Shaking Table Tests and Numerical Analysis of a Steel Frame Employing Novel Variable-Coefficient Viscous Dampers

Abstract

Variable-coefficient viscous dampers (VVDs) have a variable annular gap, allowing them to dynamically adjust the damping coefficient at different displacement stages and provide higher damping forces during large displacement phases. This study evaluates the seismic performance of a steel frame equipped with VVDs. A shaking table test was conducted on a two-story, single-span steel frame with the VVDs to assess its seismic response, and the results were compared with those of the same frame equipped with conventional viscous dampers (VD). The experimental results demonstrated that the VVDs significantly reduced the structural dynamic response at various levels of earthquake intensity, consistently outperforming the VDs in terms of the seismic reduction effectiveness. Subsequently, a constitutive model for the VVD element was developed using the open-source finite element software OpenSees3.3.0. The accuracy of the developed element was validated by comparing the finite-element analysis results with mechanical performance tests of the VVD. Based on the developed VVD element, a numerical model of test structure was established in OpenSees for time–history analyses. The results showed good agreement between the numerical simulations and shaking table test data. Finally, a parametric study was conducted on the effects of the ratio $r$ of the second-order damping coefficient to the first-order damping coefficient and the velocity index α of the VVD on the seismic response of the numerical model of the tested structure. The results indicated that the seismic reduction rate of the tested structure increased with $r$, with a maximum improvement of 24%, while it decreased with increasing α, with a maximum reduction of 27%.

1. Introduction

Energy dissipation devices [1,2] have been developed to mitigate the seismic response of structures. These devices can be classified into two main categories based on their working mechanisms: displacement-based dampers [3] and velocity-based dampers [4]. A viscous damper can enhance the structural damping ratio without affecting structural stiffness [5].

A traditional VD typically consists of a hollow cylinder filled with silicone oil and a piston rod, where energy dissipation occurs through the shear forces generated as the viscous fluid flows through the gap between the inner cylinder wall and the piston rod [6]. Numerous studies have been conducted on the seismic performance of structural systems equipped with VDs. Constantinou et al. [7] performed structural tests on steel frames fitted with VDs and proposed a simplified method for calculating the modal properties of such structures, thereby enabling the estimation of peak seismic responses. Yu et al. [8] confirmed the effectiveness of VDs in reducing seismic responses in high-rise concrete structures based on shaking table tests. Su et al. [9] introduced an open-space VD installation method that demonstrated superior shock absorption performance compared to traditional diagonal configuration. Feng et al. [10] conducted shaking table tests on the same structure equipped with different types of dampers, with the VD reducing the seismic response of the test structure by dissipating approximately 45% of the earthquake energy.

However, VDs have a constant damping coefficient, which limits their ability to satisfy energy dissipation demands under varying seismic intensities. To address this issue, staged energy dissipation devices (SEEDs) have been proposed, which are classified into semi-active and passive SEEDs. Semi-active SEEDs, such as magneto-rheological (MR) dampers [11,12] and electro-rheological (ER) dampers [13,14], adjust their damping coefficient by changing the fluid viscosity in the VD through magnetic or electric fields [15,16]. Typically, these devices are equipped with sensors that regulate the damping force in real-time based on algorithmic control rules [17]. These control strategies generally fall into two categories: the first relies on precise numerical models of the structure, such as optimal control algorithms [18] and continuous sliding mode control [19], and the second category is based on real-time structural responses, such as clipped-optimal control (COC) [20] and neural network control [21]. The effectiveness of these systems in mitigating seismic responses were experimentally validated. Dyke et al. [22] performed shaking table tests on a structure equipped with MR dampers and demonstrated the effectiveness of the COC algorithm in reducing seismic responses. Wani et al. [23] verified the efficacy of the IDRA control strategy through shaking table tests and conducted a numerical simulation of this strategy.

Passive SEEDs, which do not require external energy input, can automatically adapt their behavior to external excitation through a mechanical system. Researchers have focused on friction dampers and metallic dampers. Sha et al. [24] achieved an approximately 20% increase in the friction coefficient by paralleling two friction dampers. Xu et al. [25] designed a staged energy dissipation damper that integrates metallic and friction dampers into three operational stages. Yang et al. [26] developed an asynchronous parallel buckling restrained brace that demonstrated superior performance compared with traditional buckling restrained braces in terms of seismic reduction effect. By contrast, traditional viscous dampers (VDs) have seen fewer adaptations to achieve graded energy dissipation without external excitation. Hormozabad et al. [27] introduced an adaptive viscous damper equipped with self-adjusting nozzles that adjusted the passage areas, thereby providing an adaptive damping coefficient. Eyres et al. [28] proposed a viscous damper with relief valves, each connected to a preloaded spring; the valve opened when the fluid pressure decreased below the preload force, thereby regulating the fluid flow and controlling the damping coefficient.

Despite these innovations, passive SEEDs are yet to be experimentally validated in structural tests to confirm their effectiveness in mitigating seismic responses. Current limitations of structural analysis software have also restricted the numerical investigation of structures with these devices. In this paper, shaking table tests are conducted on a two-story, single-span steel frame equipped with VVDs to assess their effectiveness in controlling seismic responses across varying earthquake intensities. Subsequently, VVD material was developed in OpenSees. Finally, numerical analysis, including the experimental validation of the VVD material and the finite element model of the test frame, is discussed.

2. Test Set-Up

2.1. VD and VVD

The structural diagrams of the VD and VVD used in the shaking table tests are shown in Figure 1 and their design parameters are listed in

Table 1. Design parameters of VD and VVD.

Damper	L (mm)	s (mm)	d (mm)	D1 (mm)	D2 (mm)	Viscosity (×104 mm2/s)
VD	45	/	20	47	/	20
VVD	45	5	20	47	46	20

. The design parameters of the VD were first determined. Given the relatively small scale of the shaking table test structure and based on design experience, the peak damping force of the VD was limited to 5 kN and the maximum velocity of the piston head was controlled within 0.2 m/s. Based on the target capacity, the design parameters D₁, L, and d were specified. The damping coefficient of the conventional VD is related to the annular clearance. As shown in Figure 1, the VVD features a variable annular clearance that is adjusted based on the displacement of the piston head, whereas the VD has a fixed annular clearance. Consequently, the variation in the VVD annular clearance, depending on the piston head position, can be divided into three stages: the first, transition, and second. Correspondingly, the damping coefficient of the VVD is categorized into the same three stages. To enhance the damping coefficient in the early displacement stage, the parameters s and D₂ were introduced in the VVD design based on the VD. The equations for calculating the damping coefficient at each stage are provided in Equation (1).

$$C=\left\{\begin{array}{l}{C}_1,\left|u\right|\le s;\\ {\displaystyle \frac{L-\left|u\right|+s}{L}}\times C_1+{\displaystyle \frac{\left|u\right|-s}{L}}\times C_2;s<\left|u\right|<L+s;\\ C_2,\left|u\right|\ge L+s;\end{array}\right.$$

(1)

where u represents the displacement of the piston head; s and L are the structural parameters of the damper; and C₁ and C₂ are the damping coefficients for the first and second stages, respectively.

Before the shaking table test, a sinusoidal wave loading was applied to both the VD and VVD at a frequency of 0.5 Hz. The loading displacement amplitudes were set at 5, 10, 25, 35, and 50 mm. The resulting hysteresis curves are shown in Figure 2. When the loading displacement amplitude is less than 10 mm, the maximum damping force of the VVD is equal to that of the VD. However, when the loading displacement amplitude exceeds 10 mm, the maximum damping force of the VVD significantly increases compared to the VD; specifically, at a loading displacement amplitude of 50 mm, the peak damping force of the VVD is 1.47 times that of the VD.

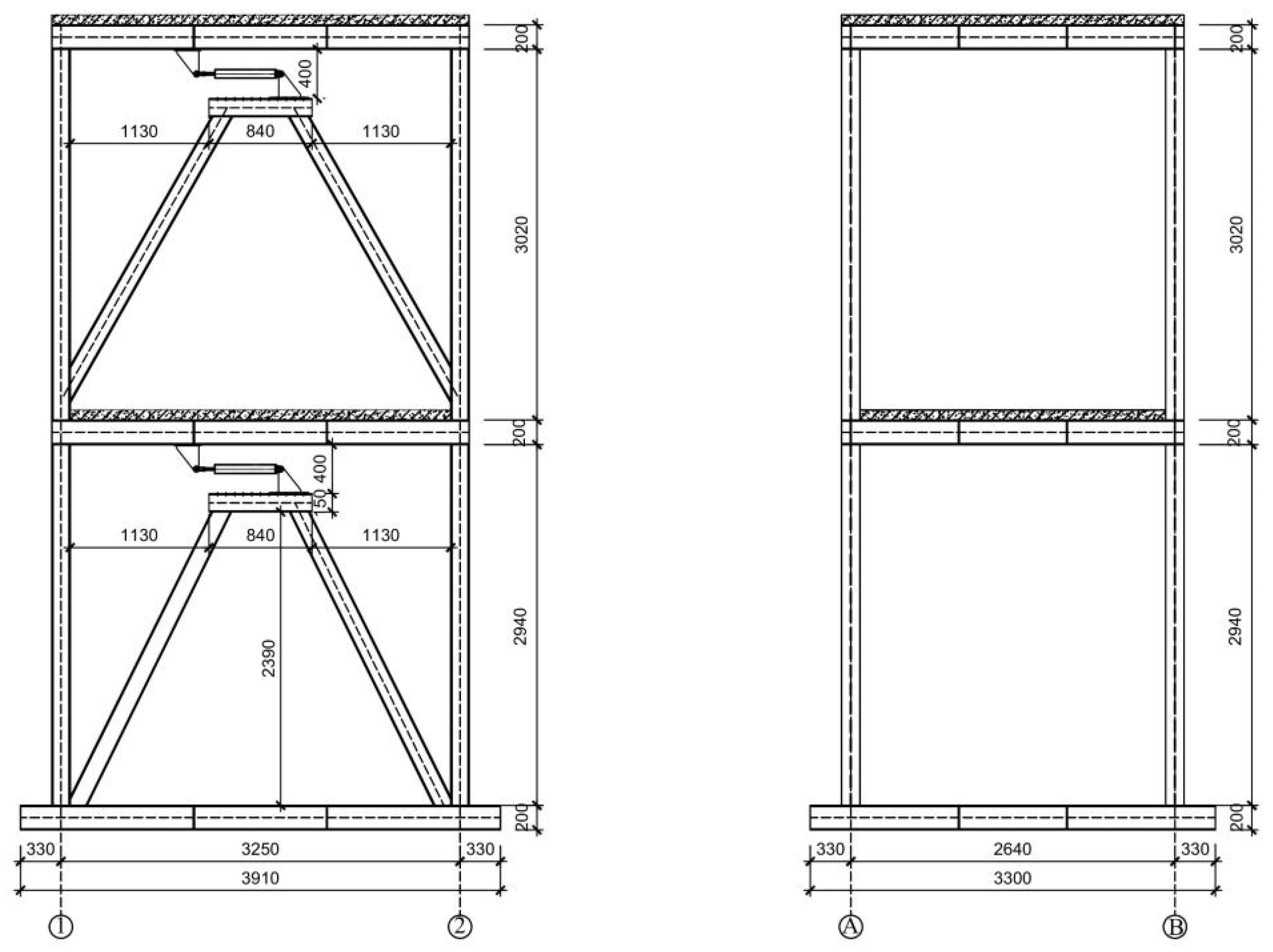
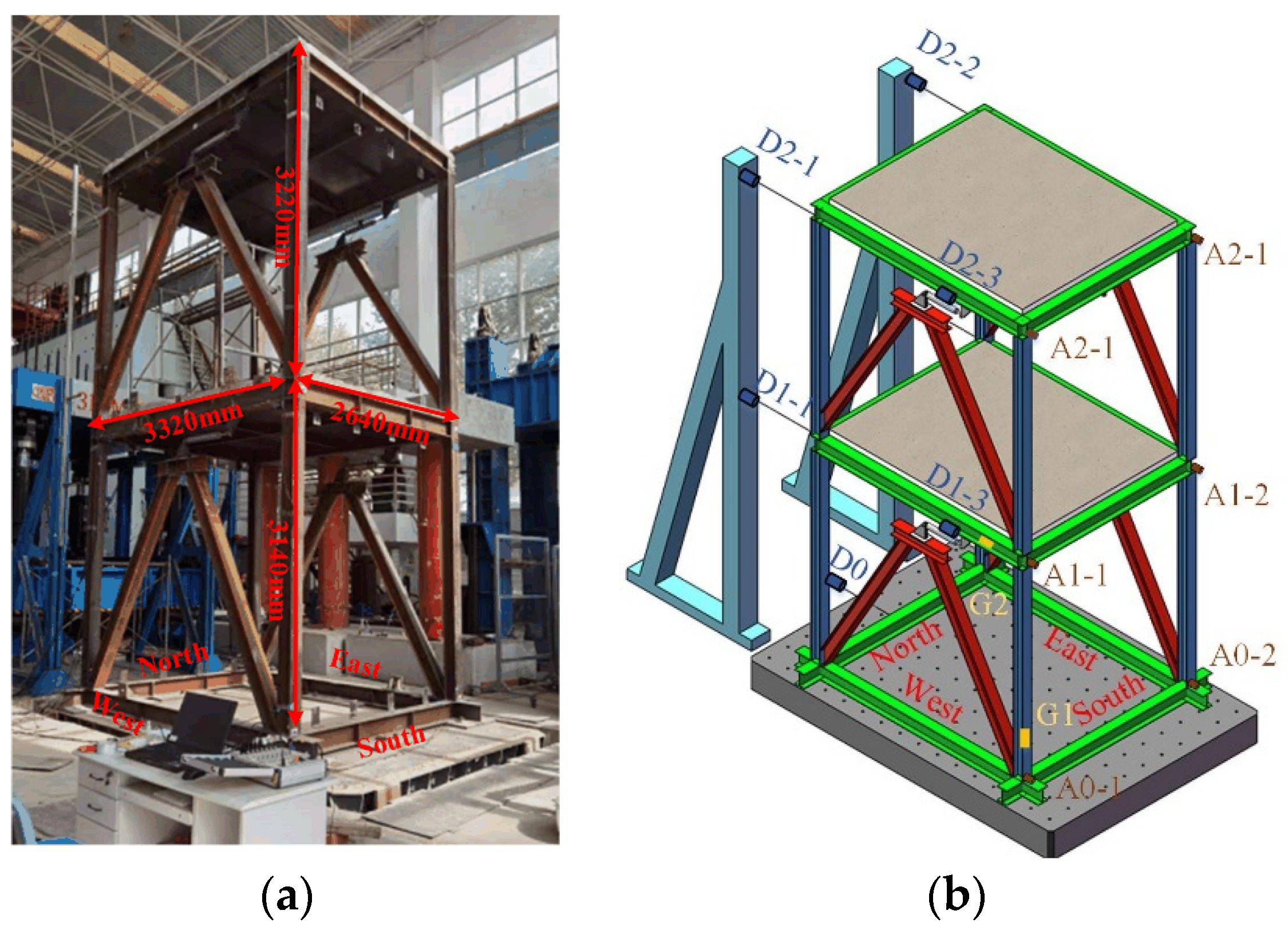
2.2. Test Structure and Instrumentation Arrangement

A two-story steel frame was selected for the shaking table tests, based on the frame developed by Kasai et al. [29] to verify the energy dissipation capacity of VDs. Its elevation view is shown in Figure 3 and section dimensions of steel members are listed in

Table 2. Section dimensions of steel members (Q235).

Steel Members	Section Dimensions
Beam	HW 200 × 150 × 6 × 9 mm
Column	HW 150 × 150 × 7 × 10 mm
Brace	HW 150 × 150 × 7 × 10 mm

. To simulate both the permanent and variable loads, four-ton lead blocks were evenly distributed across each concrete floor [15]. Beam-to-column connections were welded to ensure rigidity. The dampers were installed via a chevron connection and secured to diagonal braces with pin connections, allowing only axial deformation. The frame without dampers is referred to as the SF, whereas the steel frames equipped with four VDs and four VVDs are labeled SFVD and SFVVD, respectively. During tests, only the dampers were replaced, keeping the frame unchanged. To assess damper replacement effects, the frame was required to remain elastic.

To capture the overall seismic response and local effects, six accelerometers (A0-1, A0-2, A1-1, A1-2, A2-1, and A2-2), five displacement sensors (D-0, D1-1, D1-2, D2-1, and D2-2) and twenty strain gauges were installed on the shaking table countertop and test frame, most of which are shown in Figure 4 (only two strain gauge data points were analyzed in this study). Additionally, two displacement sensors (D1-3 and D2-3) were positioned on the dampers on the west side of the frame to measure damper deformation.

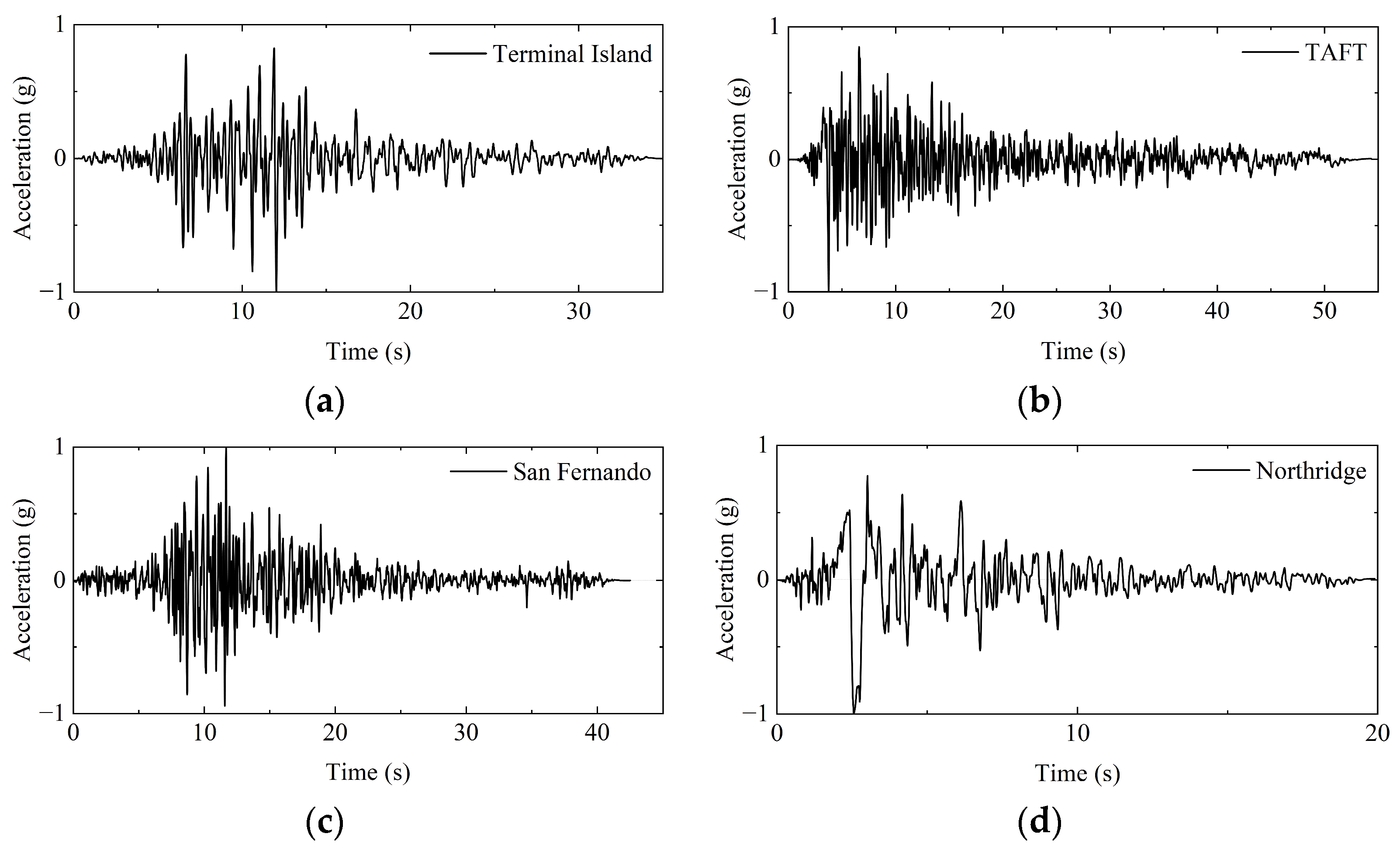
2.3. Test Conditions

Four seismic wave excitations (SWE) were selected to simulate the ground motions in the shaking table tests: (a) Terminal Island, (b) TAFT, (c) San Fernando, and (d) Northridge; the normalized acceleration time–history curves for these seismic excitation waves are shown in Figure 5. The properties of the four SWEs are shown in

Table 3. Properties of the applied ground motion records.

SWE	Year	Magnitude	Rib (km)	Rrup (km)	PGA (g)
Terminal Island	1994	6.69	53.43	57.2	0.1885
TAFT	1952	7.36	38.42	38.89	0.1803
San Fernando	1971	6.69	173.16	173.16	0.0363
Northridge	1994	6.69	0	6.5	0.8909

. To verify whether the VVD can adjust its working state according to earthquake intensity in the tested structure, the peak ground acceleration (PGA) of each SWE was scaled to 0.07 g, 0.2 g, 0.4 g, 0.6 g, and 0.8 g. To prevent structural damage and verify the effectiveness of different dampers in controlling the seismic response, the loading sequences were SFVD, SFVVD, and SF, with SF subjected to a loading of up to 0.6 g.

3. Test Results and Analysis

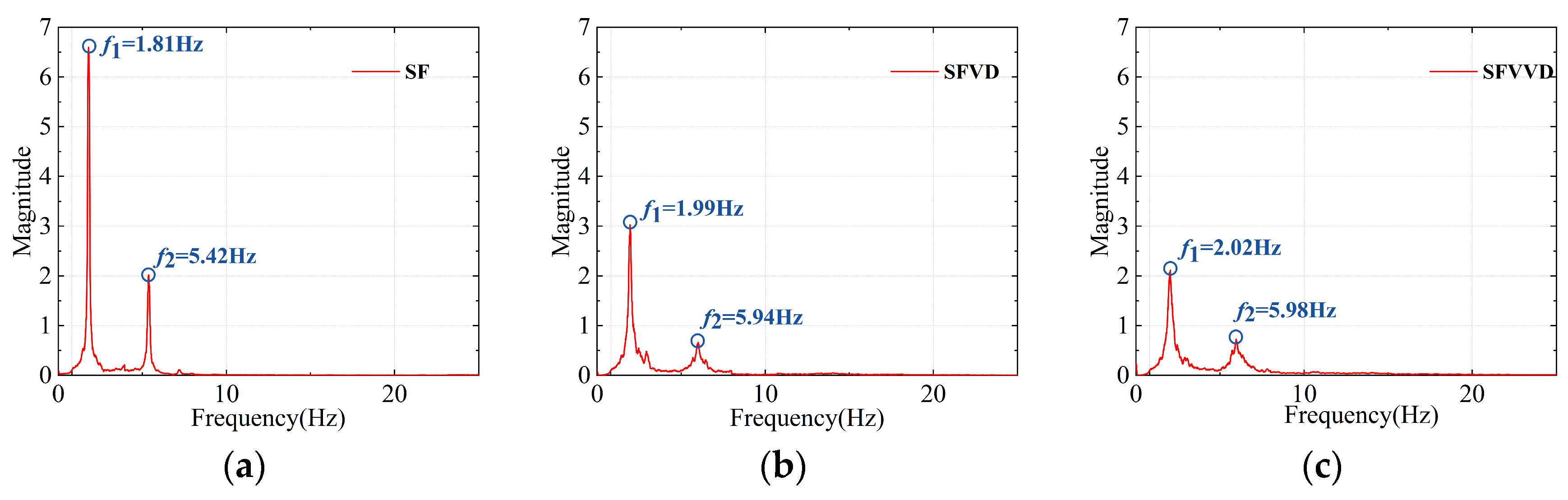
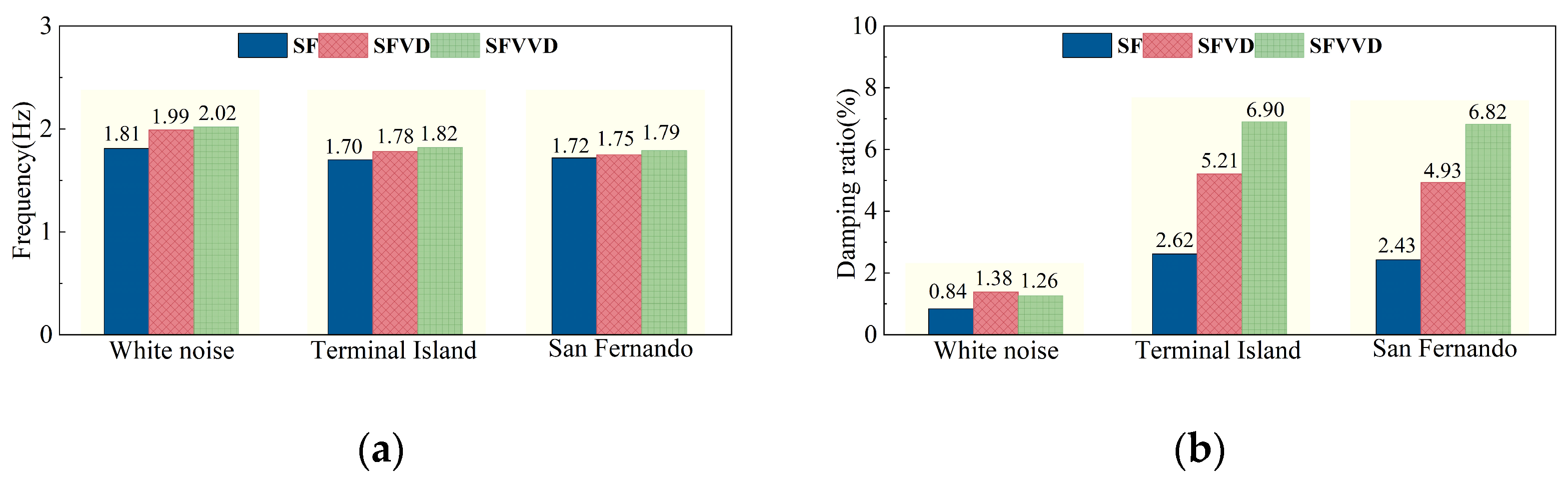
3.1. Structural Dynamic Characteristics

Before the SWEs, white noise excitation (WNE) was conducted on the test structures. The transfer function between the top-floor acceleration and the shaking table countertop is presented in Figure 6. The peak frequency in the acceleration transfer function indicates the fundamental frequency of the test models, and the structural damping ratio was determined using the half-power bandwidth approach [30]. Figure 7 shows the frequency and damping ratios of different frames under WNE and SWE with a PGA of 0.07 g. The dynamic stiffness of the VD and VVD led to an increase in the frame frequency under both the SEWs and WNE.

Under the WNE, the damping ratios of the SFVD and SFVVD improved by 40% and 30%, respectively, compared with those of the SF. Under SWE, the damping ratios of the SFVD and SFVVD increased approximately two- and three-fold, respectively, compared with the SF. This demonstrates that the installation of the VD and VVD can enhance the damping ratio of the structure with minimal impact on its natural frequency. Notably, under WNE, the damping ratio of the SFVVD was lower than that of the SFVD. However, when subjected to higher-intensity SEWs, the damping ratio of the SFVVD exceeds that of the SFVD. This is because the VVD operates primarily in its first-stage energy dissipation state when subjected to WNE. In contrast, when subjected to SWEs, the damping coefficient of the VVD enters a transition stage, increasing and surpassing that of the VD, resulting in a more significant increase in the damping ratio of the SFVVD than that of the SFVD.

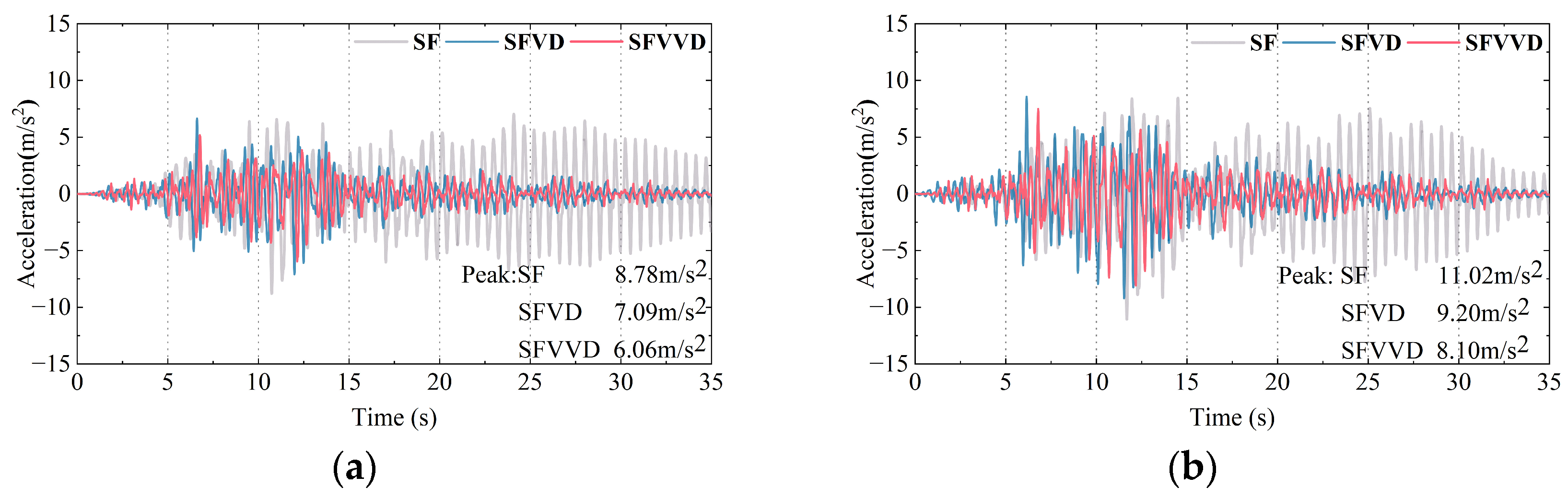
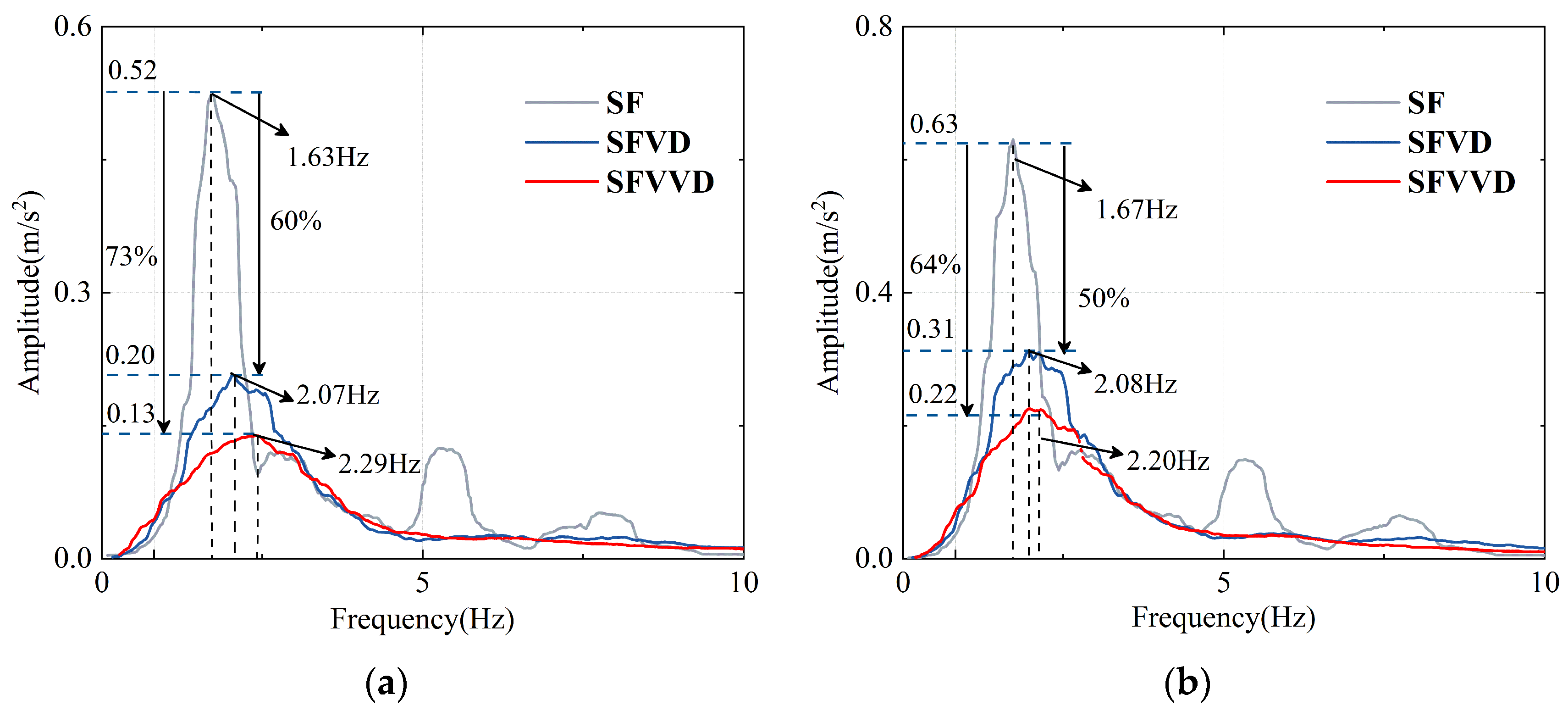
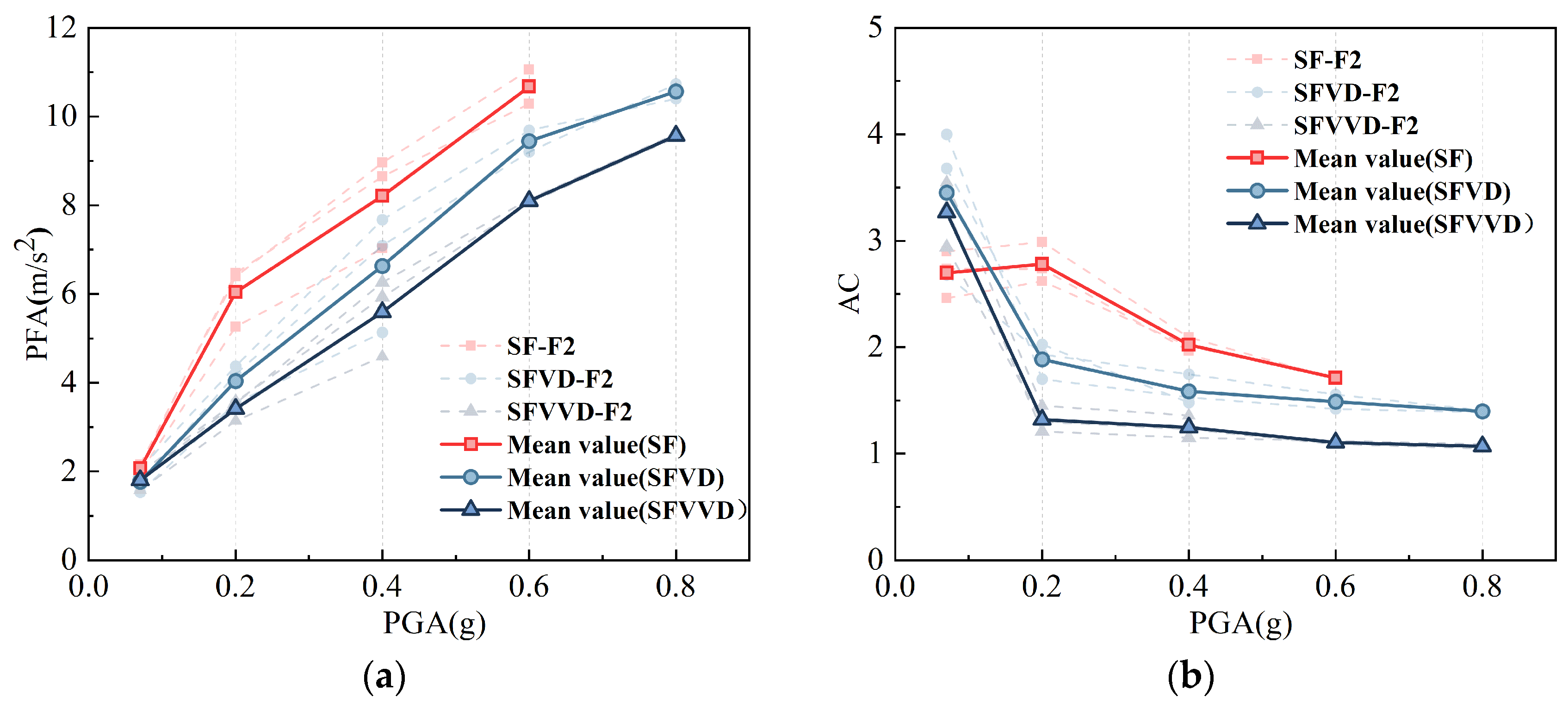
3.2. Acceleration Responses

To assess the effectiveness of the VVD in reducing acceleration response when subjected to high-intensity excitations, an acceleration time–history analysis was conducted on SF, SFVD, and SFVVD. Terminal Island seismic waves with PGAs of 0.4 g and 0.6 g were selected for this analysis. The time–history and frequency spectrum curves of top-floor acceleration are shown in Figure 8 and Figure 9, respectively. Figure 8 reveals that both the SFVD and SFVVD had lower top-floor accelerations than the SF, indicating effective suppression of acceleration. For PGAs of 0.4 g and 0.6 g, the top-floor acceleration decreased by 19% and 16% for SFVD and 31% and 26% for SFVVD compared with SF. Figure 9 shows that the amplitude response decreased by 60% and 50% for the SFVD and 73% and 64% for the SFVVD under different PGAs, respectively, indicating that the VVD provides superior damping compared with the VD.

Due to abnormal excitation recorded by the accelerometers during the TAFT earthquake wave, Figure 10a shows only the peak floor acceleration (PFA) at the top floor and the means values of PFA under the other three seismic waves at different PGAs for the tested models. The acceleration amplification coefficient (AC), which is the ratio of the peak floor acceleration to the peak acceleration on the shaking table countertop, serves as an important index for assessing the structural dynamic properties [31]. Figure 10b shows the ACs on the top floor under the same conditions, including their mean values. At a PGA of 0.07 g, both SFVD and SFVVD exhibited ACs approximately equal to 3.5; these were higher than that of SF, indicating that the VDs did not reduce the structural acceleration response and led to higher accelerations when subjected to the same excitation. This is attributed to two factors: the dynamic stiffness of the VD and VVD, which increased the acceleration responses compared with the non-seismic-reduced model, and the frequency ratio between the excitation and structure, which influenced the acceleration reduction rate. However, at PGAs exceeding 0.07 g, SFVD and SFVVD showed superior performance in terms of PFAs and ACs compared with SF. This suggests that as seismic excitation intensity increased, the VD and VVD effectively reduced the structural acceleration response.

Table 4. Reduction rates of PFA and AC for each test structure.

Test Structure	PGA	PFA	Reduction Rate	AC	Reduction Rate
SF	0.2	6.04	-	2.78	-
SFVD		4.03	0.33	1.88	0.32
SFVVD		3.71	0.38	1.52	0.45
SF	0.4	8.21	-	2.02	-
SFVD		6.63	0.19	1.58	0.22
SFVVD		5.59	0.32	1.24	0.38
SF	0.6	10.67	-	1.71	-
SFVD		9.44	0.12	1.48	0.14
SFVVD		8.10	0.24	1.01	0.35

shows the reduction rates of PFA and AC for each test structure under different PGAs. At PGAs of 0.4 g and 0.6 g, SFVVD achieved an approximately 13% greater suppression of peak acceleration and an 18% greater reduction in the acceleration amplification coefficient compared to SFVD. Moreover, at these two PGA levels, the improvement in SFVVD damping rate over SFVD is greater than that at a PGA of 0.2 g. This indicates that the VVD outperforms the VD in reducing acceleration responses under various conditions, and its effectiveness in reducing acceleration responses improves as PGA increases.

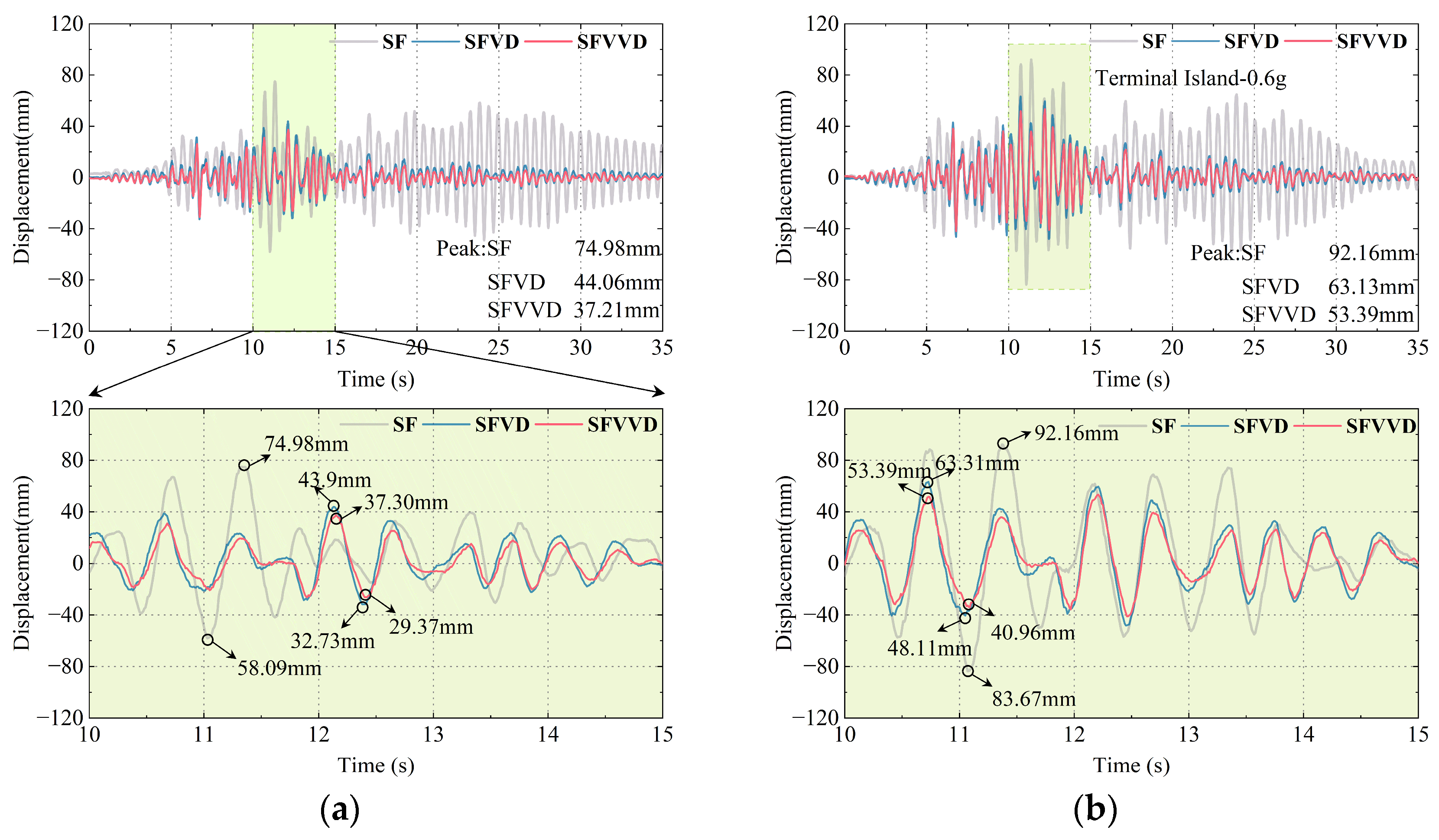
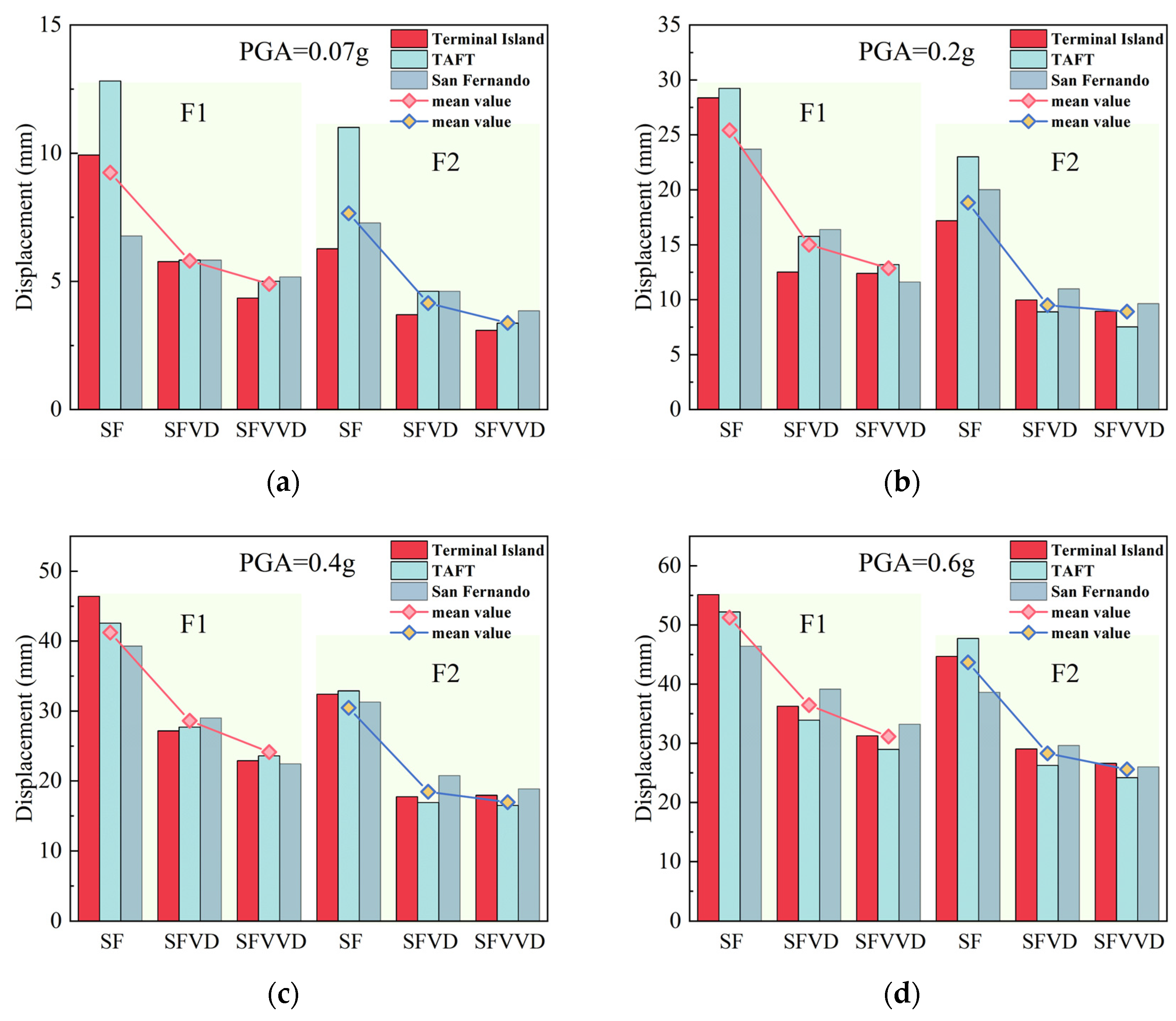
3.3. Displacement Responses

Figure 11 shows the top displacement time–history curves for SF, SFVD, and SFVVD under varying PGA from the Terminal Island seismic wave. The results indicate that the displacements for the SFVD and SFVVD were reduced compared with the SF, demonstrating the effective displacement control capabilities of the VD and VVD. They achieved this by dissipating seismic energy rather than increasing the structural stiffness. At a PGA of 0.4 g, the SFVD reduced the top-floor peak displacement by 40.5%, while the SFVVD reduced it by 52.3%. At a PGA of 0.6 g, the peak displacement reductions were 31.5% for the SFVD and 42.4% for the SFVVD. The displacement suppression effect of the VVD was superior to that of the VD under intense seismic wave excitation, providing greater damping force to the test model compared. Additionally, the dynamic stiffness of the VD and VVD led to a phase difference between the displacement time–history curves of the SFVD and SFVVD compared to those of the SF.

Owing to the detachment of the displacement sensors from the SF during the Northridge earthquake wave excitation, valid data could not be recorded. Figure 12 shows the maximum and average inter-story displacements and their mean values of SF, SFVD, and SFVVD when subjected to three seismic waves (Terminal Island, TAFT, and San Fernando) at varying earthquake intensities. The seismic reduction rate, calculated using Equation (2), was used to quantify the vibration reduction effects of VD and VVD.

$${\beta }_i={\displaystyle \frac{{\lambda }_{ucon}-{\lambda }_{con}}{{\lambda }_{ucon}}}$$

(2)

where ${\lambda }_{ucon}$ represents the maximum seismic response of the uncontrolled structure (SF), ${\lambda }_{con}$ represents the maximum seismic response of the controlled structures (SFVD and SFVVD), and $i$ denotes the floor level. The seismic reduction rate based on the maximum inter-story displacement is denoted as ${\beta }_{i\_disp}$.

As shown in Figure 12, the maximum inter-story displacements of the SFVD and SFVVD are consistently smaller than those of the SF under various conditions and PGA levels, validating the effectiveness of the VD and VVD in displacement control. Across all conditions, the first-floor inter-story displacement of the SF exceeded that of the second floor, indicating that the first floor was a weak layer. It is recommended to install dampers with enhanced energy dissipation capabilities on the first floor to reduce inter-story displacements. Compared with SFVD, SFVVD improved the ${\beta }_{i\_disp}$ for the weak layer by approximately 15% and by approximately 7% for other floors, demonstrating that the VVD provided a superior suppression of inter-story displacement compared with the VD, with the effect becoming more pronounced under stronger seismic excitation.

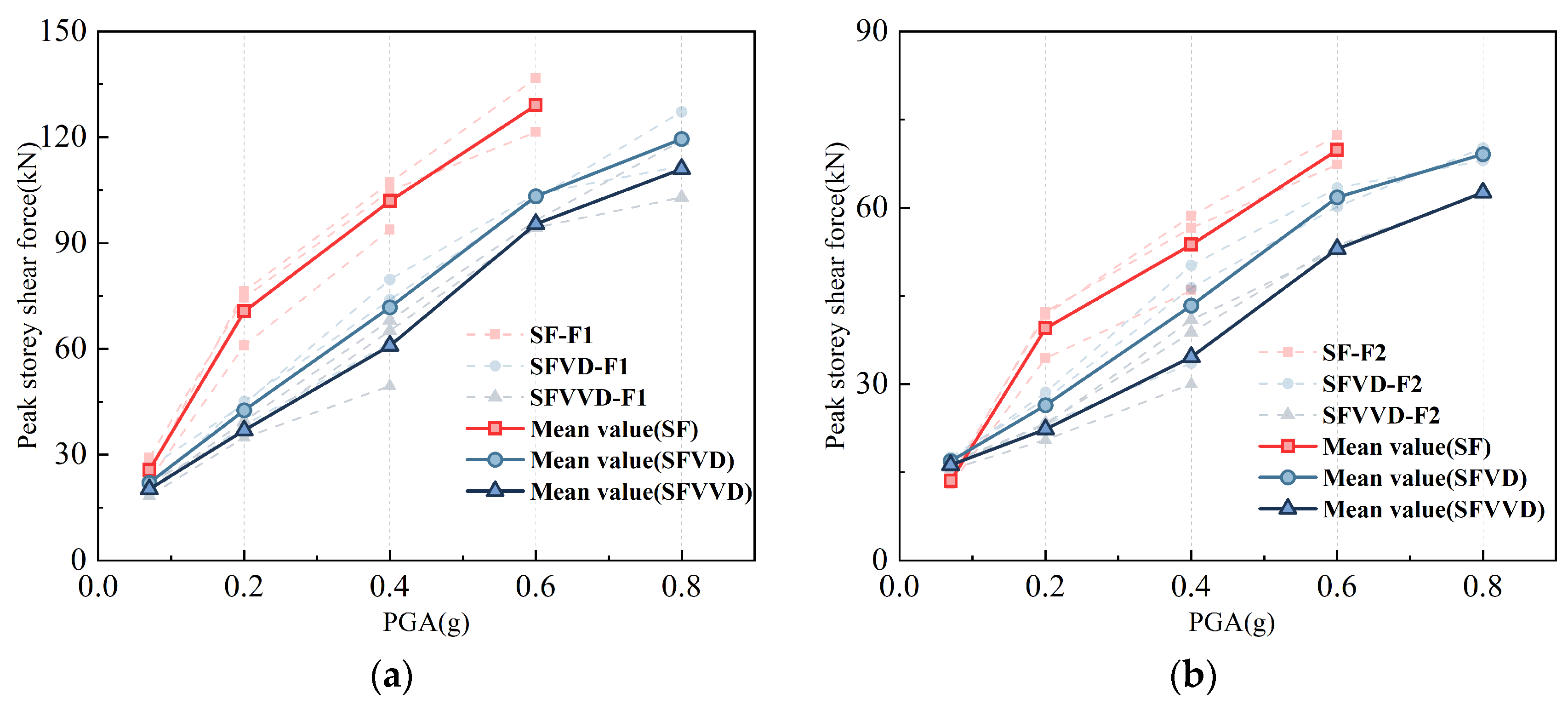
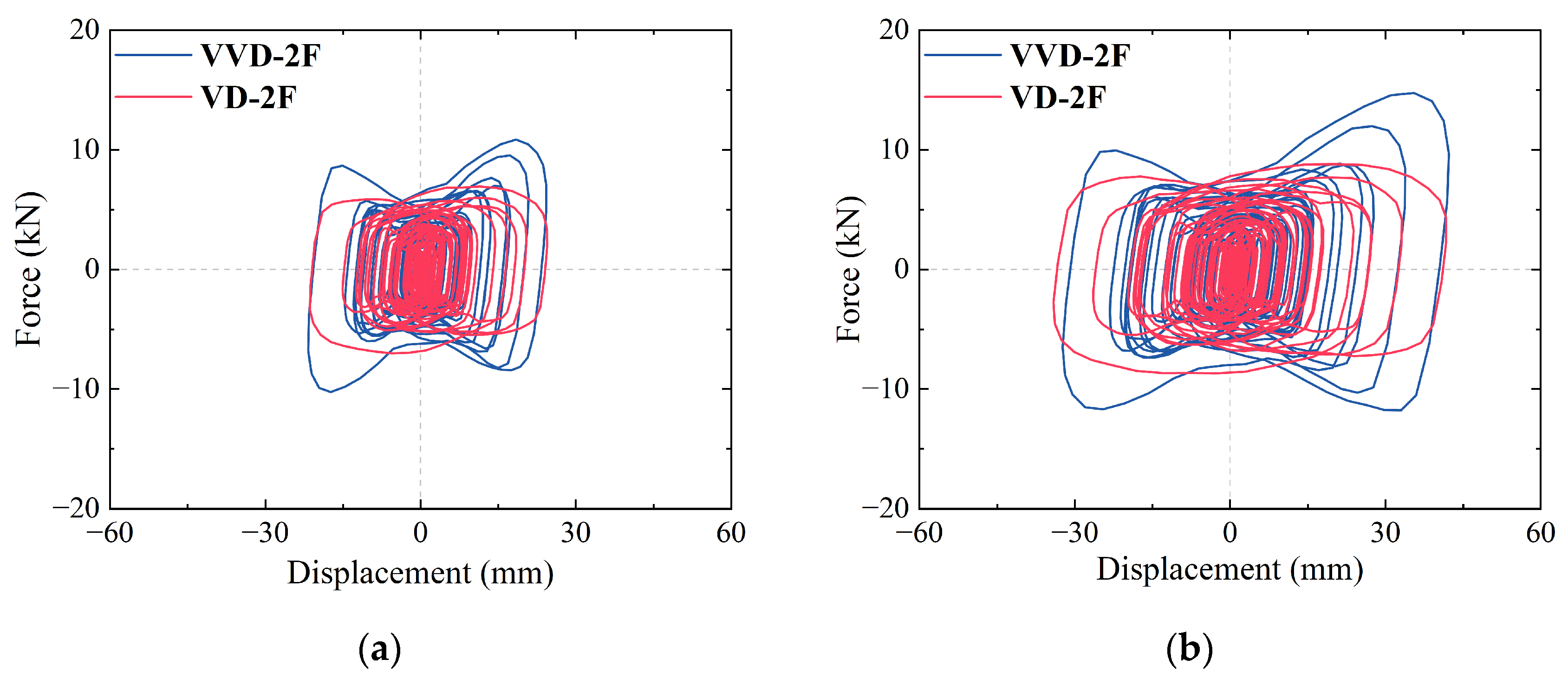
3.4. Shear Force Responses

The inter-story shear force indicates the magnitude of the internal seismic forces [32]. The peak shear force under seismic action can be approximately calculated using the following equation: $V_i{(t)}_{\max }={\left|{\displaystyle \sum _{j=i}^2{m}_j}a{(t)}_j\right|}_{\max }$, where $m_j$ represents the concentrated mass at floor level and ${a\left(t\right)}_j$ denotes the measured acceleration time history at the corresponding floor level. Figure 13 presents the peak story shear forces of SF, SFVD, and SFVVD under different conditions. The shear force reduction rate was calculated using Equation (2) and denoted as ${\beta }_{i\_shear}$. When the PGA was set to 0.07 g, the inter-story shear forces at the second floor for both the SFVD and SFVVD were higher than those for the SF. This increase was due to the additional dampers and braces in the SFVD and SFVVD, which elevated the concentrated mass between floors. Additionally, the accelerations measured on the second floor for both the SFVD and SFVVD were higher than those for the SF (as discussed in Section 3.1), which contributed to the increased inter-story shear forces. Figure 14 shows that when the PGA exceeded 0.07 g, the inter-story shear force at the first floor (F1) was consistently lower than that at the second floor (F2). The shear force was highest at the bottom floor and decreased with increasing floor height. Notably, the inter-story shear forces for the SFVVD were consistently lower than those of the SFVD under all conditions.

Table 5. ${\beta }_{1\_shear}$ and ${\beta }_{2\_shear}$ of test structure.

Test structure	PGA	${\mathit{\beta }}_{1\_\mathit{s}\mathit{h}\mathit{e}\mathit{a}\mathit{r}}$	${\mathit{\beta }}_{2\_\mathit{s}\mathit{h}\mathit{e}\mathit{a}\mathit{r}}$
SFVD	0.2	0.39	0.33
SFVVD		0.44	0.38
SFVD	0.4	0.29	0.19
SFVVD		0.38	0.35
SFVD	0.6	0.19	0.11
SFVVD		0.26	0.24

presents the damping ratio of the tested structure under different PGAs. The average ${\beta }_{1\_shear}$ of SFVVD at PGAs of 0.4 g and 0.6 g increased by 8% compared with those of the SFVD, and the average ${\beta }_{2\_shear}$ for SFVVD at these PGAs increased by 13% compared to SFVD. Additionally, at a PGA of 0.2 g, the ${\beta }_{1\_shear}$ and ${\beta }_{2\_shear}$ SFVVD was 5% higher than that of SFVD. This indicates that as the excitation intensity increases, the effectiveness of the VVD in suppressing inter-story shear forces improves.

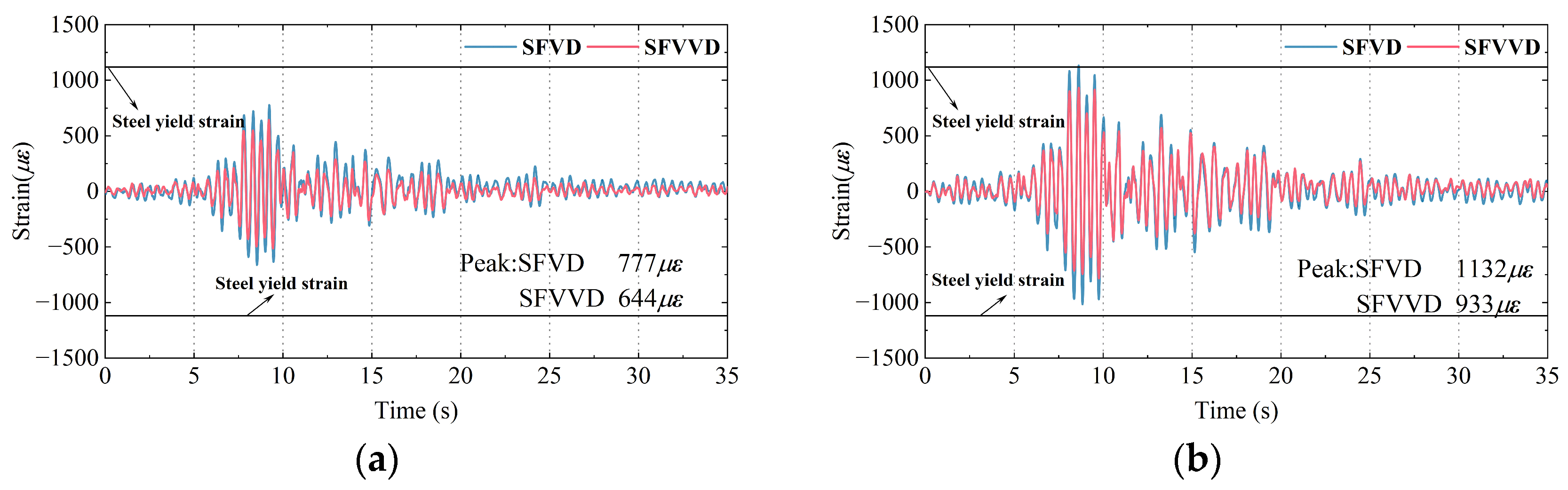
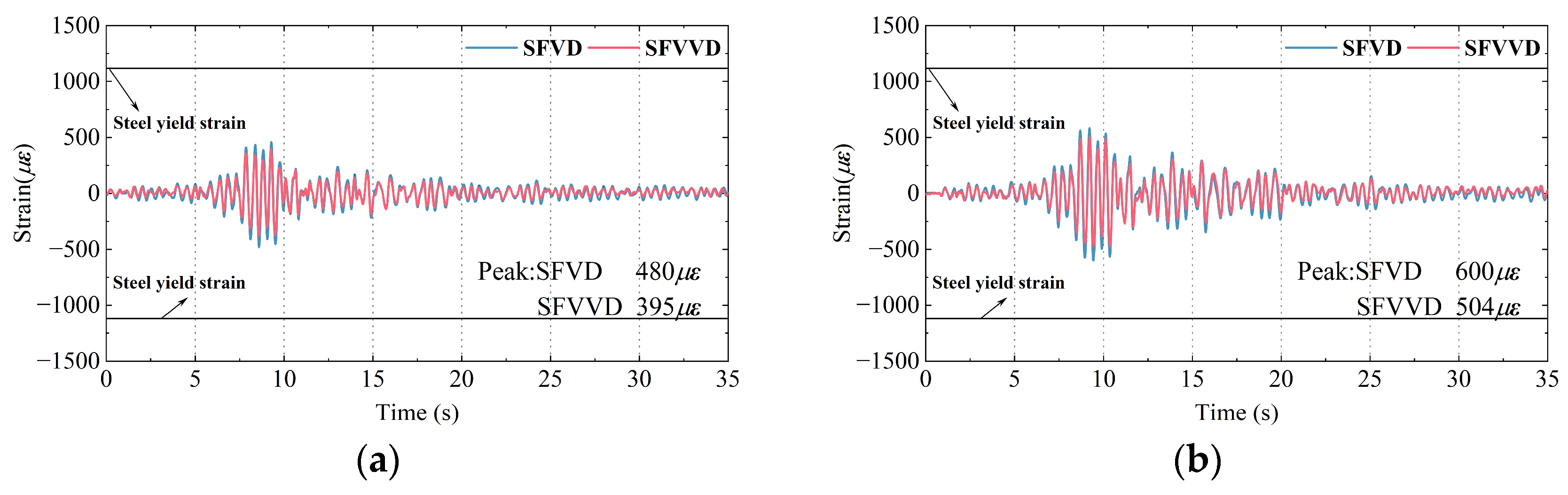
3.5. Strain Responses

Analyzing the collected strain data allows for a more accurate assessment of the strain states induced by various seismic intensities at the measurement points on the frame. Figure 14 and Figure 15, respectively, show the strain time histories at the base of the first-floor columns and beams for the SFVD and SFVVD in the case of the San Fernando seismic wave. As no material property tests were performed on the Q235 steel used for the beams and columns, the nominal yield strain value of 1119 με was calculated using standard values from the Chinese Code [33]. Figure 14b shows that only the maximum strain of the first-floor SFVD column exceeded 1119 με when the PGA was 0.6, and this exceedance was brief and only 1% above the standard value. Thus, both the SFVD and SFVVD maintained elastic behavior when subjected to SWEs with varying intensities. Under different PGAs, the maximum strain of the SFVVD columns was reduced by 17.5% compared to that of the SFVD columns, and the maximum strain of SFVVD beams was reduced by 16% compared to that of the SFVD beams at different PGAs. This demonstrates that the VVD is more effective than the VD in restraining strains and reducing the internal forces in the beams and columns.

4. Numerical Analysis

4.1. VVD Material Development and Validation

In OpenSees [34], a viscous damper material is typically used to simulate VDs [35], where the damping coefficient is constant and does not vary with damper deformation. Consequently, OpenSees cannot directly simulate structures equipped with VVDs. Therefore, a new material (VVD material) is developed and incorporated into the OpenSees library to represent the VVD constitutive model.

In OpenSees, damper elements are simulated by defining the damper material and assigning characteristic parameters to the element [36]. To incorporate a VVD element with a variable damping coefficient into OpenSees, it is essential to identify the parameters that accurately describe the VVD material properties and to provide input interfaces for these parameters. Unlike the VD, where the damping coefficient is constant, the damping coefficient of the VVD varies with damper deformation while other properties remain unchanged. Therefore, in developing the VVD material, the parameter interfaces of the viscous damper material were retained, excluding the damping coefficient C. New parameter interfaces for C₁, C₂, s, and L were added based on Equation (1). The relevant parameters and units of the VVD material are listed in

Table 6. Parameters and units of VVD material.

Parameter	C1	C2	$\mathit{\alpha }$	K	s	L
Unit	$\mathrm{N}/{(\mathrm{m}\mathrm{m}/\mathrm{s})}^{\alpha }$	$\mathrm{N}/{(\mathrm{m}\mathrm{m}/\mathrm{s})}^{\alpha }$	/	$\mathrm{N}/\mathrm{m}\mathrm{m}$	$\mathrm{m}\mathrm{m}$	$\mathrm{m}\mathrm{m}$

.

After determining the relevant parameters that describe the mechanical properties of the VVD, the following steps were taken to add the VVD material to OpenSees:

(a)

Located the viscous damper material.h and viscous damper material.cpp source files in the OpenSees 3.3.0 code. These files were modified using C++ in the Microsoft Visual Studio 2022 software.

(b)

New parameter interfaces for C₁, C₂, s, and L were added to the viscous damper material.h by extending the public class.

(c)

Modified the setTrialStrain function in viscous damper material.cpp. Implemented a conditional function to calculate the damping coefficient C for the current time step based on the VVD deformation, using Equation (1). This value was assigned to the damping coefficient parameter for the stress calculations.

(d)

Renamed the modified files to VVD material.h and VVD material.cpp. These files were added to the OpenSees uniaxial material library, and the relevant declaration and invocation files were updated to incorporate the new VVD material.

(e)

OpenSees was recompiled in Microsoft Visual Studio to include the VVD material in the updated program.

In OpenSees, a two-node link element is created to replicate the loading apparatus used in the VVD performance tests. The parameters assigned to the VVD materials in OpenSees are listed in

Table 7. Model parameters of VVD material.

Model	K	C1	C2	$\mathit{\alpha }$	s	L
VVD	6500	675	1205	0.4	5	45

. A comparison between the simulation results and the experimental data from Section 2.1 is shown in Figure 16. When the displacement exceeds 5 mm, the damping force begins to increase. The peak damping force from the VVD numerical simulation differs from the experimental value by no more than 5%. This indicates that the developed VVD unit can adjust the damping force according to the predefined working state, and the simulated results closely matched the experimental results.

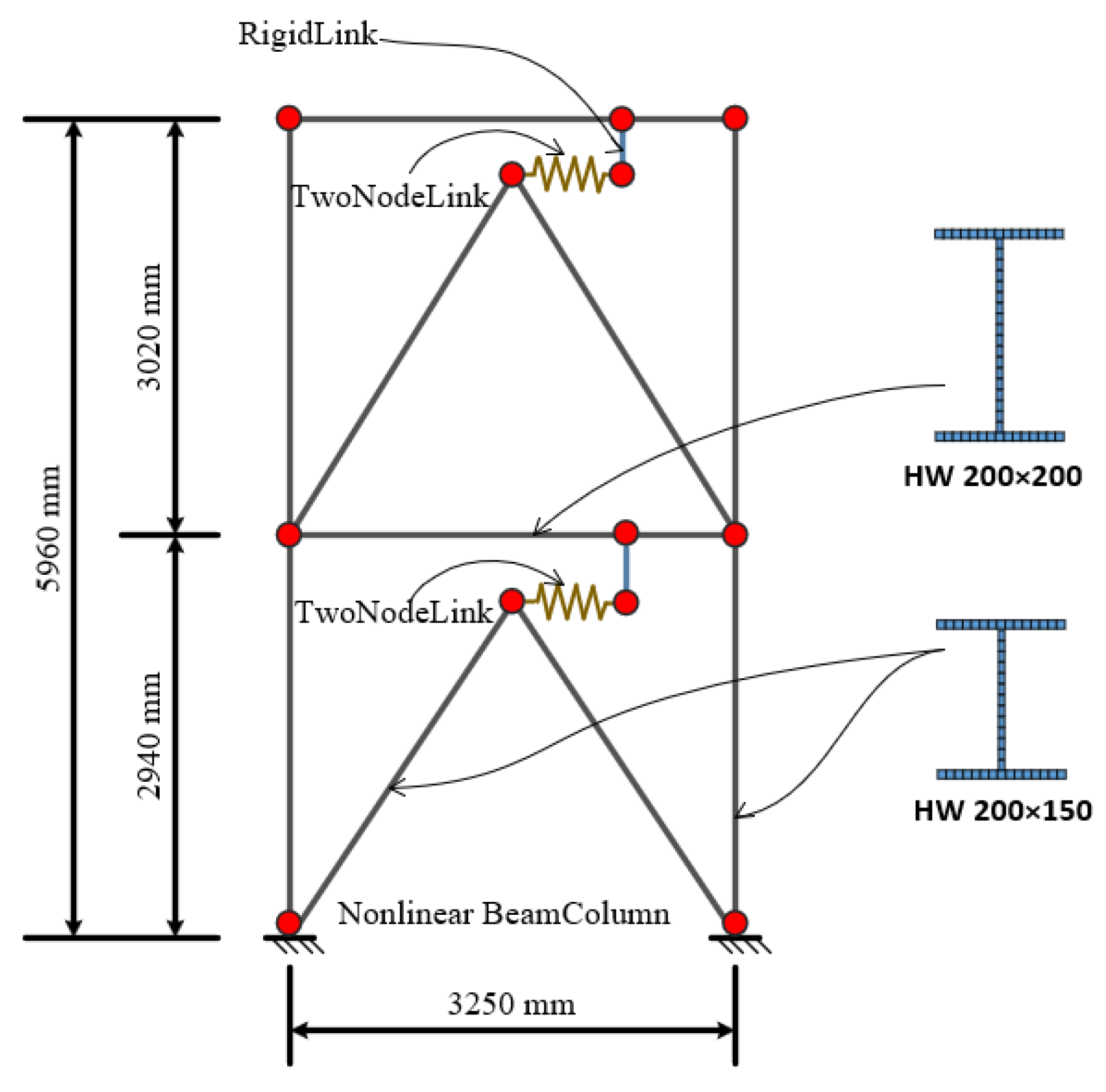
4.2. Numerical Model of SFVVD

After validating the accuracy of the developed VVD material, further analysis was conducted on the seismic response of the structures equipped with the VVD. A three-dimensional OpenSees model of the SFVVD was established, and a nonlinear structural analysis was performed. The numerical model is shown in Figure 17, where the beams, columns, and braces were modeled using fiber sections and displacement-based nonlinear beam–column elements. The concrete floors were modeled using ShellMITC4 elements, with PlateFiber components employed as the plate fiber material for shell analysis. The VVD was modeled by assigning the VVD material properties to two-node link elements [37], which were connected to the beams by rigid links.

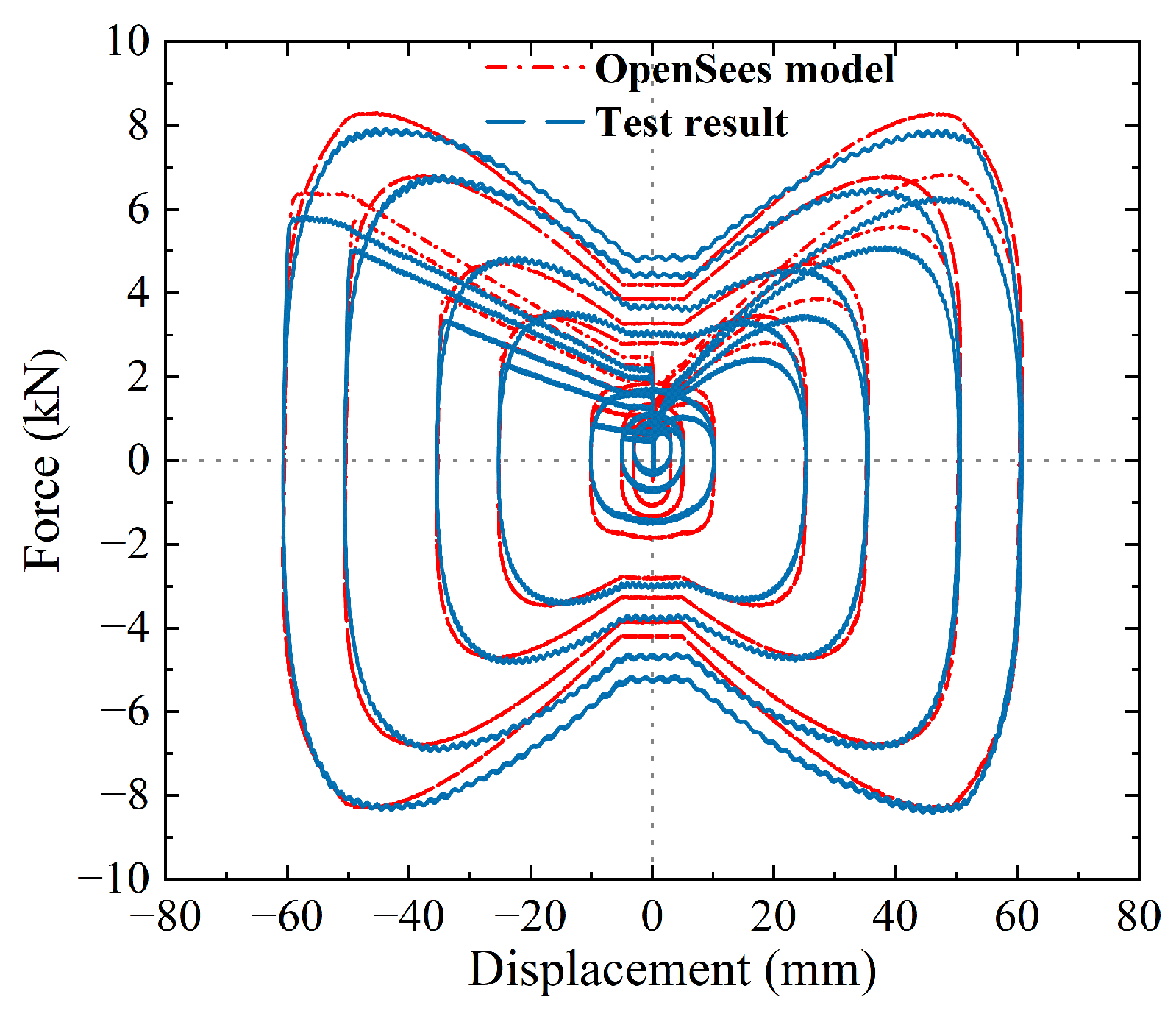
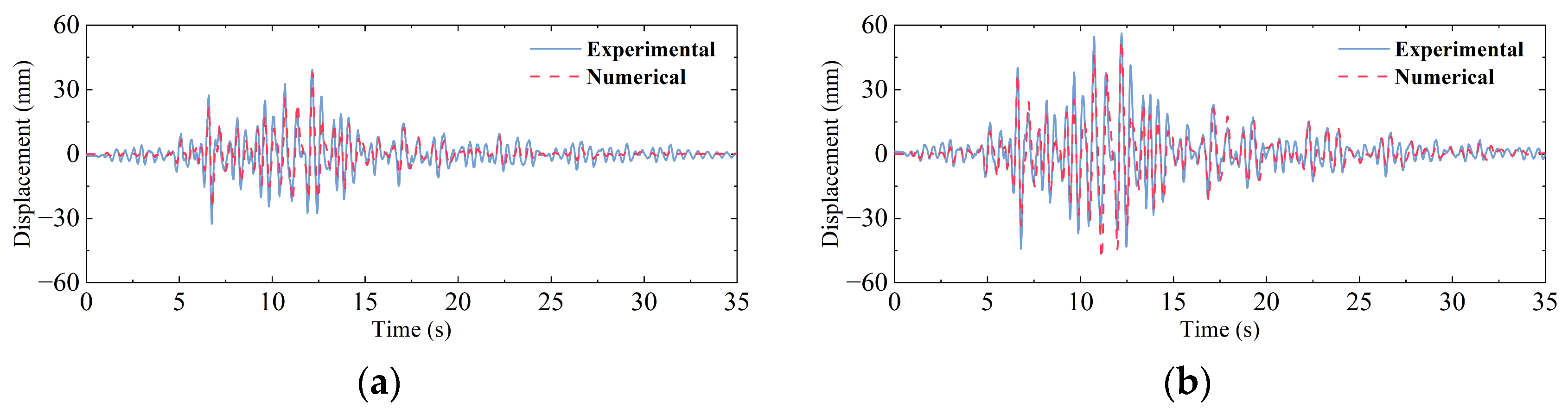
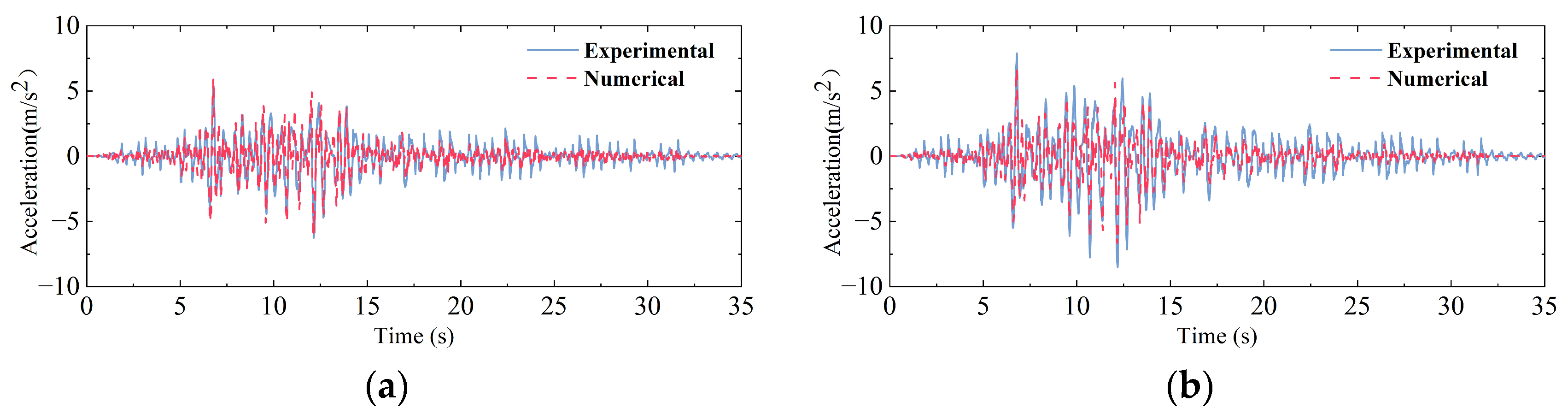
4.3. Validation Against Shaking Table Test Results

Based on the modeling method described in Section 4.2, a modal analysis was first performed on the SFVVD numerical model in OpenSees. The first modal period was 0.397 s and the second was 0.123 s, both of which are close to the values measured in the actual shaking table test (0.368 s and 0.126 s, respectively, for the SFVVD model). Subsequently, a nonlinear time–history analysis was conducted. Figure 18 and Figure 19 compare the test results with the OpenSees model outcomes, specifically for the top-floor acceleration and displacement time histories under the Terminal Island seismic wave at different PGAs. The top-floor acceleration and displacement time histories of the SFVVD show good agreement with the numerical simulation results.

Table 8. Relative Error between experimental and numerical results.

PGA (g)	Absolute Displacement (mm)		Relative Error (%)	Absolute Acceleration (m/s2)		Relative Error (%)
	Experimental Results	Numerical Results		Experimental Results	Numerical Results
0.4	41.01	42.72	4.1%	6.26	6.38	1.8%
0.6	53.44	56.21	5.1%	6.74	7.21	5.4%

lists the peak displacement and acceleration errors between the SFVVD and its numerical simulation, with a maximum error of 5.4% and the remainder within 5%. These results confirm that the SFVVD numerical model accurately reflects the seismic response observed in the shaking table tests, further validating the reliability of the VVD element developed in Section 4.1.

Figure 20 presents the hysteretic curves of VD and VVD extracted from OpenSees for the SFVD and SFVVD numerical simulation structures under the Terminal Island seismic waves with PGA of values 0.4 g and 0.6 g. It can be intuitively observed that as the earthquake intensity increases, the damping force of the VVD also increases, providing stronger energy dissipation compared with that of the VD, thus better suppressing the seismic response of the structure.

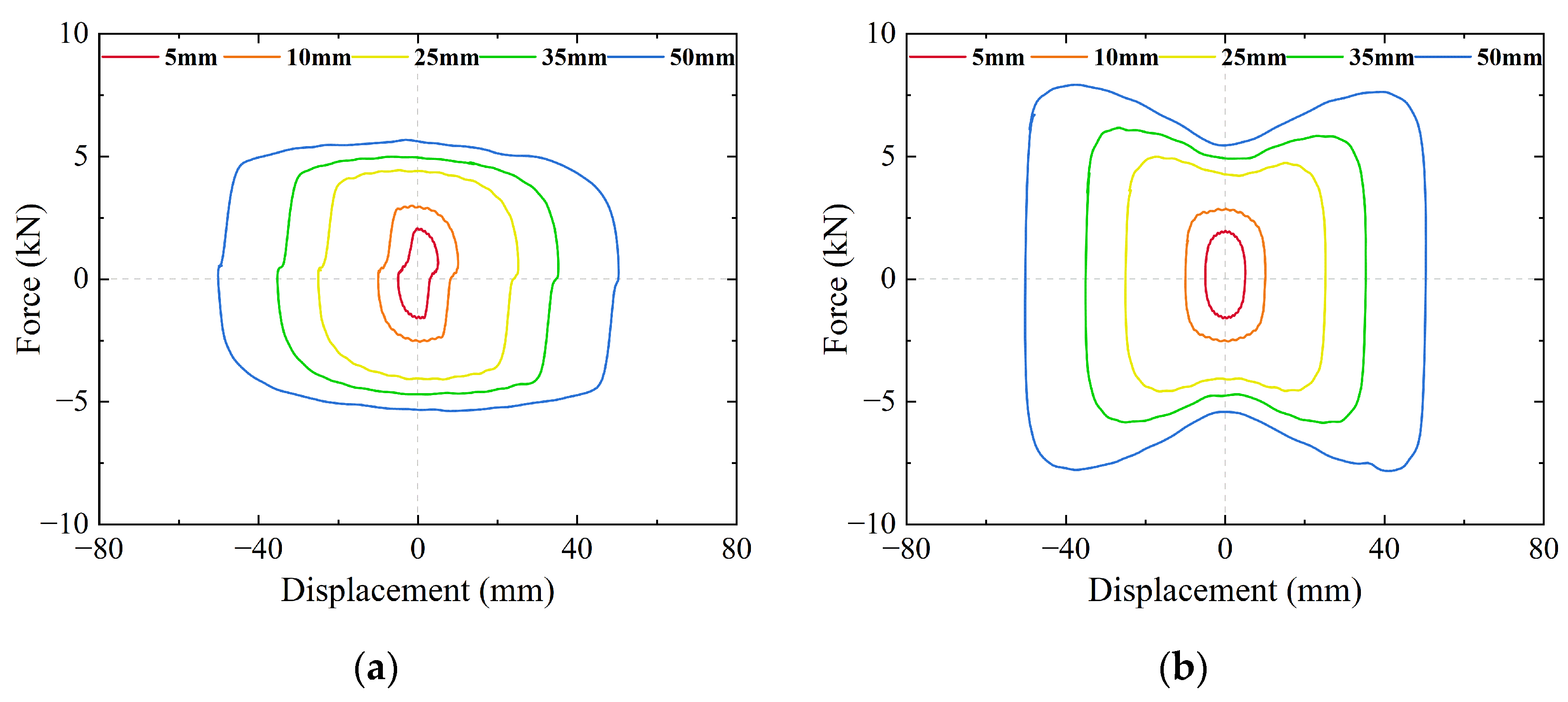
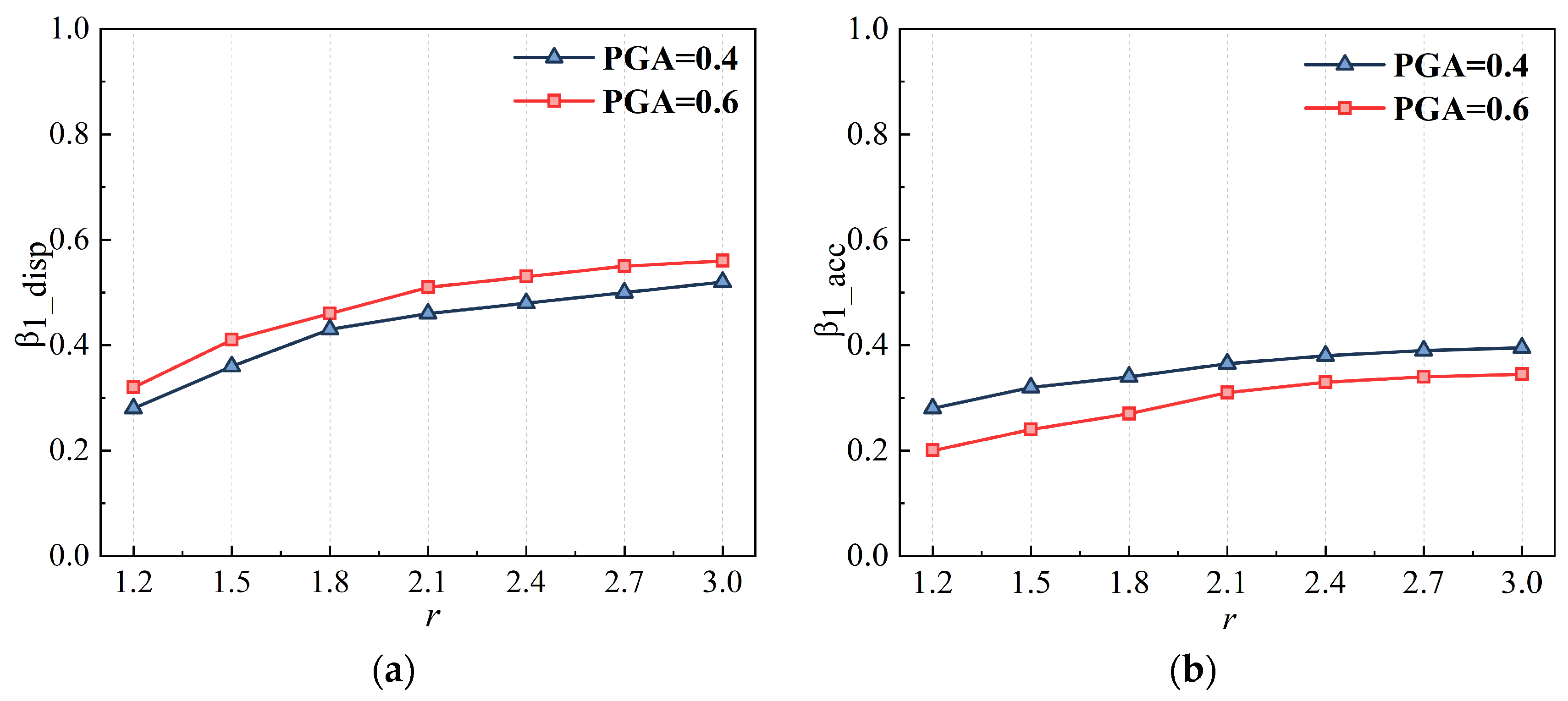
4.4. Parametric Analysis

After verifying the accuracy of the numerical model of SFVVD, a parametric analysis was conducted on this model using Terminal Island seismic waves with PGA values of 0.4 g and 0.6 g, focusing on the two VVD material parameter: the ratio of C₂ to C₁ (denoted as $r)$ and α. Given that the first floor of the structure served as a weak layer, ${\beta }_{1\_disp}$ was utilized to assess the displacement control effectiveness of various parameters, while the peak acceleration reduction rate, denoted as ${\beta }_{2\_acc}$, was employed to evaluate the acceleration control effectiveness of the parameters.

When the values of $r$ were set to 1.2, 1.5, 1.8, 2.1, 2.4, 2.7, and 3.0, respectively, and the value of C₁ was set to 675, with the other VVD material parameters as shown in Table 4, the seismic reduction rates of the SFVVD numerical model are as shown in Figure 21. It can be observed that both ${\beta }_{1\_disp}$ and ${\beta }_{2\_acc}$ generally increase with $r$. However, this increase is less pronounced when the value of $r$ exceeded 2. This trend occurred because while a higher C₂ enhanced the damping force, it also increased the fluid viscosity within the VVD, which reduced the relative deformation across the damper ends and limited energy dissipation.

When the values of α were set to 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, and 0.7, respectively, and the other VVD material parameters were as shown in Table 4, the seismic reduction rates of the SFVVD numerical model are as shown in Figure 22. Both ${\beta }_{1\_disp}$ and ${\beta }_{2\_acc}$ decrease with an increase in α. This indicates that higher α values reduce the energy dissipation capacity of the VVD, leading to weaker seismic response suppression. From Figure 22 it can also be seen that when α is less than 0.3, the seismic reduction rate at a PGA of 0.4 g is higher than at 0.6 g. Conversely, when α exceeds 0.3, the seismic reduction rate at 0.4 g is lower than at 0.6 g. This suggests that lower α values enhance seismic reduction during low-intensity earthquakes, while higher α values increase damping forces during high-intensity earthquakes.

5. Conclusions

The superiority of the VVD in mitigating structural seismic responses under high-intensity earthquakes compared with the traditional VD was been validated based on shaking table test and numerical analysis. The main conclusions of this study are as follows:

(1)

Under WNE and SWE, the first-order frequency increases for both SFVD and SFVVD compared with SF remained within 10%. Under WNE conditions, the damping ratios of the SFVD and SFVVD increased by approximately 20% and 30%, respectively. When subjected to SWEs with a PGA of 0.07 g, the damping ratios of the SFVD and SFVVD increased by approximately two and three times, respectively. As the excitation intensity increased, the VVD enhanced the structural damping ratios compared to the VD, while having a minimal impact on the structural frequencies.

(2)

Under different seismic waves with varying PGA levels, SFVVD reduced inter-story displacement at weak layers by 45–51%, a 10–17% improvement over SFVD. Top-story acceleration was reduced by 24–35% in SFVVD, reflecting a 12–15% improvement compared with that associated with the SFVD. SFVVD also decreased the inter-story shear force by 25–45%, surpassing SFVD by 10–16%. Strain in beams and columns for SFVVD were approximately 17% lower than those in SFVD. Overall, the VVD provided superior damping responses, especially under intense seismic excitation conditions, effectively reducing seismic response.

(3)

A VVD material was developed in OpenSees for simulating seismic-reduction structures with VVD. Numerical simulations of shaking table tests validated the precision of this element, with the model predicting dynamic responses with an accuracy of within 6% of experimental results.

(4)

Based on the numerical model of SFVVD, a parametric analysis was conducted to examine the effects of the ratio $r$ of C₁ to C₂ and the value of α. The results indicated that increasing $r$ enhanced the seismic reduction rate of the SFVVD, but when $r$ exceeded 2, the seismic reduction rate showed little to no further increase. Additionally, as the value of α increased, the structural seismic reduction rates decreased.