Elastoplastic Dynamic Analysis and Damage Evaluation of Reinforced Concrete Structures Based on Time Histories
Abstract
1. Introduction
2. Methodology of Design Process
3. Formulation of Computation Scheme
3.1. Numerical Modeling Scheme
3.2. Elastoplastic Dynamic Response of the Structural System
3.3. Energy Computation of Elastoplastic Time Histories of Structural System
4. Computation Results and Analysis
4.1. Control Parameters for Time-Histories Damage Program
4.2. Time-Histories Damage Program
4.3. Discussion
4.4. Practical Implications
5. Conclusions
- (1)
- This study entails the development of an extensive STHDAP with the aim of investigating structural damage within elastoplastic time histories. The program is meticulously crafted through several key steps. Firstly, a deformation energy time-history damage model is established. This model incorporates cyclic load energy dissipation damage parameters, meticulously derived from the PEER database and quasi-static test data. Additionally, it employs a degraded trilinear restoring force model. The program further investigates the conditions governing the restoring force model, particularly under loading conditions, and analyzes the uniform formula of the restoring force model in inflection point motion conditions. Subsequently, the program formulates the elastoplastic equation of motion, encompassing the uniform formula of stiffness and load, denoted as − . This equation facilitates the computation of the structural response of the system at any given time (t) using linear acceleration and incorporates a relative input energy equation for analytical purposes. Notably, this study culminates in the development of a computational method for calculating the cumulative dissipated energy, denoted as , within the single-degree-of-freedom (SDOF) system during elastoplastic time histories. Furthermore, the study encompasses the development of a computational approach based on time history and damage value . This method serves as a foundational framework for investigating elastoplastic energy dissipation within multi-degree-of-freedom (MDOF) systems. The resulting STHDAP offers comprehensive insights into the evolution of structural damage throughout elastoplastic time histories, making it a valuable tool for the analysis and determination of elastoplastic time-histories outcomes. Importantly, the proposed deformation-energy damage model is poised to facilitate the assessment of elastoplastic damage in high-strength reinforced concrete structures subjected to ground motion, thereby enhancing our understanding of their structural behavior under such conditions.
- (2)
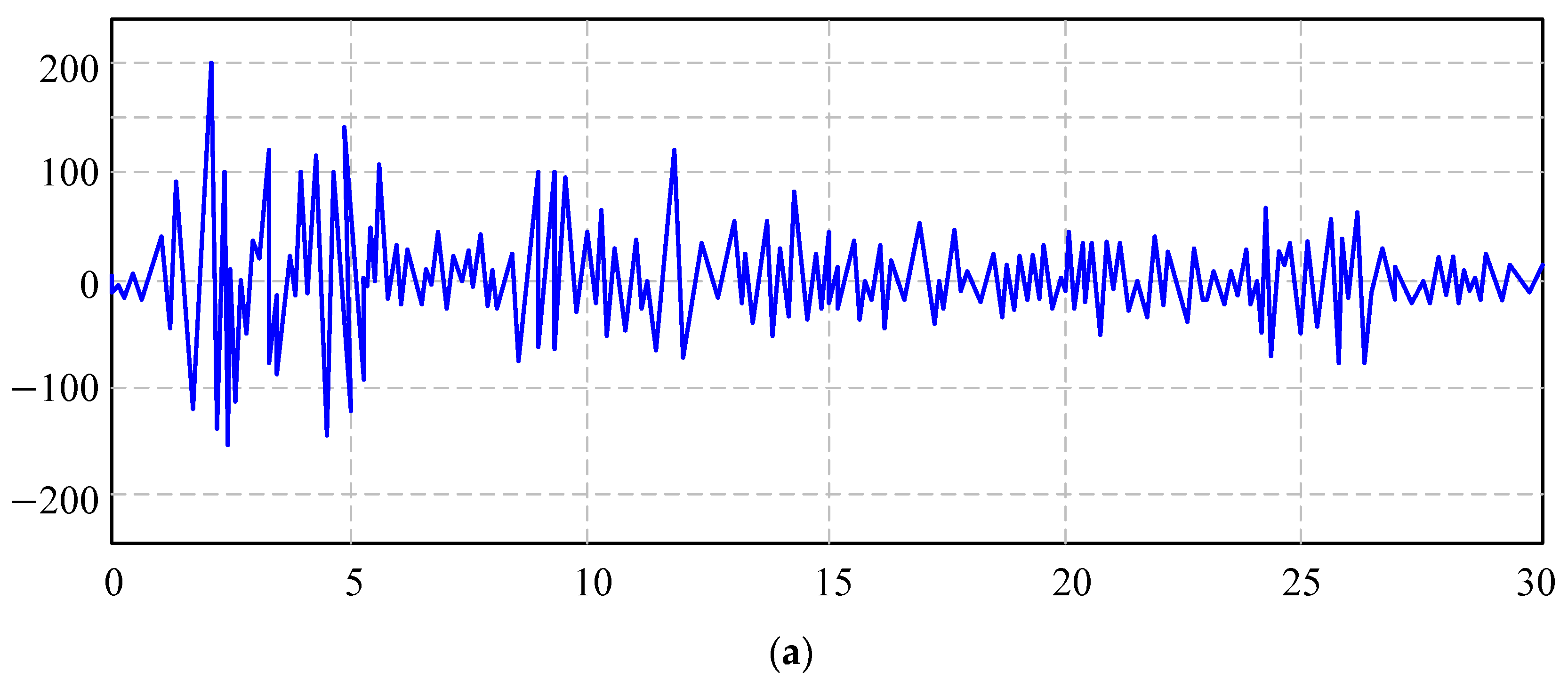
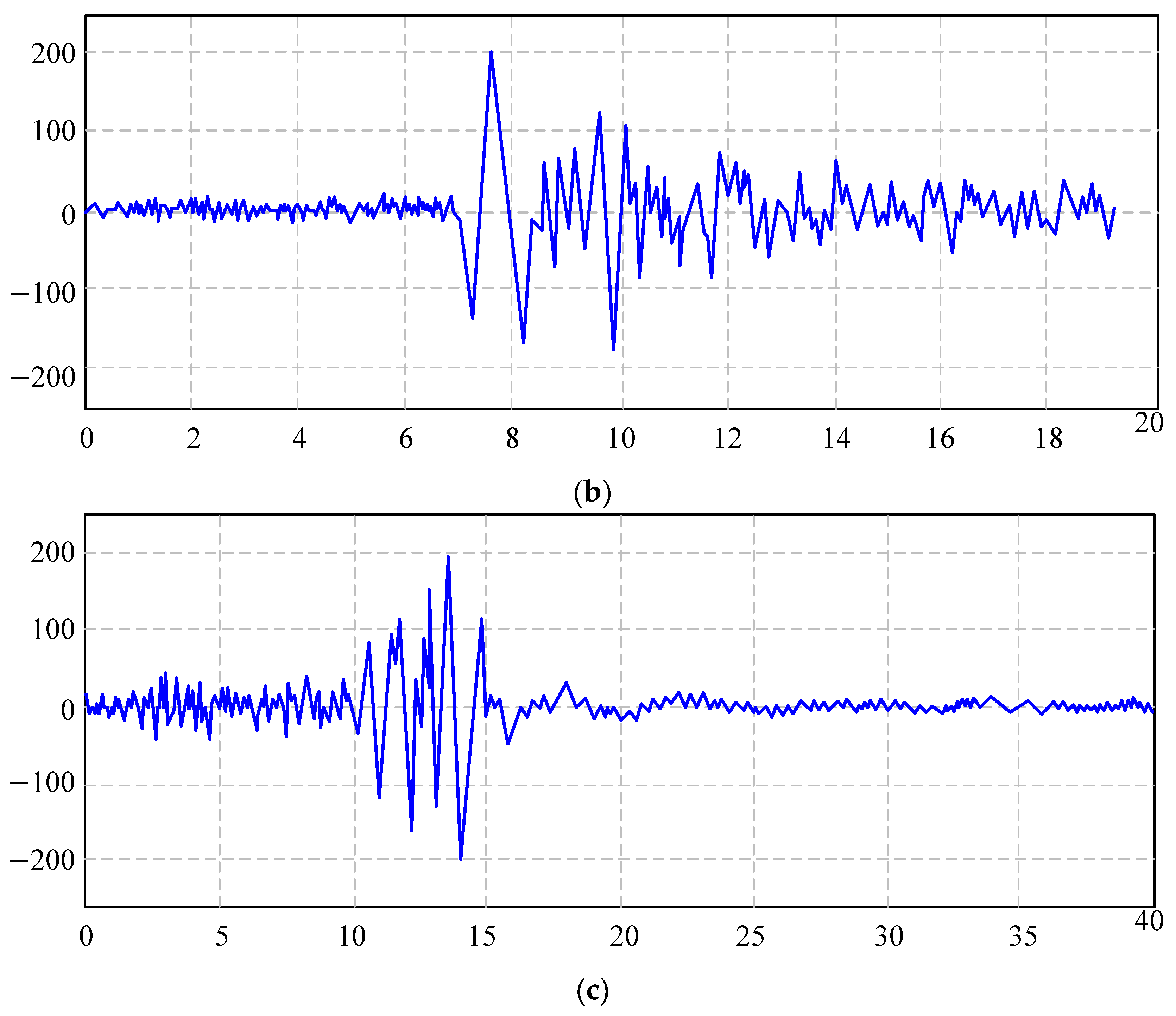
- The primary governing parameters of the restoring force model are derived through the utilization of the DECP analysis program, employing data from members denoted as SP01 through SP10. Subsequently, the pertinent test parameters associated with these members are systematically integrated into the STHDAP, facilitating a comprehensive analysis and computational evaluation. To assess the structural response, El Centro, Tri-treasure, and TianjinNS seismic waves are introduced into the STHDAP, enabling the calculation and subsequent analysis of various response characteristics of the SP01 through SP10 members. These characteristics encompass displacement response, acceleration response, time-history energy consumption, and the assessment of damage incurred. The analytical findings reveal a consistent trend wherein the cumulative damage sustained by each member tends to exhibit a progressive increase. However, it is noteworthy that these increments are characterized by variations in both amplitude and underlying patterns.
- (3)
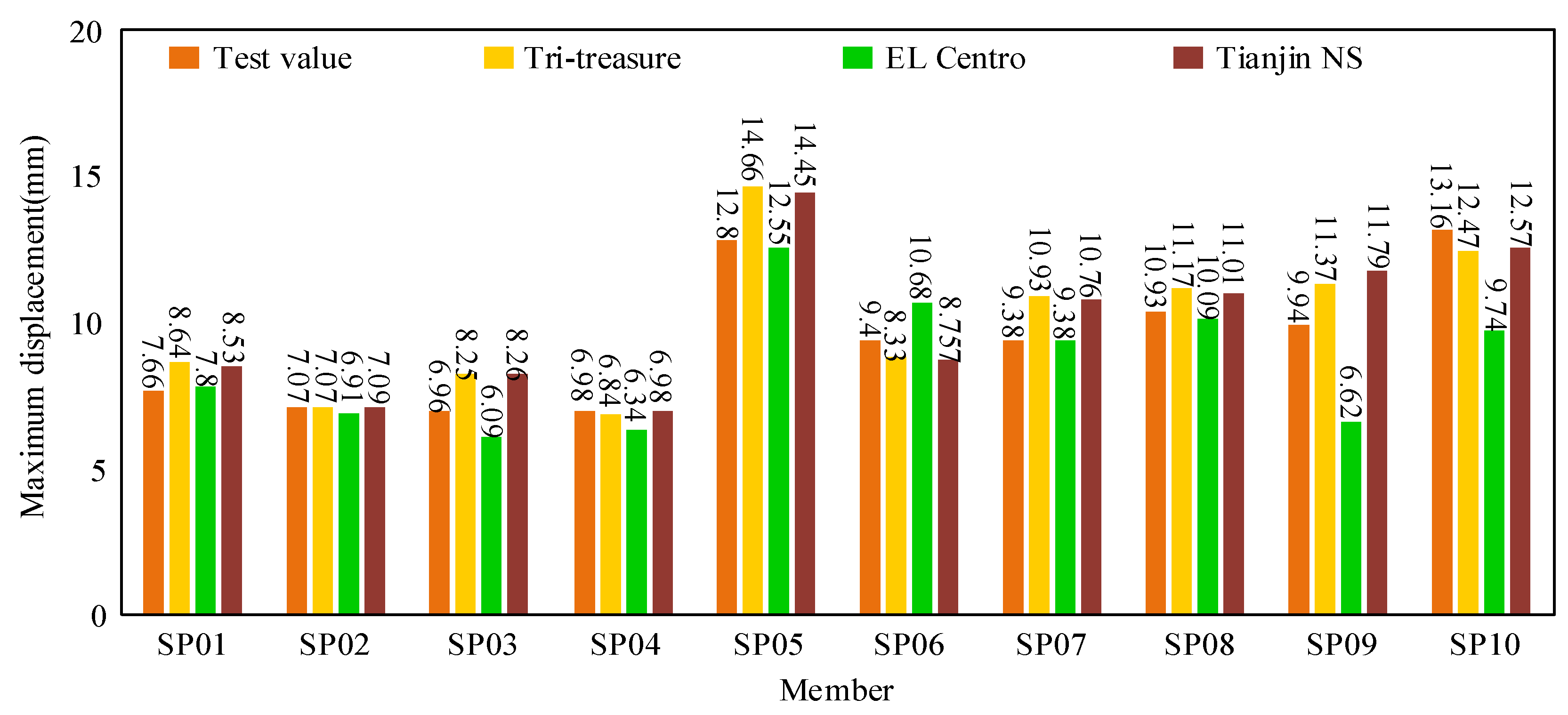
- The analysis of displacement and energy dissipation reveals noteworthy insights. When subjected to varying seismic wave inputs, the displacement response patterns exhibited by the test column align with the displacement change distributions observed in quasi-static tests. However, it is imperative to acknowledge that discrepancies arise in the specific displacement values attained when the critical limit condition is reached. Consequently, qualitative descriptions of this phenomenon become challenging. This suggests that when assessing damage factors associated with members, it is imperative to consider not only the maximum deformation but also the influence of . It is pertinent to note that hysteretic energy exhibits variability in response to changes in the loading regimen and does not adhere to a continuous regularity, as observed in quasi-static tests.
- (4)
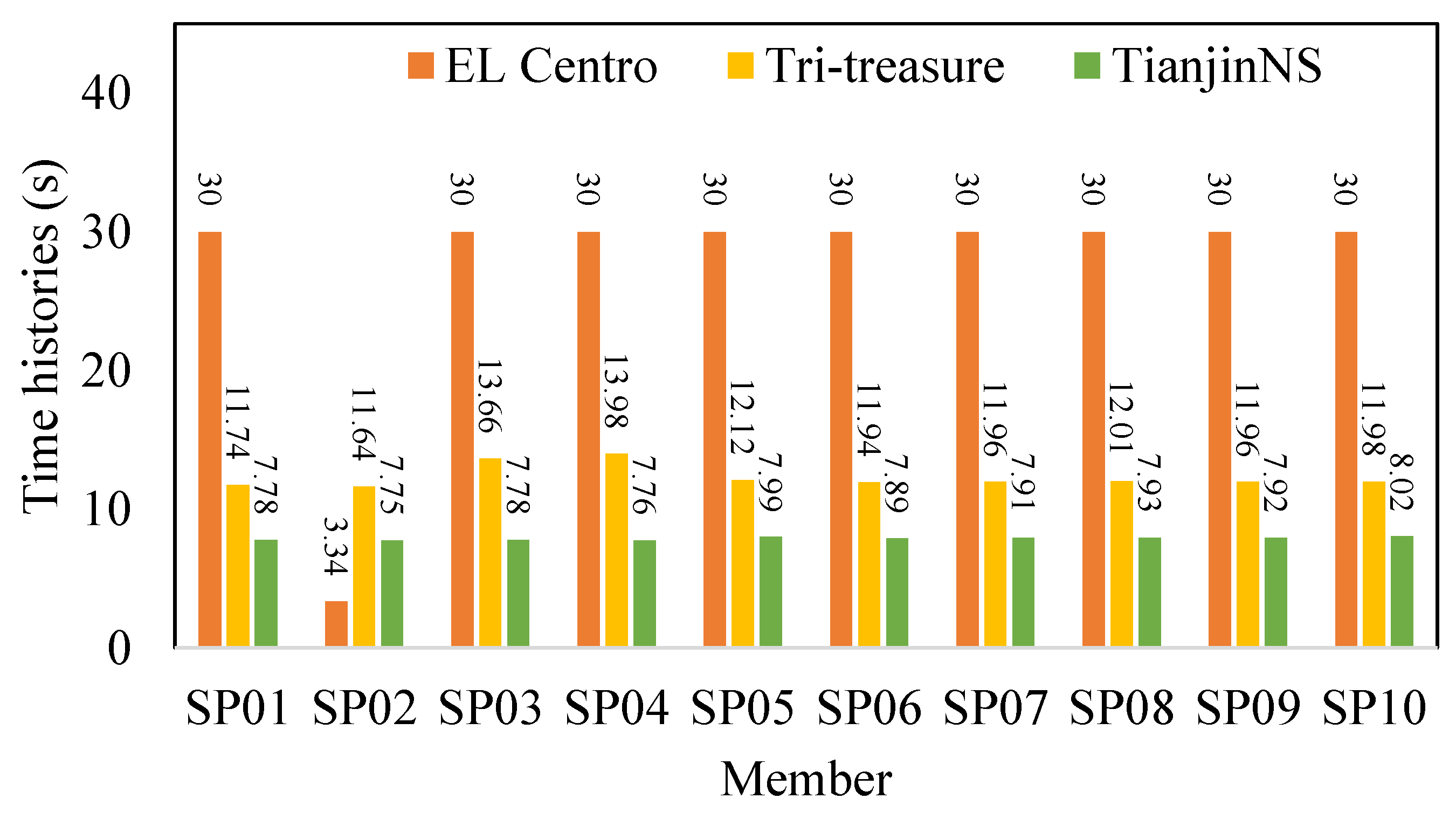
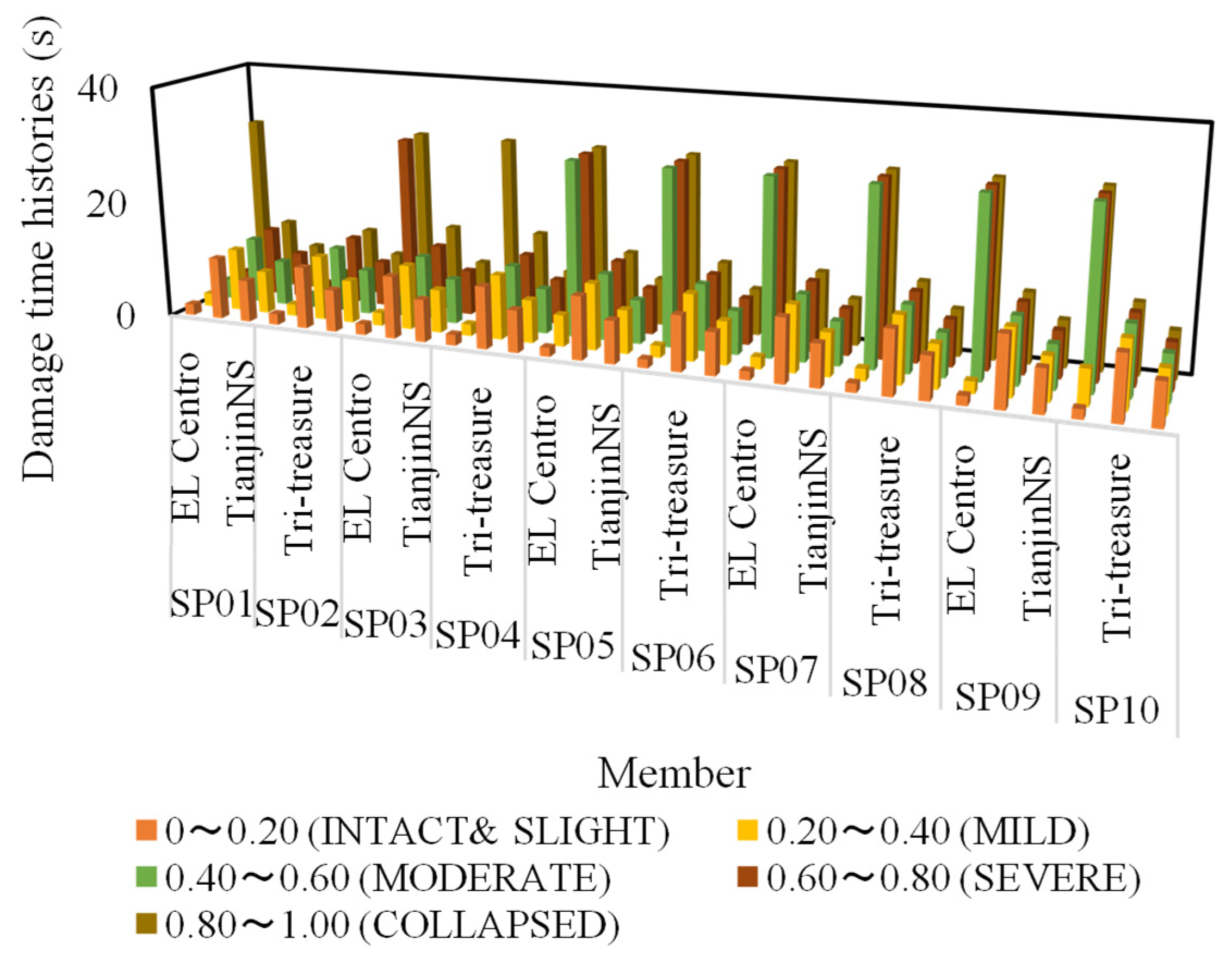
- The analysis of time histories and damage evolution under varying seismic wave inputs reveals several key findings. Firstly, differences in time histories within the same member under different seismic wave inputs stem from variations in amplitudes, spectral characteristics, and other contributing factors. Consequently, relying solely on quasi-static tests proven insufficient for accurately simulating the damage evolution process. Secondly, when subjected to the same seismic waves, the time histories of SP01~SP10 members exhibit relatively close resemblance, signifying that the numerical simulation of time-history damage within this study effectively captures the inherent characteristics of time-history damage among members. Thirdly, based on damage evaluation criteria, it becomes evident that the majority of each member’s time histories correspond to instances of slight and moderate damage, with the transition from severe damage to complete failure representing a minor fraction of the overall time history. This observation underscores the brevity of the duration spanning from initial yielding to nonlinear conditions leading to failure, aligning with the outcomes of the test analyses. Finally, when exposed to diverse seismic wave inputs, the cumulative damage value (D) for the same member exhibits gradual increments, albeit following distinct patterns and amplitudes. In the initial stages, the order of increase follows the sequence EL Centro > Tri-treasure > TianjinNS, mirroring the varying degrees of ground motion excitation during the initial phase.
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Nteres | |
| D | Damage parameter |
| Δu_i | Displacement increment at the i-th step |
| Fi | Force at the i-th step |
| H | Cumulative hysteretic energy |
| m | System mass |
| c | Damping coefficient |
| u | Displacement |
| ü | Acceleration |
| Velocity | |
| K | Uniform stiffness |
| P | Uniform load |
| β | Parameter for cyclic energy dissipation characteristics |
| α | Parameter from quasi-static tests |
| T | Time |
| D = 1.0 | Maximum damage threshold |
| SDOF | Single-degree-of-freedom system |
| STH | Seismic time histories |
| STHDAP | STH Damage Analysis Program |
| MDOF | Multi-Degree-of-Freedom |
| PEER | Pacific Earthquake Engineering Research (database) |
| EL Centro | A seismic wave dataset used in the study |
| Tri-treasure | Another seismic wave dataset |
| Tianjin NS | Third seismic wave dataset |
| DECP | Data damage energy dissipation calculation program |
| YJK | Software program referenced for seismic wave selection |
| SP | Specimen designation used in the study (e.g., SP01-SP10) |
| ξ | Damping ratio |
| k1 | First-order stiffness slope in the restoring force model |
| k2 | Second-order stiffness slope in the restoring force model |
| xfield | Parameter related to the analysis |
| xu | Ultimate deformation displacement |
| ξ | Damping ratio |
| Qyield | Yield load |
| uyield | Yield displacement |
| TH | Total seismic time histories |
| Ek | Kinetic energy increment |
| Ec | Energy dissipated by viscous damping |
| EH | Increment of hysteretic energy dissipation |
| ET | Total energy input to the structure |
| DECP | Data Damage Energy Dissipation Calculation Program |
| BP | Back Propagation (algorithm) |
| ST | Seismic wave total duration |
| SP | Specimen Designation (e.g., SP01–SP10) |
References
- Thwin, W.T. Seismic Response Evaluation of Reinforced Concrete Building with Time History Analysis. Int. J. Sci. Eng. Technol. Res. 2014, 6, 905–911. [Google Scholar]
- Memari, A.M.; Motlagh, A.Y.; Scanlon, A. Seismic evaluation of an existing reinforced concrete framed tube building based on inelastic dynamic analysis. Eng. Struct. 2000, 22, 621–637. [Google Scholar] [CrossRef]
- Boonyapinyo, V.; Choopool, N.; Warnitchai, P. Seismic performance evaluation of reinforced-concrete buildings by static pushover and nonlinear dynamic analyses. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008. [Google Scholar]
- Li, Y.C.; Gao, M. Dynamic Elasto-Plastic Analysis of a High-Rise Hybrid Structure. Appl. Mech. Mater. 2011, 71, 266–269. [Google Scholar] [CrossRef]
- Kou, X.; Li, L.; Du, X.; Zheng, X. Elastoplastic dynamic constitutive model of concrete with combined effects of temperature and strain rate. Case Stud. Constr. Mater. 2023, 18, e01905. [Google Scholar] [CrossRef]
- Oyguc, R.; Tonuk, G.; Oyguc, E.; Ucak, D. Damage accumulation modelling of two reinforced concrete buildings under seismic sequences. Bull. Earthq. Eng. 2023, 21, 4993–5015. [Google Scholar] [CrossRef]
- Zameeruddin, M.; Sangle, K.K. Review on Recent developments in the performance-based seismic design of reinforced concrete structures. Structures 2016, 6, 119–133. [Google Scholar] [CrossRef]
- ur Rehman, Z.; Zhang, G. Three-dimensional elasto-plastic damage model for gravelly soil-structure interface considering the shear coupling effect. Comput. Geotech. 2021, 129, 103868. [Google Scholar] [CrossRef]
- Feng, D.; Kolay, C.; Ricles, J.M.; Li, J. Collapse simulation of reinforced concrete frame structures. Struct. Des. Tall Spec. Build. 2016, 25, 578–601. [Google Scholar] [CrossRef]
- Dolsek, M. Development of computing environment for the seismic performance assessment of reinforced concrete frames by using simplified nonlinear models. Bull. Earthq. Eng. 2010, 8, 1309–1329. [Google Scholar] [CrossRef]
- Lin, H.B.; Tang, S.G.; Lan, C. Damage analysis and evaluation of high strength concrete frame based on deformation-energy damage model. Math. Probl. Eng. 2015, 2015, 781382. [Google Scholar] [CrossRef]
- Chou, C.C.; Uang, C.M. A procedure for evaluating seismic energy demand of framed structures. Earthq. Eng. Struct. Dyn. 2002, 32, 229–244. [Google Scholar] [CrossRef]
- Rehman, Z.U.; Zhang, G. Shear coupling effect of monotonic and cyclic behavior of the interface between steel and gravel. Can. Geotech. J. 2019, 56, 876–884. [Google Scholar] [CrossRef]
- Rehman, Z.U.; Zhang, G. Cyclic behavior of gravel–steel interface under varying rotational shear paths. Can. Geotech. J. 2021, 58, 305–316. [Google Scholar] [CrossRef]
- Rehman, Z.U.; Luo, F.; Wang, T.; Zhang, G. Large-scale test study on the three-dimensional behavior of the gravel–concrete interface of a CFR dam. Int. J. Geomech. 2020, 26, 04020046. [Google Scholar] [CrossRef]
- Yue, J.; Qian, J.; Beskos, D.E. A generalized multi-level seismic damage model for RC framed structures. Soil Dyn. Earthq. Eng. 2016, 80, 25–39. [Google Scholar] [CrossRef]
- Wang, F.; Li, H.N.; Zhang, N. A method for evaluating earthquake-induced structural damage based on displacement and hysteretic energy. Adv. Struct. Eng. 2016, 19, 1165–1176. [Google Scholar] [CrossRef]
- Huang, W.; Qian, J.; Zhou, Z. Seismic Damage Assessment of Steel Reinforced Concrete Members by a Modified Park-Ang Model. Eng. Struct. 2016, 15, 605–611. [Google Scholar] [CrossRef]
- BCUO. PEER Strong Motion Database. 2024. Available online: https://peer.berkeley.edu/peer-strong-ground-motion-databases (accessed on 1 January 2025).
- Abid, U.; Haider, A.; Alshameri, B.; ur Rehman, Z.; Khan, A.J.; Mahmood, N.; Hassan, S. Determination of ground motion parameters of urban centers of Balochistan province. Soil Dyn. Earthq. Eng. 2023, 175, 108221. [Google Scholar] [CrossRef]
- Mahmood, K.; Farooq Rehman, Z.K.; Memon, S.A. One dimensional equivalent linear ground response analysis—A case study of collapsed Margalla Tower in Islamabad during 2005 Muzaffarabad Earthquake. J. Appl. Geophys. 2016, 130, 110–117. [Google Scholar] [CrossRef]
- Mahmood, K.; Zamin, B.; Iqbal, S.; Rehman, Z.; Afzal, S.; Safdar, M.; Iqbal, Q.; Ali, A. Local site effect on seismic hazard of the relocated new Balakot town. Soil Dyn. Earthq. Eng. 2022, 162, 107451. [Google Scholar] [CrossRef]
- Uang, C.; Bertero, V.V. Evaluation of seismic energy in structures. Earthq. Eng. Struct. Dyn. 1990, 19, 77–90. [Google Scholar] [CrossRef]
- Chapman, M.C. On the use of elastic input energy for seismic hazard analysis. Earthq. Spectra 1999, 15, 607–635. [Google Scholar] [CrossRef]
- Decanini, L.D.; Mollaioli, F. Formulation of elastic earthquake input energy spectra. Earthq. Eng. Struct. Dyn. 1998, 27, 1503–1522. [Google Scholar] [CrossRef]
- De Domenico, D.; Ricciardi, G.; Takewaki, I. Design strategies of viscous dampers for seismic protection of building structures: A review. Soil Dyn. Earthq. Eng. 2019, 118, 144–165. [Google Scholar] [CrossRef]
- Symans, M.D.; Charney, F.A.; Whittaker, A.S.; Constantinou, M.C.; Kircher, C.A.; Johnson, M.W.; McNamara, R.J. Energy dissipation systems for seismic applications: Current practice and recent developments. J. Struct. Eng. 2008, 134, 3–21. [Google Scholar] [CrossRef]
- Cheng, G.Y.; Ye, L.P. Earthquake input energy spectrum for inelastic SDOF systems. Eng. Mech. 2008, 25, 28–039. [Google Scholar]
- Xiao, F.; Mao, Y.; Sun, H.; Chen, G.S.; Tian, G. Stiffness Separation Method for Reducing Calculation Time of Truss Structure Damage Identification. Struct. Control Health Monit. 2024, 2024, 5171542. [Google Scholar]
- Xiao, F.; Mao, Y.; Tian, G.; Chen, G.S. Partial-Model-Based Damage Identification of Long-Span Steel Truss Bridge Based on Stiffness Separation Method. Struct. Control Health Monit. 2024, 2024, 5530300. [Google Scholar]
- Xiao, F.; Sun, H.; Mao, Y.; Chen, G.S. Damage identification of large-scale space truss structures based on stiffness separation method. Structures 2023, 53, 109–118. [Google Scholar] [CrossRef]
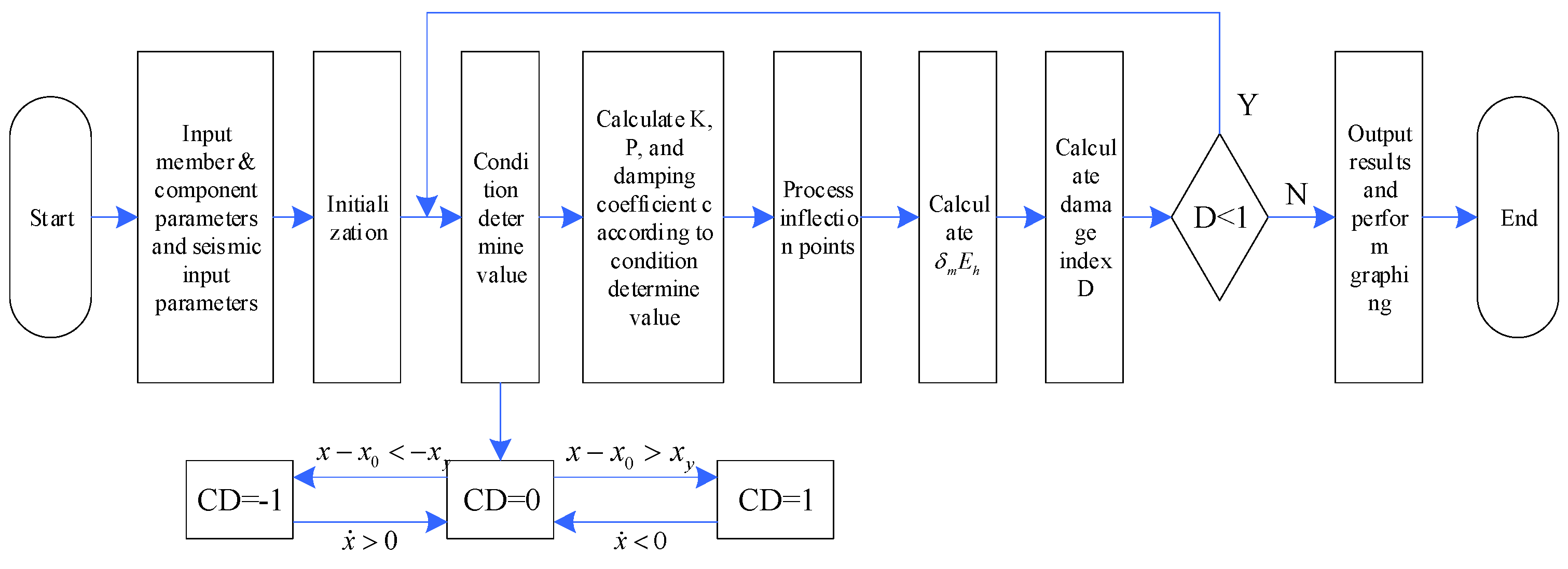
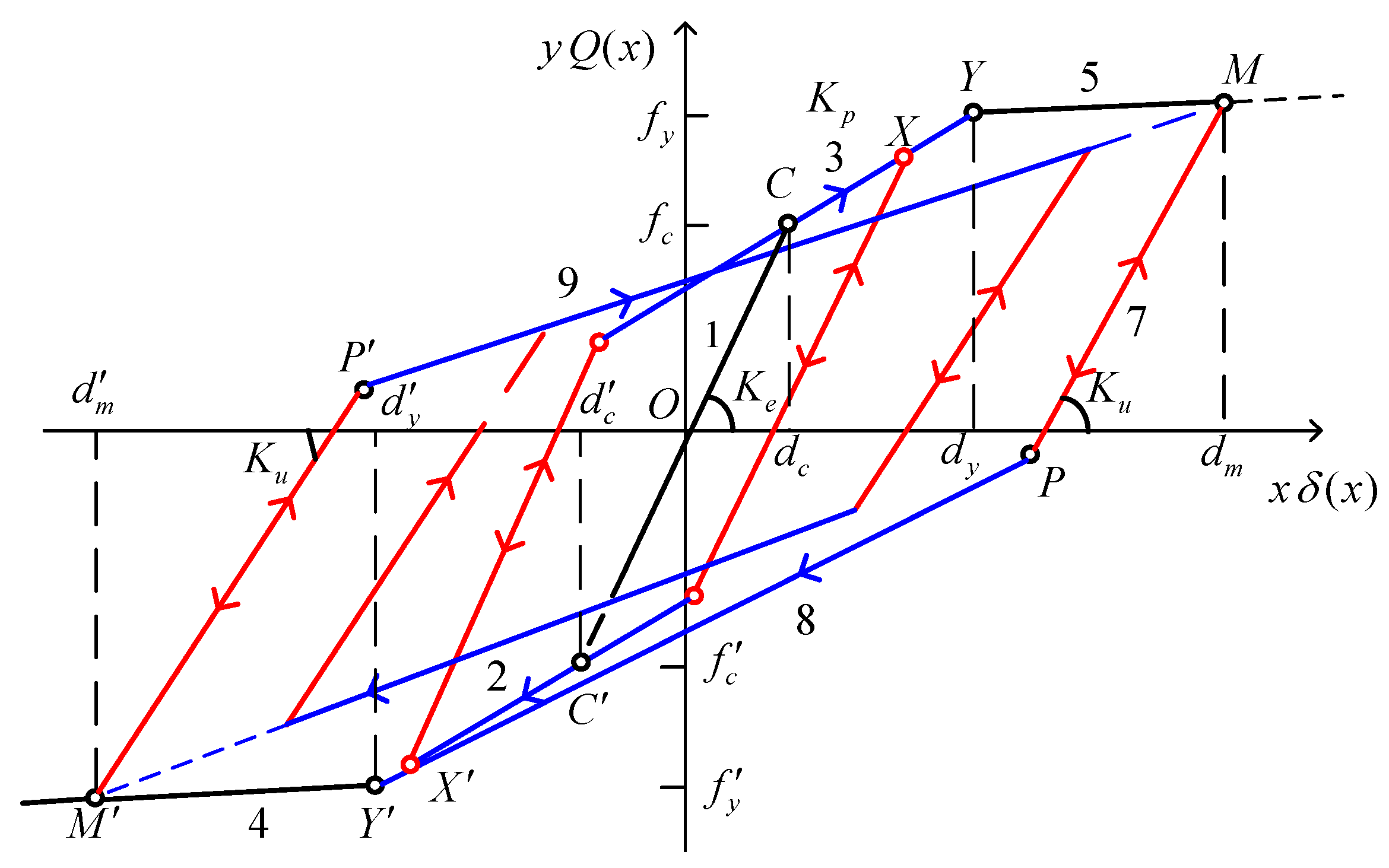
| Loading Condition | Loading Condition Description of ) | Condition Determine Value CD | Uniform Expression of ) | |
|---|---|---|---|---|
| Elastic loading | The system is in an elastic loading condition. The slope is . When the condition point ) moves along this type of straight line, the condition determine value is 0. | CD = 0 | ||
| Plastic loading | Positive loading | The system is in an elastoplastic positive loading condition. The slope of the straight line formed by joining the upper critical points is . When the condition point ) moves on this type of straight line, the condition determine value is 1. | CD = 1 | |
| Plastic loading | Negative loading | The system is in an elastoplastic negative loading condition. The slope of the straight line formed by joining the lower critical points is . When the condition point ) moves on this type of straight line, the condition determine value is −1. | CD = −1 | |
| Motion Condition at the Inflection Point | Description of Motion Condition at the Inflection Point | Abscissa of Inflection Point | Uniform Expression of Inflection Point | |
|---|---|---|---|---|
| Elastic — plastic interval | Positive direction | The acceleration within is linearly varied (Wil-son-θ method), and it is assumed that and are linearly varied, and the linear interpolation propor-tion factor: . | ||
| Negative direction | The condition determine value of the condition is: CD = −1. | |||
| Plastic — unloading interval | Positive direction | When the direction of motion changes, the value is very small, the displacement occurring within is small, and the condition point only moves slightly, so interpolation is not required. | ||
| Negative direction | Same analysis as above. | |||
| Member No. | SP01 | SP02 | SP03 | SP04 | SP05 | SP06 | SP07 | SP08 | SP09 | SP10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 67.1 | 67.1 | 75.9 | 70.7 | 57.3 | 57.3 | 57.3 | 57.3 | 57.3 | 57.3 | |
| 1.90 | 1.90 | 1.90 | 1.90 | 1.90 | 1.90 | 1.90 | 1.90 | 1.50 | 2.40 | |
| 0.20 | 0.20 | 0.20 | 0.20 | 0.20 | 0.35 | 0.50 | 0.35 | 0.20 | 0.20 | |
| 1.61 | 3.93 | 1.61 | 1.61 | 3.35 | 3.35 | 3.35 | 3.35 | 3.35 | 3.35 | |
| 0.27 | 0.27 | 0.27 | 0.27 | 0.45 | 0.45 | 0.45 | 0.67 | 0.45 | 0.45 | |
| 3.11 | 2.82 | 2.85 | 2.54 | 5.89 | 5.30 | 5.31 | 5.89 | 7.27 | 6.71 | |
| 8.39 | 7.09 | 8.26 | 7.06 | 13.25 | 9.46 | 9.88 | 10.52 | 10.02 | 13.26 | |
| 254.8 | 266.5 | 301.6 | 282.7 | 165.6 | 191.1 | 188.6 | 230.1 | 253.7 | 240.5 | |
| 0.043 | 0.049 | 0.039 | 0.070 | 0.075 | 0.090 | 0.084 | 0.049 | 0.046 | 0.084 | |
| 81.23 | 93.91 | 105.1 | 95.83 | 28.11 | 36.04 | 35.58 | 34.29 | 39.28 | 14.97 | |
| 56.91 | 75.71 | 88.96 | 96.16 | 27.17 | 25.05 | 32.69 | 29.01 | 30.15 | 20.63 |
| Member No. | SP01 | SP02 | SP03 | SP04 | SP05 | SP06 | SP07 | SP08 | SP09 | SP10 |
|---|---|---|---|---|---|---|---|---|---|---|
| EL Centro | 30.00 | 3.34 | 30.00 | 30.00 | 30.00 | 30.00 | 30.00 | 30.00 | 30.00 | 30.00 |
| Tri-treasure | 11.74 | 11.64 | 13.66 | 13.98 | 12.12 | 11.94 | 11.96 | 12.01 | 11.96 | 11.98 |
| Tianjin NS | 7.78 | 7.75 | 7.78 | 7.76 | 7.99 | 7.89 | 7.91 | 7.93 | 7.92 | 8.02 |
| Member No. | SP01 | SP02 | SP03 | SP04 | SP05 | SP06 | SP07 | SP08 | SP09 | SP10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 7.66 | 7.07 | 6.96 | 6.98 | 12.80 | 9.40 | 9.38 | 10.39 | 9.94 | 13.16 | |
| EL Centro | 7.80 | 6.91 | 6.09 | 6.34 | 12.55 | 10.68 | 9.38 | 10.09 | 6.62 | 9.74 |
| Tri-treasure | 8.64 | 7.07 | 8.25 | 6.84 | 14.66 | 8.83 | 10.93 | 11.17 | 11.37 | 12.47 |
| Tianjin NS | 8.53 | 7.09 | 8.26 | 6.98 | 14.45 | 8.757 | 10.76 | 11.01 | 11.79 | 12.57 |
| Member No. | Damage Evaluation Criteria | 0~0.20 (Intact and Slight) | 0.20~0.40 (Mild) | 0.40~0.60 (Moderate) | 0.60~0.80 (Severe) | 0.80~1.00 (Collapsed) |
|---|---|---|---|---|---|---|
| SP01 | EL Centro | 1.90 | 2.28 | 3.34 | 3.40 | 30.00 |
| Tri-treasure | 10.62 | 10.78 | 11.24 | 11.68 | 11.74 | |
| Tianjin NS | 7.22 | 7.33 | 7.73 | 7.75 | 7.78 | |
| SP02 | EL Centro | 1.88 | 2.00 | 2.30 | 2.86 | 3.34 |
| Tri-treasure | 10.60 | 11.06 | 11.12 | 11.60 | 11.64 | |
| Tianjin NS | 7.21 | 7.33 | 7.71 | 7.73 | 7.75 | |
| SP03 | EL Centro | 1.90 | 2.24 | 3.24 | 30.00 | 30.00 |
| Tri-treasure | 10.68 | 11.06 | 11.18 | 11.64 | 13.66 | |
| Tianjin NS | 7.25 | 7.38 | 7.71 | 7.74 | 7.78 | |
| SP04 | EL Centro | 1.88 | 2.00 | 2.70 | 2.76 | 30.00 |
| Tri-treasure | 10.62 | 11.04 | 11.12 | 11.60 | 13.98 | |
| Tianjin NS | 7.22 | 7.33 | 7.69 | 7.73 | 7.76 | |
| SP05 | EL Centro | 1.52 | 5.36 | 30.00 | 30.00 | 30.00 |
| Tri-treasure | 10.74 | 11.26 | 11.34 | 12.06 | 12.12 | |
| Tianjin NS | 7.26 | 7.36 | 7.46 | 7.93 | 7.99 | |
| SP06 | EL Centro | 1.48 | 2.02 | 30.00 | 30.00 | 30.00 |
| Tri-treasure | 9.36 | 11.22 | 11.30 | 11.42 | 11.94 | |
| Tianjin NS | 7.22 | 7.32 | 7.39 | 7.86 | 7.89 | |
| SP07 | EL Centro | 1.48 | 2.02 | 30.00 | 30.00 | 30.00 |
| Tri-treasure | 10.80 | 11.24 | 11.32 | 11.90 | 11.96 | |
| Tianjin NS | 7.23 | 7.33 | 7.41 | 7.87 | 7.91 | |
| SP08 | EL Centro | 1.50 | 2.06 | 30.00 | 30.00 | 30.00 |
| Tri-treasure | 10.80 | 11.32 | 11.34 | 11.90 | 12.01 | |
| Tianjin NS | 7.24 | 7.34 | 7.42 | 7.87 | 7.93 | |
| SP09 | EL Centro | 1.58 | 2.02 | 30.00 | 30.00 | 30.00 |
| Tri-treasure | 11.86 | 11.24 | 11.34 | 11.90 | 11.93 | |
| Tianjin NS | 7.24 | 7.34 | 7.43 | 7.86 | 7.92 | |
| SP10 | EL Centro | 1.64 | 6.02 | 30.00 | 30.00 | 30.00 |
| Tri-treasure | 10.88 | 11.30 | 11.88 | 11.94 | 11.98 | |
| Tianjin NS | 7.26 | 7.38 | 7.86 | 7.89 | 8.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, H. Elastoplastic Dynamic Analysis and Damage Evaluation of Reinforced Concrete Structures Based on Time Histories. Buildings 2025, 15, 971. https://doi.org/10.3390/buildings15060971
Lin H. Elastoplastic Dynamic Analysis and Damage Evaluation of Reinforced Concrete Structures Based on Time Histories. Buildings. 2025; 15(6):971. https://doi.org/10.3390/buildings15060971
Chicago/Turabian StyleLin, Huangbin. 2025. "Elastoplastic Dynamic Analysis and Damage Evaluation of Reinforced Concrete Structures Based on Time Histories" Buildings 15, no. 6: 971. https://doi.org/10.3390/buildings15060971
APA StyleLin, H. (2025). Elastoplastic Dynamic Analysis and Damage Evaluation of Reinforced Concrete Structures Based on Time Histories. Buildings, 15(6), 971. https://doi.org/10.3390/buildings15060971







