Residual Stress Distribution and Fatigue Behavior of Combined Bolted–Welded Joints
Abstract
1. Introduction
2. Tests to Measure the Residual Stress Distribution
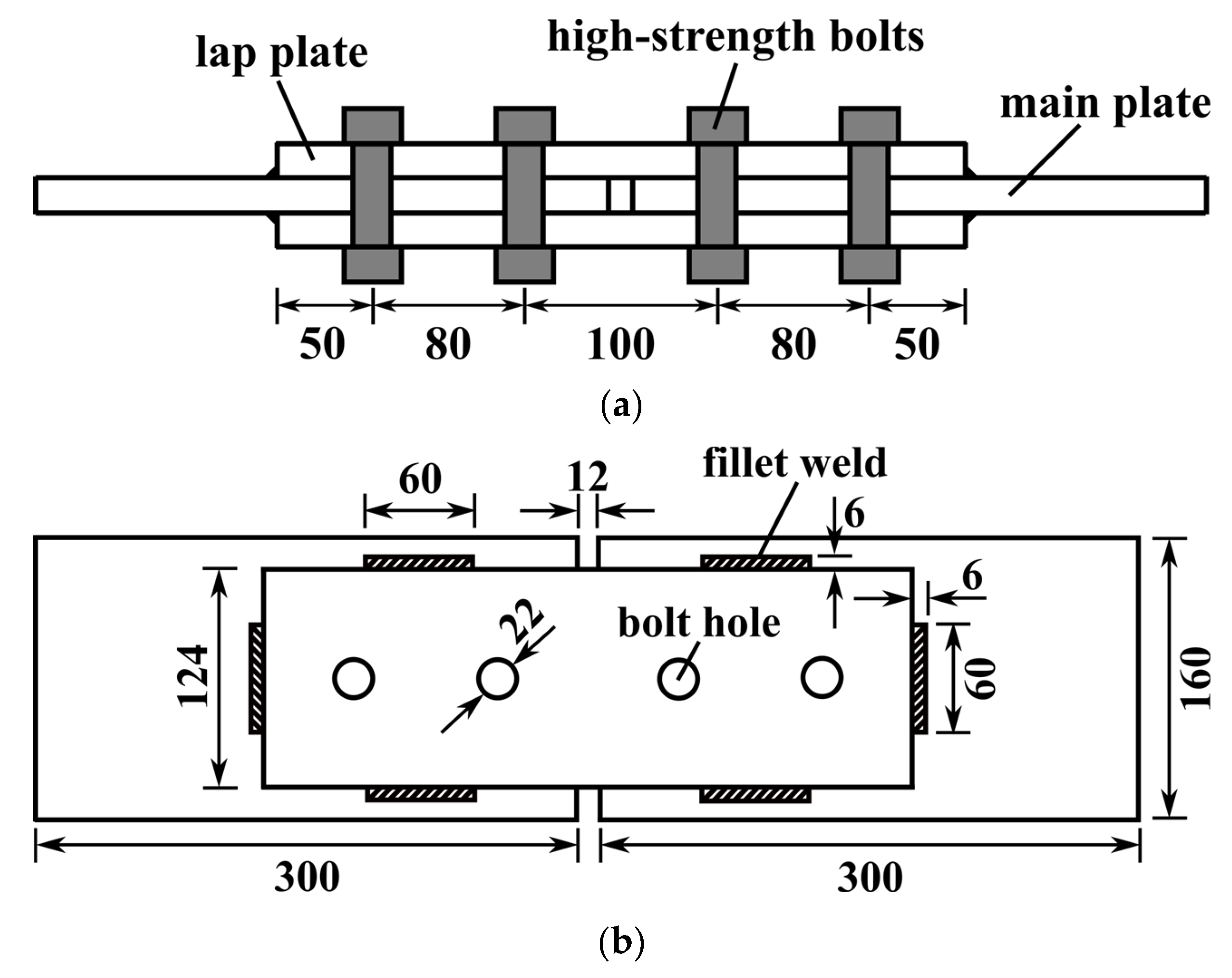
2.1. Test Specimens
2.2. Material Properties
2.3. Welding Process
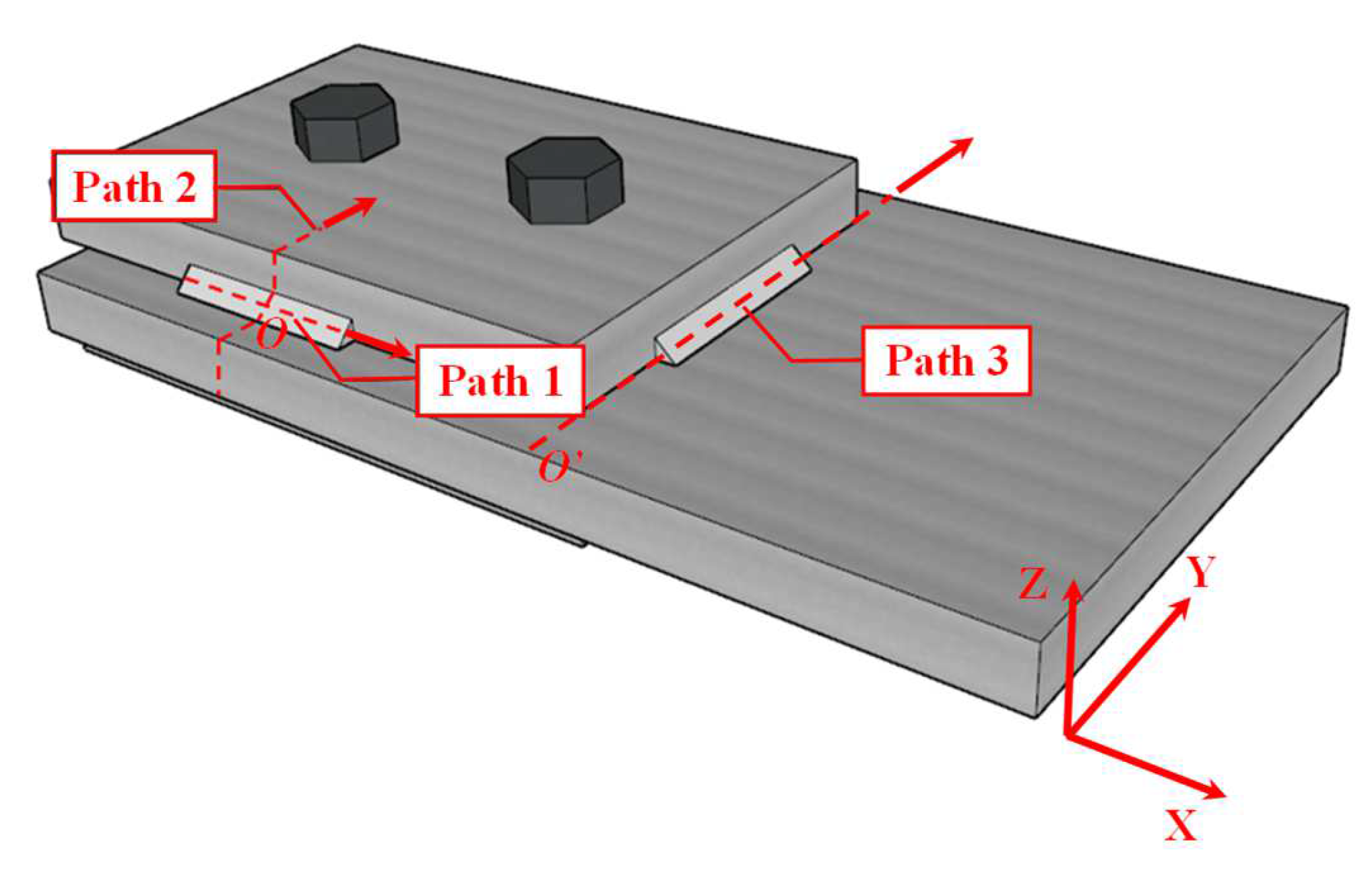
2.4. Measurement Arrangement
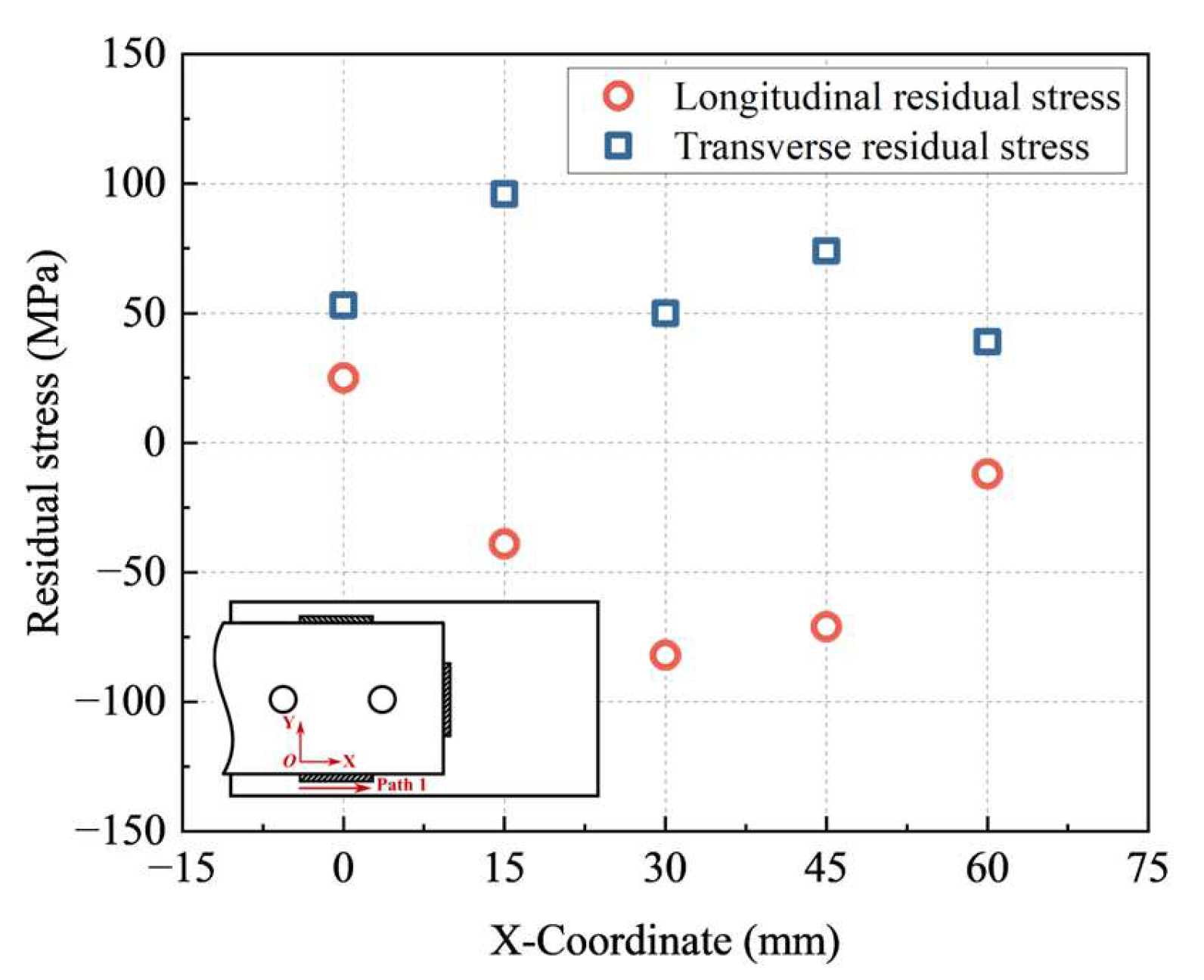
2.5. Test Results
3. Finite Element Simulation of Residual Stresses
3.1. Finite Element Model and Mesh Scheme
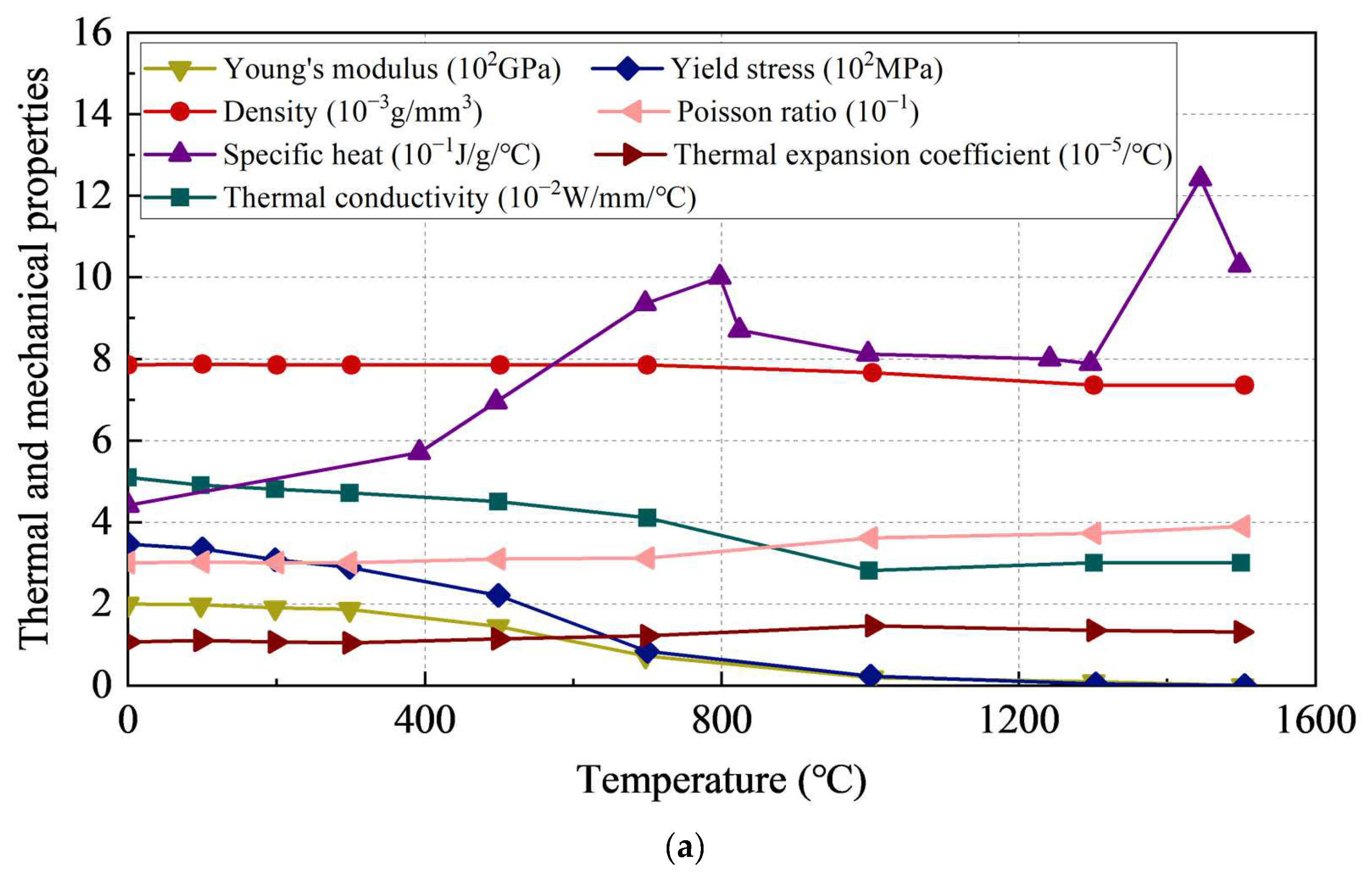
3.2. Thermal Properties of Materials
3.3. Thermal and Mechanical Analysis
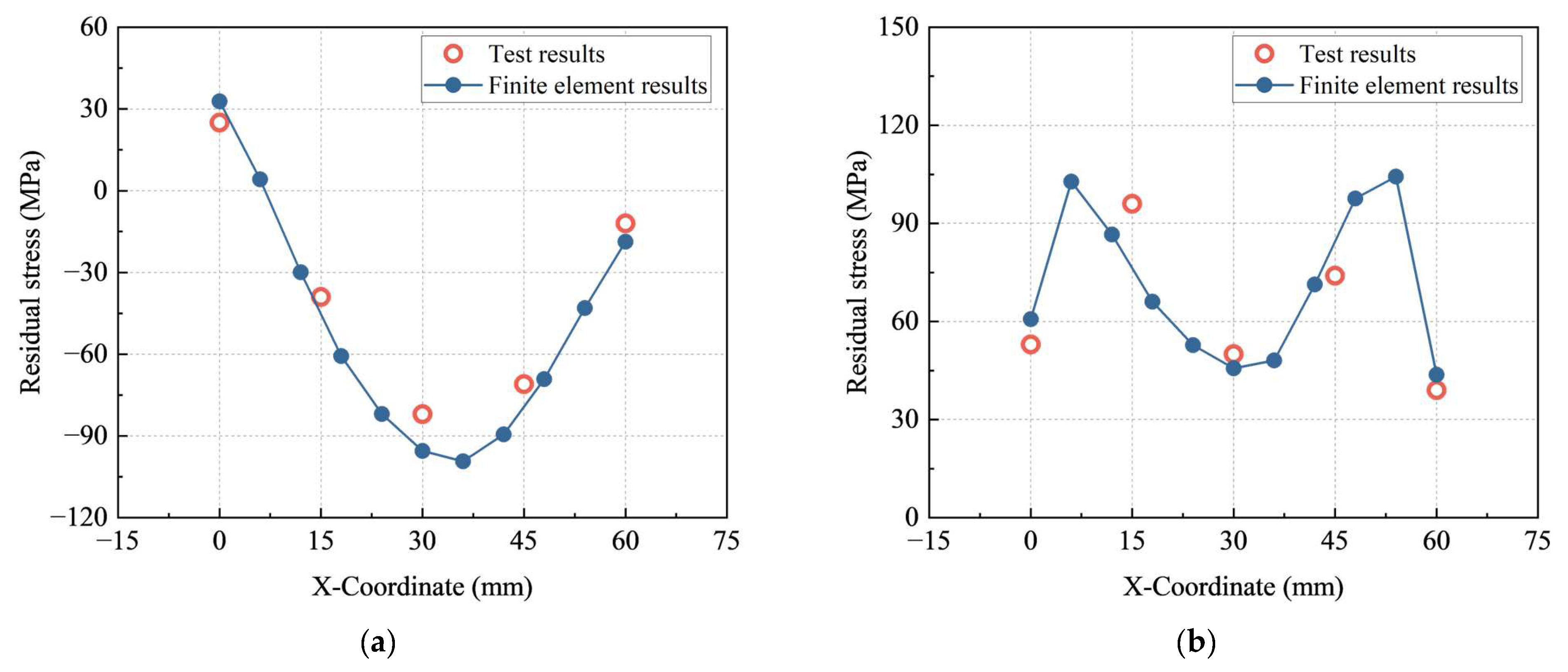
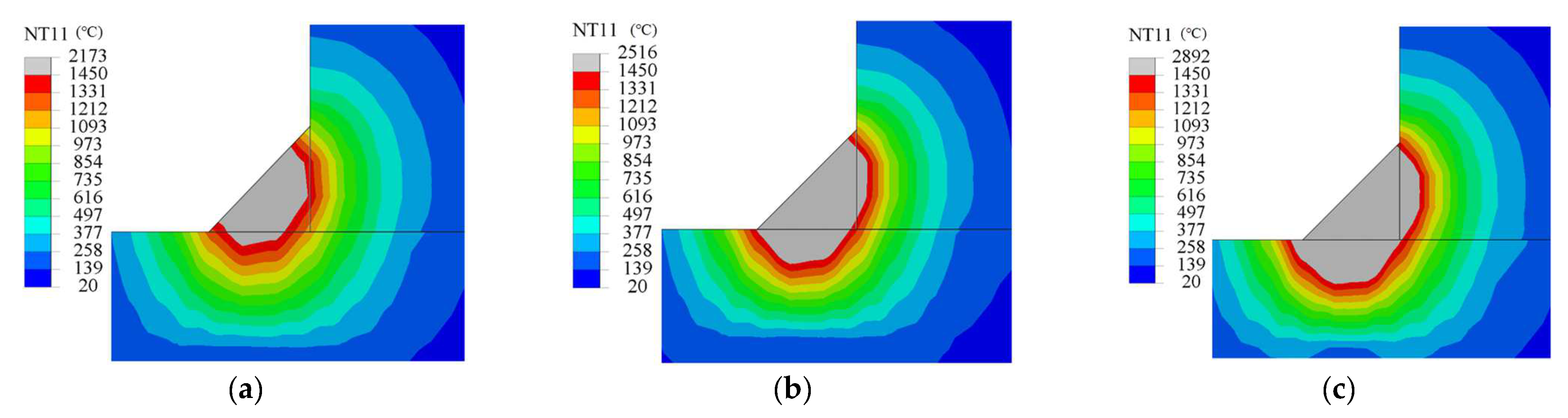
3.4. Model Validation
4. Effects of Manufacturing Processes on Residual Stress
4.1. Possible Manufacturing Processes
- Welding sequence 1: 1#→2#→3#→4#→5#→6#;
- Welding sequence 2: 1#→2#→4#→5#→3#→6#;
- Welding sequence 3: 1#→4#→2#→5#→3#→6#;
- Welding sequence 4: 1#→4#→2#→5#→3#→6# (where seams 4#, 5# and 6# are welded in the opposite direction to that shown in Figure 10).
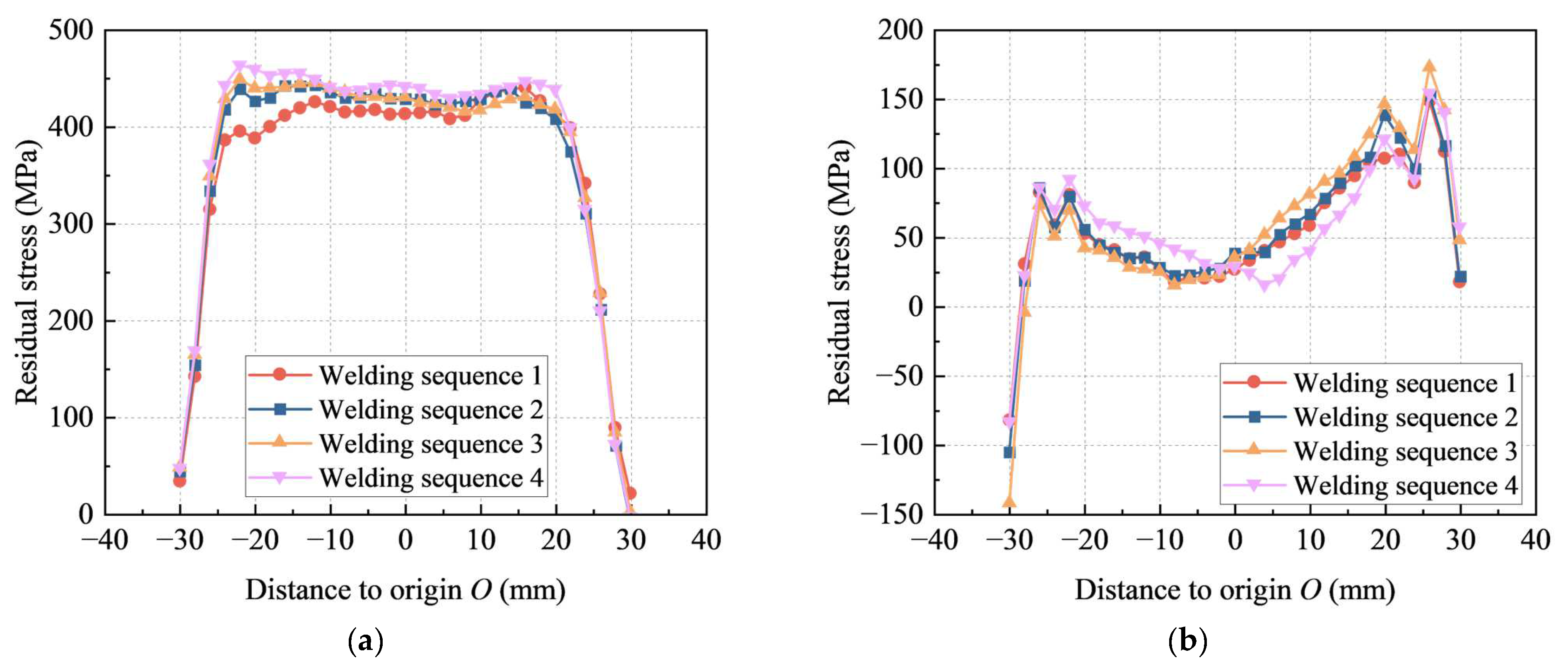
4.2. Effects of Welding Sequences on Residual Stresses
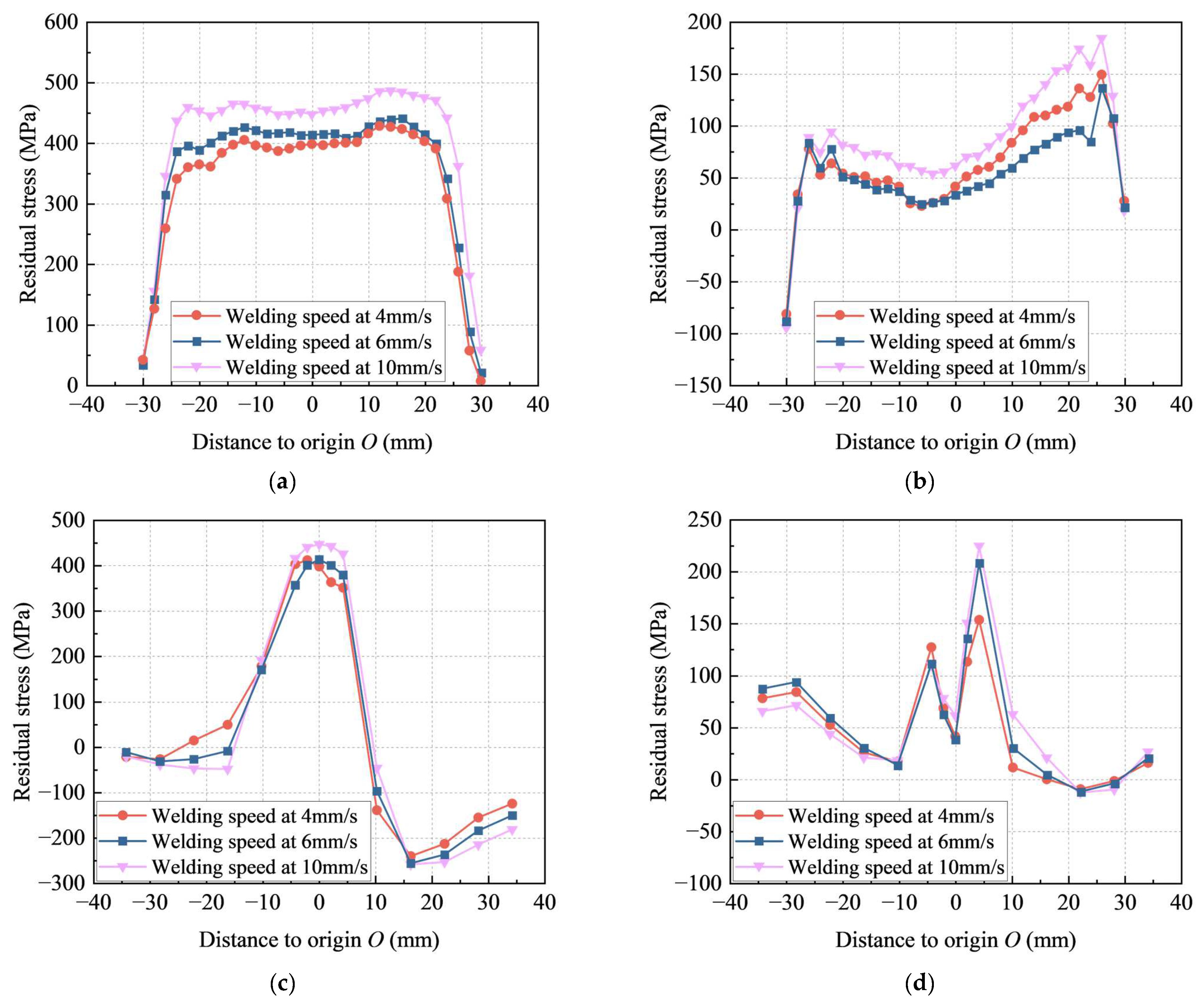
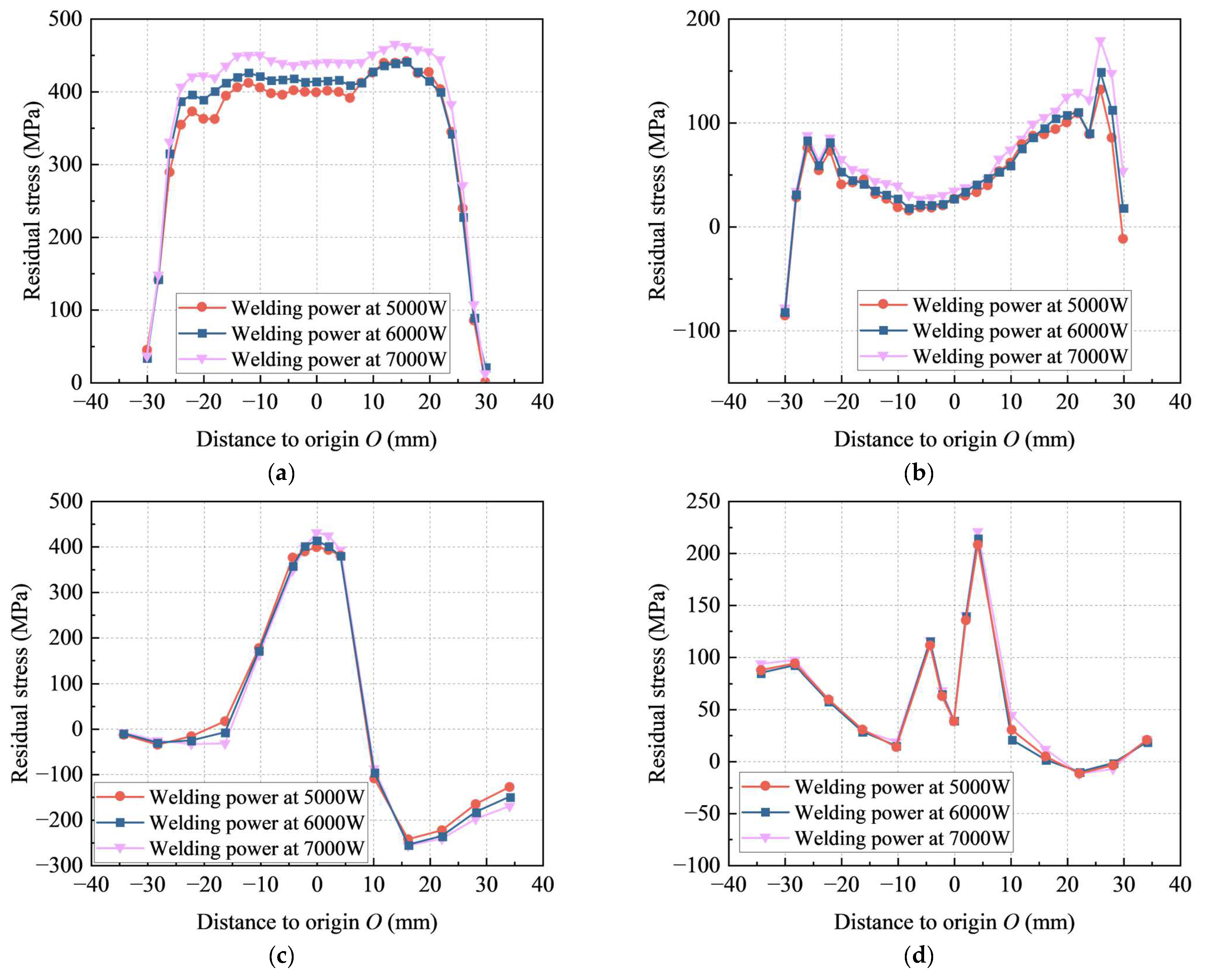
4.3. Effects of Welding Parameters on Residual Stresses
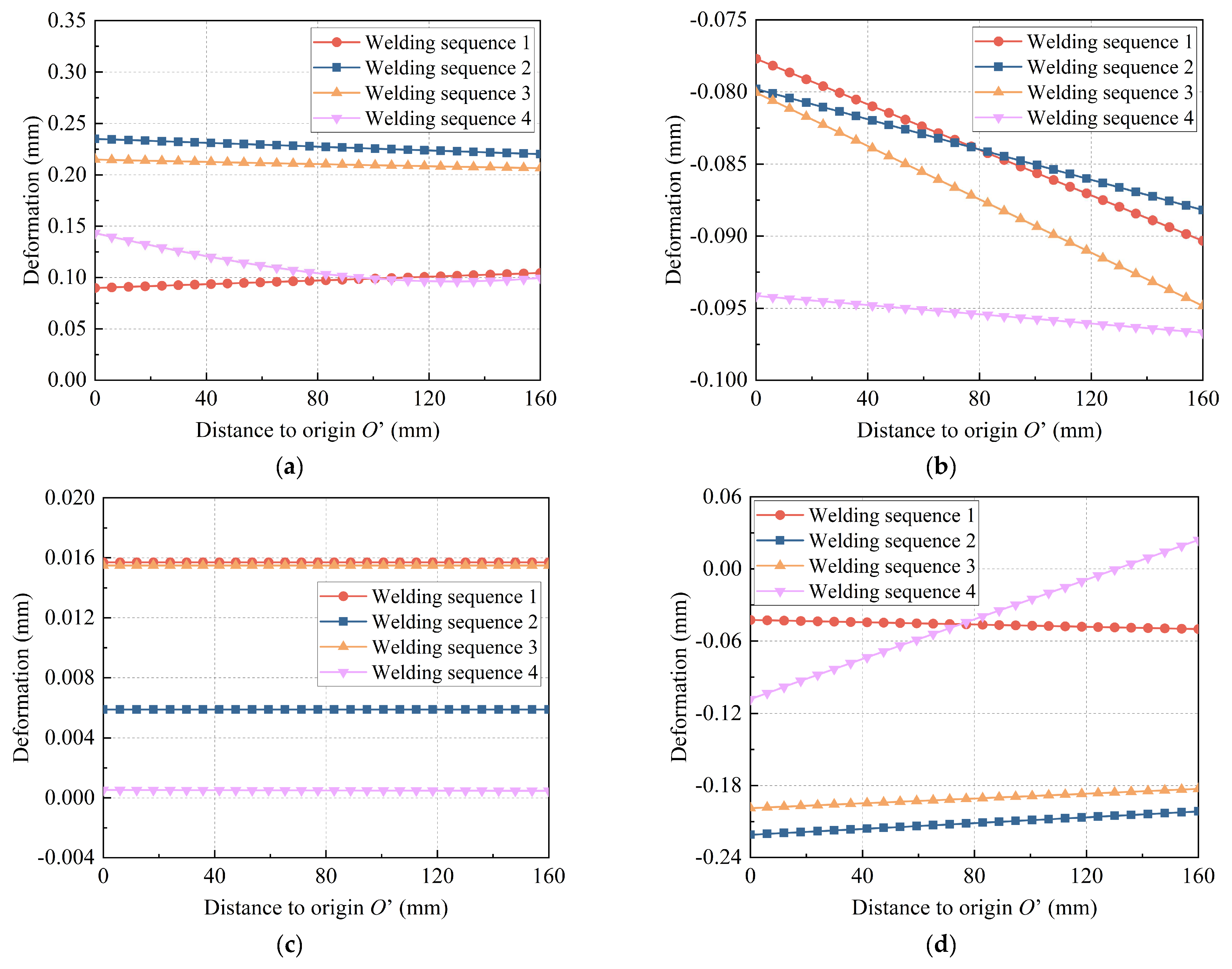
5. Effects of Manufacturing Processes on Residual Deformation
6. Effects of Residual Stresses on Fatigue Behavior
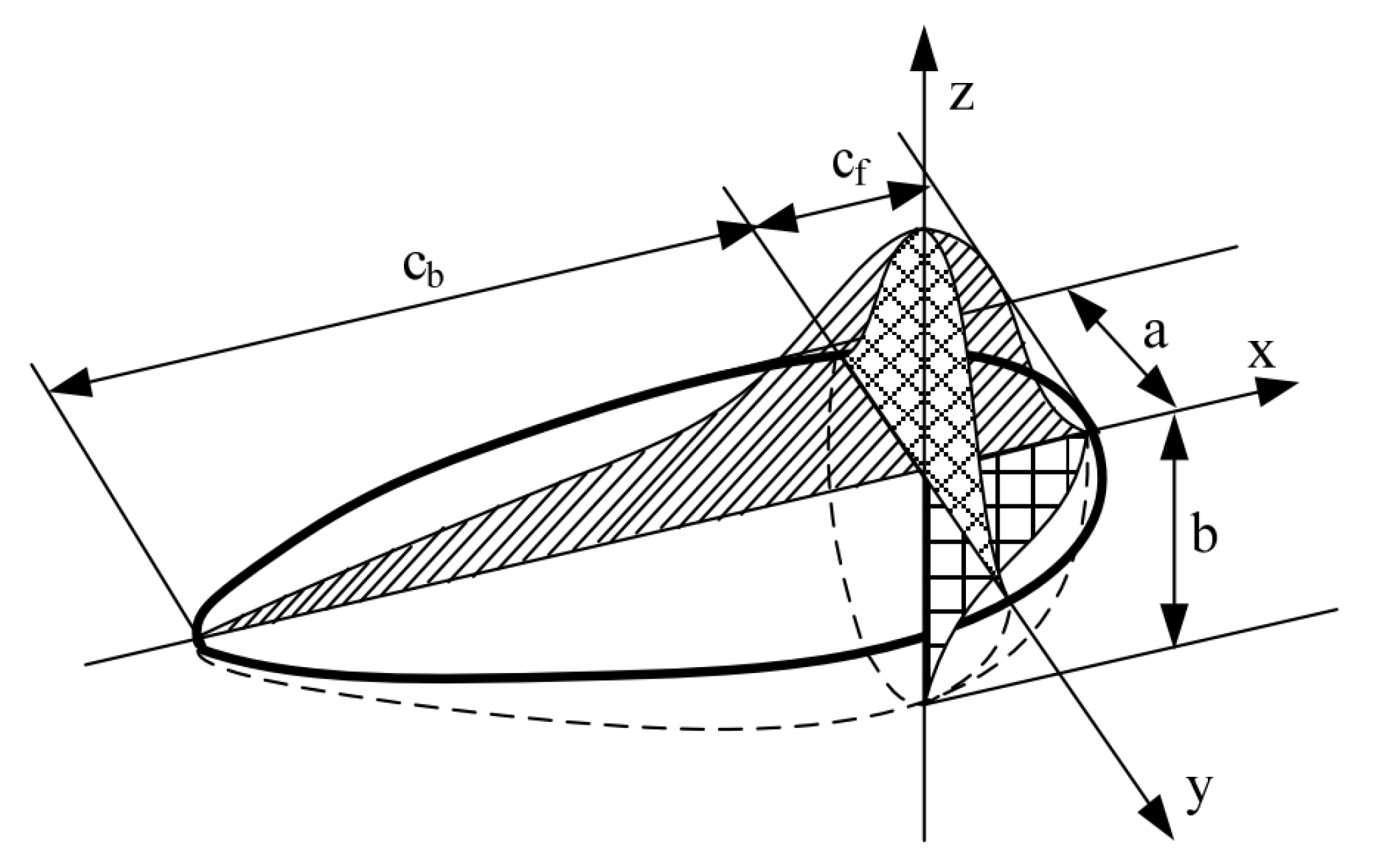
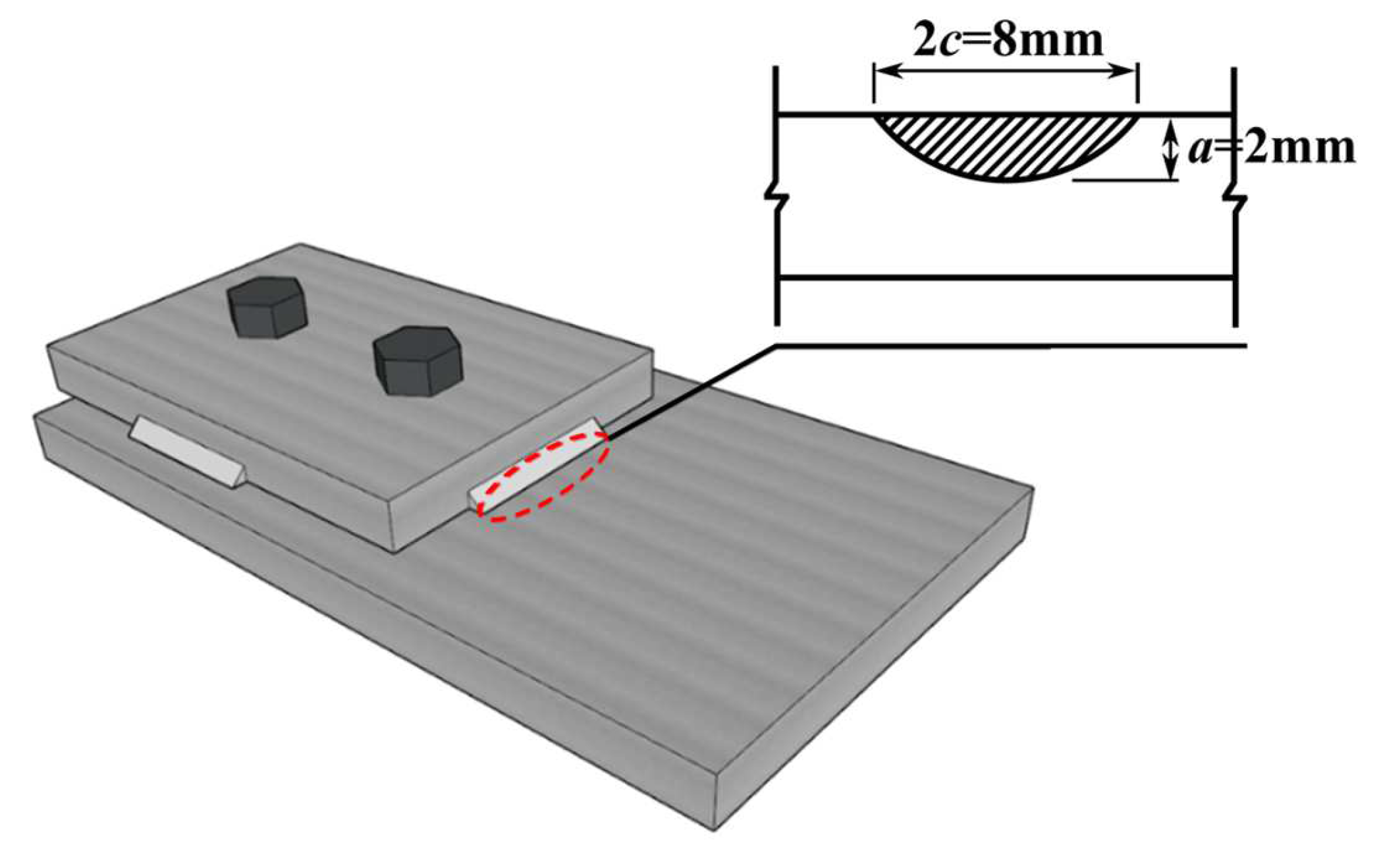
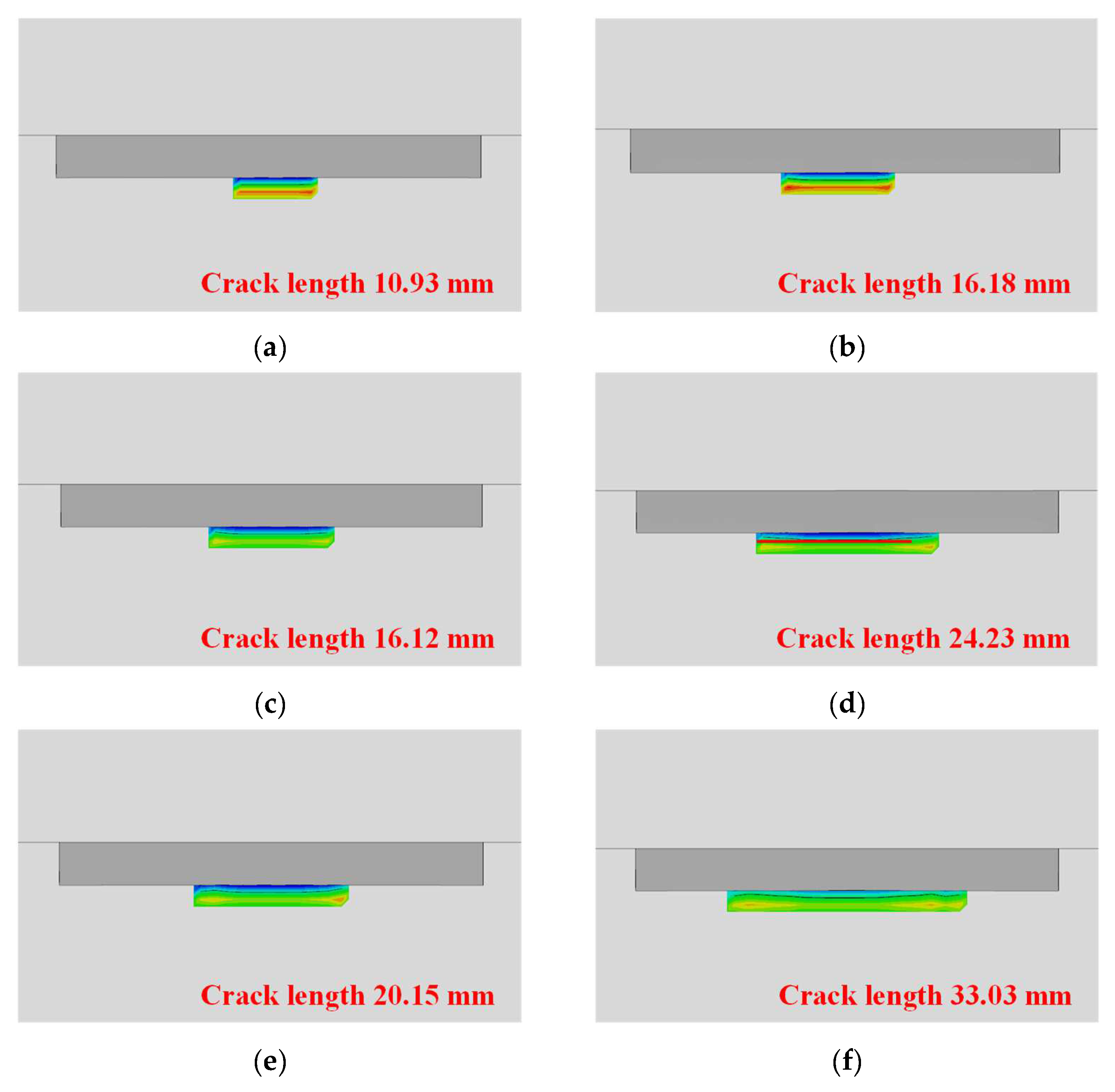
6.1. Finite Element Model with Initial Fatigue Crack
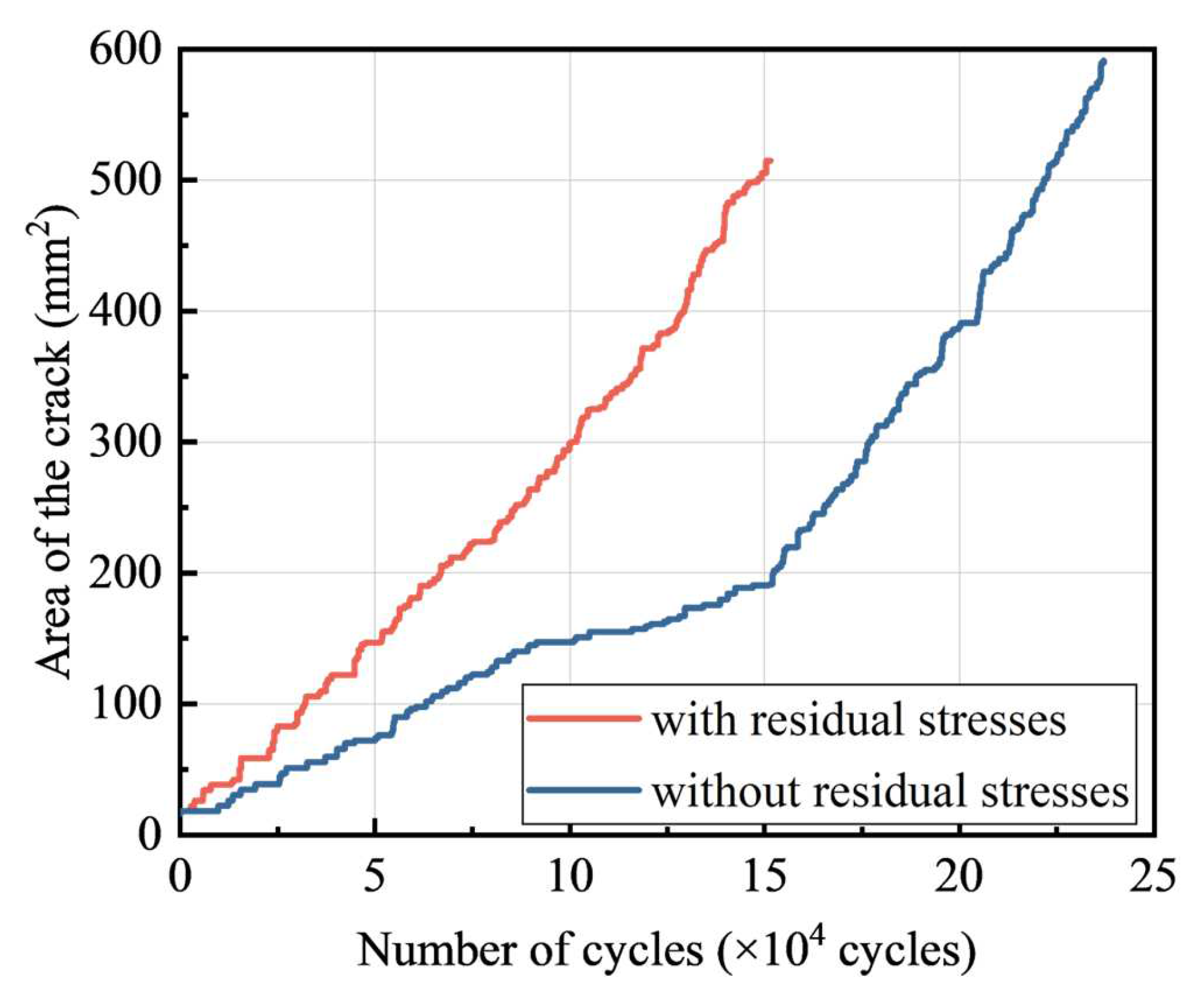
6.2. Effects of Residual Stresses on Crack Propagation
7. Summary and Conclusions
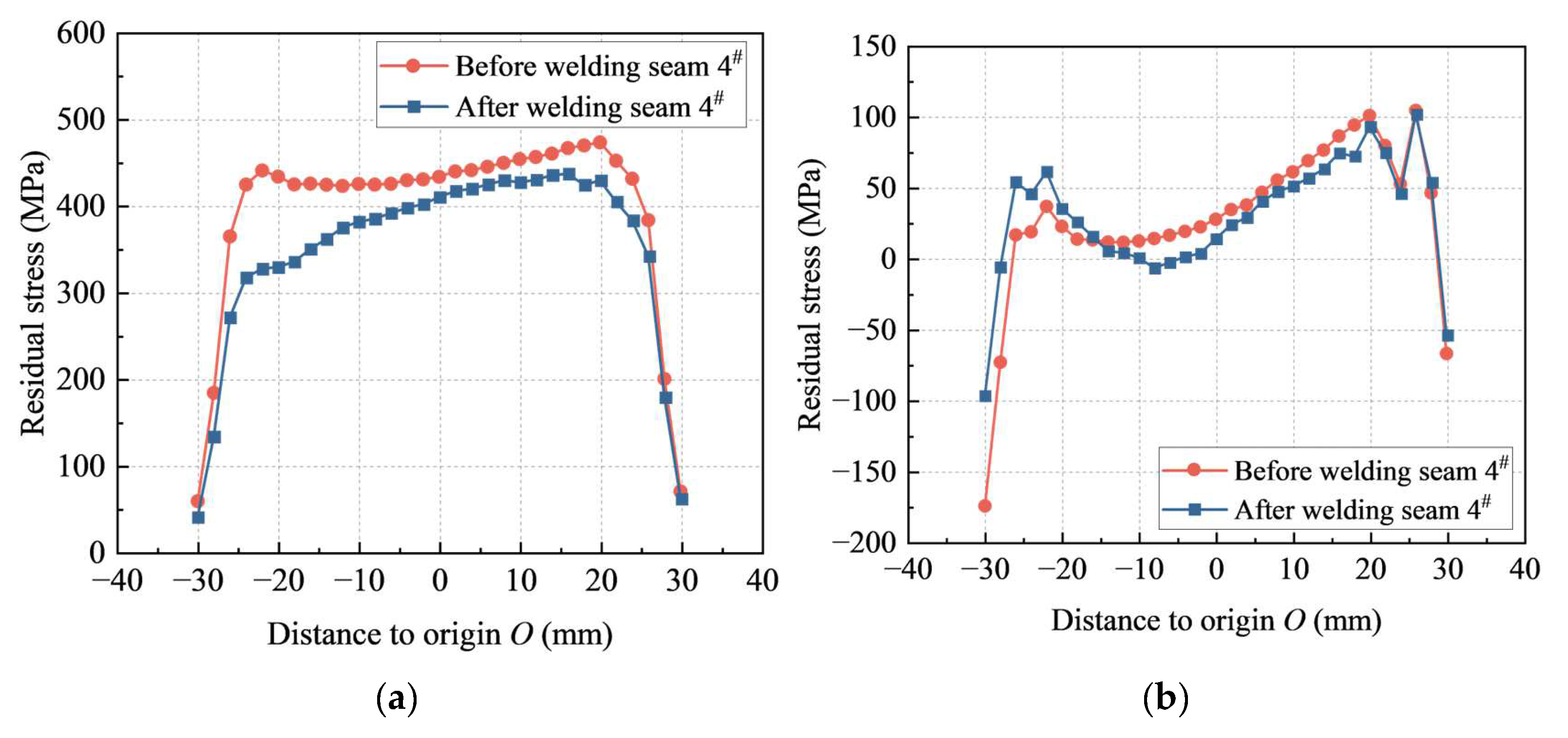
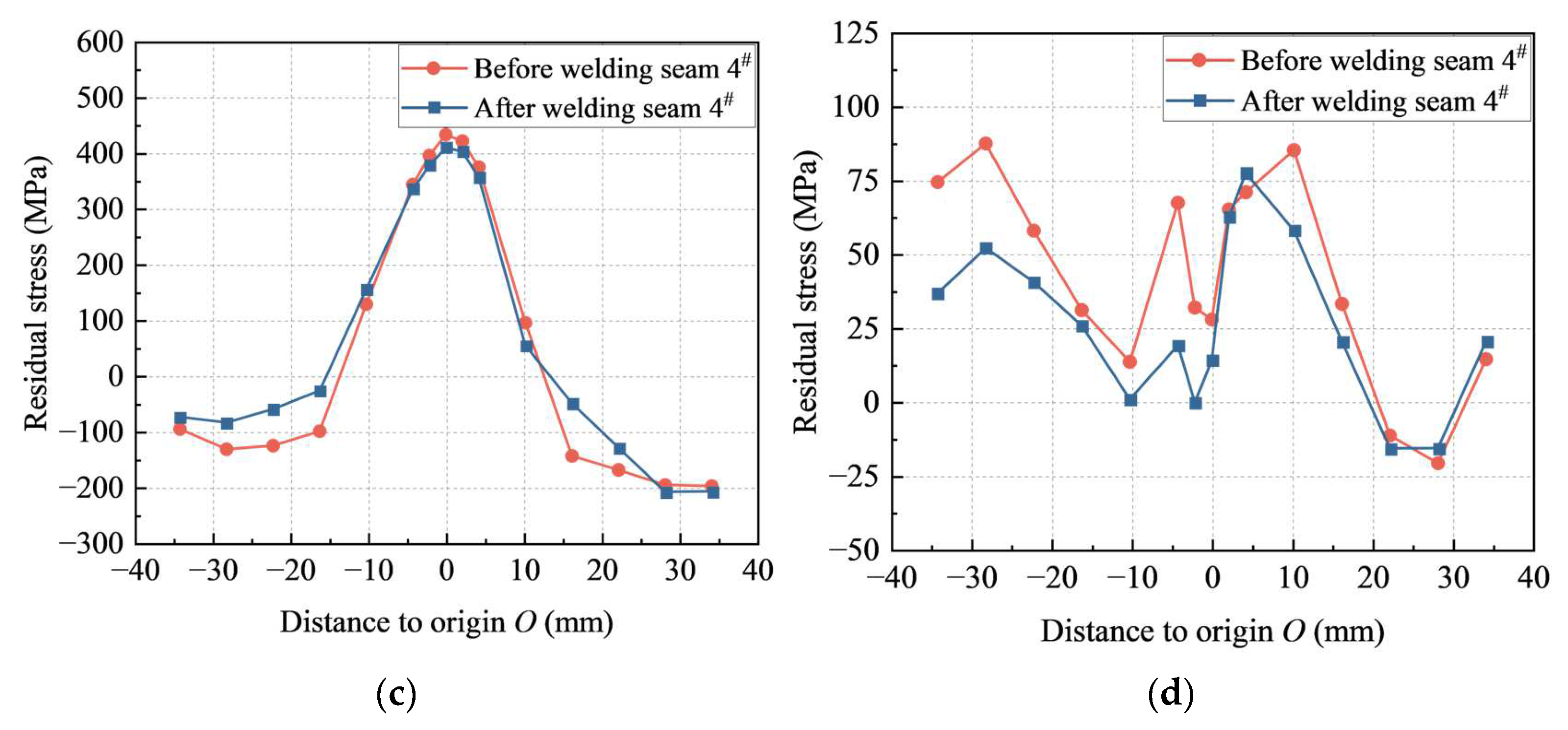
- The measured residual stresses along path 1 at a distance of 6 mm away from the longitudinal fillet weld toe showed that both the longitudinal and transverse residual stresses were basically symmetrically distributed, while the longitudinal and transverse residual stresses were generally compressive and tensile, respectively. Also, they revealed that welding seam 4# had significant effects on the residual stresses along seam 1#.
- A finite element model of combined bolted–welded joints to evaluate the residual stress was developed and validated against the test results, with an average difference of 13%. This suggested that the developed finite element model could accurately capture the residual stresses.
- For different welding sequences, the maximum residual stress was approximately 450 MPa, far exceeding the yield strength of steel plates of 335 MPa. The order was as follows: welding sequence 1 < welding sequence 2 ≈ welding sequence 3 < welding sequence 4.
- For different welding speeds, the deformation caused by the welding temperature occurred only in a relatively small area, and the ability for synchronized expansion and contraction deformation was weaker, resulting in a larger residual stress. A higher heat input caused the material to remain at high temperatures for a longer period, resulting in greater plastic deformation and larger residual stress upon cooling. Post-weld holding, as an effective heat treatment method, had a significant stress-relieving effect on the residual stress.
- Due to the presence of welding residual stresses, the fatigue life of combined bolted–welded joints was reduced by nearly 40%. This indicated that the fatigue life of the joint would be overestimated without considering the residual stresses.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shi, Y.J.; Wang, L.; Wang, Y.Q.; Ma, J.S.; Bai, R.S. Proposed design method of combined connections with bolts and longitudinal welds. Appl. Mech. Mater. 2011, 94, 923–928. [Google Scholar] [CrossRef]
- Shi, Y.J.; Wang, L.; Wang, Y.Q.; Ma, J.S.; Bai, R.S. Finite element analysis of the combined connection with bolts and welds. Appl. Mech. Mater. 2011, 94, 316–321. [Google Scholar] [CrossRef]
- Ma, J.S.; Bai, R.S.; Li, M.F.; Wang, Y.Q.; Wang, L.; Shi, Y.J. Finite element analysis of the influence of weld size on the combined connection with bolts and welds. Appl. Mech. Mater. 2014, 578, 1276–1280. [Google Scholar] [CrossRef]
- Waite, C.D.; Shen, L.; Soliman, M.; Russell, B.W. Experimental investigation into the capacity of concentrically loaded steel connections with pretensioned high-strength bolts and longitudinal fillet welds in combination. Eng. J. 2022, 59, 159–182. [Google Scholar] [CrossRef]
- Kulak, G.L.; Grondin, G.Y. Strength of joints that combine bolts and welds. Eng. J. 2003, 40, 89–98. [Google Scholar] [CrossRef]
- Manuel, T.J.; Kulak, G.L. Strength of joints that combine bolts and welds. J. Struct. Eng. 2000, 126, 279–287. [Google Scholar] [CrossRef]
- Jarosch, K.; Bowman, M.D. Tension butt joints with bolts and welds in combination. Eng. J. 1986, 23, 25–34. [Google Scholar] [CrossRef]
- Kim, D.K.; Lee, C.H. Generalized load deformation relationship for bearing-type single-bolted connections. J. Struct. Eng. 2020, 146, 04020116. [Google Scholar] [CrossRef]
- Liu, M.S.; Li, C.A.; Huang, J.R.; Ju, J.S. Numerical modeling and mechanical analysis of combined connection with bolts and welds. Strength Mater. 2016, 48, 862–869. [Google Scholar] [CrossRef]
- Tamimi, M.F.; Soliman, M.; Stringer, E.; Russell, B.W. Investigating the behavior and reliability of eccentrically loaded steel connections made with bolts and welds in combination. J. Struct. Eng. 2023, 149, 04023164. [Google Scholar] [CrossRef]
- Khandel, O.; Tamimi, M.F.; Soliman, M.; Russell, B.W.; Waite, C.D. Reliability assessment of connections with slip-critical bolts and fillet welds in combination. J. Constr. Steel Res. 2022, 188, 107036. [Google Scholar] [CrossRef]
- Kim, D.K.; Lee, C.H. Experimental and analytical study of combined bolted-welded lap joints including high-strength steel. J. Constr. Steel Res. 2020, 168, 105995. [Google Scholar] [CrossRef]
- Yokozeki, K.; Evers, T.; Vallée, T. Hybrid joints consisting of pre-tensioned bolts and a bonded connection—The influence of adhesives on the load-bearing capacity. Int. J. Adhes. Adhes. 2024, 132, 103689. [Google Scholar] [CrossRef]
- Acevedo, C.; Evans, A.; Nussbaumer, A. Neutron diffraction investigations on residual stresses contributing to the fatigue crack growth in ferritic steel tubular bridges. Int. J. Press. Vessels Pip. 2012, 95, 31–38. [Google Scholar] [CrossRef]
- Cui, C.; Zhang, Q.; Luo, Y.; Hao, H.; Li, J. Fatigue reliability evaluation of deck-to-rib welded joints in OSD considering stochastic traffic load and welding residual stress. Int. J. Fatigue 2018, 111, 151–160. [Google Scholar] [CrossRef]
- Cui, C.; Zhang, Q.; Bao, Y.; Bu, Y.; Luo, Y. Fatigue life evaluation of welded joints in steel bridge considering residual stress. J. Constr. Steel Res. 2019, 153, 509–518. [Google Scholar] [CrossRef]
- Ding, Y.; Zhong, W.; Sun, P.; Cao, B.; Song, Y. Fatigue life evaluation of welded joints in OSD for railway bridges considering welding residual stress. J. Perform. Constr. Facil. 2019, 33, 04018111. [Google Scholar] [CrossRef]
- Ding, Y.L.; Song, Y.S.; Cao, B.Y.; Wang, G.X.; Li, A.Q. Full-range S-N fatigue-life evaluation method for welded bridge structures considering hot-spot and welding residual stress. J. Bridge Eng. 2016, 21, 04016096. [Google Scholar] [CrossRef]
- Zhong, W.; Song, Y.; Ding, Y.; Fang, Z. A simplified method for fatigue life evaluation of welded joints in OSD considering welding residual stress relaxation. Structures 2023, 47, 165–176. [Google Scholar] [CrossRef]
- Van Den Berg, N.; Xin, H.H.; Veljkovic, M. Effects of residual stresses on fatigue crack propagation of an orthotropic steel bridge deck. Mater. Des. 2021, 198, 109294. [Google Scholar] [CrossRef]
- Qiang, B.; Li, Y.; Yao, C.; Wang, X. Through-thickness welding residual stress and its effect on stress intensity factors for semi-elliptical surface cracks in a butt-welded steel plate. Eng. Fract. Mech. 2018, 193, 17–31. [Google Scholar] [CrossRef]
- Choudhury, S.; Medhi, T.; Sethi, D.; Kumar, S.; Roy, B.S.; Saha, S.C. Temperature distribution and residual stress in Friction Stir Welding process. Mater. Today Proc. 2020, 26, 2296–2301. [Google Scholar] [CrossRef]
- Zhu, C.Y.; Li, H.; Huang, C.Q.; Luo, C.G.; Song, Y.L. Study on residual stress distribution of 2219 aluminum alloy. Trans. China Weld. Inst. 2017, 38, 32–36. [Google Scholar]
- Luo, W.Z.; Cheng, H.M.; Liu, H.Y.; Wang, Y.; Ye, Y.; Deng, D. Numerical Simulation of Residual Stress and Welding Deformation for High-Strength Steel Q960E Butt-Welded Joints. China Mech. Eng. 2023, 34, 2095–2105. [Google Scholar]
- Deng, D.; Murakawa, H. Numerical simulation of temperature field and residual stress in multi-pass welds in stainless steel pipe and comparison with experimental measurements. Comput. Mater. Sci. 2006, 37, 269–277. [Google Scholar] [CrossRef]
- Shariyat, M.; Asemi, K. 3D B-spline finite element nonlinear elasticity buckling analysis of rectangular FGM plates under non-uniform edge loads, using a micromechanical model. Compos. Struct. 2014, 112, 397–408. [Google Scholar] [CrossRef]
- Mondal, A.K.; Biswas, P.; Bag, S. Experimental and FE analysis of submerged arc weld induced residual stress and angular deformation of single and double sided fillet welded joint. Int. J. Steel Struct. 2017, 17, 9–18. [Google Scholar] [CrossRef]
- Barsoum, Z.; Barsoum, I. Residual stress effects on fatigue life of welded structures using LEFE. Eng. Fail. Anal. 2009, 16, 449–467. [Google Scholar] [CrossRef]
- Kollár, D. Numerical modelling on the influence of repair welding during manufacturing on residual stresses and distortions of T-joints. Results Eng. 2023, 20, 101535. [Google Scholar] [CrossRef]
- Qiang, B.; Li, Y.; Yao, C.; Wang, X.; Gu, Y. Through-thickness distribution of residual stresses in Q345qD butt-welded steel plates. J. Mater. Process. Technol. 2018, 251, 54–64. [Google Scholar] [CrossRef]
- Ghafouri, M.; Ahola, A.; Ahn, J.; Björk, T. Numerical and experimental investigations on the welding residual stresses and distortions of the short fillet welds in high strength steel plates. Eng. Struct. 2022, 260, 114269. [Google Scholar] [CrossRef]
- Gadallah, R.; Tsutsumi, S.; Yonezawa, T.; Shimanuki, H. Residual stress measurement at the weld root of rib-to-deck welded joints in orthotropic steel bridge decks using the contour method. Eng. Struct. 2020, 219, 110946. [Google Scholar] [CrossRef]
- Kollár, D.; Völgyi, I.; Joó, A. Development of residual stress model of orthotropic steel decks using measurements. Structures 2023, 58, 105601. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, R.; Zhang, S.; Chen, G.; Fu, J.; Wang, T. Experimental study on the welding residual stresses of integral joint using full-scale joint model of a steel truss bridge. Adv. Struct. Eng. 2013, 16, 1719–1727. [Google Scholar] [CrossRef]
- Gadallah, R.; Tsutsumi, S.; Tanaka, S.; Osawa, N. Accurate evaluation of fracture parameters for a surface-cracked tubular T-joint taking welding residual stress into account. Mar. Struct. 2020, 71, 102733. [Google Scholar] [CrossRef]
- Jin, D.; Hou, C.; Shen, L. Effect of welding residual stress on the performance of CFST tubular joints. J. Constr. Steel Res. 2021, 184, 106827. [Google Scholar] [CrossRef]
- Cao, Y.; Meng, Z.; Zhang, S.; Tian, H. FEM study on the stress concentration factors of K-joints with welding residual stress. Appl. Ocean. Res. 2013, 43, 195–205. [Google Scholar] [CrossRef]
- GB/T 1231-2006; Specifications of High Strength Bolts with Large Hexagon Head, Large Hexagon Nuts, Plain Washers for Steel Structures. Standards Press of China: Beijing, China, 2006.
- GB/T 1591-2018; High Strength Low Alloy Structural Steels. Standards Press of China: Beijing, China, 2018.
- GB 50661-2011; Code for Welding of Steel Structures. China Architecture & Building Press: Beijing, China, 2011.
- GB/T 11345-2023; Non-Destructive Testing of Welds—Ultrasonic Testing—Techniques, Testing Levels and Assessment. Standards Press of China: Beijing, China, 2023.
- Jiang, L.; Liu, Y.; Fam, A.; Liu, B.; Pu, B.; Zhao, R. Experimental and numerical analyses on stress concentration factors of concrete-filled welded integral K-joints in steel truss bridges. Thin-Walled Struct. 2023, 183, 110347. [Google Scholar] [CrossRef]
- Jiang, L.; Liu, Y.; Fam, A. Stress concentration factors in concrete-filled square hollow section joints with perfobond ribs. Eng. Struct. 2019, 181, 165–180. [Google Scholar] [CrossRef]
- Jiang, L.; Liu, Y.; Fam, A.; Liu, J.; Liu, B. Stress concentration factor parametric formulae for concrete-filled rectangular hollow section K-joints with perfobond ribs. J. Constr. Steel Res. 2019, 160, 579–597. [Google Scholar] [CrossRef]
- Deng, D.; Murakawa, H. Prediction of welding distortion and residual stress in a thin plate butt-welded joint. Comput. Mater. Sci. 2008, 43, 353–365. [Google Scholar] [CrossRef]
- Zhang, Y.; Su, W.; Dong, H.; Li, T.; Cao, H. Effect of welding sequence and constraint on the residual stress and deformation of thick welded butt joint made of Q345qD steel. Adv. Civ. Eng. 2022, 2022, 5966274. [Google Scholar] [CrossRef]
- Goldak, J.; Aditya, C.; Malcolm, B. A new finite element model for welding heat sources. Metall. Trans. B 1984, 15, 299–305. [Google Scholar] [CrossRef]
- Ravisankar, A.; Velaga, S.K.; Rajput, G.; Venugopal, S. Influence of welding speed and power on residual stress during gas tungsten arc welding (GTAW) of thin sections with constant heat input: A study using numerical simulation and experimental validation. J. Manuf. Process. 2014, 16, 200–211. [Google Scholar] [CrossRef]
- Patel, S.; Patel, B.P.; Ahmad, S. Estimation of Residual Stresses in Steel Welded Joints Using Three Dimensional Finite Element Analysis. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Madrid, Spain, 17–22 June 2018; American Society of Mechanical Engineers: New York, NY, USA, 2018; p. 51265. [Google Scholar]
- Javadi, Y.; Azari, K.; Ghalehbandi, S.M.; Roy, M.J. Comparison between using longitudinal and shear waves in ultrasonic stress measurement to investigate the effect of post-weld heat-treatment on welding residual stresses. Res. Nondestruct. Eval. 2017, 28, 101–122. [Google Scholar] [CrossRef]
- Li, X.; Fu, Z.; Cui, J.; Ji, B. Effect of Post-Weld heat treatment on residual stress in deck-rib double-side welded joints and process optimization. Eng. Fail. Anal. 2024, 164, 108731. [Google Scholar] [CrossRef]
- Hobbacher, A.F. Recommendations for Fatigue Design of Welded Joints and Components; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar]













Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Jiang, L.; Cheng, G.; Liu, J.; Xu, B.; Jin, R. Residual Stress Distribution and Fatigue Behavior of Combined Bolted–Welded Joints. Buildings 2025, 15, 910. https://doi.org/10.3390/buildings15060910
Liu X, Jiang L, Cheng G, Liu J, Xu B, Jin R. Residual Stress Distribution and Fatigue Behavior of Combined Bolted–Welded Joints. Buildings. 2025; 15(6):910. https://doi.org/10.3390/buildings15060910
Chicago/Turabian StyleLiu, Xiaoguang, Lei Jiang, Gao Cheng, Jun Liu, Banghao Xu, and Ruibao Jin. 2025. "Residual Stress Distribution and Fatigue Behavior of Combined Bolted–Welded Joints" Buildings 15, no. 6: 910. https://doi.org/10.3390/buildings15060910
APA StyleLiu, X., Jiang, L., Cheng, G., Liu, J., Xu, B., & Jin, R. (2025). Residual Stress Distribution and Fatigue Behavior of Combined Bolted–Welded Joints. Buildings, 15(6), 910. https://doi.org/10.3390/buildings15060910






