Dynamic Mechanical Properties and Deformation Mechanisms of Lightweight High-Strength TWIP Steel
Abstract
1. Introduction
2. Materials and Methods
2.1. Material
2.2. Experiment Method
3. Results and Discussion
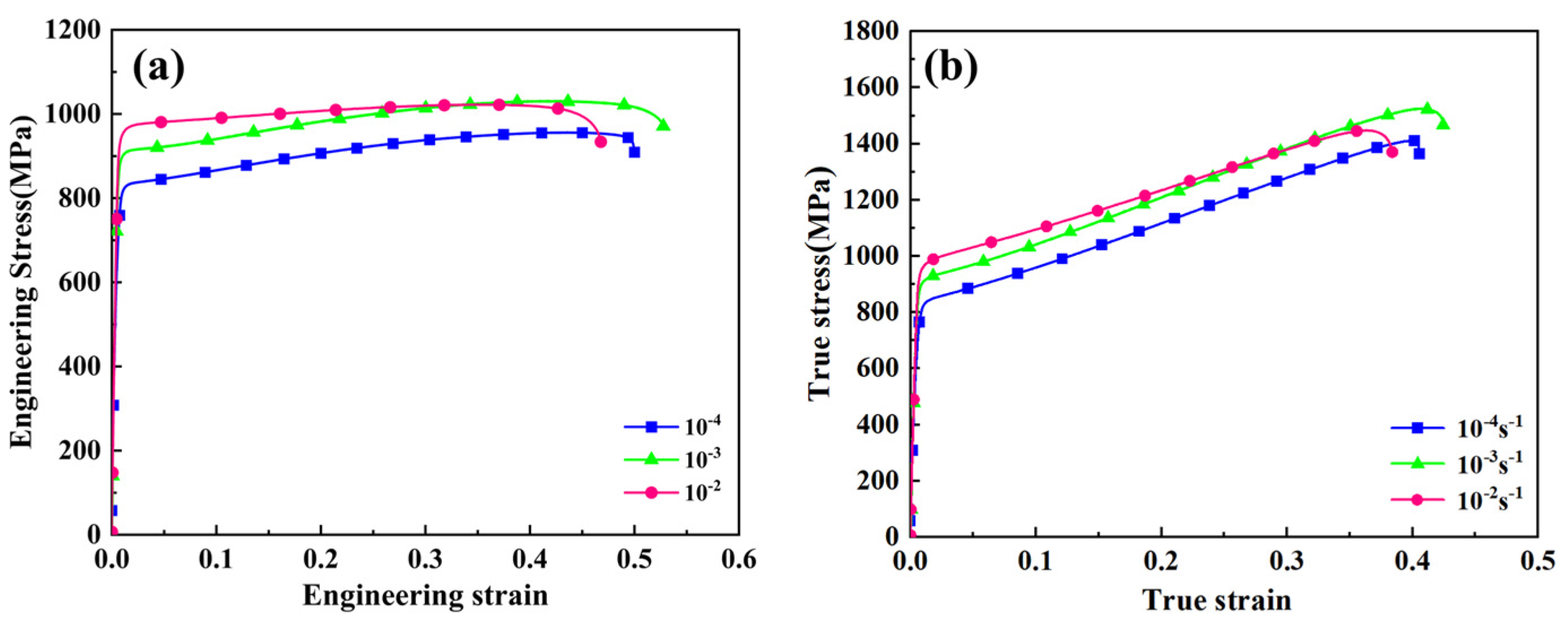
3.1. Quasi-Static Mechanical Properties
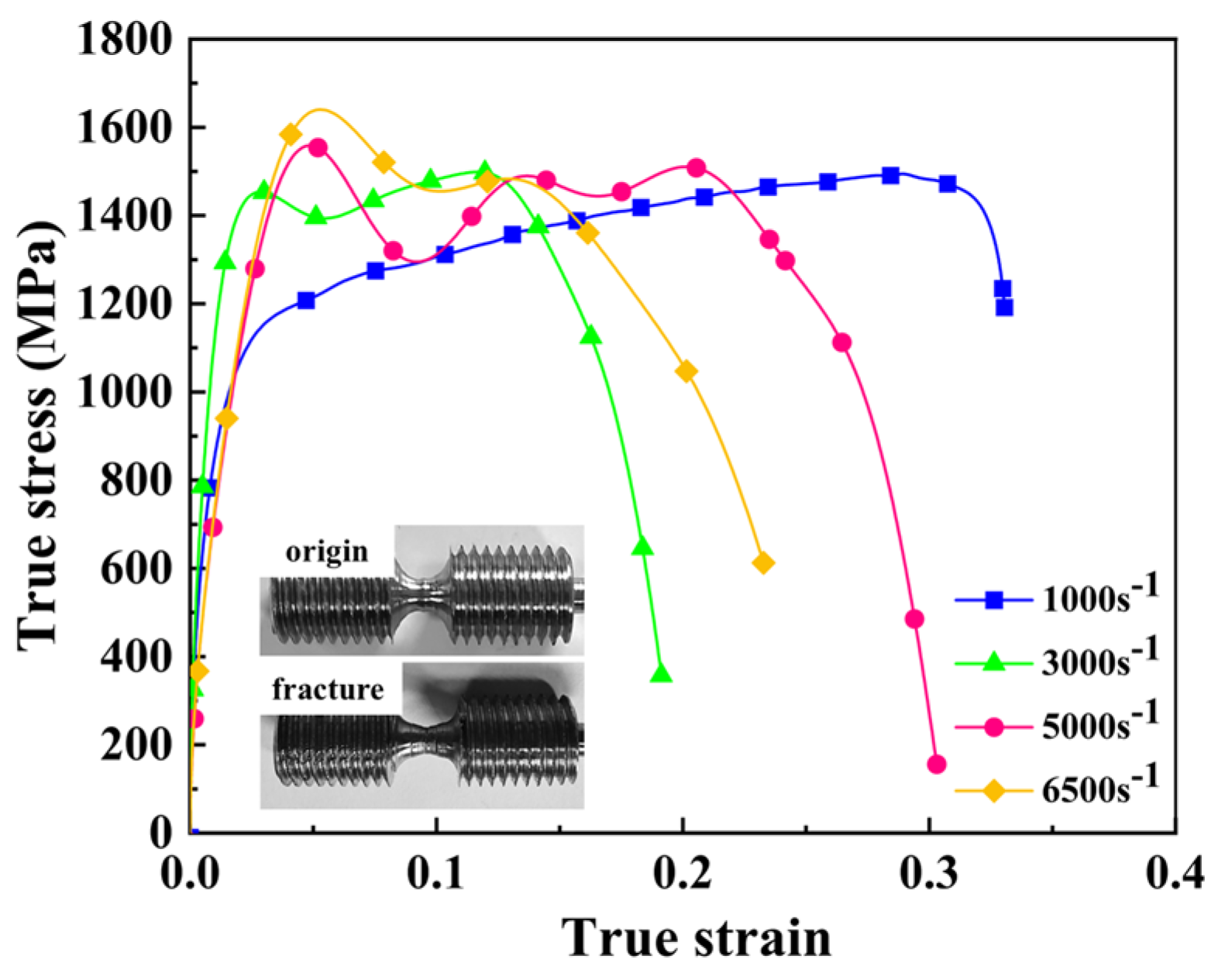
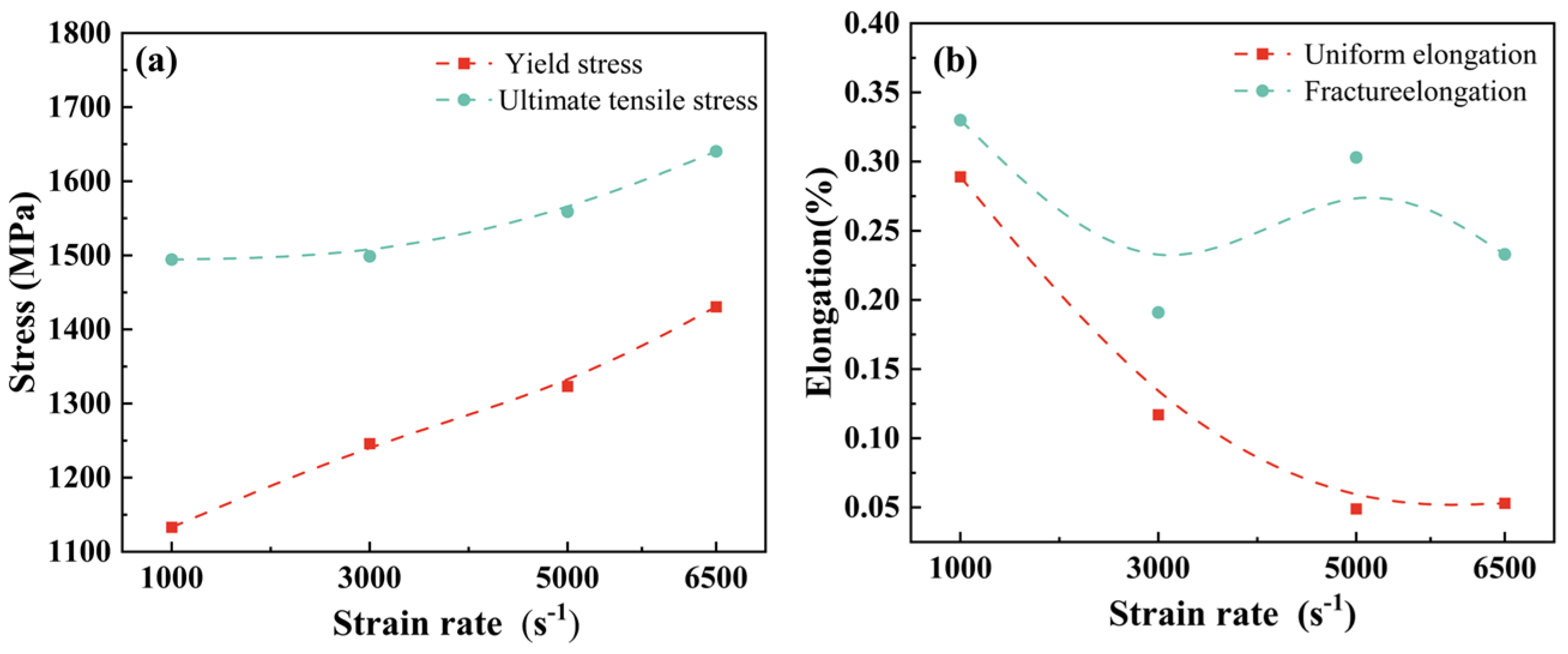
3.2. Dynamic Mechanical Properties
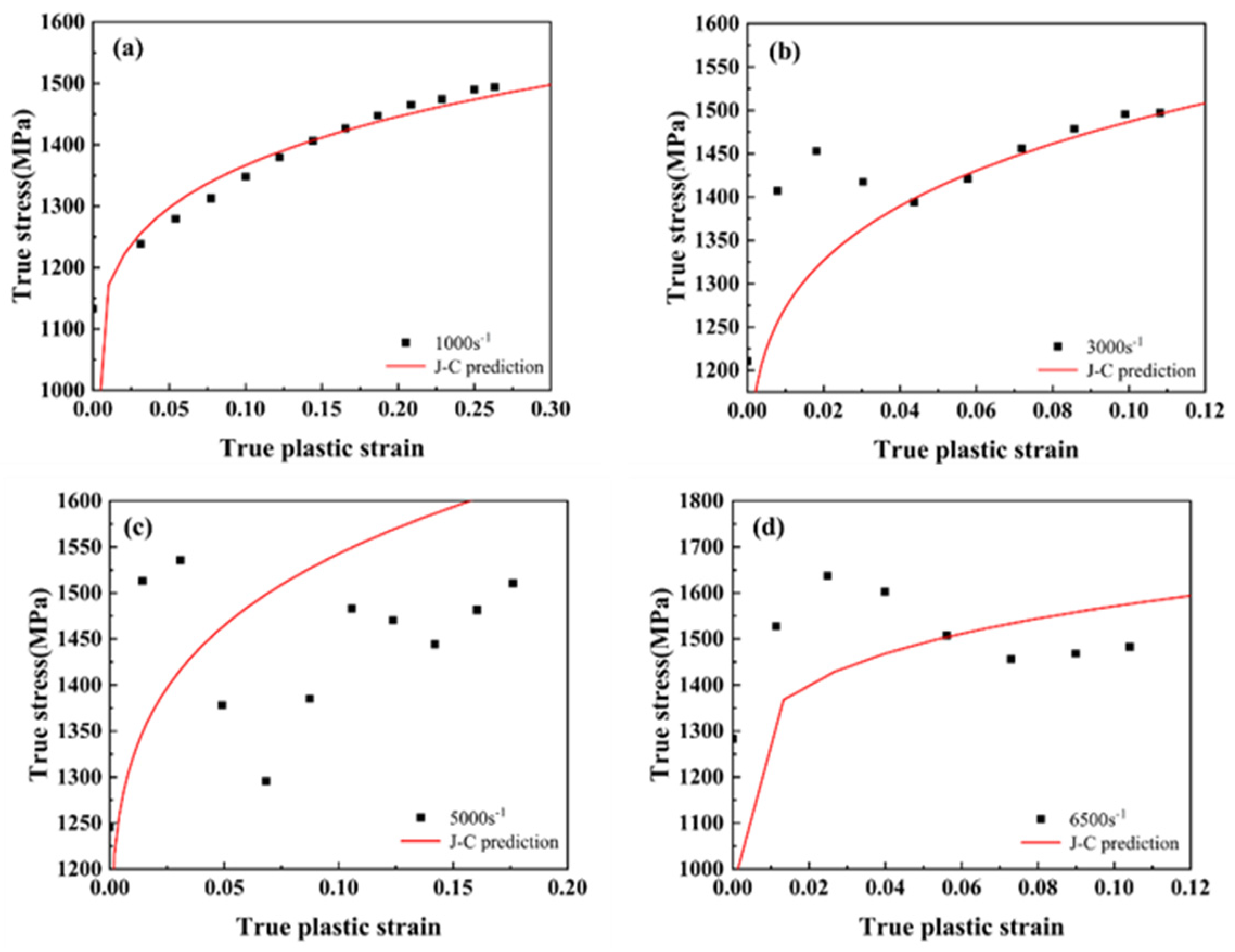
3.3. Fitting of the Material’s Johnson–Cook Constitutive Model
3.4. Fracture Failure Modes
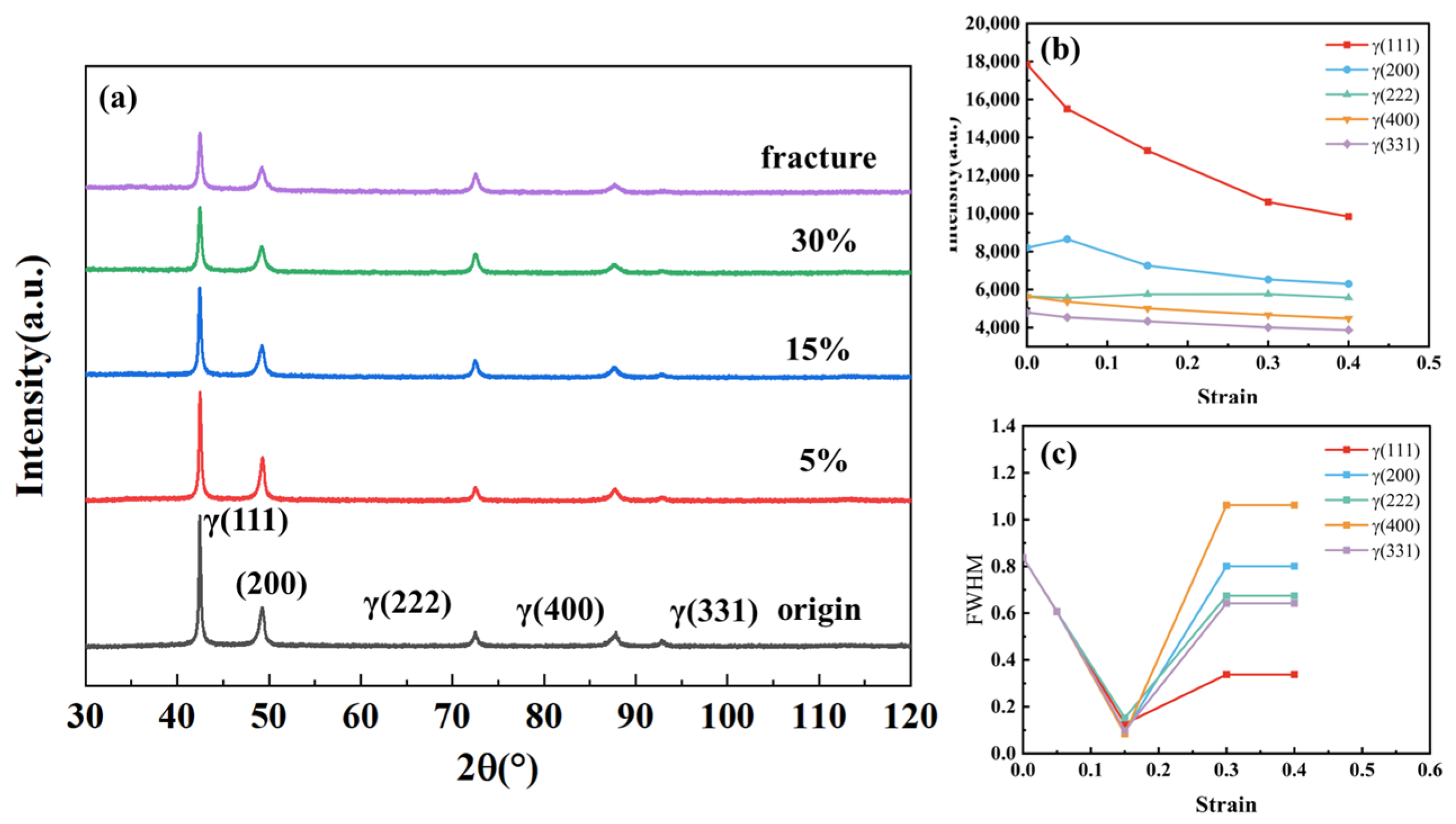
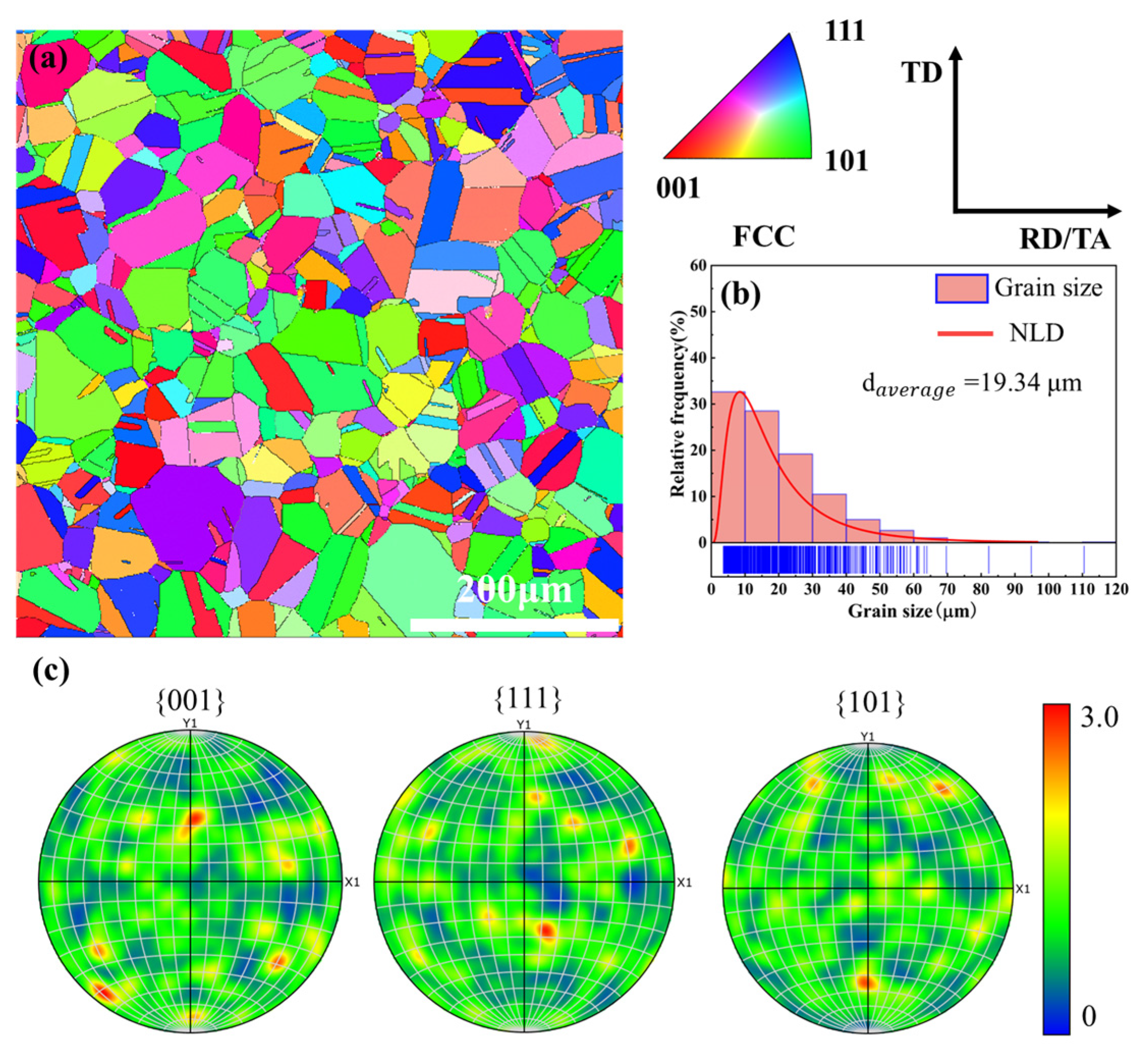
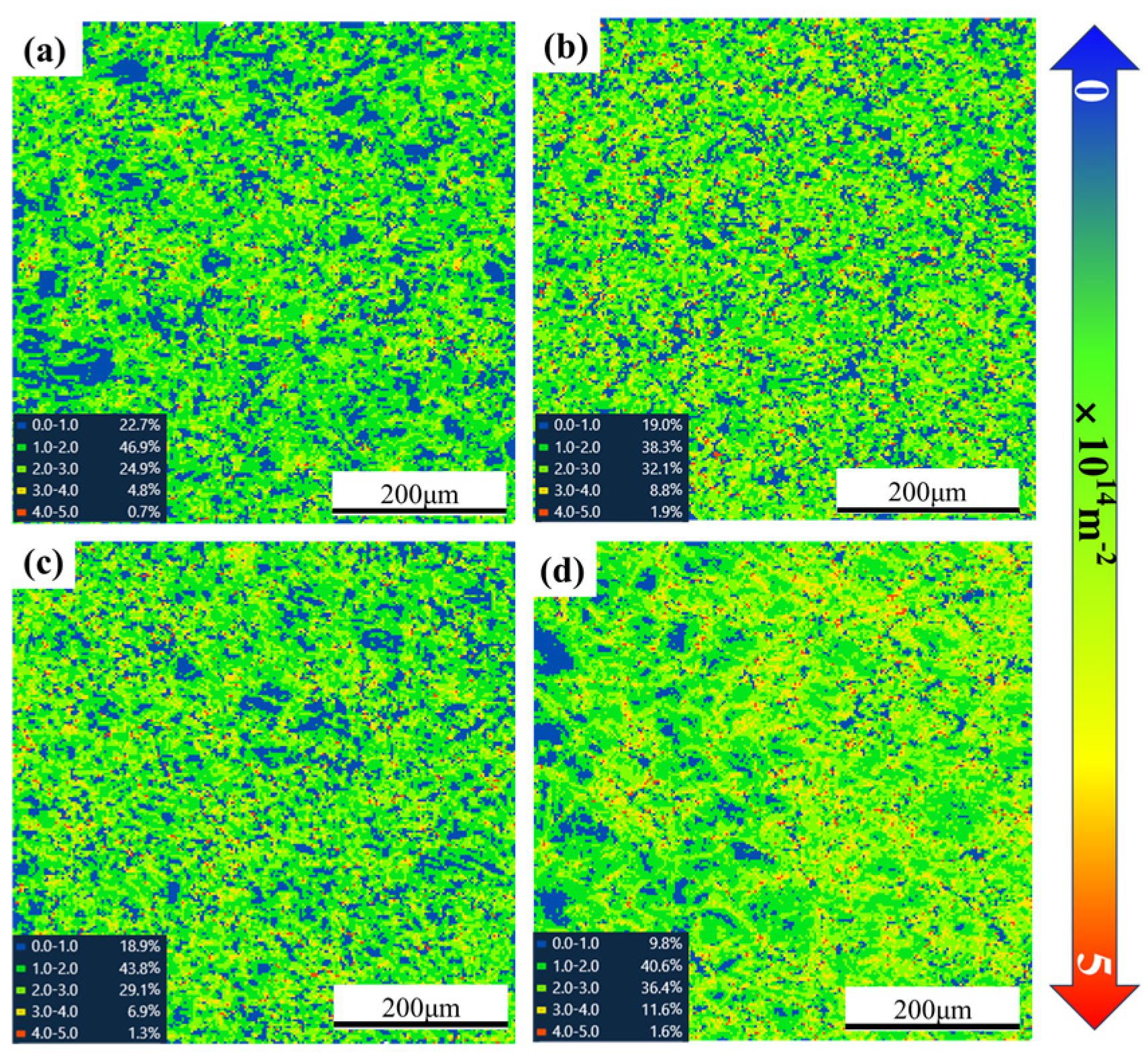
3.5. Microstructural Evolution and Deformation Mechanisms
4. Conclusions
- (1)
- Fe-Mn-Al-Ni-C TWIP steel maintains a single phase throughout varying strain conditions, suggesting that tensile deformation is characterized solely by twinning.
- (2)
- TWIP steel demonstrates PSRS under both quasi-static and dynamic conditions. Plasticity diminishes with increasing strain rate, with 5000 s−1 marking a critical point for enhanced plasticity and superior overall mechanical properties.
- (3)
- Macroscopic fracture morphology evolves with strain rate, yet the microscopic fracture mechanism remains ductile across all rates. At 5000 s−1, Fe and Mn oxides are evenly dispersed within the matrix near the dimples, contributing to plastic strengthening.
- (4)
- The J-C material constitutive equation obtained through multi-parameter fitting cannot ignore the temperature term. This is due to the complex competitive relationship between strain hardening and thermal softening effects during the deformation process of TWIP steel.
- (5)
- The twinning mechanism is more active at high strain rates compared to quasi-static conditions. As the strain rate increases, dislocations near grain boundaries and twins become increasingly entangled, leading to a rise in dislocation density. This promotes twin nucleation near grain boundaries. At a strain rate of 5000 s−1, secondary twin systems can be activated, resulting in grain refinement and further hindering dislocation slip, thereby enhancing strength.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Grässel, O.; Krüger, L.; Frommeyer, G.; Meyer, L. High strength Fe-Mn-(Al, Si) TRIP/TWIP steels development—Properties—Application. Int. J. Plast. 2000, 16, 1391–1409. [Google Scholar] [CrossRef]
- Chowdhury, P.; Canadinc, D.; Sehitoglu, H. On deformation behavior of Fe-Mn based structural alloys. Mater. Sci. Eng. R 2017, 122, 1–28. [Google Scholar] [CrossRef]
- Mintz, B.; Qaban, A. The Influence of Precipitation, High Levels of Al, Si, P and a Small B Addition on the Hot Ductility of TWIP and TRIP Assisted Steels: A Critical Review. Metals 2022, 12, 502. [Google Scholar] [CrossRef]
- Qin, X.M.; Chen, L.Q.; Deng, W.; Di, H.S. Effect of strain rate on mechanical properties of Fe-23Mn-2Al-0.2C TWIP steel. CJMR 2011, 25, 278–282. (In Chinese) [Google Scholar]
- Deng, J.H.; Li, C.W.; Wang, Z.Y.; Tong, W.; Wu, Q.Y. Effect of post-weld heat treatment on microstructure and mechanical properties of twinning-induced plasticity (TWIP) steel joints. Mater. Today Commun. 2024, 40, 109720. [Google Scholar] [CrossRef]
- Xu, J.P.; Wang, Z.; Yan, Y.; Li, J.X.; Wu, M. Effect of hot/warm rolling on the microstructures and mechanical properties of medium-Mn steels. Mater. Charact. 2020, 170, 110682. [Google Scholar] [CrossRef]
- Wesselmecking, S.; Kreins, M.; Dahmen, M.; Bleck, W. Material oriented crash-box design—Combining structural and material design to improve specific energy absorption. Mater. Des. 2022, 213, 110357. [Google Scholar] [CrossRef]
- Fajardo, S.; Llorente, I.; Jiménez, J.A.; Bastidas, J.M.; Bastidas, D.M. Effect of Mn additions on the corrosion behaviour of TWIP Fe-Mn-Al-Si austenitic steel in chloride solution. Corros. Sci. 2019, 154, 246–253. [Google Scholar] [CrossRef]
- Wang, Y.N.; Li, Q.; He, Y.L.; Fu, R.Y.; Li, L. Microstructure and properties of high strength and high plasticity TWIP steel. Heat Treat. 2006, 154, 25–30. (In Chinese) [Google Scholar]
- Liu, X.H.; Liu, W.; Liu, J.B.; Shu, K.Y. Research status of twin-induced plasticity (TWIP) steel. Mater. Rep. 2010, 11, 102–105. (In Chinese) [Google Scholar]
- Madivala, M.; Schwedt, A.; Wong, S.L.; Roters, F.; Prahl, U.; Bleck, W. Temperature dependent strain hardening and fracture behavior of TWIP steel. Int. J. Plast. 2018, 104, 80–103. [Google Scholar] [CrossRef]
- Cui, X.W.; Zhang, G.J.; Lin, S.F. Effect of Mn content on microstructure and properties of hot rolled TWIP steel. Cailiao Rechuli Xuebao 2022, 43, 92–98. (In Chinese) [Google Scholar] [CrossRef]
- An, Y.F.; Chen, X.P.; Mei, L.; Ren, P.; Wei, D.; Cao, W.Q. Precipitation transformation pathway and mechanical behavior of nanoprecipitation strengthened Fe-Mn-Al-C-Ni austenitic low-density steel. J. Mater. Sci. Technol. 2024, 7, 157–167. [Google Scholar] [CrossRef]
- Guo, P.C.; Qian, L.H.; Meng, J.Y.; Liu, S.; Zhang, F. Effect of Al on the low cycle fatigue deformation behavior and microstructure evolution of Fe-22Mn-0.6C TWIP steel. JMR&T 2024, 30, 2086–2098. [Google Scholar] [CrossRef]
- Chu, C.M.; Huang, H.; Kao, P.W.; Gan, D. Effect of alloying chemistry on the lattice constant of austenitic Fe-Mn-Al-C alloys. Scr. Metall. Mater. 1994, 30, 505–508. [Google Scholar] [CrossRef]
- Yang, Z.B.; Zhu, D.Y.; Yi, W.F.; Lin, S.M. Effect of carbon content on strain hardening behavior of Fe-Ni-Mn-Si-C TWIP steels. Iron Steel 2011, 46, 69–73. [Google Scholar]
- Wen, H.Y.; Zhu, D.Y.; Wang, M.J.; Qiao, W.; Liao, L. Effect of carbon content on microstructure and mechanical properties of new Fe-Ni-Mn-Si-C TWIP steel. Iron Steel 2010, 45, 74–78. [Google Scholar]
- Akinay, Y.; Hayat, F. Effect of Ni on the mechanical behavior of a high-Mn austenitic TWIP steel. Mater. Test. 2016, 58, 413–417. [Google Scholar] [CrossRef]
- Wang, Y.C.; Lan, P.; Li, Y.; Zhang, J.Q. Influence of alloying elements on mechanical behavior of Fe-Mn-C TWIP steel. Cailiao GongGheng 2015, 9, 30–38. (In Chinese) [Google Scholar]
- Lu, S.; Wang, Q.C.; Yao, T.T.; Feng, H.; Gao, M.; Xi, T.; Li, H.B.; Tan, L.; Yang, K. Simultaneous improvement of strength and plasticity: Nano-twin construction for a novel high-nitrogen TWIP steel. Int. J. Plast. 2024, 183, 104144. [Google Scholar] [CrossRef]
- Feng, X.C.; Liu, X.Y.; Bai, S.X.; Ye, Y.C.; Zong, L.; Tang, Y. Mechanical properties and deformation behaviour of TWIP steel at different strain rates (vol 879, 145182, 2023). Mater. Sci. Eng. A Struct. Mater. Prop. Microstruct. Process. 2023, 882, 145414. [Google Scholar] [CrossRef]
- Xue, K.R.; Qiao, K.; Zhang, T.; Gao, F.; Yao, J.C.; Wang, W.; Wang, K.S. Hot Deformation Behavior and Dynamic Recrystallization Mechanism of Fe-18.2Mn-0.52C Twinning-Induced Plasticity Steel. JOM 2024, 76, 6457–6471. [Google Scholar] [CrossRef]
- Sklate Boja, M.F.; Giordana, M.F.; Banegas, S.; Druker, A.V. Twinning-Induced Plasticity Steel for the Automotive Industry: Design Stress for Gas Tungsten Arc Welded Parts. J. Mater. Eng. Perform. 2024, 1–15. [Google Scholar] [CrossRef]
- Yang, N.; Wang, X.; Liang, J.; Deng, H.X.; Ma, J.G.; Liu, Z.H.; Han, F.S. Characterization of microstructures and mechanical properties of laser welded TWIP steel plate. J. Mater. Res. Technol. 2024, 30, 7228–7241. [Google Scholar] [CrossRef]
- Santos GJ, D.; Colombo TC, A.; REgo, R.R.; Otubo, J. Integrity evolution during dissimilar welding of TWIP steel. J. Mater. Res. Technol. 2023, 27, 4461–4468. [Google Scholar] [CrossRef]
- Deng, H.X.; Liu, Z.H.; Wang, X.F.; Ma, J.G.; Wu, J.F.; Han, F.S. Microstructure and mechanical properties of heat affected zone for high-Mn TWIP steel based on welding thermal simulation. Hanjie Xuebao/Trans. China Weld. Inst. 2023, 44, 83–89. [Google Scholar] [CrossRef]
- Zhong, Y.L.; Li, G.Q. Concept and hysteretic behavior studies of TWIP steel made metallic energy dissipater. J. Constr. Steel Res. 2021, 186 (Suppl. C), 106911. [Google Scholar] [CrossRef]
- Feng, X.C.; Liu, X.Y.; Bai, S.X.; Tang, Y.; Ye, Y.C. Investigation of dynamic tensile mechanical responses and deformation mechanism at high strain rates in a TWIP steel. J. Mater. Res. Technol. 2023, 26, 639–653. [Google Scholar] [CrossRef]
- Zhang, C.; Han, Y.; Teng, H.X.; Liu, H.S.; Xie, C.Q.; Su, Y.J. Enhancement of hydrogen embrittlement resistance in high manganese steel under in-situ electrochemical hydrogen charging by regulating the grain size and distribution. Int. J. Hydrogen Energy 2024, 82, 968–978. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, G.M.; Li, H.Y.; Zhang, X.M.; Ding, H. Microstructure, strain hardening behavior, segregation and corrosion resistance of an electron beam welded thick high-Mn TWIP steel plate. J. Mater. Res. Technol. 2023, 25, 1105–1114. [Google Scholar] [CrossRef]
- Opiela, M.; Grajcar, A.; Krukiewicz, W. Corrosion behaviour of Fe-Mn-Si-Al austenitic steel in chloride solution. J. Achiev. Mater. Manuf. Eng. 2009, 33, 159–165. [Google Scholar]
- Ai, G.G.; Jiang, F.Y.; Si, F.; Liu, J.N.; Wei, N.; Wang, J.B. Effect of annealing process on microstructure and corrosion resistance of high-Mn TWIP steel. Jinshu Rechuli/Heat Treat. Met. 2024, 49, 313–321. [Google Scholar] [CrossRef]
- Jo, Y.H.; Cho, H.J.; Yang, J.H.; Lee, S.J. Enhancing charpy absorbed energy of aged duplex lightweight steel plates through TRIP and TWIP mechanisms. Mater. Charact. 2024, 217, 114413. [Google Scholar] [CrossRef]
- Martin, S.; Weidner, A.; Ullrich, C.; Schimpf, C.; Motylenko, M.; Lehnert, R.; Biermann, H.; Rafaja, D.; Vinogradov, A.; Estrin, Y. Deformation behaviour of TWIP steels: Constitutive modelling informed by local and integral experimental methods used in concert. Mater. Charact. 2022, 184, 111667. [Google Scholar] [CrossRef]
- GB/T 228.1-2010; Metallic Materials—Tensile Tests—Part 1: Test Method at Room Temperature. Standardization Administration of China: Beijing, China, 2010.
- GB/T 30069.1-2013; High Strain Rate Tensile Tests for Metallic Materials—Part 1: Elastic Rod Type Systems. Standardization Administration of China: Beijing, China, 2013.
- Lan, P.; Zhang, J. Tensile property and microstructure of Fe-22Mn-0.5C TWIP steel. Mater. Sci. Eng. A 2017, 707, 373–382. [Google Scholar] [CrossRef]
- Lan, P.; Zhang, J. Serrated Flow and Dynamic Strain Aging in Fe-Mn-C TWIP Steel. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2018, 49A, 147–161. [Google Scholar] [CrossRef]
- Li, Y.Z.; Liang, Z.Y.; Huang, M.X. Strengthening contributions of dislocations and twins in warm-rolled TWIP steels. Int. J. Plast. 2022, 150, 103198. [Google Scholar] [CrossRef]
- Chumlyakov, Y.; Maier, H.J.; Sehitoglu, H.; Canadinc, D.; Niklasch, D. Orientation evolution in Hadfield steel single crystals under combined slip and twinning. Int. J. Solids Struct. 2007, 44, 34–50. [Google Scholar]
- Guo, Z.; Gao, B.; Guo, Z.; Zhang, W. Dynamic constitutive relationship of Q235 steel based on J-C model. Expl. Shock Wave 2018, 38, 804–810. (In Chinese) [Google Scholar] [CrossRef]
- Lin, H.; Jin, G.; Zhan, Q.; Wang, G.; Han, J. Mechanical Properties and Constitutive Model of TC4 Titanium Alloy at Cryogenic. J. Mater. Eng. Perform. 2023, 33, 13731–13743. [Google Scholar] [CrossRef]
- Li, C.; Fang, W.; Yu, H.Y.; Peng, T.; Yao, Z.T.; Liu, W.G.; Zhang, X.; Xu, P.; Yin, F. The BCC → FCC hierarchical martensite transformation under dynamic impact in FeMnAlNiTi alloy. Mater. Sci. Eng. A 2024, 892, 146096. [Google Scholar] [CrossRef]
- Ye, T.; Zhao, F.; Chen, L.Y.; Jiang, K.; Deng, Q.; Chen, Y.Z.; Wang, Q.Y.; Suo, T. Effect of strain rate and low temperature on mechanical behaviour and microstructure evolution in twinning-induced plasticity steel. Mater. Sci. Eng. A 2021, 823, 141734. [Google Scholar] [CrossRef]
- Li, D.D.; Qian, L.H.; Wei, C.Z.; Liu, S.; Zhang, F.C.; Meng, J.Y. The tensile properties and microstructure evolution of cold-rolled Fe–Mn–C TWIP steels with different carbon contents. Mater. Sci. Eng. A 2022, 839, 142862. [Google Scholar] [CrossRef]
- Jabłońska, M.B.; Archie, F. Effect of the strain rate on the deformation mechanisms of TWIP-type steel. Mater. Sci. Eng. A 2024, 915, 147219. [Google Scholar] [CrossRef]
- Shen, S.C.; Xie, P.; Wu, C.L.; Luo, J.; Ye, H.F.; Chen, J.H. Cross-slip of extended dislocations and secondary deformation twinning in a high-Mn TWIP steel. Int. J. Plast. 2024, 175, 103922. [Google Scholar] [CrossRef]
- Cai, W.; Sun, C.; Zhang, H.; Wang, C.; Meng, L.; Fu, M.W. Delving into the intrinsic co-relation between microstructure and mechanical behaviour of fine-/ultrafine-grained TWIP steels via TEM and in-situ EBSD observation. Mater. Charact. 2024, 210, 113780. [Google Scholar] [CrossRef]
- Xie, P.; Wu, C.L.; Chen, J.H. Electron microscopic characterization of deformed twin boundary defects in high manganese TWIP steel. Dianzi Xianwei Xuebao 2023, 42, 596–604. (In Chinese) [Google Scholar]
- Feng, X.C.; Liu, X.Y.; Tang, Y.; Bai, S.X.; Zhu, L.A. Study on dynamic mechanical properties and deformation mechanism of TWIP steel. Xiyou Jinshu Cailiao Yu Gongcheng 2023, 52, 1695–1707. (In Chinese) [Google Scholar]
- Wang, S.H.; Liu, Z.Y.; Wang, G.D. Influence of grain size on TWIP effect in TWIP steel. Jinshu Xuebao 2009, 45, 1083–1090. (In Chinese) [Google Scholar] [CrossRef]
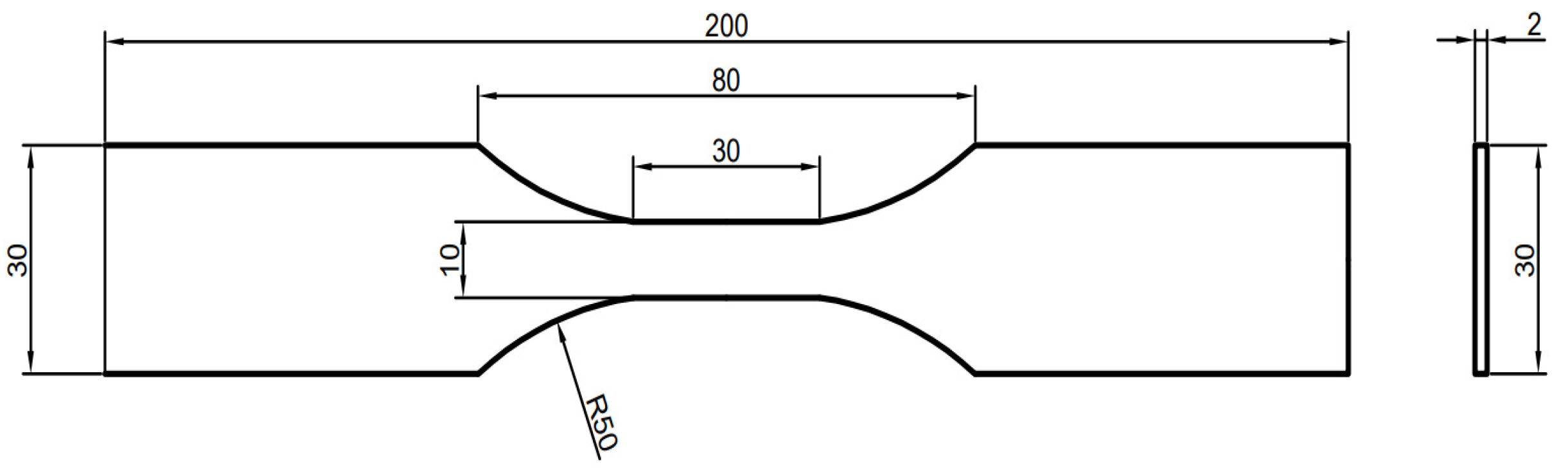
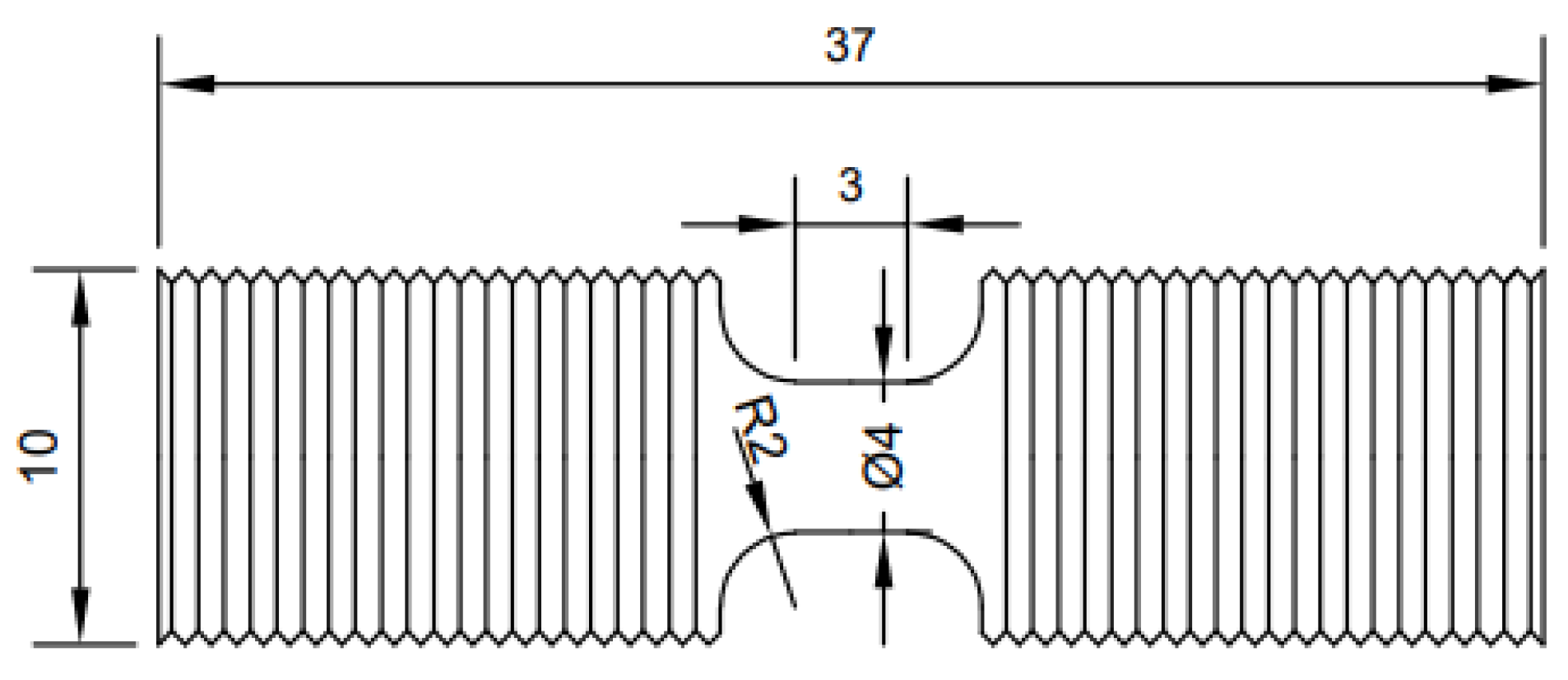







| Mn | Al | Ni | C | Si | Fe |
|---|---|---|---|---|---|
| 29.200 | 8.800 | 6.000 | 1.200 | 0.090 | Bal. |
| Strain Rate /s−1 | Yield Stress /MPa | Ultimate Tensile Stress /MPa | Yield Ratio | Uniform Elongation % | Fracture Elongation /% | PSE /MPa% |
|---|---|---|---|---|---|---|
| 10−2 | 958.61 | 1448.07 | 0.66 | 0.357 | 0.375 | 54,303 |
| 10−3 | 898.93 | 1526.13 | 0.59 | 0.410 | 0.443 | 67,608 |
| 10−4 | 833.12 | 1411.14 | 0.59 | 0.423 | 0.437 | 61,667 |
| Strain Rate /s−1 | Yield Stress /MPa | Ultimate Tensile Stress /MPa | Yield Ratio | Uniform Elongation % | Fracture Elongation /% | PSE /MPa% |
|---|---|---|---|---|---|---|
| 1000 | 1133.0 | 1494.3 | 0.76 | 0.289 | 0.330 | 49,279 |
| 3000 | 1245.9 | 1498.8 | 0.84 | 0.117 | 0.191 | 28,627 |
| 5000 | 1323.2 | 1558.9 | 0.85 | 0.049 | 0.303 | 47,234 |
| 6500 | 1430.6 | 1640.3 | 0.87 | 0.053 | 0.233 | 38,220 |
| Strain Rate | 1000 | 3000 | 5000 | 6500 |
|---|---|---|---|---|
| 123.23 | 68.84 | 108.27 | 83.94 | |
| Plastic Energy Absorption | 442.23 | 245.84 | 386.68 | 299.79 |
| /MPa | |||
|---|---|---|---|
| 833.12 | 845.56 | 0.2 | 0.08 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Liu, X.; Tang, Y.; Bai, S.; Ye, Y.; He, M.; Xia, M. Dynamic Mechanical Properties and Deformation Mechanisms of Lightweight High-Strength TWIP Steel. Buildings 2025, 15, 897. https://doi.org/10.3390/buildings15060897
Yang J, Liu X, Tang Y, Bai S, Ye Y, He M, Xia M. Dynamic Mechanical Properties and Deformation Mechanisms of Lightweight High-Strength TWIP Steel. Buildings. 2025; 15(6):897. https://doi.org/10.3390/buildings15060897
Chicago/Turabian StyleYang, Jia, Xiyue Liu, Yu Tang, Shuxin Bai, Yicong Ye, Manchao He, and Min Xia. 2025. "Dynamic Mechanical Properties and Deformation Mechanisms of Lightweight High-Strength TWIP Steel" Buildings 15, no. 6: 897. https://doi.org/10.3390/buildings15060897
APA StyleYang, J., Liu, X., Tang, Y., Bai, S., Ye, Y., He, M., & Xia, M. (2025). Dynamic Mechanical Properties and Deformation Mechanisms of Lightweight High-Strength TWIP Steel. Buildings, 15(6), 897. https://doi.org/10.3390/buildings15060897






