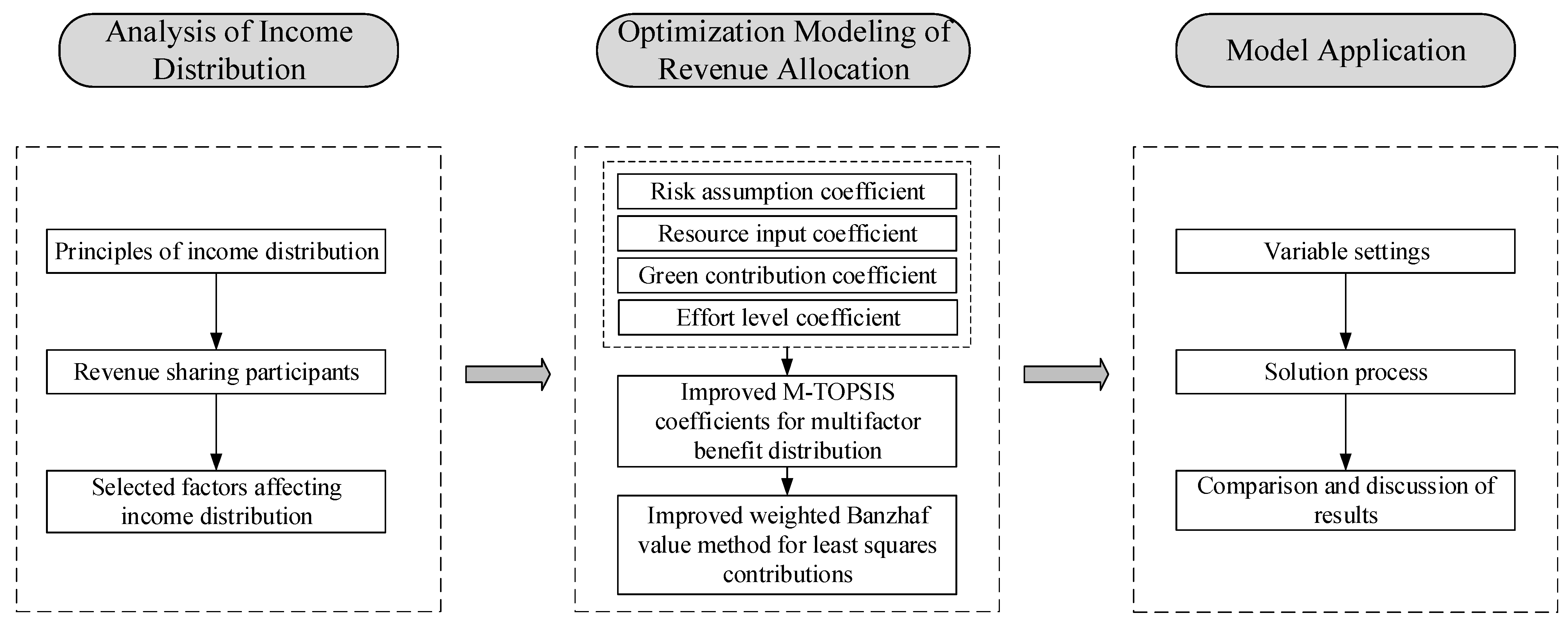
4.1. Single-Factor Benefit Distribution Coefficient Based on Triangular Fuzzy Numbers
- (1)
Risk Assumption Coefficient
To ensure the fairness of the evaluation of benefit impact factors and to minimize the influence of human factors, this paper proposes a comprehensive analytical method based on triangular fuzzy numbers combined with an improved G1 weighting method and the entropy method. Traditional hierarchical analysis methods, which rely on expert ratings to determine the importance of indicators, are susceptible to subjectivity. Therefore, this study adopts a method that combines subjective and objective weighting to allocate weights to risk factors and uses triangular fuzzy numbers from fuzzy theory to clearly express the strength of relationships between factors, effectively resolving the issue of relational ambiguity in practical applications.
- (i)
Triangular Fuzzy Numbers
The Triangular Fuzzy Number (TFN) is a widely used form of fuzzy number in decision analysis and risk assessment, effectively handling uncertainty and expressing subjective bias and fuzzy information. It is capable of describing uncertain information in complex systems, providing an expected model that covers the potential fluctuation range and reflecting the decision maker’s subjective judgment and expectations about possible outcomes under different scenarios. Compared to traditional 0–1 relationships, triangular fuzzy numbers allow for a more comprehensive and precise quantitative analysis of the relationships between influencing factors, thereby enhancing decision quality. It helps decision makers consider the various possibilities influencing the benefit distribution, providing a scientific benefit distribution coefficient and promoting a more robust and fair decision-making process.
In this study, triangular fuzzy numbers are chosen for weight assignment primarily because they can effectively handle the uncertainty of factors such as risk assumption and green contribution. Compared to precise numbers, triangular fuzzy numbers better express uncertainty and fuzziness, and compared to interval numbers, they offer greater flexibility, allowing for a more accurate reflection of the uncertain range in decision making. Through the setting of three parameters—the minimum value, most likely value, and maximum value—the triangular fuzzy number demonstrates strong applicability when dealing with weight assignment. It effectively simulates uncertainty and provides a more flexible, adaptive mathematical model for decision making, optimizing the distribution of cooperative benefits.
The specific steps are as follows:
Let
be a triangular fuzzy number, where
is the upper limit,
is the lower limit, and
is the mean value; then, its membership function is as follows:
When the values of are close to 0 or 1, the fuzziness of the triangular fuzzy number is small. When the values of are around 0.5, the fuzziness of the triangular fuzzy number is large. When , is simplified to a real number. Since the contribution values studied in this paper are non-negative, that is, the lower limit , the corresponding represents a non-negative triangular fuzzy number. Assuming any two non-negative triangular fuzzy numbers are and , their operational rules are as follows:
- ①
Addition:
- ②
Subtraction:
- ③
Scalar multiplication:
- (ii)
Improved G1 Weighting Method Based on Triangular Fuzzy Numbers
The G1 weighting method was initially a subjective weighting method based on comparing the importance ratios of evaluation indicators [
89]. To enhance the differentiation between weight values and improve the accuracy of the weights, this paper uses a scoring method for the importance of adjacent evaluation indicators to improve the G1 method. In expert scoring standards, to ensure the reliability of the scores, it is necessary to clearly understand the meanings of the scores on the scale. If the meanings of the scoring points on the scale are unclear, the reliability and validity of the measurements will be affected. Based on this, this study, referencing the
Handbook of Survey Research [
90], we propose using a 9-level scale to optimize the improved G1 weighting method. The specific calculation steps are as follows:
- ①
Expert scoring. A questionnaire survey was conducted to collect scores from several experts in related fields on the strength of the impact relationships between factors influencing benefit distribution among participants in the green supply chain for prefabricated construction. Triangular fuzzy numbers are used to fuzzify the evaluation indicators, reducing the subjective bias in expert scoring. The triangular fuzzy numbers correspond to each evaluation indicator, as shown in
Table 4, where higher values indicate greater importance of the indicator.
- ②
The ranking of the importance of evaluation indicators. Based on the importance scores given by experts to the indicators, the indicators are ranked according to the size of their scores. If the importance score of indicator is greater than the importance score of indicator , then it is denoted as , and the relative importance ranking is:
- ③
The ratio of the importance of adjacent indicators. Based on the scores given by the nth expert on the importance of the evaluation indicators, the ratio of the importance scores of adjacent indicators is used as the ratio of their weights. The weight ratio of indicator to indicator is denoted as:
In the formula, represents the weight of indicator based on the scoring of the -th expert.
- ④
The calculation of indicator weights. The weight of indicator is:
Using the recursive formula, the weights of other indicators can be calculated as:
where
.
- ⑤
The calculation of weights. Assume there are participants in the project, with evaluation indicators for each participant. The weight of the impact factors on benefit distribution in the green supply chain for prefabricated construction as assessed by the -th expert is , resulting in the initial triangular fuzzy direct relation matrix:
The initial triangular fuzzy direct relation matrix reflects the fuzzy semantic information of each expert regarding risk factors and evaluation indicators. To better utilize this information in subsequent analyses, it is necessary to defuzzify it to transform it into more specific and computable values. The purpose of defuzzification, while retaining fuzziness, is to make the values more consistent with actual situations. This paper uses the CFCS method (Converting Fuzzy data into Crisp Scores) for data defuzzification, a method that is simple to compute and results in the minimal loss of information after defuzzification, specifically as follows:
- ⑥
Standardize triangular fuzzy numbers , , and :
- ⑦
Calculate the left and right limit values of the standardized values and :
- ⑧
Calculate the precise value of the triangular fuzzy evaluation by expert :
- ⑨
Calculate the weights of each risk factor: compute the standardized precise values evaluated by experts.
- (iii)
Improved Entropy Method Based on Triangular Fuzzy Numbers
The entropy method is an objective weighting method that determines weights by analyzing the statistical characteristics of data and uses the entropy value of each risk factor to measure the degree of information loss [
91]. The higher the entropy value, the greater the uncertainty of the factor, indicating a smaller contribution to the system; conversely, a lower entropy value indicates that the factor has a greater impact on the system, and therefore, its weight should be larger. Additionally, the entropy method measures the variability of each risk factor in the dataset through a differentiation coefficient, thus reflecting the importance of different risk factors [
92]. Since the entropy method is an objective weighting method based on the statistical characteristics of data, it requires the defuzzification of the original triangular fuzzy numbers, transforming fuzzy ratings into precise values for input into the entropy method, thereby allowing for objective weight calculation. The objectivity of this method ensures the scientific and reasonable distribution of weights. The specific steps are as follows:
- ①
Construct a matrix. Collect expert ratings; this study uses the efficient CFCS method to defuzzify the rating data, following the same steps as in Formulae (7)–(10), transforming fuzzy ratings into precise ratings . Based on objective weighting methods, construct the scoring matrix X:
- ②
Quantify risk indicators. Quantify the risk indicators in the matrix:
- ③
Calculate the entropy values for each risk factor. Use the entropy formula to calculate the entropy value of each risk factor:
where
, and
and
are the number of samples.
- ④
Calculate the differentiation coefficient for each risk factor. According to the entropy value, calculate the differentiation coefficient for the indicators:
The greater the variability of , the smaller the entropy, thus the larger is, and the more important the indicator.
- ⑤
Determine the weights. Based on the differentiation coefficients, calculate the weights for each risk factor:
- (iv)
Combined Weights for Risk Assumption Factors
Combine the weights obtained from the improved G1 weighting method and the entropy method. When the sum of the squared deviations of the weights from the two methods is minimized, that is, when the weights from both subjective and objective methods each account for half, it is considered that the optimal combined weight is achieved. Derived from Equations (10) and (15), the formula for calculating the combined weight is as follows:
where
represents the weight values obtained from the improved G1 weighting method, and
represents the weight values obtained from the entropy method.
- (2)
Resource Input Coefficient
This follows the same steps as with the risk assumption coefficient.
- (3)
Green Contribution Coefficient
This follows the same steps as with the risk assumption coefficient.
- (4)
Effort Level Coefficient
In the green supply chain alliance for prefabricated construction, the level of effort by members directly relates to their contribution to the alliance, which is crucial for maintaining stability and enhancing efficiency. Additionally, the distribution of profits significantly influences the enthusiasm of cooperative enterprises to participate in alliance activities and their level of investment. Therefore, incorporating the effort level into the benefit distribution optimization model is necessary. By setting a series of conditions, it is possible to more accurately measure the contributions made by companies in the cooperation to obtain benefits and, based on this, achieve a reasonable distribution of profits.
- (i)
In constructing the benefit distribution model for the green supply chain alliance in prefabricated construction, to reflect the relative contribution of different companies’ efforts to overall benefit creation, value creation coefficients are introduced, represented by , , and . Additionally, considering other uncontrollable factors that may affect the benefits of enterprises, these factors are collectively referred to as . This setup helps to more comprehensively understand and analyze the benefit distribution situation in the alliance.
- (ii)
In the green supply chain alliance for prefabricated construction, to reasonably distribute benefits among all parties, benefit distribution coefficients , , and are introduced, corresponding to the benefit proportions of different companies in the alliance. These coefficients are set to follow the principle that their sum is 1, i.e., . Moreover, the benefit distribution coefficients are positively correlated with the level of effort in the supply chain, meaning that more effort by a company results in a larger share of benefits in the alliance. This design ensures the fairness of benefit distribution and motivates companies to increase their effort levels.
- (iii)
Costs are typically divided into fixed costs and variable costs. Fixed costs are those that do not change with production volume or business volume and can usually be determined by a company’s initial investment. For companies in the green supply chain alliance for prefabricated construction, their cost functions are represented as , , and , corresponding to the costs of different companies. Assume that the variable costs faced by participating nodes in the supply chain reflect the level of effort they expend to optimize overall profits. Specifically, each company’s effort level can be quantified by its effort cost coefficients, represented by , , and . Therefore, variable costs reflect the additional costs incurred by companies to enhance their performance in the alliance due to increased efforts.
Based on the above content, a model for the total economic income and cost functions of the enterprises participating in the supply chain collaboration can be formed:
where
,
, and
quantify the participation intensity (i.e., their level of effort) of companies A, B, and C in the alliance.
The expression for the net profit gained from cooperation among the green supply chain enterprises is:
where
,
and
represent the economic income obtained by companies a, b, and c within the supply chain, respectively.
Each cooperating enterprise, in order to maximize its own benefits, exhibits an effort level that is directly proportional to the economic benefits ultimately distributed. Based on this principle, specific expressions for the effort level of each company within the alliance can be derived. These expressions reflect the extent of effort each company puts forth to enhance its benefits within the alliance. By analyzing these expressions, further understanding of the behavioral patterns of enterprises within the alliance and how they might adjust their strategies to maximize benefits can be gained:
Following the principle of
, the economic return distribution coefficients for each cooperating enterprise from the perspective of effort levels can be calculated as:
4.2. Improved M-TOPSIS Multi-Factor Benefit Distribution Coefficient
The previous sections constructed the weight coefficients for risk assumption, resource input, green contribution, and effort level as the factors affecting the benefit distribution in the construction supply chain alliance, providing a basis for individually determining the benefit distribution schemes for each party. However, for different enterprises within the green supply chain alliance for prefabricated construction, the outcomes of different influencing factors often vary. Therefore, this paper introduces the TOPSIS method to conduct a comprehensive evaluation of the outcomes of the four factors. This method calculates the distance between the ideal solution and the negative ideal solution, comprehensively measures the differences between the factors, and is efficient and widely applicable. It has strong adaptability, enabling a more accurate reflection of the actual benefit status of the participants in the prefabricated building green supply chain alliance.
The TOPSIS method was proposed by Hwang and Yoon in 1981 [
93] and is a multi-criteria decision analysis method suitable for comprehensive evaluation with multiple variables and objectives. The method calculates the Euclidean distance between the decision object and the positive and negative ideal solutions to determine the relative closeness of each alternative, thus ranking them in order of preference. The advantages of TOPSIS lie in its simple calculation and reasonable results, allowing for the quantitative evaluation of multiple indicators. It has been widely applied in various decision-making fields. Moreover, TOPSIS has strong applicability and does not impose strict requirements on the indicators of the influencing factors, making it particularly suitable for addressing the characteristics of benefit influencing factors in the prefabricated building green supply chain alliance. By conducting a comprehensive evaluation of the contributions of each participant on different dimensions, a more scientific and comprehensive benefit distribution coefficient for the prefabricated building green supply chain can be generated. This approach takes into account the weighted importance of each factor and provides an accurate and flexible benefit distribution scheme for each participant, helping to achieve a more ideal benefit distribution coefficient.
However, the TOPSIS method may encounter a reversal issue, where sudden changes in the data for individual indicators may significantly affect the final result, sometimes even leading to a reversal in the ranking of alternatives. To address this issue, the M-TOPSIS method optimizes the traditional TOPSIS. This method enhances the reliability of the final benefit distribution coefficient by improving the relative closeness calculation rule after calculating the Euclidean distance of each scheme to the positive and negative ideal solutions.
Assuming there are
factors and
players in prefabricated construction, the initial decision matrix can be obtained from the single-factor benefit distribution coefficients:
Next, the initial decision matrix is dimensionless processed to obtain the standardized decision matrix:
Calculate the ideal and negative ideal solutions:
The Euclidean distances from each influencing factor to the ideal and negative ideal solutions are:
Calculate the relative closeness
:
where
, and the higher the closeness value, the closer it is to the ideal point, indicating a higher priority of that influencing factor. The size of the relative closeness determines the merits of the influencing factors and provides a reference for decision making.
The improved M-TOPSIS method constructs a
coordinate system, defining point E that represents the “optimal ideal solution” within the plane. The distances
between points within the plane EFGH, which represents the four influencing factors, and point E are used as the basis for ranking (as shown in
Figure 2). The influencing factors are prioritized in ascending order of these distances.
If two influencing factors have equal
values, then their
values are compared, and the factor with the smaller
value is considered superior.
Figure 2 clearly illustrates the calculation and ranking principles of the M-TOPSIS method.
The
values are normalized, resulting in a correction coefficient:
4.3. Improved Least Squares Contribution with Weighted Banzhaf Value Method
By utilizing the improved M-TOPSIS model, we calculated the composite benefit distribution coefficients under multiple factors within the green supply chain for prefabricated construction. In addressing the distribution of benefits among multiple participants, cooperative game theory methods are typically employed to ensure a fair and reasonable allocation. Cooperative game theory provides a framework for mutual negotiation and mutually beneficial outcomes, and the Banzhaf value, as a classic concept in cooperative games, provides a key basis for measuring the contributions of each party. It objectively measures the critical contributions made by each participant in all possible coalitions and uses mathematical methods to provide scientific and reasonable solutions to complex problems of cost apportionment, profit and loss distribution, and benefit distribution. Therefore, introducing the Banzhaf value in determining risk-sharing schemes allows for a more objective assessment of each party’s contributions, thereby justifying their proportions of risk assumption.
For a cooperative game
involving
people, the classical expression for the Banzhaf value is [
94]:
represents the benefits allocated to player from grand coalition , where represents the player’s marginal contribution to the grand coalition . Although the Banzhaf value effectively measures a player’s critical role in cooperative games, its methodology has certain limitations. Specifically, the Banzhaf value assesses a player’s influence by calculating their marginal contributions to the coalition, a method that performs well in symmetric, balanced games. However, the original calculation of marginal contributions is somewhat simplified and does not fully consider the interactions and complex relationships among players in cooperative games, especially as game structures become more complex and players’ heterogeneity increases. Moreover, the Banzhaf value assumes that each player’s contribution is based solely on their ability to influence the outcome of cooperation, without considering that players often have different resources, capabilities, and objectives, which may lead to varying degrees of contribution in actual cooperation. Therefore, to ensure the scientific accuracy of the risk-sharing scheme, this paper modifies the Banzhaf value based on the least squares method to more accurately reflect the actual contributions of players in projects, resulting in a more equitable distribution of risk-sharing proportions and aligning risk-sharing strategies more closely with project realities and stakeholder interests.
Liu et al. [
95] demonstrated through the optimized Shapley value based on least squares contributions that the traditional method of marginal contributions is insufficient to capture the true influence of players in complex cooperative games. Extending the least squares contributions to the improvement of the Banzhaf value in a fuzzy environment has shown good results in the distribution of benefits within a supply chain alliance. This study extends this method to the calculation of the Banzhaf value in a precise environment, using weighted least squares contributions instead of marginal contributions in the Banzhaf value, proposing a modified Banzhaf value based on player contributions.
Triangular fuzzy number weighted least squares contributions are measured by the squared distance between the benefits received by players on the distribution vector and their actual contributions. By minimizing the variance of the excess contributions of all players in the coalition, the determined solution for the triangular fuzzy number weighted least squares contribution is:
where
represents the weight of coalition
, and
.
is the profit attainable by grand coalition
excluding subset
, representing the marginal contribution of sub-coalition
to grand coalition
.
According to the membership function of the triangular fuzzy number, when , the upper and lower limits of the profits do not change, becoming certain, and at this point, the triangular fuzzy number can degenerate into an exact number. When , degenerates into the exact number . Similarly, the total revenue of the grand coalition as a triangular fuzzy number can degenerate into the exact number , and the marginal contribution of the sub-coalition as a triangular fuzzy number can also degenerate into an exact number .
Therefore, based on the weighted least squares contributions of the players, the value is:
where
represents the marginal contribution of player
to grand coalition
, and number of coalitions
is
.
Integrating the properties of the Banzhaf value with the concept of least squares, using the least squares contribution values in place of the marginal contributions in the Banzhaf value, yields a preliminary distribution function based on player contributions:
where
In this case, treating sub-coalition
as the grand coalition, where
is a sub-coalition within coalition
,
can still be obtained from the formula. To verify whether the single-value solution of this preliminary distribution function satisfies the collective rationality principle
, we calculate the excess difference:
At this time,
means
; thus, it does not satisfy collective rationality, and there exists a cooperative surplus
, requiring the surplus value to be evenly redistributed. The final result, based on the weighted contributions of players, yields an improved Banzhaf value:
The Shapley value is one of the most classic single-value solutions in cooperative game theory. For any cooperative game, the Shapley value can be expressed as [
18]:
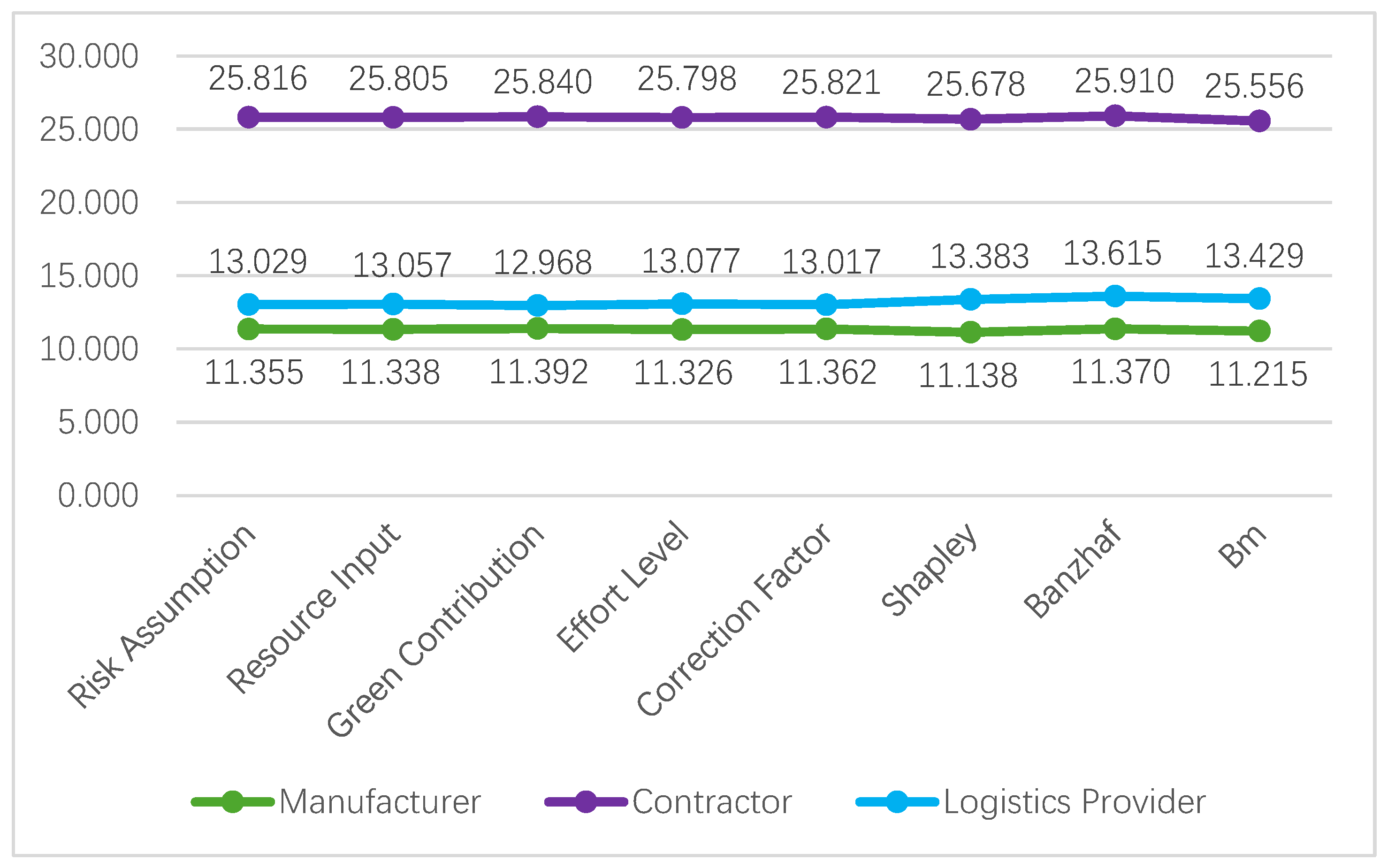
The marginal contribution of the Shapley value is equivalent to the marginal contribution of the Banzhaf value, differing only in the form of expression. The Shapley value of each participant is their average marginal contribution, with the calculation involving all possible participant combinations. Unlike the Shapley value, the Banzhaf value does not consider the probability of various coalitions forming but instead simply averages all possible marginal contributions. The least squares method selects the optimal payoff vector by minimizing the difference between expected and actual returns , thus minimizing the overall dissatisfaction of the coalition. It not only considers the marginal contributions of players within the coalition but also ensures a more stable and balanced benefit distribution through mathematical optimization. Moreover, the least squares method emphasizes reducing errors and biases, ensuring that the benefit distribution does not excessively rely on changes in specific coalition structures, thereby increasing the model’s adaptability and robustness in complex cooperative environments.
Next, we verify that the proposed improved Banzhaf value satisfies the four axioms of cooperative game theory and confirm that this cooperative game solution is uniquely determined. For any two cooperative games and , the following applies:
- 1.
Efficiency:
From Equation (33), the sum of all players’ earnings is:
This indicates that the total sum of the payoffs distributed to all players is exactly equal to the total value of the entire coalition, satisfying the efficiency axiom.
- 2.
Additivity:
The results of cooperative games are always independent:
This indicates that regardless of how the cooperative game solution is combined, the payoffs for each player are simply the direct sum of their individual game payoffs, verifying the additivity axiom of cooperative games.
- 3.
Symmetry:
The distribution of earnings between player
and player
in the cooperative game is independent of the order of distribution. If two players have the same position and contribution in the cooperative game, they should receive the same payoff. This can be derived from Equation (29):
Given the assumption that player and player have the same position and contribution in the cooperative game, obviously, . This shows that the benefit distribution is independent of the order in which players are assigned, reflecting the symmetry axiom.
- 4.
Dummy player: (when player contributes nothing to the coalition).
Since , the improved Banzhaf value assigns to player a value of , not zero as with the traditional Banzhaf value. When , . This is because the improved Banzhaf value considers principles of efficiency and fairness, providing a reasonable redistribution for . This method more accurately reflects the actual contributions of the players, enhancing the fairness and rationality of cooperative benefit distribution.
In summary, the improved Banzhaf value satisfies three fundamental axioms of cooperative game theory: efficiency, additivity, and symmetry. Additionally, it introduces a new interpretation in the virtual participant setting that considers indirect impacts and fairness, more accurately reflecting the actual contributions of the players and enhancing the fairness and rationality of the cooperative benefit distribution. Therefore, the improved Banzhaf value is the unique solution that satisfies the four aforementioned axioms, and the resulting benefit distribution has unique validity. Thus, the improved Banzhaf value satisfies these four axioms uniquely, and the distributed values possess unique validity.