Study on Dynamic Response and Anti-Collision Measures of Aqueduct Structure Under Vehicle Impact
Abstract
1. Introduction
2. Materials and Methods
2.1. Numerical Model
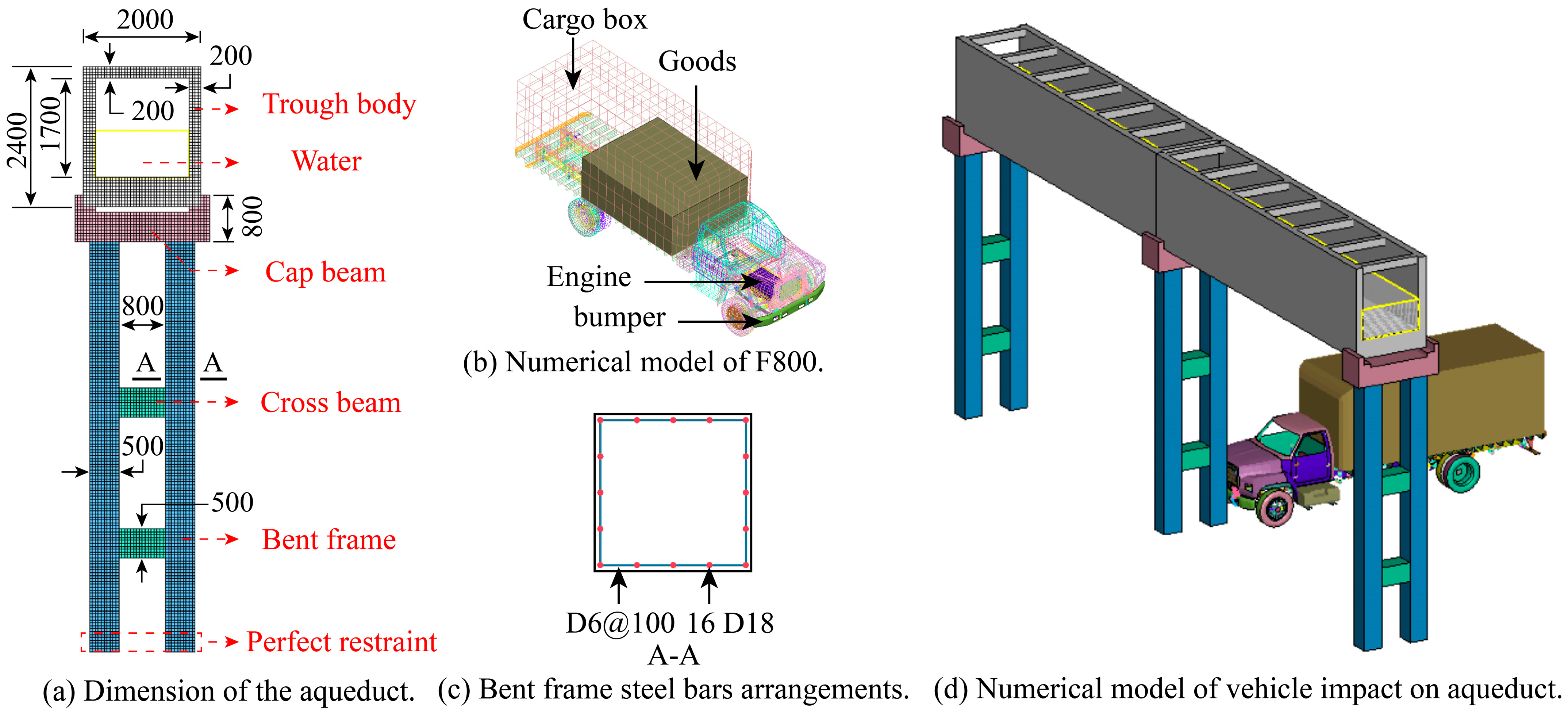
2.1.1. Aqueduct Model
2.1.2. Water Model
2.1.3. Vehicle Model
2.2. Material Models and Numerical Algorithm
| Model | Notation | Parameter | Magnitude |
|---|---|---|---|
| *Mat_003 | RO (kg/m3) | Mass density | 7850 |
| E (MPa) | Young’s modulus | 2.06 × 105 | |
| PR | Poisson’s ratio | 0.3 | |
| SIGY (MPa) | Yield stress | 400/335 | |
| ETAN | Tangent modulus | 2060 | |
| BETA | Hardening parameter | 1 | |
| SRC | Strain rate parameter, c | 40.4 | |
| SRP | Strain rate parameter, p | 5 | |
| FS | Failure strain for eroding elements | 0.2 | |
| *Mat_027 [39] | RO (kg/m3) | Mass density | 1600 |
| PR | Poisson’s ratio | 0.4995 | |
| A (MPa) | Material constant | 0.6 | |
| B (MPa) | Material constant | 0.15 | |
| *Mat_063 [37] | RO (kg/m3) | Mass density | 1200 |
| E (MPa) | Young’s modulus | 1200 | |
| PR | Poisson’s ratio | 0.3 | |
| TSC (MPa) | Tensile stress cutoff | 10 | |
| *Mat_111 [15] | RO (kg/m3) | Mass density | 2375 |
| G (MPa) | Shear modulus | 1.15 × 104 | |
| A | Normalized cohesive strength | 0.79 | |
| B | Normalized pressure hardening | 1.6 | |
| C | Strain rate coefficient | 0.007 | |
| N | Pressure hardening exponent | 0.61 | |
| FC (MPa) | Quasi-static uniaxial compressive strength | 24.5 | |
| T (MPa) | Maximum tensile hydrostatic pressure | 3.1 | |
| EPS0 | Reference strain rate | 1 × 10−6 | |
| EFMIN | Amount of plastic strain before fracture | 0.01 | |
| SFMAX | Normalized maximum strength | 7 | |
| PC (MPa) | Crushing pressure | 13.7 | |
| UC | Crushing volumetric strain | 0.0006 | |
| PL (MPa) | Locking pressure | 800 | |
| UL | Locking volumetric strain | 0.095 | |
| D1 | Damage constant | 0.03 | |
| D2 | Damage constant | 1 | |
| K1 (MPa) | Pressure constant | 8.5 × 104 | |
| K2 (MPa) | Pressure constant | −1.71 × 105 | |
| K3 (MPa) | Pressure constant | 2.08 × 105 | |
| FS | Failure type | 0.003 | |
| *Mat_159 (UHPC) [31] | RO (kg/m3) | Mass density | 2500 |
| NH | Hardening initiation | 0 | |
| CH | Hardening rate | 0 | |
| G (MPa) | Shear modulus | 1.8 × 1010 | |
| K (MPa) | Bulk modulus | 2.5 × 1010 | |
| α (MPa) | Triaxial compression surface constant term | 4.59 × 1010 | |
| θ | Triaxial compression surface linear term | 0.2873 | |
| λ (MPa) | Triaxial compression surface nonlinear term | 3.65 × 107 | |
| β (MPa−1) | Triaxial compression surface exponent | 1.26 × 10−8 | |
| α1 (MPa) | Torsion surface constant term | 1 | |
| θ1 | Torsion surface linear term | 0 | |
| λ1 (MPa) | Torsion surface nonlinear term | 0.4226 | |
| β1 (MPa−1) | Torsion surface exponent | 1.277 × 10−9 | |
| α2 (MPa) | Triaxial extension surface constant term | 1 | |
| θ2 | Triaxial extension surface linear term | 0 | |
| λ2 (MPa) | Triaxial extension surface nonlinear term | 0.5 | |
| β2 (MPa−1) | Triaxial extension surface exponent | 1.277 × 10−9 | |
| R | Cap aspect ratio | 6 | |
| X0 (MPa) | Cap initial location | 6 × 108 | |
| W | Maximum plastic volume compaction | 0.05 | |
| D1 (MPa−1) | Linear shape parameter | 6 × 10−10 | |
| D2 (MPa−1) | Quadratic shape parameter | 0 | |
| B | Ductile shape softening parameter | 100 | |
| GFC | Fracture energy in uniaxial stress | 1 × 104 | |
| D | Brittle shape softening parameter | 0.1 | |
| GFT | Fracture energy in uniaxial tension | 1000 | |
| GFS | Fracture energy in pure shear stress | 1000 | |
| pwrc | Shear-to-compression transition parameter | 5 | |
| pwrt | Shear-to-tension transition parameter | 1 | |
| pmod | Modify moderate pressure softening parameter | 0 | |
| η0c | Rate effects parameter for uniaxial compressive stress | 1.83 × 10−4 | |
| Nc | Rate effects power for uniaxial compressive stress | 0.504 | |
| η0t | Rate effects parameter for uniaxial tensile stress | 1.76 × 10−5 | |
| Nt | Rate effects power for uniaxial tensile stress | 0.56 | |
| overc | Maximum overstress allowed in compression | 1.05 × 108 | |
| overt | Maximum overstress allowed in tension | 7.76 × 106 | |
| Srate | Ratio of effective shear stress to tensile stress fluidity | 1 | |
| repow | Power which increases fracture energy with rate effects | 1 | |
| *Mat_159 (Concrete) [26] | RO (kg/m3) | Mass density | 2500 |
| IRATE | Rate effect options | 1 | |
| ERODE | Element erosion | 1.1 | |
| FPC (MPa) | Unconfined compression strength | 40 | |
| DAGG (mm) | Maximum aggregate size | 25 |
3. Results
3.1. Energy Analysis
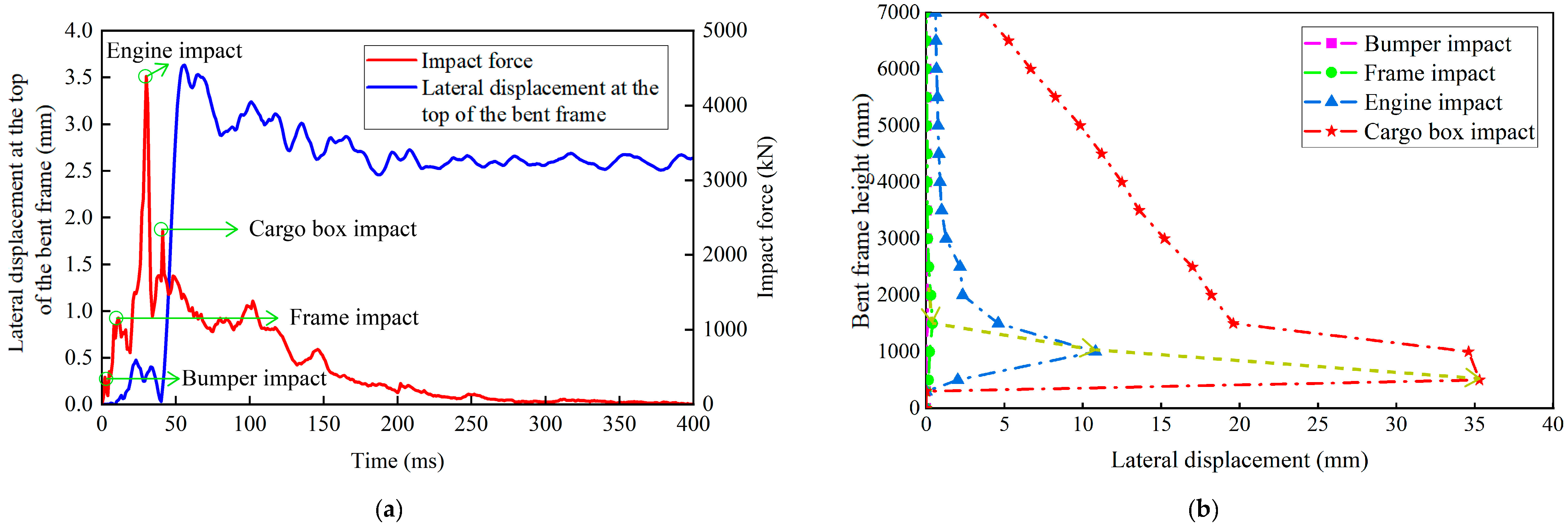
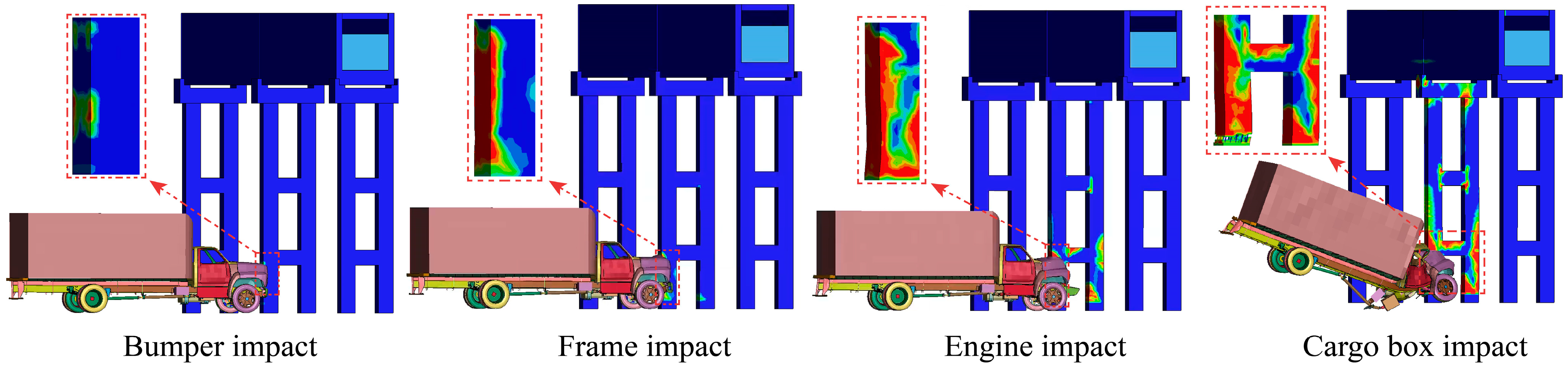
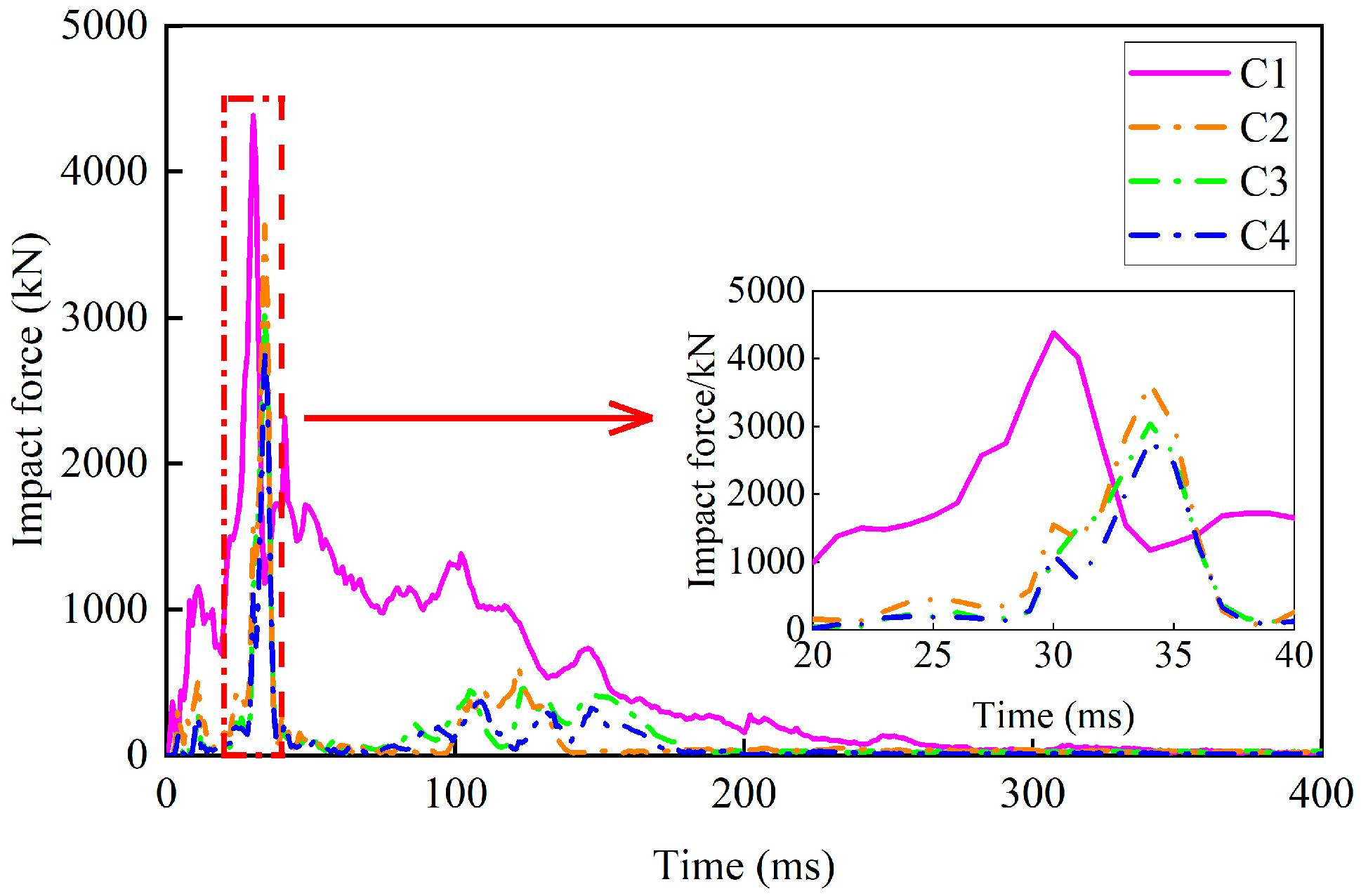
3.2. Impact Force and Damage Analysis
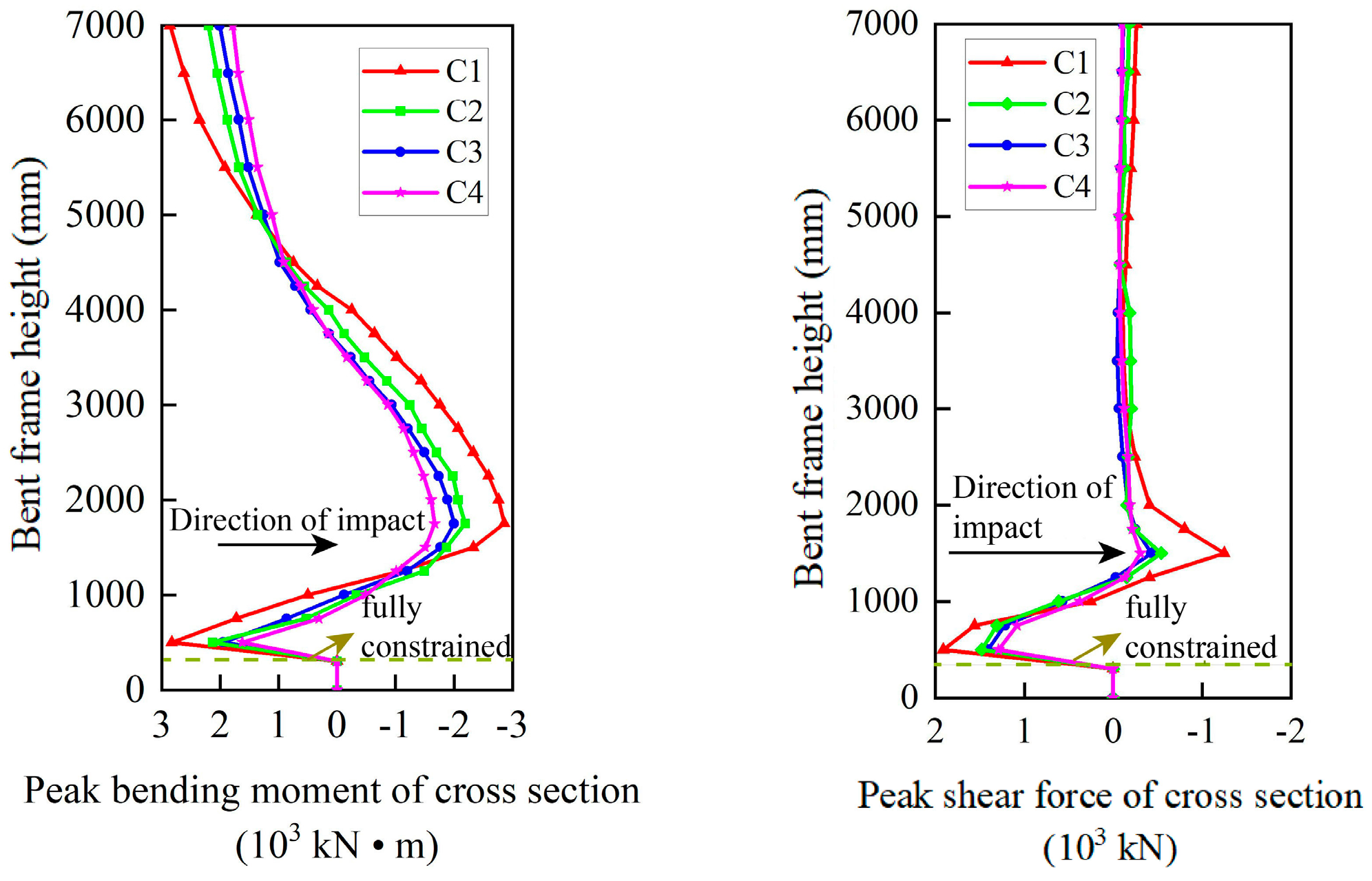
3.3. Internal Force Analysis
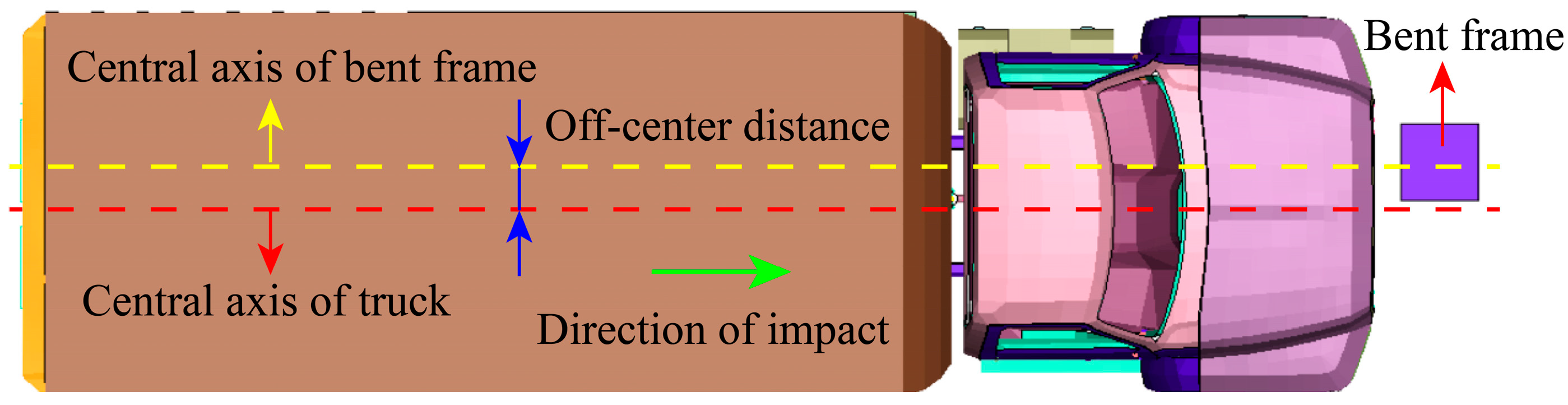
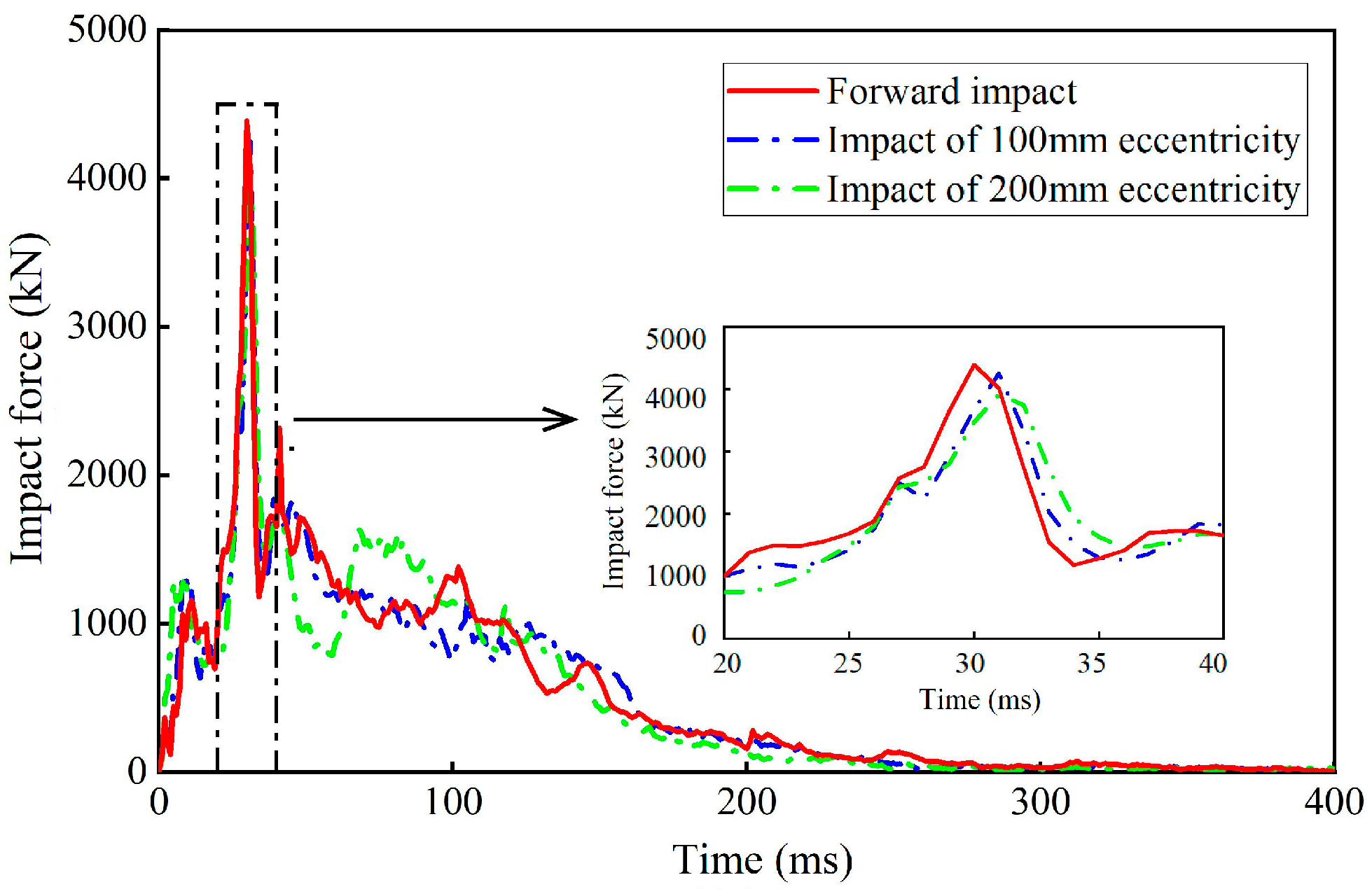
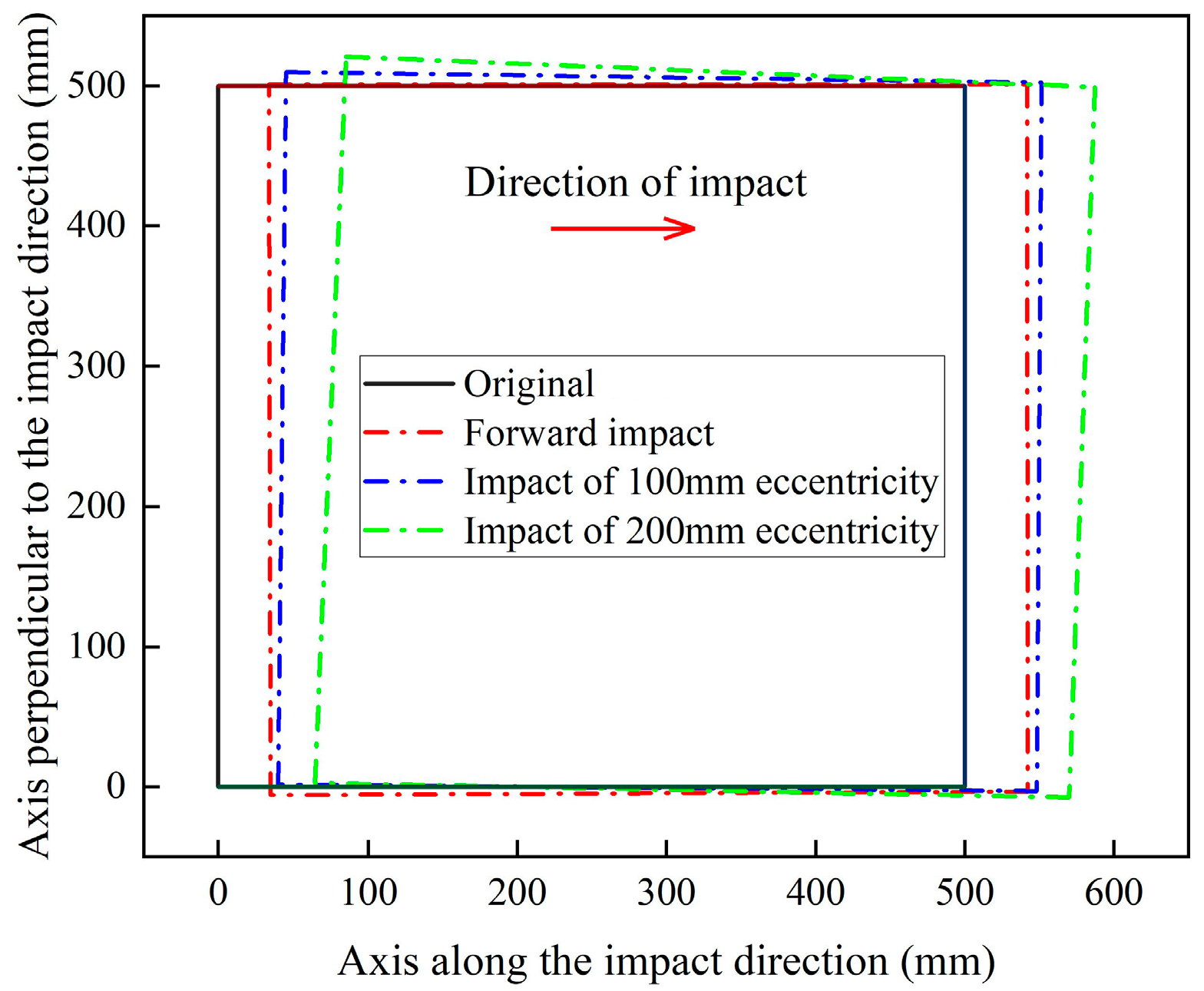
3.4. Impact Eccentricity Analysis
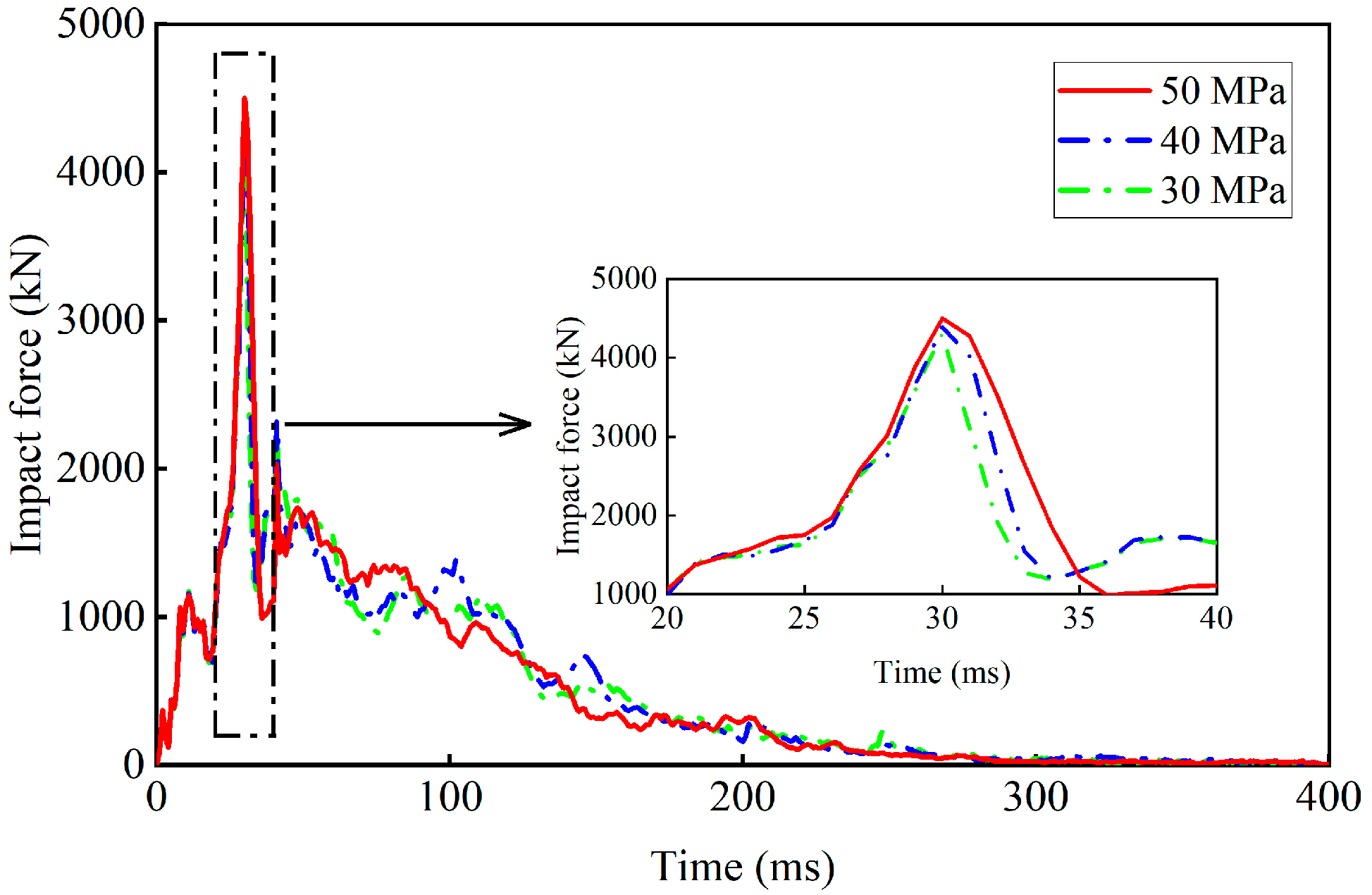
3.5. Concrete Strength Analysis
4. Discussion
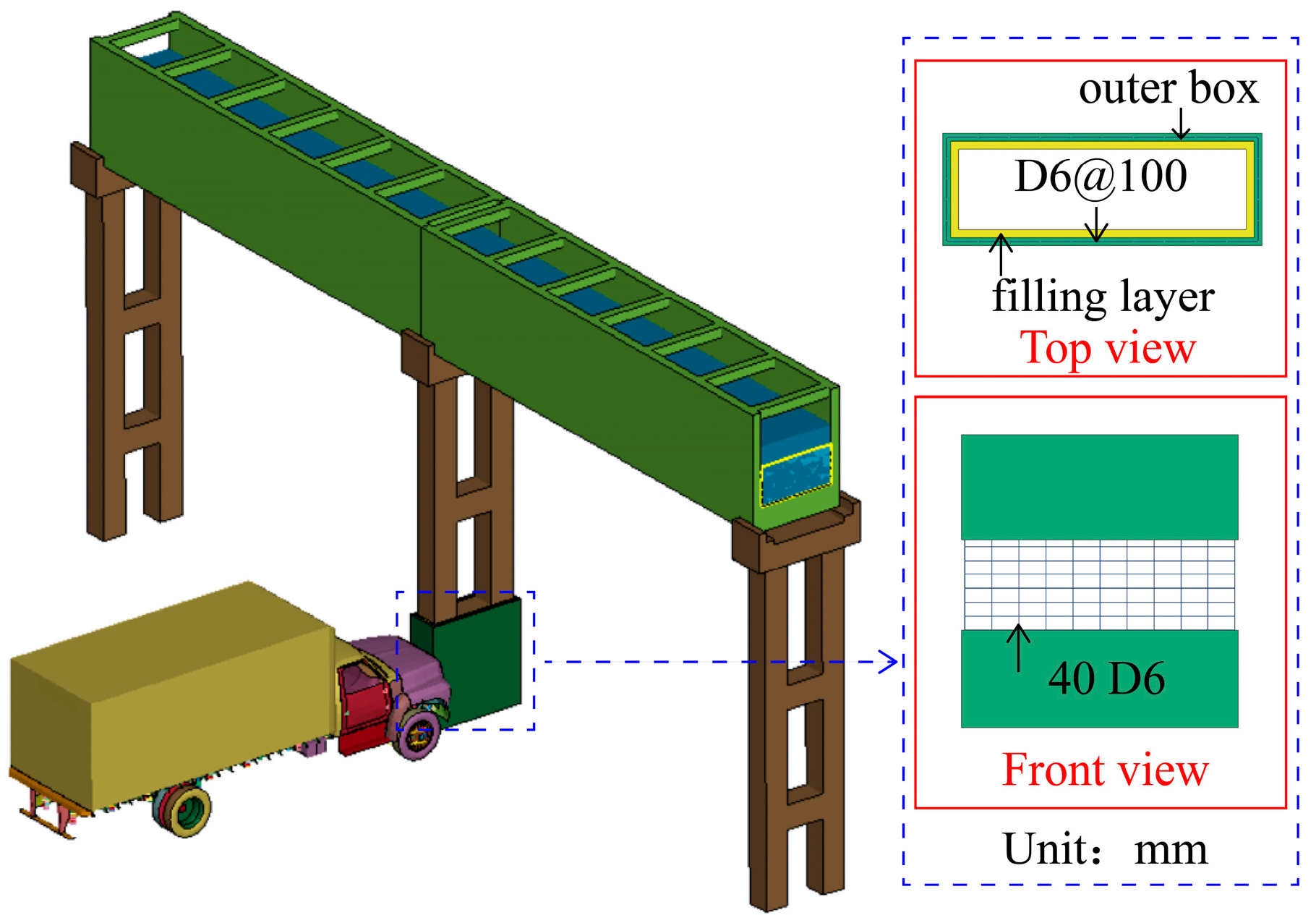
4.1. Aqueduct Model with Anti-Collision Measures
4.2. Comparative Analysis of Dynamic Response Results
4.2.1. Energy Dissipation
4.2.2. Internal Force Response
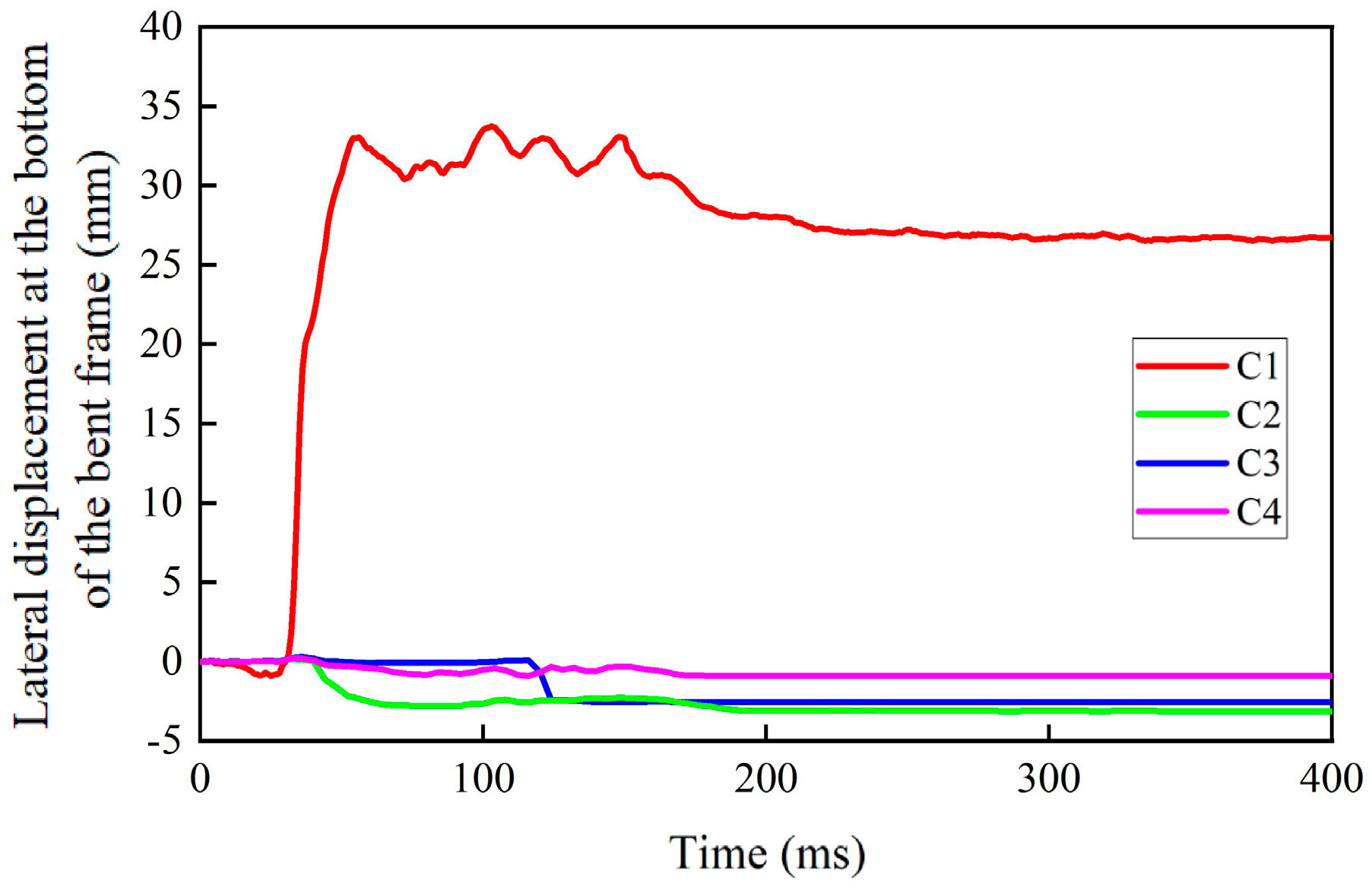
4.2.3. Displacement Response
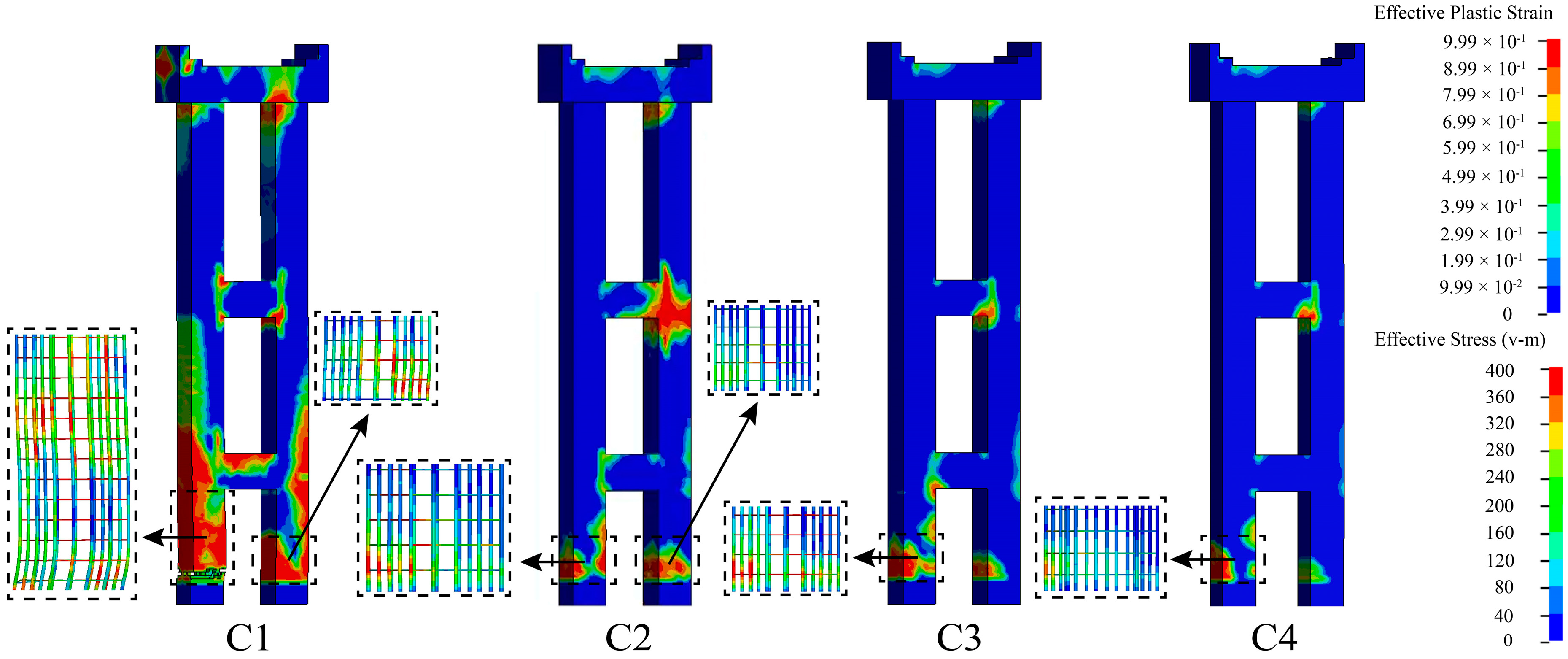
4.2.4. Damage Feature
5. Conclusions
- (1)
- The dynamic impact process of a vehicle on an aqueduct structure can be categorized into four stages: bumper impact, frame impact, engine impact, and cargo box impact. Notably, the shear failure of the concrete at the bottom of the impacted side of the bent frame, caused by the engine and cargo box impact, along with the bending failure of the concrete on the rear impact side, are the primary contributors to the instability and failure of the aqueduct structure.
- (2)
- Eccentric impact induces substantial torsional deformation of the aqueduct bent frame, thereby reducing its shear and bending resistance, which leads to more severe impact damage and greater residual deformation.
- (3)
- The peak impact force exhibits a positive correlation with concrete strength during vehicle impact on the aqueduct. Conversely, the lateral displacement at the top of the impacted bent frame shows a negative correlation with concrete strength. Enhancing concrete strength significantly improves the aqueduct structure’s resistance to vehicle impact.
- (4)
- The three anti-collision measures proposed in this paper effectively protect the aqueduct structure during the impact process. Notably, the anti-collision performance is most pronounced when the rubber concrete outer box with a foam aluminum filling layer is employed.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shen, J.J.; Bai, X.L. Research on temporal and spatial difference model of urban water use for water-saving construction. J. Hohai Univ. (Nat. Sci.) 2022, 50, 38–43. [Google Scholar]
- Li, K.B.; Tao, J. Study on water resources utilization efficiency and its influencing factors in China. J. Hydraul. Eng. 2024, 43, 11–23. [Google Scholar]
- Chen, X.N.; Jin, Y.G. Thinking on smart water dispatching in the South-to-North Water Diversion Middle Route Project. J. Hohai Univ. (Nat. Sci.) 2023, 51, 46–55. [Google Scholar]
- Li, J.; Cui, D.H. Safety detection and evaluation of aqueduct supporting structure under lateral impact load. Pearl River 2023, 44, 89–96. [Google Scholar]
- Gu, P.Y.; Wang, L.L. Summary of research on typical failure characteristics of aqueduct structures in China. Adv. Sci. Technol. Water Res. 2017, 37, 1–8. [Google Scholar]
- Nan, J.J. Research on disease treatment and roughness reduction protection technology of aqueduct in large irrigation area. Tech. Supply Water Res. 2023, 1, 195–198. [Google Scholar]
- Huang, L.; Hou, Y. Collision in the expansion joint effects on the seismic behavior of large-scale aqueduct. J. Asian Arch. Build. Eng. 2021, 20, 663–673. [Google Scholar] [CrossRef]
- Du, M.; Zhang, S.; Wang, C.; She, L.; Li, J.; Lu, T. Seismic fragility assessment of aqueduct bent structures subjected to mainshock-aftershock sequences. J. Eng. Struct. 2023, 292, 116505. [Google Scholar] [CrossRef]
- Du, M.; Zhang, S.; Wang, C.; Li, Z.; Yao, J.; Lu, T. Development of the compound intensity measure and seismic performance assessment for aqueduct structures considering fluid-structure interaction. J. Ocean Eng. 2024, 311, 118838. [Google Scholar] [CrossRef]
- Su, Z.Q.; Wang, J.M.; Yan, Q.L. Reliability analysis of water-crossing bridge under ship collision based on surrogate model. Highways 2023, 68, 176–181. [Google Scholar]
- Thilakarathna, H.M.I.; Thambiratnam, D.P.; Dhanasekar, M. Numerical simulation of axially loaded concrete columns under transverse impact and vulnerability assessment. Int. J. Impact Eng. 2010, 37, 1100–1112. [Google Scholar] [CrossRef]
- Do, T.V.; Pham, T.M.; Hao, H. Dynamic responses and failure modes of bridge columns under vehicle collision. Eng. Struct. 2018, 156, 243–259. [Google Scholar] [CrossRef]
- Chen, L.; Zeng, Y.Y.; Yan, Z.F. Dynamic response and damage characteristics of reinforced concrete piers under vehicle impact. J. Vib. Shock 2019, 38, 261–267. [Google Scholar]
- Wang, B.; Liu, J.; Yang, S. Design and numerical analysis of flexible anti-collision device for bridge pier. Jidian Gongcheng 2016, 33, 30–36. [Google Scholar]
- Liu, B.; Yang, S.; Li, W. Damping dissipation properties of rubberized concrete and its application in anti-collision of bridge piers. Constr. Build. Mater. 2020, 236, 117286. [Google Scholar] [CrossRef]
- Hirt, C.W.; Amsden, A.A.; Cook, J.L. An arbitrary lagrangian-eulerian computing method for all flow speeds. J. Comput. Phys. 1974, 14, 227–253. [Google Scholar] [CrossRef]
- Milan, K.; Mikhail, S. Conservative Multi-Material Remap for Staggered Multi-Material Arbitrary Lagrangian-Eulerian Methods. J. Comput. Phys. 2014, 258, 268–304. [Google Scholar]
- Zeng, Q.H.; Sun, W.J. MOF-MMALE Numerical Simulation of Multi-Material Large Deformation Flow Problems. Appl. Math. Mech. 2014, 35, 1163–1176. [Google Scholar]
- Xue, M.A.; Kargbo, O.; Zheng, J. Seiche oscillations of layered fluids in a closed rectangular tank with wave damping mechanism. Ocean Eng. 2020, 196, 106842. [Google Scholar] [CrossRef]
- Yu, C.C.; Mir, F.U.H.; Whittaker, A.S. Validation of numerical models for seismic fluid-structure-interaction analysis of nuclear, safety-related equipment. Nucl. Eng. Des. 2021, 379, 111179. [Google Scholar] [CrossRef]
- Zhang, D.X.; Liu, P.S.; Zhang, C.J. Study on the Applicability of Fluid-Solid Interaction Model of Dynamic Analysis of Aqueduct Structure. J. North China Univ. Water Res. Electr. Power (Nat. Sci. Ed.) 2024, 10, 1–9. [Google Scholar]
- Abdelkarim, O.I.; Elgawady, M.A. Performance of Bridge Piers Under Vehicle Collision. Eng. Struct. 2017, 140, 337–352. [Google Scholar] [CrossRef]
- Li, R.W.; Wu, H.; Yang, Q.T. Vehicular impact resistance of seismic designed RC bridge piers. Eng. Struct. 2020, 220, 111015. [Google Scholar] [CrossRef]
- Li, R.W.; Cao, D.S.; Wu, H. Collapse analysis and damage evaluation of typical simply supported double-pier RC bridge under truck collision. Structures 2021, 33, 3222–3238. [Google Scholar] [CrossRef]
- Li, R.W.; Zhou, D.Y.; Wu, H. Experimental and numerical study on impact resistance of RC bridge piers under lateral impact loading. Eng. Fail. Anal. 2019, 109, 104319. [Google Scholar] [CrossRef]
- Meng, Y.; Yi, W.J. Study on dynamic effect of concrete cylinder specimen under low velocity impact. J. Vib. Shock 2011, 30, 205–210. [Google Scholar]
- Du, J.; Meng, W.; Khayat, K.H. New development of ultra-high-performance concrete (UHPC). Compos. Part B Eng. 2021, 224, 109220. [Google Scholar] [CrossRef]
- Hung, C.C.; El-Tawil, S.; Chao, S.H. A review of developments and challenges for UHPC in structural engineering: Behavior, analysis, and design. J. Struct. Eng. 2021, 147, 03121001. [Google Scholar] [CrossRef]
- Bajaber, M.A.; Hakeem, I.Y. UHPC evolution, development, and utilization in construction: A review. J. Mater. Res. Technol. 2021, 10, 1058–1074. [Google Scholar] [CrossRef]
- Bahmani, H.; Mostafaei, H.; Santos, P.; Fallah Chamasemani, N. Enhancing the Mechanical Properties of Ultra-High-Performance Concrete (UHPC) Through Silica Sand Replacement with Steel Slag. Buildings 2024, 14, 3520. [Google Scholar] [CrossRef]
- Wang, W.; Wu, C.; Li, J. Behavior of ultra-high performance fiber-reinforced concrete (UHPFRC) filled steel tubular members under lateral impact loading. Int. J. Impact Eng. 2019, 132, 103314. [Google Scholar] [CrossRef]
- Liu, F.; Chen, G.; Li, L. Study of impact performance of rubber reinforced concrete. Constr. Build. Mater. 2012, 36, 604–616. [Google Scholar] [CrossRef]
- Turatsinze, A.; Bonnet, S.; Granju, J.L. Potential of rubber aggregates to modify properties of cement based-mortars:improvement in cracking shrinkage resistance. Constr. Build. Mater. 2007, 21, 176–181. [Google Scholar] [CrossRef]
- Xue, J.; Shinozuka, M. Rubberized concrete: A green structural material with enhanced energy-dissipation capability. Constr. Build. Mater. 2013, 42, 196–204. [Google Scholar] [CrossRef]
- Wu, Z.L.; Xu, X.X.; Liu, L. Experimental study on the compression and energy-absorbing properties of anti-collision energy-absorbing materials, metal foam, and aluminum. Transp. Sci. Technol. 2008, 4, 74–77. [Google Scholar]
- Wang, D.P.; Li, W.; He, S.M. Study on optimization of impact structure of bridge piers across debris flow reinforced by aluminum foam sandwich panels. J. Vib. Shock 2016, 35, 108–114. [Google Scholar]
- Li, Z.M.; Yang, X.D.; Hu, Q. Low-speed impact energy absorption performance of aluminum foam. Hot Work. Technol. 2019, 48, 29–33. [Google Scholar]
- Zabihi, A.; Fasihi, M.; Rasouli, S. Improving the mechanical properties and curing characteristics of styrene-butadiene rubber/butadiene rubber composites by incorporating silicon carbide. Polym. Compos. 2024, 45, 1676–1687. [Google Scholar] [CrossRef]
- Li, H.Y.; Zhou, L.Y.; Wang, Q. Research on key parameters and performance of new assembled steel-UHPC anti-ship collision device. J. Cent. South Univ. (Sci. Technol.) 2021, 52, 519–528. [Google Scholar]
- Truong, D.D.; Jang, B.S.; Janson, C.E. Benchmark study on slamming response of flat-stiffened plates considering fluid-structure interaction. Mar. Struct. 2021, 79, 103040. [Google Scholar] [CrossRef]
- Cao, R.; Agrawal, A.K.; El-Tawil, S. Heavy truck collision with bridge piers: Computational simulation study. J. Bridge Eng. 2019, 24, 04019052. [Google Scholar] [CrossRef]
- Xue, S.; Hao, H.; Hao, Y. Numerical investigation of impact response of bridge pier subjected to off-center vehicle collision. Eng. Struct. 2024, 317, 118624. [Google Scholar] [CrossRef]







| Date | Location | Impact Position | Aqueduct Damage |
|---|---|---|---|
| August 2011 | Penghu Town, Fujian Province, China | Bottom of the bent frame | Trough body collapsed |
| December 2015 | Hezhuang Village, Zhejiang Province, China | Bottom of the bent frame | Trough body collapsed |
| August 2017 | Liangfeng Village, Sichuan Province, China | Bottom of the bent frame | Trough body collapsed |
| January 2018 | Lushan City, Jiangxi Province, China | Bottom of the bent frame | Trough body collapsed |
| August 2018 | Taoxi Town, Fujian Province, China | Bottom of the bent frame | Trough body slipped and fell |
| May 2019 | Wujiachong Caokouyan Irrigation District, Hunan Province, China | Bottom of the bent frame | Trough body collapsed |
| March 2020 | Tanlei Section of G4 Beijing-Hong Kong-Macao Expressway, China | Bottom of the bent frame | Trough body slipped |
| January 2021 | Majian Aqueduct, Jiangxi Province, China | Bottom of the bent frame | Trough body collapsed |
| May 2021 | Lintou Village, Zhejiang Province, China | Bottom of the bent frame | Trough body fractured |
| June 2023 | Shenhu Aqueduct, Hunan Province, China | Bottom of the bent frame | Bent frame fractured |
| July 2023 | Shuangxikou Town, Hunan Province, China | Trough body | Cross beam fractured |
| Notation (Air) | Magnitude (Air) | Notation (Water) | Magnitude (Water) |
|---|---|---|---|
| ρ0 (kg/m3) | 1.225 | ρ0 (kg/m3) | 1000 |
| C0 | 0 | C | 1.48 × 106 |
| C1 | 0 | S1 | 1.921 |
| C2 | 0 | S2 | −0.096 |
| C3 | 0 | S3 | 0 |
| C4 | 0.4 | γ0 | 0.35 |
| C5 | 0.4 | A | 0 |
| C6 | 0 | E (MPa) | 0.2895 |
| E (MPa) | 0.25 |
| Case | Anti-Collision Measures | Fmax (kN) | Peak Bending Moment of Cross-Section (kN•m) | Peak Shear Force of the Section (kN) | ||||
|---|---|---|---|---|---|---|---|---|
| Bottom | Impact Area | Top | Bottom | Impact Area | Top | |||
| C1 | / | 4389 | 2817 | −2861 | 2874 | 1916 | −1250 | −264 |
| C2 | rubber concrete–rubber | 3636 | 2139 | −2198 | 2215 | 1482 | −552 | −188 |
| C3 | UHPC–aluminum | 3038 | 1950 | −2006 | 2032 | 1417 | −443 | −123 |
| C4 | rubber concrete–aluminum | 2787 | 1625 | −1677 | 1784 | 1293 | −233 | −113 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, J.; Wen, R.; Chen, L.; Zhou, Y.; Duan, L.; Wang, W. Study on Dynamic Response and Anti-Collision Measures of Aqueduct Structure Under Vehicle Impact. Buildings 2025, 15, 851. https://doi.org/10.3390/buildings15060851
Shi J, Wen R, Chen L, Zhou Y, Duan L, Wang W. Study on Dynamic Response and Anti-Collision Measures of Aqueduct Structure Under Vehicle Impact. Buildings. 2025; 15(6):851. https://doi.org/10.3390/buildings15060851
Chicago/Turabian StyleShi, Jiaze, Rui Wen, Li Chen, Yao Zhou, Lei Duan, and Weiqiang Wang. 2025. "Study on Dynamic Response and Anti-Collision Measures of Aqueduct Structure Under Vehicle Impact" Buildings 15, no. 6: 851. https://doi.org/10.3390/buildings15060851
APA StyleShi, J., Wen, R., Chen, L., Zhou, Y., Duan, L., & Wang, W. (2025). Study on Dynamic Response and Anti-Collision Measures of Aqueduct Structure Under Vehicle Impact. Buildings, 15(6), 851. https://doi.org/10.3390/buildings15060851







