Enhancing HVAC Control Systems Using a Steady Soft Actor–Critic Deep Reinforcement Learning Approach

Abstract

Buildings account for a substantial portion of global energy use, with about one-third of total consumption attributed to them, according to IEA statistics, significantly contributing to carbon emissions. Building energy efficiency is crucial for combating climate change and achieving energy savings. Smart buildings, leveraging intelligent control systems, optimize energy use to reduce consumption and emissions. Deep reinforcement learning (DRL) algorithms have recently gained attention for heating, ventilation, and air conditioning (HVAC) control in buildings. This paper reviews current research on DRL-based HVAC management and identifies key issues in existing algorithms. We propose an enhanced intelligent building energy management algorithm based on the Soft Actor–Critic (SAC) framework to address these challenges. Our approach employs the distributed soft policy iteration from the Distributional Soft Actor–Critic (DSAC) algorithm to improve action–state return stability. Specifically, we introduce cumulative returns into the SAC framework and recalculate target values, which reduces the loss function. The proposed HVAC control algorithm achieved 24.2% energy savings compared to the baseline SAC algorithm. This study contributes to the development of more energy-efficient HVAC systems in smart buildings, aiding in the fight against climate change and promoting energy savings.

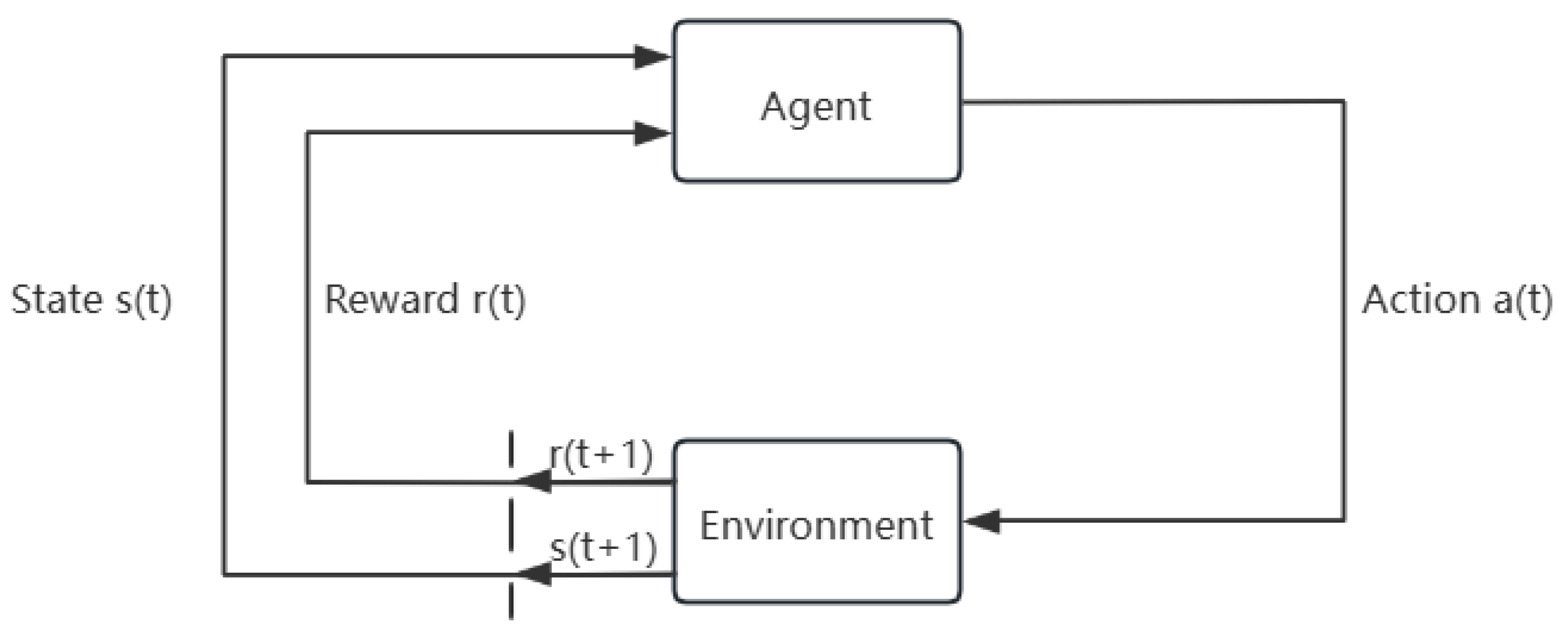
1. Introduction

With the continuous progress of human society and sustained economic development, people’s living standards have been increasing. To meet these ever-growing living standards, more resources and energy are required. In the long run, the consumption of resources and energy poses a serious problem: energy depletion. The world’s renewable energy sources may be unable to sustain human use under continuous exploitation, while non-renewable energy sources are also diminishing. In industrial production and daily life, humans also emit harmful pollutants into the atmosphere, affecting air quality and degrading quality of life. Faced with such a difficult situation, researchers worldwide have begun to focus on the conservation of resources and energy, actively adopting various preventive measures to reduce the resource and energy consumption rate and placing high emphasis on environmental protection. In recent decades, the significant growth in building energy consumption has exacerbated global warming and climate change. GlobalABC points out that the energy consumption of the construction industry accounted for more than one-third of global total energy consumption in 2021 [1]. Meanwhile, the International Energy Agency (IEA) reports that direct and indirect carbon dioxide emissions from buildings account for 9% and 18% of global total emissions, respectively. We have queried the final consumption of biofuels and waste in various global sectors from 1990 to 2021 (data source: https://www.iea.org/data-and-statistics/data-tools/, accessed on 5 February 2025), with 2019 data indicating that building energy consumption and carbon emissions accounted for 30% and 28% of global totals, respectively. In the face of resource depletion and energy consumption challenges, researchers globally have prioritized resource and energy conservation and are taking proactive measures. Against this backdrop, smart energy buildings have emerged as a new development direction, aiming to provide humans with an efficient, comfortable, and convenient building environment while focusing on energy consumption and striving to minimize energy use while meeting human needs. Smart energy buildings are based on building structures and electronic information technology, integrating various sensors, controllers, intelligent recognition and response systems, building automation systems, network communication technology, real-time positioning technology, computer virtual simulation technology, and other related technologies to form a complex system, thereby achieving high energy efficiency and a comfortable indoor environment.

Smart buildings thrive globally, with the United States and Japan excelling in this field. Since Japan first proposed the concept of smart buildings in 1984, it has completed multiple landmark projects, such as the Nomura Securities Building and the NFC Headquarters, becoming a pioneer in research and practice in this area. The Singaporean government has also invested significant funds in specialized research to promote the development of smart buildings, aiming to transform Singapore into a “Smart City Garden” [2]. Additionally, India launched the construction of a “Smart City” in the Salt Lake area of Kolkata in 1995 [3], driving the development of smart buildings and smart cities. Smart buildings, characterized by efficiency, energy conservation, and comfort, are rapidly emerging globally.

China’s smart buildings started later but have developed rapidly since the late 1980s, especially in major cities like Beijing, Shanghai, and Guangzhou, where numerous smart buildings have been constructed. According to incomplete statistics, approximately 1400 smart buildings have been built in China, mainly designed, constructed, and managed according to international standards [4]. Domestic smart buildings are shifting toward large public buildings, such as exhibition centers, libraries, and sports venues. Furthermore, China has conducted extensive technical research on smart energy buildings, covering building energy management systems, intelligent control technologies, energy-saving equipment, and more. Researchers are committed to improving building energy efficiency and reducing carbon emissions by integrating IoT technology, AI technology, and big data analytics. Smart energy buildings have gradually formed a complete industrial chain in China, encompassing smart building design, construction, operation management, intelligent equipment manufacturing, and sales, among other sectors, providing a new impetus for economic development and energy conservation.

In building energy management and control, reinforcement learning (RL) methods have garnered considerable attention in recent years. The field has witnessed rapid development since Barrett and Linder proposed an RL-based autonomous thermostat controller in 2015 [5]. In 2017, Wei et al. used deep reinforcement learning (DRL) for the optimal control of heating, ventilation, and air conditioning (HVAC) in commercial buildings [6], with multiple studies building on this foundation [7,8] and evaluating its adaptability in practical research. Mozer first applied RL to building control in 1998 [9], and with the rise of DRL, research in this area has become particularly noteworthy in recent years. Recent literature reviews [10,11] have extensively studied and summarized the applications of DRL in building energy control and HVAC.

However, smart buildings still face numerous challenges and limitations [12]. Firstly, building thermal dynamics models are influenced by complex stochastic factors, making it difficult to achieve precise and efficient energy optimization [6]. Secondly, the system involves many uncertain parameters, such as renewable energy generation, electricity prices, indoor and outdoor temperatures, carbon dioxide concentrations, and occupancy levels. Thirdly, there are spatio-temporal coupling operational constraints among energy subsystems, HVAC, and ESSs, requiring coordination between current and future decisions, as well as decisions across different subsystems [13]. Fourthly, traditional optimization methods exhibit poor real-time performance when dealing with large-scale building energy optimization problems, as they require the computation of many potential solutions [14]. Developing universal building energy management methods is also challenging, with existing methods often requiring strict applicability. For instance, stochastic programming and model predictive control (MPC) require prior or predictive information about uncertain parameters [15]. At the same time, personalized thermal comfort models demand extensive real-time occupant preference data, making implementation difficult and intrusive. When predicting thermal comfort, test subjects are often assumed to be homogeneous with no differences in thermal preferences, which reduces the accuracy of the algorithms. DRL models may have poor generalization ability in different environments. For HVAC systems, due to variations in environmental and architectural factors, the model’s performance in practical applications may need to meet expectations. HVAC systems involve multiple parameters and variables that require optimization and adjustment. DRL algorithms may struggle with balancing exploration and exploitation, leading to situations where they get stuck in local optima or over-explore. Furthermore, DRL algorithms may exhibit instability during the training process and be susceptible to factors such as initial conditions and hyperparameter choices. Stability is a crucial consideration for the reliability and safety of HVAC systems.

Based on the aforementioned issues, this paper considers addressing the balance between human comfort and energy consumption in HVAC systems through profound reinforcement learning control. In response to these problems, the following innovations are proposed in this study, which are of significant importance:

• Exploring Deep Reinforcement Learning Control for HVAC Systems: We explore using deep reinforcement learning control to address the balance between human comfort and energy consumption in HVAC systems.
• Improving Policy Evaluation Accuracy: This paper proposes a new method to address the inaccuracy of deep reinforcement learning algorithms in policy evaluation. Specifically, we select the smaller value between the random target return and the target Q-value to replace the target Q-value. This approach effectively reduces the instability of the mean-related gradient. Substituting this into the mean-related gradient and policy gradient further mitigates the risk of overestimation, resulting in a slight and more ideal underestimation. This enhancement improves the algorithm’s exploration capabilities and the stability and efficiency of the learning process.
• Building an SSAC-Based Policy Model: We construct a policy model based on Steady Soft Actor–Critic (SSAC) that can output optimized control actions based on environmental parameters to achieve the dual goals of minimizing power consumption and maximizing comfort. For each time step, based on the current state $s_t$, an action $a_t$ (i.e., adjusting the air conditioning temperature setpoint) is determined. At the end of the current time step, the next state $s_{t+1}$ is returned.

The remainder of this paper is structured as follows: Section 2 introduces related work, presenting the theoretical foundation of our research. Section 3 introduces the theoretical basis of deep reinforcement learning, smart energy buildings, and the Soft Actor–Critic. Section 4 presents the analysis and design of the algorithm proposed in this paper. This section proposes a deep reinforcement learning-based smart building energy algorithm in the HVAC domain. It comprehensively analyzes existing research and improves the model based on prior studies. Section 5 discusses the evaluation experiments and results of the algorithm. Section 6 concludes the paper, presenting the conclusions and future work.

2. Related Work

2.1. Thermal Comfort Prediction

Thermal comfort prediction refers to forecasting individuals’ sensations of thermal comfort in specific environments based on environmental conditions and individual characteristics. Researchers have proposed various thermal comfort indices, including the Temperature–Humidity Index, Temperature– Humidity–Wind Speed Index, Standard Effective Temperature, and PMV/PPD model, to assess people’s thermal comfort under specific environmental conditions. By utilizing building and heat transfer models, combined with indoor and outdoor environmental parameters and human physiological parameters, predictions can be made regarding thermal comfort within buildings. Building models can incorporate information such as architectural structure, materials, and equipment to simulate the internal thermal environments of buildings. Data-driven methods, such as machine learning and deep learning, leverage large amounts of data to train models that predict people’s thermal comfort under different environmental conditions. These methods can utilize historical and sensor data to achieve accurate thermal comfort predictions. Additionally, human physiological models are established by integrating physiological parameters and behavioral characteristics to predict people’s thermal comfort sensations under varying environmental conditions. These models consider parameters such as the human metabolic rate, sweat rate, and blood flow to assess thermal comfort from a physiological perspective.

Personalized comfort models require substantial occupant preference data to achieve accurate model performance. These preference data are typically collected through various survey tools, such as online surveys and wearable devices, which can be highly invasive and labor-intensive, especially when conducting large-scale data collection studies [16]. Individual thermal comfort models are used to predict thermal comfort responses at the individual level and, compared to comprehensive comfort models, can capture individual preferences [16].

Since the early 20th century, numerous researchers have investigated evaluation methods and standards for indoor thermal comfort, proposing a series of evaluation indices. These include the Standard Effective Temperature, Effective Temperature, New Effective Temperature, Comfort Index, and Wind Effect Index, among others. With the continuous evolution and development of thermal comfort evaluation methods, the widely recognized thermal comfort index at present is the thermal comfort theory and thermal comfort equation proposed by Danish scholar Fanger, known as the Predicted Mean Vote. Compared to other thermal comfort indices, the Predicted Mean Vote equation comprehensively considers both objective environmental factors and individual subjective sensations.

Shepherd et al. [17] and Calvino [18] introduced a fuzzy control method for managing building thermal conditions and energy costs. Kummert et al. [19] and Wang et al. [20] proposed optimal control methods for HVAC systems. Ma et al. [21] presented a model predictive control-based approach to control building cooling systems by considering thermal energy storage. Barrett et al. [5], Li et al. [22], and Nikovski et al. [23] adopted Q-learning-based methods for HVAC control. Dalamagkidis et al. [24] designed a Linear Reinforcement Learning Controller using a linear function approximation of the state–action value function to achieve thermal comfort with minimal energy consumption.

2.2. Deep Reinforcement Learning Control

DRL represents a new direction in machine learning. It integrates the technique of rewarding behaviors based on RL with the idea of learning feature representations using neural networks from deep learning, shining brightly in artificial intelligence. Consequently, it possesses both the powerful representation capabilities of deep learning and the decision-making abilities in unknown environments characteristic of reinforcement learning.

The first DRL algorithm was the Deep Q-Network (DQN), which overcame the shortcomings of Q-learning by adopting several techniques to stabilize the learning process. In addition to DQN, many other DRL algorithms exist, such as DDPG, SAC, and RSAC. DRL has been applied to robotic control, enabling robots to learn to execute tasks in complex environments, like mechanical arm control and gait learning. In autonomous driving, DRL is used to train agents to handle intricate driving scenarios, optimizing vehicle decision-making and control.

Biemann et al. compared different DRL algorithms in the Datacenter2 [25] environment. This is a well-known and commonly used test scenario in DRL-based HVAC control [26,27] to manage the temperature setpoints and fan speeds in a data center divided into two zones. They compared the SAC, TD3, PPO, and TRPO algorithms, evaluating them regarding energy savings, thermal stability, robustness, and data efficiency. Their findings revealed the advantages of non-policy algorithms, notably the SAC algorithm, which achieved approximately 15% energy reduction while ensuring comfort and data efficiency. Lastly, when training DRL algorithms under different weather patterns, a significant improvement in robustness was observed, enhancing the generalization and adaptability of the algorithms.

3. Theoretical Background

3.1. Deep Reinforcement Learning

In the reinforcement learning framework illustrated in Figure 1, the controlling agent learns the optimal control strategy through direct interaction with the environment via a trial-and-error approach. Reinforcement learning can be formalized as a Markov Decision Process (MDP), which is defined by a four-tuple consisting of states, actions, transition probabilities, and rewards. States are a set of variables whose values represent the controlled environment. Actions are the control signals executed by the agent within the control environment, aiming to maximize its objectives encoded in the reward function. Transition probabilities define the probability of the environment transitioning from state s to state s’ when action a is executed. According to MDP theory, these probabilities depend only on the value of state s and not on the previous states of the environment [28].

The RL framework for control problems in energy management can be simplified as follows: a control agent (e.g., a control module connected to a building management system) interacts with an environment (e.g., a thermally heated building zone). At each time step, the agent executes an action (e.g., setting the water heating temperature) when the environment is in a particular state (e.g., the building is occupied, but the temperature is above the comfort threshold). While observing the state, the agent receives a reward that measures its performance relative to its control objectives. Starting from a certain state of the environment, the RL algorithm seeks to determine the optimal control policy $\pi$ that maximizes the cumulative sum of future rewards. The RL agent determines the optimal policy by evaluating the state-value function and action-value function. The state-value function represents the goodness of being in a particular state $S_t$ relative to the control objectives [29]. This function provides the expected value of the cumulative sum of future rewards that the control agent will obtain by starting from state $S_t$ and following policy $\pi$, defined as follows:

$$v_{\pi }\left(s\right)=\mathbb{E}\left[r_{t+1}+\gamma v_{\pi }\left(s^{\prime }\right)\mid S_t=s,S_{t+1}=s^{\prime }\right]$$

(1)

where $\gamma \in [0,1]$ is the discount factor for future rewards. When $\gamma$ = 0, the agent places greater emphasis on immediate rewards. Conversely, when $\gamma$ = 1, the agent seeks to maximize only future rewards.

Similarly, the action-value function, which represents the value of taking a specific action $A_t$ in a certain state $S_t$ under a particular control policy $\pi$, can be expressed as

$$q_{\pi }(s,a)=\mathbb{E}\left[r_{t+1}+\gamma q_{\pi }(s^{\prime },a^{\prime })\mid S_t=s,A_t=a\right]$$

(2)

In the context of reinforcement learning algorithms, one of the most widely applied methods is Q-learning. Q-learning utilizes a tabular approach to map the relationships between state–action pairs [30]. These relationships are formalized as state–action values or q-values, which are iteratively updated by the control agent using the Bellman equation [31]:

$$Q(s,a)=Q(s,a)+\mu \left[r_t+\gamma \underset{a^{\prime }}{max}Q(s^{\prime },a^{\prime })-Q(s,a)\right]$$

(3)

where $\mu \in [0,1]$ is the learning rate, determining the speed at which new knowledge overrides old knowledge. When $\mu$ = 1, new knowledge completely overrides the previously learned knowledge of the control agent.

However, when the complexity of the environment significantly increases, traditional reinforcement learning methods often need help to manage it. This complexity may arise from a sharp expansion in the number of actions or states in the environment, and relying solely on specific methods becomes ineffective in addressing such generalization challenges. At this point, deep learning demonstrates its unique value: neural networks can learn abstract features of states and actions and estimate potential rewards based on historical data. In recent years, the integration of reinforcement learning with deep neural networks has led to the emergence of DRL. This new field opens up vast possibilities for applying reinforcement learning in complex real-world environments. DRL algorithms cleverly combine both advantages, allowing reinforcement learning to leverage the powerful representation, efficiency, and flexibility of deep learning [32].

Deep reinforcement learning algorithms, mainly DQN, DDPG, Double Deep Q-Network, and others, combine the strengths of deep learning and reinforcement learning to handle problems with high-dimensional and continuous action spaces. One commonly used method in deep reinforcement learning is using neural networks to approximate value functions, such as Q-functions or value functions. This allows for modeling and solving high-dimensional problems by handling complex state and action spaces. Deep reinforcement learning also involves optimizing the agent’s policy to maximize long-term rewards during interactions with the environment. Policy optimization methods include value iteration, policy gradients, etc., which can be implemented for end-to-end learning in combination with deep learning. In deep reinforcement learning, balancing exploration and exploitation is a crucial issue. One of the keys to designing deep reinforcement learning algorithms is determining how to adequately explore the environment while effectively utilizing existing knowledge.

3.2. Smart Energy Building

Smart energy buildings leverage intelligent technologies and energy management systems to achieve efficient energy utilization, relying on building automation, smart control, and sensing technologies. These technologies enable intelligent control and management of building facilities, enhancing energy utilization efficiency and reducing energy consumption. The sustainable development theory emphasizes the coordinated development of the economy, society, and environment. Smart energy buildings achieve sustainable growth through energy conservation, emission reduction, and the application of environmentally friendly technologies [33].

Building thermal control is crucial for providing a high-quality working and living environment. Only when the temperature and humidity of indoor thermal conditions fall within the thermal comfort zone can the occupants of the building maintain a thermally comfortable state, ensuring the smooth progress of work and life. However, environmental thermal conditions may undergo drastic changes, leading to fluctuations in indoor thermal conditions and discomfort for occupants. Therefore, building thermal control is necessary to maintain acceptable indoor thermal conditions.

HVAC systems regulate indoor temperature, humidity, and air quality, involving thermodynamics, fluid mechanics, heat and mass transfer, aerodynamics, and control theory. For HVAC systems, thermodynamic principles are used to describe heat transfer, thermal efficiency, etc.; fluid mechanics principles describe the flow characteristics of air and water in pipes, including velocity distribution, resistance losses, etc.; heat and mass transfer principles describe the transfer processes of heat and moisture in the system, including heat exchanger design, evaporative cooling, etc.; aerodynamics principles describe the flow characteristics of air in ventilation systems, including wind speed, wind pressure, airflow distribution, etc.; and control theory is used to design and optimize the control strategies of the system to achieve the precise control of indoor environmental parameters such as temperature and humidity. Energy efficiency is key in the design of HVAC systems, focusing on the energy utilization rate, energy savings, and system optimization [34].

3.3. Soft Actor–Critic

In the algorithm presented in this paper, an improved version of the SAC algorithm, a deep reinforcement learning control algorithm, is employed. SAC is an off-policy algorithm based on the maximum entropy RL framework introduced by Haarnoja et al. [35]. Unlike Q-learning, SAC can handle continuous action spaces, enhancing its applicability to various control problems. SAC utilizes a specific Actor–Critic architecture that approximates the action-value and state-value functions using two distinct deep neural networks. The Actor maps the current state to what it estimates as the optimal action, while the Critic evaluates the action by computing the value function. A key feature of SAC is entropy regularization, and the algorithm is based on the maximum entropy RL framework with the objective, as stated in Equation (4), of maximizing both the expected return and entropy [36].

$$\pi *=\arg \underset{\pi }{max}{\mathbb{E}}_{\pi }\left[\sum _{t=0}^{\infty }{\gamma }^t\left({\gamma }_t+\alpha H^{{\pi }_t}\right)\right],H\left(\pi (·\mid s_t)\right)=\mathbb{E}\left[-\log \pi (·\mid s_t)\right]$$

(4)

where H is the Shannon entropy term, which expresses the attitude of the agent in taking random actions, and $\alpha$ is a regularization coefficient that indicates the importance of the entropy term over the reward. Generally, $\alpha$ is zero when considering conventional reinforcement learning algorithms.

The strategy employed to update the found maximum total reward involves the entropy regularization coefficient, which controls the significance of entropy. This coefficient, denoted as $H\left(\pi (·\mid s_t)\right)$, represents the entropy value; a higher entropy value indicates greater exploration of the environment by the algorithm, thereby enhancing its exploratory nature. This helps to identify a relatively efficient strategy and accelerates subsequent policy learning.

The Bellman equation for the soft policy evaluation in SAC is given by Equation (5):

$$Q^{\pi }(s_t,a_t)=r_t+\gamma {\mathbb{E}}_{s_{t+1},a_{t+1}}\left[Q^{\pi }(s_{t+1},a_{t+1})-\alpha \log \pi (a_{t+1}\mid s_{t+1})\right]$$

(5)

Furthermore, this paper considers another deep reinforcement learning algorithm, the DSAC [37]. This algorithm improves policy performance by mitigating the overestimation of q-values. The DSAC algorithm first defines the random variable for the soft state–action return, as shown in Equation (6):

$$Z^{\pi }(s_t,a_t)=r_t+\gamma G_{t+1}$$

(6)

where $G_t$ represents the cumulative entropy-augmented reward obtained from state $s_t$, given by Equation (7):

$$G_t=\sum _{i=t}^{\infty }{\gamma }^{i-1}\left[r_t-\alpha \log \pi \left(a_i\right|s_i)\right]$$

(7)

The policy for the distributional soft policy iteration can then be derived, as shown in Equation (8):

$$Q^{\pi }(s,a)=\mathbb{E}\left[Z^{\pi }(s,a)\right]$$

(8)

The function is defined as a mapping to the distribution over soft state–action returns, referred to as the soft state–action return distribution or simply the value distribution. Based on this definition, the distributional soft Bellman equation in the DSAC algorithm is given by Equation (9):

$${\mathbb{T}}_{\mathrm{D}}^{\pi }Z(s_t,a_t)\stackrel{D}{=}r+\gamma \left(Z(s_{t+1},a_{t+1})-\alpha \log \pi (s_{t+1},a_{t+1})\right)$$

(9)

where

$$A\stackrel{D}{=}B$$

indicates that A and B have the same probability distribution.

4. Analysis and Design of the SSAC-HVAC Algorithm

The objective of this paper is to design a more stable deep reinforcement learning algorithm and apply it to HVAC systems to address issues such as low convergence performance and significant fluctuations during the transition to winter that arise during the training process of HVAC systems based on deep reinforcement learning. Therefore, this paper first formalizes the problem under investigation and then introduces the deep reinforcement learning model used in this study, followed by corresponding improvements tailored to address the issues above.

4.1. Formal Definition of the Research Problem

The goal of using deep reinforcement learning to control HVAC systems is to find an optimal strategy that maximizes human thermal comfort while minimizing energy consumption. Therefore, the objectives of this paper are as follows:

In terms of electrical consumption, this paper seeks a strategy to minimize it, as shown in Equation (10):

$$\pi *=\arg \underset{{\pi }_{\theta }}{min}\sum _{t=1}^T\cos \mathrm{t}\left(A_t\right)$$

(10)

In terms of comfort, this paper seeks a strategy to optimize human comfort, as shown in Equation (11):

$$\pi *=\arg \underset{{\pi }_{\theta }}{max}\sum _{t=1}^T\mathrm{comfort}\left(S_t\right)$$

(11)

Combining the minimization of electrical consumption with the optimization of comfort constitutes the overall objective of this paper, as represented in Equation (12):

$$\pi *=\omega \underset{{\pi }_{\theta }}{\arg min}\sum _{t=1}^T\cos \mathrm{t}\left(A_t\right)+(1-\omega )\underset{{\pi }_{\theta }}{\arg max}\sum _{t=1}^T\mathrm{comfort}\left(S_t\right)$$

(12)

where $\omega$ and $(1-\omega )$ are the weights assigned to each component. When considering lower electrical consumption, $\omega <0.5$; when considering optimal human thermal comfort, $\omega >0.5$.

4.2. Overview of the SSAC-HVAC Algorithm

Based on the problem formally defined in Section 4.1, this paper proposes an HVAC system algorithm, namely, the Steady Soft Actor–Critic for HVAC (SSAC-HVAC) algorithm.

Firstly, in the process of regulating the HVAC system, to mitigate the issue where some actions cannot be sampled during deep reinforcement learning training, leading to difficulties in convergence and a tendency to fall into local optimal solutions, this paper adopts the optimization strategy of the SAC method. This facilitates more exploration during training, enhancing convergence performance. Although SAC employs a double Q-network design to improve stability, its stability performance still needs to improve during HVAC system training. This paper introduces distributional soft policy iteration, which defines the soft state–action return of the policy as a random variable. Based on this definition, the distributional Bellman equation is derived, as shown in Equation (9). Compared to the Bellman equation for soft policy evaluation, this approach replaces the target Q-value with a stochastic target return, thereby enhancing the exploration of the algorithm. While increasing exploration, this may affect the related gradients’ stability, reducing the learning process’s stability and efficiency. Therefore, this paper considers combining the strength of the target Q-value with the high exploration of stochastic targets.

When calculating the target Q-value, SAC uses a double Q-network. In each training round, the smaller Q-value is selected to update the target network when searching for the optimal policy to prevent overestimation during training. The random variable for the soft state–action return is introduced in Equation (6). When searching for the optimal policy, the minimum value between the double Q and the random variable is chosen for updating. After the update, the target network is used to update the Critic network and the Actor network, constructing the gradients for the Critic and Actor for the next update.

The main steps of the SSAC-HVAC algorithm are as follows:

• Initialization: This crucial step sets the foundation for the entire SSAC-HVAC algorithm. It involves initializing the policy network (Actor network) and two Q-value networks (Critic networks), as well as their target networks (Target networks). The initial parameters of the target networks are set to be the same as the current network parameters, ensuring a consistent starting point.
• Data Sampling: In each time step, an action is sampled from the environment according to the current policy network and exploration strategy, the action is executed, and the environment’s feedback is observed to obtain the reward and the next state.
• Calculate Q-values: The two Q-value networks are used to separately calculate the Q-values corresponding to the current state–action pair, and the smaller one is selected as the Q-value for the current state–action pair. Simultaneously, the target Q-value is calculated, which is the smaller value between the obtained Q-value and the stochastic target return plus the current reward;
• Update Critic Networks: The parameters of the two Q-value networks are updated by minimizing the loss function of the Critic networks so that the Q-values of the current state–action pairs approximate the target Q-values.
• Calculate Policy Loss: Based on the output of the Critic networks, the policy network’s loss function is calculated, aiming to maximize the Q-values for the actions output by the policy network.
• Update Actor Network: The parameters of the policy network are updated by minimizing the policy loss, a process that is heavily influenced by the Critic networks. This interdependence ensures that the performance of the policy network is continually improved.
• Update Target Networks: A soft update method is adopted to gradually update the parameters of the current networks to the target networks, stabilizing the training process.
• Repeat Steps 2 to 7: The training process is iterative, requiring persistence and dedication. The above steps are repeated until the preset number of training rounds specified before training begins is reached, or until the stopping condition is met.

4.3. Strategy Model Based on SSAC

Based on the execution steps, the SSAC-HVAC algorithm designed in this paper can be divided into the specific design of the SSAC algorithm and the settings of the state space, action space, and reward function in the HVAC domain. Therefore, this subsection will introduce the SSAC-HVAC algorithm in two parts.

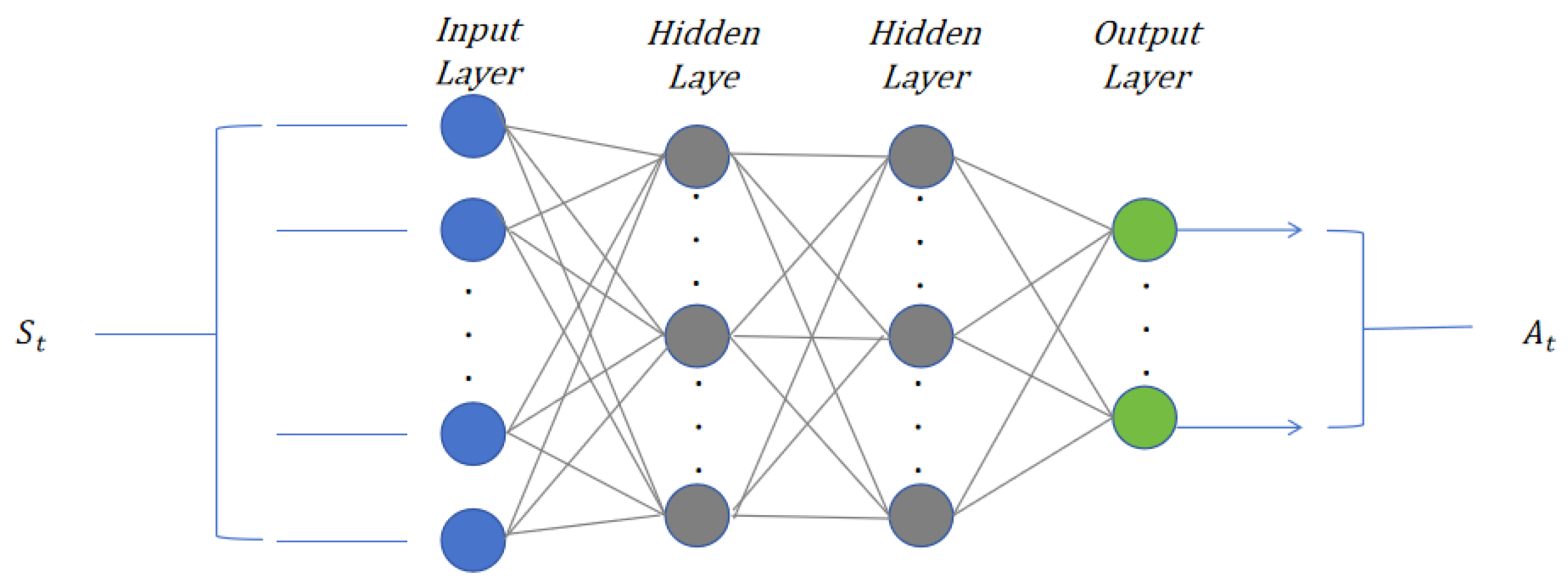
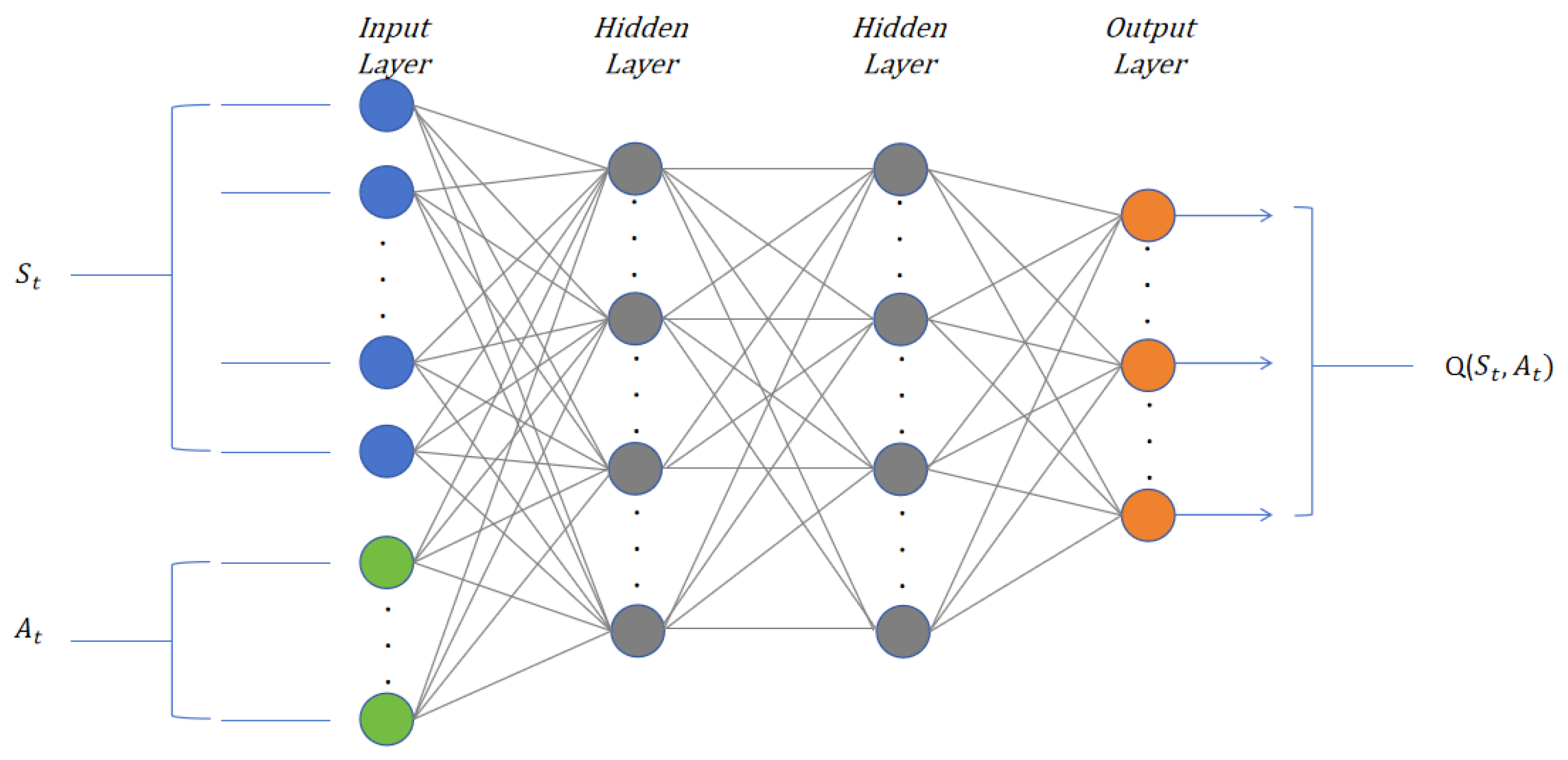
The algorithm proposed in this paper is based on the SSAC-HVAC algorithm, which considers both the exploration and stability of the algorithm, addressing reinforcement learning problems in continuous action spaces. In this algorithm, the agent has an Actor and Critic network. The network structures are shown in Figure 2 and Figure 3, respectively, consisting of an input layer, two hidden layers with activation functions, and an output layer. The input of the Actor network is the state $s_t$, and the output is the action $a_t$, which is used to approximate the action policy. The input of the Critic network is the state $s_t$ and action $a_t$, and the output is the state–action value function $Q(s_t,a_t)$.

Upon obtaining the initial state, the agent uses the Actor network to acquire the probabilities of all actions $\pi \left(a\right|s_t)$. At the beginning of each time step t, an action $a_t=a_2$ is sampled based on these probabilities according to the SSAC algorithm. The selected action $a_t$ is then input into the established reinforcement learning environment, resulting in the state $s_{t+1}$ and reward $r_{t+1}$ for the next time step. The obtained action, state, and reward are combined into a transition tuple $(s_t,a_t,s_{t+1},r_{t+1})$, which is subsequently placed into the experience pool R. In each training round, the traditional SAC algorithm updates the target value function using a double Q-network format [38], selecting the minimum Q-value to help avoid overestimation and the generation of inappropriate Q-values. The traditional objective function equation is

$$y_i=r_i+\gamma \underset{j=1,2}{min}{Q}_{{\varphi }_j^{-}}(s_{i+1},a_{i+1})-\alpha \log {\pi }_{\theta }\left(a_{i+1}\mid s_{i+1}\right)$$

(13)

where $a_{i+1}={\pi }_{\theta }(·\mid s_{i+1})$. In this paper, by combining the soft policy Bellman equation and the distributed Bellman equation, Equation (14) is introduced into the traditional objective function. This equation is compared with the Q-values in the double Q-network, and the minimum value is selected as the Q-value for the next time step. Therefore, the calculation of the objective function is updated to

$$y_i=r_i+\gamma P(s_{i+1},a_{i+1})-\alpha \log {\pi }_{\theta }(a_{i+1}\mid s_{i+1})$$

(14)

where $P(s_{i+1},a_{i+1})=min\left\{\mathbb{E}\left[Z^{\pi }(s,a)\right],{min}_{j=1,2}{Q}_{{\varphi }_j^{-}}(s_{i+1},a_{i+1})\right\}$.

After updating, the new Q-values are used to calculate the loss functions for each network. By minimizing these loss values, the optimal policy is selected to reduce the return values for state–action pairs in this study. The loss function for updating the current Actor network is shown in Equation (15).

$$L_{\pi }\left(\theta \right)={\displaystyle \frac{1}{N}}\sum _{i=1}^N\left(\alpha \log {\pi }_{\theta }(a_i\mid s_i)-P(s_i,a_i)\right)$$

(15)

The loss function for updating the Q-function, using the updated Q-values, is presented in Equation (16). This helps to mitigate the issue of overestimation caused by excessively high Q-values.

$$L_Q\left(\omega \right)={\mathbb{E}}_{(s_t,a_t,r_t,s_{t+1})\sim \mathcal{R}}\left[{\displaystyle \frac{1}{2}}{\left(Q_{\omega }(s_t,a_t)-\left(y(r_t,s_{t+1})\right)\right)}^2\right]$$

(16)

Algorithm 1 displays the pseudocode for the complete process of the SSAC algorithm. After calculating the target values, the Q-values, the policy, and the target networks are updated. The updated target values can further reduce the overestimation error, and the policy typically avoids actions with underestimated values. Simultaneously, the updated target values can also result in underestimated Q-values, serving as a performance lower bound for policy optimization and enhancing learning stability.

In deep reinforcement learning, concepts such as state, action, and reward are fundamental. The research content of this paper focuses on optimizing control strategies for HVAC systems. Hence, these concepts carry specific meanings within this context. The policy model based on SSAC can output the correct control actions based on the input environmental parameters, thereby minimizing electricity consumption and optimizing comfort. After the completion of Algorithm 1, at each time step, an action $a_t$ to be taken, i.e., adjusting the set temperature of the air conditioning, will be determined based on the current state $s_t$. At the end of the current time step, the next state $s_{t+1}$ will be returned, and the above steps will be repeated to carry out the execution algorithm. The execution algorithm pseudocode (Algorithm 2) is shown below.

Algorithm 1: Steady Soft Actor–Critic

Algorithm 2: Execute

The following instantiates the research problem of this paper into the relevant concepts of deep reinforcement learning, facilitating the subsequent experiments and research in this paper.

• State Space
  The HVAC system primarily considers human thermal comfort within a given area, and the state space should be set accordingly. The current state serves as the basis for determining the following action, and the assumed values of the state variables influence the control actions. Based on the simulation environment set up by EnergyPlus in Section 5.1, the model’s state consists of three components: indoor temperature, outdoor dry-bulb temperature, and outdoor humidity. This can be represented as a vector:

  $$S=[T_{\mathrm{in}},T_{\mathrm{out}},H_{\mathrm{out}}]$$

  where S represents the state, and $T_{\mathrm{in}}$, $T_{\mathrm{out}}$, and $H_{\mathrm{out}}$ are the indoor temperature, outdoor temperature, and outdoor humidity, respectively. This study employs the continuous state space SSAC algorithm, so the state space of the model is composed of a three-dimensional space of all possible state values S.
• Action Space
  In this study, the SSAC algorithm is employed, featuring a continuous action space. The controller is responsible for adjusting the air conditioning temperature, with an action space spanning from 15 °C to 30 °C. Thus, the selected action is formulated as follows:

  $$A_t=\{T_{\mathrm{set}}\mid 15\le T_{\mathrm{set}}\le 30\}$$
  No penalty is imposed when the selected action is within the action space. If the chosen action exceeds the action space, a corresponding penalty is applied to the exceeding temperature, as reflected in Equation (11).
• Reward Function
  In the HVAC system, the reward function needs to consider two components: one related to electricity consumption and the other related to temperature. These are combined using weights $\omega$ to alter their relative importance. The reward function adopted in this paper penalizes violations, with the total value of the reward function being negative to penalize both electricity consumption and temperatures exceeding the action space. The SSAC algorithm introduces the optimal control strategy using Equation (13). $r_E$ represents the electricity consumed by changes in air conditioning temperature, with units of kWh, and $r_T$ represents the difference between the set temperature and the temperature exceeding the set temperature in the action space, with units of °C. In this study, considering both electricity consumption and human comfort, the general expression of the reward function is given by Equation (17):

  $$\mathbf{r}=\omega {\mathbf{r}}_{\mathbf{T}}+(1-\omega ){\mathbf{r}}_{\mathbf{E}}$$

  (17)

  where the coefficients $\omega$ and $(1-\omega )$ are the weights assigned to the two parts of the reward, used to balance their relative importance. By adjusting the weight coefficients, the electricity consumption term and the temperature term can be flexibly adjusted. When $\omega$ is reduced, the importance of electricity consumption increases, and conversely, the importance of temperature, i.e., human comfort, increases.
  In the reward function, the temperature term is considered in three different expressions, classified according to whether the controlled action, i.e., the set air conditioning temperature, exceeds the action space. It is assumed that when the set temperature is within the action space, the occupants will feel comfortable, and no penalty will be incurred; otherwise, a corresponding penalty will be imposed. The specific temperature-related term is given by Equation (18):

  $$r_T=\left\{\begin{array}{cc}0,\hfill & \mathrm{if}{T}_{min}\le T_{\mathrm{set}}\le T_{max}\hfill \\ -(T_{\mathrm{set}}-T_{max}),\hfill & \mathrm{if}{T}_{\mathrm{set}}>T_{max}\hfill \\ -(T_{min}-T_{\mathrm{set}}),\hfill & \mathrm{if}{T}_{\mathrm{set}}<T_{min}\hfill \end{array}\right.$$

  (18)

  where $T_{min}$ and $T_{max}$ represent the minimum and maximum temperatures in the action space, which are 15 °C and 30 °C, respectively.
  In the reward function, the term related to HVAC system electricity consumption is defined by Equation (19):

  $$r_E=-\delta E_{\mathrm{heat}}$$

  (19)

  where $E_{\mathrm{heat}}$ is the electricity consumption at the current time step, and $\delta ={10}^{-7}$ is a coefficient. This coefficient balances the electricity consumption term with the temperature penalty, ensuring they are of the same order of magnitude, thus preventing the electricity consumption term $r_E$ from overwhelming the temperature-related term.
• Network Architecture
  The SSAC algorithm includes five neural networks: the Actor network, two Q-value networks, a target network, and a value network. The Actor network is the policy network that outputs actions for a given state. It is typically a deep neural network, which can be either a fully connected neural network or a convolutional neural network. The input is the current state, and the output is the probability distribution of each action in the action space. The Critic network, a pivotal part of the SSAC algorithm, is the value function network that rigorously evaluates the value of state–action pairs. In the SSAC algorithm used in this paper, two Q-value networks are employed to estimate the Q-values of state–action pairs in order to reduce estimation bias. These two Q-value networks can also be deep neural networks, with the input being the current state and action and the output being the corresponding Q-value. The SAC algorithm, in its quest for stability, relies on a target network to estimate the target Q-values. The target network, a copy of the Critic network, plays a crucial role in reducing oscillations during training by slowly updating its parameters to match the parameters of the current network. In the SAC algorithm, apart from the two Q-value networks, there is also a value network that estimates the value of states. The value network can also be a deep neural network, with the input being the current state and the output being the value of the state.

5. Evaluation

5.1. Experimental Setup

In this paper, EnergyPlus software (https://energyplus.net/, accessed on 5 February 2025) was utilized for collaborative simulation. EnergyPlus is building energy simulation software designed to evaluate buildings’ energy consumption and thermal comfort under various design and operational conditions. The following are the general steps for conducting simulations using EnergyPlus:

Model Construction: Create a building model using EnergyPlus’s model editor or other building information modeling software (such as OpenStudio can be downloaded at https://openstudio.net/, accessed on 5 February 2025). This includes the building’s geometry, structure, external environment, internal loads, HVAC systems, etc.

Definition of Simulation Parameters: Define the parameters for the simulation, such as the time range, time step, and weather data file.

Setting Simulation Options: Configure simulation options, including the running mode (design day, typical meteorological year, etc.) and the level of detail in the output results.

Running the Simulation: Before executing the EnergyPlus simulation, it is important to define the conditions. This action ensures the relevance of the results, such as the building’s energy consumption and indoor comfort.

In the simulation experiments conducted in this paper, an actual university lecture hall was modeled. The selected weather file is a typical meteorological year from the EnergyPlus official website. The HVAC system is configured with air-handling units for supply and exhaust air, with the target actuator set as the supply air temperature setpoint. The simulation environment is set in Miliana, Algeria, and specific city parameters are presented in

Table 1. Simulation environment parameters.

Parameter Name	Parameter Value
Name	Miliana
Latitude	36.3
Longitude	2.333
Time Zone	1

(more detailed building information can be downloaded at https://energyplus.net/weather-region/africa_wmo_region_1/DZA, accessed on 5 February 2025).

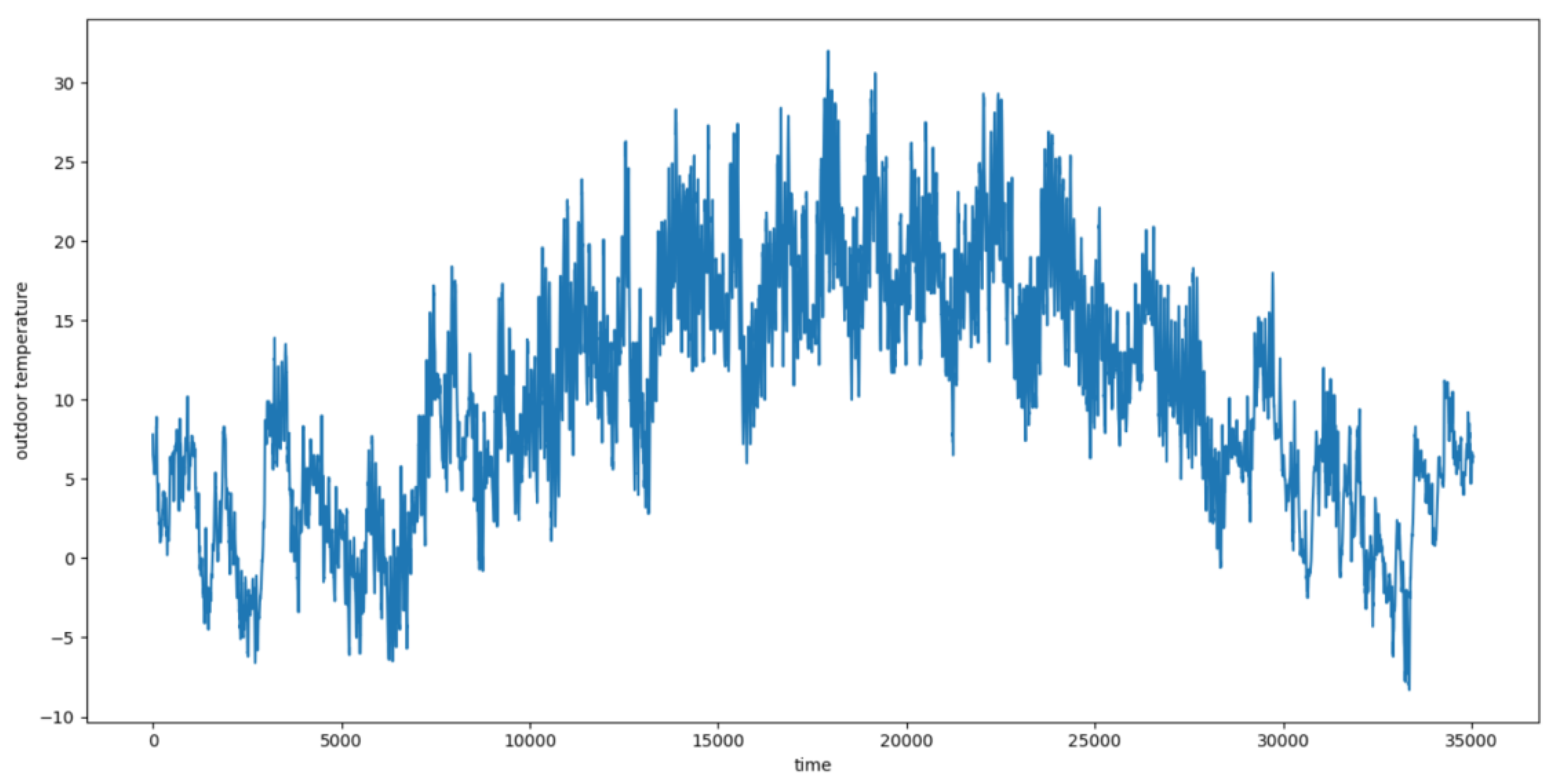
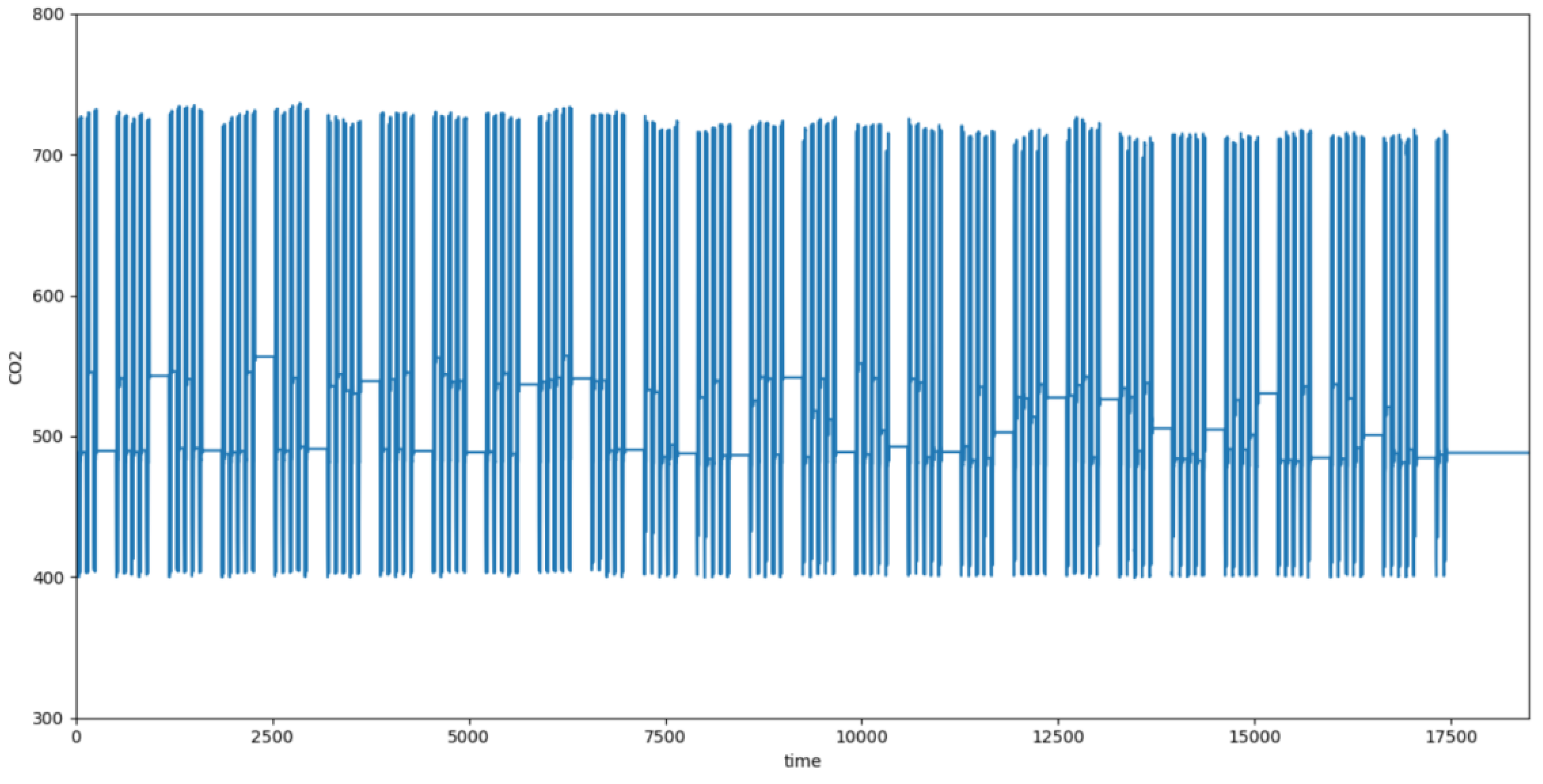
Figure 4 and Figure 5 present the real-time outdoor temperature throughout the year for the simulated building and the carbon dioxide concentration in the building’s region over the same period. Each day consists of 96 time steps, with each time step representing a 15 min interval. The horizontal axis represents the time steps. It can be observed that the temperature variations throughout the year exhibit seasonal differences, which closely align with real-life scenarios, thereby enhancing the scalability of the algorithm. The concentrations of carbon dioxide fluctuations are relatively small throughout the year and are therefore not considered a factor influencing the profound reinforcement learning control. This allows the influencing factors to focus more on outdoor dry-bulb temperature, indoor temperature, and outdoor humidity.

User comfort is also a crucial factor to consider in a simulation environment. In order to maintain user comfort at a satisfactory level within the simulation environment, maximum and minimum values for outdoor dry-bulb temperature, indoor temperature, and concentration states have been set to solve for the optimal control strategy of the HVAC system. The specific values for these state settings are presented in

Table 2. Range of state settings for the simulation environment.

Parameter	Max Value	Min Value	Unit
Outdoor dry-bulb temperature	40	−20	°C
Indoor temperature	35	10	°C
CO2 concentration	1300	0	ppm

.

When employing the SSAC algorithm for deep reinforcement learning control of the HVAC system, to ensure the rationality and comparability of hyperparameter selection, we referred to the relevant literature during the experimental design process, particularly the work by [39]. To effectively compare our results with those presented in this study from the literature, we directly adopted hyperparameter values that had been validated and demonstrated exemplary performance in the literature. Subsequently, we further verified the effectiveness of these parameter settings through our experiments, and the final determined hyperparameter values are presented in

Table 3. Hyperparameter settings for the simulation environment.

Parameter Name	Value
BATCH_SIZE	32
Discount factor	0.9
Initial $\epsilon$ value	0.9
Final $\epsilon$ value	0.05
Rate for softly updating target network parameters	0.005
$\epsilon$ Decay Rate	1000
Learning rate for Actor network	0.0003
Learning rate for Critic network	0.1
Entropy regularization coefficient	0.2
Weight $\omega$	0.5

.

The main parameters used in the proposed algorithm and model are as follows: The BATCH_SIZE is set to 32, and the discount factor for reinforcement learning is set to 0.9, serving to balance the importance of current and future rewards. A larger discount factor indicates the importance of future rewards. The initial value $\epsilon$, used for exploring the environment, ultimately represents the final $\epsilon$ value in the policy $\epsilon -\mathrm{greedy}$, which gradually decreases as training progresses. The rate for softly updating the target network parameters is used to reduce the magnitude of changes in the target network parameters. The learning rates for the Actor and Critic networks play crucial roles in these networks, influencing the convergence speed, performance, and stability of the algorithm. The entropy regularization coefficient controls the importance of entropy. For the SSAC algorithm, there are two ways to utilize entropy: one is to use a fixed entropy regularization coefficient, and the other is to automatically solve for the entropy regularization coefficient during training. In the simulation environment set up for this paper, a fixed regularization coefficient was used, while in the inverted pendulum environment and the 3D bipedal agent environment, the entropy regularization coefficient was automatically solved during training.

5.2. Analysis of Evaluation Results

In this paper, the proposed algorithm is evaluated. We primarily compare the performance of the proposed SSAC algorithm with the traditional SAC algorithm in the context of HVAC system control. However, to more comprehensively assess the performance of the SSAC algorithm, we have consulted a relevant study in the literature [39] that conducted extensive experimental comparisons between the SAC algorithm and other deep reinforcement learning algorithms (such as PPO and TD3). The study concludes that the SAC algorithm outperforms these algorithms on multiple key metrics. Therefore, in this section, we focus on comparing the performance of the SSAC algorithm with the traditional SAC algorithm. For the HVAC system problem, the reward function in this paper penalizes violations, including penalties for power consumption and temperatures exceeding the human comfort range; thus, the reward values are always negative.

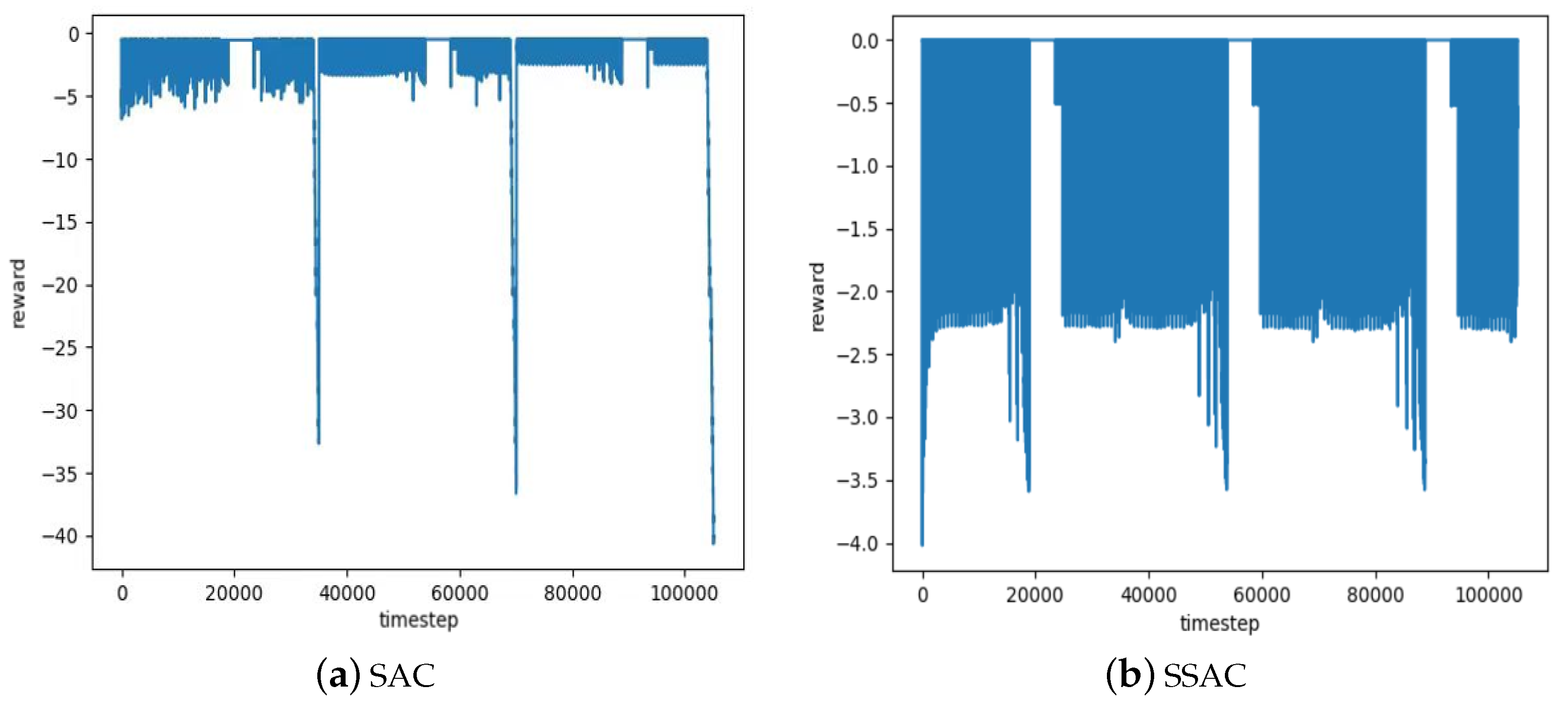
Regarding the convergence of the algorithm, Figure 6a,b show the convergence process of the action–state return values obtained by solving the HVAC system problem using the traditional SAC algorithm and the proposed SSAC algorithm, respectively. The training was conducted using weather data from the three years spanning from 2020 to 2023, with a final training time step of 100,000. The convergence processes of the reward functions using the SAC algorithm and the SSAC algorithm are presented in Figure 6a,b, respectively. The following conclusions can be drawn through comparison.

At around 35,000 steps, the cumulative return of the SAC algorithm tends to stabilize, meaning that the return values of action–state pairs reach a steady state. On the other hand, the SSAC algorithm stabilizes at around 20,000 steps and can make corresponding decisions. Therefore, the SSAC algorithm converges faster than the SAC algorithm. Due to the more minor updates to the target function, the SSAC algorithm’s loss function is smaller than that of the SAC algorithm. Consequently, the fluctuations that occur after 20,000 steps are also smaller than those of the SAC algorithm.

As the simulated building location experiences significant temperature differences across the four seasons throughout the year, there will be some fluctuations in the reward function at the moment of transitioning into winter. This issue is also considered in this paper, and through improvements, the fluctuations at the moment of entering winter are effectively reduced. Additionally, it can be seen that the SSAC algorithm converges faster than the SAC algorithm. During the subsequent training process, the SSAC algorithm also exhibits better stability than the SAC algorithm, indicating the good convergence of the SSAC algorithm.

In addition, to verify the excellent convergence of the proposed SSAC algorithm under various conditions, this paper also trained the SSAC algorithm in different environments. It compared it with the SAC algorithm in each case.

Training was conducted in both the Pendulum environment and the three-dimensional Humanoid environment. Due to the differences in these environments, the set hyperparameters differ from those in the simulation environment. The specific hyperparameter settings for the two environments are shown in

Table 4. Hyperparameter settings for two environments.

Parameter Name	Value
BATCH_SIZE	32
Discount factor	0.99
Learning rate for Actor network	0.0001
Learning rate for Critic network	0.0003
Entropy regularization coefficient	0.2

.

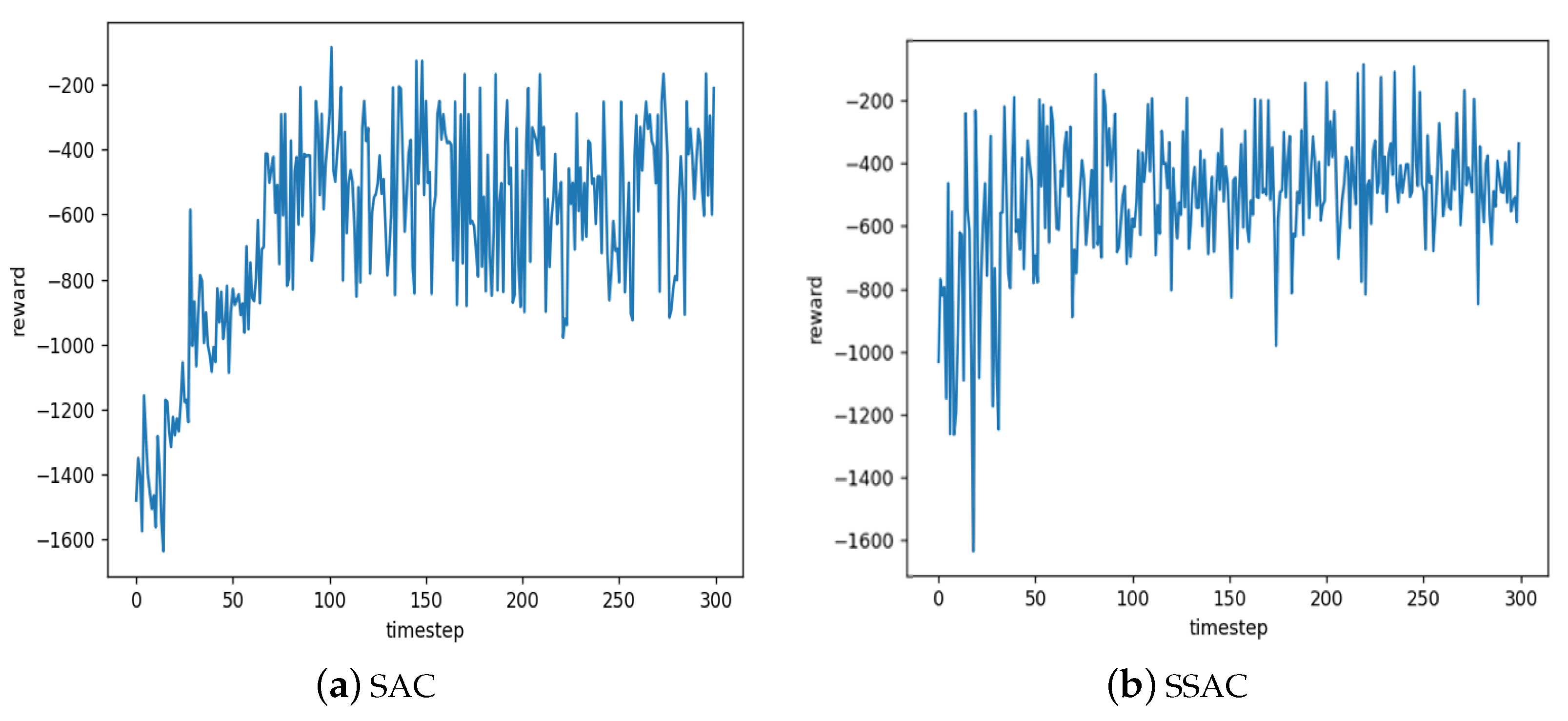
Firstly, training was conducted in the Pendulum environment for 30,000 rounds, with the rewards obtained every 100 rounds recorded in a list to facilitate algorithm comparison after training. The convergence processes of the SAC algorithm and the SSAC algorithm in this environment are shown in Figure 7a,b, respectively. The SAC algorithm begins to stabilize at around 7000 rounds, while the SSAC algorithm stabilizes at around 5000 rounds. It can be observed that the SSAC algorithm exhibits a faster convergence rate than the SAC algorithm in the inverted Pendulum environment.

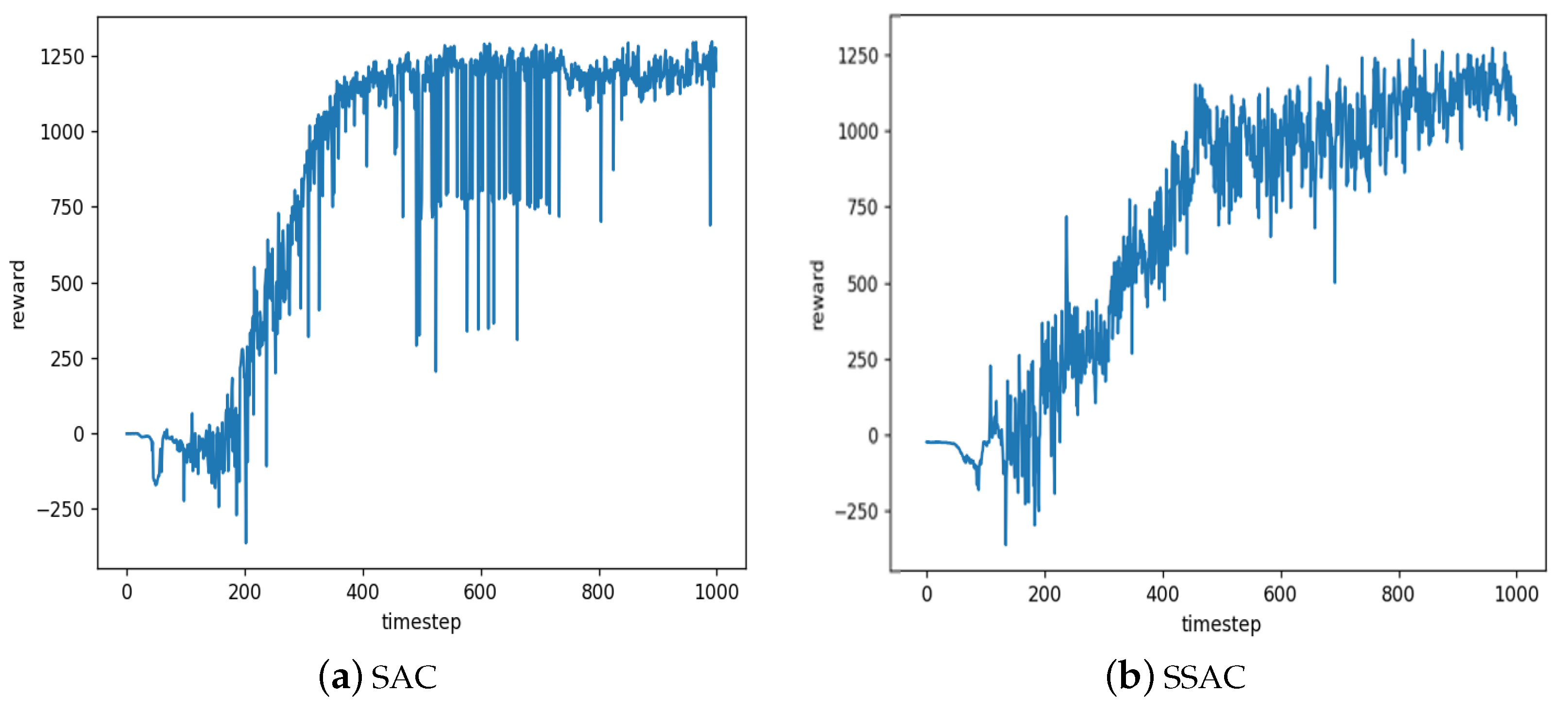
This paper also conducted training in the Humanoid environment for 100,000 rounds, with the rewards obtained every 100 rounds recorded in a list for algorithm comparison. The convergence processes of the SAC algorithm and the SSAC algorithm are illustrated in Figure 8a,b, respectively. It can be observed that during the training of the three-dimensional bipedal intelligent agent, the SSAC algorithm exhibits more minor fluctuations after stabilizing, indicating that it is more stable compared to the SAC algorithm.

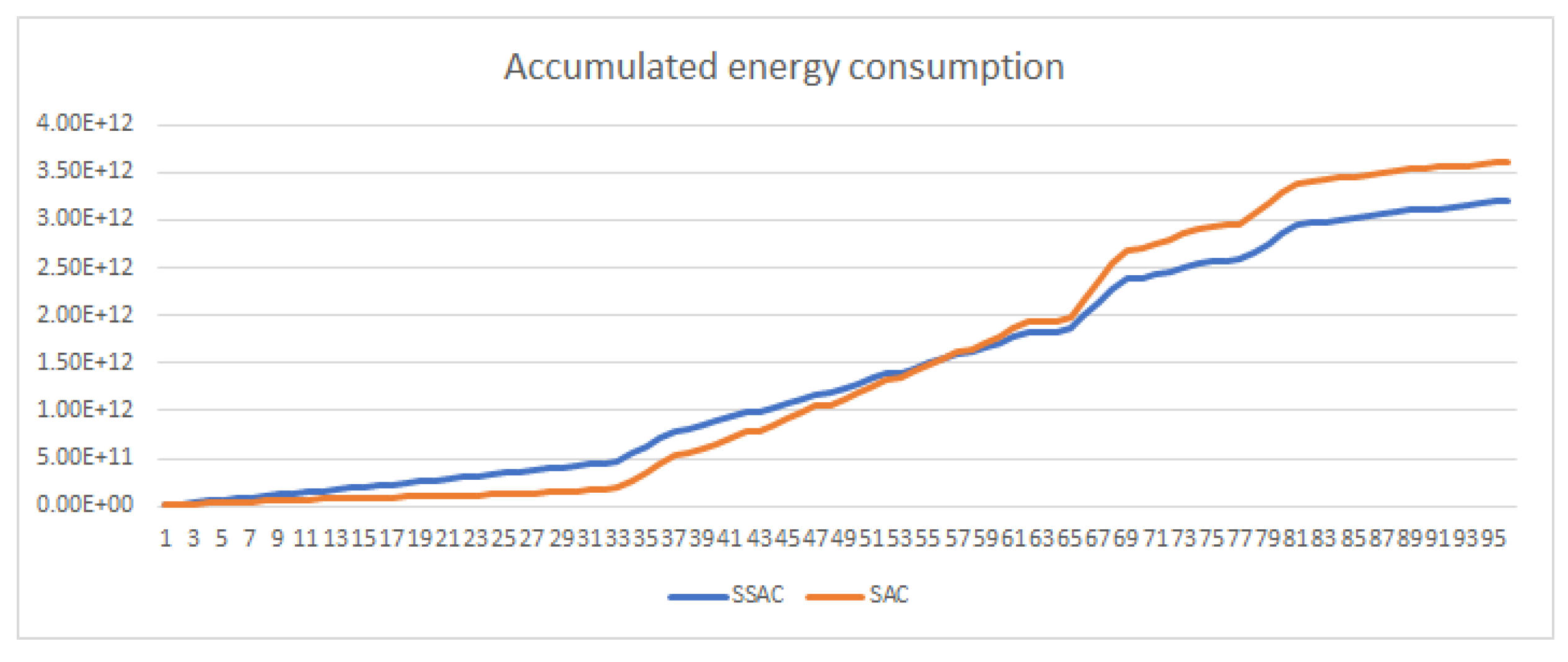
Furthermore, to demonstrate the effectiveness of the SSAC algorithm, the cumulative electricity consumption of the HVAC systems controlled by the SAC algorithm and the SSAC algorithm over 960 days is presented in the same manner as Figure 9. The horizontal axis represents the time steps, with each step corresponding to 15 min and the data being summarized and displayed every 960 time steps (i.e., 10 days). The vertical axis represents the cumulative electricity consumption. It can be observed that, while maintaining human comfort, the SSAC algorithm achieves lower cumulative electricity consumption compared to the SAC algorithm. And, the SSAC algorithm achieves cost savings of 24.2% compared to the SAC algorithm.

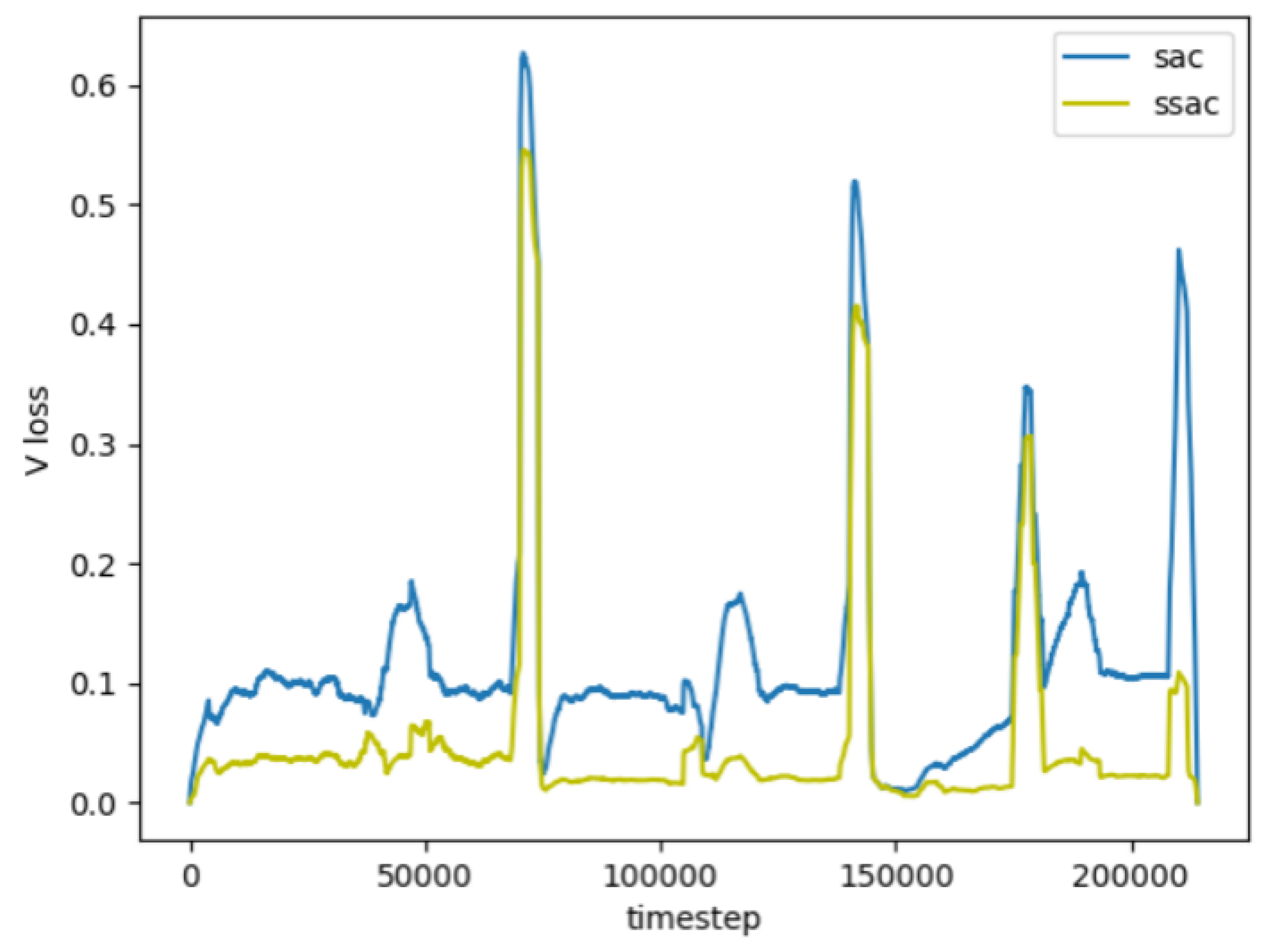
In deep reinforcement learning, Actor loss is a function that optimizes the agent’s policy during training. Specifically, when the agent takes action, it receives rewards or punishments that reflect the effectiveness of its actions. By minimizing the Actor loss, the agent can learn how to adopt the optimal policy to maximize long-term rewards or minimize long-term punishments. In the study presented in this paper, the following action is determined based on penalties for electrical consumption and human discomfort. Through improvements, a more minor Actor loss can be achieved in each training round, leading to a better policy. As shown in Figure 10, the Actor loss function of the SSAC algorithm is always smaller than that of the SAC algorithm, indicating that the SSAC algorithm outperforms the SAC algorithm in obtaining policies for the HVAC system.

In summary, by improving the objective function, the SSAC algorithm can effectively reduce the Actor loss value. The HVAC system can significantly decrease energy consumption while maintaining human comfort. Simultaneously, it facilitates the rapid convergence of the reward function, i.e., the action–state reward, in deep reinforcement learning control. Across various environments, the SSAC algorithm demonstrates a superior convergence process compared to the SAC algorithm. It is noteworthy that Reference [39] has already proven that the SAC algorithm outperforms other deep reinforcement learning algorithms, such as PPO and TD3, in multiple aspects. Furthermore, the SSAC-HVAC algorithm proposed in this paper, after further optimization, exhibits advantages over the SAC algorithm in all aspects. Therefore, it is reasonable to infer that the SSAC-HVAC algorithm also possesses more outstanding performance compared to currently popular deep reinforcement learning algorithms, providing strong support for optimal strategy decision-making in HVAC systems and achieving dual improvements in energy savings and comfort.

6. Conclusions and Future Work

This paper conducts an in-depth study on control algorithms for HVAC systems based on deep reinforcement learning. Considering the difficulties in obtaining real-time indoor and outdoor temperatures and HVAC energy consumption in real-world environments, along with uncertain system parameters and the unclear impacts of other factors on human comfort, conducting this research in a real-world setting is challenging. Therefore, this paper chose to conduct training in a simulation environment. By introducing the SSAC algorithm, we propose an innovative HVAC system control strategy named the SSAC-HVAC algorithm. Based on the deep reinforcement learning model, this algorithm improves the objective function, enhancing the algorithm’s exploration capability and maintaining good stability. Experimental results demonstrate that applying the SSAC algorithm in HVAC systems significantly reduces operating costs while ensuring appropriate human comfort. Compared with the traditional SAC algorithm, the SSAC algorithm exhibits clear advantages in convergence performance and stability, achieving an energy-saving effect of, approximately 24.2%.

Although significant results have been achieved in the simulation environment, there are still many aspects that need further exploration and optimization:

• Optimizing the Interval of Control Actions: The deep reinforcement learning control proposed in this paper is based on training in a simulation environment. In real life, frequent control may result in additional electrical consumption or damage to HVAC system components. Therefore, future work should consider the control action time interval.
• Developing a Personalized Comfort Model: The current research mainly focuses on general comfort, but different populations (such as the elderly, children, patients, etc.) may have significantly different comfort requirements for indoor environments. Future research will aim to develop personalized comfort models by collecting and analyzing preference data for temperature, humidity, and other environmental factors among different populations, providing customized comfort control strategies for each group.
• Considering More Environmental Factors: In practical applications, beyond temperature, numerous other factors, such as humidity, carbon dioxide concentration, and building wall thickness, can influence human thermal comfort and energy consumption. Future research will incorporate a broader range of sensors to monitor these factors and conduct comprehensive analyses with specific building specifications. By taking into account a greater variety of environmental factors, we can more comprehensively evaluate and optimize the algorithm’s performance, making it more reliable and effective in real-world applications.
• Enhancing the Flexibility and Reliability of the Algorithm: Future research will actively collect more practical data and conduct in-depth analyses of various potential factors to address unknown factors that may arise in real-world environments. By incorporating more real-world data and feedback mechanisms, we can continuously enhance the flexibility and reliability of deep reinforcement learning control in HVAC systems, enabling them to better adapt to complex and changing environmental conditions.
• Conducting Sensitivity Analysis and Performance Comparison: Future research will undertake a thorough sensitivity analysis to evaluate the SSAC algorithm’s performance comprehensively. By simulating HVAC operation under various conditions, we will compare the performance differences between the SAC and SSAC methods in different scenarios, aiming to better understand the strengths, weaknesses, and applicable contexts of both approaches. Additionally, we will seek out more datasets related to the comfort preferences of diverse populations and conduct new experiments to validate the usability and universality of the algorithm.

Future research will focus on collecting and analyzing real-time data on these factors to improve the adaptability and robustness of the algorithm.