Technical Review of Solar Distribution Calculation Methods: Enhancing Simulation Accuracy for High-Performance and Sustainable Buildings
Abstract
1. Introduction
2. Materials and Methods
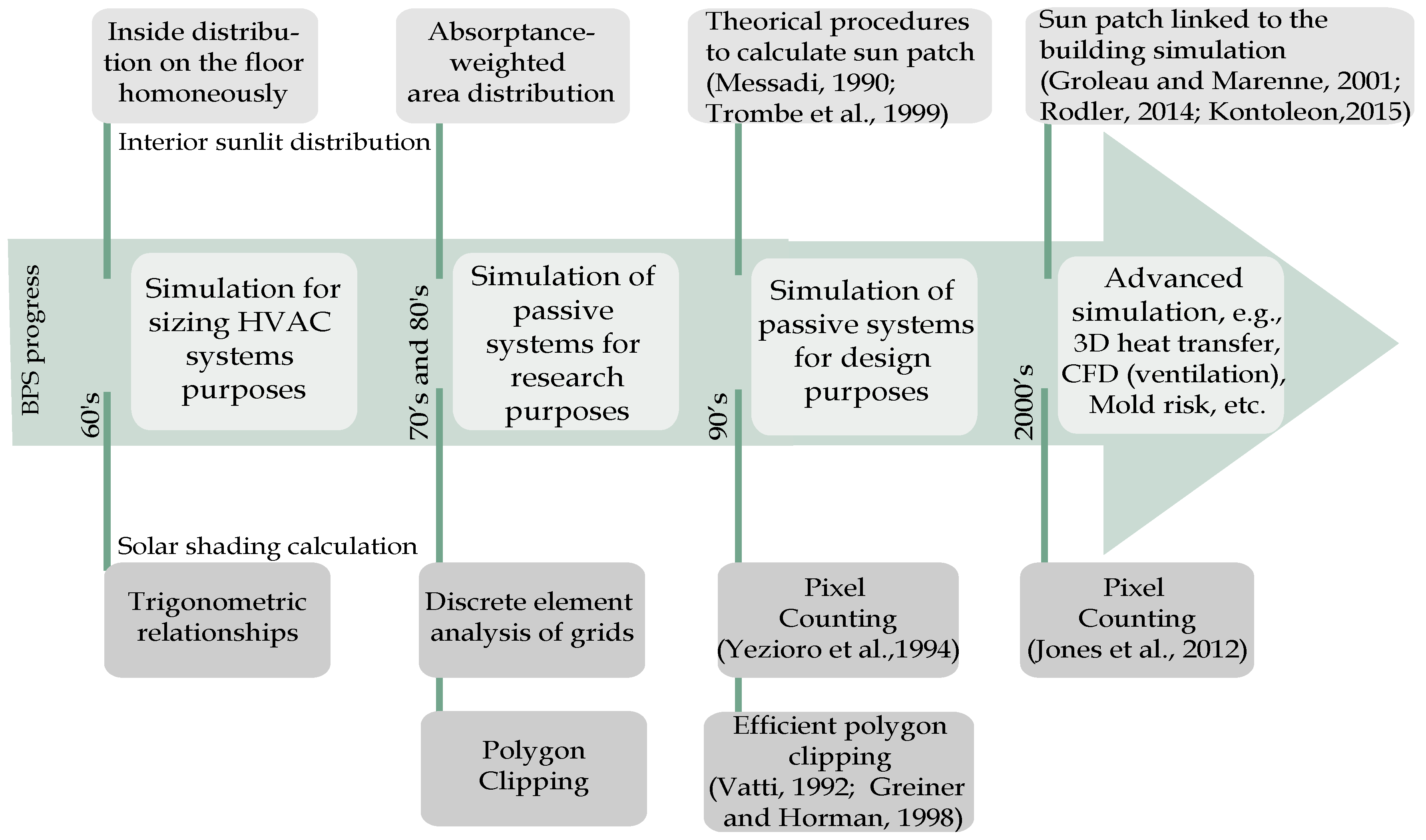
3. Timeline of Solar Shading Methods in Building Performance Simulation
4. Exterior Solar Shading Techniques
4.1. Vectorial Methods
4.2. Trigonometric Models
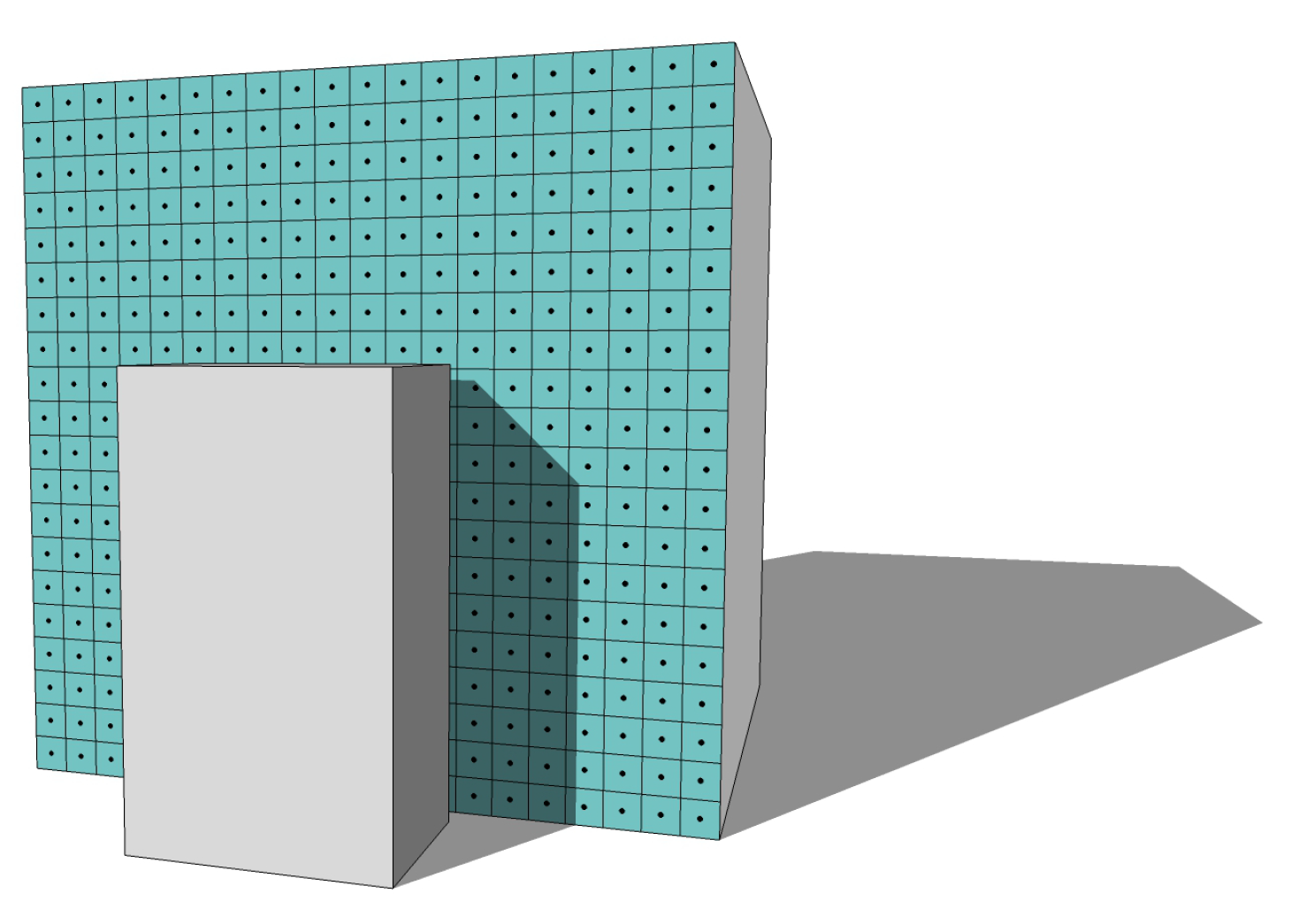
4.3. Discrete Element Analysis of Grids
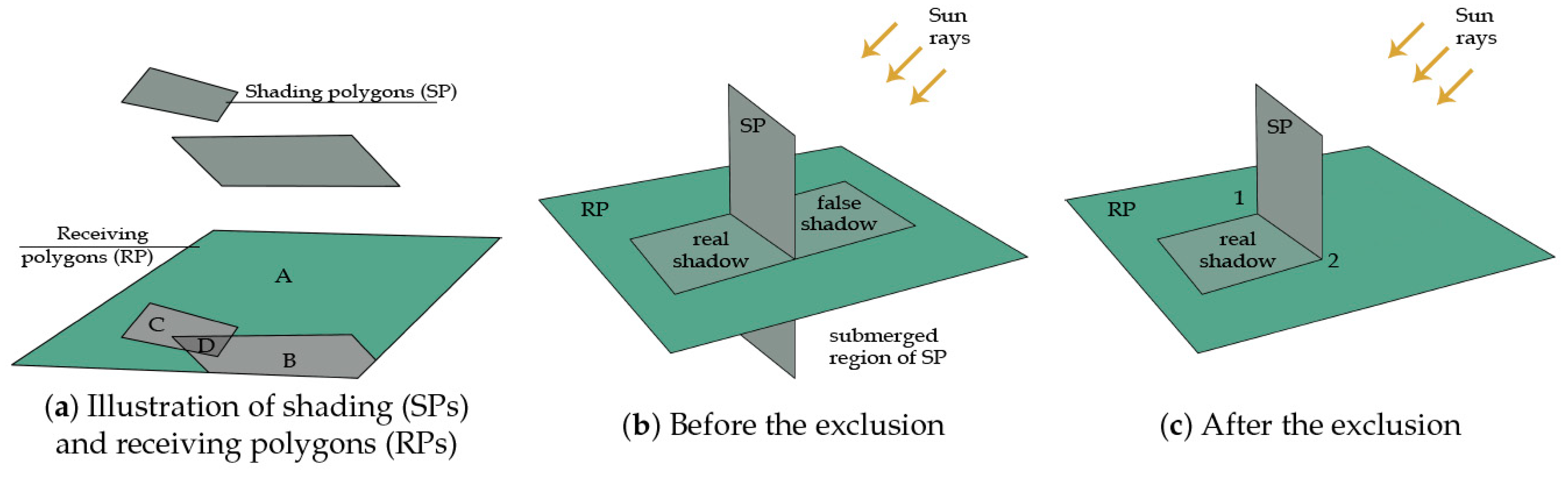
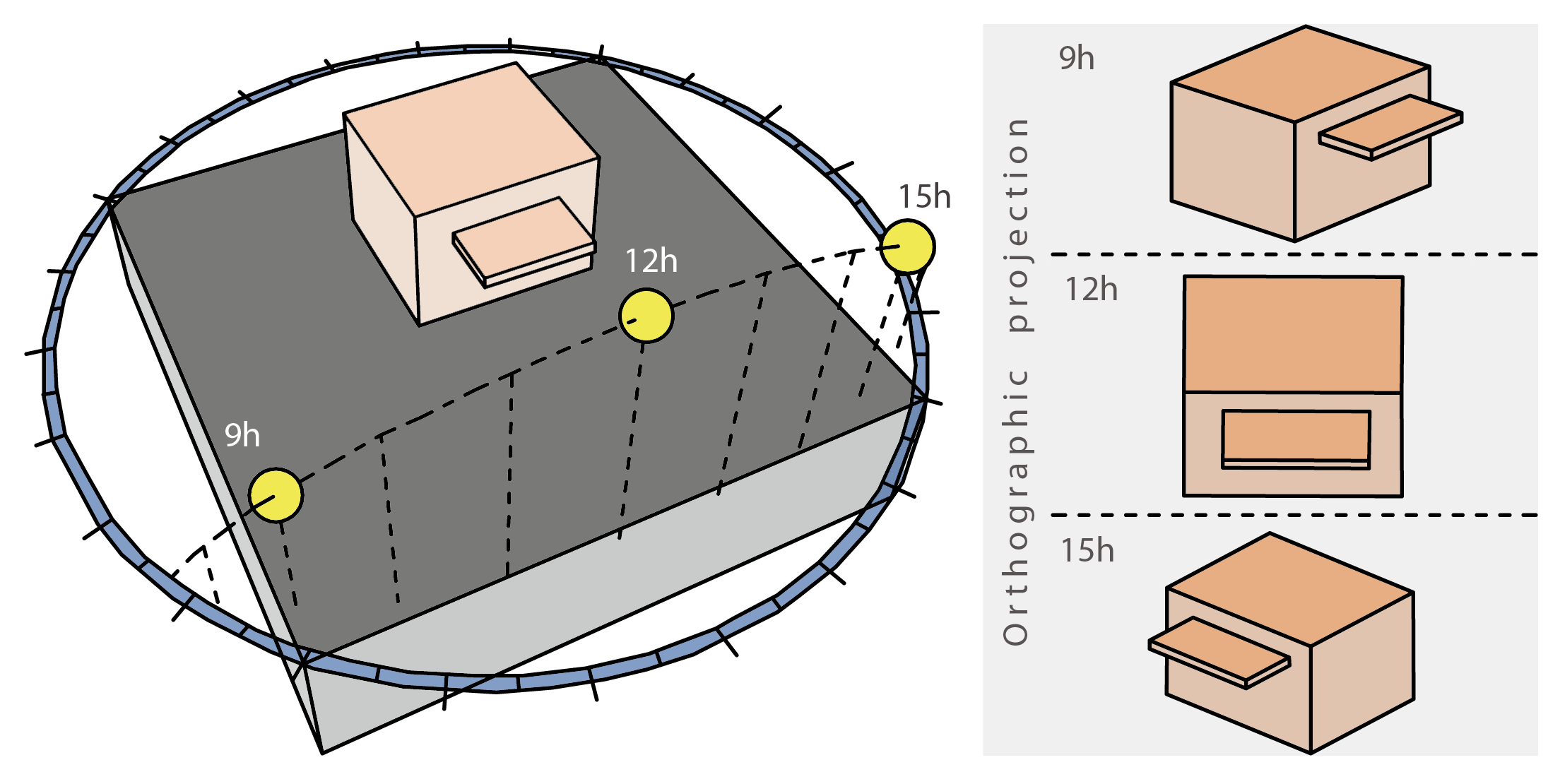
4.4. Projection and Clipping Techniques
4.4.1. Steps Involved in Projection and Clipping
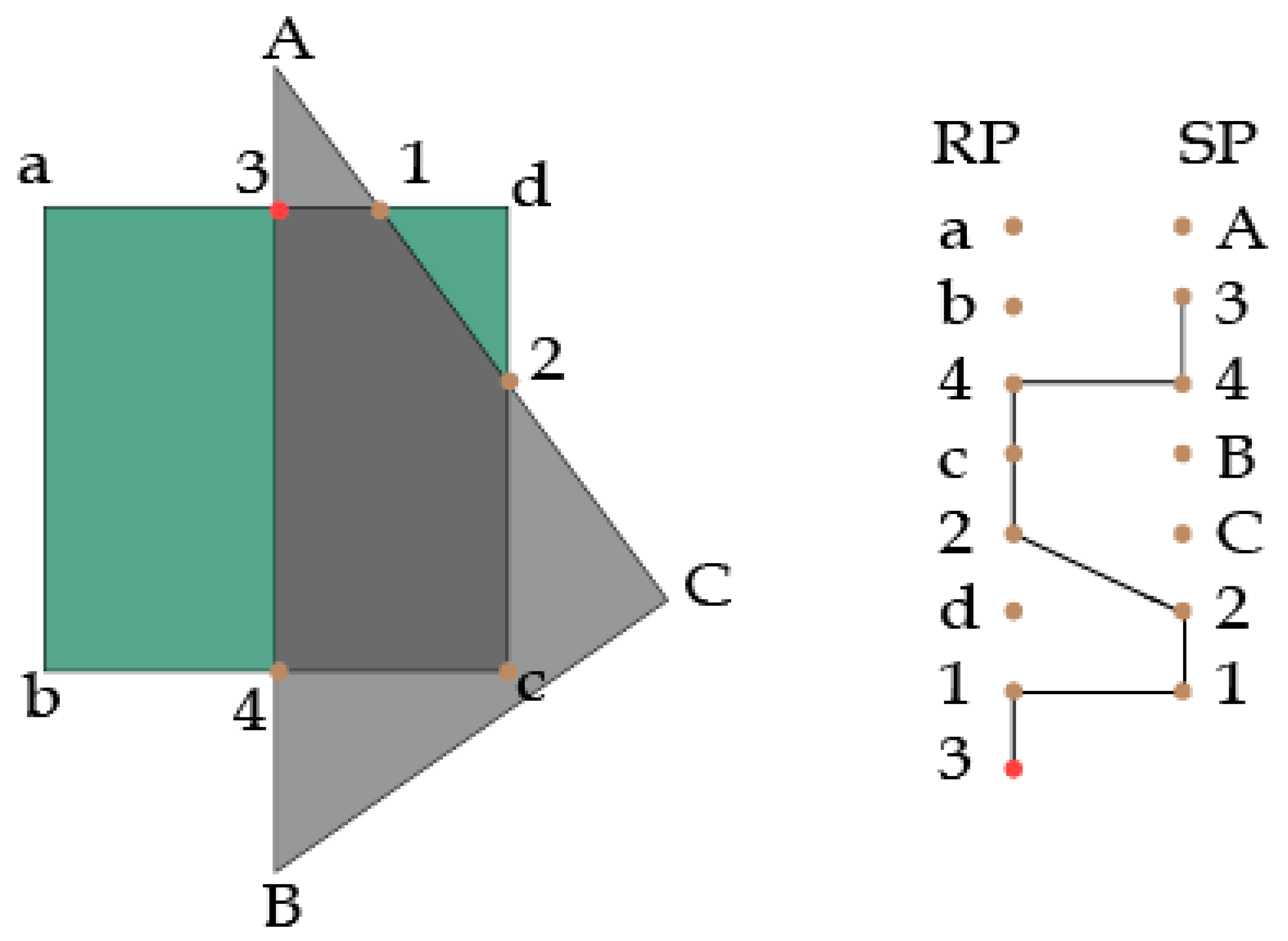
4.4.2. Clipping Algorithms
- Convex Weiler–Atherton: This method is only accurate when both the casting and receiving surfaces are convex.
- Sutherland–Hodgman: This computationally simpler algorithm is used for non-convex surfaces. It clips each edge of the shading polygon against the edges of the receiving polygon, classifying the edges into four types based on their position relative to the clipping window.
- Slater–Barsky: Particularly efficient for rectangular surfaces, this algorithm uses parametric equations to calculate intersection points. It reduces computational effort by dividing the plane into regions, minimizing unnecessary calculations.
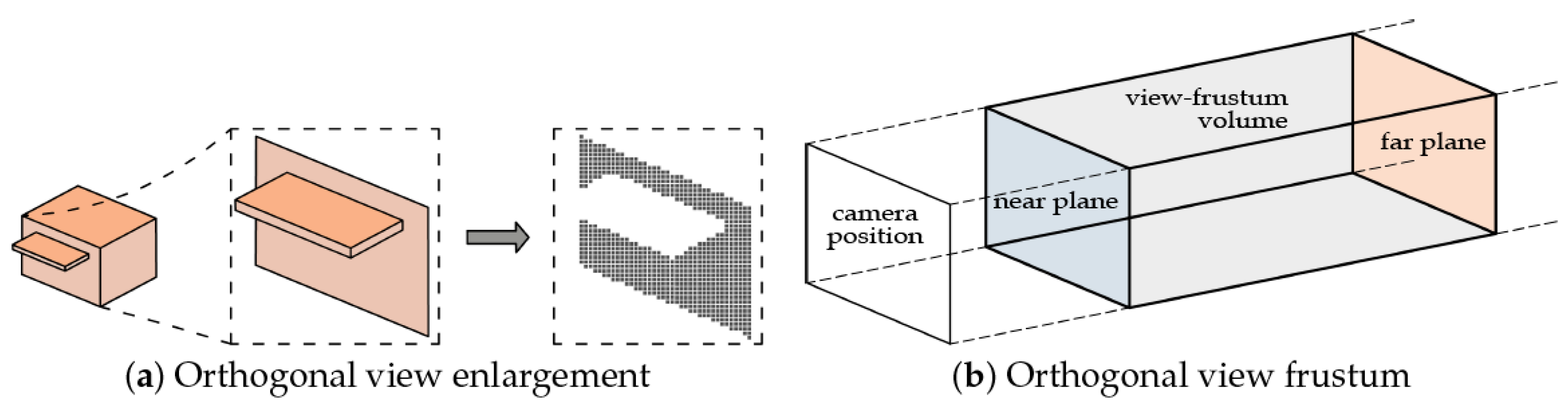
4.5. Pixel Counting Technique
4.5.1. Original Implementation of PxC
4.5.2. Enhancements for Computational Efficiency
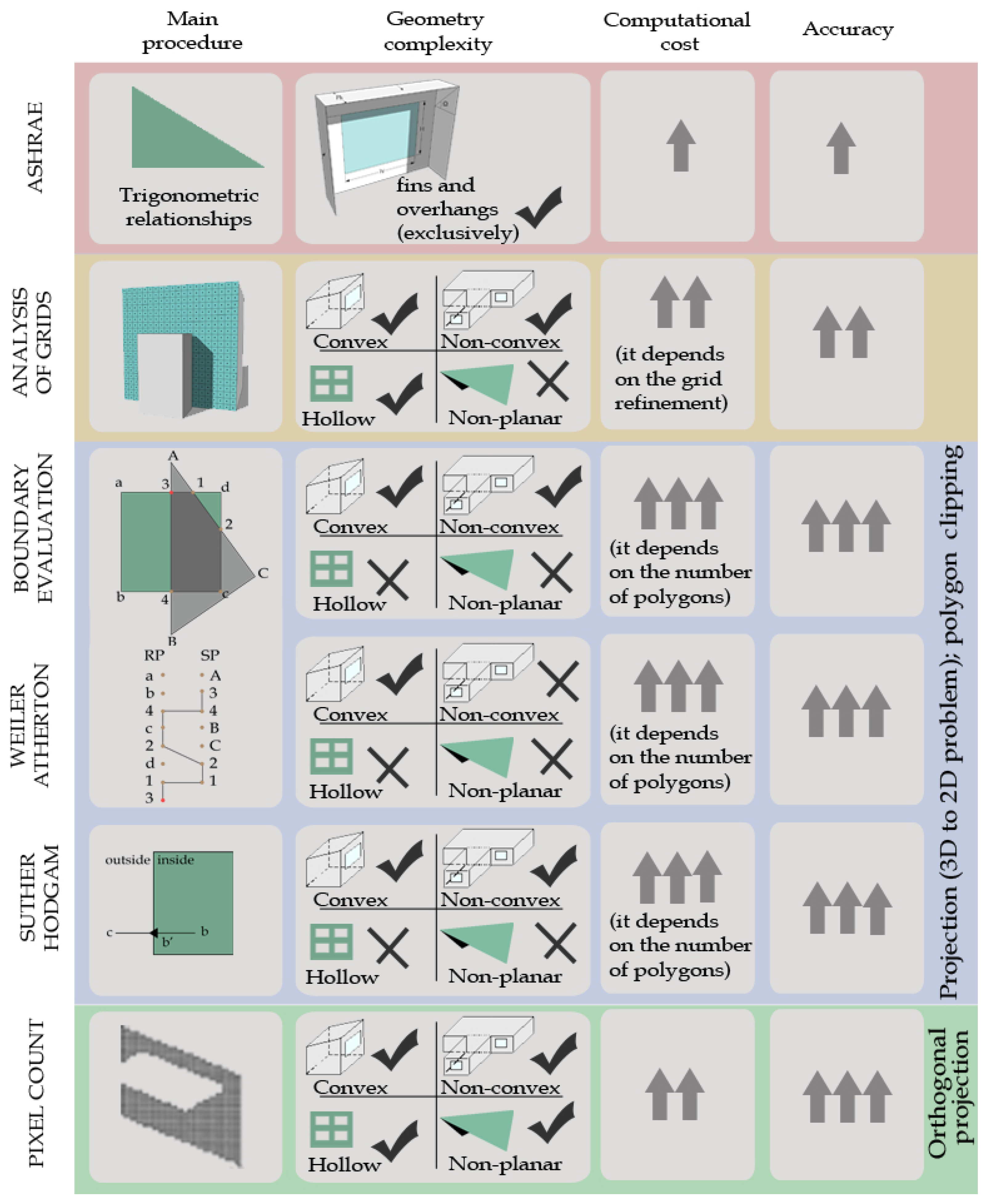
4.6. Key Features and Classifications
5. Internal Solar Distribution Methods
6. Solar Shading Calculation Features Across BPS Tools
6.1. EnergyPlus
6.2. TRNSYS
6.3. ESP-r
6.4. Domus
7. Conclusions
Future Research
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AI | Artificial Intelligence |
| BESTs | Building Energy Software Tools |
| BIM | Building Information Modeling |
| BPS | Building Performance Simulation |
| FDM | Finite-Difference Method |
| GPC | Polygon Clipper |
| GPU | Graphics Processing Unit |
| GSC | Geometric Shading Coefficient |
| HVAC | Heating, Ventilation, and Air Conditioning |
| IoT | Internet of Things |
| PgC | Polygon Clipping |
| P&C | Projection and Clipping |
| PxC | Pixel Counting |
| PSSs | Perforated Solar Screens |
| PV | Photovoltaic |
| RPs | Receiving Polygons |
| SPs | Shading Polygons |
| TgMs | Trigonometric Methods |
| VMs | Vectorial Methods |
| WWR | Window-to-Wall Ratio |
References
- Conejo-Fernández, J.; Cappelletti, F.; Gasparella, A. Including the effect of solar radiation in dynamic indoor thermal comfort indices. Renew. Energy 2021, 165, 151–161. [Google Scholar] [CrossRef]
- Chi, D.A.; Moreno, D.; Navarro, J. Design optimisation of perforated solar façades in order to balance daylighting with thermal performance. Build. Environ. 2017, 125, 383–400. [Google Scholar] [CrossRef]
- Jiang, W.; Jin, Y.; Liu, G.; Ju, Z.; Arıcı, M.; Li, D.; Guo, W. Net-zero energy optimization of solar greenhouses in severe cold climate using passive insulation and photovoltaic. J. Clean. Prod. 2023, 402, 136770. [Google Scholar] [CrossRef]
- Shirinbakhsh, M.; Harvey, L.D. Feasibility of achieving net-zero energy performance in high-rise buildings using solar energy. Energy Built Environ. 2024, 5, 946–956. [Google Scholar] [CrossRef]
- Sherif, A.; El-Zafarany, A.; Arafa, R. External perforated window Solar Screens: The effect of screen depth and perforation ratio on energy performance in extreme desert environments. Energy Build. 2012, 52, 1–10. [Google Scholar] [CrossRef]
- Lionar, R.; Kroll, D.; Soebarto, V.; Sharifi, E.; Aburas, M. A review of research on self-shading façades in warm climates. Energy Build. 2024, 314, 114203. [Google Scholar] [CrossRef]
- Kirimtat, A.; Koyunbaba, B.K.; Chatzikonstantinou, I.; Sariyildiz, S. Review of simulation modeling for shading devices in buildings. Renew. Sustain. Energy Rev. 2016, 53, 23–49. [Google Scholar] [CrossRef]
- Valladares-Rendón, L.G.; Schmid, G.; Lo, S.L. Review on energy savings by solar control techniques and optimal building orientation for the strategic placement of façade shading systems. Energy Build. 2017, 140, 458–479. [Google Scholar] [CrossRef]
- Li, T.; Merabtine, A.; Lachi, M.; Bennacer, R.; Kauffmann, J. Experimental study on the effects of a moving sun patch on heating radiant slabs: The issue of occupants’ thermal comfort. Sol. Energy 2023, 255, 36–49. [Google Scholar] [CrossRef]
- Shi, S.; Merabtine, A.; Bennacer, R.; Kauffmann, J. Experimental evaluation of the impact of real sun patch on radiant floor heating in highly glazed spaces. Build. Environ. 2023, 244, 110799. [Google Scholar] [CrossRef]
- Dubois, M.C. Solar Shading for Low Energy Use and Daylight Quality in Offices Simulations, Measurements and Design Tools; Technical Report; Department of Construction and Architecture, Lund University: Lund, Sweden, 2001. [Google Scholar]
- Bellia, L.; Marino, C.; Minichiello, F.; Pedace, A. An overview on solar shading systems for buildings. Energy Procedia 2014, 62, 309–317. [Google Scholar] [CrossRef]
- Hien, W.N.; Poh, L.K.; Feriadi, H. The use of performance-based simulation tools for building design and evaluation—A Singapore perspective. Build. Environ. 2000, 35, 709–736. [Google Scholar] [CrossRef]
- Wilde, P.D.; Augenbroe, G.; Voorden, M.V.D. Design analysis integration: Supporting the selection of energy saving building components. Build. Environ. 2002, 37, 807–816. [Google Scholar] [CrossRef]
- de Wilde, P.; Van Der Voorden, M. Providing computational support for the selection of energy saving building components. Energy Build. 2004, 36, 749–758. [Google Scholar] [CrossRef]
- Zapata-Lancaster, G.; Tweed, C. Tools for low-energy building design: An exploratory study of the design process in action design process in action. Archit. Eng. Des. Manag. 2016, 12, 279–295. [Google Scholar] [CrossRef]
- Hiller, M.D.E.; Beckman, W.A.; Mitchell, J.W. TRNSHD—A program for shading and insolation calculations. Build. Environ. 2000, 35, 633–644. [Google Scholar] [CrossRef]
- Szokolay, S. Introduction to Architectural Science: The Basis of Sustainable Design, 2nd ed.; Elsevier Ltd.: Amsterdam, The Netherlands, 2008; Volume 8, p. 345. [Google Scholar] [CrossRef]
- Cascone, Y.; Corrado, V.; Serra, V. Development of a software tool for the evaluation of the shading factor under complex boundary conditions. In Proceedings of the 12th International Building Performance Simulation Association Conference, Sydney, Australia, 14–16 November 2011; pp. 2269–2276. [Google Scholar]
- Weiler, K.; Atherton, P. Hidden surface removal using polygon area sorting. Comput. Graph. 1977, 11, 214–222. [Google Scholar] [CrossRef]
- Blinn, J.; Newell, M. Clipping Using Homogenous Coordinates. ACM SIGGRAPH Comput. Graph. 1978, 12, 245–251. [Google Scholar] [CrossRef]
- Vatti, B.R. A generic solution to polygon clipping. Commun. ACM 1992, 35, 56–63. [Google Scholar] [CrossRef]
- Jones, N.L.; Greenberg, D.P. Fast computation of incident solar radiation from preliminary to final building design. In Proceedings of the Building Simulation 2011, Sydney, Australia, 14–16 November 2011. [Google Scholar]
- de Almeida Rocha, A.P.; Oliveira, R.C.; Mendes, N. Experimental validation and comparison of direct solar shading calculations within building energy simulation tools: Polygon clipping and pixel counting techniques. Sol. Energy 2017, 158, 462–473. [Google Scholar] [CrossRef]
- Hensen, J.L.M.; Lamberts, R. (Eds.) Building Performance Simulation for Design and Operation; Spon Press: London, UK, 2011; p. 507. [Google Scholar] [CrossRef]
- Wall, M. Distribution of solar radiation in glazed spaces and adjacent buildings. A comparison of simulation programs. Energy Build. 1997, 26, 129–135. [Google Scholar] [CrossRef]
- Tittelein, P. Environnements de Simulation Adaptes a l’Etude du Comportament Energetique des Batiments Basse Consommation. Ph.D. Thesis, Universite de Savoie, Chambéry, France, 2008. [Google Scholar]
- Rodler, A.; Roux, J.J.; Virgone, J.; Kim, E.J.; Hubert, J.L. Are 3D heat transfer formulations with short time sted and sun patch evolution nececessary for building simulation? In Proceedings of the 13th International Building Performance Simulation Association Conference, Chambéry, France, 25–28 August 2013; pp. 3737–3744. [Google Scholar]
- Rodler, A.; Virgone, J.; Roux, J.J. Impact of the sun patch on heating and cooling power evaluation for a low energy cell. In Proceedings of the CISBAT 2013, Lausanne, Switzerland, 4–6 September 2013. [Google Scholar]
- Rodler, A.; Virgone, J.; Roux, J.J. Impact of sun patch and three-dimensional heat transfer descriptions on the accuracy of a building’s thermal behavior prediction. Build. Simul. 2016, 9, 269–279. [Google Scholar] [CrossRef]
- Fiorito, F.; Sauchelli, M.; Arroyo, D.; Pesenti, M.; Imperadori, M.; Masera, G.; Ranzi, G. Shape morphing solar shadings: A review. Renew. Sustain. Energy Rev. 2016, 55, 863–884. [Google Scholar] [CrossRef]
- EnergyPlus. Available online: https://www.energyplus.net/ (accessed on 10 January 2025).
- Mendes, N.; Oliveira, R.C.L.F.; dos Santos, G.H. Domus 2.0: A whole-building hygrothermal simulation program. In Proceedings of the 8th International Building Performance Simulation Association Conference, Eindhoven, The Netherlands, 11–14 August 2003; pp. 863–870. [Google Scholar]
- Jones, N.L.; Greenberg, D.P.; Pratt, K.B. Fast computer graphics techniques for calculating direct solar radiation on complex building surfaces. J. Build. Perform. Simul. 2012, 5, 300–312. [Google Scholar] [CrossRef]
- Hoover, J.; Dogan, T. Fast and Robust External Solar Shading Calculations using the Pixel Counting Algorithm with Transparency Environmental. In Proceedings of the 15th International Building Performance Simulation Association Conference, San Francisco, CA, USA, 7–9 August 2017. [Google Scholar]
- Al-Masrani, S.M.; Al-Obaidi, K.M.; Zalin, N.A.; Isma, M.I.A. Design optimisation of solar shading systems for tropical office buildings: Challenges and future trends. Sol. Energy 2018, 170, 849–872. [Google Scholar] [CrossRef]
- Avcı, P.; Ekici, B.; Kazanasmaz, Z.T. A review on adaptive and non-adaptive shading devices for sustainable buildings. J. Build. Eng. 2025, 100, 111701. [Google Scholar] [CrossRef]
- Naik, N.S.; Elzeyadi, I.; Cartwright, V. Dynamic solar screens for high-performance buildings—A critical review of perforated external shading systems. Archit. Sci. Rev. 2022, 65, 217–231. [Google Scholar] [CrossRef]
- Shum, C.; Zhong, L. A review of smart solar shading systems and their applications: Opportunities in cold climate zones. J. Build. Eng. 2023, 64, 105583. [Google Scholar] [CrossRef]
- Yezioro, A.; Shaviv, E. Shading: A design tool for analyzing mutual shading between buildings. Sol. Energy 1994, 52, 27–37. [Google Scholar] [CrossRef]
- Greiner, G.; Hormann, K. Efficient clipping of arbitrary polygons. ACM Trans. Graph. 1998, 17, 71–83. [Google Scholar] [CrossRef]
- Messadi, M.T. A theoretical procedure to determine configurations of sunlit room surfaces. In Proceedings of the Transactions of ASHRAE, 1990, Peachtree Corners, GA, USA; pp. 39–52. Available online: https://store.accuristech.com/standards/3384-a-theoretical-procedure-to-determine-configurations-of-sunlit-room-surfaces?product_id=1717450&srsltid=AfmBOoomVw8Fh3xG-ptna2jeKlAdTQ5CX8zUcr_--K5GqG1p2QFF_1Xs (accessed on 12 March 2016).
- Trombe, A.; Serres, L.; Moisson, M. Solar radiation modelling in a complex enclosure. Sol. Energy 1999, 67, 297–307. [Google Scholar] [CrossRef]
- Groleau, D.; Marenne, C. Simula_3D: A Multi-Zone Unsteady Thermal Simulation Tool Based on a 3D Modelling of the Building. In Proceedings of the 7th International Building Performance Simulation Association Conference, Rio de Janeiro, RJ, Brazil, 13–15 August 2001; pp. 585–592. [Google Scholar]
- Kontoleon, K. Glazing solar heat gain analysis and optimization at varying orientations and placements in aspect of distributed radiation at the interior surfaces. Appl. Energy 2015, 144, 152–164. [Google Scholar] [CrossRef]
- Niewienda, A.; Heidt, F.D. Sombrero: A pc-tool to calculate shadows on arbitrarily oriented surfaces. Sol. Energy 1996, 58, 253–263. [Google Scholar] [CrossRef]
- Shaviv, E.; Yezioro, A. Analyzing mutual shading among buildings*. Sol. Energy 1997, 59, 83–88. [Google Scholar] [CrossRef]
- Pongpattana, C.; Rakkwamsuk, P. Efficient algorithm and computing tool for shading calculation. Songklanakarin J. Sci. Technol. 2006, 28, 375–386. [Google Scholar]
- Jones, N.L.; Greenberg, D.P. Hardware accelerated computation of direct solar radiation through transparent shades and screens. In Proceedings of the Fifth National Conference of IBPSA-USA, Madison, WI, USA, 1–3 August 2012. [Google Scholar]
- Maestre, I.R.; Pérez-Lombard, L.; Foncubierta, J.L.; Cubillas, P.R. Improving direct solar shading calculations within building energy simulation tools. J. Build. Perform. Simul. 2013, 6, 437–448. [Google Scholar] [CrossRef]
- Gladt, M.; Bednar, T. A fully automated calculation of shadow casting with matrix-based coordinate transformations and polygon clipping. In Proceedings of the 13th International Building Performance Simulation Association Conference, Chambery, France, 25–28 August 2013; pp. 403–410. [Google Scholar]
- Choi, S.J.; Lee, D.S.; Jo, J.H. Method of Deriving Shaded Fraction According to Shading Movements of Kinetic Façade. Sustainability 2017, 9, 1449. [Google Scholar] [CrossRef]
- Chi, F.; Zhu, Z.; Jin, L.; Bart, D. Calculation method of shading area covering southerly orientated windows for the Tangwu building in Sizhai village. Sol. Energy 2019, 180, 39–56. [Google Scholar] [CrossRef]
- Schmiedt, J.E.; Schiricke, B. A Projection and Clipping Method to Calculate Direct, Diffuse, and Reflected Irradiation. In Proceedings of the 16th IBPSA Conference, IBPSA, Rome, Italy, 2–4 September 2019; pp. 4777–4784. [Google Scholar] [CrossRef]
- Arias-Rosales, A.; LeDuc, P.R. Shadow modeling in urban environments for solar harvesting devices with freely defined positions and orientations. Renew. Sustain. Energy Rev. 2022, 164, 112522. [Google Scholar] [CrossRef]
- Elmalky, A.M.; Araji, M.T. A new trigonometric model for solar radiation and shading factor: Varying profiles of building façades and urban eccentricities. Energy Build. 2023, 282, 112803. [Google Scholar] [CrossRef]
- Elmalky, A.M.; Araji, M.T. Computational procedure of solar irradiation: A new approach for high performance façades with experimental validation. Energy Build. 2023, 298, 113491. [Google Scholar] [CrossRef]
- Voivret, C.; Bigot, D.; Rivière, G. A Method to Compute Shadow Geometry in Open Building Information Modeling Authoring Tools: Automation of Solar Regulation Checking. Buildings 2023, 13, 3120. [Google Scholar] [CrossRef]
- Liu, Z.; Zhou, X.; Shen, X.; Sun, H.; Yan, D. A novel acceleration approach to shadow calculation based on sunlight channel for urban building energy modeling. Energy Build. 2024, 315, 114244. [Google Scholar] [CrossRef]
- Zhou, X.; Shen, X.; Liu, Z.; Sun, H.; An, J.; Yan, D. A novel shadow calculation approach based on multithreaded parallel computing. Energy Build. 2024, 312, 114237. [Google Scholar] [CrossRef]
- ASHRAE. Handbook of Fundamentals; American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc.: Atlanta, GA, USA, 2013. [Google Scholar]
- Groth, C.G.; Lokmanhekim, M. SHADOW—A new technique for the calculation of shadow shapes and areas by digital computer. In Proceedings of the 2nd Hawaii International Conference on System Sciences, Honolulu, HI, USA, 22–24 January 1969; pp. 471–474. [Google Scholar]
- Hiller, M.D. TRNSHD a Program for Shading and Insolation Calculations. Master’s Thesis, University of Wisconsin-Madison, Madison, WI, USA, 1996. [Google Scholar]
- Escrivà, E.J.S. Cálculo de Sombras en Programas de Simulación Térmica de Edificios. Ph.D. Thesis, Universidad Politecnica de Valencia, Valencia, Spain, 2010. [Google Scholar]
- ESRU. The ESP-r System for Building Energy Simulation—User Guide Version 10 Series, 2002. ESRU Manual U02/1. University of Strathclyde. Glasgow, Scotland. Available online: https://www.esru.strath.ac.uk/Documents/ESP-r_userguide.pdf (accessed on 10 January 2025).
- Liu, Y.K.; Wang, X.Q.; Bao, S.Z.; Gombosi, M.; Zalik, B. An algorithm for polygon clipping, and for determining polygon intersections and unions. Comput. Geosci. 2007, 33, 589–598. [Google Scholar] [CrossRef]
- York, D.A.; Charlene, C.C. (Editors) DOE-2 Engineers Manual; Lawrence Berkeley Laboratory, University of California: Berkeley, CA, USA, 1982; p. 56. [Google Scholar]
- Kallblad, K. A method to estimate the shading of solar radiation theory and implementation in a computer program. In Proceedings of the the 6th International Building Performance Simulation Association Conference, Kyoto, Japan, 13–15 September 1999; pp. 595–601. [Google Scholar]
- Walton, G.N. The application of homogeneous coordinates to shadowing calculations. ASHRAE Trans. 1979, 85, 174–180. [Google Scholar]
- EnergyPlus. EnergyPlus Engineering Reference: The Reference to EnergyPlus Calculations. 2024. Available online: https://energyplus.net (accessed on 29 January 2025).
- Yezioro, A.; Gutman, T. SHADING Tools Plugin v1.0. 2016. Available online: http://ayezioro.technion.ac.il/Downloads/ShadingII/index.php (accessed on 2 March 2016).
- da Cunha, V.M.R. Remoção HieráRquica de Geometria por Oclusão em Simulações em Tempo Real. Master’s Thesis, Instituto Politecnico do Porto, Porto, Portugal, 2009; p. 106. [Google Scholar]
- Bouia, H.; Roux, J.J.; Teodosiu, C. Modélisation de la tache solaire dans une pièce équipée d’un vitrage utilisant un maillage en surface de Delaunay. Energy Build. 2002, 34, 57–70. [Google Scholar]
- Grau, K.; Wittchen, K.B.; Sorensen, C.G. Visualisation of building models. In Proceedings of the 8th International Building Performance Simulation Association Conference, Eindhoven, The Netherlands, 11–14 August 2003; pp. 415–420. [Google Scholar]
- Chatziangelidis, K.; Bouris, D. Calculation of the distribution of incoming solar radiation in enclosures. Appl. Therm. Eng. 2009, 29, 1096–1105. [Google Scholar] [CrossRef]
- Boukhris, Y.; Gharbi, L.; Ghrab-Morcos, N. Coupling the building simulation tool ZAER with a sunspot model. Case study in Tunis. Energy Build. 2014, 70, 1–14. [Google Scholar] [CrossRef]
- Benzaama, M.H.; Lachi, M.; Maalouf, C.; Mokhtari, A.M.; Polidori, G.; Makhlouf, M. Study of the effect of sun patch on the transient thermal behaviour of a heating floor in Algeria. Energy Build. 2016, 133, 257–270. [Google Scholar] [CrossRef]
- de Almeida Rocha, A.P.; Rodler, A.; Oliveira, R.C.; Virgone, J.; Mendes, N. A pixel counting technique for sun patch assessment within building enclosures. Sol. Energy 2019, 184, 173–186. [Google Scholar] [CrossRef]
- Bellagh, L.; Merabtine, A.; Kheiri, A.; Mokraoui, S.; Kauffmann, J. Studies on how to counteract overheating caused by sun patch exposure in ventilated highly glazed spaces heated by floor heating systems. Sol. Energy 2021, 220, 991–1005. [Google Scholar] [CrossRef]
- de Almeida Rocha, A.P.; Mendes, N.; Oliveira, R.C.L.F. Domus method for predicting sunlit areas on interior surfaces. Ambiente Construído 2018, 18, 83–95. [Google Scholar] [CrossRef][Green Version]
- IBPSA-USA. Available online: https://www.ibpsa.us/ (accessed on 10 March 2018).
- Crawley, D.B.; Lawrie, L.K.; Winkelmann, F.C.; Buhl, W.F.; Huang, Y.J.; Pedersen, C.O.; Strand, R.K.; Liesen, R.J.; Fisher, D.E.; Witte, M.J.; et al. EnergyPlus: Creating a new-generation building energy simulation program. Energy Build. 2001, 33, 319–331. [Google Scholar] [CrossRef]
- Meeus, J. Astronomical Algorithms; Willmann-Bell: Richmond, VA, USA, 1999; p. 477. [Google Scholar]
- TRNSYS TRaNsient SYstems Simulation Program. Available online: https://sel.me.wisc.edu/trnsys/ (accessed on 31 January 2025).
- Duffy, M.J.; Hiller, M.; Bradley, D.E.; Keilholz, W.; Thornton, J.W. TRNSYS—Features and functionalitity for building simulation 2009 conference. In Proceedings of the 11th International Building Performance Simulation Association Conference, Glasgow, UK, 27–30 July 2009; pp. 1950–1954. [Google Scholar]
- Klein, S.A. Trnsys 17—A TRaNsient SYstem Simulation Program—Volume 4—Mathematical Reference, 2009, Solar Energy Laboratory, University of Wisconsin-Madison, USA. Available online: https://web.mit.edu/parmstr/Public/TRNSYS/04-MathematicalReference.pdf (accessed on 28 January 2025).
- Aschaber, J.; Hiller, M.; Weber, R. Trnsys 17: New Features of the Multizone Building Model. In Proceedings of the 11th International Building Performance Simulation Association Conference, Glasgow, UK, 27–30 July 2009; pp. 1983–1988. [Google Scholar]
- Braun, J.E.; Mitchell, J.C. Solar Geometry for fixed and tracking surfaces. Sol. Energy 1983, 31, 439–444. [Google Scholar] [CrossRef]
- ASHRAE. ASHRAE Handbook: 1997 Fundamentals; ASHRAE: American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc.: Atlanta, GA, USA, 1997. [Google Scholar]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes, 4th ed.; John Wiley and Sons: Hoboken, NJ, USA, 2013; p. 936. [Google Scholar]
- ESP-r. Available online: http://www.esru.strath.ac.uk/Programs/ESP-r.htm (accessed on 30 January 2025).
- Hand, J.W. Strategies for Deploying Virtual Representations of the Built Environment; University of Strathclyde: Glasgow, UK, 2015. [Google Scholar]
- Clarke, J.A. Energy Simulation in Building Design, 2nd ed.; Taylor and Francis: Oxford, UK, 2001; p. 362. [Google Scholar]
- DOMUS. Available online: http://www.domus.pucpr.br/ (accessed on 10 January 2025).
- Mendes, N.; Barbosa, R.M.; Freire, R.; Oliveira, R.C.L.F. A Simulation Environment for Performance Analysis of HVAC Systems. Build. Simul. 2008, 1, 129–143. [Google Scholar] [CrossRef]
- Reda, I.; Andreas, A. Solar position algorithm for solar radiation applications. Sol. Energy 2004, 76, 577–589. [Google Scholar] [CrossRef]
| Ref. | Year | Output Data | Method | Details | Tools | Comparison with Tools | Study Case | Context | Shadow Source | Studied Surfaces | Location | Simulation Timeframe | Max. Runtime |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [40] | 1994 | GIC [%] | PxC | Uses orthographic projection from the Sun’s point of view; bitmap technique for pixel analysis; evaluates solar rights and shading requirements. | SHADING | Compared with traditional CAD methods | Modeled case | Building | Surrounding buildings, Trees and other vegetation | Façades and Openings | Israel | Specific Dates and Times | 6 s per view |
| [46] | 1996 | GSC [%] | PxC | Projection of shadow-casting surfaces onto a receiving surface, combined with pixel counting to determine the proportion of the shaded area. | TRNSYS, Suncode | Not directly compared | Modeled case | Building | Overhangs | Façades and Openings | Germany | Monthly | Not specified |
| [47] | 1997 | GIC [%] | PxC | Uses orthographic projection from the Sun’s point of view; bitmap technique for pixel analysis; evaluates solar rights and shading requirements. | SHADING | Not directly compared | Real case | Urban | Surrounding buildings | Façades and Openings | Israel | Specific Dates and Times | Not specified |
| [17] | 2000 | Sunlit area [m²] | PgC | Handles complex surface geometries, including self-shading and external obstructions. | TRNSYS | Compared with Simulation and Standards | Modeled case | Building | Self-shading, Surrounding buildings | Façades and Openings | USA | Specific Dates and Times | Not specified |
| [48] | 2006 | Shaded area [m²] | Vectorial | Uses vector algebra for calculating shadow projections | Custom-developed model | Compared with Experimental | Real case | Generic | Overhangs | Generic surface | Thailand | Specific Times | Not specified |
| [19] | 2011 | Sunlit area [m²] | Vectorial | Uses vector algebra and homogeneous coordinate systems for shading | Custom-developed model | Not directly compared | Modeled case | Generic | Trees and other vegetation | Generic surface | Italy | Specific Times | Not specified |
| [34] | 2012 | PSSF [%] | PxC | A module calculates incident radiation using a pixel-based depth buffer and B-Spline interpolation. | Custom-developed model | Compared with Analytical | Real case | Building | Trees and other vegetation, Self-shading | Façades and Openings | USA | Annual | 6.2 min |
| [49] | 2012 | PSSF [%] | PxC | Uses programmable shaders to handle complex transparent and perforated shading surfaces. | Custom-developed model | Compared with Simulation | Modeled case | Building | Trees and other vegetation | Façades and Openings | USA, Abu Dhabi | Specific Dates and Times | 209 s |
| [50] | 2012 | Sunlit area [m²] | PgC | Improved method projects all polygons on a single plane orthogonal to the sunray; uses Vatti’s clipping algorithm for shadow intersection. | Custom-developed model | Compared with Standards and Experimental | Real case | Building | Surrounding buildings | Façades and Openings | Spain | Annual | 8.3 min for a whole year, every Sun hour. |
| [51] | 2013 | PSSF [%] | PgC | Matrix-based coordinate transformations and polygon clipping. | Custom-developed model | Compared with OpenGL | Modeled case | Generic | Trees and other vegetation | Generic surface | Not specified | Not specified | 264.7 s |
| [24] | 2017 | Sunlit fraction [%] | PxC | Experimental validation of two solar shading calculation techniques. PxC and PgC are compared based on their accuracy and computational time. | Domus, EnergyPlus, Shading II SketchUp plug-in | Compared with Simulation, Compared with Experimental | Modeled case | Building | Shading devices, surrounding buildings, trees | Façade surfaces | Brazil | Specific Times | Varies by software; Domus: <1 h, EnergyPlus: ~18 h |
| [35] | 2017 | PSSF [%] | PxC | Uses OpenGL to calculate shading with pixel counting. Transparency feature enables more accurate shading in vegetated or complex urban environments. | Modified version of EnergyPlus | Compared with Standards, Compared with Experimental | Modeled case | Urban | Surrounding buildings, Self-shading | Façades and Openings | USA | Annual | 40–50% faster than EnergyPlus |
| [52] | 2017 | Shaded area [m²] | PgC | Projection of the geometry of shading elements onto a surface using 3D coordinates and resolves overlaps with the Planar-Polygon method and General Polygon Clipper (GPC). | Custom-developed model | Not directly compared | Modeled case | Generic | Kinetic façades | Generic surface | Repulic of Korea | Specific Dates and Times | Not specified |
| [53] | 2019 | Shaded area [m²] | TgM | Uses empirical equations based on trigonometric models for shading calculation | Custom-developed model | Compared with SketchUp | Real case | Building | Overhangs; Self-shading | Façades and Openings | China | Specific Times | Not specified |
| [54] | 2019 | Shaded area [m²] | PgC | Improved PgC method for solar radiation calculations, including direct and sky diffuse irradiance, and reflections on building surfaces. | Custom-developed model | Compared with Simulation | Modeled case | Urban | Surrounding buildings | Façades and Openings | Germany | Specific Dates and Times | Similar to Energyplus simulations |
| [55] | 2022 | Sunlit area [m²] | PxC | Comparison of four shadow modeling approaches: forward ray tracing, focused ray tracing, pixel-counting, and analytical areas. PV panels. | Custom-developed model | Compared with Simulation | Modeled case | Building | Overhangs | Façades and Openings | USA | Specific Dates and Times | Not specified |
| [56] | 2023 | Shading factor (SF) [%] | TgM | Mesh elements and solar exposure analysis of a building façade within linear and elliptical site contexts. | Custom-developed model | Compared with Experimental | Modeled case | Urban | Surrounding buildings | Façades and Openings | Canada | Annual | 6.1 min per façade |
| [57] | 2023 | Shading factor (SF) [%] | TgM | Mesh elements and solar exposure analysis of a building façade within linear and elliptical site contexts. | Custom-developed model | Compared with Experimental | Modeled case | Urban | Surrounding buildings | Façades and Openings | Not specified | Annual | 0.8 s per façade |
| [58] | 2023 | Shaded area [m²] | PgC | Uses a solid clipping technique that extrudes a 3D sunpath and calculates the intersections with building geometry to accurately compute shadow areas for solar regulation checks in BIM environments. | Custom-developed model | Compared with Simulation | Modeled case | Building | Overhangs | Façades and Openings | France | Specific Dates and Times | Not specified |
| [59] | 2024 | Shaded area [m²] | PgC | Combines polygon clipping, distance filtering, and the sunlight channel to calculate shadows in urban environments by eliminating irrelevant surfaces and focusing on the most relevant ones based on proximity, height, and the Sun’s position, significantly speeding up the process. | Custom-developed model | Compared with Simulation | Modeled case, Real case | Urban | Surrounding buildings | Façades and Roofs | China | Annual | 10 times faster over the baseline runtime |
| [60] | 2024 | Shaded area [m²] | PgC | Uses multithreaded parallel processing to accelerate shadow calculations, combining sunlight channel and celestial sphere methods. | DeST | Compared with Simulation | Real case | Building, Urban | Surrounding buildings | Façades and Roofs | China | Annual | 2.4× faster for complex buildings |
| Method | Advantages and Limitations |
|---|---|
| Vectorial Methods (VMs) | Advantages: Effective for simple geometries (e.g., overhangs, inclined planes). High precision in shadow projections. |
| Limitations: Computationally expensive for complex geometries. Requires considerable hardware resources. | |
| Trigonometric Models (TgMs) | Advantages: Extremely efficient in computation time. Ideal for early-stage design simulations. Low learning curve. |
| Limitations: Relies on simplified assumptions. Accuracy diminishes with irregular geometries. Integration challenges with BPS tools. | |
| Discrete Element Analysis of Grids | Advantages: Highly flexible, simple. Handles convex and concave shapes. Easy to implement. |
| Limitations: Accuracy compromised with coarse grids. Long processing time with high-density configurations. | |
| Projection and Clipping Techniques (PgCs) | Advantages: High precision for planar surfaces. Handles a wide range of geometries, especially non-convex surfaces. |
| Limitations: Computationally intensive. Difficulty handling irregular shapes. Requires specialized hardware and programming. | |
| Pixel Counting (PxC) | Advantages: Very efficient in computation time. Leverages GPU power for large models. High accuracy with better hardware. |
| Limitations: Dependent on compatible graphics hardware. Pixelation effects cause small inaccuracies. |
| Ref. | Year | Location | Output Data | Study | Sunlit Patch | Tools | Comparison with Tools | Study Case |
|---|---|---|---|---|---|---|---|---|
| [42] | 1990 | - | Sunpatch area, solar radiation impact on walls, floor, ceiling | Vectorial analysis, analytical methods for projection | Vectorial analysis, analytical methods for projection | Custom-developed model | Comparison with conventional methods | Rectangular single-zone room |
| [26] | 1997 | Denmark | Solar heat gain, surface temperature, heating/cooling loads | Comparison of four simulation programs calculating solar radiation based on the building’s geometry, considering direct and diffuse radiation. | Different sunpatch models are used in the tested software, respectively: grid elements, volume, area factor, decided by the user. | DEROB-LTH, SUNREP (TRNSYS), FRES, tsbi3 | Compared with Simulation | Glazed space with adjacent room |
| [43] | 1999 | France | Sunpatch area, solar radiation flux, surface temperature, thermal comfort | 3D dynamic simulation with sunpatch modeling and heat transfer calculations, computing solar radiation distribution, including direct and diffuse radiation, with surface interactions (absorption, reflection). | Projection and polygon clipping | TRNSYS, custom heat transfer and sunpatch models | Compared with Experimental | Room with multiple obstacles (furniture and occupant), highly glazed wall configuration |
| [44] | 2001 | - | Sunpatch area, surface temperature | Multizone unsteady thermal simulation with 3D modeling for solar radiation and thermal exchanges, using volumetric modeling with thermal zones, solar radiation simulation, and multi-reflection calculations. | Solar ray projection: solar rays are traced along a square grid to calculate sunlit areas by determining intersections with building surfaces. The grid size (dx) controls the accuracy of the normal solar flux, accounting for opaque, transparent, or masked surfaces. | SIMULA_3D software | Not directly compared | Glazed space with adjacent room |
| [73] | 2002 | France | Sunpatch area | Delaunay triangulation for mesh generation on walls, ceiling, and floor, used to model solar radiation over time. | Uses a triangular mesh, with visibility calculated through ray tracing by casting rays from each triangle’s center towards the sun, checking for obstructions, and considering the angle of incidence to model solar radiation distribution. | Computational tools for triangulation, ray tracing for solar load modeling | Not directly compared | Rectangular single-zone room |
| [74] | 2003 | Denmark | Sunpatch area | 3D model creation using BSim2002 for thermal, moisture, and daylight simulation, with solar analysis using XSun and OpenGL for virtual tours. | Projection and polygon clipping by Xsun | BSim2002 (SimView, XSun, SimLight), Radiance, DirectX for visualization | Not directly compared | Real Building |
| [75] | 2009 | Greece | Solar radiation impact on walls, floor, ceiling, thermal loads, surface temperatures | Numerical methodology based on view factor theory, linked to TRNSYS, for solar radiation distribution on internal surfaces, considering multiple openings and orientations. | Solar radiation distribution through view factor methodology, considering geographical location and opening orientation. | TRNSYS for thermal simulation, Fortran for view factor-based distribution | Comparison with TRNSYS absorptance-weighted area ratio method for solar distribution | Single-zone and dual-zone building models with varying window placements |
| [29,30] | 2013 2016 | France | Solar heat gain, temperature distributions, heating and cooling demand, energy consumption | 3D transient heat transfer model with sunpatch projection and time-stepping solver, incorporating heat transfer and sunpatch projection onto internal surfaces with an adaptive time step. | The sunpatch is projected on walls using geometrical tests, and thermal properties are calculated for each control volume. | Custom-developed model, HEAT3 meshing for 3D calculations | Comparison with 1D models (M1D, M1D, sp) that simplify solar radiation distribution and neglect 3D heat transfer | Rectangular single-zone room with high insulation |
| [76] | 2014 | Tunisia | Sunpatch area, temperature distribution, thermal comfort | Numerical simulation coupling sunspot model with ZAER for solar radiation distribution and air temperature, calculating sunspot distribution based on Sun position and room geometry. | Divides walls into facets, projects solar rays from their centroids towards the window to determine irradiation, computes projection coordinates using vector equations, and calculates the sunspot area by summing the irradiated facet areas. | ZAER software for thermal comfort and energy simulation, Fortran for sunspot model | Comparison with other simulation models (e.g., TRNSYS, EnergyPlus) | Two parallelepiped rooms |
| [45] | 2015 | Greece | Sunpatch area, solar heat gain | Pattern-based simulation of sunlit areas for solar heat gain, optimizing glazing size and placement based on solar angle and room geometry. | Using a four-character sunlit pattern, projecting solar rays through four vertices of an orthogonal glazing onto interior surfaces (floor, left wall, back wall) to calculate direct solar radiation impact, forming footprints labeled 1-B, 2-L, 3-F, and 4-L. | Custom-developed model | Not directly compared | Single-zone building model with varying glazing sizes and placements, and wall orientations |
| [77] | 2016 | Algeria | Surface temperature, surface temperature | Numerical simulation using TRNSYS for room and floor heating, and FLUENT for sunpatch modeling and solar radiation simulation. | Moving sunpatch simulated using Ray Tracing model as proposed in FLUENT. | TRNSYS 16 and FLUENT 6.3 software, Ray Tracing model for sunpatch calculation | Comparison with models that neglect sunpatch effects | Single room with south-facing window, multiple orientations (South, West) |
| [78] | 2019 | France | Sunpatch area, surface temperature | Pixel counting technique for sunpatch calculation using 2D orthogonal projections from the Sun’s perspective. | Pixel counting with occlusion query and Z-buffer techniques | Domus, Shading II SketchUp plugin, EnergyPlus | Compared with simulation | Rectangular single-zone room with various shading elements (e.g., cobogó), window configurations |
| [79] | 2021 | France | Indoor temperature, radiant floor temperature, temperature gradients in the slab | Numerical simulation using a validated 2D finite-difference model (FDM) with dynamic sunpatch heat load (moving patch) for transient conditions. | Simulated sunpatch exposure with heating film, dynamic sunpatch movement (3 × 20 cm every 1.5 h). | Matlab for parametric studies and model simulations | Comparison with other studies | Full-scale test cell with radiant floor heating system, varying sunpatch intensity, different air ventilation rates |
| [9] | 2023 | France | Floor surface temperature, air temperature, thermal comfort, thermal manikin data | Experimental study with dynamic sunpatch simulation using heating films on the floor and a thermal manikin for comfort evaluation. | Moving sunpatch simulated by heating films in different positions (1 m × 0.5 m per patch). | SketchUp for sunpath calculation, ANSYS Fluent® for solar intensity | Not directly compared | Case with small window (5.8% WWR), case with large window (11.6% WWR) |
| Software | External Shading | Internal Distribution | Pre-Processing | Simulation Frequency | Default Time Step (min) | Simulation Method |
|---|---|---|---|---|---|---|
| EnergyPlus | Polygon Clipping; Pixel Counting | Floor incidence (homogeneous); Polygon Clipping | No | 1 day every 20 days | 15 | Finite Differences |
| TRNSYS | ASHRAE; Polygon Clipping | Absorptance-weighted ratios; Polygon Clipping | Yes | 1 day every 30 days | 60 | Finite Differences |
| ESP-r | Analysis of grids | Analysis of grids | Yes | 1 day every 30 days | 60 | Finite Differences and Finite Elements |
| Domus | Pixel Counting | Pixel Counting | Yes | 1 day every 7 days | 20 | Finite Differences |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rocha, A.P.d.A.; Oliveira, R.C.L.F.; Mendes, N. Technical Review of Solar Distribution Calculation Methods: Enhancing Simulation Accuracy for High-Performance and Sustainable Buildings. Buildings 2025, 15, 578. https://doi.org/10.3390/buildings15040578
Rocha APdA, Oliveira RCLF, Mendes N. Technical Review of Solar Distribution Calculation Methods: Enhancing Simulation Accuracy for High-Performance and Sustainable Buildings. Buildings. 2025; 15(4):578. https://doi.org/10.3390/buildings15040578
Chicago/Turabian StyleRocha, Ana Paula de Almeida, Ricardo C. L. F. Oliveira, and Nathan Mendes. 2025. "Technical Review of Solar Distribution Calculation Methods: Enhancing Simulation Accuracy for High-Performance and Sustainable Buildings" Buildings 15, no. 4: 578. https://doi.org/10.3390/buildings15040578
APA StyleRocha, A. P. d. A., Oliveira, R. C. L. F., & Mendes, N. (2025). Technical Review of Solar Distribution Calculation Methods: Enhancing Simulation Accuracy for High-Performance and Sustainable Buildings. Buildings, 15(4), 578. https://doi.org/10.3390/buildings15040578






