1. Introduction
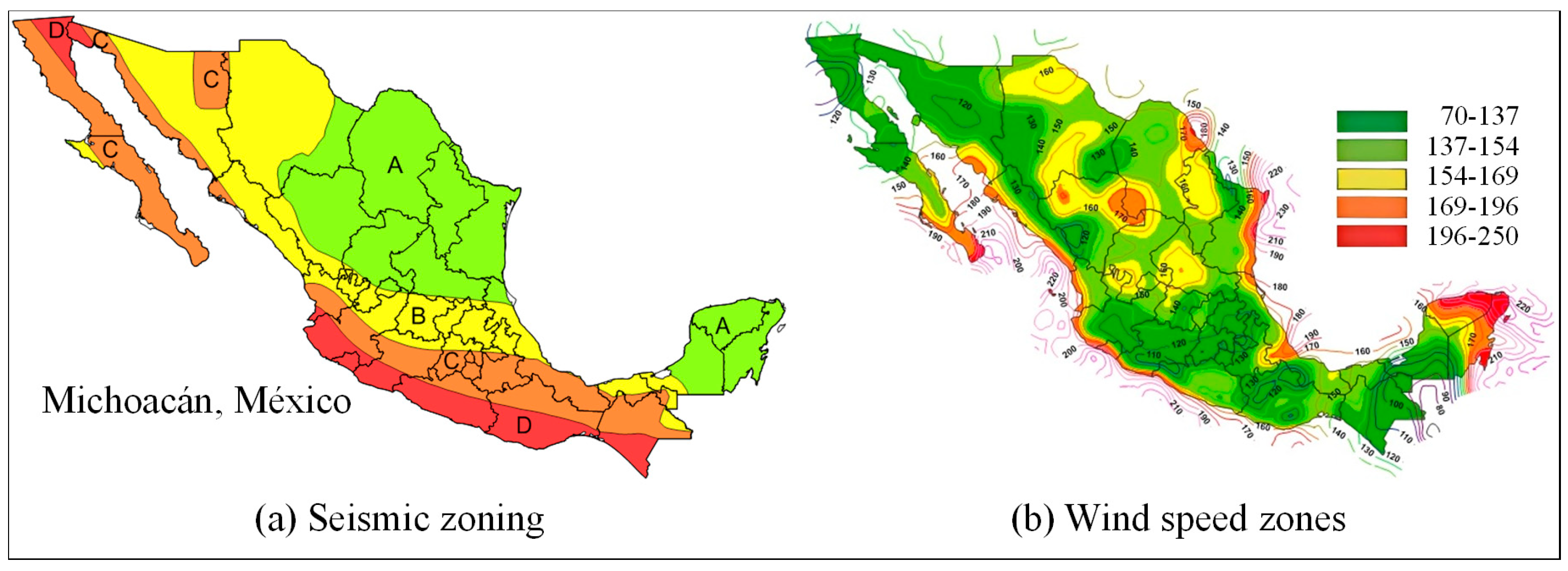
The coastal region of Michoacán, Mexico, is a crucial area for international trade due to its strategic geographical location, serving as the primary point of importation in the country. This region is also abundant in mineral resources, which has led to the development of significant steel production and processing industries. However, the civil infrastructure in Mexico’s Pacific coastal zones faces significant challenges from two main sources: the strong winds generated by frequent tropical cyclones and high-magnitude seismic events. Notably, two of the most devastating earthquakes in Mexican history, which resulted in substantial economic losses and fatalities, originated in Michoacán. The earthquake on 19 September 1985 (Mw 8.1) inflicted extensive damage in Mexico City and surrounding areas, claiming an estimated 10,000 lives and leading to the destruction or severe damage of thousands of buildings. More recently, the earthquake on 19 September 2022 (Mw 7.6) caused damage to approximately 3300 homes, 863 schools, and 41 hospital buildings.
Figure 1a illustrates the seismic zoning map of Mexico, where Zone D corresponds to seismic accelerations on rock exceeding 200 cm/s
2 [
1], designating it as the region with the highest seismic activity.
Tropical cyclones in this region occur most frequently between September and November, and their frequency and intensity have been exacerbated in recent years due to climate change.
Figure 1b illustrates a wind regionalization map of a 200-year return period, averaged over a 3 s interval [
2]. Along the Pacific Coast, design wind speeds at a height of 10 m over flat terrain can attain levels as high as 250 km/h (69.44 m/s).
The performance of civil infrastructure in this area, classified as both seismic and wind-prone, presents significant challenges, particularly for slender structures. These structures are particularly vulnerable to high dynamic demands, which necessitates innovative design solutions along with effective vibration mitigation strategies. This study specifically examines a chimney, which is a common component in power generation plants, refineries, and industrial complexes, used for the release of gases and vapors. Their slenderness ratio makes them susceptible to important vibrations under seismic and wind loads, underscoring the critical need for vibration control strategies to preserve structural integrity and functionality.
The dynamic behavior of chimneys in response to wind loads has been the subject of extensive study. Previous research has explored the responses of both steel chimneys [
3,
4,
5,
6,
7] and reinforced concrete chimneys [
8,
9,
10,
11,
12], primarily concentrating on phenomena such as vortex shedding, crosswind responses, and dynamic property identification through wind tunnel testing and numerical simulations. However, many analyses operate under the assumption of a fixed-base condition, ignoring the impact of soil–structure interaction (SSI), which can lead to an underestimation of the dynamic response. Other studies [
13,
14] highlight the significance of incorporating soil flexibility as it affects the natural frequency and effective damping of the structure, particularly in slender chimneys.
Additionally, accounting for material nonlinearity is essential for analyzing chimneys subjected to seismic and wind loads. These structures may exhibit inelastic behavior under extreme conditions, necessitating analytical methods that incorporate this nonlinearity. Traditional approaches, such as stiffness matrix updates and finite element methods, have been utilized in prior research to model nonlinear behavior [
15,
16,
17]. In this work, we employ the Force Analogy Method (FAM), a computationally efficient alternative to conventional stiffness-based approaches [
18]. Despite its underexplored status, the FAM facilitates the analysis of inelastic responses while reducing computational demands, making it particularly suitable for studies involving prolonged durations or combined loading scenarios, such as seismic and extreme wind events. The FAM has proven effective in analyzing the inelastic responses of buildings and bridges under seismic and wind demands with high precision and efficiency [
18,
19,
20,
21,
22,
23,
24,
25,
26,
27,
28,
29,
30,
31,
32,
33,
34,
35,
36,
37,
38,
39,
40,
41,
42,
43,
44,
45,
46,
47,
48,
49,
50].
Structural vibration control has proven effective in mitigating excessive responses in chimneys. Passive control systems, such as tuned mass dampers (TMDs), have been utilized to reduce wind-induced displacements and accelerations in slender structures, including steel [
51,
52], concrete [
53], and masonry chimneys [
54]. However, the application of TMDs to reinforced concrete chimneys with soil–structure interaction (SSI) under extreme wind or seismic loads remains relatively unexplored.
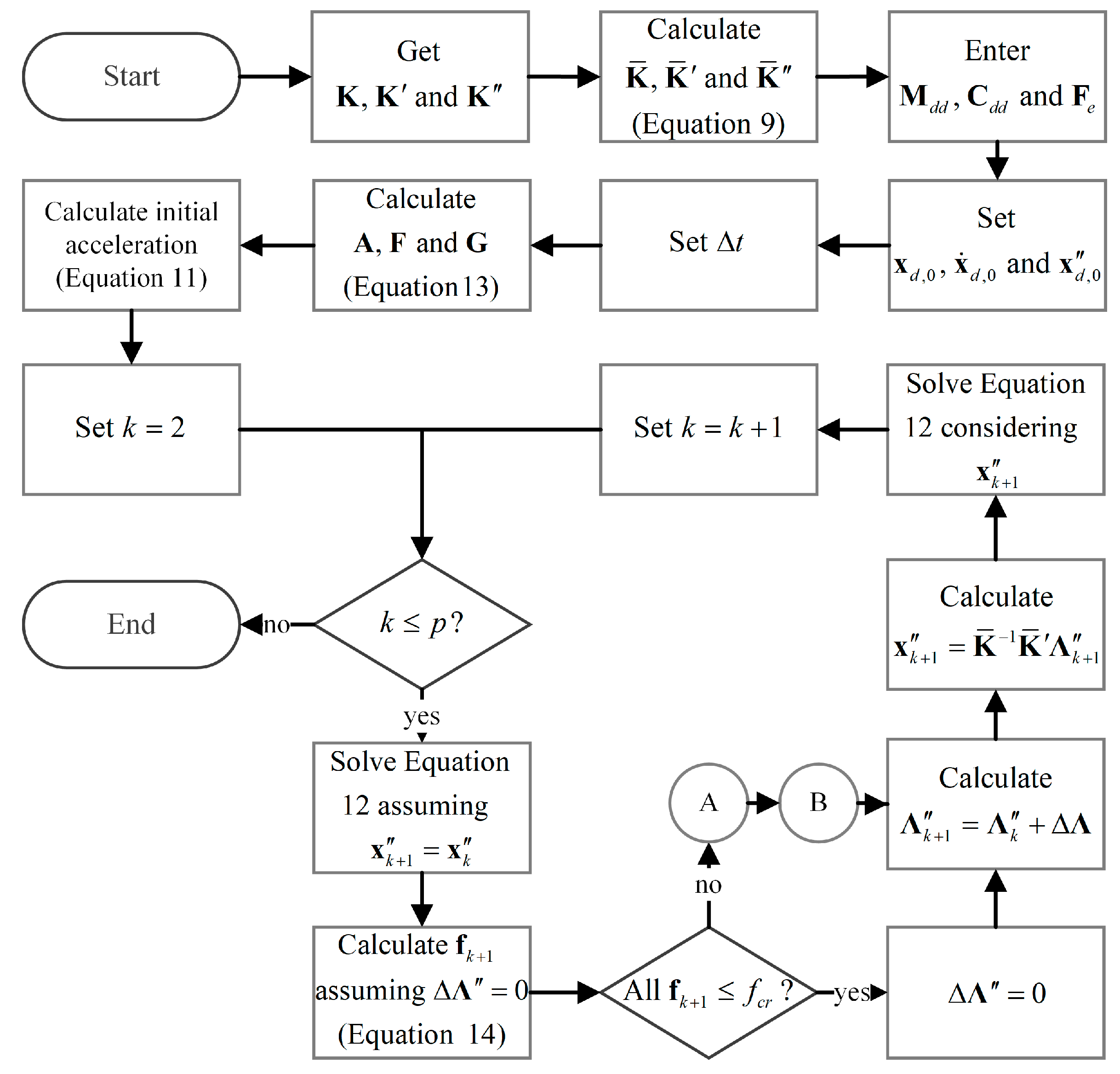
This study assesses the nonlinear dynamic response of an 80 m tall reinforced concrete chimney situated in Mexico’s Pacific coastal region and proposes a vibration control system based on a TMD installed at the chimney cap. The methodology incorporates SSI, material nonlinearity through the FAM, and the effects of seismic sequences as well as high-velocity wind scenarios.
Wind actions are modeled using synthetic records generated through spectral techniques, considering mean wind speeds ranging from 5 m/s to 25 m/s for synoptic winds and from 30 m/s to 65 m/s for tropical cyclones. For the seismic analysis, two ground motion records from the same station, representing a mainshock and its aftershock, were employed.
The results offer guidelines for the application of TMDs in slender chimneys subjected to high dynamic and wind demands, taking into account different soil types. These findings contribute to enhancing the structural safety and resilience of this critical infrastructure in the face of extreme environmental events.
3. Application Example
A reinforced concrete chimney located in Michoacán, Mexico, was chosen as the application example due to its strategic significance in the industrial and port sector along the Pacific Coast. This region is distinguished by a high level of seismic activity and frequent hurricane winds. The chimney, depicted in
Figure 9a, is a non-prismatic cylindrical structure with variable cross-sections and a total height of 80 m. It features an interior masonry lining supported by concrete corbels placed at 10 m intervals, as illustrated in
Figure 9b.
The longitudinal reinforcement of the flue is detailed in
Figure 9c, with transverse reinforcement spaced 240 mm apart. The concrete used possesses a compressive strength of 24.52 MPa and a modulus of elasticity of 24,623.10 MPa, while the steel reinforcement has an elasticity modulus of 200 GPa.
The structure was discretized into 16 elements, each measuring 5 m in height. The mass matrix was established by calculating the weight of the materials, including both the concrete shell and the interior masonry lining.
Figure 10a schematically illustrates the nodal distribution along with the corresponding concentrated masses at each node. A total of 31 plastic hinges were modeled, with their flexural behavior defined by moment–rotation relationships.
Figure 10b shows the locations of these plastic hinges.
The system features a total of 31 degrees of freedom (DOFs), including 16 translational DOFs and 15 rotational DOFs. The stiffness matrix of element
is determined by
where
Here, is the stiffness matrix in the local coordinate system; is the elastic modulus of the material; is the moment of inertia; is the element length; is a parameter that accounts for shear deformation; is the cross-sectional shear correction factor, valued at 1.5 for the section under consideration; and is the cross-sectional area.
The stiffness matrix that relates plastic rotation to the restoring force of element
is defined as follows:
Likewise, the stiffness matrix relating plastic rotation to the residual moment of element
is expressed as
The stiffness matrices for each element are transformed to align with the global coordinate system and are assembled following the standard procedures of finite element analysis. In this assembly, translational DOFs are positioned first within the global matrix, followed by rotational DOFs.
The resulting global stiffness matrices are
where elements indexed with subscript
correspond to translational DOFs, while those with subscript
correspond to rotational DOFs. The condensed matrices obtained are
,
, and
.
The plastic hinges were characterized analytically using moment–curvature diagrams. The specifications for longitudinal and transverse reinforcement utilized in this analysis are detailed in
Table 2. In this context,
represents the longitudinal reinforcement ratio, while
denotes the transverse volumetric reinforcement ratio.
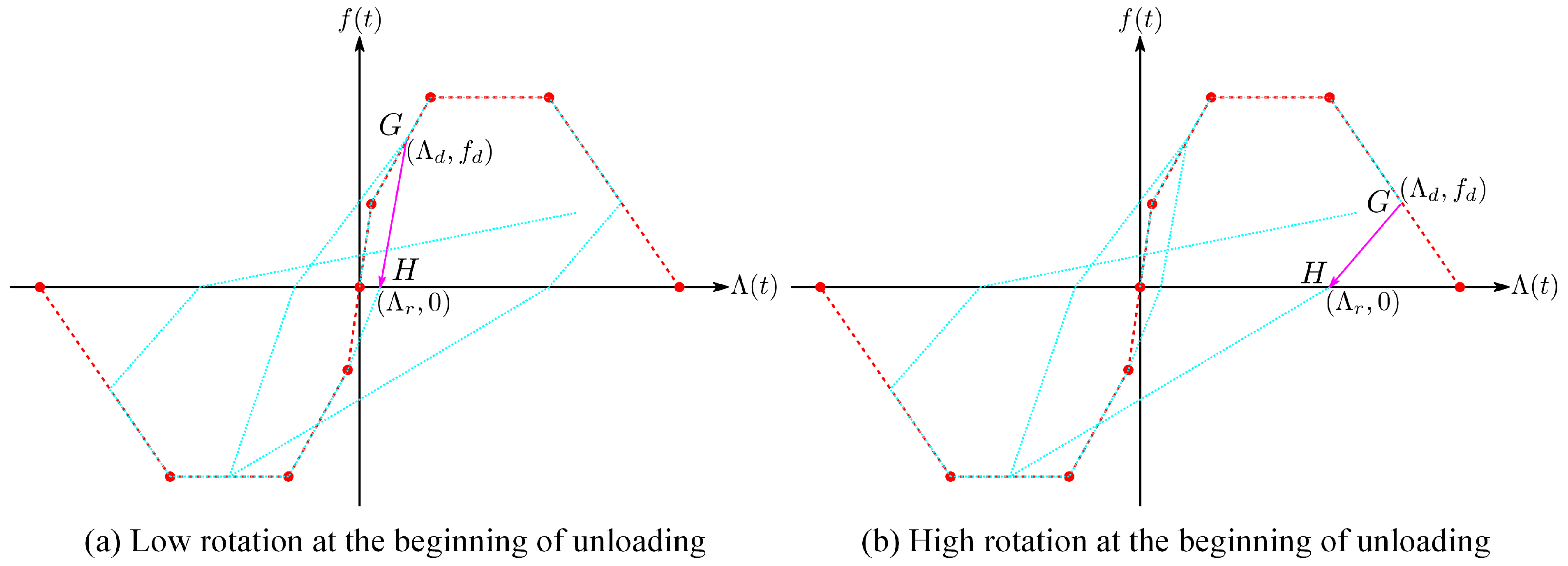
The cracking moment, denoted as
, and the plastic rotation at cracking,
, were calculated using the transformed section properties along with the following equations:
and
where
is the applied axial load (N),
is the area of the transformed section (mm
2),
is the moment of inertia of the transformed section (mm
4),
is the modulus of elasticity of the concrete (MPa),
is the distance to the furthest tension fiber in MPa, and
is the tensile strength of the concrete, determined using the following equation:
The calculated values for the hinges are summarized in
Table 3.
To evaluate the yield
, ultimate
, and fracture
curvatures, the XTRACT software version 3.0.8 [
61] was employed to compute the moment–curvature diagrams for each section. The ultimate curvature was defined as 85% of the maximum curvature (see
Table 4).
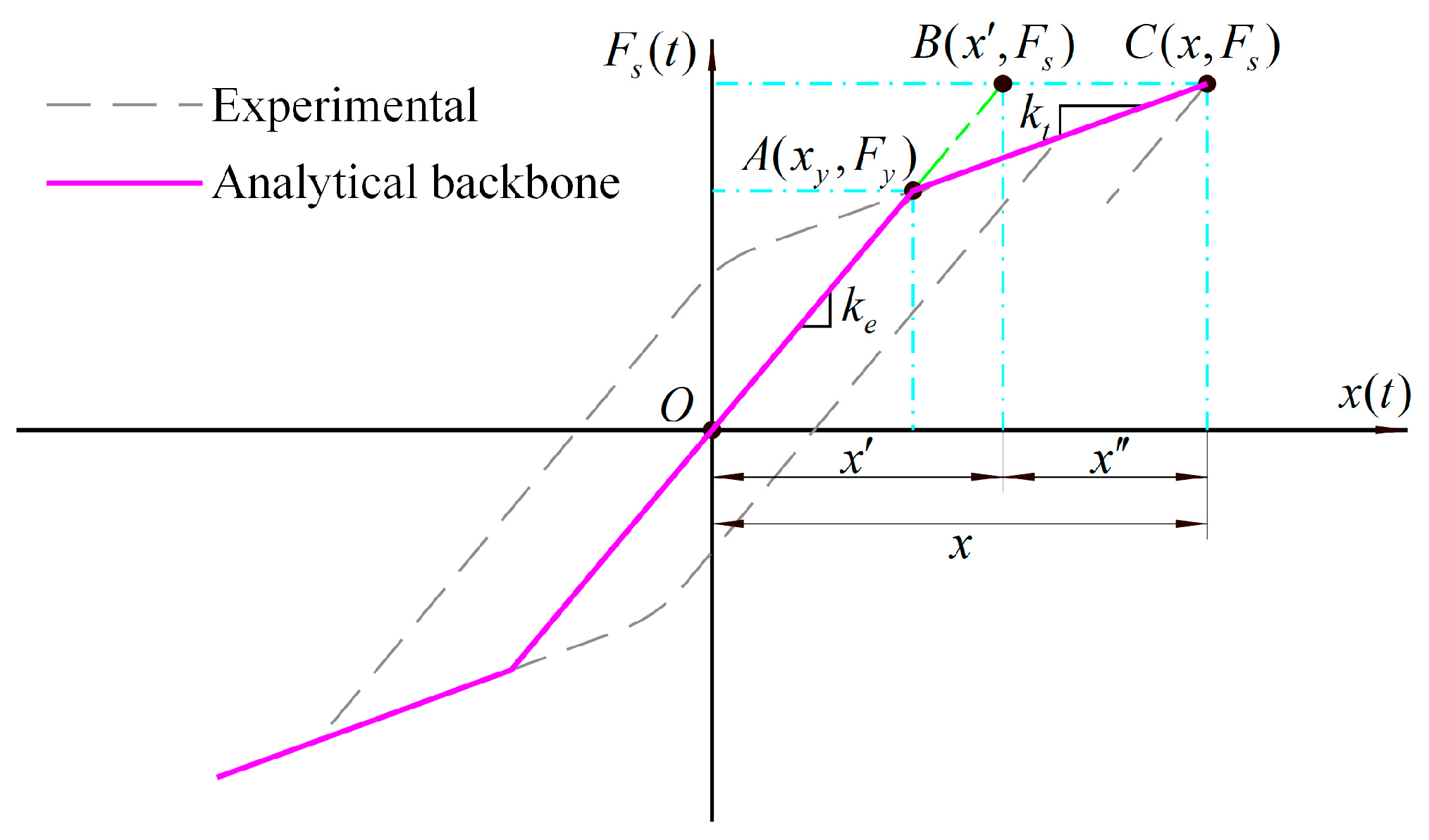
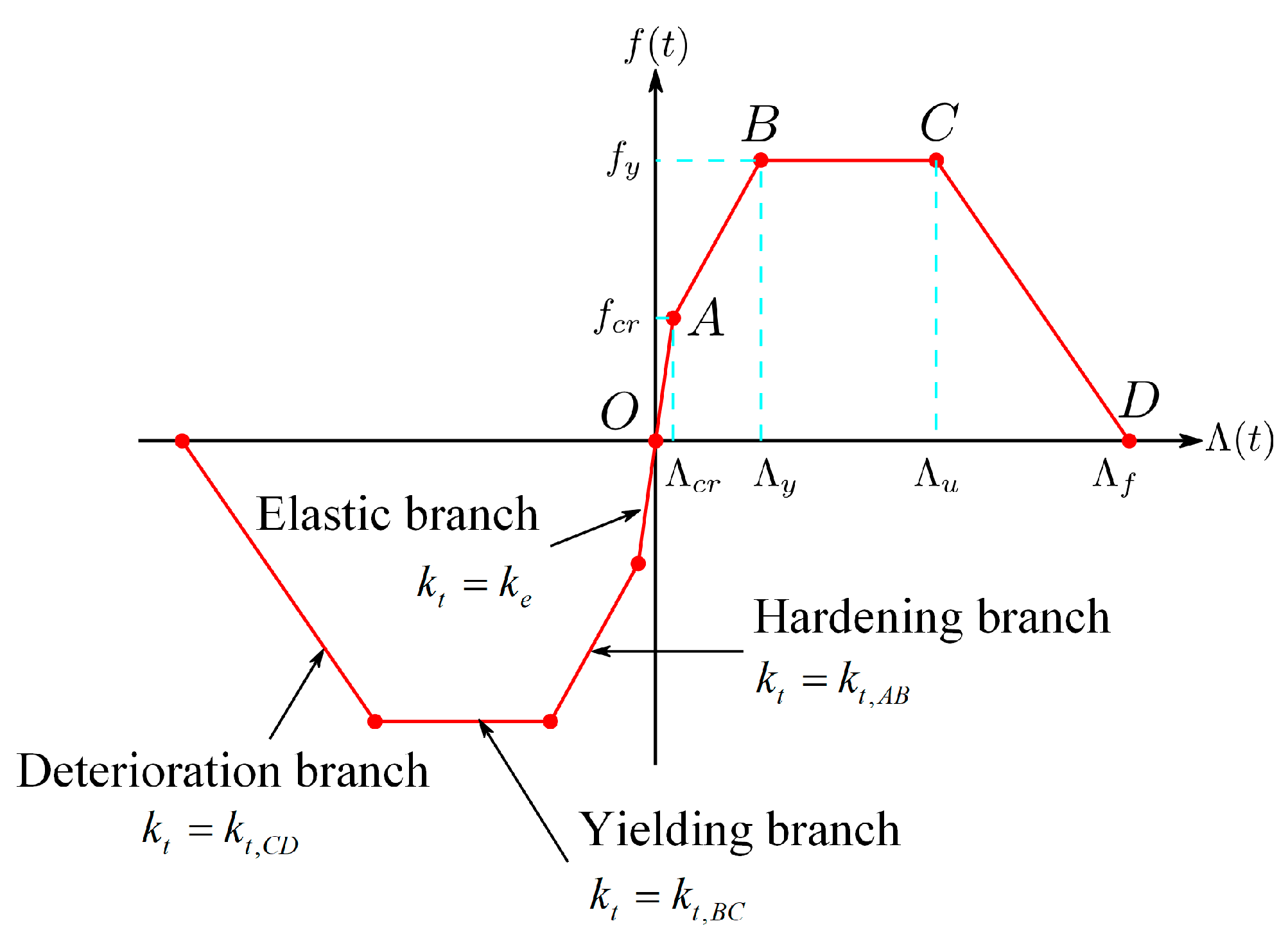
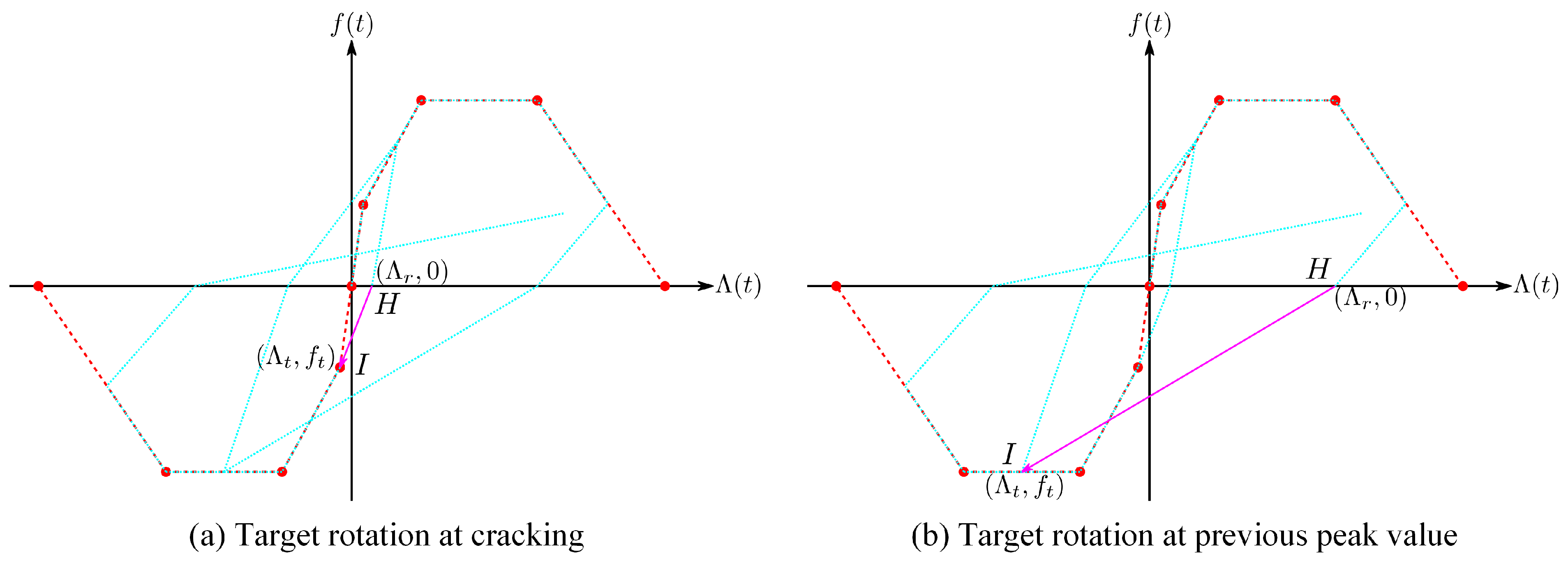
The plastic hinge backbones were characterized by the cracking moment and yield moment , along with the curvatures at cracking , yield , ultimate , and fracture points.
The plastic rotations were calculated based on the obtained curvatures, utilizing the plastic hinge length,
, defined by the following equation:
Various methodologies for determining the plastic hinge length have been proposed in the literature [
62,
63,
64,
65,
66,
67,
68]. In this study, we adopted the expression by Bae and Bayrak [
68], which considers the impact of the axial load level on the element.
The plastic hinge length is given by
where
is the frame length,
is the cross-sectional diameter, and
is the nominal axial load expressed as
In Equations (25) and (26), refers to the area of the longitudinal steel reinforcement, while indicates the total cross-sectional area of the concrete.
Using Equation (24), we determined the plastic hinge lengths and corresponding rotations to characterize the 16 backbones. A summary of the plastic hinge backbones is provided in
Table 5.
3.1. Model Considering Soil–Structure Interaction
Based on the properties described, four models incorporating foundation flexibility were developed. The foundation mass is denoted as , and its moment of inertia is .
The soil–structure interaction analysis considered four representative soil types: rock, dense soil, stiff soil, and soft soil. The stiffness and damping coefficients for these soil types were derived using expressions proposed by Gazetas [
69]. A summary of the soil and foundation properties is provided in
Table 6.
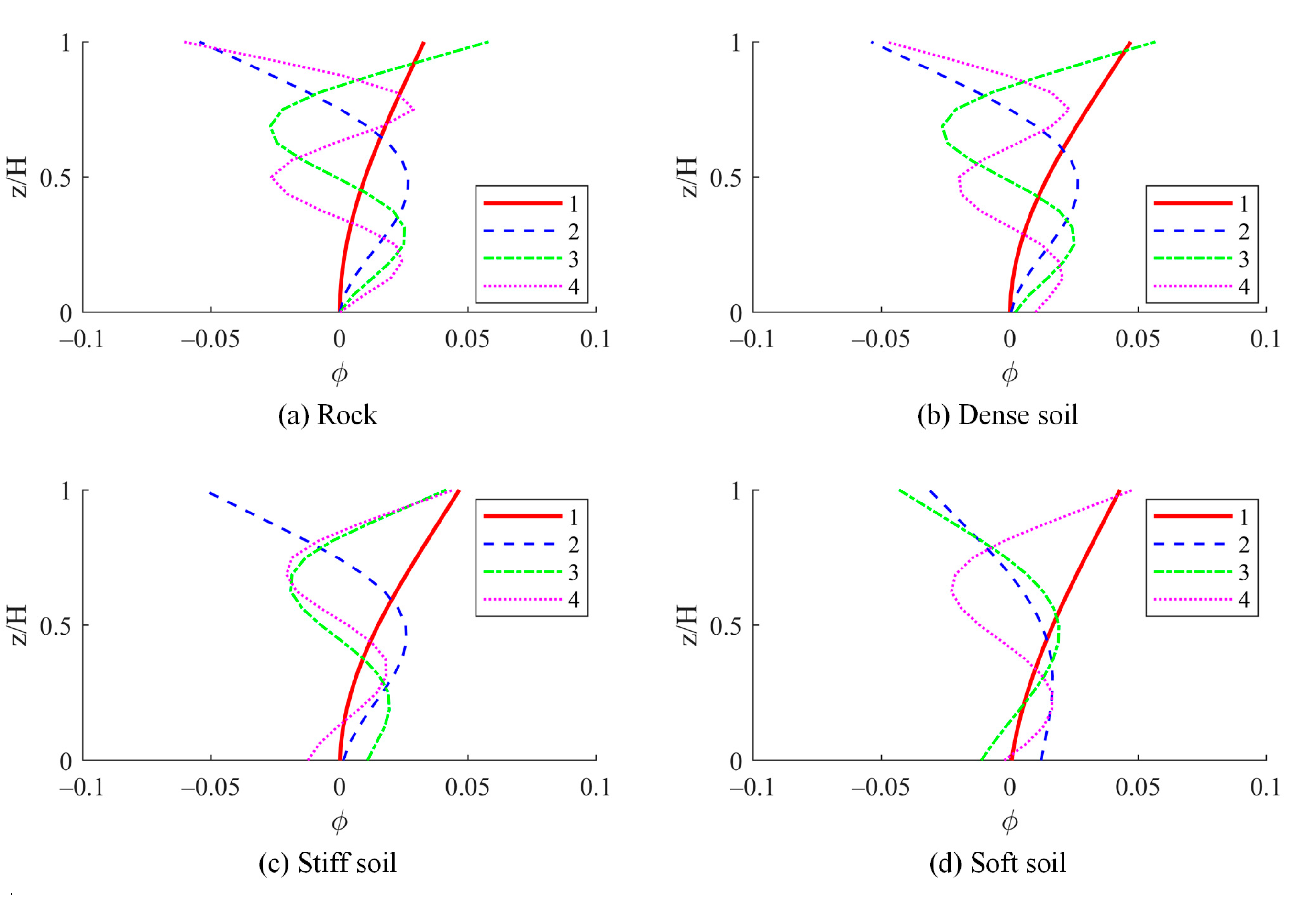
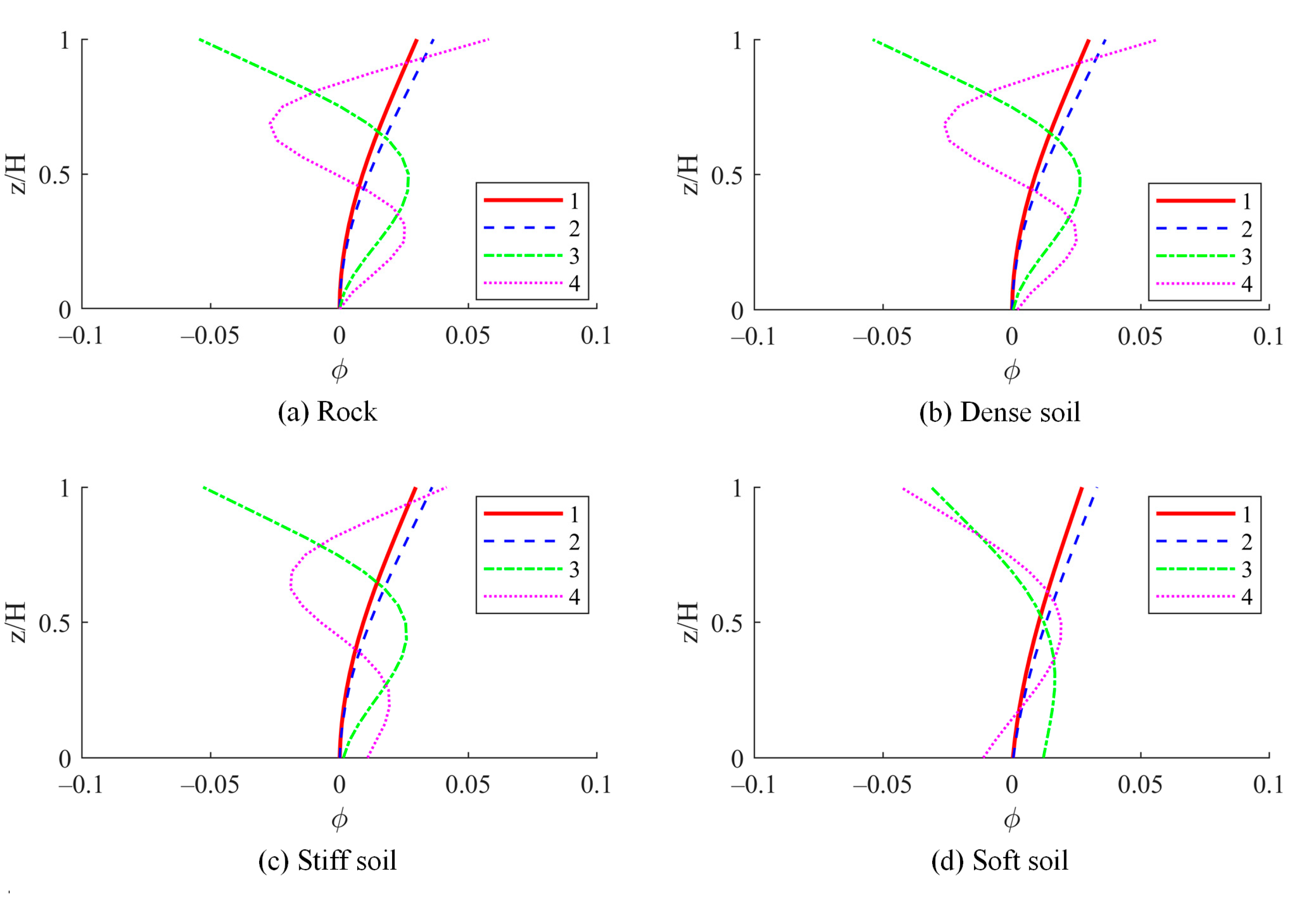
The modal periods and shapes of the chimney were determined with consideration for soil–structure interaction.
Table 7 compares the first four periods of fixed-base versus flexible-base models. It is evident that the fundamental period varies according to the soil type, while the other periods remain relatively stable. Additionally,
Figure 11 illustrates a comparison of the first four mode shapes of the chimney across different soil conditions.
3.2. Model Considering a Control Device
To mitigate the response of the chimney, a tuned mass damper (TMD) was installed at the chimney cap. This device was tuned to the fundamental period, utilizing a mass ratio of 2%. Given the different support conditions exhibited by the models, the fundamental period varied among them. As a result, the mass ratio for the TMD design remained constant, while only the period was adjusted.
The dynamic properties of the models featuring a TMD at the chimney cap, designed according to the guidelines established by Bachmann et al. [
70], are summarized in
Table 8.
The vibration periods and modes of the models that incorporate a TMD were determined. The periods for the first four modes are detailed in
Table 9. Furthermore,
Figure 12 illustrates a comparison of the first four vibration modes of the chimney with a TMD across various soil conditions.
3.3. Earthquake Analysis
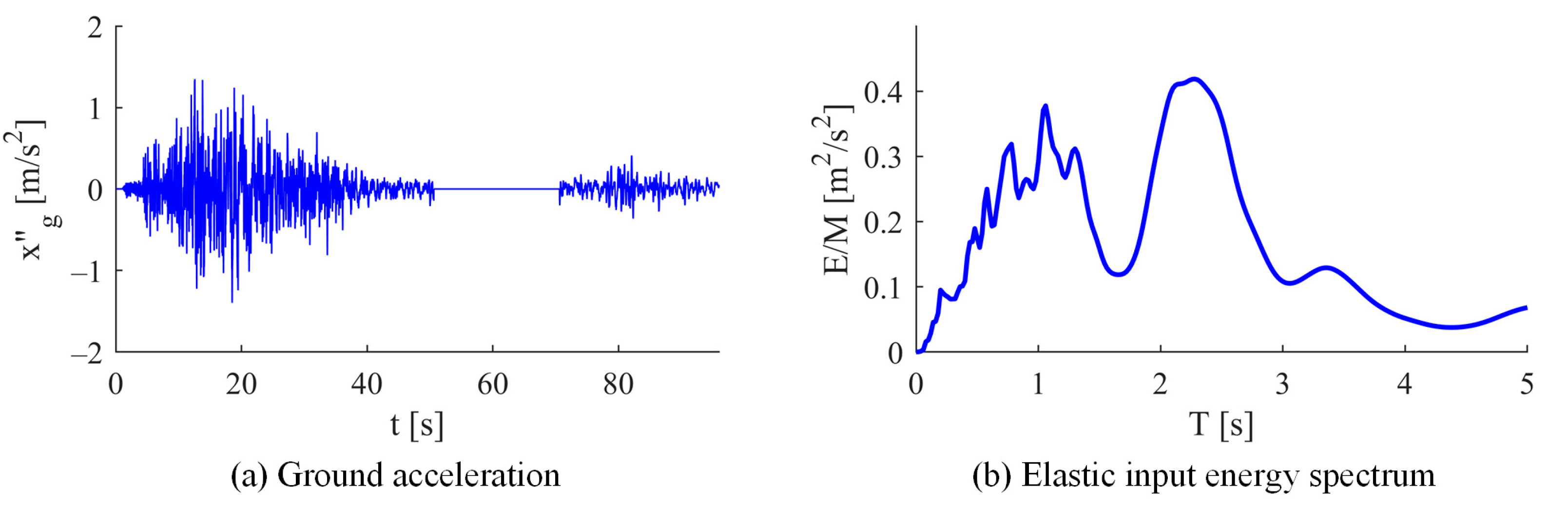
For the earthquake analysis, records obtained from the Caleta de Campos station in Michoacán, oriented along the S00E direction, were utilized. This seismic sequence encompasses the mainshock that occurred on 19 September and its subsequent aftershock on 21 September 1985.
Figure 13 illustrates the ground acceleration record and the input energy spectrum corresponding to the analyzed sequence.
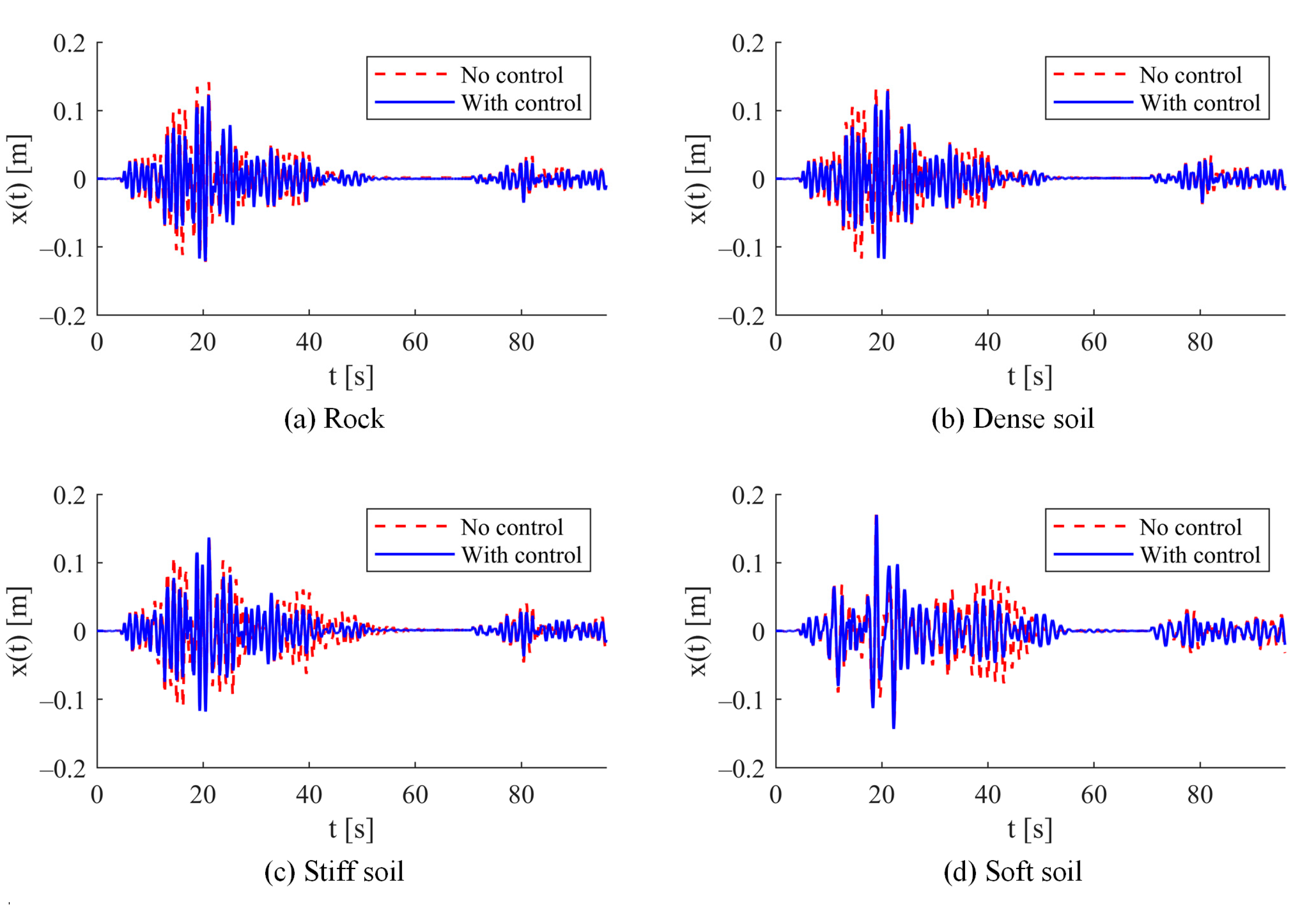
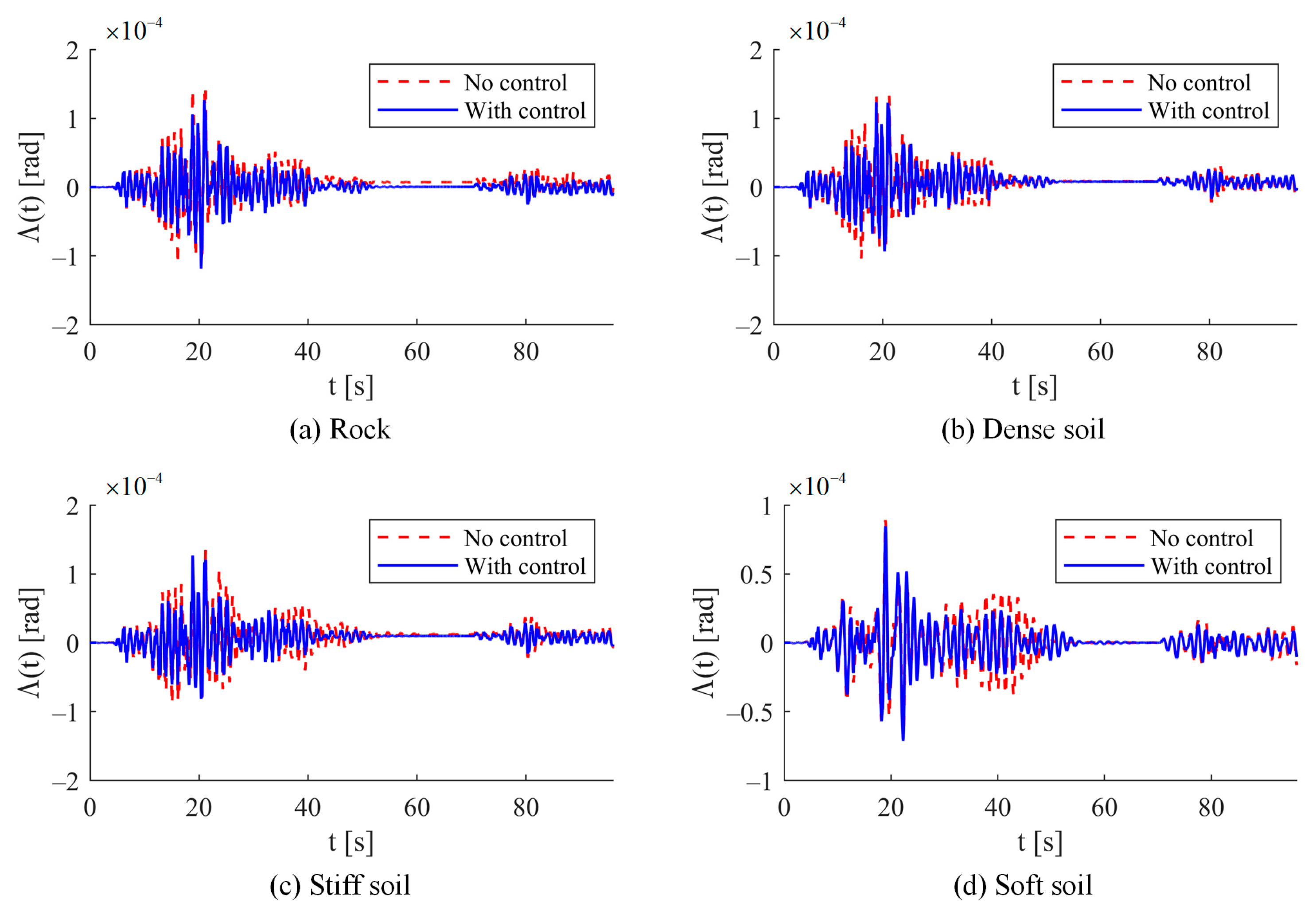
The dynamic response was determined considering a damping factor of 3% in the first two vibration modes of the structure. The inelastic response of the models, both uncontrolled and equipped with a TMD, was evaluated for foundations on various soil types: rock, dense soil, stiff soil, and soft soil.
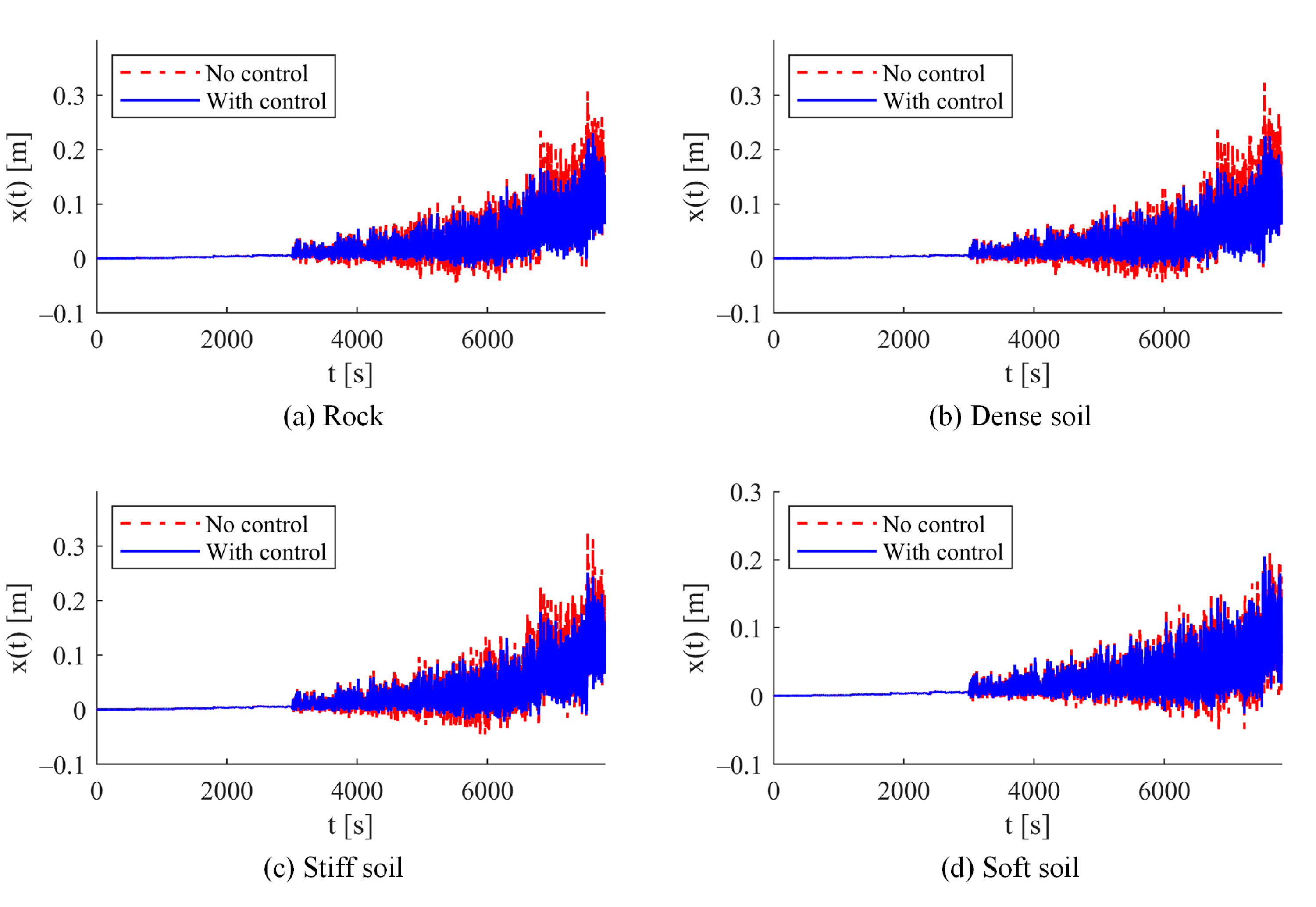
Figure 14,
Figure 15 and
Figure 16 show the displacements at the chimney cap, as well as the moments and rotations at the plastic hinge at the base. The highest amplitude of response was obtained during the mainshock. The maximum displacement without control reached 18 cm on soft soil, which is 28% greater than that observed on the other soil types. The response at the plastic hinge at the base of the chimney surpassed the cracking rotation in all scenarios, although it did not achieve the yield point of the section. The maximum recorded rotation was 1.404 × 10
−4 rad, occurring on rock.
Soil–structure interaction altered the dynamic properties, with notable differences being observed among the various soil types, particularly pronounced in soft soil. The TMD significantly reduced the response across all conditions, demonstrating greater efficiency on rigid soils. In the case of soft soil, the effectiveness of the control was more evident following the intense phase of the mainshock.
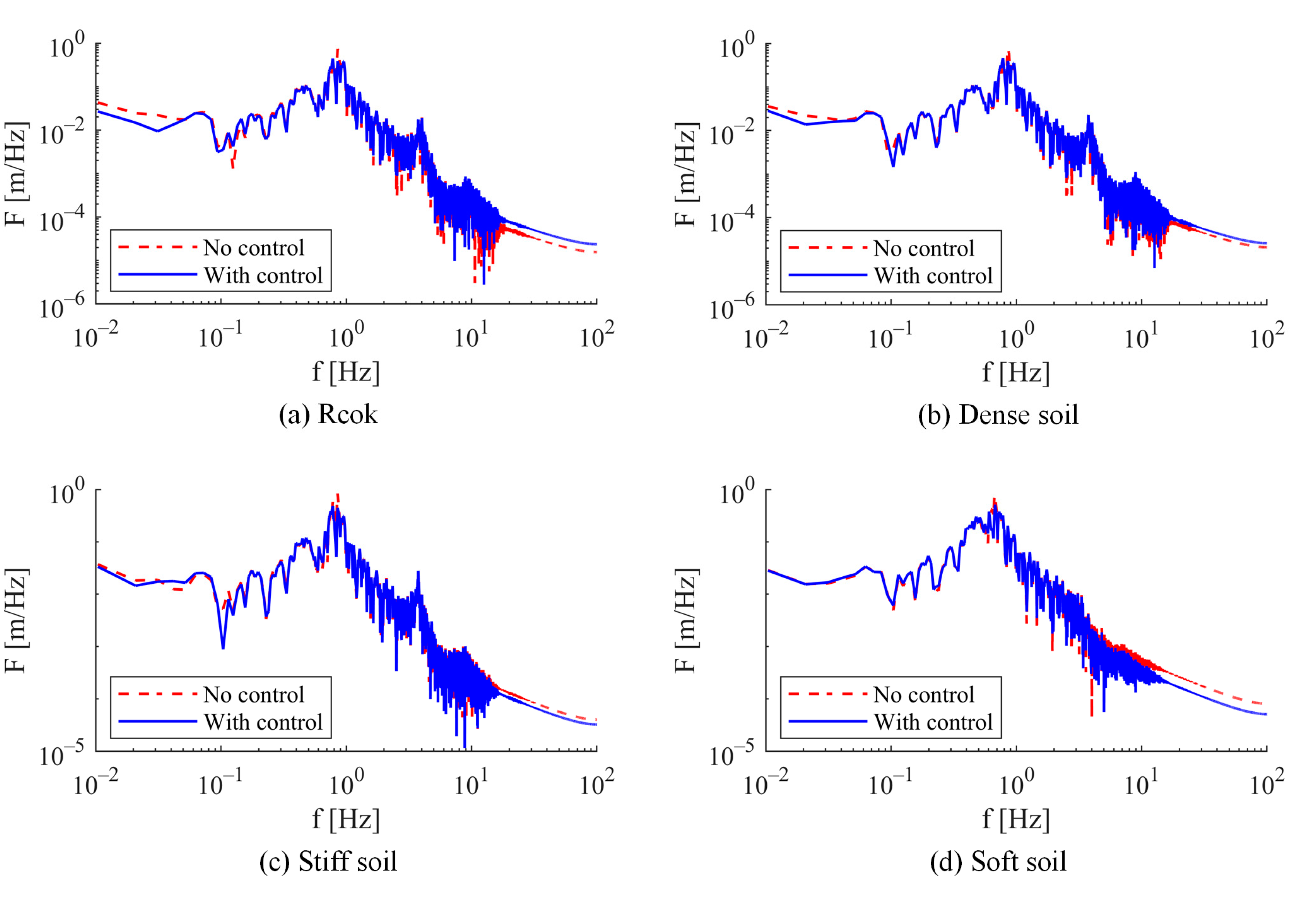
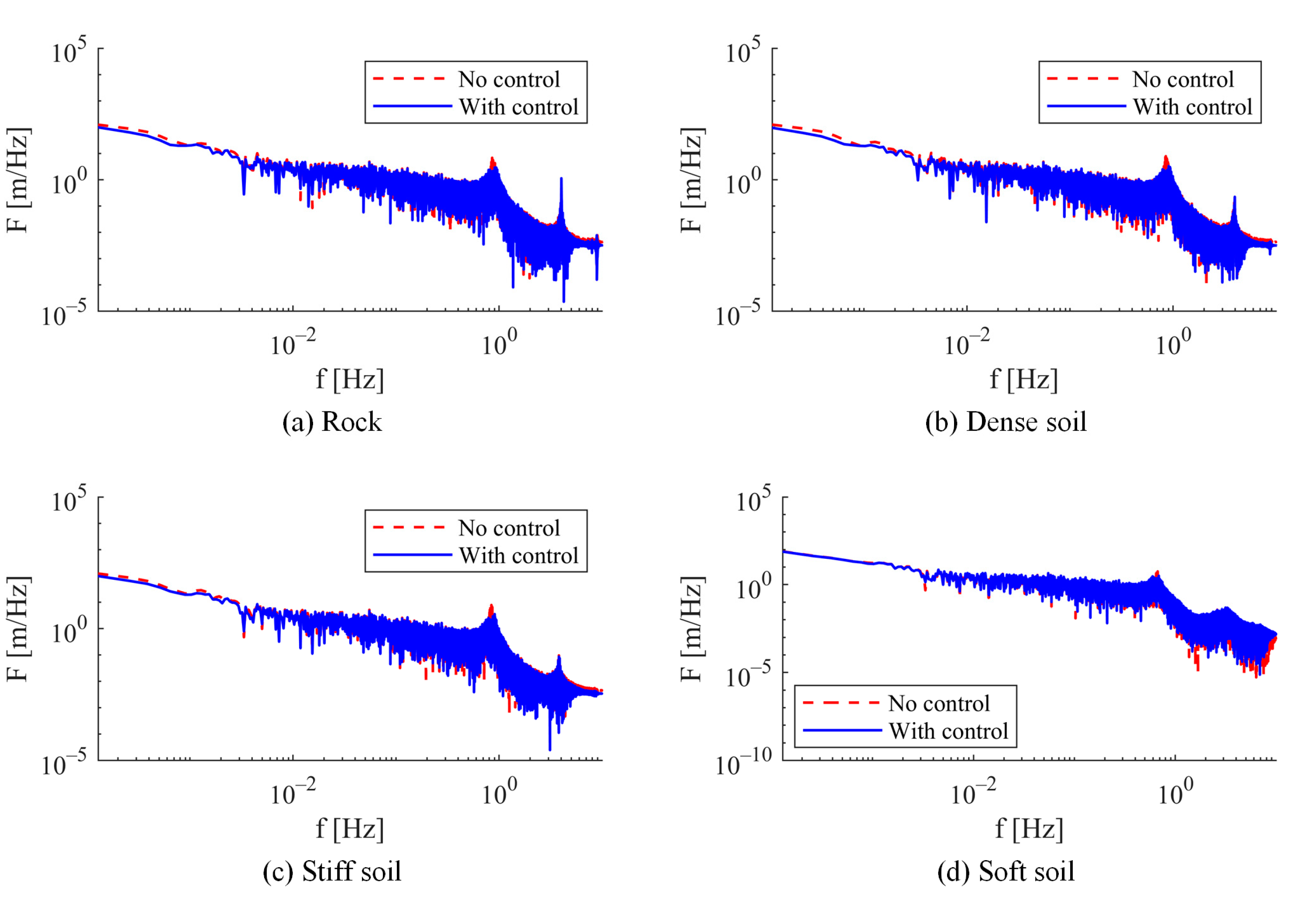
The displacement response at the chimney cap was analyzed in the frequency domain, with the Fourier amplitude spectrum presented in
Figure 17. The findings reveal that the maximum amplitude without control aligns with the fundamental period of the system for each soil type. Upon implementing the control system, a reduction in amplitude at the fundamental frequency was observed. Conversely, at frequencies higher than the fundamental, the controlled response exceeds that of the uncontrolled response, particularly in the case of firmer soils. This trend gradually diminishes with increasing soil flexibility, ultimately resulting in a lower amplitude compared to the uncontrolled response. This phenomenon can be attributed to soil–structure interaction, which modifies the dynamic properties of the system and channels more energy into the fundamental mode.
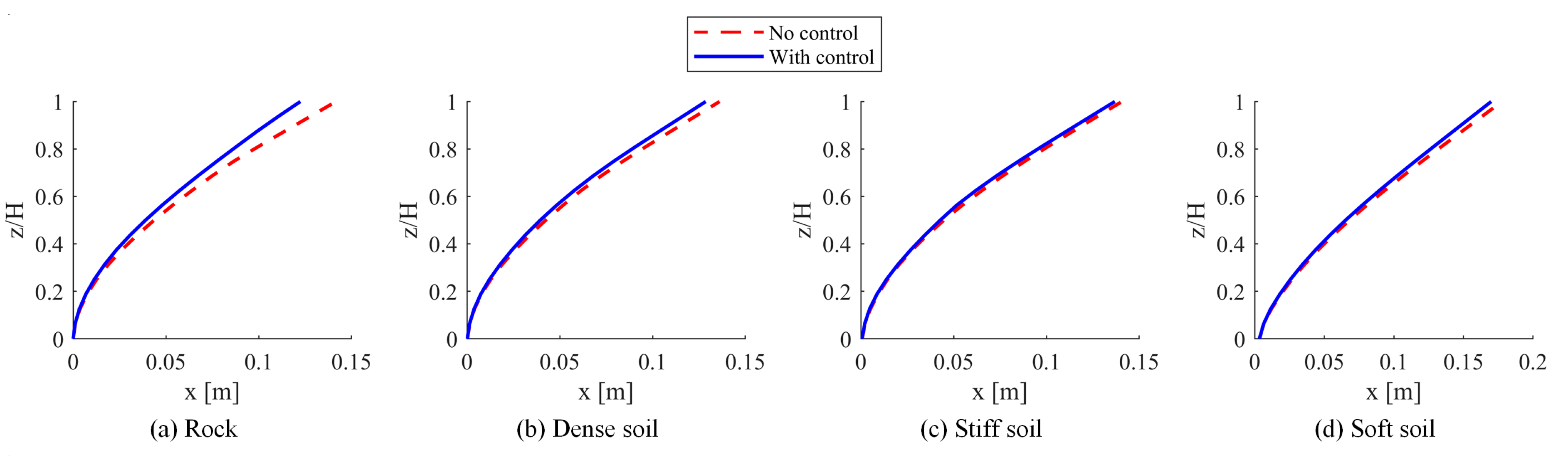
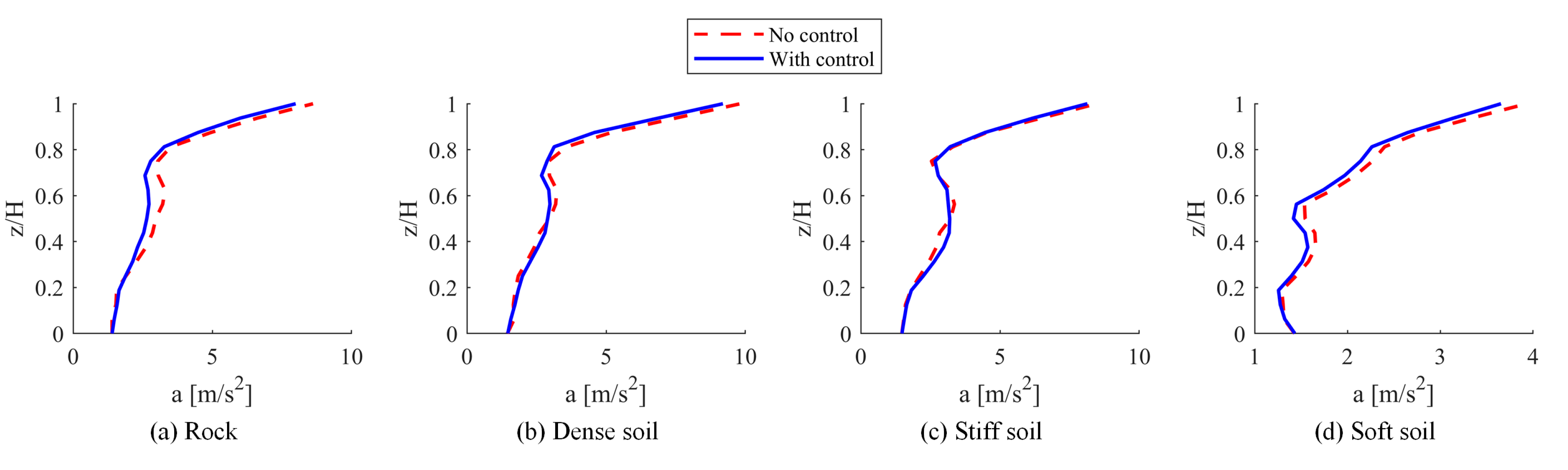
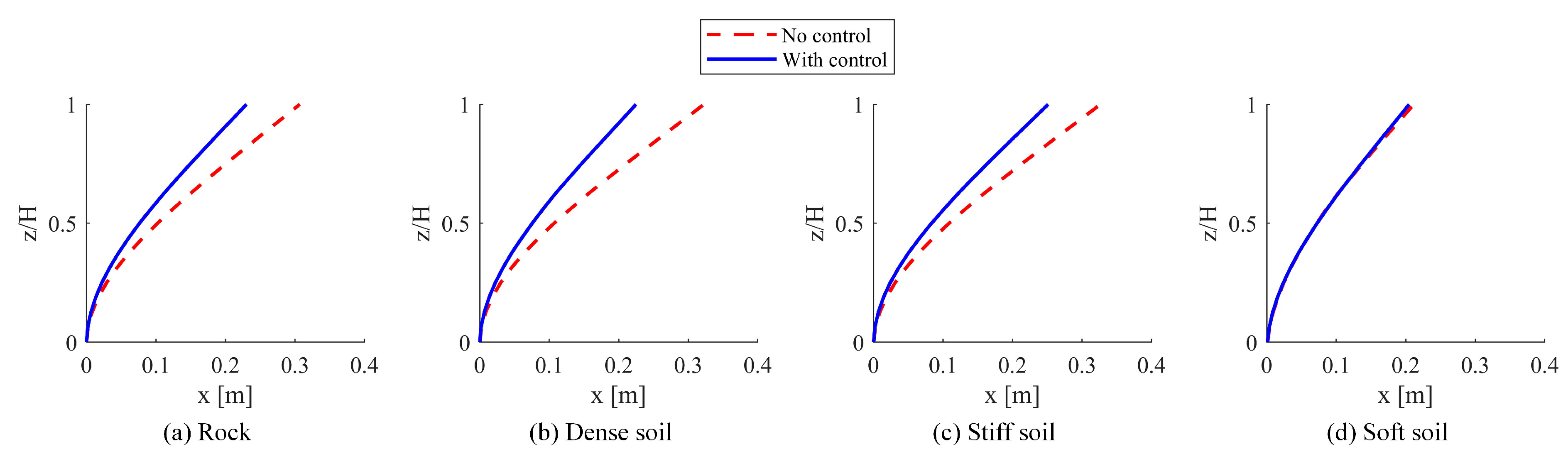
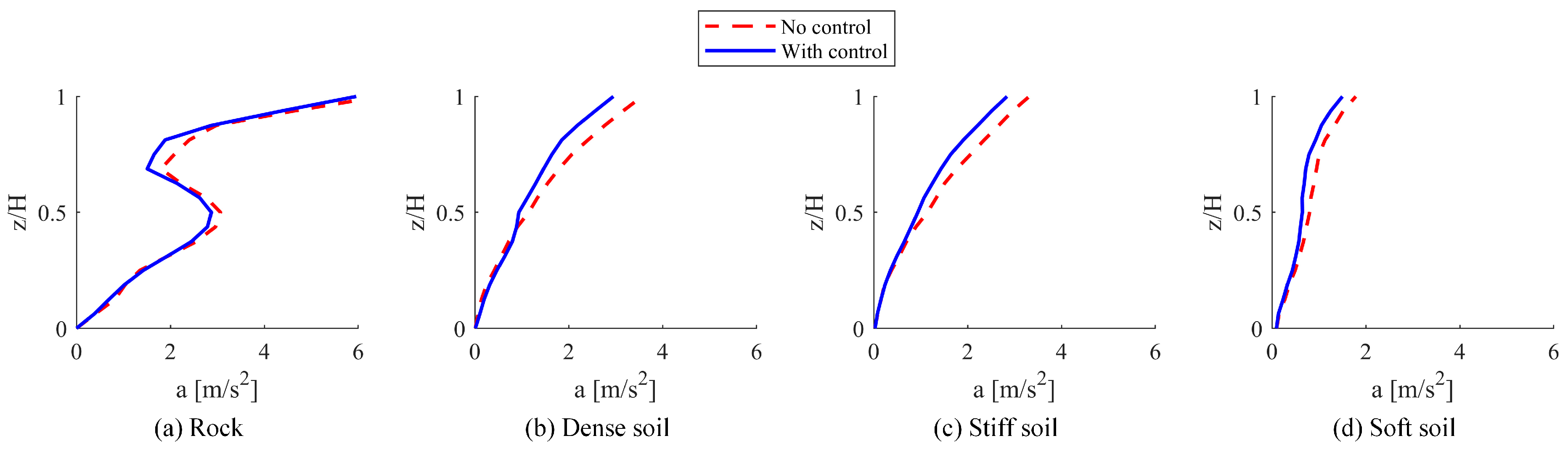
The maximum response profiles for displacements and accelerations, illustrated in
Figure 18 and
Figure 19, were evaluated across various soil types, both with and without the implementation of the TMD. The most significant overall reduction in displacement was recorded on rock, achieving a reduction of 12.4%, while the smallest reduction, measured at 3.46%, was observed on stiff soil. In terms of accelerations, the greatest overall reduction was 9.8% on rock, whereas the smallest reduction of 4.8% was noted on stiff soil. These findings suggest that the effectiveness of the TMD diminishes as the flexibility of the soil increases.
Table 10 and
Table 11 summarize the maximum mechanical response values along with their corresponding reduction percentages. The highest percentage reduction was recorded for displacements
, with a 13.6% decrease on rock, contrasted with a modest reduction of only 2.7% on stiff soil. This indicates that the flexibility of the soil significantly reduces the effectiveness of the TMD compared to the reductions achieved on rock.
3.4. Wind Analysis
The chimney under study is situated in a region with a latitude of 17°57′, an elevation of 10 m above mean sea level, an average annual temperature of , a barometric pressure of 759.14 mmHg, and a terrain roughness height of . The drag coefficient of the structure is assumed to be .
The wind excitations consist of synthetic wind records representing a storm’s development over a duration of 7800 s. The initial mean wind speeds varied from 5 m/s to 25 m/s, considering increments of 5 m/s. These were modeled as synoptic winds using the methodology proposed by Shinozuka and Deodatis [
71], with a vertical decay coefficient set at 5. For wind speeds ranging between 30 m/s and 65 m/s, also in 5 m/s increments, hurricane gusts were evaluated. This was carried out by employing the approach described by Fernández Lorenzo et al. [
72] and the empirical velocity profile suggested by Snaiki and Wu [
73], using a vertical decay coefficient of 10.
Figure 20 shows the wind history simulations used for wind analysis.
Incremental dynamic analyses were performed to assess the chimney’s response, incorporating 1% viscous damping for the fundamental modes, soil–structure interaction across four different soil types, and utilizing a TMD installed at the chimney cap.
Figure 21,
Figure 22 and
Figure 23 illustrate the displacements at the chimney cap, along with the moments and rotations occurring at the plastic hinge located at the base. The results demonstrate that the maximum response is achieved near the conclusion of the analysis, coinciding with peak wind velocity. The maximum displacement recorded without control was 33 cm on stiff soil, while the minimum displacement noted was 21 cm on soft soil. In terms of moments, the maximum value without control reached 290,200 kN·m, and the corresponding rotation was 3.46 × 10
−4 rad on dense soil; the minimum values recorded were 221,470 kN·m and 2.20 × 10
−4 rad on soft soil.
The tuned mass damper proves to be more effective in mitigating the response on firmer soils, although its efficiency decreases as the soil becomes more flexible. Moreover, the response control significantly influences displacements and rotations at the plastic hinge, more so than it does at the moments.
The Fourier amplitude spectrum of the chimney cap displacement is illustrated in
Figure 24. The results indicate that the displacement response exhibits a broader frequency range compared to the seismic excitation, with significant amplitudes observed at lower frequencies. This broadening is attributed to the synthetic wind record, which covers a wider frequency range. In the uncontrolled response, the amplitude at the structure’s fundamental frequency is pronounced, along with a substantial contribution from the second mode. When the control system is implemented, a noticeable reduction in the amplitude of the spectrum is observed compared to the uncontrolled response, which aligns with the expected outcomes of this system.
The maximum response profiles illustrated in
Figure 25 and
Figure 26 were assessed across various soil types, both with and without the TMD. The most significant reduction in displacement was recorded on dense soil, achieving a decrease of 30.2%. In a similar vein, the highest overall reduction in accelerations reached 19.0%, also on dense soil. These findings highlight that the effectiveness of the TMD diminishes as soil flexibility increases.
Table 12 and
Table 13 present a summary of the maximum values for mechanical components along with their respective response reductions. The most significant percentage of reduction was noted in dense soil, with similar values observed in rock and rigid soil. Specifically, both displacement and acceleration in dense soil were reduced by up to 30.3% and 17.1%, respectively. In contrast, on soft soil, the reduction was limited to just 3.1% for displacements. These findings consistently demonstrate that the effectiveness of the control system diminishes as soil flexibility increases.
4. Discussion of Results
The results indicate that the TMD significantly enhances the chimney’s response to earthquake and wind excitations. The device achieved reductions of up to 13.6% for earthquakes and 30.3% for wind actions in displacement response. Similar reductions were noted in base moments across rock, rigid, and dense soil conditions. However, maximum acceleration and base shear exhibited the smallest decreases among the analyzed parameters.
Soil flexibility played a critical role in the effectiveness of the control device. More substantial reductions in response were observed on firmer soils compared to soft soil, where the reduction percentages were generally less than half of those achieved on firmer soils. Consequently, soil flexibility adversely affects the efficiency of the control device.
In terms of the inelastic behavior of the structure, the control device significantly reduced the maximum rotation demand at the plastic hinge located at the base of the chimney across most soil types. This reduction was greater than that observed in the moments at the hinge. However, for soft soil, the impact of the control system on response was limited. For earthquakes, the reduction was only notable outside of the intense phase, while for wind excitation, the differences were negligible.
Incremental analyses demonstrated that the use of a TMD enhances the structural response when accounting for soil–structure interaction. The most favorable results were achieved on firm soils. This simple device reduces the demands on the original structure, making it a suitable solution for reducing the structural response of similar constructions subjected to seismic and wind forces, particularly when founded on firm soil.
The findings of this study are consistent with those reported by Elias [
53] regarding earthquake response control of a reinforced concrete chimney with consideration for SSI. Specifically, reduction percentages on rock were recorded as 13.6% in this study, compared to 19.6% reported by Elias [
53]. Differences arise because Elias [
53] performed elastic analyses, while this study used the FAM to include material nonlinearity.
In terms of wind excitation, the uncontrolled structural response on soft soil was found to be less than that on more rigid soils without control. This suggests that wind demands are more destructive for chimneys under firm soil conditions, a conclusion also supported by Galsworthy and Naggar [
13].
The results indicate that soil flexibility may reduce the effectiveness of the control device when subjected to both earthquake and wind excitations. This finding aligns with other studies [
53], which demonstrated that the response with the TMD could surpass the uncontrolled response depending on the excitation.
Comparing the numerical results obtained in this study with experimental data proves challenging due to the absence of real vibration records for chimneys fitted with vibration control systems. Nonetheless, the numerical findings align with the conclusions drawn by Galsworthy and Naggar [
13] as well as Elias [
53].
The FAM has demonstrated reliability in reproducing experimental results through the flexural model utilized in this study, as evidenced in Li et al. [
44]. Moreover, previous research [
29,
30,
39,
41] has compared the FAM with refined finite element models, revealing that the FAM not only accurately predicts outcomes but also does so with significantly reduced computational costs for both static and nonlinear dynamic analyses. Additional validations supporting the FAM’s results are presented by Patlán, Hernández-Barrios, and Gómez [
49], as well as Patlán [
74,
75]. These validations reinforce the application of the FAM for the nonlinear dynamic analyses conducted in this study.
5. Conclusions
This study examines the control of vibrations caused by extreme earthquake and wind forces in slender structures, taking into account the effects of soil–structure interaction (SSI) and material nonlinearity by using the Force Analogy Method (FAM). Through extensive dynamic analyses, the effectiveness of a tuned mass damper (TMD) was assessed across various soil types, identifying the conditions under which this control system operates most efficiently.
The implementation of the FAM introduces a novel approach in this context, providing a robust framework for understanding the nonlinear behavior and the complex interactions between soil and structure, including control devices. Its application proved crucial in accurately predicting the dynamic response of the structure under extreme loading conditions, revealing insights that the linear analysis failed to capture. This innovative methodology facilitated a thorough evaluation of the TMD’s performance in mitigating responses induced by earthquake and wind forces, emphasizing its potential for broader applications in structural control.
In the context of earthquake analysis, the implementation of the TMD resulted in substantial reductions in displacements and base moments, with peak displacements being reduced by as much as 13.6% under rock conditions. The presence of SSI modified the dynamic properties of the structure, with the most significant effects being observed on soft soils, where the TMD’s efficacy was primarily evident during the post-intense phase of the earthquake. The findings indicate that the TMD performs optimally on rock, with its effectiveness diminishing as soil flexibility increases.
For wind excitations, the TMD achieved a remarkable reduction of up to 30.3% in maximum displacements when evaluated under dense soil conditions, with comparable performance noted on rock and rigid soils. However, its effectiveness diminishes in soft soils due to alterations in dynamic properties arising from SSI, highlighting the necessity for adaptive control systems in such scenarios. Incremental analyses demonstrated that as the wind velocity increases, the maximum response of the structure intensifies, emphasizing the importance of utilizing optimized control devices for extreme conditions.
Incorporating material nonlinearity through the FAM and SSI in the analysis revealed critical effects that a linear model would overlook. This approach underscores the significance of considering these factors when designing control systems. The findings suggest that while the TMD is effective in mitigating dynamic responses, its design must be specifically tailored to the soil and structural characteristics to maximize performance.
These results highlight the importance of integrating SSI effects and material nonlinearity into the design of slender structures with passive control systems subjected to extreme events. This integration promotes more informed and responsible design practices, ensuring the effectiveness of these systems under realistic and complex conditions.
Future research should prioritize the development of alternative control systems aimed at enhancing effectiveness on soft soils and during extreme events, especially for structures that are highly vulnerable. Moreover, extending the analyses conducted in this study to encompass more complex structures, such as bridges or communication towers, would be beneficial for validating the general applicability of the findings.