Local Full-Scale Model Test on Mechanical Performance of the Integral Splicing Composite Structure of Adjacent Existing Box Girder Bridges

Abstract

Adjacent existing box girder bridges should be spliced in the long-span bridge expansion project. A type of integral splicing composite structure for connecting the adjacent flange plates is designed herein. The mechanical characteristic of the integral splicing composite structure is tested using a local full-scale model, and a refined simulation model is also proposed for the optimization of the integral splicing composite structure. The loop bar in the joint connection segment and the application of Ultra-High-Performance Concrete (UHPC) material can guarantee the effective connection between the existing flange plate and the splicing structure. The embedded angled bar can delay the interface debonding failure and interface slip. The UHPC composite segment below the flange plate (segment CF) can bend together with the existing flange plate. In this study, an innovative integral splicing composite structure for a long-span bridge extension project is proposed and verified using both a local full-scale model test and finite element simulation. The adaptation of UHPC material and loop bar joint connection form can meet the cracking loading requirements of the splicing box girder structure. By proposing a refined simulation model and comparing the calculation result with the test result, it is found that the flexural performance of the integral splicing composite structure depends on the size of the composite segment below the flange plate (segment CF). Increasing the width of segment CF is beneficial to delay the interface debonding failure, and increasing its thickness can effectively delay the cracking load of the flange plate. Finally, the scheme of segment CF with one side width of 200 cm and a minimum thickness of 15 cm can improve the flexural resistance of the spliced structure and avoid the shear effect caused by the lane layout scheme and the location of the segment CF end. Through the research in this paper, the reasonable splicing form of a long-span old bridge is innovated and verified, which can be used as a reference for other long-span bridge splicing projects.

1. Introduction

In the traditional reconstruction and expansion of existing long-span bridge projects, a separated expansion scheme without splicing bridges is generally adopted to avoid the problem of excessive stress levels after splicing [1,2]. At this time, the road structure connected to the bridge needs to adopt a separate roadbed scheme to smooth the route alignment, which may cause a lot of waste of land resources [3,4,5]. If the width of the roadbed is compressed and the diversion facilities are set at the bridge head, the sudden change in the traffic environment becomes a safety risk point, which may easily lead to accidents [6,7]. Therefore, it is necessary to explore the reasonable splicing structure and materials for the expansion of long-span bridges. In this way, the residual performance of the long-span old bridge can be fully excavated and ensure the safety and long-term performance of the bridge [8,9].

Several studies have included the splicing method and splicing material development. Tan et al. [10] proposed a multi-technology hybrid bridge splicing method, which mainly follows the principle of maximum material stress at the splicing interface. The number of splicing partitions of widened bridges can be easily calculated, and the relevant research results have been applied in short- and medium-span bridges. However, the mechanical properties of the splicing structure in long-span bridges are completely different from those of short- or middle-span bridges, and the applicability of the bridge splicing method still needs further verification. Wen et al. [11] proposed a new type of transverse splicing structure to reduce the transverse deformation caused by concrete shrinkage and creep between old and new bridges. This type of structure can reduce the transverse tensile stress in the joint and effectively avoid the concrete cracking of the top flange of the box girder at the beam end. In addition, Nie et al. [12] studied the mechanical behavior of composite joints between existing concrete bridges and steel–concrete composite beams. They found that the interface failure mode between the old and new concrete is usually caused by the failure of composite joints. Moreover, they also found from tests that the increase in concrete strength can improve the ultimate shear strength of the interface. Although several studies have been conducted on the splicing of long-span bridges, the existing studies mainly concentrate on the splicing method between old and new bridges, and even the splicing of two bridges with different structural forms. There are relatively few studies on the splicing between two long-span old bridges, and reasonable splicing forms between old bridges need to be developed.

In addition, some studies have been carried out on the excellent performance of ring bars and other types of joint connections. The research content is not only limited to the joint structure forms, but also includes the development of joint materials [13]. Gu et al. [14] investigated the effect of traffic vibration on the splitting interface strength and found that the interface between the new and old concrete specimens needs to be connected with steel bars to ensure the bonding performance at the interface. Wang et al. [15] experimentally compared the performance of loop joints with different parameters and concluded that enough overlap length can meet the stress requirements of the joint. Shi et al. [16] obtained similar conclusions by numerical analysis. Through refined numerical analysis, they also found that excellent material properties can reduce the overlapping length of loop bars to a certain extent. Lu et al. [17] focused on the cracking problem of wet joints under fatigue load, where the fatigue performance of Ultra-High-Performance Concrete (UHPC) specimens with a field-cast dovetail joint were tested using the full-scale test method. They found that dovetail wet joints can disperse fatigue stress to some extent. However, the box section form is often adopted in long-span bridges, and the thickness of the flange plate end is usually low. Therefore, it is difficult to use the method of planting steel bars to make the two adjacent flange plates effectively connected. In addition, the design scheme of three-dimensional prestress is often adopted for long-span bridges, and the arrangement of transverse prestressed steel wire bundles often has an important impact on the feasibility of splicing forms. Therefore, more attention should also be paid to the safety of the splicing effect. According to the analysis of relevant research, the application of high-performance materials and the development of reliable lap schemes should be focused on.

In this study, different types of integral splicing composite structure are proposed for the existing Xinfengjiang Bridge (XFJ Bridge), which can be divided into left and right spans, and the distance between the ends of adjacent flange plates is 40 cm. Local full-scale specimens with sizes of 5.6 m × 3.0 m × 0.62 m are designed and prepared according to the splicing construction process. Local full-scale specimens with different splicing schemes are tested, and the crack propagation characteristics, failure mode, and loading-force–displacement curve are especially compared. The significant effect of the composite segment below the flange plate (segment CF) has been recognized in terms of improving the flexural and tensile properties. In addition, the integral splicing composite structure is optimized based on this finding, and the schemes with different segment CF widths and thicknesses are proposed. A refined simulation model is proposed and verified by comparing the simulation results with the test results. By adopting this proposed simulation model, the schemes with different segment CF widths and thicknesses are compared. The simulation results are also compared in the aspects of the failure mode and cracking force, and the optimal scheme with the 200 cm segment CF width and 15 cm minimum thickness segment CF is recommended.

Through the research of this paper, some novelties have been achieved. Firstly, an innovative integral splicing composite structure for a long-span bridge extension project is proposed and verified. This type of integral splicing composite structure is a novel sandwich composite structure composed of the composite segment as the integral layer (segment CI), the joint connection segment (segment JC), and the composite segment below the flange plate (segment CF). This structure can surround the flange plate so that the end of the adjacent flange plate is cooperatively deformed. In addition, properly chiseling off the concrete at the end of the flange plate between the transverse prestressed wire bundles provides a new idea for the connection of the joint steel bar, and the low-thickness flange plate that cannot be straightly embedded into the steel bars. The adaptation of UHPC material can effectively improve the connection performance of the loop bar after partially chiseling off the flange plate concrete. In addition, the preparation of the specimen is in full accordance with the proposed splicing construction process, which can verify the splicing construction technology and ensure the rationality of the boundary conditions of the local model test at the same time. Moreover, the combination of the local full-scale model test method and the finite element simulation method assists the in-depth study of the rationality of the proposed spliced composite structure and the joint material.

However, in the following stage of study, the local full-scale model test method can still be applied to verify the optimized splicing scheme with maximum composite width. Moreover, actual bridge monitoring can also be carried out on the XFJ bridge to evaluate the long-term performance of the proposed integral splicing composite structure.

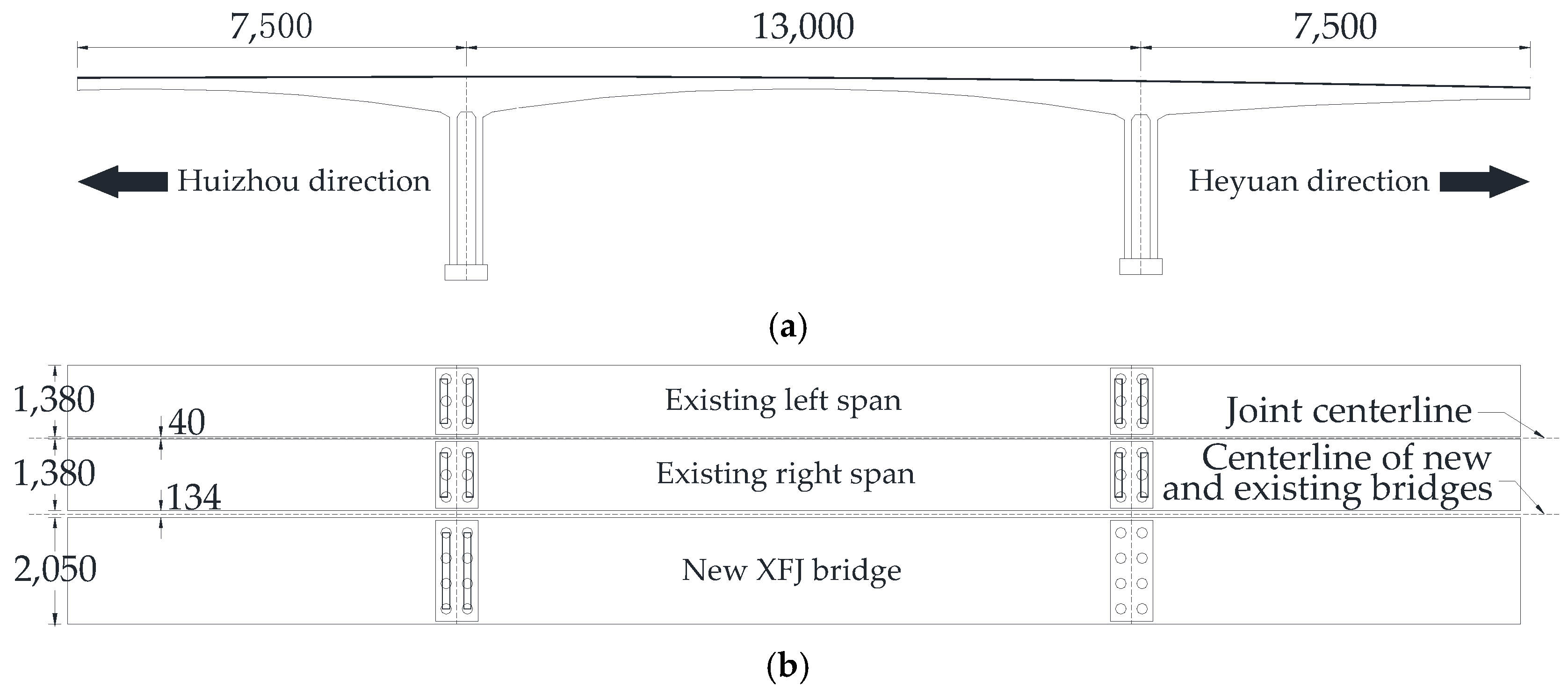
2. Background

2.1. Target Box Girder Bridge

Xinfengjiang Bridge (XFJ Bridge) is an existing bridge located in the Heyuan to Huizhou section of G15 National Highway. It is a three-span continuous rigid frame bridge with a span combination of 75 m + 130 m + 75 m, as shown in Figure 1a. The left and right spans of the XFJ Bridge were constructed separately. A box girder structure with a single box and a single chamber is adopted by each span, and its width is 1380 cm. The width of the flange plate is 315 cm, and the minimum thickness of its end is 18 cm.

The XFJ Bridge is equipped with three-direction prestress. The vertical prestressing adopts 25 mm finish-rolled screw-thread steel bars, and the longitudinal spacing is 0.5 m. The transverse prestressing adopts three bunches of standard steel wire bundles (3 × 7∅5), and the longitudinal spacing is 1.0 m. The transverse prestressed steel wire bundles are set to be tensioned at one end and fixed at the other end, with staggered arrangement. VLM 15BP-3 and VLM 15B-3 flat-shape anchorage are adopted by the fixed end and tension end, respectively.

According to the highway expansion design scheme of the Heyuan to Huizhou section of G15, it has been proposed to build a new bridge with a similar structural form on the side of the existing XFJ bridge, and the left and right spans of the existing XFJ Bridge are designed to be continually used after being integrally spliced, as presented in Figure 1b.

The distance between the end of the adjacent flange plates is 40 cm, as shown in Figure 1c. After the integral splicing of adjacent box girders, the span of the spliced flange plate reaches 670 cm, and its stress mode has also changed. When the left and right sides of the integral splicing box girder are subjected to asymmetric vehicle load, the root of the spliced flange plate will be subjected to positive flexural moment. This conflicts with the structural design concept that the flange plate was originally subjected to negative bending moment, which is extremely unfavorable to the stress of the spliced flange plate. Therefore, it is necessary to determine a reasonable integral splicing structure to ensure the safety of the box girder bridge after integral splicing.

In addition, a road traffic marking scheme for the spliced XFJ bridge is also proposed to ensure the safety of the splicing joints under local stress. A vehicle-restricted zone is set up on both sides of the joint within a certain range, and the lanes are arranged on both sides of the restricted zone, as shown in Figure 1c. It can be considered that, in the case of compliance with traffic rules, there will be no vehicles crossing the restricted zone.

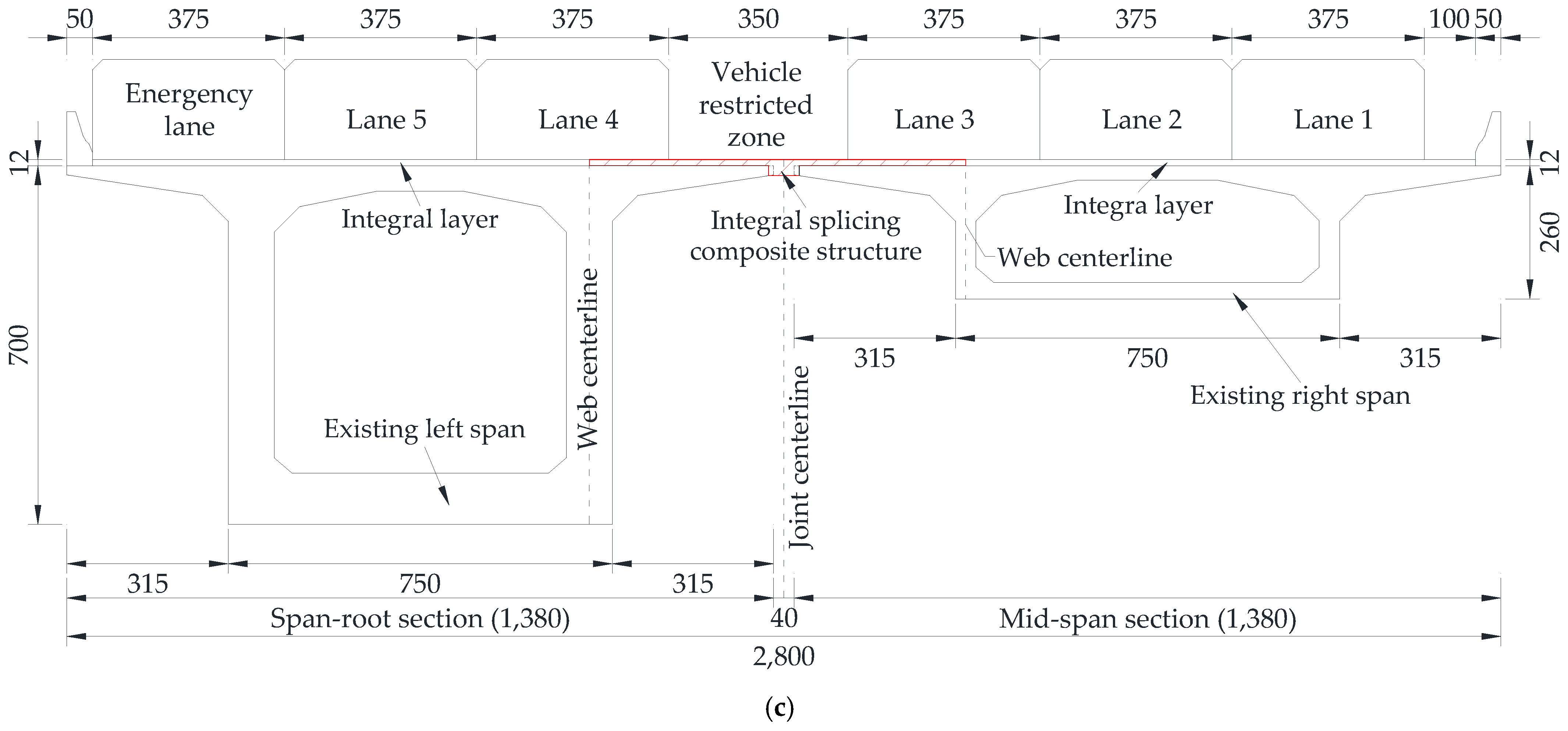
2.2. Integral Splicing Scheme of Adjacent Flange Plates

After several rounds of splicing scheme comparison, the overall splicing scheme of the XFJ Bridge is preliminarily determined as follows:

• Scheme ZL: The adjacent flange plate ends are directly connected by the splicing region. The thickness of the splicing region is the same as that of the flange plate ends, as shown in Figure 2a.

The integral splicing structure of scheme ZL mainly includes a joint connection segment (segment JC) and a composite segment as the integral layer (segment CI). The transverse range of segment CI extends to the midline of the box girder web, and its thickness is 12 cm, which is the same as the designed thickness of the integral layer. At the position of the joint centerline, the section height is 31.5 cm, including 12 cm thick segment CI and 19.5 cm thick segment JC.

• Scheme ZH: The adjacent flange plate ends are connected by a thickened splicing region, and part of the flange plate end is wrapped, as shown in Figure 2b.

The integral splicing structure of scheme ZH is similar to that of scheme ZL, which mainly includes segments JC, CI, and a composite segment below the flange plate (segment CF). Segment CF is added to the lower edge of the flange plate, and its main function is to increase the section height at the position of joint centerline, which can prevent the flange plate end and segment JC from directly bearing various loads. The thickness of segment JC is from 5 to 14 cm, and the width is 2 × 80 cm.

Additionally, the ends of the adjacent existing flange plate box girders need to be specially treated in advance to increase the connection between segment JC and the flange plate and improve the mechanical properties of the integral splicing composite structure. Before the joint splicing operation, it is necessary to partially chisel off the concrete at the flange plate end, while retaining the existing steel bars in the flange plate. The size of the partially chiseled region is only 60~70 cm (longitudinal) × 10 cm (transverse) × 18 cm (minimum thickness), as illustrated in Figure 2c. The ends of the flange plate in the range of 10 to 15 cm on both sides of the prestressed steel wire bundles are retained, which can prevent stress concentration at the end of the flange plate. When performing the joint splicing operation, the connection between the loop bar in segment JC and the existing steel bar at the end of the flange plate enables the integral splicing composite structure to effectively transmit force.

3. Test Design

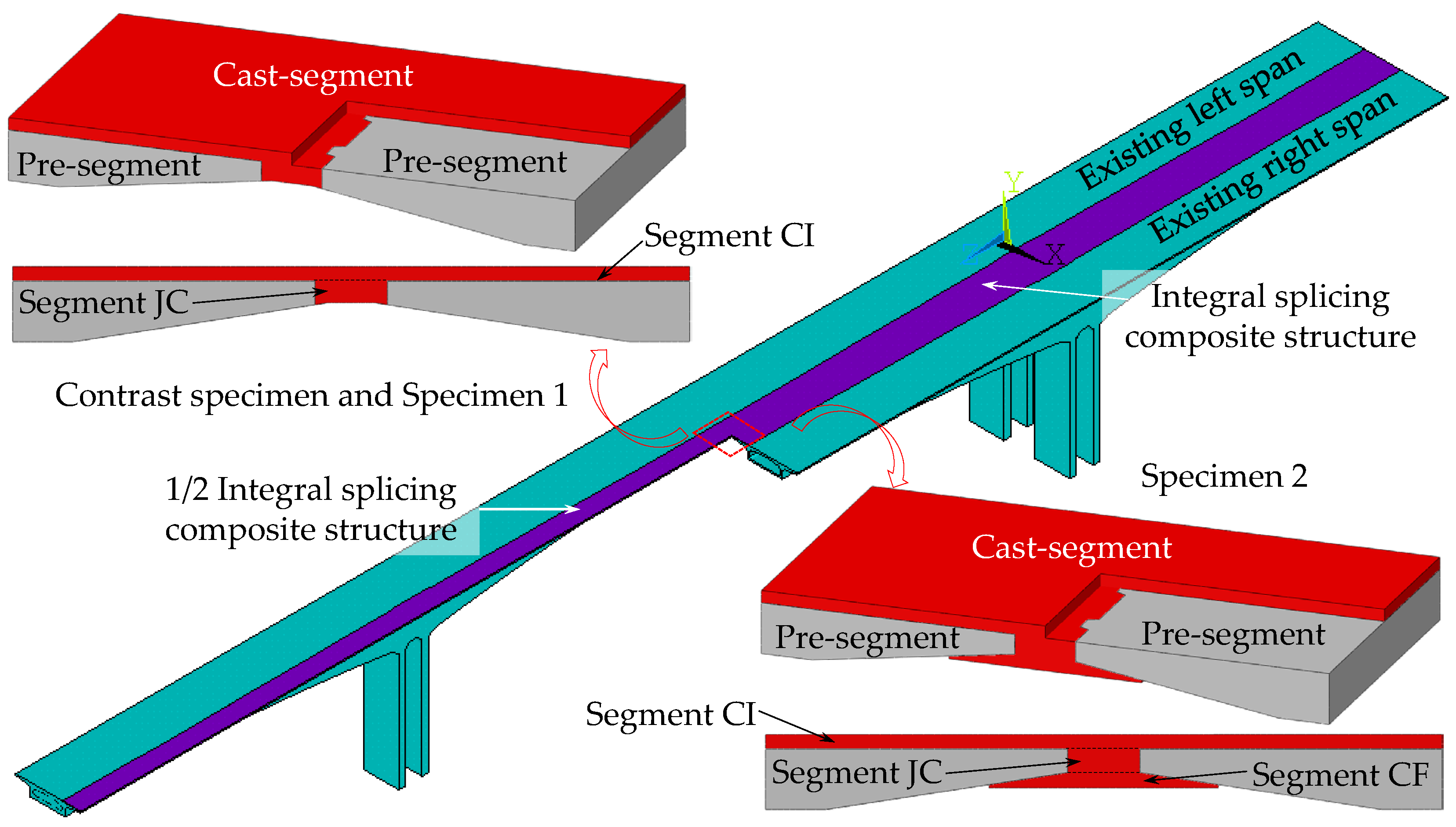
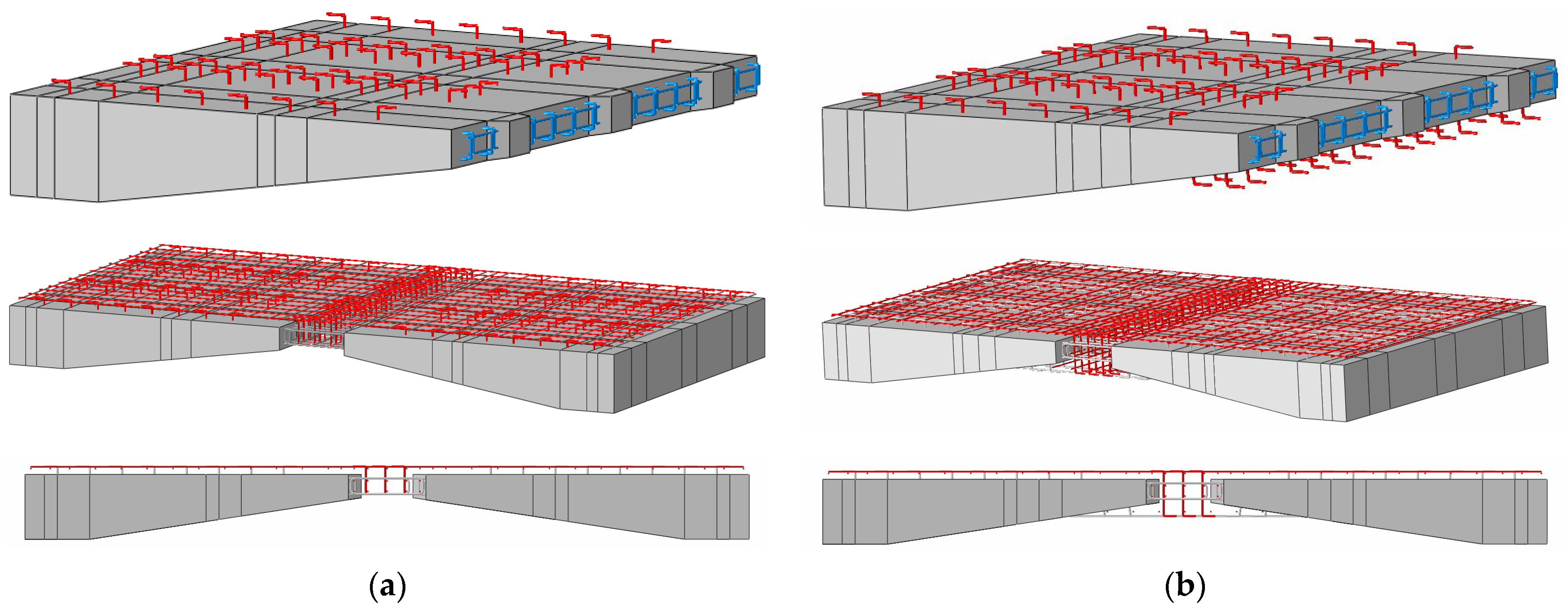
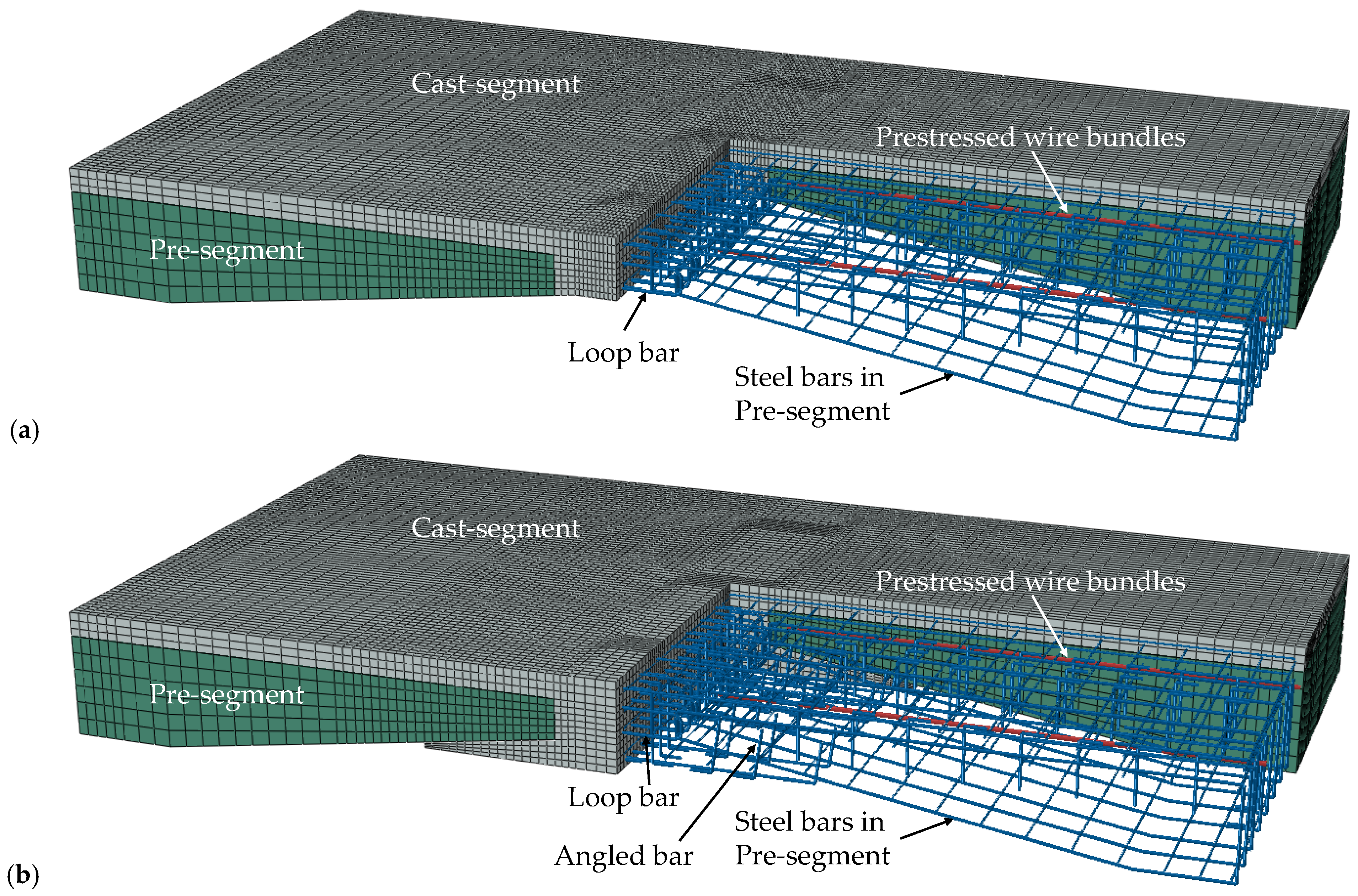
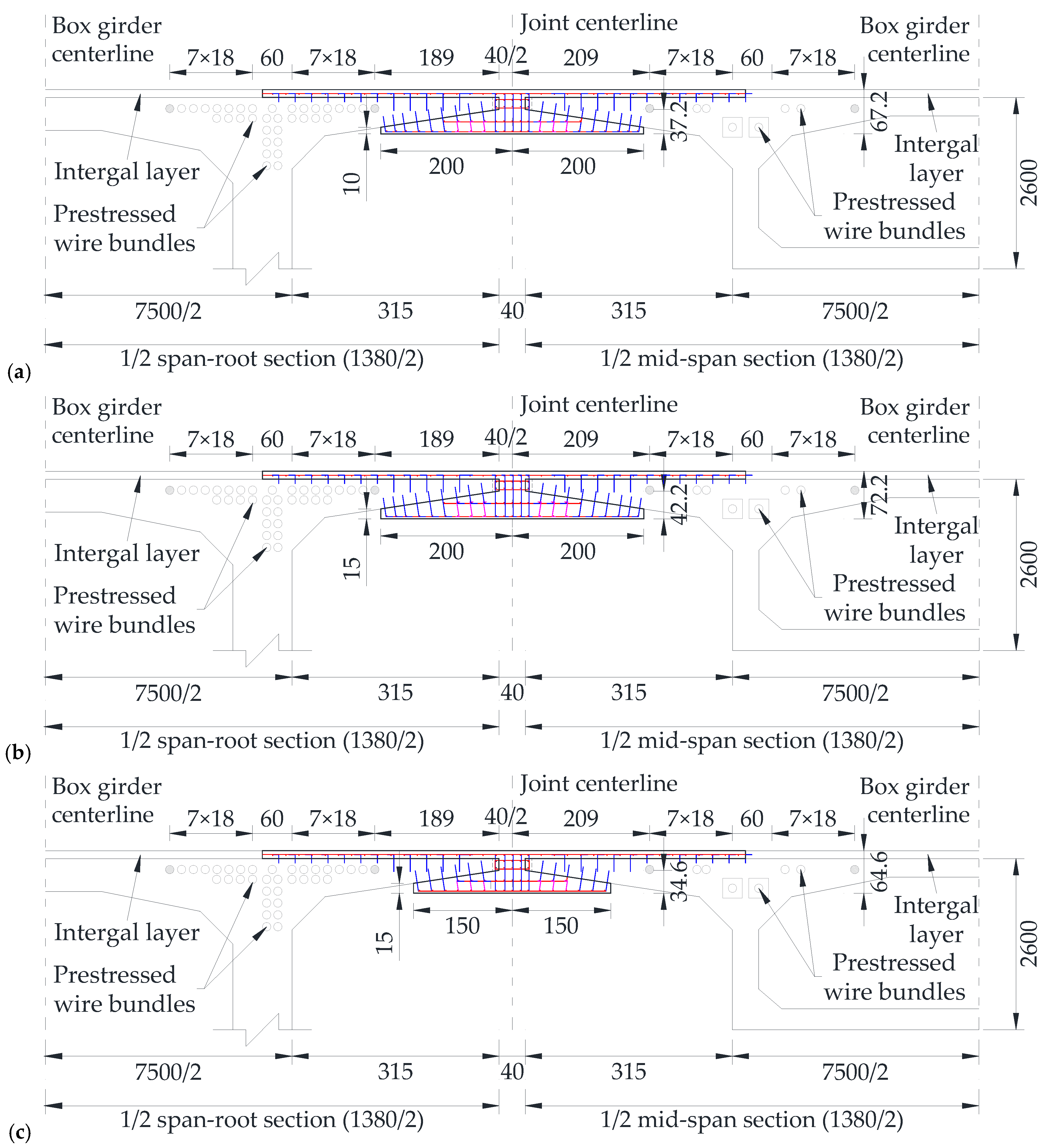
3.1. Design of Local Full-Scale Specimen

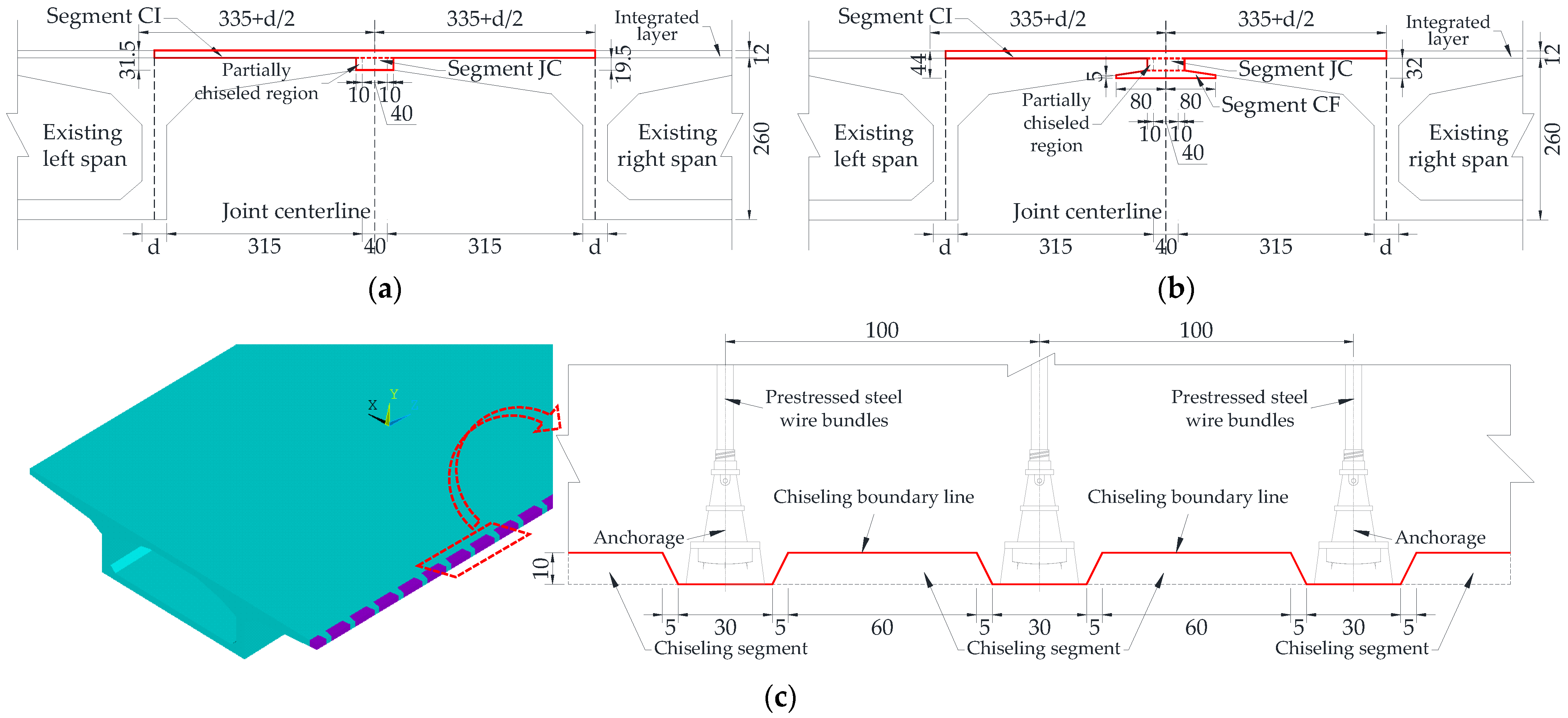
3.1.1. Specimen Size

According to the integral splicing scheme mentioned above, the finite element analysis model of the XFJ bridge can be established. The transverse stress distribution law of the upper and lower edges of the flange plate can be obtained by simulation [18]. It can be found that the inflexion point of the spliced flange plate is located 1.25 m away from both sides of the joint centerline.

In order to reduce the influence of local stress concentration [19], the region within 2.8 m on both sides of the joint centerline and 3 m in the longitudinal direction of the bridge is selected as the research object of the local full-scale model test. In this test, three specimens are designed, including Specimen 1 and Specimen 2, as well as the contrast specimen. The structure of Specimen 1 and the contrast specimen corresponds to scheme ZL, while that of Specimen 2 corresponds to scheme ZH. The size of each specimen is 5.6 m (transverse) × 3.0 m (longitudinal) × 0.62 m (maximum thickness), as shown in Figure 3.

Each specimen has a composite structure, including two prefabricated segments of flange plate (Pre-segment) and one joint cast-in-place segment (Cast-segment). The Pre-segment of each specimen is the same and needs to be prefabricated in advance.

For the Pre-segment, the appearance size, the arrangement of the steel bar and prestressed steel wire bundles, and the type of anchorage are consistent with the existing structure of the XFJ Bridge. In addition, similar to schemes ZL and ZH described in Figure 2, before operating the Cast-segment, the concrete at the end of the Pre-segment needs to be partially chiseled off, but the steel bars are retained.

The Cast-segment is mainly composed of segments CI, JC, and CF (only for Specimen 2). The structural form of the Cast-segment is consistent with that of schemes ZL and ZH. After the arrangement of the steel bars is completed, the concrete in the Cast-segment is poured at one time.

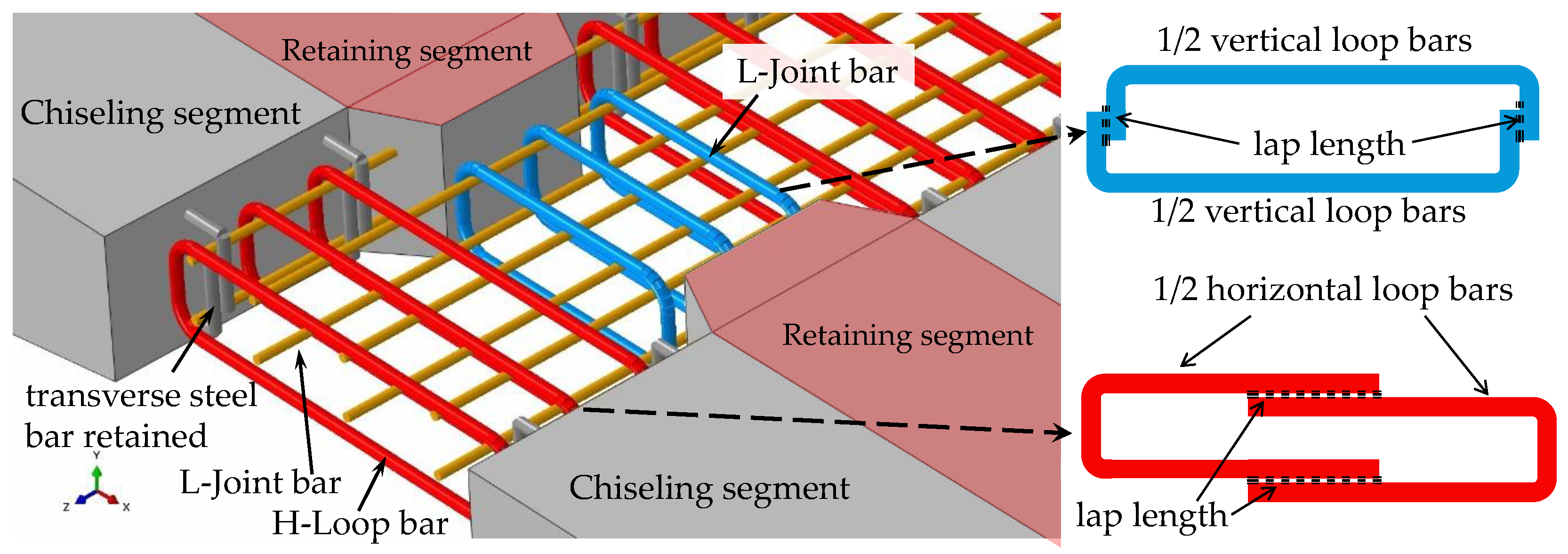
3.1.2. Steel Bar Arrangement Form of Cast-Segment

• Joint connection segment (segment JC)

Different forms of loop bar and longitudinal steel bars are adopted in segment JC, as presented in Figure 4 [20].

Segment JC can also be divided into two segments according to whether the concrete is chiseled off, as follows: the chiseling segment between adjacent prestressed wire bundles (chiseling segment) and the retaining segment of prestressed anchorage end (retaining segment).

For the chiseling segment, a horizontally lapped loop bar (H-Loop bar) with a diameter of 16 mm is adopted, which is composed of the left and right half of the horizontal loop bars, and the lap length is not less than 32 cm. In particular, the H-Loop bar needs to be aligned with the transverse steel bar retained in the chiseling segment, and the retained longitudinal steel bar should pass through the middle of these two types of steel bar.

For the retaining segment, a vertically lapped loop bar (V-Loop bar) with a diameter of 16 mm is adopted, which is composed of the upper and lower halves of the vertical loop bars, and the lap length is not less than 10 cm.

Additionally, the H-Loop bar and V-Loop bars are vertically lapped with the longitudinal bar of joints (L-Joint bar) with a diameter of 12 mm.

2.

Composite segment as an integral layer (segment CI)

In the middle height of this segment, a steel net composed of steel bars with a diameter of 12 mm is set up, for which the spacing of the steel bars is 20 cm. In addition, a type of angled steel bar should be partially embedded in the upper edge of flange plate, and the embedment depth should not be less than 20 cm. After the angled steel bar is embedded, it should also be lapped with the steel net, as shown in Figure 5. In particular, the position of the angled steel bar needs to be at least 20 cm away from the transverse prestressed steel wire bundles to ensure the safety of the transverse prestress of the box girder.

3.

Composite segment below the flange plate (segment CF)

Segment CF only exists in Specimen 2. The transverse bar of the composite segment (CF transverse bar) with a diameter of 16 mm is set in this segment. Similarly, another type of angled steel bar should be partially embedded in the upper edge of the flange plate, and the angle of the angled steel bar is set to be perpendicular to the lower surface of the flange plate. The embedment depth should not be less than 20 cm as well. After the embedment, the CF transverse bar is lapped with the angled steel bar and the L-Joint bar, as shown in Figure 5b.

Furthermore, different heights of near the Z-shaped vertical steel bars are set between segments JC, CI, and CF (only for Specimen 2) for vertical connection so that collaborative deformation can be achieved in each segment.

3.1.3. Material Composition and Properties

The material composition of the specimens and key parameters of the material properties are listed in

Table 1. Material composition and material properties of the specimens.

Material	Specimen Number	Segment	Item	Parameter
Steel bar	Contrast specimen Specimens 1 and 2	All segments	Characteristic value of tension strength	400 MPa
			Elastic modulus	200 GPa
Concrete C50	Contrast specimen Specimens 1 and 2	Pre-segment of all specimens and Cast-segment of contrast specimen	Characteristic value of compression strength	32.4 MPa
			Characteristic value of tension strength	2.65 MPa
			Elastic modulus	34.5 GPa
			Passion ratio	0.2
UHPC	Specimens 1 and 2	Cast-segment	Compression strength	≥130 MPa
			Flexural tension strength of 28 d	≥22 MPa
			Tensile strength in elastic stage	≥7 MPa
			Ultimate tensile strength	≥9 MPa
			Elastic modulus	45 GPa
			Shrinkage rate of 28 days	<200 × 10−6

.

In the Pre-segment, the steel bar type and concrete grade are the same as those of the existing XFJ Bridge, as follows: the steel bar is grade HRB400, the concrete is grade C50, the prestressed steel wire bundle is of high strength and low relaxation type of grade 1860, and the anchorage is type VLM15B-3.

In the Cast-segment, the steel bar is grade HRB400 as well. Specimens 1 and 2 are poured with Ultra-High-Performance Concrete (UHPC), while the contrast specimen is still poured with normal concrete of grade C50.

3.2. Preparation Process of Specimens

3.2.1. Preparation of Prefabricated Segments

The process of preparing the Pre-segment mainly includes the following steps: steel bar banding, concrete pouring, prestress wire tension, and pipeline grouting, as shown in Figure 6.

In the steel bar arrangement form, the position of the prestress corrugated pipe and prestress anchorage is basically consistent with the actual situation of the XFJ Bridge. Before concrete pouring, strain gauges are embedded in advance according to the arrangement scheme of the steel strain measuring points, as presented in Figure 6a.

In order to facilitate concrete pouring, the steel skeleton can be flipped in advance, and then the concrete of the Pre-segment is poured. After the pouring is completed, concrete curing should be started immediately, and the curing time should not be less than 7 days. After the curing is completed, the Pre-segment is flipped again.

The tension force of the prestressed wire bundles should be calibrated with the pressure ring before the formal tension operation, as shown in Figure 6b, so that the actual tension stress of the prestressed wire bundles can be consistent with the design scheme of the XFJ Bridge, both of which are 1302 MPa.

3.2.2. Concrete Chiseling at the Splicing End

The cutter is applied to pre-cut along the boundary line of the chiseled area, then the air pick is used to chisel the concrete within the design range of the Pre-segment, and the steel bar should be retained. The effect after chiseling is shown in Figure 7.

It can be observed from the chiseled regions that the upper edge of the chiseling segment is relatively complete along the boundary line, as shown in Figure 6a,c. There is a local concrete over-chiseling phenomenon along the boundary line of the lower edge, but the over-drilling region is only limited to the thickness range of the concrete protective layer, as presented in Figure 6b. After the concrete chiseling operation, no obvious cracks are found in the Pre-segment, and the phenomenon that the anchorage end of the prestressed wire bundles is destroyed due to excessive local stress concentration is not observed.

3.2.3. Reinforcement Connection and Concrete Pouring in the Splicing Region

According to the spatial position relationship of the adjacent flange plates described in Figure 1, two Pre-segments are symmetrically arranged along the midline of the joint, and the minimum spacing between the two is 40 cm.

The embedded angle bar of a typical specimen is presented in Figure 8a–c. After the completion of the layout of the steel bar in the Cast-segment, the effect diagram is shown in Figure 8b,c. The pouring process of the Cast-segment concrete is shown in Figure 8d.

3.3. Test Setup

3.3.1. Loading Setup

A self-balancing loading device is designed to meet the test loading requirements, as presented in Figure 9.

It can be divided into three parts from top to bottom, as follows:

• Upper counterforce framework: composed of two 4.5 m double-splicing I-shaped steel beams of I63 and two 2.4 m I-shaped steel beams of I20a.
• Test platform framework: composed of two 6.0 m double-splicing I-shaped steel beams of I63 and two 2.0 m I-shaped steel beams of I20a.
• Lower counterforce framework: composed of two 4.5 m double-splicing I-shaped steel beams of I56 and two 2.4 m I-shaped steel beams of I20a.
• The steel grade of these frames is Q235.
• Counterforce connecting rods: composed of eight thread steel rods of PSB930 with a diameter of 40 mm.

It can be seen from the previous calculation that the maximum deformation of the loading device is only 5.58 mm at 1.5 times that of the estimated ultimate load level (about 2000 kN), and the maximum steel stress of that is 135.13 MPa at this time, which still has a lot of security redundancies and meets the safety requirements of the loading process.

The specimen layout form is presented in Figure 9. Between the specimen and the test platform framework, four different types of steel plate support are arranged as supporting points, then the specimen can be simply supported. The supporting point is 20 cm away from both ends of the specimen. In addition, two jacks are arranged under the upper counterforce framework as loading points. A distribution beam is also set between the specimen and the jack. The loading point is located at 120 cm on both sides of the centerline of the specimen. It is designed according to the lane layout scheme, as described in Figure 1c, where the distance between the edge line of lane 3 and the midline of the joint is about 1.2 m [21]. In addition, segment JC can be subjected to pure flexural load during the test.

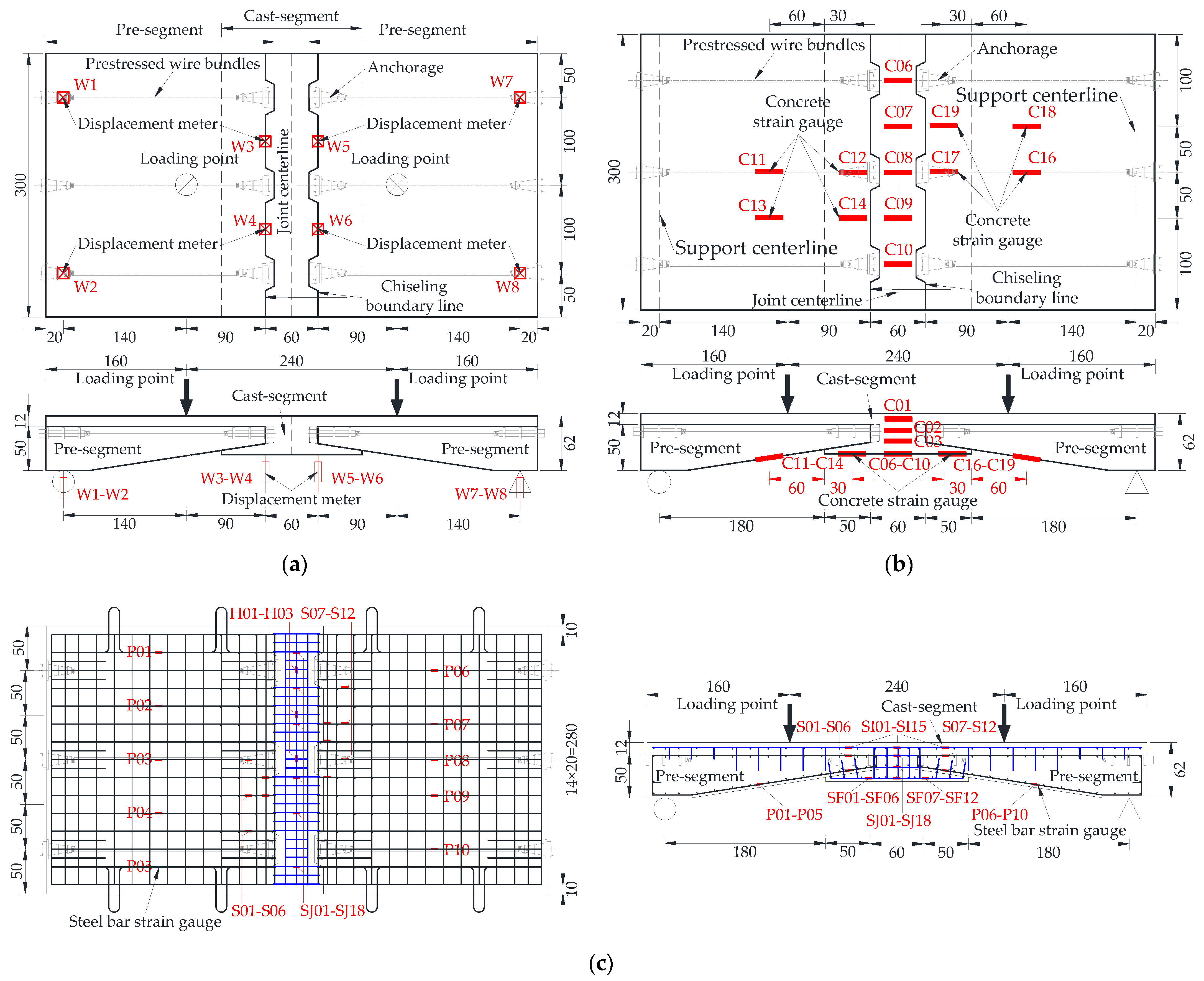
3.3.2. Measurement Setup

The load on the specimen, the displacement at the key position, and the strain of the concrete and steel bar should mainly be obtained during this test.

• Measurement of loading force

The loading force is tested with the pressure ring, which is arranged between the jack and the distribution beam, as presented in Figure 9.

• Measurement of displacement

The displacement meter is arranged as follows to test the displacement of the key positions: four displacement meters are arranged near each support, and the other four are symmetrically arranged on the lower edge of the Cast-segment, which are used to measure the displacement of the bearing position and the pure flexural segment, respectively. The arrangement of the support is depicted in Figure 10a.

• Measurement of concrete strain

The concrete strain gauge is adopted to test the concrete strain. The measuring points are mainly arranged on the side and bottom of the specimen. Among them, the strain measuring points on the side are mainly used to measure the concrete strain at the end of the Pre-segment and the centerline of the Cast-segment at different cross-section heights.

The measuring points at the bottom of the specimen are mainly arranged on both sides of the interface of the Pre-segment and the Cast-segment, and their positions also follow the rule that they are located at the projection position of the prestressed wire bundles or between the adjacent prestressed wire bundles in the longitudinal direction. It is mainly applied to evaluate the influence of prestressed wire bundles on the strain of concrete at the lower edge. Taking Specimen 1 as an example, the arrangement of the concrete strain gauge is presented in Figure 10b.

• Measurement of steel bar strain

The steel bar strain of the Pre-segment and the Cast-segment are tested using the pre-embedded strain gauge. Measuring points P01 to P10 are set for testing the stain of the transverse bar on the lower edge of the Pre-segment. Measuring points S01 to S12, SJ01 to SJ18, and SF01 to SF12 can be applied to test the stain of the H-Loop bar and the V-Loop bar (only for Specimen 2) in segment JC and the stain of the transverse bar in segments CI and CF. Furthermore, measuring points H01 to H03 are used to test the strain of the longitudinal bar in the Pre-segment. The layout of the steel bar strain measuring points is illustrated in Figure 10c.

4. Test Results and Analysis

Based on the observation results of the crack propagation characteristics, failure mode, strain of the steel bar and concrete, and other aspects in each loading step, the test results are comprehensively analyzed.

4.1. Crack Propagation Characteristics and Failure Mode

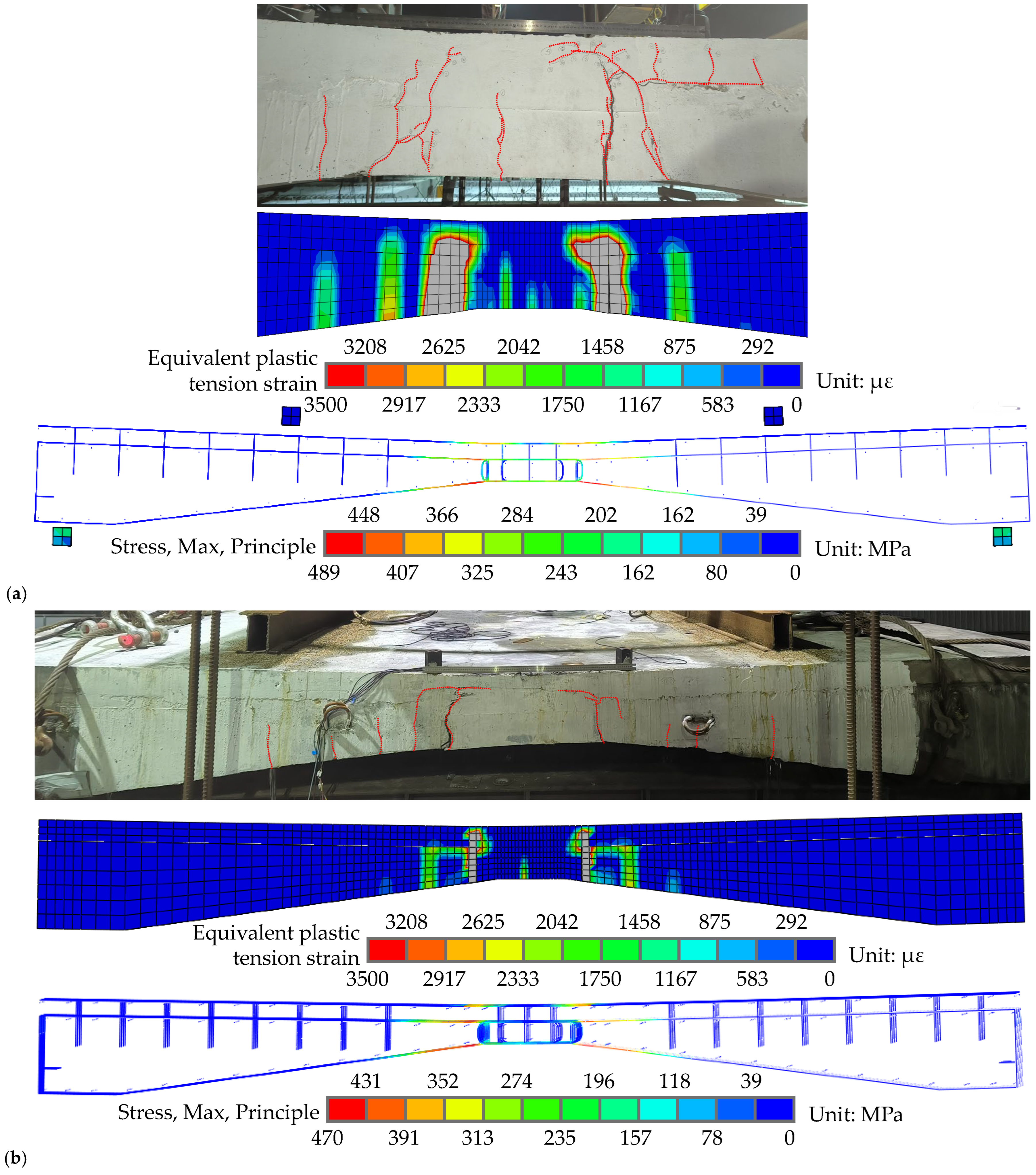
4.1.1. Contrast Specimen

• Crack Propagation Characteristics

When the loading force is about 25 kN, a crack appears at the interface between segment JC and the Pre-segment. This crack orientates from the upper part of the joint centerline, and the maximum cracking height reaches the steel bar of the integral layer. In addition, a crack appears at the position of the joint centerline as well, and the cracking height reaches almost half that of the section height. When the loading force is about 100 kN, the concrete of the Pre-segment near the interface is cracked, and the cracking height reaches to the position of the prestressed wire bundles. However, no obvious crack extension at other positions can be observed. When the loading force reaches 310 kN, the crack on the right side of the Cast-segment continues to propagate upward. The width of the existing crack continues to increase, and the sound of steel bar fracture can be heard.

• Final failure mode

The final cracking morphology of the contrast specimen is presented in Figure 11.

The interface between the Pre-segment and the Cast-segment has obvious cracks, but the cracks are only limited to a certain range on both sides of the interface, and there is no obvious cracking in the Pre-segment far away from the interface. It can be considered that the failure of the contrast specimen is mainly caused by the failure of the joint connection form. Normal concrete fails to keep long-term effective force transmission between the integral splicing composite structure and the existing flange plate, and the loop bars withdraw from the force transmission mechanism prematurely.

In addition, in the interface between segment CI and the Pre-segment, there is debonding as well, and cracks exist in segment CI. This means that the interface adhesive strength between segment CI made of normal concrete and the flange plate is not enough, and the stiffness of segment CI is not enough. Thus, UHPC should be adopted to maintain the interfacial performance between the integral splicing composite structure and the existing flange plate.

In addition, for the lower edge of the specimen, concrete crushing around the area of the prestressed bundle anchorage ends can be observed. The concrete damage on both sides of the interface is more serious, and the concrete in this region can also be easily removed.

It can be observed that the concrete of the retaining segment has a certain degree of cracking, but the crack width is narrow. This is mainly caused by the extrusion of the concrete at segment JC to that at the retaining segment during the flexural loading process, which makes the prestressed bundle anchorage end of the flange plate subject to a certain flexural moment. The concrete of segment JC is completely debonded from the retaining segment, and the debonding interface is smooth. It can be considered that the V-Loop bar fails to exert the connection performance with the flange plate.

In addition, a W-shaped interface fracture line can be observed in the overlapping region of the H-loop bar and the transverse steel bar of the flange plate, which is similar to the failure mode of the typical loop bar connection mentioned in existing studies [22]. Due to the short lap length of the H-loop bars, normal concrete fails to play a connecting role at 25 kN.

4.1.2. Specimen 1

• Crack Propagation Characteristics

When the loading force is about 500 kN, the first cracking at the interface can be clearly observed, which means that the cracking load of the integral splicing composite structure can be significantly improved by adopting UHPC.

With the increase in loading force, the height of the interface crack continues to increase and extends to the height of segment CI. During this period, there are also many vertical cracks at the lower edge of the Pre-segment, but there were no cracks in segment JC made of UHPC. It can be summarized that the interface is the first to crack, followed by the flange plate.

When the loading force continues to increase before the yield failure state of the specimen, the interface between segment JC and the Pre-segment completely debonds, and the interface between segment JC and segment CI also cracks. It can be considered that the connection performance of the integral splicing composite structure can still be effectively guaranteed by the loop bar arrangement forms. The integral layer in the composite structure can sustain force due to the high strength of UHPC.

• Final failure mode

The final failure mode of Specimen 1 is shown in Figure 12.

The interface between segment JC and the Pre-segment completely debonds, and steel fiber can be seen at the debonding position. The interface between segments JC and CI cracks as well, and the crack at this position is extended from that caused by the interface debonding between segment JC and the Pre-segment. In addition, obvious plastic slip can be observed at the interface between segment CI and the Pre-segment after unloading. Based on these interface debonding and slip phenomena and strain test results, it can be considered that the flange plate and the integral splicing composite structure can effectively transfer force through the loop bar when the splicing composite structure adopts the connection form of Specimen 1. In addition, the embedded angled steel bar can effectively delay the occurrence of interface failure after the interface debonding between the integral layer and the flange plate, which can make the integral splicing composite structure maintain functionality.

Before stopping loading, the number and the height of cracks in the Pre-segment does not increase significantly, and only the crack width expands slightly with the increase in load. The prestressed wire bundles in the Pre-segment exert the effect of inhibiting cracking. After chiseling out the UHPC near the anchorage end of the prestressed wire bundles, no concrete cracking can be observed at the end of the retaining segment, and the UHPC integral splicing composite structure will not adversely affect the prestressed wire bundle anchorage at the end of the flange plate.

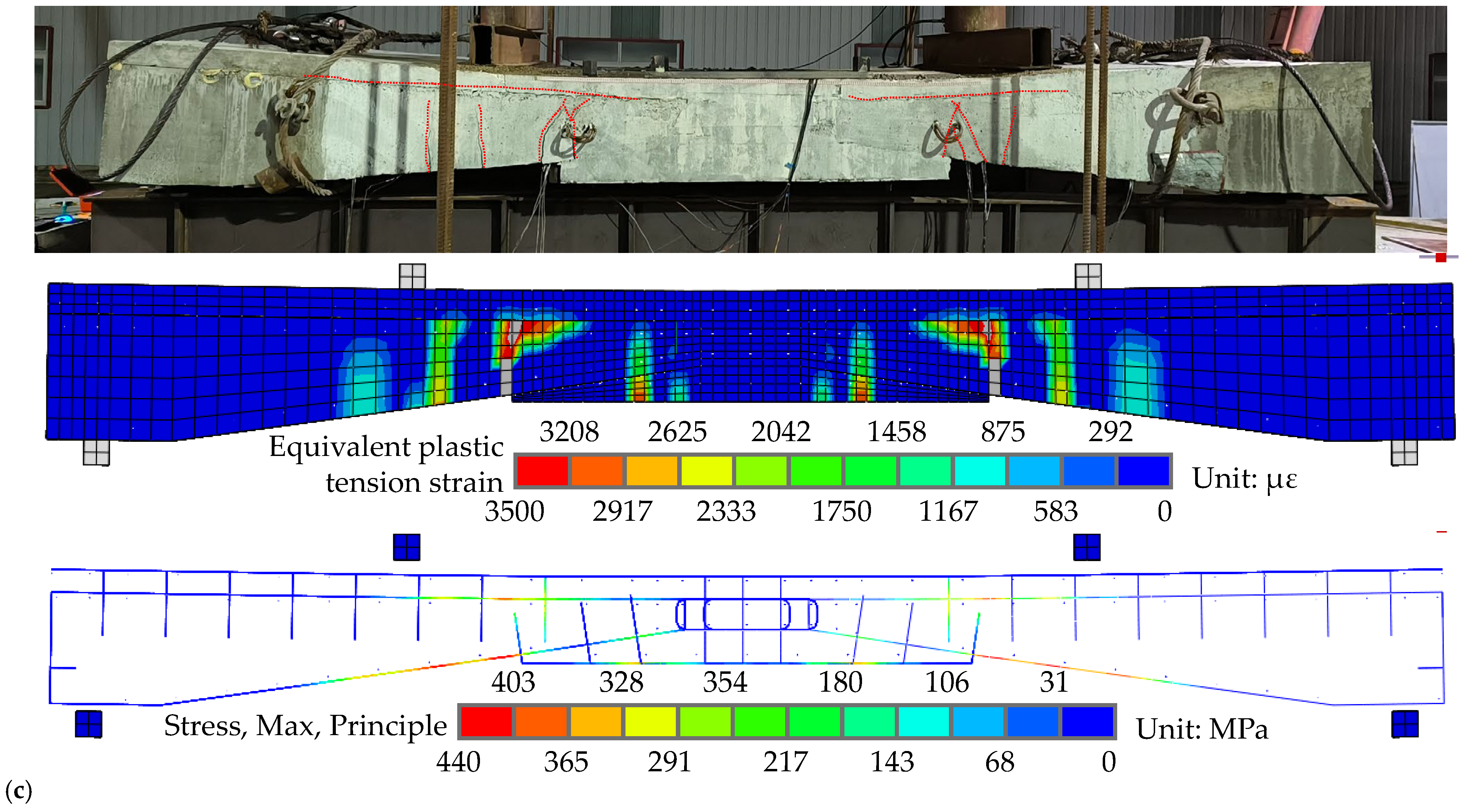
4.1.3. Specimen 2

• Crack Propagation Characteristics

When the loading force is 175 kN, cracks first appear at the position of the lower edge of the Pre-segment near the end of segment CF, and the height of these cracks extends approximately to half the height of the Pre-segment. Among them, the crack on the right Pre-segment of the specimen is located within the overlapping range of segment CF, so the interface between segment CF and the flange plate may debond before the flange plate cracks. However, there are no obvious cracks in the UHPC integral splicing composite structure.

When the loading force increases to 400 kN, the number of cracks in the Pre-segment increase, but the cracking range is outside of the overlapping range of segment CF. No obvious cracks can be observed still in the UHPC integral splicing composite structure. The interface between the Pre-segment and segment JC is still well bonded.

• Final failure mode

The final failure mode of Specimen 2 is depicted in Figure 13.

The cracking of Specimen 2 mainly exists in the Pre-segment made of normal concrete. The cracking range is mainly concentrated between the end of segment CF and the supports, while there is no obvious cracking in the UHPC Cast-segment. The height of these cracks basically reaches the section height where the prestressed wire bundle is located. However, due to the preloading effect of the prestressed wire bundles, the Pre-segment is not completely shear fractured. The cracks between the support and the distribution beam are mainly concentrated in the flexural shear section near the distribution beam, which may be caused by the sudden change in shear force in Specimen 2. For the interface between the Pre-segment and the Cast-segment, only the interface between the integral layer and the flange plate has debonding and obvious plastic slip. This is mainly due to the excellent tension and compression performance of the UHPC Pre-segment. With the increase in loading force, segment CI is completely in the compassion state, and the Pre-segments are in the tension state. Due to the arrangement of simple support boundaries, a virtual rotating hinge is formed between the Pre-segment and the Cast-segment, the Pre-segment and the Cast-segment move in different directions, and interface slip occurs. However, there is no obvious interface debonding between the flange plate and segments JC and CF, indicating that there is still a good force transmission performance between these two segments, and segment CF plays a good protective role in the interface.

Based on the comprehensive analysis of the cracking process and final failure mode mentioned above, the end of the flange plate can be effectively protected when the integral splicing composite structure similar to that of Specimen 2 is adopted. After adding the composite segment below the flange plate, the connection performance between the splicing structure and the flange plate can be guaranteed. In addition, similar to Specimen 1, the embedded angle bar between the integral layer and the flange plate can effectively delay the interface failure.

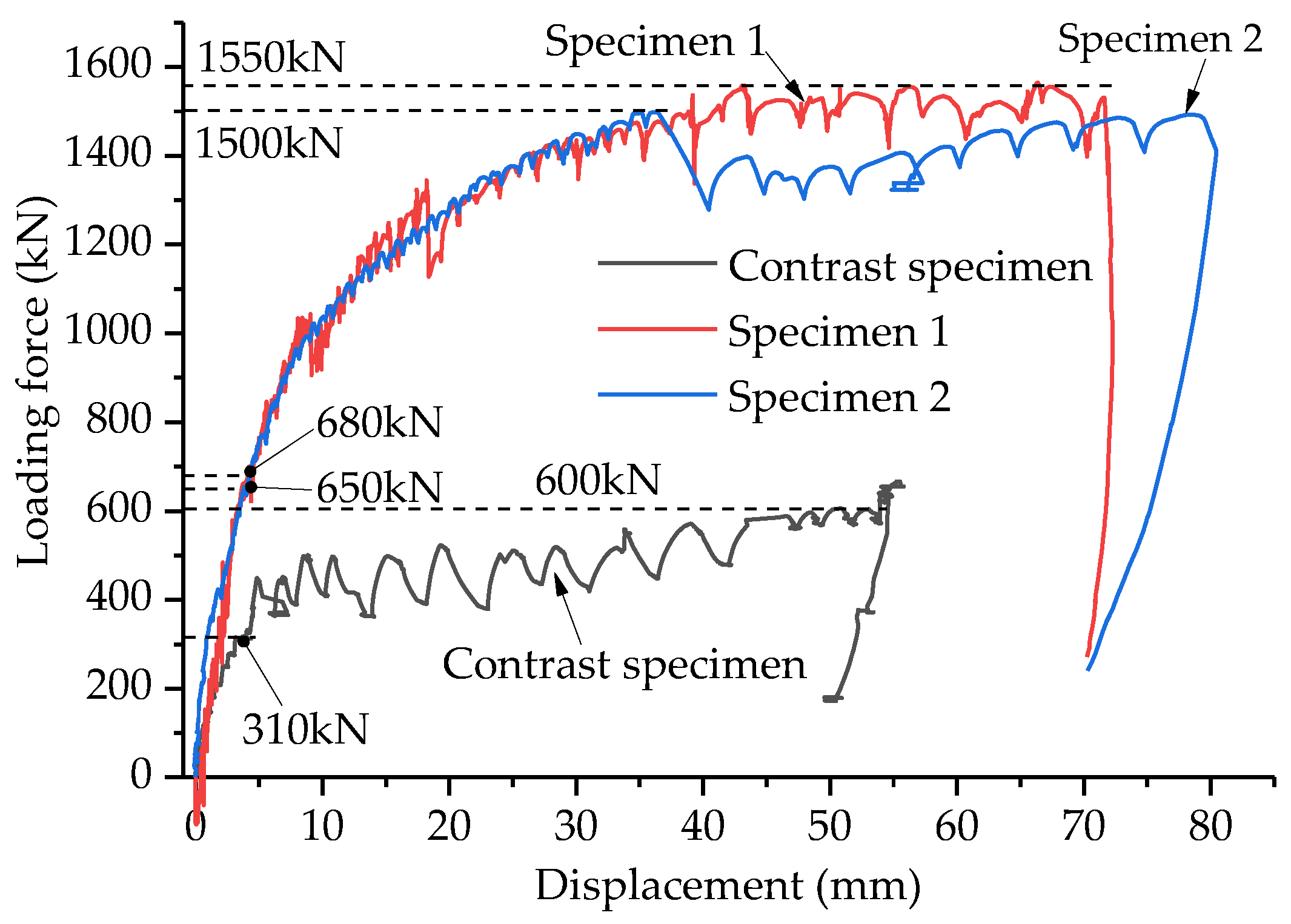
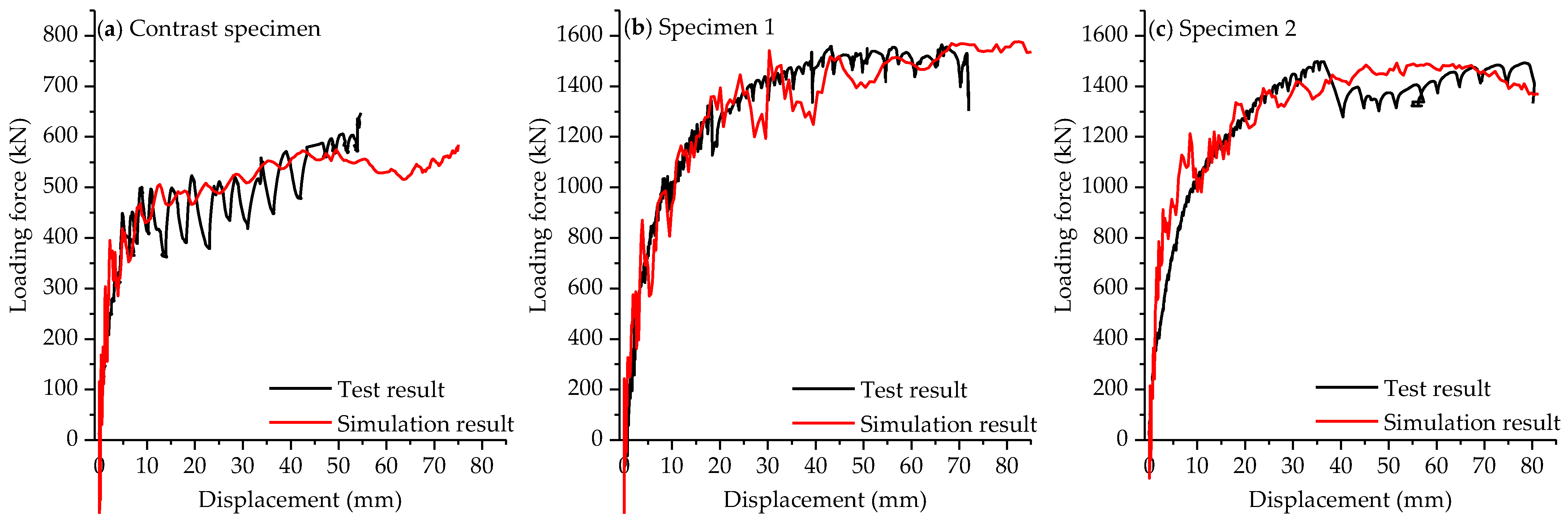
4.2. Relationship of Loading-Force–Displacement

The loading-force-to-displacement curves of each specimen are compared, as illustrated in Figure 14.

The curve shape of the contrast specimen is similar to that of a typical steel bar with an obvious yield point [22]. The specimen reaches yield strength at a loading force of 310 kN and reaches ultimate strength at a loading force of 600 kN. Combined with the failure mode of the specimen, it can be considered that the failure mode of the contrast specimen is mainly controlled by the interface between the Pre-segment and segment JC.

The curve shape of Specimens 1 and 2 is similar to that of a typical steel bar without an obvious yield point [23]. The yield strength and ultimate strength of Specimen 1 are 680 kN and 1550 kN, respectively, while those of Specimen 2 are 650 kN and 1500 kN, respectively.

Segment JC of Specimen 1 is not obviously damaged due to the high tensile strength of UHPC. The main failure modes of Specimen 1 are interface debonding and Pre-segment cracking, which are mainly controlled by the prestressed wire bundles in the Pre-segment and the loop bar connection in segment JC. Several yield steps can be observed in the loading-force-to-displacement curve, which may correspond to the tensile yield failure of transverse reinforcement at different positions.

Both segment JC and the end of the Pre-segment of Specimen 2 are not obviously damaged due to the protection of its segment CF, while other parts of the Pre-segment crack obviously. Therefore, the failure mode of Specimen 2 mainly corresponds to the prestressed wire bundles in the Pre-segment.

The relevant calculation results show that the safety of the integral splicing composite structure and the existing XFJ bridge can be fully guaranteed when adopting UHPC in the Cast-segment, and the performance redundancy is particularly large under the standard vehicle live load [24]. However, for the direct users of the spliced bridge, whether there is cracking is the focus of attention [25]. Thus, different cracking load levels are summarized by the comprehensive consideration of the strain test results, the load–displacement curves and failure process, as listed in

Table 2. Typical cracking force of each specimen.

Specimen Number	Splicing Material	Splicing Scheme	Cracking at the Interface *		Cracking at The Flange Plate
			Loading Force (kN)	Flexural Moment (kN·m)	Loading Force (kN)	Flexural Moment (kN·m)
Contrast specimen	C50	Scheme ZL	25	142.1	100	194.6
Specimen 1	UHPC	Scheme ZL	70	173.6	500	474.6
Specimen 2	UHPC	Scheme ZH	175	255.1	400	412.6

* For the contrast specimen and Specimen 1, the cracking at the interface corresponds to the interface between segment JC and the Pre-segment, while, for Specimen 2, it corresponds to the interface between segment CF and the Pre-segment.

.

It can be seen from Table 2 that when normal concrete C50 is applied in the Cast-segment, the tensile performance of the interface between segment CF and the Pre-segment is poor. This is mainly due to the short lap length between the H-loop bar and the transverse bar of the chiseling segment, and the connection performance of such joints cannot be well exerted when normal concrete is used. Therefore, the prestressed wire bundles in the Pre-segment fail to work well with the Cast-segment, and the contrast specimen enters the yield state soon after interface cracking. However, the application of UHPC in the Cast-segment, such as that in Specimen 1 and Specimen 2, can well guarantee the connection performance between the H-loop bar and the transverse bar, thus significantly improving the cracking force of at the interface. The H-loop bar and the transverse bar of the chiseling segment wrapped with UHPC can still transfer the force well, even after interface debonding, so that the composite structure composed of the prestressed Pre-segment and the non-prestressed Cast-segment can continue to bear the force together.

For Specimens 1 and 2 with the UHPC Cast-segment, whether segment CF is set has little influence on the cracking force at the flange plate, but the cracking force at the interface is significantly improved, which is mainly due to the difference in the debonding position of the interface. Due to the existence of the angled bar embedded in the Pre-segment, the tension force in the Cast-segment can be effectively transferred to the Pre-segment. Even after the interface debonding between segment CF and the Pre-segment, the interface between segment JC and the Pre-segment can continue to work. When the Cast-segment adopts UHPC, its tensile strength is stronger than that of the Pre-segment with normal concrete, with either the interface between the normal concrete or UHPC. Therefore, the cracking forces at the flange plate of Specimens 1 and 2 are still controlled by the normal concrete at the lower edge of the Pre-segment, so these values of the two specimens are relatively close.

Through the comparison of the test results, it can be observed that segment CF has a significant effect on improving the flexural and tensile resistance of the integral splicing composite structure, which can delay the interface debonding between the flange plate and the joint connection segment (segment JC). However, in order to further improve the crack resistance of the integral splicing composite structure, it is necessary to explore the optimization of the splicing scheme on the basis of this test.

5. Discussion

5.1. Simulation Model and Results Comparison

5.1.1. Simulation Model

A refined finite element simulation model is proposed for the optimization of an integral splicing composite structure based on the mentioned local full-scale model test.

• Material constitutive model

Appropriate material constitutive models are selected for each material of the specimen. The concrete damaged plastic model and the double-fold linear model are adopted for concrete and steel, respectively [26].

The elastic modulus of concrete C50 and UHPC is taken as 34,584.6 MPa and 45,000 MPa, respectively, and the passion ratio of such is taken as 0.2 and 0.3, respectively. The standard values of the compressive strength and tension strength of concrete C50 are taken as 26.62 MPa and 3.15 MPa, and those of the UHPC are taken as 40.64 MPa and 6.60 MPa. The elastic modulus of the steel bar and prestress steel wire is taken as 206,000 MPa and 195,000 MPa, respectively. Especially, the linear expansion coefficient of the prestressed wire bundle is 1.1 × 10⁻⁵. In addition, the material of the bearing and the distribution beam is idealized to ensure the bearing performance of the supports, and its elastic modulus is taken as ten times that of the steel bar.

2.

Mesh subdivision

The finite element simulation model with a mesh subdivision is depicted in Figure 15.

The standard mesh size is 20 mm and is locally densified in the key area. The steel bar and prestressed wire bundle are simulated by element T3D2, and the concrete is simulated by element C3D8R. The support and balanced beams are simulated by element C3D8R as well. A mesh convergence study has been carried out on each specimen, and a balance has been obtained between the computation time and the accuracy of the simulation result.

3.

Boundary conditions

The supports and balanced beams are tied with the specimen, and the load and support boundary conditions are applied by a coupling point tied with the support and the distribution beam. The elements of the steel bar and prestressed wire bundle are treated as an embedded region, and the adhesive–slip relationship between the steel bar and the concrete is ignored.

The relationship between the Pre-segment and the Cast-segment is simulated by the surface-based cohesive behavior, and the key parameters are K_nn = K_ss = K_tt = 3450 N/mm. The maximum nominal stress criterion is used for describing the damage, the maximum tensile and shear stress of the interface is 2.65 MPa, and the damage criterion is based on the fracture energy constitutive [27].

In addition, the prestress is applied by changing the temperature field. The linear expansion coefficient of the prestressed wire bundle is 1.1 × 10⁻⁵, and the terminal prestress is also 1302 MPa, which is the same as the value in the test.

4.

Analysis type performed

The explicit dynamics analysis procedure is adopted in this simulation model. The total calculation time is 0.6 s and is divided into three loading steps. The first two loading steps are both 0.15 s, which are used to apply prestress to the Pre-segments. The third loading step is 0.3 s, which is used to apply loading force to the distribution beams.

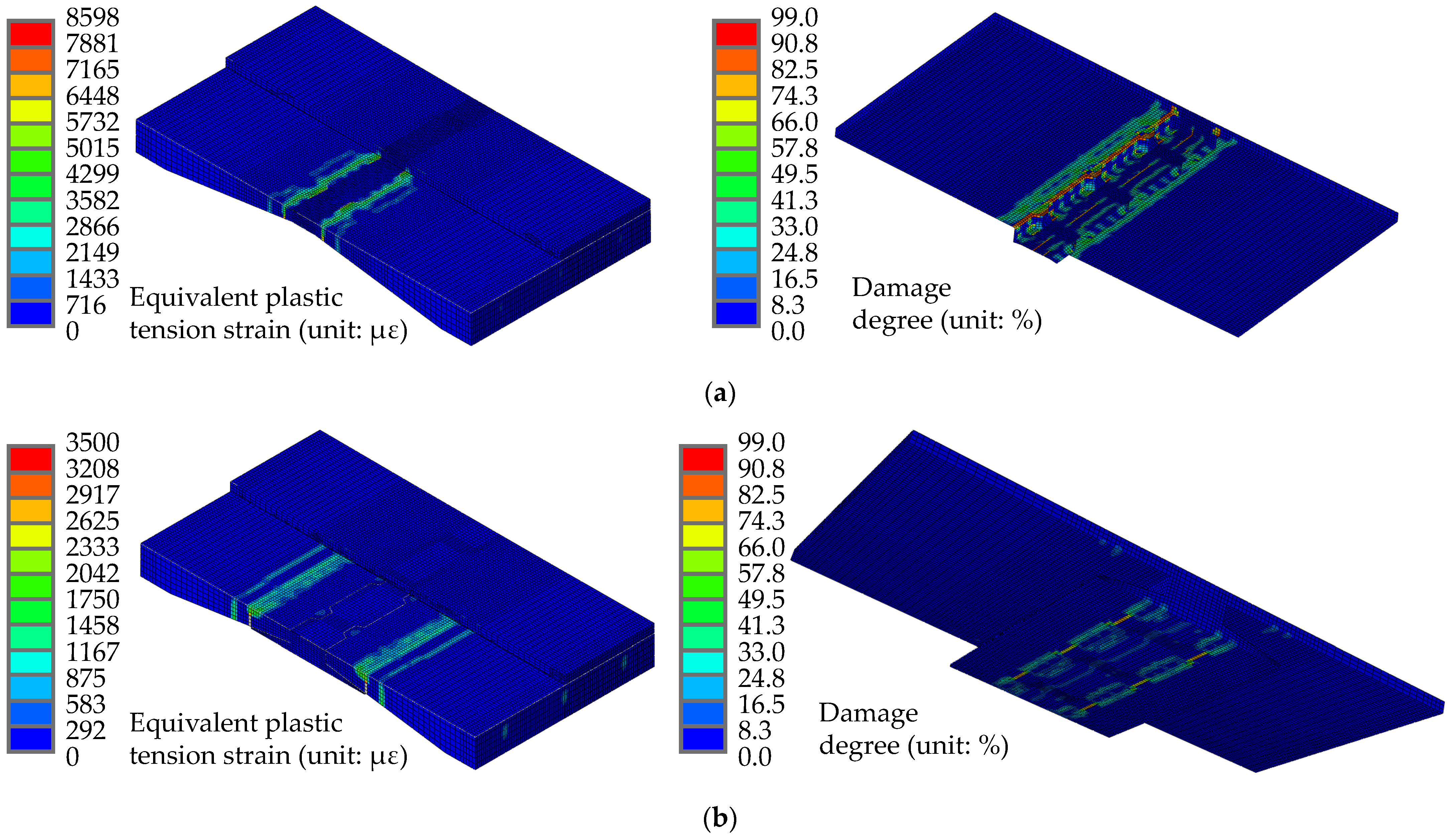
5.1.2. Comparison of Simulation Results with Test Results

The simulation effect of the proposed model is evaluated from different aspects.

Firstly, in the aspect of crack propagation morphology, the simulation results and test results are compared in Figure 16. It can be seen from the comparison that the failure process and crack morphology of the proposed model are in good agreement with the test results.

In addition, the stress distribution of the steel framework is also presented in Figure 16. It can be observed from the steel framework stress distribution that the steel bars in the Pre-segment have reached the yield strength when the specimen is damaged. For the contrast specimen with normal concrete in its Cast-segment, the loop bars are also obviously tensioned, which may lead to premature failure of the integral splicing composite structure. However, for Specimens 1 and 2 with UHPC in their Cast-segment, the stress of the loop bar and the L-Joint bar is lower, indicating that the adaptation of UHPC can enhance the splicing performance obviously. Especially for Specimen 2, the stress of the steel bar in segment CI is also lower than that of the other two specimens. This may be due to the increase in the cross-section height of the Cast-segment, so it is beneficial to increase the thickness of segment CF.

In order to compare the failure of the interface between the Pre-segment and Cast-segment when the specimen reaches the yield state (that is, the maximum stress of the steel bar is 400 MPa), the strain distribution of Specimens 1 and 2 is compared in Figure 17. In addition, the damage of UHPC is also depicted in the figure.

For Specimen 1, the damage is mainly located at the interface between the Pre-segment and segment JC, but no obvious interface damage can be observed at the interface between the Pre-segment segment CI when the specimen reaches the yield state. In addition, the damage region of the chiseling segment is obviously not larger than that of the retaining segment. This means that the L-loop bar can still function well in segment JC, even after interface debonding.

For Specimen 2, the damage is mainly located at the end of segment CF when the specimen reaches the yield state. No obvious interface damage can be observed at the interface between the Pre-segment and the Cast-segment, indicating that segment CF is conducive to the role of the loop bars in both the retaining segment and the chiseling segment. The proposed steel bar arrangement forms of scheme ZH can function well in the integral splicing composite structure.

Furthermore, the loading-force–displacement curves are also compared in Figure 18. The similarity of the loading-force–displacement curve can be clearly seen from the comparison.

For the contrast specimen, when the load is less than 400 kN, the simulation results are similar to the test results, and the deviation between the two is less than 2%. After the displacement is greater than 10 mm, the curve of the test result fluctuates around the curve of the result. This may be caused by the multi-stage loading in the actual test process. After loading, the contrast specimen may be damaged, and the deformation increases, which may lead to a decrease in the load value measured with the pressure ring. This development process lasts for a certain period of time in the actual test process. However, the loading conditions of the simulation model are continuous, which is relatively ideal. If the load–displacement relationship when the loading step is just completed is adopted to characterize the loading effect of the current loading step, the simulated result is relatively close to the test result, and the maximum deviation is only about 5%.

For Specimen 1, when the displacement is less than 20 mm, the simulation results are basically the same as the test results, for which the deviation is less than 1%. When the displacement is greater than 20 mm, the curve of the simulation results fluctuates around that of the test results, which may be caused by the yield of the steel bar. In the actual test, due to the non-uniformity difference in the material quality of the concrete and steel bar, no obvious fluctuation caused by the yield of the steel bar can be observed. Although the maximum deviation between the test result and the simulated result is about 7%, the overall change trend is still basically similar, and the calculation model can still be considered to be relatively reliable.

For Specimen 2, when the loading force is less than 400 kN, the simulation results are basically the same as the experimental results, for which the deviation is less than 1%. When the loading force is between 400 kN and 1200 kN, the curve of the simulation result shows an obvious yield process of the steel bar. Under the same load level, the test result of displacement is 15% greater than the simulated value. This may be due to the relatively ideal constitutive relationship of the steel bar in the simulation model, while the quality of the concrete and steel bar materials used in practice has a certain non-uniformity. This leads to no obvious yield step in the loading-force–displacement curve of Specimen 2. When the displacement is more than 10 mm, the curve of the simulation results almost fluctuates around that of the test result. Only when the displacement is about 35 mm do the test results show obvious fluctuation, which may be caused by the sudden change in the deformation of the specimen caused by the yield of the steel bar, but the maximum deviation is still less than 7%.

In general, the displacement simulation result is close to the test result under the same load level. Therefore, it can be considered that the proposed finite element simulation model has a good simulation effect and can be applied to further analysis.

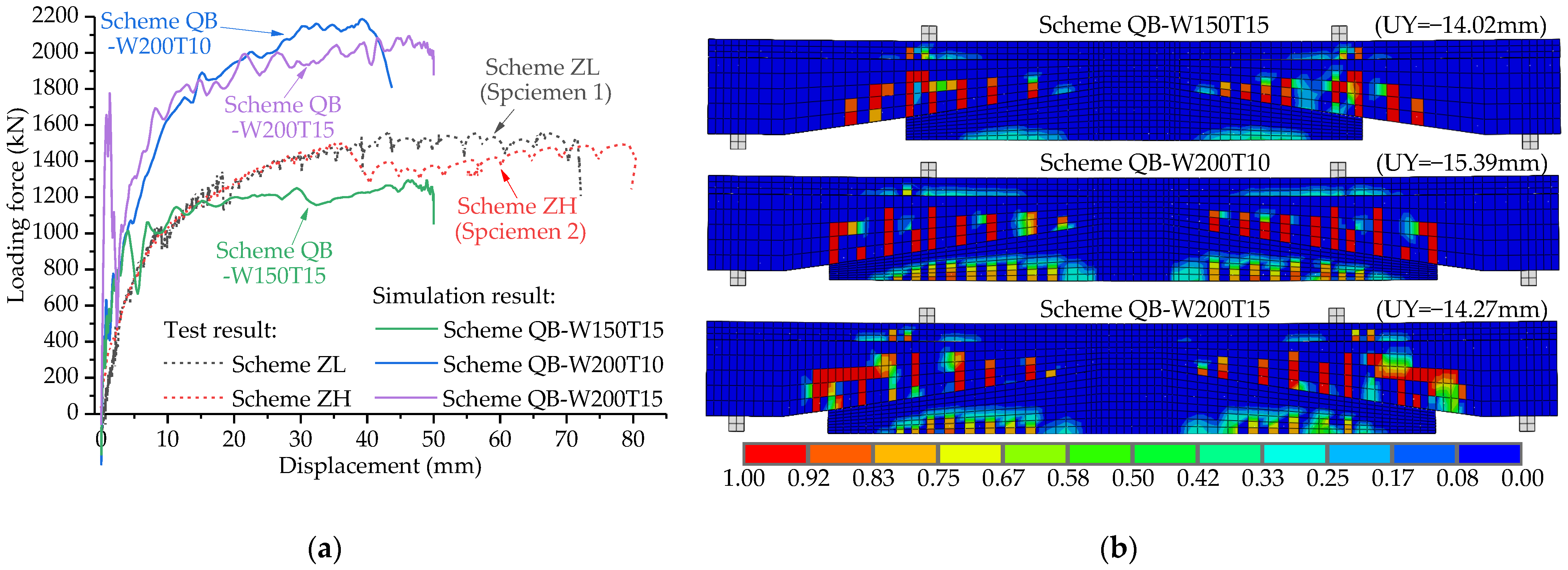
5.2. Optimization of Splicing Scheme

To fully ensure the safety of the flange plate of the existing XFJ bridge and even avoid the interface debonding between the flange plate and the splicing joint, different optimized splicing schemes are proposed. The width and thickness of segment CF are increased based on scheme ZH, and the optimized splicing scheme is described as follows:

• Optimized for maximum composite width

The end of segment CF is extended to the root of the flange plate as much as possible. However, considering that the longitudinal prestressed wire bundles are roughly located in the range of 126 cm on both sides of the web, the safety area of the flange plate that can be embedded with the angled bar is limited within the range of 1.89 m from the flange plate end. A type of splicing scheme with segment CF with a width of 2 × 200 cm is proposed, and the minimum thickness of segment CF is taken as 10 cm and 15 cm for comparison. These two schemes are marked as scheme QB-W200T10 and scheme QB-W200T15, and the steel bar arrangement forms are presented in Figure 19a and Figure 19b, respectively.

• Optimized for construction convenience

Properly reducing the composite width of segment CF is more beneficial to construction convenience, which can also ensure the rigidity of the formwork. Thus, the width of segment CF is reduced to 150 cm, but the minimum thickness of segment CF is still set as 15 cm. This scheme is marked as scheme QB-W150T15, and the steel bar arrangement form is presented in Figure 19c.

The finite element analysis model of the XFJ bridge is still applied to obtain the inflexion point of the spliced flange plate corresponding to the above optimized splicing scheme. From the calculation results, the inflexion point of the flange plate spliced with scheme QB is located at 2.10 m on both sides of the joint centerline. With the protection of the wide segment CF, the tensile stress at the lower edge of the flange plate can be significantly reduced, which makes the inflexion point move towards the web. The location of the inflexion point is still within the range of the selected local full-scale model, so the boundary conditions of the proposed simulation model are still applicable.

The force characteristics of specimens with scheme QB are simulated, and the loading-force–displacement curve of each specimen is presented in Figure 20a.

The ultimate loading force of schemes QB-W200T10 and QB-W200T15 are almost 2200 kN, which is obviously higher than the test results of schemes ZL and ZH. However, the ultimate loading force of scheme QB-W150T15 is only 1100 kN, which is close to the test results of schemes ZL and ZH. This means that segment CF with a width of 2.0 m can improve the bearing capacity of the integral splicing composite structure to a certain extent, but the improvement in ductility is still relatively limited.

Compared with the test results of ZL and ZH, it can be seen that the corresponding loading force of scheme QB-W150T15 is lower than that of ZL and ZH when the displacement is higher than 20 mm. This may be due to the greater thickness of segment CF in scheme QB-W150T15, and its stiffness will be greater when UHPC is adopted. For scheme QB-W150T15 with a segment CF width of 150 cm, the end of segment CF is located just below the distribution beam. This makes the stress mode of the flange plate under the distribution beam change after cracking. The original flexural tension stress mode at this position is transformed into a flexural shear stress mode, which will adversely affect the flange plate. From another point of view, the distribution beam can represent the vehicle load in practical engineering. According to the designed lane layout scheme depicted in Figure 1c, when the width of segment CF is 150 cm, its end is located near the lane edge. The flange plate may be damaged by shear stress under the limit state of stress, which should be avoided in practical engineering. Therefore, this scheme is not recommended.

Particularly for scheme QB-W200T15, when the specimen is loaded with a small displacement, the loading-force–displacement curve has an obvious curve peak. Combined with the strain and fracture morphology in the simulation model, it can be seen that this mainly occurs in the process of debonding failure of the interface between the Pre-segment and segment CF. When the interface between segment CF and the flange plate is well bonded, the bearing capacity of the integral splicing composite structure with scheme QB-W200T15 is mainly controlled by segment CF. The superior material properties of UHPC provide strong tensile properties for such structure. However, after the interface debonding between segment CF and the flange plate, the bearing capacity of such a structure mainly depends on the connection performance of the embedded angle bar. The tensile capacity provided by the UHPC segment CF is weakened, and the bearing capacity of this kind of structure is mainly controlled by the flexural tensile performance of the flange plate. Compared with scheme QB-W200T10, it can be seen that due to the decrease in the thickness of segment CF, the flexural tensile performance provided by segment CF is weakened. The interface debonding failure of the Pre-segment and segment CF occurs earlier; therefore, no obvious peak can be observed in the loading-force–displacement curve. Therefore, when the displacement is greater than 5 mm, the law of the loading-force–displacement curve of schemes QB-W200T15 and QB-W200T10 is roughly similar.

In addition, when the specimen is loaded to a vertical displacement of about 14 mm, the crack propagation morphology of scheme QB is compared, as shown in Figure 20b. The cracks are mainly concentrated in the Pre-segment and the lower edge of segment CF, and there is almost no obvious cracking in the UHPC region on both sides of the joint centerline. Especially for the crack propagation morphology of segment CF, scheme QB-W150T15 is compared with schemes QB-W200T15 and QB-W200T10, and some opinions can be analyzed from the comparison, as follows:

When the width of segment CF is 150 cm, the projection position of the distribution beam is close to the end of segment CF. The force can only be transmitted through the embedded angle bar between the interface after the interface debonding between the Pre-segment and segment CF, the flexural performance of segment CF cannot be well exerted. Therefore, the concrete of the Pre-segment close to the end of segment CF is seriously cracked.

However, when the width of segment CF is 200 cm, the force transfer of the embedded angle bars makes the UHPC segment CF give full play to its tensile effect, even after the interface debonding failure between the Pre-segment and segment CF. When the thickness of segment CF is increased, such as in scheme QB-W200T15, due to the high stiffness of the UHPC segment CF, the flexural performance of segment CF will be weakened, and the concrete of the Pre-segment will be seriously damaged at the angled bar position.

In addition, the interface between segment CI and the Pre-segment has a certain degree of debonding for each scheme QB. Similarly, the angled bars between the interfaces can effectively delay interface slip and failure, so it is particularly necessary to set angled bars between the interfaces.

Similarly, the key loading force of scheme QB is extracted from the simulation model, and the corresponding flexural moment is calculated.

Table 3. Cracking force comparison among schemes ZL, ZH, and QB.

Splicing Scheme	Size of Segment CF		Cracking at the Interface *		Cracking at the Flange Plate
	Width (cm)	Thickness (cm)	Loading Force (kN)	Flexural Moment (kN·m)	Loading Force (kN)	Flexural Moment (kN·m)
Scheme ZL 1	0	0	70	173.6	500	474.6
Scheme ZH 1	2 × 80	5~14	175	255.1	400	412.6
Scheme QB-W150T15 2	2 × 150	15~34.6	616	431.3	1226	858.2
Scheme QB-W200T10 2	2 × 200	10~37.2	436	305.2	839	583.3
Scheme QB-W200T15 2	2 × 200	15~42.2	785	549.5	1559	1091.3

¹ The cracking force of schemes ZL and ZH is obtained from the local full-scale model test. ² The cracking force of scheme QB is obtained from the proposed simulation model. * For scheme ZL, the cracking at the interface corresponds to the interface between segment JC and the Pre-segment, while, for schemes ZH and QB, it corresponds to the interface between segment CF and the Pre-segment.

outlines the comparison of the test values of schemes ZL and ZH with the simulation results of scheme QB. It can be seen from the comparison results that increasing the width of segment CF is beneficial to delaying the cracking of the interface between segment CF and the flange plate, and increasing the thickness of segment CF is beneficial to delaying the cracking loading force of the flange plate.

In order to meet the psychological expectations of the direct users of the spliced box girder bridge without cracks, it is necessary to increase the cracking load of the integral spliced composite structure as much as possible. For scheme ZL, the cracking load of the interface and flange plate can be considered as the minimum load requirement for such composite structures. Therefore, in order to ensure that the interface does not debond as much as possible, schemes QB-W150T15 and QB-W200T15 with a segment CF thickness of 15 cm can meet the interface debonding load better than the flange plate cracking load of scheme ZL, and the existing flange plate can be completely protected. However, as mentioned above, the segment CF end of scheme QB-W150T15 is close to the lane edge line of the designed lane layout, where it is easy to make the existing flange plate in an unfavorable state of shear stress. Therefore, it is recommended to adopt scheme QB-W200T15 as the optimal scheme for the integrated splicing composite structure.

6. Conclusions

An integral splicing composite structure is proposed for the connection of adjacent existing box girder bridges, the mechanical characteristics are tested using local full-scale mode tests, and a refined simulation model is proposed for the optimization of an integral splicing composite structure. The following conclusions can be summarized:

• The loop bar in the joint connection segment (segment JC) should be connected to the traverse steel bar of the existing flange plate, and the application of UHPC material can ensure the effective anchorage length of the loop bar so that the integral splicing structure can effectively transfer the force to the existing flange plate.
• The failure process of the proposed integral splicing composite structure is firstly debonding at the interface and then cracking at the flange plate of the existing box girder. In order to ensure the safety of the bridge users during the normal operation of the bridge, the cracking load of the interface should be increased as much as possible. Through the calculation and test results, it is well verified that the interface cracking loads of integral splicing schemes ZL and ZH are obviously less than the load of the bridge suffered under normal condition.
• The embedded angled bar can delay the interface debonding failure and interface slip. It can make the composite segment below the flange plate (segment CF) bend together with the existing flange plate, which is beneficial to the protection of the existing flange plate.
• The refined simulation model proposed is in good agreement with the test results, and the model can be applied to optimize the splicing scheme. The size of the composite segment below the flange plate (segment CF) has a significant effect on the flexural performance of the integral splicing composite structure. Increasing its width is beneficial to delaying the interface debonding failure, and increasing its thickness can effectively delay the cracking load of the flange plate.
• When the width of segment CF is 150 cm, its end is close to the lane edge line of the designed lane layout, which puts the existing flange plate in an unfavorable state of shear stress. Segment CF with a thickness of 15 cm can increase the interface debonding load and the flange plate cracking load. Therefore, optimized splicing scheme QB-W200T15 is recommended, in which the width of segment CF is 200 cm and the minimum thickness is 15 cm.