A Short-Term Building Load Prediction Method Based on Modal Decomposition and Deep Learning

Abstract

Accurate cooling load prediction is essential for energy-efficient HVAC system operation. However, the stochastic and nonlinear nature of load data challenges conventional neural networks, causing prediction delays and errors. To address this, a novel hybrid model is developed. The approach first applies a two-stage decomposition (CEEMDAN with K-means and VMD) to process complex cooling load data. Then, a CNN-BiLSTM network optimized by the Crested Porcupine Optimizer and integrated with an attention mechanism is constructed for prediction. Experimental results demonstrate the model’s high performance, achieving a 96.75% prediction accuracy with a MAPE of 3.25% and an R² of 0.9929. The proposed model shows strong robustness and generalization, providing a reliable reference for intelligent building energy management.

1. Introduction

As a core contributor to global energy consumption and carbon emissions, the building sector has rendered energy conservation and carbon reduction in related fields a key issue for sustainable development [1] while simultaneously undergoing a transformative shift from being merely energy-intensive to becoming smart and responsive [2,3]. This paradigm shift is fueled by advancements in data processing, storage, and transmission, which now enable the design and deployment of sophisticated control systems [4]. Among these, predictive control stands out by optimizing Heating, Ventilating and Air-conditioning (HVAC) system operation based on forecasts of future conditions. It is this critical dependence on accurate and anticipatory energy demand forecasts that elevates building load prediction from a supportive tool to a cornerstone technology for improving energy system performance and achieving significant energy efficiency [5].

Broadly, building load prediction methods fall into two categories: physics-based modeling and data-driven modeling [6]. Physics-based approaches incorporate detailed building envelope and system parameters to simulate building loads. Although these methods can represent physical processes with high fidelity, they require extensive, labor-intensive data collection, and inaccuracies in input parameters can lead to significant discrepancies between simulated and actual performance. Data-driven approaches avoid such dependencies by learning the mapping between operational and environmental variables and load values directly from historical data, using algorithms such as Artificial Neural Networks (ANN), Extreme Learning Machines (ELM), Regression Trees (RT), and Support Vector Machines (SVM). Representative work includes Hu et al. [7], who applied ANN to predict the thermal load of a zonally divided office building in Tianjin, enabling accurate room-level temperature estimation, and Guo et al. [8], who compared Back Propagation Neural Network (BPNN), SVM, and ELM for short-term load forecasting, showing superior performance for ELM when incorporating thermal response time as input.

Compared to shallow architectures, deep learning models capture more complex, non-linear relationships between features, enabling end-to-end learning without manual feature engineering [9]. LSTM networks, owing to their ability to handle long-sequence data, are especially valuable in load forecasting. Wang et al. [10] used LSTM to estimate internal heat gains in U.S. office buildings, identifying miscellaneous electrical loads as the most influential variable, and later compared shallow learning with deep learning, concluding that LSTM excels in short-term forecasting, whereas Extreme Gradient Boosting (XGBoost) performs better for long-term tasks.

Recent efforts increasingly combine complementary neural network architectures into hybrid frameworks. An et al. [11] employed a hybrid modeling framework that incorporated data processing and model optimization procedures with BP and ELMAN networks, resulting in accurate short-term residential load predictions. Li et al. [12] integrated Convolutional Neural Networks (CNN) with Gated Recurrent Units (GRU), adopting transfer learning to address small dataset scenarios. Bui et al. [13] proposed an electromagnetism-inspired Firefly Algorithm–ANN hybrid for thermal load prediction, assisting energy-efficient building design.

Alongside these developments, a wave of newer studies adopt more sophisticated feature engineering, decomposition techniques, and metaheuristic optimization. Feng et al. [14] demonstrated that CNN-based spatial feature extraction, BiLSTM temporal modeling, and multi-head self-attention, optimized via an improved Rime algorithm, substantially enhanced cooling load accuracy in public buildings. Kong et al. [15] addressed non-stationary loads from cascaded phase-change material buildings using SSA–VMD–PCA to preprocess data, thereby reducing prediction error by nearly 60%. Guo et al. [16] improved Artificial Rabbit Optimization with adaptive crossover to fine-tune LSTM hyperparameters, yielding performance gains in dynamically varying heat load scenarios. Song et al. [17] integrated gated multi-head temporal convolution with improved BiLSTM to robustly capture multi-scale temporal patterns, lowering prediction error over diverse forecasting horizons. Lu et al. [18] further showed how attention mechanisms coupled with time representation learning and XGBoost correction can improve both accuracy and robustness under varying occupancy schedules.

Other contributions emphasize interpretability, such as Zhang et al., [19] who combined clustering decision trees with adaptive multiple linear regression, matching black-box model accuracy while revealing that historical cooling loads and outdoor temperature are the most critical predictors. Salami et al. [20] leveraged Bayesian metaheuristic optimization in explainable tree-based models, achieving high alignment between design parameters and load outcomes. Additionally, Fouladfar et al. [21] developed adaptive ANN models retrained daily for residential thermal load prediction, enhancing flexibility and responsiveness. However, intelligent optimization algorithms often suffer from limitations such as slow convergence, premature convergence to local optima, and poor balance between global and local search—all affecting prediction accuracy. Therefore, integrating more advanced optimization algorithms with neural networks is essential to improve model accuracy and training speed. In the context of building energy consumption, load forecasting is generally classified into short-term and long-term horizons. Short-term load forecasting, typically spanning from minutes to several days, is particularly valuable for supporting real-time control of HVAC systems.

Accurate prediction of complex, dynamic building cooling loads remains a critical challenge in building energy efficiency. While data-driven models have advanced development, they still struggle with the stochastic, highly nonlinear, and non-smooth nature of cooling load data, leading to inadequate accuracy and robustness. To address these limitations, this study develops a high-accuracy hybrid model tailored to non-stationary and complex load characteristics. The proposed model provides more reliable support for intelligent control, real-time monitoring, and efficient management of HVAC systems. The shortcomings of existing research, along with the key contributions and innovations of this work, are summarized below:

(1) Limitations of Existing Research:

(a) Inadequate handling of non-stationary and complex cooling load data: Conventional single neural network models often struggle with the stochastic fluctuations, nonlinear variations, and non-stationary characteristics of building cooling load data, leading to compromised prediction accuracy and limited adaptability to complex real-world operational conditions.

(b) Room for improvement in data decomposition methods: Existing modal decomposition techniques may suffer from incomplete decomposition or insufficient processing of high-frequency components. As a result, data preprocessing may fail to adequately reduce data complexity, thereby constraining further improvements in prediction model performance.

(c) Suboptimal efficiency and accuracy in model parameter optimization: Parameter configuration in traditional neural networks often relies on empirical or trial-and-error approaches, which are inefficient and unlikely to yield optimal parameter sets. Meanwhile, intelligent optimization algorithms may exhibit slow convergence or a tendency to become trapped in local optima during the parameter search process.

(d) Lack of comprehensive validation of model robustness and generalizability: Many existing studies focus predominantly on accuracy metrics while paying insufficient attention to validating model robustness and generalization capability under varying operational and data conditions. This undermines the reliability of such models in practical engineering applications.

(2) Contributions and Innovations:

(a) Developed an innovative ICEEMDAN-Kmeans-VMD secondary decomposition framework that sequentially applies ICEEMDAN for initial decomposition, sample entropy-based K-means clustering for component aggregation, and VMD for refining high-frequency components. This multi-stage approach overcomes limitations of single decomposition methods, achieving more thorough data denoising and providing higher-quality inputs for prediction.

(b) Constructed a CPO-CNN-BiLSTM-Attention hybrid model that effectively combines CNN’s local feature extraction, BiLSTM’s long-term dependency capture, and Attention’s focus on critical temporal information. This integration enhances the model’s capability to learn complex cooling load patterns.

(c) Introduced the Crested Porcupine Optimizer for automated hyperparameter tuning, addressing the challenge of manual parameter adjustment in deep hybrid models. CPO demonstrates faster convergence, superior optimization results, and higher efficiency compared to traditional methods, significantly improving model performance.

(d) Established comprehensive validation through case studies using real building data with multiple metrics and benchmark comparisons. Extensive analysis across decomposition effectiveness, feature engineering impact, optimization performance, and model robustness confirms the superiority of the proposed approach in accuracy, robustness, and generalization capability.

2. Methodology

The proposed short-term building load prediction method integrating modal decomposition and deep learning is presented in Figure 1.

2.1. Data Processing

2.1.1. Primary Decomposition of Data

To initially reduce the nonlinearity and non-stationarity of the original load time series, the study employs the Improved Complete Ensemble Empirical Mode Decomposition with Adaptive Noise (ICEEMDAN) algorithm to decompose the raw load data. As an enhanced Empirical Mode Decomposition (EMD) technique, ICEEMDAN effectively addresses mode mixing and residual noise issues present in conventional EMD and Ensemble EMD (EEMD) methods by incorporating adaptive noise during each decomposition stage and utilizing local mean values for signal processing. This enables more accurate decomposition of complex signals into a series of Intrinsic Mode Functions (IMFs) and one residual component. The ICEEMDAN procedure can be outlined as follows:

(1) Initialization: Let the residual signal be r₀(t) = X(t), where X(t) is the original load time series. Set the iteration count i = 1.

(2) First-stage decomposition: Add white noise n^(j)(t) with zero mean and standard deviation ϵ_i to the residual signal r_i−1(t), obtaining the noise-added signal:

$$X^{(j)}(t)=r_{i-1}(t)+{\in }_i{n}^{(j)}(t),j=1,2,...,N$$

(1)

where N is the number of noise ensembles and ϵ_i specifies the noise amplitude for the i-th step.

Perform EMD decomposition on the noise-added signal X^(j)(t) and extract the first IMF component. Calculate the average of the first IMF components obtained from all noise-added signal decompositions, which serves as the first IMF component IMF₁(t) of the ICEEMDAN algorithm:

$$IM{F}_1(t)={\displaystyle \frac{1}{N}}{\displaystyle \sum _{j=1}^N{\widetilde{IMF}}_1^{(j)}}(t)$$

(2)

Compute the first residual signal r₁(t)

$$r_1(t)=r_0(t)-IM{F}_1(t)$$

(3)

(3) Subsequent-stage decomposition: Use r_i−1(t) as the input, repeat the preceding step to obtain IMF_i(t) and r_i(t). Continue until r_m(t) becomes monotonic or satisfies the termination criteria.

(4) Final decomposition result: The original series X(t) is expressed as

$$X(t)={\displaystyle \sum _{i=1}^{m}IM{F}_i(t)}-R(t)$$

(4)

where m is the number of IMFs produced, and R(t) is the residual term representing the long-term trend or low-frequency content of the load signal.

2.1.2. Data Component Aggregation

To streamline the decomposition results and extract load subsequences of varying frequencies, the IMF components from ICEEMDAN decomposition are aggregated using K-means clustering. This unsupervised algorithm partitions components into K clusters by minimizing within-cluster variance. Each IMF is characterized by its Sample Entropy (SampEn), where higher values indicate more complex, high-frequency components while lower values correspond to more predictable, low-frequency patterns.

(1) Sample entropy calculation

For a time series {x(t)}_t=1^L of length L, the procedure is as follows:

a. Parameters: Set embedding dimension m and tolerance r.

b. Vector formation: For t = 1, 2, ..., L − m + 1, form m-dimensional vectors X_m(t) = [x(t), x(t + 1), ..., x(t + m − 1)].

c. Distance calculation: Compute the chebyshev distance d[X_m(i), X_m(j)] between any two vectors X_m(i) and X_m(j):

$$d\left[X_m\left(i\right),X_m\left(j\right)\right]=\underset{k=0,1,...,m-1}{\max }\left|x\left(i+k\right)-x\left(j+k\right)\right|$$

(5)

d. Similarity count: For each i, count the number of vectors within tolerance r, denoted as B_i. Define B_m(r) as the average of B_i/(L − m).

$$B^m\left(r\right)={\displaystyle \frac{1}{L-m}}{\displaystyle \sum _{i=1}^{L-m}\frac{B_i}{L-m}}$$

(6)

e. Dimensional increase: Repeat steps b–d for dimension m + 1 to obtain A^m+1(r).

f. Sample entropy: Calculate as

$$SampEn\left(m,r,L\right)=-\ln \left({\displaystyle \frac{A^{m+1}(r)}{B^m(r)}}\right)$$

(7)

(2) K-means clustering procedure

a. Compute sampEn: Calculate the Sample Entropy of each IMF.

b. Cluster specification: Set cluster number K = 3 (high-, medium-, and low-frequency).

c. Center initialization: Randomly select three SampEn values as initial centroids.

d. Cluster assignment: Assign each IMF to the nearest centroid based on SampEn distance.

e. Centroid update: Recalculate centroids as the mean SampEn of assigned IMFs.

f. Iteration: Repeat steps d–e until convergence or maximum iterations.

g. Component aggregation: Sum IMFs within each cluster to form three subsequences.

2.1.3. Secondary Decomposition of Data

To mitigate the complexity inherent in the high-frequency IMF subsequences, a secondary analysis was carried out through Variational Mode Decomposition (VMD). VMD is a variational principle-based approach capable of adaptively separating a signal into a fixed number of modes, each characterized by a distinct center frequency and finite bandwidth. In this framework, the goal is to partition the original signal into K sub-components (VMD-IMFs), with each mode localized around its own central frequency. This partitioning process is formulated as the following constrained variational optimization problem:

$$SampEn\left(m,r,L\right)=-\ln \left({\displaystyle \frac{A^{m+1}(r)}{B^m(r)}}\right)$$

(8)

$$s.t.{\displaystyle \sum _{k=1}^K{\parallel u_k\left(t\right)\parallel }_2^2}=IM{F}_{HF}(t)$$

(9)

where {u_k} = {u₁, u₂, ..., u_K} denotes the extracted VMD-IMFs, and {ω_k} = {ω₁, ω₂, ..., ω_K} represents the central frequencies for each mode. The term δ(t) is the Dirac delta function, ∗ stands for convolution, ∂_t refers to differentiation with respect to time t, and ∇ is the gradient operator, α is the penalty factor balancing data fidelity and mode smoothness, ||·|| represents the squared L2 norm.

Based on this methodology, an ICEEMDAN-Kmeans-VMD secondary decomposition framework was developed, as depicted in Figure 2. The process begins with initial noise reduction through ICEEMDAN decomposition, which generates multi-frequency IMF components. It then employs sample entropy-based dynamic clustering to identify high-frequency subsequences, and finally applies secondary VMD decomposition to these components to reduce their complexity. This dual-stage decomposition approach with dynamic clustering aims at smoothing input uncertainty while enhancing high-frequency processing capability, thereby significantly optimizing computational efficiency.

2.2. CPO-CNN-BiLSTM-Attention Model Establishment

2.2.1. Convolutional Neural Network

A Convolutional Neural Network (CNN) is a deep feedforward architecture designed to process grid-structured data through convolution-based feature extraction, as shown in Figure 3. CNNs form the cornerstone of modern computer vision and underpin numerous advanced frameworks, such as Generative Adversarial Networks (GANs). Typically, a CNN comprises three main components: convolutional layers for hierarchical feature representation, pooling layers for dimensionality reduction and spatial abstraction, and fully connected layers that convert extracted features into task-specific outputs. This hierarchical design effectively suppresses redundancy while preserving robust generalization under complex and large-scale data environments [22]. Although CNN have been extensively applied in the computer vision domain, their local feature extraction capability is equally applicable to one-dimensional time series such as building cooling loads [23]. Short-term cooling load variations often contain localized, high-frequency patterns induced by rapid outdoor environmental changes, adjustments in occupant schedules, or sudden increases in equipment usage. By sliding convolution kernels along the temporal axis, CNN can efficiently identify these local temporal-dependency features, enabling the model to capture and respond to transient peaks, troughs, and short-term fluctuations more effectively than purely recurrent architectures [24].

During the forward propagation, information flows sequentially from the input to the output through a chain of weighted linear operations followed by non-linear activations. The convolutional process for the i-th layer can be expressed as [25]

$$a^i=f\left(z^i\right)=f\left(W^i\ast a^{i-1}+b^i\right)$$

(10)

where Wⁱ denotes the convolution kernel (weight tensor), * indicates the convolution operator, aⁱ⁻¹ is the output from the (i − 1)-th layer, bⁱ is the bias term, zⁱ denotes the pre-activation linear output, f is the nonlinear activation function, and aⁱ represents the activated output of the i-th layer.

After the forward pass, backpropagation computes gradients to adjust network parameters by minimizing the difference between model predictions and actual labels. The residual (error term) at the output layer equals the partial derivative of the loss function L with respect to the output z_i:

$${\delta }^i={\displaystyle \frac{\partial L}{\partial z^i}}={\displaystyle \frac{\partial L}{\partial a^i}}{\displaystyle \frac{\partial a^i}{\partial z^i}}={\displaystyle \frac{\partial L}{\partial a^i}}{\displaystyle \frac{\partial f\left(z^i\right)}{\partial z^i}}={\displaystyle \frac{\partial L}{\partial a^i}}{f}^{\prime }\left(z^i\right)$$

(11)

where L quantifies the discrepancy between predicted outputs and ground truth.

Given the residual δⁱ of one convolutional layer, the residual δⁱ⁻¹ propagated to the preceding hidden layer (which may be convolutional or pooling) is expressed as

$${\delta }^{i-1}={\delta }^i\ast rot180\left(W^i\right)°f^{\prime }\left(z^{i-1}\right)$$

(12)

where rot180 indicates a 180° rotation of the convolutional kernel, ° signifies the Hadamard (element-wise) product.

Once the residual δⁱ is obtained for any convolutional layer, the corresponding weights and biases are updated through the gradient descent mechanism as follows:

$$W^i=W^i-\alpha {\displaystyle \sum _{n=1}^m{\delta }^i\ast rot180\left(a^{i-1}\right)}$$

(13)

$$b^i=b^i-\alpha {\displaystyle \sum _{n=1}^m{\displaystyle \sum _{u,v}{\left({\delta }^i\right)}_{u,v}}}$$

(14)

where u and v represent the spatial dimensions of the residual matrix, α is the learning rate, and m denotes the number of training samples.

2.2.2. Bidirectional Long Short-Term Memory Network

The Bidirectional Long Short-Term Memory (BiLSTM) network extends the capabilities of the conventional Long Short-Term Memory (LSTM) architecture to improve modeling of long-range temporal dependencies. Unlike a standard unidirectional LSTM, BiLSTM processes sequence data in both forward and backward directions, enabling the network to incorporate context from preceding and subsequent time steps simultaneously.

An LSTM unit comprises a memory cell and a set of gating mechanisms, namely the forget gate, input gate, and output gate [26], as depicted in Figure 4. These gates regulate the flow of information entering, leaving, or being preserved within the cell state, allowing selective retention of relevant features while discarding unnecessary ones. This design addresses limitations found in traditional RNNs—most notably the vanishing gradient issue—by maintaining a stable pathway for long-term information propagation. The cell state functions as a persistent memory vector that is updated at each time step through the combined action of the three gates. The forward computation within an LSTM cell is defined by the following set of equations [27]:

$$f_t=\sigma \left(W_f\cdot \left[h_{t-1},x_t\right]+b_f\right)$$

(15)

$$i_t=\sigma \left(W_i\cdot \left[h_{t-1},x_t\right]+b_i\right)$$

(16)

$${\tilde{C}}_t=\sigma \left(W_c\cdot \left[h_{t-1},x_t\right]+b_c\right)$$

(17)

$$C_t=f_t\ast C_{t-1}+i_t\ast {\tilde{C}}_t$$

(18)

$$o_t=\sigma \left(W_o\cdot \left[h_{t-1},x_t\right]+b_o\right)$$

(19)

$$h_t=o_t\cdot \tanh \left(C_t\right)$$

(20)

where i_t, f_t, and o_t represent the input, forget, and output gates, respectively, σ denotes the sigmoid (logistic) activation function, tanh is the hyperbolic tangent activation function, C_t−1 and C_t are the internal states of the cell at time t − 1 and t, ℎ_t is the hidden state at time t, W_i, W_f, W_o, and W_c are weight matrices for the input gate, forget gate, output gate, and cell state, respectively, b_i, b_f, b_o, and b_c are bias vectors for the corresponding gates and cell state, * indicates element-wise multiplication.

2.2.3. Attention Mechanism

The Attention Mechanism is an essential concept in deep learning that enables neural networks to dynamically emphasize more relevant information within complex input sequences, similar to the way humans concentrate on salient details when perceiving large amounts of data. Rather than treating each input element equally, the attention framework assigns learnable coefficients—often termed attention weights or alignment scores—to quantify the relative importance of individual components in the input. Through this adaptive weighting, the model selectively enhances informative features while diminishing redundant or irrelevant signals. A general formulation of the attention operation can be represented in three main stages:

(1) Score generation: The relationship between a query and a collection of keys is assessed using a similarity or relevance function as

$$e_t=\tanh \left(W_h\cdot h_t+b_h\right)$$

(21)

(2) Weight normalization: The raw scores are transformed into a probability distribution through a softmax activation, yielding normalized attention coefficients for every key:

$${\alpha }_t={\displaystyle \frac{\exp \left(e_t\right)}{{\displaystyle \sum _{t=1}^T\exp \left(e_t\right)}}}$$

(22)

(3) Context aggregation: The attention output is obtained by performing a weighted combination of the corresponding value vectors, resulting in the final context representation:

$$c={\displaystyle \sum _{t=1}^T{\alpha }_t\cdot h_t}$$

(23)

where e_t denotes the attention score, α_t is the normalized attention weight, c is the aggregated context vector.

While CNNs are powerful for extracting regional features and local patterns from time-series inputs, their capability to capture extended temporal dependencies remains limited. In contrast, the BiLSTM network effectively models sequential relationships by incorporating both past and future contextual information through forward and backward propagation. To capitalize on their complementary advantages, a CNN–BiLSTM hybrid architecture is employed, where CNN layers handle spatial or short-term feature extraction, and BiLSTM layers refine temporal correlation learning. However, in scenarios involving high-dimensional or large-volume input sequences, the hybrid CNN–BiLSTM may underrepresent crucial information at certain moments, thereby weakening its learning efficiency and predictive accuracy. Integrating the Attention Mechanism into this framework resolves this limitation by adaptively quantifying the contribution of different time steps to the final prediction. Consequently, the model enhances interpretability and improves overall forecasting performance for complex time-dependent data.

As shown in Figure 5, the CNN-BiLSTM-Attention model processes input features through a structured pipeline: the CNN layer extracts and condenses local patterns via convolutional and pooling operations; the BiLSTM layer then captures long-term temporal dependencies using forward and backward LSTM units; subsequently, the Attention layer dynamically weights the significance of different time steps; and finally, the output layer synthesizes these refined representations to generate accurate predictions.

2.2.4. Crested Porcupine Optimizer

The Crested Porcupine Optimizer (CPO) is a recently proposed metaheuristic method that abstracts characteristic behaviors of crested porcupines, including adaptive foraging, defensive strategies, and social cooperation, into computational search rules. Within this framework, the optimization problem’s search space is analogized to the porcupines’ activity environment, and each candidate solution corresponds to an individual agent. In a D-dimensional search domain, the position of the i-th individual at iteration t is expressed as X_i^t = (x_i1^t, x_i2^t, ···, x_iD^t).

(1) Exploration phase

During the exploration of food resources, porcupines perform random long-distance movements to expand the search range. Position updating in this stage follows:

$$X_i^{t+1}=X_i^t+\alpha \times \beta \times \left(X_{best}^t-X_i^t\right)$$

(24)

where α is a parameter controlling step size, typically within (0, 1); β is a random variable sampled from the normal distribution N(0, 1); and $X_{best}^t$ represents the global best solution found up to the t-th iteration.

(2) Exploitation phase

When a porcupine identifies a potentially resource-rich area, it performs a local search to locate the food more precisely. The position update formula during the exploitation phase is

$$X_i^{t+1}=X_{best}^t+\gamma \times \left(X_j^t-X_k^t\right)$$

(25)

where γ is a random number within (0, 1) and $X_j^t$, and $X_k^t$ are the coordinates of two randomly chosen distinct agents from the current population.

(3) Collective cooperation mechanism

In CPO, a collective cooperation mechanism is introduced to enhance search capability. When a porcupine discovers a better position X_new, it signals nearby companions, prompting them to move toward this position. The position update formula for other porcupine individuals is

$$X_i^{t+1}=\left(1-\delta \right)X_{best}^t+\delta X_{new}$$

(26)

where δ is a weight coefficient within (0, 1), balancing the influence of the individual’s current position and the newly discovered position.

2.2.5. Hybrid Prediction Model Establishment

Building on these strengths—CNN’s efficiency in local feature extraction, BiLSTM’s ability to model long-term dependencies, and Attention’s focus on influential time steps—this study integrates CPO as an efficient metaheuristic optimizer for hyperparameter tuning. The resulting CPO-CNN-BiLSTM-Attention hybrid model combines multi-stage decomposition to reduce time series complexity with adaptive hyperparameter optimization, enabling accurate prediction of complex temporal patterns. The implementation process, outlined in Figure 6, proceeds as follows:

Step 1: Primary modal decomposition

Apply ICEEMDAN to decompose the input time series into multiple IMF components, effectively handling nonlinear and non-stationary characteristics to reduce initial complexity.

Step 2: IMF grouping via K-means clustering

Calculate the sample entropy of each IMF to quantify complexity and randomness. Cluster all IMFs into high-, medium-, and low-frequency subsequences using K-means for targeted model construction.

Step 3: Secondary modal decomposition

Perform VMD on high-frequency IMFs to refine complex features. Combine the resulting new IMFs with existing medium- and low-frequency components for comprehensive decomposition.

Step 4: Hyperparameter optimization with CPO

Input each IMF into the CPO algorithm to adaptively optimize three key hyperparameters of the CNN-BiLSTM model: L2 regularization coefficient, initial learning rate, and number of hidden units, enhancing prediction performance per component.

Step 5: Sub-model construction

Build individual CNN-BiLSTM-Attention sub-models for each IMF using CPO-optimized hyperparameters. Each sub-model employs CNN for local feature extraction and BiLSTM for long-term dependency capture.

Step 6: Integrated prediction

Generate predictions for each IMF using its corresponding sub-model, then aggregate all results through weighted summation to produce the final prediction of the original time series.

Step 7: Performance evaluation

Conduct comprehensive assessment using metrics such as MAE and CV-RMSE, comparing the hybrid model against benchmark methods to validate its effectiveness and superiority.

3. Case Study

3.1. Case Building

A three-story office building in Tianjin, China, shown in Figure 7a, serves as the case study. The building measures 43 m × 35 m × 12 m (length × width × height), with key parameters listed in

Table 1. Building model parameter settings.

Parameter	Value	Parameter	Value
Length	43 m	External wall heat transfer coefficient	0.54 W/(m2·K)
Width	35 m	Window heat transfer coefficient	1.8 W/(m2·K)
Height	12 m	Occupant density	5 persons/100 m2
Window-to-wall ratio	0.7	Lighting power density	9.5 W/m2
Roof heat transfer coefficient	0.33 W/(m2·K)	Equipment power density	75 W/m2

. Weather inputs, including ambient dry-bulb temperature and incident solar radiation, were sourced from the Chinese Standard Weather Data (CSWD).

The operational schedules and occupant behavior settings are critical behavioral characteristics of typical office buildings [28]. The operational schedules and occupant behavior settings are critical behavioral characteristics of typical office buildings. Internal heat gains from occupants, lighting, and equipment were determined based on operational schedules prescribed in the Chinese Design Standard for Energy Efficiency of Public Buildings (GB50189-2015 [29]) for standard office building operation patterns. For typical working days (Monday to Friday), the building operates between 08:00 and 18:00, with reduced lighting and equipment power during the lunch break. On weekends and public holidays, the building remains in a non-operational or low-load state. The designed occupant density is approximately 0.05–0.06 persons/m², with activity levels corresponding to light office work as defined by ASHRAE (metabolic rate ~1.2 met). Recommended equipment and lighting power densities are 10–15 W/m² and 8–12 W/m², respectively. These operational schedules directly affect occupant presence during working and non-working days, equipment usage frequency, and variations in internal heat gains; they were converted into building operation calendars for EnergyPlus simulation inputs. Cooling load data from June 1 to September 1 were simulated, with a time step of one hour, to build a dataset for developing and validating the CPO-CNN-BiLSTM-Attention prediction model. The dataset contains a total of 2208 records, with the building cooling load shown in Figure 7b, solar radiation variation in Figure 7c, and outdoor temperature together with relative humidity variation in Figure 7d.

3.2. Data Preprocessing

The cooling load dataset encompasses several categories of explanatory variables, including temporal descriptors, outdoor environmental factors, and the cooling load from the previous time step. In building load prediction, the current load is influenced not only by instantaneous meteorological and operational parameters but also by the pronounced thermal inertia of the building envelope and indoor air. Particularly over short prediction horizons, cooling load exhibits strong autocorrelation, while meteorological variables—such as solar radiation—demonstrate notable temporal continuity. Incorporating lagged features of cooling load and solar radiation from the previous time step into the model allows for more effective capture of these temporal dependencies, thereby enhancing prediction accuracy.

During feature engineering, categorical variables such as time type and weekday type were encoded into numerical values to facilitate model training. Specifically, the time type was sequentially assigned integers from 0 to 23 representing each hour of the day; the weekday type was assigned integers from 1 (Monday) to 7 (Sunday), and public holidays were uniformly encoded as 0 to distinguish their operational patterns from regular weekdays. Outdoor environmental parameters (temperature, humidity, and solar irradiance) retained their original numeric form, but missing entries were removed and gaps filled via linear interpolation. Lagged features for cooling load and solar radiation were constructed by shifting the dataset backward by one hour, appending these lagged values as independent predictors.

A Pearson correlation analysis was then performed on all collected feature parameters, with the results shown in Figure 8. Based on the correlation analysis, a threshold of ±0.3 was adopted for feature selection. The parameters ultimately chosen as model inputs include time type, weekday type, outdoor temperature, outdoor humidity, cooling load at the previous time step, and solar radiation at the previous time step, as detailed in

Table 2. Input parameters.

Variable Name	Unit
Time type	0, 1, …, 23
Weekday type	Monday, Tuesday, …, Sunday
Outdoor temperature	°C
Outdoor humidity	%
Cooling load at previous time step	W/m2
Solar radiation at previous time step	W/m2

.

To address the adverse effects of different feature scales on training speed, convergence stability, and predictive accuracy, all numerical features were first checked to ensure the absence of anomalies before normalization. Subsequently, a unified min–max scaling was applied to map values to the range [0, 1], as calculated by Equation (27).

$${x^{\prime }}_j={\displaystyle \frac{x_j-x_{\min }}{x_{\max }-x_{\min }}}$$

(27)

where x_j and x_j′ represent the original and normalized values, respectively, while x_max and x_min refer to the highest and lowest values within the dataset, respectively.

3.3. Evaluation Metrics

Four metrics were employed to evaluate prediction accuracy. The calculations are defined as follows:

$$R^2=1-{\displaystyle \frac{{\displaystyle \sum _{i=1}^n{\left(y_i-x_i\right)}^2}}{{\displaystyle \sum _{i=1}^n{\left(y_i-\overline{y}\right)}^2}}}$$

(28)

$$\mathrm{MAE}={\displaystyle \frac{1}{n}}{\displaystyle {\sum }_{i=1}^n\left|x_{\mathrm{i}}-y_{\mathrm{i}}\right|}$$

(29)

$$\mathrm{MAPE}={\displaystyle \frac{100\%}{n}}{\displaystyle {\sum }_{i=1}^n\left|\frac{y_{\mathrm{i}}-x_{\mathrm{i}}}{y_{\mathrm{i}}}\right|}$$

(30)

$$\mathrm{CV}\text{-}\mathrm{RMSE}={\displaystyle \frac{n}{{\displaystyle \sum _{i=1}^n{y}_i}}}\sqrt{{\displaystyle \frac{{\displaystyle \sum _{i=1}^n{\left(y_i-x_i\right)}^2}}{n}}}$$

(31)

where n represents the sample size, x_i denotes the i-th simulated value (kW), y_i denotes the i-th measured value (kW), $\overline{x}$ represents the mean of simulated values (kW), $\overline{y}$ represents the mean of measured values (kW).

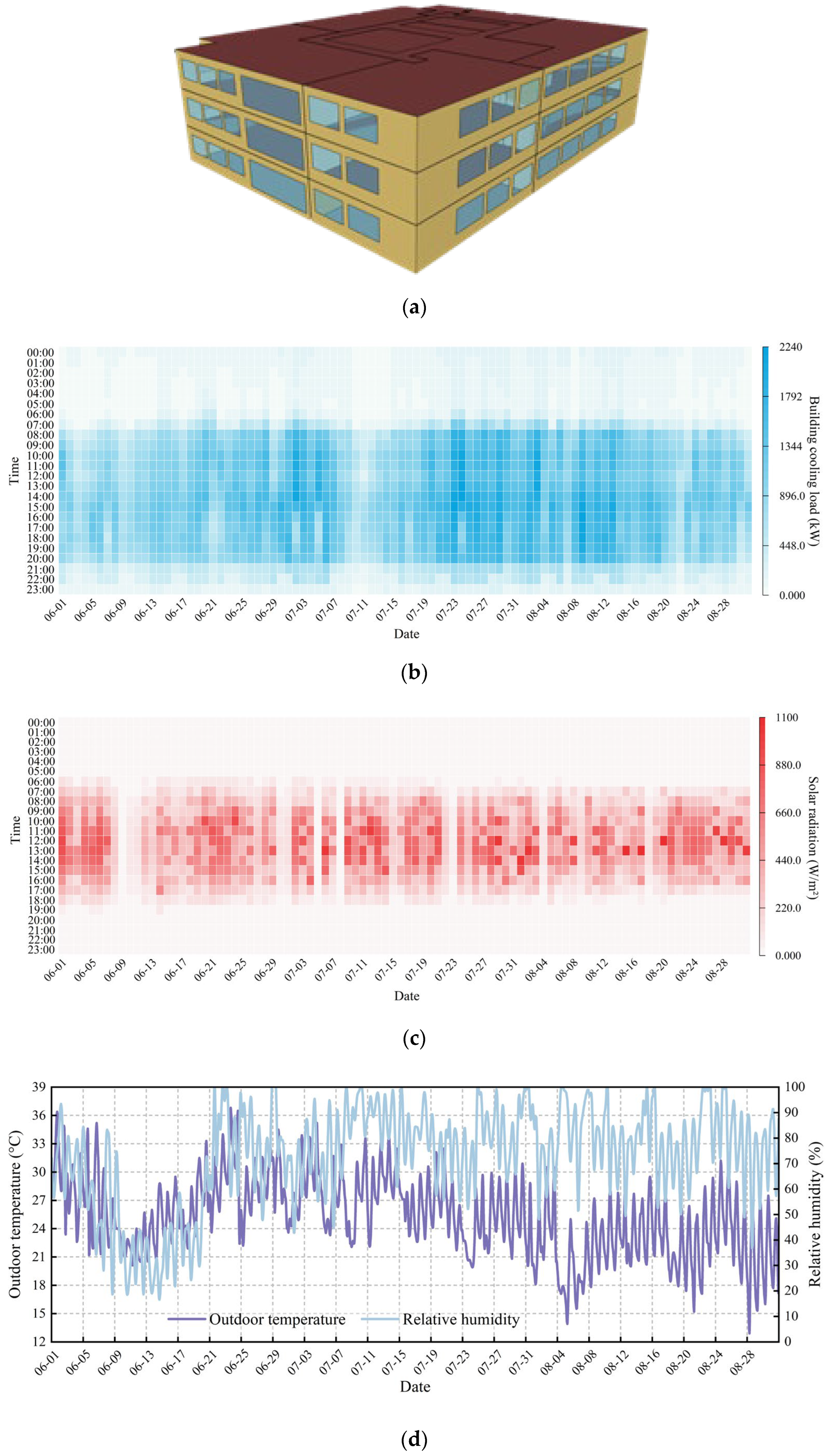
4. Results and Discussion

4.1. Data Decomposition Results

The ICEEMDAN method was employed to process the load profile of the case-study building. The decomposition was performed with a white noise amplitude of 0.2, 50 realizations of noise addition, and 100 iterations, yielding multiple IMF components. As shown in Figure 9, the IMFs exhibit a distinct stratification in both frequency and amplitude. From IMF 1 to IMF 10, the oscillation frequency gradually decreases: IMF 1 to IMF 3 represent high-frequency oscillations, characterized by dense waveforms and large amplitude fluctuations. IMF 4 to IMF 6 show a marked reduction in frequency, with the waveforms transitioning from dense oscillations to relatively smooth fluctuations and a narrower amplitude range. IMF 7 to IMF 9 exhibit even lower-frequency, trend-like oscillations with further extended oscillation periods. Finally, IMF 10 reflects a slowly varying trend component with a relatively stable amplitude range and no apparent oscillations. This hierarchical decomposition demonstrates that the ICEEMDAN algorithm effectively separates the original cooling load signal into components with distinct frequency and amplitude characteristics, thereby laying the groundwork for precise prediction of each individual component in subsequent analysis.

To address the model complexity from excessive ICEEMDAN-generated IMFs, sample entropy analysis with K-means clustering was implemented. This grouped components into three frequency-based Co-IMFs (high, medium, low), effectively reducing the components from 10 to 3 as shown in Figure 10 and significantly cutting training costs.

The high-frequency time series obtained from K-means clustering undergoes secondary modal decomposition via VMD to reduce complexity. As shown in Figure 11, the Co-IMF components are decomposed into three VMD-IMFs. These are combined with the medium- and low-frequency components from the initial ICEEMDAN decomposition to form a new IMF set. Based on the classification criteria, VMD-IMF1 and VMD-IMF3 are categorized as high-frequency components, VMD-IMF4 as medium-frequency, and VMD-IMF5 as low-frequency. From the perspective of HVAC process dynamics, each frequency band corresponds to distinct physical phenomena influencing cooling load variations [30]. High-frequency components are primarily driven by rapid changes in outdoor meteorological conditions, such as solar radiation spikes and wind disturbances, as well as instantaneous internal gains from occupant activities or equipment cycling. Medium-frequency components reflect daily operational cycles dictated by the building schedule and moderate thermal inertia of the envelope. Low-frequency components capture long-term trends arising from substantial envelope thermal inertia, indoor air heat storage, and seasonal climate variations. Subsequent to decomposition, each VMD-IMF is combined with the existing feature variables to construct new component-specific sample datasets, which are later used for feature selection and prediction testing.

4.2. Prediction Results

After undergoing secondary modal decomposition and feature selection, the processed cooling load dataset was partitioned into training (80%) and testing (20%) subsets. Simulations were conducted in MATLAB R2023a to implement and evaluate four models: CPO-CNN, CPO-BiLSTM, CPO-CNN-BiLSTM, and CPO-CNN-BiLSTM-Attention. The prediction performance of the CPO-CNN-BiLSTM-Attention model was thoroughly validated and analyzed. Through extensive testing and adjustment, an optimal parameter set was determined for the case study, as detailed in

Table 3. Model hyperparameter settings.

Hyperparameter	Value	Hyperparameter	Value
Convolution kernel size	[3, 1]	Dropout probability	0.1
Number of convolution kernels	16	Optimizer type	Adam
Number of filters	128	Maximum training epochs	30
Stride	[1, 1]	Gradient clipping threshold	1
Pooling window size	2

. The results in Figure 12 indicate that the CPO-CNN-BiLSTM-Attention model produces forecasts that align closely with the actual load profiles, demonstrating strong predictive accuracy.

Table 4. Prediction performance of the hybrid models.

Model	Evaluation Metric
	R2	MAE	MAPE (%)	CV-RMSE (%)
CPO-CNN-BiLSTM-Attention	0.9929	31.0252	3.2462	6.7212
CPO-CNN-BiLSTM	0.9896	38.4950	5.3146	8.1546
CPO-BiLSTM	0.9812	56.1133	8.4137	10.9487
CPO-CNN	0.9721	71.4175	10.0618	13.3426
BiLSTM	0.9713	68.5972	9.7881	13.5312
CNN	0.9673	69.9111	9.6380	9.6380

provides a comparative overview of the evaluation results for the five predictive models. The CPO-CNN-BiLSTM-Attention approach attained a MAPE of 3.2462% (96.7538% accuracy), meeting practical requirements. This configuration consistently surpasses all alternatives in the assessed criteria, yielding MAE, MAPE, and CV-RMSE values of 31.0252, 3.2462%, and 6.7212%, respectively—representing reductions of 7.47–40.39, 2.07–6.82%, and 1.43–7.72% over other models. Its R² value of 0.9929 also exceeds others by 0.0033–0.0256. The attention mechanism contributes a 2.07% accuracy gain, while CPO-optimized CNN and BiLSTM models show marked improvement over their base versions, confirming CPO’s effectiveness in parameter tuning.

4.3. Prediction Performance Analysis

4.3.1. Performance of Modal Decomposition

Figure 13 compares the predictive performance of secondary modal decomposition, primary modal decomposition, and non-decomposition methods using MAPE and CV-RMSE as evaluation metrics. Experimental results demonstrate the significant advantages of the proposed secondary modal decomposition method in both prediction accuracy and stability. Specifically, its MAPE (3.246%) and CV-RMSE (6.721%) are reduced by 6.542% and 6.81%, respectively, compared to primary decomposition, and by 10.879% and 10.751% compared to the non-decomposition approach.

To address the limitations of traditional single-stage decomposition—particularly its inadequate handling of high-frequency components leading to suboptimal prediction accuracy—this study constructs a hierarchical optimization framework of “decomposition-clustering-re-decomposition”. The process begins with initial noise reduction via ICEEMDAN decomposition, generating multi-frequency IMF components. Based on sample entropy dynamic clustering (high-frequency components: entropy >1.5; low-frequency components: entropy <0.8), high-frequency subsequences are selected. These high-frequency components then undergo secondary decomposition using VMD, where adaptive bandwidth adjustment restricts mode mixing error below 0.8%, effectively reducing high-frequency complexity. Experimental evidence confirms that this method, through its dual-stage decomposition and dynamic clustering mechanism, effectively mitigates input uncertainty while enhancing high-frequency processing capability, thereby optimizing computational efficiency.

To quantitatively evaluate the contribution of modal decomposition and its smoothing effect to prediction performance, three experimental schemes were designed using the CNN model as the baseline. Scheme 1: a CNN model without any decomposition; Scheme 2: a CPO–CNN–BiLSTM–Attention model without decomposition; Scheme 3: a CNN model incorporating dual-stage modal decomposition. The results are presented in

Table 5. Performance comparison under different decomposition schemes.

No.	Modal Decomposition	Model Type	MAPE (%)	CV-RMSE (%)
Scheme 1	No	CNN	15.2051	21.8377
Scheme 2	No	CPO–CNN–BiLSTM–Attention	14.1250	17.4720
Scheme 3	Yes	CNN	9.6380	9.6380

. Compared with the baseline CNN model, the deep model without decomposition reduced the MAPE by approximately 7.1% and the CV-RMSE by about 20.0%. In contrast, introducing dual-stage modal decomposition into the simple CNN framework reduced the MAPE by approximately 36.6% and the CV-RMSE by around 55.8%. These findings indicate that dual-stage modal decomposition plays a critical role in reducing the high-frequency complexity of the input signal and enhancing its predictability. Moreover, the improvement is not solely attributed to the smoothing effect; the decomposition also provides more stable and informative input features to the predictive model, thereby further improving forecasting accuracy.

4.3.2. Impact of Feature Engineering and Attention Mechanism on Model Prediction Accuracy

Feature engineering plays a crucial role in improving model prediction accuracy. To analyze its specific impact on load forecasting, a comparative study was designed with two model groups: an experimental group using input features processed by feature engineering—including fine-grained time types (e.g., hour, period), day type (weekday/weekend/holiday), outdoor temperature, outdoor humidity, cooling load at the previous timestep, and solar radiation at the previous timestep—and a control group using raw features without such processing. As shown in Figure 14, the engineered features were filtered and transformed to reduce redundancy and noise. In contrast, the raw feature set, while more comprehensive—including current solar radiation, wind direction, and wind speed in addition to the same temporal and environmental variables—may suffer from multicollinearity and scale variation, potentially impairing model training and prediction.

Meanwhile, the attention mechanism in the CNN-BiLSTM-Attention model also plays a vital role by adaptively highlighting the importance of different timesteps in the sequential data. When handling long and complex time series, it learns varying weights for each step, amplifying relevant information while suppressing less useful inputs. This helps the model capture truly salient temporal patterns and further improves predictive accuracy. Further analysis of the attention weight distribution reveals that several timesteps corresponding to peaks in solar radiation received notably higher weights. This indicates that the model successfully identified the strong coupling between solar gains and building cooling demand [31]. Solar radiation increases the heat load on the building envelope, directly affecting indoor thermal conditions and substantially raising cooling requirements during clear-sky periods. In this study, the close alignment between high-weight timesteps and solar radiation peaks further confirms that solar radiation is a critical physical driver of building load variations.

As summarized in Figure 14, the contributions of feature engineering and attention mechanism to prediction accuracy were quantified. Models trained with feature-engineered inputs showed significant improvement over those using raw features, with accuracy gains ranging from 7.17% to 10.74% and averaging 9.29%. This substantially exceeded the gains from the attention mechanism, which ranged from 2.06% to 6.81% with feature engineering and 2.33% to 3.67% without. These results demonstrate that for building cooling load forecasting, improving input quality through feature engineering—by removing redundancy, reducing noise, and constructing informative features—is essential. It substantially enhances the model’s ability to capture dynamic load patterns and leads to markedly more accurate predictions.

4.3.3. Performance of Different Optimization Algorithms

To evaluate the optimization capability of the Crested Porcupine Optimizer (CPO) algorithm on three key parameters—L2 regularization coefficient, initial learning rate, and number of hidden units—of the CNN and BiLSTM models, convergence iteration count, error metrics, and runtime were used as performance metrics. For benchmarking, conventional optimization approaches including Genetic Algorithm (GA), Particle Swarm Optimization (PSO), and Bayesian Optimization (BO) were implemented under identical experimental conditions. Specifically, the search space for the L2 regularization coefficient was set to [1 × 10⁻⁵, 1 × 10⁻²], the initial learning rate to [1 × 10⁻⁴, 1 × 10⁻²], and the number of hidden units to [32, 256]. The maximum number of iterations was fixed at 100, the population size was kept constant across algorithms, and the same random seed was applied for initialization to ensure reproducibility and fairness of comparison. As summarized in

Table 6. Performance comparison results of different optimization algorithms.

Optimization Algorithm	Convergence Iterations	CV-RMSE	Runtime/s
GA	81	10.698	35.2
PSO	78	8.0597	33.7
BO	73	7.5762	26.8
CPO	63	6.7212	23.9

, CPO achieved superior optimization results with the shortest runtime and faster convergence speed compared to GA, PSO, and BO, demonstrating its effectiveness in tuning parameters for both CNN and BiLSTM. This approach significantly enhances model accuracy and accelerates the training process.

4.3.4. Robustness of the Models

The robustness assessment, illustrated in Figure 15, displays box plots of relative errors across six prediction approaches. Among these, the CPO-CNN-BiLSTM-Attention configuration produces the most compact error spread, characterized by the smallest interquartile distance and minimal presence of outliers. This outcome implies that the model consistently confines prediction deviations within a limited range, underscoring its strong resilience against variability.

To assess the stability of the proposed method under different data-splitting conditions, multiple random splits of the dataset were performed within the original framework of 80% training and 20% testing sets. A total of six independent experiments were conducted. As shown in

Table 7. Stability verification results of model prediction performance under different random data splits.

Run	Evaluation Metric
	R2	MAE	MAPE (%)	CV-RMSE (%)
Run 1	0.9929	31.0252	4.2462	6.7212
Run 2	0.9913	34.4574	4.7350	7.4467
Run 3	0.9925	30.6647	4.7616	6.9265
Run 4	0.9911	34.4826	5.3559	7.5470
Run 5	0.9923	33.6359	4.8135	7.0018
Run 6	0.9918	33.3607	4.5466	7.2530
Mean	0.9920	32.9378	4.7431	7.1494

, the R² values remained consistently high, ranging from 0.9911 to 0.9929, with an average of 0.9920, indicating strong fitting capability across different splits. The MAE and MAPE metrics were kept within low ranges of 30.6647–34.4826 and 4.2462–5.3559%, with averages of 32.9378 and 4.7431%, respectively. The average CV-RMSE was 7.1494%, with fluctuations across runs not exceeding 0.83%. These results demonstrate that the proposed modal decomposition and deep learning-based short-term building load forecasting method maintains stable and high predictive performance under varying random data splits, exhibiting strong generalization ability and robustness of conclusions.

4.3.5. Configuration of Hyperparameters

The hyperparameters for the CNN and BiLSTM components in the CPO-CNN-BiLSTM-Attention model were optimized following a predefined structure [32]. A sequential tuning approach was applied to four key parameters: convolutional filters (16, 32, 64, 128), kernel number (2, 4, 8, 16), pooling window size (2, 4, 8, 16), and dropout rate (0.05, 0.1, 0.2, 0.3). Initial tests identified kernel number 16 and Dropout rate 0.1 as optimal, which were subsequently fixed. The model was trained and evaluated on each IMF component, with results visualized in Figure 16. This systematic optimization established the final parameter set, enhancing the model’s cooling load prediction capability.

To verify the rationality of parameter selection and the stability of decomposition results, a sensitivity analysis was conducted on three key parameters in the decomposition framework: the white noise amplitude in ICEEMDAN, the number of clusters in K-means, and the preset number of modes in VMD. The relative prediction error of the proposed model was used as the evaluation metric, and the results are presented in Figure 17. In the ICEEMDAN stage, the white noise amplitude was tested at 0.1, 0.2, and 0.3. As shown in Figure 17a, an amplitude of 0.2 yielded a lower median prediction error and reduced dispersion, effectively suppressing mode mixing while preserving the dominant characteristics of the original signal. For K-means clustering, the cluster number K was set to 2, 3, and 4. As illustrated in Figure 17b, K = 3 provided a stable error range and a lower maximum relative error, while reasonably distinguishing high-, medium-, and low-frequency IMF groups, thereby facilitating targeted secondary decomposition and modeling for each frequency band. For the secondary VMD decomposition applied to the high-frequency IMF sequence, the preset number of modes K was varied between 3, 4, and 5. As shown in Figure 17c, K = 3 achieved lower errors and stable decomposition performance, effectively separating high-frequency components without excessively increasing computational complexity. Based on comparative analysis, the optimal parameter configuration in this study was determined as follows: the white noise standard deviation coefficient in ICEEMDAN was set to 0.2; the cluster number in K-means was fixed at K = 3, corresponding to high-, medium-, and low-frequency IMF groups; and the number of modes in the secondary VMD decomposition of high-frequency IMF sequences was set to K = 3, resulting in three VMD-IMF components.

4.3.6. Generalization Analysis of the Model

To evaluate the generalization capability of the proposed prediction model, the dataset was split into three non-overlapping subsets corresponding to 1–30 June, 1–31 July, and 1–31 August. Each subset was divided into training and testing sets at a ratio of 8:2, and simulations were conducted using the proposed hybrid prediction framework. As shown in

Table 8. Generalization verification results of model prediction performance under different monthly datasets.

Time Period	R2	MAE	MAPE (%)	CV-RMSE (%)
1–30 June	0.9920	26.3135	4.1532	7.0188
1–31 July	0.9948	29.4909	3.7700	5.7339
1–31 August	0.9897	42.0436	5.7937	7.9132

, consistently high predictive performance was achieved across all periods. Overall, the model shows strong and stable generalization ability under diverse monthly and climatic conditions.

4.4. Limitations and Future Work

Although the proposed hybrid prediction framework demonstrated strong performance on simulated datasets, its practical deployment in real-world scenarios still faces several limitations and challenges. To advance the engineering implementation and broaden the applicability of the method, future studies will focus on aspects including data acquisition, model optimization, adaptation to multiple prediction horizons, robustness under complex scenarios, and deep integration with intelligent control systems. The key directions are outlined as follows:

(1) At present, model validation has been conducted primarily on simulated data, without leveraging real measured data from buildings. As a result, the model may not fully capture the complexities of real-world scenarios, such as random noise, load fluctuations driven by occupant behavior, and control deficiencies of HVAC systems. Future work will prioritize real-data-driven optimization by collecting hourly load profiles, meteorological parameters, occupant behavior patterns, and HVAC operation records from representative buildings, thereby constructing a multi-scenario real energy consumption dataset. Model input processing and training strategies will be tailored to the statistical properties of measured data, and a fault diagnosis module will be incorporated to improve robustness and practicality in engineering applications. Computational efficiency will also be systematically evaluated across different hardware platforms, accompanied by the development of lightweight or pruned versions of the model and exploration of simplified decomposition strategies within acceptable accuracy trade-offs. Finally, deployment tests will be conducted in actual building management systems to assess scalability, latency, and operational stability in real-world environments.

(2) Incorporating behavioral and psychological correction factors could further enhance the dynamic responsiveness and realism of the model [33,34]. Future studies will integrate building behavior monitoring data—such as variations in occupant density and equipment usage triggered by meetings, holidays, or unexpected events—along with psychological state indicators obtained through surveys or sensors, and investigate their integration into deep learning-based prediction models.

(3) Performance evaluation under varying temporal resolutions is a prerequisite for effective integration of the model with control strategies. In addition to the default one-hour prediction horizon, this study also assessed a one-day time step, showing that the proposed hybrid prediction framework maintained high accuracy for long-horizon forecasts (R² = 0.9857, MAE = 472.45, MAPE = 2.63%, CV-RMSE = 3.51%). Future research will systematically investigate performance across minute-, hourly, and daily level forecasts under diverse building load scenarios and climate zones. This will enable comprehensive assessment of model robustness and adaptability, thereby ensuring its capability to meet heterogeneous operational and planning needs in real-world applications.

(4) Complex or unexpected scenarios in building load forecasting can challenge the adaptability of prediction models. For instance, abrupt changes in occupant behavior—such as unscheduled meetings, gatherings, or extended absences—can lead to non-periodic load spikes that are difficult to capture in real time; equipment faults or control system failures may disrupt established load patterns; extreme weather events or other external disturbances could introduce unseen data distributions, undermining prediction reliability. Future work will address these challenges by incorporating real-time monitoring data, developing anomaly detection modules, and adopting online learning methods capable of rapidly adapting to new operational conditions, thereby enhancing adaptability and robustness in dynamic, non-stationary environments.

(5) The proposed hybrid prediction model is currently evaluated in an offline setting, and its forecasts have not yet been directly integrated into active HVAC control strategies. Future research will focus on deep integration of the prediction model with intelligent control systems, using real-time forecasts as inputs for load balancing, indoor temperature–humidity optimization, and peak shaving operations. Prediction-driven control experiments will be designed to quantitatively assess the actual benefits in terms of energy savings, peak load reduction, and occupant comfort improvement. In addition, applicability across various building types and climate conditions will be explored to ensure multi-scenario robustness and scalability of the approach.

5. Conclusions

This study proposes a novel ICEEMDAN-Kmeans-VMD-CPO-CNN-BiLSTM-Attention model for predicting building cooling loads. The model demonstrates outstanding predictive accuracy, along with excellent robustness and generalization capabilities. The main conclusions are as follows:

(1) The proposed secondary modal decomposition method significantly outperforms both primary modal decomposition and non-decomposition methods in terms of predictive accuracy and stability. Its MAPE (3.2462%) and CV-RMSE (6.7212%) are reduced by 6.542% and 6.81%, respectively, compared to primary modal decomposition, and by 10.879% and 10.751% compared to the non-decomposition approach. The proposed dual-stage decomposition and dynamic clustering strategy effectively smooths and reduces the uncertainty in the model inputs.

(2) The CPO-CNN-BiLSTM-Attention model achieved excellent predictive results for building load data across different periods, with R², MAE, MAPE, and CV-RMSE reaching 0.9929, 31.0252, 3.2462%, and 6.7212%, respectively. This indicates that the proposed model can fully leverage the strengths of both the CNN and the BiLSTM.

(3) Feature engineering contributed more significantly to improving predictive accuracy than the attention mechanism. Feature engineering yielded an average accuracy improvement of 9.29%, while the attention mechanism provided a maximum improvement of 6.81%. Nevertheless, both components enhanced the model’s predictive performance.

(4) Both the CPO-CNN and CPO-BiLSTM models outperformed their unoptimized, single neural network counterparts across performance metrics. Their box plots of relative errors showed narrower interquartile ranges and fewer outliers, indicating that the CPO algorithm provides a reliable method for optimizing parameters in both CNN and BiLSTM models. In comparison with classical approaches such as GA, PSO, and BO, the CPO framework achieved higher optimization efficiency, reduced computational overhead, and quicker convergence, demonstrating its suitability for fine-tuning deep learning architectures of this type.

This study will evolve along two primary pathways: validating the model’s generalizability across a wider range of buildings and multi-energy load (cooling, heating, electricity, and gas), and exploring advanced data-driven structures for enhanced prediction accuracy. These efforts are aimed at transforming high-fidelity load prediction into a practical tool for optimizing building energy systems, thereby directly contributing to energy efficiency improvement and carbon neutrality.