A ConvLSTM-Based Hybrid Approach Integrating DyT and CBAM(T) for Residential Heating Load Forecast
Abstract
1. Introduction
2. Methodology
2.1. Data Preprocessing
2.2. eXtreme Gradient Boosting
2.3. Convolutional Long Short-Term Memory (ConvLSTM)
2.4. Dynamic Tanh (DyT)
2.5. Channel–Temporal Attention (CBAM(T))
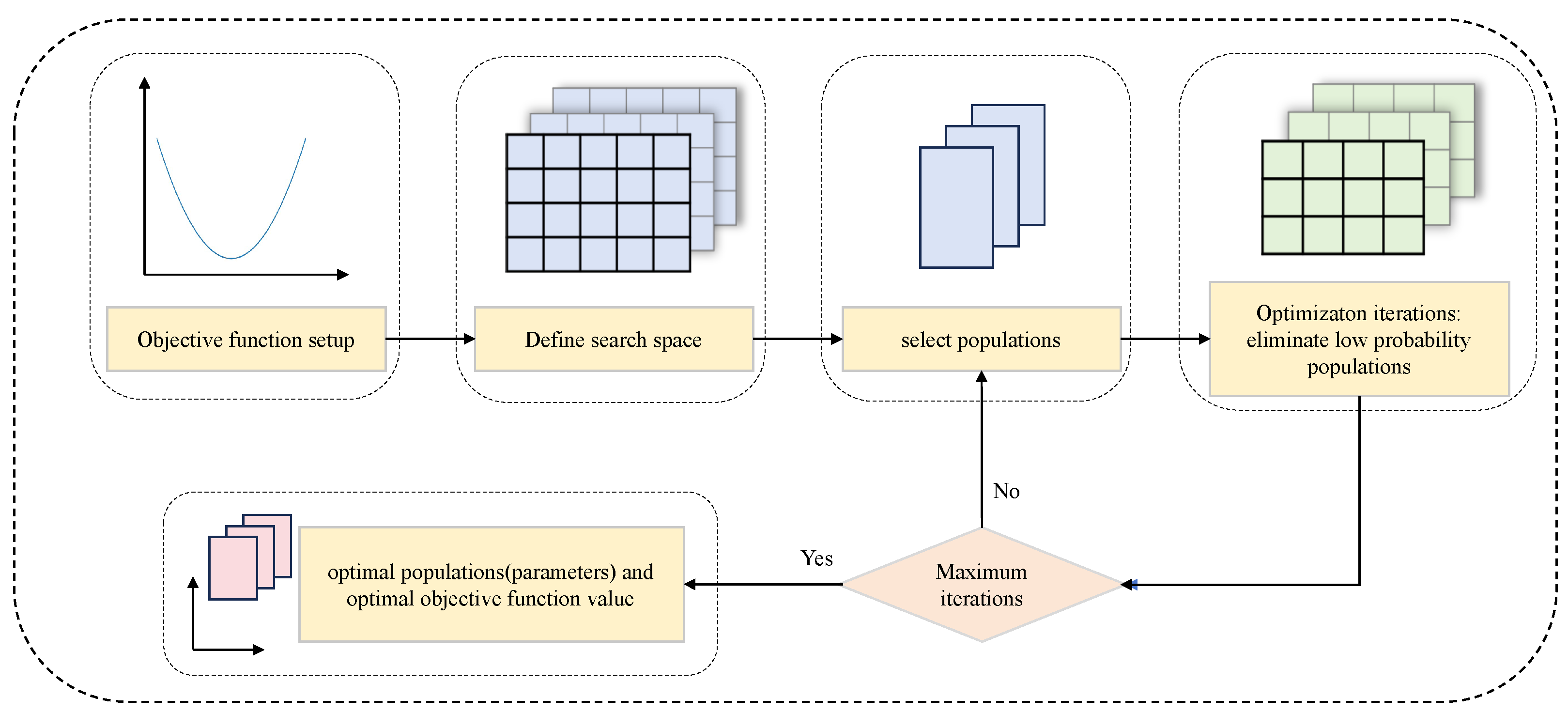
2.6. Optuna
2.7. ConvLSTM-DyT-CBAM(T)
2.8. Evaluation Metrics
3. Research Design
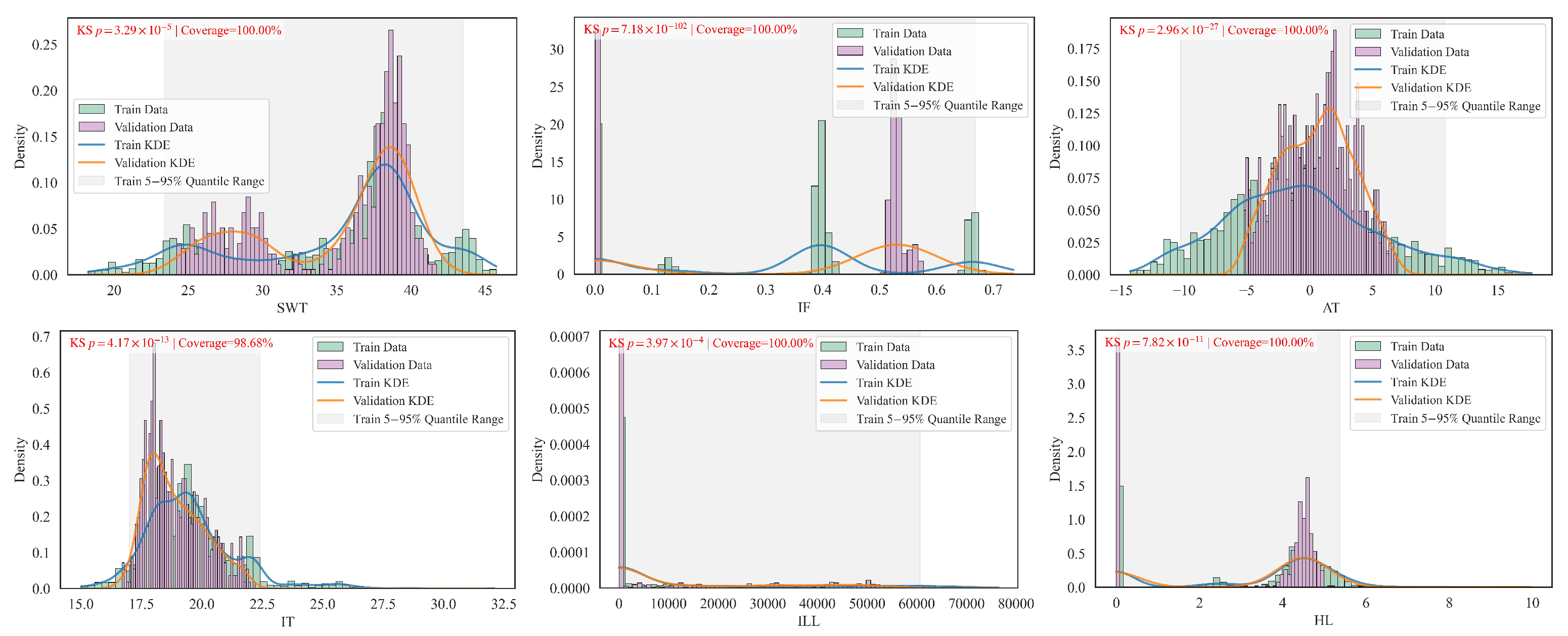
3.1. Dataset and Preprocessing
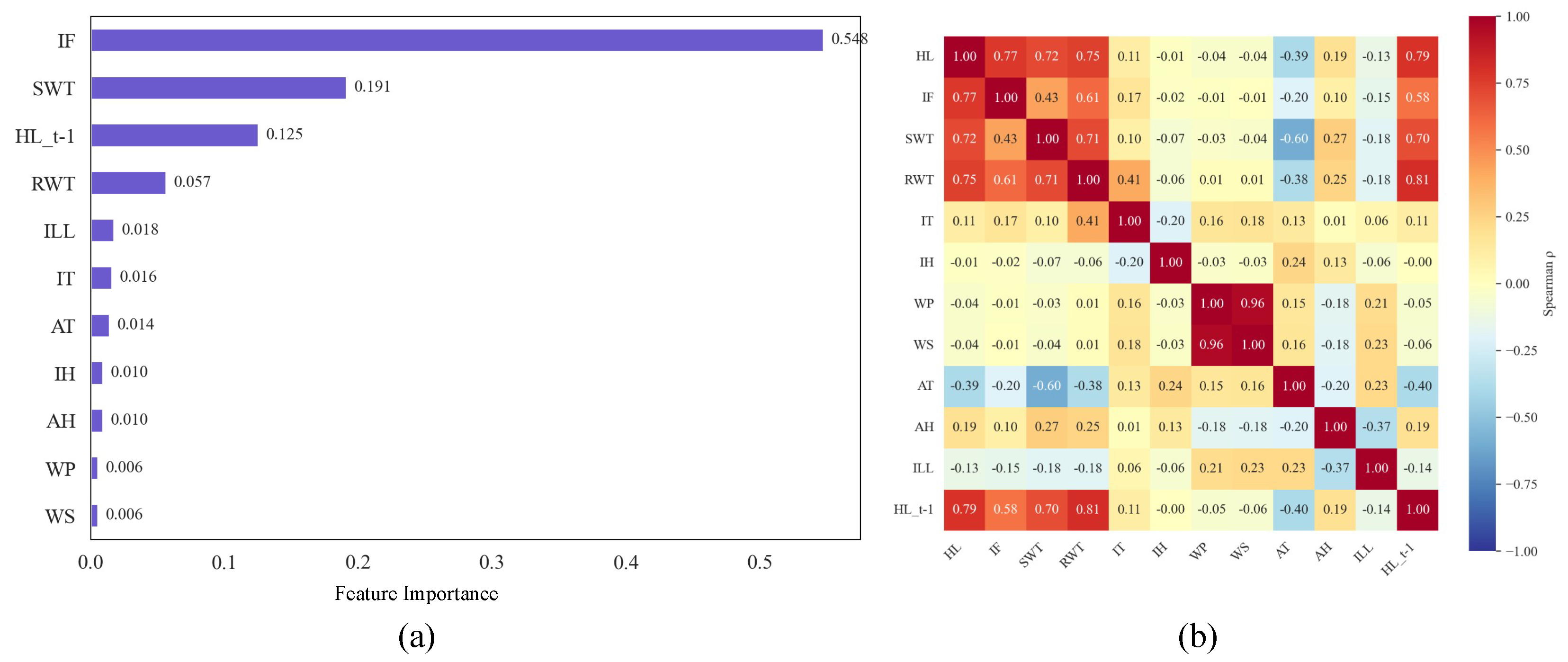
3.2. Feature Selection
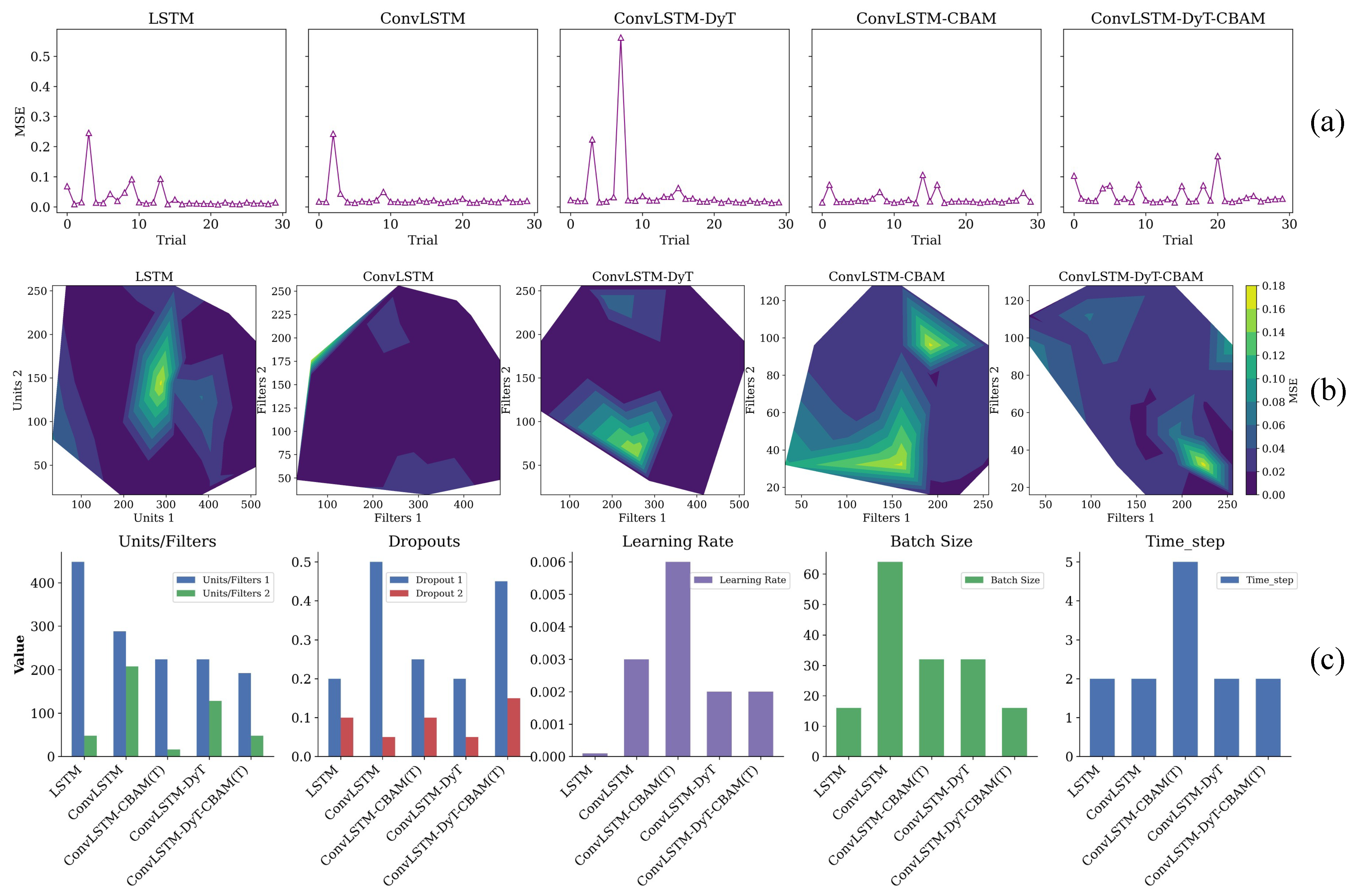
3.3. Hyperparameter Optimization Based on Optuna
4. Prediction Results and Analysis
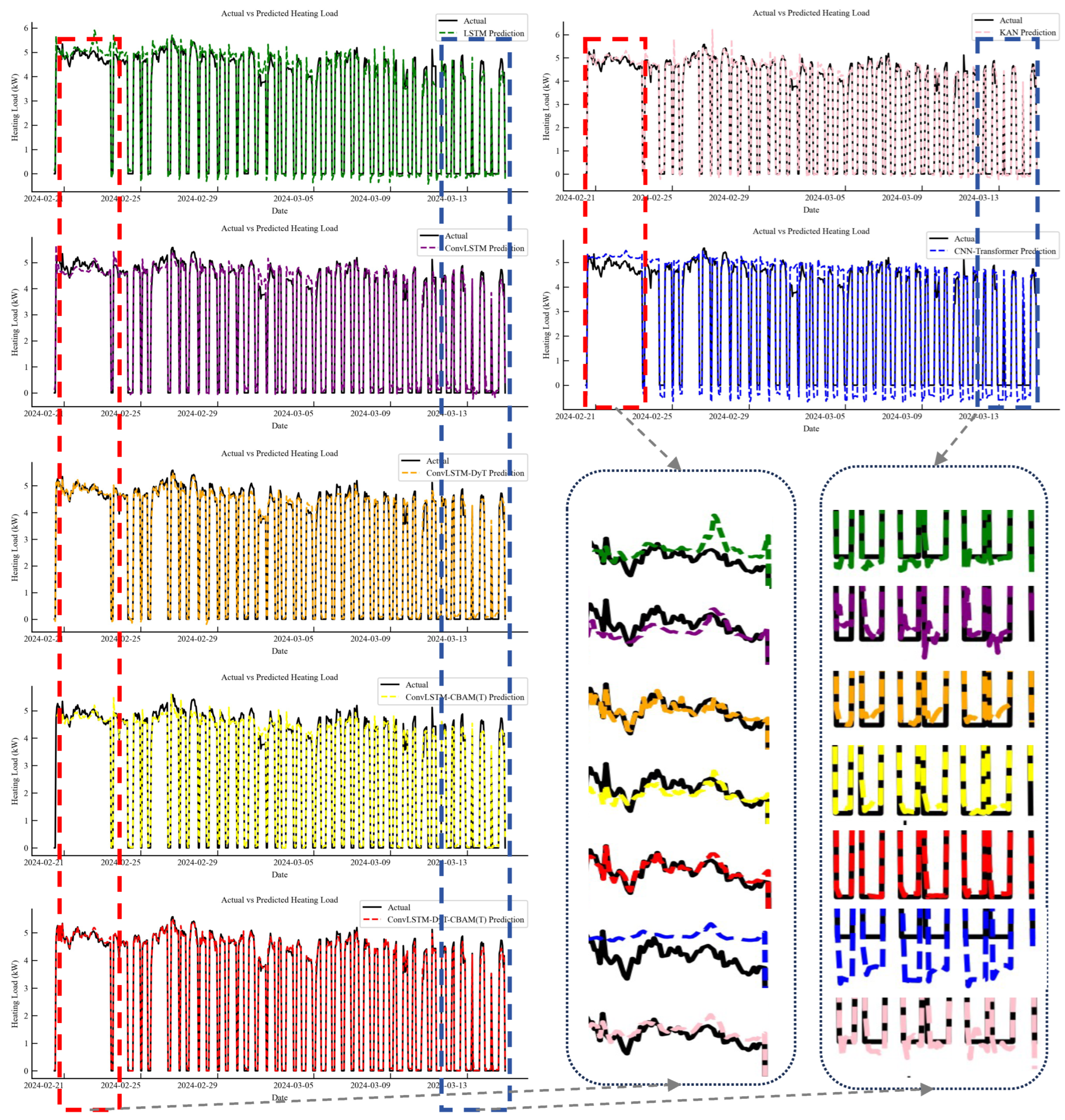
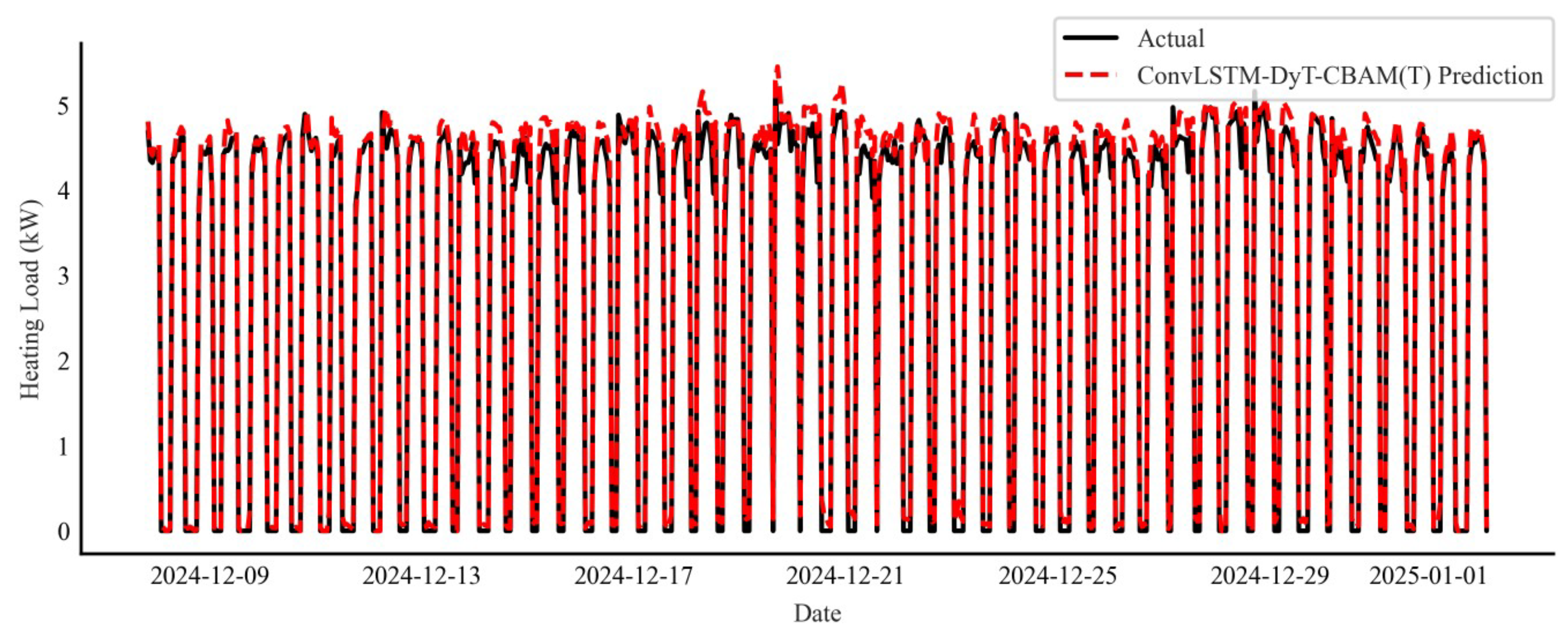
4.1. Prediction Results of Residential Heating Load
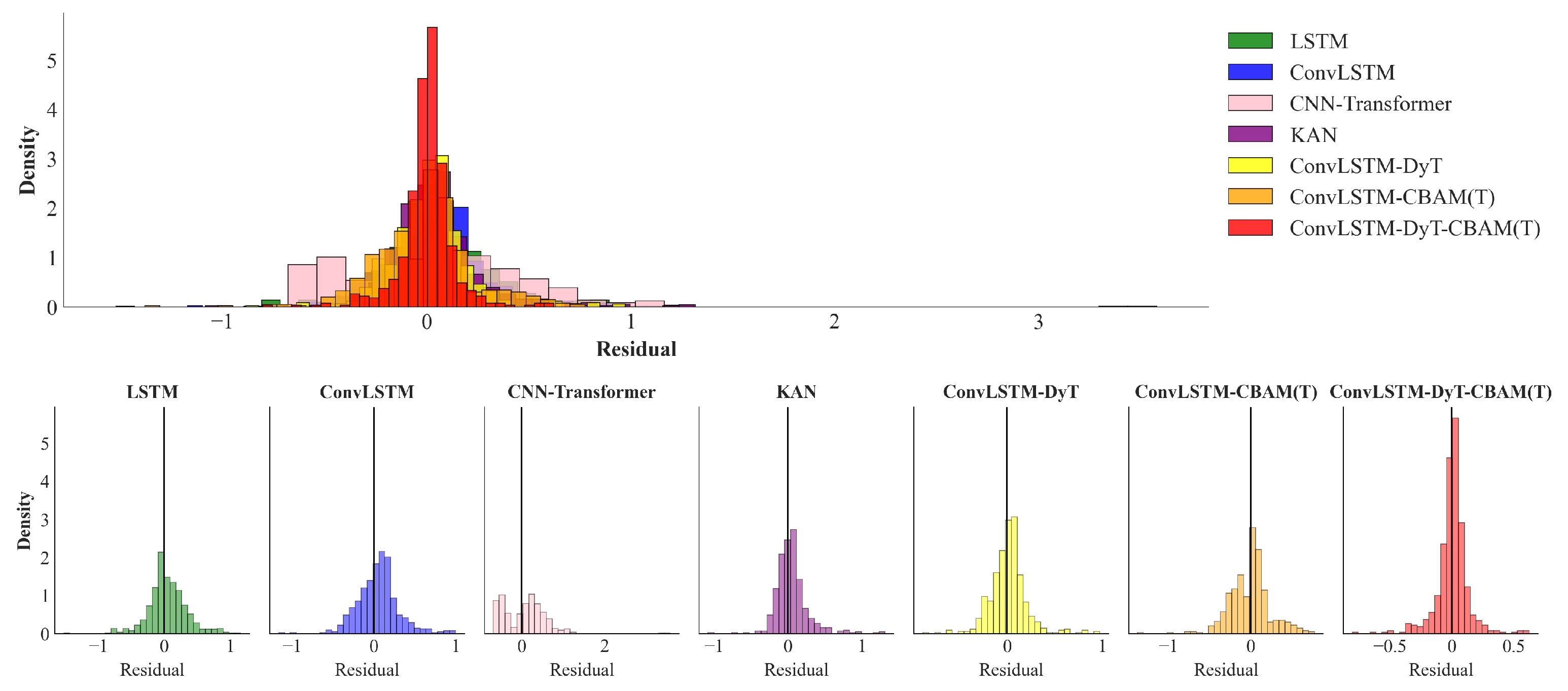
4.2. Analysis of Prediction Results
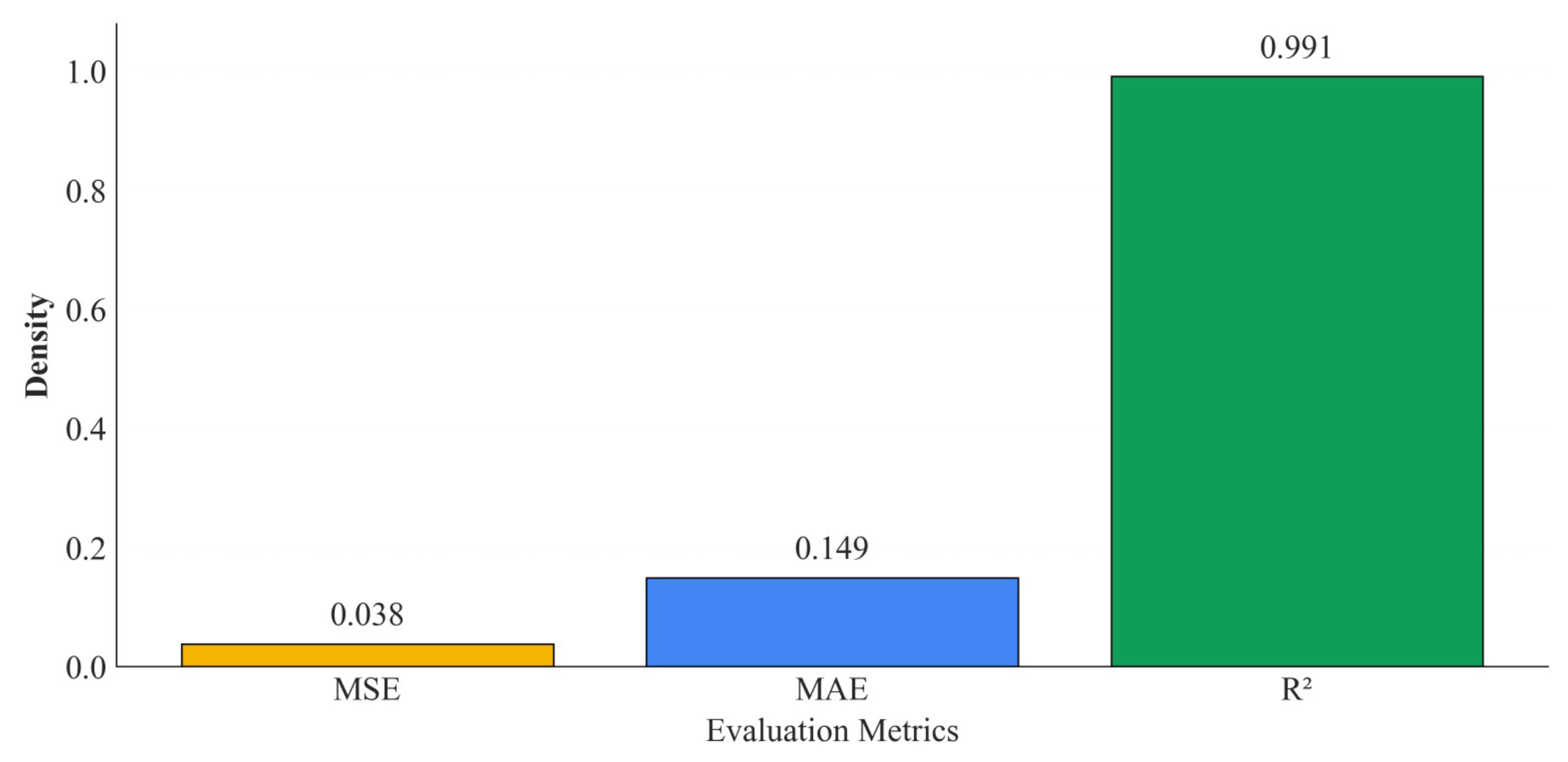
4.3. Analysis of Cross-Season Validation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Uerge-Vorsatz, D.; Cabeza, L.F.; Serrano, S.; Barreneche, C.; Petrichenko, K. Heating and cooling energy trends and drivers in buildings. Renew. Sust. Energy Rev. 2015, 41, 85–98. [Google Scholar] [CrossRef]
- Dahl, M.; Brun, A.; Andresen, G.B. Using ensemble weather predictions in district heating operation and load forecasting. Appl. Energy 2017, 193, 455–465. [Google Scholar] [CrossRef]
- Yu, H.; Zhong, F.; Du, Y.; Xie, X.; Wang, Y.; Zhang, X.; Huang, S. Short-term cooling and heating loads forecasting of building district energy system based on data-driven models. Energy Build. 2023, 298, 113513. [Google Scholar] [CrossRef]
- Jiang, W.; Wang, P.; Ma, X.; Liu, Y. Development of a grey-box heat load prediction model by subspace identification method for heating building. Build. Environ. 2025, 280, 113119. [Google Scholar] [CrossRef]
- Kazmi, H.; Fu, C.; Miller, C. Ten questions concerning data-driven modelling and forecasting of operational energy demand at building and urban scale. Build. Environ. 2023, 239, 110407. [Google Scholar] [CrossRef]
- Quanwei, T.; Guijun, X.; Wenju, X. Cakformer: Transformer model for long-term heat load forecasting based on cauto-correlation and KAN. Energy 2025, 324, 135460. [Google Scholar] [CrossRef]
- Zhao, J.; Li, J.; Shan, Y. Research on a forecasted load-and time delay-based model predictive control (MPC) district energy system model. Energy Build. 2021, 231, 110631. [Google Scholar] [CrossRef]
- Xiao, Z.; Gang, W.; Yuan, J.; Zhang, Y.; Fan, C. Cooling load disaggregation using a NILM method based on random forest for smart buildings. Sustain. Cities Soc. 2021, 74, 103202. [Google Scholar] [CrossRef]
- Liu, H.; Yu, J.; Dai, J.; Zhao, A.; Wang, M.; Zhou, M. Hybrid prediction model for cold load in large public buildings based on mean residual feedback and improved SVR. Energy Build. 2023, 294, 113229. [Google Scholar] [CrossRef]
- Wei, Z.; Zhang, T.; Yue, B.; Ding, Y.; Xiao, R.; Wang, R.; Zhai, X. Prediction of residential district heating load based on machine learning: A case study. Energy 2021, 231, 120950. [Google Scholar] [CrossRef]
- Cai, W.; Wen, X.; Li, C.; Shao, J.; Xu, J. Predicting the energy consumption in buildings using the optimized support vector regression model. Energy 2023, 273, 127188. [Google Scholar] [CrossRef]
- Mohan, R.; Pachauri, N. An ensemble model for the energy consumption prediction of residential buildings. Energy 2025, 314, 134255. [Google Scholar] [CrossRef]
- Yan, R.; Ma, Z.; Zhao, Y.; Kokogiannakis, G. A decision tree based data-driven diagnostic strategy for air handling units. Energy Build. 2016, 133, 37–45. [Google Scholar] [CrossRef]
- Le, L.T.; Nguyen, H.; Dou, J.; Zhou, J. A comparative study of PSO-ANN, GA-ANN, ICA-ANN, and ABC-ANN in estimating the heating load of buildings’ energy efficiency for smart city planning. Appl. Sci. 2019, 9, 2630. [Google Scholar] [CrossRef]
- Lu, C.; Li, S.; Penaka, S.R.; Olofsson, T. Automated machine learning-based framework of heating and cooling load prediction for quick residential building design. Energy 2023, 274, 127334. [Google Scholar] [CrossRef]
- Kavaklioglu, K. Robust modeling of heating and cooling loads using partial least squares towards efficient residential building design. J. Build. Eng. 2018, 18, 467–475. [Google Scholar] [CrossRef]
- Guo, Z.; Moayedi, H.; Foong, L.K.; Bahiraei, M. Optimal modification of heating, ventilation, and air conditioning system performances in residential buildings using the integration of metaheuristic optimization and neural computing. Energy Build. 2020, 214, 109866. [Google Scholar] [CrossRef]
- Al-Selwi, S.M.; Hassan, M.F.; Abdulkadir, S.J.; Muneer, A.; Sumiea, E.H.; Alqushaibi, A.; Ragab, M.G. RNN-LSTM: From applications to modeling techniques and beyond—systematic review. J. King Saud Univ.-Comput. Inf. Sci. 2024, 36, 102068. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, X.; Huang, Y.; Zhang, P.; Fu, Y. A multivariate time series graph neural network for district heat load forecasting. Energy 2023, 278, 127911. [Google Scholar] [CrossRef]
- Chen, B.; Yang, W.; Yan, B.; Zhang, K. An advanced airport terminal cooling load forecasting model integrating SSA and CNN-transformer. Energy Build. 2024, 309, 114000. [Google Scholar] [CrossRef]
- Zhao, Z.; Yun, S.; Jia, L.; Guo, J.; Meng, Y.; He, N.; Li, X.; Shi, J.; Yang, L. Hybrid VMD-CNN-GRU-based model for short-term forecasting of wind power considering spatio-temporal features. Eng. Appl. Artif. Intell. 2023, 121, 105982. [Google Scholar] [CrossRef]
- Xue, G.; Qi, C.; Li, H.; Kong, X.; Song, J. Heating load prediction based on attention long short term memory: A case study of Xingtai. Energy 2020, 203, 117846. [Google Scholar] [CrossRef]
- Ni, Z.; Zhang, C.; Karlsson, M.; Gong, S. A study of deep learning-based multi-horizon building energy forecasting. Energy Build. 2024, 303, 113810. [Google Scholar] [CrossRef]
- Huang, Y.; Zhao, Y.; Wang, Z.; Liu, X.; Liu, H.; Fu, Y. Explainable district heat load forecasting with active deep learning. Appl. Energy 2023, 350, 121753. [Google Scholar] [CrossRef]
- Zhou, M.; Wang, L.; Hu, F.; Zhu, Z.; Zhang, Q.; Kong, W.; Zhou, G.; Wu, C.; Cui, E. ISSA-LSTM: A new data-driven method of heat load forecasting for building air conditioning. Energy Build. 2024, 321, 114698. [Google Scholar] [CrossRef]
- Zhu, J.; Yang, J.; Cui, X.; Peng, M.; Liang, X. A novel adaptive adjustment kolmogorov-arnold network for heat load prediction in district heating systems. Appl. Therm. Eng. 2025, 274, 126552. [Google Scholar] [CrossRef]
- Wan, A.; Chang, Q.; AL-Bukhaiti, K.; He, J. Short-term power load forecasting for combined heat and power using CNN-LSTM enhanced by attention mechanism. Energy 2023, 282, 128274. [Google Scholar] [CrossRef]
- Yan, Q.; Lu, Z.; Liu, H.; He, X.; Zhang, X.; Guo, J. An improved feature-time transformer encoder-bi-LSTM for short-term forecasting of user-level integrated energy loads. Energy Build. 2023, 297, 113396. [Google Scholar] [CrossRef]
- Li, X.; Wang, S.; Chen, Z. Hierarchical reconciliation of convolutional gated recurrent units for unified forecasting of branched and aggregated district heating loads. Energy 2024, 313, 134097. [Google Scholar] [CrossRef]
- Zhu, J.; Ge, Z.; Song, Z.; Gao, F. Review and big data perspectives on robust data mining approaches for industrial process modeling with outliers and missing data. Annu. Rev. Control 2018, 46, 107–133. [Google Scholar] [CrossRef]
- Ding, Y.; Su, H.; Liu, K.; Wang, Q. Robust commissioning strategy for existing building cooling system based on quantification of load uncertainty. Energy Build. 2020, 225, 110295. [Google Scholar] [CrossRef]
- Li, J.; Cheng, K.; Wang, S.; Morstatter, F.; Trevino, R.P.; Tang, J.; Liu, H. Feature selection: A data perspective. ACM Comput. Surv. 2018, 50, 94. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Wang, Z.; Hong, T.; Piette, M.A. Building thermal load prediction through shallow machine learning and deep learning. Appl. Energy 2020, 263, 114683. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, N.; Hou, Y. A novel hybrid model for building heat load forecasting based on multivariate empirical modal decomposition. Build. Environ. 2023, 237, 110317. [Google Scholar] [CrossRef]
- Agga, A.; Abbou, A.; Labbadi, M.; El Houm, Y. Short-term self consumption PV plant power production forecasts based on hybrid CNN-LSTM, ConvLSTM models. Renew. Energy 2021, 177, 101–112. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.-Y.; Wong, W.; Woo, W. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Montreal, QC, Canada, 7–12 December 2015. [Google Scholar]
- Parkes, E.J. Observations on the tanh–coth expansion method for finding solutions to nonlinear evolution equations. Appl. Math. Comput. 2010, 217, 1749–1754. [Google Scholar] [CrossRef]
- Zhu, J.; Chen, X.; He, K.; LeCun, Y.; Liu, Z. Transformers without normalization. arXiv 2025, arXiv:2503.10622. [Google Scholar] [CrossRef]
- Woo, S.; Park, J.; Lee, J.-Y.; Kweon, I.S. CBAM: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Nguyen, T.V.; Song, Z.; Yan, S. STAP: Spatial-temporal attention-aware pooling for action recognition. IEEE Trans. Circuits Syst. Video Technol. 2015, 25, 77–86. [Google Scholar] [CrossRef]
- Wu, Y.; Tan, H.; Qin, L.; Ran, B.; Jiang, Z. A hybrid deep learning based traffic flow prediction method and its understanding. Transp. Res. Pt. C-Emerg. Technol. 2018, 90, 166–180. [Google Scholar] [CrossRef]
- Cui, Z.; Ke, R.; Pu, Z.; Wang, Y. Stacked bidirectional and unidirectional LSTM recurrent neural network for forecasting network-wide traffic state with missing values. Transp. Res. Pt. C-Emerg. Technol. 2020, 118, 102674. [Google Scholar] [CrossRef]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A next-generation hyperparameter optimization framework. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 2623–2631. [Google Scholar]
- Hoang-Phuong, N.; Liu, J.; Zio, E. A long-term prediction approach based on long short-term memory neural networks with automatic parameter optimization by tree-structured parzen estimator and applied to time-series data of NPP steam generators. Appl. Soft Comput. 2020, 89, 106116. [Google Scholar]



| Data Category | Feature | Unit | Symbol |
|---|---|---|---|
| Heating Network Parameters | Heating load | kW | HL |
| Instantaneous flow rate | m3/h | IF | |
| Supply water temperature | °C | SWT | |
| Return water temperature | °C | RWT | |
| Outdoor Meteorological Data | Air temperature | °C | AT |
| Air relative humidity | % | AH | |
| Wind force (Beaufort scale) | Bft | WP | |
| Wind speed | m/s | WS | |
| Illuminance | Lux | ILL | |
| Indoor Environmental Parameters | Indoor air temperature | °C | IT |
| Indoor relative humidity | % | IH |
| Variable | Coverage | KS p-Value |
|---|---|---|
| HL | 100% | |
| IF | 100% | |
| SWT | 100% | |
| IT | 98.68% | |
| AT | 100% | |
| ILL | 100% |
| # | Hyperparameter | Values |
|---|---|---|
| 1 | n_estimators | 500 |
| 2 | Learning Rate | 0.005 |
| 3 | Max_depth | 5 |
| 4 | subsample | 0.8 |
| 5 | Min_child_weight | 1 |
| 6 | Reg_ | 0 |
| # | Hyperparameter | Search Space | Step |
|---|---|---|---|
| 1 | Units1 or Filters1 | [16, 512] | 16 |
| 2 | Units2 or Filters2 | [16, 256] | 16 |
| 3 | Num_heads | [2, 8] | 2 |
| 4 | Key_dim | [16, 128] | 16 |
| 3 | Dropout1 | [0, 0.5] | 0.05 |
| 4 | Dropout2 | [0, 0.5] | 0.05 |
| 5 | Learning rate | [, ] | |
| 6 | Batch size | {16, 32, 64} | – |
| 7 | Time steps | [1, 6] | 1 |
| 8 | CBAM(T) ratio | [4, 16] | 4 |
| 9 | Temporal kernel | [3, 12] | 3 |
| 10 | DyT_alpha1 | [0.1, 1.5] | 0.1 |
| 11 | DyT_alpha2 | [0.1, 1.5] | 0.1 |
| Hyper Parameters | LSTM | CNN -Transformer | KAN | ConvLSTM | ConvLSTM -CBAM(T) | ConvLSTM -DyT | ConvLSTM -DyT -CBAM(T) |
|---|---|---|---|---|---|---|---|
| Units1/Filters1 | 448 | 256 | 208 | 288 | 224 | 224 | 192 |
| Units2/Filters2 | 48 | 112 | 208 | 208 | 16 | 128 | 48 |
| Num_heads | - | 4 | - | - | - | - | - |
| Key_dim | - | 80 | - | - | - | - | - |
| Dropout1 | 0.20 | 0.35 | 0.05 | 0.50 | 0.25 | 0.20 | 0.45 |
| Dropout2 | 0.10 | - | 0.30 | 0.05 | 0.10 | 0.05 | 0.15 |
| Learning_rate | 0.001 | 0.002 | 0.001 | 0.003 | 0.007 | 0.002 | 0.002 |
| Batch_size | 16 | 16 | 16 | 64 | 32 | 32 | 16 |
| Time_step | 2 | 2 | 3 | 2 | 5 | 2 | 2 |
| DyT_alpha1 | - | - | - | - | - | 1.9 | 0.5 |
| DyT_alpha2 | - | - | - | - | - | 0.9 | 0.9 |
| CBAM(T)_ratio | - | - | 16 | - | - | 8 | - |
| Temporal_kernel | - | - | 6 | - | 6 | - | 6 |
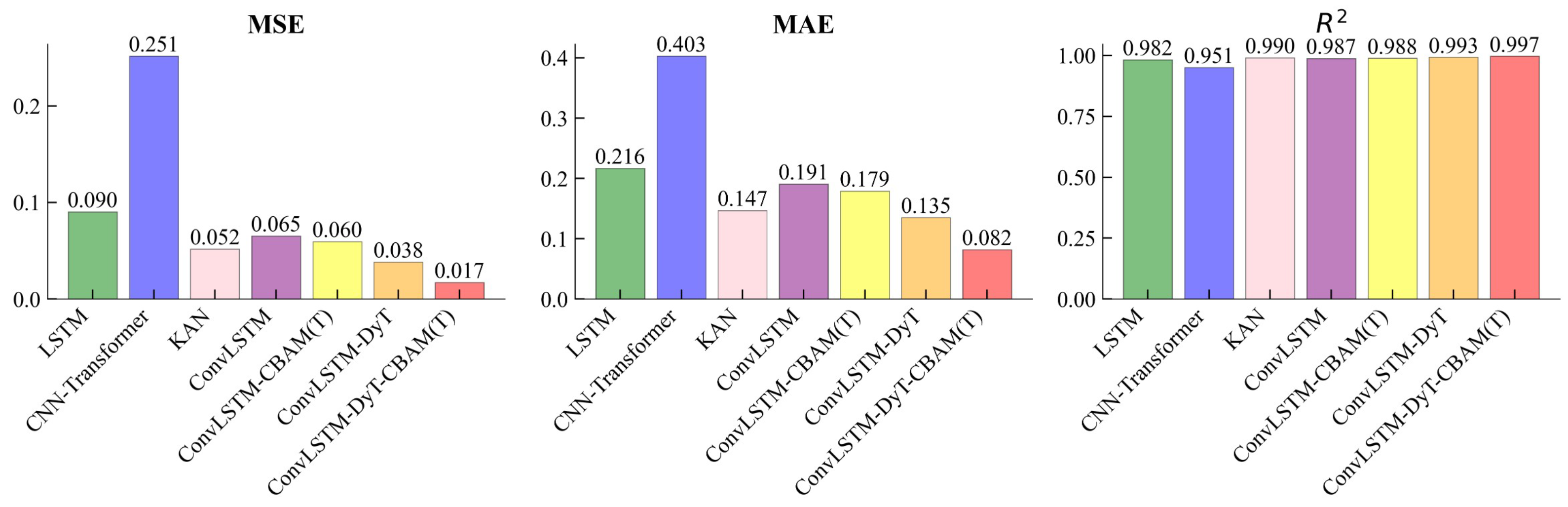
| # | Model | MSE | MAE | R2 |
|---|---|---|---|---|
| 1 | LSTM | 0.090 | 0.216 | 0.972 |
| 2 | CNN-Transformer | 0.251 | 0.403 | 0.951 |
| 3 | KAN | 0.052 | 0.147 | 0.990 |
| 4 | ConvLSTM | 0.065 | 0.191 | 0.987 |
| 5 | ConvLSTM-CBAM(T) | 0.060 | 0.179 | 0.988 |
| 6 | ConvLSTM-DyT | 0.038 | 0.135 | 0.993 |
| 7 | ConvLSTM-DyT-CBAM(T) | 0.017 | 0.082 | 0.997 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Gao, X.; Liu, X.; Liu, Z. A ConvLSTM-Based Hybrid Approach Integrating DyT and CBAM(T) for Residential Heating Load Forecast. Buildings 2025, 15, 3781. https://doi.org/10.3390/buildings15203781
Zhang H, Gao X, Liu X, Liu Z. A ConvLSTM-Based Hybrid Approach Integrating DyT and CBAM(T) for Residential Heating Load Forecast. Buildings. 2025; 15(20):3781. https://doi.org/10.3390/buildings15203781
Chicago/Turabian StyleZhang, Haibo, Xiaoxing Gao, Xuan Liu, and Zhibin Liu. 2025. "A ConvLSTM-Based Hybrid Approach Integrating DyT and CBAM(T) for Residential Heating Load Forecast" Buildings 15, no. 20: 3781. https://doi.org/10.3390/buildings15203781
APA StyleZhang, H., Gao, X., Liu, X., & Liu, Z. (2025). A ConvLSTM-Based Hybrid Approach Integrating DyT and CBAM(T) for Residential Heating Load Forecast. Buildings, 15(20), 3781. https://doi.org/10.3390/buildings15203781





