A Macro-Scale Modeling Approach for Capturing Bending-Shear Coupled Dynamic Behavior in High-Rise Structures Using Deep Learning
Abstract
1. Introduction
2. FSC Behavior Parameterization and Modeling Method
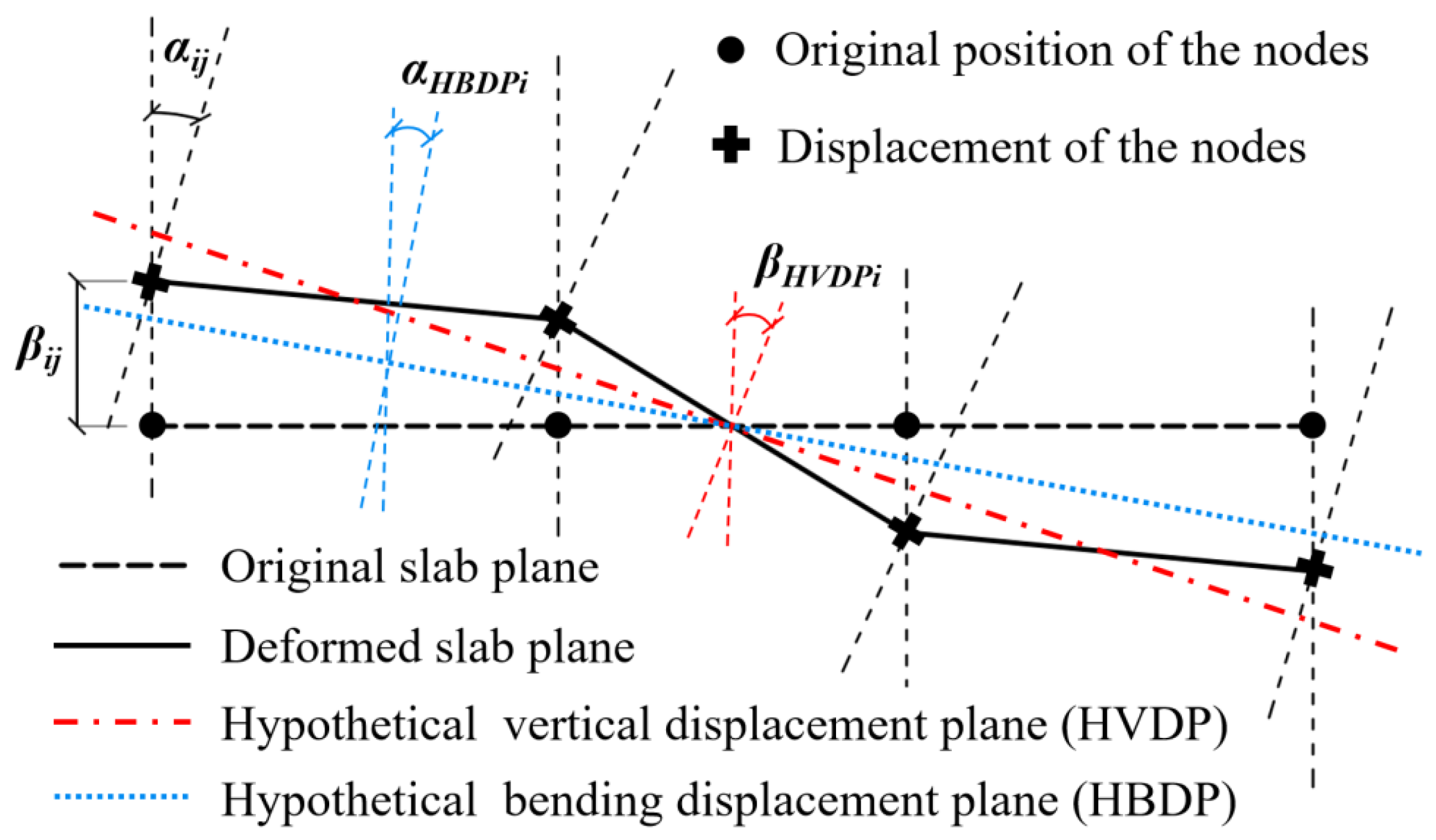
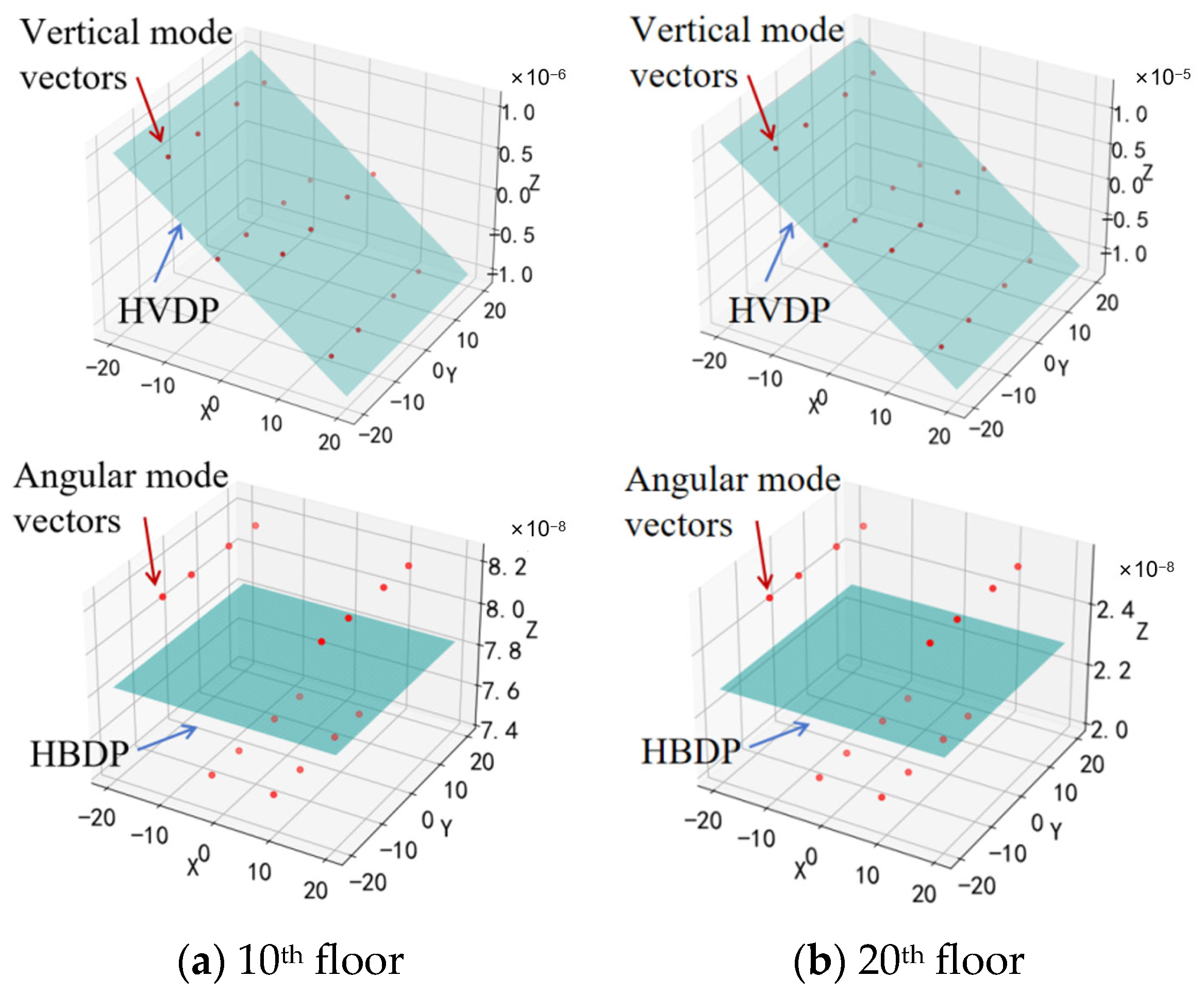
2.1. Displacement Interaction Coefficients
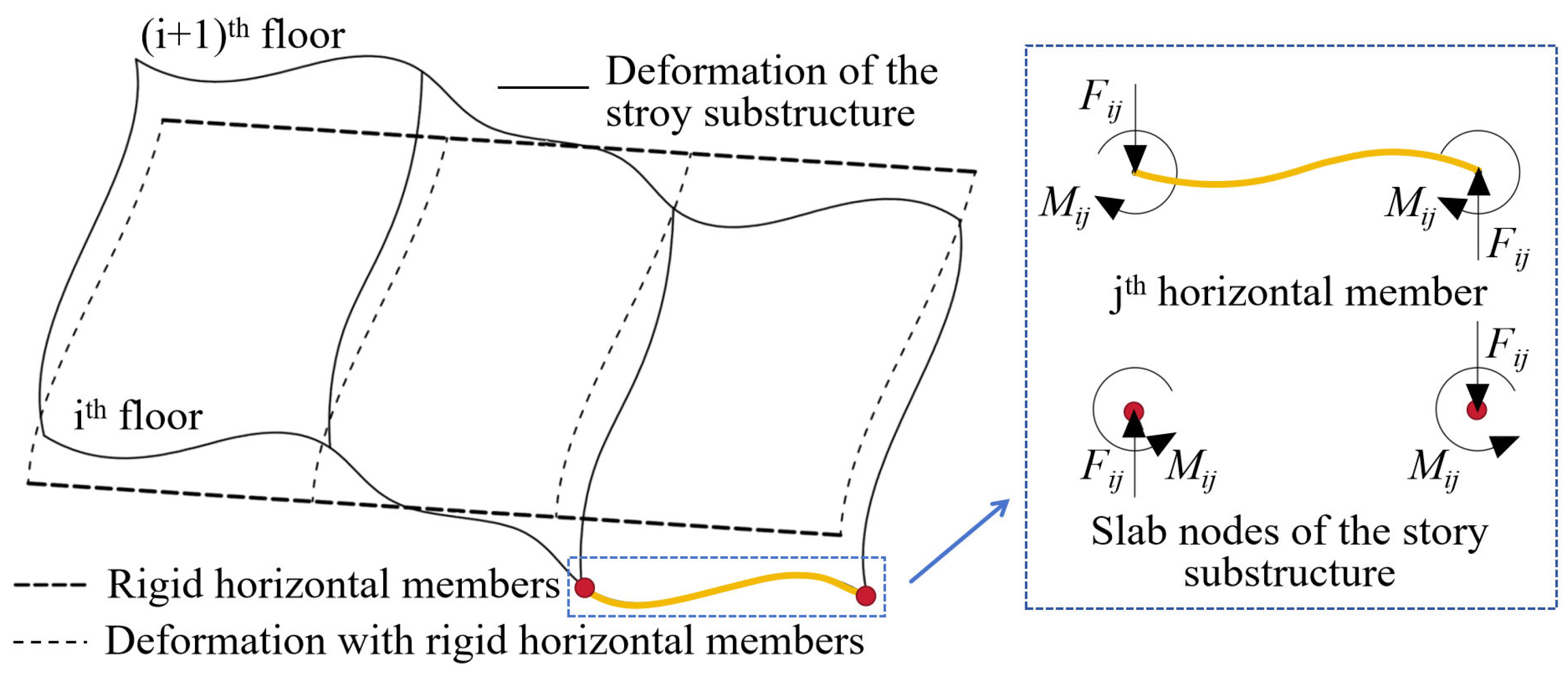
2.2. Enhanced LPMs for FSC Dynamic Behavior
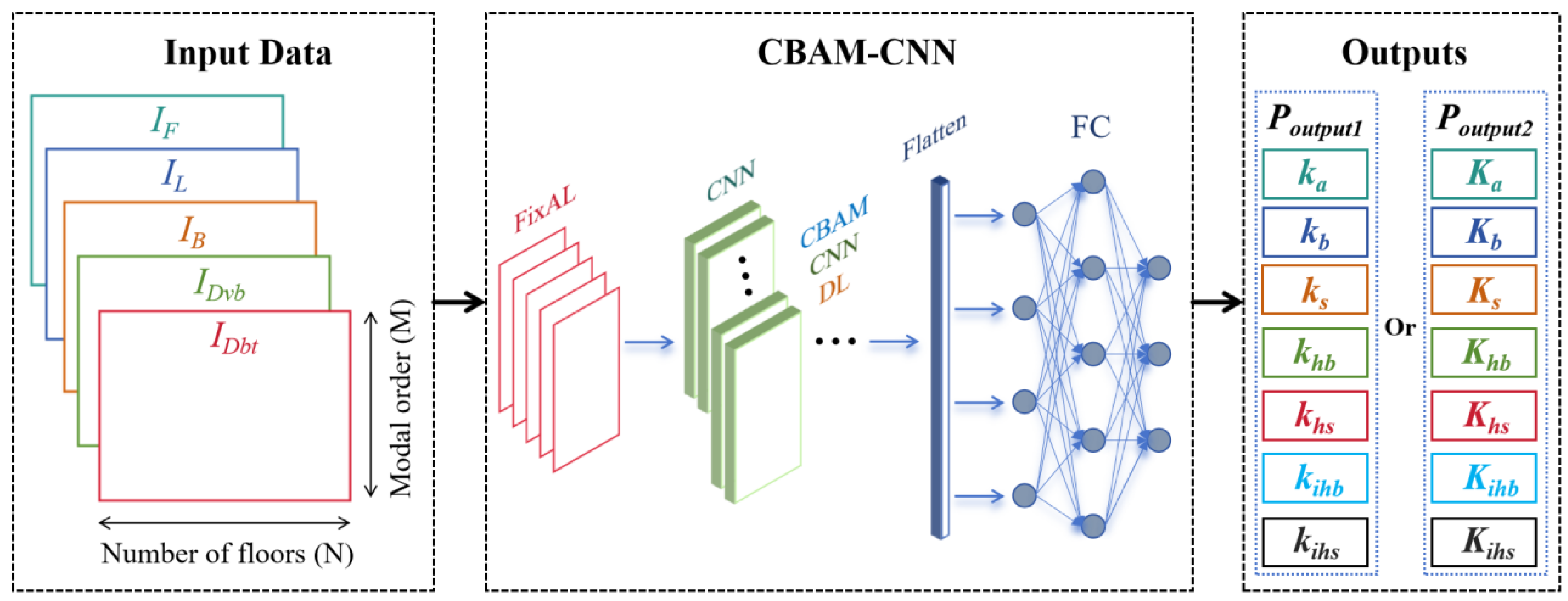
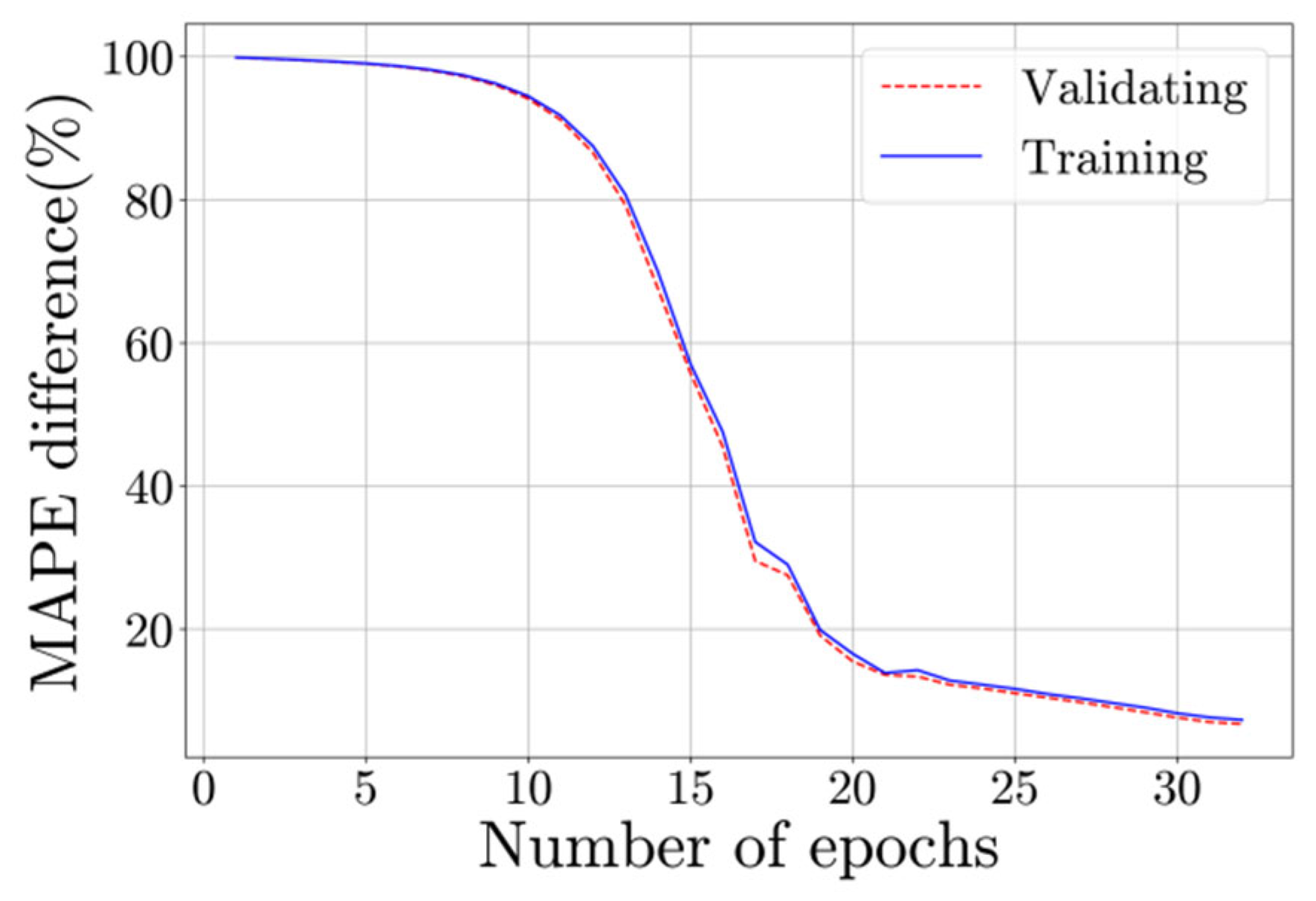
2.3. Parameter Identification with CNN
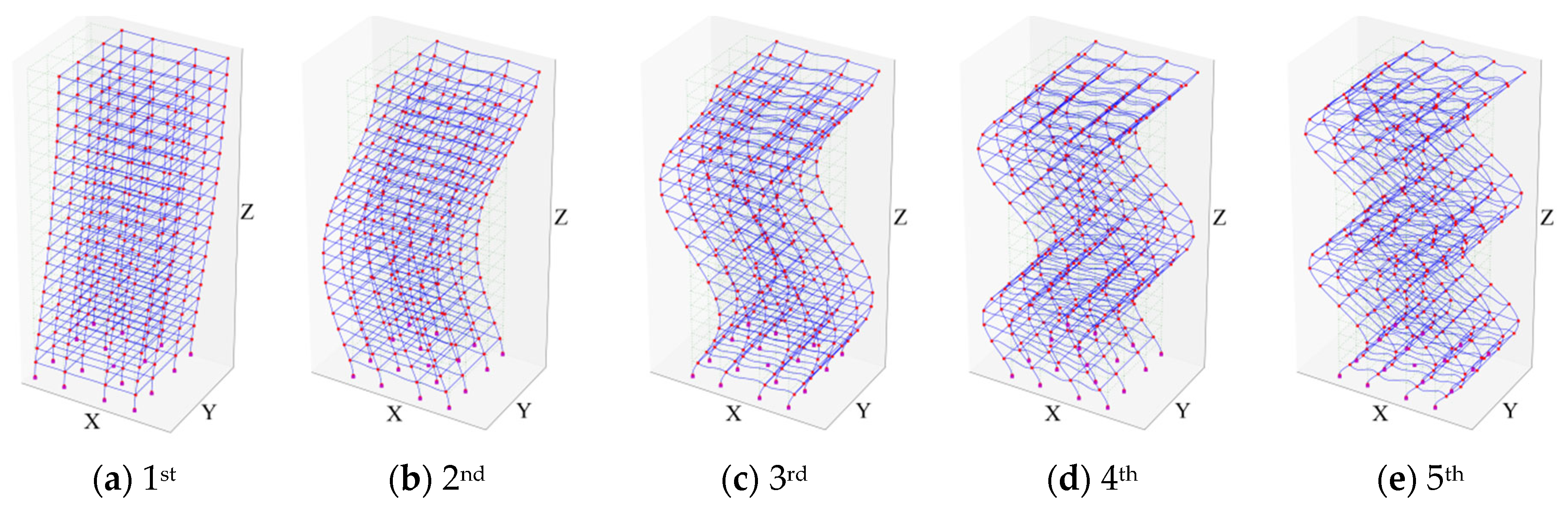
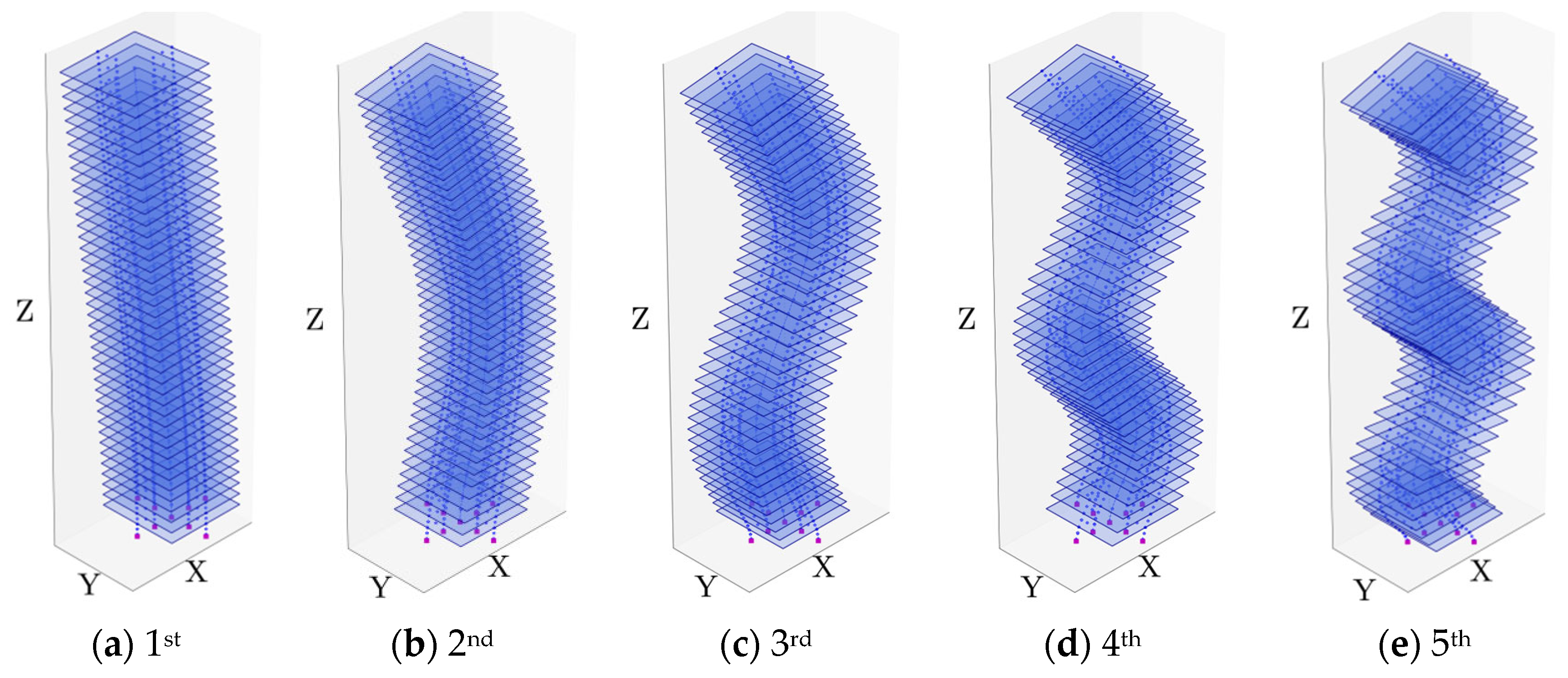
3. Application in Frame and Frame-Tube Core Structures
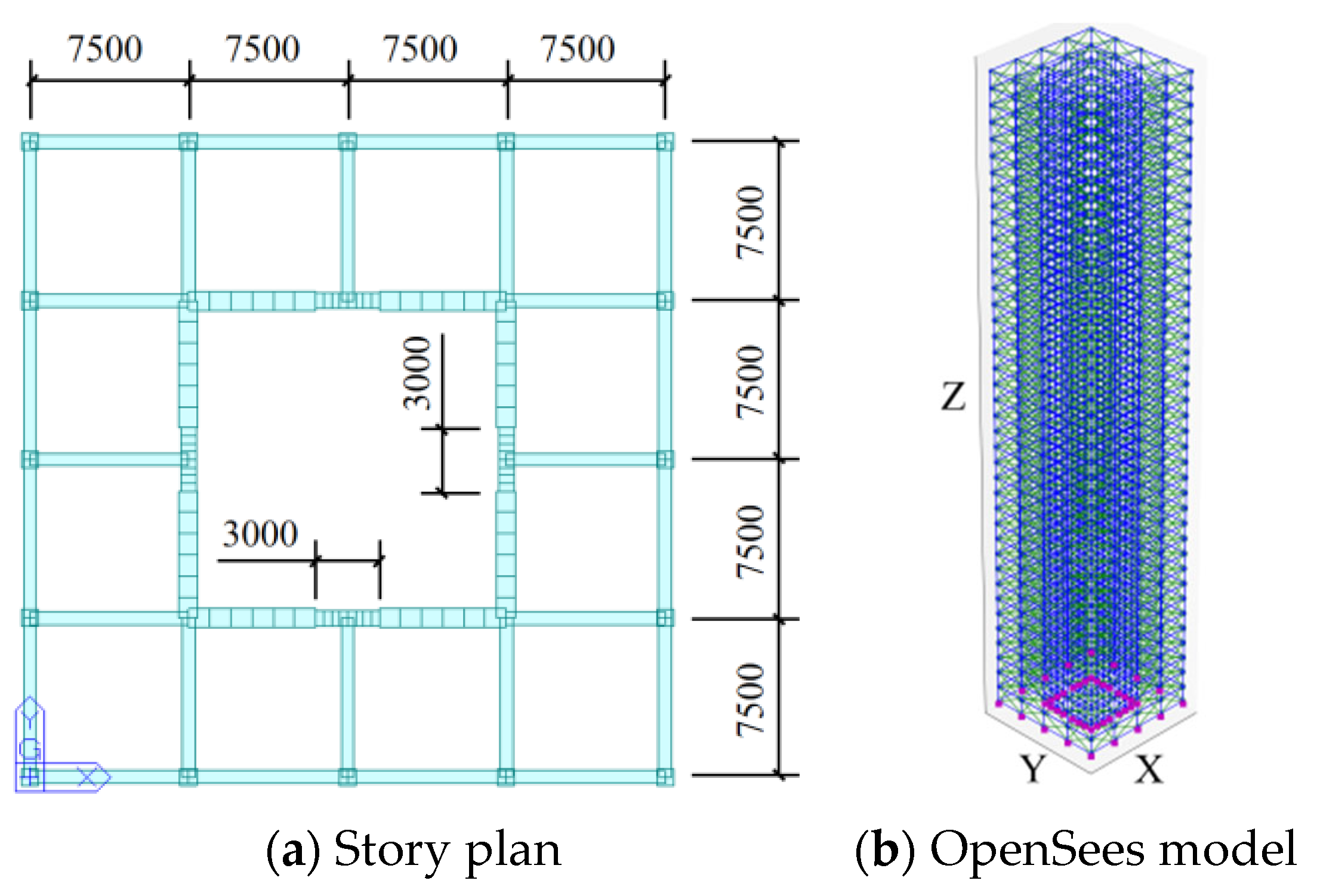
3.1. Frame Structures and Conventional Macro-Scale Model
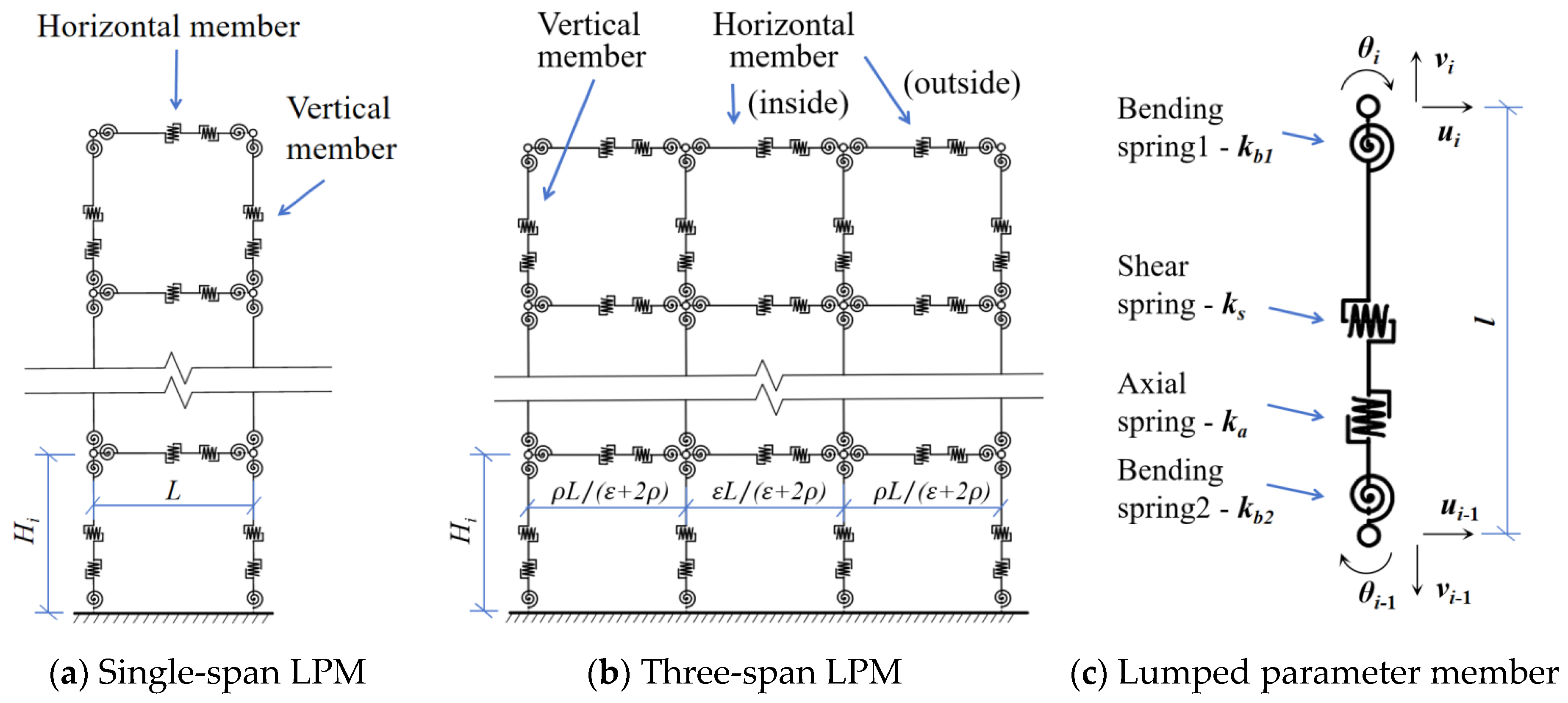
3.2. Single-Span LPM for Frame Structure
3.3. Three-Span LPM for Frame-Core Tube Structure
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Stiffness Parameters | Initial Values | Recognized Values | ||
|---|---|---|---|---|
| LPM-1 (Step-1) | LPM-2 | LPM-1 (Step-1) | LPM-2 | |
| (N/m) | 1.20 × 1012 | 7.00 × 107 | 1.42 × 1012 | 6.96 × 107 |
| (Nm/rad) | 3.50 × 109 | 1.50 × 1014 | 3.57 × 109 | 1.45 × 1014 |
| (N/m) | 7.50 × 108 | 1.00 × 1012 | 5.74 × 108 | 9.92 × 1011 |
| (Nm/rad) | 2.00 × 1011 | 8.00 × 1013 | 2.10 × 1011 | 7.98 × 1013 |
| (N/m) | 3.00 × 109 | 1.00 × 1014 | 8.18 × 109 | 9.99 × 1013 |
| (Nm/rad) | - | 4.00 × 1013 | - | 3.95 × 1010 |
| (N/m) | - | 1.00 × 1014 | - | 1.00 × 1013 |
| Parameters | LPM-1 (Step 1) | LPM-1 (Step 2) | LPM-2 |
|---|---|---|---|
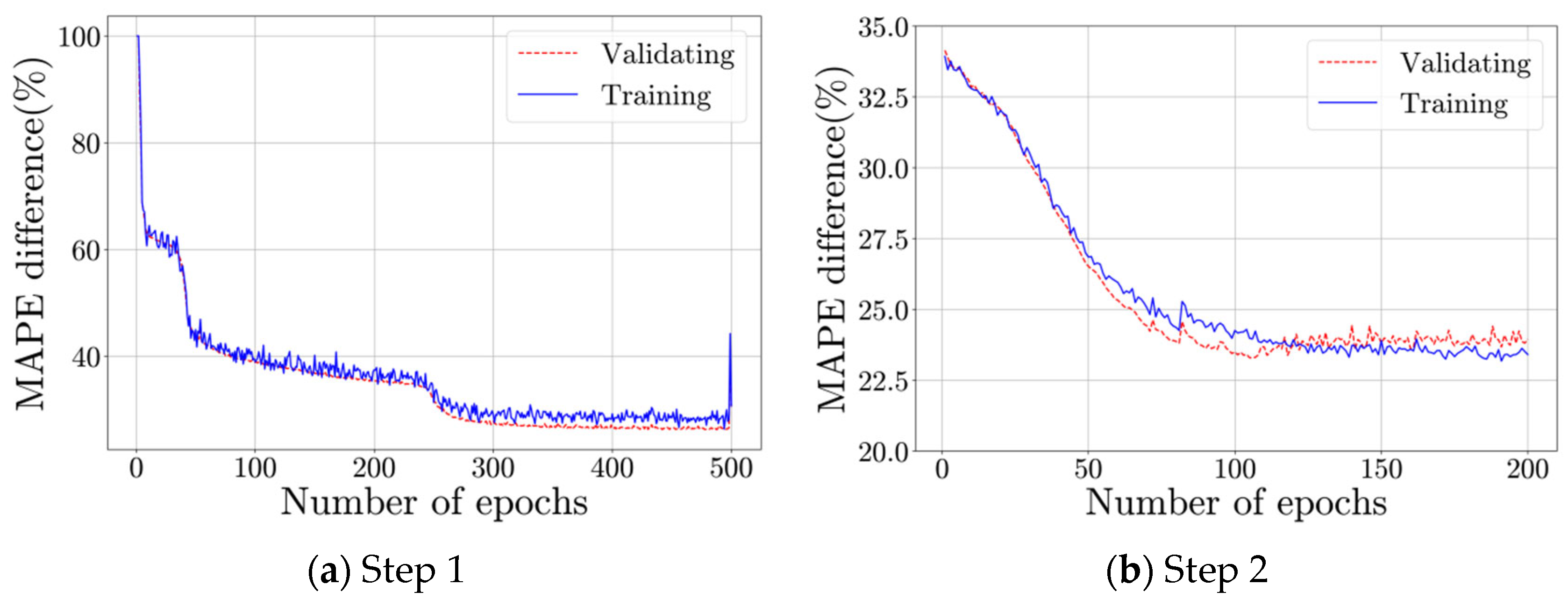
| Number of epochs | 500 | 200 | 32 |
| Batch size | 256 | 256 | 2048 |
| Learning rate | 0.02 | 0.1 | 0.0001 |
| Kernel size of Conv3d | 3 × 3 × 3 | 3 × 3 × 3 | 3 × 3 × 3 |
| Weight decay (L2 regularization) | 1.0 × 10−8 | 1.0 × 10−10 | 1.0 × 10−3 |
| Dropout rate | 0.3 | 0.1 | 0.2 |
| Layer | Type | Output Size | ||
|---|---|---|---|---|
| LPM-1(Step 1) | LPM-1(Step 2) | LPM-2 | ||
| Input | Modal data | bs 1 × 1 × 5 × 5 × 20 | bs × 1 × 5 × 5 × 40 | |
| FixAL 2 | Weight matrix-1 | bs × 1 × 5 × 5 × 20 | bs × 1 × 5 × 5 × 40 | |
| Weight matrix-2 | bs × 1 × 5 × 5 × 20 | bs × 1 × 5 × 5 × 40 | ||
| CNN 3 | Conv3d | bs × 32 × 5 × 5 × 20 | bs × 16 × 5 × 5 × 40 | |
| ReLU | - | - | ||
| Max pooling | bs × 32 × 2 × 2 × 10 | bs × 16 × 2 × 2 × 20 | ||
| CBAM 4 | Channel attention | bs × 32 × 2 × 2 × 10 | - | |
| Spatial attention | bs × 32 × 2 × 2 × 10 | |||
| CNN | Conv3d | bs × 64 × 2 × 2 × 10 | bs × 32 × 2 × 2 × 20 | |
| ReLU | - | - | ||
| Max pooling | bs × 64 × 1 × 1 × 5 | bs × 32 × 2 × 2 × 10 | ||
| CNN | Conv3d | - | bs × 64 × 2 × 2 × 10 | |
| ReLU | - | |||
| Max pooling | bs × 64 × 1 × 1 × 5 | |||
| CBAM | Channel attention | - | bs × 64 × 1 × 1 × 5 | |
| Spatial attention | bs × 64 × 1 × 1 × 5 | |||
| DL 5 | - | - | - | |
| FC 6 | Flatten | bs × 320 | bs × 320 | bs × 320 |
| FC cells | bs × 64 | bs × 256 | bs × 1000 | |
| ReLU | - | - | - | |
| FC cells | bs × 16 | bs × 128 | bs × 640 | |
| ReLU | - | - | - | |
| FC cells | bs × 5 | bs × 100 | bs × 256 | |
| Output | Stiffness parameters | bs × 5 | bs × 100 | bs × 7 |
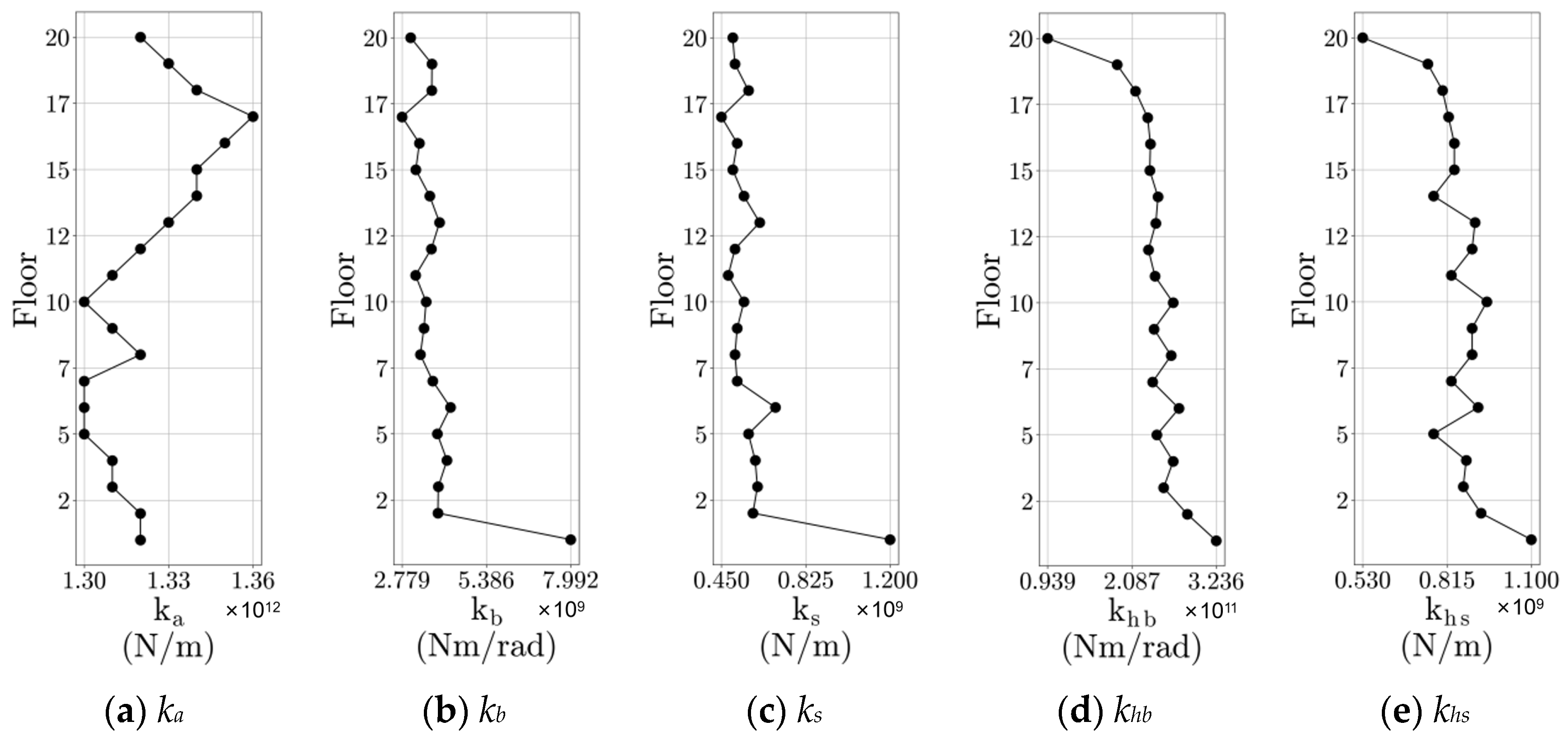
References
- Zhou, K.; Li, Q.S.; Li, X. Dynamic behavior of supertall building with active control system during Super Typhoon Mangkhut. J. Struct. Eng. 2020, 146, 04020077. [Google Scholar] [CrossRef]
- Naeim, F.; Lew, M.; Carpenter, L.D.; Youssef, N.F.; Rojas, F.; Saragoni, G.R.; Adaros, M.S. Performance of tall buildings in Santiago, Chile during the 27 February 2010 offshore Maule, Chile earthquake. Struct. Des. Tall. Build. 2011, 20, 1–16. [Google Scholar] [CrossRef]
- Yu, S.; Guo, T.; Wang, Y.; Han, X.; Du, Z.; Wang, J. Visualization of regional seismic response based on oblique photography and point cloud data. Structures 2023, 56, 104916. [Google Scholar] [CrossRef]
- Xu, Z.; Chen, J.; Shen, J.; Xiang, M. Regional-scale nonlinear structural seismic response prediction by neural network. Eng. Fail. Anal. 2023, 154, 107707. [Google Scholar] [CrossRef]
- Lam, H.F.; Hu, J.; Yang, J.H. Bayesian operational modal analysis and Markov chain Monte Carlo-based model updating of a factory building. Eng. Struct. 2017, 132, 314–336. [Google Scholar] [CrossRef]
- Prajapat, K.; Ray-Chaudhuri, S. Prediction error variances in Bayesian model updating employing data sensitivity. J. Eng. Mech. 2016, 142, 04016096. [Google Scholar] [CrossRef]
- Sun, H.; Büyüköztürk, O. Probabilistic updating of building models using incomplete modal data. Mech. Syst. Signal. Process. 2016, 75, 27–40. [Google Scholar] [CrossRef]
- Deng, Y.; Li, Y.; Li, A. Seismic safety assessments of historical timber buildings using updated finite element models: Case study of Yingxian wooden pagoda, China. J. Build. Eng. 2023, 63, 105454. [Google Scholar] [CrossRef]
- Lee, D.G.; Kim, H.S.; Chun, M.H. Efficient seismic analysis of high-rise building structures with the effects of floor slabs. Eng. Struct. 2002, 24, 613–623. [Google Scholar] [CrossRef]
- Minami, Y.; Yoshitomi, S.; Takewaki, I. System identification of super high-rise buildings using limited vibration data during the 2011 Tohoku (Japan) earthquake. Struct. Control Health Monit. 2013, 20, 1317–1338. [Google Scholar] [CrossRef]
- Encina, J.; de la Llera, J.C. A simplified model for the analysis of free plan buildings using a wide-column model. Eng. Struct. 2013, 56, 738–748. [Google Scholar] [CrossRef]
- Pan, Y.; Ventura, C.E.; Xiong, H.; Zhang, F.L. Model updating and seismic response of a super tall building in Shanghai. Comput. Struct. 2020, 239, 106285. [Google Scholar] [CrossRef]
- Shan, J.; Zhuang, C.; Chao, X.; Loong, C.N. Model updating of a shear-wall tall building using various vibration monitoring data: Accuracy and robustness. Struct. Des. Tall. Spec. Build. 2024, 33, e2114. [Google Scholar] [CrossRef]
- Amoussou, C.P.D.; Lei, H.; Alhaddad, W.; Halabi, Y. Simplified modeling and analysis method for skyscrapers with outrigger system. Structures 2021, 33, 1033–1050. [Google Scholar] [CrossRef]
- Li, X.; Kurata, M. Probabilistic updating of fishbone model for assessing seismic damage to beam–column connections in steel moment-resisting frames. Comput.-Aided Civ. Infrastruct. Eng. 2019, 34, 790–805. [Google Scholar] [CrossRef]
- Qu, Z.; Gong, T.; Li, Q.; Wang, T. Evaluation of the fishbone model in simulating the seismic response of multistory reinforced concrete moment-resisting frames. Earthq. Eng. Eng. Vib. 2019, 18, 315–330. [Google Scholar] [CrossRef]
- Tang, Y.; Cai, C.; Xie, Y. Improved lumped parameter model for shear wall–frame structures with geometric and material nonlinearities. J. Build. Eng. 2024, 91, 109633. [Google Scholar] [CrossRef]
- Ji, X.; Fenves, G.L.; Kajiwara, K.; Nakashima, M. Seismic damage detection of a full-scale shaking table test structure. J. Struct. Eng. 2011, 137, 14–21. [Google Scholar] [CrossRef]
- Shan, J.; Zhuang, C.; Loong, C.N. Parametric identification of Timoshenko-beam model for shear-wall structures using monitoring data. Mech. Syst. Signal. Process. 2023, 189, 110100. [Google Scholar] [CrossRef]
- Zapico, J.L.; González, M.P. Numerical simulation of a method for seismic damage identification in buildings. Eng. Struct. 2006, 28, 255–263. [Google Scholar] [CrossRef]
- González, M.P.; Zapico, J.L. Seismic damage identification in buildings using neural networks and modal data. Comput. Struct. 2008, 86, 416–426. [Google Scholar] [CrossRef]
- Li, Z.; Liu, F.; Yang, W.; Peng, S.; Zhou, J. A survey of convolutional neural networks: Analysis, applications, and prospects. IEEE. Trans. Neural. Netw. 2021, 33, 6999–7019. [Google Scholar] [CrossRef]
- Yao, G.; Lei, T.; Zhong, J. A review of convolutional-neural-network-based action recognition. Pattern. Recognit. Lett. 2019, 118, 14–22. [Google Scholar] [CrossRef]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. Cbam: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. Available online: https://link.springer.com/conference/eccv (accessed on 5 October 2024).
- Zhang, L.; Cosmo, L.; Minello, G.; Torsello, A.; Rossi, L. GraFix: A graph transformer with fixed attention based on the wl kernel. In Lecture Notes in Computer Science, Proceedings of the International Conference on Pattern Recognition, Kolkata, India, 1–5 December 2024; Springer Nature: Cham, Switzerland, 2024; Volume 15304, pp. 435–450. [Google Scholar] [CrossRef]
- McKenna, F.; Scott, M.H.; Fenves, G.L. Nonlinear finite-element analysis software architecture using object composition. J. Comput. Civ. Eng. 2010, 24, 95–107. [Google Scholar] [CrossRef]
- Chen, W.H.; Lu, Z.R.; Lin, W.; Chen, S.H.; Ni, Y.Q.; Xia, Y.; Liao, W.Y. Theoretical and experimental modal analysis of the Guangzhou New TV Tower. Eng. Struct. 2011, 33, 3628–3646. [Google Scholar] [CrossRef]



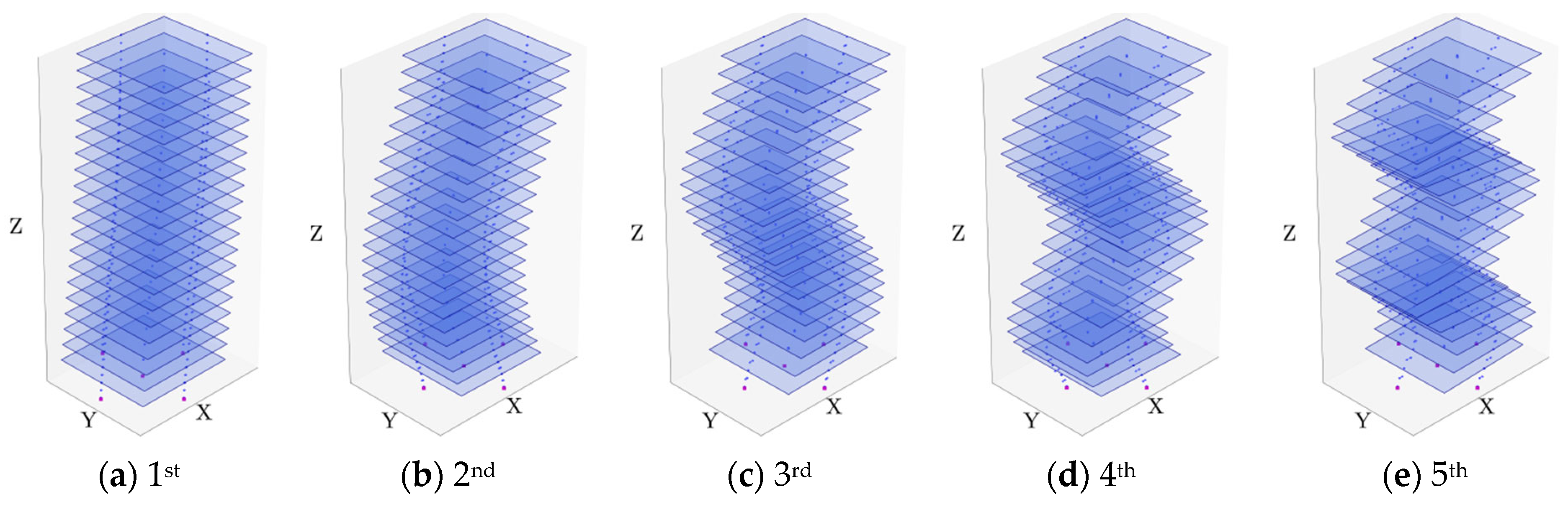

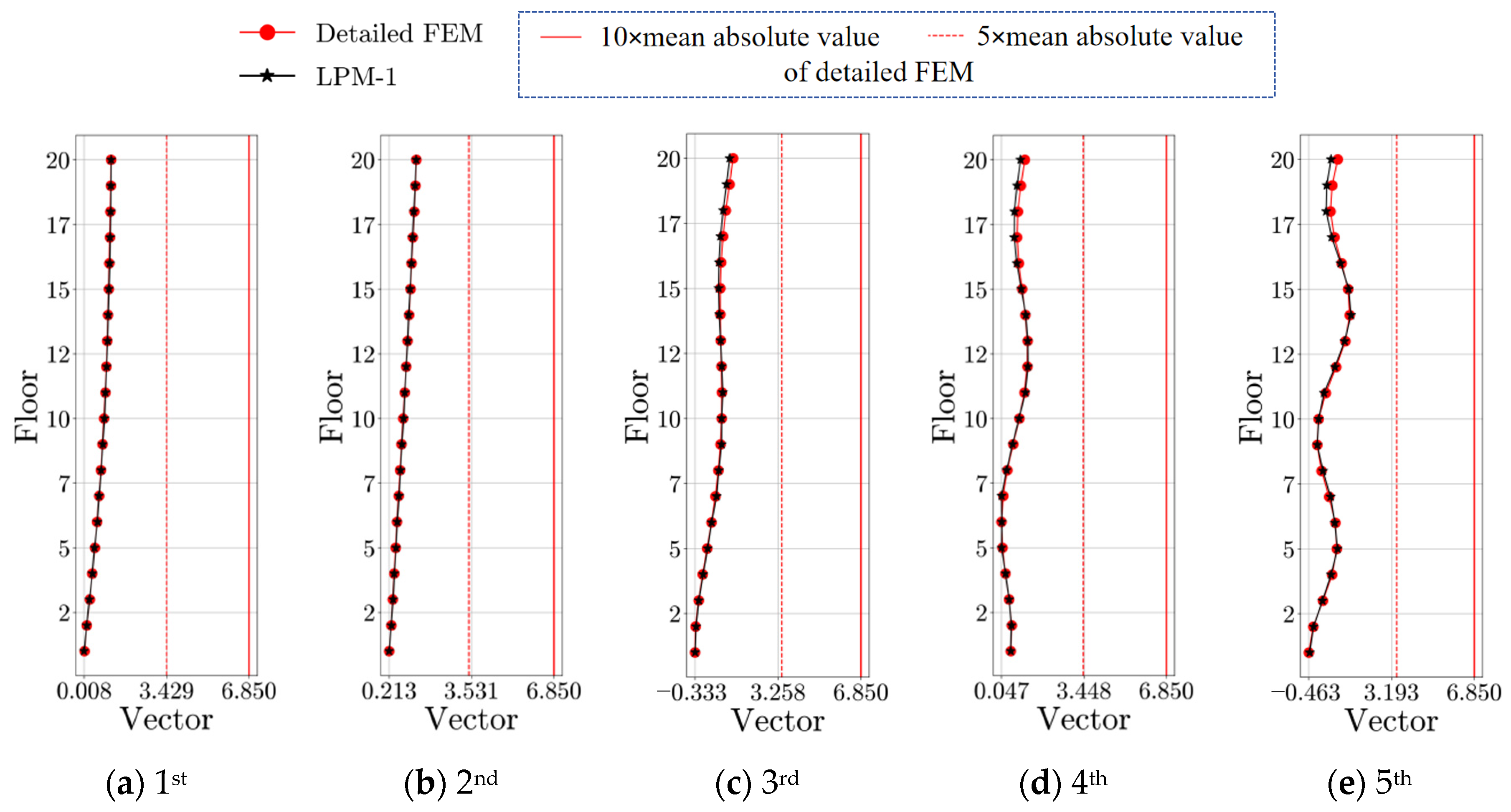
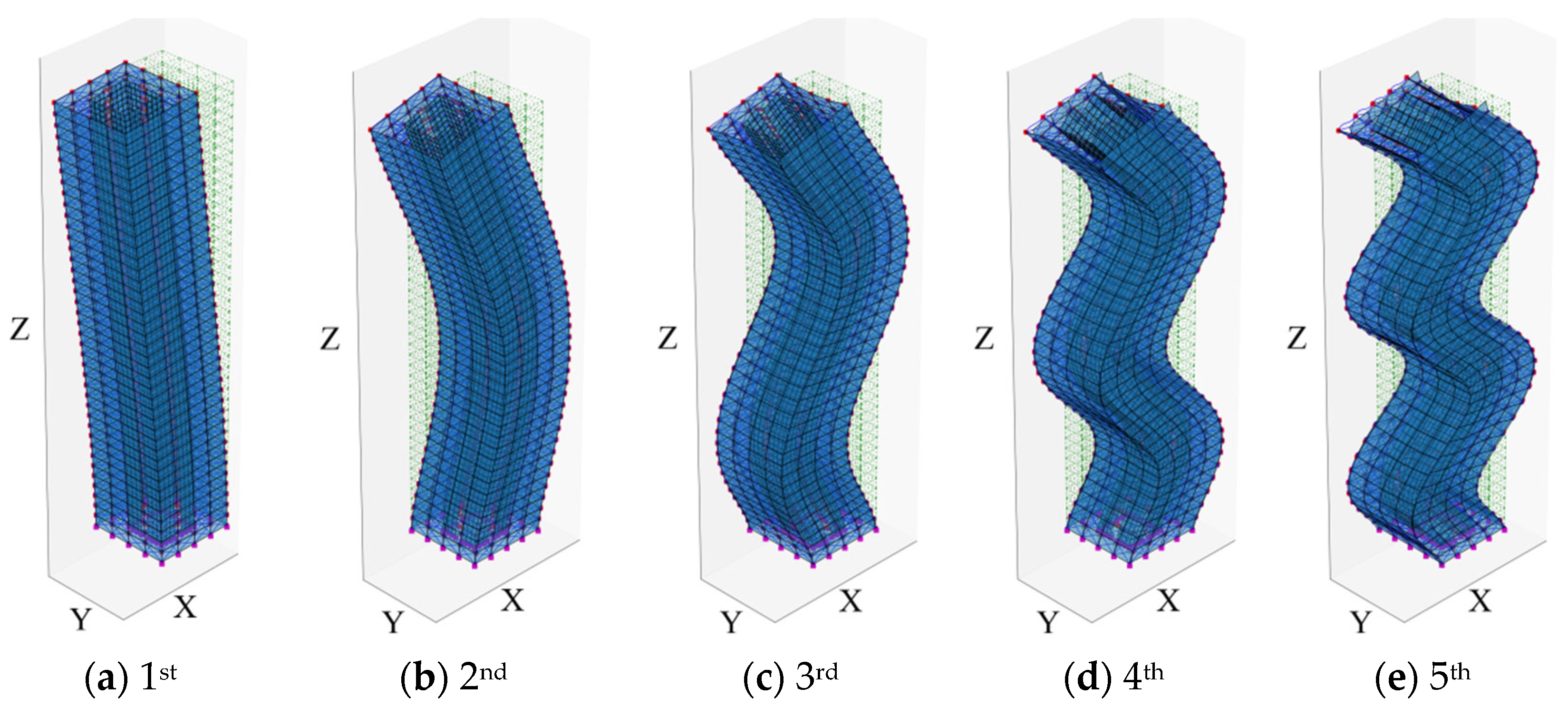
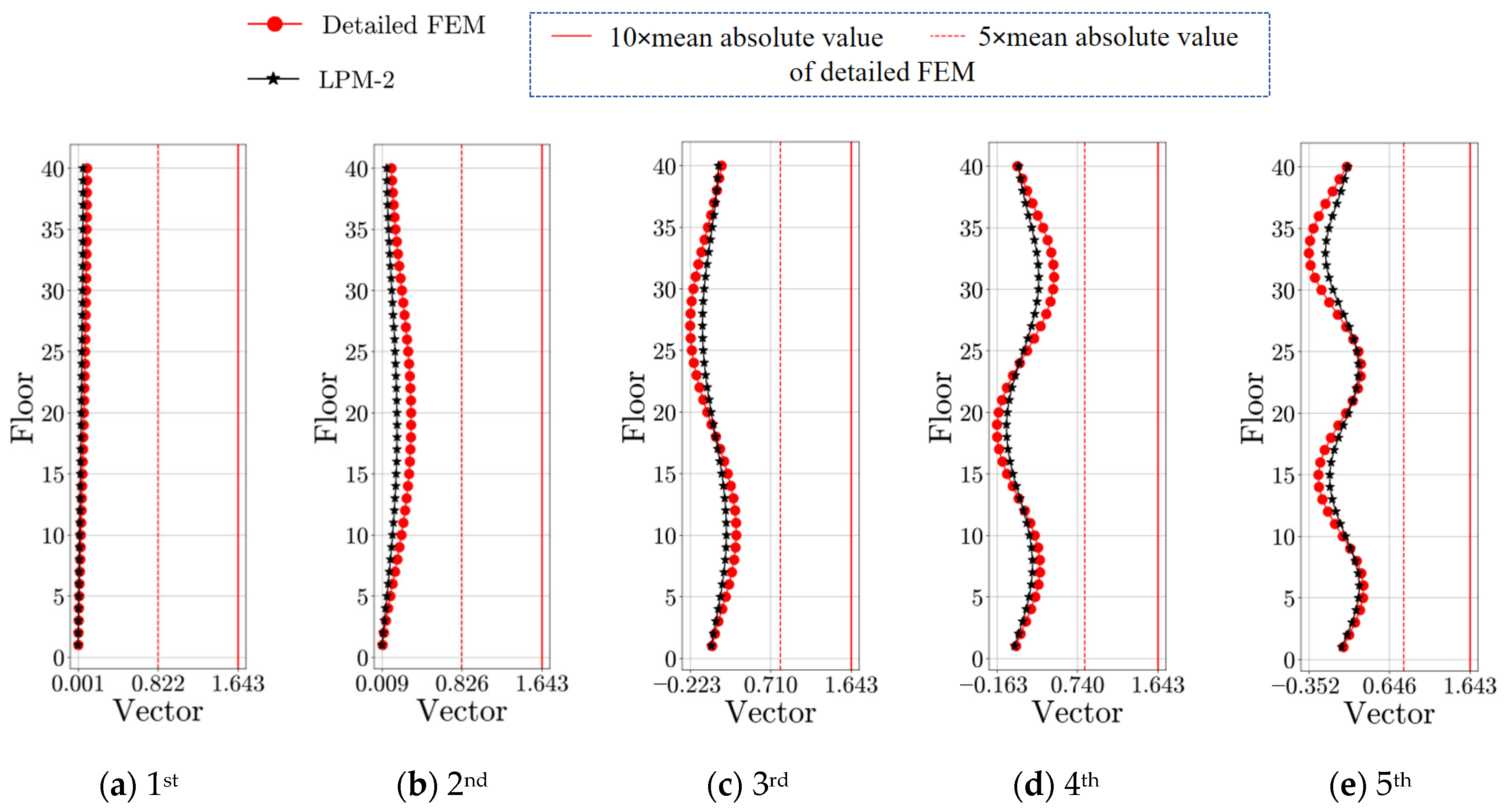
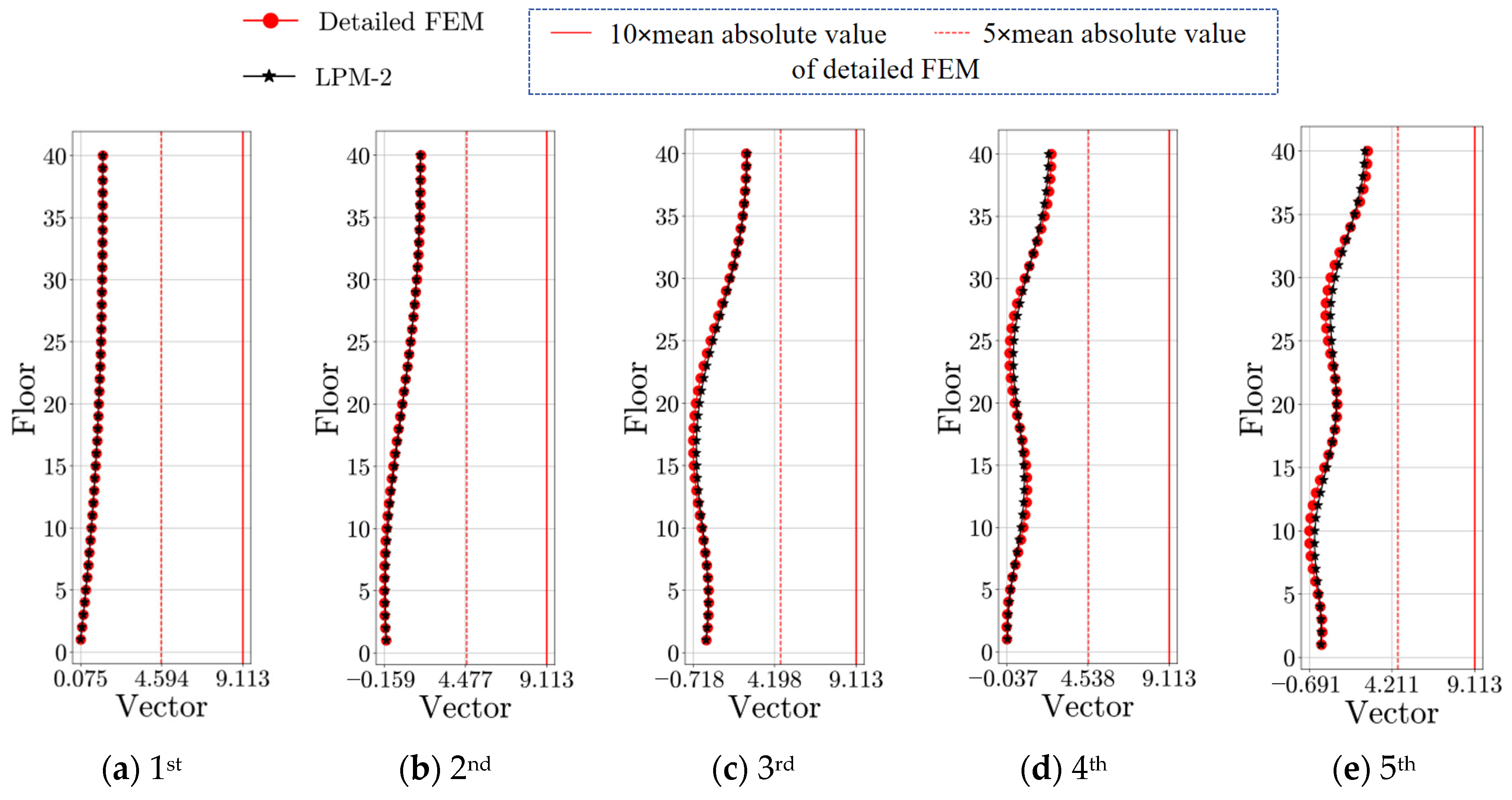
| Modal Order | Detailed FEM | SM | BM | |||||
|---|---|---|---|---|---|---|---|---|
| Freq. 1 (Hz) | Freq. (Hz) | Δf 2 (%) | Lateral MAC (%) | Freq. (Hz) | Δf (%) | Lateral MAC (%) | Angular MAC (%) | |
| 1 | 0.30 | 0.30 | −0.23 | 0.9999 | 0.30 | 0.13 | 0.9998 | 0.8314 |
| 2 | 0.92 | 0.88 | −4.55 | 0.9994 | 0.90 | −1.64 | 0.9974 | 0.7233 |
| 3 | 1.62 | 1.45 | −10.45 | 0.9982 | 1.59 | −2.26 | 0.9923 | 0.5006 |
| 4 | 2.35 | 2.02 | −14.04 | 0.9954 | 2.22 | −5.73 | 0.9844 | 0.3437 |
| 5 | 3.14 | 2.58 | −18.12 | 0.9918 | 2.84 | −9.64 | 0.9776 | 0.2385 |
| Modal Order | Freq. 1 (Hz) | Δf 2 (%) | Lateral MAC (%) | Angular MAC (%) |
|---|---|---|---|---|
| 1 | 0.30 | 0.94 | 0.9997 | 0.9963 |
| 2 | 0.90 | −1.77 | 0.9995 | 0.9995 |
| 3 | 1.47 | −10.01 | 0.9992 | 0.9986 |
| 4 | 2.09 | −12.29 | 0.9984 | 0.9979 |
| 5 | 2.67 | −17.82 | 0.954 | 0.9879 |
| Modal Order | Detailed FEM Freq. 1 (Hz) | LPM-2 Freq. 1 (Hz) | Δf 2 (%) | Lateral MAC (%) | Angular MAC (%) |
|---|---|---|---|---|---|
| 1 | 0.35 | 0.36 | 1.19 | 0.9999 | 0.9984 |
| 2 | 1.43 | 1.41 | 1.07 | 0.9999 | 0.9984 |
| 3 | 3.00 | 2.94 | 1.58 | 1.0000 | 0.9990 |
| 4 | 4.67 | 4.58 | 1.37 | 0.9998 | 0.9986 |
| 5 | 6.54 | 6.40 | 1.33 | 0.9995 | 0.9984 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, H.; Lu, W.; Zheng, W.; Hu, W.; Teng, J.; Lui, E.M. A Macro-Scale Modeling Approach for Capturing Bending-Shear Coupled Dynamic Behavior in High-Rise Structures Using Deep Learning. Buildings 2025, 15, 3727. https://doi.org/10.3390/buildings15203727
Shao H, Lu W, Zheng W, Hu W, Teng J, Lui EM. A Macro-Scale Modeling Approach for Capturing Bending-Shear Coupled Dynamic Behavior in High-Rise Structures Using Deep Learning. Buildings. 2025; 15(20):3727. https://doi.org/10.3390/buildings15203727
Chicago/Turabian StyleShao, Hetian, Wei Lu, Wenchang Zheng, Weihua Hu, Jun Teng, and Eric M. Lui. 2025. "A Macro-Scale Modeling Approach for Capturing Bending-Shear Coupled Dynamic Behavior in High-Rise Structures Using Deep Learning" Buildings 15, no. 20: 3727. https://doi.org/10.3390/buildings15203727
APA StyleShao, H., Lu, W., Zheng, W., Hu, W., Teng, J., & Lui, E. M. (2025). A Macro-Scale Modeling Approach for Capturing Bending-Shear Coupled Dynamic Behavior in High-Rise Structures Using Deep Learning. Buildings, 15(20), 3727. https://doi.org/10.3390/buildings15203727








