Macro–Micro Quantitative Model for Deformation Prediction of Artificial Structural Loess
Abstract
1. Introduction
2. Materials and Methods
2.1. Test Materials
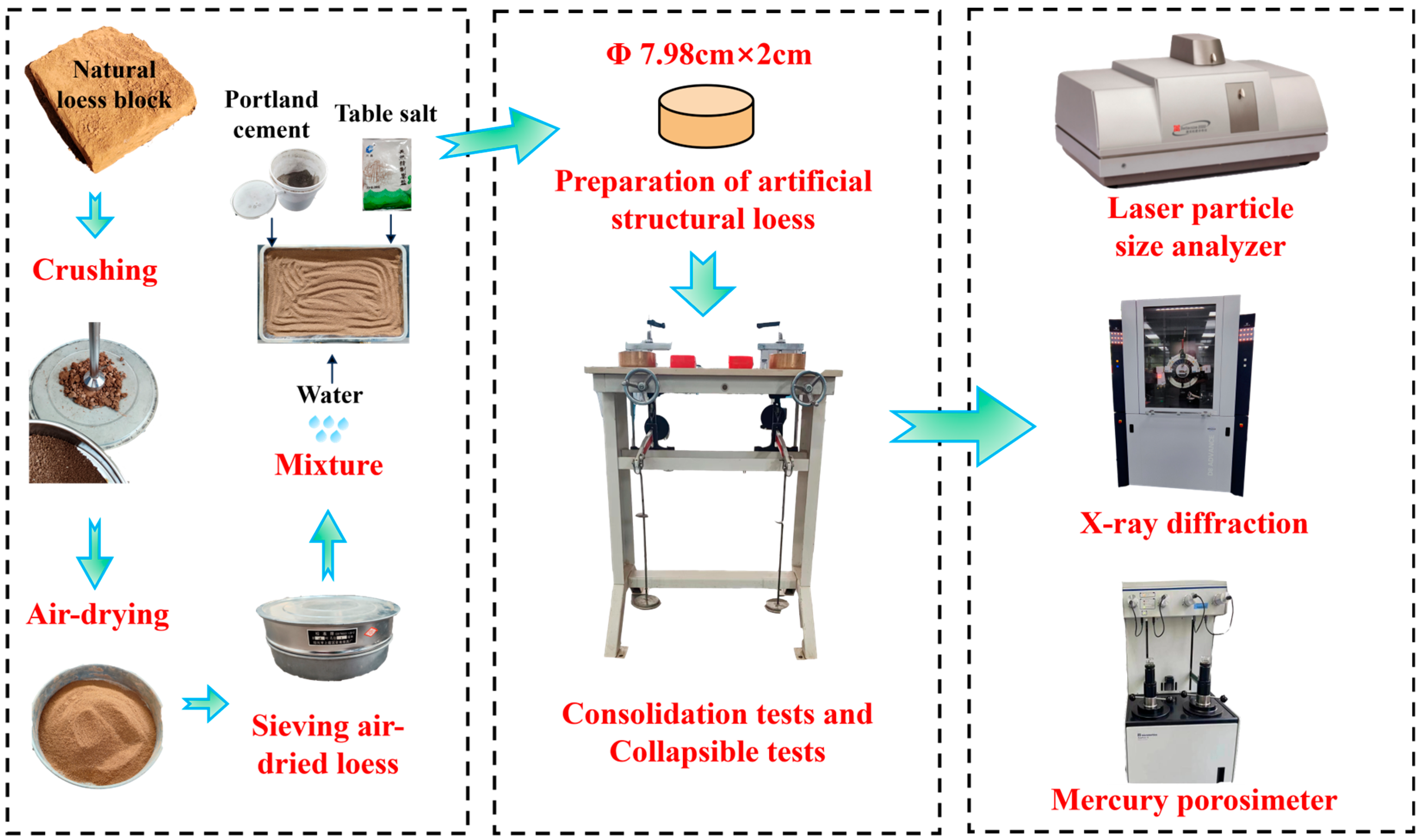
2.2. Sample Preparation
2.3. Test Method
2.3.1. Consolidation, Compression, and Collapsibility Test
2.3.2. Microscopic Test
2.3.3. Construction of Multivariate Nonlinear Models
2.3.4. Model Validation and Generalization Ability Evaluation
3. Results and Analysis
3.1. Mechanical Test Results and Analysis
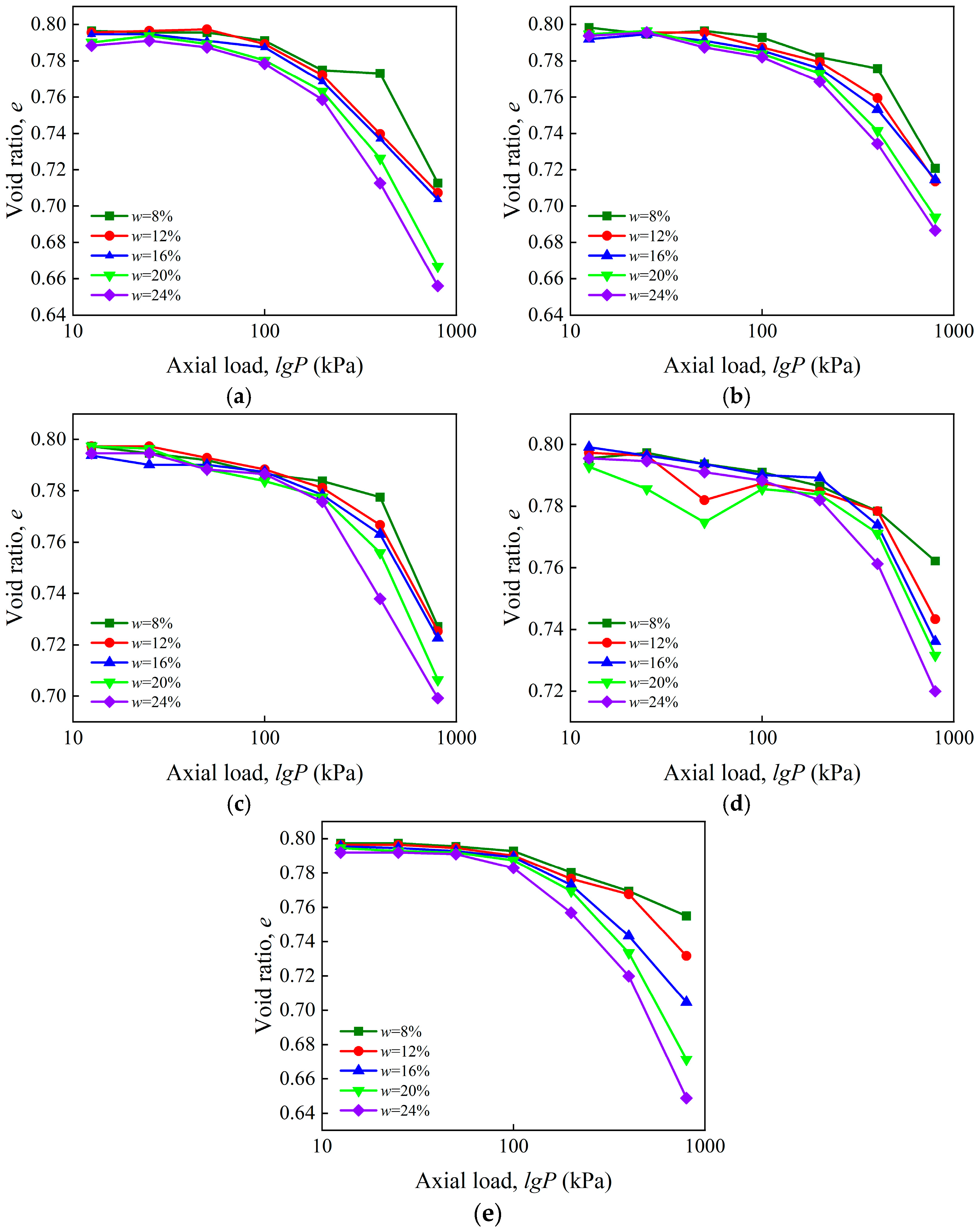
3.1.1. Compression Curve
3.1.2. Compression Coefficient and Compression Modulus
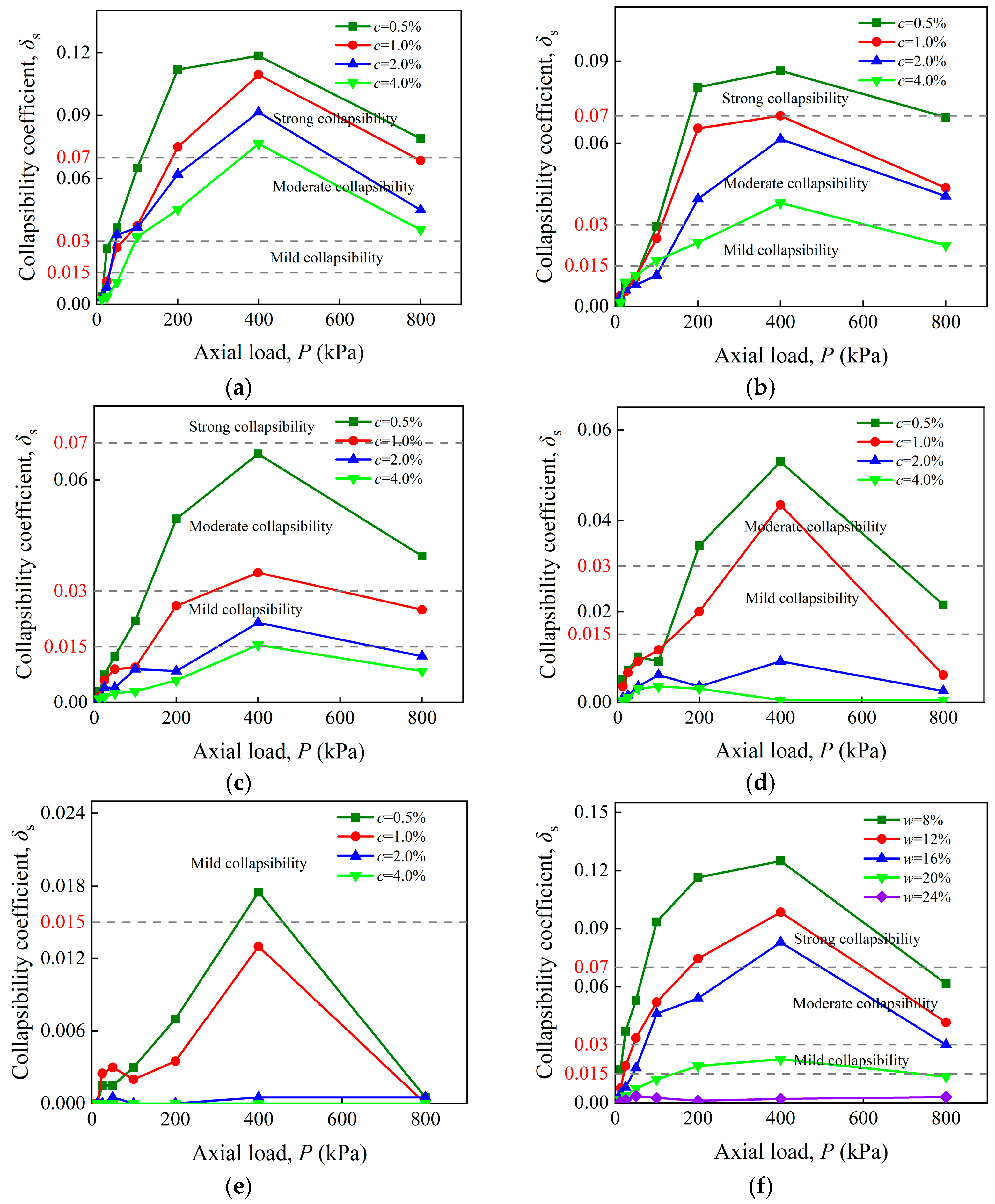
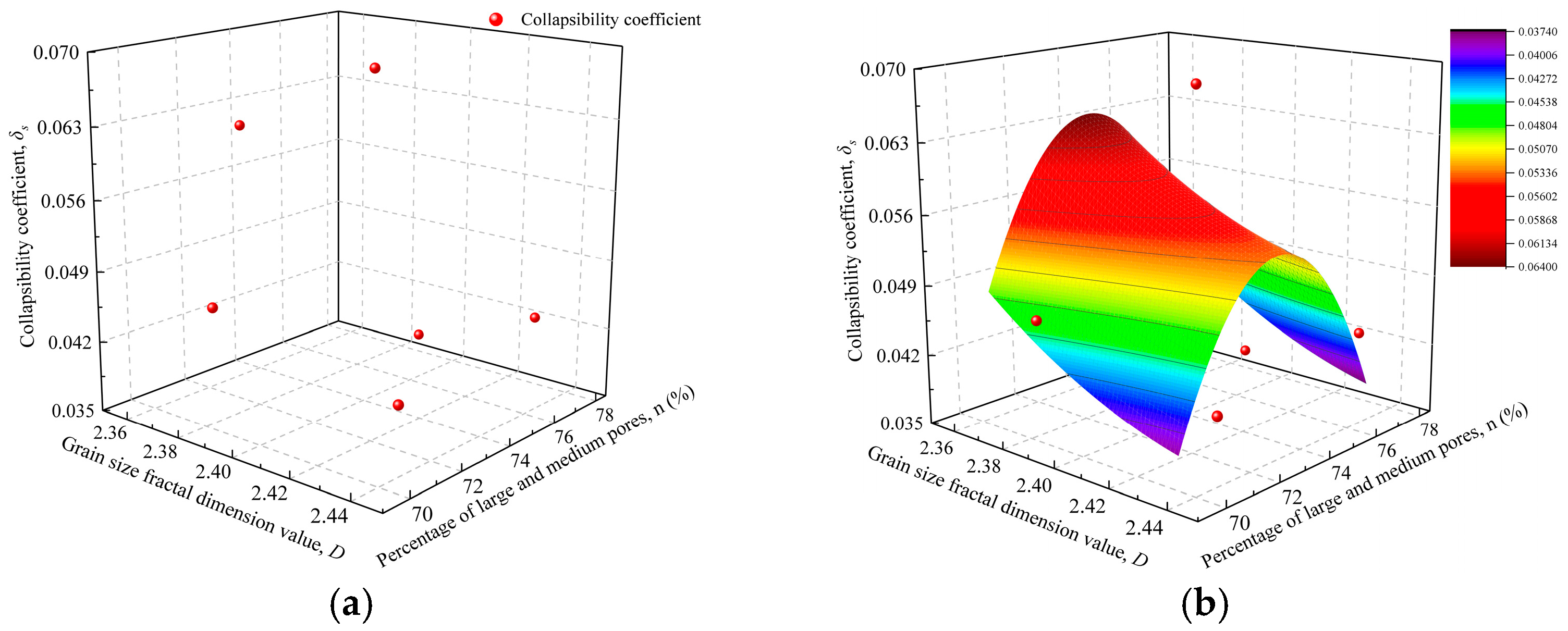
3.1.3. Collapsibility Coefficient
3.2. Microstructure and Material Composition Test Results and Analysis
3.2.1. Particle Analysis Test Results
3.2.2. XRD Test Results
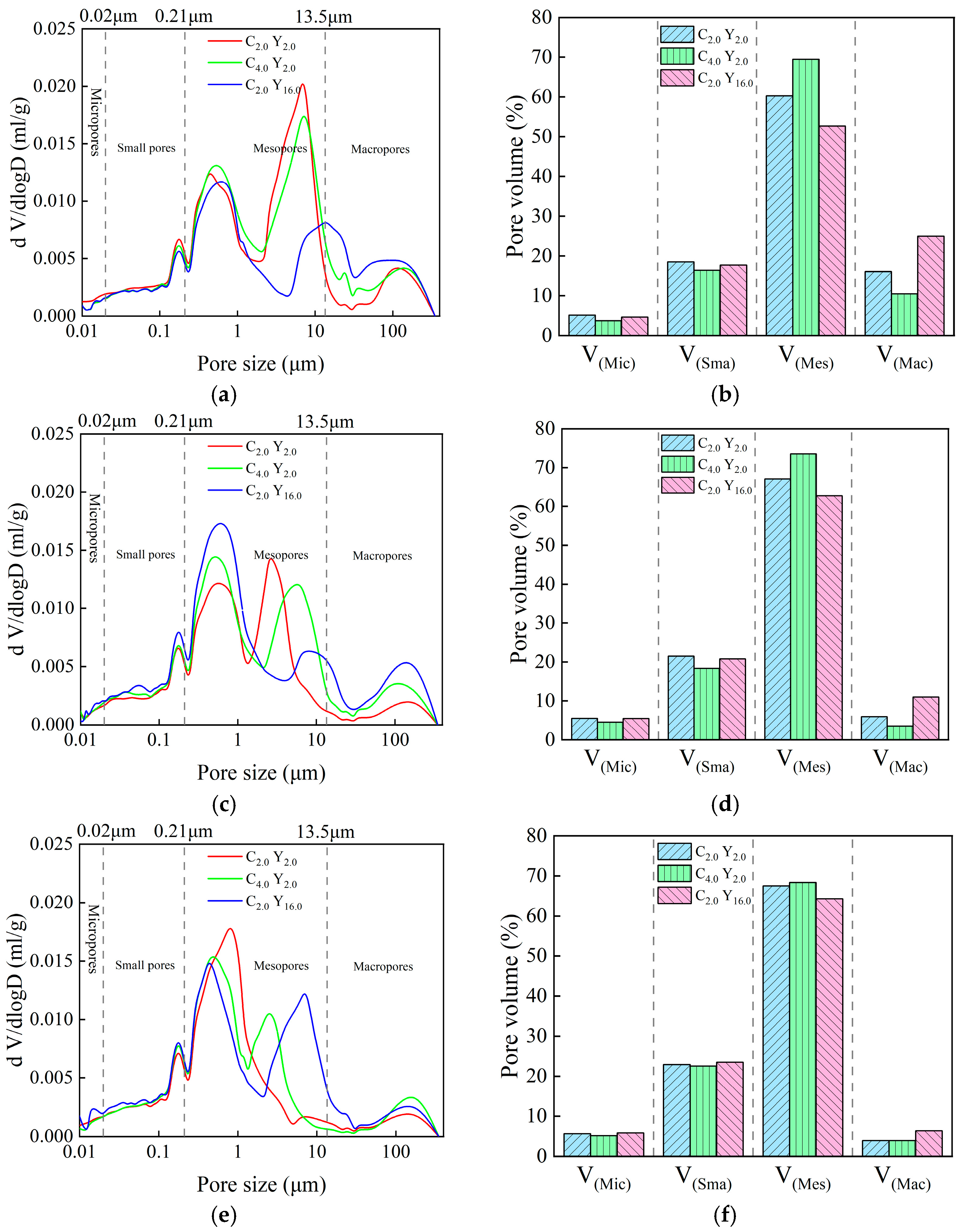
3.2.3. Mercury Intrusion Porosimetry Results
3.3. Correlation Analysis and Calculation Between Macroscopic Deformation Indicators and Microscopic Structural Parameters
3.3.1. Linear Correlation Analysis
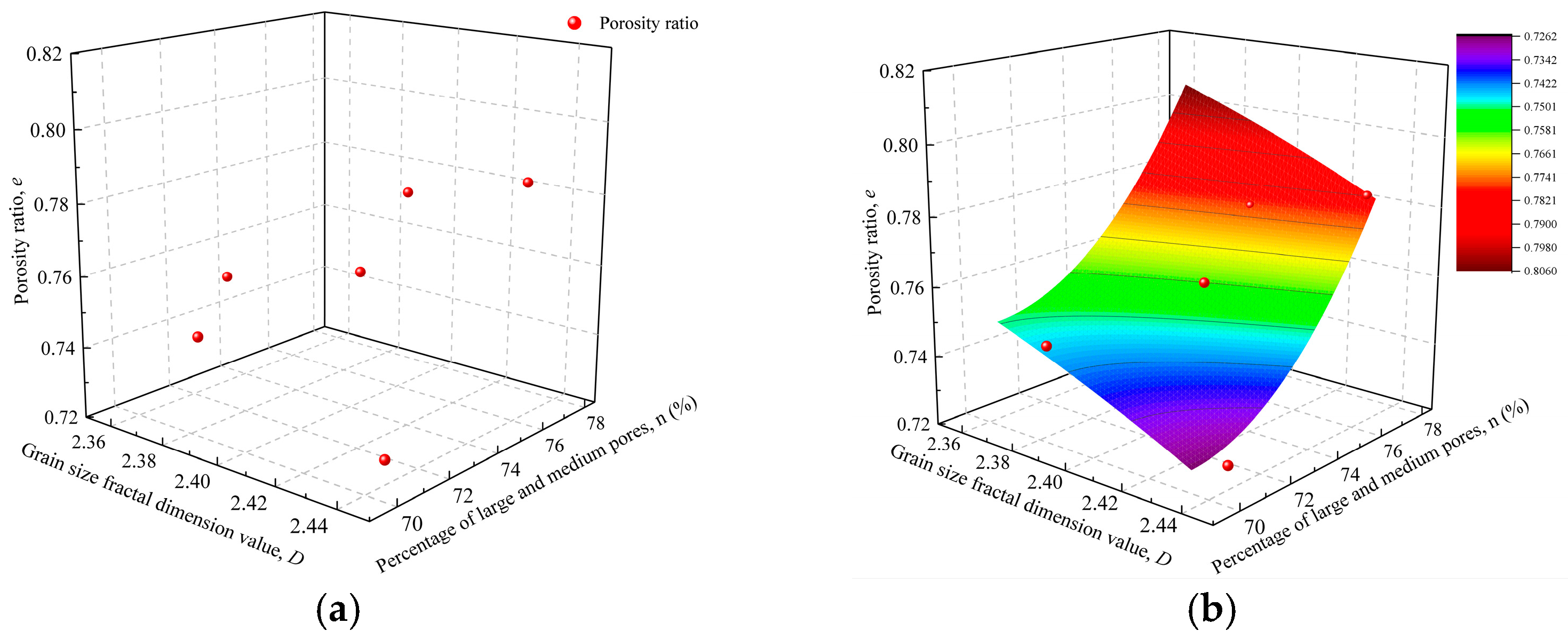
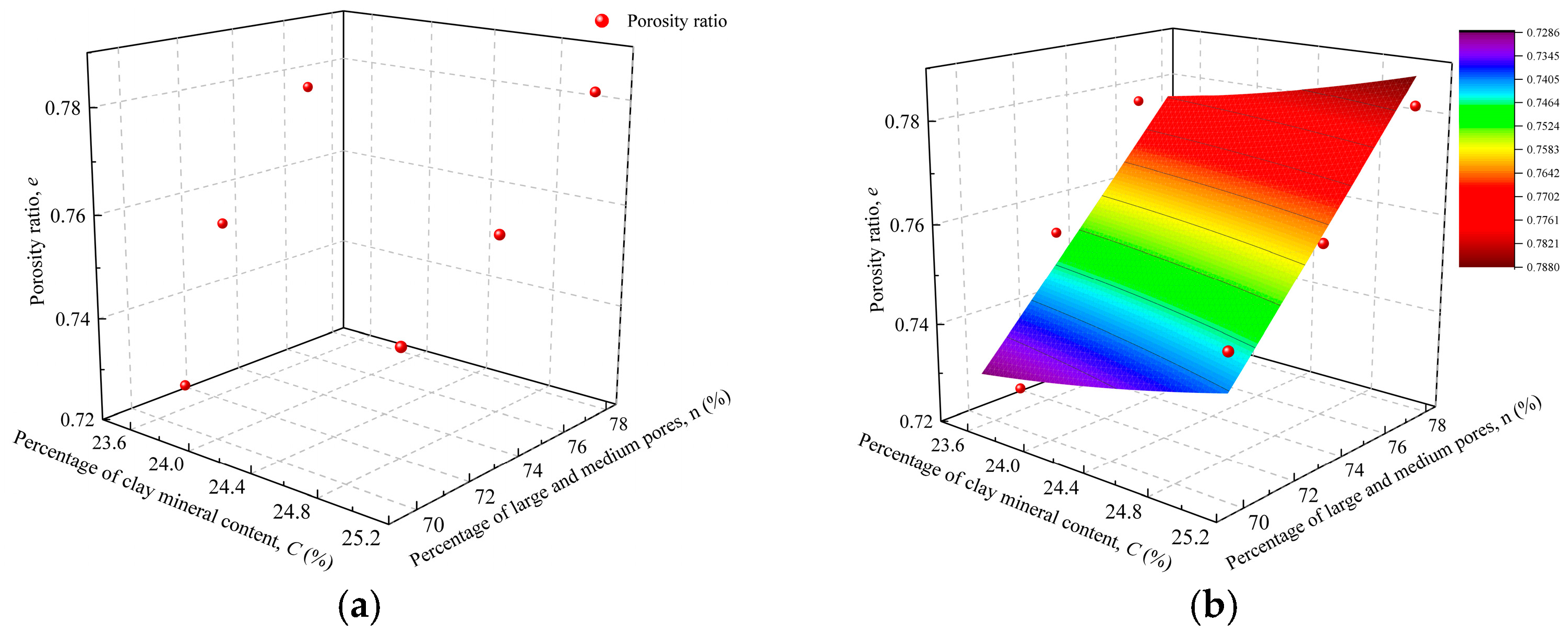
3.3.2. Quantitative Calculation of Loess Deformation Based on Macro–Micro Correlation
3.3.3. Feasibility Verification of the Computational Model
4. Conclusions
- 1.
- The compressibility and collapsibility of artificial structured loess are governed by cement content and moisture conditions. Increased moisture reduces the porosity ratio but elevates compressibility due to the disintegration of cementitious bonds and the redistribution of fine particles. In contrast, higher cement content enhances void ratio and structural strength through improved particle bonding. The transition from point-to-surface contacts among particles, induced by cementation, reduces compressibility during consolidation and suppresses post-immersion collapse. Under high-moisture conditions, pre-filled pores further dimmish the collapse potential by facilitating particle rearrangement during compression.
- 2.
- Microstructural analyses reveal that cementation fundamentally alters the mechanical behavior of loess through multiple mechanisms. Particle size analysis indicates that cement encapsulation enhances interparticle bonding and promotes gradation refinement, leading to the formation of a densified skeletal structure that improves deformation resistance. XRD results demonstrate that hydration generates cementitious materials, increasing clay mineral content to 29.5% and producing secondary calcite that effectively blocks micropores. Concurrent consumption of quartz contributes to particle refinement and reduced skeletal stiffness. MIP data confirm that applied loads cause structural yielding characterized by the collapse of large pores into smaller classes. While cement bonding strengthens the matrix and suppresses large-pore formation, salt crystallization creates weakly bonded medium–large pores susceptible to brittle collapse under pressure.
- 3.
- Pearson correlation analysis shows the esopore volume ratio controls collapsibility (Pearson |r| > 0.96), while increased porosity raises macropore proportion and exacerbates compressibility. Small-pore variations indirectly regulate deformation by altering water migration paths.
- 4.
- A three-dimensional nonlinear model was developed and validated, comprising a porosity ratio model and a collapsibility coefficient model. The model predictions demonstrate good agreement with experimental results, with the porosity ratio model yielding an R2 value of 0.893 and the collapsibility model achieving an R2 value of 0.746. These results indicate that the model can serve as a quantitative analytical tool for engineering deformation assessment and disaster prevention in loess regions.
- 5.
- This study establishes a novel quantitative framework correlating microstructural evolution with macroscopic deformation in artificially structured loess, providing a reliable approach for deformation prediction under controlled cementation and moisture conditions. However, the research is limited to controlled laboratory conditions and static loading, without incorporating environmental cyclic processes such as wetting–drying or freeze–thaw actions. Future work should focus on validating the model under field conditions, extending it to incorporate coupled thermo-hydro-mechanical loading paths, and accounting for temporal changes in microstructure to enhance long-term predictive capability.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yao, C.; Zhang, Q.; Wang, C.; Ren, J.; Li, H.; Wang, H.; Wu, F. Response of sediment transport capacity to soil properties and hydraulic parameters in the typical agricultural regions of the Loess Plateau. Sci. Total Environ. 2023, 879, 163090. [Google Scholar] [CrossRef] [PubMed]
- Crouvi, O.; Sun, J.; Rousseau, D.; Muhs, D.R.; Zárate, M.A.; Marx, S. Loess records. In Encyclopedia of Quaternary Science, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2025; Volume 3, pp. 505–528. [Google Scholar] [CrossRef]
- Wang, L.; Liu, Q.; Li, X.; Qin, B.; Hong, B.; Shi, J. Effect of nanosilica on the hydrological properties of loess and the microscopic mechanism. Sci. Rep. 2024, 14, 3420. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Yan, Z.; Song, Y.; Fitzsimmons, K.E.; Yi, S.; Kang, S.; E, C.; Stevens, T.; Lai, Z.; Dave, A.K.; et al. A comprehensive dataset of luminescence chronologies and environmental proxy indices of loess-paleosol deposits across Asia. npj Clim. Atmos. Sci. 2024, 7, 7. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Aydin, A. Loess structure: Evolution and a scale-based classification. Earth-Sci. Rev. 2023, 249, 104665. [Google Scholar] [CrossRef]
- Schlüter, S.; Sammartino, S.; Koestel, J. Exploring the relationship between soil structure and soil functions via pore-scale imaging. Geoderma 2020, 370, 114370. [Google Scholar] [CrossRef]
- Cui, C.; Liang, Z.; Xu, C.; Xin, Y.; Wang, B. Analytical solution for horizontal vibration of end-bearing single pile in radially heterogeneous saturated soil. Appl. Math. Model. 2022, 116, 65–83. [Google Scholar] [CrossRef]
- Yang, J.; Li, X.; Li, L.; Jing, Z.; Wang, W. Formation mechanism of metastable internal support microstructure in Malan Loess and its implications for collapsibility. Eng. Geol. 2024, 346, 107892. [Google Scholar] [CrossRef]
- Filho, H.C.S.; Venson, G.I.; Centofante, R.; Festugato, L. Discussion of “Analysis and optimization of tensile strength for LOESs stabilized by calcium carbide residue”. J. Mater. Civ. Eng. 2024, 37, 06024004. [Google Scholar] [CrossRef]
- Zhang, J.; Jia, M.; Jiang, T.; Kato, S.; Sun, D.; Gao, Y.; Yang, Z. Dynamic deformation characteristics and microscopic analysis of xanthan gum-treated silty soil during wetting process. J. Rock Mech. Geotech. Eng. 2024, 17, 1149–1162. [Google Scholar] [CrossRef]
- Pei, Q.Q.; Wang, X.D.; Zhao, L.Y.; Zhang, B.; Guo, Q.L. A sticky rice paste preparation method for reinforcing earthen heritage sites. J. Cult. Herit. 2020, 44, 98–109. [Google Scholar] [CrossRef]
- Yang, X.; Hu, Z.; Li, H.; Wang, Y.; Zhang, Y.; She, H.; Wang, X. Effect of freeze-thaw cycles on mechanical properties and microstructure of artificially prepared site soil. Constr. Build. Mater. 2025, 485, 141878. [Google Scholar] [CrossRef]
- Xi, Y.; Sun, M.; Hua, X.; Zhang, Y.; Yuan, Y. Study on the dynamic Deformation Characteristics of artificial Structural Loess. Buildings 2025, 15, 1198. [Google Scholar] [CrossRef]
- Yu, H.; Liu, E. Cyclic properties of artificially cemented Gravel-Silty clay mixed soils. Exp. Tech. 2020, 44, 573–589. [Google Scholar] [CrossRef]
- Yan, X.; Xu, Q.; Deng, M.; Sun, Y.; He, X.; Dong, S.; Ma, L.; Hai, C.; Zhou, Y. Investigation on the solidification effect and mechanism of loess utilizing magnesium oxysulfate cement as a curing agent. Sci. Total Environ. 2024, 951, 175214. [Google Scholar] [CrossRef]
- Guo, S.; Zhang, H.; Bi, Y.; Zhang, J. Mechanical experiment and microstructural characteristics of water glass solidified loess. Bull. Eng. Geol. Environ. 2024, 83, 411. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, E.; Wu, J.; Zhang, S. Mechanical Properties and Constitutive Model for Artificially Structured Soils under Undrained Conditions. Mathematics 2024, 12, 2226. [Google Scholar] [CrossRef]
- Zhang, Y.; Song, Z.; Chen, H.; Ruan, L.; He, S. Experimental study on collapsible and structural characteristics of artificially prepared loess material. Sci. Rep. 2023, 13, 4113. [Google Scholar] [CrossRef]
- Kong, B.; Yan, Y.; He, H.; Yu, J.; Zou, B.; Chen, Q. Strength and fractal characteristics of artificial Frozen–Thawed sandy soft soil. Fractal Fract. 2024, 8, 393. [Google Scholar] [CrossRef]
- Konstantinou, C.; Biscontin, G.; Jiang, N.; Soga, K. Application of microbially induced carbonate precipitation to form bio-cemented artificial sandstone. J. Rock Mech. Geotech. Eng. 2021, 13, 579–592. [Google Scholar] [CrossRef]
- Chen, H.; Li, H.; Jiang, Y.; Yu, Q.; Yao, M.; Shan, W. Feasibility study on artificial preparation of structured loess. Geosci. Lett. 2022, 9, 21. [Google Scholar] [CrossRef]
- Liu, W.; Bai, R.; Sun, X.; Yang, F.; Zhai, W.; Su, X. Rainfall- and Irrigation-Induced Landslide Mechanisms in Loess Slopes: An Experimental Investigation in Lanzhou, China. Atmosphere 2024, 15, 162. [Google Scholar] [CrossRef]
- Bai, R.; Lai, Y.; Zhang, M.; Jiang, H. Investigating the Thermo-Hydro-Mechanical Behavior of Loess Subjected to Freeze–Thaw Cycles. Acta Geotech. 2024, 19, 6305–6318. [Google Scholar] [CrossRef]
- Huang, X.; Horn, R.; Ren, T. Soil structure effects on deformation, pore water pressure, and consequences for air permeability during compaction and subsequent shearing. Geoderma 2021, 406, 115452. [Google Scholar] [CrossRef]
- Yu, Q.; Yan, X.; Wang, Q.; Yang, T.; Kong, Y.; Huang, X.; Mehmood, Q. X-ray computed tomography-based evaluation of the physical properties and compressibility of soil in a reclamation area. Geoderma 2020, 375, 114524. [Google Scholar] [CrossRef]
- Wang, H.; Cui, Y.; Zhang, F.; Liu, J. Effect of grain breakage on the compressibility of soils. Acta Geotech. 2021, 17, 769–778. [Google Scholar] [CrossRef]
- Jia, R.; Lei, H.; Li, K. Compressibility and Microstructure Evolution of Different Reconstituted Clays during 1D Compression. Int. J. Geomech. 2020, 20, 04020181. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, D.; Wang, S.; Liang, C.; Zhao, D. Dynamic-response characteristics and deformation evolution of loess slopes under seismic loads. Eng. Geol. 2020, 267, 105507. [Google Scholar] [CrossRef]
- Yang, J.; Niu, X.; Guo, Q.; Wen, Z.; Cao, H. Strength and deformation characteristics of compacted loess with different water content and compaction energy. Results Eng. 2023, 20, 101637. [Google Scholar] [CrossRef]
- Cai, G.; Han, B.; Wei, J.; Yang, R.; Li, J.; Cui, Y. Wetting-induced deformation characteristics of unsaturated compacted sandy loess. Acta Geotech. 2023, 19, 177–195. [Google Scholar] [CrossRef]
- Xie, D.Y.; Qi, J.L.; Zhang, Z.Z. A constitutive law considering soil structural properties. China Civ. Eng. J. 2000, 33, 35–41. [Google Scholar] [CrossRef]
- Li, X.; Sun, J.; Ren, H.; Lu, T.; Ren, Y.; Pang, T. The effect of particle size distribution and shape on the microscopic behaviour of loess via the DEM. Environ. Earth Sci. 2022, 81, 294. [Google Scholar] [CrossRef]
- Luo, F.; Zhang, G.; Yao, Y. Macro-micro tests of cohesive soil under varied normal and shear stresses subjected to drying-wetting cycles. J. Rock Mech. Geotech. Eng. 2024, 17, 5893–5905. [Google Scholar] [CrossRef]
- GB/T 50123-2019; Standard for Geotechnical Testing Method. Construction Ministry of PRC: Beijing, China, 2019.
- Li, Y.; Liu, E.; He, M. Mechanical properties of artificially structured soil and Binary-medium-based constitutive model under undrained conditions. PLoS ONE 2024, 19, e0296441. [Google Scholar] [CrossRef] [PubMed]
- Qin, B.; Li, X.; Wang, L.; Gao, R.; Chai, H. Model interpretation and microscopic characteristics of collapsibility evolution of compacted loess under dry-wet cycles. CATENA 2024, 246, 108413. [Google Scholar] [CrossRef]
- Liu, Q.; Xie, W.; Yang, H.; Yuan, K.; Zhang, S.; Li, X.; Qu, P.; Wu, Z.; Zhou, J.; Gao, X. Intrinsic Mechanisms of Differences in Wetting-Induced Deformation of Soils on Chinese Loess Plateau: Insights into Land Stability and Sustainable Management. Land 2025, 14, 312. [Google Scholar] [CrossRef]
- Shen, J.; Wang, Q.; Chen, Y.; Zhang, X.; Han, Y.; Liu, Y. Experimental investigation into the salinity effect on the physicomechanical properties of carbonate saline soil. J. Rock Mech. Geotech. Eng. 2023, 16, 1883–1895. [Google Scholar] [CrossRef]
- Zhao, X.; Cui, Y.; Zhang, R.; Tian, G.; Satyanaga, A.; Zhai, Q. Experimental investigation of the collapsibility of loess subjected to water invasion. Bull. Eng. Geol. Environ. 2023, 83, 33. [Google Scholar] [CrossRef]
- Wei, Y.; Fan, W.; Yu, B.; Deng, L.; Wei, T. Characterization and evolution of three-dimensional microstructure of Malan loess. CATENA 2020, 192, 104585. [Google Scholar] [CrossRef]
- Basham, M.R.; Cerato, A.B.; Tabet, W.E. Using fractal geometry theory to quantify pore structure evolution and particle morphology of stabilized kaolinite. J. Mater. Civ. Eng. 2024, 36, 04024247. [Google Scholar] [CrossRef]
- Yuan, K.; Wang, H.; Ni, W.; Ren, S.; Guo, Y. New insights into the dynamic changes of loess collapsibility under climate-induced wetting-drying cycles: A case study of the loess Plateau of China. CATENA 2025, 250, 108782. [Google Scholar] [CrossRef]
- Lavagna, L.; Nisticò, R. An Insight into the Chemistry of Cement—A Review. Appl. Sci. 2022, 13, 203. [Google Scholar] [CrossRef]
- Yan, R.; Zhang, L.; Zhang, J.; Peng, J.; Chen, L.; Zhang, Y. Pore characteristics and micro-structure change of undisturbed loess induced by acid corrosion. Eng. Geol. 2022, 310, 106880. [Google Scholar] [CrossRef]
- Yuan, K.; Liu, K.; Yi, G.; Yang, B. Mechanical properties and evolution of microstructure of cement stabilized loess. J. Renew. Mater. 2022, 10, 3611–3627. [Google Scholar] [CrossRef]
- Wu, J.; Liu, L.; Deng, Y.; Zhang, G.; Zhou, A.; Wang, Q. Distinguishing the effects of cementation versus density on the mechanical behavior of cement-based stabilized clays. Constr. Build. Mater. 2020, 271, 121571. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, Q.; Yuan, M.; Chen, X.; Xiao, Z.; Hao, X.; Zhang, J.; Tang, Q. The Effect of MICP on Physical and Mechanical Properties of Silt with Different Fine Particle Content and Pore Ratio. Appl. Sci. 2021, 12, 139. [Google Scholar] [CrossRef]
- Wei, Y.; Yao, Z.; Chong, X.; Zhang, J.; Zhang, J. Microstructure of unsaturated loess and its influence on strength characteristics. Sci. Rep. 2022, 12, 1502. [Google Scholar] [CrossRef]
- Zhang, L.; Yan, R.; Peng, J.; Shen, Y.; Zhang, J.; Zhang, Y. Microstructure damage characteristics and its mechanism of undisturbed loess suffering to weak acid leaching. Bull. Eng. Geol. Environ. 2023, 82, 71. [Google Scholar] [CrossRef]
- Feng, P.; Cao, P.; Ren, S.; Ren, J.; Dong, Y.; Wu, G.; Tang, R. The mechanical and hydrochemical properties of cemented calcareous soil under long-term soaking. Sci. Rep. 2024, 14, 24532. [Google Scholar] [CrossRef]
- Ulusoy, U. A review of particle shape effects on material properties for various engineering applications: From macro to nanoscale. Minerals 2023, 13, 91. [Google Scholar] [CrossRef]
- He, J.; Li, T.; Rui, Y. Discrete element method analyses of bond degradation evolutions for cemented soils. Fractal and Fractional 2024, 8, 119. [Google Scholar] [CrossRef]
- Li, Z.; Qi, Z.; Qi, S.; Zhang, L.; Hou, X. Microstructural changes and micro–macro-relationships of an intact, compacted and remolded loess for land-creation project from the Loess Plateau. Environ. Earth Sci. 2021, 80, 593. [Google Scholar] [CrossRef]
- Ying, Z.; Cui, Y.; Benahmed, N.; Duc, M. Salinity effect on the compaction behaviour, matric suction, stiffness and microstructure of a silty soil. J. Rock Mech. Geotech. Eng. 2021, 13, 855–863. [Google Scholar] [CrossRef]
- Yang, X.; Hu, Z.; Wang, Y.; Zhang, Y.; Wang, X.; Hou, B.; Wei, Y.; Liu, C. Mechanical properties and micro-mechanisms of geopolymer solidified salinized loess. Constr. Build. Mater. 2024, 455, 139211. [Google Scholar] [CrossRef]
- Ji, G.; Peng, X.; Wang, S.; Li, J.; Sun, K.; Chi, H. Influence of ground quartz sand finesses on the formation of poorly ordered calcium silicate hydrate prepared by dynamically hydrothermal synthesis. Case Stud. Constr. Mater. 2023, 20, e02746. [Google Scholar] [CrossRef]
- Ibrahim, M.A.; Jaafar, M.Z.; Yusof, M.A.M.; Shye, C.A.; Idris, A.K. Influence of size and surface charge on the adsorption behaviour of silicon dioxide nanoparticles on sand particles. Colloids Surf. A Physicochem. Eng. Asp. 2023, 674, 131943. [Google Scholar] [CrossRef]
- Ravindran, S.; Gratchev, I. Effect of Water Content on Apparent Cohesion of Soils from Landslide Sites. Geotechnics 2022, 2, 385–394. [Google Scholar] [CrossRef]
- Bunimovich, L.; Skums, P. Fractal networks: Topology, dimension, and complexity. Chaos Interdiscip. J. Nonlinear Sci. 2024, 34, 042101. [Google Scholar] [CrossRef] [PubMed]
- Datseris, G.; Kottlarz, I.; Braun, A.P.; Parlitz, U. Estimating fractal dimensions: A comparative review and open source implementations. Chaos Interdiscip. J. Nonlinear Sci. 2023, 33, 102101. [Google Scholar] [CrossRef]

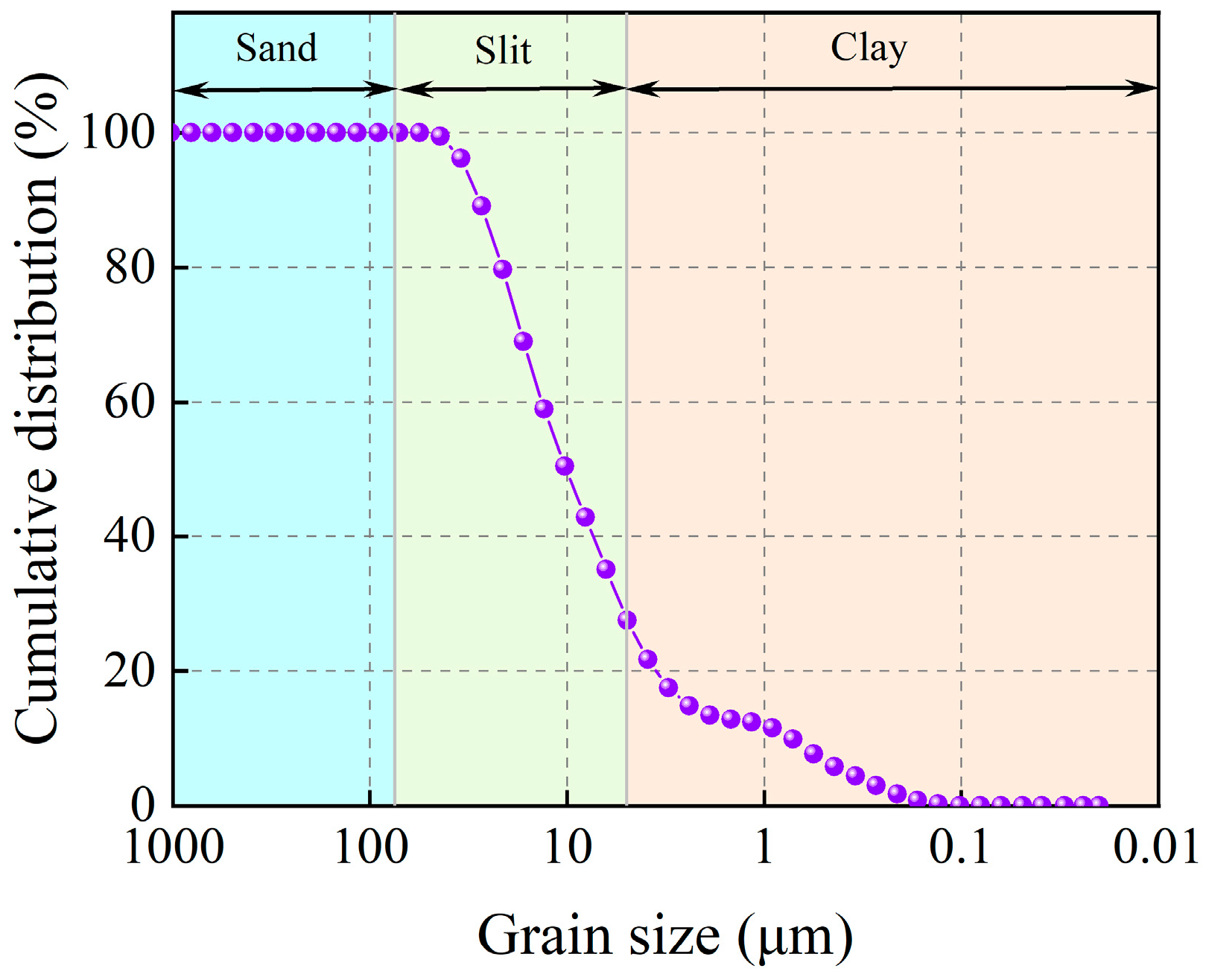





| Specific Gravity Gs | Natural Density ρ (g/cm3) | Natural Water Content w0 (%) | Dry Density ρd (g/cm3) | Plasticity Limit wp (%) | Liquid Limit wL (%) | Natural Void Ratio e0 |
|---|---|---|---|---|---|---|
| 2.69 | 1.78 | 21.80 | 1.46 | 21.08 | 28.02 | 0.84 |
| Test Type | Research Subject | Water Content (%) | Salt Content (%) | Cement Content (%) | Vertical Pressure (kPa) | |
|---|---|---|---|---|---|---|
| ASL | RL | |||||
| Consolidation test | √ | √ | 8.00, 12.00, 16.00, 20.00, 24.00 | 2.00 | 0.50, 1.00, 2.00, 4.00 | 12.5, 25.0, 50.0, 100.0, 200.0, 400.0, 800.0 |
| Collapsibility test | √ | √ | 8.00, 12.00, 16.00, 20.00, 24.00 | 2.00, 4.00, 8.00 | 1.00, 2.00, 4.00 | 12.5, 25.0, 50.0, 100.0, 200.0, 400.0, 800.0 |
| Particle size analysis | √ | √ | 16.00 | 2.00, 16.00 | 2.00 | 200.0, 400.0, 800.0 |
| XRD | √ | √ | 16.00 | 2.00 | 2.00, 4.00 | 400.0 |
| MIP | √ | 16.00 | 2.00, 16.00 | 2.00, 4.00 | 200.0, 400.0, 800.0 | |
| Sample Name | Quartz (%) | Potash Feldspar (%) | Plagioclase (%) | Calcite (%) | Salt (%) | Amphibolite (%) | TCCM (%) |
|---|---|---|---|---|---|---|---|
| Remolded loess (B) | 42.40 | 2.20 | 20.50 | 9.80 | / | 1.60 | 23.50 |
| Structural loess (C2.0 Y2.0) | 41.10 | 2.30 | 17.20 | 11.20 | 2.10 | / | 25.10 |
| Structural loess (C4.0 Y2.0) | 38.50 | 2.50 | 14.90 | 12.30 | 2.30 | / | 29.50 |
| Load P (kPa) | Void Ratio e | Collapsibility Coefficient δs | Granularity Fractal Dimension Value D | Proportion of Large and Medium-Sized Pores n (%) | Proportion of Clay Minerals C (%) |
|---|---|---|---|---|---|
| 200 | 0.7766 | 0.0395 | 2.4000 | 76.38 | 25.10 |
| 0.7820 | 0.0425 | 2.4310 | 77.66 | 23.70 | |
| 400 | 0.7531 | 0.0615 | 2.3640 | 72.96 | 25.10 |
| 0.7611 | 0.0685 | 2.4060 | 73.71 | 23.70 | |
| 800 | 0.7226 | 0.0405 | 2.4340 | 71.44 | 25.10 |
| 0.7478 | 0.0470 | 2.3830 | 70.03 | 23.70 |
| Load P (kPa) | Actual Measured Values | Fit Predicted Values | Absolute Error Δ | Relative Error (%) | ||||
|---|---|---|---|---|---|---|---|---|
| e | δs | e | δs | e | δs | e | δs | |
| 200 | 0.7685 | 0.0495 | 0.7669 | 0.0489 | 0.0015 | 0.0005 | 0.21 | 1.12 |
| 0.7757 | 0.0260 | 0.7819 | 0.0286 | 0.0062 | 0.0026 | 0.81 | 10.20 | |
| 400 | 0.7370 | 0.0670 | 0.7361 | 0.0640 | 0.0009 | 0.0029 | 0.12 | 4.45 |
| 0.7532 | 0.0350 | 0.7527 | 0.0398 | 0.0004 | 0.0048 | 0.06 | 13.82 | |
| 800 | 0.7037 | 0.0395 | 0.6930 | 0.0428 | 0.0106 | 0.0033 | 1.51 | 8.45 |
| 0.7145 | 0.0250 | 0.7316 | 0.0414 | 0.0171 | 0.0164 | 2.41 | 65.73 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Zhou, C.; Zhang, H.; Li, Z.; Fan, X.; Guo, P. Macro–Micro Quantitative Model for Deformation Prediction of Artificial Structural Loess. Buildings 2025, 15, 3714. https://doi.org/10.3390/buildings15203714
Zhang Y, Zhou C, Zhang H, Li Z, Fan X, Guo P. Macro–Micro Quantitative Model for Deformation Prediction of Artificial Structural Loess. Buildings. 2025; 15(20):3714. https://doi.org/10.3390/buildings15203714
Chicago/Turabian StyleZhang, Yao, Chuhong Zhou, Heng Zhang, Zufeng Li, Xinyu Fan, and Peixi Guo. 2025. "Macro–Micro Quantitative Model for Deformation Prediction of Artificial Structural Loess" Buildings 15, no. 20: 3714. https://doi.org/10.3390/buildings15203714
APA StyleZhang, Y., Zhou, C., Zhang, H., Li, Z., Fan, X., & Guo, P. (2025). Macro–Micro Quantitative Model for Deformation Prediction of Artificial Structural Loess. Buildings, 15(20), 3714. https://doi.org/10.3390/buildings15203714





