Research on the Coupling Coordination Characteristics of Affordable Housing Market and Urban Development
Abstract
1. Introduction
2. Materials and Methods
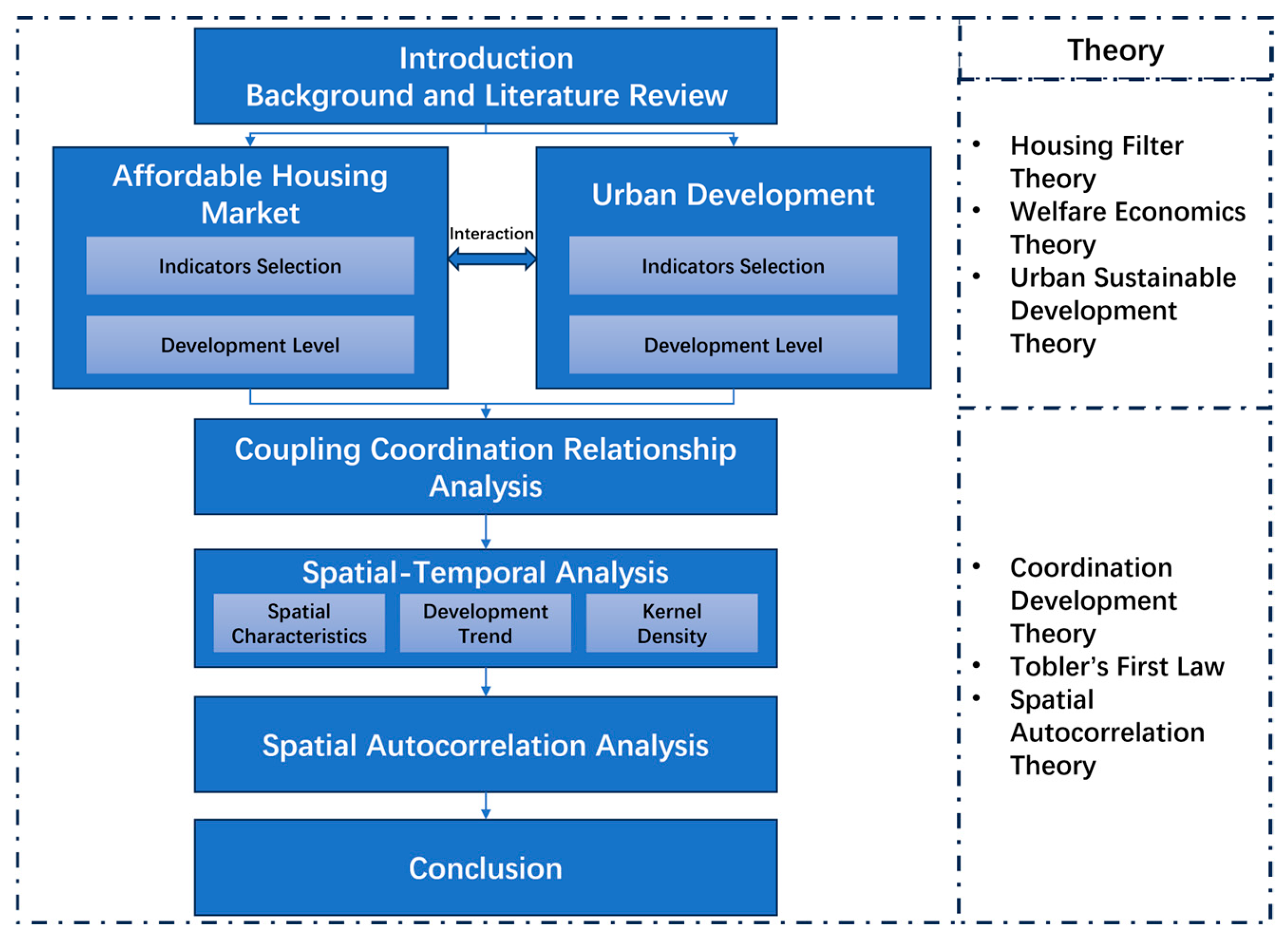
2.1. Research Framework
2.2. Research Scope and Data Sources
2.3. Research Methods
2.3.1. Entropy Weight Model
- Step 1:
- Normalization of indicator values
- Step 2:
- Calculating indicator weights
2.3.2. Coupling Coordination Degree Model
2.3.3. Growth Distribution Dynamic Analysis
2.3.4. Spatial Correlation Analysis Model
- Step 1:
- Construction of spatial weight matrix
- Step 2:
- Construction of spatial correlation analysis model
- (1)
- Global spatial autocorrelation analysis
- (2)
- Local spatial autocorrelation analysis
3. Results
3.1. Affordable Housing Market Evaluation
3.1.1. Affordable Housing Market Evaluation System Construction
3.1.2. Affordable Housing Market Evaluation Results
3.2. Urban Development Evaluation
3.2.1. Urban Development Evaluation System Construction
3.2.2. Urban Development Evaluation Results
3.3. Coupling Coordination Degree Evaluation Results
3.3.1. Systematic Comprehensive Development Level
3.3.2. Coupling Degree
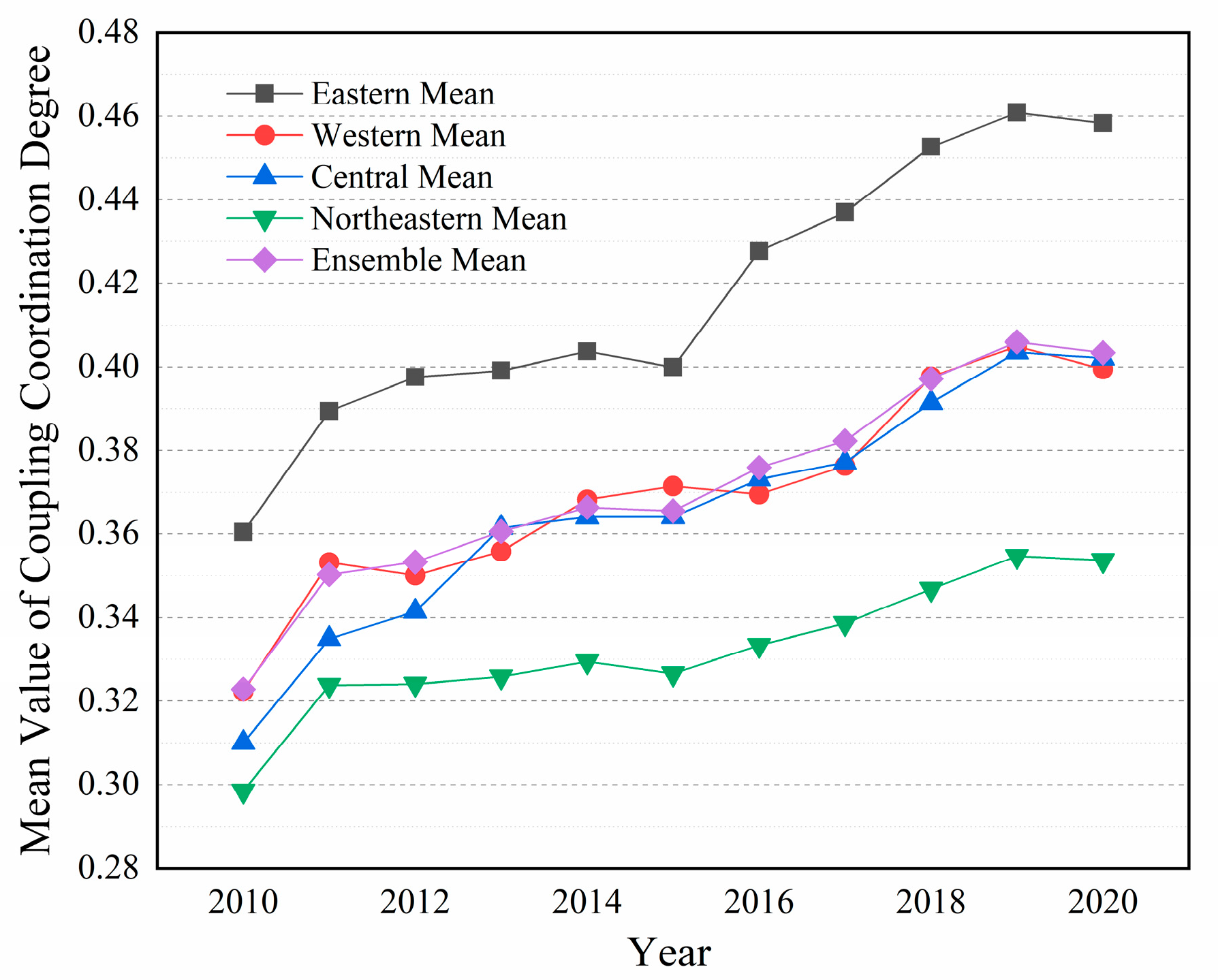
3.3.3. Coupling Coordination Degree
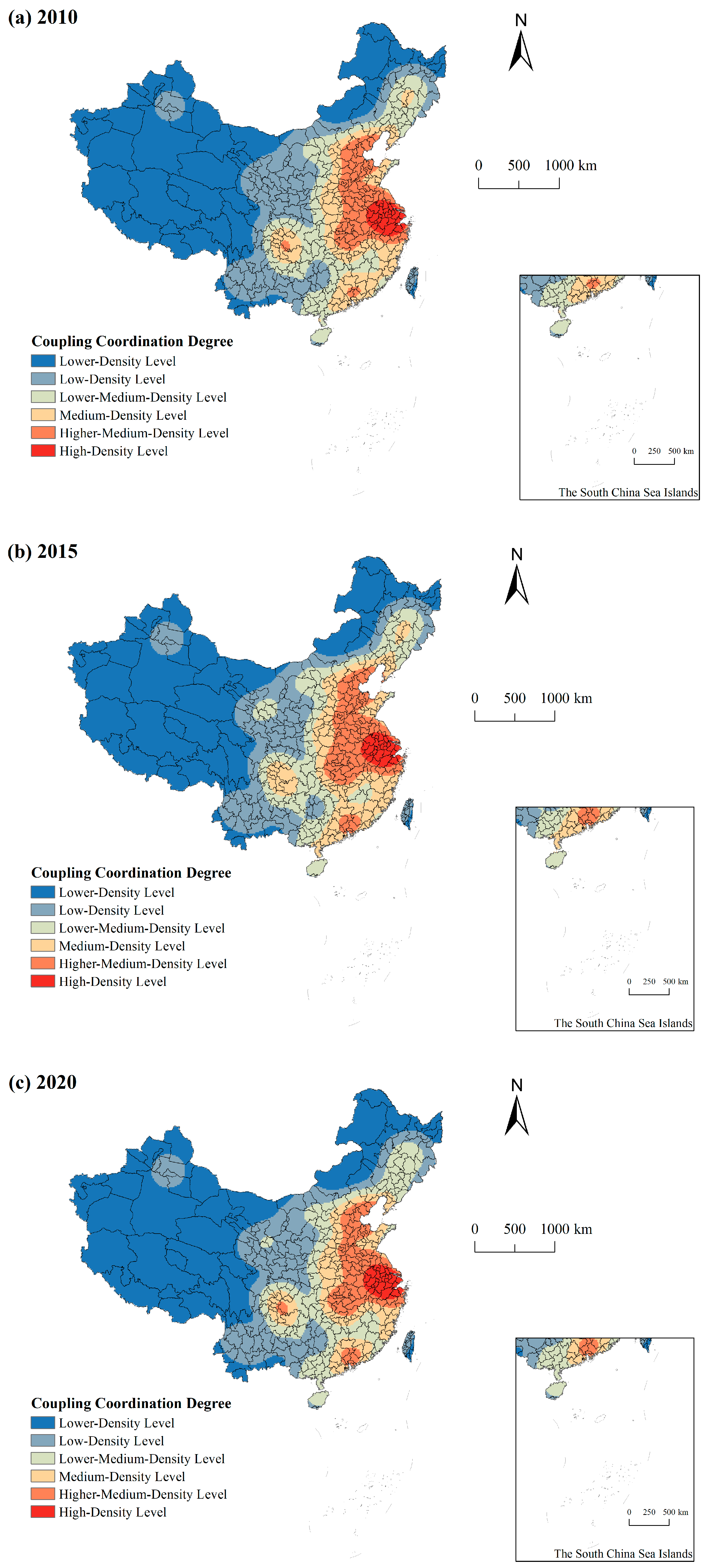
3.4. Coupling Coordination Degree Spatial Characteristics
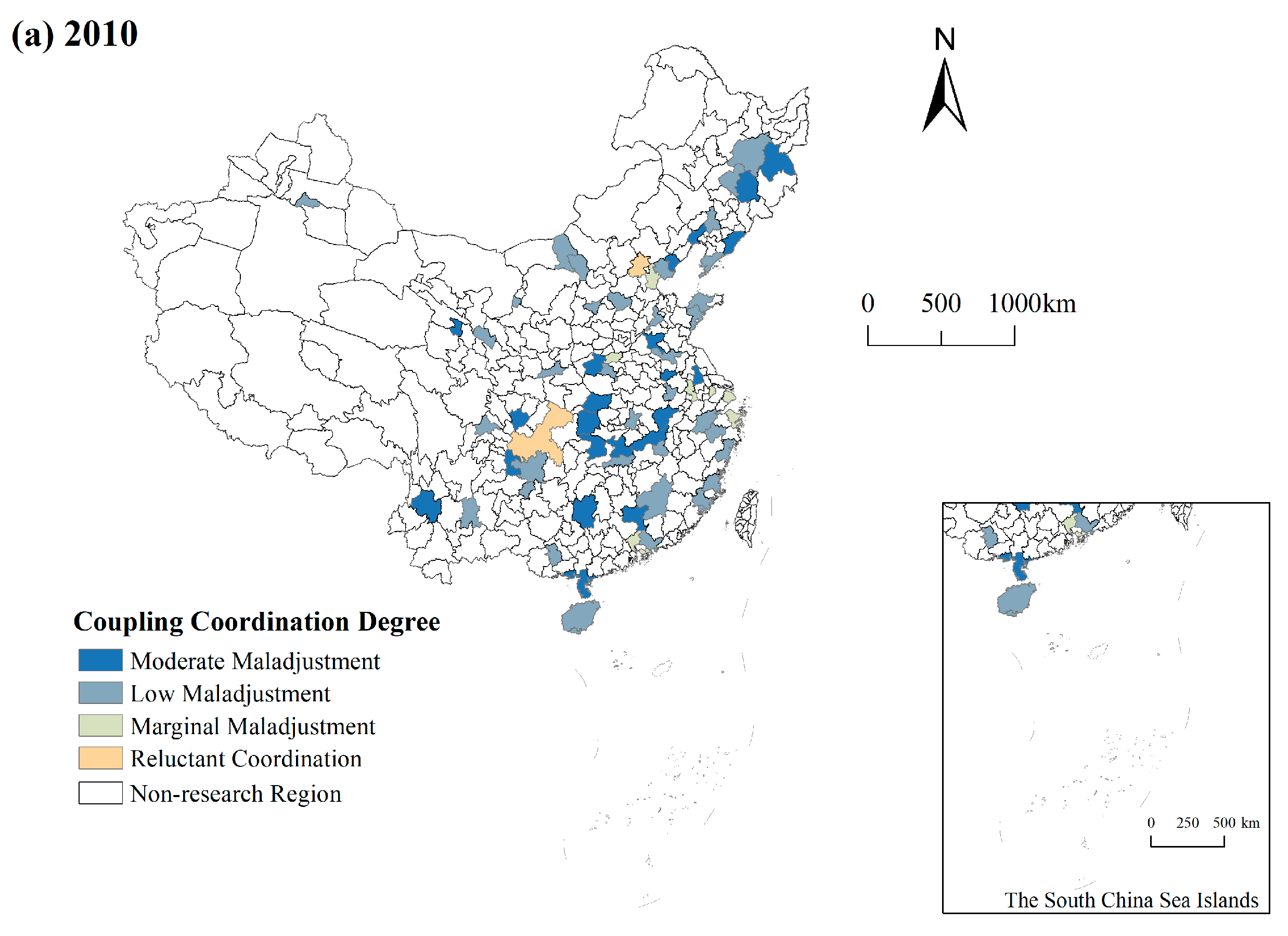
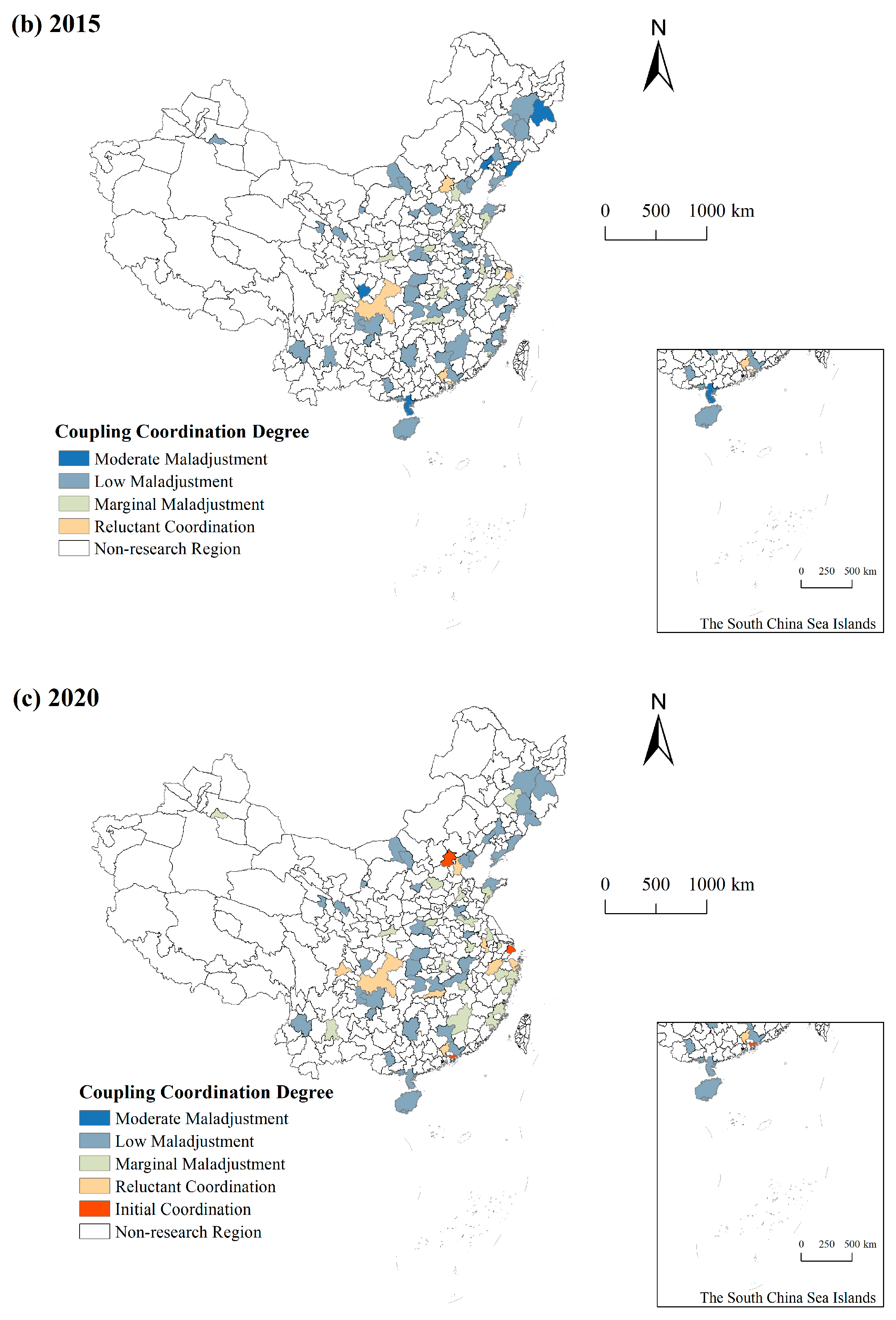
3.4.1. Spatial Distribution Analysis
3.4.2. Development Level Trend Analysis
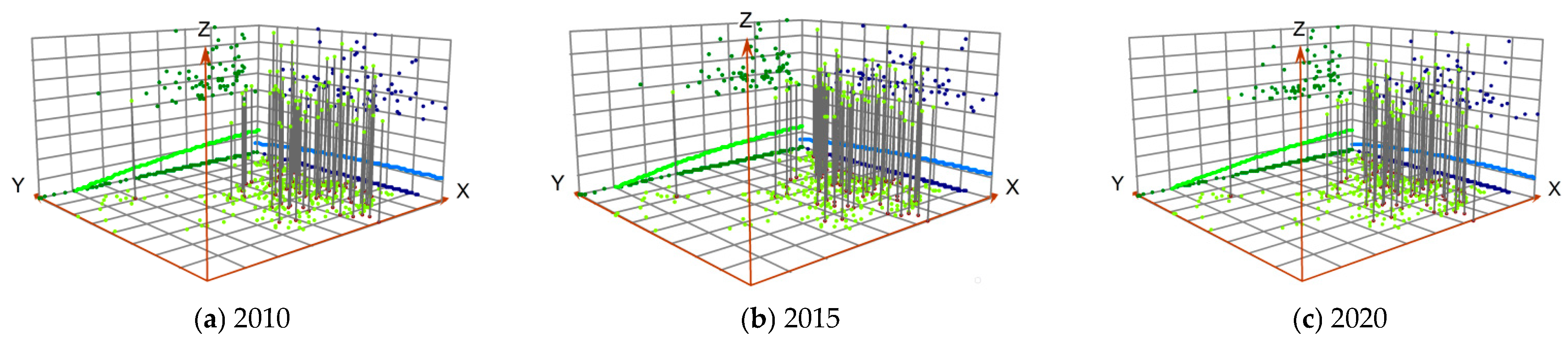
3.4.3. Kernel Density Regional Distribution Analysis
3.4.4. Kernel Density Development Trend Analysis
4. Discussion
4.1. Global Spatial Autocorrelation Analysis of Coupling Coordination Degree
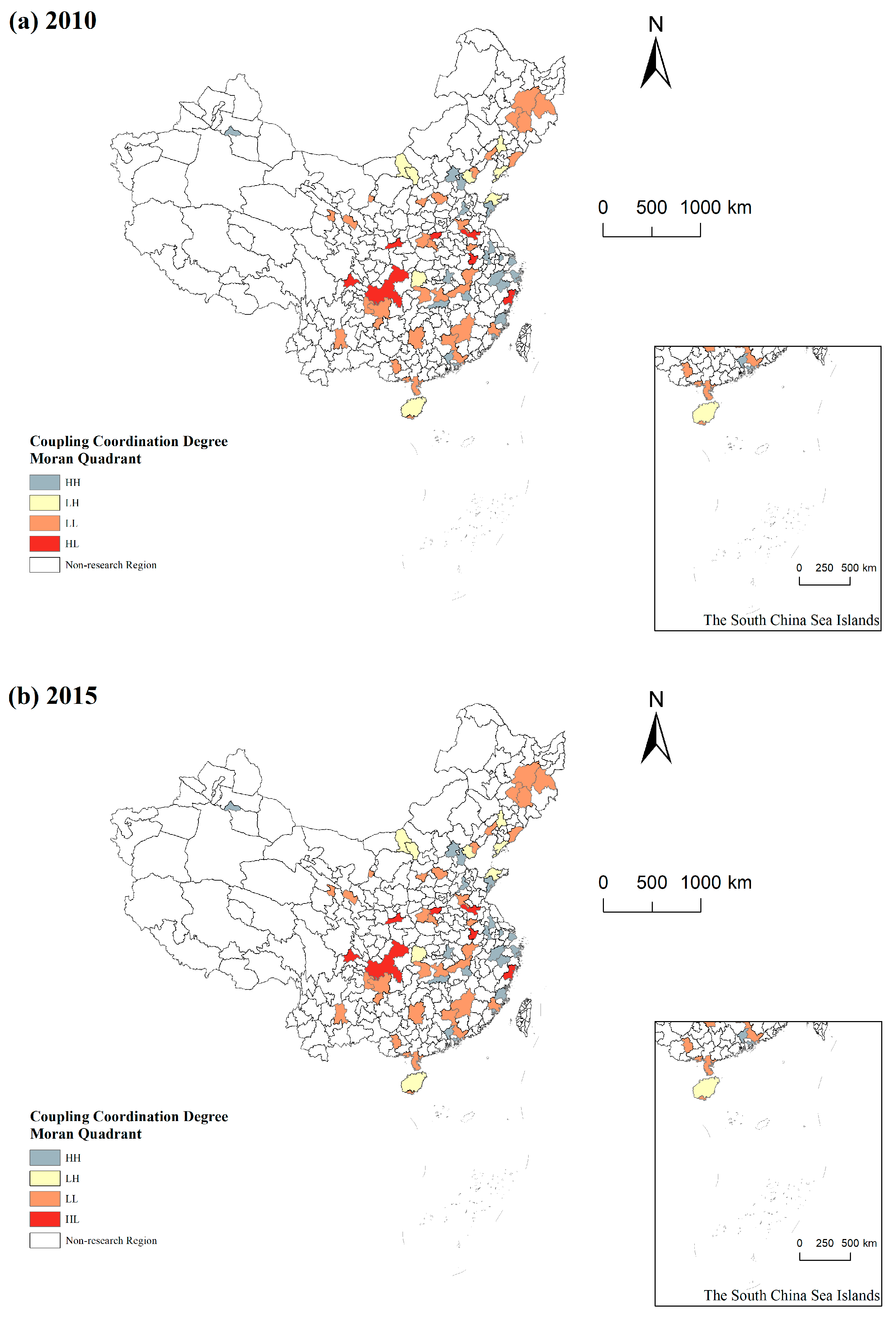
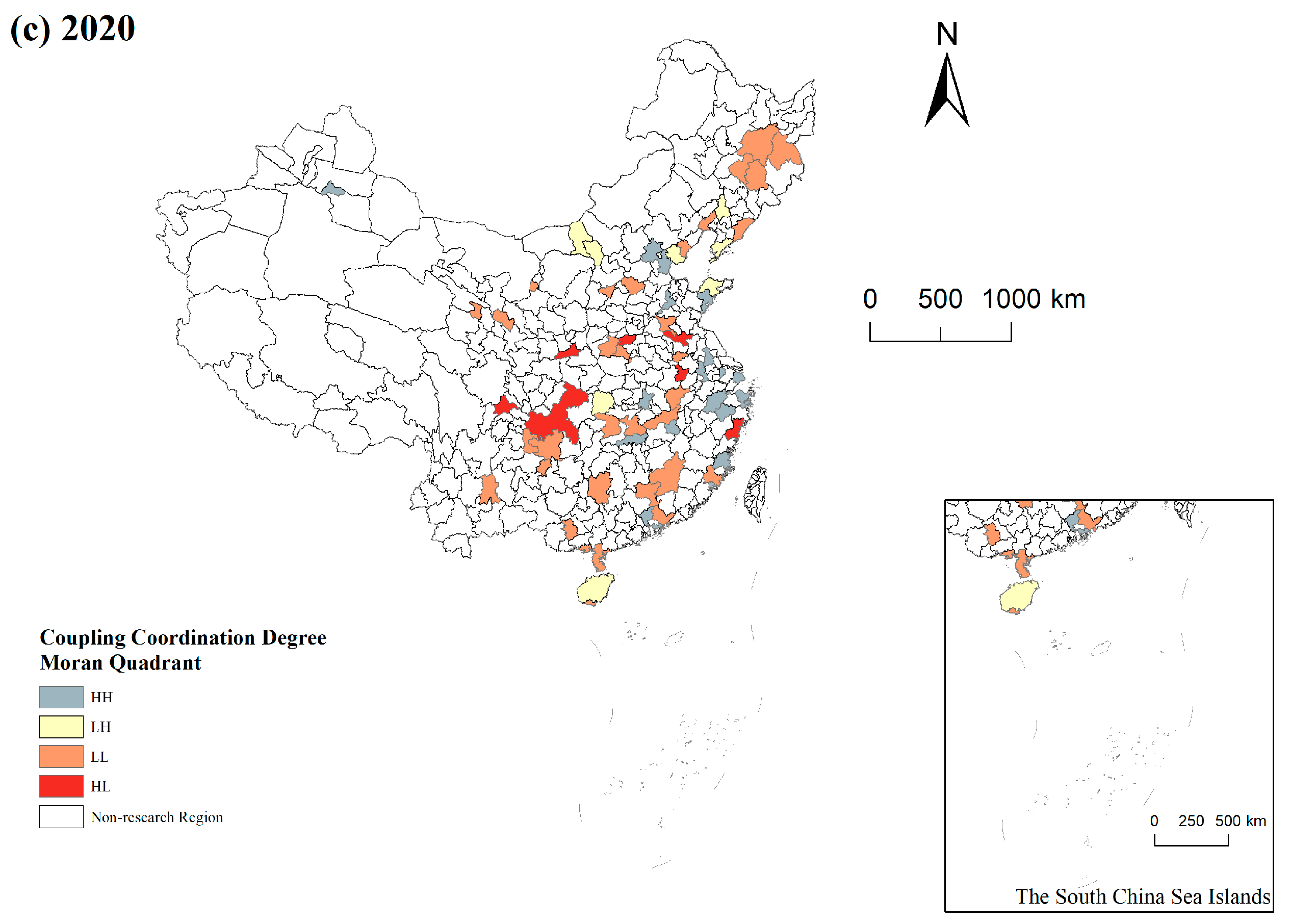
4.2. Local Spatial Autocorrelation Analysis of Coupling Coordination Degree
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| City | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Beijing | 0.231 | 0.264 | 0.254 | 0.251 | 0.230 | 0.247 | 0.374 | 0.327 | 0.299 | 0.324 | 0.314 |
| Tianjin | 0.246 | 0.349 | 0.335 | 0.196 | 0.209 | 0.118 | 0.247 | 0.181 | 0.286 | 0.295 | 0.273 |
| Shijiazhuang | 0.081 | 0.116 | 0.109 | 0.125 | 0.114 | 0.118 | 0.151 | 0.149 | 0.171 | 0.153 | 0.158 |
| Hohhot | 0.086 | 0.114 | 0.113 | 0.113 | 0.111 | 0.109 | 0.128 | 0.113 | 0.129 | 0.134 | 0.121 |
| Taiyuan | 0.070 | 0.103 | 0.105 | 0.093 | 0.089 | 0.096 | 0.104 | 0.097 | 0.104 | 0.122 | 0.121 |
| Shenyang | 0.085 | 0.088 | 0.105 | 0.122 | 0.121 | 0.105 | 0.119 | 0.112 | 0.123 | 0.133 | 0.129 |
| Dalian | 0.078 | 0.174 | 0.108 | 0.119 | 0.097 | 0.098 | 0.104 | 0.102 | 0.119 | 0.130 | 0.130 |
| Changchun | 0.117 | 0.118 | 0.143 | 0.097 | 0.118 | 0.095 | 0.104 | 0.116 | 0.132 | 0.145 | 0.150 |
| Harbin | 0.114 | 0.146 | 0.101 | 0.081 | 0.098 | 0.090 | 0.097 | 0.104 | 0.110 | 0.122 | 0.118 |
| Shanghai | 0.170 | 0.313 | 0.262 | 0.214 | 0.248 | 0.253 | 0.289 | 0.327 | 0.345 | 0.355 | 0.363 |
| Nanjing | 0.181 | 0.375 | 0.214 | 0.227 | 0.237 | 0.165 | 0.256 | 0.309 | 0.303 | 0.314 | 0.339 |
| Hangzhou | 0.140 | 0.158 | 0.268 | 0.270 | 0.215 | 0.164 | 0.261 | 0.226 | 0.271 | 0.319 | 0.323 |
| Ningbo | 0.322 | 0.155 | 0.372 | 0.317 | 0.240 | 0.172 | 0.233 | 0.200 | 0.305 | 0.320 | 0.319 |
| Hefei | 0.107 | 0.150 | 0.185 | 0.169 | 0.180 | 0.104 | 0.189 | 0.186 | 0.192 | 0.219 | 0.206 |
| Fuzhou | 0.087 | 0.111 | 0.105 | 0.111 | 0.121 | 0.130 | 0.135 | 0.139 | 0.163 | 0.165 | 0.166 |
| Xiamen | 0.099 | 0.124 | 0.113 | 0.109 | 0.111 | 0.116 | 0.134 | 0.144 | 0.154 | 0.160 | 0.156 |
| Nanchang | 0.076 | 0.093 | 0.089 | 0.210 | 0.113 | 0.108 | 0.142 | 0.134 | 0.156 | 0.176 | 0.179 |
| Jinan | 0.128 | 0.128 | 0.122 | 0.140 | 0.156 | 0.145 | 0.165 | 0.178 | 0.188 | 0.201 | 0.216 |
| Qingdao | 0.110 | 0.194 | 0.169 | 0.184 | 0.158 | 0.133 | 0.164 | 0.154 | 0.216 | 0.213 | 0.222 |
| Zhengzhou | 0.204 | 0.172 | 0.113 | 0.149 | 0.236 | 0.250 | 0.230 | 0.225 | 0.247 | 0.237 | 0.259 |
| Wuhan | 0.105 | 0.194 | 0.194 | 0.283 | 0.190 | 0.181 | 0.160 | 0.173 | 0.215 | 0.218 | 0.212 |
| Changsha | 0.136 | 0.142 | 0.200 | 0.179 | 0.202 | 0.160 | 0.213 | 0.175 | 0.241 | 0.239 | 0.248 |
| Guangzhou | 0.139 | 0.181 | 0.162 | 0.168 | 0.178 | 0.203 | 0.189 | 0.216 | 0.221 | 0.235 | 0.266 |
| Shenzhen | 0.117 | 0.161 | 0.151 | 0.154 | 0.158 | 0.182 | 0.303 | 0.407 | 0.272 | 0.286 | 0.292 |
| Nanning | 0.097 | 0.111 | 0.080 | 0.117 | 0.089 | 0.102 | 0.099 | 0.108 | 0.120 | 0.119 | 0.135 |
| Haikou | 0.061 | 0.069 | 0.079 | 0.072 | 0.077 | 0.080 | 0.091 | 0.103 | 0.097 | 0.101 | 0.099 |
| Chongqing | 0.392 | 0.610 | 0.518 | 0.344 | 0.302 | 0.292 | 0.269 | 0.232 | 0.380 | 0.400 | 0.414 |
| Chengdu | 0.125 | 0.292 | 0.159 | 0.210 | 0.252 | 0.212 | 0.171 | 0.227 | 0.275 | 0.271 | 0.270 |
| Guiyang | 0.123 | 0.118 | 0.099 | 0.114 | 0.105 | 0.118 | 0.100 | 0.117 | 0.149 | 0.150 | 0.141 |
| Kunming | 0.083 | 0.144 | 0.174 | 0.133 | 0.124 | 0.129 | 0.136 | 0.134 | 0.140 | 0.154 | 0.155 |
| Xi’an | 0.114 | 0.135 | 0.187 | 0.227 | 0.208 | 0.193 | 0.192 | 0.173 | 0.201 | 0.243 | 0.239 |
| Lanzhou | 0.075 | 0.088 | 0.081 | 0.085 | 0.093 | 0.125 | 0.115 | 0.108 | 0.139 | 0.138 | 0.152 |
| Xining | 0.042 | 0.070 | 0.066 | 0.079 | 0.073 | 0.113 | 0.117 | 0.107 | 0.115 | 0.112 | 0.115 |
| Yinchuan | 0.093 | 0.141 | 0.151 | 0.131 | 0.168 | 0.168 | 0.140 | 0.129 | 0.183 | 0.175 | 0.171 |
| Urumqi | 0.068 | 0.079 | 0.070 | 0.064 | 0.124 | 0.092 | 0.104 | 0.127 | 0.159 | 0.171 | 0.158 |
| Tangshan | 0.088 | 0.134 | 0.098 | 0.101 | 0.105 | 0.115 | 0.119 | 0.120 | 0.133 | 0.140 | 0.136 |
| Qinhuangdao | 0.073 | 0.122 | 0.091 | 0.182 | 0.099 | 0.103 | 0.126 | 0.126 | 0.138 | 0.145 | 0.147 |
| Baotou | 0.095 | 0.144 | 0.123 | 0.128 | 0.139 | 0.131 | 0.139 | 0.129 | 0.142 | 0.144 | 0.143 |
| Dandong | 0.033 | 0.059 | 0.052 | 0.059 | 0.063 | 0.069 | 0.073 | 0.076 | 0.082 | 0.090 | 0.090 |
| Jinzhou | 0.056 | 0.074 | 0.076 | 0.092 | 0.085 | 0.082 | 0.080 | 0.082 | 0.090 | 0.095 | 0.096 |
| Jilin | 0.070 | 0.085 | 0.102 | 0.090 | 0.090 | 0.093 | 0.085 | 0.087 | 0.092 | 0.092 | 0.094 |
| Mudanjiang | 0.050 | 0.055 | 0.067 | 0.067 | 0.072 | 0.082 | 0.097 | 0.092 | 0.094 | 0.096 | 0.100 |
| Wuxi | 0.236 | 0.283 | 0.253 | 0.194 | 0.215 | 0.158 | 0.180 | 0.181 | 0.250 | 0.267 | 0.259 |
| Yangzhou | 0.083 | 0.143 | 0.119 | 0.110 | 0.121 | 0.130 | 0.157 | 0.179 | 0.184 | 0.202 | 0.204 |
| Xuzhou | 0.099 | 0.096 | 0.255 | 0.108 | 0.172 | 0.099 | 0.172 | 0.151 | 0.203 | 0.220 | 0.246 |
| Wenzhou | 0.112 | 0.141 | 0.232 | 0.267 | 0.291 | 0.156 | 0.212 | 0.289 | 0.290 | 0.286 | 0.285 |
| Jinhua | 0.122 | 0.131 | 0.157 | 0.202 | 0.199 | 0.161 | 0.195 | 0.191 | 0.218 | 0.227 | 0.225 |
| Bengbu | 0.070 | 0.067 | 0.077 | 0.077 | 0.142 | 0.124 | 0.129 | 0.103 | 0.117 | 0.127 | 0.131 |
| Anqing | 0.060 | 0.104 | 0.087 | 0.112 | 0.115 | 0.102 | 0.108 | 0.134 | 0.134 | 0.138 | 0.133 |
| Quanzhou | 0.104 | 0.140 | 0.133 | 0.134 | 0.138 | 0.142 | 0.149 | 0.150 | 0.159 | 0.173 | 0.175 |
| Jiujiang | 0.071 | 0.100 | 0.159 | 0.185 | 0.178 | 0.135 | 0.133 | 0.125 | 0.147 | 0.166 | 0.167 |
| Ganzhou | 0.103 | 0.162 | 0.149 | 0.293 | 0.145 | 0.117 | 0.115 | 0.139 | 0.198 | 0.242 | 0.207 |
| Yantai | 0.086 | 0.104 | 0.109 | 0.119 | 0.125 | 0.122 | 0.126 | 0.138 | 0.167 | 0.142 | 0.145 |
| Jining | 0.076 | 0.110 | 0.101 | 0.088 | 0.099 | 0.105 | 0.131 | 0.143 | 0.151 | 0.126 | 0.122 |
| Luoyang | 0.076 | 0.143 | 0.101 | 0.111 | 0.116 | 0.137 | 0.134 | 0.120 | 0.143 | 0.155 | 0.164 |
| Pingdingshan | 0.096 | 0.080 | 0.110 | 0.079 | 0.096 | 0.086 | 0.106 | 0.122 | 0.126 | 0.122 | 0.115 |
| Yichang | 0.059 | 0.084 | 0.095 | 0.128 | 0.152 | 0.212 | 0.157 | 0.165 | 0.175 | 0.167 | 0.154 |
| Xiangyang | 0.058 | 0.069 | 0.078 | 0.098 | 0.153 | 0.137 | 0.135 | 0.130 | 0.140 | 0.151 | 0.151 |
| Yueyang | 0.085 | 0.117 | 0.124 | 0.121 | 0.129 | 0.123 | 0.141 | 0.147 | 0.141 | 0.154 | 0.149 |
| Changde | 0.074 | 0.118 | 0.107 | 0.129 | 0.130 | 0.148 | 0.140 | 0.136 | 0.149 | 0.151 | 0.163 |
| Huizhou | 0.081 | 0.101 | 0.099 | 0.079 | 0.101 | 0.094 | 0.105 | 0.122 | 0.115 | 0.127 | 0.138 |
| Zhanjiang | 0.043 | 0.067 | 0.063 | 0.062 | 0.070 | 0.073 | 0.079 | 0.082 | 0.085 | 0.090 | 0.097 |
| Shaoguan | 0.060 | 0.080 | 0.083 | 0.082 | 0.081 | 0.107 | 0.093 | 0.095 | 0.098 | 0.104 | 0.107 |
| Guilin | 0.058 | 0.091 | 0.085 | 0.103 | 0.187 | 0.170 | 0.112 | 0.096 | 0.154 | 0.172 | 0.197 |
| Beihai | 0.086 | 0.113 | 0.110 | 0.080 | 0.100 | 0.094 | 0.091 | 0.094 | 0.100 | 0.108 | 0.095 |
| Sanya | 0.060 | 0.072 | 0.074 | 0.080 | 0.086 | 0.099 | 0.097 | 0.095 | 0.112 | 0.123 | 0.108 |
| Luzhou | 0.063 | 0.075 | 0.081 | 0.096 | 0.117 | 0.107 | 0.079 | 0.105 | 0.123 | 0.124 | 0.124 |
| Nanchong | 0.061 | 0.101 | 0.064 | 0.063 | 0.137 | 0.094 | 0.098 | 0.105 | 0.122 | 0.132 | 0.128 |
| Zunyi | 0.083 | 0.088 | 0.088 | 0.121 | 0.113 | 0.142 | 0.166 | 0.157 | 0.172 | 0.155 | 0.149 |
| Dali | 0.058 | 0.076 | 0.075 | 0.077 | 0.093 | 0.094 | 0.113 | 0.110 | 0.115 | 0.122 | 0.123 |
| Average | 0.104 | 0.139 | 0.138 | 0.140 | 0.143 | 0.133 | 0.148 | 0.151 | 0.171 | 0.179 | 0.180 |
| City | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Beijing | 0.301 | 0.320 | 0.337 | 0.364 | 0.374 | 0.401 | 0.427 | 0.446 | 0.465 | 0.485 | 0.461 |
| Tianjin | 0.197 | 0.215 | 0.234 | 0.260 | 0.285 | 0.291 | 0.312 | 0.312 | 0.313 | 0.303 | 0.285 |
| Shijiazhuang | 0.144 | 0.148 | 0.151 | 0.151 | 0.154 | 0.160 | 0.165 | 0.169 | 0.179 | 0.180 | 0.185 |
| Hohhot | 0.151 | 0.143 | 0.168 | 0.184 | 0.170 | 0.172 | 0.177 | 0.170 | 0.175 | 0.182 | 0.154 |
| Taiyuan | 0.141 | 0.153 | 0.161 | 0.165 | 0.170 | 0.175 | 0.180 | 0.187 | 0.185 | 0.195 | 0.175 |
| Shenyang | 0.150 | 0.160 | 0.169 | 0.179 | 0.180 | 0.181 | 0.175 | 0.185 | 0.192 | 0.197 | 0.193 |
| Dalian | 0.160 | 0.168 | 0.175 | 0.187 | 0.181 | 0.182 | 0.178 | 0.192 | 0.200 | 0.195 | 0.185 |
| Changchun | 0.140 | 0.147 | 0.152 | 0.158 | 0.161 | 0.169 | 0.170 | 0.175 | 0.184 | 0.183 | 0.182 |
| Harbin | 0.135 | 0.140 | 0.145 | 0.145 | 0.149 | 0.156 | 0.159 | 0.166 | 0.170 | 0.163 | 0.161 |
| Shanghai | 0.313 | 0.335 | 0.348 | 0.371 | 0.384 | 0.420 | 0.453 | 0.480 | 0.513 | 0.544 | 0.554 |
| Nanjing | 0.197 | 0.211 | 0.223 | 0.243 | 0.256 | 0.269 | 0.282 | 0.294 | 0.309 | 0.320 | 0.306 |
| Hangzhou | 0.174 | 0.184 | 0.193 | 0.204 | 0.214 | 0.227 | 0.241 | 0.259 | 0.272 | 0.282 | 0.267 |
| Ningbo | 0.143 | 0.153 | 0.158 | 0.172 | 0.175 | 0.184 | 0.195 | 0.221 | 0.226 | 0.240 | 0.231 |
| Hefei | 0.139 | 0.144 | 0.155 | 0.145 | 0.146 | 0.160 | 0.169 | 0.184 | 0.186 | 0.205 | 0.200 |
| Fuzhou | 0.140 | 0.140 | 0.147 | 0.156 | 0.155 | 0.165 | 0.173 | 0.184 | 0.188 | 0.200 | 0.199 |
| Xiamen | 0.236 | 0.253 | 0.264 | 0.275 | 0.278 | 0.289 | 0.295 | 0.311 | 0.315 | 0.325 | 0.265 |
| Nanchang | 0.123 | 0.129 | 0.142 | 0.158 | 0.151 | 0.163 | 0.167 | 0.162 | 0.173 | 0.181 | 0.177 |
| Jinan | 0.159 | 0.167 | 0.168 | 0.179 | 0.197 | 0.206 | 0.214 | 0.219 | 0.229 | 0.239 | 0.237 |
| Qingdao | 0.152 | 0.166 | 0.179 | 0.196 | 0.204 | 0.214 | 0.224 | 0.232 | 0.252 | 0.255 | 0.248 |
| Zhengzhou | 0.151 | 0.159 | 0.165 | 0.172 | 0.184 | 0.198 | 0.208 | 0.223 | 0.235 | 0.250 | 0.240 |
| Wuhan | 0.170 | 0.183 | 0.197 | 0.214 | 0.218 | 0.228 | 0.241 | 0.258 | 0.282 | 0.300 | 0.283 |
| Changsha | 0.150 | 0.156 | 0.159 | 0.169 | 0.186 | 0.202 | 0.214 | 0.227 | 0.239 | 0.249 | 0.255 |
| Guangzhou | 0.259 | 0.271 | 0.285 | 0.312 | 0.310 | 0.329 | 0.342 | 0.354 | 0.390 | 0.409 | 0.361 |
| Shenzhen | 0.320 | 0.282 | 0.377 | 0.404 | 0.430 | 0.468 | 0.504 | 0.550 | 0.566 | 0.602 | 0.627 |
| Nanning | 0.132 | 0.136 | 0.139 | 0.142 | 0.147 | 0.149 | 0.154 | 0.156 | 0.162 | 0.170 | 0.169 |
| Haikou | 0.152 | 0.169 | 0.177 | 0.166 | 0.161 | 0.167 | 0.178 | 0.194 | 0.194 | 0.194 | 0.161 |
| Chongqing | 0.173 | 0.198 | 0.214 | 0.221 | 0.228 | 0.242 | 0.250 | 0.268 | 0.275 | 0.296 | 0.292 |
| Chengdu | 0.147 | 0.156 | 0.174 | 0.186 | 0.199 | 0.203 | 0.212 | 0.234 | 0.248 | 0.261 | 0.259 |
| Guiyang | 0.131 | 0.128 | 0.137 | 0.139 | 0.152 | 0.151 | 0.154 | 0.172 | 0.167 | 0.173 | 0.152 |
| Kunming | 0.149 | 0.150 | 0.161 | 0.163 | 0.178 | 0.183 | 0.189 | 0.193 | 0.192 | 0.189 | 0.169 |
| Xi’an | 0.147 | 0.157 | 0.168 | 0.178 | 0.183 | 0.190 | 0.195 | 0.204 | 0.209 | 0.225 | 0.211 |
| Lanzhou | 0.121 | 0.125 | 0.139 | 0.137 | 0.134 | 0.149 | 0.155 | 0.162 | 0.170 | 0.161 | 0.146 |
| Xining | 0.090 | 0.094 | 0.111 | 0.097 | 0.109 | 0.135 | 0.130 | 0.126 | 0.131 | 0.143 | 0.144 |
| Yinchuan | 0.122 | 0.126 | 0.128 | 0.138 | 0.137 | 0.143 | 0.150 | 0.159 | 0.163 | 0.155 | 0.140 |
| Urumqi | 0.154 | 0.162 | 0.169 | 0.181 | 0.191 | 0.202 | 0.205 | 0.232 | 0.244 | 0.277 | 0.199 |
| Tangshan | 0.104 | 0.110 | 0.114 | 0.119 | 0.121 | 0.125 | 0.131 | 0.131 | 0.145 | 0.148 | 0.149 |
| Qinhuangdao | 0.098 | 0.100 | 0.101 | 0.104 | 0.107 | 0.113 | 0.116 | 0.122 | 0.129 | 0.133 | 0.132 |
| Baotou | 0.126 | 0.133 | 0.136 | 0.142 | 0.144 | 0.147 | 0.153 | 0.144 | 0.154 | 0.148 | 0.134 |
| Dandong | 0.077 | 0.077 | 0.082 | 0.092 | 0.094 | 0.091 | 0.105 | 0.106 | 0.098 | 0.106 | 0.101 |
| Jinzhou | 0.075 | 0.082 | 0.091 | 0.091 | 0.087 | 0.084 | 0.095 | 0.093 | 0.093 | 0.099 | 0.096 |
| Jilin | 0.084 | 0.088 | 0.091 | 0.097 | 0.107 | 0.107 | 0.103 | 0.109 | 0.112 | 0.114 | 0.119 |
| Mudanjiang | 0.079 | 0.082 | 0.081 | 0.085 | 0.090 | 0.086 | 0.087 | 0.099 | 0.092 | 0.102 | 0.102 |
| Wuxi | 0.162 | 0.178 | 0.189 | 0.207 | 0.203 | 0.211 | 0.219 | 0.230 | 0.245 | 0.251 | 0.239 |
| Yangzhou | 0.086 | 0.098 | 0.102 | 0.108 | 0.115 | 0.123 | 0.130 | 0.138 | 0.148 | 0.157 | 0.159 |
| Xuzhou | 0.101 | 0.108 | 0.115 | 0.123 | 0.128 | 0.134 | 0.139 | 0.143 | 0.150 | 0.154 | 0.160 |
| Wenzhou | 0.113 | 0.117 | 0.127 | 0.129 | 0.134 | 0.141 | 0.147 | 0.154 | 0.160 | 0.169 | 0.168 |
| Jinhua | 0.086 | 0.088 | 0.092 | 0.095 | 0.102 | 0.111 | 0.118 | 0.125 | 0.132 | 0.140 | 0.137 |
| Bengbu | 0.095 | 0.096 | 0.102 | 0.106 | 0.104 | 0.109 | 0.113 | 0.124 | 0.120 | 0.130 | 0.138 |
| Anqing | 0.089 | 0.090 | 0.090 | 0.099 | 0.095 | 0.094 | 0.099 | 0.099 | 0.106 | 0.107 | 0.115 |
| Quanzhou | 0.118 | 0.123 | 0.128 | 0.131 | 0.135 | 0.139 | 0.144 | 0.159 | 0.163 | 0.172 | 0.165 |
| Jiujiang | 0.100 | 0.099 | 0.088 | 0.091 | 0.093 | 0.098 | 0.096 | 0.105 | 0.103 | 0.109 | 0.114 |
| Ganzhou | 0.103 | 0.101 | 0.105 | 0.110 | 0.111 | 0.117 | 0.118 | 0.122 | 0.125 | 0.129 | 0.136 |
| Yantai | 0.103 | 0.110 | 0.116 | 0.121 | 0.127 | 0.130 | 0.138 | 0.147 | 0.165 | 0.165 | 0.166 |
| Jining | 0.090 | 0.099 | 0.108 | 0.116 | 0.117 | 0.118 | 0.122 | 0.128 | 0.134 | 0.139 | 0.148 |
| Luoyang | 0.104 | 0.108 | 0.110 | 0.111 | 0.114 | 0.116 | 0.118 | 0.125 | 0.120 | 0.130 | 0.136 |
| Pingdingshan | 0.087 | 0.089 | 0.096 | 0.099 | 0.101 | 0.103 | 0.105 | 0.114 | 0.112 | 0.120 | 0.116 |
| Yichang | 0.070 | 0.073 | 0.079 | 0.086 | 0.099 | 0.107 | 0.109 | 0.110 | 0.114 | 0.123 | 0.115 |
| Xiangyang | 0.066 | 0.069 | 0.072 | 0.080 | 0.080 | 0.094 | 0.103 | 0.108 | 0.110 | 0.119 | 0.115 |
| Yueyang | 0.079 | 0.077 | 0.080 | 0.081 | 0.083 | 0.100 | 0.099 | 0.111 | 0.105 | 0.112 | 0.123 |
| Changde | 0.069 | 0.071 | 0.077 | 0.080 | 0.078 | 0.091 | 0.090 | 0.095 | 0.105 | 0.110 | 0.107 |
| Huizhou | 0.116 | 0.118 | 0.123 | 0.127 | 0.139 | 0.141 | 0.150 | 0.154 | 0.161 | 0.165 | 0.144 |
| Zhanjiang | 0.100 | 0.100 | 0.103 | 0.101 | 0.092 | 0.102 | 0.098 | 0.104 | 0.105 | 0.109 | 0.123 |
| Shaoguan | 0.077 | 0.077 | 0.080 | 0.084 | 0.079 | 0.083 | 0.087 | 0.095 | 0.096 | 0.101 | 0.102 |
| Guilin | 0.084 | 0.087 | 0.085 | 0.091 | 0.089 | 0.090 | 0.088 | 0.108 | 0.105 | 0.112 | 0.109 |
| Beihai | 0.087 | 0.092 | 0.089 | 0.094 | 0.095 | 0.099 | 0.100 | 0.107 | 0.115 | 0.118 | 0.121 |
| Sanya | 0.140 | 0.148 | 0.156 | 0.163 | 0.171 | 0.182 | 0.180 | 0.183 | 0.207 | 0.216 | 0.163 |
| Luzhou | 0.068 | 0.071 | 0.075 | 0.084 | 0.082 | 0.082 | 0.068 | 0.093 | 0.099 | 0.107 | 0.117 |
| Nanchong | 0.064 | 0.067 | 0.070 | 0.078 | 0.077 | 0.081 | 0.086 | 0.093 | 0.098 | 0.102 | 0.106 |
| Zunyi | 0.100 | 0.100 | 0.099 | 0.103 | 0.095 | 0.096 | 0.101 | 0.109 | 0.106 | 0.111 | 0.115 |
| Dali | 0.140 | 0.135 | 0.139 | 0.135 | 0.133 | 0.138 | 0.143 | 0.152 | 0.149 | 0.153 | 0.165 |
| Average | 0.131 | 0.137 | 0.145 | 0.153 | 0.156 | 0.164 | 0.171 | 0.180 | 0.187 | 0.194 | 0.188 |
| City | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Beijing | 0.266 | 0.292 | 0.296 | 0.307 | 0.302 | 0.324 | 0.400 | 0.387 | 0.382 | 0.405 | 0.388 |
| Tianjin | 0.221 | 0.282 | 0.284 | 0.228 | 0.247 | 0.204 | 0.279 | 0.247 | 0.300 | 0.299 | 0.279 |
| Shijiazhuang | 0.112 | 0.132 | 0.130 | 0.138 | 0.134 | 0.139 | 0.158 | 0.159 | 0.175 | 0.166 | 0.171 |
| Hohhot | 0.119 | 0.129 | 0.141 | 0.148 | 0.141 | 0.140 | 0.153 | 0.141 | 0.152 | 0.158 | 0.137 |
| Taiyuan | 0.106 | 0.128 | 0.133 | 0.129 | 0.129 | 0.136 | 0.142 | 0.142 | 0.144 | 0.159 | 0.148 |
| Shenyang | 0.118 | 0.124 | 0.137 | 0.151 | 0.151 | 0.143 | 0.147 | 0.148 | 0.158 | 0.165 | 0.161 |
| Dalian | 0.119 | 0.171 | 0.142 | 0.153 | 0.139 | 0.140 | 0.141 | 0.147 | 0.160 | 0.162 | 0.157 |
| Changchun | 0.129 | 0.132 | 0.147 | 0.128 | 0.139 | 0.132 | 0.137 | 0.146 | 0.158 | 0.164 | 0.166 |
| Harbin | 0.124 | 0.143 | 0.123 | 0.113 | 0.123 | 0.123 | 0.128 | 0.135 | 0.140 | 0.142 | 0.140 |
| Shanghai | 0.241 | 0.324 | 0.305 | 0.292 | 0.316 | 0.337 | 0.371 | 0.403 | 0.429 | 0.449 | 0.458 |
| Nanjing | 0.189 | 0.293 | 0.218 | 0.235 | 0.247 | 0.217 | 0.269 | 0.301 | 0.306 | 0.317 | 0.322 |
| Hangzhou | 0.157 | 0.171 | 0.230 | 0.237 | 0.214 | 0.195 | 0.251 | 0.243 | 0.271 | 0.301 | 0.295 |
| Ningbo | 0.232 | 0.154 | 0.265 | 0.244 | 0.207 | 0.178 | 0.214 | 0.210 | 0.266 | 0.280 | 0.275 |
| Hefei | 0.123 | 0.147 | 0.170 | 0.157 | 0.163 | 0.132 | 0.179 | 0.185 | 0.189 | 0.212 | 0.203 |
| Fuzhou | 0.114 | 0.126 | 0.126 | 0.134 | 0.138 | 0.148 | 0.154 | 0.161 | 0.175 | 0.182 | 0.183 |
| Xiamen | 0.167 | 0.189 | 0.189 | 0.192 | 0.195 | 0.203 | 0.214 | 0.227 | 0.235 | 0.243 | 0.210 |
| Nanchang | 0.099 | 0.111 | 0.116 | 0.184 | 0.132 | 0.136 | 0.155 | 0.148 | 0.164 | 0.179 | 0.178 |
| Jinan | 0.143 | 0.147 | 0.145 | 0.159 | 0.177 | 0.175 | 0.189 | 0.198 | 0.209 | 0.220 | 0.226 |
| Qingdao | 0.131 | 0.180 | 0.174 | 0.190 | 0.181 | 0.174 | 0.194 | 0.193 | 0.234 | 0.234 | 0.235 |
| Zhengzhou | 0.177 | 0.165 | 0.139 | 0.161 | 0.210 | 0.224 | 0.219 | 0.224 | 0.241 | 0.244 | 0.249 |
| Wuhan | 0.137 | 0.189 | 0.196 | 0.249 | 0.204 | 0.205 | 0.201 | 0.215 | 0.249 | 0.259 | 0.247 |
| Changsha | 0.143 | 0.149 | 0.180 | 0.174 | 0.194 | 0.181 | 0.214 | 0.201 | 0.240 | 0.244 | 0.251 |
| Guangzhou | 0.199 | 0.226 | 0.223 | 0.240 | 0.244 | 0.266 | 0.266 | 0.285 | 0.306 | 0.322 | 0.313 |
| Shenzhen | 0.218 | 0.222 | 0.264 | 0.279 | 0.294 | 0.325 | 0.404 | 0.479 | 0.419 | 0.444 | 0.459 |
| Nanning | 0.114 | 0.123 | 0.109 | 0.129 | 0.118 | 0.126 | 0.127 | 0.132 | 0.141 | 0.145 | 0.152 |
| Haikou | 0.107 | 0.119 | 0.128 | 0.119 | 0.119 | 0.124 | 0.134 | 0.149 | 0.146 | 0.147 | 0.130 |
| Chongqing | 0.283 | 0.404 | 0.366 | 0.282 | 0.265 | 0.267 | 0.259 | 0.250 | 0.327 | 0.348 | 0.353 |
| Chengdu | 0.136 | 0.224 | 0.167 | 0.198 | 0.225 | 0.208 | 0.191 | 0.230 | 0.261 | 0.266 | 0.264 |
| Guiyang | 0.127 | 0.123 | 0.118 | 0.127 | 0.129 | 0.134 | 0.127 | 0.144 | 0.158 | 0.162 | 0.146 |
| Kunming | 0.116 | 0.147 | 0.168 | 0.148 | 0.151 | 0.156 | 0.162 | 0.163 | 0.166 | 0.171 | 0.162 |
| Xi’an | 0.131 | 0.146 | 0.177 | 0.203 | 0.195 | 0.192 | 0.193 | 0.188 | 0.205 | 0.234 | 0.225 |
| Lanzhou | 0.098 | 0.107 | 0.110 | 0.111 | 0.114 | 0.137 | 0.135 | 0.135 | 0.155 | 0.150 | 0.149 |
| Xining | 0.066 | 0.082 | 0.088 | 0.088 | 0.091 | 0.124 | 0.124 | 0.116 | 0.123 | 0.128 | 0.130 |
| Yinchuan | 0.108 | 0.134 | 0.140 | 0.135 | 0.152 | 0.155 | 0.145 | 0.144 | 0.173 | 0.165 | 0.155 |
| Urumqi | 0.111 | 0.121 | 0.120 | 0.122 | 0.158 | 0.147 | 0.154 | 0.180 | 0.201 | 0.224 | 0.178 |
| Tangshan | 0.096 | 0.122 | 0.106 | 0.110 | 0.113 | 0.120 | 0.125 | 0.126 | 0.139 | 0.144 | 0.143 |
| Qinhuangdao | 0.085 | 0.111 | 0.096 | 0.143 | 0.103 | 0.108 | 0.121 | 0.124 | 0.133 | 0.139 | 0.139 |
| Baotou | 0.111 | 0.138 | 0.129 | 0.135 | 0.141 | 0.139 | 0.146 | 0.136 | 0.148 | 0.146 | 0.139 |
| Dandong | 0.055 | 0.068 | 0.067 | 0.076 | 0.079 | 0.080 | 0.089 | 0.091 | 0.090 | 0.098 | 0.095 |
| Jinzhou | 0.066 | 0.078 | 0.083 | 0.091 | 0.086 | 0.083 | 0.087 | 0.088 | 0.091 | 0.097 | 0.096 |
| Jilin | 0.077 | 0.086 | 0.097 | 0.093 | 0.099 | 0.100 | 0.094 | 0.098 | 0.102 | 0.103 | 0.106 |
| Mudanjiang | 0.064 | 0.068 | 0.074 | 0.076 | 0.081 | 0.084 | 0.092 | 0.095 | 0.093 | 0.099 | 0.101 |
| Wuxi | 0.199 | 0.230 | 0.221 | 0.201 | 0.209 | 0.185 | 0.199 | 0.205 | 0.248 | 0.259 | 0.249 |
| Yangzhou | 0.085 | 0.120 | 0.111 | 0.109 | 0.118 | 0.127 | 0.143 | 0.159 | 0.166 | 0.179 | 0.181 |
| Xuzhou | 0.100 | 0.102 | 0.185 | 0.116 | 0.150 | 0.117 | 0.156 | 0.147 | 0.177 | 0.187 | 0.203 |
| Wenzhou | 0.113 | 0.129 | 0.180 | 0.198 | 0.213 | 0.148 | 0.179 | 0.222 | 0.225 | 0.228 | 0.227 |
| Jinhua | 0.104 | 0.110 | 0.124 | 0.148 | 0.150 | 0.136 | 0.157 | 0.158 | 0.175 | 0.183 | 0.181 |
| Bengbu | 0.082 | 0.081 | 0.090 | 0.092 | 0.123 | 0.116 | 0.121 | 0.113 | 0.118 | 0.129 | 0.134 |
| Anqing | 0.075 | 0.097 | 0.088 | 0.106 | 0.105 | 0.098 | 0.104 | 0.116 | 0.120 | 0.123 | 0.124 |
| Quanzhou | 0.111 | 0.131 | 0.131 | 0.133 | 0.137 | 0.140 | 0.146 | 0.154 | 0.161 | 0.173 | 0.170 |
| Jiujiang | 0.085 | 0.099 | 0.124 | 0.138 | 0.135 | 0.117 | 0.114 | 0.115 | 0.125 | 0.138 | 0.141 |
| Ganzhou | 0.103 | 0.131 | 0.127 | 0.202 | 0.128 | 0.117 | 0.117 | 0.131 | 0.161 | 0.185 | 0.171 |
| Yantai | 0.094 | 0.107 | 0.112 | 0.120 | 0.126 | 0.126 | 0.132 | 0.143 | 0.166 | 0.153 | 0.156 |
| Jining | 0.083 | 0.105 | 0.104 | 0.102 | 0.108 | 0.112 | 0.127 | 0.135 | 0.143 | 0.133 | 0.135 |
| Luoyang | 0.090 | 0.125 | 0.105 | 0.111 | 0.115 | 0.127 | 0.126 | 0.123 | 0.132 | 0.143 | 0.150 |
| Pingdingshan | 0.091 | 0.084 | 0.103 | 0.089 | 0.099 | 0.095 | 0.106 | 0.118 | 0.119 | 0.121 | 0.116 |
| Yichang | 0.065 | 0.079 | 0.087 | 0.107 | 0.126 | 0.159 | 0.133 | 0.138 | 0.144 | 0.145 | 0.135 |
| Xiangyang | 0.062 | 0.069 | 0.075 | 0.089 | 0.117 | 0.115 | 0.119 | 0.119 | 0.125 | 0.135 | 0.133 |
| Yueyang | 0.082 | 0.097 | 0.102 | 0.101 | 0.106 | 0.111 | 0.120 | 0.129 | 0.123 | 0.133 | 0.136 |
| Changde | 0.071 | 0.095 | 0.092 | 0.104 | 0.104 | 0.120 | 0.115 | 0.115 | 0.127 | 0.130 | 0.135 |
| Huizhou | 0.098 | 0.110 | 0.111 | 0.103 | 0.120 | 0.118 | 0.128 | 0.138 | 0.138 | 0.146 | 0.141 |
| Zhanjiang | 0.071 | 0.084 | 0.083 | 0.082 | 0.081 | 0.088 | 0.088 | 0.093 | 0.095 | 0.099 | 0.110 |
| Shaoguan | 0.069 | 0.078 | 0.081 | 0.083 | 0.080 | 0.095 | 0.090 | 0.095 | 0.097 | 0.102 | 0.104 |
| Guilin | 0.071 | 0.089 | 0.085 | 0.097 | 0.138 | 0.130 | 0.100 | 0.102 | 0.129 | 0.142 | 0.153 |
| Beihai | 0.087 | 0.102 | 0.100 | 0.087 | 0.097 | 0.096 | 0.095 | 0.100 | 0.107 | 0.113 | 0.108 |
| Sanya | 0.100 | 0.110 | 0.115 | 0.121 | 0.129 | 0.141 | 0.138 | 0.139 | 0.160 | 0.169 | 0.136 |
| Luzhou | 0.065 | 0.073 | 0.078 | 0.090 | 0.100 | 0.094 | 0.074 | 0.099 | 0.111 | 0.116 | 0.121 |
| Nanchong | 0.063 | 0.084 | 0.067 | 0.071 | 0.107 | 0.087 | 0.092 | 0.099 | 0.110 | 0.117 | 0.117 |
| Zunyi | 0.091 | 0.094 | 0.094 | 0.112 | 0.104 | 0.119 | 0.134 | 0.133 | 0.139 | 0.133 | 0.132 |
| Dali | 0.099 | 0.106 | 0.107 | 0.106 | 0.113 | 0.116 | 0.128 | 0.131 | 0.132 | 0.137 | 0.144 |
| Average | 0.283 | 0.404 | 0.366 | 0.307 | 0.316 | 0.337 | 0.404 | 0.479 | 0.429 | 0.449 | 0.459 |
| City | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Beijing | 0.991 | 0.995 | 0.990 | 0.983 | 0.971 | 0.971 | 0.998 | 0.988 | 0.976 | 0.980 | 0.982 |
| Tianjin | 0.994 | 0.971 | 0.984 | 0.990 | 0.988 | 0.906 | 0.993 | 0.964 | 0.999 | 0.999 | 0.999 |
| Shijiazhuang | 0.960 | 0.993 | 0.987 | 0.996 | 0.989 | 0.988 | 0.999 | 0.998 | 0.999 | 0.997 | 0.997 |
| Hohhot | 0.961 | 0.994 | 0.981 | 0.971 | 0.978 | 0.974 | 0.987 | 0.980 | 0.988 | 0.988 | 0.993 |
| Taiyuan | 0.941 | 0.981 | 0.977 | 0.960 | 0.950 | 0.957 | 0.963 | 0.949 | 0.960 | 0.973 | 0.983 |
| Shenyang | 0.961 | 0.957 | 0.972 | 0.982 | 0.980 | 0.964 | 0.982 | 0.969 | 0.976 | 0.981 | 0.980 |
| Dalian | 0.940 | 0.999 | 0.971 | 0.975 | 0.953 | 0.955 | 0.966 | 0.952 | 0.968 | 0.980 | 0.984 |
| Changchun | 0.996 | 0.994 | 0.999 | 0.971 | 0.988 | 0.960 | 0.971 | 0.980 | 0.987 | 0.993 | 0.995 |
| Harbin | 0.996 | 0.999 | 0.984 | 0.960 | 0.978 | 0.964 | 0.970 | 0.973 | 0.977 | 0.990 | 0.988 |
| Shanghai | 0.955 | 0.999 | 0.990 | 0.963 | 0.977 | 0.969 | 0.975 | 0.982 | 0.981 | 0.978 | 0.978 |
| Nanjing | 0.999 | 0.960 | 0.999 | 0.999 | 0.999 | 0.971 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 |
| Hangzhou | 0.994 | 0.997 | 0.986 | 0.990 | 0.999 | 0.987 | 0.999 | 0.998 | 0.999 | 0.998 | 0.995 |
| Ningbo | 0.923 | 0.999 | 0.915 | 0.955 | 0.988 | 0.999 | 0.996 | 0.999 | 0.989 | 0.990 | 0.987 |
| Hefei | 0.991 | 0.999 | 0.996 | 0.997 | 0.995 | 0.978 | 0.998 | 0.999 | 0.999 | 0.999 | 0.999 |
| Fuzhou | 0.973 | 0.993 | 0.987 | 0.986 | 0.992 | 0.993 | 0.992 | 0.990 | 0.998 | 0.995 | 0.996 |
| Xiamen | 0.912 | 0.939 | 0.916 | 0.901 | 0.902 | 0.905 | 0.926 | 0.930 | 0.939 | 0.941 | 0.966 |
| Nanchang | 0.972 | 0.987 | 0.974 | 0.990 | 0.990 | 0.979 | 0.997 | 0.995 | 0.999 | 0.999 | 0.999 |
| Jinan | 0.994 | 0.991 | 0.988 | 0.993 | 0.993 | 0.985 | 0.991 | 0.995 | 0.995 | 0.996 | 0.999 |
| Qingdao | 0.987 | 0.997 | 0.999 | 0.999 | 0.992 | 0.973 | 0.988 | 0.979 | 0.997 | 0.996 | 0.998 |
| Zhengzhou | 0.989 | 0.999 | 0.982 | 0.997 | 0.992 | 0.993 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 |
| Wuhan | 0.972 | 0.999 | 0.999 | 0.990 | 0.998 | 0.993 | 0.979 | 0.980 | 0.991 | 0.987 | 0.989 |
| Changsha | 0.999 | 0.999 | 0.994 | 0.999 | 0.999 | 0.994 | 0.999 | 0.991 | 0.999 | 0.999 | 0.999 |
| Guangzhou | 0.954 | 0.980 | 0.961 | 0.954 | 0.962 | 0.972 | 0.958 | 0.970 | 0.961 | 0.963 | 0.988 |
| Shenzhen | 0.886 | 0.962 | 0.904 | 0.894 | 0.886 | 0.898 | 0.968 | 0.989 | 0.937 | 0.934 | 0.931 |
| Nanning | 0.988 | 0.995 | 0.963 | 0.995 | 0.970 | 0.982 | 0.976 | 0.983 | 0.989 | 0.984 | 0.994 |
| Haikou | 0.903 | 0.907 | 0.924 | 0.920 | 0.935 | 0.936 | 0.946 | 0.952 | 0.942 | 0.949 | 0.971 |
| Chongqing | 0.922 | 0.860 | 0.909 | 0.976 | 0.990 | 0.996 | 0.999 | 0.997 | 0.987 | 0.989 | 0.985 |
| Chengdu | 0.997 | 0.953 | 0.999 | 0.998 | 0.993 | 0.999 | 0.994 | 0.999 | 0.999 | 0.999 | 0.999 |
| Guiyang | 0.999 | 0.999 | 0.987 | 0.995 | 0.984 | 0.992 | 0.977 | 0.982 | 0.998 | 0.997 | 0.999 |
| Kunming | 0.958 | 0.999 | 0.999 | 0.995 | 0.984 | 0.984 | 0.987 | 0.984 | 0.988 | 0.995 | 0.999 |
| Xi’an | 0.992 | 0.997 | 0.999 | 0.993 | 0.998 | 0.999 | 0.999 | 0.997 | 0.999 | 0.999 | 0.998 |
| Lanzhou | 0.972 | 0.984 | 0.964 | 0.972 | 0.983 | 0.996 | 0.989 | 0.980 | 0.995 | 0.997 | 0.999 |
| Xining | 0.933 | 0.988 | 0.968 | 0.994 | 0.980 | 0.996 | 0.999 | 0.997 | 0.998 | 0.993 | 0.994 |
| Yinchuan | 0.991 | 0.998 | 0.997 | 0.999 | 0.995 | 0.997 | 0.999 | 0.995 | 0.998 | 0.998 | 0.995 |
| Urumqi | 0.923 | 0.939 | 0.911 | 0.879 | 0.977 | 0.928 | 0.945 | 0.956 | 0.978 | 0.971 | 0.993 |
| Tangshan | 0.997 | 0.995 | 0.997 | 0.996 | 0.998 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 |
| Qinhuangdao | 0.989 | 0.995 | 0.999 | 0.963 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 |
| Baotou | 0.991 | 0.999 | 0.999 | 0.999 | 0.999 | 0.998 | 0.999 | 0.998 | 0.999 | 0.999 | 0.999 |
| Dandong | 0.916 | 0.992 | 0.974 | 0.976 | 0.980 | 0.990 | 0.984 | 0.986 | 0.996 | 0.997 | 0.998 |
| Jinzhou | 0.990 | 0.999 | 0.996 | 0.999 | 0.999 | 0.999 | 0.997 | 0.998 | 0.999 | 0.999 | 0.999 |
| Jilin | 0.996 | 0.999 | 0.998 | 0.999 | 0.996 | 0.998 | 0.996 | 0.993 | 0.995 | 0.994 | 0.993 |
| Mudanjiang | 0.974 | 0.980 | 0.996 | 0.993 | 0.994 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 |
| Wuxi | 0.983 | 0.974 | 0.989 | 0.999 | 0.999 | 0.990 | 0.995 | 0.993 | 0.999 | 0.999 | 0.999 |
| Yangzhou | 0.999 | 0.983 | 0.997 | 0.999 | 0.999 | 0.999 | 0.996 | 0.992 | 0.994 | 0.992 | 0.992 |
| Xuzhou | 0.999 | 0.998 | 0.926 | 0.998 | 0.989 | 0.988 | 0.994 | 0.999 | 0.989 | 0.984 | 0.977 |
| Wenzhou | 0.999 | 0.996 | 0.956 | 0.937 | 0.930 | 0.999 | 0.983 | 0.953 | 0.957 | 0.966 | 0.966 |
| Jinhua | 0.985 | 0.980 | 0.964 | 0.933 | 0.947 | 0.983 | 0.970 | 0.978 | 0.969 | 0.971 | 0.970 |
| Bengbu | 0.989 | 0.985 | 0.991 | 0.987 | 0.988 | 0.998 | 0.998 | 0.995 | 0.999 | 0.999 | 0.999 |
| Anqing | 0.982 | 0.997 | 0.999 | 0.998 | 0.996 | 0.999 | 0.999 | 0.989 | 0.993 | 0.992 | 0.997 |
| Quanzhou | 0.998 | 0.998 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 |
| Jiujiang | 0.985 | 0.999 | 0.957 | 0.940 | 0.949 | 0.988 | 0.987 | 0.996 | 0.984 | 0.978 | 0.982 |
| Ganzhou | 0.999 | 0.973 | 0.985 | 0.891 | 0.991 | 0.999 | 0.999 | 0.998 | 0.974 | 0.953 | 0.978 |
| Yantai | 0.996 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.997 | 0.998 |
| Jining | 0.996 | 0.998 | 0.999 | 0.991 | 0.997 | 0.998 | 0.999 | 0.998 | 0.998 | 0.999 | 0.995 |
| Luoyang | 0.988 | 0.990 | 0.999 | 0.999 | 0.999 | 0.996 | 0.998 | 0.999 | 0.996 | 0.996 | 0.995 |
| Pingdingshan | 0.999 | 0.999 | 0.998 | 0.994 | 0.999 | 0.996 | 0.999 | 0.999 | 0.998 | 0.999 | 0.999 |
| Yichang | 0.997 | 0.998 | 0.996 | 0.981 | 0.977 | 0.944 | 0.983 | 0.980 | 0.977 | 0.989 | 0.989 |
| Xiangyang | 0.998 | 0.999 | 0.999 | 0.995 | 0.951 | 0.983 | 0.990 | 0.996 | 0.993 | 0.993 | 0.991 |
| Yueyang | 0.999 | 0.978 | 0.976 | 0.981 | 0.976 | 0.995 | 0.985 | 0.990 | 0.989 | 0.987 | 0.995 |
| Changde | 0.999 | 0.968 | 0.986 | 0.972 | 0.969 | 0.971 | 0.977 | 0.984 | 0.985 | 0.988 | 0.978 |
| Huizhou | 0.984 | 0.997 | 0.994 | 0.972 | 0.988 | 0.980 | 0.984 | 0.993 | 0.986 | 0.991 | 0.999 |
| Zhanjiang | 0.917 | 0.981 | 0.972 | 0.970 | 0.991 | 0.987 | 0.994 | 0.993 | 0.995 | 0.995 | 0.993 |
| Shaoguan | 0.992 | 0.999 | 0.999 | 0.999 | 0.999 | 0.992 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 |
| Guilin | 0.983 | 0.999 | 0.999 | 0.998 | 0.935 | 0.951 | 0.993 | 0.998 | 0.982 | 0.977 | 0.958 |
| Beihai | 0.999 | 0.995 | 0.994 | 0.997 | 0.999 | 0.999 | 0.999 | 0.998 | 0.997 | 0.999 | 0.992 |
| Sanya | 0.917 | 0.939 | 0.935 | 0.939 | 0.945 | 0.955 | 0.954 | 0.949 | 0.955 | 0.961 | 0.979 |
| Luzhou | 0.999 | 0.999 | 0.999 | 0.998 | 0.985 | 0.991 | 0.997 | 0.998 | 0.994 | 0.997 | 0.999 |
| Nanchong | 0.999 | 0.979 | 0.999 | 0.994 | 0.959 | 0.997 | 0.998 | 0.998 | 0.994 | 0.992 | 0.996 |
| Zunyi | 0.996 | 0.998 | 0.998 | 0.997 | 0.996 | 0.981 | 0.970 | 0.984 | 0.972 | 0.986 | 0.992 |
| Dali | 0.911 | 0.960 | 0.955 | 0.961 | 0.984 | 0.982 | 0.993 | 0.987 | 0.991 | 0.993 | 0.989 |
| Average | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 |
| City | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Beijing | 0.513 | 0.539 | 0.541 | 0.550 | 0.541 | 0.561 | 0.632 | 0.618 | 0.611 | 0.630 | 0.617 |
| Tianjin | 0.469 | 0.524 | 0.529 | 0.475 | 0.494 | 0.430 | 0.527 | 0.488 | 0.547 | 0.547 | 0.528 |
| Shijiazhuang | 0.328 | 0.361 | 0.358 | 0.370 | 0.364 | 0.371 | 0.397 | 0.399 | 0.418 | 0.407 | 0.413 |
| Hohhot | 0.338 | 0.358 | 0.371 | 0.379 | 0.371 | 0.369 | 0.389 | 0.372 | 0.388 | 0.395 | 0.369 |
| Taiyuan | 0.315 | 0.354 | 0.360 | 0.352 | 0.350 | 0.361 | 0.370 | 0.368 | 0.372 | 0.393 | 0.381 |
| Shenyang | 0.336 | 0.344 | 0.365 | 0.385 | 0.384 | 0.371 | 0.380 | 0.379 | 0.392 | 0.403 | 0.397 |
| Dalian | 0.335 | 0.414 | 0.371 | 0.387 | 0.364 | 0.366 | 0.369 | 0.374 | 0.393 | 0.399 | 0.394 |
| Changchun | 0.358 | 0.363 | 0.384 | 0.352 | 0.371 | 0.356 | 0.365 | 0.378 | 0.395 | 0.403 | 0.406 |
| Harbin | 0.352 | 0.378 | 0.347 | 0.330 | 0.347 | 0.344 | 0.352 | 0.362 | 0.370 | 0.375 | 0.372 |
| Shanghai | 0.480 | 0.569 | 0.550 | 0.531 | 0.556 | 0.571 | 0.602 | 0.629 | 0.648 | 0.663 | 0.670 |
| Nanjing | 0.435 | 0.530 | 0.467 | 0.485 | 0.496 | 0.459 | 0.519 | 0.549 | 0.553 | 0.563 | 0.567 |
| Hangzhou | 0.395 | 0.413 | 0.477 | 0.484 | 0.463 | 0.439 | 0.501 | 0.492 | 0.521 | 0.548 | 0.542 |
| Ningbo | 0.463 | 0.392 | 0.493 | 0.483 | 0.453 | 0.422 | 0.462 | 0.458 | 0.513 | 0.527 | 0.521 |
| Hefei | 0.349 | 0.383 | 0.411 | 0.396 | 0.403 | 0.359 | 0.423 | 0.430 | 0.435 | 0.460 | 0.450 |
| Fuzhou | 0.333 | 0.353 | 0.353 | 0.363 | 0.370 | 0.383 | 0.391 | 0.400 | 0.418 | 0.426 | 0.427 |
| Xiamen | 0.390 | 0.421 | 0.416 | 0.416 | 0.419 | 0.428 | 0.446 | 0.460 | 0.469 | 0.478 | 0.451 |
| Nanchang | 0.310 | 0.331 | 0.336 | 0.427 | 0.361 | 0.364 | 0.393 | 0.384 | 0.405 | 0.423 | 0.422 |
| Jinan | 0.378 | 0.382 | 0.378 | 0.398 | 0.419 | 0.416 | 0.433 | 0.444 | 0.456 | 0.469 | 0.475 |
| Qingdao | 0.360 | 0.423 | 0.417 | 0.436 | 0.424 | 0.411 | 0.437 | 0.435 | 0.483 | 0.483 | 0.484 |
| Zhengzhou | 0.419 | 0.407 | 0.370 | 0.400 | 0.457 | 0.472 | 0.468 | 0.473 | 0.491 | 0.493 | 0.499 |
| Wuhan | 0.365 | 0.434 | 0.442 | 0.496 | 0.451 | 0.451 | 0.443 | 0.460 | 0.496 | 0.505 | 0.495 |
| Changsha | 0.378 | 0.386 | 0.423 | 0.417 | 0.440 | 0.424 | 0.462 | 0.446 | 0.490 | 0.494 | 0.501 |
| Guangzhou | 0.435 | 0.471 | 0.463 | 0.479 | 0.485 | 0.509 | 0.504 | 0.526 | 0.542 | 0.557 | 0.557 |
| Shenzhen | 0.440 | 0.462 | 0.488 | 0.499 | 0.511 | 0.540 | 0.625 | 0.688 | 0.626 | 0.644 | 0.654 |
| Nanning | 0.336 | 0.350 | 0.325 | 0.359 | 0.338 | 0.351 | 0.352 | 0.360 | 0.373 | 0.377 | 0.389 |
| Haikou | 0.310 | 0.328 | 0.344 | 0.331 | 0.333 | 0.340 | 0.356 | 0.376 | 0.370 | 0.374 | 0.355 |
| Chongqing | 0.511 | 0.590 | 0.577 | 0.525 | 0.512 | 0.515 | 0.509 | 0.499 | 0.568 | 0.587 | 0.589 |
| Chengdu | 0.368 | 0.462 | 0.408 | 0.444 | 0.473 | 0.455 | 0.436 | 0.480 | 0.511 | 0.515 | 0.514 |
| Guiyang | 0.356 | 0.350 | 0.341 | 0.355 | 0.356 | 0.365 | 0.352 | 0.376 | 0.398 | 0.401 | 0.383 |
| Kunming | 0.333 | 0.383 | 0.409 | 0.384 | 0.385 | 0.392 | 0.400 | 0.401 | 0.404 | 0.413 | 0.402 |
| Xi’an | 0.360 | 0.382 | 0.421 | 0.448 | 0.442 | 0.438 | 0.440 | 0.433 | 0.453 | 0.483 | 0.474 |
| Lanzhou | 0.309 | 0.324 | 0.325 | 0.329 | 0.334 | 0.369 | 0.365 | 0.364 | 0.392 | 0.386 | 0.386 |
| Xining | 0.248 | 0.285 | 0.292 | 0.296 | 0.299 | 0.352 | 0.351 | 0.341 | 0.350 | 0.356 | 0.359 |
| Yinchuan | 0.327 | 0.365 | 0.373 | 0.367 | 0.389 | 0.394 | 0.381 | 0.379 | 0.415 | 0.406 | 0.393 |
| Urumqi | 0.320 | 0.337 | 0.330 | 0.328 | 0.392 | 0.370 | 0.382 | 0.414 | 0.444 | 0.467 | 0.421 |
| Tangshan | 0.310 | 0.348 | 0.325 | 0.331 | 0.335 | 0.347 | 0.353 | 0.355 | 0.373 | 0.379 | 0.378 |
| Qinhuangdao | 0.290 | 0.332 | 0.310 | 0.371 | 0.321 | 0.328 | 0.347 | 0.352 | 0.365 | 0.373 | 0.373 |
| Baotou | 0.331 | 0.372 | 0.360 | 0.367 | 0.376 | 0.373 | 0.382 | 0.369 | 0.385 | 0.382 | 0.372 |
| Dandong | 0.225 | 0.260 | 0.256 | 0.272 | 0.278 | 0.281 | 0.296 | 0.300 | 0.299 | 0.312 | 0.309 |
| Jinzhou | 0.255 | 0.279 | 0.288 | 0.302 | 0.293 | 0.288 | 0.295 | 0.296 | 0.302 | 0.311 | 0.310 |
| Jilin | 0.277 | 0.294 | 0.311 | 0.306 | 0.314 | 0.316 | 0.306 | 0.312 | 0.318 | 0.320 | 0.325 |
| Mudanjiang | 0.250 | 0.259 | 0.271 | 0.274 | 0.284 | 0.290 | 0.303 | 0.308 | 0.305 | 0.314 | 0.317 |
| Wuxi | 0.442 | 0.474 | 0.468 | 0.448 | 0.457 | 0.427 | 0.445 | 0.451 | 0.498 | 0.509 | 0.499 |
| Yangzhou | 0.291 | 0.344 | 0.332 | 0.330 | 0.343 | 0.356 | 0.378 | 0.397 | 0.406 | 0.422 | 0.424 |
| Xuzhou | 0.316 | 0.319 | 0.414 | 0.340 | 0.385 | 0.339 | 0.394 | 0.384 | 0.418 | 0.429 | 0.445 |
| Wenzhou | 0.336 | 0.359 | 0.414 | 0.431 | 0.445 | 0.385 | 0.420 | 0.459 | 0.464 | 0.469 | 0.468 |
| Jinhua | 0.320 | 0.328 | 0.346 | 0.372 | 0.377 | 0.366 | 0.390 | 0.393 | 0.412 | 0.422 | 0.419 |
| Bengbu | 0.286 | 0.283 | 0.298 | 0.301 | 0.349 | 0.340 | 0.348 | 0.336 | 0.344 | 0.359 | 0.366 |
| Anqing | 0.271 | 0.311 | 0.297 | 0.325 | 0.323 | 0.313 | 0.322 | 0.339 | 0.346 | 0.349 | 0.352 |
| Quanzhou | 0.332 | 0.362 | 0.361 | 0.364 | 0.370 | 0.375 | 0.383 | 0.393 | 0.401 | 0.416 | 0.412 |
| Jiujiang | 0.290 | 0.315 | 0.344 | 0.360 | 0.358 | 0.339 | 0.336 | 0.339 | 0.351 | 0.367 | 0.372 |
| Ganzhou | 0.321 | 0.357 | 0.354 | 0.424 | 0.357 | 0.342 | 0.342 | 0.361 | 0.396 | 0.420 | 0.409 |
| Yantai | 0.307 | 0.327 | 0.335 | 0.347 | 0.355 | 0.355 | 0.363 | 0.378 | 0.407 | 0.391 | 0.394 |
| Jining | 0.287 | 0.323 | 0.323 | 0.318 | 0.328 | 0.334 | 0.356 | 0.368 | 0.378 | 0.364 | 0.366 |
| Luoyang | 0.299 | 0.352 | 0.324 | 0.333 | 0.339 | 0.355 | 0.355 | 0.350 | 0.362 | 0.377 | 0.386 |
| Pingdingshan | 0.302 | 0.290 | 0.320 | 0.297 | 0.314 | 0.307 | 0.325 | 0.343 | 0.345 | 0.348 | 0.340 |
| Yichang | 0.254 | 0.280 | 0.294 | 0.324 | 0.350 | 0.388 | 0.362 | 0.367 | 0.376 | 0.379 | 0.365 |
| Xiangyang | 0.249 | 0.263 | 0.274 | 0.298 | 0.333 | 0.337 | 0.343 | 0.345 | 0.352 | 0.366 | 0.363 |
| Yueyang | 0.287 | 0.308 | 0.316 | 0.315 | 0.322 | 0.333 | 0.344 | 0.357 | 0.349 | 0.362 | 0.368 |
| Changde | 0.267 | 0.303 | 0.301 | 0.319 | 0.317 | 0.341 | 0.335 | 0.337 | 0.353 | 0.359 | 0.363 |
| Huizhou | 0.311 | 0.330 | 0.333 | 0.317 | 0.345 | 0.340 | 0.355 | 0.370 | 0.369 | 0.381 | 0.376 |
| Zhanjiang | 0.256 | 0.286 | 0.284 | 0.281 | 0.283 | 0.294 | 0.297 | 0.304 | 0.307 | 0.315 | 0.331 |
| Shaoguan | 0.261 | 0.279 | 0.285 | 0.288 | 0.283 | 0.307 | 0.300 | 0.309 | 0.311 | 0.320 | 0.323 |
| Guilin | 0.264 | 0.298 | 0.292 | 0.311 | 0.359 | 0.352 | 0.314 | 0.319 | 0.356 | 0.372 | 0.383 |
| Beihai | 0.294 | 0.319 | 0.315 | 0.294 | 0.312 | 0.310 | 0.309 | 0.317 | 0.327 | 0.336 | 0.327 |
| Sanya | 0.303 | 0.321 | 0.328 | 0.338 | 0.349 | 0.366 | 0.363 | 0.363 | 0.390 | 0.403 | 0.365 |
| Luzhou | 0.256 | 0.270 | 0.279 | 0.299 | 0.313 | 0.306 | 0.271 | 0.315 | 0.332 | 0.340 | 0.347 |
| Nanchong | 0.250 | 0.287 | 0.259 | 0.265 | 0.320 | 0.295 | 0.303 | 0.314 | 0.331 | 0.340 | 0.342 |
| Zunyi | 0.302 | 0.306 | 0.306 | 0.334 | 0.322 | 0.342 | 0.360 | 0.361 | 0.368 | 0.362 | 0.362 |
| Dali | 0.300 | 0.319 | 0.320 | 0.319 | 0.333 | 0.338 | 0.356 | 0.360 | 0.362 | 0.369 | 0.378 |
| Average | 0.513 | 0.590 | 0.577 | 0.550 | 0.556 | 0.571 | 0.632 | 0.688 | 0.648 | 0.663 | 0.670 |
References
- Zhang, X.; Chen, N.C.; Sheng, H.; Ip, C.; Yang, L.; Chen, Y.; Sang, Z.; Tadesse, T.; Lim, T.P.Y.; Rajabifard, A.; et al. Urban drought challenge to 2030 sustainable development goals. Sci. Total Environ. 2019, 693, 133536. [Google Scholar] [CrossRef]
- He, Q.; Yang, J.; Gong, L. Study on micro-mechanism of the affordable housing community in urban renewal the case of Zunyi city, Guizhou province. Front. Environ. Sci. 2023, 11, 1149661. [Google Scholar] [CrossRef]
- Xiong, N.; Wong, S.; Ren, Y.; Shen, L. Regional Disparity in Urbanizing China: Empirical Study of Unbalanced Development Phenomenon of Towns in Southwest China. J. Urban Plan. Dev. 2020, 146, 05020013. [Google Scholar] [CrossRef]
- Xia, X.; Lin, K.; Ding, Y.; Dong, X.; Sun, H.; Hu, B. Research on the Coupling Coordination Relationships between Urban Function Mixing Degree and Urbanization Development Level Based on Information Entropy. Int. J. Environ. Res. Public Health 2021, 18, 242. [Google Scholar] [CrossRef] [PubMed]
- Zhou, R.; Chen, S.; Zhang, B. Smart city construction and new-type urbanization quality improvement. Sci. Rep. 2023, 13, 21074. [Google Scholar] [CrossRef]
- Adabre, M.A.; Chan, A.P.C. Critical success factors (CSFs) for sustainable affordable housing. Build. Environ. 2019, 156, 203–214. [Google Scholar] [CrossRef]
- Napoli, G.; Trovato, M.; Barbaro, S. Social Housing and Affordable Rent: The Effectiveness of Legal Thresholds of Rents in Two Italian Metropolitan Cities. Sustainability 2022, 14, 7172. [Google Scholar] [CrossRef]
- Han, X.; Zhao, X. Foreign experience and enlightenment of solving the problem of indemnificatory housing. Soc. Sci. 2018, 64–68. [Google Scholar]
- Zimmer, B.G. Participation of Migrants in Urban Structures. Read. Sociol. Migr. 1970, 20, 71–83. [Google Scholar]
- Guo, Y.; Yang, K. The Study on Identifying Housing Security Objects. Urban Stud. 2009, 16, 15–19+36. [Google Scholar]
- Wu, J.; Niu, Y. Research on the Definition of Scope of Housing Security Objects and Construction of Mechanism. Econ. Probl. 2018, 85–89. [Google Scholar] [CrossRef]
- Murry, M. Subsidized and unsubsidized housing starts: 1961–1977. Rev. Econ. Stat. 1983, 4, 590–597. [Google Scholar]
- Sinai, T.; Waldfogel, J. Do low-income housing subsidies increase housing consumption. J. Public Econ. 2005, 89, 2137–2164. [Google Scholar]
- Zhang, Y.; Li, G.; Xie, Y. A VAR-based Study on the Impaction of the Affordable Housing to the Private Housing. J. Cent. Univ. Financ. Econ. 2013, 79–82+96. [Google Scholar]
- Zou, X.; Ma, X.; Shi, X. How does Affordable Housing Supply Affect Commercial Housing Prices:Crowd out Supply or Divert Demand? J. Financ. Econ. 2021, 47, 49–63. [Google Scholar] [CrossRef]
- Wang, L.; Rong, X.; Mu, L. The Coupling Coordination Evaluation of Sustainable Development between Urbanization, Housing Prices, and Affordable Housing in China. Discret. Dyn. Nat. Soc. 2021, 2021, 3937226. [Google Scholar] [CrossRef]
- Baltagi, B.H.; Jing, L.I. Further evidence on the spatio–temporal model of house prices in the united states. J. Appl. Econom. 2014, 29, 515–522. [Google Scholar]
- Marom, N.; Carmon, N. Affordable housing plans in london and new york: Between marketplace and social mix. Hous. Stud. 2015, 30, 993–1015. [Google Scholar] [CrossRef]
- Casas, G.B.D.L. Can community land trust models work in peru? Researching community-based land tenure models for affordable housing. J. Prop. Plan. Environ. Law 2023, 15, 194–211. [Google Scholar]
- Abelson, P. Affordable housing: Concepts and policies. Econ. Pap. A J. Appl. Econ. Policy 2009, 28, 27. [Google Scholar] [CrossRef]
- Holden, M. Urban indicators and the integrative ideals of cities. Cities 2006, 23, 170–183. [Google Scholar] [CrossRef]
- Martínez, J.; Mboup, G.; Sliuzas, R.; Stein, A. Trends in urban and slum indicators across developing world cities, 1990–2003. Habitat Int. 2008, 32, 86–108. [Google Scholar] [CrossRef]
- World Health Organization (WHO). CBR—A Strategy for Rehabilitation, Equalization of Opportunities, Poverty Reduction and Social Inclusion of People with Disabilities; Joint position paper; UNESCO: Paris, France, 2010. [Google Scholar]
- Taylor, P.J. New political geographies: Global civil society and global governance through world city networks. Political Geogr. 2005, 24, 703–730. [Google Scholar] [CrossRef]
- Taylor, P.J. World City Network: A Global Urban Analysis; Routledge: London, UK, 2010. [Google Scholar]
- Mosannenzadeh, F.; Bisello, A.; Vaccaro, R.; D’ALonzo, V.; Hunter, G.W.; Vettorato, D. Smart energy city development: A story told by urban planners. Cities 2017, 64, 54–65. [Google Scholar] [CrossRef]
- Hao, P.; Hooimeijer, P.; Sliuzas, R.; Geertman, S. What drives the spatial development of urban villages in china? Urban Stud. 2013, 50, 3394–3411. [Google Scholar] [CrossRef]
- Zhang, S.; Xia, Y.; Li, Z.; Li, X.; Wu, Y.; Liu, P.; Du, S. An assessment of urban residential environment quality based on multi-source geospatial data: A case study of Beijing, China. Land 2024, 13, 13060823. [Google Scholar] [CrossRef]
- Tang, D. A Study on the Interactive Relationship Between the Development of New Towns and Housing Security in the Process of the Rapid Urbanization. Ph.D. Thesis, Southeast University, Nanjing, China, 2019. [Google Scholar]
- Wang, W. Research on the Mechanism and Impact of Affordable Housing Supply on Urban Inclusive Growth: A Framework Based on the Integration of Citizenization and Domestic Demand. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2019. [Google Scholar]
- Yan, J.; Feng, C.; Li, L. Sustainability assessment of machining process based on extension theory and entropy weight approach. Int. J. Adv. Manuf. Technol. 2014, 71, 1419–1431. [Google Scholar] [CrossRef]
- Sun, Y.; Cui, Y. Analyzing the coupling coordination among economic, social, and environmental benefits of urban infrastructure: Case study of four chinese autonomous municipalities. Math. Probl. Eng. 2018, 2018, 1–13. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.; Zhou, Y.; Shi, Y.; Zhu, X. Investigation of a coupling model of coordination between urbanization and the environment. J. Environ. Manag. 2012, 98, 127–133. [Google Scholar] [CrossRef]
- Liao, K.; Yue, M.; Sun, S.; Xue, H.-B.; Liu, W.; Tsai, S.-B.; Wang, J.-T. An evaluation of coupling coordination between tourism and finance. Sustainability 2018, 10, 2320. [Google Scholar] [CrossRef]
- Liu, P.; Zhu, B.; Yang, M.; De Baets, B. High-quality marine economic development in china from the perspective of green total factor productivity growth: Dynamic changes and improvement strategies. Technol. Econ. Dev. Econ. 2024, 30, 22018. [Google Scholar] [CrossRef]
- Iseki, H.; Eom, H. Impacts of rail transit accessibility on firm spatial distribution: Case study in the metropolitan area of washington, DC. Transp. Res. Rec. 2019, 2673, 220–232. [Google Scholar]
- Yu, T.; Jia, S.; Cui, X. From efficiency to resilience: Unraveling the dynamic coupling of land use economic efficiency and urban ecological resilience in yellow river basin. Sci. Rep. 2024, 14, 16518. [Google Scholar] [CrossRef]
- Zhang, J.; Lin, B.; Zhou, Y. Kernel density estimation for partial linear multivariate responses models. J. Multivar. Anal. 2021, 185, 104768. [Google Scholar] [CrossRef]
- Wu, G.; Li, C.; Niu, X. Housing affordability evaluation based on the third-generation prospect theory and the improved VIKOR method. J. Intell. Fuzzy Syst. 2022, 42, 1405–1420. [Google Scholar] [CrossRef]
- Zhou, B.; Zhang, L. Research on Evaluation Method and Index System of Public Housing Policy. Urban Dev. Stud. 2020, 27, 111–117. [Google Scholar]
- Tannis, C.; Senerat, A.; Garg, M.; Peters, D.; Rajupet, S.; Garland, E. Improving physical activity among residents of affordable housing: Is active design enough? Int. J. Environ. Res. Public Health 2019, 16, 151. [Google Scholar] [PubMed]
- Shi, J.; Li, J. Research on Shanghai housing security policy effect based on the evaluation method of prospect theory. Syst. Eng. Theory Pract. 2019, 39, 89–99. [Google Scholar]
- Zhang, Y.; Zhang, Y.; Jia, Q. Study on Coordination of the Affordable and Commercialized Housing Market Under the Background of Coordinated Development of Beijing, Tianjin and Hebei Based on Coupling Model. J. Eng. Manag. 2018, 32, 141–146. [Google Scholar]
- Grossman, V.; Martínez-García, E.; Torres, L.; Sunc, Y. Drilling Down: The Impact of Oil Price Shocks on Housing Prices. Energy J. 2019, 40, 59–84. [Google Scholar] [CrossRef]
- Li, B. Analysis on Performance Characteristics of Affordable Housing Policy in China. J. Financ. Econ. 2008, 34, 129–139. [Google Scholar]
- Xie, Q.; Yi, F.; Tian, X. Disparate changes of living standard in China: Perspective from Engel’s coefficient. China Agric. Econ. Rev. 2023, 15, 481–505. [Google Scholar] [CrossRef]
- Berto, R.; Cechet, G.; Stival, C.; Rosato, P. Affordable housing vs. urban land rent in widespread settlement areas. Sustainability 2020, 12, 3129. [Google Scholar] [CrossRef]
- Song, X.; Wang, S. Housing investment model under high housing prices in Beijing. In International Conference on Education, Management, Computer and Society (ICEMCS), Proceeding of the 2017 International Conference on Society Science (ICOSS 2017), Colombo, Sri Lanka, 21–22 September 2017; Atlantis Press: Paris, France, 2017; pp. 288–293. [Google Scholar]
- Lin, Y.; Ma, Z.; Zhao, K.; Hu, W.; Wei, J. The impact of population migration on urban housing prices: Evidence from China’s major cities. Sustainability 2018, 10, 3169. [Google Scholar] [CrossRef]
- Xing, L.; Xue, M.; Hu, M. Dynamic simulation and assessment of the coupling coordiantion degree of the economy-resource-environment system: Case of Wuhan city in China. J. Environ. Manag. 2019, 230, 474–487. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Cui, Z.; Lin, J.; Xie, J.; Su, K. Coupling relationship between urbanization and ecological resilience in the Pearl River Delta. Acta Geogr. Sin. 2021, 76, 973–991. [Google Scholar] [CrossRef]
- Cui, X.; Fang, C.; Liu, H.; Liu, X. Assessing sustainability of urbanization by a coordinated development index for an urbanization-resources-environment complex system: A case study of Jing-jin-ji region, China. Ecol. Indic. 2019, 96, 383–391. [Google Scholar] [CrossRef]
- Jia, J.; Liang, X. Local Government Competition Strategy of Fiscal Revenue and Expenditure and Residents’ Income Distribution. China Ind. Econ. 2020, 38, 5–23. [Google Scholar]
- Ren, B.; Zhang, Q. The Gold Content of GDP, Wealth Creation Ability of Provincial-Level Governments and Regional Economic Disparities. Southeast Acad. Res. 2021, 148–158+248. [Google Scholar]
- Zhang, M.; Bi, J. Spatial Differences and Pattern Evolution of Urban Land Economic Density of the Yangtze River Delta Urban Agglomeration. J. Manag. 2020, 33, 17–26. [Google Scholar]
- Li, J.; Zhao, M.; Han, R.; Shen, W. Spatial-Temporal Differentiation and Its Influencing Factors of the Comprehensive Carrying Capacity in Shandong Province. Ecol. Econ. 2021, 37, 85–92. [Google Scholar]
- Ren, B.; He, M. An Analysis of Spatial-Temporal Evolution of China’s Economic Gap and Its Influencing Mechanism. J. Xi’an Jiaotong Univ. (Soc. Sci.) 2019, 39, 47–57. [Google Scholar]
- Li, J.; Yuan, W.; Qin, X.; Qi, X.; Meng, L. Coupling coordination degree for urban green growth between public demand and government supply in urban agglomeration: A case study from China. J. Environ. Manag. 2022, 304, 10. [Google Scholar] [CrossRef] [PubMed]
- Gan, L.; Shi, H.; Hu, Y.; Qi, X.; Meng, L. Coupling coordination degree for urbanization city-industry integration level: Sichuan case. Sustain. Cities Soc. 2020, 58, 102136. [Google Scholar] [CrossRef]
- Tan, Y.; Jiao, L.; Shuai, C.; Shen, L. A system dynamics model for simulating urban sustainability performance: A case study. J. Clean. Prod. 2018, 199, 1107–1115. [Google Scholar] [CrossRef]
- Yang, Z.; Yang, H.; Wang, H. Evaluating urban sustainability under different development pathways: A case study of the Beijing-Tianjin-Hebei region. Sustain. Cities Soc. 2020, 61, 102226. [Google Scholar]
- Ding, C.; Gao, W. Land Urbanization and Land Issues in China. Urban Dev. Stud. 2018, 25, 29–36. [Google Scholar]
- Jiang, Y.; Jin, X.; Qin, L.; Xue, Q.; Cheng, Y.; Long, Y.; Yang, X.; Zhou, Y. Process and Characteristics of Urban Built-Up Area Expansion in Jiangsu-Shanghai Region in the Past 600 Years. City Plan. Rev. 2019, 43, 55–68. [Google Scholar]


| Research Region | Eastern Region | Central Region | Western Region | Northeast Region |
|---|---|---|---|---|
| Research urban area | Beijing, Tianjin, Shijiazhuang, Shanghai, Nanjing, Hangzhou, Ningbo, Fuzhou, Xiamen, Jinan, Qingdao, Guangzhou, Shenzhen, Haikou, Tangshan, Qinhuangdao, Wuxi, Yangzhou, Xuzhou, Wenzhou, Jinhua, Quanzhou, Yantai, Jining, Huizhou, Zhanjiang, Shaoguan, Sanya | Taiyuan, Hefei, Nanchang, Zhengzhou, Wuhan, Changsha, Bengbu, Anqing, Jiujiang, Ganzhou, Luoyang, Pingdingshan, Yichang, Xiangyang, Yueyang, Changde | Hohhot, Nanning, Chongqing, Chengdu, Guiyang, Kunming, Xi’an, Lanzhou, Xining, Yinchuan, Urumqi, Baotou, Guilin, Beihai, Luzhou, Nanchong, Zunyi, Dali | Shenyang, Dalian, Changchun, Harbin, Dandong, Jinzhou, Jilin, Mudanjiang |
| Coupling Coordination Stage | Indicator Value | Coupling Coordination Classification |
|---|---|---|
| Low Level Stage | Extreme maladjustment | |
| Serious maladjustment | ||
| Moderate maladjustment | ||
| Antagonism Stage | Low maladjustment | |
| Marginal maladjustment | ||
| Running-in Stage | Reluctant coordination | |
| Initial coordination | ||
| Moderate coordination | ||
| High Level Stage | Satisfactory coordination | |
| Superior coordination |
| Quadrant List | Implication | |||
|---|---|---|---|---|
| First quadrant (HH) | Region i and adjacent regions are high-value regions | |||
| Second quadrant (LH) | Region i is the low value region, and the adjacent region is the high value region | |||
| Third quadrant (LL) | Region i and adjacent regions are low-value regions | |||
| Fourth quadrant (HL) | Region i is the high value region, and the adjacent region is the low value region |
| Research Dimension | Index Layer | No. | Properties | References |
|---|---|---|---|---|
| Supply dimension | Housing affordable expenditure | A1 | + | [16,38,39,40,41] |
| Affordable housing land supply | A2 | + | [39,40,42,43] | |
| Affordable housing supply | A3 | + | [39,41,42,43] | |
| Demand dimension | Per capita disposable income—low-income | A4 | + | [26,38,39,40,41,42,43,44] |
| Per capita disposable income—low- and middle- income | A5 | + | [26,38,39,40,41,42,44] | |
| Per capita housing area of low-income households | A6 | + | [40,41,42,43,45,46] | |
| Per capita housing area of low- and middle-income households | A7 | + | [40,41,42,43,45,46] | |
| Engel coefficient | A8 | − | [42,46,47,48] | |
| Housing income ratio of low- and middle-income households | A9 | − | [26,44,45,46,47,48] |
| Research Dimension | Index Layer | Weight |
|---|---|---|
| Supply dimension | A1 | 0.259 |
| A2 | 0.281 | |
| A3 | 0.213 | |
| Demand dimension | A4 | 0.072 |
| A5 | 0.071 | |
| A6 | 0.037 | |
| A7 | 0.035 | |
| A8 | 0.024 | |
| A9 | 0.008 |
| Research Dimension | Index Layer | No. | Properties | References |
|---|---|---|---|---|
| Economic dimension | Gross Domestic Product (GDP) | U1 | + | [49,50,51,52,53,54,55] |
| Economic density | U2 | + | [55,56,57] | |
| Financial dependence | U3 | + | [53,56,57,58] | |
| The proportion of tertiary industry | U4 | + | [51,52,54,55,56,59,60,61] | |
| Local general public finance budgets | U5 | + | [49,51,52,54,56,58,59] | |
| Social dimension | Number of health technicians per 1000 people | U6 | + | [52,56,58,60,61] |
| Number of primary and secondary schools per 1000 people | U7 | + | [52,60,61] | |
| Number of buses per 1000 people | U8 | + | [52,58,60,61] | |
| Urban registered unemployment rate | U9 | − | [16,49,51,56,59] | |
| Resident dimension | The number of permanent residents | U10 | + | [49,50,52,53] |
| Population density | U11 | + | [49,53,54,58] | |
| Per capita GDP | U12 | + | [49,50,51,53,54,57,59] | |
| Per capita GDP contains gold | U13 | + | [51,53,54,57] | |
| Spatial dimension | Green coverage rate | U14 | + | [49,51,56,62] |
| Per capita built-up area | U15 | + | [49,56,60,62,63] | |
| Per capita road area | U16 | + | [52,54,58,62] |
| Research Dimension | Index Layer | Weight |
|---|---|---|
| Economic dimension | U1 | 0.107 |
| U2 | 0.208 | |
| U3 | 0.045 | |
| U4 | 0.028 | |
| U5 | 0.133 | |
| Social dimension | U6 | 0.024 |
| U7 | 0.033 | |
| U8 | 0.083 | |
| U9 | 0.026 | |
| Resident dimension | U10 | 0.056 |
| U11 | 0.069 | |
| U12 | 0.043 | |
| U13 | 0.033 | |
| Spatial dimension | U14 | 0.004 |
| U15 | 0.055 | |
| U16 | 0.053 |
| Year | Moran’s I | Z Score | p Value |
|---|---|---|---|
| 2010 | 0.397 | 6.945 | 0.000 *** |
| 2011 | 0.420 | 7.379 | 0.000 *** |
| 2012 | 0.409 | 7.159 | 0.000 *** |
| 2013 | 0.414 | 7.191 | 0.000 *** |
| 2014 | 0.434 | 7.544 | 0.000 *** |
| 2015 | 0.399 | 7.030 | 0.000 *** |
| 2016 | 0.467 | 8.216 | 0.000 *** |
| 2017 | 0.443 | 7.865 | 0.000 *** |
| 2018 | 0.453 | 7.904 | 0.000 *** |
| 2019 | 0.446 | 7.785 | 0.000 *** |
| 2020 | 0.412 | 7.235 | 0.000 *** |
| Quadrants | 2010 | 2015 | 2020 |
|---|---|---|---|
| HH | Beijing, Tianjin, Hohhot, Shenyang, Dalian, Shanghai, Nanjing, Hangzhou, Ningbo, Hefei, Fuzhou, Xiamen, Jinan, Qingdao, Wuhan, Changsha, Guangzhou, Shenzhen, Wuxi, Wenzhou | Beijing, Tianjin, Shanghai, Nanjing, Hangzhou, Ningbo, Fuzhou, Xiamen, Jinan, Qingdao, Wuhan, Changsha, Guangzhou, Shenzhen, Wuxi, Yichang | Beijing, Tianjin, Shanghai, Nanjing, Hangzhou, Ningbo, Fuzhou, Xiamen, Nanchang, Jinan, Qingdao, Wuhan, Changsha, Guangzhou, Shenzhen, Urumqi, Wuxi, Yangzhou, Jinhua |
| LH | Nanchang, Haikou, Urumqi, Tangshan, Baotou, Yangzhou, Yantai, Yichang | Hohhot, Taiyuan, Dalian, Hefei, Nanchang, Haikou, Urumqi, Tangshan, Baotou, Yangzhou, Quanzhou, Yantai, Huizhou | Hohhot, Shenyang, Dalian, Haikou, Tangshan, Baotou, Yantai, Yichang, Xiangyang |
| LL | Shijiazhuang, Taiyuan, Lanzhou, Xining, Yinchuan, Qinhuangdao, Dandong, Jinzhou, Jilin, Mudanjiang, Xuzhou, Jinhua, Bengbu, Anqing, Jiujiang, Ganzhou, Jining, Luoyang, Pingdingshan, Xiangyang, Yueyang, Changde, Huizhou, Zhanjiang, Shaoguan, Guilin, Beihai, Sanya, Luzhou, Nanchong, Zunyi, Dali | Shijiazhuang, Shenyang, Changchun, Harbin, Nanning, Guiyang, Lanzhou, Xining, Qinhuangdao, Dandong, Jinzhou, Jilin, Mudanjiang, Xuzhou, Jinhua, Bengbu, Anqing, Jiujiang, Ganzhou, Jining, Luoyang, Pingdingshan, Xiangyang, Yueyang, Changde, Zhanjiang, Shaoguan, Guilin, Beihai, Sanya, Luzhou, Nanchong, Zunyi, Dali | Shijiazhuang, Taiyuan, Changchun, Harbin, Nanning, Guiyang, Kunming, Lanzhou, Xining, Yinchuan, Qinhuangdao, Dandong, Jinzhou, Jilin, Mudanjiang, Bengbu, Anqing, Quanzhou, Jiujiang, Ganzhou, Jining, Luoyang, Pingdingshan, Yueyang, Changde, Huizhou, Zhanjiang, Shaoguan, Guilin, Beihai, Sanya, Luzhou, Nanchong, Zunyi, Dali |
| HL | Changchun, Harbin, Zhengzhou, Nanning, Chongqing, Chengdu, Guiyang, Kunming, Xi’an, Quanzhou | Zhengzhou, Chongqing, Chengdu, Kunming, Xi’an, Yinchuan, Wenzhou | Hefei, Zhengzhou, Chongqing, Chengdu, Xi’an, Xuzhou, Wenzhou |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Shi, C.; Mu, L.; Yin, Q.; Shi, X. Research on the Coupling Coordination Characteristics of Affordable Housing Market and Urban Development. Buildings 2025, 15, 3707. https://doi.org/10.3390/buildings15203707
Wang L, Shi C, Mu L, Yin Q, Shi X. Research on the Coupling Coordination Characteristics of Affordable Housing Market and Urban Development. Buildings. 2025; 15(20):3707. https://doi.org/10.3390/buildings15203707
Chicago/Turabian StyleWang, Lida, Chengcheng Shi, Lingling Mu, Qiaomeng Yin, and Xiaona Shi. 2025. "Research on the Coupling Coordination Characteristics of Affordable Housing Market and Urban Development" Buildings 15, no. 20: 3707. https://doi.org/10.3390/buildings15203707
APA StyleWang, L., Shi, C., Mu, L., Yin, Q., & Shi, X. (2025). Research on the Coupling Coordination Characteristics of Affordable Housing Market and Urban Development. Buildings, 15(20), 3707. https://doi.org/10.3390/buildings15203707






