Experimental and Numerical Investigation of Welding Residual Stress of U-Rib Joints in Orthotropic Steel Bridge Decks
Abstract
1. Introduction
2. U-Rib Joint Experimental Results
2.1. Dimensions of U-Rib Specimens and Welding Parameters
2.2. Thermal History Measurement
2.3. Residual Stress Measurement
3. FEA of the U-Rib Joint Welding
3.1. Mesh Model
3.2. Heat Source Model
3.3. Thermophysical and Mechanical Properties of Steels
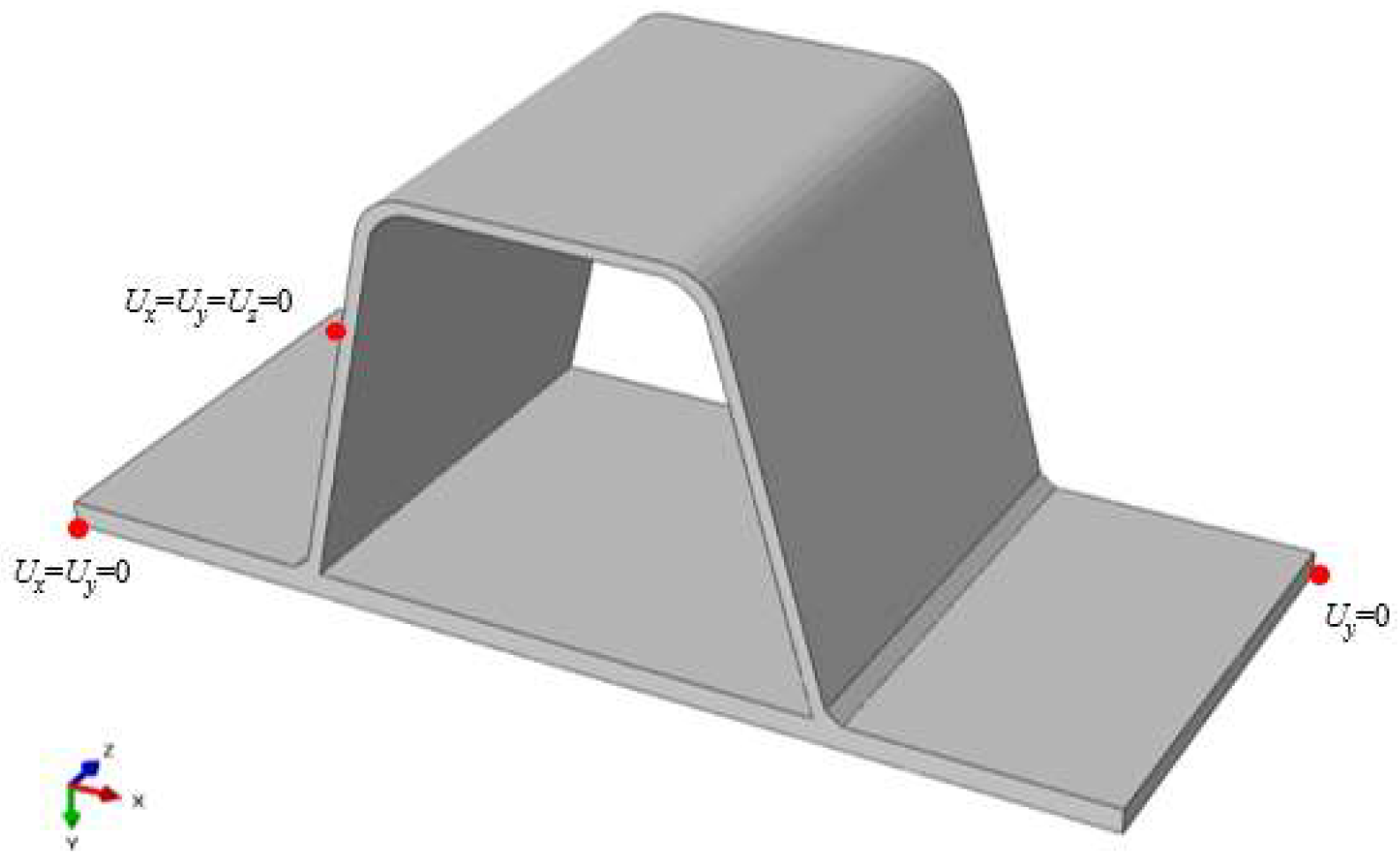
3.4. Boundary Conditions for the Temperature and Stress Analyses
4. FEA Verification
4.1. Temperature Comparison
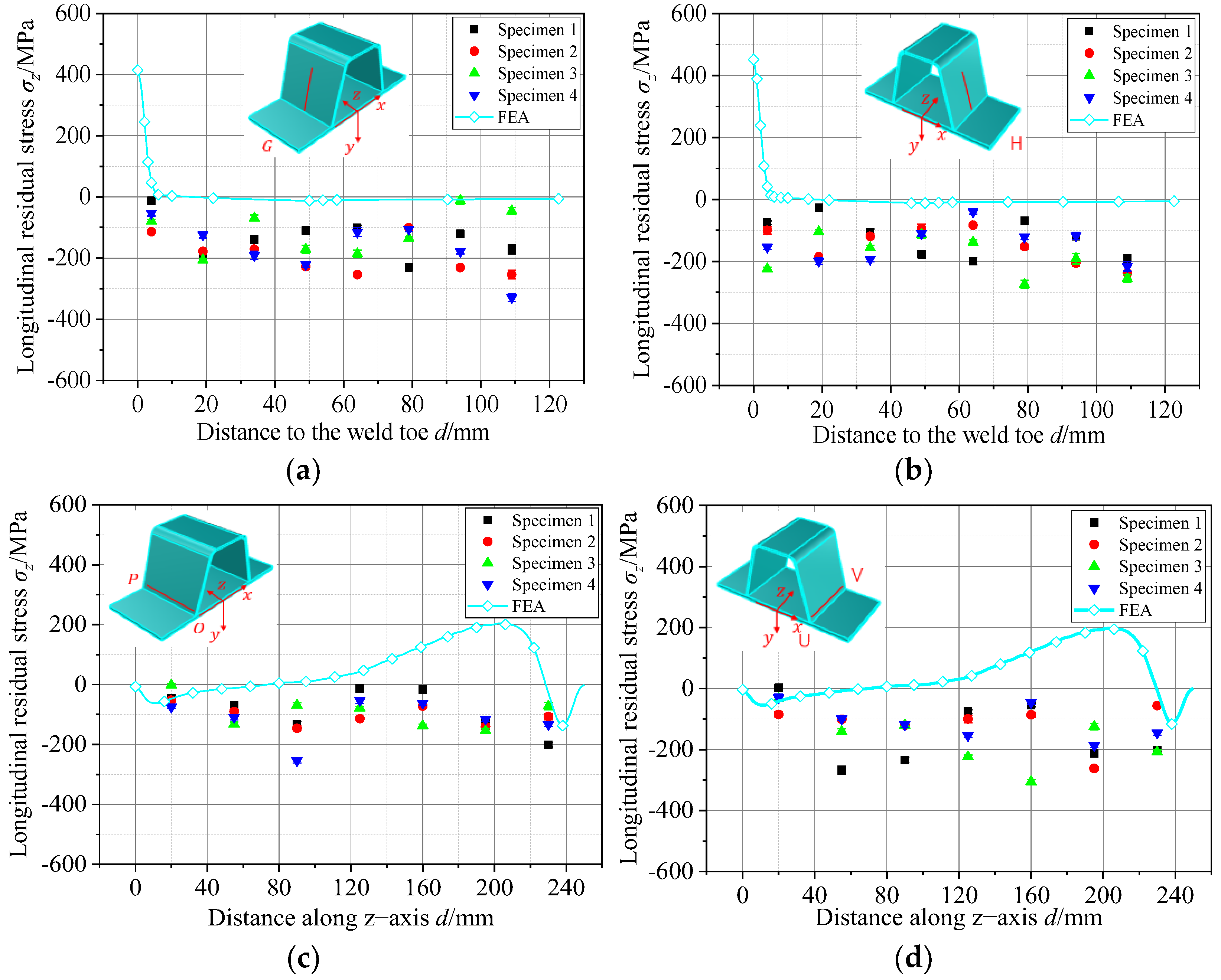
4.2. Comparison of the Residual Stresses
5. FE Parametric Study
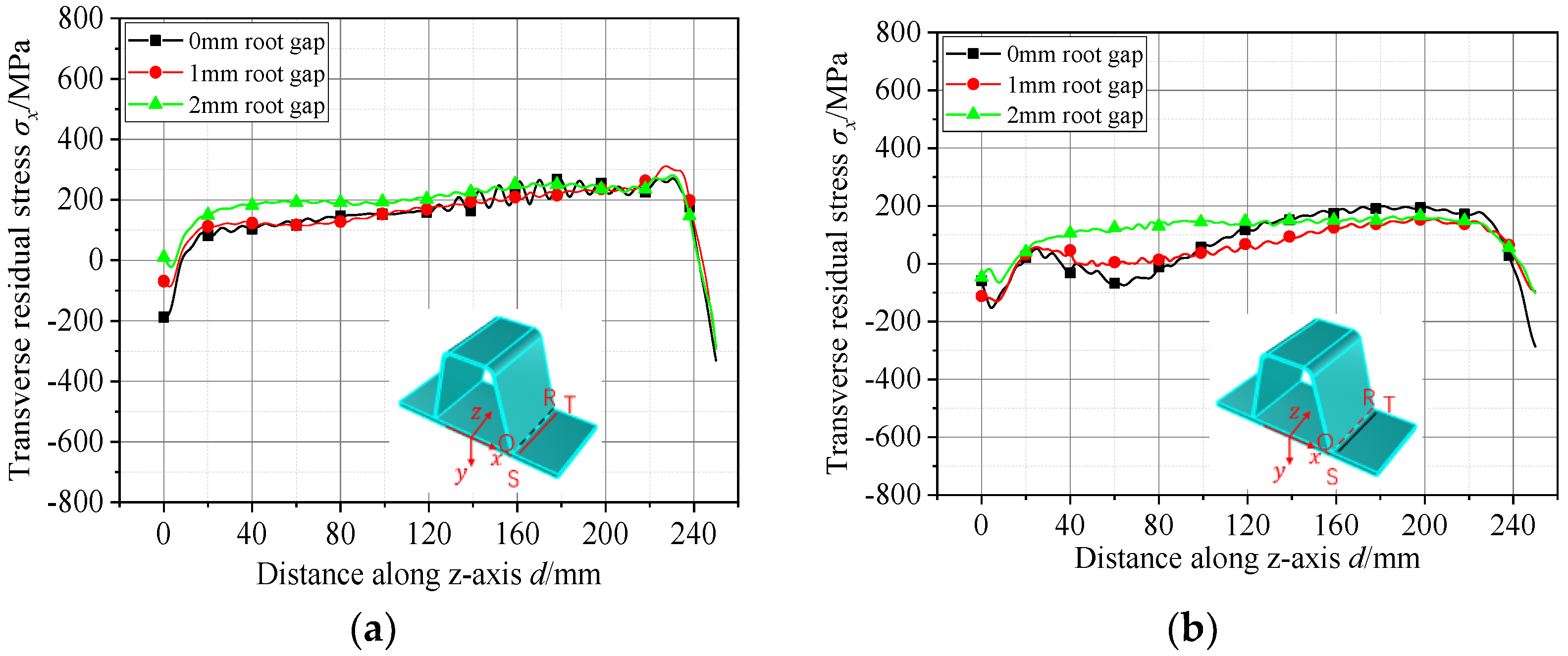
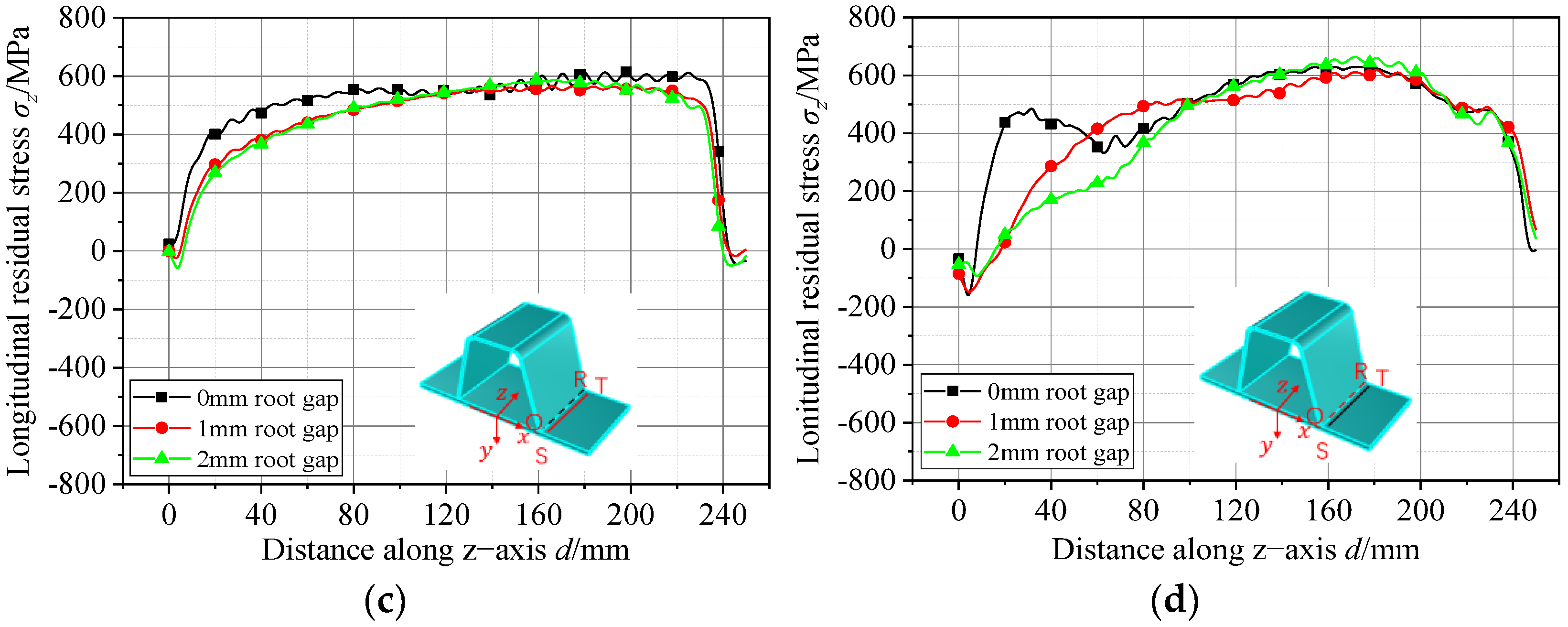
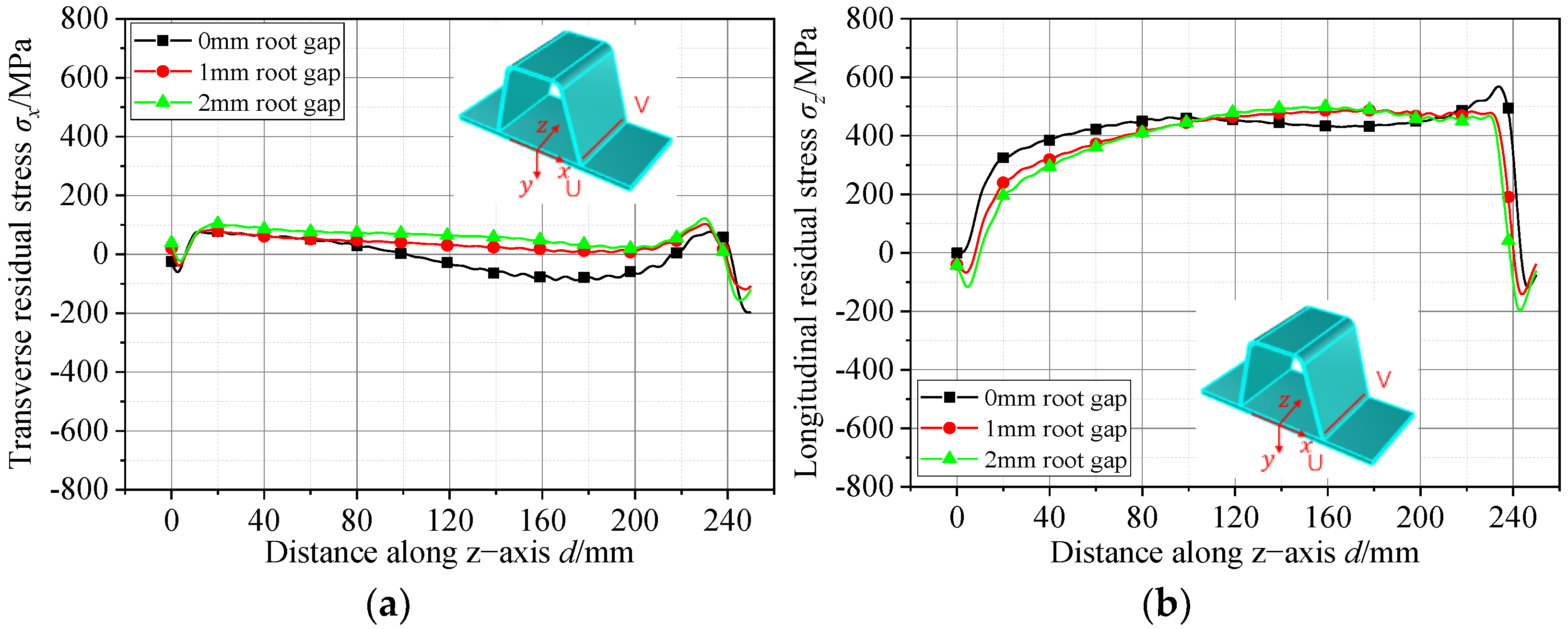
5.1. Effect of Root Gap on Residual Stresses
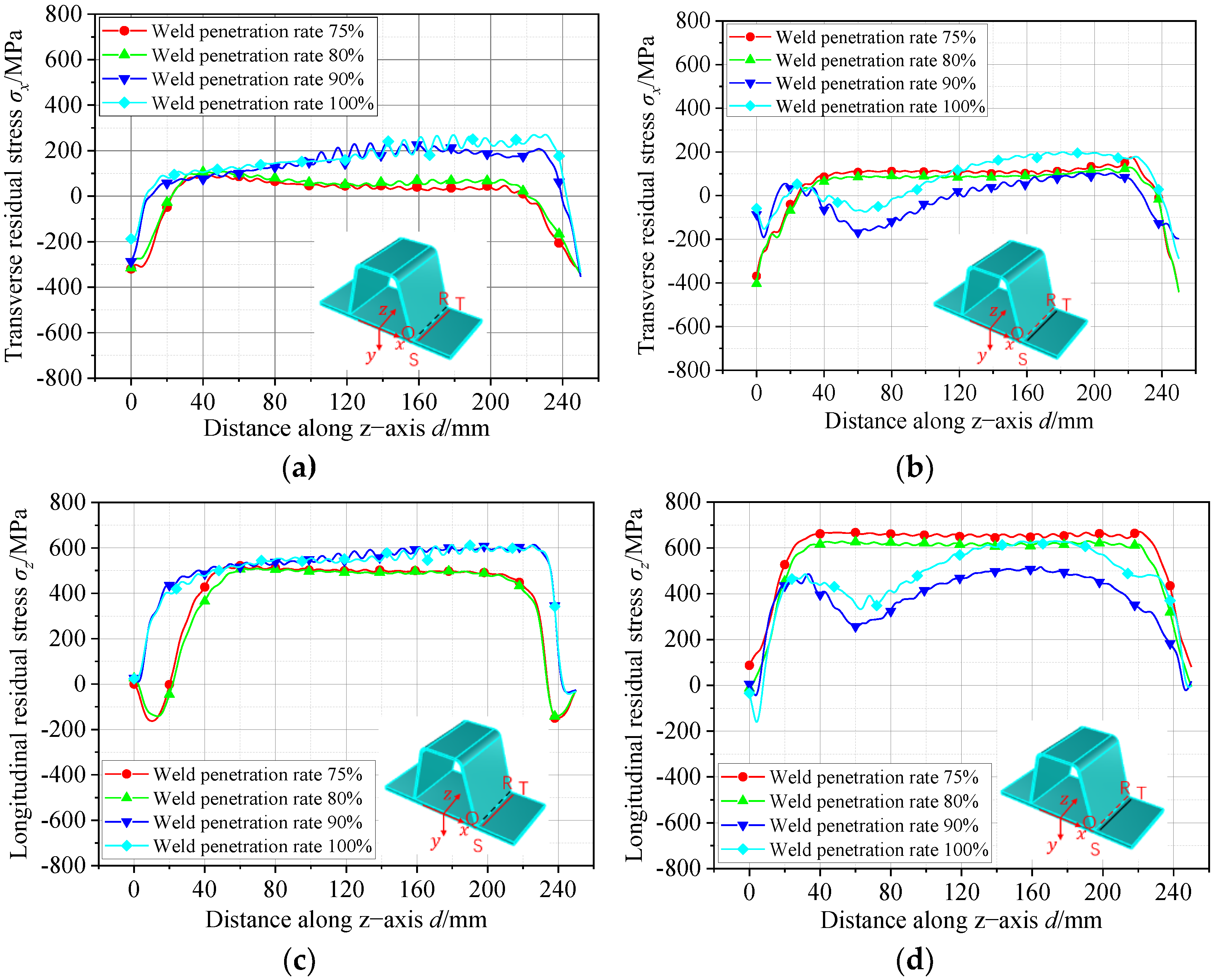
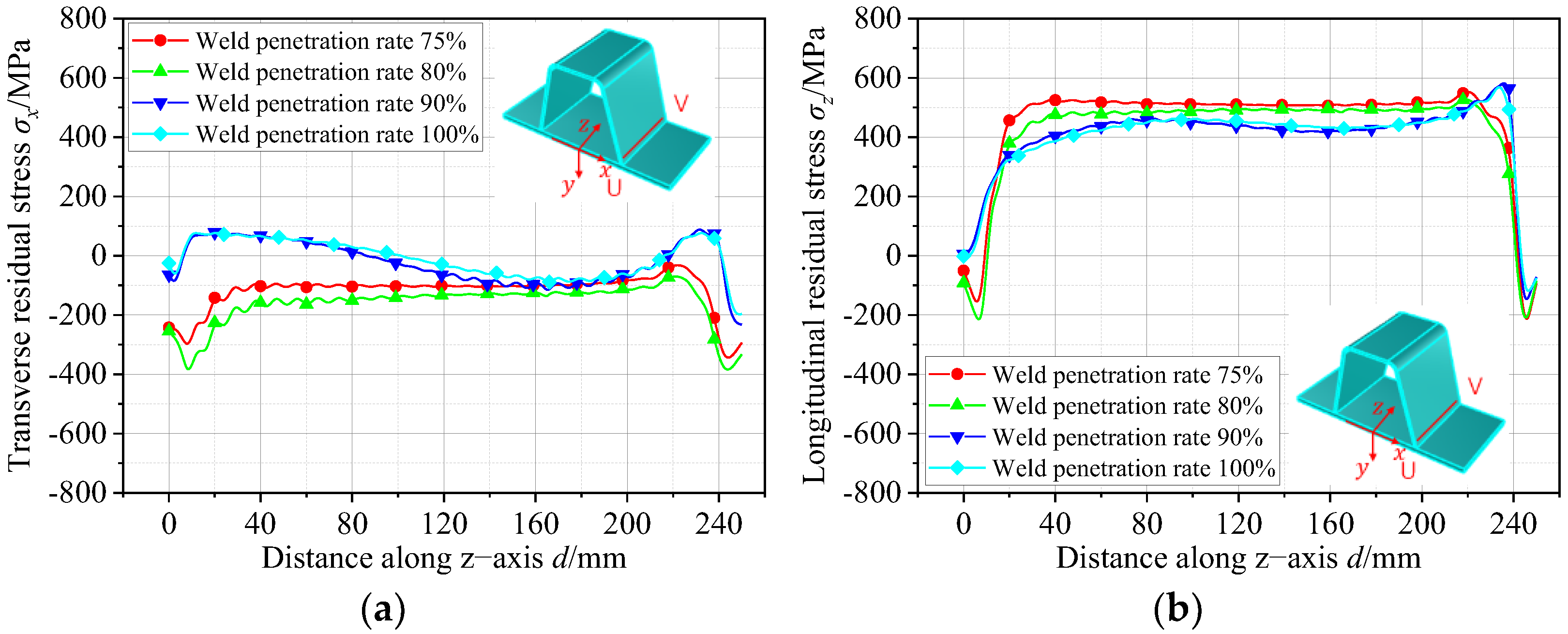
5.2. Effect of Weld Penetration Rate on Residual Stresses
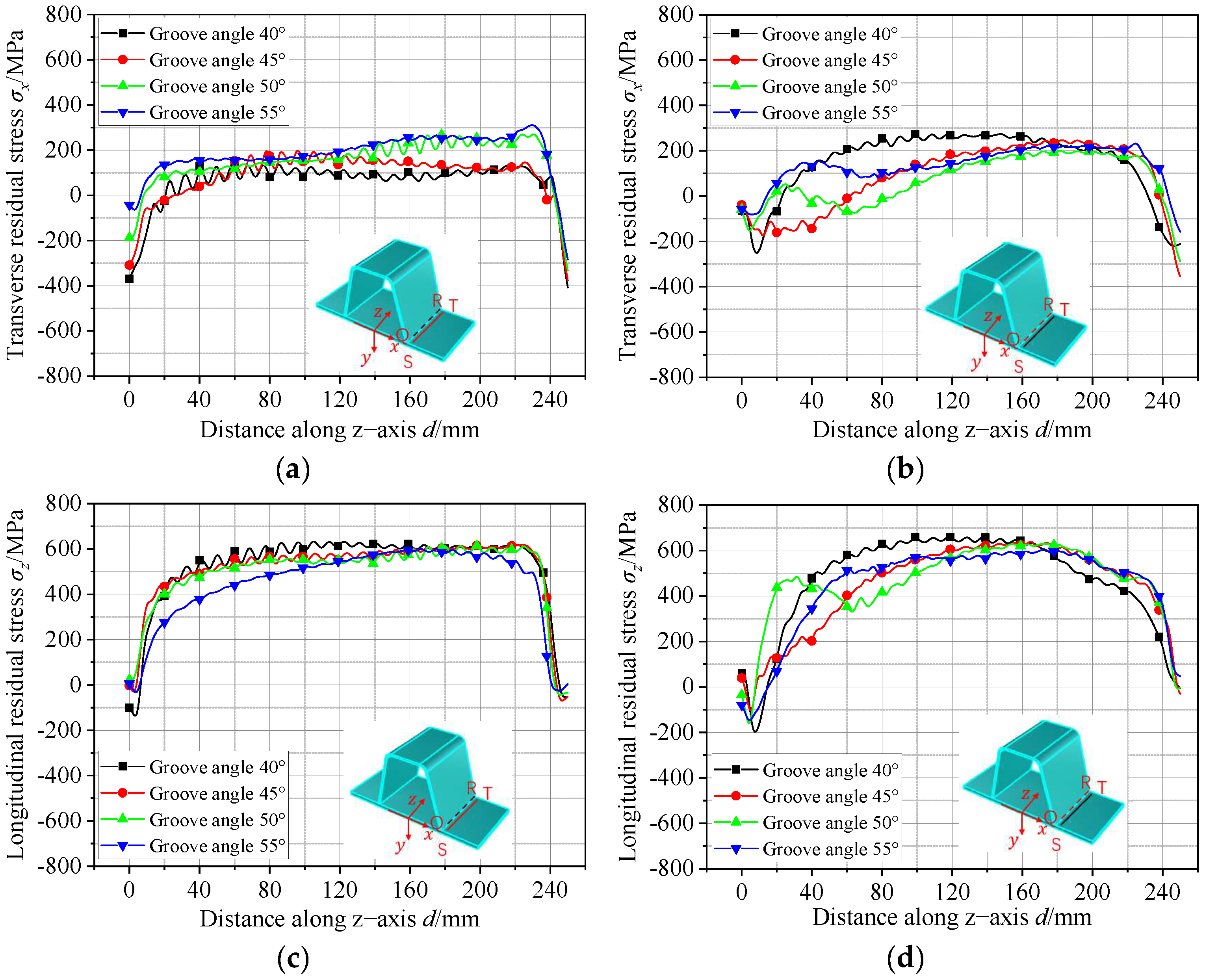
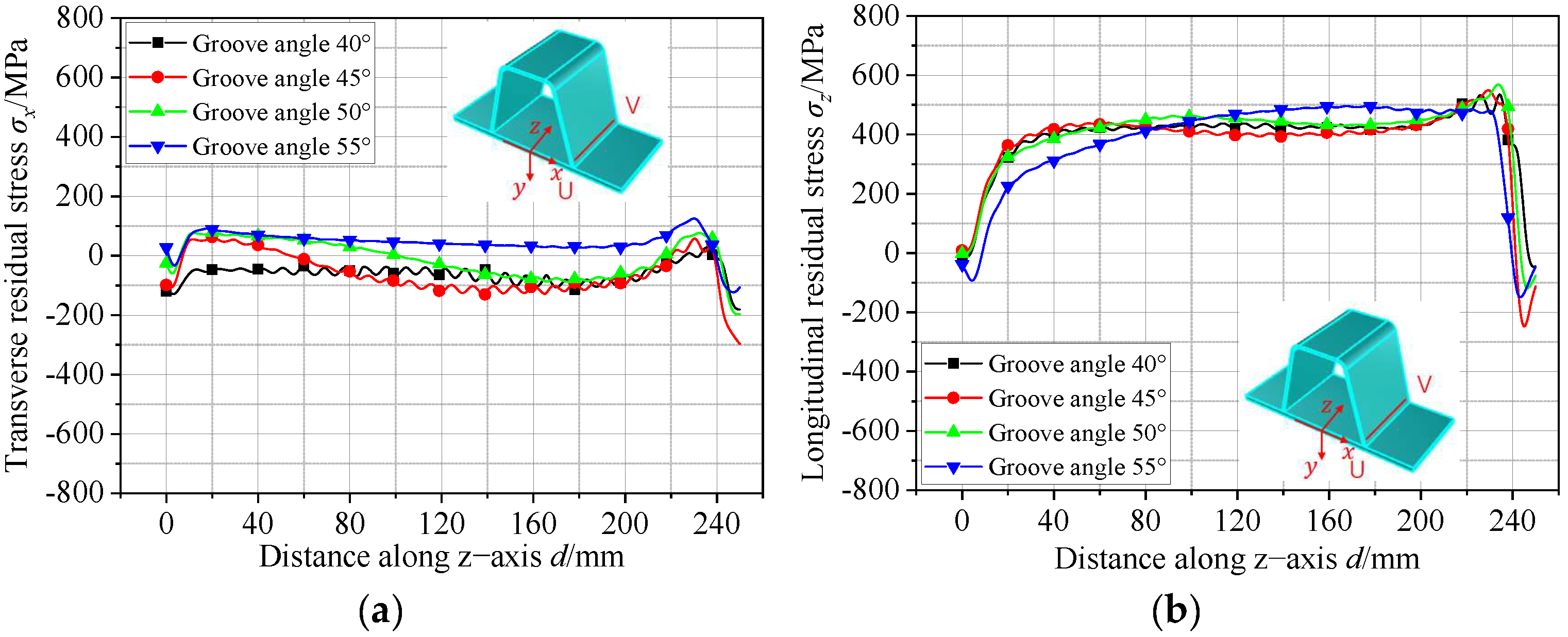
5.3. Effect of Groove Angle on Residual Stresses
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jiang, F.; Fu, Z.; Ji, B. Fatigue life evaluation of deck to U-rib welds in orthotropic steel deck integrating weldment size effects on welding residual stress. Eng. Fail. Anal. 2021, 124, 105359. [Google Scholar] [CrossRef]
- Wang, Q.; Ji, B.; Li, C. Fatigue evaluation of rib-deck welds: Crack-propagation-life predictive model and parametric analysis. J. Constr. Steel Res. 2020, 173, 106248. [Google Scholar] [CrossRef]
- Wu, J.; Qiang, B.; Liao, X. Experimental investigation and numerical simulation of welding residual stress in the orthotropic steel deck with diaphragm considering solid-state phase transformation. Eng. Struct. 2022, 250, 113415. [Google Scholar] [CrossRef]
- Chen, J.; Wei, C.; Zhao, Y. Fatigue resistance of orthotropic steel deck system with double-side welded rib-to-deck joint. Adv. Struct. Eng. 2023, 26, 952–965. [Google Scholar] [CrossRef]
- Chen, F.; Zhang, H.; Li, Z.; Luo, Y.; Xiao, X.; Liu, Y. Residual stresses effects on fatigue crack growth behavior of rib-to-deck double-sided welded joints in orthotropic steel decks. Adv. Struct. Eng. 2024, 27, 35–50. [Google Scholar] [CrossRef]
- Matos, J.C.; Nicoletti, V.; Kralovanec, J.; Sousa, H.S.; Gara, F.; Moravcik, M.; Morais, M.J. Comparison of Condition Rating Systems for Bridges in Three European Countries. Appl. Sci. 2023, 13, 12343. [Google Scholar] [CrossRef]
- Issa, M.A.; Shumin, T.; Yousif, A. Application of knowledge-based expert systems for rating highway bridges. Eng. Fract. Mech. 1995, 50, 923–934. [Google Scholar] [CrossRef]
- Boulton, N.S.; Lance Martin, H.E. Residual Stresses in Arc-Welded Plates. Proc. Inst. Mech. Eng. 1936, 133, 295–347. [Google Scholar] [CrossRef]
- Ueda, Y.; Fukuda, K.; Nakacho, K. A New Measuring Method of Residual Stresses with the Aid of Finite Element Method and Reliability of Estimated Values. Trans. JWRI 1975, 4, 123–131. [Google Scholar] [CrossRef]
- Kainuma, S.; Young-Soo, J.; Yang, M.Y. Welding residual stress in roots between deck plate and U-rib in orthotropic steel decks. Measurement 2016, 92, 475–482. [Google Scholar] [CrossRef]
- Kong, W.; Huang, W.; Wei, Y. Numerical study on welding residual stress of double-sided submerged arc welding for orthotropic steel deck. Eng. Struct. 2024, 302, 117445. [Google Scholar] [CrossRef]
- Wang, Q.; Ji, B.; Fu, Z. Experimental study on the determination of welding residual stress in rib-deck by sharp indentation testing. Thin-Walled Struct. 2021, 161, 107516. [Google Scholar] [CrossRef]
- Liu, X.; Qiang, B.; Wu, H. Distribution and relaxation of welding residual stress in U-rib-to-deck joints considering actual material properties. Thin-Walled Struct. 2022, 180, 109747. [Google Scholar] [CrossRef]
- Li, Y.; Wu, J.; Qiang, B. Measurement of residual stresses in a welded orthotropic steel deck by the hole-drilling method considering stress biaxiality. Eng. Struct. 2021, 230, 111690. [Google Scholar] [CrossRef]
- Wang, F.; Lyu, Z.; Zhao, Z. Experimental and numerical study on welding residual stress of U-rib stiffened plates. J. Constr. Steel Res. 2020, 175, 106362. [Google Scholar] [CrossRef]
- Inspection and Quarantine of the People’s Public of China. Non-Destructive Testing-Practice for Residual Stress Measurement by X-Ray, General Administration of Quality Supervision; Inspection and Quarantine of the People’s Public of China: Beijing, China, 2017.
- Qiang, B.; Li, Y.D.; Yao, C.R. Through-thickness Welding Residual Stress and Its Effect on Stress Intensity Factors for Semi-elliptical Surface Cracks in a Butt-welded Steel Plate. Eng. Fract. Mech. 2018, 193, 17–31. [Google Scholar] [CrossRef]
- Goldak, J.; Chakravarti, A.; Bibby, M. A New Finite Element Model for Welding Heat Sources. Metall. Mater. Trans. B 1984, 15, 299–305. [Google Scholar] [CrossRef]
- Attarha, M.J.; Sattari-Far, I. Study on Welding Temperature Distribution in Thin Welded Plates Through Experimental Measurements and Finite Element Simulation. J. Mater. Process. Technol. 2011, 211, 688–694. [Google Scholar] [CrossRef]
- Qiang, B.; Wang, X. Evaluating Stress Intensity Factors for Surface Cracks in an Orthotropic Steel Deck Accounting for the Welding Residual Stresses. Theor. Appl. Fract. Mech. 2020, 110, 102827. [Google Scholar] [CrossRef]
- Gu, Y.; Li, Y.; Zhou, Z. Numerical simulation and measurement of welding residual stresses in orthotropic steel decks stiffened with U-shaped ribs. Int. J. Steel Struct. 2020, 20, 856–869. [Google Scholar] [CrossRef]
- Wang, H.; Qin, S.; Wang, B. Welding-indued residual stresses in U-ribs of a steel bridge deck. Period. Polytech. Civ. Eng. 2021, 65, 1239–1246. [Google Scholar]
- Yang, H.; Wang, P.; Qian, H. An experimental investigation into fatigue behaviors of single- and double-sided U rib welds in orthotropic bridge decks. Int. J. Fatigue 2022, 159, 106827. [Google Scholar] [CrossRef]
- Qiang, B.; Xie, Y.; Xie, Q. Influence of post-weld heat treatment on welding residual stress in U-rib-to-deck joint. Thin-Walled Struct. 2024, 196, 111550. [Google Scholar] [CrossRef]
- European Committee for Standardization. EN 1993-2: Eurocode 3—Design of Steel Structures—Part 2: Steel Bridges; CEN: Brussels, Belgium, 2012. [Google Scholar]
- American Association of State Highway and Transportation of Officials. LRFD Bridge Design Specifications, 3rd ed.; AASHTO: Washington, DC, USA, 2012. [Google Scholar]
- Ministry of Transport of the People’s Republic of China. Specifications for Design of Highway Steel Bridge; China Communications Press: Beijing, China, 2015.
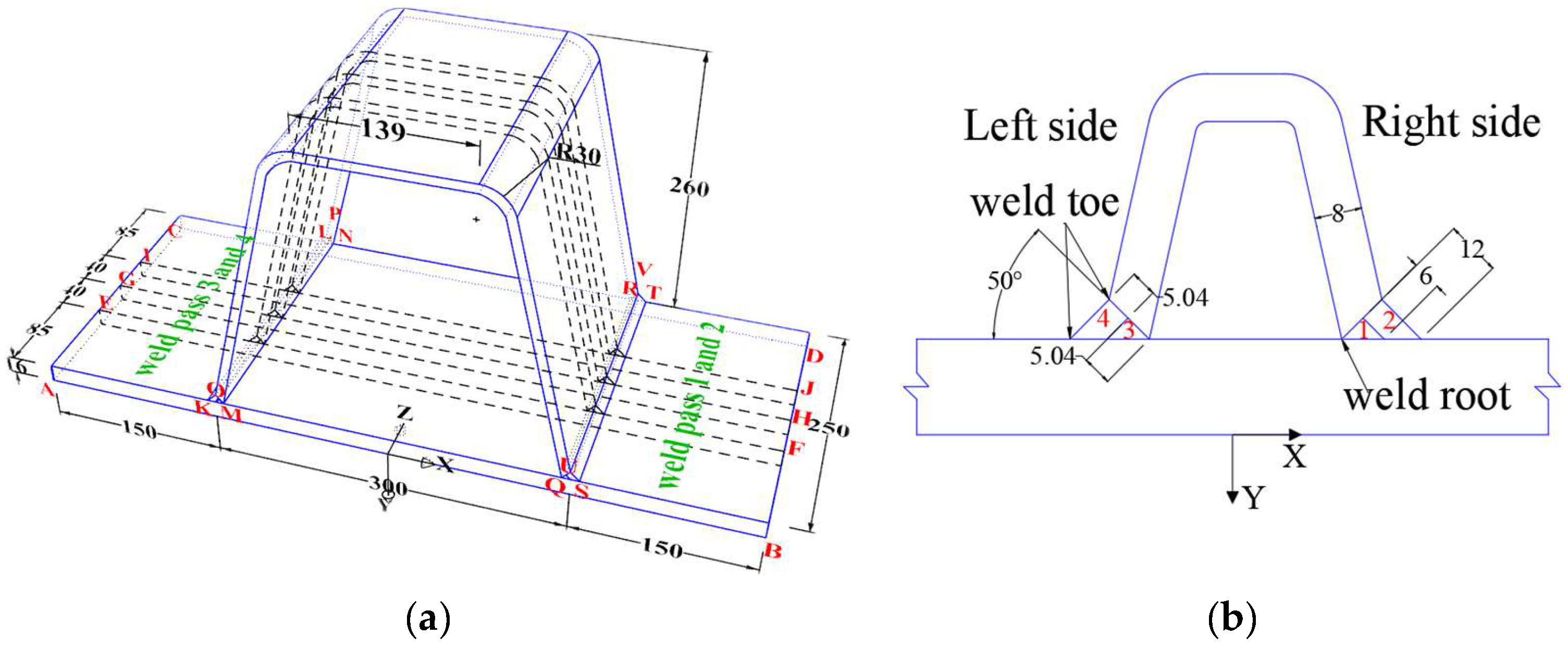
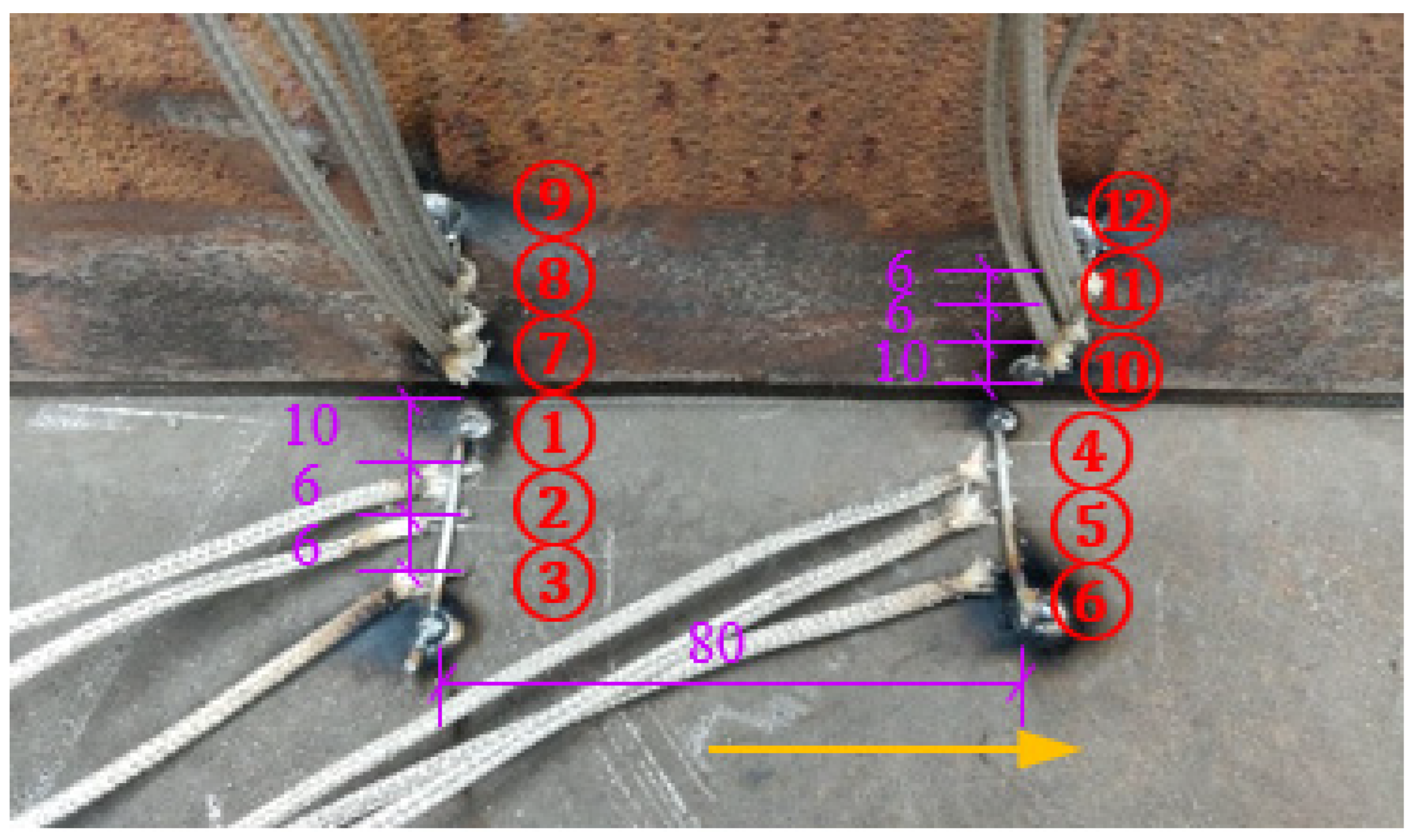

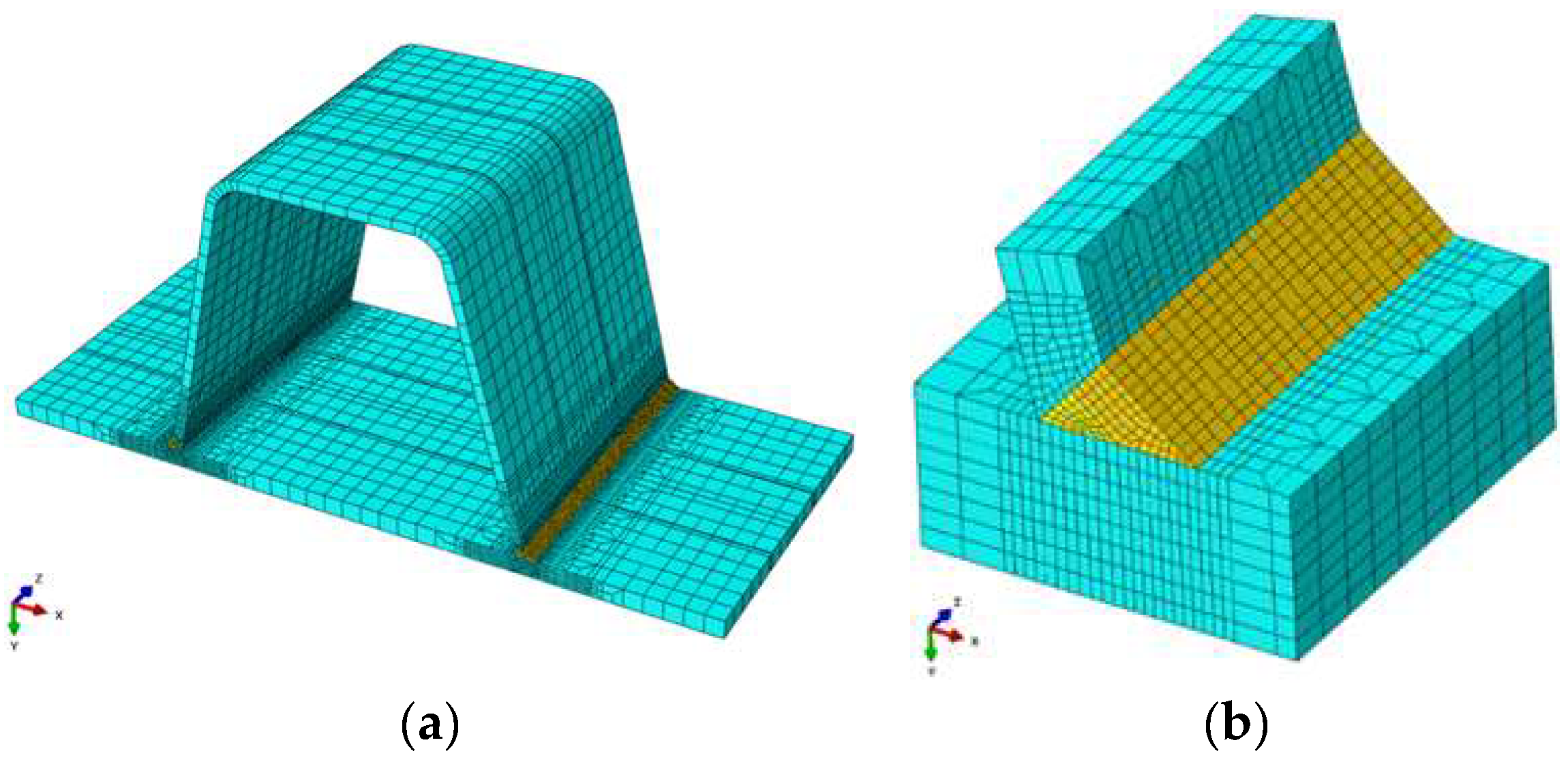

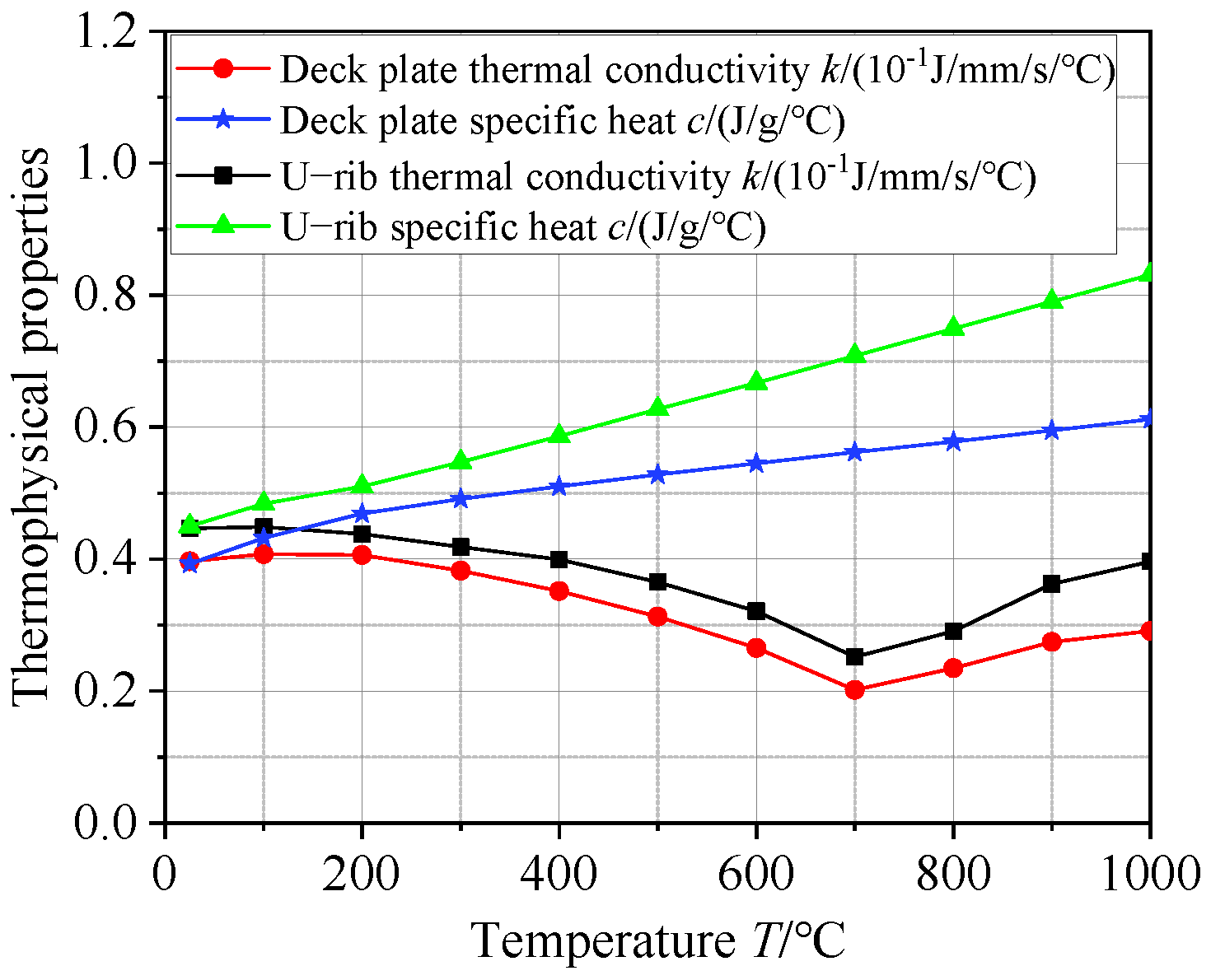







| Welding Pass No. | Welding Current (A) | Welding Voltage (V) | Welding Speed (mm/s) |
|---|---|---|---|
| 1, 3 | 140 | 23 | 2.10 |
| 2, 4 | 140 | 23 | 3.13 |
| Welding Pass No. | b (mm) | c (mm) | af (mm) | ar (mm) |
|---|---|---|---|---|
| 1, 3 | 2.97 | 7.42 | 2.97 | 5.94 |
| 2, 4 | 5.78 | 6.52 | 5.78 | 11.56 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Z.; Su, W.; Shi, J.; Li, T.; Cao, H. Experimental and Numerical Investigation of Welding Residual Stress of U-Rib Joints in Orthotropic Steel Bridge Decks. Buildings 2025, 15, 262. https://doi.org/10.3390/buildings15020262
Huang Z, Su W, Shi J, Li T, Cao H. Experimental and Numerical Investigation of Welding Residual Stress of U-Rib Joints in Orthotropic Steel Bridge Decks. Buildings. 2025; 15(2):262. https://doi.org/10.3390/buildings15020262
Chicago/Turabian StyleHuang, Zhiqiang, Wenxue Su, Jun Shi, Tao Li, and Hongyou Cao. 2025. "Experimental and Numerical Investigation of Welding Residual Stress of U-Rib Joints in Orthotropic Steel Bridge Decks" Buildings 15, no. 2: 262. https://doi.org/10.3390/buildings15020262
APA StyleHuang, Z., Su, W., Shi, J., Li, T., & Cao, H. (2025). Experimental and Numerical Investigation of Welding Residual Stress of U-Rib Joints in Orthotropic Steel Bridge Decks. Buildings, 15(2), 262. https://doi.org/10.3390/buildings15020262







