Assessment of Masonry-Infilled Steel Frames Using Existing Experimental Tests Database in Comparison to Standards
Abstract
1. Introduction
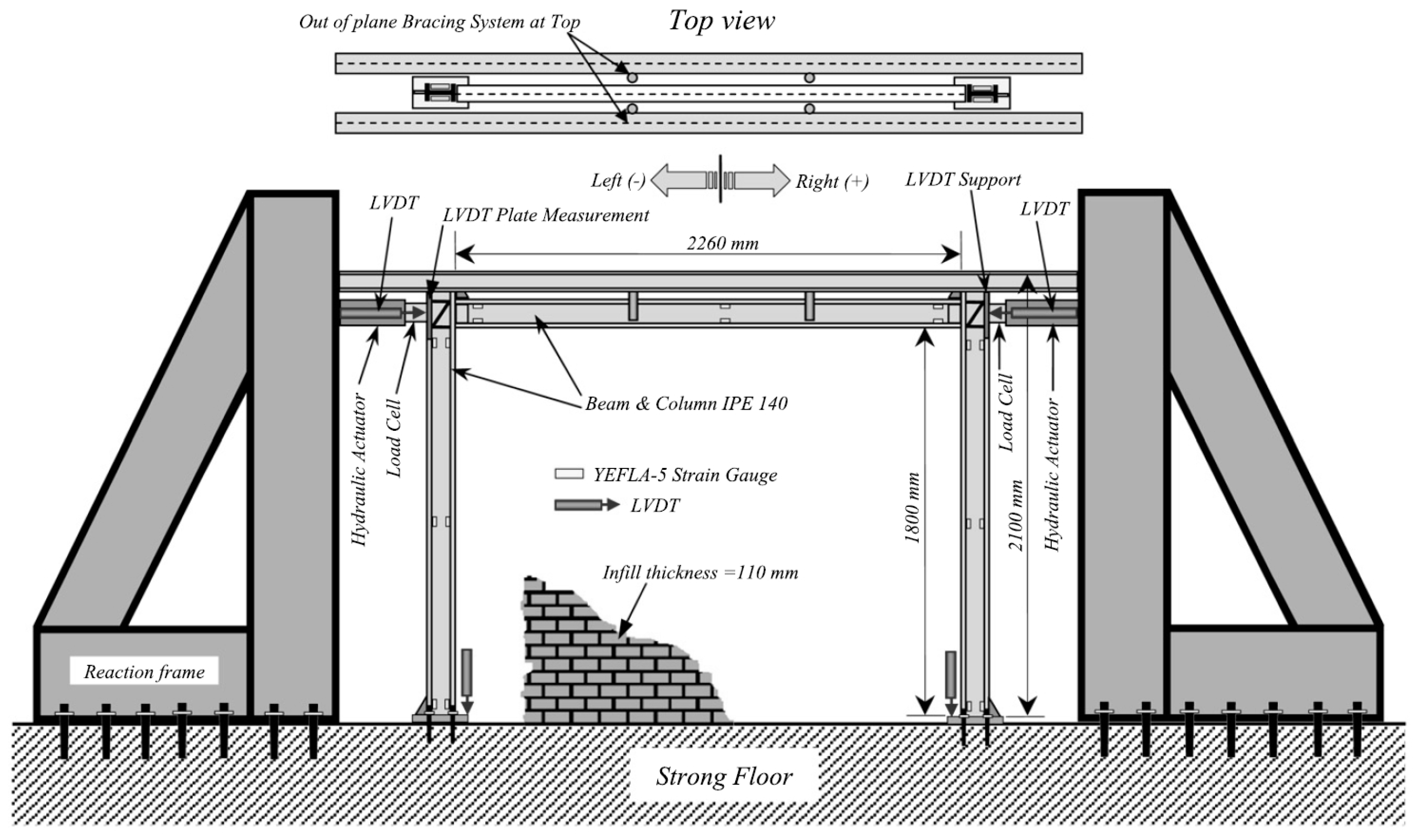
2. Database of the Masonry-Infilled Steel Frame Structures
- Em—modulus of elasticity of masonry;
- Em,AAC—modulus of elasticity of aerated concrete infill;
- fk—compressive strength of masonry.
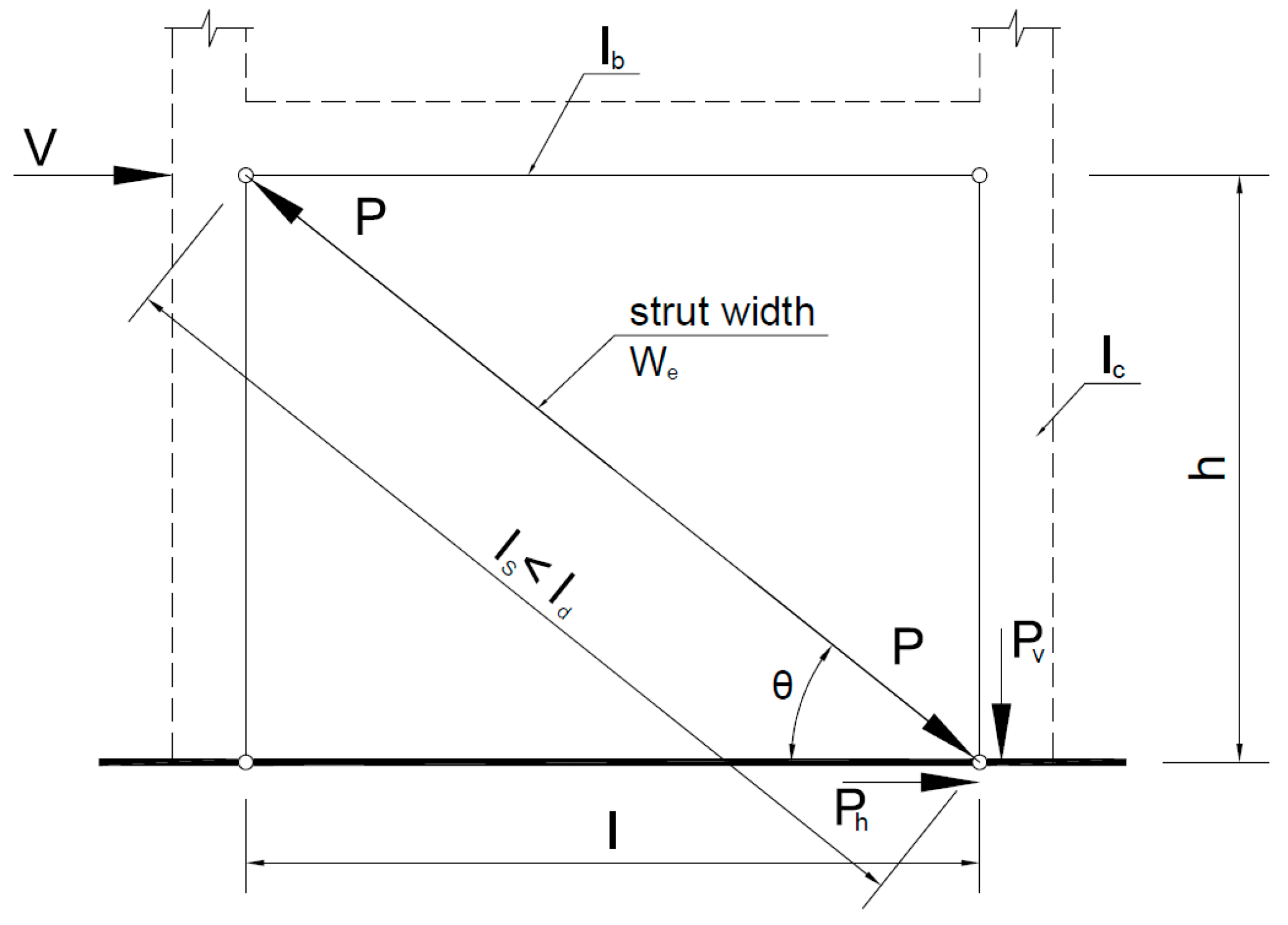
3. Database Analytical Terms/Expressions Used for Estimating the Load-Bearing Capacity and Stiffness
4. Comparison of CSA S304-14 [49] Standard with Experimental Data
- Participating infill (diagonal strut approach). For frame structures with an infill wall that lacks openings and where there is no direct connection between the frame and the wall, the diagonal failure model is applied (Figure 5). However, if openings are present, it must be demonstrated that diagonal failure remains a feasible failure mechanism.
- Frame and infill composite action. When the infill shear wall is tied and bonded to the frame to create a composite shear wall.
- Isolated infill masonry.
4.1. Experimental Database—Markulak et al. (2013) [34] and Markulak et al. (2020) [35]
4.2. Experimental Database—Liu and Soon (2012) [36] and Liu and Manesh (2013) [38]
4.3. Experimental Database—Tsantilis and Triantafillou (2020) [37]
4.4. Experimental Database—Moghadam (2004) [39] and Moghadam et al. (2006) [45]
4.5. Experimental Database—Mohammadi and Emami (2019) [41], Mohammadi et al. (2011) [43], and Mohammadi et al. (2017) [44]
4.6. Experimental Database—Ravichandran (2009) [42]
4.7. Experimental Database—Tasnimi and Mohebkhah (2011) [46]
5. Comparison of Analytical Expressions and Experimental Data
- Vuk—the total load-bearing capacity of the system;
- VFR—frame bearing capacity;
- Vinf,min—the minimum load-bearing capacity value of the infill masonry, depending on the norm.
- VFR—frame bearing capacity;
- Mpl—plastic flexural resistance of column;
- h—the height of the column.
5.1. Calculation of the Load-Bearing Capacity of the Frame with Infill Elements According to FEMA 306 [50]
- Vislide—initial sliding-shear capacity of the infill;
- Vc—the shear force (horizontal component of the diagonal strut capacity);
- Vcr—the cracking shear in the infill;
- Vmf—final shear capacity as a result of cyclic loading effects;
- Vmi—available initial shear capacity that is consumed during the first half-cyclic (monotonic) loading;
- Linf—length of infill panel;
- tinf—thickness of infill panel and equivalent strut;
- hinf—height of infill panel;
- a—equivalent strut width;
- t—infill thickness;
- Em—Young’s modulus of the masonry;
- θ—angle whose tangent is the infill height-to-length aspect ratio;
- μ—coefficient of sliding friction along the bed joint;
- —the angle of sliding friction of the masonry along a bed joint;
- τ0—cohesive capacity of the mortar beds;
- σcr—the cracking capacity of masonry;
- f’me,90—expected strength of masonry in the horizontal direction, which may be set at 50% of the expected stacked prism strength f’m.
5.2. Calculation of Load-Bearing Capacity of Frames with Infill Masonry According to CSA S304-14 (R2019) [49]
- Pr—the factored axial load resistance;
- Vr—factored shear resistance;
- Vm—shear strength attributed to the masonry;
- Vrs—shear resistance of masonry;
- Pd—axial compressive load on the section under consideration, based on 0.9 times dead load plus any factored axial load arising from bending in coupling beams where applicable;
- χ—factor used to account for the direction of compressive stress in a masonry member relative to the direction used for the determination of f’m;
- Фm—resistance factor for masonry;
- f’m—compressive strength of masonry normal to the bed joint at 28 days;
- d—distance from extreme compression fiber to centroid of tension reinforcement;
- Ae—effective cross-sectional area of masonry;
- Auc—uncracked area of the cross-section;
- vm—factored shear resistance of masonry members provided by the masonry;
- bw—overall web width, which does not include flanges or projections formed by intersecting walls when calculating factored shear resistance of walls;
- dv—effective depth for shear calculations, taken as the greater of 0.9d or 0.72hb but need not be taken as less than 0.8lw for walls;
- lw—wall length;
- hb—overall height of a beam;
- γg—factor to account for partially grouted walls or columns or ungrouted walls and columns when calculating the shear resistance;
- μ—the friction coefficient;
- θ—angle of diagonal strut measured from the horizontal.
5.3. Calculation of the Load-Bearing Capacity of the Frame with Infill Masonry According to Paulay and Priestley (1991) [52]
- Rc—the diagonal compression failure force;
- z—vertical length between panel and column;
- t—infill thickness;
- f’m—compression strength of the masonry;
- θ—the angle between the diagonal strut and the horizontal;
- Vs—shear resistance of the masonry infill panel
- fv0—design shear strength of masonry;
- tw—thickness of web of a flanged wall;
- Lw—length of the infill masonry wall (between the columns)
- h—overall thickness of member;
- L—interaxis length (between the columns axis)
- μ—the friction coefficient.
5.4. Calculation of the Load-Bearing Capacity of the Masonry-Infilled Frame According to EN 1996-1 and EN 1998-1 [48,51]
- VRd—the design value of the shear resistance;
- Vc,Ed—the shear force in the columns;
- Mc,Rd—the flexural capacity of the column;
- fv—is the design shear strength of masonry;
- tw—is the thickness of the wall;
- Lw—is the length of the wall;
- lc—contact length, should be assumed to be equal to the full vertical width of the diagonal strut of the infill;
- γRd—is the factor accounting for possible overstrength due to steel strain hardening.
5.5. Calculation of the Load-Bearing Capacity of the Frame with Infill Masonry According to Liauw and Kwan (1983) [53]
- Hu—collapse shear;
- Mpj—plastic moment of the (the smallest value of Mpc and Mpb);
- Mpc—plastic moment of the column;
- Mpb—plastic moment of the beam;
- σc—crushing stress of the panel material;
- s—shear strength of interface connection (force per unit length);
- t—thickness of the infill wall;
- h—story height;
- l—span of the infilled frame;
- θ—angle between the diagonal of the infilled panel and the horizontal.
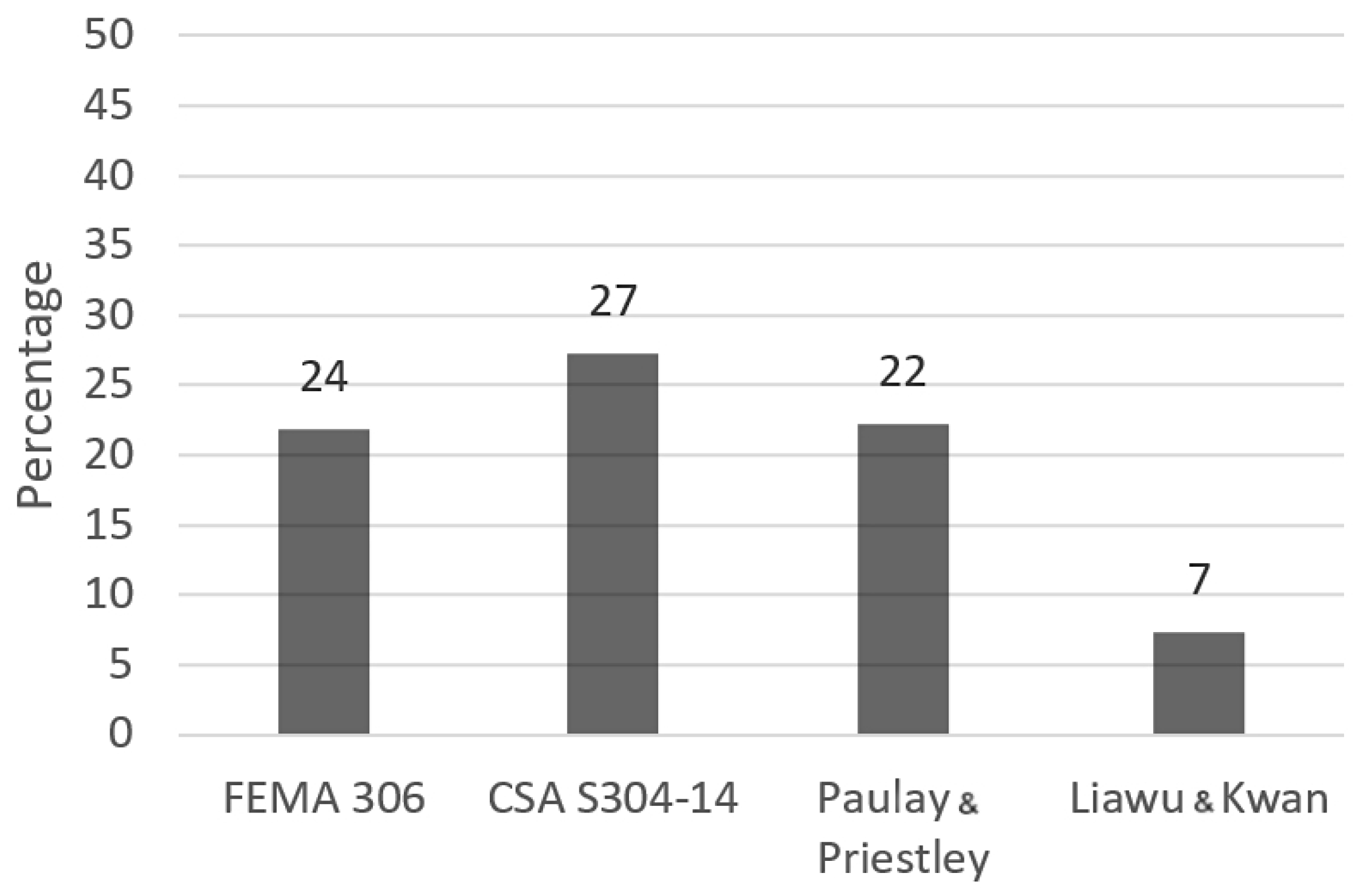
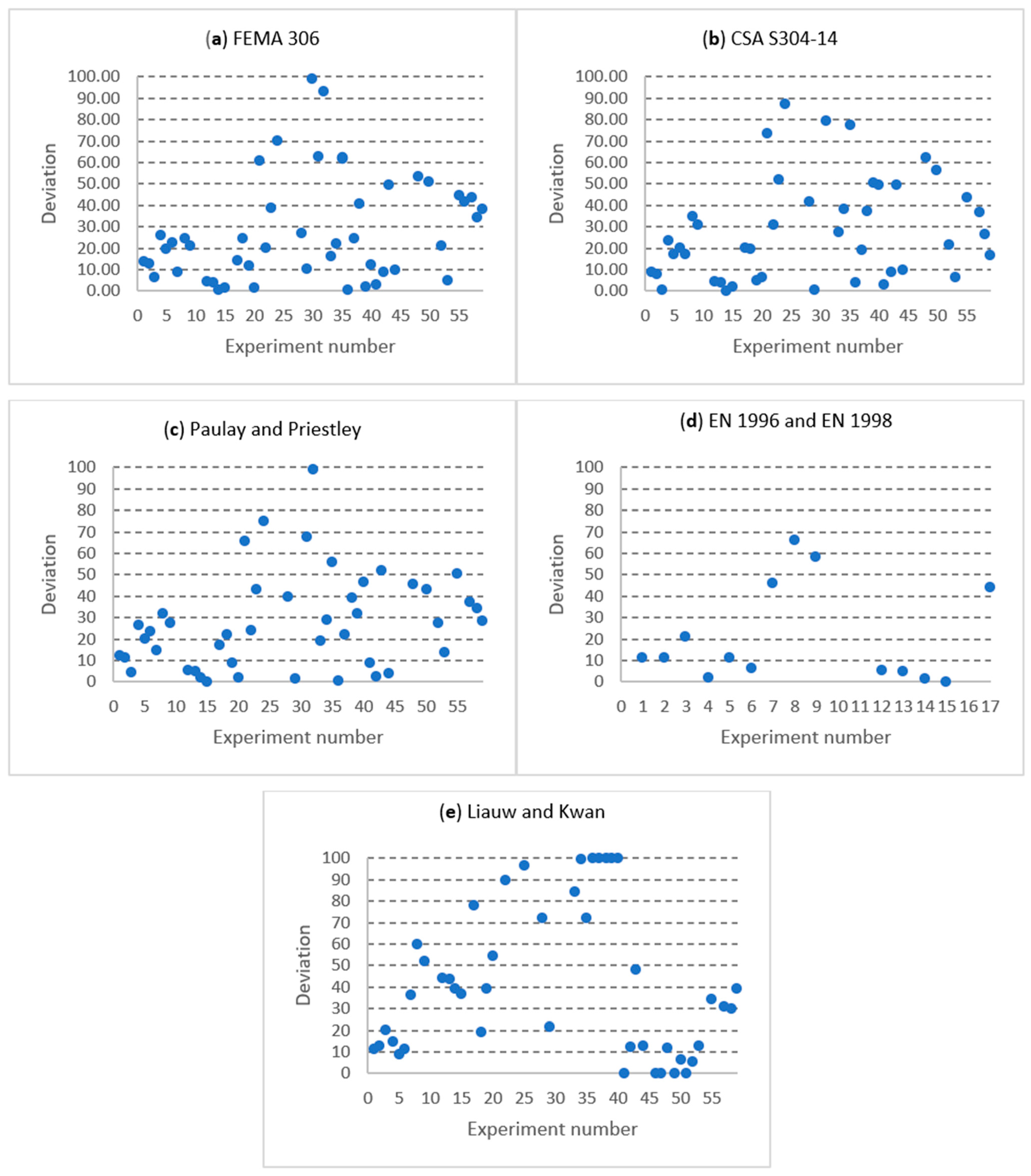
5.6. Conclusions on the Analytical Expressions and Experimental Data Comparison
6. Conclusions
- The equivalent diagonal model, utilized in all analytical expressions, can provide highly accurate estimations of load-bearing capacities that closely align with the experimental results. However, this accuracy is significantly influenced by the configuration of both the frame and the infill wall, as well as their interaction and interconnection. It is important to note that the behavior observed before failure cannot be captured by the equivalent diagonal model, as the interaction between the frame and the infill wall exhibits distinctly nonlinear characteristics, which the model does not account for.
- The type of infill element, whether hollow or solid, as well as the size of the vertical compressive strength, did not significantly impact the obtained results. Regardless of the type of infill element, the analytical expressions consistently overestimated the load-bearing capacity.
- The influence of longitudinal force enhances the load-bearing capacity of the frame, with the load-bearing capacity increasing as the longitudinal force increases. In the presence of longitudinal force, analytical expressions tend to be conservative, providing significantly lower load-bearing values compared with experimental results, which ensures a safety margin.
- The manner in which the force is transferred to the frame—whether directly or indirectly—significantly influences the analytical results. In the equivalent diagonal model, the force is applied directly to the node, the column and the beam, and experiments with this type of load application yield more accurate results compared with those where the load is applied indirectly.
- Steel frames with an infill wall, where the failure mode occurred diagonally along the compression diagonal and ultimately led to corner crushing, show better agreement with analytical expressions. This is in contrast to cases where failure occurs through shear failure in the mortar joints, which tend to exhibit discrepancies with the analytical predictions.
- The database can be utilized to develop numerical models, which can subsequently serve as the foundation for probabilistic methods used in conducting reliability assessments.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cheng, C.; Kawaguchi, K.I. A preliminary study on the response of steel structures using surveillance camera image with vision-based method during the Great East Japan Earthquake. Measurement 2015, 62, 142–148. [Google Scholar] [CrossRef]
- Tremblay, R.; Filiatrault, A.; Timler, P.; Bruneau, M. Performance of steel structures during the 1994 Northridge earthquake. Can. J. Civ. Eng. 1995, 22, 338–360. [Google Scholar] [CrossRef]
- Miller, D.K. Lessons learned from the Northridge earthquake. Eng. Struct. 1998, 20, 249–260. [Google Scholar] [CrossRef]
- Mahin, S.A. Lessons from damage to steel buildings during the Northridge earthquake. Eng. Struct. 1998, 20, 261–270. [Google Scholar] [CrossRef]
- Okazaki, T.; Lignos, D.G.; Midorikawa, M.; Ricles, J.M.; Love, J. Damage to steel buildings observed after the 2011 Tohoku-Oki earthquake. Earthq. Spectra 2013, 29 (Suppl. 1), 219–243. [Google Scholar] [CrossRef]
- De Risi, M.T.; Del Gaudio, C.; Ricci, P.; Verderame, G.M. In-plane behaviour and damage assessment of masonry infills with hollow clay bricks in RC frames. Eng. Struct. 2018, 168, 257–275. [Google Scholar] [CrossRef]
- Furtado, A.; Rodrigues, H.; Arêde, A.; Varum, H. Out-of-plane behavior of masonry infilled RC frames based on the experimental tests available: A systematic review. Constr. Build. Mater. 2018, 168, 831–848. [Google Scholar] [CrossRef]
- Dolsek, M.; Fajfar, P. The effect of masonry infills on the seismic response of a four-storey reinforced concrete frame- a deterministic assessment. Eng. Struct. 2008, 30, 1991–2001. [Google Scholar] [CrossRef]
- Dilmac, H.; Ulutas, H.; Tekeli, H.; Demir, F. The investigation of seismic performance of existing RC buildings with and without infill walls. Comput. Concr. 2018, 22, 439–447. [Google Scholar] [CrossRef]
- Timurağaoğlu, M.Ö.; Doğangün, A.; Livaoğlu, R. Comparison and assessment of material models for simulation of infilled RC frames under lateral loads. Građevinar 2019, 71, 45–56. [Google Scholar] [CrossRef]
- Radić, I.; Markulak, D.; Sigmund, V. Controlled seismic behaviour of masonry-infilled steel frames. Građevinar 2016, 68, 883–893. [Google Scholar] [CrossRef][Green Version]
- Cetisli, F. Effect of openings on infilled frame stiffness. Građevinar 2015, 67, 787–798. [Google Scholar] [CrossRef]
- Hak, S.; Morandi, P.; Magenes, G. Evaluation of infill strut properties based on in-plane cyclictests. Građevinar 2013, 65, 509–522. [Google Scholar] [CrossRef]
- Shendkar, M.R.; Kontoni, D.P.N.; Işık, E.; Mandal, S.; Maiti, P.R.; Harirchian, E. Influence of Masonry Infill on Seismic Design Factors of Reinforced-Concrete Buildings. Shock Vib. 2022, 2022, 1–15. [Google Scholar] [CrossRef]
- Athanasiou, A.; Dakour, M.; Pejmanfar, S.; Tirca, L.; Stathopoulos, T. Multihazard performance-based assessment framework for multistory steel buildings. J. Struct. Eng. 2022, 148, 04022054. [Google Scholar] [CrossRef]
- Tapia-Hernández, E.; Geneş, M.C.; Gülkan, P. Damage assessment and seismic response of steel buildings during the Kahramanmaraş, Turkey earthquakes of February 6, 2023. Earthq. Spectra 2022, 4, 102–122. [Google Scholar] [CrossRef]
- Georgiev, T. Field observations and assessment of performance level of steel structures after the Kahramanmaras Earthquake Sequence of 2023. In Proceedings of the International Conference on the Behaviour of Steel Structures in Seismic Areas; Springer Nature: Cham, Switzerland, 2024; pp. 633–645. [Google Scholar]
- Qiu, C.; Zhang, A.; Jiang, T.; Du, X. Seismic performance analysis of multi-story steel frames equipped with FeSMA BRBs. Soil Dyn. Earthq. Eng. 2022, 161, 107392. [Google Scholar] [CrossRef]
- Clifton, G.C.; Bruneau, M.; MacRae, G.; Leon, R.; Fussell, A. Multistorey steel framed building damage from the Christchurch earthquake series of 2010/2011. In Proceedings of the 7th International Conference on Behaviour of Steel Structures in Seismic Areas, Santiago, Chile, 9–11 January 2012. [Google Scholar]
- Clifton, C.; Bruneau, M.; MacRae, G.; Leon, R.; Fussell, A. Steel structures damage from the Christchurch earthquake series of 2010 and 2011. Bull. N. Z. Soc. Earthq. Eng. 2011, 44, 297–318. [Google Scholar] [CrossRef]
- Kadhum, A.K.; Abdul-Razzaq, K.S. Effect of seismic load on steel frame multistory building from economical point of view. In Proceedings of the AIP Conference Proceedings 2020, Baghdad, Iraq, 25–29 September 2019; Volume 2213. [Google Scholar]
- Zou, C.; Chen, Y. Study on Damage Law of Multistory and High-rise Steel Frame Structures under Strong Earthquake. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2020; Volume 525, No. 1; p. 012116. [Google Scholar]
- Di Sarno, L.; Freddi, F.; D’Aniello, M.; Kwon, O.-S.; Wu, J.-R.; Gutiérrez-Urzúa, F.; Landolfo, R.; Park, J.; Palios, X.; Strepelias, E. Assessment of existing steel frames: Numerical study, pseudo-dynamic testing and influence of masonry infills. J. Constr. Steel Res. 2021, 185, 106873. [Google Scholar] [CrossRef]
- Shan, S.; Li, S.; Wang, S. Effect of infill walls on mechanisms of steel frames against progressive collapse. J. Constr. Steel Res. 2019, 162, 105720. [Google Scholar] [CrossRef]
- Hadzima-Nyarko, M.; Čolak, S.; Bulajić, B.Đ.; Ademović, N. Assessment of Selected Models for FRP-Retrofitted URM Walls under In-Plane Loads. Buildings 2021, 11, 559. [Google Scholar] [CrossRef]
- Chinese Standards. Design Guidance for FRP Strengthened Structures (Provisional); Ministry of Construction: Beijing, China, 2006.
- ACI 440.7R-10; Guide for the Design and Construction of Externally Bonded Fiber-Reinforced Polymer Systems for Strengthening Unreinforced Masonry Structures. American Concrete Institute Committee 440: Farmington Hills, MI, USA, 2010.
- De Luca, F.; Morciano, E.; Perrone, D.; Aiello, M.A. Masonry Infilled RC Frame Experimental Database. Proc. Ital. Concr. Days 2018, 10, 147–160. [Google Scholar] [CrossRef]
- Sun, H.; Burton, H.V.; Huang, H. Machine learning applications for building structural design and performance assessment: State-of-the-art review. J. Build. Eng. 2021, 33, 101816. [Google Scholar] [CrossRef]
- El-Dakhakhni, W.W.; Mohamed, E.; Ahmad, H.A. Three-Strut Model for Concrete Masonry-Infilled Steel Frames. J. Struct. Eng. 2003, 129, 177–185. [Google Scholar] [CrossRef]
- Mohebkhah, A.; Sarhosis, V. Discrete Element Modeling of Masonry-Infilled Frames, 1st ed.; Sarhosis, V., Bagi, K., Lemos, J.V., Milani, G., Eds.; Engineering Science Reference; IGI Global: Hershey, PA, USA, 2016; Chapter 9; pp. 200–234. [Google Scholar] [CrossRef]
- Asteris, P.G.; Antoniou, S.T.; Sophianopoulos, D.S.; Chrysostomou, C.Z. Mathematical Macromodeling of Infilled Frames: State of the Art. J. Struct. Eng. 2011, 137, 1508–1517. [Google Scholar] [CrossRef]
- Farshidnia, P. Behavior and analysis of masonry-infilled reinforced concrete frames subjected to lateral load. WIT Trans. Built Environ. 2009, 104, 13–23. [Google Scholar] [CrossRef]
- Markulak, D.; Radic, I.; Sigmund, V. Cyclic testing of single bay steel frames with various types of masonry infill. Eng. Struct. 2013, 51, 267–277. [Google Scholar] [CrossRef]
- Markulak, D.; Dokšanović, T.; Radić, I.; Zovkić, J. Behaviour of steel frames infilled with environmentally and structurally favourable masonry units. Eng. Struct. 2020, 204, 109909. [Google Scholar] [CrossRef]
- Liu, Y.; Soon, S. Experimental study of concrete masonry infills bounded by steel frames. Can. J. Civ. Eng. 2012, 39, 180–190. [Google Scholar] [CrossRef]
- Tsantilis, A.; Triantafillou, T. Innovative Seismic Isolation of Masonry Infills in Steel Frames using Cellular Materials at the Frame-Infill Interface. J. Earthq. Eng. 2018, 24, 1–18. [Google Scholar] [CrossRef]
- Liu, Y.; Manesh, P. Concrete masonry infiltrated steel frames subjected to combined in-plane lateral and axial loading—An experimental study. Eng. Struct. 2013, 52, 331–339. [Google Scholar] [CrossRef]
- Moghaddam, H.A. Lateral Load Behavior of Masonry Infilled Steel Frames with Repair and Retrofit. J. Struct. Eng. 2004, 130, 56–63. [Google Scholar] [CrossRef]
- Dawe, J.L.; Seah, C.K. Behaviour of masonry infilled steel frames. Can. J. Civ. Eng. 1989, 16, 865–876. [Google Scholar] [CrossRef]
- Emami, S.M.M.; Mohammadi, M. Multi-bay and pinned connection steel infilled frames; an experimental and numerical study. Eng. Struct. 2019, 188, 43–59. [Google Scholar] [CrossRef]
- Ravichandran, S.S. Design Provisions for Autoclaved Aerated Concrete (AAC) Infiltrated Steel Moment Frames. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 2009; 342p. Available online: http://hdl.handle.net/2152/7529 (accessed on 4 December 2024).
- Mohammadi, M.; Akrami, V.; Mohammadi-Ghazi, R. Methods to Improve Infilled Frame Ductility. J. Struct. Eng. 2011, 137, 646–653. [Google Scholar] [CrossRef]
- Najarkolaie, K.; Mohammadi, M.; Fanaie, N. Realistic behavior of infilled steel frames in seismic events: Experimental and analytical study. Bull. Earthq. Eng. 2017, 15, 5365–5392. [Google Scholar] [CrossRef]
- Moghadam, H.; Mohammadi, M.; Ghaemian, M. Experimental and analytical investigation into crack strength determination of infiltrated steel frames. J. Constr. Steel Res. 2006, 62, 1341–1352. [Google Scholar] [CrossRef]
- Tasnimi, A.A.; Mohebkhah, A. Investigation on the behavior of brick-infilled steel frames with openings, experimental and analytical approaches. Eng. Struct. 2011, 33, 968–980. [Google Scholar] [CrossRef]
- Hashemi, S.J.; Razzaghi, J.; Moghadam, A.S.; Lourenço, P.B. Cyclic testing of steel frames infilled with concrete sandwich panels. Archit. Civ. Mech. Eng. 2018, 18, 557–572. [Google Scholar] [CrossRef]
- EN1996-1-1; Eurocode 6: Design of Masonry Structures-Part 1-1: General Rules for Reinforced and Unreinforced Masonry Structures. European Committee for Standardization: Brussels, Belgium, 1996.
- CSA S304-14; (R2019) Design of Masonry Structures. Canadian Standards Association: Toronto, ON, Canada, 2019.
- Federal Emergency Management Agency. FEMA 306 Evaluation of Earthquake Damaged Concrete and Masonry Wall Buildings; Basic Procedures Manual; Federal Emergency Management Agency: Washington, DC, USA, 1998.
- Eurocode 8: Design of Structures for Earthquake Resistance–Part 1: General Rules, Seismic Actions and Rules for Buildings; European Committee for Standardization: Brussels, Belgium, 2005.
- Paulay, T.; Priestley, M.J.N. Seismic Design of Reinforced Concrete and Masonry Buildings; John Wiley & Sons: New York, NY, USA; Chichester, UK; Brisbane, Australia; Toronto, ON, Canada; Singapore, 1991. [Google Scholar]
- Liauw, T.; Kwan, K. Plastic theory of infilled frames with finite interface shear strength. Proc. Inst. Civ. Eng. 1983, 75, 707–723. [Google Scholar] [CrossRef]
- Saneinejad, A. Non-Linear Analysis of Infilled Frames; University of Sheffield: Sheffield, UK, 1990; Available online: https://books.google.ro/books?id=_NIuGwAACAAJ (accessed on 12 November 2024).
- Salmon, C.G.; Johnson, J.E. Steel Structures: Design and Behavior: Emphasizing Load and Resistance Factor Design. HarperCollins College Publishers, University of Michigan. 1996. Available online: https://books.google.ro/books?id=I-pRAAAAMAAJ (accessed on 10 October 2024).
- Saneineja, A.; Hobbs, B. Inelastic Design of Infilled Frames. J. Struct. Eng. 1995, 121, 634–650. [Google Scholar] [CrossRef]
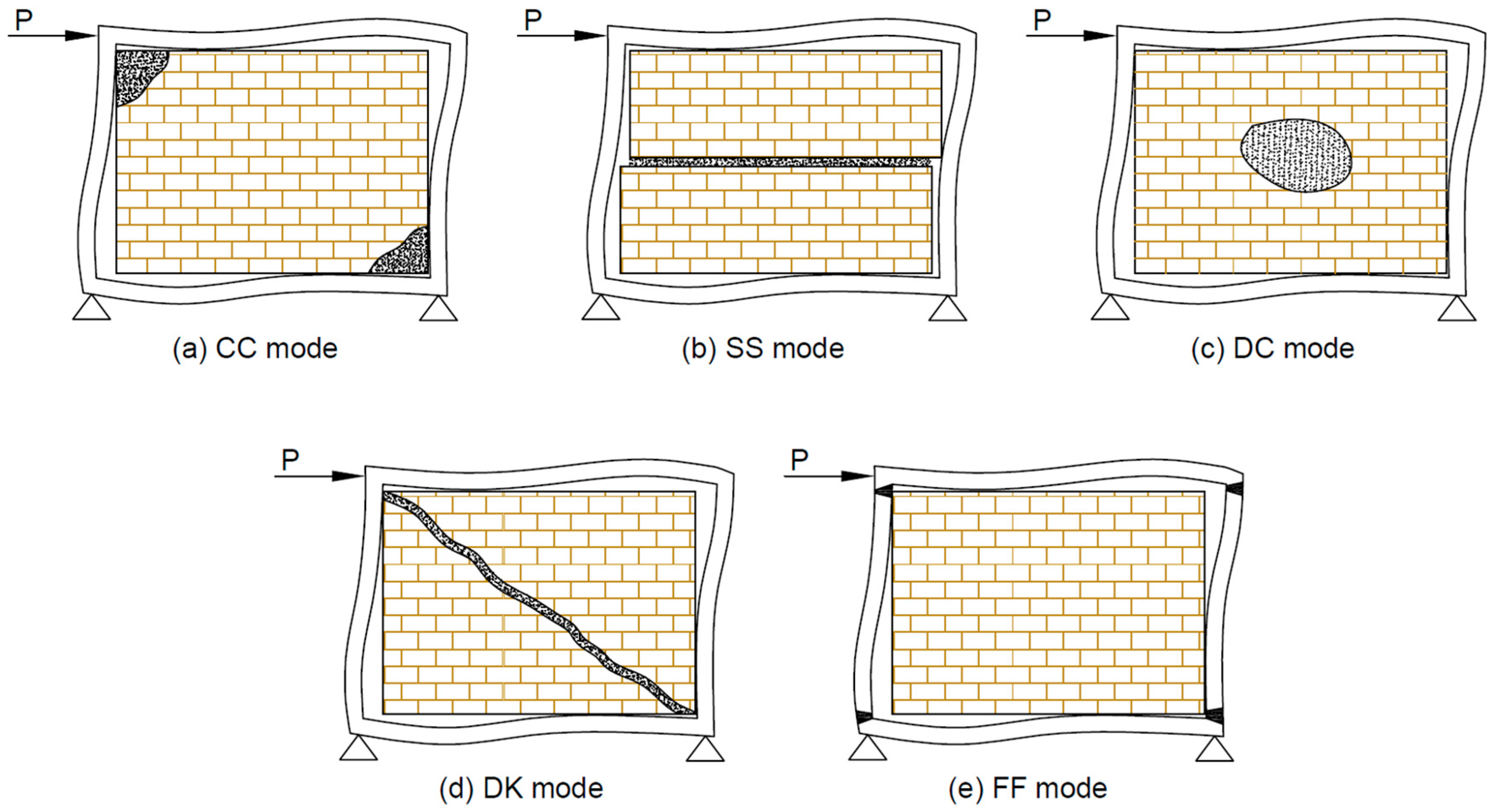
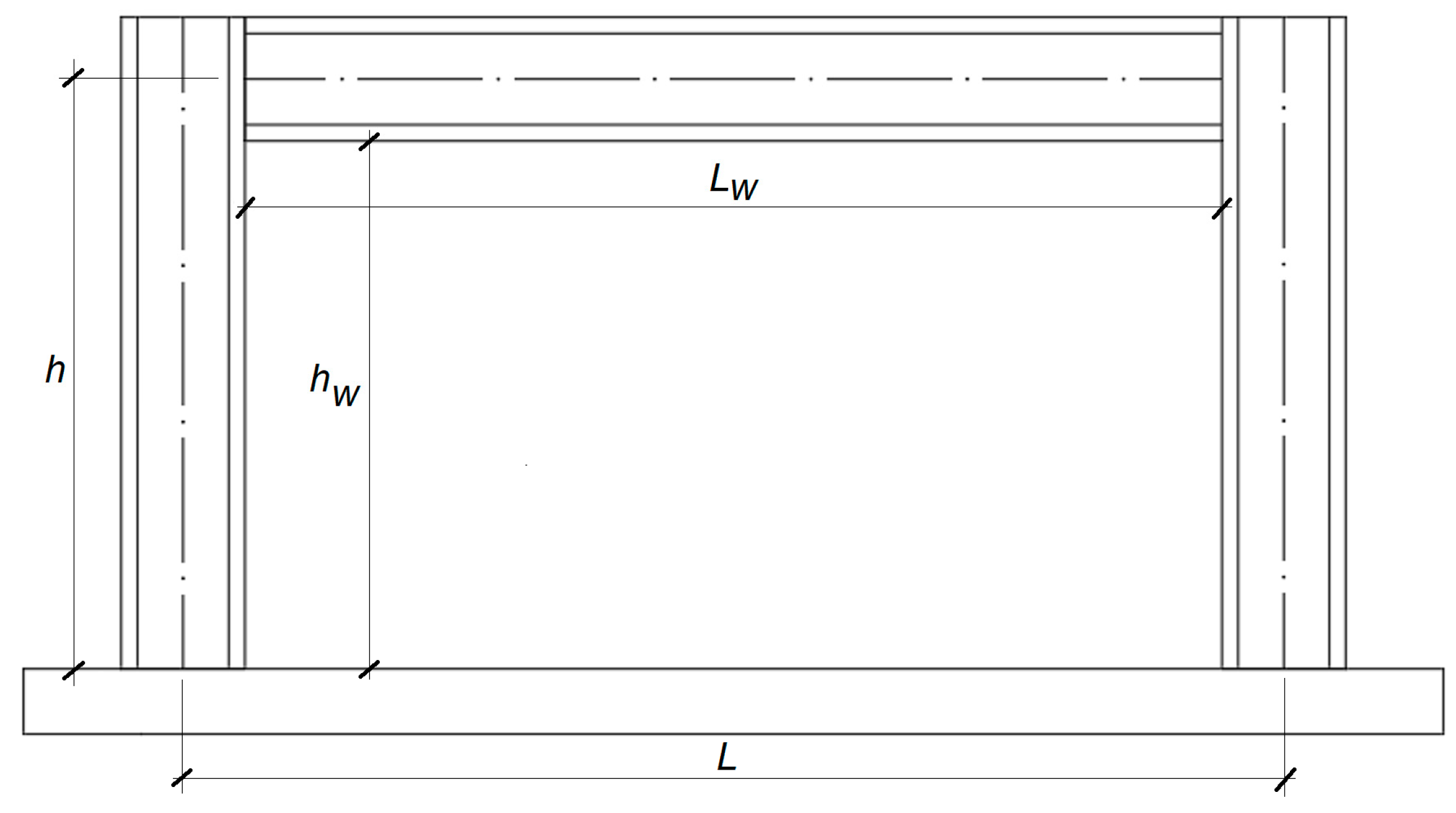
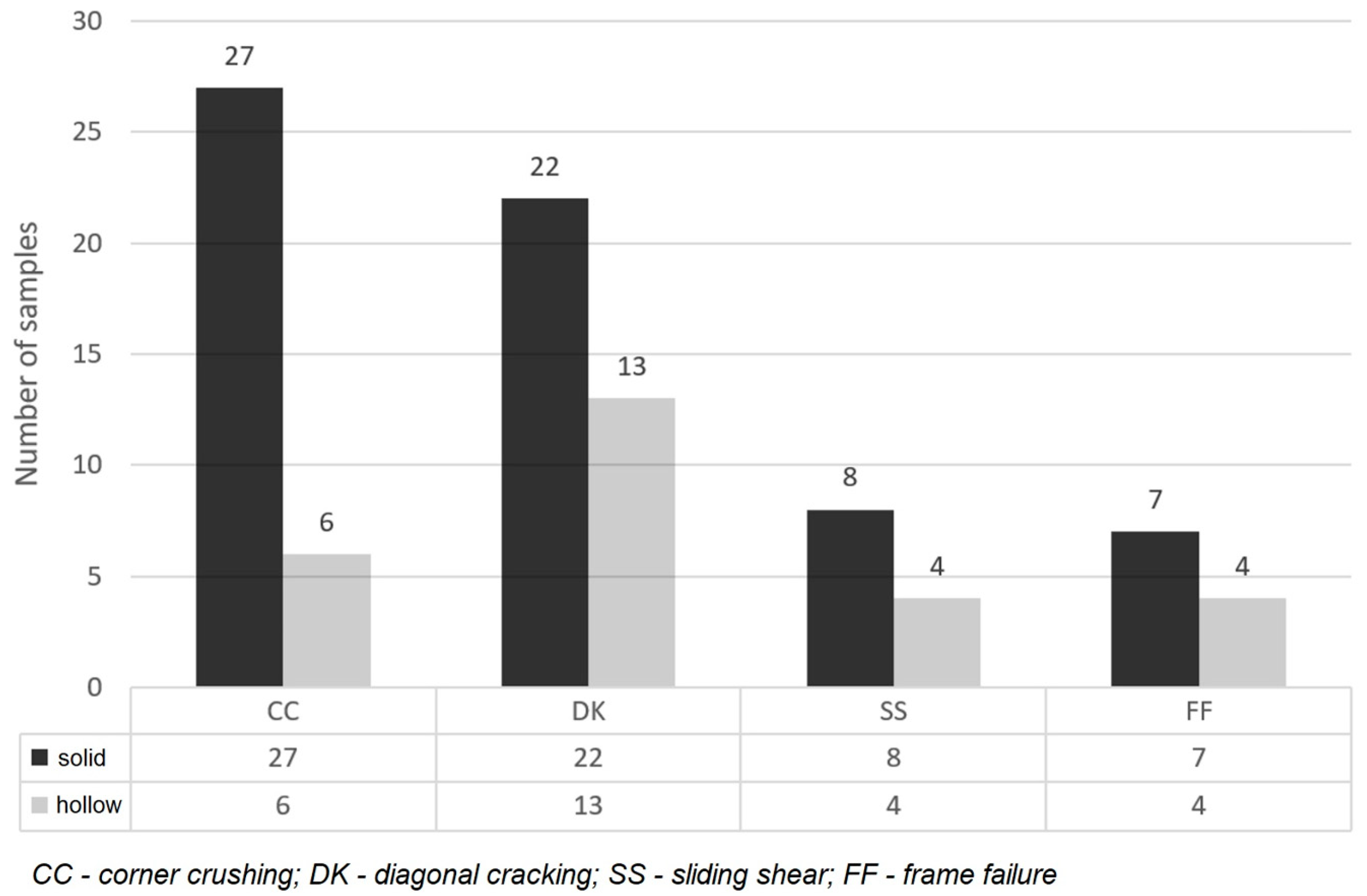
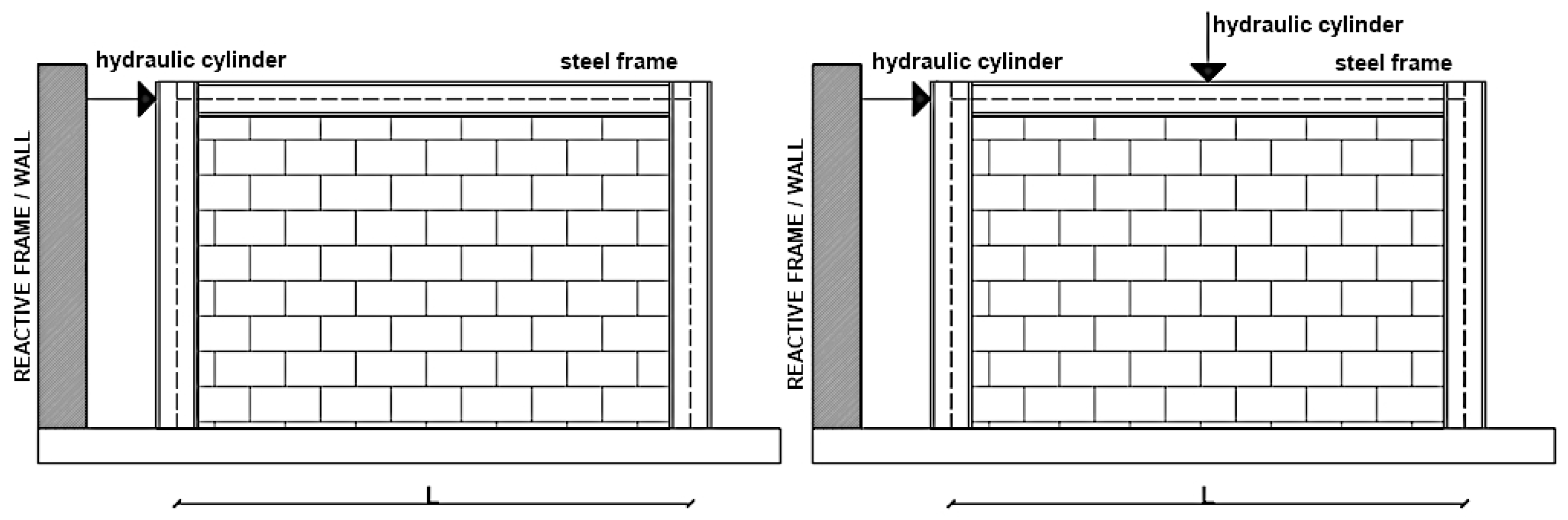
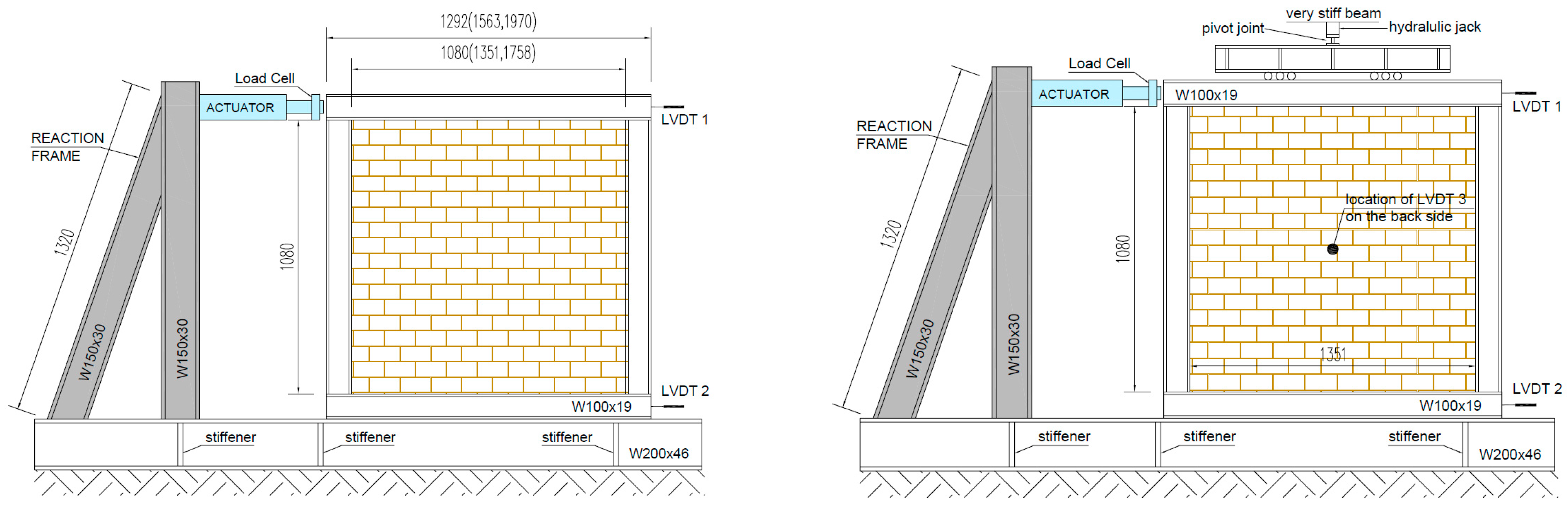
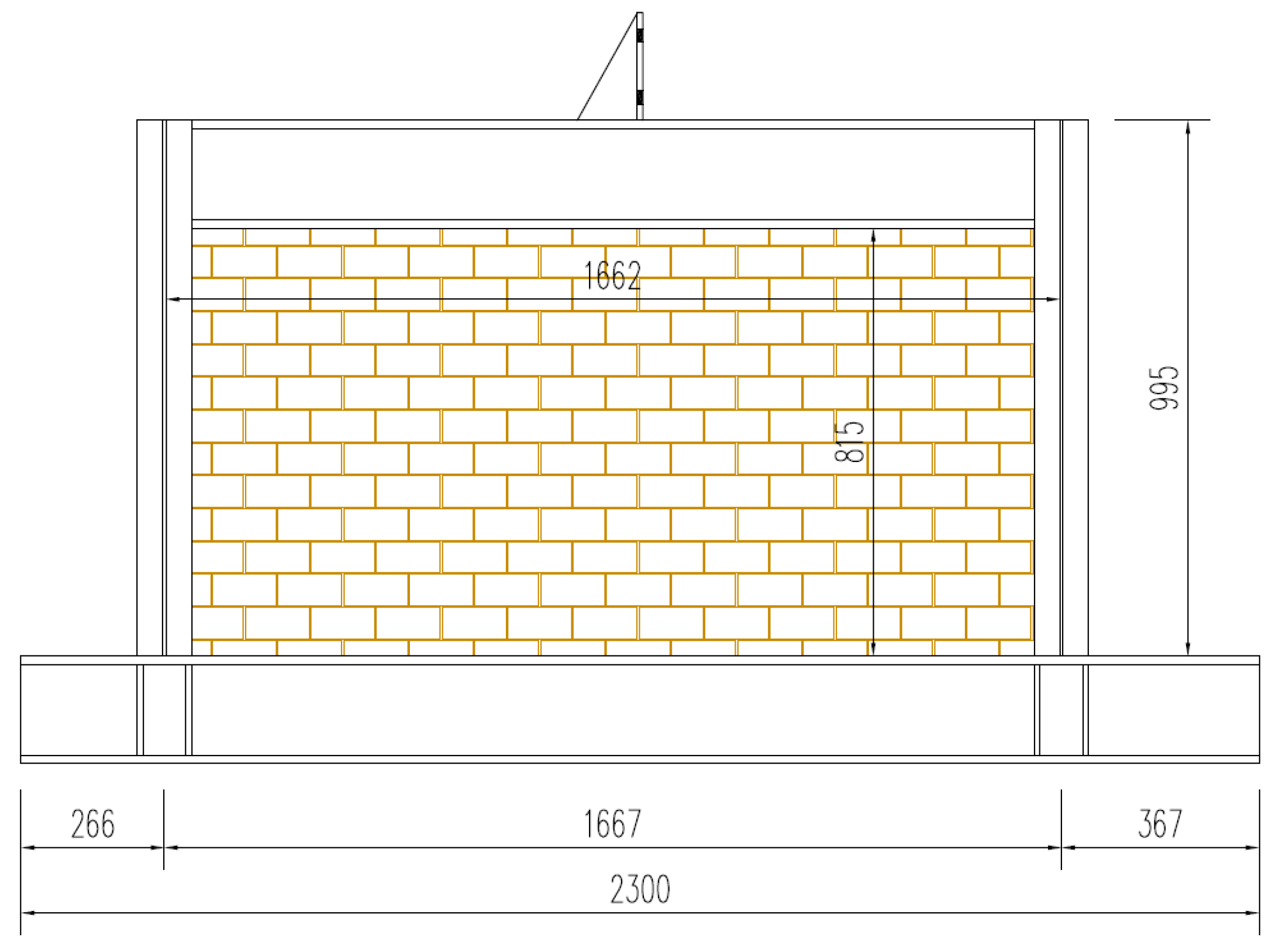
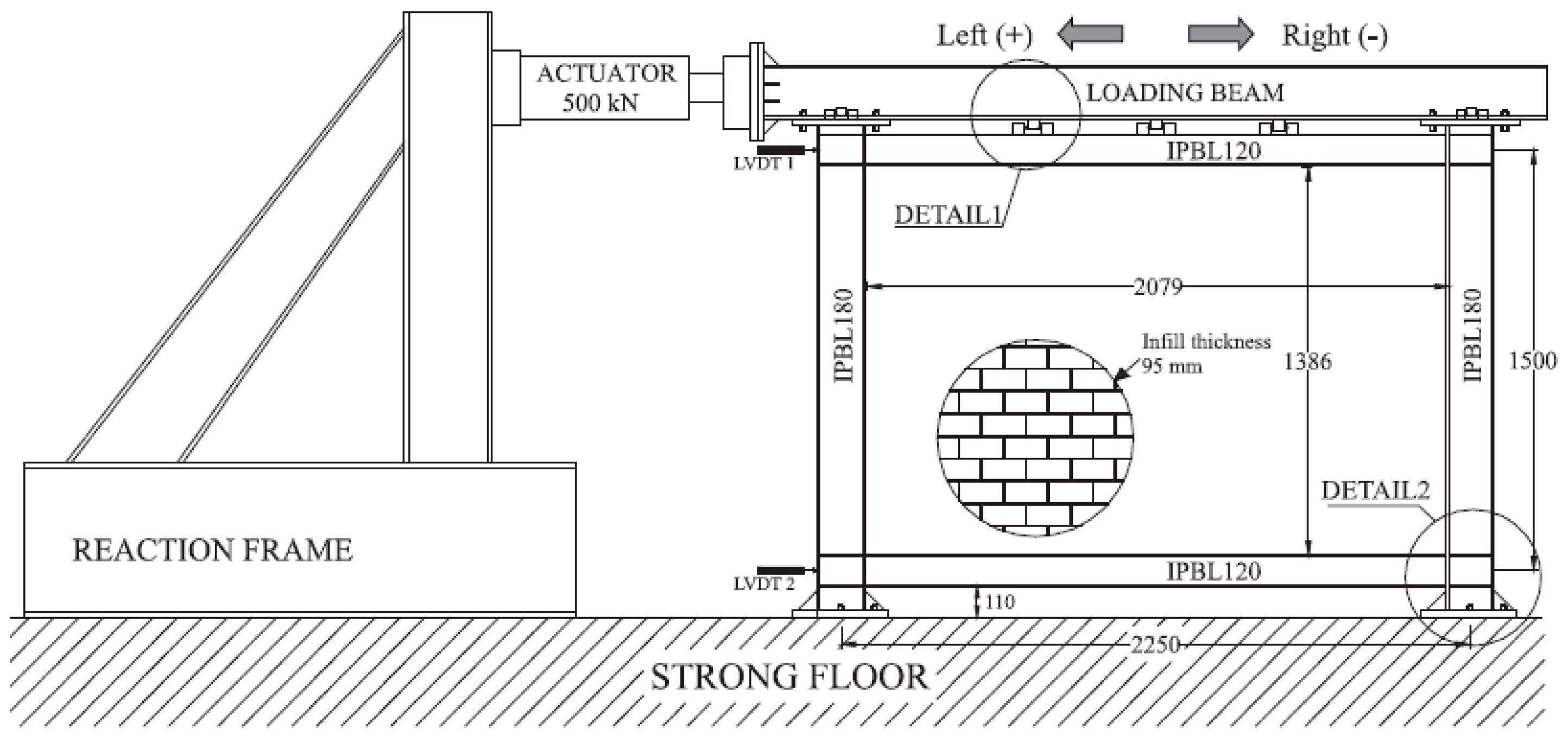
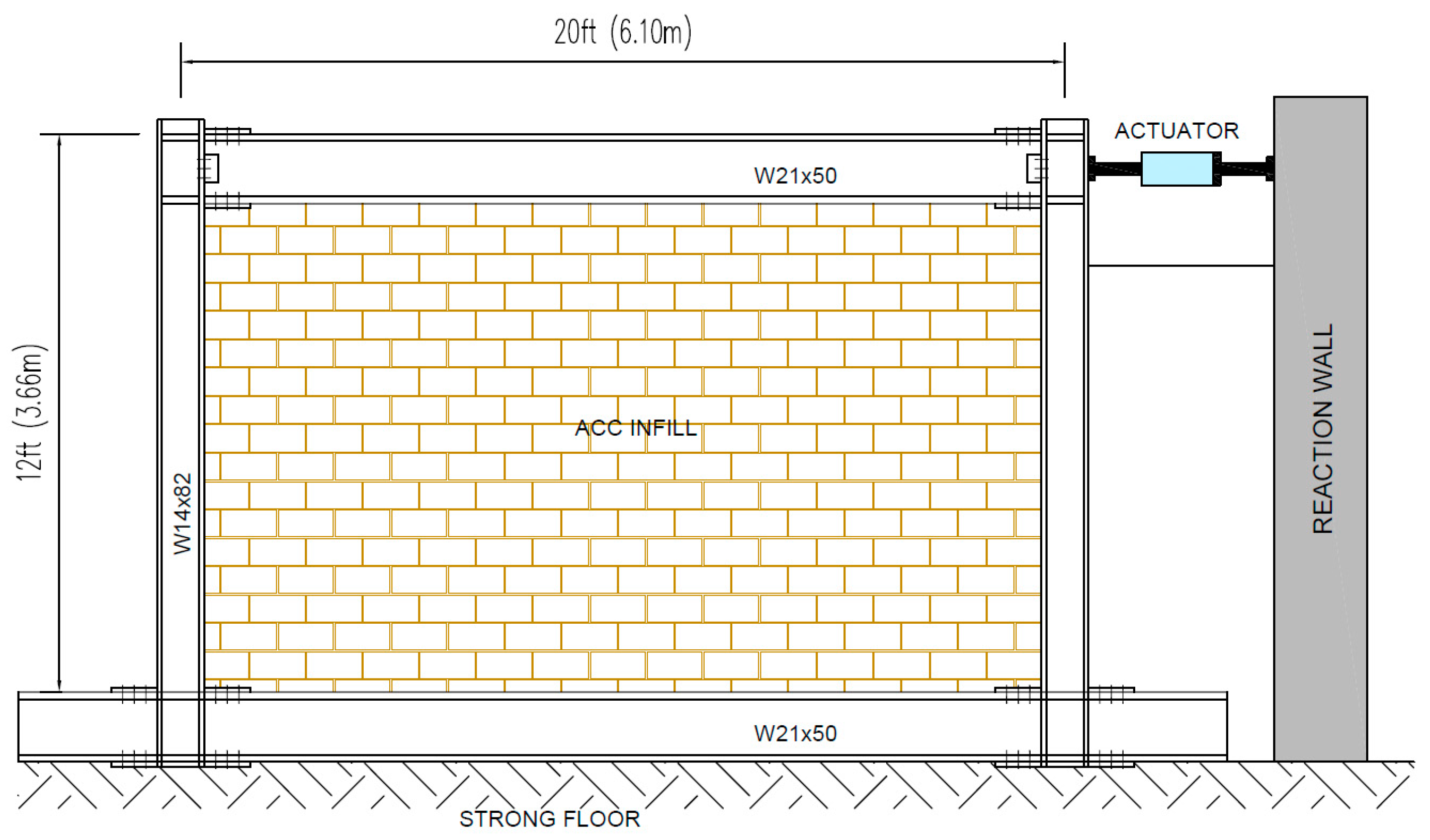
| # | References | Label | H (m) | L (m) | Andc (cm4) | Andb (cm4) | Wpl.c (mm3) | Es (GPa) |
|---|---|---|---|---|---|---|---|---|
| 1 | Markulak et al. (2013) [34] | C-1 | 1.613 | 2.176 | 606.2 | 606.2 | 119,500 | 210 |
| 2 | C-2 | 1.613 | 2.176 | 606.2 | 606.2 | 119,500 | 210 | |
| 3 | C-3 | 1.613 | 2.176 | 606.2 | 606.2 | 119,500 | 210 | |
| 4 | AAC-1 | 1.613 | 2.176 | 606.2 | 606.2 | 119,500 | 210 | |
| 5 | AAC-2 | 1.613 | 2.176 | 606.2 | 606.2 | 119,500 | 210 | |
| 6 | AAC-3 | 1.613 | 2.176 | 606.2 | 606.2 | 119,500 | 210 | |
| 7 | CA-1 | 1.613 | 2.176 | 606.2 | 606.2 | 119,500 | 210 | |
| 8 | CA-2 | 1.613 | 2.176 | 606.2 | 606.2 | 119,500 | 210 | |
| 9 | CA-3 | 1.613 | 2.176 | 606.2 | 606.2 | 119,500 | 210 | |
| where: C—hollow clay blocks; AAC—autoclaved aerated blocks. | ||||||||
| 10 | Markulak et al. (2020) [35] | PF-M-1 | 1.613 | 2.176 | 13.670 | 13.670 | 111,200 | 210 |
| 11 | PF-M-2 | 1.613 | 2.176 | 13.670 | 13.670 | 111,200 | 210 | |
| 12 | RF-M-1 | 1.613 | 2.176 | 606.2 | 606.2 | 119,500 | 210 | |
| 13 | RF-M-2 | 1.613 | 2.176 | 606.2 | 606.2 | 119,500 | 210 | |
| 14 | RF-MF-1 | 1.613 | 2.176 | 606.2 | 606.2 | 119,500 | 210 | |
| 15 | RF-MF-1 | 1.613 | 2.176 | 606.2 | 606.2 | 119,500 | 210 | |
| where: PF-M—Pinned steel frame infilled with masonry units of Type A; RF-M—Rigid steel frame infilled with masonry units of Type A; RF-MF—Steel frame infilled with masonry units of Type A and Type B. | ||||||||
| 16 | Liu and Soon (2012) [36] | N-0 | 1.239 | 1.407 | 476 | 476 | 103,000 | 199.5 |
| 17 | F-0 | 1.239 | 1.407 | 476 | 476 | 103,000 | 199.5 | |
| 18 | CF-1 | 1.239 | 1.407 | 476 | 476 | 103,000 | 199.5 | |
| 19 | CF-2 | 1.239 | 1.407 | 476 | 476 | 103,000 | 199.5 | |
| 20 | CF-3 | 1.239 | 1.407 | 476 | 476 | 103,000 | 199.5 | |
| 21 | P-0 | 1.239 | 1.407 | 476 | 476 | 103,000 | 199.5 | |
| 22 | CP-1 | 1.239 | 1.407 | 476 | 476 | 103,000 | 199.5 | |
| 23 | CP-2 | 1.239 | 1.407 | 476 | 476 | 103,000 | 199.5 | |
| 24 | CP-3 | 1.239 | 1.407 | 476 | 476 | 103,000 | 199.5 | |
| where: C—combined load; N—ungrouted infill; F—fully grouted infill; P—partially grouted infill | ||||||||
| 25 | Tsantilis and Triantafillou (2018) [37] | S0 | 0.905 | 1.667 | 1.317 | 1.317 | 16,640 | 210 |
| 26 | S2 | 0.905 | 1.667 | 1.317 | 1.317 | 16,640 | 210 | |
| 27 | S4 | 0.905 | 1.667 | 1.317 | 1.317 | 16,640 | 210 | |
| where: S0—infilled frame; S2—cellular material 2mm at vertical slits; S4—cellular material 4 mm perimets. | ||||||||
| 28 | Liu and Manesh (2013) [38] | P1NA | 1.239 | 1.136 | 476 | 476 | 103,000 | 199.5 |
| 29 | F1NA | 1.239 | 1.136 | 476 | 476 | 103,000 | 199.5 | |
| 30 | N3NA | 1.239 | 1.136 | 476 | 476 | 103,000 | 199.5 | |
| 31 | P3NA | 1.239 | 1.136 | 476 | 476 | 103,000 | 199.5 | |
| 32 | F3NA | 1.239 | 1.136 | 476 | 476 | 103,000 | 199.5 | |
| 33 | P3NI | 1.239 | 1.136 | 476 | 476 | 103,000 | 199.5 | |
| 34 | F3NI | 1.239 | 1.136 | 476 | 476 | 103,000 | 199.5 | |
| 35 | P6NA | 1.239 | 1.814 | 476 | 476 | 103,000 | 199.5 | |
| where: P—partially grouted; F—fully grouted; N—non-grouted; A—major column orientation in frame; I—minor column orientation in frame. | ||||||||
| 36 | H. Moghaddam (2004) [39] | S1 | 1.300 | 1.500 | 328 | 328 | 6,360 | 210 |
| 37 | S2 | 1.300 | 1.500 | 328 | 328 | 6,360 | 210 | |
| 38 | S3 | 1.300 | 1.500 | 328 | 328 | 6,360 | 210 | |
| where: S1—solid brick, intact condition; S2—solid brick repaired (corner strengthened); S3—perforated brick intact condition. | ||||||||
| 39 | Dawe and Seah (1989) [40] | WA4 | 2.697 | 3.600 | 8.730 | 4.540 | 770,000 | 210 |
| 40 | WC7 | 2.697 | 3.600 | 8.730 | 4.540 | 770,000 | 210 | |
| where: WA4—mortar between column flange and panel, but without bed-join reinforcement; WC7—mortar packed between column flanges and panel, without mortar between panel and column flanges, with no joint reinforcement. | ||||||||
| 41 | Mohammadi and Emami (2019) [41] | M-RC-1B | 1.500 | 2.250 | 2.510 | 606.2 | 324,900 | 185 |
| 42 | M-PC-1B | 1.500 | 2.250 | 2.510 | 606.2 | 324,900 | 185 | |
| 43 | M-RC-2B | 1.500 | 2.250 | 2.510 | 606.2 | 324,900 | 185 | |
| 44 | M-PC-2B | 1.500 | 2.250 | 2.510 | 606.2 | 324,900 | 185 | |
| where: M—masonry unit; R—rigid; P -pinned; 1—one way; 2—two bay. | ||||||||
| 45 | Ravichandran (2009) [42] | AAC | 3.139 | 6.100 | 36.691 | 40.934 | 139,000 | 210 |
| where: AAC—Autoclaved aerated concrete | ||||||||
| 46 | Mohammadi et al. (2011) [43] | SP1 | 2.070 | 3.000 | 541.20 | 541.20 | 88,340 | 210 |
| 47 | CL-SP1 | 2.070 | 3.000 | 541.20 | 541.20 | 88,340 | 210 | |
| 48 | SP-2 | 2.070 | 3.000 | 541.20 | 541.20 | 88,340 | 210 | |
| 49 | CF-SP2 | 2.070 | 3.000 | 541.20 | 541.20 | 88,340 | 210 | |
| 50 | CP3 | 2.070 | 3.000 | 541.20 | 541.20 | 88,340 | 210 | |
| 51 | SF-SP3 | 2.070 | 3.000 | 541.20 | 541.20 | 88,340 | 210 | |
| where: SP1—three-layer infill, composed of 25 mm concrete, 100 mm brick, 25 mm concrete; CL-SP1—corner less; SP2—three-layer infill, two 100 mm masonry wall with 75 mm RC wall at the middle; CF-SP2—column fuse; CP3—three-layer infill, two 100mm masonry wall with 50 mm RC wall at the middle; SF-SP3—sliding fuse in the infill. | ||||||||
| 52 | Najarkolaie et al. (2017) [44] | DL | 2.226 | 2.219 | 2.510 | 606.00 | 324,900 | 199 |
| 53 | CL | 2.226 | 2.219 | 2.510 | 606.00 | 324,900 | 199 | |
| where: DL—specimen distributed loading; CL—specimen concentrated loading. | ||||||||
| 54 | Moghadam et al. (2006) [45] | MS | 2.020 | 1.800 | 541.20 | 541.20 | 88,340 | 170 |
| 55 | MM | 2.070 | 3.000 | 541.20 | 541.20 | 88,340 | 170 | |
| where: M—masonry. | ||||||||
| 56 | Tasnimi and Mohebkhah (2011) [46] | SW | 1.870 | 2.400 | 541.20 | 541.20 | 88,340 | 210 |
| where: SW—solid infilled frame | ||||||||
| 57 | Hashemi et al. (2018) [47] | IFS | 1.753 | 1.100 | 1.673 | 1.033 | 245,100 | 203 |
| 58 | IFM | 1.753 | 1.752 | 1.673 | 1.033 | 245,100 | 203 | |
| 59 | IFL | 1.753 | 2.502 | 1.673 | 1.033 | 245,100 | 203 | |
| where: IFS—infilled frame with small aspect ratio; IFM—infilled frame with medium aspect ratio; IFL—infilled frame with large aspect ratio. | ||||||||
| # | References | Label | Fill | Hw (m) | Lw (m) | tw (mm) | fb (MPa) | fk (MPa) | Em (MPa) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Markulak et al. (2013) [34] | C-1 | HC | 1.556 | 2.062 | 120 | 13.05 | 1.9 | 4600 |
| 2 | C-2 | HC | 1.556 | 2.062 | 120 | 13.05 | 2.0 | 4600 | |
| 3 | C-3 | HC | 1.556 | 2.062 | 120 | 13.05 | 1.9 | 4600 | |
| 4 | AAC-1 | AAC | 1.556 | 2.062 | 120 | 2.13 | 1.06 | 1174 | |
| 5 | AAC-2 | AAC | 1.556 | 2.062 | 120 | 2.13 | 0.97 | 1174 | |
| 6 | AAC-3 | AAC | 1.556 | 2.062 | 120 | 2.13 | 1.05 | 1174 | |
| 7 | CA-1 | HC+AAC | 1.556 | 2.062 | 120 | 2.12 | 1.9 | 4600 | |
| 8 | CA-2 | HC+AAC | 1.556 | 2.062 | 120 | 2.03 | 2.0 | 4600 | |
| 9 | CA-3 | HC+AAC | 1.556 | 2.062 | 120 | 1.6 | 1.9 | 4600 | |
| 10 | Markulak et al. (2020) [35] | PF-M-1 | RBA-EP | 1.548 | 2.062 | 120 | 4.04 | 3.13 | 2746 |
| 11 | PF-M-2 | RBA-EP | 1.548 | 2.062 | 120 | 4.04 | 3.13 | 2746 | |
| 12 | RF-M-1 | RBA-EP | 1.548 | 2.062 | 120 | 4.04 | 3.13 | 2746 | |
| 13 | RF-M-2 | RBA-EP | 1.548 | 2.062 | 120 | 4.04 | 3.13 | 2746 | |
| 14 | RF-MF-1 | RBA-EP | 1.548 | 2.062 | 120 | 4.04 | 3.13 | 2746 | |
| 15 | RF-MF-1 | RBA-EP | 1.548 | 2.062 | 120 | 4.04 | 3.13 | 2746 | |
| 16 | Liu and Soon (2012) [36] | N-0 | CMB | 1.080 | 1.351 | 64 | 20.5 | 10.5 | 9920 |
| 17 | F-0 | CMB | 1.080 | 1.351 | 64 | 20.5 | 9.10 | 10,100 | |
| 18 | CF-1 | CMB | 1.080 | 1.351 | 64 | 20.5 | 9.10 | 12,800 | |
| 19 | CF-2 | CMB | 1.080 | 1.351 | 64 | 20.5 | 9.10 | 12,800 | |
| 20 | CF-3 | CMB | 1.080 | 1.351 | 64 | 20.5 | 9.10 | 12,800 | |
| 21 | P-0 | CMB | 1.080 | 1.351 | 64 | 20.5 | 9.40 | 12,800 | |
| 22 | CP-1 | CMB | 1.080 | 1.351 | 64 | 20.5 | 9.40 | 12,800 | |
| 23 | CP-2 | CMB | 1.080 | 1.351 | 64 | 20.5 | 9.40 | 12,800 | |
| 24 | CP-3 | CMB | 1.080 | 1.351 | 64 | 20.5 | 9.40 | 12,800 | |
| 25 | Tsantilis and Triantafillou (2018) [37] | S0 | HC | 1.662 | 0.815 | 58 | 14.26 | 4.19 | 3890 |
| 26 | S2 | HC | 1.662 | 0.815 | 58 | 14.26 | 4.19 | 3890 | |
| 27 | S4 | HC | 1.662 | 0.815 | 58 | 14.26 | 4.19 | 3890 | |
| 28 | Liu and Manesh (2013) [38] | P1NA | CMB | 1.080 | 1.080 | 64 | 20.5 | 9.7 | 10,940 |
| 29 | F1NA | CMB | 1.080 | 1.080 | 64 | 20.5 | 9.7 | 10,940 | |
| 30 | N3NA | CMB | 1.080 | 1.080 | 64 | 20.5 | 9.7 | 10,940 | |
| 31 | P3NA | CMB | 1.080 | 1.080 | 64 | 20.5 | 9.7 | 10,940 | |
| 32 | F3NA | CMB | 1.080 | 1.080 | 64 | 20.5 | 9.7 | 10,940 | |
| 33 | P3NI | CMB | 1.080 | 1.080 | 64 | 20.5 | 9.7 | 10,940 | |
| 34 | F3NI | CMB | 1.080 | 1.080 | 64 | 20.5 | 9.7 | 10,940 | |
| 35 | P6NA | CMB | 1.080 | 1.080 | 64 | 20.5 | 9.7 | 10,940 | |
| 36 | H. Moghaddam (2004) [39] | S1 | SB | 1.240 | 1.380 | 110 | - | 3.50 | 782 |
| 37 | S2 | HC | 1.240 | 1.380 | 110 | - | 2.95 | 782 | |
| 38 | S3 | HC | 1.240 | 1.380 | 110 | - | 2.28 | 1350 | |
| 39 | Dawe and Seah (1989) [40] | WA4 | HCB | 2.597 | 3.348 | 200 | 24.4 | 18.92 | 31,303 |
| 40 | WC7 | HCB | 2.597 | 3.348 | 200 | 33.4 | 23.57 | 33,691 | |
| 41 | Mohammadi and Emami (2019) [41] | M-RC-1B | SB | 1.386 | 2.079 | 55 | - | 8.30 | 1892 |
| 42 | M-PC-1B | SB | 1.386 | 2.079 | 55 | - | 8.30 | 1892 | |
| 43 | M-RC-2B | SB | 1.386 | 2.079 | 55 | - | 8.30 | 1892 | |
| 44 | M-PC-2B | SB | 1.386 | 2.079 | 55 | - | 8.30 | 1892 | |
| 45 | Ravichandran (2009) [42] | RF-AAC | AAC | 3.131 | 5.736 | 203 | - | 4.90 | 2041 |
| 46 | Mohammadi et al. (2011) [43] | SP1 | SB | 2.000 | 2.860 | 150 | 6.70 | 4.90 | 4900 |
| 47 | CL-SP1 | SB | 2.000 | 2.860 | 150 | 6.70 | 4.90 | 4900 | |
| 48 | SP-2 | SB | 2.000 | 2.860 | 275 | 13.0 | 4.90 | 4900 | |
| 49 | CF-SP2 | SB | 2.000 | 2.860 | 275 | 17.40 | 4.90 | 4900 | |
| 50 | CP3 | SB | 2.000 | 2.860 | 250 | 6.20 | 4.90 | 4900 | |
| 51 | SF-SP3 | SB | 2.000 | 2.860 | 250 | 10 | 4.90 | 4900 | |
| 52 | Najarkolaie et al. (2017) [44] | DL | SB | 2.079 | 1.386 | 55 | - | 7.50 | 1425 |
| 53 | CL | SB | 2.079 | 1.386 | 55 | - | 7.50 | 1425 | |
| 54 | Moghadam et al. (2006) [45] | MS | SB | 1.630 | 0.960 | 56 | 29.0 | 4.90 | 2321 |
| 55 | MM | SB | 1.630 | 0.960 | 56 | 29.0 | 4.90 | 2321 | |
| 56 | Tasnimi and Mohebkhah (2011) [46] | SW | SB | 1.800 | 2.260 | 110 | 12.60 | 7.40 | - |
| 57 | Hashemi et al. (2018) [47] | IFS | CSP | 0.950 | 1.620 | 140 | 28.20 | 4.13 | 16,700 |
| 58 | IFM | CSP | 1.600 | 1.620 | 140 | 28.20 | 4.13 | 16,700 | |
| 59 | IFL | CSP | 2.650 | 1.620 | 140 | 28.20 | 4.13 | 16,700 |
| # | References | Label | Kini (kN/mm) | Ksec (kN/mm) | Fy (kN) | Fmax (kN) |
|---|---|---|---|---|---|---|
| 1 | Markulak et al. (2013) [34] | C-1 | 32.07 | - | 59.0 | 139.0 |
| 2 | C-2 | 27.89 | - | 70.0 | 139.0 | |
| 3 | C-3 | 34.00 | - | 51.0 | 128.0 | |
| 4 | AAC-1 | 26.93 | - | 54.0 | 152.0 | |
| 5 | AAC-2 | 15.07 | - | 51.0 | 139.0 | |
| 6 | AAC-3 | 17.50 | - | 49.0 | 146.0 | |
| 7 | CA-1 | 23.93 | - | 39.0 | 106.0 | |
| 8 | CA-2 | 23.26 | - | 40.0 | 93.0 | |
| 9 | CA-3 | 19.49 | - | 50.0 | 95.0 | |
| 10 | Markulak et al. (2020) [35] | PF-M-1 | 7.90 | - | 24.80 | 60.0 |
| 11 | PF-M-2 | 8.20 | - | 19.00 | 50.0 | |
| 12 | RF-M-1 | 14.40 | - | 69.50 | 130.0 | |
| 13 | RF-M-2 | 14.90 | - | 30.50 | 130.70 | |
| 14 | RF-MF-1 | 14.00 | - | 65.00 | 135.0 | |
| 15 | RF-MF-1 | 14.30 | - | 68.50 | 137.0 | |
| 16 | Liu and Soon (2012) [36] | N-0 | - | 18.70 | 62.00 | 77.0 |
| 17 | F-0 | - | 26.90 | 128.0 | 132.0 | |
| 18 | CF-1 | - | 36.70 | 165.0 | 198.0 | |
| 19 | CF-2 | - | 32.0 | 150.0 | 169.0 | |
| 20 | CF-3 | - | 29.10 | 130.0 | 152.0 | |
| 21 | P-0 | - | 24.80 | 94.0 | 94.0 | |
| 22 | CP-1 | - | 26.30 | 80.0 | 126.0 | |
| 23 | CP-2 | - | 24.90 | 65.0 | 109.0 | |
| 24 | CP-3 | - | 25.60 | 75.0 | 89.0 | |
| 25 | Tsantilis and Triantafillou (2018) [37] | S0 | - | 11.98 | - | 107.54 |
| 26 | S2 | - | 7.79 | - | 87.52 | |
| 27 | S4 | - | 6.66 | - | 98.0 | |
| 28 | Liu and Manesh (2013) [38] | P1NA | 27.10 | 19.90 | 92.0 | 111.0 |
| 29 | F1NA | 38.80 | 22.60 | 109.0 | 157.0 | |
| 30 | N3NA | 24.30 | 18.70 | 62.0 | 77.0 | |
| 31 | P3NA | 35.40 | 24.80 | 94.0 | 94.0 | |
| 32 | F3NA | 17.90 | 13.10 | 63.0 | 79.0 | |
| 33 | P3NI | 56.40 | 26.90 | 128.0 | 132.0 | |
| 34 | F3NI | 21.40 | 18.40 | 46.0 | 128.0 | |
| 35 | P6NA | 29.70 | 23.40 | 104.0 | 104.0 | |
| 36 | H. Moghaddam (2004) [39] | S1 | 22.10 | - | - | 82.13 |
| 37 | S3 | 31.65 | - | - | 116.0 | |
| 38 | S5 | 42.85 | - | - | 139.3 | |
| 39 | Dawe and Seah (1989) [40] | WA4 | 63.0 | - | 211.0 | 4760 |
| 40 | WC7 | 64.0 | - | 310.0 | 534.0 | |
| 41 | Mohammadi and Emami (2019) [41] | M-RC-1B | 10.64 | - | - | 325.0 |
| 42 | M-PC-1B | 5.60 | - | - | 290.0 | |
| 43 | M-RC-2B | 17.20 | - | - | 623.0 | |
| 44 | M-PC-2B | 13.90 | - | - | 288.0 | |
| 45 | Ravichandran (2009) [42] | RF-AAC | - | - | - | 431.0 |
| 46 | Mohammadi et al. (2011) [43] | SP1 | - | - | - | - |
| 47 | CL-SP1 | - | - | - | - | |
| 48 | SP-2 | - | - | 304.0 | 412.0 | |
| 49 | CF-SP2 | - | - | - | - | |
| 50 | CP3 | - | - | 196.0 | 368.0 | |
| 51 | SF-SP3 | - | - | 31.0 | - | |
| 52 | Najarkolaie et al. (2017) [44] | DL | 13.40 | - | - | 325.0 |
| 53 | CL | 10.60 | - | - | 272.0 | |
| 54 | Moghadam et al. (2006) [45] | MS | 7.23 | - | - | 21.85 |
| 55 | MM | 6.79 | - | - | 147.16 | |
| 56 | Tasnimi and Mohebkhah (2011) [46] | SW | - | - | - | 212.0 |
| 57 | Hashemi et al. (2018) [47] | IFS | 20.10 | - | - | 315.0 |
| 58 | IFM | 28.40 | - | - | 394.0 | |
| 59 | IFL | 31.90 | - | - | 391.0 |
| FEMA 306 [35] | Sliding-shear capacity of the infill | |
| Compression resistance of the diagonal | ||
| Resistance to diagonal tensile cracking | ||
| Sheer resistance of infill masonry | ||
| EN 1996, EN 1998 [33,36] | Sheer resistance of infill masonry | |
| Sheer force in the columns | ||
| CSA S304-14 [34] | Compression resistance of the diagonal | |
| Resistance to diagonal tensile cracking | ||
| Sheer resistance of infill masonry | ||
| Paulay and Priestley [37] | Sheer resistance of infill masonry | |
| Compression resistance of the diagonal | ||
| Liauw and Kwan [38] | Corner crushing with failure in columns and infill/beam connections | |
| Corner crushing with failure in beams and infill/column connections. | ||
| Diagonal crushing with failure in infill/beam connection | ||
| Diagonal crushing with failure in infill/column connections |
| # | Label | Infill Type | VFR (kN) | Ph (kN) | Vm (kN) | Vrs (kN) | Vuk (kN) | Vuk/Vexp (%) |
|---|---|---|---|---|---|---|---|---|
| 1 | C-1 | HC | 99.68 | 29.97 | 13.10 | 27.63 | 127.31 | 0.92 |
| 2 | C-2 | HC | 99.68 | 31.55 | 13.44 | 28.35 | 128.03 | 0.92 |
| 3 | C-3 | HC | 99.68 | 29.97 | 13.10 | 27.63 | 127.31 | 0.99 |
| 4 | AAC-1 | AAC | 99.68 | 16.72 | 9.78 | 20.64 | 116.40 | 0.77 |
| 5 | AAC-2 | AAC | 99.68 | 15.30 | 9.36 | 19.74 | 114.98 | 0.83 |
| 6 | AAC-3 | AAC | 99.68 | 16.56 | 9.74 | 20.54 | 116.24 | 0.80 |
| 7 | CA-1 | HC+AAC | 99.68 | 24.45 | 10.68 | 26.68 | 124.13 | 1.17 |
| 8 | CA-2 | HC+AAC | 99.68 | 25.73 | 10.96 | 27.38 | 125.42 | 1.35 |
| 9 | CA-3 | HC+AAC | 99.68 | 24.45 | 10.68 | 26.68 | 124.13 | 1.31 |
| 10 | PF-M-1 | RBA-EP | 745.30 | 49.37 | 12.61 | 35.34 | 780.64 | 13.01 |
| 11 | PF-M-2 | RBA-EP | 745.30 | 49.37 | 12.61 | 35.34 | 780.64 | 15.61 |
| 12 | RF-M-1 | RBA-EP | 99.71 | 49.37 | 12.61 | 35.34 | 135.05 | 1.04 |
| 13 | RF-M-2 | RBA-EP | 99.71 | 49.37 | 12.61 | 35.34 | 135.05 | 1.03 |
| 14 | RF-MF-1 | RBA-EP | 99.71 | 49.37 | 12.61 | 35.34 | 135.05 | 1.00 |
| 15 | RF-MF-1 | RBA-EP | 99.71 | 49.37 | 12.61 | 35.34 | 135.05 | 0.99 |
| # | Label | Infill Type | VFR (kN) | Ph (kN) | Vm (kN) | Vrs (kN) | Vuk (kN) | Vuk/Vexp (%) |
|---|---|---|---|---|---|---|---|---|
| 16 | N-0 | CMB | 114.72 | 57.88 | 15.47 | 45.55 | 160.27 | 2.08 |
| 17 | F-0 | CMB | 114.72 | 50.16 | 14.71 | 43.51 | 158.23 | 1.20 |
| 18 | CF-1 | CMB | 114.72 | 50.16 | 15.02 | 44.61 | 159.33 | 0.80 |
| 19 | CF-2 | CMB | 114.72 | 50.16 | 15.34 | 45.71 | 160.43 | 0.95 |
| 20 | CF-3 | CMB | 114.72 | 50.16 | 15.65 | 46.81 | 161.53 | 1.06 |
| 21 | P-0 | CMB | 114.72 | 51.81 | 16.22 | 48.70 | 163.42 | 1.74 |
| 22 | CP-1 | CMB | 114.72 | 51.81 | 16.54 | 49.82 | 164.54 | 1.31 |
| 23 | CP-2 | CMB | 114.72 | 51.81 | 16.86 | 50.94 | 165.66 | 1.52 |
| 24 | CP-3 | CMB | 114.72 | 51.81 | 17.18 | 52.06 | 166.54 | 1.87 |
| 28 | P1NA | CMB | 114.72 | 42.74 | 14.98 | 56.72 | 157.46 | 1.42 |
| 29 | F1NA | CMB | 114.72 | 42.74 | 15.24 | 57.84 | 157.46 | 1.00 |
| 30 | N3NA | CMB | 114.72 | 53.47 | 19.39 | 59.70 | 168.19 | 2.18 |
| 31 | P3NA | CMB | 114.72 | 53.47 | 19.71 | 60.84 | 168.19 | 1.79 |
| 32 | F3NA | CMB | 114.72 | 53.47 | 20.04 | 61.98 | 168.19 | 2.13 |
| 33 | P3NI | CMB | 114.72 | 53.47 | 20.36 | 63.12 | 168.19 | 1.27 |
| 34 | F3NI | CMB | 114.72 | 53.47 | 20.68 | 64.25 | 168.19 | 1.38 |
| 35 | P6NA | CMB | 114.72 | 69.57 | 27.33 | 72.36 | 184.30 | 1.77 |
| # | Label | Infill Type | VFR (kN) | Ph (kN) | Vm (kN) | Vrs (kN) | Vuk (kN) | Vuk/Vexp (%) |
|---|---|---|---|---|---|---|---|---|
| 25 | S0 | HC | 42.06 | 25.75 | 14.37 | 33.76 | 67.80 | 0.63 |
| 26 | S2 | HC | 42.06 | 25.75 | 14.63 | 34.47 | 67.80 | 0.77 |
| 27 | S4 | HC | 42.06 | 25.75 | 14.89 | 35.18 | 67.80 | 0.69 |
| # | Label | Infill Type | VFR (kN) | Ph (kN) | Vm (kN) | Vrs (kN) | Vuk (kN) | Vuk/Vexp (%) |
|---|---|---|---|---|---|---|---|---|
| 36 | S1 | SB | 65.54 | 19.71 | 13.09 | 45.06 | 85.24 | 1.04 |
| 37 | S2 | HC | 65.54 | 28.55 | 12.20 | 42.08 | 94.09 | 0.81 |
| 38 | S3 | HC | 65.54 | 22.06 | 10.88 | 37.62 | 87.60 | 0.63 |
| 54 | MS | SB | 55.98 | 28.51 | 23.42 | 62.58 | 84.49 | 3.87 |
| 55 | MM | SB | 54.63 | 28.51 | 23.69 | 63.39 | 83.14 | 0.56 |
| # | Label | Infill Type | VFR (kN) | Ph (kN) | Vm (kN) | Vrs (kN) | Vuk (kN) | Vuk/Vexp (%) |
|---|---|---|---|---|---|---|---|---|
| 41 | M-RC-1B | SB | 254.78 | 60.50 | 32.66 | 91.28 | 315.29 | 0.97 |
| 42 | M-PC-1B | SB | 254.78 | 60.50 | 33.12 | 92.72 | 315.29 | 1.09 |
| 43 | M-RC-2B | SB | 254.78 | 60.50 | 33.58 | 94.16 | 315.29 | 0.51 |
| 44 | M-PC-2B | SB | 254.78 | 60.50 | 34.04 | 95.59 | 315.29 | 1.09 |
| 46 | SP1 | SB | 47.80 | 134.01 | 36.95 | 107.03 | 154.82 | - |
| 47 | CL-SP1 | SB | 47.80 | 134.01 | 37.44 | 108.59 | 156.39 | - |
| 48 | SP-2 | SB | 47.80 | 245.68 | 37.92 | 110.15 | 157.95 | 0.38 |
| 49 | CF-SP2 | SB | 47.80 | 245.68 | 38.41 | 111.71 | 159.51 | - |
| 50 | CP3 | SB | 47.80 | 223.35 | 38.90 | 113.28 | 161.07 | 0.44 |
| 51 | SF-SP3 | SB | 47.80 | 223.35 | 39.38 | 114.84 | 162.64 | - |
| 52 | DL | SB | 186.82 | 69.25 | 40.60 | 115.34 | 256.07 | 0.79 |
| 53 | CL | SB | 186.82 | 69.25 | 41.09 | 116.88 | 256.07 | 0.94 |
| # | Label | Infill Type | VFR (kN) | Ph (kN) | Vm (kN) | Vrs (kN) | Vuk (kN) | Vuk/Vexp (%) |
|---|---|---|---|---|---|---|---|---|
| 45 | RF-AAC | AAC | 61.05 | 298.72 | 66.25 | 169.10 | 230.15 | 0.53 |
| # | Label | Infill Type | VFR (kN) | Ph (kN) | Vm (kN) | Vrs (kN) | Vuk (kN) | Vuk/Vexp (%) |
|---|---|---|---|---|---|---|---|---|
| 56 | SW | SB | 59,52 | 117.28 | 42.26 | 135.87 | 363.52 | 0.83 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bratu, C.; Šokić, D.; Ademović, N.; Isik, E.; Bulajić, B.; Radu, D.; Hadzima-Nyarko, M. Assessment of Masonry-Infilled Steel Frames Using Existing Experimental Tests Database in Comparison to Standards. Buildings 2025, 15, 190. https://doi.org/10.3390/buildings15020190
Bratu C, Šokić D, Ademović N, Isik E, Bulajić B, Radu D, Hadzima-Nyarko M. Assessment of Masonry-Infilled Steel Frames Using Existing Experimental Tests Database in Comparison to Standards. Buildings. 2025; 15(2):190. https://doi.org/10.3390/buildings15020190
Chicago/Turabian StyleBratu, Ciprian, Dario Šokić, Naida Ademović, Ercan Isik, Borko Bulajić, Dorin Radu, and Marijana Hadzima-Nyarko. 2025. "Assessment of Masonry-Infilled Steel Frames Using Existing Experimental Tests Database in Comparison to Standards" Buildings 15, no. 2: 190. https://doi.org/10.3390/buildings15020190
APA StyleBratu, C., Šokić, D., Ademović, N., Isik, E., Bulajić, B., Radu, D., & Hadzima-Nyarko, M. (2025). Assessment of Masonry-Infilled Steel Frames Using Existing Experimental Tests Database in Comparison to Standards. Buildings, 15(2), 190. https://doi.org/10.3390/buildings15020190











