Integrated Scheduling Optimization for Multi-Line Production and Transportation of Prefabricated Components Considering Shared Resources

Abstract

With the increasing popularity of prefabricated buildings, more and more precast plants have been equipped with multiple production lines to increase productivity and meet the growing market demand. Sharing equipment, human, and transportation resources is a typical feature of integrated scheduling management for precast production and transportation on multiple production lines. In response to these characteristics, this article studies the integrated scheduling optimization of multi-line production and transportation for prefabricated components. With on-time delivery and lower costs as the goals, a scheduling optimization mathematical model is established for this scenario. This article adopts the genetic algorithm to design the solution algorithm for this model, and the effectiveness of the model and algorithm is verified through an example. The results show that compared with the traditional scheduling scheme, this method can prominently reduce costs while promoting on-time delivery. The model and method can help the precast plant with multiple production lines improve efficiency and reduce costs, as well as enhancing the practicability of the precast production and transportation scheduling scheme.

1. Introduction

In the fiercely competitive construction industry, prefabrication is used as an innovative technology to enhance the competitiveness of enterprises and projects [1,2,3,4]. In some mature economies, such as America, Germany, Australia, and Canada, prefabricated buildings have been widely promoted due to their reliable quality, rapid construction, environmental friendliness, and intelligent technology [5,6,7,8]. In some emerging economies, such as China, Turkey, Pakistan, and Albania, with the implementation of urbanization strategies, prefabricated buildings are increasingly valued for their excellence [9,10,11,12]. The building sector dominates energy consumption and carbon emissions in cities [13], and in China, prefabricated buildings are considered an effective way to improve the transformation and upgrading of the construction industry, achieve green progression in urban and rural construction, and realize intelligent operation throughout the entire life cycle of buildings. China’s Ministry of Housing and Urban-Rural Development in the 14th Five-Year Construction Industry Development Plan set the goal of domestic prefabricated buildings to account for more than 30% of new construction by 2035 [14].

Prefabricated component production encompasses two typical methods: job shop and flow shop. Different methods are adopted to solve the optimization problems of these two typical production methods. The job shop production method is suitable for beams, columns, and stairs. Many advanced technologies are developed around this production model. Huang et al. [15] and Huang et al. [16] study the seismic behavior of a replaceable artificial controllable plastic hinge and a friction-type artificial plastic hinge for prefabricated concrete beam–column, while Shu et al. [17] use advanced methods, such as point cloud and machine learning, to identify the position of steel reinforcement and fittings in prefabricated beam components. The flow shop production method is suitable for plate and wall components, which is also the subject of this study. The flow production line is an efficient piece of equipment for precast production. The long period of a construction project usually causes it to face the risk of a large amount of capital occupation and project delay. In order to support the rapid construction of prefabricated buildings, many precast plants have installed multiple production lines, such as Jiangsu Longxin Construction Group (Nantong City, Jiangsu Province, China), Changsha Broad Homes Industrial Group Co. Ltd. (Changsha City, Hunan Province, China), and Shanghai Construction Engineering Group (Shanghai City, China) in China. Scientific scheduling management is an important means to ensure timely project progress and reduce risks. Therefore, the production scheduling problem of prefabricated components around the flow production line has been widely explored by scholars [18,19,20,21,22,23,24,25,26]. The research on production scheduling optimization of prefabricated components on the flow line is essential work in the development of prefabricated buildings, and it is also an important branch of workshop scheduling academic research in the field of construction engineering. The flow precast production line needs to continuously produce many prefabricated components of diverse shapes, sizes, and specifications, and the characteristics of each production process are inconsistent, which makes prefabricated component production scheduling optimization on the flow line both challenging and unique.

With the gradual popularity of prefabricated buildings, the prefabricated component orders rise, and precast plants become increasingly busy. Many precast plants have installed multiple production lines to meet the escalating market demand. How can we fully and realistically depict the multi-line integrated production scenario of prefabricated components? How can we fully utilize resources to maximize production efficiency in multi-line scenarios? These questions pose newer and higher requirements for scheduling levels on precast plants. In reality, for the full utilization of space, equipment resources, and energy, the configuration of multiple production lines is complex and not simply the accumulation of single production lines. The curing chamber is a device with numerous stations, occupying a large space. In addition, the curing chamber requires a daily supply of high-temperature steam to maintain the normal operation of the curing process, resulting in high operating costs [9]. To fully utilize this valuable equipment and achieve more reasonable space planning, it is common for multiple production lines to share the curing chamber. In terms of space, this is reflected in the parallel arrangement of multiple U-shaped production lines, with a long and through-type curing chamber at their U-shaped ends. In addition to sharing space and equipment resources, integrated management of multiple production lines will also share human resources. After completing the demolding process, the prefabricated components start the quality inspection process, which shares human resources. The workers responsible for this process move back and forth between different production lines, and the inspection sequence of all prefabricated component groups is comprehensively arranged. This further enhances the difficulty of integrating multi-line production scheduling and managing prefabricated components.

The construction of prefabricated buildings begins with the production of components in precast plants, and then, the components are transported to the construction site for assembly. For precast plant customers, the complete service ranges from the production of prefabricated components to transportation to the construction site. The on-time delivery of prefabricated components is crucial. If delivered too early, prefabricated components would occupy large space resources on the small construction site, generating additional management risks and secondary transfer costs. If delivered too late, this would delay the overall construction progress of prefabricated buildings. Customers usually agree with precast plants on certain early and late penalty costs for not-on-time delivery of prefabricated components. Whether the prefabricated component can be delivered on time depends on the production time and transportation time. The production and transportation processes also have a certain degree of correlation. A scientific, rational, and integrated scheduling scheme for prefabricated component production and transportation on multiple production lines is the key to ensuring the timely progress and effective cost control of prefabricated construction projects. Obtaining such a scheduling scheme is a complex problem.

Therefore, to decrease the cost, enhance capacity utilization, and reach on-time delivery of prefabricated components from a global perspective, this article studies the integrated scheduling optimization problem of multi-line production and transportation of prefabricated components. The characteristics of integrated scheduling of multi-line production and transportation for prefabricated components are analyzed, and an integrated scheduling optimization model of multi-line production and transportation for prefabricated components with shared resources is established. Based on realistic constraints, this model depicts the situation of shared equipment, human, and transportation resources among multiple lines. It considers blocking caused by the lack of buffer on the flow line, the different number of stations for diverse processes, and the limitation of working time every day. It also calculates the natural curing process time more closely than the actual situation. It also aims to promote the on-time delivery of prefabricated components. Then, a solution scheme based on a genetic algorithm is designed for the model, so that the optimal solution can be obtained in a short time. The effectiveness of the model and the algorithm is proved by an example.

At present, scholars have investigated the single-line precast production scheduling issue [9,27,28,29,30] and the integrated scheduling issue of single-line precast production and transportation [25,26,31,32]. These studies have not addressed the cooperative scheduling issue of multiple production lines, whereas multiple lines exist in the real-world production environment [24]. Although some scholars have explored multi-line scenarios, the production and transportation stages managed by precast plants both affect the delivery and cost of prefabricated components [26,32]. Only Wang and Hu [33] and Wang et al. [24] have studied the integrated scheduling problem of multi-line production and transportation. These two papers, similar to previous research on multi-line scheduling, decompose multiple production lines into independent single lines for scheduling and do not consider the cooperative scheduling of multiple lines. Consequently, contrary to the multiple independent production lines in past multi-line scheduling studies, the distinctiveness of this article lies in the interrelation and mutual influence among multiple production lines during the production stage, with the shared utilization of curing chamber equipment and quality inspection process personnel. In addition to being produced successively on their respective production lines, all components converge at the curing process and the quality inspection process, and the operation sequence is comprehensively arranged. After completing the curing process, the components return to their respective production lines. In addition, distinct from the majority of past multi-line scheduling studies that merely concentrated on the production stage, the characteristic of this article lies in integrating both the production and transportation stages for investigation. The difficulty of this article lies in the fact that, during the modeling process, the abovementioned characteristics and constraints need to be depicted in the model, and a suitable solution algorithm needs to be sought to solve the model within a reasonable time.

The rest of this article is organized as follows. The second chapter is the literature review, exploring research gaps. The third chapter depicts the characteristics of integrated scheduling optimization of multi-line production and transportation for prefabricated components and provides relevant explanations for the research problem. The fourth chapter establishes an integrated scheduling optimization model for multi-line production and transportation of prefabricated components with shared resources. The fifth chapter develops a set of solving algorithms based on a genetic algorithm. The sixth chapter proves the effectiveness of the model by an example. The seventh chapter provides some conclusive conclusions.

2. Literature Review

Effective and optimized scheduling management is crucial for successfully constructing prefabricated buildings. It not only guarantees the construction progress but also promotes the full utilization of construction resources to cut costs [34,35,36]. Different from the traditional buildings built on the construction site entirely, for prefabricated buildings, prefabricated components are manufactured and produced in precast plants, firstly located far away from the construction site and then transported to the construction site and finally assembled there. Therefore, the scheduling of prefabricated buildings has a phased characteristic. Since the beginning of this century, most scholars have focused their interest on the precast production stage of prefabricated buildings [20,29,30,36,37,38,39,40,41,42,43,44]. They apply mathematical models and computer-aided technology to meet optimization goals, such as on-time delivery and minimizing costs.

Normally, a precast plant is equipped with a flow production line. Many scholars have studied the scheduling optimization of prefabricated components produced on a single production line in the most common scenarios. Chan and Hu [19,45] studied classic optimization that distinguished sequential and parallel processes, as well as interruptible and non-interruptible processes. Leu and Hwang [37] studied precast production scheduling under constrained resources and mixed production. Benjaoran and Dawood [20] explored the optimization of enhancing the utilization rate of specialized precast molds for bespoke prefabricated components. Ko and Wang [46] researched optimization that considered limited buffer zones between processes. Arashpour et al. [22] studied the comprehensive production scheduling of different types of prefabricated components under shared concrete mixers and concrete vibration tables. Nasirian et al. [34] evaluated and optimized the operational performance of various management strategies for multi-skilled workers related to bottleneck configuration. Wang et al. [47] researched rescheduling under the interference of new order insertion. Jiang and Wu [27] explored the comprehensive production scheduling optimization for non-standard components produced for order and standard components produced for inventory. Yazdani et al. [28] proposed a new insight into the theory of scheduling dealing with sequence-dependent due dates. Kim et al. [48] used reinforcement learning methods to study the intelligent scheduling optimization. Liu et al. [30] researched production scheduling optimization with multiple stations in each process. Podolski [29] presented a new model for precast production scheduling with the possibility of parallel performance of some tasks. Dan et al. [9] explored multi-shift production scheduling optimization with urgent delivery due dates. Kosse et al. [49] utilized digital twin technology to study the dynamic scheduling of prefabricated components.

Considering that the production and transportation of prefabricated components are two correlated phases that precast plants need to complete, some scholars have attempted to research the scheduling optimization of single-line production and transportation of prefabricated components by linking these two stages. Wang and Hu [50] enriched the classical production scheduling model and built a comprehensive scheduling model that considers the entire process from mold manufacturing, precast production to transportation. Kim et al. [31] established a production and transportation dynamic scheduling model based on discrete event simulation considering full-load transportation of curtain walls. Xiong et al. [26] considered the congestion situation of roads at different time periods and solved a comprehensive scheduling problem for the production and transportation of prefabricated components with time-dependent transportation times. Du et al. [32] incorporated value management and just-in-time principles in lean construction into the precast production process and conducted real-time scheduling of prefabricated component production and transportation according to resource occupation and sudden events. Dan and Liu [25] sought a method for integrated scheduling of prefabricated component production and transportation that balances on-time delivery and transportation economy while considering multiple transportation constraints. However, the above papers do not address the cooperative scheduling problem of multiple production lines.

In order to increase the production capacity of precast plants and meet the growing market demand, some precast plants have installed multiple production lines. Accordingly, precast production scheduling optimization research is extended from a single production line to multiple production lines. Yang et al. [51] studied multi-objective cooperative scheduling optimization of multiple production lines under the constraints of limited resources, such as productivity, the number of stations, buffer size, the number of molds, and the number of bench formworks. Altaf et al. [52] utilized radio frequency identification technology and simulation technology to automate the scheduling of multiple production lines. Ma et al. [23] utilized the difference between the excessive production time allocated in each process and the estimated production time to cope with emergencies under multi-line production. Zhang et al. [53] took carbon emission as one of the optimization objectives and studied the rescheduling optimization of two production lines under disturbance events. Gartner et al. [54] enhanced the productivity of a precast plant with three different wall production lines by improving worker resource allocation and utilizing product rotation to avoid production bottlenecks. However, the above research only focuses on the internal production phase of the precast plant and does not integrate in-plant production and off-plant transportation, which have a close relationship with time and space.

Considering that transportation is necessary for precast plants to serve customers, optimizing the entire service process of order manufacturing and delivery has become one of the ways for precast plants to perfect service quality. A few scholars have studied the multi-line production and transportation of prefabricated components, which is also most relevant to the research in this article. Wang and Hu [33] explored the rescheduling of multiple production lines under demand changes from two levels of line selection and prefabricated component priority, and they studied two production scheduling scenarios where certain molds are shared or not shared. On this basis, Wang et al. [24] researched precast multi-line rescheduling influenced by product interruption and sought a balance between high service level and profit maximization. The above research decomposed multiple lines into an independent single line for scheduling and did not consider the comprehensive scheduling of multiple lines.

Table 1. Recent research comparison on prefabricated component production and transportation scheduling optimization.

Literature	Year	Schedule Subject		Stage		Features
		Single Production Line	Multiple Production Line	Production	Production and Transportation
Arashpour et al. [22]	2016	√		√		shared concrete mixers and concrete vibration tables
Nasirian et al. [34]	2019	√		√		multi-skilled workers
Wang et al. [47]	2020	√		√		new order insertion
Jiang and Wu [27]	2021	√		√		non-standard components for order and standard components for inventory
Yazdani et al. [28]	2021	√		√		sequence-dependent due dates
Kim et al. [48]	2022	√		√		reinforcement learning methods
Liu et al. [30]	2023	√		√		multiple workstations in each process
Podolski [29]	2022	√		√		parallel performance of some tasks
Dan et al. [9]	2024	√		√		multi-shift production scheduling optimization
Kosse et al. [49]	2024	√		√		digital twin technology
Kim et al. [31]	2021	√			√	full-load transportation, curtain walls
Xiong et al. [26]	2023	√			√	time-dependent transportation times
Du et al. [32]	2023	√			√	just-in-time principles, resource occupation and sudden events
Dan and Liu [25]	2024	√			√	balancing on-time delivery and transportation economy
Altaf et al. [52]	2018		√	√		radio frequency identification technology and simulation technology
Ma et al. [23]	2018		√	√		utilizing the time difference to cope with emergencies
Zhang et al. [53]	2023		√	√		taking carbon emission as one of the optimization objectives, disturbance events
Gartner et al. [54]	2024		√	√		three different wall production lines
Wang and Hu [33]	2018		√		√	demand changes, certain molds are not shared or shared
Wang et al. [24]	2021		√		√	influenced by product interruption
This article			√		√	shared curing chamber equipment, quality inspection personnel, and transportation resources among multiple production lines

summarizes the research focus and features of some important literature works in the above four fields in recent years and, at the same time, explains the uniqueness and contribution of this study in the last row of the table.

In reality, the configuration of multiple production lines is more complex due to the full utilization of space, equipment, and energy resources. For example, in precast production equipment, the curing chamber is a key resource to ensure the quality of prefabricated components and a valuable resource with high configuration and usage costs. In many precast plants, multiple production lines share the curing chamber to fully utilize the curing chamber and make space planning more reasonable. In this way, all stations of the curing chamber can be fully utilized. As only one through-type curing chamber needs to be supplied with high-temperature steam, the energy consumption for curing is also reduced. Therefore, prefabricated components from different lines are gathered for the first time after concrete casting, and their curing sequence is comprehensively arranged. Their specific time to enter the curing chamber is determined based on the vacancy situation at that time. After curing, each prefabricated component group returns to the previous production line for the following process: demolding. After demolding, prefabricated components leave their production line for the second time, and their sequence of quality inspection is also arranged comprehensively due to shared personnel.

In addition, previous studies handle the natural curing process simply, i.e., after quality inspection, prefabricated components are placed at the yard for 48 h to achieve assembly strength. Such simple handling process wastes time to some extent. In fact, the start time of natural curing is when the prefabricated component reaches the demolding strength, i.e., when the high-temperature curing process ends, even though the component has not left the curing chamber at that time [25]. Scheduling closer to real-world settings can cut total production and transportation time and make scheduling management more flexible.

Given this fact, this study intends to establish an improved production and transportation scheduling model for prefabricated components—considering that multiple production lines share the curing chamber, quality inspection personnel, and transportation resources and handle the natural curing process time more accurately—to facilitate on-time delivery of prefabricated components and cut costs. The main feature of this study lies in the following. Firstly, all previous multi-line scheduling studies featured multiple production lines that were decomposed into independent single ones for scheduling, neglecting the correlation among multiple lines resulting from the equipment and personnel configuration in some plants. The multiple production lines in this study are not independent during production but are correlated. This is mainly manifested in the fact that the prefabricated components on different production lines, in the curing process and the quality inspection process, require a comprehensive and reasonable arrangement of the operation sequence due to the shared curing chamber equipment and the quality inspection team personnel. Secondly, distinct from the majority of past multi-line scheduling studies that merely focused on the production stage, this article integrates the production and transportation stages for scheduling from a comprehensive perspective to reduce costs.

3. Model Establishment

3.1. Problem Description

Some precast plants have installed multiple flow production lines to increase production efficiency; therefore, they must consider the integrated scheduling of multi-line production and transportation of prefabricated components. In this case, when developing a production schedule plan, it is necessary to allocate production lines for each prefabricated component and determine the production sequence of prefabricated components on each line. This problem is much more complex than the integrated scheduling problem of single-line production and transportation.

Before being delivered to the construction site, prefabricated components go through two phases: production and transportation. As shown in Figure 1, they can be regarded as going through eight processes: Mold assembling (M1), Reinforcement setting (M2), Concrete casting (M3), High-temperature curing (M4), Demolding (M5), Quality inspection (M6), Natural curing (M7), and Transportation (M8). In order to rationalize the space layout of the plant and maximize resource utilization, multiple production lines often share the curing chamber. The prefabricated components on multiple production lines go through the M1–M3 processes on their respective production lines and then gather in the High-temperature curing (M4) process. They then return to their previous production lines in M5. After M5, they leave the production line again and proceed to the M6 and M8 processes. M7 starts when M4 ends and is a parallel process with M5 and M6. Whether the components are on the production line does not affect the progress of M7.

The basic assumptions of this study are as follows:

(1)

Once each process starts, it cannot be interrupted to avoid wasting time and cost due to work handover;

(2)

The quality inspection area of the plant is sufficient; therefore, the quality inspection stations are regarded as unlimited, but only one group of staff is set up for the Quality inspection (M6) process;

(3)

After the prefabricated components reach assembly strength through natural curing, they would be immediately arranged to be sent to the construction site.

3.2. Parameter Settings

The parameters are set as follows:

$N$ is the set of prefabricated component group numbers, $N=\left\{1,2,\dots ,j,\dots ,n\right\}$, where $n$ indicates the total number of prefabricated component groups. $j$ is the number of one prefabricated component group, and one to three prefabricated components are placed on one bench formwork to a group.

$L$ is the set of flow production lines, $L=\left\{1,2,\dots ,k,\dots ,n_L\right\}$. $k$ is the number of production lines, assuming that there are $n_L$ production lines.

${\pi }_k$ is the set of production sequence numbers of the prefabricated component groups from M1 to M3 and M5 on the line $k$, ${\pi }_k=\left\{\left[1\right],\left[2\right],\dots ,\left[p\right],\dots \right\}$, where $\left[p\right]$ represents the prefabricated component group occupying position $p$ in the sequence.

${\pi }_r$ is the set of the sequence numbers in which the prefabricated component groups enter the curing chamber of M4 successively, $\pi =\left\{\left[1\right],\left[2\right],\dots ,\left[r\right],\dots ,\left[n\right]\right\}$, where $\left[r\right]$ represents the prefabricated component group occupying position $r$ in the sequence.

${\pi }_s$ is the set of the sequence numbers in which the prefabricated component groups start M6 successively, $\pi =\left\{\left[1\right],\left[2\right],\dots ,\left[s\right],\dots ,\left[n\right]\right\}$, where $\left[s\right]$ represents the prefabricated component group occupying position $s$ in the sequence.

$H$ is the working hours of each day (unit: hour).

$h$ is the number of curing chamber stations.

$x_{j,k}=\left\{\begin{array}{l}1\\ 0\end{array}\right. j\in N,k\in L$, $x_{j,k}=1$ indicates that the prefabricated component group $j$ selects the line $k$, and $x_{j,k}=0$ indicates that the prefabricated component group $j$ does not select the line $k$.

$d_j$ represents the delivery due date of the prefabricated component group $j$.

$P_{i,k,\left[p\right]}, i=1,2,3,5$ is the operation time of the process $i$ of the prefabricated component group $\left[p\right]$ on the line $k$.

$S_{i,k,\left[p\right]}, i=1,2,3,5$ is the start time of the process $i$ of the prefabricated component group $\left[p\right]$ on the line $k$.

$C_{i,k,\left[p\right]}, i=1,2,3,5$ is the completion time of the process $i$ of the prefabricated component group $\left[p\right]$ on the line $k$.

$D_{i,k,\left[p\right]}, i=1,2,3,5$ is the time when the prefabricated component group $\left[p\right]$ on the line $k$ leaves the process $i$ station and also the time when it enters the process $i+1$ station.

$P_{i,\left[r\right]} i=4,7$ is the operation time of M4 or M7 of the prefabricated component group $\left[r\right]$.

$S_{i,\left[r\right]} i=4,7$ is the start time of M4 or M7 of the prefabricated component group $\left[r\right]$.

$C_{i,\left[r\right]} i=4,7$ is the completion time of M4 or M7 of the prefabricated component group $\left[r\right]$.

$D_{4,\left[r\right]}$ is the time when the prefabricated component group $\left[r\right]$ leaves the curing chamber (M4) station.

$P_{i,\left[s\right]} i=6,8$ is the operation time of M6 or M8 of the prefabricated component group $\left[s\right]$.

$S_{i,\left[s\right]} i=6,8$ is the start time of M6 or M8 of the prefabricated component group $\left[s\right]$.

$C_{i,\left[s\right]} i=6,8$ is the completion time of M6 or M8 of the prefabricated component group $\left[s\right]$.

$D_{6,\left[s\right]}$ is the time when the prefabricated component group $\left[s\right]$ leaves the M6 station.

$C{\prime }_{3,k,\left[p\right]}$ is the end time of process M3 without considering the constraints of working time $H$ and the number of M4 stations.

$\phi$ is the set of all $C{\prime }_{k,3,[p]}$, $\phi =\left\{C{\prime }_{3,1,[1]},\dots ,C{\prime }_{3,k,[p]},\dots \right\}$.

$\gamma$ is the permutation of elements in $\phi$ from small to large, which also corresponds to the sequence of prefabricated component groups starting M4, $\gamma =\left\{S{\prime }_{4,\left[1\right]},\dots S{\prime }_{4,\left[j\right]},\dots S{\prime }_{4,\left[n\right]}\right\}$.

$\eta$ is the set of all $D_{5,k,\left[p\right]}$, $\eta =\left\{D_{5,1,\left[1\right]},\dots ,D_{5,k,\left[p\right]},\dots \right\}$.

$\lambda$ is the permutation of elements in $\eta$ from small to large, which also corresponds to the sequence of prefabricated component groups starting M6, $\lambda =\left\{D_{5,\left[1\right]},\dots ,D_{5,\left[h\right]},\dots ,D_{5,\left[n\right]}\right\}$.

$W_j$ is the completion time of the prefabricated component group $j$.

${\alpha }_j$ is the unit early cost of the prefabricated component group $j$.

${\beta }_j$ is the unit late cost of the prefabricated component group $j$.

${\Phi }_j$ is the early delivery time of the prefabricated component group $j$.

${\Gamma }_j$ is the late delivery time of the prefabricated component group $j$.

$Z$ is the total delivery penalty cost.

$T{L}_k$ is the time during which the production line $k$ is occupied.

$TLS$ is the total time during which all the production lines are occupied, $TLS={\displaystyle \sum _{L}T{L}_k}$

3.3. Objective Function

On-time delivery of prefabricated components is significant to the entire project’s success. If the delivery of prefabricated components is late, it would affect the construction progress on site, causing additional losses to the customer, and the precast plant would also be punished for default (late cost). If the delivery of prefabricated components is early, the small construction site needs to free up space to store the prefabricated components, increasing additional storage and management costs for customers, and the precast plant would also be punished for default (early cost). Therefore, this study builds a scheduling optimization model aiming at on-time delivery, which minimizes the sum of early and late costs (referred to as total penalty costs), as shown below.

$$\min Z={\displaystyle \sum _{j\in N}\left({\alpha }_j{\Phi }_j+{\beta }_j{\Gamma }_j\right)}$$

(1)

The first and second terms in Equation (1) represent the early cost and late cost of the prefabricated component group $j$, respectively. ${\Phi }_j$ is the early time of the prefabricated component group $j$, calculated according to the following equation.

$${\Phi }_j=\max \left\{0,d_j-W_j\right\}$$

(2)

${\Gamma }_j$ is the late time of the prefabricated component group $j$, calculated according to the following equation.

$${\Gamma }_j=\max \left\{0,W_j-d_j\right\}$$

(3)

3.4. Time and Space Constraints

(1)

Selection of the production line for prefabricated component groups

The precast plant is configured with multiple production lines. Each prefabricated component group must choose a certain production line, and only one production line can be selected, as shown below.

$${\displaystyle \sum _{k=1}^{n_L}{x}_{j,k}=1}, j=1,2,\dots ,n$$

(4)

(2)

Start time of the process

For the convenience of modeling, a Virtual process (M0) is set before the Mold assembling (M1), and its operation time $P_{0,k,\left[p\right]}=0$.

For the start time of the process, different processes are calculated in different ways, and the start time of the Virtual process (M0) is 0.

$$S_{0,k,\left[p\right]}=0$$

(5)

The four processes—Mold assembling (M1), Reinforcement setting (M2), Concrete casting (M3), and Demolding (M5)—are completed on different production lines, and the calculation of their start time is related to the parameter $k$. The other processes—High-temperature curing (M4), Quality inspection (M6), Natural curing (M7), and Transportation (M8)—are not affected by the production line they are on; therefore, the calculation of their start time is independent of the parameter $k$.

The start time of Mold assembling (M1), Reinforcement setting (M2), and Concrete casting (M3) is related to the parameter, production line number, $k$, and it is calculated as follows.

$$S_{i,k,\left[p\right]}=\left\{\begin{array}{l}{D}_{i-1,k,\left[p\right]} \mathrm{if} D_{i-1,k,\left[p\right]}+P_{i,k,\left[p\right]}\le 24⌊D_{i-1,k,\left[p\right]}/24⌋+H\\ 24*⌈D_{i,k,\left[p\right]}/24⌉ \mathrm{otherwise}\end{array}\right.i=1,2,3,5$$

(6)

The sequence of prefabricated component groups entering the curing chamber (M4) is in accordance with the sequence of elements in $\gamma$. To determine this sequence, $C{\prime }_{3,k,\left[p\right]}$ needs to be calculated first. $C{\prime }_{3,k,\left[p\right]}$ is the end time of process M3 without considering the constraints of working time $H$ and the number of M4 stations. $C{\prime }_{3,k,\left[p\right]}=\left\{\begin{array}{l}{C}_{2,k,\left[p\right]}+P_{3,k,\left[p\right]}\\ \max \left\{C_{2,k,\left[p\right]},C{\prime }_{3,k,[p-1]}\right\}+P_{3,k,\left[p\right]}\end{array}\right.$. $\phi$ is the set of all $C{\prime }_{k,3,[p]}$. Simultaneously, $S{\prime }_{4,[r]}=S{\prime }_{4,k,\left[p\right]}=C{\prime }_{3,k,\left[p\right]}$, where the value of $r$ needs to be calculated. $\gamma$ is the permutation of elements in $\phi$ from small to large, which also corresponds to the sequence of prefabricated component groups starting M4. If there are two identical values, the one with the smaller $k$ value is entered first by default, that is, the element with the smaller $k$ value is placed closer to the front, $\gamma =\left\{S{\prime }_{4,\left[1\right]},\dots S{\prime }_{4,\left[j\right]},\dots S{\prime }_{4,\left[n\right]}\right\}$. The start time of High-temperature curing (M4) is independent of the parameter, production line number, $k$, and it is calculated as follows.

$$S_{4,\left[r\right]}=D_{3,\left[r\right]}$$

(7)

The sequence of prefabricated component groups starting Quality inspection (M6) is in accordance with the sequence of elements in $\lambda$. First, obtain the set, $\eta$. $\eta$ is the set of all $D_{5,k,\left[p\right]}$, $\eta =\left\{D_{5,1,\left[1\right]},\dots ,D_{5,k,\left[p\right]},\dots \right\}$. $\lambda$ is the permutation of elements in $\eta$ from small to large, which also corresponds to the sequence of prefabricated component groups starting M6. If there are two identical values, the one with the smaller $k$ value is entered first by default, that is, the element with the smaller $k$ value is placed closer to the front, $\lambda =\left\{D_{5,\left[1\right]},\dots ,D_{5,\left[h\right]},\dots ,D_{5,\left[n\right]}\right\}$. The start time of Quality inspection (M6), Natural curing (M7), and Transportation (M8) is independent of the parameter, production line number, $k$, and it is calculated as follows.

$$S_{6,[1]}=\left\{\begin{array}{l}{D}_{5,[1]} \mathrm{if} D_{5,[1]}+P_{6,[1]}\le 24⌊D_{5,[1]}/24⌋+H\\ 24*⌈D_{5,[1]}/24⌉ \mathrm{otherwise}\end{array}\right.$$

(8)

$$S_{6,\left[s\right]}=\left\{\begin{array}{l}\max \left\{D_{5,\left[s\right]},C_{6,\left[s\right]}\right\} \mathrm{if}\max \left\{D_{5,\left[s\right]},C_{6,\left[s-1\right]}\right\}+P_{6,\left[s\right]}\le 24⌊\max \left\{D_{5,\left[s\right]},C_{6,\left[s-1\right]}\right\}/24⌋+H\\ 24*⌈\max \left\{D_{5,\left[s\right]},C_{6,\left[s-1\right]}\right\}/24⌉ \mathrm{otherwise}\end{array}\right.s>1$$

(9)

$$S_{7,\left[r\right]}=C_{4,\left[r\right]}$$

(10)

$$S_{8,j}=\max \left\{D_{6,j},C_{7,j}\right\}$$

(11)

(3)

Completion time of the process

A process’s completion time equals its start time plus its operation time. The calculation principle of the completion time for different processes is the same, but their expression methods are different, as shown below.

$$C_{i,k,\left[p\right]}=S_{i,k,\left[p\right]}+P_{i,k,\left[p\right]}\hspace{1em}i=0,1,2,3,5$$

(12)

$$C_{4,\left[r\right]}=S_{4,\left[r\right]}+P_{4,\left[r\right]}$$

(13)

$$C_{6,\left[s\right]}=S_{6,\left[s\right]}+P_{6,\left[s\right]}$$

(14)

$$C_{7,\left[r\right]}=S_{7,\left[r\right]}+P_{7,\left[r\right]}$$

(15)

$$C_{8,\left[s\right]}=S_{8,\left[s\right]}+P_{8,\left[s\right]}$$

(16)

(4)

Departure time from different process stations

The precast production is operated on a large bench formwork. During the Virtual process (M0), Mold assembling (M1), Reinforcement setting (M2), and Concrete casting (M3), the bench formwork is on different production lines. Therefore, the departure time from these process stations is related to the parameter, production line number, $k$, as shown below. Among them, for the Virtual process (M0), Mold assembling (M1), and Reinforcement setting (M2), it not only needs to consider the completion time of the current prefabricated component group but also the departure time of the previous prefabricated component group from the next process station.

$$D_{i,k,\left[p\right]}=\left\{\begin{array}{l}{C}_{i,k,\left[p\right]} \mathrm{if} \left[p\right]=\left[1\right]\\ \max \left\{C_{i,k,\left[p\right]},D_{i+1,k,\left[p-1\right]}\right\} \mathrm{otherwise}\end{array}\right.i=0,1,2$$

(17)

$$D_{3,k,\left[p\right]}\ge C_{3,k,\left[p\right]}$$

(18)

After Concrete casting (M3), the prefabricated component group leaves its production line and enters the curing chamber shared by multiple lines for M4. The departure time from the M3 station is also the time to enter the curing chamber. The number of the curing chamber stations is $h$. For the first $h$ prefabricated component groups entering the curing chamber, there is sufficient space to place them. Therefore, their departure times from the M3 station are only subject to their M3 completion times. For the subsequent prefabricated component group $\left[r\right]$, it has to wait for a vacant station before entering the curing chamber, that is, it is necessary to consider the blocking caused by the limited M4 stations of the curing chamber. Therefore, its departure time from the M3 station is subject both to its M3 completion time and the departure time of the prefabricated component group $\left[r-h\right]$ from the curing chamber (M4). The calculation is as follows:

$$D_{3,\left[r\right]}=\left\{\begin{array}{l}{C}_{3,\left[r\right]} \mathrm{if} \left[r\right]\le h\\ \max \left\{C_{3,\left[r\right]},D_{4,\left[r-h\right]}\right\} \mathrm{otherwise}\end{array}\right.$$

(19)

After High-temperature curing (M4), the prefabricated component group leaves the curing chamber and returns to its previous line for Demolding (M5). This departure time is subject both to its M4 completion time and the departure time of the previous prefabricated component group from the M5 station. The calculation is as follows:

$$D_{4,k,\left[p\right]}=\left\{\begin{array}{l}\max \left\{C_{4,k,\left[p\right]},D_{5,k,\left[p-1\right]}\right\} \mathrm{if} C_{4,k,\left[p\right]}\le 24⌊C_{4,k,\left[p\right]}/24⌋+H \\ \max \left\{24*⌈C_{4,k,\left[p\right]}/24⌉,D_{5,k,\left[p-1\right]}\right\} \mathrm{otherwise}\end{array}\right.$$

(20)

After Demolding (M5), the prefabricated component group leaves the M5 station and enters the quality inspection area for M6. Quality inspection can be operated not only in the quality inspection area but also in the storage area. The quality inspection stations are sufficient; therefore, there is no need to consider the blocking caused by limited stations. Therefore, the departure time of the prefabricated component group from the M5 station is only subject to M5 completion time. After Quality inspection (M6), the prefabricated components are lifted off the bench formwork and stored in the storage area. Therefore, the departure time from the M6 station is calculated as follows.

$$D_{i,k,\left[p\right]}=C_{i,k,\left[p\right]}\hspace{1em}i=5,6$$

(21)

Natural curing (M7) is independent of its location. Transportation (M8) is the process of transporting prefabricated components from the precast plant to the construction site by truck. Therefore, there is no fixed station for M7 and M8, and these two processes only need to calculate the completion time without calculating the departure time from their stations.

(5)

Delivery time to the construction site

The delivery time of the prefabricated components to the construction site is the end time of transportation.

$$W_j=C_{8,j}$$

(22)

4. Algorithm Design

The genetic algorithm (GA) is a computational model that simulates the process of biological evolution. It gradually searches for the optimal solution to a problem by simulating the natural evolution process and performing operations such as competition, selection, crossover, and mutation among individuals in a population. The GA demonstrates distinct superiority in addressing prefabricated component production and transportation scheduling issues. For instance, through the GA, scholars have solved the production scheduling optimization problem for prefabricated components [19,20,21,30,37,44,51], addressed the transport scheduling optimization problem [55,56], or tackled the integrated scheduling problem of production and transportation [25,50,57]. Heuristic algorithms, including the GA, can improve problem-solving efficiency when the range of solutions is extensive [58]. Chan and Hu [19,45] and Ko and Wang [21] demonstrated the superiority of the GA over Palmer’s heuristic algorithm, Gupta’s heuristic algorithm, Campbell Dudek Smith heuristic algorithm, and rapid access heuristic algorithm through case operations. Yang et al. [51] also pointed out that group solution search algorithms, such as GAs, without specific information are more suitable for scheduling optimization of prefabricated components than single-solution search algorithms, such as simulated annealing algorithms, and gradient information algorithms, such as particle swarm algorithms. This article uses the GA to design a method for seeking the optimal solution of integrated scheduling optimization for multi-line production and transportation of prefabricated components considering shared resources. Figure 2 shows the specific algorithm flow and implementation form. The following provides detailed explanations of the key steps.

4.1. Encoding

The GA designed in this article encodes the chromosome into a 2 × $n$ matrix. The genes in the first row of the matrix are the numbers of the prefabricated component groups, namely the parameter $j$. The genes in the second row of the matrix are the numbers of the production line where the prefabricated component group in the first row is located, namely the parameter $k$. The data in two rows of the matrix need to be read correspondingly. Select the same genes in the second row, and the arrangement sequence of the prefabricated component groups represented by the corresponding genes in the first row is the production sequence of the prefabricated component groups on the production line of that number. Taking the chromosome in Figure 2 as an example, the production sequence of the prefabricated component group on line 1 is 6 → 11 → 7 → 14 → 5 → 19 → 2 → 18 → 9 → 20, and the production sequence on line 2 is 3 → 16 → 17 → 8 → 15 → 1 → 4 → 13 → 10 → 12. After determining the chromosome, other parameters used in this study can all be calculated through Equations (1)–(22).

4.2. Fitness Calculation

The optimization objective function, i.e., Equation (1), was adopted to assess the fitness of the scheduling scheme corresponding to each chromosome. The lower the cost, the higher the fitness. The chromosome with the lowest objective function value in each generation is considered the optimal chromosome. Through continuous iteration, the objective function value of the optimal chromosome in each generation gradually decreases, and the fitness gradually increases and tends to converge.

4.3. Selection

The GA designed in this article adopts the classical roulette wheel method to select parent chromosomes. In each round of wheel rotation selection, the higher the chromosome’s fitness, the greater its probability of being selected. Therefore, it is essential to ensure that excellent chromosomes, i.e., chromosomes corresponding to production plans with low objective function cost values, are selected as much as possible. The number of selected parent chromosomes is the same as the population size.

4.4. Crossover

In the GA of this design, the chromosome is a 2 × $n$ matrix. The first row of the matrix adopts the Order Crossover 2 (OX2) method, and the second row employs the Partial-Mapped Crossover (PMX) method. When designing the crossover method, the individual characteristics of the genes in the two rows and the correlation between the two rows need to be considered. Consequently, the two randomly selected gene points in the two rows of the chromosome should be consistent to utilize the advantages of the GA. The specific crossover process is shown in Figure 2. Two positions of the genes in a pair of parent chromosomes are randomly selected, and the positions of the corresponding genes in this pair of chromosomes are exchanged to generate the offspring chromosomes. By exchanging the positions of the two parent chromosomes, another offspring chromosome can be generated.

4.5. Mutation

In the GA of this design, the chromosome is a 2 × $n$ matrix. In the first row of the matrix, two positions are randomly selected, and these two genes are swapped. In the second row of the matrix, a position is randomly selected, and the gene value at this position is changed to some other feasible value. As shown in Figure 2, the genes in the first row represent the number of prefabricated component groups, and the positions of genes 14 and 4 are exchanged. The genes in the second row represent the number of production lines, and the gene at position nine changes from 1 to 2.

4.6. Determining the Optimal Solution

This article determines the appropriate number of iterations through trial-and-error experiments to ensure reasonable operation time and convergence effect. When the number of iterations reaches the set limit, the chromosome with the minimum value of the objective function and the highest fitness would be regarded as the optimal chromosome and output and decoded.

5. Result and Discussion

5.1. Case Data Collection

This article uses the actual data of a precast plant in China to validate the effectiveness of the model and algorithm. The precast plant has two flow production lines, and the products include laminated plates, interior walls, exterior walls, etc. To enhance production efficiency, 2–3 prefabricated components are formed into a group and produced on the same bench formwork. The total number of prefabricated component groups is $n=20$ in this case. The process operation time, due date, unit late cost, and unit early cost of each prefabricated component group are presented in

Table 2. Case data for the integrated multi-line scheduling model.

Items	Operation Time of Each Process for Prefabricated Component Group (h)								Due Date (h)	Delivery Penalty Cost
	Process Number
Prefabricated Component Group Number	M1	M2	M3	M4	M5	M6	M7	M8		Unit Early Cost	Unit Late Cost
1	0.29	0.94	0.29	10.00	0.26	0.25	48.00	2.00	80	2	10
2	0.28	0.85	0.26	10.00	0.25	0.25	48.00	2.00	80	2	10
3	0.20	0.46	0.14	10.00	0.22	0.25	48.00	2.00	80	2	10
4	0.25	0.71	0.22	10.00	0.24	0.25	48.00	2.00	80	2	10
5	0.27	0.85	0.27	10.00	0.25	0.25	48.00	2.00	80	2	10
6	0.23	0.54	0.15	10.00	0.23	0.25	48.00	2.00	80	2	10
7	0.25	0.72	0.22	10.00	0.24	0.25	48.00	2.00	80	2	10
8	0.28	0.84	0.26	10.00	0.25	0.25	48.00	2.00	80	2	10
9	0.26	0.73	0.23	10.00	0.24	0.25	48.00	2.00	80	2	10
10	0.29	0.94	0.31	10.00	0.26	0.25	48.00	2.00	80	2	10
11	0.26	0.78	0.27	10.00	0.24	0.25	48.00	2.00	80	2	10
12	0.24	0.68	0.23	10.00	0.24	0.25	48.00	2.00	80	2	10
13	0.27	0.74	0.24	10.00	0.25	0.25	48.00	2.00	80	2	10
14	0.21	0.48	0.15	10.00	0.22	0.25	48.00	2.00	80	2	10
15	0.29	1.01	0.32	10.00	0.26	0.25	48.00	2.00	80	2	10
16	0.24	0.61	0.19	10.00	0.23	0.25	48.00	2.00	80	2	10
17	0.25	0.73	0.22	10.00	0.24	0.25	48.00	2.00	80	2	10
18	0.23	0.62	0.19	10.00	0.23	0.25	48.00	2.00	80	2	10
19	0.28	0.88	0.28	10.00	0.25	0.25	48.00	2.00	80	2	10
20	0.25	0.64	0.20	10.00	0.24	0.25	48.00	2.00	80	2	10

. The precast plant agrees with the customer on the delivery due date of prefabricated components. If the delivery is earlier than the agreed due date, the plant has to pay an early penalty cost to the customer, mainly guard management fees, secondary handling fees, etc. If the delivery is later than the agreed due date, the plant has to pay a late penalty cost to the customer to compensate for the loss of delaying the customer’s project progress to a certain extent. According to the law, the precast plant stipulates that the working hours per day are $H=8$. The operation time of M4 is related to the steam temperature in the curing chamber. In this case, the temperature in the curing chamber is 50 °C; the operation time of M4 is 10 h; and the total number of curing stations in the curing chamber is $h=20$.

5.2. Results

In this study, the result of the traditional scheduling method of shortest processing time (SPT) is used as the control group. SPT is a classic scheduling scheme, which makes the production sequence of prefabricated component groups consistent with the ascending sequence of their M1 operation times. If the operation times of M1 are the same, the production sequence of the prefabricated component groups is the same as the ascending sequence of M2 operation times, and so on. Moreover, the production lines are allocated in a sequential, even manner. This plant employs this scheduling method for manual production scheduling. The scheduling result of SPT is that the production sequence of prefabricated component groups on line 1 is 3 → 6 → 16 → 20 → 7 → 9 → 13 → 8 → 19 → 10, and the production sequence on line 2 is 14 → 18 → 12 → 4 → 17 → 11 → 5 → 2 → 1 → 15. Under this scheduling scheme, the sequence of the prefabricated component group entering the curing chamber is 3 → 14 → 6 → 18 → 16 → 12 → 20 → 4 → 7 → 17 → 9 → 11 → 13 → 5 → 8 → 2 → 19 → 1 → 10 → 15, and the sequence of the quality inspection process is 3 → 14 → 6 → 18 → 16 → 12 → 20 → 4 → 7 → 17 → 9 → 11 → 13 → 5 → 8 → 2 → 19 → 1 → 10 → 15. The total penalty cost for delivery is 656.32, including an early penalty cost of 613.12 and a late penalty cost of 43.20. The total completion time is 84.32 h. Except for the 15th group, which is late, the other prefabricated component groups are delivered before their due dates.

A trial-and-error experiment is a common method for the GA to determine control parameters. This article uses trial-and-error experiments to determine crossover probability, mutation probability, population size, and the maximum iteration number. The basic parameters are finally determined as follows: population size of 300, maximum iteration number of 2500, crossover probability of 0.85, and mutation probability of 0.2. This experiment was conducted on the Microsoft Windows 11 system, with an Intel Core i7-1260U CPU @2.50GHz processor. The steps of the GA were implemented through programming in MATLAB R2021a, and multiple operations were run to obtain the optimal solution that minimized the objective function. The scheduling result of the optimal scheme is that the production sequence of prefabricated component groups on line 1 is 10 → 1 → 5 → 8 → 13 → 7 → 12 → 20 → 6 → 3, and the production sequence on line 2 is 15 → 19 → 2 → 11 → 9 → 17 → 4 → 18 → 16 → 14. Under this scheduling scheme, the sequence of the prefabricated component group entering the curing chamber is 10 → 15 → 1 → 19 → 5 → 2 → 11 → 8 → 9 → 13 → 17 → 7 → 4 → 12 → 18 → 20 → 6 → 16 → 3 → 14, and the sequence of the quality inspection process is 10→ 15 → 19 → 1 → 2 → 5 → 11 → 8 → 9 → 13 → 17 → 7 → 4 → 12 → 18 → 20 → 16 → 6 → 14 → 3. The total penalty cost for delivery is 600.18, including an early penalty cost of 600.18 and a late penalty cost of 0. The total completion time is 67.84 h. All prefabricated component groups can be delivered before their due dates.

The effectiveness of the optimization model and algorithm design in this study is validated. The fitness value convergence curve of the solution process is shown in Figure 3, where the optimized fitness value stabilized after the 1000th generation, and the optimal solution was obtained in the 1680th generation. Figure 4 is the Gantt chart of the optimal scheduling scheme, where the horizontal axis refers to time; each tick refers to 12 h, and the initial time is set to 0. 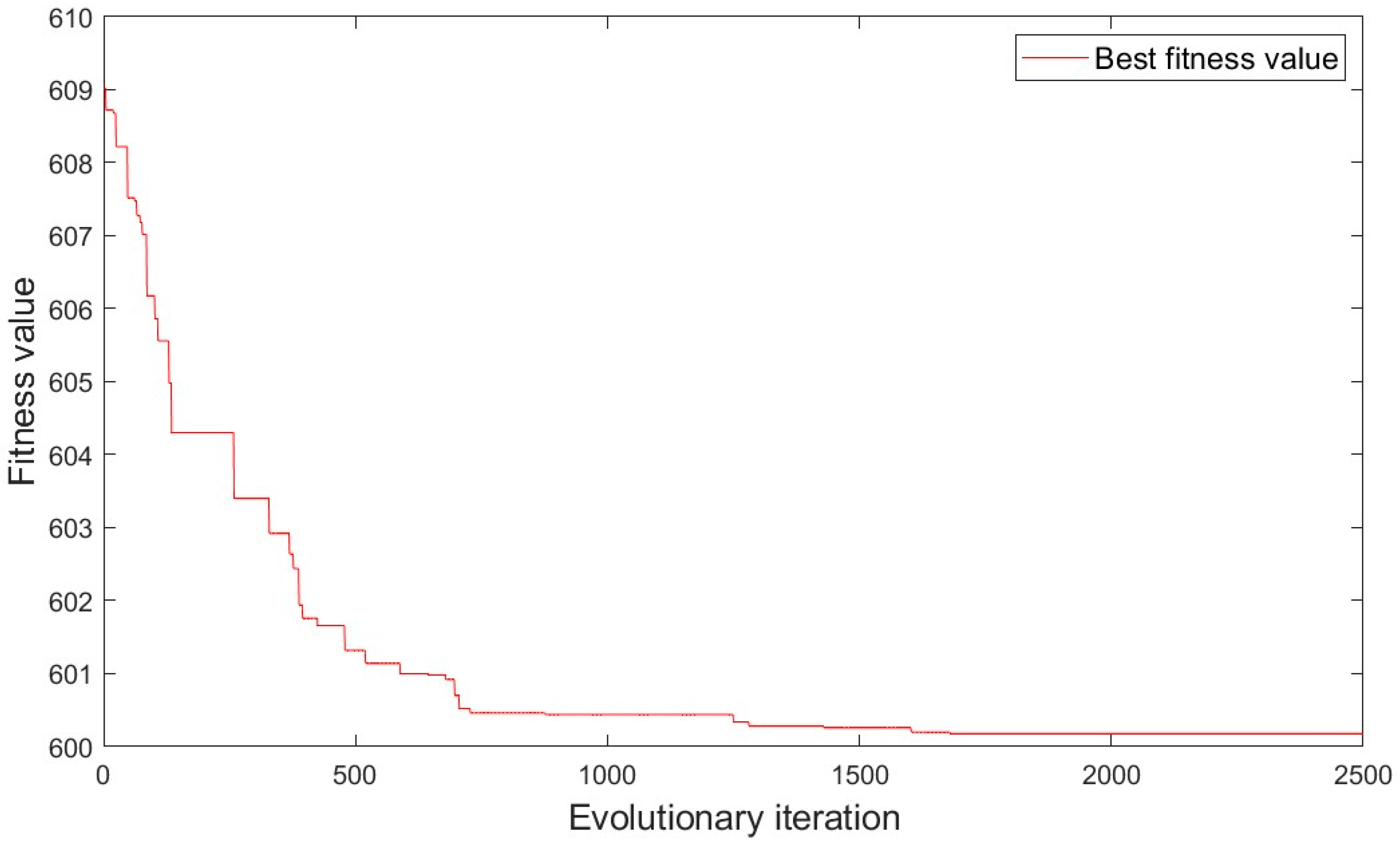Meanwhile, the vertical axis represents the prefabricated component group number; the blocks represent different processes, and the corresponding abscissa values on the left and right sides of the block, respectively, refer to the start time and the end time of the process.

5.3. Discussion

To evaluate the performance of the proposed model and algorithm, the optimal scheme’s results are compared with the SPT method.

(1)

The optimal scheme can cut costs compared to the SPT scheme. Compared with the traditional SPT method, the result of the optimal scheme can cut the cost (656.32–600.18)/656.32 = 8.55%, and the cost-cutting effect is significant. The cost of prefabricated buildings is generally higher than that of cast-in-site buildings [59]. Reducing the cost has a positive significance for promoting the development of prefabricated buildings.

(2)

The optimal scheme can ensure on-time delivery compared to the SPT scheme. At the same time, it can ensure that all prefabricated components are delivered before due dates, improving customer satisfaction. In contrast, in the SPT scheme, a group of prefabricated components are delayed by 4.32 h. Prefabricated buildings are constructed floor by floor, with each lower floor serving as the foundation for the upper ones. If prefabricated components are delivered late, this will delay the project’s construction progress, causing losses for the client. The plant needs to make a breach of contract compensation as stipulated in the contract. Therefore, ensuring the on-time delivery of prefabricated components is very important.

(3)

The optimal scheme can reduce the total production line occupancy time compared to the SPT solution. Next, an analysis and comparison of the two schemes’ total production line occupancy time, $TLS$, are conducted. This can not only measure the production efficiency of the schemes but also reflect the levels of energy consumption and carbon emissions of the schemes to a certain extent. The occupancy time on the production lines is 74.67 h for the SPT scheme and 52.84 h for the optimal scheme, respectively. The shortening of the time occupied on the production lines, to a certain extent, indicates a reduction in energy consumption and carbon emissions. Hence, optimal scheduling, while minimizing the penalty costs, also incentivizes practices that might be at odds with environmental responsibility.

6. Conclusions

Multi-line production is an increasingly common scenario in precast concrete plants to meet the growing market demand, and production and transportation of prefabricated components are two consecutive services that precast plants need to provide for customers. Unlike the previous multi-line scheduling studies that merely decomposed multiple production lines into independent single ones for scheduling, disregarding the correlations among multiple lines resulting from the equipment and personnel configuration in some plants, in this article, multiple production lines have shared use of curing chamber equipment and shared quality inspection personnel. They are not independent, and the situation is more complicated. Prefabricated components are produced sequentially on different production lines, which will be comprehensively scheduled at specific processes, and then returned to the original production lines after these processes are finished. In this article, an integrated scheduling optimization model for multi-line production and transportation of prefabricated components is established to minimize the early and late delivery penalty costs. A genetic algorithm using double-layer coding chromosomes is designed for this model. The model is validated via numerical analysis using actual data from a precast plant. Additionally, the practicality of the scheduling optimization model is improved by considering various realistic constraints, which is beneficial for extending prefabricated component scheduling theory to practice. The specific contributions of this article to prefabricated component production and transportation scheduling are as follows.

(1)

For a multi-line production scenario, the integrated scheduling optimization of precast production and transportation is studied. Considering multiple practical constraints, such as the shared curing chamber, shared quality inspection personnel resources, and shared transportation resources, an integrated scheduling optimization model of multi-line production and transportation of prefabricated components is established. This model could guide precast plants to integrate precast production and transportation scheduling optimization from a global perspective while managing multiple production lines and minimizing costs while meeting customer needs.

(2)

Based on a genetic algorithm and computer programming technology, a solution algorithm is designed for the model, which realizes the integrated scheduling of multiple lines through the double-layer coding of chromosomes. At the same time, a reasonable method of selection, crossover, and mutation is designed to ensure that the genes of excellent parent chromosomes are more likely to be inherited by their offspring chromosomes, and the fitness value can converge in a reasonable time.

(3)

Based on the case data of a precast plant, the operation analysis is carried out to validate the model and algorithm. The optimal scheduling result reveals the effective allocation of production lines and the corresponding production sequence of the prefabricated component groups, which can meet the customer’s order requirements and significantly reduce the cost. Compared with the traditional SPT scheduling scheme, the optimal scheduling result can ensure that all prefabricated components are delivered before the due dates and cut the cost by 8.55%.

In the future, our research will consider more realistic constraints and significant optimization goals. For instance, factors that influence employee morale and operational stress levels, along with their effects on production efficiency, will be considered as constraints in the model. Moreover, reducing carbon emissions will be regarded as one of the optimization targets. Based on the calculation formula of production process time and data such as the power of related equipment on the assembly line, carbon emissions will be accounted for, seeking an optimized equilibrium among reducing carbon emissions, cutting production costs, and enhancing production efficiency. Furthermore, the joint scheduling of production, transportation, and on-site construction can be investigated to support the enhancement of on-site construction efficiency for construction enterprises.