Design and Shear Bearing Capacity Calculation of All-Welded Irregular Joints in Steel Traditional Chinese Buildings
Abstract
1. Introduction
2. Experimental Investigation
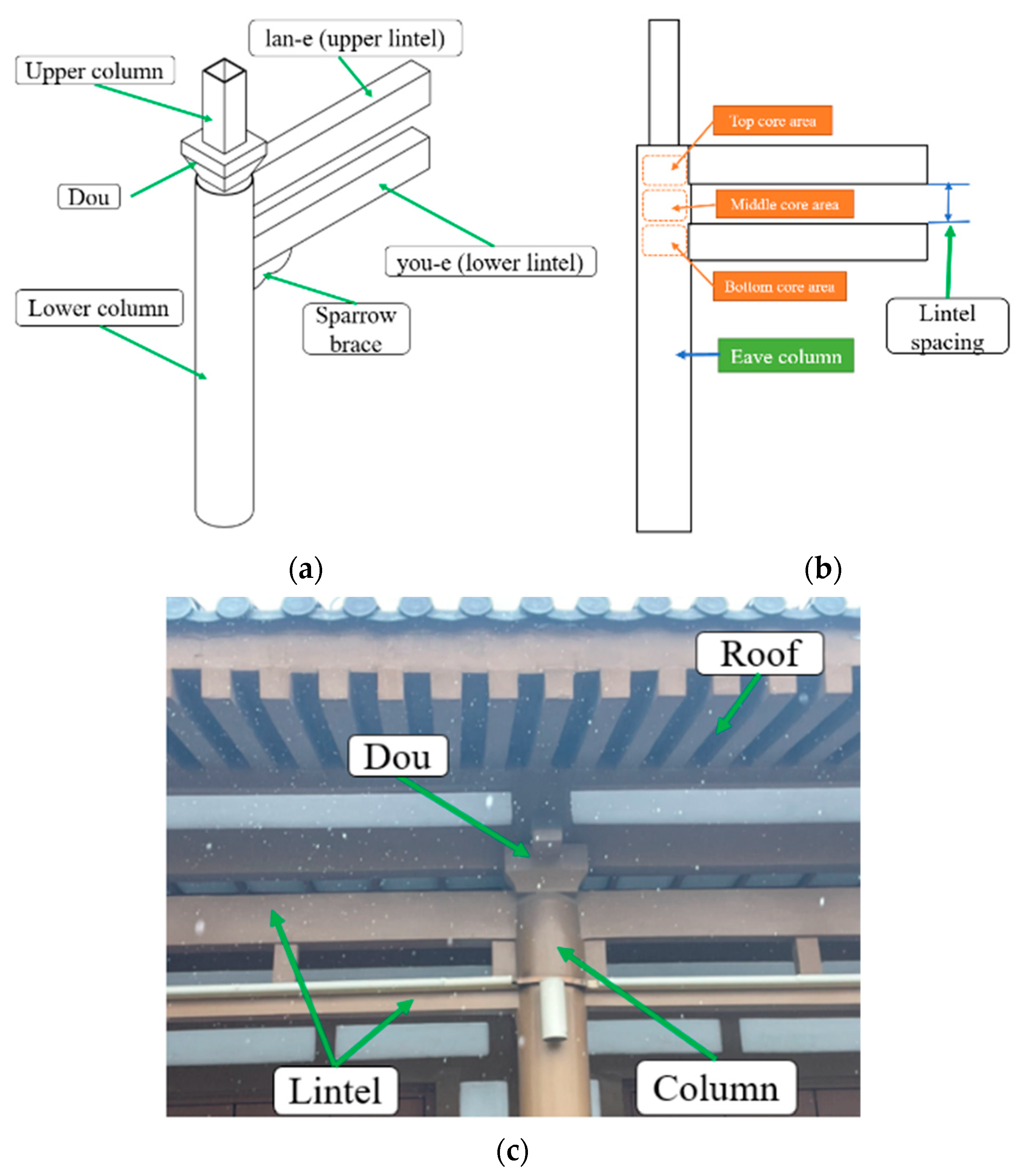
2.1. Construction and Design Method
2.2. Specimen Design
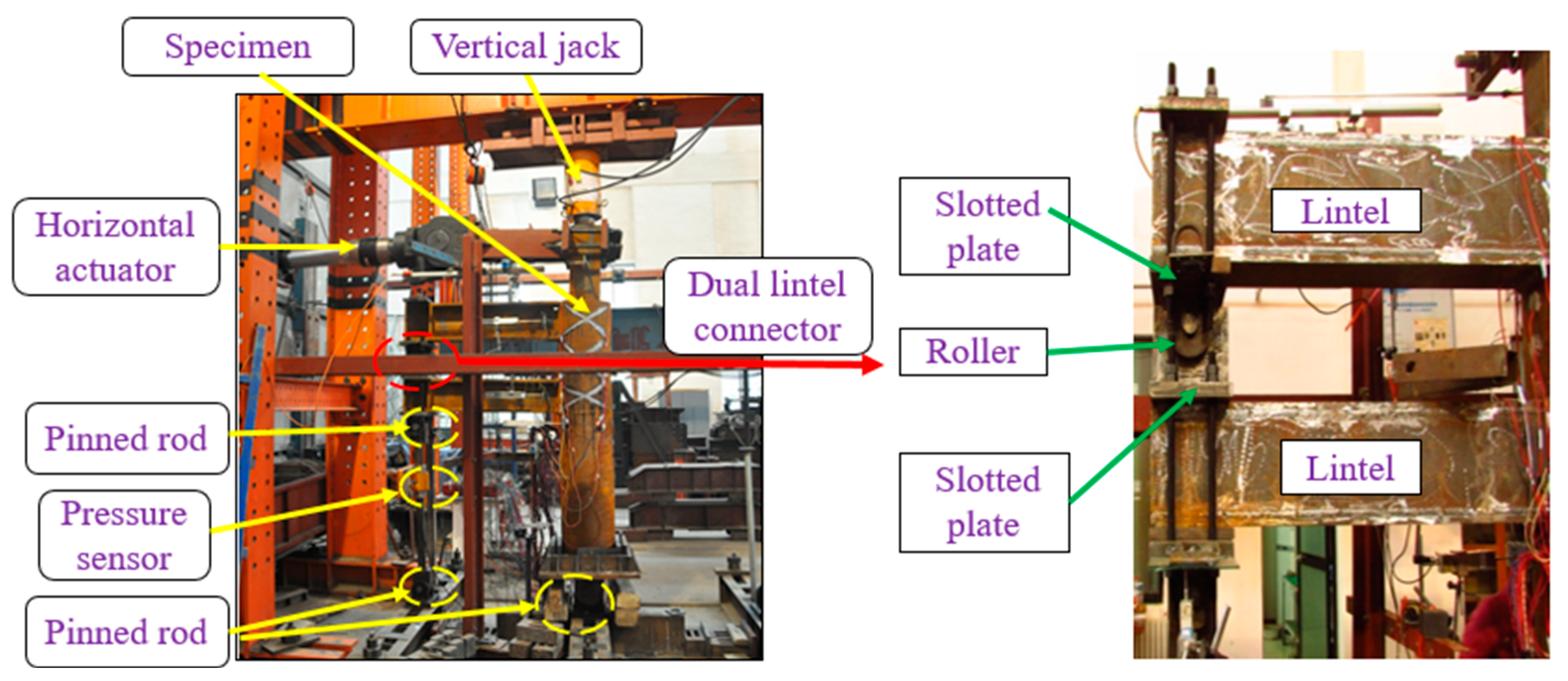
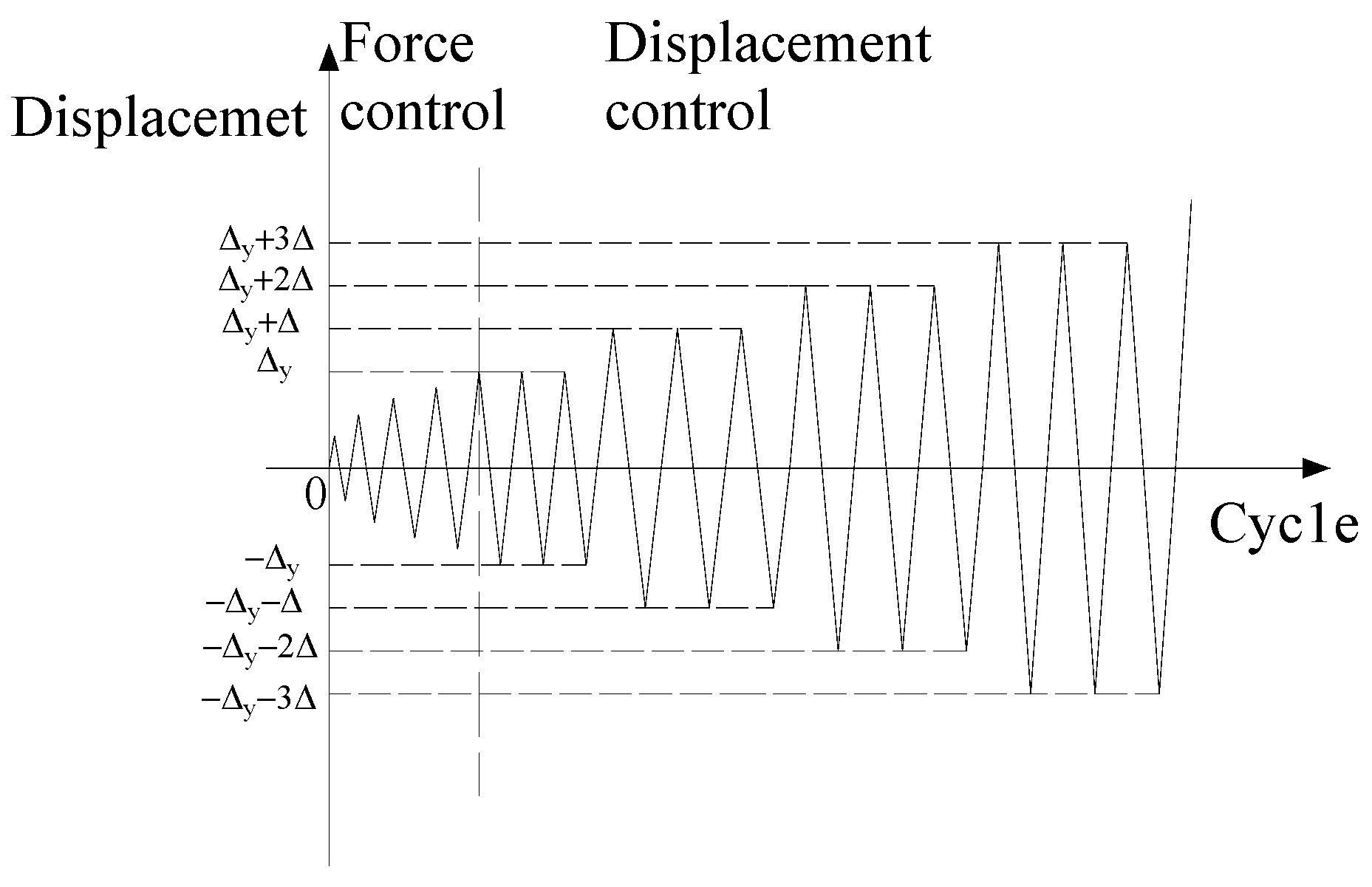
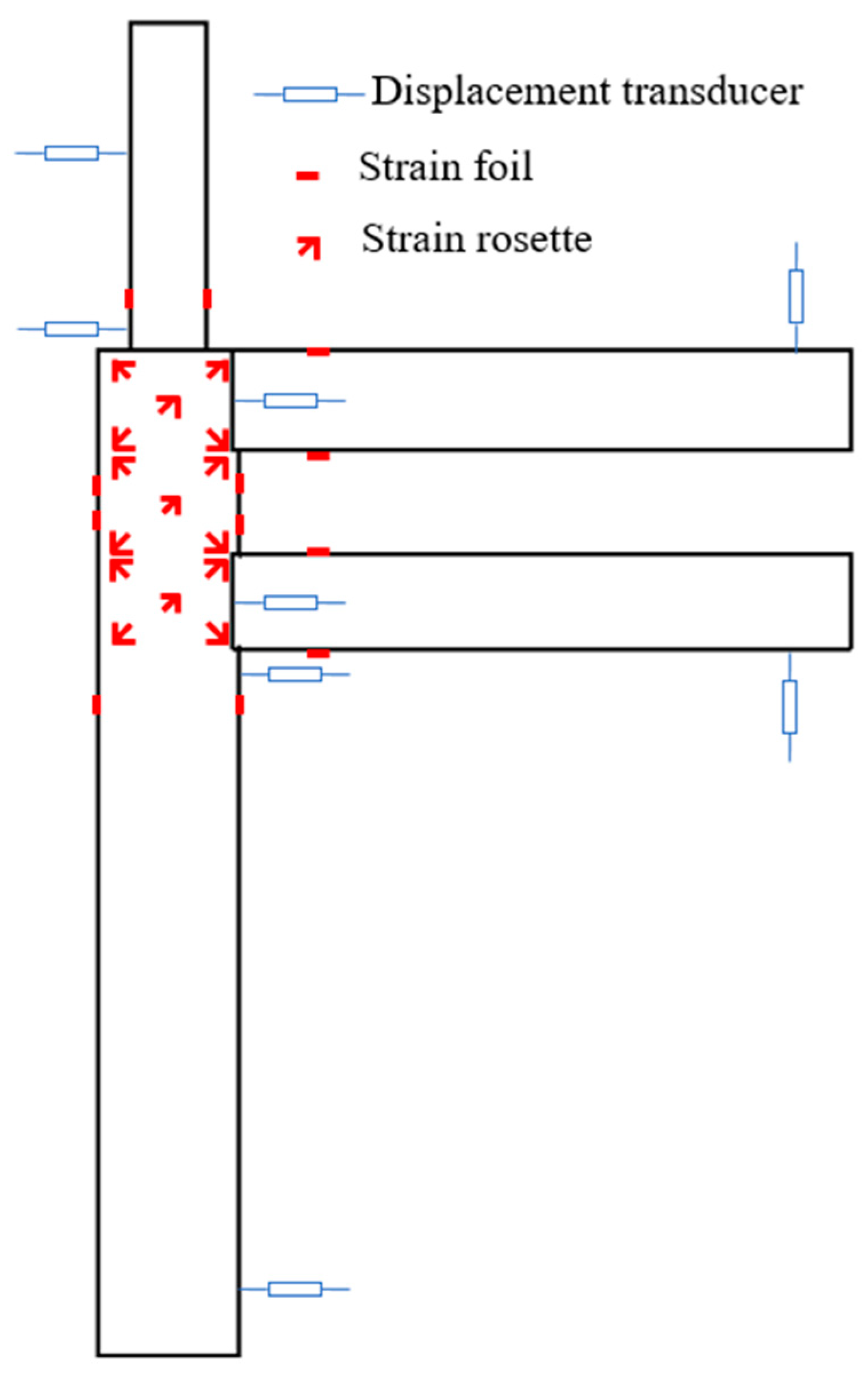
2.3. Test Methods
3. Test Results
3.1. Failure Patterns
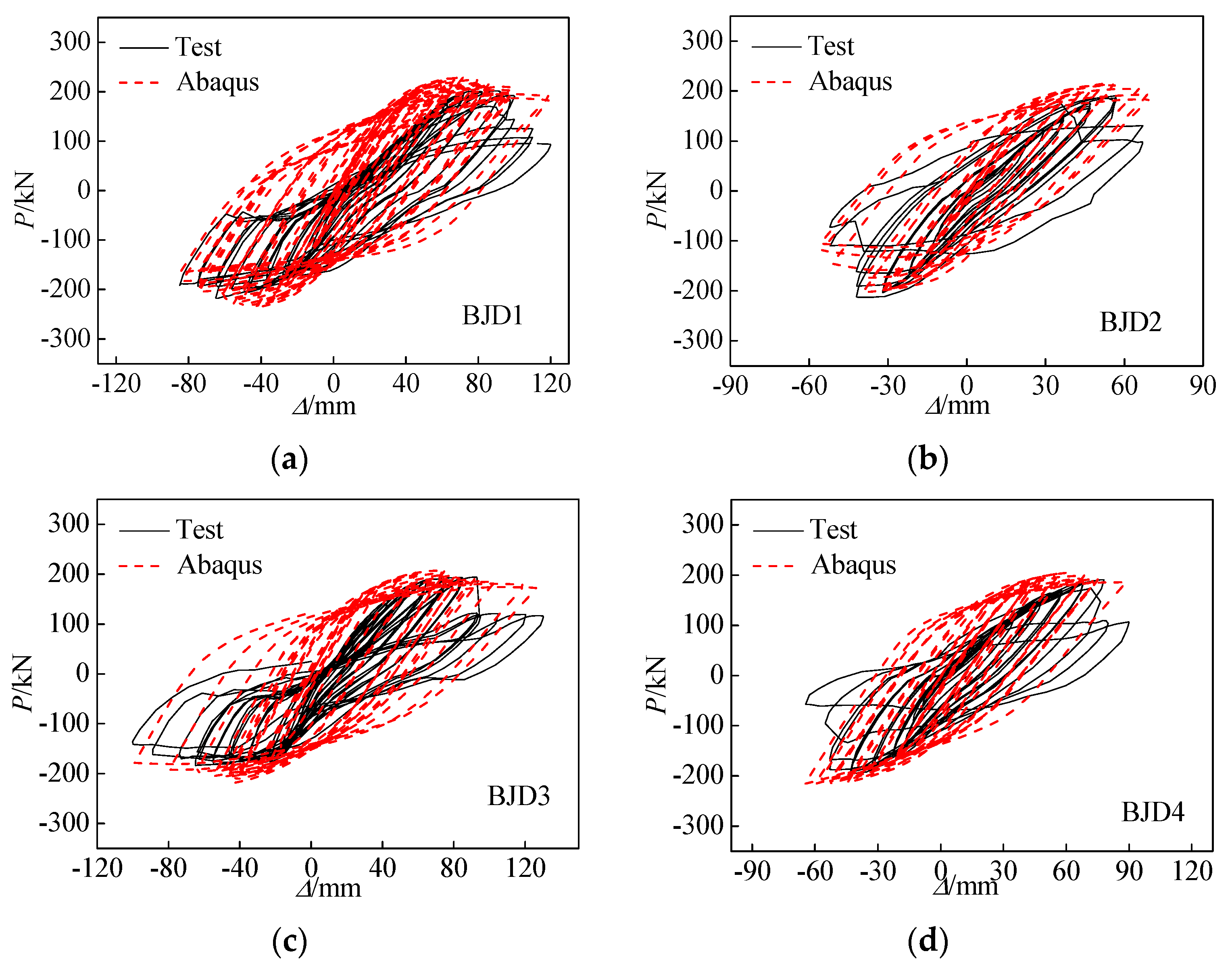
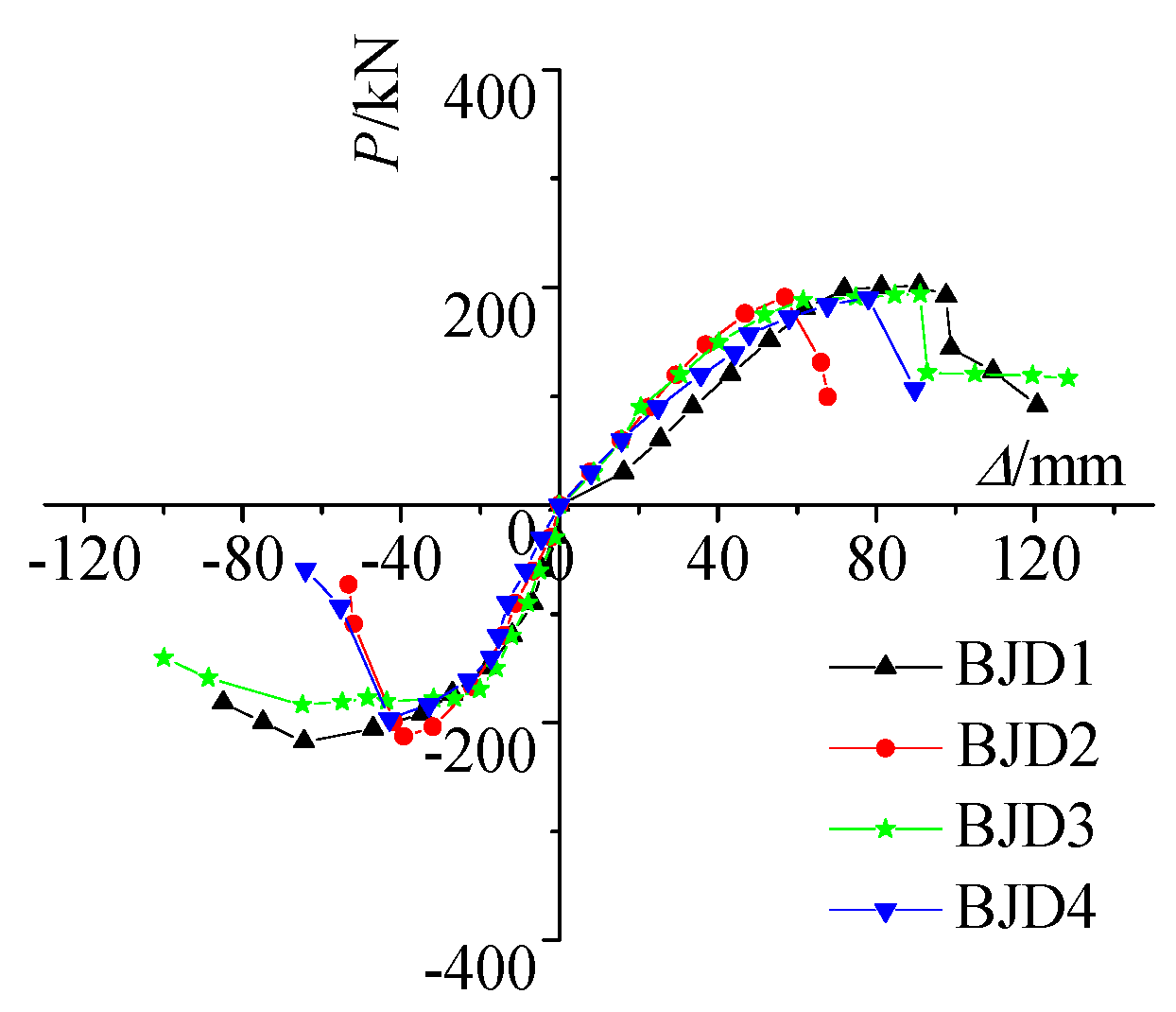
3.2. Load–Displacement Curves
4. Finite Element Analysis
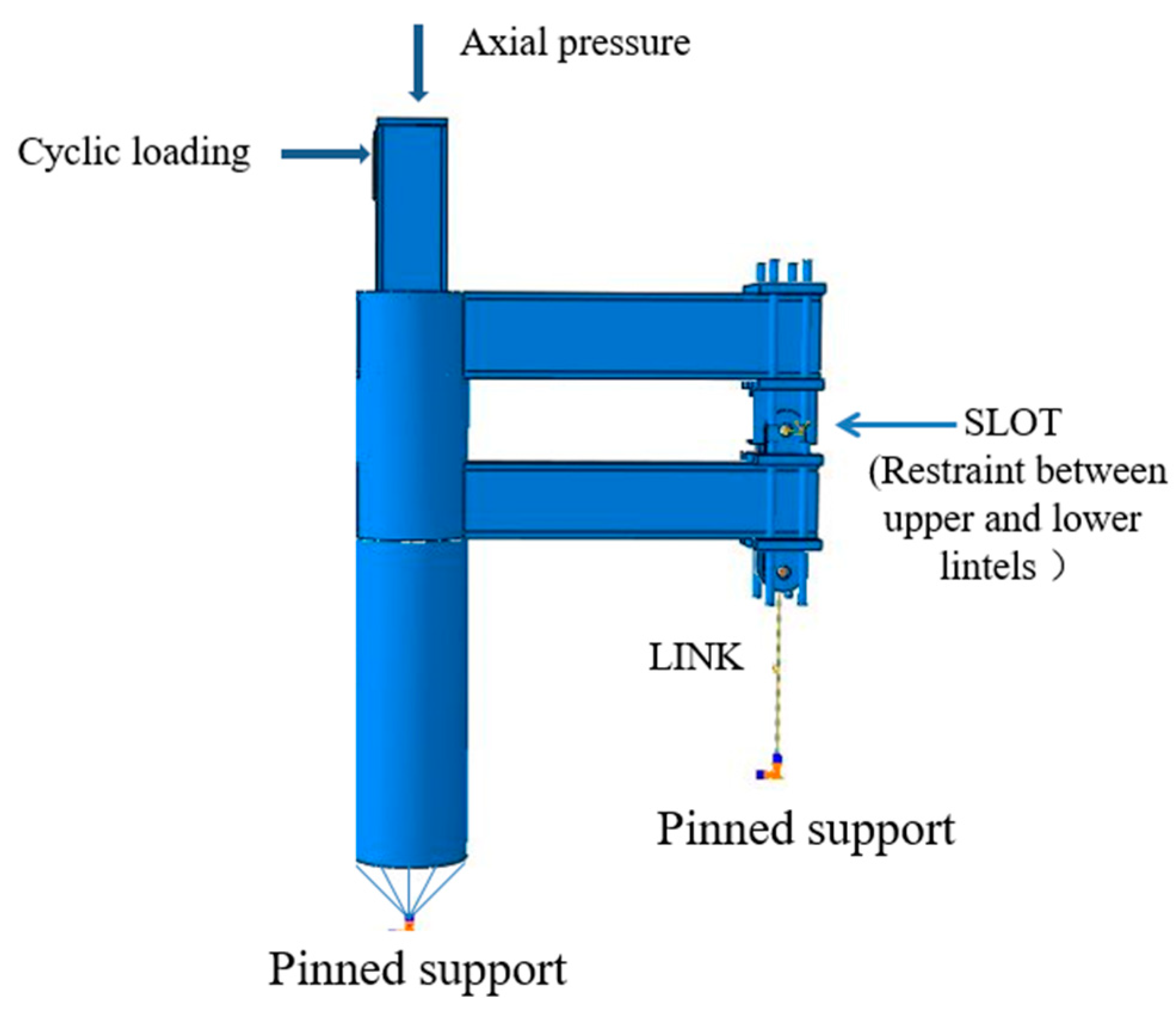
4.1. FEA Models
4.2. Verification of Finite Element Model
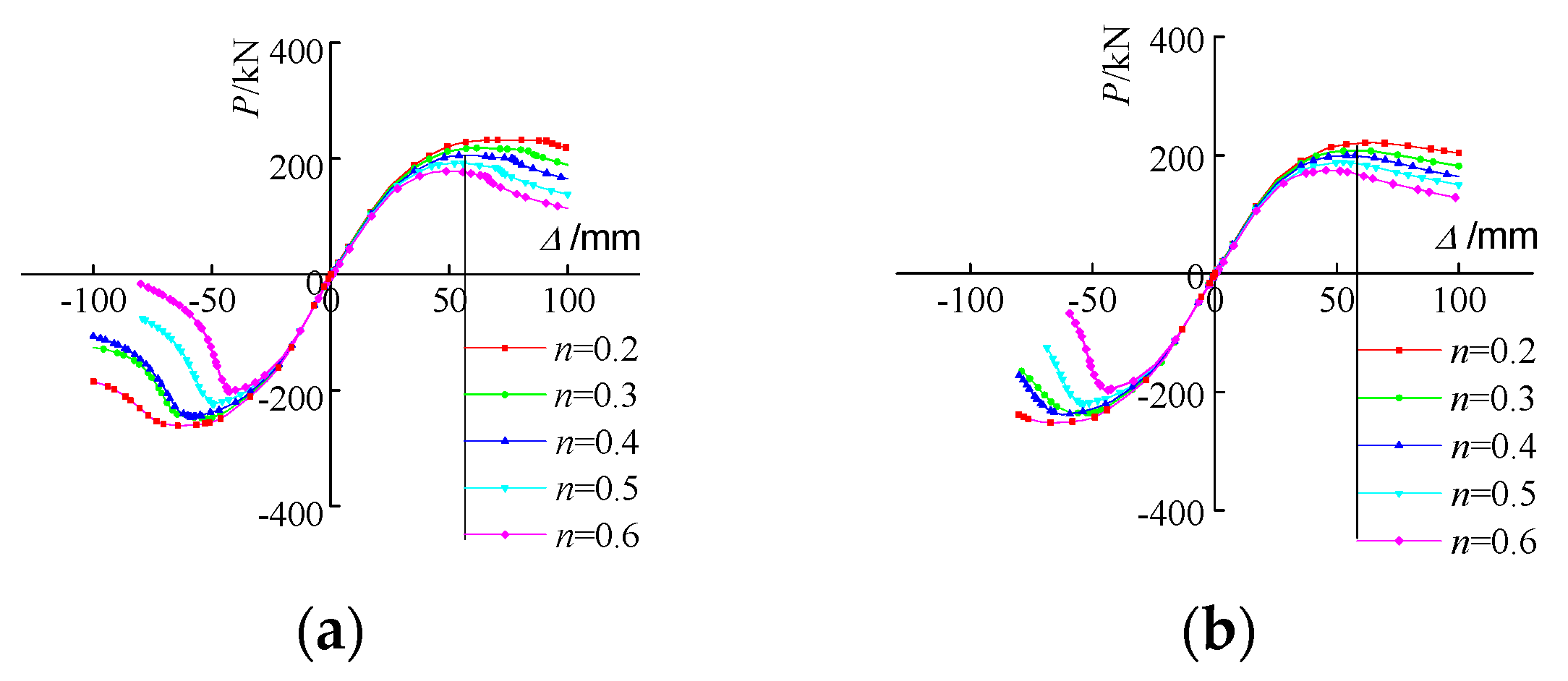
4.3. Effects of the Axial Compression Ratio
5. Analysis of Shear Capacity
6. Conclusions
- WIJs in STCBs are characterized by their dual-lintel configuration, which forms three distinct small core regions. The primary failure mode is shear failure in the lower core. Under late-stage loading, the joint between the column wall and the beam tends to crack, which should be carefully considered in the design.
- The axial compression ratio and the section shape of the lintel have significant effects on the failure mode and bearing capacity of the joint. As the axial compression ratio increases, shear failure in the lower core region becomes more pronounced. The deformation of the lower core region in the box beam specimen is larger than that in the H-section beam specimen.
- Based on the proportional relationship outlined in the Song Dynasty construction manual, a simplified calculation formula for the shear strength of the core region is derived. This formula is applicable to the traditional style of temple buildings in the Tang Dynasty. The calculated results are in good agreement with the experimental findings, providing a theoretical foundation for the seismic design of WIJs in STCBs.
- Future research will be carried out in the field of STCBs of prefabricated fully bolted connection, while increasing the research on hall and Qing architecture. There will be a focus on joint optimization design using artificial intelligence and machine learning.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, Q.; Yu, P.; Law, S.S. Load resisting mechanism of the mortise-tenon connection with gaps under in-plane forces and moments. Eng. Struct. 2020, 219, 110755. [Google Scholar] [CrossRef]
- Chen, Z.; Zhu, E.; Lam, F.; Pan, J. Structural performance of Dou-Gong brackets of Yingxian Wood Pagoda under vertical load-An experimental study. Eng. Struct. 2014, 80, 274–288. [Google Scholar] [CrossRef]
- Song, D.; Xue, J.; Wu, C. Experimental and theoretical study on seismic behavior of Tou-kung brackets on column under the load in overhanging and width directions. Eng. Struct. 2024, 299, 117138. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, L.; Qiu, Z.; Cui, L.; Hu, C. Replaceable Displacement-Amplifying Rotary Friction Damper: Experimental and Numerical Investigation. Struct. Control Health Monit. 2024, 1, 9402792. [Google Scholar] [CrossRef]
- Dai, N.; Cui, L.; Li, Y.; Fan, L.; Chen, J. A numerical simulation study on the out-of-plane performance of timber framework-brick wall systems in traditional residential Buildings of northern China. Buildings 2024, 14, 1224. [Google Scholar] [CrossRef]
- Cui, L.; Zhang, X.; Hu, W.; Meng, Z.; Chen, J.; Qiu, Z. Seismic performance analysis of ancient palace-style building considering column rocking effect. J. Earthq. Eng. 2024, 28, 3175–3190. [Google Scholar] [CrossRef]
- Xue, J.; Guo, R.; Qi, L. Experimental study on the seismic performance of traditional timber mortise tenon joints with different looseness under low-cyclic reversed loading. Adv. Struct. Eng. 2019, 22, 1312–1328. [Google Scholar] [CrossRef]
- Zhao, H.; Zhang, F.; Xue, J.; Xie, Q.; Zhang, X.; Ma, H. Research review on structural performance of ancient timber structure. J. Build. Struct. 2012, 33, 1–10. [Google Scholar]
- Rabi, M.; Abarkan, I.; Shamass, R. Buckling resistance of hot-finished CHS beam-columns using FE modelling and machine learning. Steel Constr. Des. Res. 2024, 17, 93–103. [Google Scholar] [CrossRef]
- Abarkan, I.; Rabi, M.; Ferreira, F.P.V.; Shamass, R.; Limbachiya, V.; Jweihan, Y.S.; Santos, L.F.P. Machine learning for optimal design of circular hollow section stainless steel stub columns: A comparative analysis with Eurocode 3 predictions. Eng. Appl. Artif. Intell. 2024, 132, 107952. [Google Scholar] [CrossRef]
- Rabi, M.; Jweihan, Y.S.; Abarkan, I.; Ferreira, F.P.V.; Shamass, R.; Limbachiya, V.; Tsavdaridis, K.D.; Santos, L.F.P. Machine learning-driven web-post buckling resistance prediction for high-strength steel beams with elliptically-based web openings. Results Eng. 2024, 21, 101749. [Google Scholar] [CrossRef]
- Wu, K.; Jia, J.; Che, S. Structural material evolution and key component design of traditional style building. Build. Struct. 2017, 47, 61–65. [Google Scholar]
- Che, S.; Jia, J.; Wu, K.; Wei, S.; Mu, M. Steel structure design of a traditional style pavilion architecture. Build. Struct. 2017, 47, 47–50, 81. [Google Scholar]
- Qi, L.; Xue, J.; Leon, R.T. Experimental and analytical investigation of transition steel connections in traditional-style buildings. Eng. Struct. 2017, 150, 438–450. [Google Scholar] [CrossRef]
- Xue, J.; Zhai, L.; Gao, W.; Dong, J.; Wu, K. Experimental study on seismic performances of connections between rectanglar steel pipe column and circular steel pipe column in imitated ancient building. J. Build. Struct. 2016, 37, 81–91. [Google Scholar]
- Xue, J.; Ma, L.; Wu, Z.; Gao, W. Influence analysis of bracket set on seismic performance of steel eave columns in Chinese traditional style buildings. Struct. Des. Tall Spec. Build. 2018, 27, e1462. [Google Scholar] [CrossRef]
- Xue, J.; Qi, L.; Yang, K.; Wu, Z. Dynamic experimental study on single and double beam-column joints in steel traditional-style buildings. Struct. Eng. Mech. 2017, 63, 617–628. [Google Scholar]
- Xue, J.; Ma, L.; Wu, Z. Seismic performance of steel joints between double beams and column in Chinese traditional style buildings. Int. J. Steel Struct. 2018, 18, 417–432. [Google Scholar] [CrossRef]
- Xue, J.; Qi, L. Experimental studies on steel frame structures of traditional-style buildings. Steel Compos. Struct. 2016, 22, 235–255. [Google Scholar] [CrossRef]
- Qi, L.; Xue, J. Pseudo dynamic test and time-history analyses of traditional-style steel frame structures. Int. J. Steel Struct. 2018, 18, 402–416. [Google Scholar] [CrossRef]
- Ling, H.; Xue, J.; Qi, L. Shaking table test and numerical analyses of a multi-story traditional tower-style building. Earthq. Eng. Struct. Dyn. 2024, 53, 3184–3204. [Google Scholar] [CrossRef]
- Sui, Y.; He, Z.; Xue, J.; Wu, Z. Experimental study and numerical analysis on seismic performance of steel beam-column damping joint in Chinese traditional style buildings. Struct. Des. Tall Spec. Build. 2020, 29, e1710. [Google Scholar] [CrossRef]
- Wu, Z.; Xue, J.; Ke, X.; Sui, Y.; Dong, J. Dynamic experimental and numerical study of double beam-column joints in modern traditional-style steel buildings with viscous damper. Struct. Des. Tall Spec. Build. 2020, 29, e1677. [Google Scholar] [CrossRef]
- Yuan, Z.; Xue, J.; Qi, L. Seismic performance of steel semi-rigid friction-damped joints with replaceable angles in modern Chinese traditional-style buildings. J. Constr. Steel Res. 2023, 207, 107948. [Google Scholar] [CrossRef]
- Qi, L.; Yuan, Z.; Xue, J. Experimental and numerical study on seismic performance of steel semi-rigid joints equipped with SMA bars and friction dampers. Eng. Struct. 2024, 301, 117320. [Google Scholar] [CrossRef]
- Qi, L.; Cao, Y.; Xue, J.; Yuan, Z.; Ling, H.; Meng, R. Seismic performance evaluation and engineering application of modern Chinese traditional-style buildings: The state-of-art review. Structures 2023, 56, 105022. [Google Scholar] [CrossRef]
- Liang, S. A Pictorial History of Chinese Architecture; MTT Press: Boston, MA, USA, 1984. [Google Scholar]
- GB 50011-2010; Code for Seismic Design of Buildings. China Architecture & Building Press: Beijing, China, 2010.
- GB 50661-2011; Code for Welding of Steel Structures. Standards Press of China: Beijing, China, 2011.
- GB/T 228; Metallic Materials-Tensile Testing at Ambient Temperature. Chinese Standard Press: Beijing, China, 2002.
- JGJ 101-2015; Specification of Testing Methods for Earthquake Resistant Building. China Building Industry Press: Beijing, China, 2015. (In Chinese)
- AISC. Load and Resistance Factor Design Specification for Structural Steel Buildings; American Institute of Steel Construction: Chicago, IL, USA, 2005. [Google Scholar]

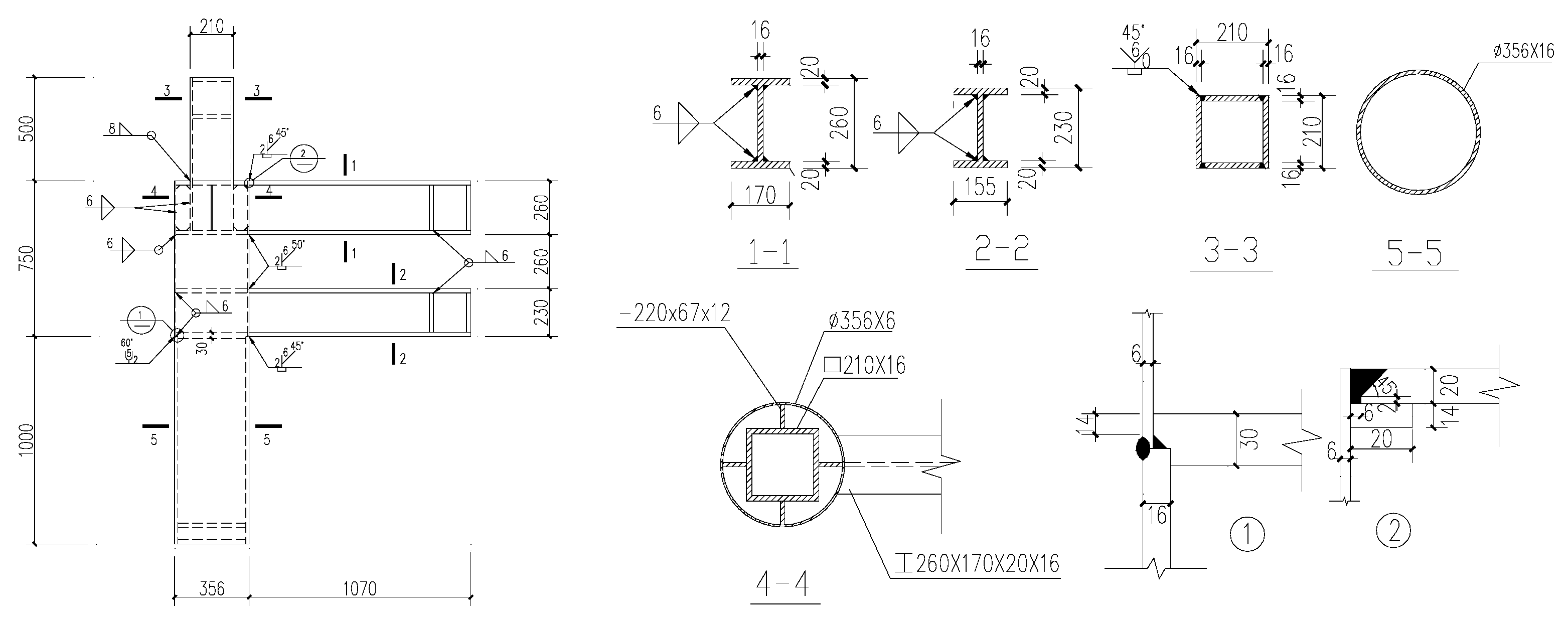


| Specimen ID | Axial Comparison Ratio | Top Box Column (mm) | Circular Column | Beam | Beam Spacing (mm) | ||
|---|---|---|---|---|---|---|---|
| Other Area (mm) | Panel Zone (mm) | Lan-e (Upper Lintel) (mm) | You-e (Lower Lintel) (mm) | ||||
| BJD1 | 0.3 | 10 × 210 × 16 × 16 | 356 × 16 | 356 × 6 | 260 × 170 × 20 × 16 | 230 × 155 × 20 × 16 | 260 |
| BJD2 | 0.6 | 210 × 210 × 16 × 16 | 356 × 16 | 356 × 6 | 260 × 170 × 20 × 16 | 230 × 155 × 20 × 16 | 260 |
| BJD3 | 0.3 | 210 × 210 × 16 × 16 | 356 × 16 | 356 × 6 | 260 × 170 × 20 × 16 | 230 × 155 × 20 × 16 | 260 |
| BJD4 | 0.6 | 210 × 210 × 16 × 16 | 356 × 16 | 356 × 6 | 260 × 170 × 20 × 16 | 230 × 155 × 20 × 16 | 260 |
| Material | Thickness t (mm) | Yield Stress fy (MPa) | Tensile Strength fu (MPa) | Elastic Modulus E (MPa) | Yield Strain εy |
|---|---|---|---|---|---|
| Plate | 12 | 318.9 | 472.3 | 2.077 × 105 | 1535 × 10−6 |
| 16 | 289.7 | 436.7 | 2.106 × 105 | 1375 × 10−6 | |
| 20 | 268.9 | 406.6 | 2.130 × 105 | 1262 × 10−6 | |
| Tube | 6 | 310.5 | 425.6 | 2.101 × 105 | 1537 × 10−6 |
| 16 | 301.7 | 438.9 | 2.121 × 105 | 1472 × 10−6 |
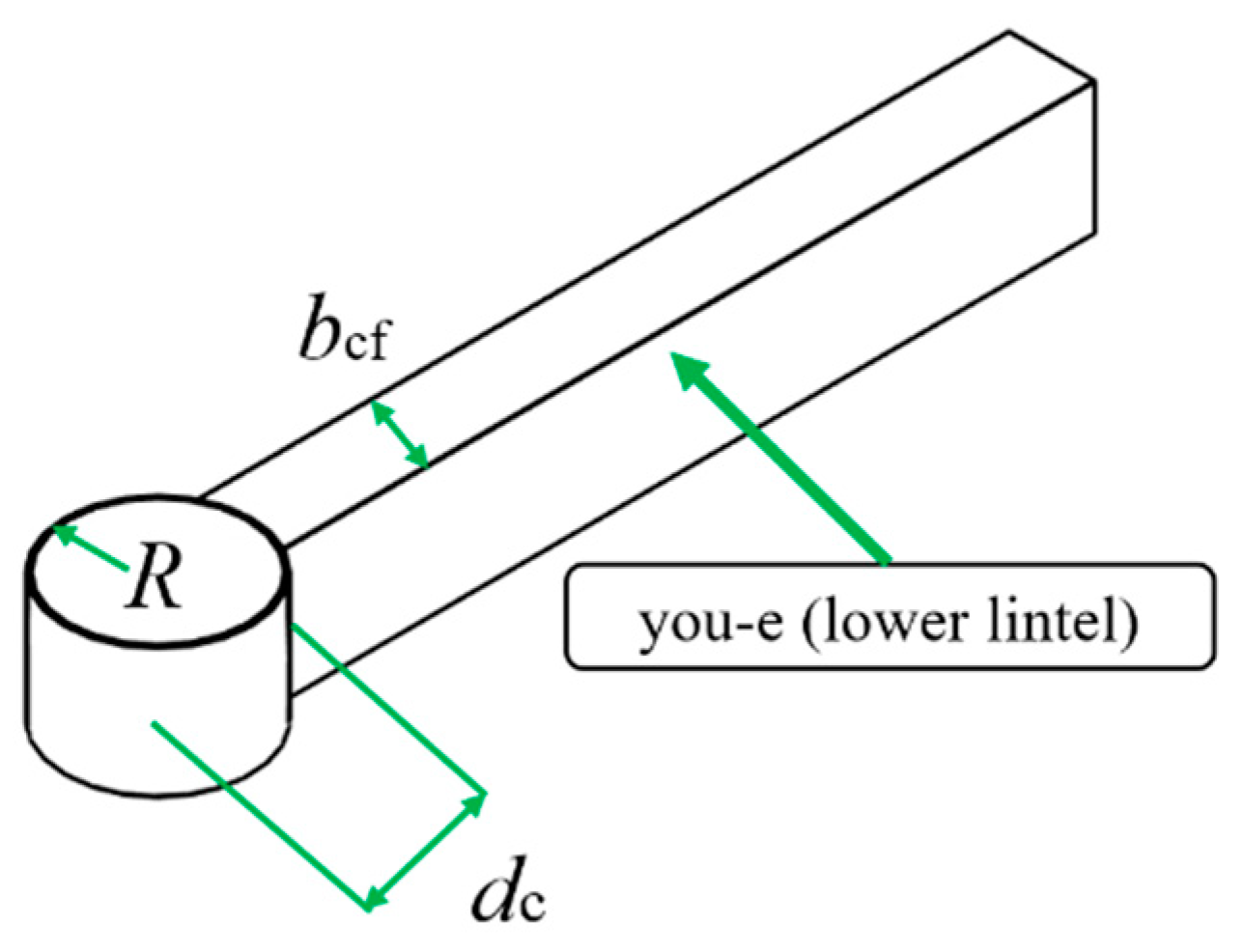
| Parameter | Unit: fen |
|---|---|
| D | 42 |
| dc | 36 |
| db | 27 |
| bcf | 18 |
| No | Section Form of Lintel | D /mm | t /mm | fy /MPa | n | Vc /kN | Vt /kN | Vc/Vt |
|---|---|---|---|---|---|---|---|---|
| JD1 | Box-section | 356 | 6 | 323 | 0.3 | 518.87 | 559.86 | 0.98 |
| JD2 | 356 | 6 | 323 | 0.6 | 470.87 | 474.63 | 1.05 | |
| JD3 | H-section | 356 | 6 | 323 | 0.3 | 533.91 | 554.27 | 0.93 |
| JD4 | 356 | 6 | 323 | 0.6 | 503.38 | 506.41 | 0.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Wang, X.; Bu, X.; Dong, J. Design and Shear Bearing Capacity Calculation of All-Welded Irregular Joints in Steel Traditional Chinese Buildings. Buildings 2025, 15, 184. https://doi.org/10.3390/buildings15020184
Wu Z, Wang X, Bu X, Dong J. Design and Shear Bearing Capacity Calculation of All-Welded Irregular Joints in Steel Traditional Chinese Buildings. Buildings. 2025; 15(2):184. https://doi.org/10.3390/buildings15020184
Chicago/Turabian StyleWu, Zhanjing, Xinwu Wang, Xin Bu, and Jinshuang Dong. 2025. "Design and Shear Bearing Capacity Calculation of All-Welded Irregular Joints in Steel Traditional Chinese Buildings" Buildings 15, no. 2: 184. https://doi.org/10.3390/buildings15020184
APA StyleWu, Z., Wang, X., Bu, X., & Dong, J. (2025). Design and Shear Bearing Capacity Calculation of All-Welded Irregular Joints in Steel Traditional Chinese Buildings. Buildings, 15(2), 184. https://doi.org/10.3390/buildings15020184





