Graph-RWGAN: A Method for Generating House Layouts Based on Multi-Relation Graph Attention Mechanism
Abstract
1. Introduction
- Multi-relational graph attention mechanism: For the first time, multi-relational graph attention is introduced into house layout generation to capture the complex spatial and functional relationships between room nodes and improve the rationality of room layout.
- Iterated prediction generator: Through multiple iterations, the node features and room relationships are gradually optimized to achieve accurate generation of the layout. It supports iterative modification and dynamic optimization to make up for the shortcomings of traditional methods that cannot adjust the layout.
- Conditional graph discriminator combined with Wasserstein loss: A conditional graph discriminator with Wasserstein loss enforces global consistency in generated layouts, ensuring realistic spatial connectivity and rationality while enhancing training stability and layout diversity.
- Efficient layout generation under weak constraints: The proposed method generates house layouts under partial constraints with flexibility, controllability, and strong adaptability, while enhancing style diversity to provide rich solutions for diverse building types and personalized design needs.
2. Related Work
2.1. Graph Attention Module
2.2. Generators in Different Domains
2.3. Boundary-Aware Graph Convolution Module
2.4. Conditional Graph Discriminator
3. Preparatory Work
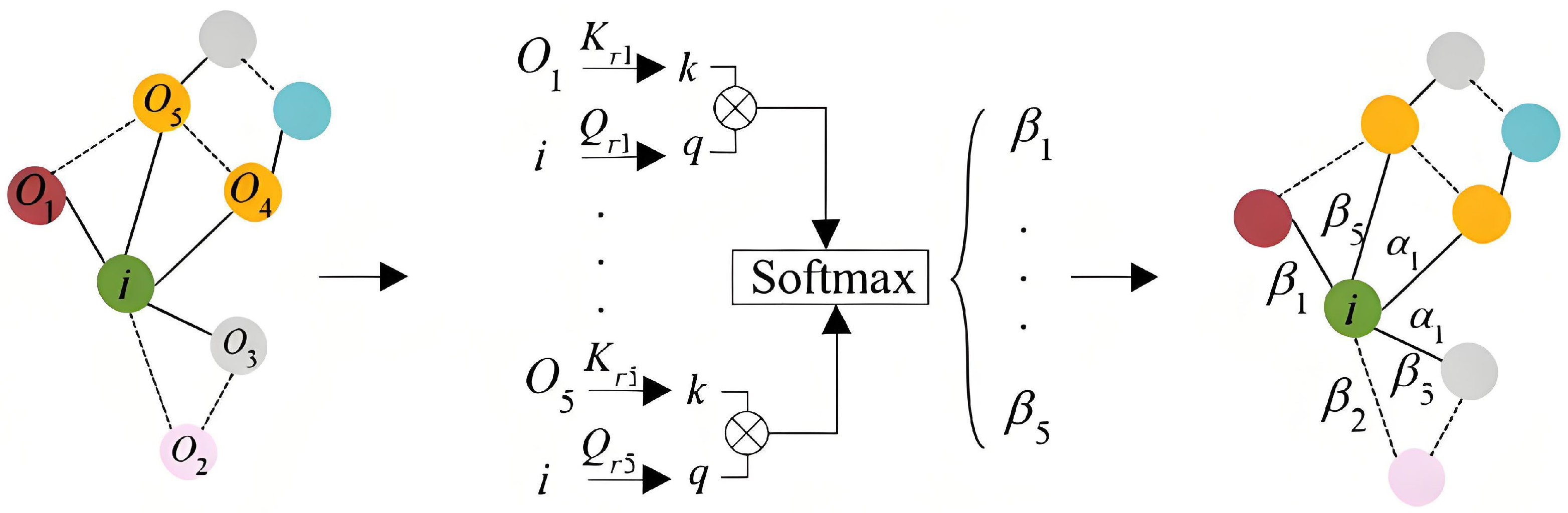
3.1. Captures the Relationship Between Room Nodes
3.2. Iterative Prediction Generator for Complete Room Graph Inference
3.3. Conditional Graph Discriminator with Wasserstein Loss
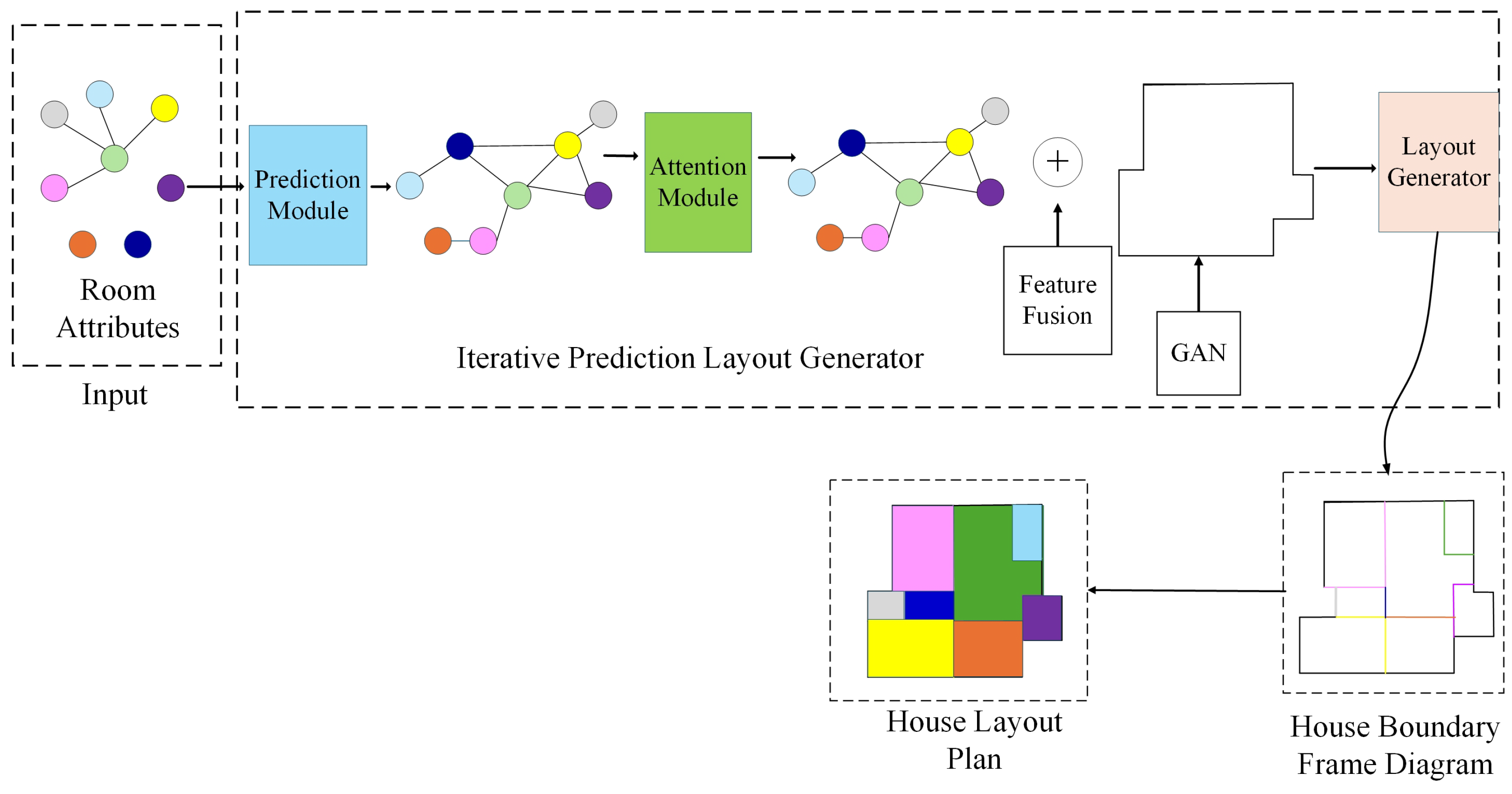
4. Methodology
4.1. Graph-RWGAN Network Framework
4.2. Relationship Prediction Module
4.3. Multi-Relation Graph Attention Module
4.4. Layout Generation Module
4.5. Conditional Graph Discriminator with Wasserstein Loss
4.6. User Input and Weak Constraint Specification
5. Experimental Setup
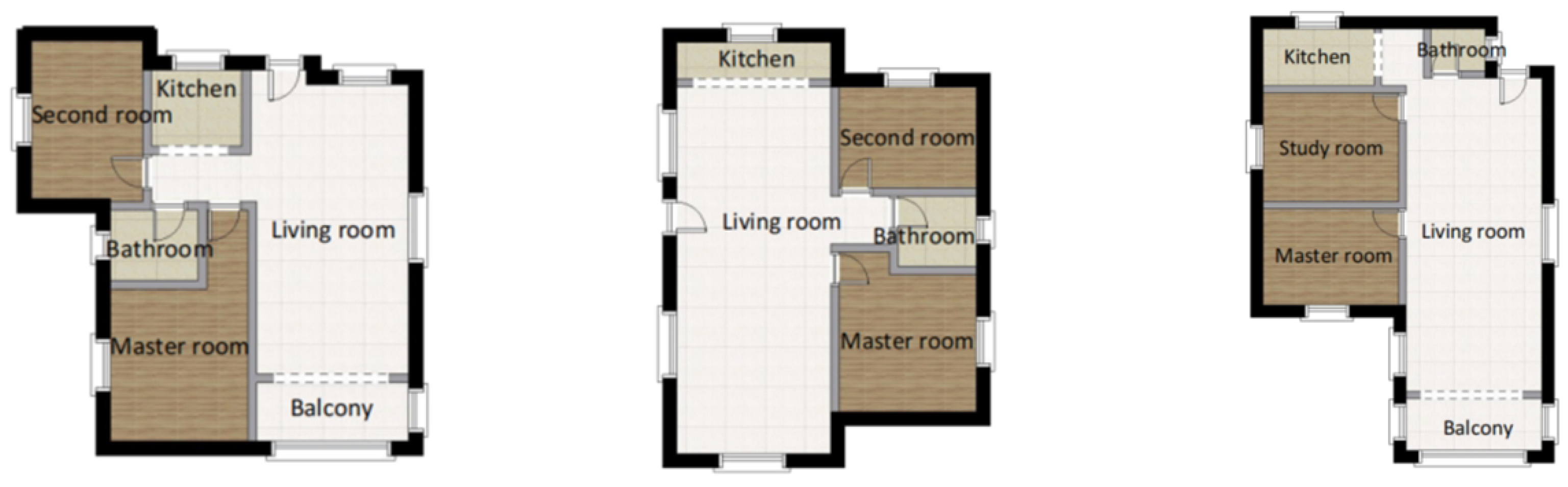
5.1. Dataset Introduction
5.2. Experimental Environment
5.3. Evaluation Indicators
6. Evaluation and Analysis
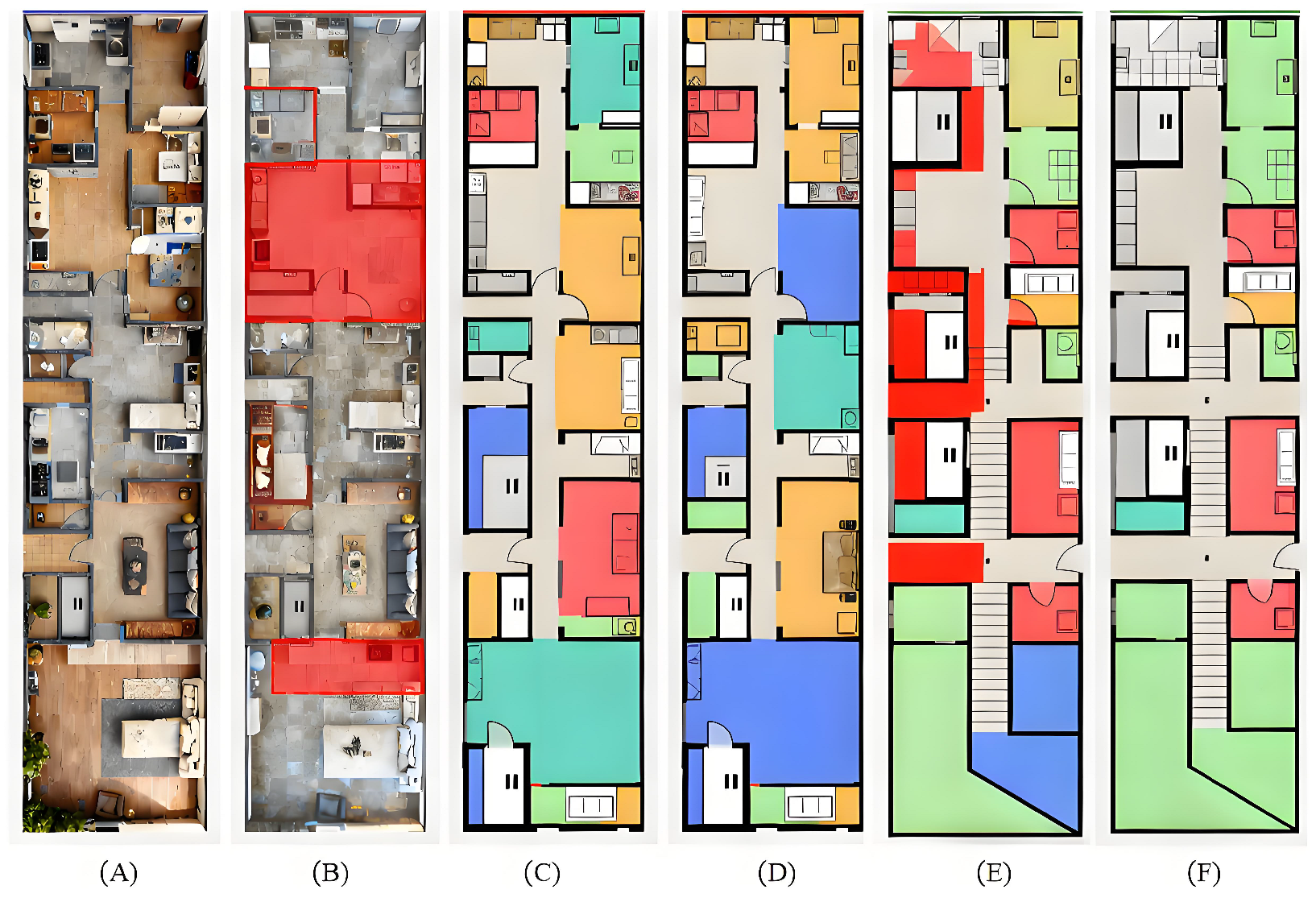
6.1. Preprocessing of Data
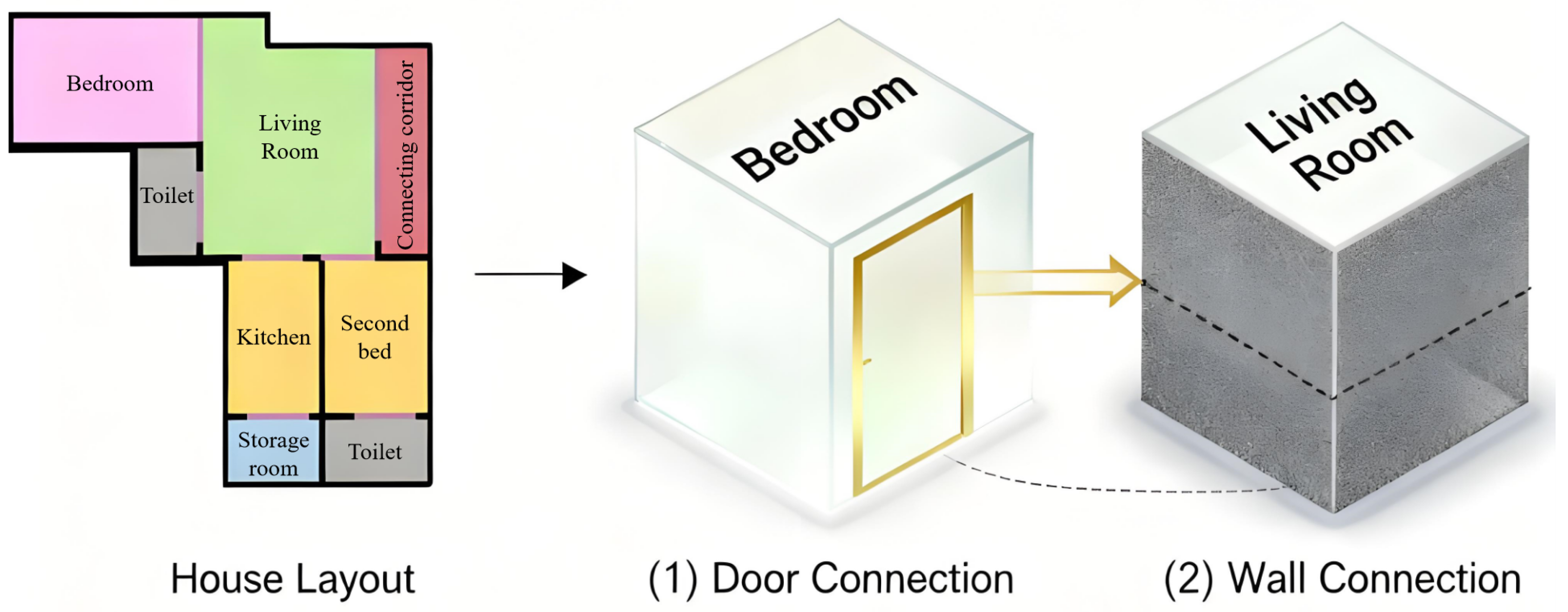
- Door connections: These edges represent rooms that are directly accessible via a door, allowing for movement or functional interaction between the spaces.
- Wall connections: These edges signify rooms that share a common wall, indicating a physical separation that prevents direct spatial flow between them but still establishes a structural connection.
- General connections: This category encompasses both door and wall connections, representing broader neighborhood relationships between rooms that might not necessarily require direct access but still form part of the layout’s overall connectivity.
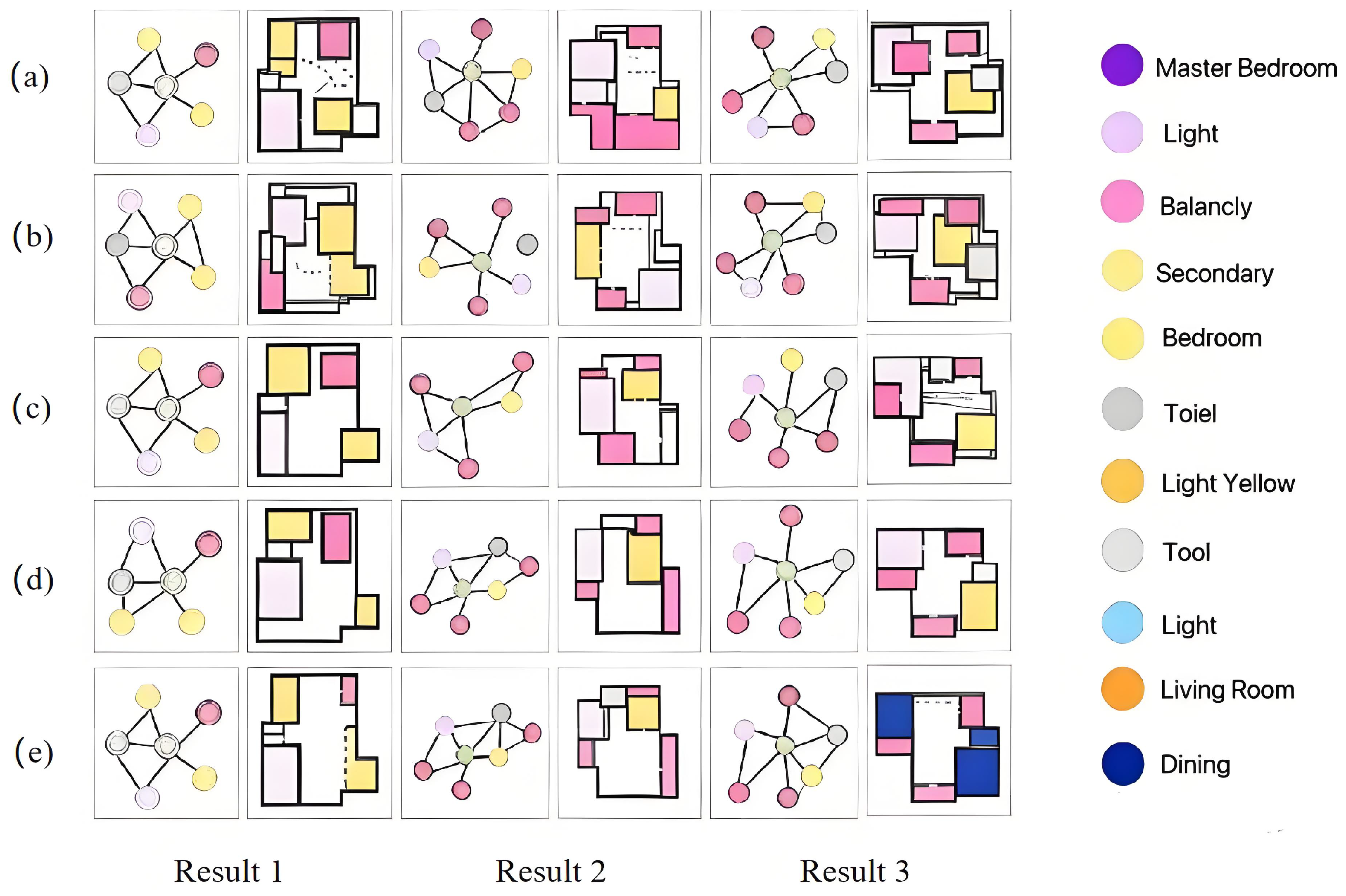
6.2. Experimental Results
6.3. Ablation Study
- Iterative Learning Mechanism: This mechanism allows the model to progressively improve its predictions over time. By disabling this component, we observe a significant decrease in the model’s ability to predict unknown relationships, as reflected in lower accuracy and poorer layout generation quality.
- Relation Prediction Module: This module plays a crucial role in predicting spatial relationships between rooms. Without it, the model’s accuracy decreases, indicating the importance of precise relationship prediction for generating realistic and coherent layouts.
- Multi-Relation Graph Attention Module: This module consolidates information from multiple edge relationship types, improving the model’s capacity to capture intricate spatial dependencies. Its removal results in noticeable performance drops, especially in terms of structural consistency and the accuracy of room topology.
6.4. Runtime and Efficiency Evaluation
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, Y.; Dong, J.; Wang, W.; Duan, H. A multi-typed multi-relational heterogeneous graph neural network model for complex networks. Knowl.-Based Syst. 2025, 329, 114291. [Google Scholar] [CrossRef]
- Ai, W.; Liu, Y.; Wei, C.; Meng, T.; Shao, H.; He, Z.; Li, K. MFLM-GCN: Multi-Relation Fusion and Latent-Relation Mining Graph Convolutional Network for Entity Alignment. Knowl.-Based Syst. 2025, 325, 113974. [Google Scholar] [CrossRef]
- Shakeel, H.M.; Iram, S.; Farid, H.M.A.; Hill, R.; Rehman, H. EPCDescriptor: A Multi-Attribute Visual Network Modeling of Housing Energy Performance. Buildings 2025, 15, 2929. [Google Scholar] [CrossRef]
- Wang, F.; Liu, X.; Li, W.; Tian, W.; Jia, Z.; Ran, C. MRGCE: A Multi-Relational Graph Contrastive Enhancement Learning Framework for High-Value Patent Identification. Scientometrics 2025, 130, 10. [Google Scholar] [CrossRef]
- Li, W.; Gao, Y.; Li, A.; Zhang, X.; Gu, J.; Liu, J. Sparse Subgraph Prediction Based on Adaptive Attention. Appl. Sci. 2023, 13, 8166. [Google Scholar] [CrossRef]
- Zhou, X.; Zeng, Y.; Hao, Z.; Wang, H. A Robust Graph Attention Network with Dynamic Adjusted Graph. Eng. Appl. Artif. Intell. 2024, 129, 107619. [Google Scholar] [CrossRef]
- Yin, H.; Zhong, J.; Wang, C.; Li, R.; Li, X. GS-InGAT: An Interaction Graph Attention Network with Global Semantic for Knowledge Graph Completion. Expert Syst. Appl. 2023, 228, 120380. [Google Scholar] [CrossRef]
- Li, J.; Yang, J.; Zhang, J.; Liu, C.; Wang, C.; Xu, T. Attribute-Conditioned Layout GAN for Automatic Graphic Design. IEEE Trans. Vis. Comput. Graph. 2020, 27, 4039–4048. [Google Scholar] [CrossRef]
- Wang, S.; Zeng, W.; Chen, X.; Ye, Y.; Qiao, Y.; Fu, C.-W. ActFloor-GAN: Activity-Guided Adversarial Networks for Human-Centric Floorplan Design. IEEE Trans. Vis. Comput. Graph. 2021, 29, 1610–1624. [Google Scholar] [CrossRef]
- Zhou, Y.; Xia, H.; Yu, D.; Cheng, J.; Li, J. Outlier detection method based on high-density iteration. Inf. Sci. 2024, 662, 120286. [Google Scholar] [CrossRef]
- Ong, Y.Z.; Zheng, L.; Feng, C.; Song, K. VG-GAN: Conditional GAN Framework for Graphical Design Generation. In Proceedings of the 2022 IEEE International Conference on Image Processing (ICIP), Bordeaux, France, 16–19 October 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 781–785. [Google Scholar]
- Johnson, J.; Gupta, A.; Li, F.-F. Image Generation from Scene Graphs. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1219–1228. [Google Scholar]
- Nauata, N.; Chang, K.H.; Cheng, C.Y.; Mori, G.; Furukawa, Y. House-GAN: Relational Generative Adversarial Networks for Graph-Constrained House Layout Generation. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Part I. Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 162–177. [Google Scholar]
- Yao, S.; Guan, R.; Wu, Z.; Ni, Y.; Huang, Z.; Liu, R.W.; Yue, Y.; Ding, W.; Lim, E.G.; Seo, H.; et al. Waterscenes: A multi-task 4D radar-camera fusion dataset and benchmarks for autonomous driving on water surfaces. IEEE Trans. Intell. Transp. Syst. 2024, 25, 16584–16598. [Google Scholar] [CrossRef]
- Chang, K.H.; Cheng, C.Y.; Luo, J.; Murata, S.; Nourbakhsh, M.; Tsuji, Y. Building-GAN: Graph-Conditioned Architectural Volumetric Design Generation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 11956–11965. [Google Scholar]
- Pan, X.; Song, S.; Chen, Y.; Wang, L.; Huang, G. PLAM: A Plug-in Module for Flexible Graph Attention Learning. Neurocomputing 2022, 480, 76–88. [Google Scholar] [CrossRef]
- Pan, T.; Zhang, L.; Song, Y.; Liu, Y. Hybrid Attention Compression Network With Light Graph Attention Module for Remote Sensing Images. IEEE Geosci. Remote Sens. Lett. 2023, 20, 6005605. [Google Scholar] [CrossRef]
- Feng, Z.; Li, Y.; Chen, W.; Su, X.; Chen, J.; Li, J.; Liu, H.; Li, S. Infrared and Visible Image Fusion Based on Improved Latent Low-Rank and Unsharp Masks. Spectrosc. Spectr. Anal. 2025, 45, 2034–2044. [Google Scholar]
- Wu, Y.; Wang, G.; Wang, Z.; Wang, H.; Li, Y. Triplet Attention Fusion Module: A Concise and Efficient Channel Attention Module for Medical Image Segmentation. Biomed. Signal Process. Control 2023, 82, 104515. [Google Scholar] [CrossRef]
- Carneiro, P.M.R.; Vidal, J.V.; Rolo, P.; Peres, I.; Ferreira, J.A.F.; Kholkin, A.L.; Soares dos Santos, M.P. Instrumented Electromagnetic Generator: Optimized Performance by Automatic Self-Adaptation of the Generator Structure. Mech. Syst. Signal Process. 2022, 171, 108898. [Google Scholar] [CrossRef]
- Du, J.; Li, B.; Yang, J. Boundary-aware Graph Convolutional Network for Building Roof Detection from High-Resolution Remote Sensed Imagery. PFG J. Photogramm. Remote Sens. Geoinf. Sci. 2025, 93, 443–455. [Google Scholar] [CrossRef]
- Li, Q.; Sun, X.; Dong, J. Transductive zero-shot learning via knowledge graph and graph convolutional networks. Sci. Rep. 2025, 15, 28708. [Google Scholar] [CrossRef]
- Liu, H.; Li, D.; Zeng, B.; Xu, Y. Learning discriminative features for multi-hop knowledge graph reasoning. Appl. Intell. 2025, 55, 468. [Google Scholar] [CrossRef]
- Wen, X.; Yang, X.-H.; Ma, G.-F. ConDiff: Conditional graph diffusion model for recommendation. Inf. Process. Manag. 2026, 63, 104303. [Google Scholar] [CrossRef]
- Hu, R.; Huang, Z.; Tang, Y.; van Kaick, O.; Zhang, H.; Huang, H. Graph2Plan: Learning Floorplan Generation from Layout Graphs. arXiv 2020, arXiv:2004.13204. [Google Scholar] [CrossRef]
- Wang, Z.; Fang, X.; Zhang, W.; Ding, X.; Wang, L.; Chen, C. Multi-relation spatiotemporal graph residual network model with multi-level feature attention: A novel approach for landslide displacement prediction. J. Rock Mech. Geotech. Eng. 2025, 17, 4211–4226. [Google Scholar] [CrossRef]
- Nauata, N.; Hosseini, S.; Chang, K.-H.; Chu, H.; Cheng, C.-Y.; Furukawa, Y. House-GAN++: Generative Adversarial Layout Refinement Networks. arXiv 2021, arXiv:2103.02574. [Google Scholar]
- Wu, W.; Fu, X.-M.; Tang, R.; Wang, Y.; Qi, Y.-H.; Liu, L. Data-driven interior plan generation for residential buildings. ACM Trans. Graph. 2019, 38, 1–12. [Google Scholar] [CrossRef]
- Nauata, N.; Chang, K.-H.; Cheng, C.-Y.; Mori, G.; Furukawa, Y. House-GAN: Relational generative adversarial networks for graph-constrained house layout generation. arXiv 2020, arXiv:2003.06988. [Google Scholar]
- Li, J.; Yang, J.; Hertzmann, A.; Zhang, J.; Xu, T. LayoutGAN: Generating graphic layouts with wireframe discriminators. arXiv 2019, arXiv:1901.06767. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, Y.; Zhang, Y.; Wang, S.; Liu, H. Multi-relational graph attention networks for knowledge graph completion. Knowl.-Based Syst. 2022, 251, 109262. [Google Scholar] [CrossRef]
- Zhang, J.; Guo, J.; Sun, S.; Lou, J.-G.; Zhang, D. LayoutDiffusion: Improving Graphic Layout Generation by Discrete Diffusion Probabilistic Models. arXiv 2023, arXiv:2303.11589. [Google Scholar] [CrossRef]
- Tang, H.; Zhang, Z.; Shi, H.; Li, B.; Shao, L.; Sebe, N.; Timofte, R.; Van Gool, L. Graph Transformer GANs for Graph-Constrained House Generation. arXiv 2023, arXiv:2303.08225. [Google Scholar] [CrossRef]
| Model | FID ↓ | SSIM ↑ | Acc (%) ↑ | IS ↑ | Room Adjacency Score ↑ |
|---|---|---|---|---|---|
| House-GAN [29] | 109.27 | 0.784 | 81.34 | 2.85 | 0.71 |
| LayoutGAN [30] | 175.36 | 0.525 | 68.22 | 2.12 | 0.60 |
| MR-GAT [31] | 94.69 | 0.813 | 82.37 | 3.05 | 0.74 |
| Graph-RWGAN | 92.73 | 0.828 | 85.96 | 3.12 | 0.78 |
| Model | Room Topology Accuracy (%) | Layout Quality (%) | Structural Coherence (%) |
|---|---|---|---|
| House-GAN | 60% | 70% | 65% |
| LayoutGAN | 45% | 50% | 55% |
| MR-GAT | 75% | 85% | 80% |
| Graph-RWGAN | 95% | 90% | 95% |
| Method | IoU (%) | Position Error | Structural Consistency | Visual Realism |
|---|---|---|---|---|
| MA-GAN | 62.3 | 15.8 | 0.68 | 0.72 |
| MR-GAT | 68.5 | 12.5 | 0.75 | 0.78 |
| House-GAN | 71.2 | 10.3 | 0.80 | 0.82 |
| LayoutDiffusion | 83.0 | 6.0 | 0.90 | 0.96 |
| Our Method | 85.6 | 5.2 | 0.92 | 0.95 |
| Model Variant | FID ↓ | SSIM ↑ | Acc ↑ |
|---|---|---|---|
| w/o Iterative Learning | 112.87 | 0.729 | 74.17 |
| w/o Relation Prediction Module | 98.49 | 0.752 | 72.67 |
| w/o Multi-Relation Graph Attention | 109.15 | 0.693 | 69.29 |
| Ours (Graph-RWGAN) | 92.73 | 0.828 | 85.96 |
| Model | Generation Time (s) | Memory Consumption (GB) | Inference Time (s) | Time for 1000 Layouts (min) |
|---|---|---|---|---|
| Graph-RWGAN | 1.2 | 2.1 | 0.8 | 20 |
| MA-GAN | 1.8 | 2.3 | 1.0 | 25 |
| MR-GAT | 2.0 | 2.5 | 1.2 | 28 |
| House-GAN | 2.4 | 3.5 | 1.6 | 30 |
| LayoutGAN | 3.1 | 4.2 | 2.0 | 40 |
| LayoutDiffusion | 1.5 | 2.0 | 0.9 | 22 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, Z.; Liu, S.; Tian, Z.; Chen, Y.; Zheng, L.; Chen, J. Graph-RWGAN: A Method for Generating House Layouts Based on Multi-Relation Graph Attention Mechanism. Buildings 2025, 15, 3623. https://doi.org/10.3390/buildings15193623
Ye Z, Liu S, Tian Z, Chen Y, Zheng L, Chen J. Graph-RWGAN: A Method for Generating House Layouts Based on Multi-Relation Graph Attention Mechanism. Buildings. 2025; 15(19):3623. https://doi.org/10.3390/buildings15193623
Chicago/Turabian StyleYe, Ziqi, Sirui Liu, Zhen Tian, Yile Chen, Liang Zheng, and Junming Chen. 2025. "Graph-RWGAN: A Method for Generating House Layouts Based on Multi-Relation Graph Attention Mechanism" Buildings 15, no. 19: 3623. https://doi.org/10.3390/buildings15193623
APA StyleYe, Z., Liu, S., Tian, Z., Chen, Y., Zheng, L., & Chen, J. (2025). Graph-RWGAN: A Method for Generating House Layouts Based on Multi-Relation Graph Attention Mechanism. Buildings, 15(19), 3623. https://doi.org/10.3390/buildings15193623










