Numerical Investigation of Modified Punching Shear Behavior in Precast Prestressed Hollow Core Slabs Under Concentrated Loads

Abstract

Precast prestressed hollow-core slabs (HCSs), primarily designed for uniformly distributed loads, frequently encounter concentrated loads, causing complex stress states. Load distribution occurs through longitudinal joints; however, the hollow cross-section and absence of transverse reinforcement increase susceptibility to shear, including punching. Existing guidelines offer limited guidance, often conflicting with experimental results. While limited previous studies have examined concentrated load effects on various HCS types, research on the Spancrete system—distinguished by unique core geometries—is lacking. This study presents a detailed numerical investigation of modified punching shear behavior in Spancrete HCS floors using a 3D finite element (FE) model developed in ABAQUS. The model, comprising three interconnected HCS units, was validated against experimental data from single-unit and full-scale floor tests exhibiting modified punching shear failure. Results show that modified punching shear in HCSs is driven initially by localized stress distribution in the top flange along one direction and secondarily by compression stresses in the loaded region, unlike the symmetric failure in solid slabs. While variations in loading area affected post-peak response, shifting the load closer to the longitudinal joints led to earlier joint debonding, reducing ultimate capacity. These insights challenge the adequacy of current design guidance and emphasize the necessity of refined HCS provisions.

1. Introduction

Precast, prestressed, Hollow Core Slabs (HCSs) have become a popular choice for floor and roof systems in many modern multi-story buildings due to their durability, resilience, economy, and ease of placement. The design of HCSs includes continuous voids, separated by thin webs, running longitudinally through the slabs, effectively reducing the weight of the structure without compromising its strength compared to solid concrete slabs. There are three basic geometries commonly used for HCSs with (1) the oldest one featuring circular cores, (2) another one featuring closely spaced openings with an oval shape that is topped by a peaked crown (such as the Spancrete system), and (3) a newer system featuring wider, rectangular shaped cores with radiused corners (such as the Elematic system). While most common in the US, the Spancrete system has also been introduced to other countries through Spancrete Global Services. Being prefabricated off-site, they can be quickly and efficiently installed on-site, significantly reducing construction time and labor costs. HCS units are integrated with longitudinal prestressing strands which effectively delay cracking. As a result, service loads are primarily supported by uncracked concrete [1].

HCS floors are typically designed as an assembly of single, one-way, simply supported units primarily intended to resist uniformly distributed loads. The floor system is constructed by connecting adjacent units through cast-in-place concrete longitudinal joints at the keyways, facilitating force transfer between slabs. However, in many applications, individual units are also subjected to concentrated and line loads. In such cases, non-uniform loads applied to a single unit are transversely distributed to surrounding units via shear keys, which function as hinges, redistributing a portion of the applied load and reducing the demand on the directly loaded element.

The manufacturing process of HCS restricts the inclusion of shear or other transverse reinforcement, limiting their structural response to rely exclusively on the tensile strength of the concrete. Due to concrete’s inherently low tensile capacity and its complex behavior under concentrated loading, which induces transverse bending moments and localized shear forces, HCS systems appear to be susceptible to punching shear failure, as they are not explicitly configured to resist such effects.

Although extensive research has addressed individual HCS units [2,3,4,5,6,7,8,9,10,11,12,13,14], only a small amount of work has been conducted on full-scale HCS floor assemblies, where the effects of load distribution could be examined [15,16,17,18,19,20,21,22,23,24,25]. Tests on 400 mm (16 in.) deep HC floors under concentrated loads at Technical Research Centre of Finland (VTT) [18,19] revealed brittle modified form of punching failures, characterized by longitudinal cracks on both top and bottom surfaces, with failure occurring under different loading positions. Aswad and Jacques [22] examined 200 mm (8 in.) deep single and double-unit assemblies, finding that slabs loaded at midspan, and one-third of the span failed in modified punching, while those loaded closer to supports exhibited a combined shear–torsion failure. Pajari [24] investigated a 400 mm (16 in.) deep HC floor with pre-cracked longitudinal joints, where tests under varying transverse load positions showed that while a single point load led to modified punching failure, load redistribution using a spreader beam resulted in shear–torsion failure, significantly increasing load capacity. Lucio and Castilho [25] studied the local failure of single HC slabs, noting that slabs without filled cores initially developed longitudinal cracks before experiencing brittle shear failure, whereas edge-loaded slabs failed without longitudinal cracking. Their findings demonstrated that filling the cores improved modified punching resistance by approximately 30% under different loading conditions.

While the above-mentioned studies have examined the overall failure mechanisms of HCSs subjected to concentrated loads, a dedicated focus on their punching shear behavior remains lacking. As a consequence of the resulting gap in the knowledge base, the PCI design manual [26] does not provide specific guidance for evaluating punching shear capacity. Moreover, according to EN 1168 [27], the applied concentrated load must not exceed a calculated punching load, which is based on the effective width of the webs, slab height, and concrete properties. However, analysis of experimental tests on HCS floors performed by Jeziorski and Derkowski [28] suggest that the actual modified punching capacity is significantly higher than current code estimates. Their findings indicate that defining the control perimeter using a stress dispersion angle of 35°, rather than the conventional 45°, offers a more accurate representation of the failure mechanism. Using numerical analyses, Broo [29] examined torsion and shear–torsion interaction in HCS and showed that presence of adjacent slabs enhances the ultimate capacity of the directly loaded unit. These discrepancies highlight the constraints of existing design provisions, which are compounded by the shortage of well-documented experimental data and the relatively small number of numerical studies [29,30,31] addressing modified punching shear in full-scale HCS floor systems under point loads. Therefore, this topic remains insufficiently explored, and this failure in hollow-core slabs is still not fully understood, particularly because it differs significantly from conventional punching shear observed in solid slabs. This underscores the need for more detailed and targeted finite element (FE) analyses to better predict the structural response and ensure safe design under concentrated loading conditions.

While most existing studies focus on HCSs with circular or rectangular voids, research on Spancrete units is lacking. Due to their unique core geometry, which modifies stress flow and crack development under concentrated loading, they may exhibit a potentially distinct failure response. For this purpose, this study investigates the structural response of Spancrete hollow-core slabs using a detailed numerical approach, based on a 3D non-linear FE model developed in ABAQUS [32] for formulating a conceptual framework of the modified punching shear phenomenon in HCSs. The modeling approach also considers more realistic construction scenarios, such as the absence of joint reinforcement and the use of high-strength grout, both of which are common in modern precast floor systems in the US. In addition, the present study explores the effect of loading area size and load location, providing further insights into the structural response and failure characteristics of these slabs.

2. Numerical Simulations

A numerical approach using the software ABAQUS/Explicit 2024 was formulated to simulate the prestressed precast hollow-core concrete slabs for FE analysis. In the following, it is described in relation to the Spancrete hollow-core sections. However, the same modeling approach was applied to sections with circular and rectangular cores (e.g., Elematic) used for numerical validation, notwithstanding changes in the HCS sections. The next section describes the experimental verification of the FE approach used here. The principal difference in the analysis of the three types of HCS section is the mesh which has distinct geometric features for each. In the experimental studies considered, different prestressing strand layouts and support conditions were also used.

2.1. Geometry and Mesh Considerations

The FE mesh was developed based on the dimensions of each HCS section, with Figure 1 illustrating the Spancrete section used in this study. Individual slabs were connected via cast-in-place concrete longitudinal joints, functioning as shear keys, to form the complete floor system. The longitudinal joint consists of a narrow keyway located between adjacent units. During assembly, this keyway is filled with grout to interlock the units and enable shear transfer across the floor system.

The concrete in the HCS units and longitudinal joints were modelled using 8-node solid brick elements with reduced integration (C3D8R). The 8-node solid brick elements can introduce shear locking during the bending of thin members, leading to a stiffer response. To mitigate this issue, reduced integration was applied, in which the number of integration points were reduced from eight to one. However, the use of a single integration point introduces kinematic modes, and this challenge was addressed using the hourglass control technique. Mesh sensitivity analysis was used to determine the dimensions of the elements, with Figure 2 showing the mesh for the Spancrete section.

The prestressing strands were represented by two-node linear 3D truss elements (T3D2). Perfect bond between strands and concrete was assumed through embedding. The transfer length was assumed to be 50 times the strand diameter (d_b), as suggested by the ACI Code [33]. To accurately model the transfer length, the strands in the end regions were subdivided into five longitudinal segments, with the cross-sectional area gradually increasing from strand tip along the transfer length.

2.2. Boundary Conditions and Load Application

Due to floor symmetry with respect to the mid-span, only one-half of the HCS was modeled. Symmetry boundary conditions were applied along the longitudinal direction (z-axis) on the mid-span surface. The end of the slabs was constrained against vertical and transversal displacement (y and x-axes) along a line spanning the entire width at the support area. The details of elements type and boundary conditions are depicted in Figure 3.

A multi-step dynamic explicit analysis was performed. The initial loading step was designed to simulate the transfer of prestressing forces from the strands to the surrounding concrete, effectively representing the process of strand release and the resulting camber along the slab length. The prestressing forces were introduced by defining a negative temperature to the 3D truss elements representing the strands through the “predefined field” option available in ABAQUS. The second step accounted for the self-weight of the floor system. In the final step, a concentrated load was applied to represent the assumed external loads or experimental loading protocol. In this study, a smooth step amplitude was used to apply load gradually, minimizing inertial effects and ensuring stable results to achieve quasi-static solutions. To further verify quasi-static behavior, the ratio of kinetic energy to internal energy was monitored throughout all simulations and remained consistently below 0.5%. This is well under the commonly accepted 5% threshold, confirming that inertial effects did not influence the results.

2.3. Material Properties

2.3.1. Concrete

The Concrete Damage Plasticity (CDP) model was employed to simulate the concrete behavior of both the slab and the cast-in-place shear keys. The CDP model in ABAQUS relies on the yield function models proposed by Lubliner et al. [34], with the modifications suggested by Lee and Fenves [35], incorporating concepts from both plasticity and damage mechanics. This model assumes a non-associated plastic flow based on the Drucker-Prager hyperbolic function.

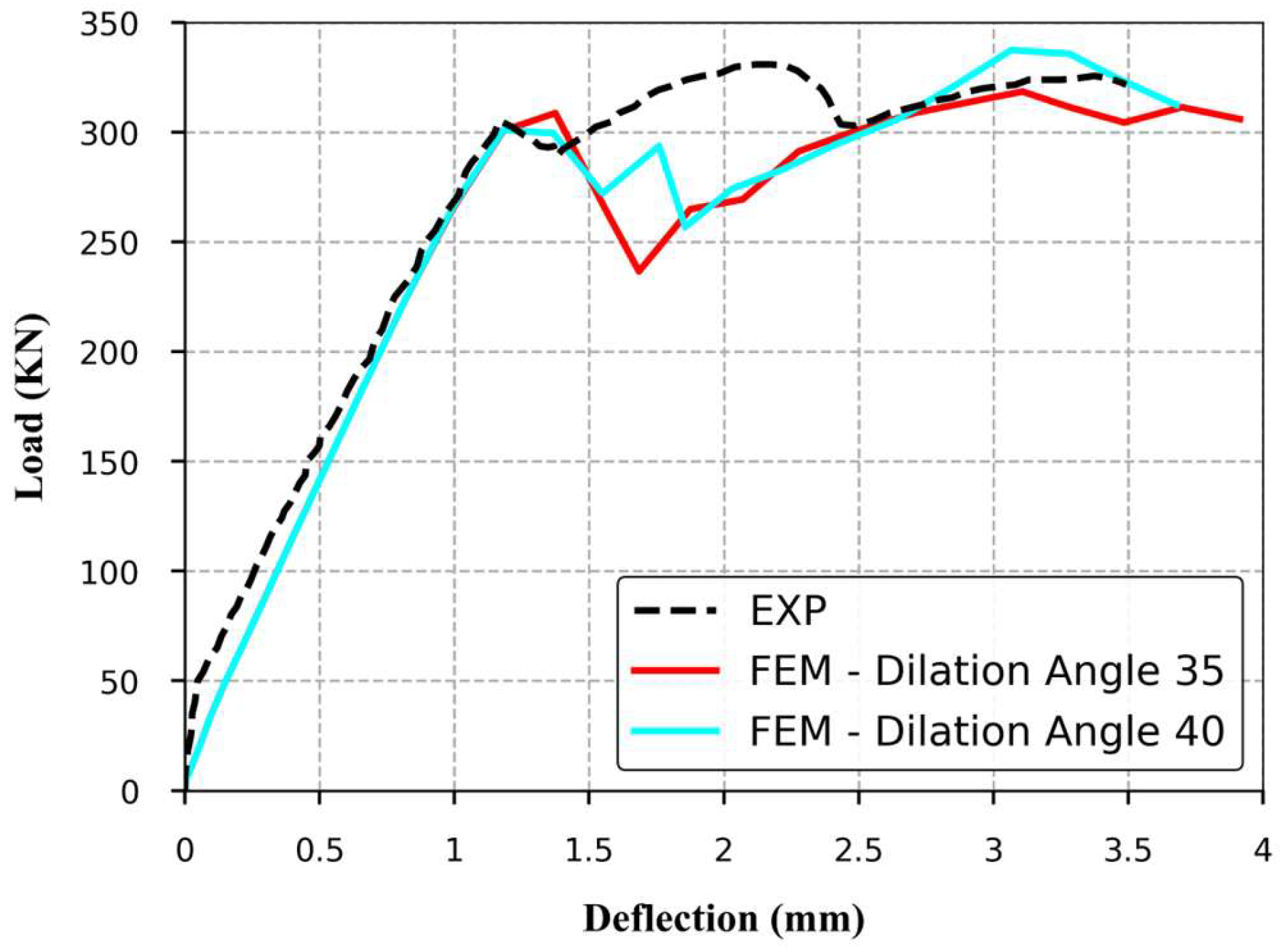
To fully define the plastic behavior of concrete within this model, five parameters, are needed: $\psi$, ε, σ_b0/σ_c0, K_c, and μ. In addition, the uniaxial stress–strain relationship of the concrete must be specified. The dilation angle ($\psi$), which is a term defining inelastic volumetric change in granular materials, can be interpreted as an internal friction angle. A dilation angle between 30° and 40° is typically recommended for normal-strength reinforced concrete [36]. However, various studies have applied a wider range of values depending on specific modeling needs [37,38,39,40]. In this study, a broader range from 25° to 40° was initially considered, and sensitivity analysis was performed. The maximum load varied slightly, with less than 6% difference across the range and about 1% between 35° and 40°. This confirms that the model response was not highly sensitive to the dilation angle. A value of 35° was selected, accounting for the self-confinement effect within the HCS floor system due to the placement of adjacent units.

The eccentricity parameter (ε) affects the yield surface’s curvature within the deviatoric stress space. Following ABAQUS recommendations, a value of 0.1 was adopted for ε in this study, suggesting that the material exhibits nearly constant dilation across a broad range of confining pressures. The ratio σ_b0/σ_c0, which reflects the relationship between initial equibiaxial and uniaxial compressive yield stresses, was set to the default value of 1.16, as recommended by Lubliner et al. [34]. The parameter $K_c$ represents the ratio of the second stress invariant on the tensile meridian to that on the compressive meridian at initial yield, was set to the default value of 2/3. The viscosity parameter (μ) was set to zero to avoid introducing artificial viscosity. These values have been widely adopted in previous studies of prestressed concrete, including HCS systems, and have been shown to have no significant influence on the overall behavior [37,38,39,40,41,42].

Table 1. Summary of the parameters of the CDP model.

Parameter	Value
Dilation angle ($\psi$)	25–40°
Eccentricity (ε)	0.1
σb0/σc0	1.16
Kc	0.667
Viscosity parameter (μ)	0

summarizes the CDP model parameters used in this analysis.

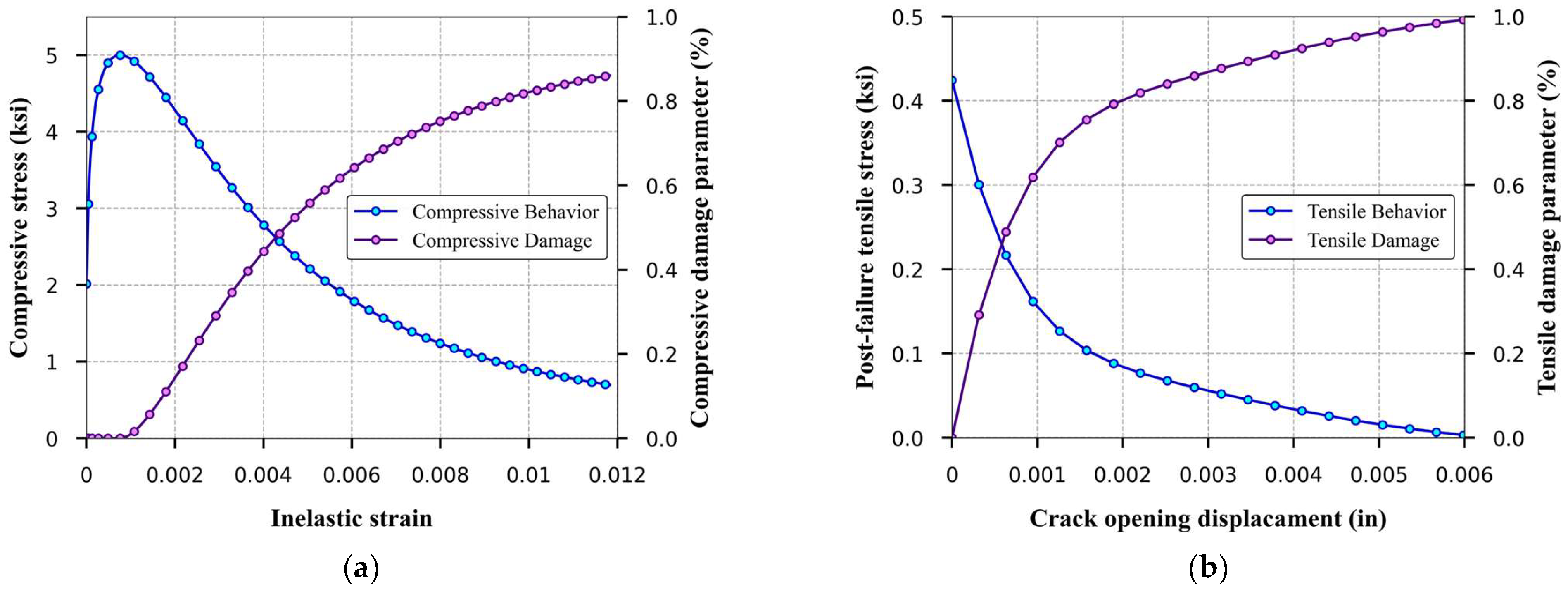
The CDP model represents the compressive behavior of concrete under uniaxial loading as initially linear until the material reaches its yield point. Beyond this point, the model captures stress hardening up to the ultimate stress, followed by strain softening as the material begins to fail. The uniaxial stress–strain behavior for concrete under compression was determined in accordance with the model proposed by Mander et al. [43]. Figure 4a exhibits the uniaxial stress–inelastic strain curve in compression, along with the corresponding compressive damage evolution.

The response of the CDP model under uniaxial tensile loading is characterized by an initial linear–elastic stress–strain relationship until the peak stress is reached, at which micro–cracks begin to form within the concrete matrix and merge into larger, macro-cracks. As they continue to open, the model captures this transition through a softening stress–strain relationship. This softening behavior reflects the tensile cracking process of concrete and is typically represented by a “tension stiffening” mechanism, which can be defined using either a post-failure stress–strain relationship or a fracture energy cracking criterion. In this study, the tension softening model by Reinhardt et al. [44], which describes the tensile stress vs. cracking displacement behavior, was used. Figure 4b shows the uniaxial tensile stress-crack opening displacement curve used as input in ABAQUS, as well as the relationship between the damage variable and displacement in tension. The interaction between cracked concrete and reinforcement, known as “bond-slip”, was indirectly considered through the ‘tension stiffening’ effect for concrete under tension.

2.3.2. Prestressing Steel Strand

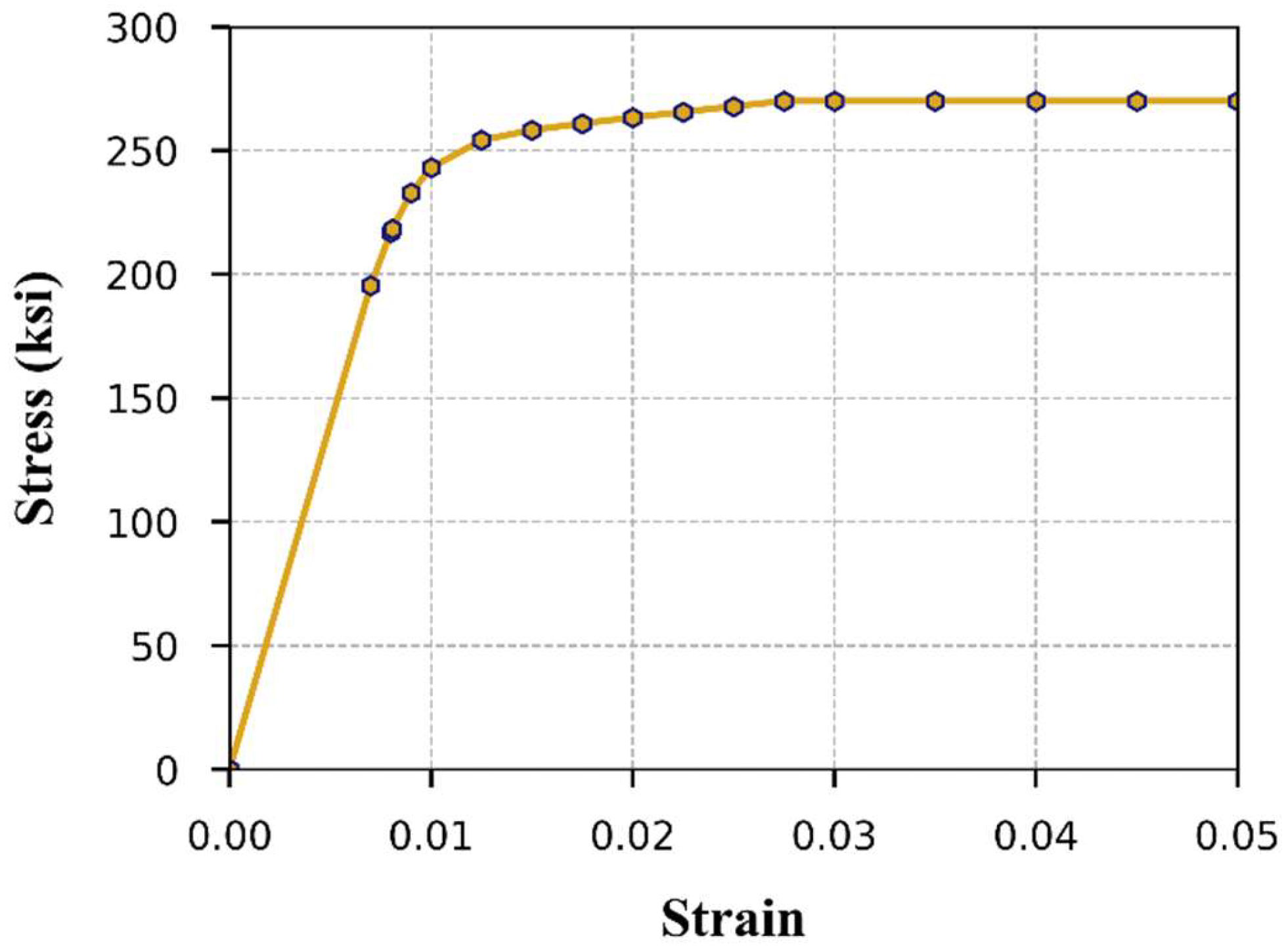
The model incorporated 7-wire low relaxation strands with an ultimate tensile strength of 1860 MPa (270 ksi). The density of steel used for prestressing strands was equal to 7850 kg/m³ (490 pcf). The elastic modulus for the strands was set to 196.5 GPa (28,500 ksi), with a Poisson’s ratio of 0.3 applied in the modeling process. To capture the steel material behavior of the strands, a non-linear elastoplastic model was employed. This model follows the stress–strain relationship proposed by Devalapura and Tadros [45], which refines the power formula originally developed by Skogman et al. [46]. According to ASTM A-416 [47], the minimum yield stress f_py at 1 percent strain for this type of strand should be equal to 0.9 times the ultimate tensile strength f_pu. Figure 5 shows the obtained stress–strain response of the prestressing strands chosen for this study.

2.4. Interactions Between Contact Surfaces

The FE model of the precast prestressed HCS floor system was composed of three HCS units with cast-in-place concrete acting as shear keys between them. This configuration created four contact surfaces between the slabs and the longitudinal joints, which were subject to both normal and shear stresses, leading to a mixed-mode response. To accurately capture this behavior, a surface-based contact cohesive behavior was implemented at the interface between the precast and in situ concrete, allowing for mixed-mode debonding through the application of a traction-separation law.

The failure mechanism consists of two components: a damage initiation criterion and a damage evolution law. Prior to damage, cohesive behavior follows a linear traction-separation law. As the bond stiffness progressively degrades, bond failure arises. Damage initiation marks the onset of degradation in the cohesive response at the contact interface. Following damage initiation, the cohesive stiffness undergoes gradual degradation, described by the damage evolution process. This process can be specified using either the total fracture energy or the post-damage initiation effective separation at failure. The scalar damage variable D represents the overall damage at the contact point, evolving from 0 to 1 as loading progresses. This evolution was modeled using a linear softening law based on effective separation. Bond failure in ABAQUS can be tracked using two output variables: the maximum contact stress damage initiation criterion (CSMAXSCRT) and the damage variable for cohesive surfaces (CSDMG). Damage initiation is considered to occur when the first variable reaches a value of 1, and full debonding is assumed to take place when the second variable also reaches unity.

Barbieri et al. [48] mentioned that all three stiffness components typically range from 5.0 MPa/mm (18.4 ksi/in.) to 15.0 MPa/mm (55.3 ksi/in.), with the ratio of displacement at complete damage (D = 1) to displacement at damage initiation (D = 0) $({\delta }^f/{\delta }^0)$ ranging from 1.5 (indicating brittle fracture) to 3.0 (indicating extended rupture) for all three directions. Hu et al. [49] simulated hinge joints to transfer shear stress between HCSs, finding a tangential shear stress stiffness of 10 MPa/mm (36.8 ksi/in.) for undamaged joints through a trial-and-error process to match the predictions of the hinge-joint plate method and minimize the difference in the lateral load distribution coefficients. Based on the information, contact interaction stiffness values in all three directions were assumed to be 10 MPa/mm (36.8 ksi/in).

Based on laboratory tests, Ye et al. [50] proposed a formula for calculating the shear strength of concrete hinge joints with a smooth interface in HCSs, with a 95% assurance rate: $f_v^0=0.017f_c^0$. Additionally, the normal strength of the interface can be expressed as $f_n=c{f}_{ct}$, where the cohesion coefficient c is assumed to be 0.7. Here, $f_c^0$ and $f_{ct}$ represent the minimum compressive and tensile strengths of the concrete between the HCSs and joints, respectively. However, according to EN 1992-1-1 [51], c ranges from 0.025 to 0.1 for very smooth interfaces and up to 0.2 for smooth surfaces typical of precast concrete elements, although 0.5 can be obtained on machine finished HCSs [52]. A sensitivity analysis was conducted using varying the cohesion coefficient and comparing the results against experimental data. The results demonstrated that different values of c had a negligible impact on the load–deflection behavior, with minimal variation observed in the maximum deflection, so a value of 0.7 was used recognizing Ye’s laboratory test results.

Finally, the PCI HCS manual [26] recommends a shear capacity of 0.55 MPa (80 psi) for grouted keyways between HCS units to transfer longitudinal shear from one slab to the next. Consequently, maximum normal and shear stresses were assumed to be 2.05 MPa (296.8 psi) and 0.55 MPa (80 psi), respectively, with a ${\delta }^f/{\delta }^0$ value of 2 for all three components in the traction-separation law.

3. Experimental Validation

Given the lack of experimental data on Spancrete systems, the proposed FE models were validated against two experimental studies using other HCS sections in which modified version of punching shear failure was observed. The responses of the HCS test specimens were compared with computational results that were reproduced using the FE modelling approach described in the preceding. The first study, by McGinnis et al. [14], utilized single HCS unit with circular cores. The second study, by Pajari [24], tested a floor system made of Elematic HCS slabs. The latter is one of the limited available full-scale floor tests that exhibited modified punching shear failure.

3.1. McGinnis et al. [14]

Experimental tests conducted by McGinnis et al. [14] were considered as they provided valuable insight into the performance of an isolated HCSs under load. The test focused on the flexural and punching shear behavior of a HCS specimen, designated as NDS3. The geometric cross-section and load application for this specimen are shown in Figure 6. The slab had an overall length of 4.57 m (15 ft) and incorporated five 7-wire, low-relaxation prestressing strands, each with a nominal diameter of 9.5 mm (0.375 in.) and a cross-sectional area of 55 mm² (0.085 in²). The strands were initially prestressed to 0.7f_pu, corresponding to a jacking stress of 1300 MPa (189 ksi). The concrete used had a measured cylindrical compressive strength of 50.6 MPa (7.34 ksi), and a Poisson’s ratio of 0.2 was adopted for modeling purposes. Relevant material properties derived from this strength are summarized in

Table 2. Concrete properties derived from experimental program by McGinnis et al. [14].

Parameter	Value
Cylindrical compressive strength [MPa] (ksi)	50.60 (7.34)
Tensile strength [MPa] (ksi)	3.62 (0.52)
Young’s modulus [GPa] (ksi)	35.65 (5170.60)
Poisson ratio	0.2

. The element size was set to 25 mm (1 in.) for both solid and linear elements.

Regarding the testing procedure in McGinnis’s study, the slabs were first subjected to 90-day sustained service loading and then sequentially tested in flexure, shear, and punching shear. Following flexural failure, each slab was repositioned for shear testing on the intact portion, and subsequently for punching on the remaining part. The flexural bending test was conducted over the full slab length, with end supports and two line loads applied symmetrically about the midspan to create a four-point loading condition. For the punching shear test, the slab length was 2134 mm (7 ft), and a concentrated load was applied at midspan on one of the HCS webs, as illustrated in Figure 6.

The models were validated by comparing the load–deflection curves obtained from both the experimental data and the finite element simulations. As shown in Figure 7a, which represents flexural behavior, the FE models accurately capture the structural stiffness within the elastic range up to the cracking point. While some deviation is observed in the post-cracking region, the predicted peak loads closely match the experimental results, with only 3% discrepancy, as summarized in

Table 3. Comparison of maximum capacity obtained from numerical models and McGinnis tests results.

Model	P_EXP [kN] (kips)	P_FEM [kN] (kips)	P_FEM/P_EXP
Flexural loading	63.11 (14.20)	65.31 (14.68)	1.03
Punching shear loading	93.70 (21.06)	97.41 (21.90)	1.04

. Moreover, the experiments were stopped prior to complete failure to maintain the integrity of the specimens for subsequent shear and punching shear tests, whereas the FE model was carried to larger deflections until ultimate failure. Since the McGinnis study did not provide a load-deflection curve to represent modified punching shear case, only the ultimate capacity was reported and is represented in Figure 7b as a reference (blue) line. The numerical model developed in this study slightly overestimates the modified punching shear capacity but remains in close agreement with the experimental result, supporting the accuracy of the modeling approach.

3.2. Pajari [24]

The behavior of a complete floor system composed of multiple interconnected units was investigated using a full-scale experimental test conducted by Pajari [24]. The layout and load configuration of this test setup are presented in Figure 8. The test floor comprised four 400 mm (16 in.)-thick HCS units, each spanning 7 m (23 ft), joined together with the grout and supported by reinforced concrete beams, as illustrated in Figure 9a. A mortar layer was placed between the slabs and the support beams, and a tie beam was cast over the supports, as detailed in Figure 9b. In the FE model, this setup was modeled by restraining the rotational degrees of freedom in the support region to replicate the stiffness provided by the tie beam. L-shaped reinforcement bars were embedded in each joint and to simulate shrinkage-induced cracking, the joints were pre-cracked prior to testing. In the Abaqus model, joint cracking was simulated by assigning zero normal stiffness to specific interfaces between the joints and the slabs. The floor was tested to failure under three different loading configurations. However, only the test involving a single-point load is discussed here, as it is most relevant to the objectives of this study.

The compressive strength of the concrete was determined from 50 × 50 mm core samples extracted from the slabs and 150 mm cubes cast for the longitudinal joints. For analysis, it was assumed that the strength of the 50 mm cores corresponded to the cube strength of the 150 mm specimens. The equivalent cylindrical compressive strength was estimated to be 85% of the cube strength. Other mechanical properties, including tensile strength and modulus of elasticity, were calculated based on the compressive strength using empirical formulas from ACI 318-19 [33] and are provided in

Table 4. Concrete properties derived from experimental program by Pajari [24].

Parameter	Slab	Joint
Cubic compressive strength [MPa] (ksi)	74.83 (10.85)	38.42 (5.57)
Cylindrical compressive strength [MPa] (ksi)	63.61 (9.23)	32.64 (4.73)
Tensile strength [MPa] (ksi)	4.95 (0.72)	3.54 (0.51)
Young’s modulus [GPa] (ksi)	40.32 (5847.92)	31.37 (4549.83)
Poisson ratio	0.2	0.2

. The slabs were prestressed using 11 strands with a diameter of 12.5 mm (0.5 in.), each stressed initially to 1000 MPa (145.04 ksi). An average mesh size of 50 mm (2 in.) was used for solid elements in the cross-section and along the span near the load application area to ensure accurate stress distribution. To optimize computational efficiency, the mesh was gradually enlarged to 100 mm (4 in.) along the span in regions away from the loading zone. Additionally, the truss elements representing the prestressing strands were assigned a uniform element length of 200 mm (8 in.).

To assess the validity of the FE models, their performance was compared against experimental observations in terms of load–deflection response, crack propagation patterns, and failure modes. As displayed in Figure 10, the load–deflection behavior obtained from the numerical simulations using two different dilation angles closely follow the experimental curve up to peak load. Some discrepancies are observed in the post-peak response of the model, particularly during the softening phase, which can be attributed to the brittle behavior of concrete in shear and tension, which is highly variable and challenging to simulate precisely. The model with a dilation angle of 35° slightly underestimates the peak load, while the higher dilation angle produces a stiffer post-peak response and better captures the residual strength, whereas the lower angle reflects a more brittle softening behavior. Nevertheless, the model accurately captures the ultimate load and maximum deflection, both critical for evaluating structural performance, and the results are comparable to those reported in other FE studies [29,31]. A quantitative comparison of peak loads between the experimental and numerical results is provided in

Table 5. Comparison of maximum capacity obtained from numerical models and Pajari test result.

Model	P_EXP [kN] (kips)	P_FEM [kN] (kips)	P_FEM/F_EXP
Dilation Angle 35	331.50 (74.52)	318.45 (71.60)	0.96
Dilation Angle 40		337.37 (75.84)	1.02

, further supporting the model’s reliability.

Crack pattern comparison is presented in Figure 11 and shows strong agreement between experimental observations (Figure 11a) and the FE model (Figure 11b,c). Both the top and bottom surfaces exhibited similar longitudinal cracking. However, two minor differences were observed: the long crack located far from the loading point on the top surface in the experiment did not appear in the simulation, and the other two cracks were longer in the FE model. Despite these localized differences, the numerical model demonstrated good predictive capability for crack development, reinforcing the credibility of the simulation methodology.

4. Evaluation of Spancrete HCS Floor System Behavior

After validating the FE modeling technique against two experimental studies, the behavior of Spancrete HCS floors was evaluated for a system consisting of three interconnected units with longitudinal joints, each with characteristics described in Section 4.1. The performance of the system was assessed in terms of load–deflection response, extent of cracking damage, failure modes, strain and stress distribution in concrete and prestressing strands, and the integrity of longitudinal joints. Furthermore, the influence of both loading area and load location on the response of the HCS floor was also investigated.

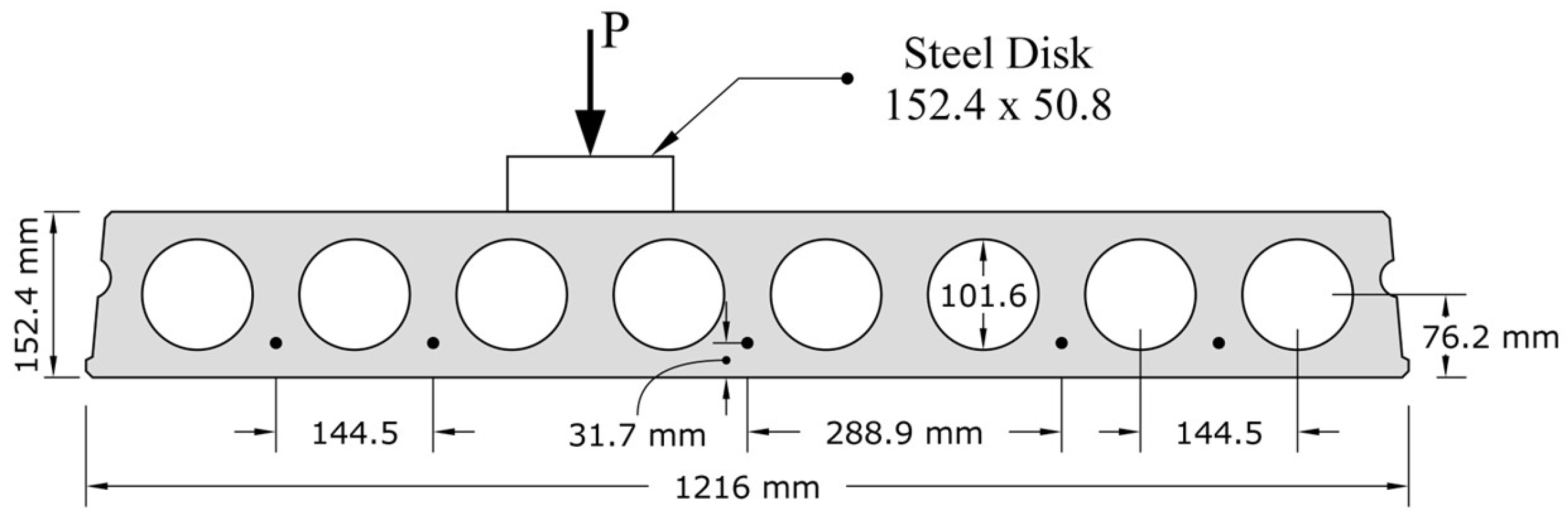
4.1. Details of the Spancrete Floor System

The Spancrete HCS section has a depth of 305 mm (12 in.), a width of 1219 mm (48 in.), and a span length of 7.3 m (24 ft). It includes eight prestressing strands with an effective depth of 273 mm (10.75 in.) and an eccentricity of 128 mm (5 in.). The strands, with a diameter of 12.7 mm (0.5 in.), were stressed to 70% of their ultimate strength, with a 15% prestressing loss assumed. Pajari [11,24] considered prestress losses of 5%, 10%, and 15%, in resistance calculations and noted that exact value is of little importance. After performing mesh sensitivity analysis, the element size for the concrete elements was set to 19 mm (0.75 in.) across the width and 38 mm (1.5 in.) along the length. Furthermore, a mesh size of 127 mm (5 in.) was selected for prestressing strands elements. Assumed external loading was a concentrated force applied to a 152 mm (6in.) square area at the center of the slabs to simulate a column load in a building system. Concrete properties used for both the HCS, and longitudinal joints are detailed in

Table 6. Concrete properties for Spancrete floor system.

Properties	HCS	Joint
Density [kg/m3] (pcf)	2400 (150)	2400 (150)
Poisson ratio	0.2	0.2
Compressive strength f’c [MPa] (ksi)	34.50 (5)	48.30 (7)
Young’s modulus Ec [GPa] (ksi)	27.80 (4030.51)	32.88 (4768.96)
Tensile strength ft [MPa] (ksi)	2.92 (0.424)	4.83 (0.70)

with the latter having higher strength than the former. These properties are typical of Spancrete HCS construction in the USA. The modulus of elasticity of the concrete and tensile strength were calculated according to ACI 318 [33].

4.2. Load-Deflection Behavior

The load versus midspan deflection curve is presented in Figure 12. As the load increased, the slab initially exhibited a linear response, reflecting the elastic behavior of the system. The curve starts to deviate from linearity as microcracks formed (A), leading to a gradual increase in the deflection with the continued load. At roughly 169.94 kN (38.20 kips), longitudinal cracks began to form at the midspan on the bottom surface, reducing the stiffness of the slab. With continued loading, these cracks propagated toward the support regions. Upon reaching a load of approximately 374.43 kN (84.18 kips), transverse flexural cracks initiated at the bottom of the middle slab (B). Beyond this peak, the curve plateaued (C), indicating the onset of damage propagation, with additional cracks developing and extending into the side slabs. Subsequently, a longitudinal crack formed (D) and rapidly advanced along the top surface (compression zone) of the slab, resulted in the penetration of the loaded column through the slab depth within the defined loading patch. During column penetration, crushing of the concrete due to the large stresses and strains in all three directions (longitudinal, transverse, and vertical) occurred in the loading area, leading to numerical instability and non-convergence of the analysis.

4.3. Failure Modes and Damage Progression

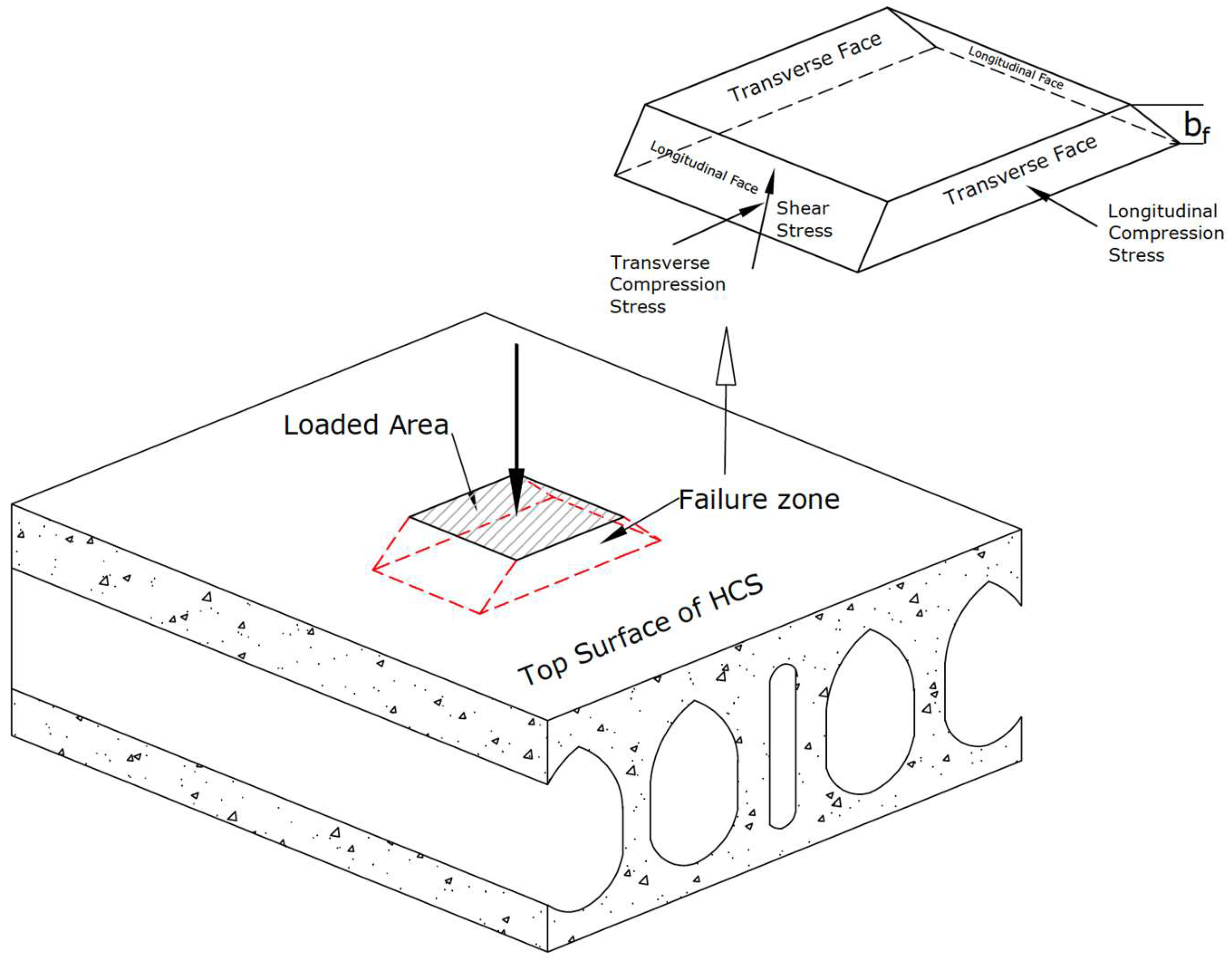
In HCS floor systems subjected to heavy concentrated loads, several failure modes, such as flexural failure, web shear failure, longitudinal joint failure, and punching shear failure, can occur. However, due to the large cavities, HCSs may be more susceptible to punching shear failure under concentrated loads. The lack of reinforcement in the transverse direction increases the risk of this brittle failure mode. This is a localized failure that occurs when shear stresses from loading exceed the slab shear stress capacity around the perimeter of a concentrated load. In this mode for solid flat slabs, a cone-shaped or truncated pyramid-like failure surface forms around the loaded area, as the slab “punches” through. For HCS, this mechanism develops in a different manner and is referred to here as modified punching shear, which is investigated in the following using the analysis results from ABAQUS.

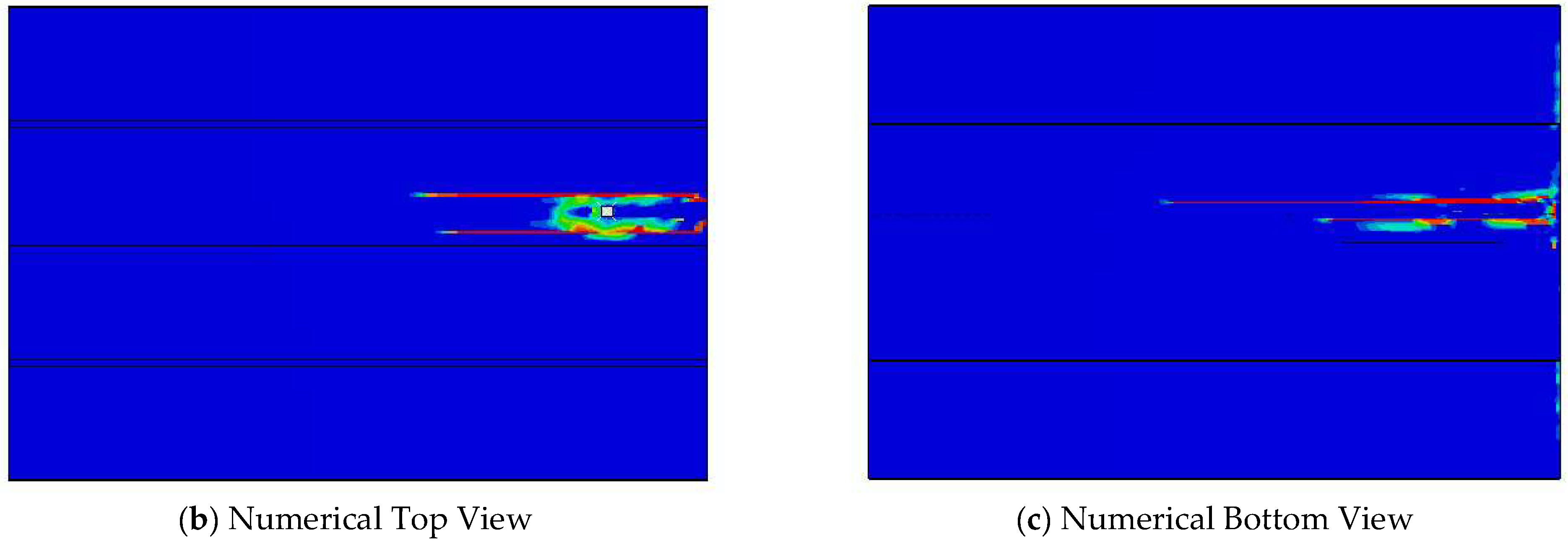
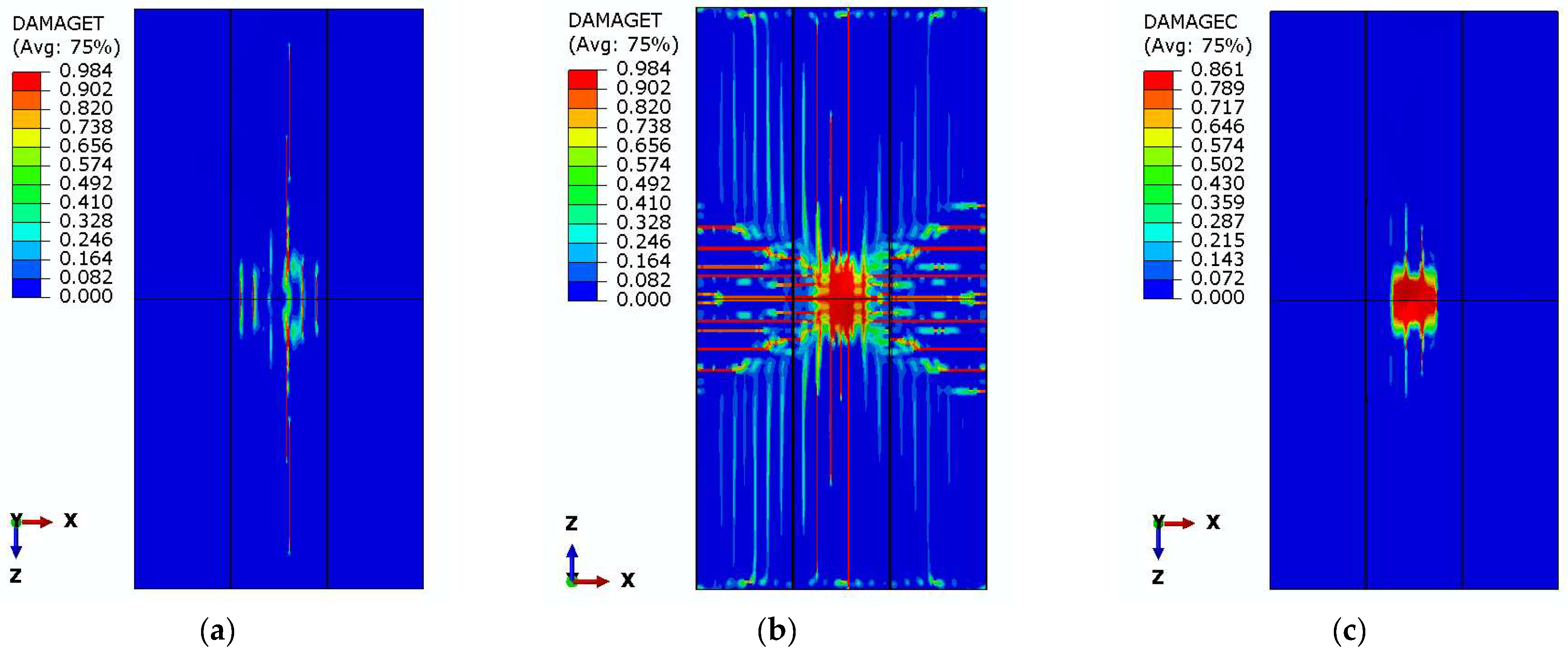
The crack propagation of the system on the top surface is depicted in Figure 13a, which aligns with the findings of other studies regarding the formation of wide longitudinal cracks under the load on the top surface of the slab. Figure 13b shows extreme damage on the bottom surface around loading area. In the CDP model, these variables evolve between 0 (undamaged) and the maximum value defined by the stress–strain laws in Section 2.3.1 (Figure 4), with higher values indicating more severe cracking or crushing. Based on Figure 13c the failure mode was characterized by concrete crushing near the loading point, causing the simulation in ABAQUS to fail by column penetration through the slab. The failure mechanism observed here consisted of two sequential events: the formation of shear cracks, followed by crushing resulting from large compression stresses and strains concentrated in the loaded region. This process was initiated by the slab’s susceptibility to shear cracking due to its hollow-core configuration and lack of transverse reinforcement and ultimately resulted in localized concrete crushing caused by the highly concentrated load, that led to the larger displacements observed in the analysis. In Figure 14, the deflected shape of the model at the end of the analysis is shown, which is consistent with modified punching shear failure, where the failure surface of the slab “punches” along inclined longitudinal shear planes, and the longitudinal crushing completes the mechanism along the transverse faces through around the loading device.

4.4. Deflection Response

The overall deflection curves of the HCS model at different load levels along a transverse line at the load point are plotted in Figure 15. The horizontal axis represents the distance across the width of the slabs from the center. At the cracking load (169.94 kN (38.20 kips)), deflection across the slab is minimal and uniform, reflecting elastic behavior. As the load increases, the deflection becomes more pronounced, suggesting the onset of cracking and reduced stiffness. At failure, the central deflection sharply increases, reaching 35 mm (1.4 in.). The shape of the curve shows that most of the deflection is concentrated in the center, which suggests significant localized deformation, indicating a potential progression toward failure, likely due to modified punching shear and significant cracking in the middle region.

4.5. Shear Stress

Figure 16 shows the vertical shear stress distribution at the peak load in the HCS. The shear stress pattern started from the periphery of the loaded area and extended downward through the slab, primarily confined to the top flange, with an approximate propagation angle of 45° which is consistent with dispersion angle recommended by EN1168 [27] and differ from those of Jeziorski and Derkowski [28]. However, unlike the symmetric stress distribution typically observed in punching shear failure of solid slabs, the stress in the HCS is concentrated along two faces, on either side of the loaded area of the top flange, in the longitudinal direction. The observed pattern differs from punching shear in solid reinforced concrete flat slabs in which the shear cracks generally initiate around all faces of the loaded area and radiate outwards diagonally through the entire depth of the slab, forming a truncated cone or pyramid-shaped failure surface around the loaded area as we see in Figure 17.

The modified punching shear behavior of the HCS, as observed in this study, deviates significantly due to its unique structural configuration. The high shear stress was confined primarily to the top flange and concentrated in a single direction, extending transversely only as far as the nearest row of cores in the longitudinal direction, the failure surface extends until failure from a different mode is generated, as observed by Pajari [24] and McGinnis et al. [14]. It is noted here that as a consequence of the inclined cracks, there is a rapid increase in longitudinal compressive stress in the top flange. After shear cracking, these stresses are concentrated over a small portion of the width of the section, namely between the longitudinal crack faces produced by the vertical shear stresses because the full magnitude of the vertical load is applied within this segment. The longitudinal compressive stress continues to increase until the concrete crushes and the column punches through the top flange.

The presence of voids in the slab not only reduces the effective cross-sectional area available to resist shear forces but also alters the stress distribution, and the shape of the punched surface has a longer longitudinal dimension than the transverse one, leading to a modified form of punching shear failure. Consequently, the failure perimeter and critical section in the HCS exhibits a distinctly different shape compared to those in solid slabs. Thus, this indicates that revised procedures need to be developed to evaluate the shear resistance of HCSs under concentrated loads.

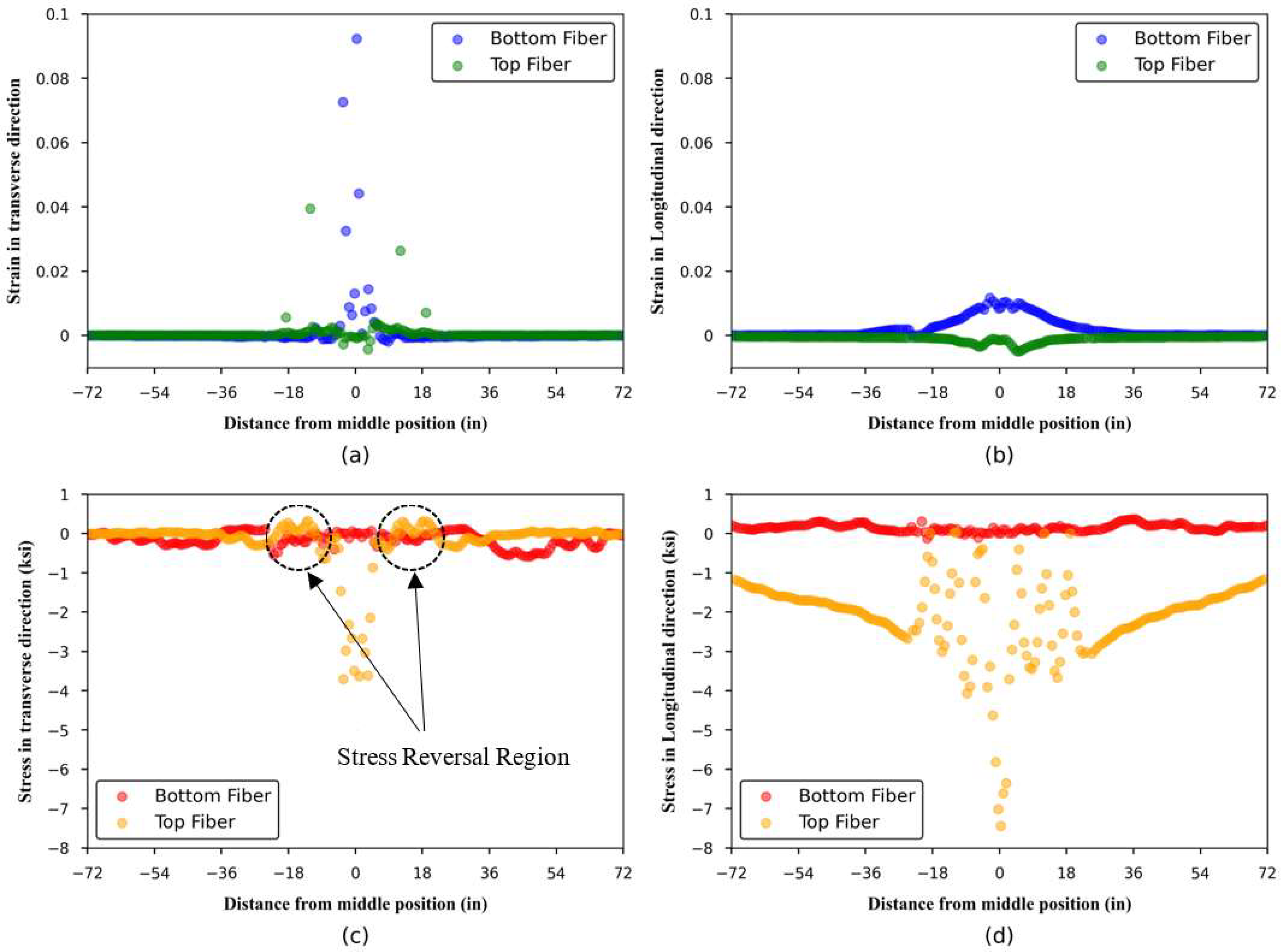
4.6. Concrete Strain and Stress Distribution

To further investigate the failure mode of the HCS floor system under a concentrated load, the strain and stress distributions at different locations are illustrated in Figure 18 and Figure 19. These plots depict the strain and stress values in both transverse and longitudinal directions at the extreme top and bottom concrete fibers across the width and along the span length of the model, respectively. In all these plots, negative values show compression and positive ones show tension.

Figure 18a shows significant transverse strain in the transverse direction at the bottom fiber in a few elements near the center of the cross-section, associated with longitudinal cracking due to transverse bending moments. Since these slabs lack transverse reinforcement, crack opening is controlled solely by confinement between the slabs, as noted by Lucio [25]. By examining tensile strain values in both directions, it is observed that the region of high longitudinal strain is wider than the region of high transverse strain. Another notable observation is the presence of high tensile strain in the transverse direction at the top fiber, which is indicative of longitudinal cracking potentially associated with modified punching shear failure.

In terms of stress distribution, Figure 18c,d reveal that the top fiber experiences pronounced stress concentrations in both transverse and longitudinal directions near the slab center, directly beneath the applied load. These large compressive stresses occur at relatively small strains which in the longitudinal direction are primarily affected by flexure and influenced by Poisson’s effect and transverse bending in the transverse direction. The most significant of these results are the transverse tensile stresses at the top fiber, as well as the reversal of strain and stress patterns, which are characteristic of punching shear behavior. Another insight from these figures is that in the transverse direction, only top and bottom flanges are actively engaged in resisting stresses across the width, whereas along the span, the webs also contribute, allowing for stress redistribution and enhanced load-carrying capacity until failure. This distinction highlights the fact that the HCS is structurally weaker in the transverse direction.

Figure 19 further supports this behavior, showing that both strain and stress remain largely uniform along most of the slab length, with minimal variation, except near the center, where a sharp increase (both negative and positive) is observed. This spike near the loading point suggests localized deformations due to stress concentrations. However, while significant strain and stress across the width are confined to a small central region, along the length of the slab, elevated values extend more gradually away from the load point. This distribution allows cracks to propagate farther in the longitudinal direction.

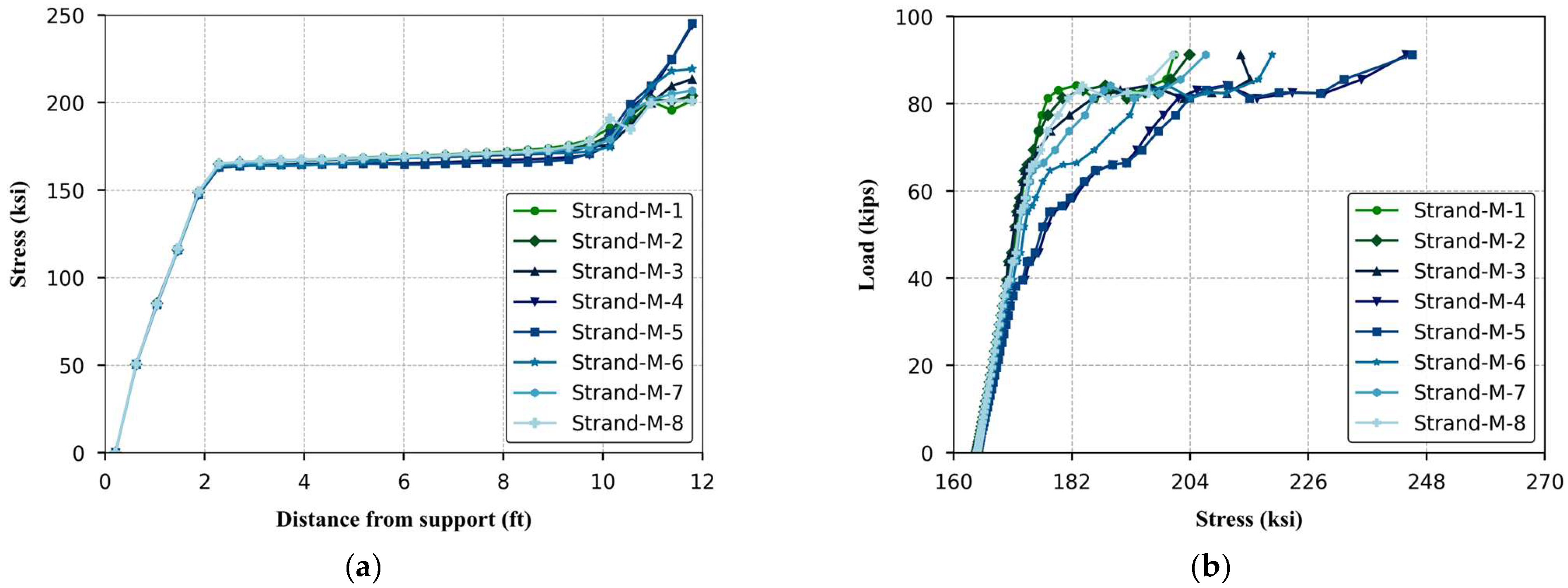
4.7. Strands Strain and Stress Distribution

Figure 20a illustrates the stress distribution along the length of different prestressing strands in the middle slab of the HCS system at failure and Figure 20b portrays the relationship between applied load and strand stress. The numbering of strands ranges from 0 to 8, corresponding to the first strand on the right edge of the slab to the last one on the left as shown in Figure 1. The initial region of Figure 20a corresponds to the transfer length. Beyond this region, the stress became relatively constant, indicating uniform prestress along the span. The strands were in a state of equilibrium, carrying the applied load evenly, with no significant changes in stress.

Near the slab center, there was a noticeable rise in stress, particularly for the central strands (M-4 and M-5), reflecting localized stress concentrations beneath the applied load and these strands were taking on a larger portion of the load. Only these two strands reached the proportional limit of the strand material (1689 MPa (243 ksi)). This indicates that concrete crushing occurred before the strands became nonlinear. So, when modified punching shear failure developed, the concrete in the top flange lost its load-carrying capacity, requiring the strands to carry additional internal stress to resist bending.

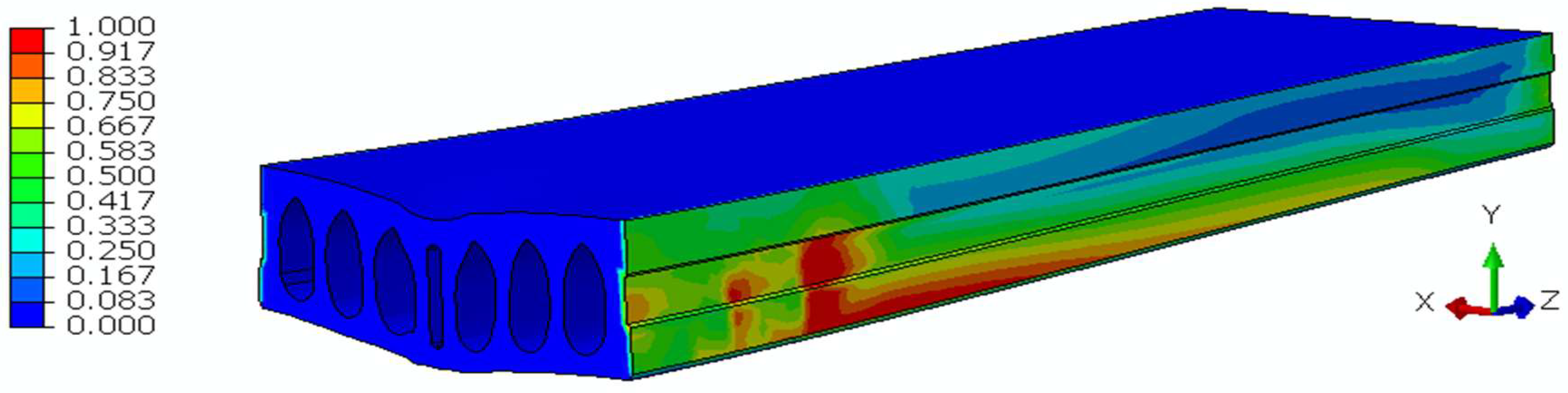
4.8. Damage in Longitudinal Joints

Figure 21 exhibits the impact of the contact damage criterion (CSMAXSCRT), highlighting the initiation of damage in red at the conclusion of the analysis for the symmetrical surfaces between the middle slab and the longitudinal joints. From the figure, it is evident that there was negligible damaged area close to midspan and loading area, indicating that shear key failure did not happen before the modified punching shear failure in this model. The shear keys were still functioning and capable of transferring load between the slabs. This observation confirms that, despite the presence of localized stress concentrations, the shear keys retained their load-bearing capability, allowing for load redistribution across the slab system until modified punching shear failure became the dominant failure mode in this model with mentioned configuration. The influence of geometry and material properties should be further investigated in future studies.

4.9. Effect of Loading Area

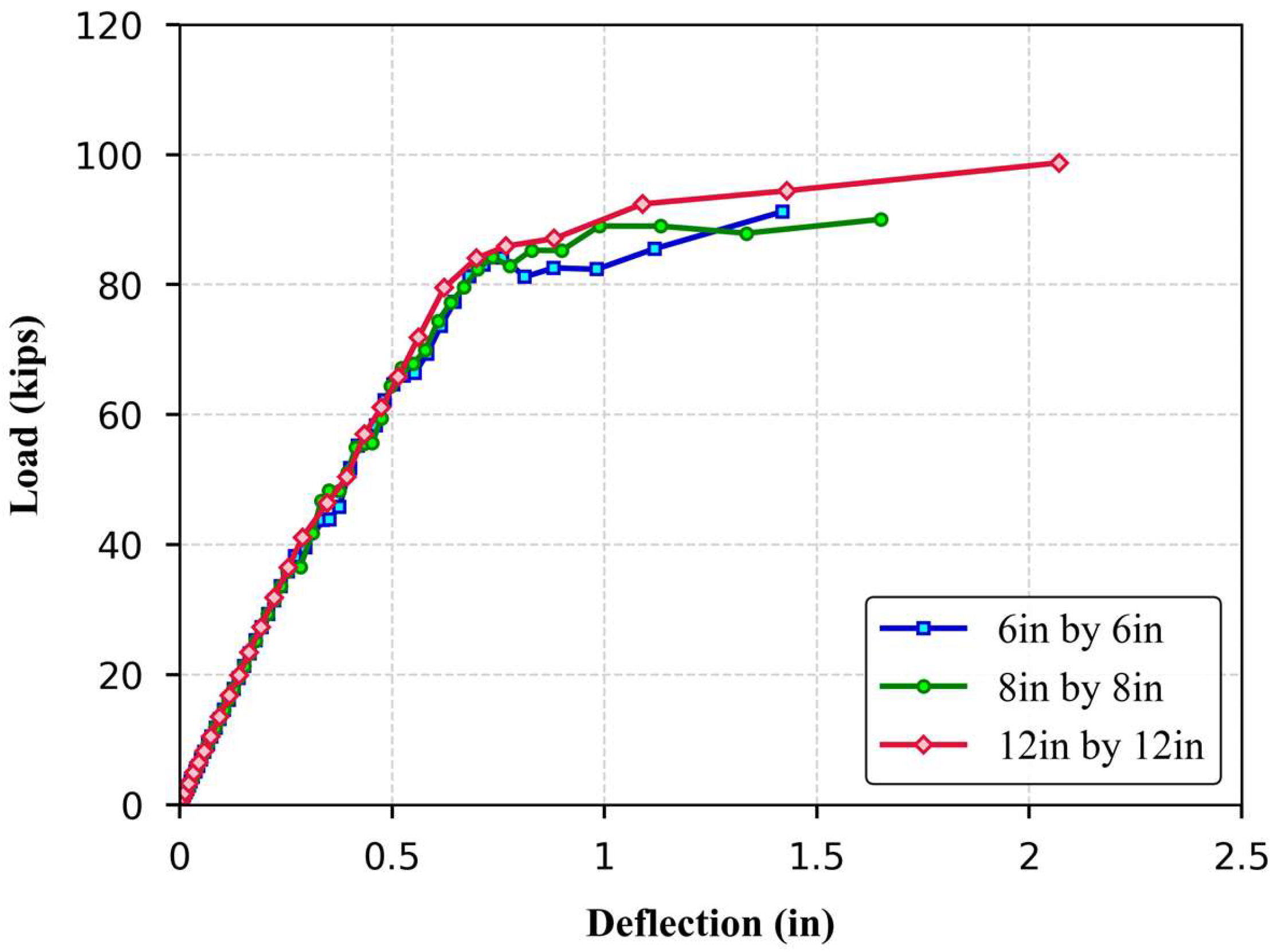
The sensitivity of the HCSs response to various loading areas is illustrated in Figure 22. During the initial loading phase, all specimens exhibited a similar linear trend, indicating comparable initial stiffness and elastic behavior regardless of the load area. However, divergence became apparent at higher load levels. The slab subjected to the 203 × 203 mm (8 in × 8 in) load area reached a peak load similar to that of the 152 × 152 mm (6 in × 6 in) patch but exhibited better post-peak performance, suggesting marginal improvements in ductility. In contrast, increasing the load area to 305 × 305 mm (12 in × 12 in) resulted in approximately an 8% increase in ultimate capacity, along with an extended deflection range. The slab continued to carry increasing loads beyond 50 mm (2 in.) of deflection, indicating a more ductile response and enhanced post-peak performance. The observed behavior can be attributed to the distribution of stresses over a wider region in the larger loading areas, which reduces the intensity of localized stresses and delays modified punching shear failure. In the case of the 152 mm (6 in.) loading area, the concentrated stress led to an earlier onset of modified punching shear, limiting both the load capacity and post-peak ductility. Furthermore, increasing the patch size was observed to promote the formation of shear cracks at the supports, suggesting a potential transition in the failure mechanism.

4.10. Effect of Loading Point

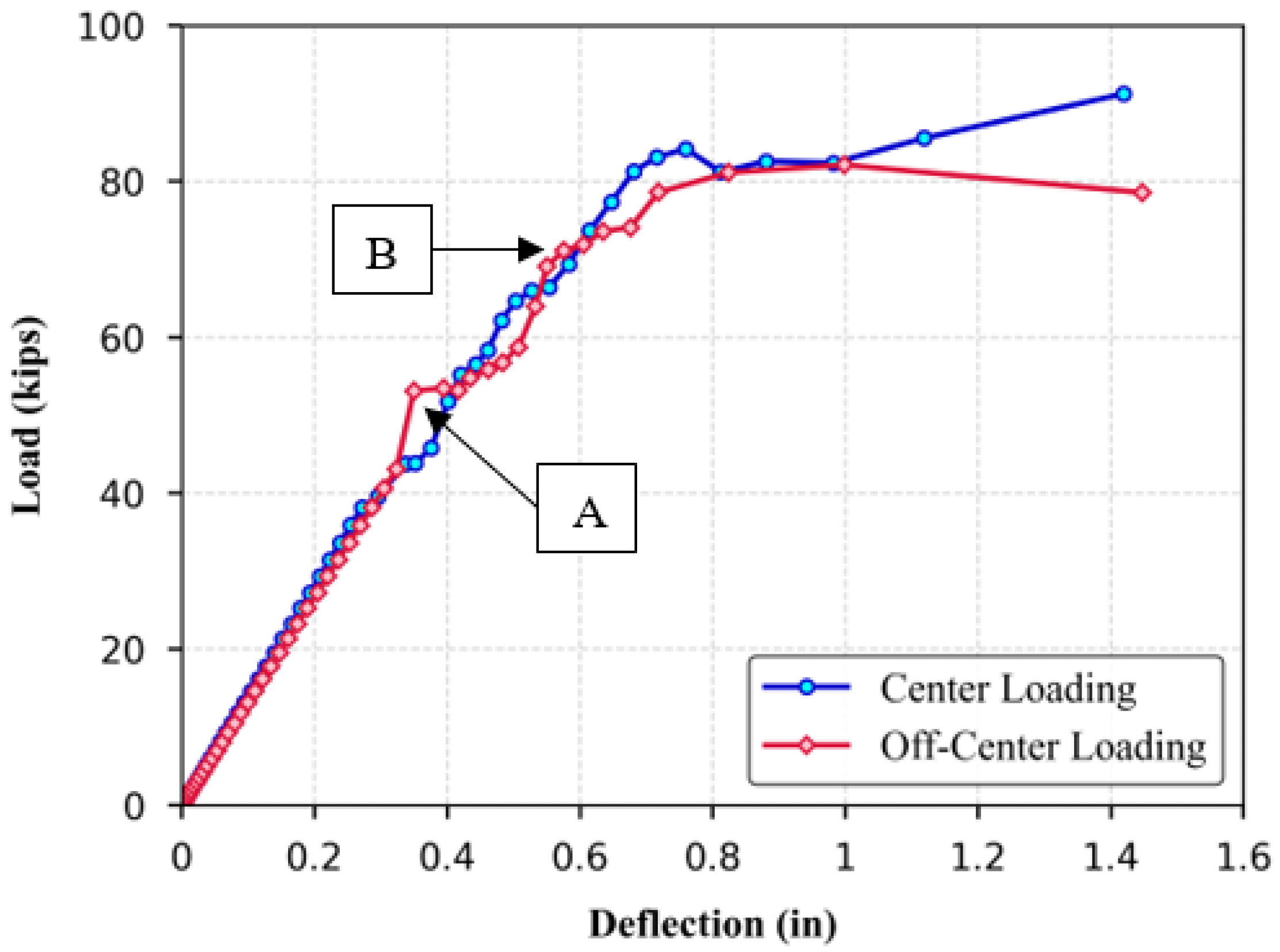
To bridge the gap of knowledge regarding the performance of longitudinal joints in HCS floors under concentrated loads, the present study includes a preliminary investigation on the influence of load location. Specifically, the effect of shifting the point load closer to the joint was assessed to evaluate its impact on the structural response and failure mode. Figure 23 presents the two loading configurations considered: one at the slab center and another near the inside edge adjacent to the joint. The resulting load–deflection curves, shown in Figure 24, reveal how load location influences overall performance, including load-carrying capacity, crack propagation, and failure patterns.

At Point A on the load-deflection curve for off-center loading, a wide crack forms on the bottom surface of the middle slab directly beneath the loading point. Simultaneously, damage initiates at the interface between the joint surface (near the loading point) and the adjacent side slab. As the load increases further, Point B is reached, marking the onset of debonding between the joint surface and the loaded slab. These two points signify the initiation of local failure driven by contact debonding at the joint. The peak load attained in this configuration is approximately 365.27 kN (82.12 kips), representing about 97% of the capacity recorded under center loading. At this stage, a longitudinal crack propagates along the top surface of the slab from the load application point toward the support. Beyond the peak load, the response softens due to continued crack propagation and joint degradation. The system ultimately fails through a combined mechanism involving joint debonding and modified punching shear failure. The resulting crack patterns closely resemble those observed in center loading, particularly the development of wide longitudinal cracks on the top surface beneath the loading point, indicating similar failure progression but triggered earlier due to proximity to the joint.

Figure 25 and Figure 26 illustrate the deflected shape and joint debonding area for the off-center loading configuration at the end of the analysis. In Figure 26, the red-highlighted regions indicate the debonded interfaces between the joint and the adjacent slabs. In this case, the response is dominated by torsional deformation of the loaded slab about its longitudinal axis. This torsion arises from the limited torsional stiffness, primarily due to the proximity of the longitudinal joint whose shear stiffness is significantly lower than that of the slab. The resulting twisting induces premature joint debonding on the loaded side, triggering failure through a torsion-driven mechanism that precedes—or replaces—the modified punching shear sequence observed under centered loading. The joint farther from the load remains intact, confirming that the failure is localized near the loading region. These findings highlight that, under off-center loading, the longitudinal joint integrity is critical to the structural performance and can significantly influence both the load-carrying capacity and failure mode of the system.

5. Conclusions

Three-dimensional non-linear finite element models of Spancrete HCS floor systems were developed using ABAQUS/Explicit. Due to the lack of experimental data for Spancrete HCSs under concentrated loads, the model was calibrated and validated using available test results from other HCS systems. This approach allowed for assessment of model robustness across different HCS geometries and provided confidence in the general applicability of the modeling technique. The analysis provided several key insights into the structural performance of these systems:

• The developed finite element modeling technique effectively captured the behavior and failure mechanisms of HCS systems under concentrated loading, reproducing the experimental peak loads of the McGinnis and Pajari tests with discrepancies of approximately 4% and 2%, respectively.
• Longitudinal cracking due to transverse bending moments altered lateral load distribution and increased demand on the most heavily loaded webs. This led to loss of load-bearing capacity and concrete crushing around the load, triggering a modified form of punching shear failure.
• The modified punching shear failure is distinct from the typical symmetric pattern in solid slabs. Shear stress was confined to the top flange at about a 45° angle, along the slab longitudinal direction, and crushing from flexural compression stress caused concrete failure in the regions located longitudinally on either side of the loaded area.
• The shear stress along the critical perimeter reached approximately 13 MPa (2 ksi), while the longitudinal compressive stress at the top fiber beneath the loading area reached about 50 MPa (7 ksi), exceeding the concrete uniaxial compressive strength.
• Longitudinal joints remained undamaged under center loading, effectively transferring the load between slabs until modified punching failure.
• Increasing loading area size enhanced post-peak stability, improved ductility, and increased ultimate load capacity about 8% by reducing stress concentration.
• Applying loads near longitudinal joints generated torsional deformation and caused earlier joint debonding and reduced load capacity by 2.5%, combining joint failure with modified punching shear. So, load position influenced failure mode and capacity, highlighting the need to consider load location in design.
• These findings demonstrate that existing design provisions, which are primarily based on solid slab behavior, are inadequate for HCSs. Future research should be directed toward refining design rules to account for their unique failure mechanisms.
• Lastly, future research should address bond–slip behavior, different concrete properties for joints and slabs, different geometries, and varied load locations to improve understanding of modified punching shear in HCS and enable more accurate generalization of the results.