Experimental Study on the Shear Performance of Epoxy Resin-Bolted Steel-Cross Laminated Timber (CLT) Connections
Abstract
1. Introduction
2. Materials and Methods
2.1. Specimen Details
2.2. Material Properties
2.3. Loading Method
3. Experimental Results
3.1. Load–Displacement Curves
- (1)
- Elastic stage: In the initial loading stage, the connection exhibited a linear load–displacement relationship, indicating that both the bolt and timber were deforming elastically. With increasing load, the specimen gradually yields, and the joints stiffness begins to exhibit non-linear degradation, subsequently entering the elastic-plastic stage.
- (2)
- Elasto-plastic stage: This stage is characterized by the non-linear smooth degradation of joint stiffness. Wood fibers are compressed by the bolt, gradually undergoing plastic deformation, causing the joint’s tangential stiffness to continuously decrease. However, the load-bearing capacity of the joint continued to increase due to the compaction of the wood. This resulted in the curve exhibiting a distinct convex non-linear characteristic.
- (3)
- Plastic development stage: As deformation accumulates, the joint enters a stage dominated by material plasticity, characterized by strengthening and increased ductility. The bolts exhibit significant bending deformation and gradually form one or more plastic hinges. The compressed wood areas below the pin slots or washers become denser, and the load-bearing capacity continues to increase, eventually reaching the peak load, with the specimen exhibiting some ductility. During the continued loading process, the wood fibers experience sustained and non-uniform fracture, which manifests as slight fluctuations in the load displacement curve.
- (4)
- Failure stage: When the displacement exceeds the peak load point, the curve enters the load-bearing capacity decline segment, marking the beginning of the loss of structural integrity at the joint. Due to the compressive failure of the pin slot wall, shear fracture of the bolt, or local compressive failure of the wood beneath the washer, the bearing capacity of the joint significantly decreases and the specimen fails.
3.2. Failure Modes
4. Discussion
4.1. Mechanical Properties
- (1)
- The maximum load observed throughout the test is denoted as the peak load Fmax. A peak load is deemed valid only when the load–displacement curve shows a clear maximum, followed by a period of sustained load decay. For specimens where the load continues to increase until the end of loading, the peak load is not defined.
- (2)
- As illustrated in Figure 8, two distinct methods are employed to determine the yield point (vy, Fy), corresponding to the different types of load–displacement curves observed for the various connectors.
- (3)
- The ultimate displacement vu is defined as the smallest of the following three criteria: (a) the displacement corresponding to a significant decrease in load due to shear failure of the connector; (b) the displacement corresponding to a load equal to 0.8 Fmax of the load on the descending segment of the curve; (c) a maximum displacement limit of 30 mm.
- (4)
- The ultimate load Fu is identified as the load value on the curve corresponding to the ultimate displacement vu.
- (5)
- The joint’s initial stiffness Ks,0.4 and secondary stiffness Ks,0.7 are calculated according to Equations (1) and (2), respectively.
| Group | Shear Connector | CLT Local Compression Failure | Failure Mode | ||
|---|---|---|---|---|---|
| Single Plastic Hinge | Double Plastic Hinges | Shear Damage | |||
| 1B-12 | √ | Severe | II | ||
| 1BF-12 | √ | √ | Moderate | II + III | |
| 1B#-12 | √ | √ | Moderate | II + III | |
| 1BE-8 | √ | √ | Slight | II + III | |
| 1BE-12 | √ | Severe | II | ||
| 1BE-16 | √ | Severe | II | ||
| 1S#-8 | √ | II | |||
| 1S#-12 | √ | I | |||
| 2S#-12 | √ | I | |||
- (6)
- The ratio of the ultimate displacement to the yield displacement is used to define the ductility coefficient Δ. Table 8 presents the method for determining the minimum required ductility and corresponding ductility classes for Cross-Laminated Timber (CLT) structures, as specified in prEN 1998-1-2:2023 [41].
| Group | Fmax (kN) | Fy (kN) | Fu (kN) | vy (mm) | vu (mm) | Ks,0.4 (kN/mm) | Ks,0.7 (kN/mm) | Δ |
|---|---|---|---|---|---|---|---|---|
| 1B-12 | / | 113.43 [6.04] | 181.47 [3.75] | 8.45 [9.04] | 30 [0.00] | 12.76 [3.46] | 5.78 [15.86] | 3.56 [9.04] |
| 1BF-12 | 184.46 [4.44] | 93.17 [1.27] | 181.84 [4.13] | 7.83 [3.70] | 29.62 [2.22] | 11.97 [0.90] | 5.21 [8.90] | 3.79 [5.77] |
| 1B#-12 | 144.85 [0.60] | 69.55 [6.47] | 139.15 [3.31] | 7.39 [1.64] | 30 [0.00] | 10.32 [9.10] | 3.98 [6.44] | 4.06 [1.62] |
| 1BE-8 | 131.01 [4.79] | 54.12 [3.44] | 131.01 [4.79] | 6.33 [3.24] | 24.98 [1.05] | 8.12 [4.41] | 4.78 [4.76] | 3.95 [4.29] |
| 1BE-12 | / | 137.18 [8.56] | 203.37 [5.82] | 9.03 [10.89] | 30 [0.00] | 14.27 [16.54] | 5.14 [17.78] | 3.35 [11.61] |
| 1BE-16 | / | 143.52 [10.76] | 232.24 [7.84] | 8.45 [3.60] | 30 [0.00] | 18.23 [17.81] | 6.00 [31.50] | 3.55 [3.57] |
| 1S#-8 | 46.58 [4.94] | 41.39 [6.45] | 37.29 [4.34] | 7.17 [10.56] | 30 [0.00] | 5.74 [8.60] | 4.38 [18.49] | 4.22 [11.22] |
| 1S#-12 | 68.91 [5.56] | 57.83 [6.79] | 68.29 [5.79] | 5.71 [33.81] | 30 [0.00] | 11.75 [37.44] | 10.84 [10.59] | 5.75 [38.47] |
| 2S#-12 | 62.53 [5.25] | 54.09 [2.73] | 61.55 [6.42] | 8.58 [9.19] | 30 [0.00] | 7.04 [13.04] | 7.15 [7.10] | 3.52 [9.10] |
| Structural Type | Dissipative Sub-Assembly/Joint/2D-or 3D Connector/Connection | Type of Ductility | Δ DC2 | Δ DC3 |
|---|---|---|---|---|
| Cross laminated timber structures | Shear wall | Displacement | 1.5 | 2.5 |
| Hold-downs, tie-downs, foundation tie-downs, angle brackets, shear plates | Displacement | 1.5 | 1.5 | |
| Screwed wall panel-to-panel joints | Displacement | - | 5.5 |
4.2. Comparison of Test Results with Eurocode 5 Predictions
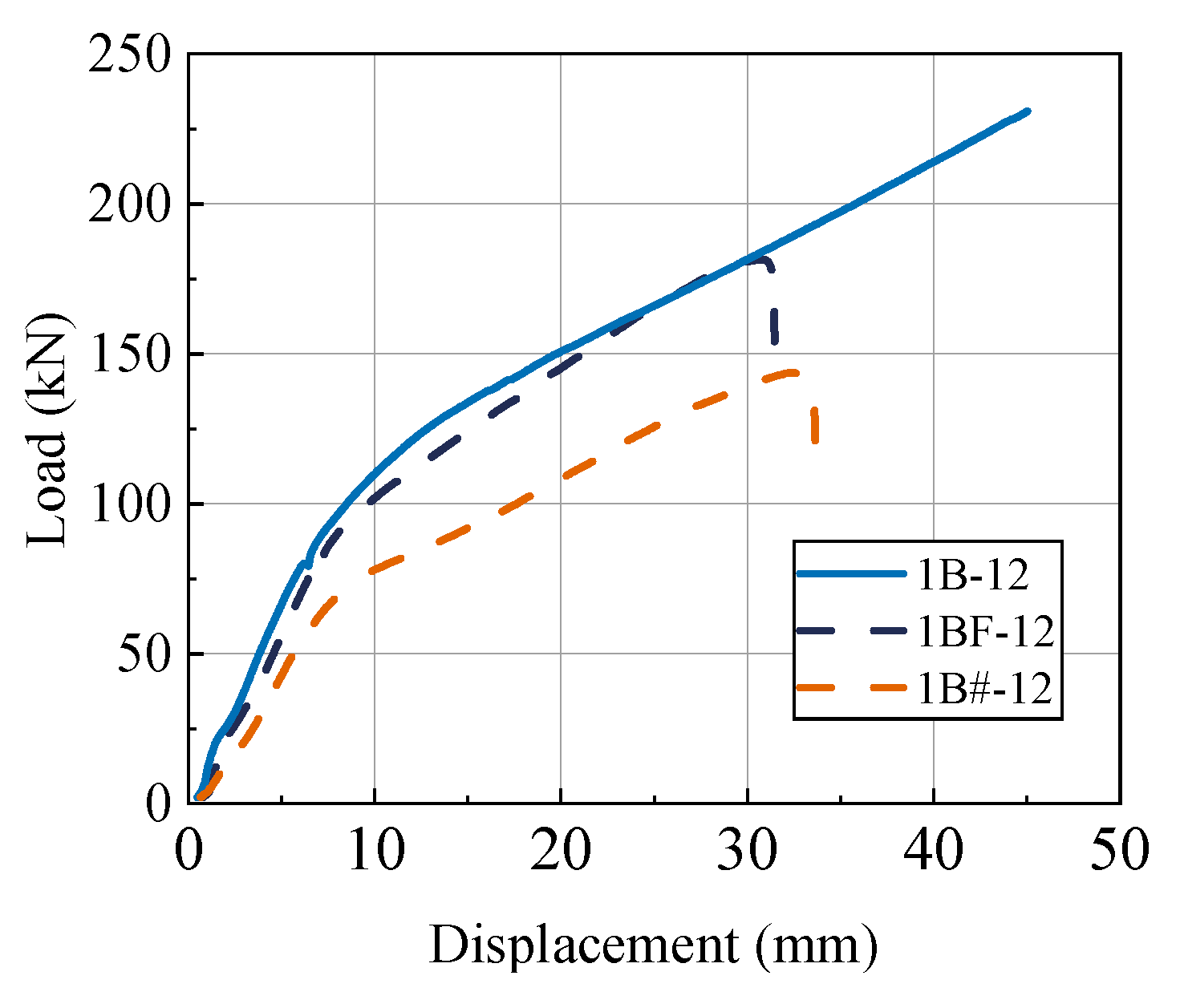
4.3. Comparison of the Performance of Ordinary Bolt Joints
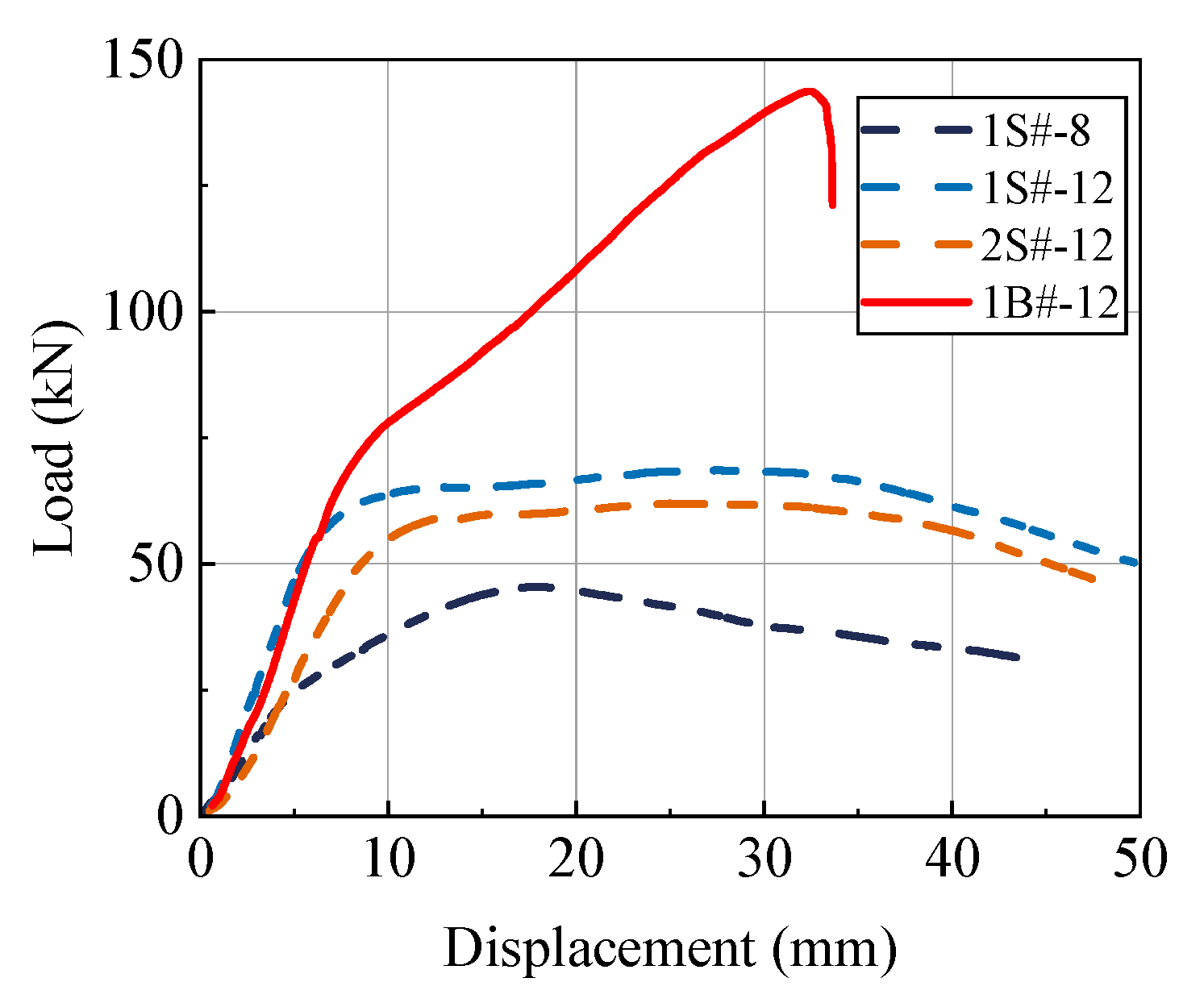
4.4. Comparison of Bolt and Screw Joint Performance
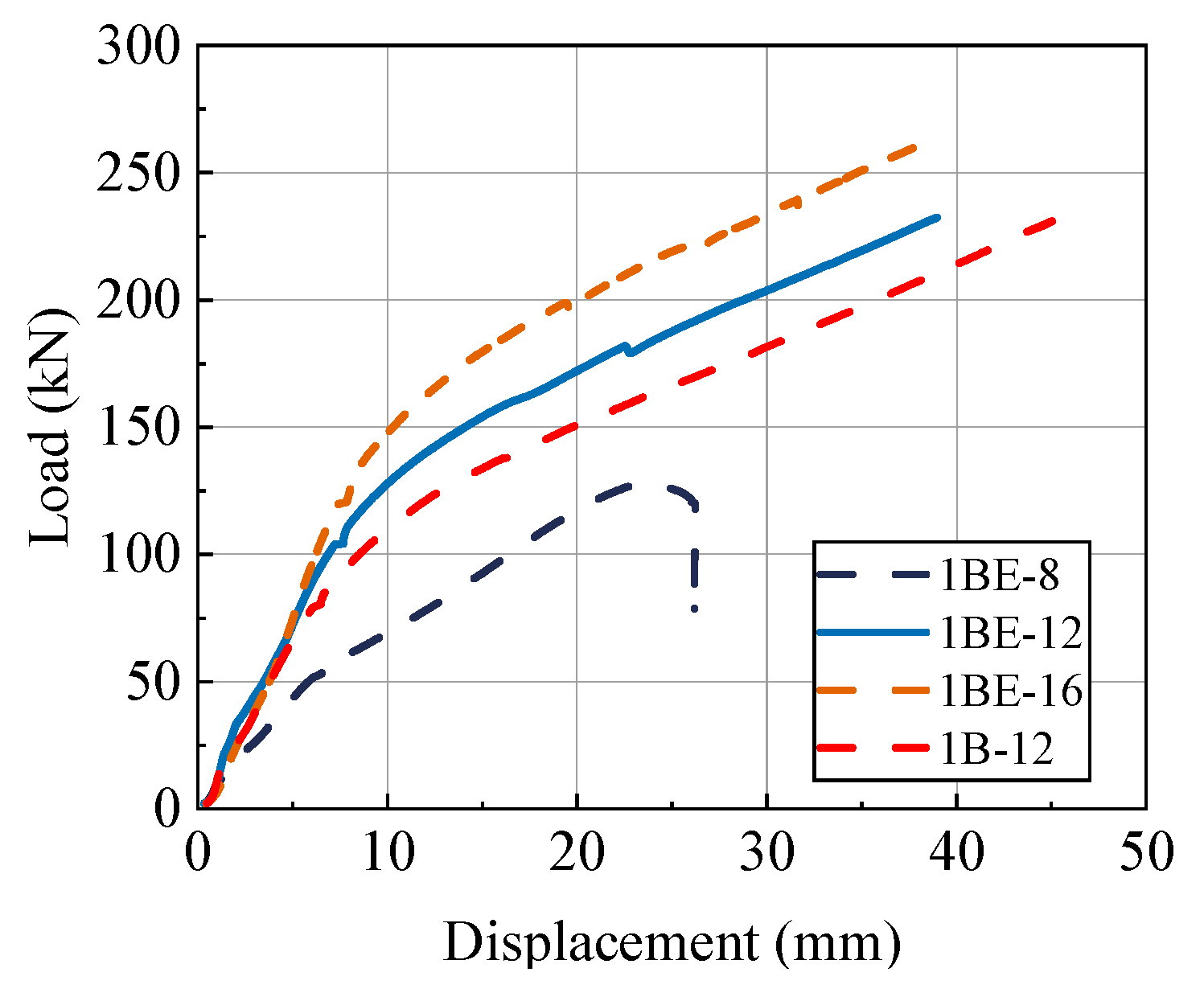
4.5. Comparison of the Performance of Ordinary Bolts and Epoxy Resin-Bolted Joints
5. Conclusions and Design Recommendations
5.1. Conclusions
- (1)
- Using high-strength bolts was found to be a direct way to enhance the ultimate load-bearing capacity of connection joints. Additionally, compared to fully threaded bolts, partially threaded bolts had a larger effective cross-sectional area, resulting in higher shear load-bearing capacity. Furthermore, by forming a plastic hinge at the root of the bolt, the failure mode of partially threaded bolts transitioned from brittle shear failure to the desired ductile failure.
- (2)
- Ordinary bolt specimens exhibited significantly higher ultimate load-bearing capacity than screw specimens of the same diameter due to the anchoring effect at the nut end. However, screw specimens effectively utilized the wood’s anchoring capacity through the close thread-wood engagement interface, thereby demonstrating superior initial stiffness. Regarding the number of screw rows, increasing the number of connection elements enhanced load-bearing capacity and stiffness. However, due to the ‘cluster nail effect,’ performance improvements were not linearly increased, and the efficiency reduction of group nails needs to be considered in the design.
- (3)
- Compared with ordinary bolts, the epoxy resin–bolt joint formed by injecting epoxy resin into the bolt slot increased the initial stiffness and ultimate load of the connection by 12% and 11.8%, respectively, without sacrificing ductility. However, when the wood end is sufficiently reinforced, smaller-diameter bolts became the weak link in the connection system, which caused the failure mode to shift from the ideal ductile yielding to unexpected bolt brittle fracture.
5.2. Design Recommendations
- (1)
- This study demonstrated that 12 mm and 16 mm diameter bolts can establish a good synergistic mechanism with the epoxy-reinforced timber, leading to ductile failure. To ensure the connection possesses adequate ductility and reliability by avoiding brittle failure of the bolt itself, it is recommended to use high-strength bolts with a diameter of no less than 12 mm.
- (2)
- The 2 mm epoxy layer thickness used in this study performed well experimentally. This thickness represents an effective balance between constructability and mechanical performance. In the absence of further parametric studies, a 2 mm thickness is recommended as a reference. Designers should ensure that the oversized hole is large enough for uniform epoxy filling but avoid excessive thickness that could increase material consumption and potential issues related to volumetric shrinkage.
- (3)
- To mitigate the group nail effect, proper spacing is essential. In this composite system, the load is transferred by the ‘epoxy resin-bolt’ composite dowel, which has a diameter of the hole (D). This is different from the bare bolt diameter. Therefore, all spacing calculations should be based on this composite diameter D. With reference to the provisions for dowel-type fasteners in Eurocode 5, we suggest: Spacing parallel to the load direction of no less than 4D and spacing perpendicular to the load direction of no less than 4D. This recommendation is a rational inference but requires validation through future dedicated experimental studies. Until more precise reduction factors for this specific composite connection are developed, a conservative approach should be taken in design by applying the capacity reduction factors for conventional multi-row bolted connections to ensure structural safety.
- (4)
- For the epoxy resin-bolted connections, which exhibited a ductile failure mode governed by bolt yielding and progressive wood crushing, Eurocode 5 provided a reasonable prediction of the bearing capacity, making it suitable for design applications.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CLT | Cross laminated timber |
| STC | Steel–timber composite |
| GLT | Glue laminated timber |
References
- Quintana Gallo, P.; Carradine, D.M.; Bazaez, R. State of the art and practice of seismic-resistant hybrid timber structures. Eur. J. Wood Wood Prod. 2021, 79, 5–28. [Google Scholar] [CrossRef]
- Chiniforush, A.A.; Akbarnezhad, A.; Valipour, H.; Xiao, J. Energy implications of using steel-timber composite (STC) elements in buildings. Energy Build. 2018, 176, 203–215. [Google Scholar] [CrossRef]
- Liu, W.; Yang, H. Research progress on modern timber structures. J. Build. Struct. 2019, 40, 16–43. [Google Scholar]
- Brandner, R.; Flatscher, G.; Ringhofer, A.; Schickhofer, G.; Thiel, A. Cross laminated timber (CLT): Overview and development. Eur. J. Wood Wood Prod. 2016, 74, 331–351. [Google Scholar] [CrossRef]
- Fan, Y.; Zhang, L.; Chen, S.; Yamahiro, S. Technological Iteration and Design Evolution of Medium and Large Timber Architecture in Japan. Archit. J. 2023, 9, 24–31. [Google Scholar] [CrossRef]
- Svatoš-Ražnjević, H.; Orozco, L.; Menges, A. Advanced timber construction industry: A review of 350 multi-storey timber projects from 2000–2021. Buildings 2022, 12, 404. [Google Scholar] [CrossRef]
- Ataei, A.; Valipour, H.R.; Bradford, M.A.; Chiniforush, A.A. Experimental study of steel-timber composite beam-to-column joints with extended end plates. Constr. Build. Mater. 2019, 226, 636–650. [Google Scholar] [CrossRef]
- Ascione, F.; Esposito, F.; Iovane, G.; Faiella, D.; Faggiano, B.; Mele, E. Sustainable and efficient structural systems for tall buildings: Exploring timber and steel–timber hybrids through a case study. Buildings 2024, 14, 524. [Google Scholar] [CrossRef]
- Ataei, A.; Bradford, M.A.; Valipour, H.R. Sustainable high strength steel flush and plate beam-to-column composite joints with deconstructable bolted shear connectors. In Proceedings of the Second International Conference on Performance-Based and Lifecycle Structural Engineering, Brisbane, QLD, Australia, 9–11 December 2015; pp. 749–757. [Google Scholar]
- Wang, X.; He, Q.; An, Z.; Liu, G.; Wen, X.; Wang, Y.; Zhong, Z. Experimental study of perfobond rib shear connector under lateral force. Appl. Sci. 2021, 11, 9088. [Google Scholar] [CrossRef]
- Xu, X.; Liu, Y.; He, J. Study on mechanical behavior of rubber-sleeved studs for steel and concrete composite structures. Constr. Build. Mater. 2014, 53, 533–546. [Google Scholar] [CrossRef]
- Zhuang, B.; Liu, Y.; Yang, F. Experimental and numerical study on deformation performance of Rubber-Sleeved Stud connector under cyclic load. Constr. Build. Mater. 2018, 192, 179–193. [Google Scholar] [CrossRef]
- He, X.; Yam, M.C.; Ke, K.; Zhou, X.; Zhang, H.; Gu, Z. Behaviour insights on damage-control composite beam-to-beam connections with replaceable elements. Steel Compos. Struct. 2023, 46, 773–791. [Google Scholar]
- He, X.; Ke, K.; Chen, Y.; Yam, M.C.; Shao, T. An experimental study of steel-concrete composite connections equipped with fuse angles. J. Constr. Steel Res. 2022, 195, 107357. [Google Scholar] [CrossRef]
- Wang, C.-L.; Lyu, J.; Zhao, J.; Yang, H. Experimental investigation of the shear characteristics of steel-to-timber composite joints with inclined self-tapping screws. Eng. Struct. 2020, 215, 110683. [Google Scholar] [CrossRef]
- Ataei, A.; Chiniforush, A.; Bradford, M.; Valipour, H. Cyclic behaviour of bolt and screw shear connectors in steel-timber composite (STC) beams. J. Constr. Steel Res. 2019, 161, 328–340. [Google Scholar] [CrossRef]
- Yang, R.; Li, H.; Lorenzo, R.; Ashraf, M.; Sun, Y.; Yuan, Q. Mechanical behaviour of steel timber composite shear connections. Constr. Build. Mater. 2020, 258, 119605. [Google Scholar] [CrossRef]
- Chiniforush, A.A.; Valipour, H.R.; Bradford, M.A.; Akbarnezhad, A. Long-term behaviour of steel-timber composite (STC) shear connections. Eng. Struct. 2019, 196, 109356. [Google Scholar] [CrossRef]
- Li, Z.; Wang, X.; He, M.; Dong, W. Experimental investigation of timber-steel hybrid walls and seismic design method for timber-steel hybrid structural system. J. Build. Struct. 2018, 39, 191–197. [Google Scholar]
- Hassanieh, A.; Valipour, H.R.; Bradford, M.A. Experimental and numerical study of steel-timber composite (STC) beams. J. Constr. Steel Res. 2016, 122, 367–378. [Google Scholar] [CrossRef]
- Hassanieh, A.; Valipour, H.R.; Bradford, M.A. Load-slip behaviour of steel-cross laminated timber (CLT) composite connections. J. Constr. Steel Res. 2016, 122, 110–121. [Google Scholar] [CrossRef]
- Hassanieh, A.; Valipour, H.R.; Bradford, M.A. Experimental and analytical behaviour of steel-timber composite connections. Constr. Build. Mater. 2016, 118, 63–75. [Google Scholar] [CrossRef]
- Hassanieh, A.; Valipour, H.; Bradford, M.; Sandhaas, C. Modelling of steel-timber composite connections: Validation of finite element model and parametric study. Eng. Struct. 2017, 138, 35–49. [Google Scholar] [CrossRef]
- Hassanieh, A.; Valipour, H.R.; Bradford, M.A. Experimental and numerical investigation of short-term behaviour of CLT-steel composite beams. Eng. Struct. 2017, 144, 43–57. [Google Scholar] [CrossRef]
- Loss, C.; Piazza, M.; Zandonini, R. Connections for steel–timber hybrid prefabricated buildings. Part I: Experimental tests. Constr. Build. Mater. 2016, 122, 781–795. [Google Scholar] [CrossRef]
- Loss, C.; Piazza, M.; Zandonini, R. Connections for steel–timber hybrid prefabricated buildings. Part II: Innovative modular structures. Constr. Build. Mater. 2016, 122, 796–808. [Google Scholar] [CrossRef]
- He, M.; Ni, S.; Ma, R.; Bai, X. Loading Tests of Prestressed Tube Bolted Joint with Slotted-in Steel Plate. J. Tongji Univ. (Nat. Sci.) 2013, 41, 1353–1358. [Google Scholar]
- He, M.; Zhao, Y.; Ma, R. Experimental investigation on lateral performance of pre-stressed tube bolted connection with high initial stiffness. Adv. Struct. Eng. 2016, 19, 762–776. [Google Scholar] [CrossRef]
- Ling, Z.; Liu, C.; Zhang, H. Shear performance of grouted stud connections for steel-cross laminated timber composite beams. J. Build. Struct. 2024, 45, 232–242. [Google Scholar]
- Hassanieh, A.; Valipour, H.R.; Bradford, M.A. Composite connections between CLT slab and steel beam: Experiments and empirical models. J. Constr. Steel Res. 2017, 138, 823–836. [Google Scholar] [CrossRef]
- Hassanieh, A.; Valipour, H.R.; Bradford, M.A. Bolt shear connectors in grout pockets: Finite element modelling and parametric study. Constr. Build. Mater. 2018, 176, 179–192. [Google Scholar] [CrossRef]
- Zhao, Y.; Yuan, Y.; Wang, C.-L.; Zheng, J.; Zhou, Y. Experimental study on shear performance of steel-timber screw connectors with grout pockets. Eng. Struct. 2022, 266, 114535. [Google Scholar] [CrossRef]
- GB/T 50329-2012; Standard for Methods Testing of Timber Structures. China Architecture & Building Press: Beijing, China, 2012.
- GB/T 26899-2011; Structural Glued Laminated Timber. Standards Press of China: Beijing, China, 2011.
- GB/T 228.1-2021; Metallic Materials: Tensile Testing: Part 1, Method of Test at Room Temperature. Standards Press of China: Beijing, China, 2021.
- GB 50017-2017; Standard for Design of Steel Structures. China Architecture & Building Press: Beijing, China, 2017.
- GB 50011-2010; Code for Seismic Design of Buildings. China Architecture & Building Press: Beijing, China, 2016.
- BS EN 26891:1991; Timber Structures-Joints Made with Mechanical Fasteners-General Principles for the Determination of Strength and Deformation Characteristics. CEN: Brussels, Belgium, 1991.
- GB 50005-2017; Standard for Design of Timber Structures. China Architecture & Building Press: Beijing, China, 2017.
- BS EN 12512-2001; Timber Structures-Test Methods-Cyclic Testing of Joints Made with Mechanical Fasteners. CEN: Brussels, Belgium, 2001.
- prEN 1998-1-2:2023; Design of Structures for Earthquake Resistance—Part 1-2, Buildings. CEN: Brussels, Belgium, 2023.
- EN 1995-1-1; Eurocode 5, Design of Timber Structures—Part 1-1, General Common Rules and Rules for Buildings. European Committee for Standardization: Brussels, Belgium, 2004.
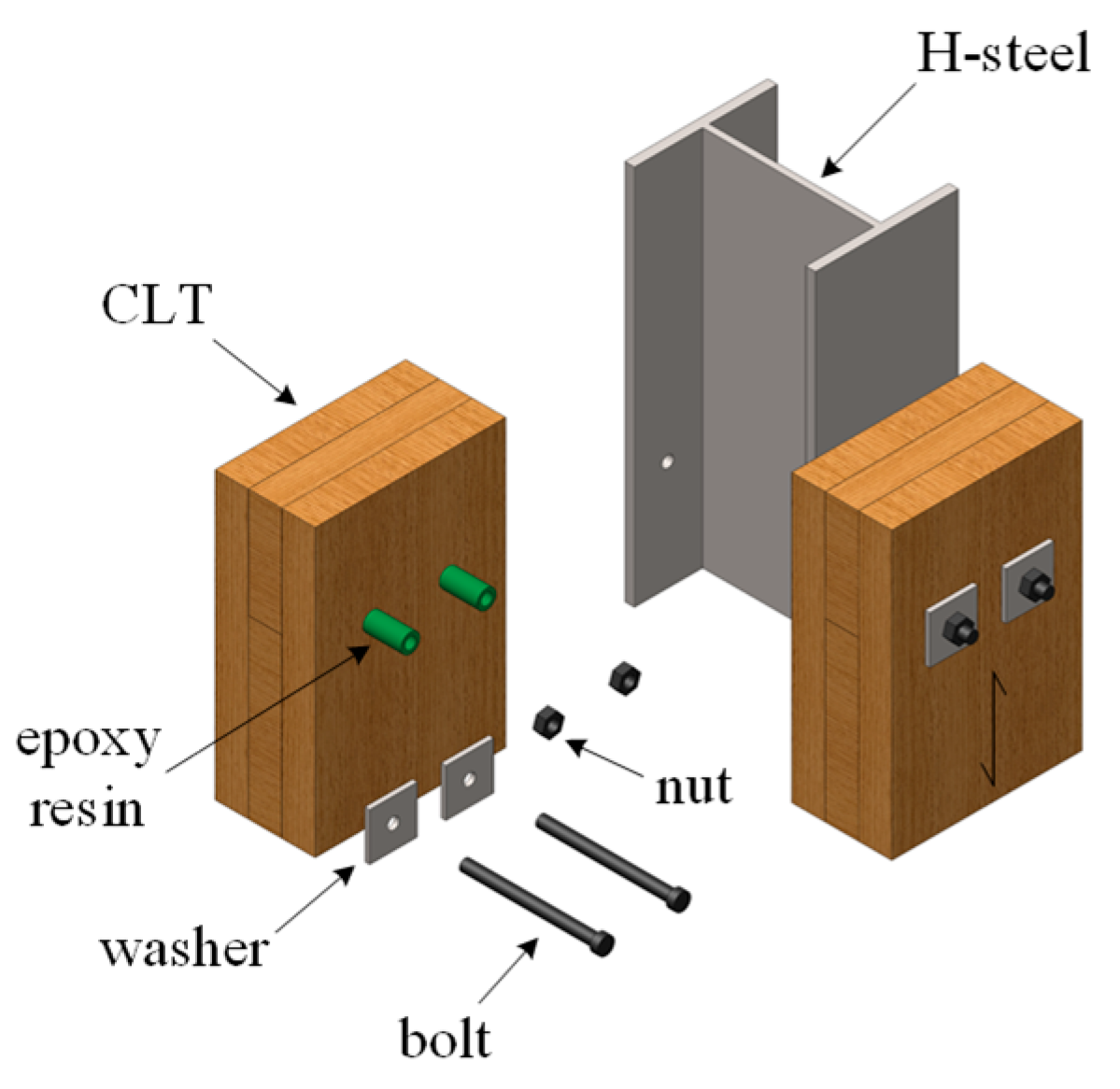

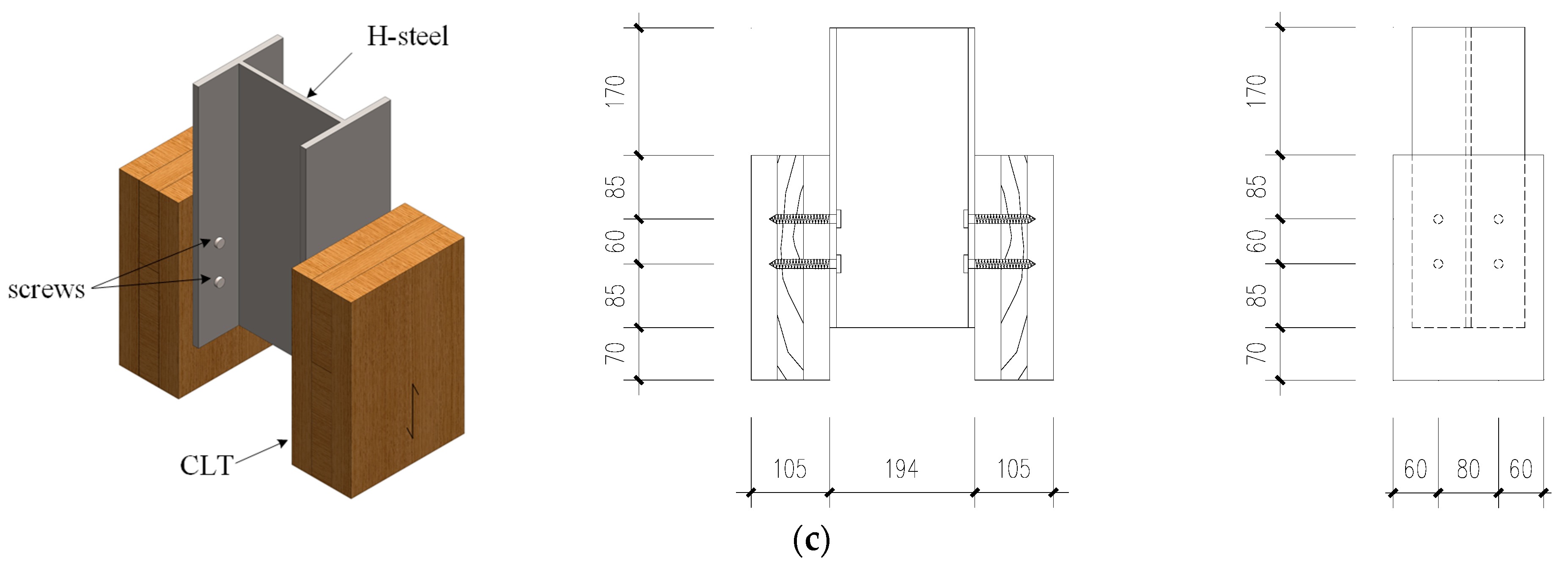

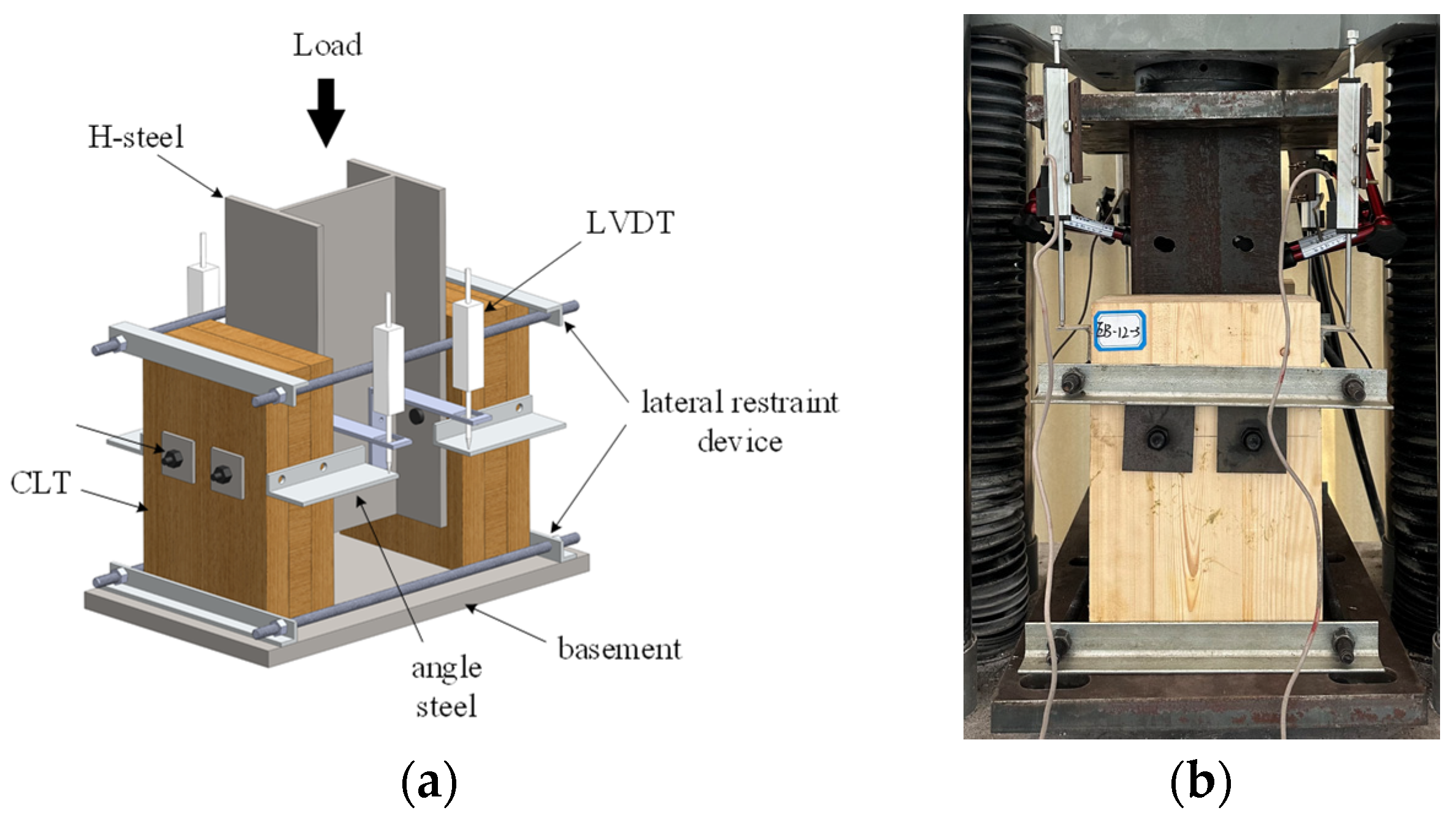
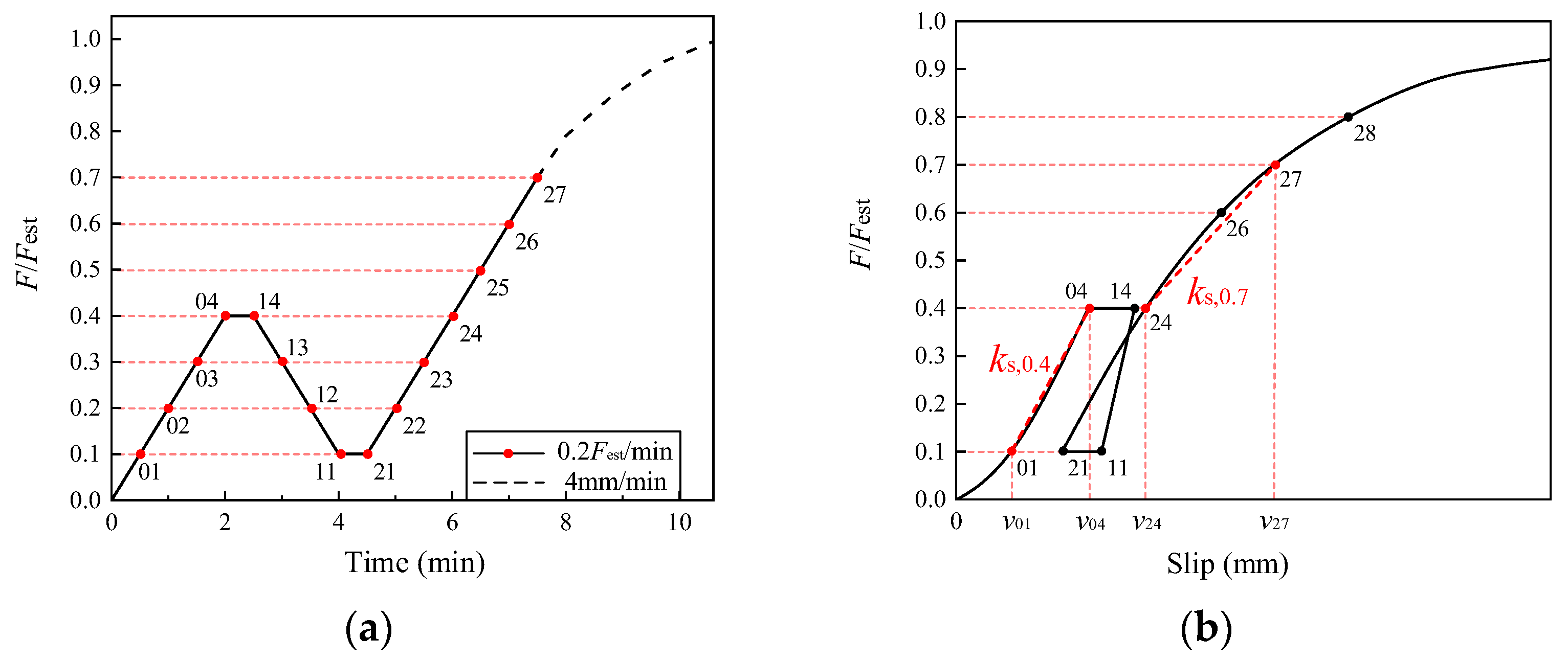



| Group | Shear Connector | Epoxy Resin | |||||
|---|---|---|---|---|---|---|---|
| Number of Rows | Number of Columns | D (mm) | L (mm) | Type | Strength Grade | ||
| 1B-12 | 1 | 2 | 12 | 140 | Partially threaded bolt | 8.8 | Without |
| 1BF-12 | 1 | 2 | 12 | 140 | Fully threaded bolt | 8.8 | Without |
| 1B#-12 | 1 | 2 | 12 | 140 | Partially threaded bolt | 4.8 | Without |
| 1BE-8 | 1 | 2 | 8 | 140 | Partially threaded bolt | 8.8 | With |
| 1BE-12 | 1 | 2 | 12 | 140 | Partially threaded bolt | 8.8 | With |
| 1BE-16 | 1 | 2 | 16 | 140 | Partially threaded bolt | 8.8 | With |
| 1S#-8 | 1 | 2 | 8 | 80 | Screw | 4.8 | Without |
| 1S#-12 | 1 | 2 | 12 | 80 | Screw | 4.8 | Without |
| 2S#-12 | 2 | 2 | 12 | 80 | Screw | 4.8 | Without |
| Fc, max (kN) | Ec (GPa) | fc (MPa) | τc (MPa) | ρ (kg/m3) | ω (%) | μ |
|---|---|---|---|---|---|---|
| 362.11 | 8.48 | 28.74 | 1.19 | 464.88 | 11.6 | 0.43 |
| Strength Grade | Type | Nominal Diameter (mm) | Maximum Load (kN) | Average Value (kN) | Tensile Strength (MPa) | ||
|---|---|---|---|---|---|---|---|
| Specimen 1 | Specimen 2 | Specimen 3 | |||||
| 4.8 | Screw | 8 | 17.24 | 18.23 | 18.42 | 17.96 | 357.48 |
| Screw | 12 | 40.25 | 40.06 | 37.93 | 39.41 | 348.63 | |
| Partially threaded bolt | 12 | 48.14 | 48.83 | 49.61 | 48.86 | 432.01 | |
| 8.8 | Partially threaded bolt | 8 | 43.43 | 41.48 | 41.01 | 41.97 | 835.39 |
| Partially threaded bolt | 12 | 103.06 | 101.03 | 105.04 | 103.04 | 911.53 | |
| Partially threaded bolt | 16 | 185.85 | 181.36 | 176.52 | 181.24 | 901.87 | |
| Fully threaded bolt | 12 | 70.93 | 79.54 | 73.46 | 74.64 | 660.29 | |
| Tensile Strength (MPa) | Bending Strength (MPa) | Compressive Strength (MPa) | Steel-to-Steel Tensile Shear Strength (MPa) | Complete Curing Time (h) |
|---|---|---|---|---|
| 19.57 | 77.5 | 107.6 | 21.3 | 24 |
| Environmental Resistance | Stress Resistance | Resistance to Medium Corrosion | ||||||
|---|---|---|---|---|---|---|---|---|
| Damp-Heat Aging Resistance (%) | Heat Aging Resistance (%) | Freeze–Thaw Resistance (%) | Long-Term Stress Resistance | Fatigue Stress Resistance | Salt Spray Resistance (%) | Seawater Immersion Resistance (%) | Resistance to Alkaline Medium | Resistance to Acidic Medium |
| −4.4 | −2.9 | −3.4 | Specimen does not fail | Specimen does not fail | −3.7 | −3.5 | Strength did not decrease, failure in concrete | Failure in concrete |
| Group | Fy (kN) | Eurocode 5 (kN) | Error (%) | Group | Fy (kN) | Eurocode 5 (kN) | Error (%) | Group | Fy (kN) | Eurocode 5 (kN) | Error (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1B-12 | 113.43 | 99.09 | −12.6 | 1BE-8 | 54.12 | 64.76 | +19.6 | 1S#-8 | 41.39 | 45.27 | +9.4 |
| 1BF-12 | 93.17 | 95.96 | +2.9 | 1BE-12 | 137.18 | 99.09 | −27.7 | 1S#-12 | 57.83 | 57.29 | −0.9 |
| 1B#-12 | 69.55 | 93.08 | +33.8 | 1BE-16 | 143.52 | 135.29 | −5.7 | 2S#-12 | 54.09 | 44.63 | −17.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lyu, Q.; Ye, J.; Wang, H.; Xu, J.; Xiao, Y.; Fu, B.; Li, X.; Zhang, Z. Experimental Study on the Shear Performance of Epoxy Resin-Bolted Steel-Cross Laminated Timber (CLT) Connections. Buildings 2025, 15, 3400. https://doi.org/10.3390/buildings15183400
Lyu Q, Ye J, Wang H, Xu J, Xiao Y, Fu B, Li X, Zhang Z. Experimental Study on the Shear Performance of Epoxy Resin-Bolted Steel-Cross Laminated Timber (CLT) Connections. Buildings. 2025; 15(18):3400. https://doi.org/10.3390/buildings15183400
Chicago/Turabian StyleLyu, Qing, Jinxun Ye, Huake Wang, Jiale Xu, Yunfeng Xiao, Bo Fu, Xianlei Li, and Zhaoyang Zhang. 2025. "Experimental Study on the Shear Performance of Epoxy Resin-Bolted Steel-Cross Laminated Timber (CLT) Connections" Buildings 15, no. 18: 3400. https://doi.org/10.3390/buildings15183400
APA StyleLyu, Q., Ye, J., Wang, H., Xu, J., Xiao, Y., Fu, B., Li, X., & Zhang, Z. (2025). Experimental Study on the Shear Performance of Epoxy Resin-Bolted Steel-Cross Laminated Timber (CLT) Connections. Buildings, 15(18), 3400. https://doi.org/10.3390/buildings15183400








