Towards a Generative Frame System of Ancient Chinese Timber Architecture: Structural Generation and Optimization of “Column Reduction” and “Column Relocation”
Abstract
1. Introduction
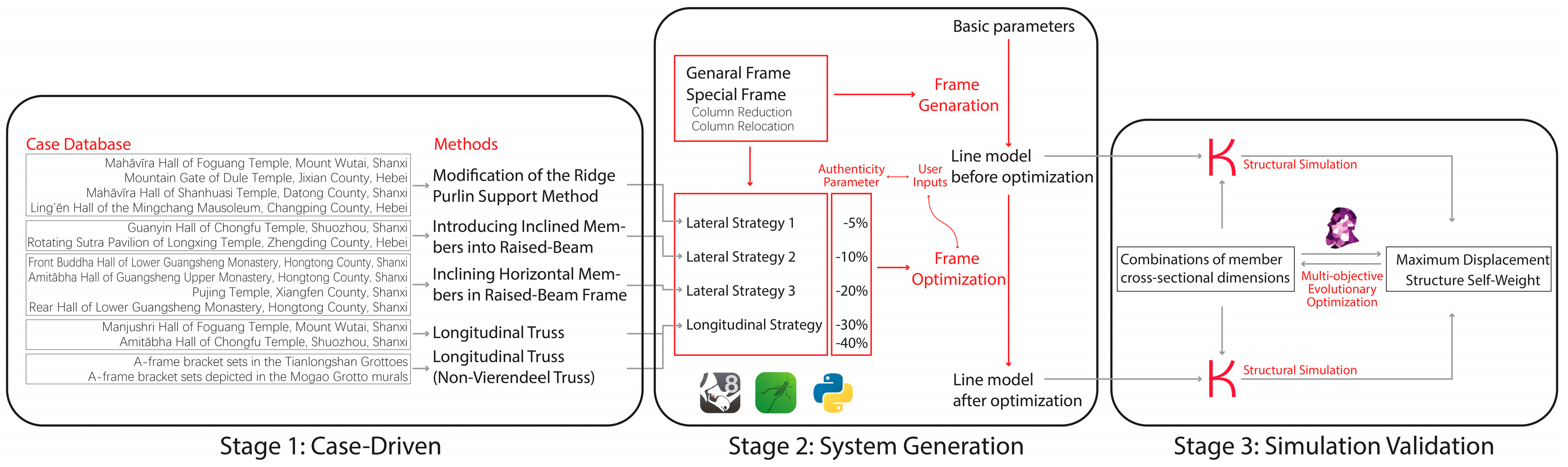
2. Materials and Methods
- (1)
- Stage One: Case-Driven—Extraction of Traditional Construction Prototypes
- (2)
- Stage Two: Generative System—Development of Structural Generation and Optimization System
- (3)
- Stage Three: Simulation Validation—Evaluation of Structural Mechanical Performance
3. Research Results
3.1. Stage 1: Case Studies for Algorithm Logic Identification
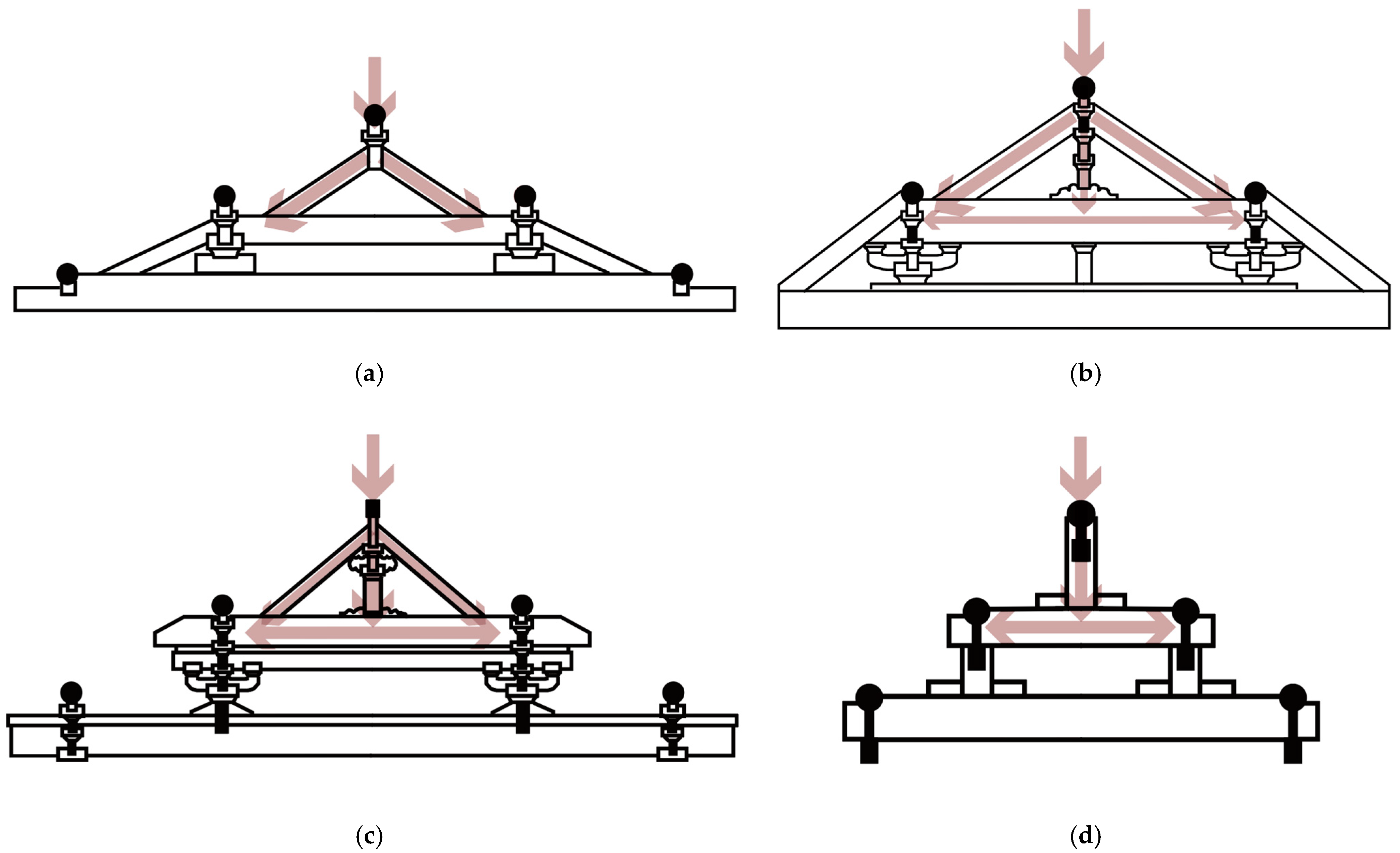
3.1.1. Lateral Load Transfer Utilizing Inclined Members
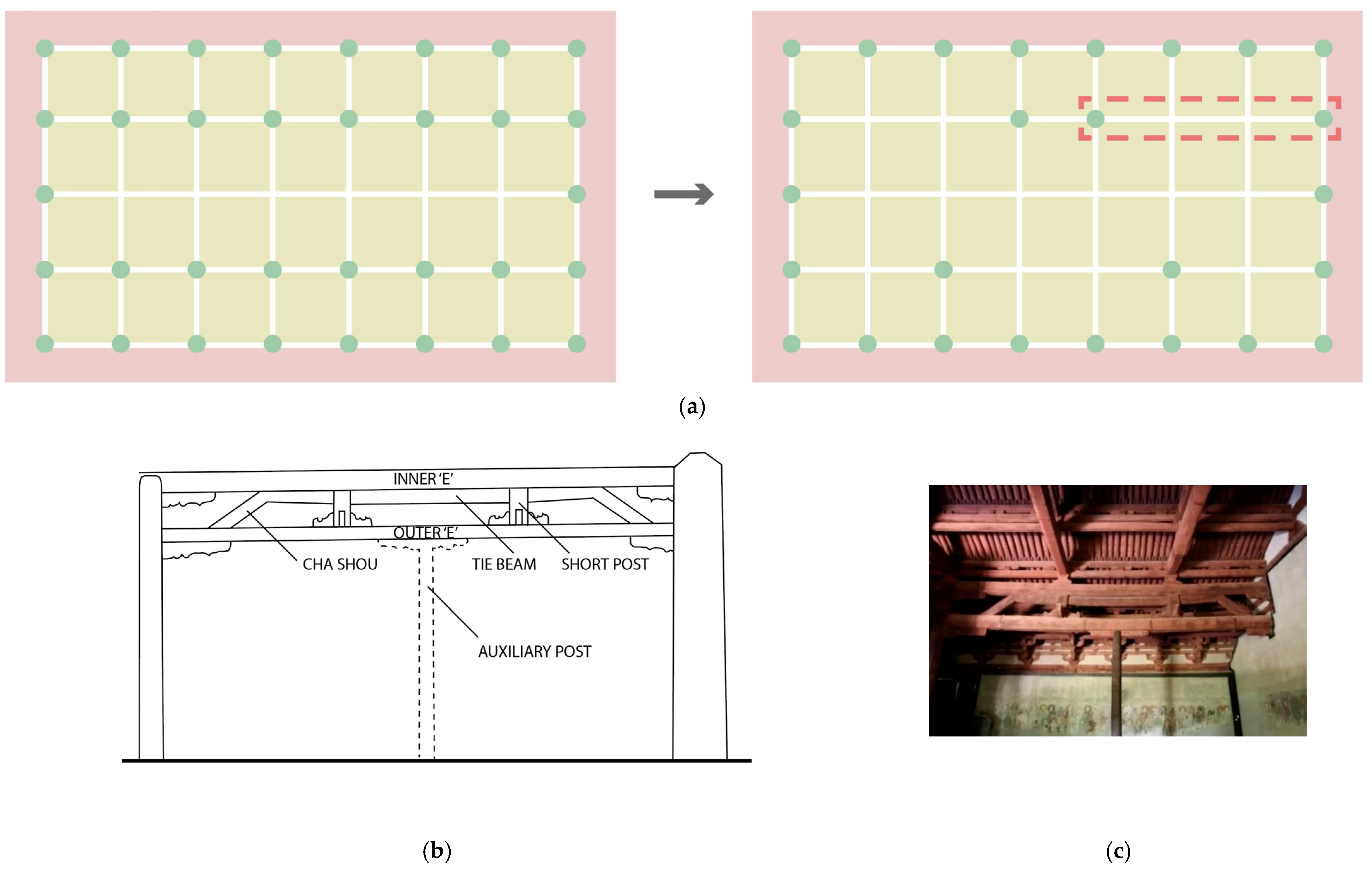
- (1)
- Cha Shou (Forked Brackets)
- (2)
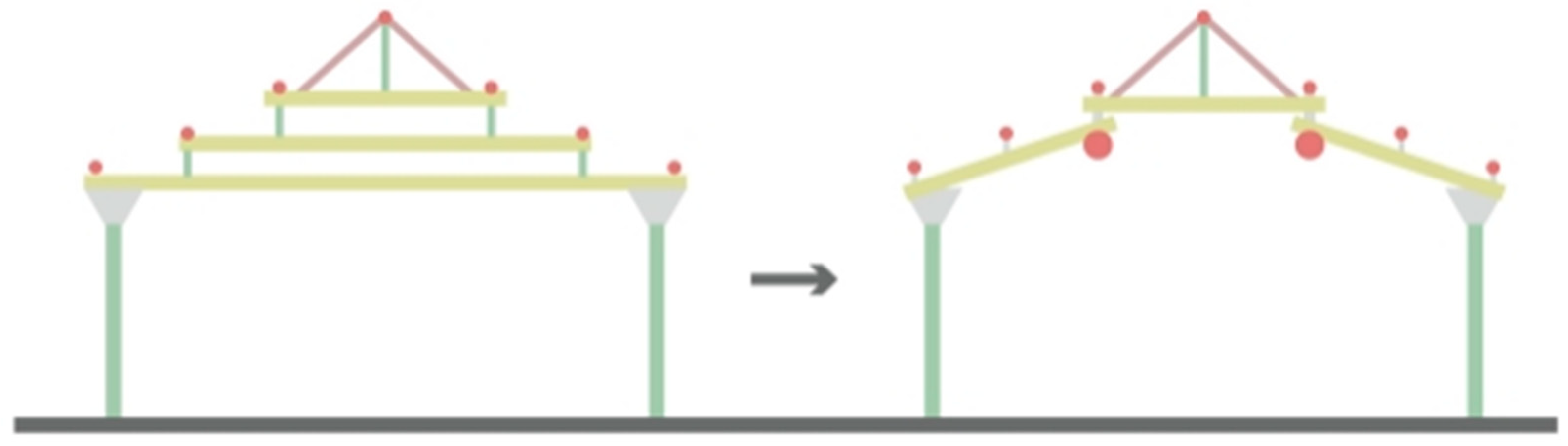
- Addition of Inclined Members to Existing Raised Beam Frame
- (3)
- Inclining Horizontal Members in Original Raised Beam Frames
3.1.2. Longitudinal Load Transfer Utilizing Inclined Members
- (1)
- Longitudinal Truss
- (2)
- Renzi Gong (Inverted-V Brackets)
3.1.3. Planar Oblique Application of Inclined Members
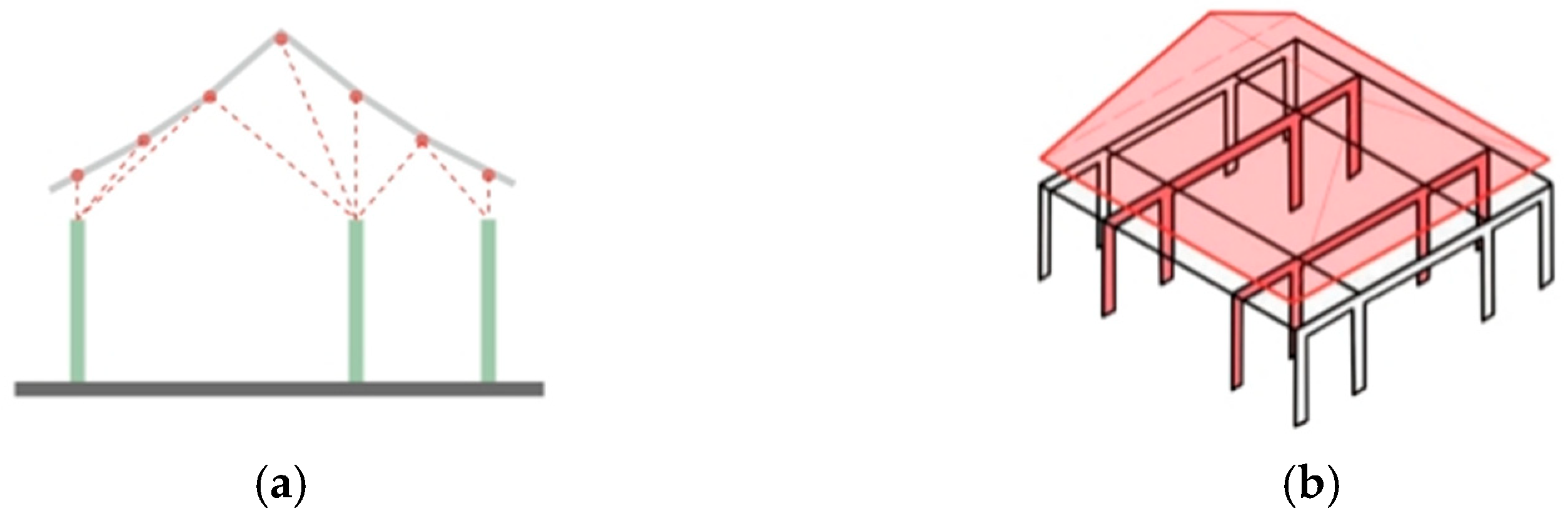
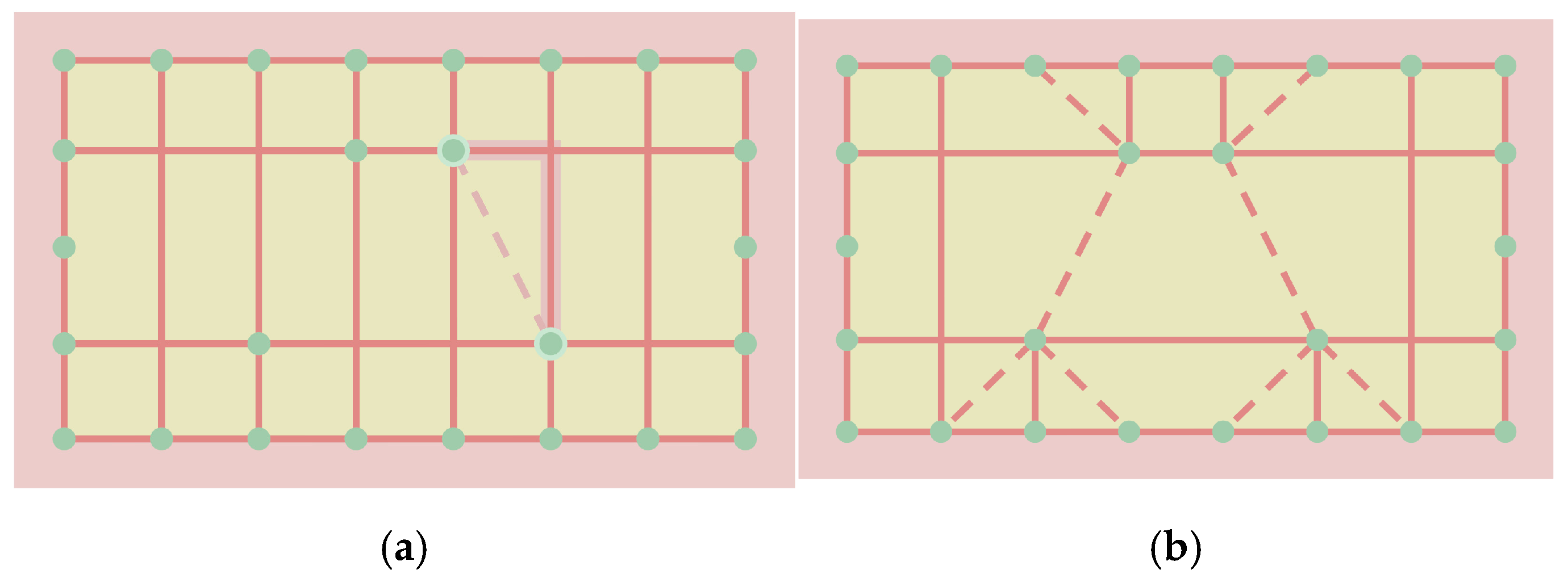
3.1.4. Strategy of Structural Optimization
3.2. Stage 2: Prototype of the Generative Frame System
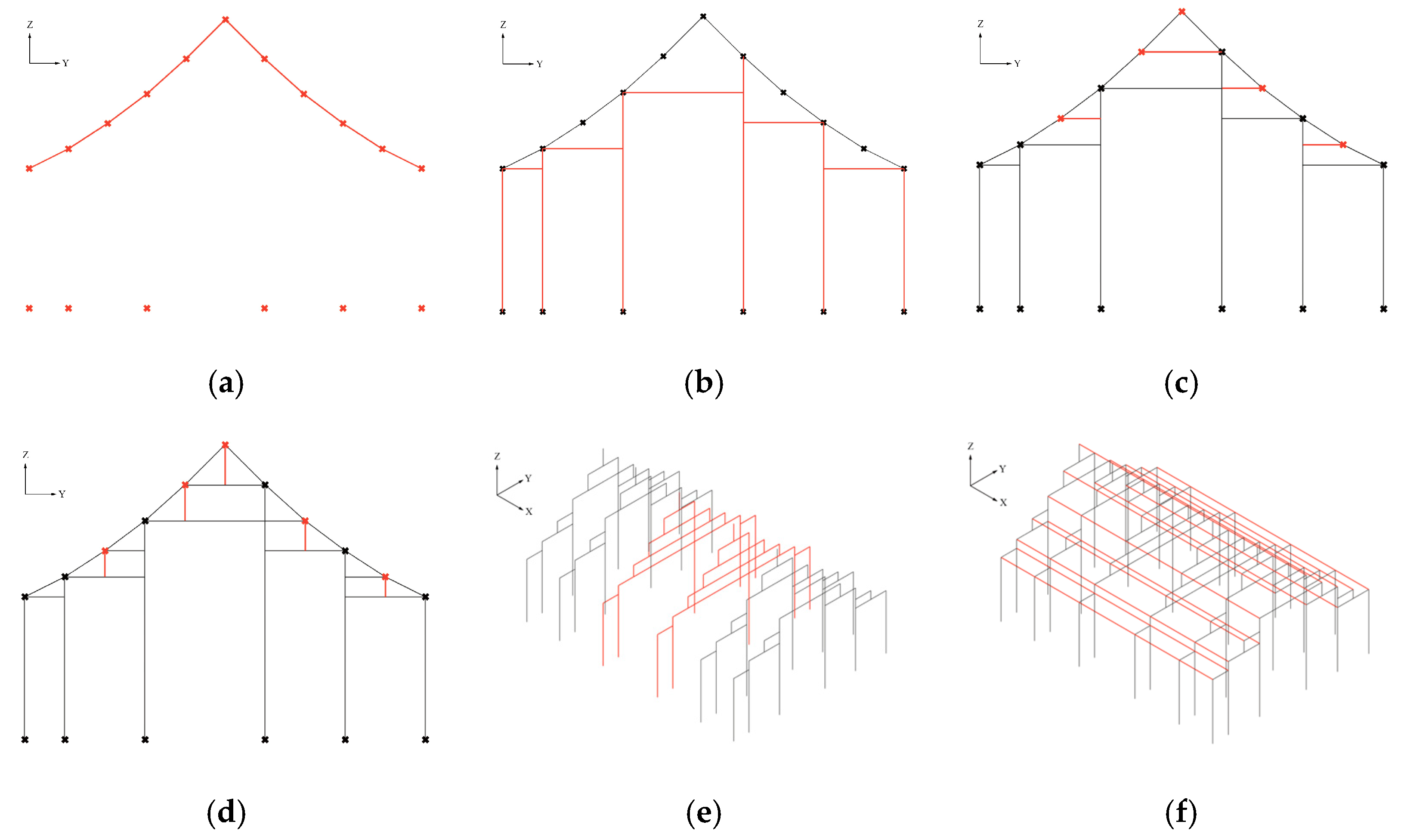
3.2.1. Step 1: Generation of the Raised Beam Frame
- (1)
- Component 1-1: Generate the column bottom points and purlin line
- (2)
- Component 1-2: Generate the columns and main beams
- (3)
- Component 1-3: Generate the secondary beams and short posts
- (4)
- Component 1-4: Generate all bays of frame, as well as the purlins and tiebeams.
3.2.2. Step 2: Generation of the Frame Line Model After Optimization
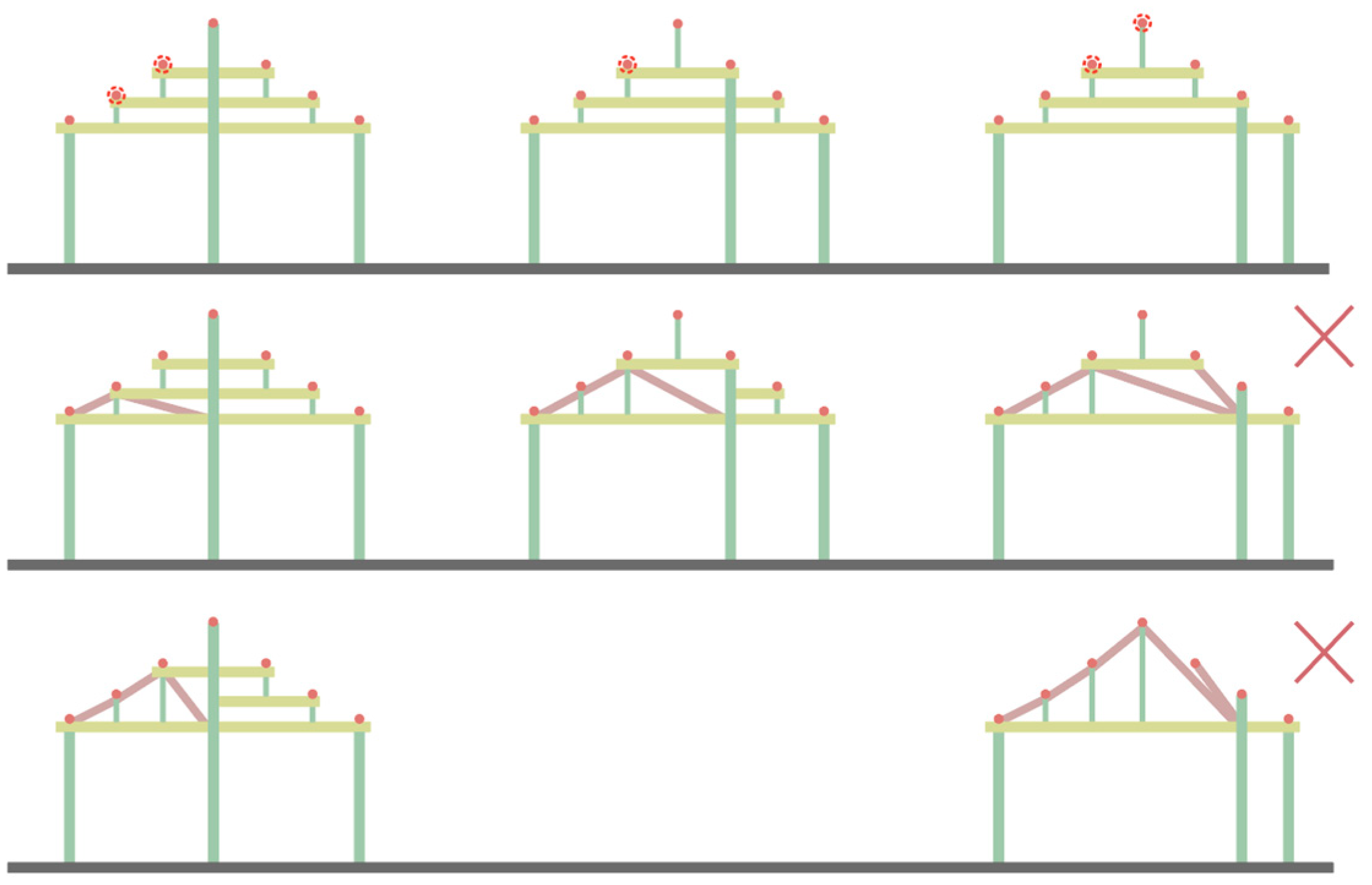
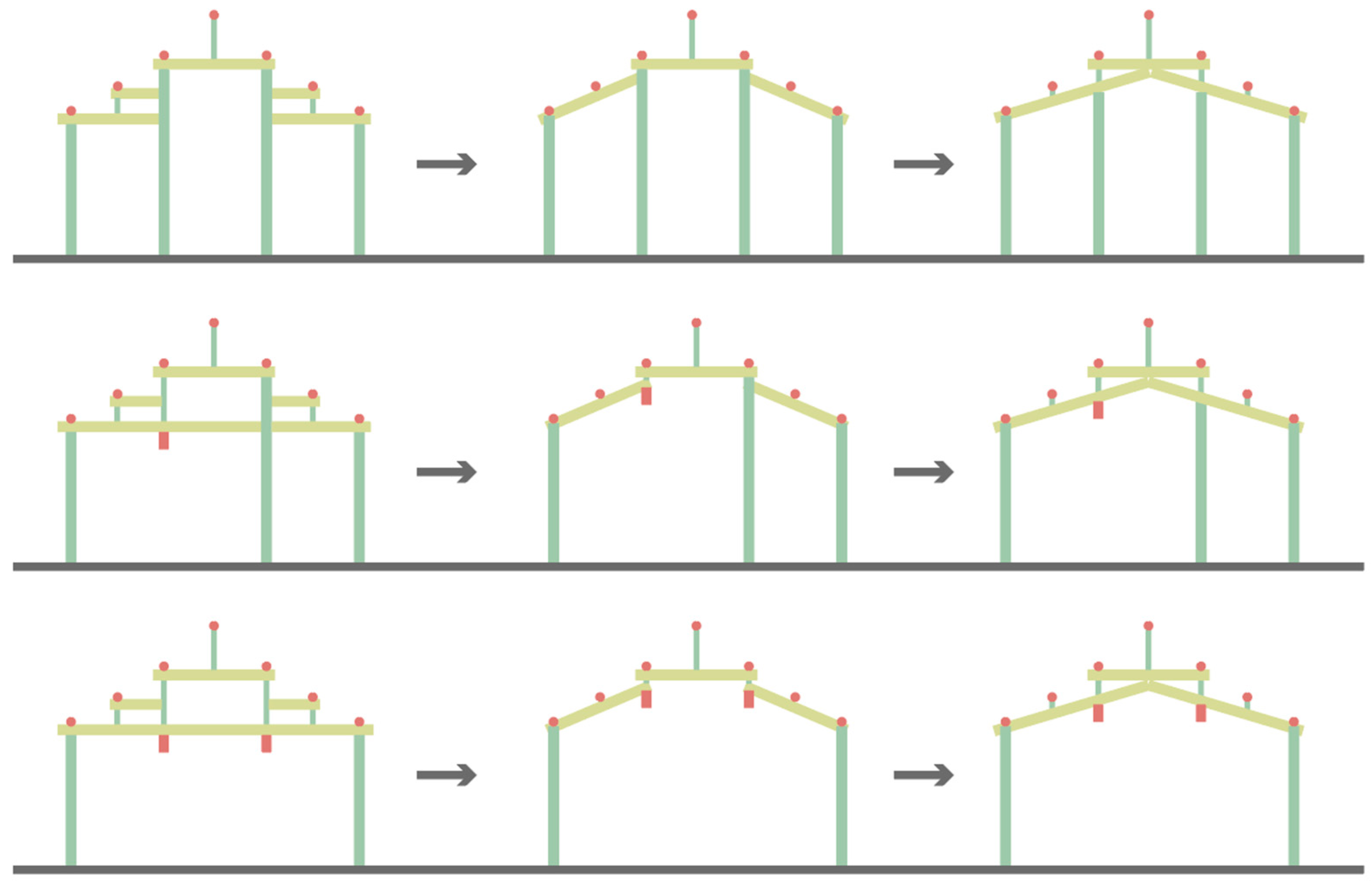
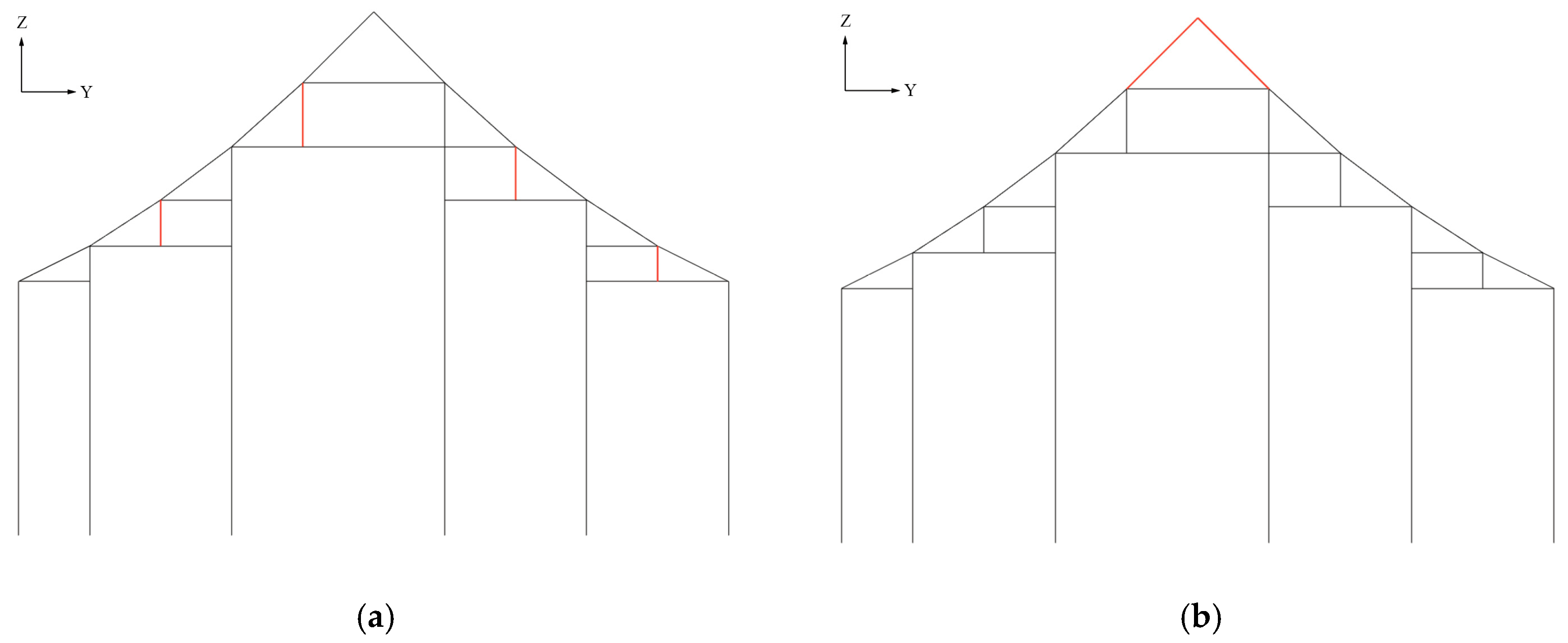
Lateral Optimization Strategy 1—Modification of the Ridge Purlin Support Method
- (1)
- Component 2-1-1: Determine if any column lies at the center and remove the top short post
- (2)
- Component 2-1-2: Preserve the top Purlin line (top chords) and generate the frame after optimization
Lateral Optimization Strategy 2—Introducing Inclined Members into the Original Raise-Beam Frame
- (1)
- Component 2-2-1: Identify the column spans to be optimized
- (2)
- Component 2-2-2: Identify the purlin points at mid-span
- (3)
- Component 2-2-3: Generate the frame after optimization
Lateral Optimization Strategy 3—Inclining Horizontal Members into the Original Raise-Beam Frame
- (1)
- Component 2-3-1: Identify the column spans to be optimized
- (2)
- Component 2-3-2: Generate the inclined member
- (3)
- Component 2-3-3: Generate the frame after optimization
Longitudinal Optimization Strategy—Generate the Longitudinal Truss
- (1)
- Component 2-4-1: Identify the column spans to be optimized
- (2)
- Component 2-4-2: Generate the longitudinal truss
- (3)
- Component 2-4-3: Revise some members and generate the frame after optimization
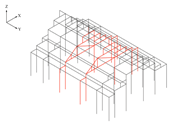
3.3. Stage 3: Validation via Structural Simulation
3.3.1. Step 1: Structural Simulation Analysis Based on Karamba3D
- (1)
- Member Specification: Reflecting authentic traditional Chinese timber construction characteristics, four categories—columns, short post, purlins, and slender rods introduced by lateral optimization strategy 3—are modeled with solid circular cross-sections. Main beams, secondary beams, longitudinal tie beams (fang), and inclined members resulting from lateral optimization strategies adopt solid rectangular cross-sections. Material properties for timber members are defined as follows: Young’s Modulus: 1050 kN/cm2; in-plane shear modulus: 360 kN/cm2; transverse shear modulus: 360 kN/cm2; specific weight: 6 kN/m3; coefficient of thermal expansion: 5.0 × 10−6 °C−1; tensile strength: 1.3 kN/cm2; compressive strength: −1.3 kN/cm2.
- (2)
- Support Conditions: In traditional Chinese timber architecture, columns typically rest on masonry bases, forming hinged connections via the “column plinth—column base—column foot” support system. This study models column base supports as hinged at ground level, restricting translational movements in all three directions while allowing for rotational freedom. It should be noted that column base tenons, socketed stone plinths, iron ties, interface friction, and localized bearing crushing collectively provide a finite, state-dependent rotational stiffness at the base. Modeling the support as an ideal hinge suppresses this restraint, thereby reducing lateral support stiffness, lengthening the fundamental period, and shifting part of the bending demand to neighboring joints. Such an idealization can bias predictions of drift and member demand, thereby reducing the accuracy of the simulation.
- (3)
- Load Conditions: Ancient Chinese structures primarily experience three load types: vertical loads (self-weight, snow, and rain), horizontal loads (wind and seismic activities), and incidental loads (temperature and moisture variations, uneven foundation settlement). For single-story hall structures, vertical loads dominate. Given that traditional strategies for addressing horizontal loads mainly involve brick shear walls and subtle column adjustments, such as “column inclination” and “raising,” which have limited direct interaction with the beam frame system, this study simplifies the load model to structural self-weight and uniformly distributed linear loads (5 kN/m) on each purlin, excluding horizontal and other special loads.
- (4)
- Joint definition: Traditional mortise–tenon joints are neither perfectly pinned, nor perfectly rigid. Geometric interlock and frictional pre-tightening provide rotational restraint, whereas assembly tolerance, wood compressibility, and micro-slip make the joint softer at small rotations and stiffer after bearing closes; under cyclic actions, energy dissipation and stiffness degradation occur, yielding an overall semi-rigid behavior. For computational tractability, all joints are idealized as rigid in this study. This increases global stiffness and alters internal force paths and deformation patterns, potentially underestimating drifts and overestimating end actions, thereby imposing inherent limits on simulation accuracy.
3.3.2. Step 2: Multi-Objective Optimization Design Based on Wallacei
4. Conclusions and Discussions
4.1. Conclusions
4.2. Cross-System Adaptability
4.3. Limitations and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Pseudo-Code of All Components in Stage 2
Appendix A.1. Step 1: Generation of the Raised Beam Frame
- (1)
- Component 1-1: Generate the column bottom points and purlin line
| Figure | Component |
|---|---|
 | Input: depthRafterCounts, rafterLength, eaveColumnHeight, raiseFactors |
| Output: columnBottomPoints, purlinPoints, purlinLine | |
|
- (2)
- Component 1-2: Generate the columns and main beams
| Figure | Component |
|---|---|
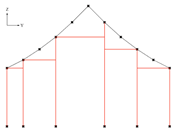 | Input: columnBottomPoints, purlinLine, yCoordinateOfPurlinMidpoint |
| Output: columns, mainBeams | |
project point i toward −Y until it intersects the columns, create a new line from point i to that intersection, and append it to mainBeams. elif y(i) < yCoordinateOfPurlinMidpoint: project point i toward +Y until it intersects the columns, create a new line from point i to that intersection, and append it to mainBeams. |
- (3)
- Component 1-3: Generate the secondary beams and short post
| Figure | Component |
|---|---|
  | Input: purlinPoints, columnTopPoints, columns, mainBeams |
| Output: secondaryBeams, shortPosts, frame | |
project i in the −Y direction until it intersects the columns, and create a line connecting i to that intersection, and append it to secondaryBeams elif y(i) is less than yCoordinateOfPurlinMidpoint: project i in +Y direction and append the line to secondaryBeams
if y(i) is equal to y(j): for each point m in columnBottomPoints: if no m exists whose Y coordinate lies between y(i) and y(j): create a line connecting i and j, and append it to secondaryBeams.
|
- (4)
- Component 1-4: Generate all bays of frame, as well as the purlins and tiebeams
| Figure | Component |
|---|---|
 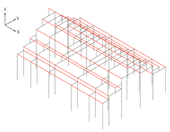 | Input: widths, frame, purlin Points, column Bottom Points |
| Output: frames, purlins, tie beams | |
|
Appendix A.2. Step 2: Generation of the Frame Line Model After Optimization
- Lateral Optimization Strategy 1—Modification of the Ridge Purlin Support Method
- (1)
- Component 2-1-1: Determine if any column lies at the center and remove the top short post
| Figure | Component |
|---|---|
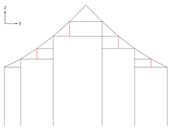 | Input: columnTopPoints, yCoordinateOfPurlinMidpoint, shortPosts, frame |
| Output: newShortPosts or frame | |
return frame and stop further steps else: proceed to the next steps
|
- (2)
- Component 2-1-2: Preserve the top Purlin line (top chords) and generate the frame after optimization
| Figure | Component |
|---|---|
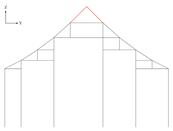 | Input: purlinLine, columns, mainBeams, secondaryBeams |
| Output: topChords, frameAfterOptimization1 | |
only keep two line i with the highest endpoint return two segments collectively labeled as topChords
|
- Lateral Optimization Strategy 2—Introducing inclined members into the original raise-beam frame
- (1)
- Component 2-2-1: Identify the column spans to be optimized
| Figure | Component |
|---|---|
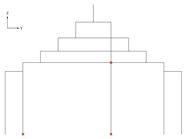 | Input: columnBottomPoints, purlinLine, yCoordinateOfPurlinMidpoint, frame |
| Output: columnABottomPoint, columnBBottomPoint, PointX or frame | |
for each point j in purlinLine: sort the absolute differences in y(j) from yCoordinateOfPurlinMidpoint. keep the three smallest values in centralPurlinPointYDifference. if (y(j) − yCoordinateOfPurlinMidpoint) is within centralPurlinPointYDifference: append j in centralPurlinPoints. if the y(columnABottomPoint) is contained in the y(centralPurlinPoints): return columnABottomPoint and proceed to the next steps. else: return frame and stop further steps.
append i in columnBottomPointsOpposite for each point i in columnBottomPointsOpposite: sort the absolute differences between y(i) and y(columnABottomPoint). take the smallest result and assign i as columnBBottomPoint.
define columnBTopPoint as point m. project columnBTopPoint along either +Y or −Y until it intersects columnA, define PointX as the intersection point. |
- (2)
- Component 2-2-2: Identify the purlin points at mid-span
| Figure | Component |
|---|---|
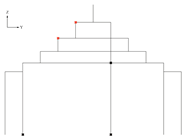 | Input: purlinPoints, columnABottomPoint, columnBBottomPoint, rafterLength |
| Output: pointM, pointN | |
append point i in purlinPointsInBetween.
pointM is the element at index (count/2) − 1, and pointN is the element at index (count/2). elif this number is odd: pointM and pointN both refer to the middle element at index (count − 1)/2.
|
- (3)
- Component 2-2-3: Generate the frame after optimization
| Figure | Component |
|---|---|
 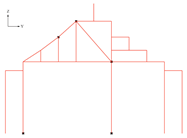  | Input: columns, mainBeams, secondaryBeams, shortPosts, columnA, columnB, PointX, pointM, pointN |
| Output: frameAfterOptimization2 | |
for each point i in purlinPoints: if the y coordinate of i lies between y(columnBBottomPoints) and y(PointM): append point i in inclinedMember2Points. inclinedMember2 is the polyline connecting all inclinedMember2Points.
project point i in the −Z direction until it intersects lineAB. connect the point i and the intersection point to form the newShortPosts. for each line i in shortPosts: for each line j in newShortPosts: if line i’ s endpoint shares a Y coordinate with line j’s endpoint: remove line i. append the newShortPosts to the shortPosts.
remove line i.
|
- Lateral Optimization Strategy 3—Inclining horizontal members into the original raise-beam frame
- (1)
- Component 2-3-1: Identify the column spans to be optimized
| Figure | Component |
|---|---|
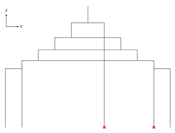 | Input: columnBottomPoints, yCoordinateOfPurlinMidpoint |
| Output: columnABottomPoint, columnBBottomPoint or frame | |
append each y difference to yDifferenceLargeColumnBottomPoints. for each i in yDifferenceLargeColumnBottomPoints: if i is equal to one rafter: return frame and stop further steps. else: proceed to the next steps.
|
- (2)
- Component 2-3-2: Generate the inclined member
| Figure | Component |
|---|---|
 | Input: columnABottomPoint, columnBBottomPoint, purlinLine, rafterLength |
| Output: inclinedMember | |
|
- (3)
- Component 2-3-3: Generate the frame after optimization
| Figure | Component |
|---|---|
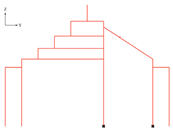  | Input: columns, mainBeams, secondaryBeams, shortPosts, inclinedMember |
| Output: frameAfterOptimization3 | |
remove line i from mainBeams.
Project those points in the +Z direction until they intersect purlinLine. Define the lines connecting those points with intersections as tinyMembers.
|
- Longitudinal optimization strategy
- (1)
- Component 2-4-1: Identify the column spans to be optimized
| Figure | Component |
|---|---|
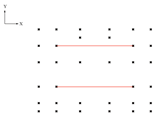 | Input: columnBottomPoints, widths |
| Output: maxSpanLine | |
create the spanLines connecting points one by one.
if i is not strictly larger than any widths: remove i. |
- (2)
- Component 2-4-2: Generate the longitudinal truss
| Figure | Component |
|---|---|
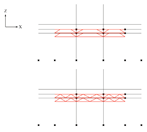 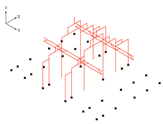 | Input: All inputs of generation of raised beam structure, normalMainBeams, trussSpanHeightRatio, vierendeelTrussBool |
| Output: newFrames, truss | |
remove the middle two diagonalWebs.
|
- (3)
- Component 2-4-3: Revise some members and generate the frame after optimization
| Figure | Component |
|---|---|
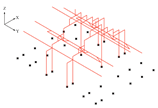  | Input: newFrames, newColumns, newMainBeams, newSecondaryBeams, newShortPosts, tieBeams, truss, normalFrames |
| Output: revisedFrames, frameAfterOptimization4 | |
if line i intersects line j: shorten line i at the intersection.
remove segment i.
|
References
- Liang, W.; Ahmad, Y.; Mohidin, H.H.B. The Development of the Concept of Architectural Heritage Conservation and Its Inspiration. Built Herit. 2023, 7, 21. [Google Scholar] [CrossRef]
- Karadag, İ. Machine Learning for Conservation of Architectural Heritage. OHI 2023, 48, 23–37. [Google Scholar] [CrossRef]
- Yamato, S. The Tradition of Wooden Architecture in Japan; Agency for Cultural Affairs: Kyoto, Japan, 2006. [Google Scholar]
- Wibowo, A.S. Conservation of Wooden Architecture: Willingness, Support and Tradition. Procedia-Soc. Behav. Sci. 2015, 184, 388–393. [Google Scholar] [CrossRef][Green Version]
- Zhang, J.; Wang, Z.; Wang, W. Application of Smart Modelling Framework for Traditional Wooden Architecture. Buildings 2024, 14, 2130. [Google Scholar] [CrossRef]
- Abdelmoniem, A.M. Preserving the Wooden Heritage of the National Police Museum: Challenges and Conservation Strategies. J. Infrastruct. Preserv. Resil. 2025, 6, 14. [Google Scholar] [CrossRef]
- Jardim, P.I.L.G.; Monteiro, S.N.; Azevedo, A.R.G.D.; De Araújo, V.A.; Panzera, T.H.; Christoforo, A.L. Preservation and Maintenance of Wood-Based Structures of Historic Buildings: A Systematic Literature Review on Structural Recovery Techniques. Case Stud. Constr. Mater. 2025, 22, e04706. [Google Scholar] [CrossRef]
- Lapshina, E.G.; Eshchin, D.V. Wooden Houses of Penza Town of the 19th–Early 20th Centuries and the Problem of Heritage Preservation. IOP Conf. Ser. Mater. Sci. Eng. 2020, 775, 012068. [Google Scholar] [CrossRef]
- Valetti, L.; Floris, F.; Pellegrino, A. Renovation of Public Lighting Systems in Cultural Landscapes: Lighting and Energy Performance and Their Impact on Nightscapes. Energies 2021, 14, 509. [Google Scholar] [CrossRef]
- Han, Y.; Chun, Q.; Xu, X.; Teng, Q.; Dong, Y.; Lin, Y. Wind Effects on Chinese Traditional Timber Buildings in Complex Terrain: The Case of Baoguo Temple. J. Build. Eng. 2022, 59, 105088. [Google Scholar] [CrossRef]
- Guo, Q. Yingzao Fashi: Twelfth-Century Chinese Building Manual. Archit. Hist. 1998, 41, 1–13. [Google Scholar] [CrossRef]
- Shiqiao, L. Reconstituting Chinese Building Tradition: The Yingzao Fashi in the Early Twentieth Century. J. Soc. Archit. Hist. 2003, 62, 470–489. [Google Scholar] [CrossRef]
- Lin, F.C.-h. Chinese Architecture and Metaphor: Song Culture in the Yingzao Fashi Building Manual. Asian Stud. Rev. 2014, 38, 301–302. [Google Scholar] [CrossRef]
- Hang, T. Beside Yingzao: An Index of Chinese Building Traditions. Master’s Thesis, Yale University, New Haven, CT, USA, 2022. (In Chinese). [Google Scholar]
- Liang, S.C. History of Chinese Architecture; Hualing Press: Beijing, China, 2023; ISBN 978-7-5169-2638-3. (In Chinese) [Google Scholar]
- Lin, H.Y. Lin Huiyin on Architecture; Jiuzhou Press: Beijing, China, 2005; ISBN 978-7-80195-313-1. (In Chinese) [Google Scholar]
- Piao, S.Y.; Phoenix Space. The Wisdom Hidden in Wood: Notes on Traditional Chinese Architecture; Jiangsu Phoenix Science and Technology Press: Nanjing, China, 2020; ISBN 978-7-5713-1493-4. (In Chinese) [Google Scholar]
- Wang, Q.J. The Miracle of Timber Frames: Great Ancient Chinese Architecture; China Architecture & Building Press: Beijing, China, 2023; ISBN 978-7-111-72581-7. (In Chinese) [Google Scholar]
- Zheng, W. A Study on the Technique of Reducing and Shifting Columns in the Timber Structure of Huizhou-Style Residential Halls in Hongcun, Southern Anhui. Archit. Cult. 2019, 227–229. (In Chinese) [Google Scholar]
- Zou, C.; Li, H. A study on the reasons for the prevalence and historical significance of the column-reduction technique in Yuan Dynasty timber architecture. Anhui Archit. 2014, 20, 33–35. (In Chinese) [Google Scholar]
- Gámez, O.; Bignon, J.-C.; Duchanois, G. Assisted Construction of Non-Standard Wooden Walls and Envelope Structures by Parametric Modeling. In Communications in Computer and Information Science; Springer: Berlin/Heidelberg, Germany, 2015; pp. 291–308. ISBN 978-3-662-47385-6. [Google Scholar]
- Khidmat, R.P.; Fukuda, H. Kustiani Design Optimization of Hyperboloid Wooden House Concerning Structural, Cost, and Daylight Performance. Buildings 2022, 12, 110. [Google Scholar] [CrossRef]
- Massafra, A.; Prati, D.; Predari, G.; Gulli, R. Wooden Truss Analysis, Preservation Strategies, and Digital Documentation through Parametric 3D Modeling and HBIM Workflow. Sustainability 2020, 12, 4975. [Google Scholar] [CrossRef]
- Prati, D.; Zuppella, G.; Mochi, G.; Guardigli, L.; Gulli, R. Wooden trusses reconstruction and analysis through parametric 3D modeling. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2019, XLII–2/W9, 623–629. [Google Scholar] [CrossRef]
- Wang, X.; Wu, C.; Que, R.; Bai, C. Algorithm modeling of ancient architecture for heritage documentation. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2019, XLII–2/W15, 1209–1213. [Google Scholar] [CrossRef]
- Ren, P.; Zhou, M.; Wu, Z.; Zhang, J.; Huang, Y.; Shui, W. Data-Driven Modeling for Chinese Ancient Architectures. In Proceedings of the Symposium on VR Culture and Heritage—Volume 2, Proceedings of the the 15th International Conference on Virtual-Reality Continuum and its Applications in Industry, Zhuhai, China, 3–4 December 2016; ACM: New York, NY, USA, 2016; pp. 59–62. [Google Scholar]
- Song, X.; Wu, X.; Yan, B.; Meng, J.; Chen, S. Design Principles and Case Analysis of Student Structural Design Competition Projects. Mech. Pract. 2020, 42, 388–393. [Google Scholar]
- Li, B. A Study on the Main Inclined Timber Components in Traditional Chinese Architecture. Master’s Thesis, Shaanxi Normal University, Xi’an, China, 2017. [Google Scholar]
- Liang, S.; Fei, W. Illustrated History of Chinese Architecture: Chinese–English Bilingual Edition; Liang, C., Translator; Baihua Literature and Art Publishing House: Beijing, China, 2001. [Google Scholar]
- Liu, J. An Investigation of the Architectural Artistic Characteristics of the Jin Dynasty Based on Chongfu Temple at Shuozhou. Master’s Thesis, Shanxi University, Taiyuan, China, 2015. (In Chinese). [Google Scholar]
- Zhang, Y. Measured Drawings of Guangsheng Temple in Hongtong, Shanxi. J. Chin. Archit. Hist. Theory 2014, 433–443. (In Chinese) [Google Scholar]
- Hua, Y. Archaeological Observations on the Curved-Foot Transformation of Renzi Gong Brackets. J. Image Hist. 2022, 135–161. (In Chinese) [Google Scholar]
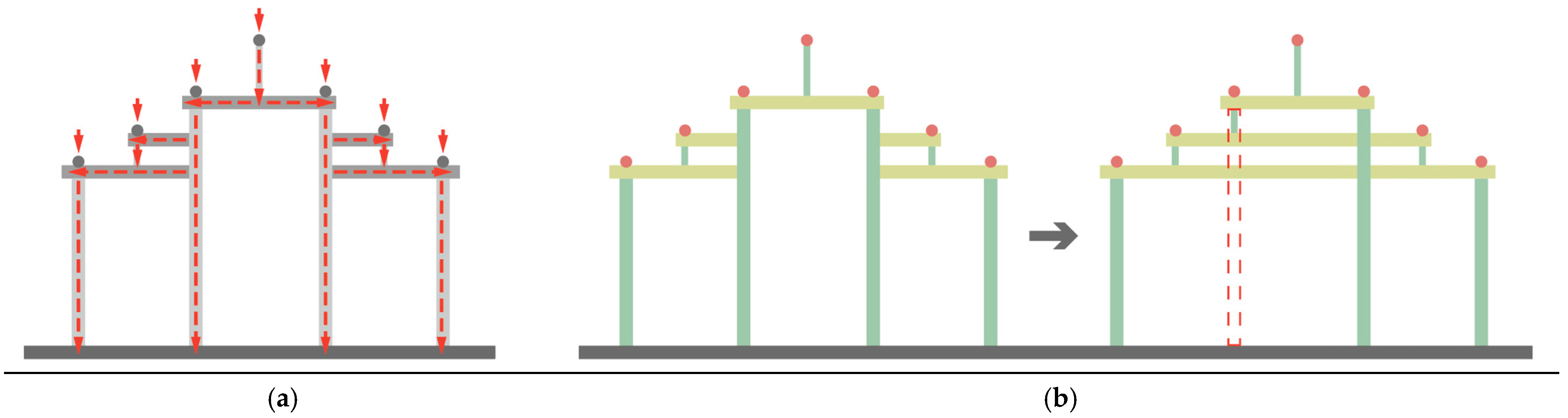












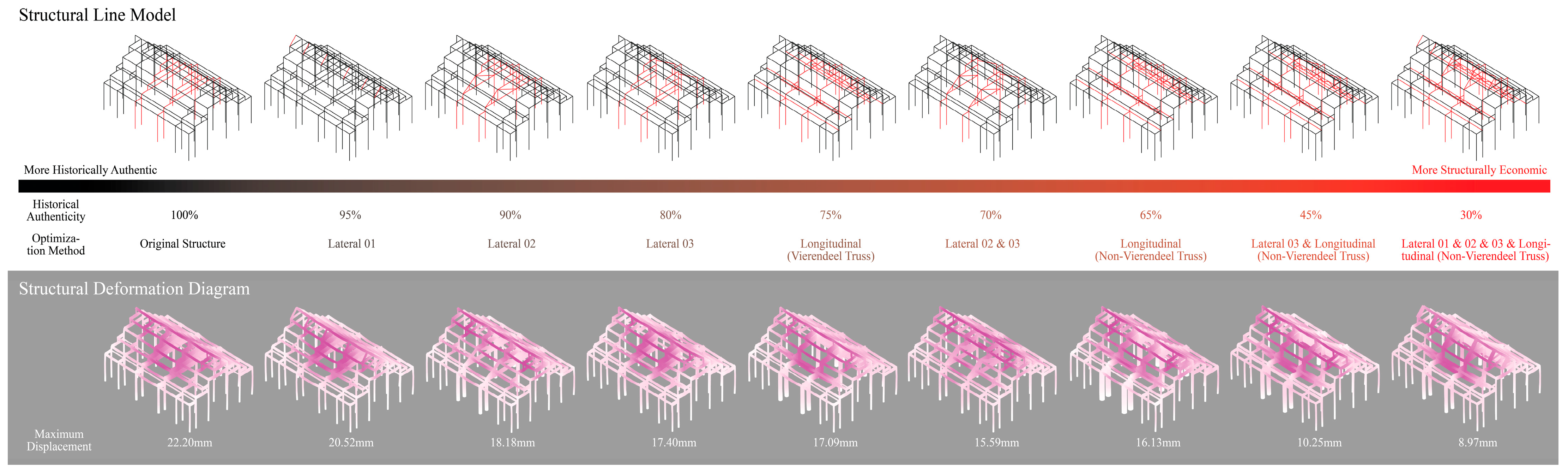
| NO. | Before Optimization | After Optimization | ||
|---|---|---|---|---|
| Structure Self-Weight (t) | Maximum Displacement (mm) | Structure Self-Weight (t) | Maximum Displacement (mm) | |
| 1 | 64.40 | 17.79 | 56.49 | 14.56 |
| 2 | 81.66 | 13.49 | 56.49 | 14.56 |
| 3 | 75.50 | 14.59 | 51.49 | 16.55 |
| 4 | 82.33 | 13.45 | 84.35 | 11.56 |
| 5 | 45.89 | 23.38 | 51.49 | 16.55 |
| 6 | 45.89 | 23.38 | 50.36 | 16.85 |
| 7 | 64.40 | 17.79 | 45.18 | 21.19 |
| 8 | 82.33 | 13.45 | 69.55 | 11.99 |
| 9 | 68.70 | 14.60 | 84.35 | 11.56 |
| 10 | 75.50 | 14.59 | 45.18 | 21.19 |
| 11 | 44.35 | 25.12 | 50.36 | 16.85 |
| 12 | 44.01 | 27.12 | 45.18 | 21.19 |
| 13 | 64.40 | 17.79 | 58.23 | 13.69 |
| 14 | 44.65 | 25.02 | 45.55 | 19.90 |
| 15 | 43.51 | 27.14 | 50.36 | 16.85 |
| 16 | 52.15 | 21.73 | 58.23 | 13.69 |
| 17 | 82.33 | 13.45 | 56.49 | 14.56 |
| 18 | 68.70 | 14.60 | 49.42 | 17.24 |
| 19 | 46.56 | 23.33 | 50.36 | 16.85 |
| 20 | 56.23 | 18.40 | 45.18 | 21.19 |
| 21 | 52.34 | 20.29 | 83.38 | 11.56 |
| 22 | 54.99 | 18.78 | 86.29 | 11.53 |
| 23 | 80.72 | 13.69 | 70.49 | 11.85 |
| 24 | 53.96 | 19.98 | 52.65 | 15.55 |
| 25 | 82.33 | 13.45 | 45.55 | 19.90 |
| 26 | 39.39 | 38.63 | 58.23 | 13.69 |
| 27 | 82.33 | 13.45 | 86.29 | 11.53 |
| 28 | 46.56 | 23.33 | 47.87 | 17.72 |
| 29 | 56.74 | 18.31 | 45.90 | 19.61 |
| 30 | 54.99 | 18.78 | 51.24 | 16.68 |
| 31 | 38.88 | 38.80 | 70.49 | 11.85 |
| 32 | 43.51 | 27.14 | 47.34 | 18.04 |
| 33 | 35.56 | 66.16 | 58.23 | 13.69 |
| 34 | 64.40 | 17.79 | 48.60 | 17.39 |
| 35 | 37.51 | 44.05 | 74.25 | 11.60 |
| 36 | 43.51 | 27.14 | 52.65 | 15.55 |
| 37 | 55.92 | 18.78 | 46.54 | 19.40 |
| 38 | 76.87 | 14.22 | 51.51 | 15.55 |
| 39 | 56.74 | 18.31 | 57.87 | 14.06 |
| 40 | 65.02 | 15.11 | 55.79 | 15.38 |
| 41 | 47.64 | 21.93 | 45.55 | 19.90 |
| 42 | 45.32 | 24.92 | 62.16 | 13.46 |
| 43 | 39.90 | 35.49 | 56.49 | 14.56 |
| 44 | 39.39 | 38.63 | 62.46 | 12.79 |
| 45 | 56.74 | 18.31 | 65.67 | 12.45 |
| 46 | 66.39 | 15.10 | 45.55 | 19.90 |
| 47 | 39.69 | 38.40 | 47.34 | 18.04 |
| 48 | 82.33 | 13.45 | 68.01 | 12.40 |
| 49 | 78.36 | 14.06 | 58.23 | 13.69 |
| 50 | 46.40 | 23.37 | 72.96 | 11.66 |
| Average | 57.96 | 22.20 | 57.60 | 15.59 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, T.; Zhang, B.; Zhao, Y. Towards a Generative Frame System of Ancient Chinese Timber Architecture: Structural Generation and Optimization of “Column Reduction” and “Column Relocation”. Buildings 2025, 15, 3329. https://doi.org/10.3390/buildings15183329
Liu T, Zhang B, Zhao Y. Towards a Generative Frame System of Ancient Chinese Timber Architecture: Structural Generation and Optimization of “Column Reduction” and “Column Relocation”. Buildings. 2025; 15(18):3329. https://doi.org/10.3390/buildings15183329
Chicago/Turabian StyleLiu, Tonghao, Binyue Zhang, and Yamin Zhao. 2025. "Towards a Generative Frame System of Ancient Chinese Timber Architecture: Structural Generation and Optimization of “Column Reduction” and “Column Relocation”" Buildings 15, no. 18: 3329. https://doi.org/10.3390/buildings15183329
APA StyleLiu, T., Zhang, B., & Zhao, Y. (2025). Towards a Generative Frame System of Ancient Chinese Timber Architecture: Structural Generation and Optimization of “Column Reduction” and “Column Relocation”. Buildings, 15(18), 3329. https://doi.org/10.3390/buildings15183329





