Development of Seismic Fragility Curve for Railway Tunnel Crossing Fracture Zone
Abstract
1. Introduction
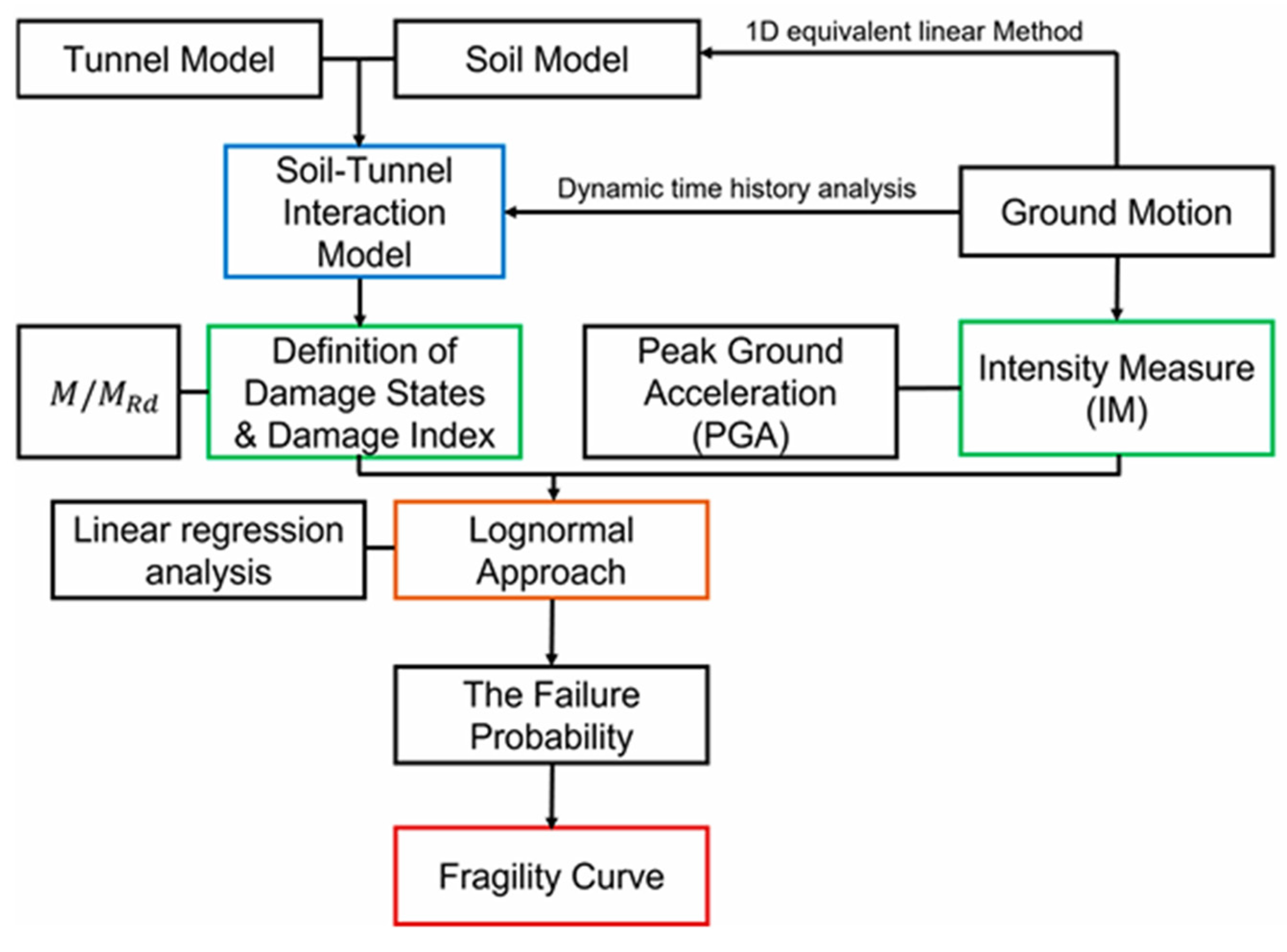
2. Numerical Modeling
2.1. Numerical Modeling Methodology
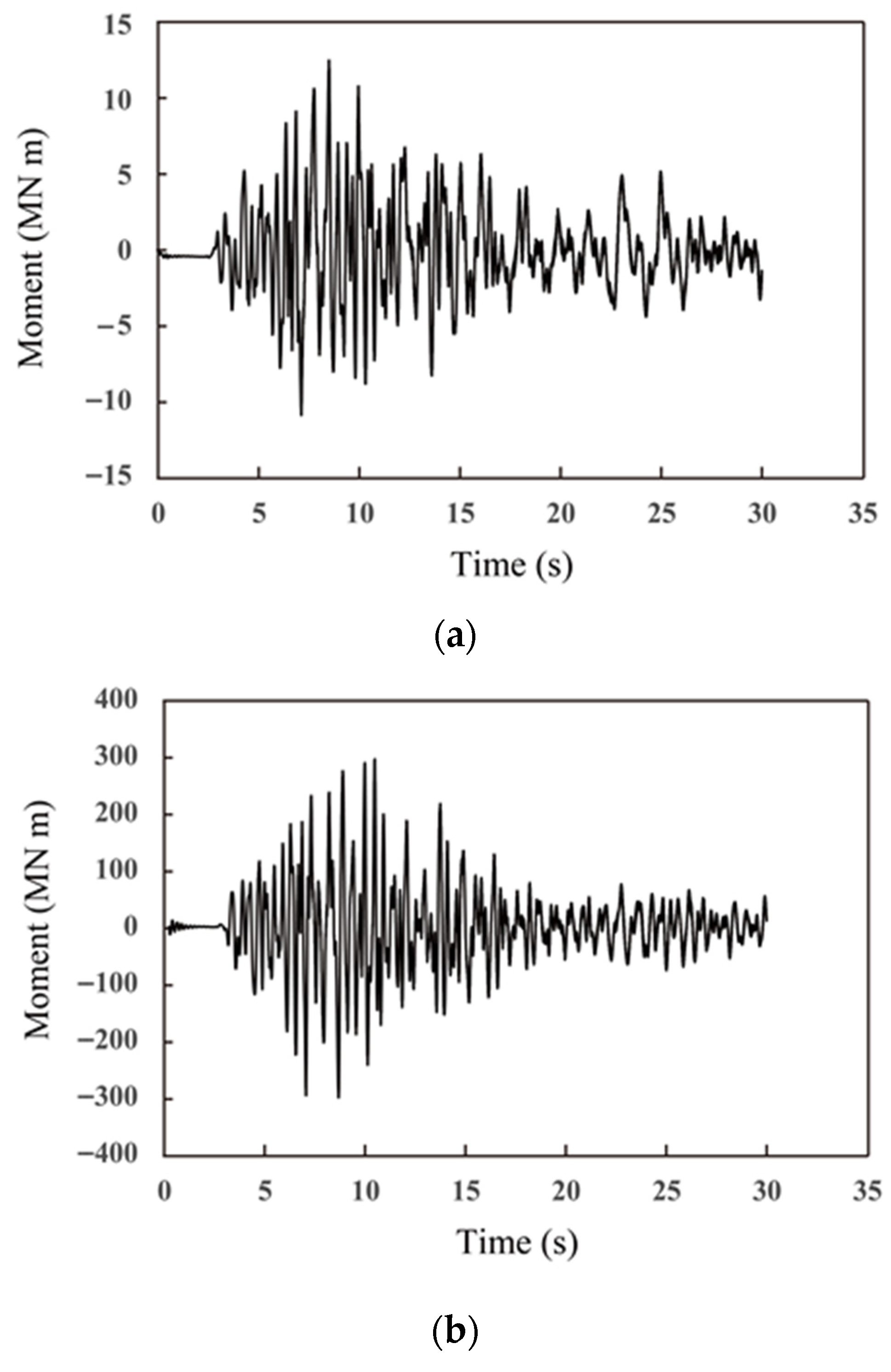
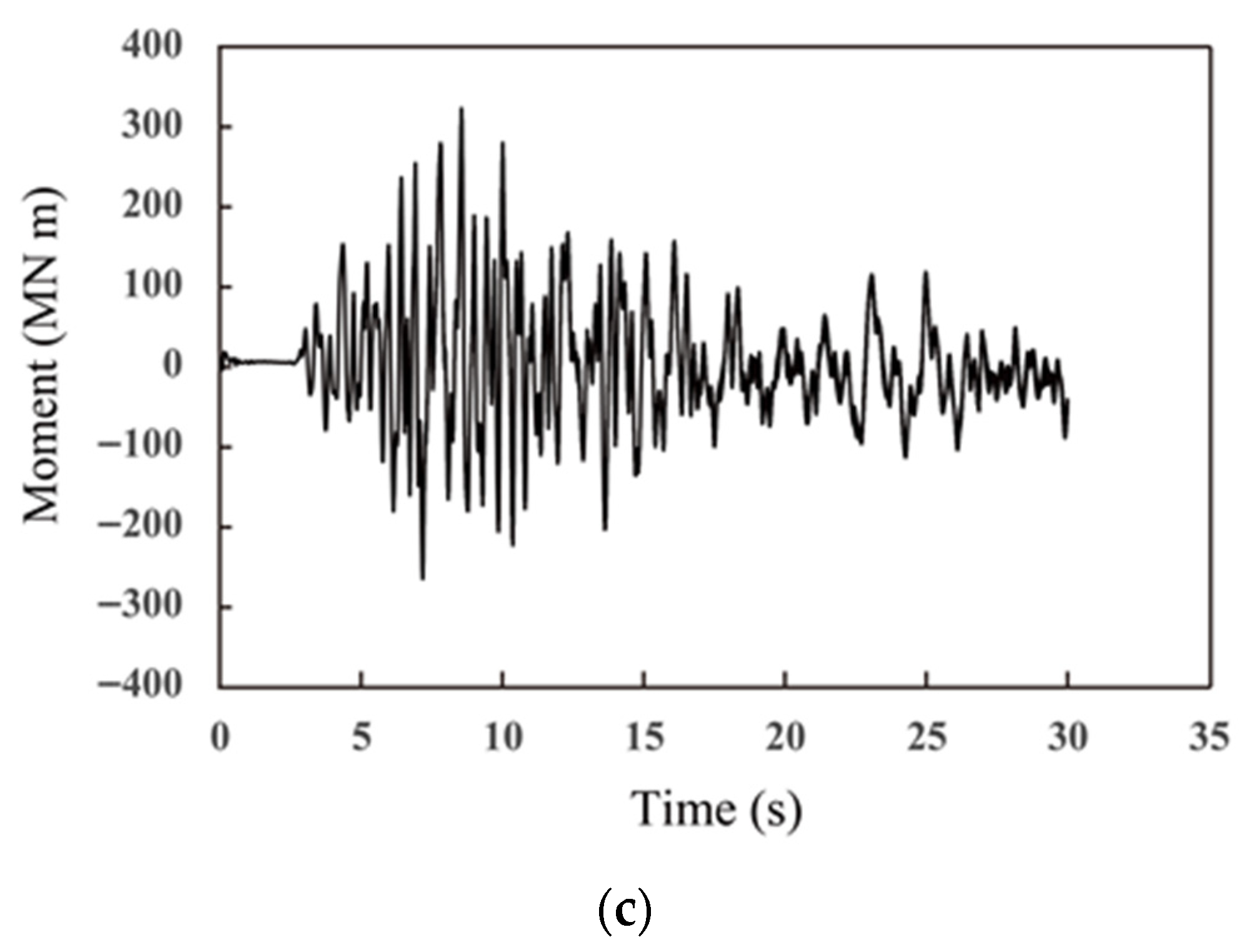
2.2. Numerical Analysis Result
3. Development of Seismic Fragility Curve for Railway Tunnel Crossing Fracture Zone
3.1. Derivation of Damage Index
3.2. Determination Procedure of Seismic Fragility Curve
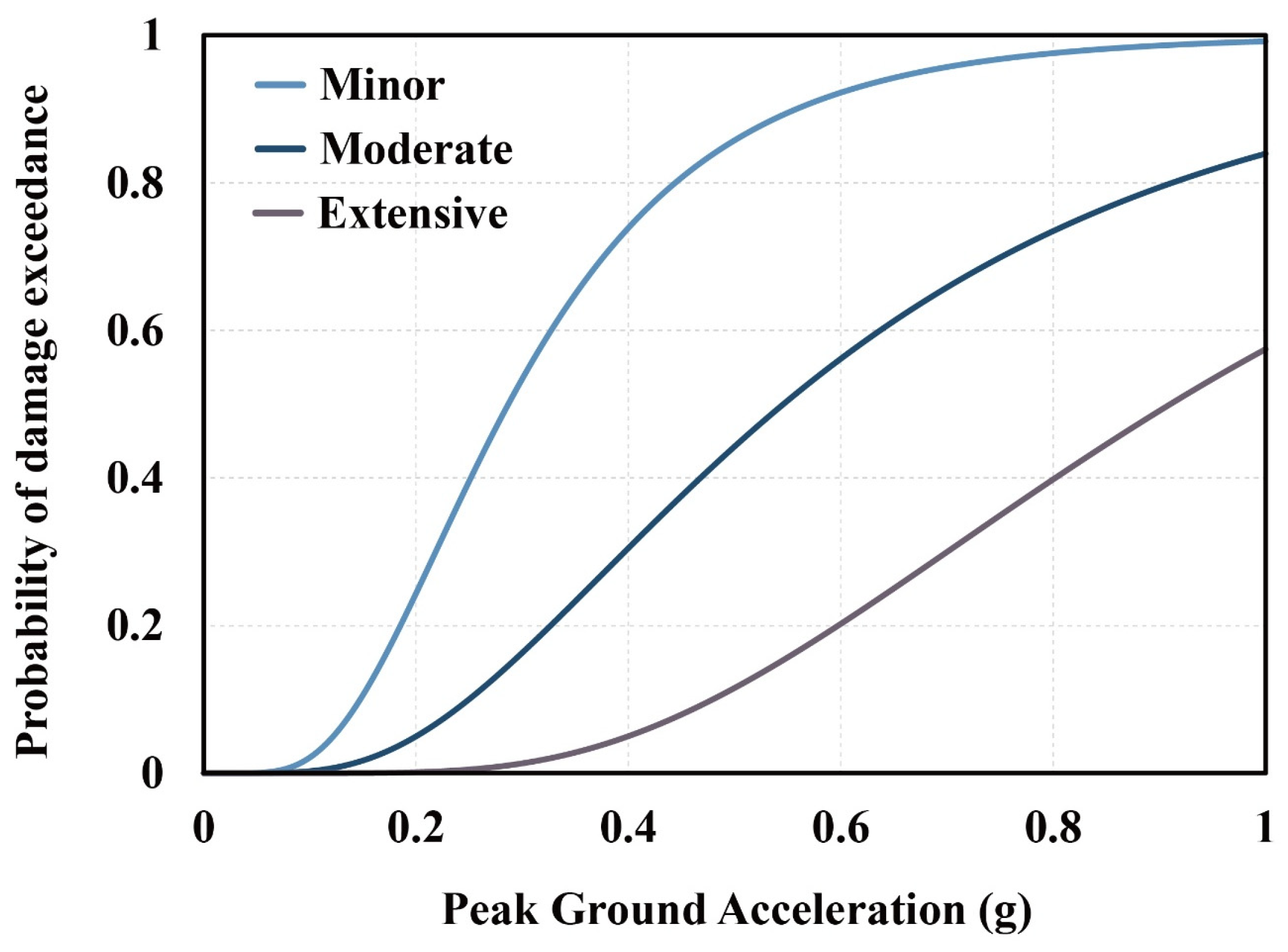
3.3. Seismic Fragility Curve for Tunnel Structure Crossing the Fracture Zone
3.4. Analysis and Discussion
4. Conclusions
- The presence of fractured zones significantly amplified the seismic response of tunnel linings. Compared with tunnels embedded in hard rock, those intersecting fractured zones exhibited higher bending moments and larger deformations under identical ground motion conditions.
- Damage indices (DI) were computed using moment-based structural responses, and the tunnel damage states were classified accordingly. The DI-based classification allowed for a systematic quantification of seismic damage levels.
- Using the DI-derived classifications, the seismic fragility functions were established for tunnels intersecting fractured zones. The fragility curves were constructed based on a lognormal cumulative distribution, with PGA as the intensity measure.
- The resulting fragility curves indicated that the probability of exceeding minor, moderate, and extensive damage states surpassed 50% at PGAs of approximately 0.289 g, 0.578 g, and 0.91 g, respectively. These results demonstrate the increased seismic vulnerability of tunnels traversing fractured geological formations and underscore the need for site-specific seismic design considerations.
- It is acknowledged that the limited number of input ground motions may affect the statistical robustness of the derived fragility curves. This limitation stems from the significant computational cost associated with FLAC3D-based 3D nonlinear dynamic analyses, which constrained the number of ground motions in this initial study. Future work will address this limitation by incorporating a larger suite of input motions through cloud analysis or incremental dynamic analysis (IDA) frameworks, thereby enhancing the statistical reliability and general applicability of the fragility functions. In addition, while both 2.0 m and 10.0 m fracture zone cases were analyzed, the limited number of ground motions within each case made it statistically unreliable to derive separate fragility curves. Moreover, the presence of a fracture zone itself caused a much greater increase in seismic demand than the incremental effect of its width. Therefore, the fragility functions were developed by pooling all fracture zone cases, and the effect of fracture zone thickness will be further investigated in future work using a larger set of seismic inputs.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yoo, M.; Kwak, C.; Lee, H.U.; Park, J. Development of seismic fragility curve for subsea railway tunnel based on 3D numerical analysis. KSCE J. Civ. Eng. 2024, 29, 100149. [Google Scholar] [CrossRef]
- Pakbaz, M.C.; Yareevand, A. 2-D analysis of circular tunnel against earthquake loading. Tunn. Undergr. Space Technol. 2005, 20, 411–417. [Google Scholar] [CrossRef]
- Asheghabadi, M.S.; Matinmanesh, H. Finite element seismic analysis of cylindrical tunnel in sandy soils with consideration of soil-tunnel interaction. Procedia Eng. 2011, 14, 3162–3169. [Google Scholar] [CrossRef]
- Jiang, L.; Chen, J.; Li, J. Seismic response of underground utility tunnels: Shaking table testing and FEM analysis. Earthq. Eng. Eng. Vib. 2010, 9, 555–567. [Google Scholar] [CrossRef]
- Bao, X.; Xia, Z.; Ye, G.; Fu, Y.; Su, D. Numerical analysis on the seismic behavior of a large metro subway tunnel in liquefiable ground. Tunn. Undergr. Space Technol. 2017, 66, 91–106. [Google Scholar] [CrossRef]
- Tsinidis, G.; Pitilakis, K.; Anagnostopoulos, C. Circular tunnels in sand: Dynamic response and efficiency of seismic analysis methods at extreme lining flexibilities. Bull. Earthq. Eng. 2016, 14, 2903–2929. [Google Scholar] [CrossRef]
- Do, N.A.; Dias, D.; Oreste, P. 2D seismic numerical analysis of segmental tunnel lining behaviour. Bull. N. Z. Soc. Earthq. Eng. 2014, 47, 206–216. [Google Scholar] [CrossRef]
- Nong, X.; Bai, W.; Yi, S.; Lu, Z.; Lu, Y. Numerical simulation for risk assessment of tunnel construction through fault fracture zones. Buildings 2024, 14, 3161. [Google Scholar] [CrossRef]
- Cho, Y.G.; Park, J.G. Effect of orientation of fracture zone on tunnel behavior—Numerical investigation. J. Korean Tunn. Undergr. Space Assoc. 2013, 15, 253–270. [Google Scholar]
- Ji, M.; Wang, X.; Luo, M.; Wang, D.; Teng, H.; Du, M. Stability analysis of tunnel surrounding rock when TBM passes through fracture zones with different deterioration levels and dip angles. Sustainability 2023, 15, 5243. [Google Scholar] [CrossRef]
- Yang, S.; Kwak, D.; Kim, S.; Yoo, B.; Yoo, M. Evaluation and Development of Seismic Fragility Models for Cut-and-Cover Underground Station. J. Korean Soc. Railw. 2024, 27, 202–212. Available online: https://scholarworks.bwise.kr/gachon/handle/2020.sw.gachon/90831 (accessed on 1 July 2025). [CrossRef]
- Kwon, S.Y.; Kim, J.; Kwak, D.; Yang, S.; Yoo, M. Development of seismic fragility function for underground railway station structures in Korea. Buildings 2024, 14, 1200. [Google Scholar] [CrossRef]
- Osmi, S.K.C.; Ahmad, S.M. Seismic fragility curves for shallow circular tunnels under different soil conditions. World Acad. Sci. Eng. Technol. Int. J. Civ. Environ. Eng. 2016, 10, 1281–1287. [Google Scholar]
- Argyroudis, S.A.; Pitilakis, K.D. Seismic fragility curves of shallow tunnels in alluvial deposits. Soil Dyn. Earthq. Eng. 2012, 35, 1–12. [Google Scholar] [CrossRef]
- Zhong, Z.; Shen, Y.; Zhao, M.; Li, L.; Du, X.; Hao, H. Seismic fragility assessment of the Daikai subway station in layered soil. Soil Dyn. Earthq. Eng. 2020, 132, 106044. [Google Scholar] [CrossRef]
- Hu, X.; Zhou, Z.; Chen, H.; Ren, Y. Seismic fragility analysis of tunnels with different buried depths in a soft soil. Sustainability 2020, 12, 892. [Google Scholar] [CrossRef]
- KDS 17 10 00; Korean Design Standard 17 10 00: Seismic Design Standard. Ministry of Land. Infrastructure and Transportation: Sejong, Republic of Korea, 2024.
- Nieto-Samaniego, A.F.; Alaniz-Álvarez, S.A.; Velázquez-Morales, L.; Xu, S.; Ramos-Arias, M.A.; Delgado-Granados, H. Effect of Mineral Processes and Deformation on the Petrophysical Properties of Soft Rocks during Active Faulting. Minerals 2020, 10, 444. [Google Scholar] [CrossRef]
- KR C-12040:Concrete Lining; Korea National Railway Construction Standard. Korea Rail Network Authority: Daejeon, Republic of Korea, 2021.
- Straub, D.; Der Kiureghian, A. Improved seismic fragility modeling from empirical data. Struct. Saf. 2008, 30, 320–336. [Google Scholar] [CrossRef]
- Ghosh, S.; Ghosh, S.; Chakraborty, S. Seismic fragility analysis in the probabilistic performance-based earthquake engineering framework: An overview. Int. J. Adv. Eng. Sci. Appl. Math. 2021, 13, 122–135. [Google Scholar] [CrossRef]
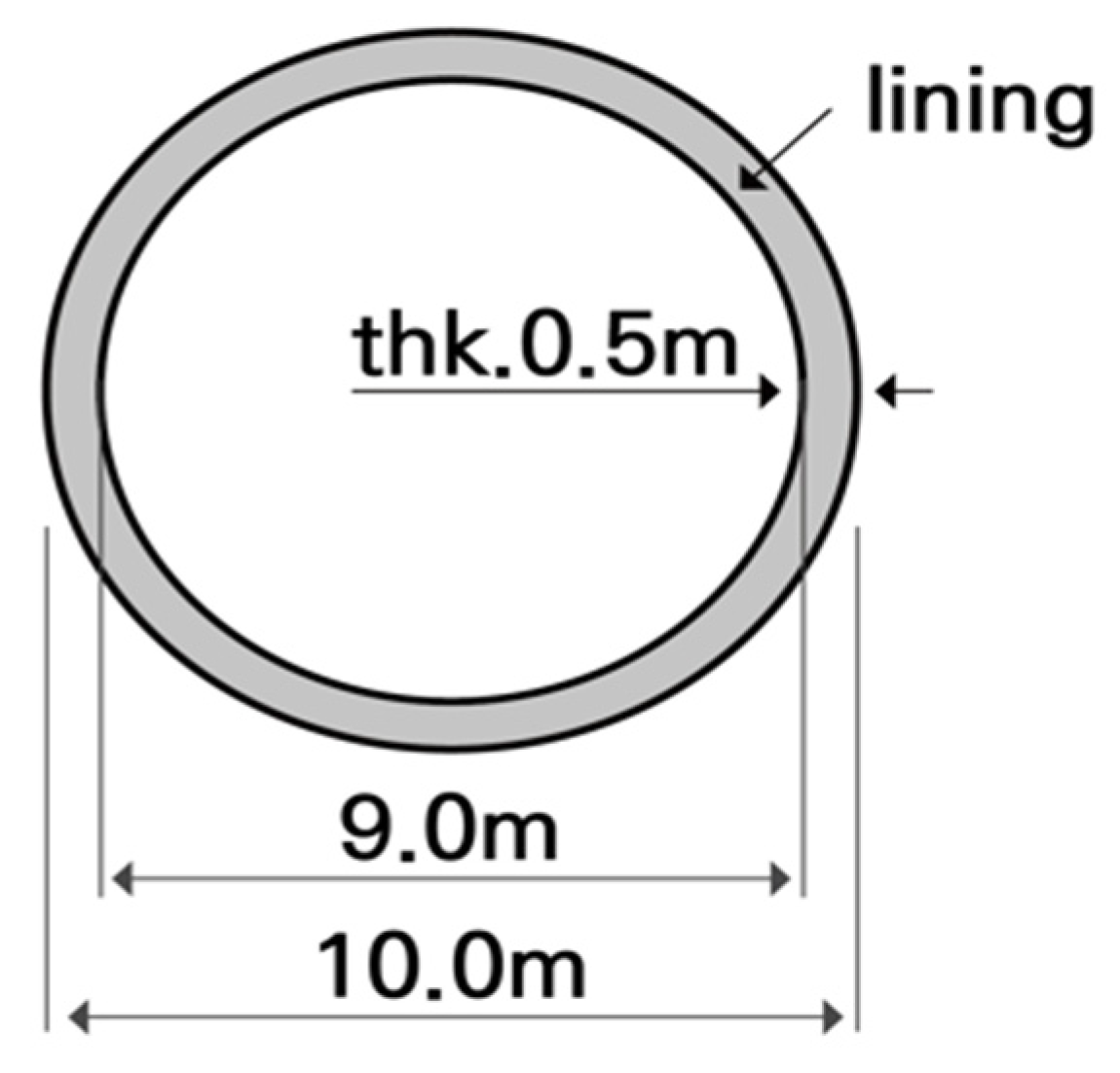
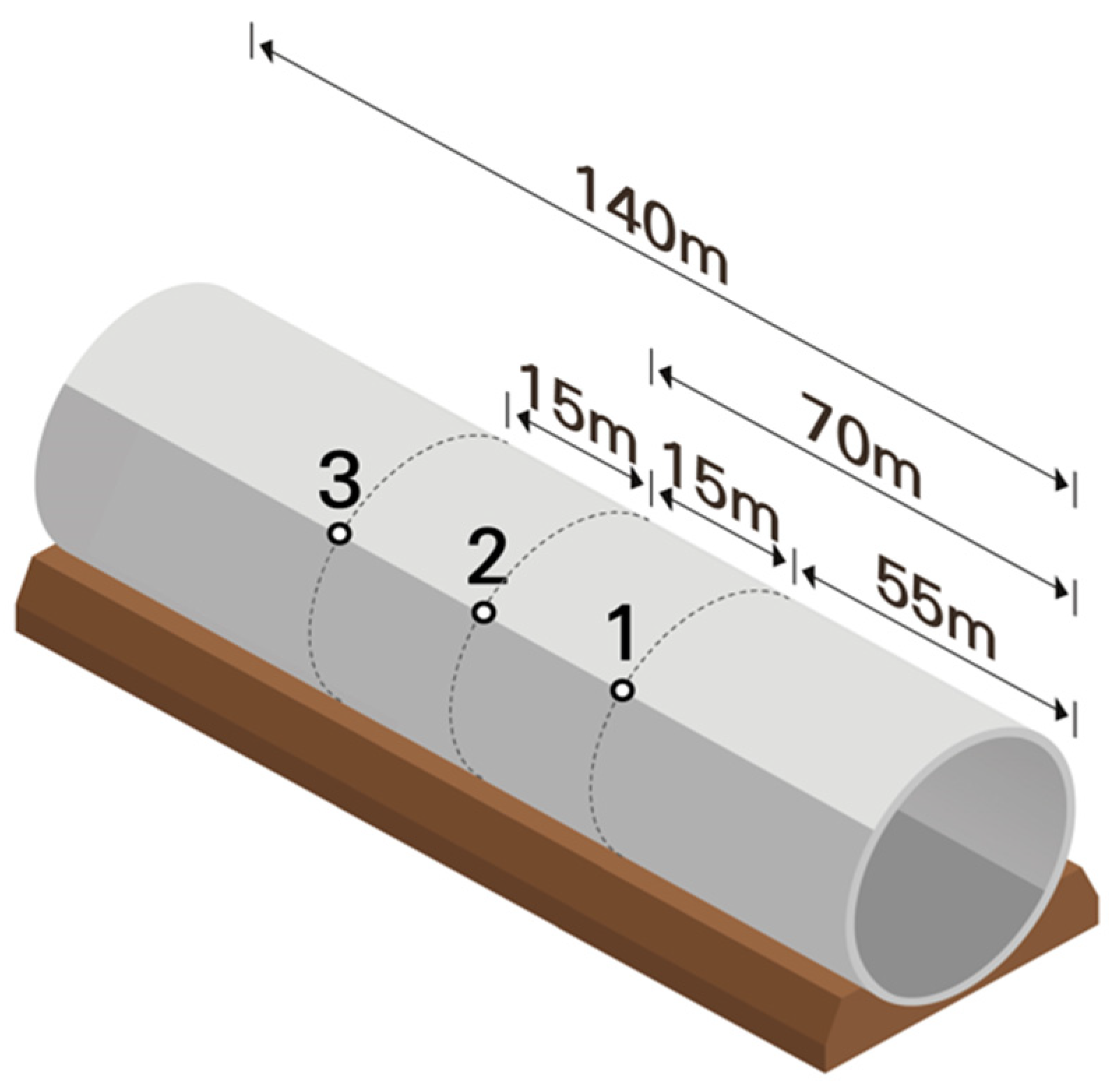
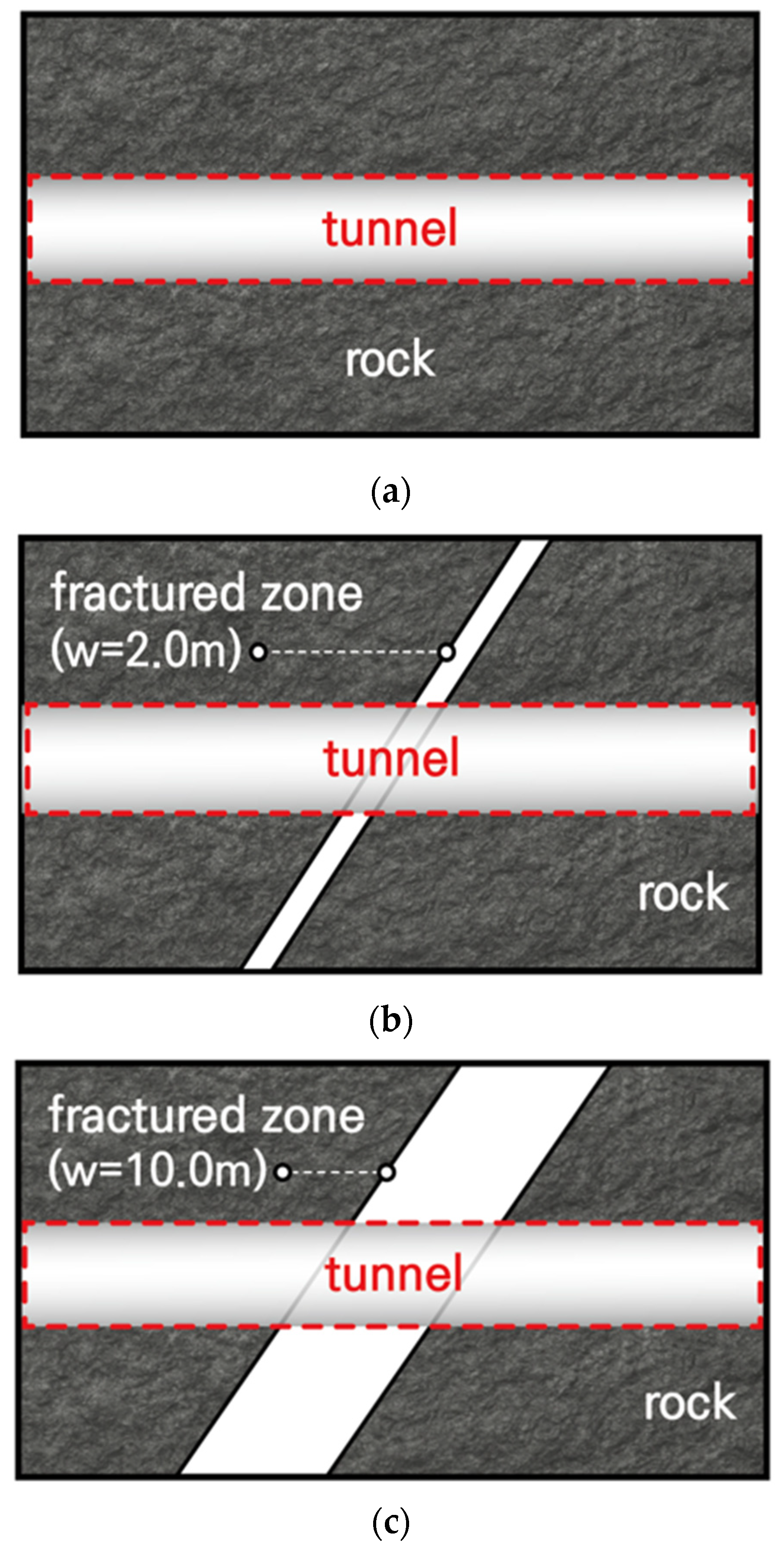
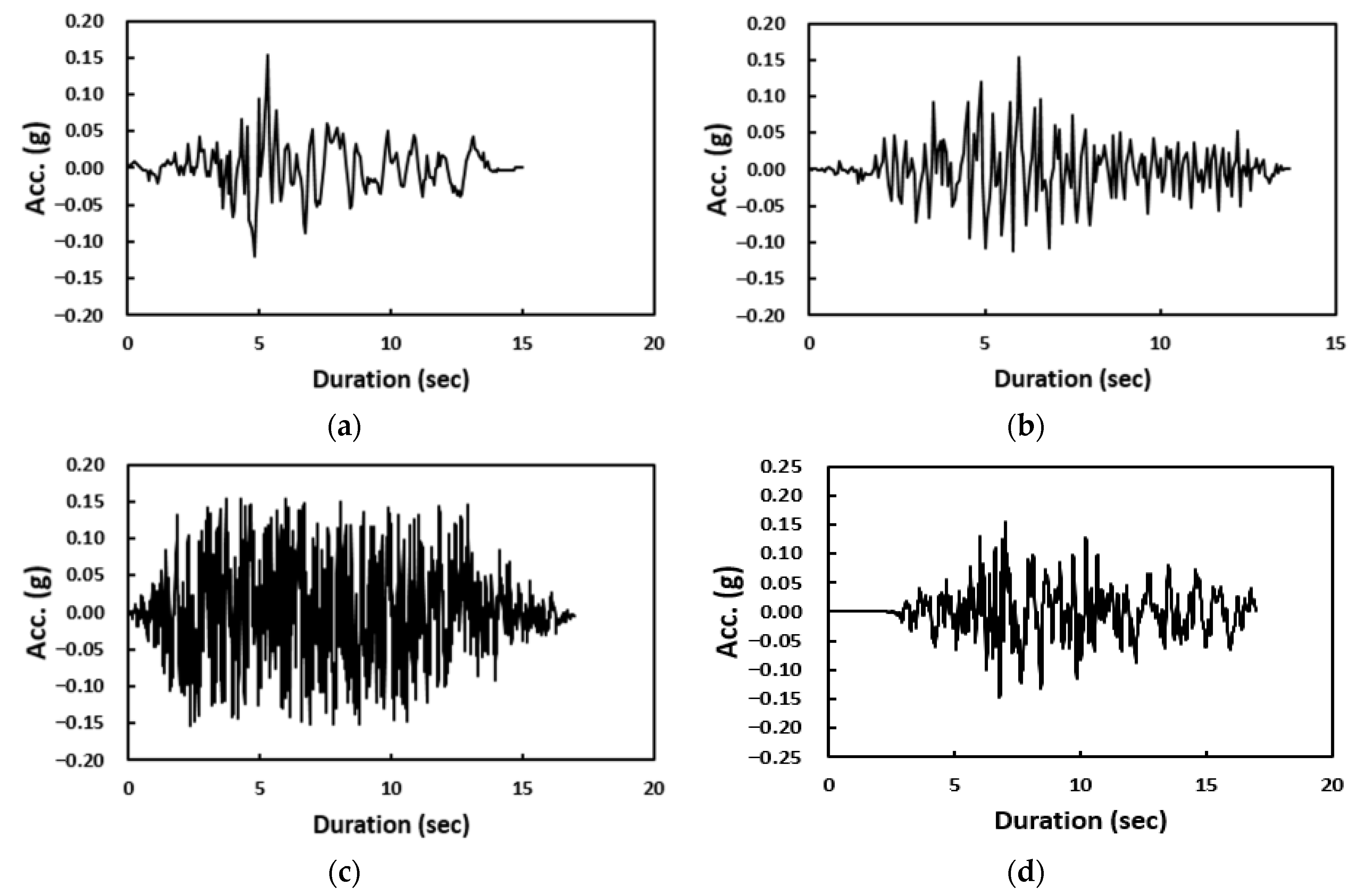
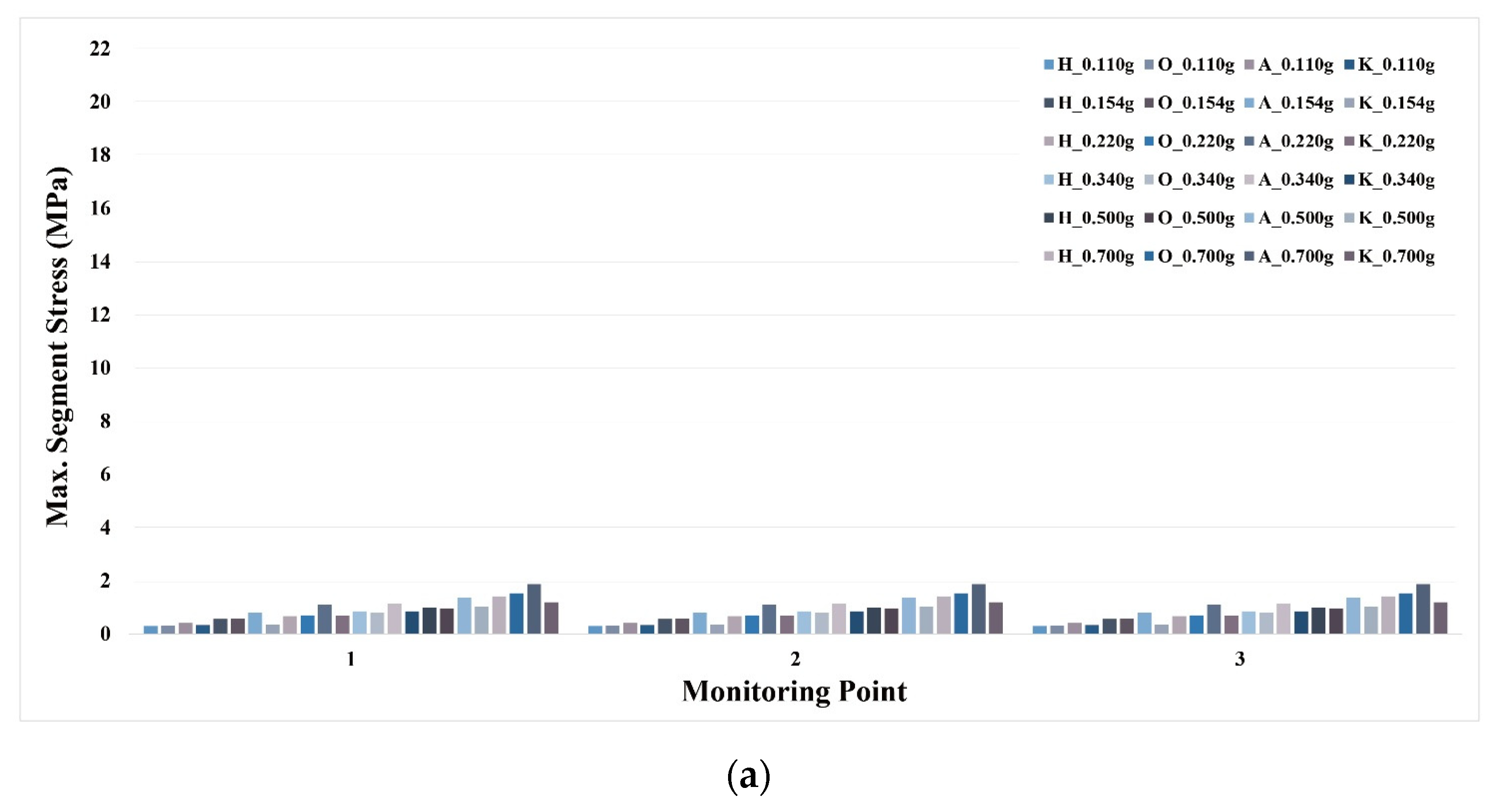
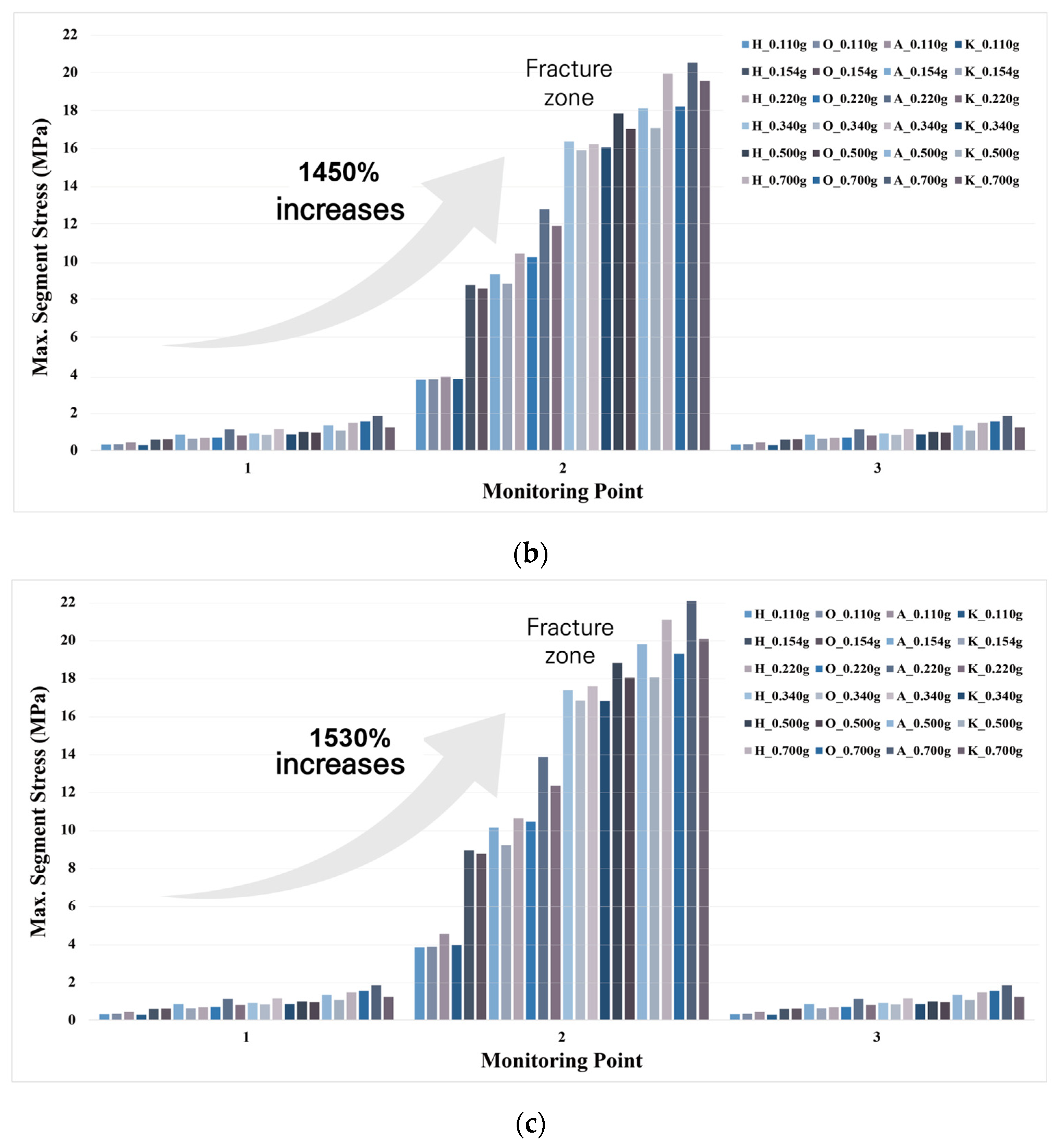
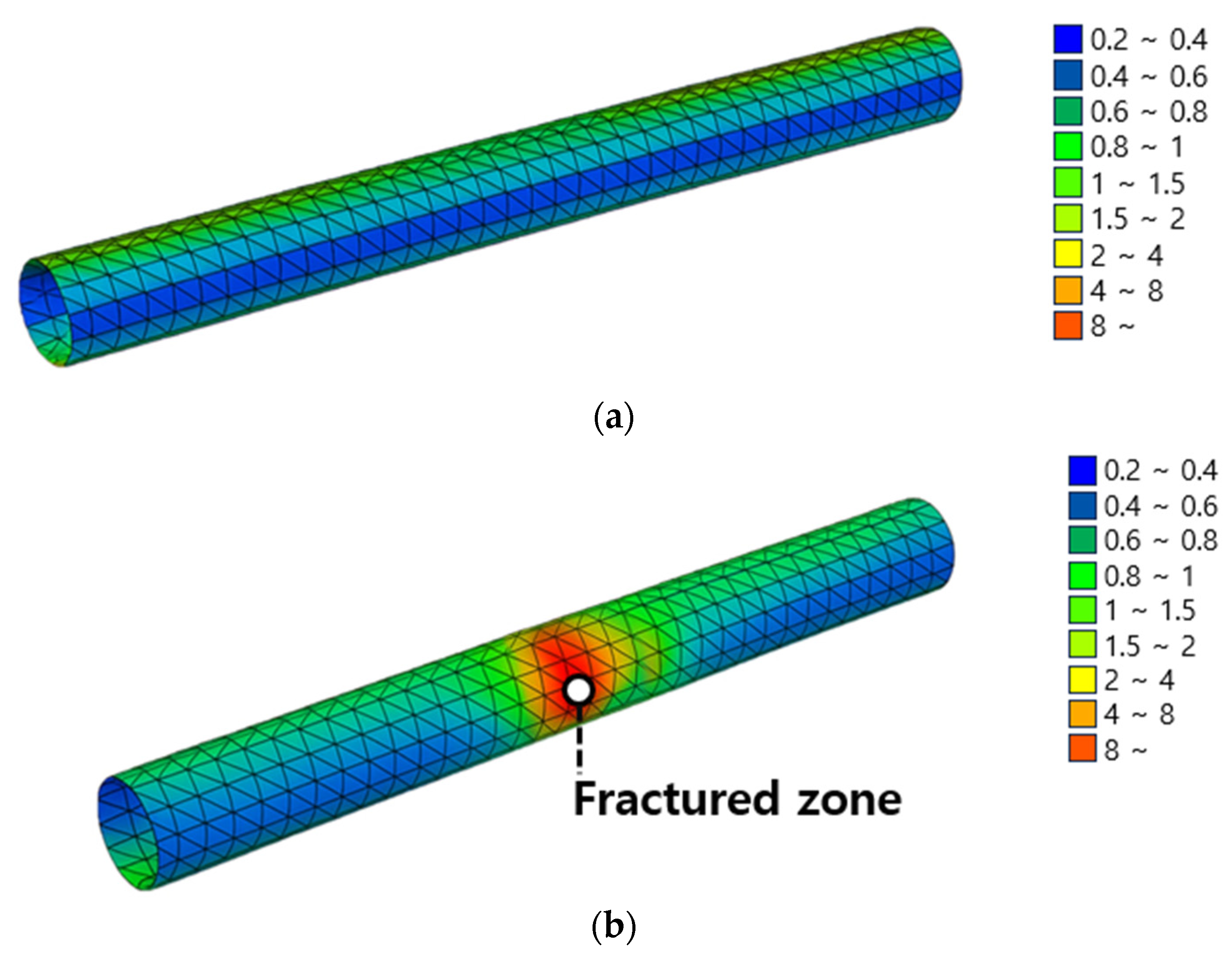
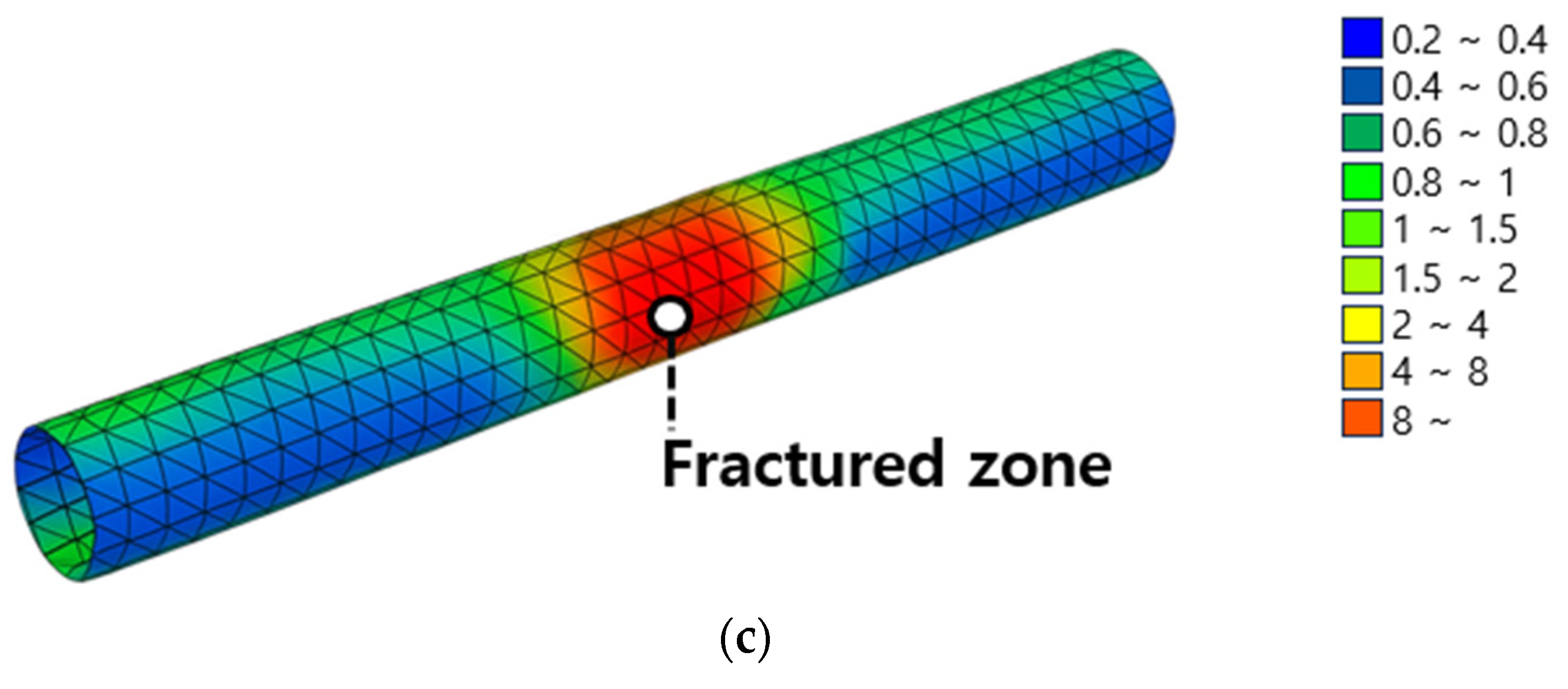
| CASE | Site Condition | Seismic Wave | Maximum Amplitude (g) |
|---|---|---|---|
| 1 | Hard rock | Hachinohe, Ofunato, Artificial, Kobe | 0.110 g/0.154 g/0.220 g/0.340 g /0.500 g/0.700 g |
| 2 | Hard rock w/narrow fracture zone | ||
| 3 | Hard rock w/wide fracture zone |
| Type | Young’s Modulus (MPa) | Unit Weight (kN/m3) | Poisson’s Ratio | Friction Angle (deg) | Cohesion (kPa) |
|---|---|---|---|---|---|
| Hard rock | 35,000 | 26.264 | 0.20 | 45 | 6000 |
| Fractured zone | 400 | 20.972 | 0.30 | 30 | 50 |
| Lining | 25,600 | 2400 | 0.20 | - | - |
| Case | 1 | 2 | 3 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Input Acc. | Point | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 |
| 0.110 g | Hachinohe | 10.4 | 10.4 | 10.4 | 10.4 | 126.0 | 10.5 | 11.3 | 129.1 | 10.9 |
| Ofuato | 11.0 | 11.0 | 11.0 | 11.0 | 126.7 | 11.0 | 11.8 | 130.0 | 11.5 | |
| Artificial | 14.3 | 14.3 | 14.3 | 14.3 | 132.0 | 13.8 | 16.3 | 153.2 | 16.6 | |
| Kobe | 11.5 | 11.5 | 11.5 | 9.2 | 127.7 | 16.1 | 12.8 | 133.5 | 12.5 | |
| 0.154 g | Hachinohe | 19.2 | 19.2 | 19.2 | 19.3 | 295.5 | 19.4 | 20.8 | 301.2 | 20.2 |
| Ofuato | 19.8 | 19.8 | 19.8 | 19.8 | 288.9 | 19.8 | 21.2 | 294.8 | 20.8 | |
| Artificial | 27.1 | 27.1 | 27.1 | 27.1 | 314.9 | 26.2 | 31.0 | 341.3 | 31.5 | |
| Kobe | 12.3 | 12.3 | 12.3 | 20.0 | 297.6 | 17.1 | 20.7 | 310.0 | 20.7 | |
| 0.220 g | Hachinohe | 22.9 | 22.9 | 22.9 | 23.0 | 351.4 | 23.1 | 24.8 | 358.2 | 24.1 |
| Ofuato | 23.6 | 23.6 | 23.6 | 23.7 | 345.1 | 23.7 | 25.3 | 352.1 | 24.8 | |
| Artificial | 37.1 | 37.1 | 37.1 | 37.1 | 430.9 | 35.8 | 42.4 | 467.1 | 43.0 | |
| Kobe | 23.5 | 23.5 | 23.5 | 23.5 | 401.1 | 23.6 | 27.6 | 415.9 | 26.1 | |
| 0.340 g | Hachinohe | 28.7 | 28.7 | 28.7 | 28.7 | 552.0 | 28.4 | 37.5 | 585.8 | 37.5 |
| Ofuato | 27.2 | 27.2 | 27.2 | 27.0 | 536.2 | 27.1 | 31.1 | 567.5 | 31.4 | |
| Artificial | 38.9 | 38.9 | 38.9 | 38.6 | 546.9 | 38.5 | 53.8 | 592.8 | 54.6 | |
| Kobe | 28.9 | 28.9 | 28.9 | 28.8 | 541.2 | 28.7 | 32.1 | 566.5 | 32.0 | |
| 0.500 g | Hachinohe | 33.8 | 33.8 | 33.8 | 33.4 | 602.0 | 32.9 | 36.5 | 634.4 | 36.3 |
| Ofuato | 32.5 | 32.5 | 32.5 | 31.1 | 574.3 | 30.9 | 33.4 | 608.1 | 33.8 | |
| Artificial | 46.1 | 46.1 | 46.1 | 44.6 | 611.0 | 44.3 | 47.6 | 667.8 | 48.3 | |
| Kobe | 34.9 | 34.9 | 34.9 | 34.1 | 575.7 | 33.8 | 37.5 | 608.4 | 37.8 | |
| 0.700 g | Hachinohe | 47.9 | 47.9 | 47.9 | 47.5 | 672.8 | 47.2 | 51.3 | 711.4 | 50.6 |
| Ofuato | 51.7 | 51.7 | 51.7 | 51.0 | 614.4 | 50.9 | 54.4 | 650.6 | 54.3 | |
| Artificial | 63.4 | 63.4 | 63.4 | 62.6 | 692.4 | 62.4 | 66.5 | 744.5 | 65.7 | |
| Kobe | 40.5 | 40.5 | 40.5 | 37.5 | 660.0 | 37.4 | 44.2 | 676.9 | 40.8 | |
| Case | 1 | 2 | 3 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Input Acc. | Point | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 |
| 0.110 g | Hachinohe | 0.03 | 0.03 | 0.03 | 0.03 | 0.37 | 0.03 | 0.03 | 0.38 | 0.03 |
| Ofuato | 0.03 | 0.03 | 0.03 | 0.03 | 0.38 | 0.03 | 0.04 | 0.39 | 0.03 | |
| Artificial | 0.04 | 0.04 | 0.04 | 0.04 | 0.39 | 0.04 | 0.05 | 0.45 | 0.05 | |
| Kobe | 0.03 | 0.03 | 0.03 | 0.03 | 0.38 | 0.05 | 0.04 | 0.40 | 0.04 | |
| 0.154 g | Hachinohe | 0.06 | 0.06 | 0.06 | 0.06 | 0.88 | 0.06 | 0.06 | 0.89 | 0.06 |
| Ofuato | 0.06 | 0.06 | 0.06 | 0.06 | 0.86 | 0.06 | 0.06 | 0.87 | 0.06 | |
| Artificial | 0.08 | 0.08 | 0.08 | 0.08 | 0.93 | 0.08 | 0.09 | 1.01 | 0.09 | |
| Kobe | 0.04 | 0.04 | 0.04 | 0.06 | 0.88 | 0.05 | 0.06 | 0.92 | 0.06 | |
| 0.220 g | Hachinohe | 0.07 | 0.07 | 0.07 | 0.07 | 1.04 | 0.07 | 0.07 | 1.06 | 0.07 |
| Ofuato | 0.07 | 0.07 | 0.07 | 0.07 | 1.02 | 0.07 | 0.08 | 1.04 | 0.07 | |
| Artificial | 0.11 | 0.11 | 0.11 | 0.11 | 1.28 | 0.11 | 0.13 | 1.38 | 0.13 | |
| Kobe | 0.07 | 0.07 | 0.07 | 0.07 | 1.19 | 0.07 | 0.08 | 1.23 | 0.08 | |
| 0.340 g | Hachinohe | 0.09 | 0.09 | 0.09 | 0.09 | 1.64 | 0.08 | 0.11 | 1.74 | 0.11 |
| Ofuato | 0.08 | 0.08 | 0.08 | 0.08 | 1.59 | 0.08 | 0.09 | 1.68 | 0.09 | |
| Artificial | 0.12 | 0.12 | 0.12 | 0.11 | 1.62 | 0.11 | 0.16 | 1.76 | 0.16 | |
| Kobe | 0.09 | 0.09 | 0.09 | 0.09 | 1.60 | 0.09 | 0.10 | 1.68 | 0.10 | |
| 0.500 g | Hachinohe | 0.10 | 0.10 | 0.10 | 0.10 | 1.78 | 0.10 | 0.11 | 1.88 | 0.11 |
| Ofuato | 0.10 | 0.10 | 0.10 | 0.09 | 1.70 | 0.09 | 0.10 | 1.80 | 0.10 | |
| Artificial | 0.14 | 0.14 | 0.14 | 0.13 | 1.81 | 0.13 | 0.14 | 1.98 | 0.14 | |
| Kobe | 0.10 | 0.10 | 0.10 | 0.10 | 1.71 | 0.10 | 0.11 | 1.80 | 0.11 | |
| 0.700 g | Hachinohe | 0.14 | 0.14 | 0.14 | 0.14 | 1.99 | 0.14 | 0.15 | 2.11 | 0.15 |
| Ofuato | 0.15 | 0.15 | 0.15 | 0.15 | 1.82 | 0.15 | 0.16 | 1.93 | 0.16 | |
| Artificial | 0.19 | 0.19 | 0.19 | 0.19 | 2.05 | 0.19 | 0.20 | 2.21 | 0.20 | |
| Kobe | 0.12 | 0.12 | 0.12 | 0.11 | 1.96 | 0.11 | 0.13 | 2.01 | 0.12 | |
| Damage State | Damage Index |
|---|---|
| None | DI < 1.0 |
| Minor | 1.0 < DI < 1.2 |
| Moderate | 1.2 < DI < 2.0 |
| Extensive | 2.0 < DI |
| Input Acc. | Input motion | Case 1 | Case 2 | Case 3 |
|---|---|---|---|---|
| 0.110 g | Hachinohe | None | None | None |
| Ofuato | None | None | None | |
| Artificial | None | None | None | |
| Kobe | None | None | None | |
| 0.154 g | Hachinohe | None | None | None |
| Ofuato | None | None | None | |
| Artificial | None | None | Minor | |
| Kobe | None | None | None | |
| 0.220 g | Hachinohe | None | Minor | Minor |
| Ofuato | None | Minor | Minor | |
| Artificial | None | Moderate | Moderate | |
| Kobe | None | Minor | Moderate | |
| 0.340 g | Hachinohe | None | Moderate | Moderate |
| Ofuato | None | Moderate | Moderate | |
| Artificial | None | Moderate | Moderate | |
| Kobe | None | Moderate | Moderate | |
| 0.500 g | Hachinohe | None | Moderate | Moderate |
| Ofuato | None | Moderate | Moderate | |
| Artificial | None | Moderate | Moderate | |
| Kobe | None | Moderate | Moderate | |
| 0.700 g | Hachinohe | None | Moderate | Extensive |
| Ofuato | None | Moderate | Extensive | |
| Artificial | None | Extensive | Extensive | |
| Kobe | None | Moderate | Extensive |
| Damage State | Median (μ) | Standard Deviation (β) |
|---|---|---|
| Minor | 0.289 | 0.519 |
| Moderate | 0.578 | 0.609 |
| Extensive | 0.91 | 0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, W.S.; Haam, S.; Lee, S.K.; Kim, J.; Song, H.; Yoo, M.; Kim, S. Development of Seismic Fragility Curve for Railway Tunnel Crossing Fracture Zone. Buildings 2025, 15, 3304. https://doi.org/10.3390/buildings15183304
Song WS, Haam S, Lee SK, Kim J, Song H, Yoo M, Kim S. Development of Seismic Fragility Curve for Railway Tunnel Crossing Fracture Zone. Buildings. 2025; 15(18):3304. https://doi.org/10.3390/buildings15183304
Chicago/Turabian StyleSong, Woo Seung, Sunnie Haam, Sang Ki Lee, Jinsoo Kim, Hyunmin Song, Mintaek Yoo, and Seokjung Kim. 2025. "Development of Seismic Fragility Curve for Railway Tunnel Crossing Fracture Zone" Buildings 15, no. 18: 3304. https://doi.org/10.3390/buildings15183304
APA StyleSong, W. S., Haam, S., Lee, S. K., Kim, J., Song, H., Yoo, M., & Kim, S. (2025). Development of Seismic Fragility Curve for Railway Tunnel Crossing Fracture Zone. Buildings, 15(18), 3304. https://doi.org/10.3390/buildings15183304







