Aseismic Experimental Research on Safety-Belt System of a Low-Gravity-Center Cable-Stayed Bridge
Abstract
1. Introduction
2. Safety-Belt System
2.1. Design of Safety-Belt Device
2.2. Mechanical Principles
3. Experiment Design
3.1. Design of Experimental Structure
3.1.1. Similarity Ratio
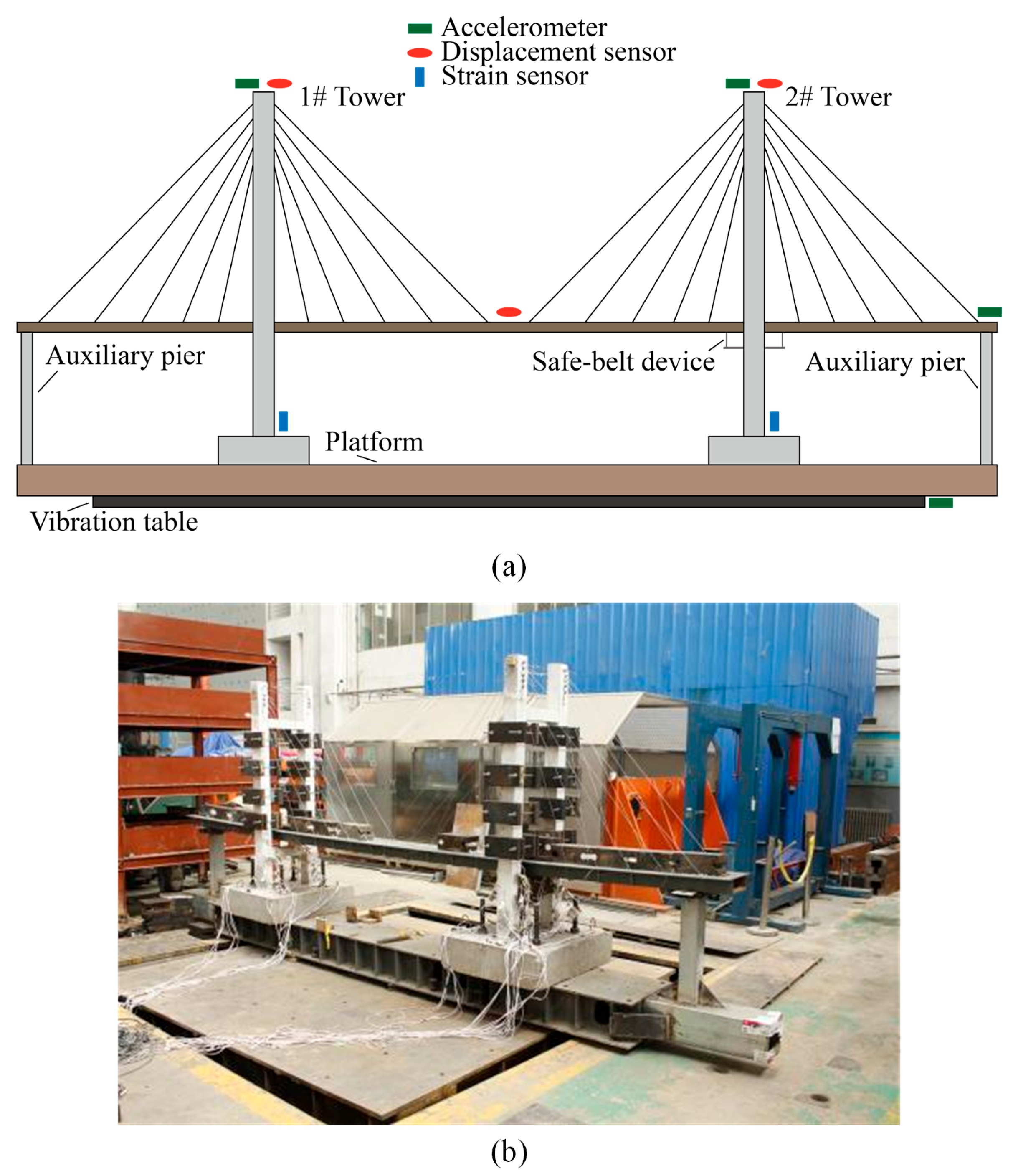
3.1.2. Experimental Structure
3.1.3. Counterweight
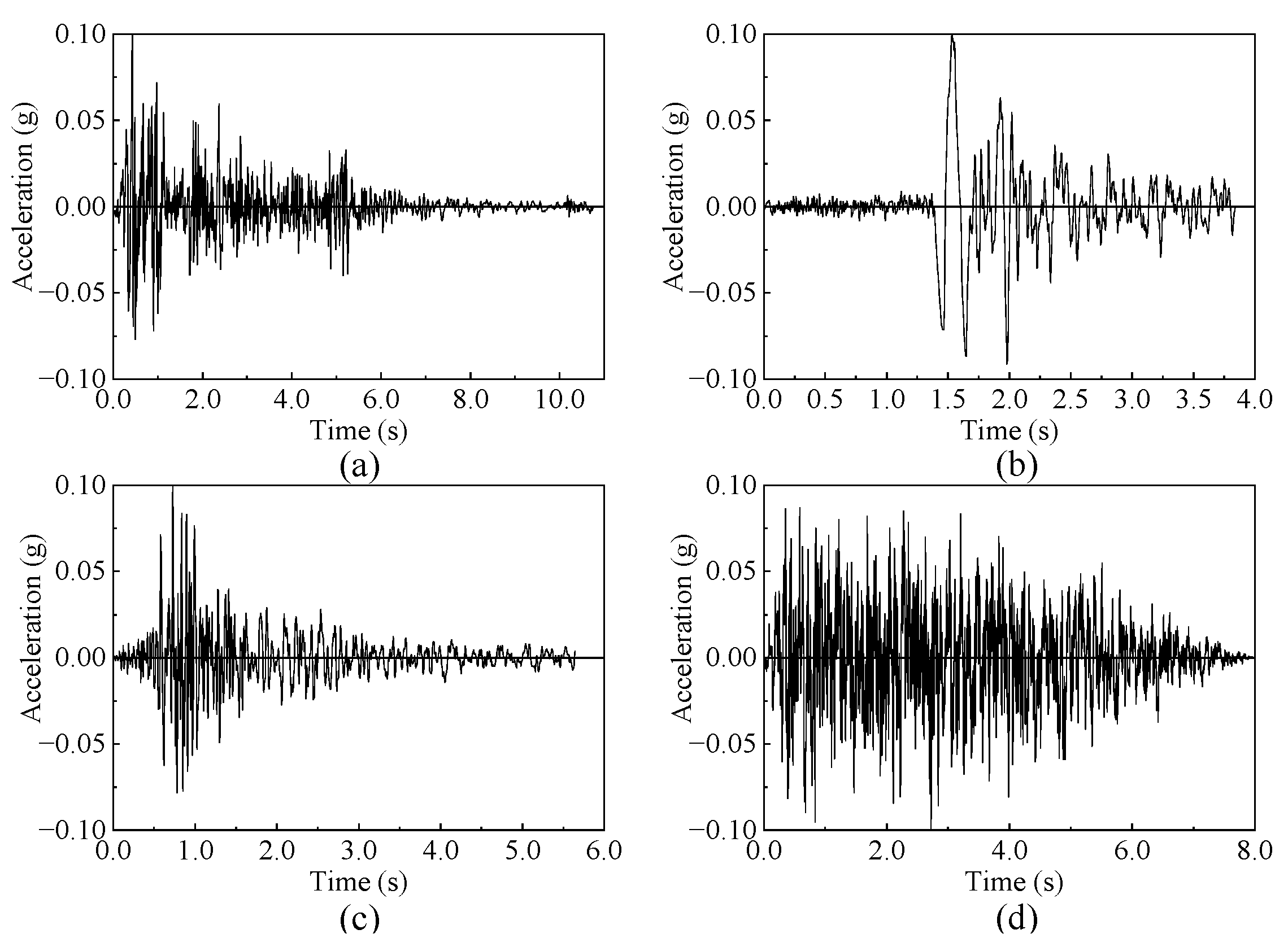
3.2. Design of Ground Motions
3.3. Experimental Arrangement
4. Results
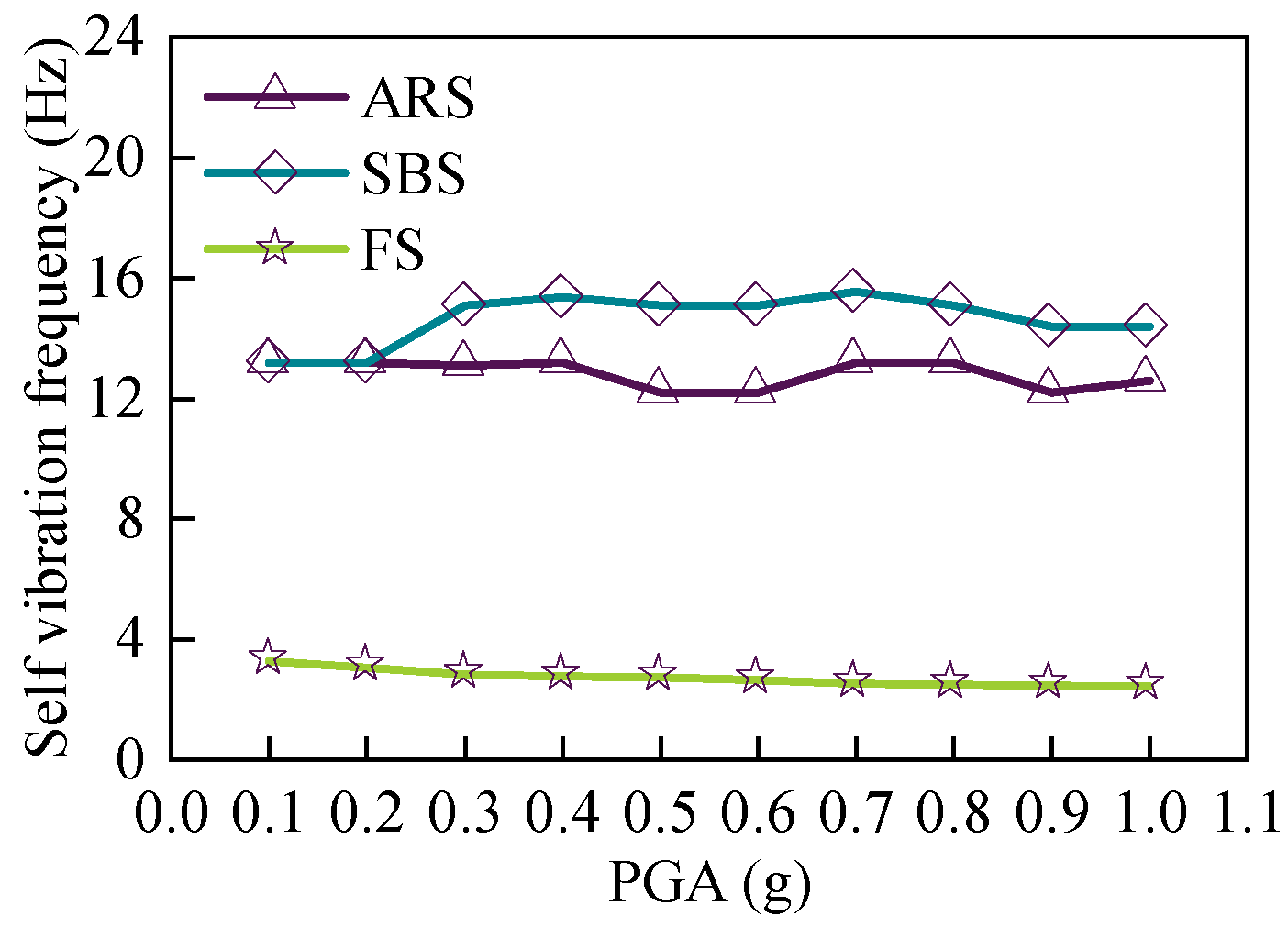
4.1. Self-Vibration Frequency
4.2. Experimental Phenomenon
| PGA | Phenomena |
|---|---|
| 0.1 g~0.7 g | No damage |
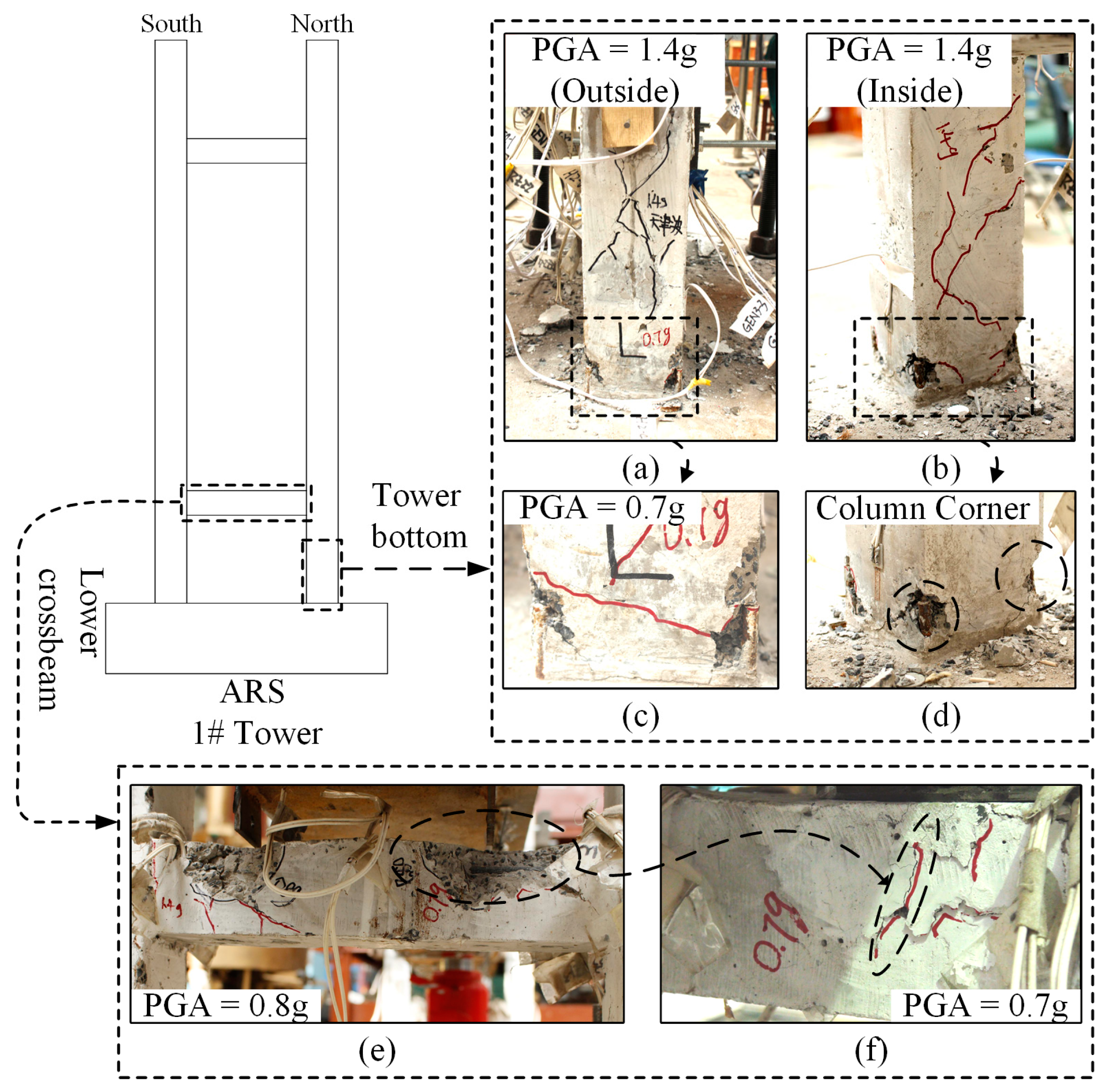
| 0.8 g | Obvious cracks with some concrete surface peeling appeared on 1# tower crossbeam, as Figure 8a,b show. |
| 1 g | Horizontal cracks appeared on the two tower bottoms of 1# tower, as Figure 8g,h show. The original cracks on the lower crossbeam of 1# tower extended and concrete fragmentation occurred, as Figure 8c,d show. |
| 1.1 g | The original cracks on 1# tower bottom extended to an around-tower-bottom circle crack and aggravated concrete fragmentation occurred. Reinforcement at the column corner of the tower bottom was exposed. The lower crossbeam had further concrete damage, as Figure 8f shows. |
| 1.2 g | New oblique cracks appeared on the 1# tower nearing the lower crossbeam, as Figure 8e shows. |
| 1.4 g | On the lower crossbeam of the 2# tower, the bolt used in fixing the safety-belt device and main girder broke under shearing, and the safety-belt device was broken, as Figure 8i shows. |

4.3. Experimental Phenomena Comparison
| PGA | Phenomena |
|---|---|
| 0.1 g~0.6 g | No damage |
| 0.7 g | A crack located at the lower tower column of 1# tower appeared as Figure 9c shows. A diagonal crack at the location of the fixed support of 1# tower appeared as Figure 9f shows. |
| 0.8 g | The extension of original cracks of 1# lower crossbeam beam occurred with local concrete fragmentation, as Figure 9e shows. |
| 1.1 g | A through crack appeared at 1# tower bottom with a large amount of concrete fragmentation, and the main reinforcements of the column corner of the 1# tower bottom were exposed, as Figure 9d shows. |
| 1.4 g | A large amount of concrete fragmentation occurred at the lower crossbeam of 1# tower, and the reinforcements were exposed. Meanwhile, many cracks appeared at the bottom of the 1# tower, as Figure 9a,b show. |
| PGA | Phenomenon |
|---|---|
| 0.1 g~0.4 g | No damage |
| 0.5 g | Two obvious cracks appeared at the location near the lower crossbeam of 1# tower, as Figure 10a shows. One crack appeared at the location near the lower crossbeam of the 2# tower, as Figure 10c shows. |
| 0.6 g | A new crack appeared at the location near the lower crossbeam of the 2# tower, as Figure 10c shows. The obvious collision between the girder and the auxiliary pier occurred under the action of the TJ wave. |
| 0.8 g | Four parallel cracks appeared at the central part of the 2# tower column, as Figure 10b shows. Two cracks appeared at 2# tower bottom, as Figure 10d shows. |
| 1 g | The collisions between the girder and auxiliary pier occurred under the action of the ELC wave, TJ wave, and SA wave. |
| 1.1 g | The outermost diagonal cable of 2# tower lost the anchored state. |

5. Analysis of Seismic Response
5.1. Displacement Response
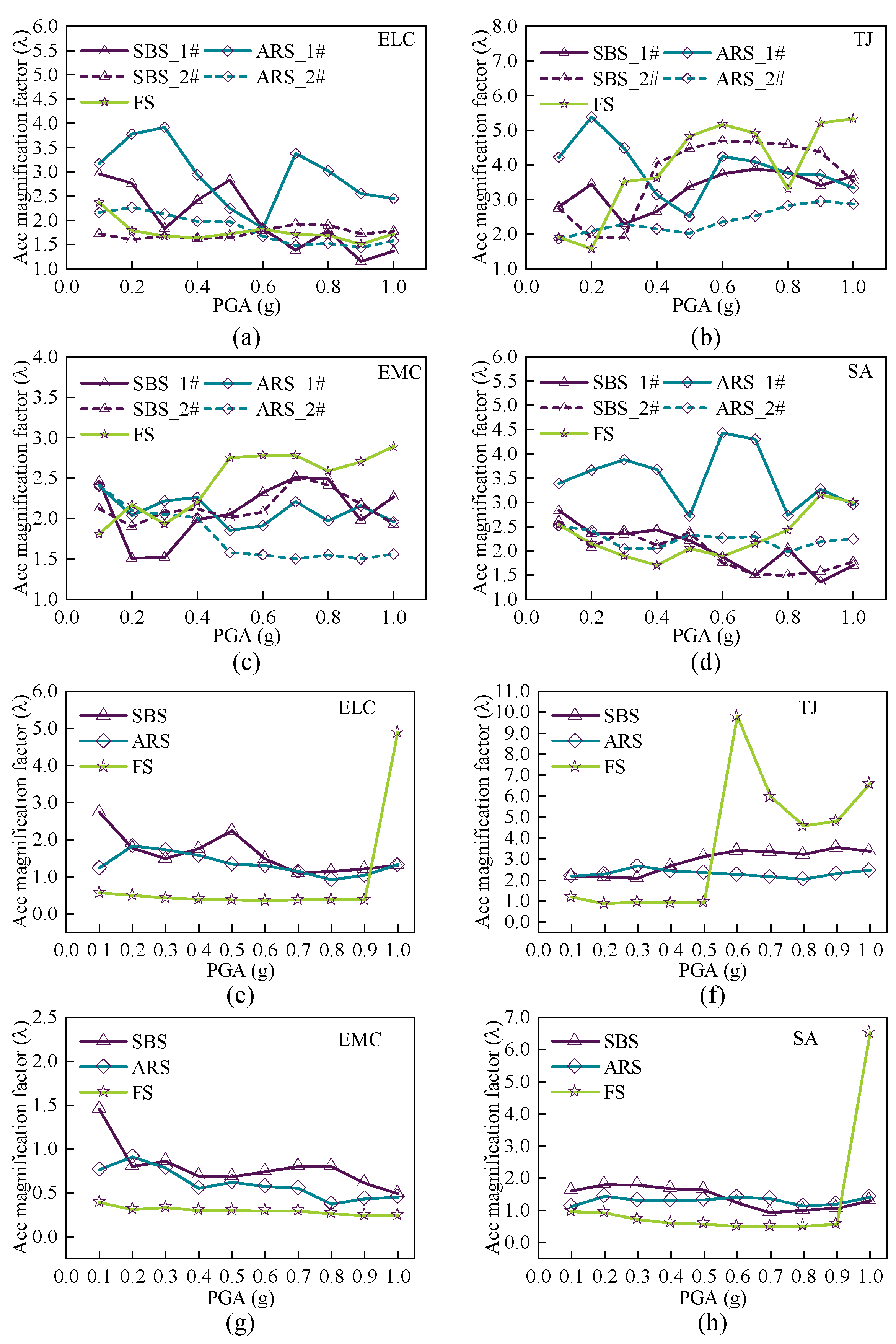
5.2. Acceleration Response
5.3. Strain Response
5.4. Evaluation of Decreasing Amplitude Effect
6. Conclusions
- (1)
- The installation of the safety-belt device has no obvious impact on the dynamic characteristics (self-vibration frequency) of the low-gravity-center cable-stayed bridge, before the activation of the safety-belt device. It will not influence the daily operation of the bridge. In the aspect of alleviating the influence of secondary internal force caused by the deformation of a girder, the SBS is the same as the ARS.
- (2)
- The seismic damage characteristics of low-gravity-center cable-stayed bridges are related to the type of structural system and the characteristics of seismic sites.
- (3)
- The safety-belt device can improve the seismic performance of low-gravity-center cable-stayed bridges. The functioning safety-belt device may reduce the internal force response of the restrained tower and the displacement response of the girder by letting the free tower with the safety-belt device bear the seismic action together.
- (4)
- The SBS has potential value in the seismic resistance of low-gravity-center cable-stayed bridges. In this paper, preliminary research was conducted on the seismic performance of the SBS low-gravity-center cable-stayed bridge by shaking table tests. The study on the seismic design theory and seismic fortification level division of the SBS low-gravity-center cable-stayed bridge should be carried out in the future.
7. Limitations and Recommendations
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, Y.; Wang, Y.; Zhang, W.; Liang, K.; Du, X. Simplified Criterion for Low Gravity Center Cable-Stayed Bridge Based on Response Spectrum Analyses. Sustainability 2022, 14, 10570. [Google Scholar] [CrossRef]
- Zhang, W.; Li, J.; Li, H. Study of Seismic Response Characteristics of Low Gravity Center Cable-Stayed Bridge. Bridge Constr. 2007, 5, 21–23+41. [Google Scholar]
- Franchini, A.; Sebastian, W.; D’Ayala, D. Surrogate-based fragility analysis and probabilistic optimisation of cable-stayed bridges subject to seismic loads. Eng. Struct. 2022, 256, 113949. [Google Scholar] [CrossRef]
- Li, H.; Liu, J.; Ou, J. Investigation of Seismic Damage of Cable-Stayed Bridges with Different Connection Configuration. J. Earthq. Tsunami 2009, 03, 227–247. [Google Scholar] [CrossRef]
- Xu, Y.; Zeng, S.; Duan, X.; Ji, D. Seismic experimental study on a concrete pylon from a typical medium span cable-stayed bridge. Front. Struct. Civ. Eng. 2018, 12, 401–411. [Google Scholar] [CrossRef]
- Javanmardi, A.; Ibrahim, Z.; Ghaedi, K.; Jameel, M.; Khatibi, H.; Suhatril, M. Seismic response characteristics of a base isolated cable-stayed bridge under moderate and strong ground motions. Arch. Civ. Mech. Eng. 2017, 17, 419–432. [Google Scholar] [CrossRef]
- Yoo, H.; Na, H.S.; Choi, D.H. Approximate method for estimation of collapse loads of steel cable-stayed bridges. Steel Constr. 2012, 72, 143–154. [Google Scholar] [CrossRef]
- Song, W.K.; Kim, S.E. Analysis of the overall collapse mechanism of cable-stayed bridges with different cable layouts. Eng. Struct. 2007, 29, 2133–2142. [Google Scholar] [CrossRef]
- Raheem, S.E.A.; Hayashikawa, T. Parametric Study on Steel Tower Seismic Response of Cable-Stayed Bridges Under Great Earthquake Ground Motion. Doboku Gakkai Ronbunshu 2003, 2003, 25–41. [Google Scholar] [CrossRef][Green Version]
- Guo, R. Research on Static and Dynamic Performance of Different Structural Systems of 140 m+240m+140m Single Cable-Stayed Bridge. Master’s Thesis, Shijiazhuang Tiedao University, Shijiazhuang, China, 2015. [Google Scholar]
- Ye, A.; Hu, S.; Fan, L. Research on Aseismatic Structural System of Cable-stayed Bridge. Bridge Constr. 2002, 4, 1–4. [Google Scholar][Green Version]
- Soong, T.T.; Spencer, B.F., Jr. Supplemental energy dissipation: State-of-the-art and state-of-the-practice. Eng. Struct. 2002, 24, 243–259. [Google Scholar] [CrossRef]
- Soong, T.T. Supplemental Energy Dissipation: State-of-the-Art and State-of-the-Practice. In Proceedings of the International Conference on Advances in Structural Dynamics Vol. I, Hong Kong, China, 13–15 December 2000. [Google Scholar]
- Shen, X.; Wang, X.; Ye, Q.; Ye, A. Seismic performance of Transverse Steel Damper seismic system for long span bridges. Eng. Struct. 2017, 141, 14–28. [Google Scholar] [CrossRef]
- Ahmad, F.; Rawat, S.; Yang, R.C.; Zhang, L.; Zhang, Y.X. Fire resistance and thermal performance of hybrid fibre-reinforced magnesium oxychloride cement-based composites. Constr. Build. Mater. 2025, 472, 140867. [Google Scholar] [CrossRef]
- Nasir, A.; Butt, F.; Ahmad, F. Enhanced mechanical and axial resilience of recycled plastic aggregate concrete reinforced with silica fume and fibers. Innov. Infrastruct. Solut. 2025, 10, 4. [Google Scholar] [CrossRef]
- Niu, J.; Ding, Y.; Shi, Y.; Li, Z. A simplified design method for metallic dampers used in the transverse direction of cable-stayed bridges. Earthq. Eng. Eng. Vib. 2020, 19, 15. [Google Scholar] [CrossRef]
- Raza, M.U.; Butt, F.; Ahmad, F.; Waqas, R.M. Seismic safety assessment of buildings and perceptions of earthquake risk among communities in Mingora, Swat, Pakistan. Innov. Infrastruct. Solut. 2025, 10, 124. [Google Scholar] [CrossRef]
- Ahmad, F.; Rawat, S.; Yang, R.; Zhang, L.; Fanna, D.J.; Soe, K.; Zhang, Y.X. Effect of metakaolin and ground granulated blast furnace slag on the performance of hybrid fibre-reinforced magnesium oxychloride cement-based composites. Int. J. Civ. Eng. 2025, 23, 853–868. [Google Scholar] [CrossRef]
- Ahmad, F.; Qureshi, M.I.; Rawat, S.; Alkharisi, M.K.; Alturki, M. E-waste in concrete construction: Recycling, applications, and impact on mechanical, durability, and thermal properties—A review. Innov. Infrastruct. Solut. 2025, 10, 246. [Google Scholar] [CrossRef]
- Rawat, S.; Saliba, P.; Estephan, P.C.; Ahmad, F.; Zhang, Y. Mechanical performance of hybrid fibre reinforced magnesium oxychloride cement-based composites at ambient and elevated temperature. Buildings 2024, 14, 270. [Google Scholar] [CrossRef]
- Pang, Y. Seismic Fragility Assessment of an Isolated Multipylon Cable-Stayed Bridge Using Shaking Table Tests. Adv. Civ. Eng. 2017, 2017, 9514086. [Google Scholar] [CrossRef]
- Li, J.; Yan, J.; Peng, T.; Han, L. Shake Table Studies of Seismic Structural Systems of a Taizhou Changjiang Highway Bridge Model. J. Bridge Eng. 2015, 20, 04014065. [Google Scholar] [CrossRef]
- Zhou, R.; Zong, Z.H.; Huang, X.Y.; Xia, Z.H. Seismic response study on a multi-span cable-stayed bridge scale model under multi-support excitations. Part II: Numerical analysis. J. Zhejiang Univ. Sci. A Appl. Phys. Eng. 2014, 15, 405–418. [Google Scholar] [CrossRef]
- Zong, Z.H.; Zhou, R.; Huang, X.Y.; Xia, Z.H. Seismic response study on a multi-span cable-stayed bridge scale model under multi-support excitations. Part I: Shaking table tests. J. Zhejiang Univ. Sci. A Appl. Phys. Eng. 2014, 15, 351–363. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, W.; Fang, R.; Zhao, H. Dynamic Model Testing of Low-Gravity-Center Cable-Stayed Bridges with Different Girder-to-Tower Connections. J. Bridge Eng. 2021, 26, 04020112. [Google Scholar] [CrossRef]
- Zhao, L.; Huang, J.; Zhang, W. Influence of Height of Gravity Center on Tower-girder Elastic Connecting Device’s Damping Effect in Cable-stayed Bridge. Highway 2015, 60, 79–82. [Google Scholar]
- Yi, R.; Li, X.; Zhu, S.; Li, Y.; Xu, X. A deep leaning method for dynamic vibration analysis of bridges subjected to uniform seismic excitation. Soil Dyn. Earthq. Eng. 2023, 168, 107830. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, Z.Y.; Yuan, D.P.; Zheng, S.X.; Hu, Y.R. Seismic Response of Two Site Models and Their Effects on the Railway Cable-Stayed Bridge. KSCE J. Civ. Eng. 2021, 25, 4724–4741. [Google Scholar] [CrossRef]
- Fang, R.; Zhang, W.; Chen, Y.; Zhang, L. Aseismic effect and parametric analysis of the safe-belt device for a continuous bridge with equal height piers. Eng. Struct. 2019, 199, 109553. [Google Scholar] [CrossRef]
- Ahamed, I.Z.A.K.; Magar, R.B. Dynamic Response of Cable-Stayed Bridge Under Seismic Vulnerability Analysis: State of the Art. In Emerging Trends in Composite Structures Select Proceedings of ICC-IDEA 2023; Lecture Notes in Civil Engineering; Springer: Singapore, 2024; Volume 387. [Google Scholar]
- Yan, X.; Cunyu, C.; Zeng, Z.; Shijie, Z. Shake table experimental study of cable-stayed bridges with two different design strategies of H-shaped towers. Earthq. Eng. Eng. Vib. 2021, 20, 483–493. [Google Scholar] [CrossRef]
- Liao, R.; Zhang, Y.; Wang, H.; Lu, L.; Chen, Z.; Wang, X.; Zuo, W. An effective ship detection approach combining lightweight networks with supervised simulation-to-reality domain adaptation. Comput.‐Aided Civ. Infrastruct. Eng. 2025, 1–26. [Google Scholar] [CrossRef]



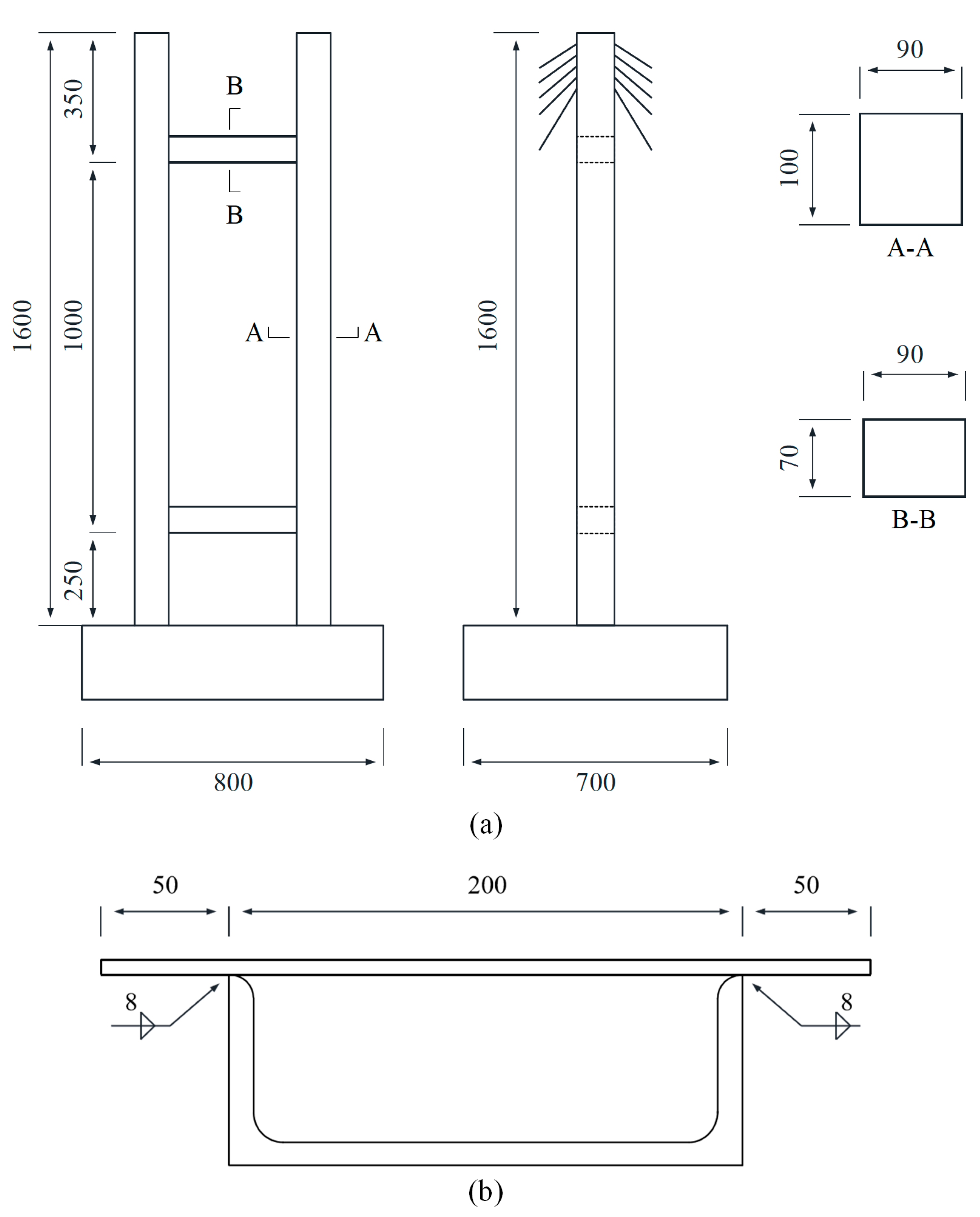



| Type | Physics Parameters | Symbol | Similarity Ratio (Model/Prototype) |
|---|---|---|---|
| Geometry property | Geometry | Sl | 0.0133 |
| Material properties | Strain | Sε | 1.0 |
| Elastic modulus | SE = Sσ | 0.3 | |
| Stress | Sσ | 0.3 | |
| Mass density | Sρ = SE/SaSL | 22.5 | |
| Poisson’s ratio | Sμ | 1.0 | |
| Mass | Sm = SρSl3 | 0.000053 | |
| Dynamic properties | Time | St = (Sm/Sk) 0.5 | 0.1155 |
| Frequency | Sf = 1/St | 8.66 | |
| Damping ratio | Sc = Sm/St | 0.00046 | |
| Velocity | Sv = Sl/St | 0.1155 | |
| Acceleration | Sa | 1.0 |
| Classification | 1# Tower–Girder Connection | 2# Tower–Girder Connection |
|---|---|---|
| FS | Free sliding | Free sliding |
| ARS | Fixed constraint | Free sliding |
| SBS | Fixed constraint | Safety-belt device |
| Index | Compressive Strength of Concrete (MPa) | Elastic Modulus of Concrete (GPa) | Yield Stress of Steel Bar (MPa) |
|---|---|---|---|
| Measured value | 17.57 | 12.1 | 367 |
| 16.82 | 10.1 | 362 | |
| 15.64 | 14.14 | 376 | |
| Average value | 16.68 | 12.11 | 368 |
| Component | Self-Weight (kg) | Additional Mass (kg) | Total Mass (kg) | Theoretical Mass (kg) |
|---|---|---|---|---|
| Steel girder | 193.36 | 320 | 513.36 | 514.13 |
| Single tower | 82.71 | 140 | 222.71 | 224.64 |
| Seismic Waves | ELC | TJ | EMC | SA |
|---|---|---|---|---|
| PGA (Activated) | 0.4 g | 0.3 g | 1.0 g | 0.5 g |
| PGA (Functioned) | 0.8 g | 0.5 g | 1.0 g | 0.8 g |
| PGA | FS | ARS | SBS |
|---|---|---|---|
| 0.5 g | 2 cracks occurred (1# tower) 1 crack occurred (2# tower) | No damage | No damage |
| 0.6 g | 1 new crack occurred (2# tower) Pier-girder collision | No damage | No damage |
| 0.7 g | — | 1 crack occurred (1# tower) 1 crack occurred (1# tower fixed pier) | No damage |
| 0.8 g | 4 parallel cracks occurred (2# tower) 2 cracks occurred (2# tower) | Original cracks extended (1# tower) Concrete fragmentation (1# tower) | Concrete fragmentation (of 1# tower crossbeam) |
| 1.0 g | Intense pier-girder collision (ELC, TJ, and SA wave) | — | Horizontal cracks occurred (1# tower column) Original cracks extended (1# tower bottom) |
| 1.1 g | Outmost stayed cable unanchored (2# tower) | Penetrating cracks occurred (1# tower bottom) Intense fragmentation occurred (1# tower column corner) | Original cracks extended (1# tower bottom) |
| 1.2 g | — | — | 1 new crack occurred (1# tower) 1 oblique crack occurred (1# tower) |
| 1.4 g | — | Intense fragmentation (1# tower lower crossbeam) Plenty of cracks occurred (1# tower) | Bolt was broken (safety belt device) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Lu, X.; Wang, Z.; Fang, R. Aseismic Experimental Research on Safety-Belt System of a Low-Gravity-Center Cable-Stayed Bridge. Buildings 2025, 15, 3268. https://doi.org/10.3390/buildings15183268
Li Q, Lu X, Wang Z, Fang R. Aseismic Experimental Research on Safety-Belt System of a Low-Gravity-Center Cable-Stayed Bridge. Buildings. 2025; 15(18):3268. https://doi.org/10.3390/buildings15183268
Chicago/Turabian StyleLi, Qing, Xiangtao Lu, Zhen Wang, and Rong Fang. 2025. "Aseismic Experimental Research on Safety-Belt System of a Low-Gravity-Center Cable-Stayed Bridge" Buildings 15, no. 18: 3268. https://doi.org/10.3390/buildings15183268
APA StyleLi, Q., Lu, X., Wang, Z., & Fang, R. (2025). Aseismic Experimental Research on Safety-Belt System of a Low-Gravity-Center Cable-Stayed Bridge. Buildings, 15(18), 3268. https://doi.org/10.3390/buildings15183268






