Rapid Regional Liquefaction Probability Assessment Based on Transfer Learning
Abstract
1. Introduction
2. Liquefaction Event in Target Region
2.1. General Overview of the Liquefaction Event
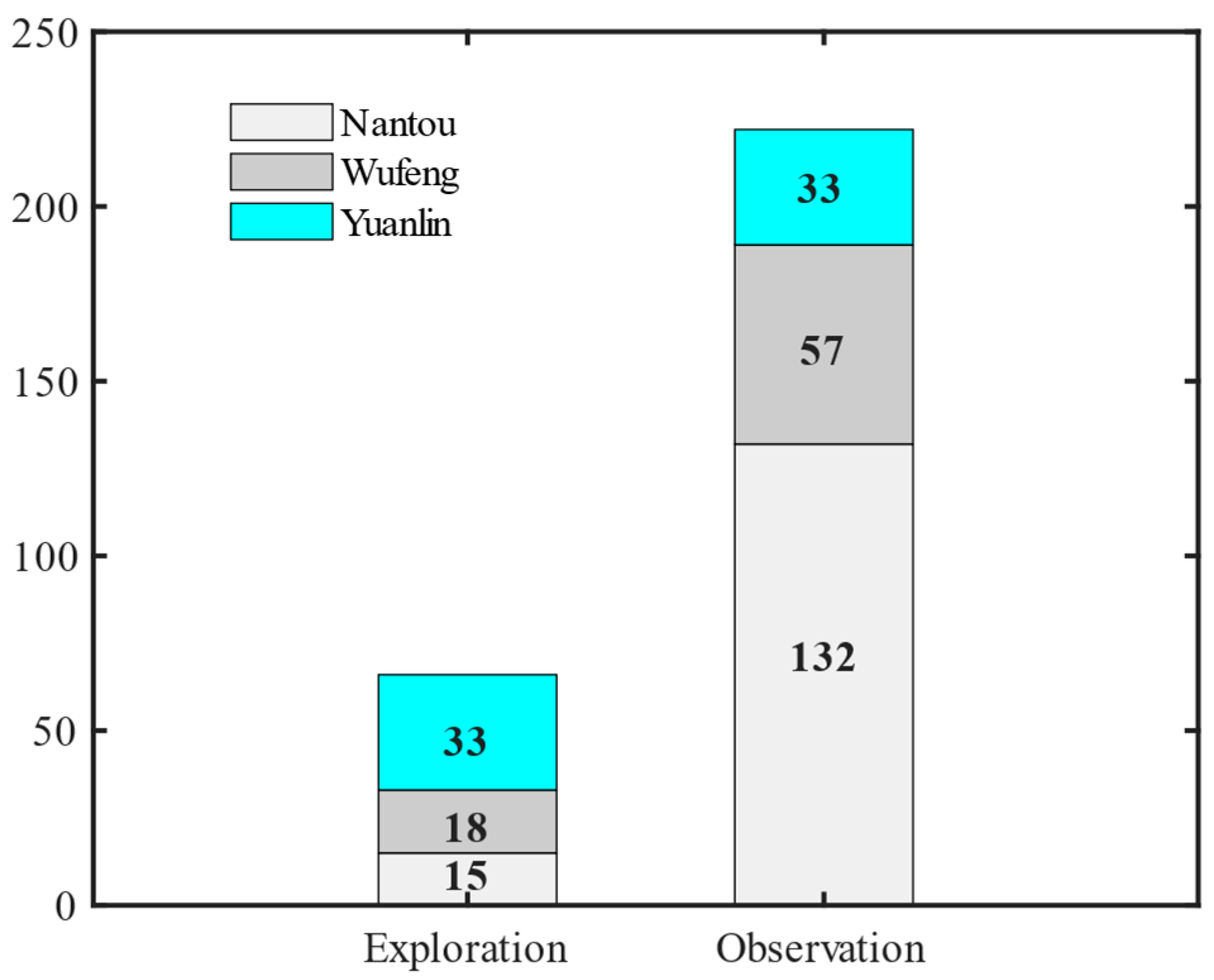
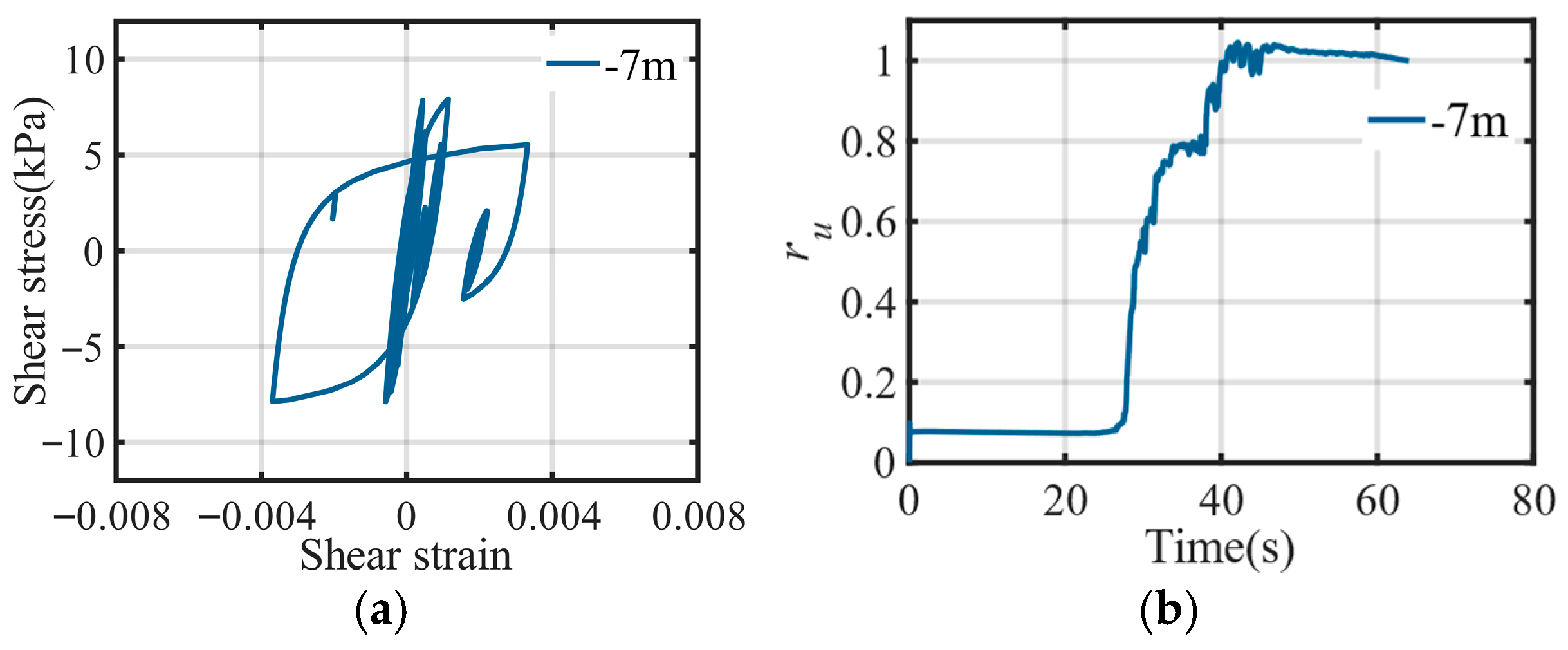
2.2. Liquefaction Data
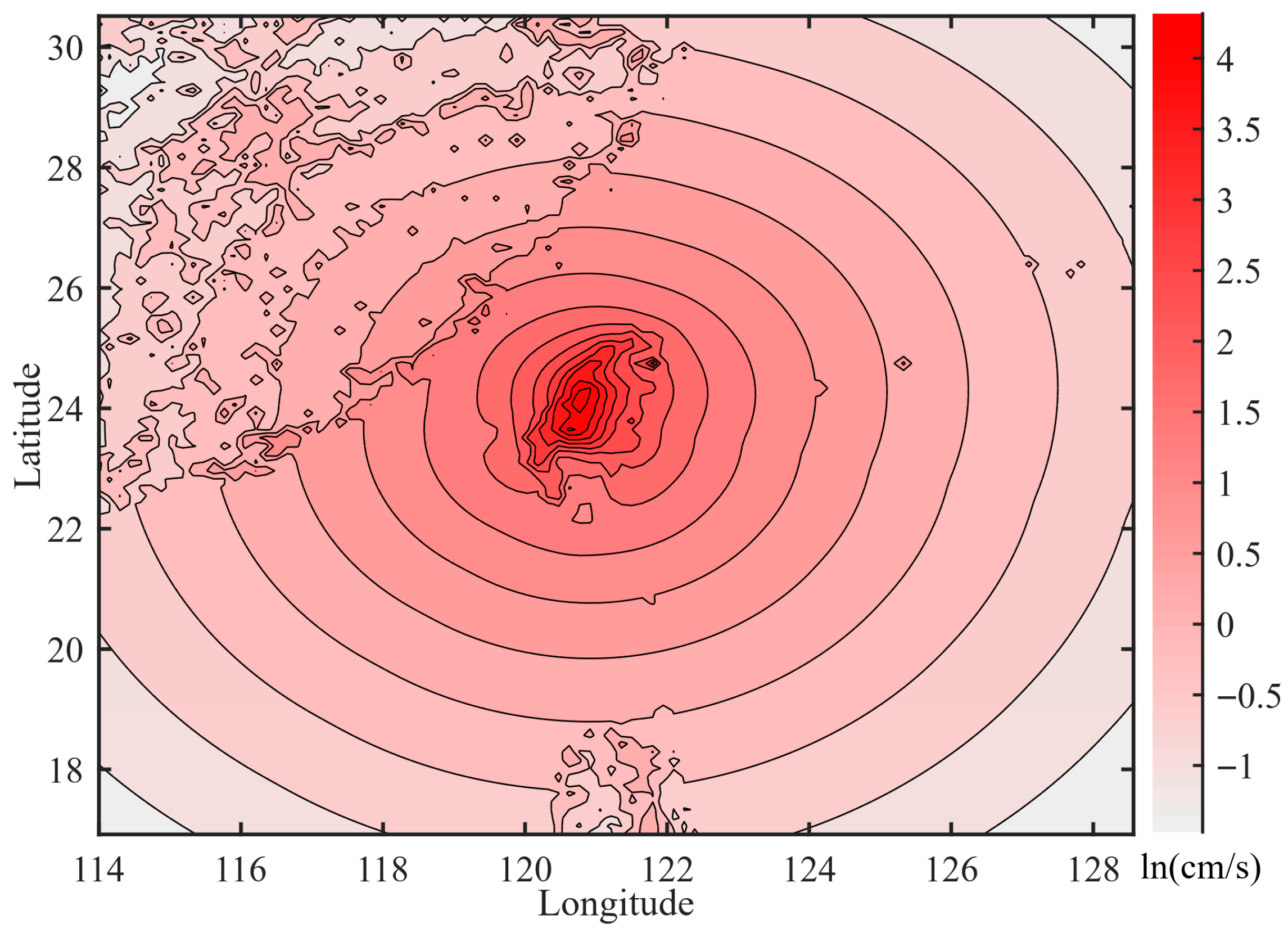
2.3. Distribution of Seismic Ground Motion Intensity
3. Rapid Assessment Procedure of Regional Probabilistic Liquefaction Based on Transfer Learning
3.1. Conditions for Rapid Assessment of Regional Seismic Liquefaction
3.1.1. Limitations of Liquefaction Data
3.1.2. Seismic Information
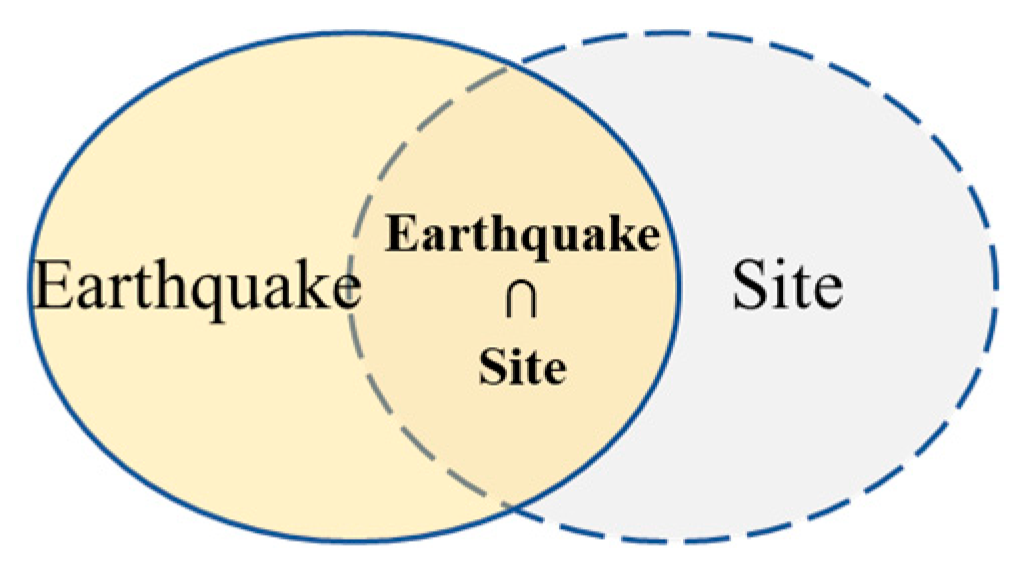
3.1.3. Feasibility of Rapid Regional Liquefaction Assessment
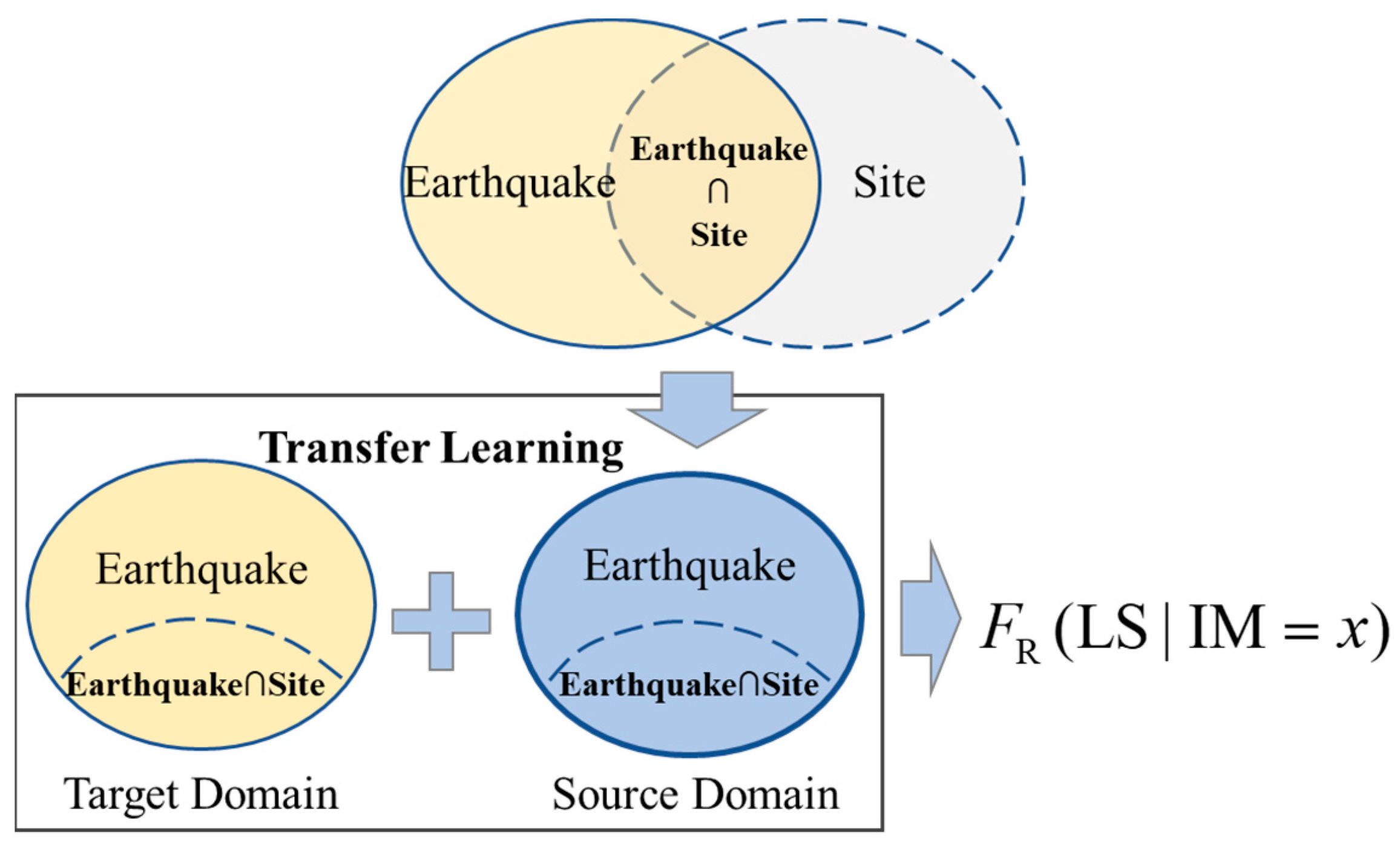
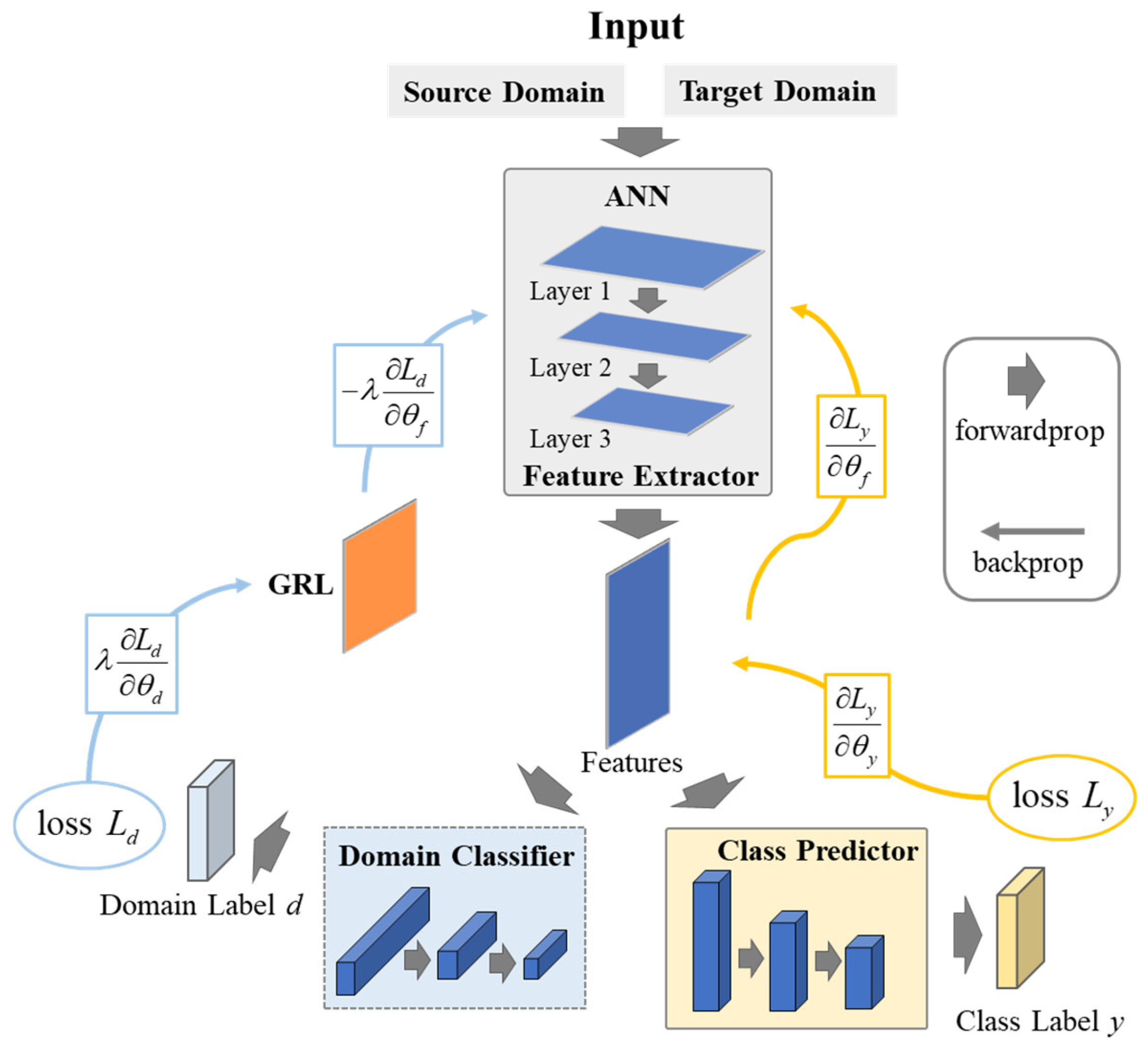
3.2. Feature-Based Transfer Learning
3.2.1. Transfer Learning Architecture
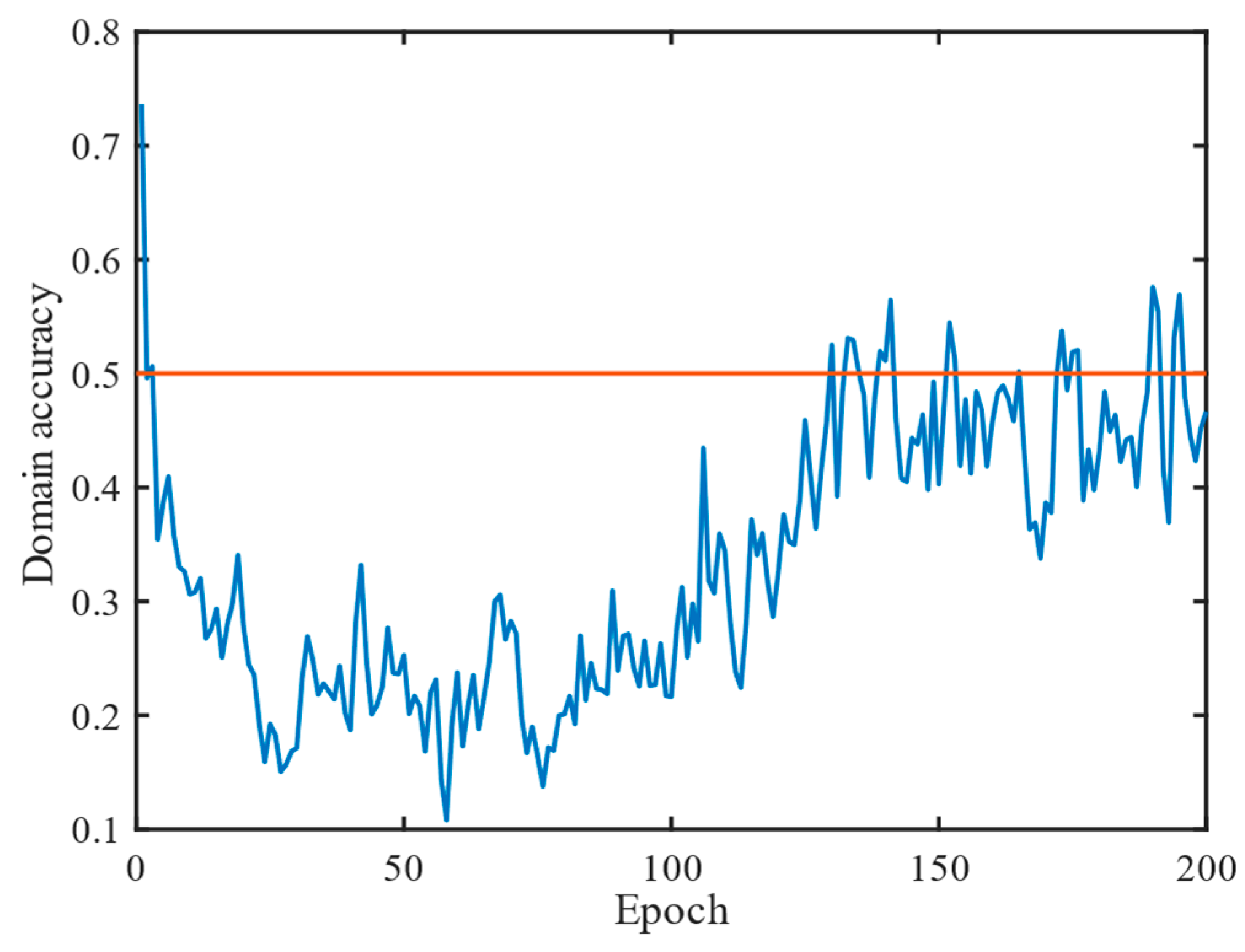
3.2.2. Domain-Invariant and Discriminative Feature Training
3.2.3. Dataset Construction
Source Domain Dataset
- Burial depth of sand layers: The burial depth of sand layers is found to follow a log-normal distribution with parameters θ = 1.62 and β = 0.7596. This distribution is validated through a Kolmogorov–Smirnov (KS) test at a significance level of 0.05.
- Groundwater level: Analysis of groundwater-level probability distributions from sample library A reveals that the log-normal distribution is appropriate, as verified by a KS test at a significance level of 0.01. To improve statistical robustness, three outliers are removed, as their exclusion does not affect the overall sample range. The refined groundwater-level data follow a log-normal distribution with parameters θ = 0.299 and β = 0.6856, passing the KS test at a significance level of 0.05.
- Sand layer thickness: The thickness of the sand layer follows a log-normal distribution with parameters θ = 0.4071 and β = 0.7053, which is validated through the KS test at a significance level of 0.05.
Target Domain Dataset
Model Parameters
3.3. Rapid Assessment Procedure of Regional Probabilistic Liquefaction Based on Transfer Learning
- (a)
- Establishment of the Target Domain Dataset: For this component, the liquefaction data from the Chi-Chi earthquake event are chosen as the target domain. This target domain encompasses three regions: Wufeng, Nantou, and Yuanlin, with Yuanlin being designated as the research object.
- (b)
- Construction of the Source Domain Dataset: When it comes to constructing the source domain dataset, data-driven approaches are employed to generate site conditions that are rich enough. After conducting the modeling process with OpenSees, we input a substantial number of actual ground motions. Subsequently, through the seismic liquefaction response analysis, a source domain dataset that is abundant in both seismic information and site information is acquired.
- (c)
- Transfer Learning-based Model Training across Source and Target Domains: In the process of training a model across the source and target domains based on transfer learning, we leverage the data from both these domains. Through transfer learning techniques, a seismic liquefaction assessment model is trained. This model primarily relies on the ground motion information and the post-earthquake liquefaction survey data of the region.
- (d)
- Regional Liquefaction Probability Assessment: To evaluate the liquefaction probability of the target region, we utilize the transfer learning model established in component (c) along with the seismic information specific to the target region.

4. Liquefaction Probability Assessment of the Target Region
4.1. Model Training Schemes
4.2. Model Performance Evaluation
- Accuracy:
- Kappa:
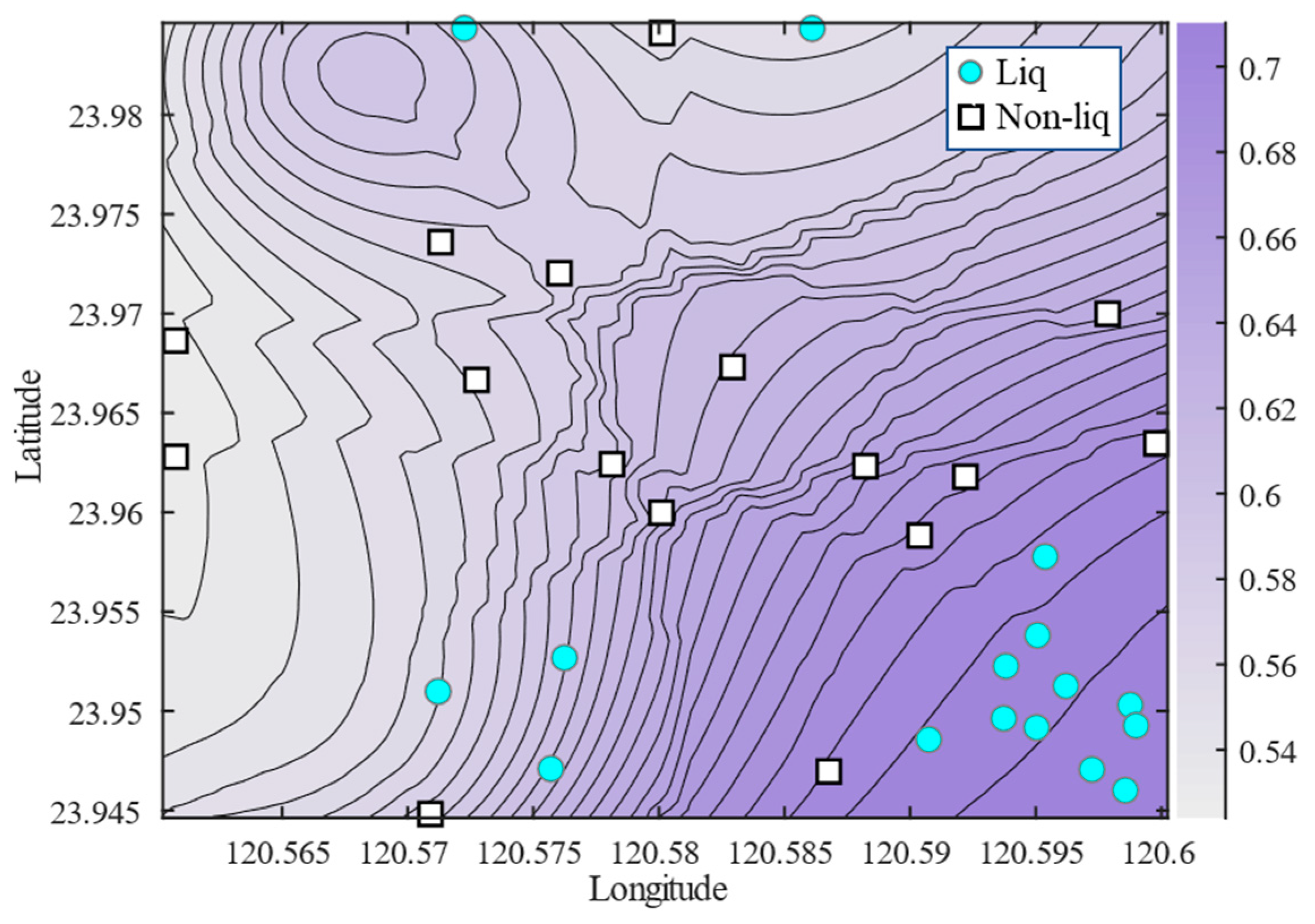
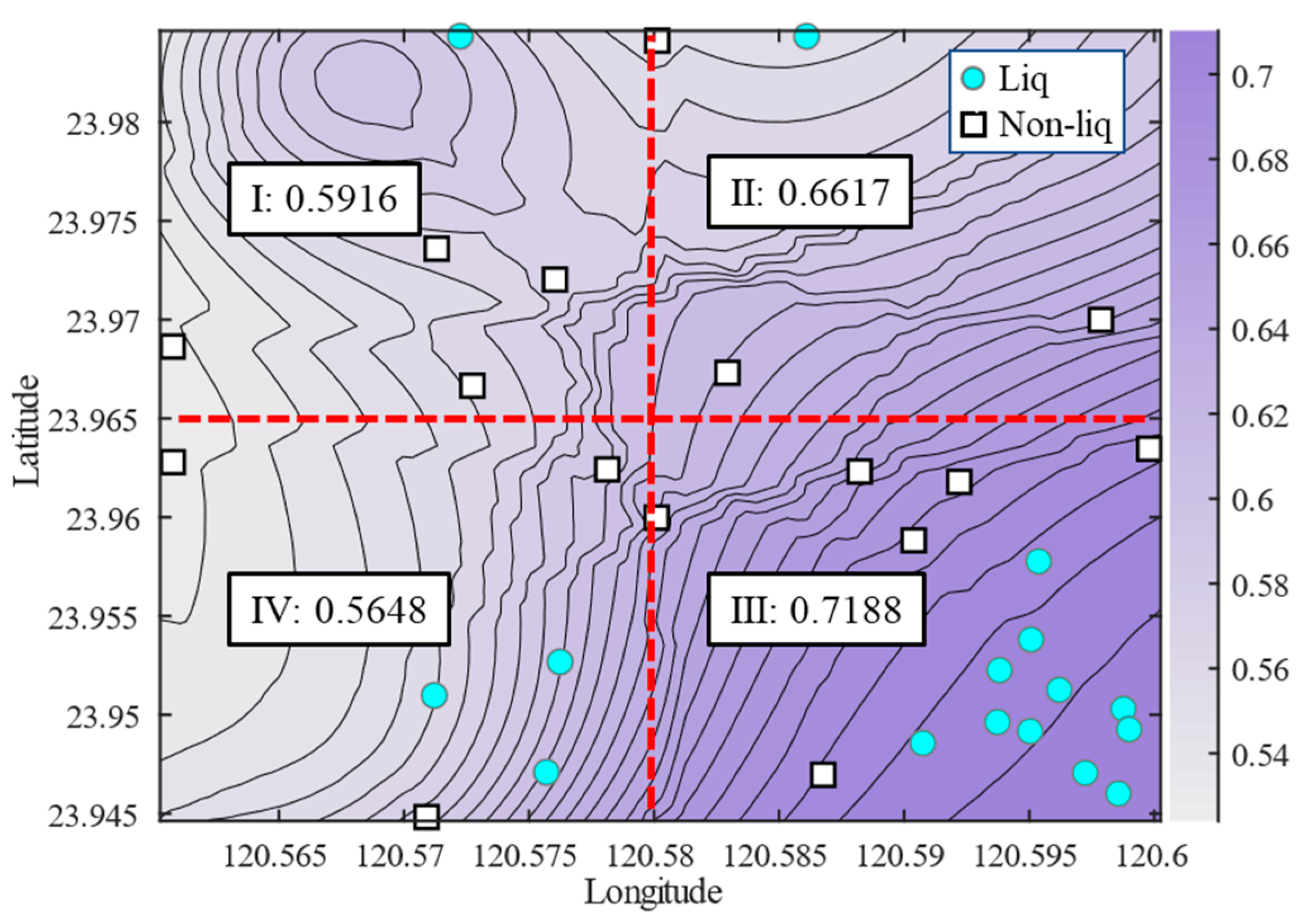
4.3. Liquefaction Probability Assessment of the Target Region
5. Regional Liquefaction Probability Index
5.1. Definition and Formula of the Regional Liquefaction Probability Index
5.2. Applications of the Regional Liquefaction Probability Index
5.2.1. Application Based on Transfer Learning
5.2.2. Simplified Application
6. Conclusions
- (1)
- A rapid assessment procedure of regional probabilistic liquefaction based on transfer learning is proposed in this study (DANN model in Scheme 1), which relies solely on earthquake information and liquefaction observations in the absence of site-related data. It exhibits performance comparable to the site-incorporating DANN model and significantly outperforms all ANN models, regardless of site data inclusion. Additionally, its model parameters can be acquired more quickly, conveniently, and at lower cost, making it suitable for large-scale regional liquefaction assessments.
- (2)
- Regional liquefaction probability assessment for Yuanlin reveals that the southeastern area is the most prone to liquefaction. This finding matches post-earthquake survey results, where actual liquefaction instances are predominantly concentrated in this region.
- (3)
- The proposed regional liquefaction probability index, when applied to Yuanlin, identifies the southeastern area as having the highest index values, consistent with both the regional probabilistic liquefaction distribution and observed liquefaction patterns. A simplified calculation method for the index is provided, which depends on the distribution and density of post-earthquake observation points, ensuring strong practical applicability.
- (4)
- The developed procedure and index rely principally on the uniformity of post-earthquake liquefaction observation point distribution and their density, offering notable advantages in real-world applications, including high efficiency, low cost, and strong implementability.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dungca, J.R.; Kuwano, J.; Takahashi, A.; Saruwatari, T.; Izawa, J.; Suzuki, H.; Tokimatsu, K. Shaking table tests on the lateral response of a pile buried in liquefied sand. Soil Dyn. Earthq. Eng. 2006, 26, 287–295. [Google Scholar] [CrossRef]
- Fairless, G.J.; Berrill, J.B. Liquefaction during historic earthquakes in New Zealand. Earthq. Eng. 1984, 17, 4. [Google Scholar] [CrossRef]
- Huang, Y.; Jiang, X. Field-observed phenomena of seismic liquefaction and subsidence during the 2008 Wenchuan earthquake in China. Nat. Hazards 2010, 54, 839–850. [Google Scholar] [CrossRef]
- Huang, Y.; Yu, M. Review of soil liquefaction characteristics during major earthquakes of the twenty-first century. Nat. Hazards 2013, 65, 2375–2384. [Google Scholar] [CrossRef]
- Ledezma, C.; Hutchinson, T.; Ashford, S.A.; Moss, R.; Arduino, P.; Bray, J.D.; Olson, S.; Hashash, Y.M.; Verdugo, R.; Frost, D.; et al. Effects of ground failure on bridges, roads, and railroads. Earthq. Spectra 2012, 28, S119–S143. [Google Scholar] [CrossRef]
- Robertson, P.K.; Wride, C.E.; Boulanger, R.W.; Mejia, L.H.; Idriss, I.M. Liquefaction at moss landing during loma prieta earthquake. J. Geotech. Geoenviron. Eng. 1999, 125, 91–95. [Google Scholar] [CrossRef]
- Andrews, D.C.; Martin, G.R. Criteria for Liquefaction of Silty Soils. 1999. Available online: https://www.iitk.ac.in/nicee/wcee/article/0312.pdf (accessed on 7 May 2025).
- Bray, J.D.; Sancio, R.B.; Durgunoğlu, H.T.; Onalp, A.; Youd, T.L.; Stewart, J.P.; Seed, R.B.; Cetin, O.K.; Bol, E.; Baturay, M.B.; et al. Subsurface characterization at ground failure sites in Adapazari Turkey. J. Geotech. Geoenviron. Eng. 2004, 130, 673–685. [Google Scholar] [CrossRef]
- Bray, J.D.; Sancio, R.B. Assessment of the liquefaction susceptibility of fine-grained soils. J. Geotech. Geoenviron. Eng. 2006, 132, 1165–1177. [Google Scholar] [CrossRef]
- Boulanger, R.W.; Idris, I.M. Liquefaction susceptibility criteria for silts clays. J. Geotech. Geoenviron. Eng. 2006, 132, 1413–1426. [Google Scholar] [CrossRef]
- Idriss, I.; Boulanger, R. Soil Liquefaction During Earthquakes; EERI Publication: Oakland, CA, USA, 2008. [Google Scholar]
- Martin, G.; Lew, M.; Arulmoli, K.; Baez, J.; Blake, T.; Earnest, J.; Gharib, F.; Goldhammer, J.; Hsu, D.; Kupferman, S.; et al. Recommended Procedures for Implementation of DMG Special Publication 117 Guidelines for Analyzing and Mitigating Liquefaction Hazard in California; The Southern California Earthquake Center: Los Angeles, CA, USA, 1999; Available online: https://scecinfo.usc.edu/resources/catalog/LiquefactionproceduresJun99.pdf (accessed on 7 May 2025).
- Seed, H.B.; Idriss, I.M.; Arango, I. Evaluation of liquefaction potential using field performance data. J. Geotech. Eng. 1983, 109, 458–482. [Google Scholar] [CrossRef]
- Youd, T.L.; Idriss, I.M.; Andrus, R.D. Liquefaction resistance of soils: Summary report from the 1996, NCEER and 1998 NCEER/NSF workshops on evaluation of liquefaction resistance of soils. J. Geotech. Geoenviron. Eng. 2001, 127, 817–833. [Google Scholar] [CrossRef]
- Seed, H.B.; Idriss, I.M. Ground Motions and Soil Liquefaction During Earthquakes; Earthquake Engineering Research Institute: Berkeley, CA, USA, 1982. [Google Scholar]
- Tan, C.S.; Marto, A.; Leong, T.K.; Teng, L.S. The role of fines in liquefaction susceptibility of sand matrix soils. Electron. J. Geotech. Eng. 2013, 18, 2355–2368. [Google Scholar]
- Xenakia, V.C.; Athanasopoulos, G.A. Liquefaction resistance of sand–silt mixtures: An experimental investigation of the effect of fines. Soil Dyn. Earthq. Eng. 2003, 23, 183–194. [Google Scholar] [CrossRef]
- Andrus, R.D.; Kenneth, I.I. Liquefaction resistance of soils from shear-wave velocity. J. Geotech. Geoenviron. Eng. 2000, 126, 1015–1025. [Google Scholar] [CrossRef]
- Cao, Z.Z.; Youd, T.L.; Yuan, X.M. Chinese dynamic penetration test for liquefaction evaluation in gravelly soils. J. Geotech. Geoenviron. Eng. 2013, 139, 1320–1333. [Google Scholar] [CrossRef]
- Guan, Z.; Wang, Y. Assessment of liquefaction-induced differential ground settlement lateral displacement using standard penetration tests with consideration of soil spatial variability. J. Geotech. Geoenviron. Eng. 2022, 148, 04022018. [Google Scholar] [CrossRef]
- Howie, J.A.; Vaid, Y.P. Evaluating cyclic liquefaction potential using the cone penetration test: Discussion. Can. Geotech. J. 2011, 37, 270–271. [Google Scholar] [CrossRef]
- Lin, P.S.; Chang, C.W.; Chang, W.J. Characterization of liquefaction resistance in gravelly soil: Large hammer penetration test and shear wave velocity approach. Soil Dyn. Earthq. Eng. 2004, 24, 675–687. [Google Scholar] [CrossRef]
- Robertson, P.K.; Wride, C.E. Evaluating cyclic liquefaction potential using the cone penetration test. Can. Geotech. J. 1998, 35, 442–459. [Google Scholar] [CrossRef]
- Cetin, K.O.; Seed, R.B.; Kiureghian, A.; Tokimatsu, K.; Harder, L.F.; Kayen, R.E.; Moss, R.E.S. Standard penetration test-based probabilistic and deterministic assessment of seismic soil liquefaction potential. J. Geotech. Geoenviron. Eng. 2004, 130, 1314–1340. [Google Scholar] [CrossRef]
- Guan, Z.; Wang, Y. SPT-based probabilistic evaluation of soil liquefaction potential considering design life of civil infrastructures. Comput. Geotech. 2022, 148, 104807. [Google Scholar] [CrossRef]
- Jas, K.; Mangalathu, S.; Dodagoudar, G.R. Evaluation and analysis of liquefaction potential of gravelly soils using explainable probabilistic machine learning model. Comput. Geotech. 2024, 167, 106051. [Google Scholar] [CrossRef]
- Huang, H.W.; Zhang, J.; Zhang, L.M. Bayesian network for characterizing model uncertainty of liquefaction potential evaluation models. KSCE J. Civ. Eng. 2012, 16, 714–722. [Google Scholar] [CrossRef]
- Kalantary, F.; Ardalan, H.; Nariman-Zadeh, N. An investigation on the Su–NSPT correlation using GMDH type neural networks and genetic algorithms. Eng. Geol. 2009, 104, 144–155. [Google Scholar] [CrossRef]
- Demir, S.; Sahin, E. Comparison of tree-based machine learning algorithms for predicting liquefaction potential using canonical correlation forest, rotation forest, and random forest based on CPT data. Soil Dyn. Earthq. Eng. 2022, 154, 107130. [Google Scholar] [CrossRef]
- Hu, X.; Zhang, H.; Mei, H.; Xiao, D.; Li, Y.; Li, M. Landslide susceptibility mapping using the stacking ensemble machine learning method in Lus hui, Southwest China. Appl. Sci. 2020, 10, 4016. [Google Scholar] [CrossRef]
- Ozsagir, M.; Erden, C.; Bol, E.; Sert, S.; Özocak, A. Machine learning approaches for prediction of fine-grained soils liquefaction. Comput. Geotech. 2022, 152, 105014. [Google Scholar] [CrossRef]
- Qiu, Z.; Zhu, J.; Ebeido, A.; Prabhakaran, A.; Zheng, Y. Data-driven probabilistic seismic demand prediction and sustainability optimization of stone columns for liquefaction mitigation in regional mildly sloping ground. Comput. Geotech. 2025, 181, 107125. [Google Scholar] [CrossRef]
- Sahin, E.; Demir, S. Greedy-AutoML: A novel greedy-based stacking ensemble learning framework for assessing soil liquefaction potential. Eng. Appl. Artif. Intell. 2023, 119, 105732. [Google Scholar] [CrossRef]
- Xie, Y.; Sichani, M.E.; Padgett, J.E.; Desroches, R. The promise of implementing machine learning in earthquake engineering: A state-of-the-art review. Earthq. Spectra 2020, 36, 875529302091941. [Google Scholar] [CrossRef]
- Anderson, L.R.; Keaton, J.R.; Aubry, K.; Ellis, S.J. Liquefaction Potential Map for Davis County Utah; Utah State University: Logan, UT, USA, 1982; Unpublic Final Tech Report, USA Geological Survey Contract No. 14-08-0001. [Google Scholar]
- Brankman, C.M.; Baise, L.G. Liquefaction susceptibility mapping in Boston, Massachusetts. Environ. Eng. Geosci. 2008, 14, 1–16. [Google Scholar] [CrossRef]
- Baise, L.G.; Daley, D.; Zhu, J.; Thompson, E.M.; Knudsen, K. Geospatial liquefaction hazard model for Kobe, Japan and Christchurch, New Zealand, Seismol. Res. Lett. 2012, 83, 458. [Google Scholar]
- Holzer, T.L.; Bennett, M.J.; Noce, T.E.; Padovani, A.C.; Tinsley, J.C. Liquefaction hazard mapping with LPI in the greater Oakland, California, area. Earthq. Spectra 2006, 22, 693–708. [Google Scholar] [CrossRef]
- Holzer, T.L.; Noce, T.E.; Bennett, M.J. Scenario liquefaction hazard maps of Santa Clara Valley, northern California. Bull. Seismol. Soc. Amer. 2009, 99, 367–381. [Google Scholar] [CrossRef]
- Rashidian, V.; Baise, L.G. Regional efficacy of a global geospatial liquefaction model. Eng. Geol. 2020, 272, 105644. [Google Scholar] [CrossRef]
- Zhu, J.; Daley, D.; Baise, L.G.; Thompson, E.M.; Wald, D.J.; Knudsen, K.L. A geospatial liquefaction model for rapid response and loss estimation. Earthq. Spectra 2015, 31, 1813–1837. [Google Scholar] [CrossRef]
- Zhu, J.; Baise, L.G.; Thompson, E.M. An updated geospatial liquefaction model for global application. Bull. Seismol. Soc. Amer. 2017, 107, 1365–1385. [Google Scholar] [CrossRef]
- Raja, M.N.A.; Mercado, V.; Abdoun, T.; El-Sekelly, W. Seismic site amplification prediction- an integrated Bayesian optimisation explainable machine learning approach. In Georisk: Assessment and Management of Risk for Engineered Systems and Geohazards; Taylor & Francis: Abingdon, UK, 2025; pp. 1–20. [Google Scholar] [CrossRef]
- Ulmer, K.J.; Zimmaro, P.; Brandenberg, S.J.; Stewart, J.P.; Hudson, K.S.; Stuedlein, A.W.; Jana, A.; Dadashiserej, A.; Kramer, S.L.; Cetin, K.O.; et al. Next-Generation Liquefaction Database [Dataset]. Version 2. Next-Generation Liquefaction Consortium. 2023. [Google Scholar] [CrossRef]
- Meng, J.Y.; Lu, D.G.; Shan, B.H. Probabilistic-based seismic fragility assessment of earthquake-induced site liquefaction. Soil Dyn. Earthq. Eng. 2023, 175, 108250. [Google Scholar] [CrossRef]
- Baker, J.; Bradley, B.; Stafford, P. Seismic Hazard and Risk Analysis; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Kramer, S.; Astaneh Asl, B.; Ozener, P.; Sideras, S. Effects of Liquefaction on Ground Surface Motions; Springer: Cham, Switzerland, 2015. [Google Scholar] [CrossRef]
- Liu, L.; Lu, D.G. Probabilistic seismic hazard analysis for China based on Bayesian network. Seismol. Res. Lett. 2023, 95, 50–63. [Google Scholar] [CrossRef]
- Liu, C.; Lu, D. Aftershock probabilistic seismic hazard analysis based on enhanced Bayesian network considering frequency information. Comput.-Aided Civil. Infrastruct. Eng. 2024, 39, 1963–1987. [Google Scholar] [CrossRef]
- Gingery, J. Effects of Liquefaction on Earthquake Ground Motions. Ph.D. Thesis, The University of California, San Diego, San Diego, CA, USA, 2014. Available online: https://escholarship.org/uc/item/3q3212r5 (accessed on 7 May 2025).
- Hashash, Y.M.A.; Park, D. Non-linear one-dimensional seismic ground motion propagation in the Mississippi embayment. Eng. Geol. 2001, 62, 185–206. [Google Scholar] [CrossRef]
- Hashash, Y.M.A.; Park, D. Viscous damping formulation and high frequency motion propagation in nonlinear site response analysis. Soil. Dyn. Earthq. Eng. 2002, 22, 611–624. [Google Scholar] [CrossRef]
- Idriss, I.M.; Sun, J.I. SHAKE91—A computer program for conducting equivalent linear seismic response analysis of horizontally layered soils. In User’s Guide; University of California, Davis: Davis, CA, USA, 1992. [Google Scholar]
- Yang, Z.; Elgamal, A.; Parra, E. Computational model for cyclic mobility associated shear deformation. J. Geotech. Geoenviron. Eng. 2003, 129, 1119–1127. [Google Scholar] [CrossRef]
- Ganin, Y.; Ustinova, E.; Ajakan, H.; Germain, P.; Larochelle, H.; Laviolette, F.; Marchand, M.; Lempitsky, V. Domain-adversarial training of neural networks. J. Mach. Learn. Res. 2016, 17, 1–35. [Google Scholar]
- Hu, J. Study on the Risk Analysis Model of Seismic Liquefaction based on Bayesian Network. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2016. (In Chinese). [Google Scholar]
- Moss, R. CPT-Based Probabilistic Assessment of Seismic Soil Liquefaction Initiation. Ph.D. Thesis, University of California–Berkeley, Berkeley, CA, USA, 2003. [Google Scholar]
- Olsson, A.M.J.; Sandberg, G.E. Latin hypercube sampling for stochastic finite element analysis. J. Eng. Mech. 2002, 128, 121–125. [Google Scholar] [CrossRef]

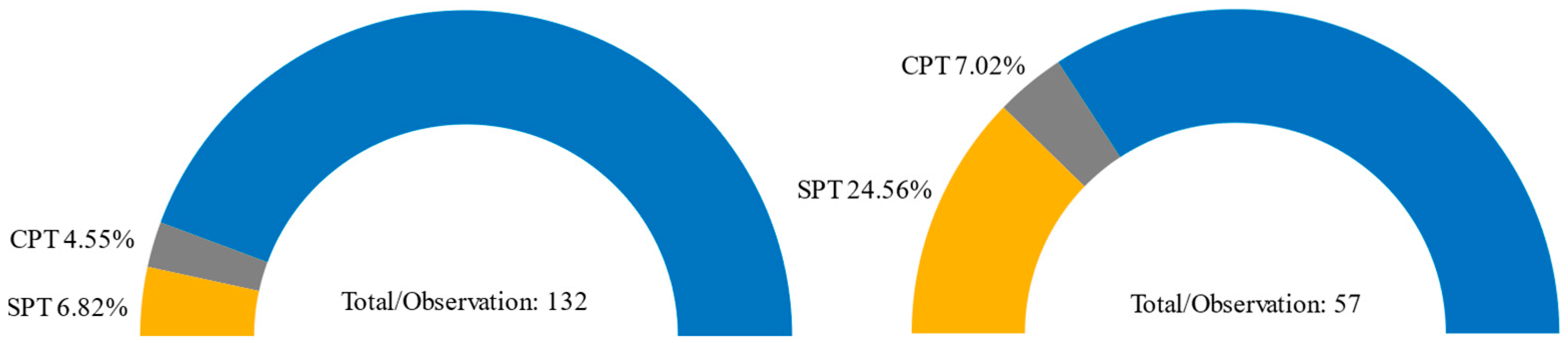
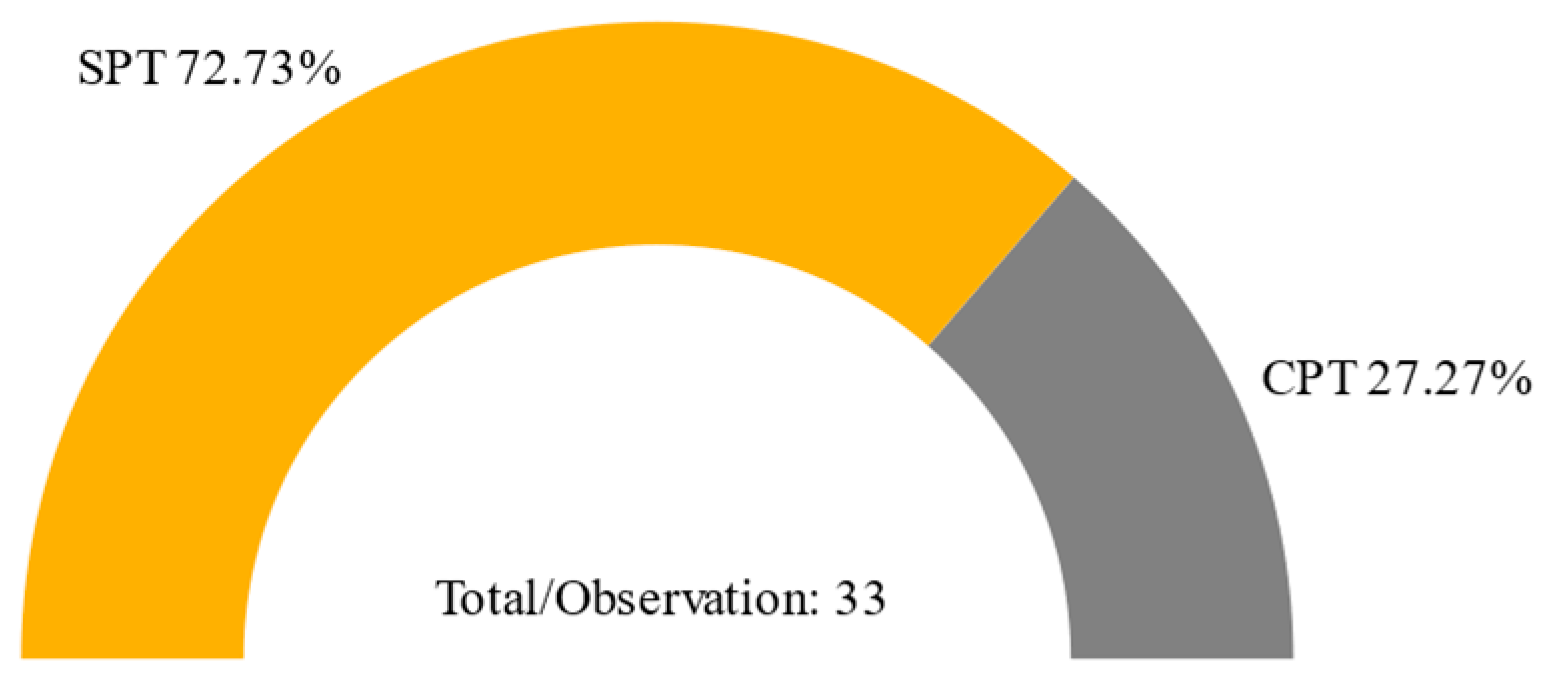
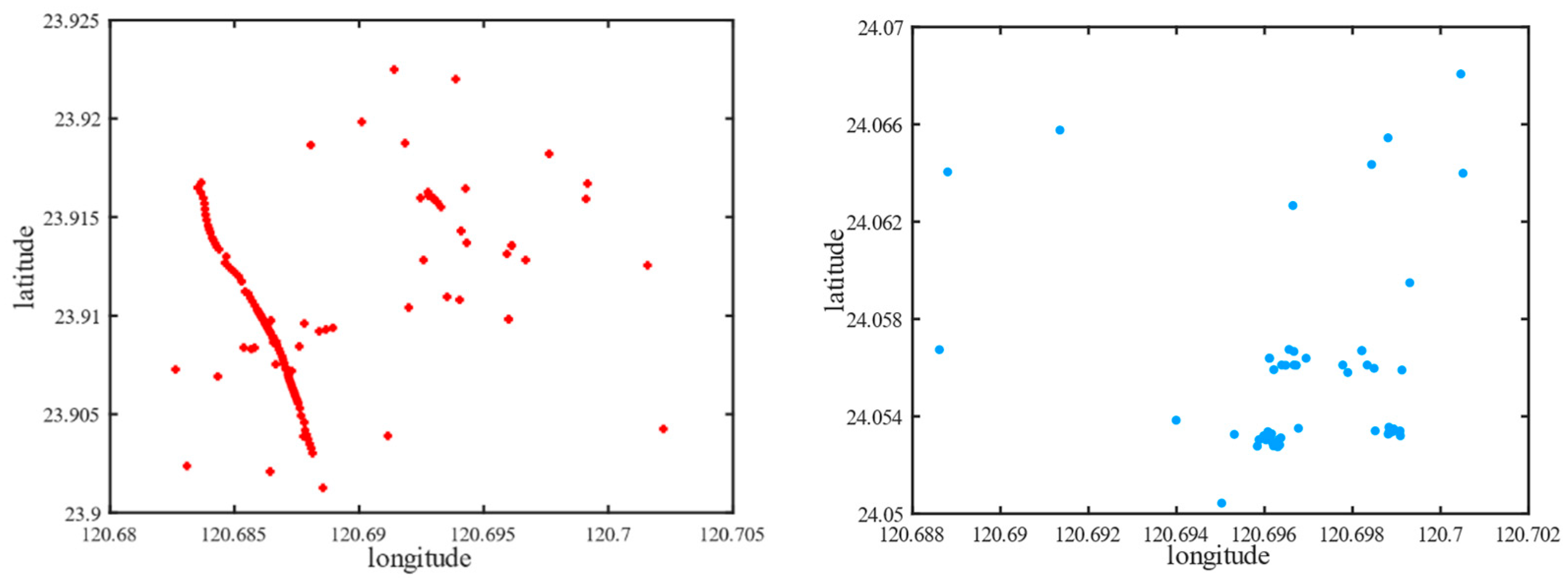
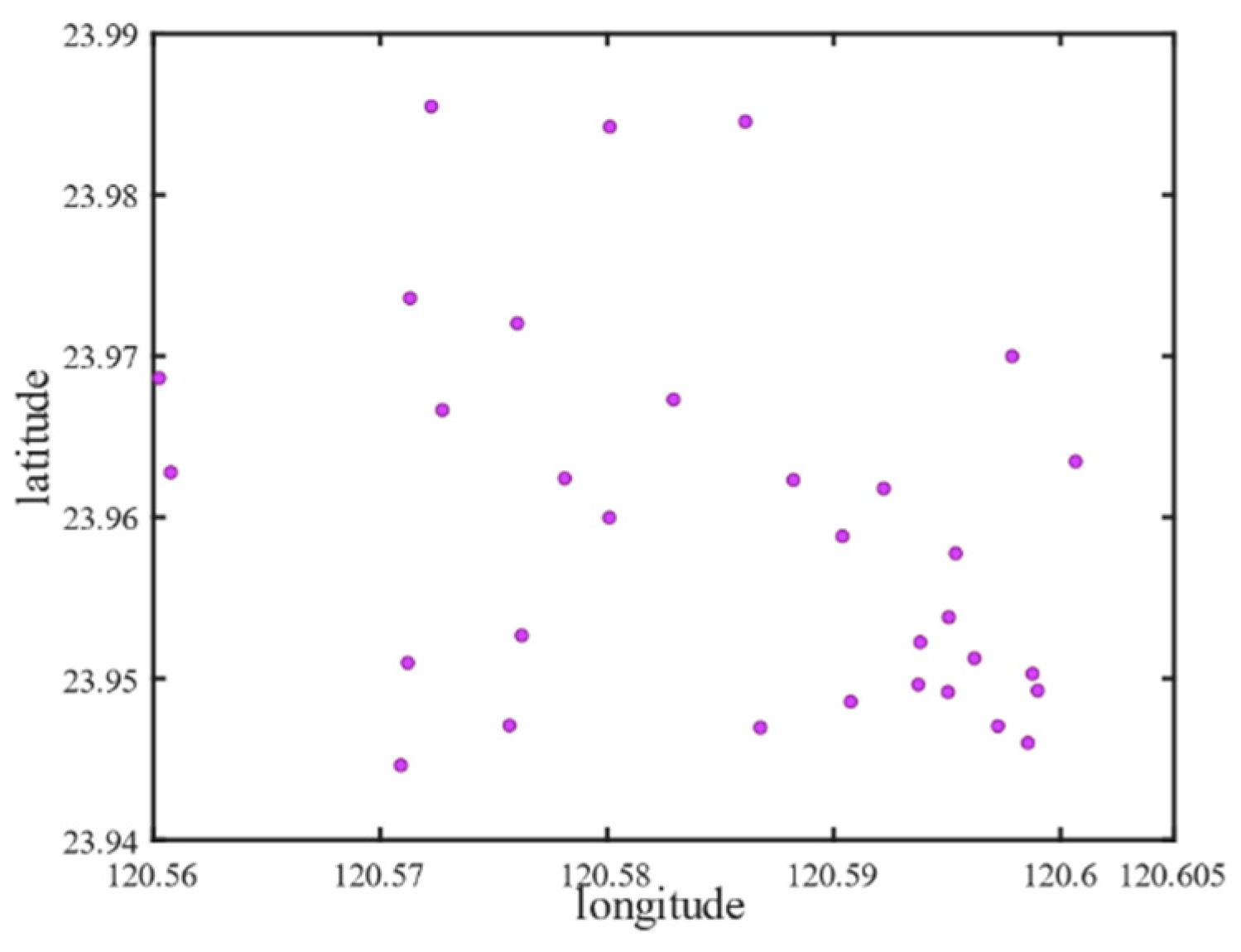


| Region | Exploration Points SPT/Others | Observation Points | Total |
|---|---|---|---|
| Nantou | 9/6 | 132 | 132 |
| Wufeng | 14/4 | 57 | 57 |
| Yuanlin | 24/9 | 33 | 33 |
| Database | Size | Size (Liquefied) | Proportion (Liquefied) | Range |
|---|---|---|---|---|
| Source domain | 188,400 | 47,581 | 25.3% | Sand layer depth 0.70~17.33 m |
| Groundwater level 0.21~4.13 m | ||||
| Sand layer thickness 0.20~4.65 m |
| Scheme | Model | Train Size | Test Size | Earthquake-Related Parameters | Site-Related Parameters | Notes |
|---|---|---|---|---|---|---|
| 1 | DANN | Nantou, Wufeng 189 | Yuanlin 33 | √ | × | Rapid Assessment Procedure |
| 2 | ANN | Nantou, Wufeng 189 | Yuanlin 33 | √ | × | - |
| 3 | DANN | Nantou, Wufeng 23 | Yuanlin 24 | √ | √ | - |
| 4 | ANN | Nantou, Wufeng 23 | Yuanlin 24 | √ | √ | - |
| Reference | |||
|---|---|---|---|
| No | Yes | ||
| Prediction | No | TN | FN |
| Yes | FP | TP | |
| Scheme | Model | Model Parameters | Confusion Matrix | Performance |
|---|---|---|---|---|
| 1 | DANN | lnMw, R, PGV | 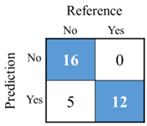 | Accuracy: 0.849 Kappa: 0.700 |
| 2 | ANN | lnMw, R, PGV |  | Accuracy: 0.697 Kappa: 0.380 |
| Scheme | Model | Model Parameters | Confusion Matrix | Performance |
|---|---|---|---|---|
| 3 | DANN | lnMw, R, PGV N1, D1, N2, D2, N3, D3, DW | 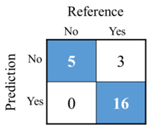 | Accuracy: 0.875 Kappa: 0.690 |
| 4 | ANN | lnMw, R, PGV N1, D1, N2, D2, N3, D3, DW |  | Accuracy: 0.750 Kappa: 0.308 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, J.-Y.; Shan, B.-H.; Lu, D.-G. Rapid Regional Liquefaction Probability Assessment Based on Transfer Learning. Buildings 2025, 15, 3243. https://doi.org/10.3390/buildings15173243
Meng J-Y, Shan B-H, Lu D-G. Rapid Regional Liquefaction Probability Assessment Based on Transfer Learning. Buildings. 2025; 15(17):3243. https://doi.org/10.3390/buildings15173243
Chicago/Turabian StyleMeng, Jian-Yu, Bao-Hua Shan, and Da-Gang Lu. 2025. "Rapid Regional Liquefaction Probability Assessment Based on Transfer Learning" Buildings 15, no. 17: 3243. https://doi.org/10.3390/buildings15173243
APA StyleMeng, J.-Y., Shan, B.-H., & Lu, D.-G. (2025). Rapid Regional Liquefaction Probability Assessment Based on Transfer Learning. Buildings, 15(17), 3243. https://doi.org/10.3390/buildings15173243






