Explainable Prediction of UHPC Tensile Strength Using Machine Learning with Engineered Features and Multi-Algorithm Comparative Evaluation

Abstract

To explore a direct predictive model for the tensile strength of ultra-high-performance concrete (UHPC), machine learning (ML) algorithms are presented. Initially, a database comprising 178 samples of UHPC tensile strength with varying parameters is established. Then, feature engineering strategies are proposed to optimize the robustness of ML models under a small-sample condition. Further, the performance and efficiency of algorithms are compared under default hyperparameters and hyperparameter tuning, respectively. Moreover, the utilization of SHapley Additive exPlanations (SHAP) enables the analysis of the relationships between UHPC tensile strength and its influencing factors. The quantitative analysis results indicate that ensemble algorithms exhibit superior performance, indicated by R² values of above 0.92, under default hyperparameters. After hyperparameter tuning, both conventional and ensemble models achieve R² values exceeding 0.94. However, Bayesian ridge regression (BRR) consistently demonstrates a suboptimal performance, irrespective of hyperparameter tuning. Notably, Categorical Boosting (CatBoost) requires a substantial duration of 1208 s, which is notably more time-consuming than that of other algorithms. The most influential feature identified is fiber reinforcement index with a contribution of 37.5%, followed by the water-to-cement ratio, strain rate, and cross-sectional size. The nonlinear relationship between UHPC tensile strength and the top four factors is visualized, and the critical thresholds are identified.

1. Introduction

Ultra-high-performance concrete (UHPC) has demonstrated considerable promise in the fields of bridge structures, marine structures, and high buildings due to its excellent mechanical properties and durability [1]. Although compressive strength constitutes the primary characteristic of most concretes, including UHPC, tensile properties play a significant role in their practical applications, especially in cases where tensile strength is a decisive requirement [2,3,4]. The tensile strength directly determines the crack control ability and ductility performance of a UHPC-based structure [5,6]. The tensile strength of UHPC is typically determined through either time-consuming and labor-intensive experimental testing or by estimation using empirical relationships. Given the enhanced tensile strength and strain-hardening of UHPC compared with normal concretes, it is imperative to explore a more direct predictive model for the tensile strength of UHPC.

The unique composition and microstructure of UHPC present significant challenges for the prediction of its tensile strength [7,8]. Conventionally, experimental testing has been the prevailing method of obtaining the tensile strength. Nevertheless, it usually requires a specialized experimental setup and equipment, which are cost-consuming and labor-intensive [9]. To reduce the dependence on experimental testing, various empirical formulas have been developed for estimating the tensile strength of UHPC [10,11,12,13,14]. However, these formulas have obvious limitations when dealing with component-tailored UHPC materials [9]. In addition, the prediction accuracy of empirical formulas has been questioned, since they are typically derived from limited experimental data and may not fully account for the potential influence of all relevant factors [7,8,15,16,17].

Recently, machine learning (ML) technology has attracted significant attention in the field of material strength prediction due to its efficiency, accuracy and advanced data-processing capabilities [18,19,20,21,22]. ML is capable of extracting complex nonlinear relationships from massive experimental data, providing substantial support for the prediction of material properties. This process enhances prediction efficiency and accuracy while reducing the time and cost consumption required for traditional experimental methods. ML methods have been successfully applied to predict the compressive, flexural, and tensile properties of UHPC [9,15,23]. Notably, their applications have expanded to the prediction of long-term performance in advanced cement-based sensors [24].

A variety of studies have demonstrated the potential of ML algorithms in predicting the tensile strength of UHPC with an acceptable accuracy [18,25,26,27,28]. For instance, Sun et al. [26] employed the XGBoost algorithm to predict the splitting tensile strength of a basalt fiber-reinforced coral aggregate concrete, utilizing three optimization algorithms for hyperparameter calibration. Abellan-Garcia et al. [27] estimated the uniaxial tensile properties of ultra-high-performance fiber-reinforced concrete (UHPFRC) using a Random Forest (RF) model. Diab et al. [28] utilized an artificial neural network (ANN) model to examine the tensile behavior of UHPC under varying strain rates. Their study revealed that both the cracking tensile stress and tensile strength increased at higher strain rates, while the strain corresponding to tensile strength remained unaffected by the strain rate.

The selection of input features constitutes a primary challenge in the ML modeling process. Typically, the selection of the most appropriate method is determined by the distinct characteristics exhibited by the samples. In most cases, Pearson’s correlation coefficient method [19,29,30] and the feature-importance-ranking method [26,28] are employed to identify the input features. Several advanced techniques, such as sequential feature selection [31], recursive feature elimination [32], and dimensionality reduction based on principal component analysis (PCA) [18], are also proposed to select the input features. Ke et al. [33] even employed a combination of RF, Maximum Information Coefficient (MIC) and Distance Correlation Coefficient (DCC) to identify optimal feature combinations.

The importance of hyperparameter optimization has been emphasized by numerous scholars [18,26,30,34,35,36]. Abbas et al. [37] pointed out that there is a tendency toward overfitting under the default hyperparameters. Thus, it is necessary to adjust the hyperparameters through fine-tuning to optimize model performance, while hyperparameter tuning is among the most time-consuming tasks in ML projects [8]. Researchers have developed a range of hyperparameter sampling algorithms [8,16,38], and it is found that several algorithmic models exhibit notably improved performance metrics after hyperparameter tuning [32].

Despite their ability to provide highly precise predictions, the “black box” nature of ML models significantly restricts their application in engineering field. In response to the inherent nature of ML models, interpretability methods such as SHapley Additive exPlanations (SHAP) have been widely adopted in recent years [21,33,39,40,41]. The SHAP framework utilizes quantitative methods to identify the key factors influencing the mechanical properties of concrete through additive feature attribution methods, thereby providing intuitive model interpretations.

Despite significant progress in predicting the mechanical properties of UHPC using ML methods, their application remains in an emergent phase of development. At present, existing research is deficient in the implementation of systematic solutions with regard to feature engineering, algorithm selection, and model interpretability. First, research on feature engineering for ML methods with small samples is relatively inadequate. The prediction of UHPC tensile strength is a paradigmatic example of a small-sample problem.

Although some feature engineering techniques such as feature fusion have been proven to directly affect model performance [42], there are few application cases in predicting the tensile strength of UHPC. Second, the optimal algorithm is not a consensus topic among researchers. Ensemble algorithms are generally considered to perform better [16,36,43,44,45], though some studies have shown that ANNs outperform the least absolute shrinkage and selection operator (LASSO), support vector regression (SVR), and tree-based ensemble algorithms [15,46]. There is even inconsistent evaluation within ensemble algorithms [19,29,41,45]. Moreover, further investigations are required to determine the balance between the computational resource consumption caused by hyperparameter tuning and the resulting performance gains [33]. Finally, the limited interpretability of ML models restricts their practical applications in engineering [15], and the utilization of interpretability methods such as SHAP in the analysis of UHPC tensile strength requires further exploration.

This study aims to explore the potential of ML in predicting the tensile strength of UHPC from three aspects, namely, modeling algorithms, performance comparison of multiple algorithms, and interpretable engineering insights. Initially, a series of feature engineering strategies are proposed to optimize model robustness and generalization ability under small-sample conditions. Additionally, several ML algorithms are selected to compare the model performance and operational efficiency of various algorithms with and without hyperparameter optimization, respectively. The selection of ML algorithms is conducted for the purpose of predicting the tensile strength of UHPC using a comparative evaluation analysis of multiple algorithms. Finally, the influencing factors of UHPC tensile strength are analyzed using a combination of SHAP analysis and the Partial Dependence Plot (PDP) method. The nonlinear relationship between the key influencing factors and the UHPC tensile strength is interpreted through the utilization of visualization curves.

2. Materials and Methodologies

2.1. Database Preparation and Pre-Processing

2.1.1. Experimental Database Acquisition and Engineered Feature Selection

The database of UHPC tensile strength is established through a systematic literature review method. In total, 17 scientific papers [12,25,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61] are identified as the sources of the dataset, and a total of 178 experimental samples of UHPC tensile strength are collected.

As previously mentioned, a multitude of factors influence the tensile strength of UHPC, including the properties and proportions of matrix components, fiber characteristics and dosage, the mixing program employed, the curing conditions, specimen dimensions, and testing conditions, among others. To balance model accuracy and practical implementation, the amount of input features is streamlined with rationality and efficiency. From the perspective of material science, the present study examines the component ratios of the matrix, fiber type, fiber volume fraction and aspect ratio. Additionally, it assesses specimen cross-section sizes and strain rate of testing as the input features contributing to the UHPC tensile strength. Given Ground Granulated Blast-furnace Slag (GGBS), the ash fly and the glass powder are deemed auxiliary cementitious materials, and they are classified into a single feature named reactive powder. Silica powder, quartz powder and micro-limestone powder in the UHPC primarily serve the function of filling the voids. Consequently, these powders are combined into a single feature and designated as inert powder. According to a relevant study [49], the volume fraction of fiber and the fiber aspect ratio should be incorporated into the fiber reinforcing factor as a novel feature. In addition, the specimen’s cross-sectional height and width should be included as a new feature of the area. Following the aforementioned processing, ten input features are selected for further analysis (see

Table 1. Input features and target variable.

Category	No.	Name	Symbol	Unit	Data Type and Range
Experimental condition	1	Strain rate	SR	1/s	N (0.833 × 10−5~0.1)
Specimen sizes	2	Sectional area	Section	mm2	N (390~5000)
UHPC components	3	Fiber type	FS	-	C (N, S, H, T)
	4	Fiber reinforcing index	FRI	-	N (0~487.5)
	5	Water/cement	W/C	-	N (0.19~0.42)
	6	Water reducer/cement	SP/C	-	N (0.005~0.033)
	7	Sand/cement	S/C	-	N (0.3~3.1)
	8	Inert powder/cement	IP/C	-	N (0~0.94)
	9	Reactive powder/cement	RP/C	-	N (0~1)
	10	Silica fume/cement	F/C	-	N (0.125~0.5)
Target variable	11	Tensile strength	TS	MPa	N (4.4~24.9)

).

It is worth noting that the dosages of water, sand, inert powder, reactive powder, silica fume, and water reducer are all proportioned relative to the cement content (by mass). The dataset in Table 1 contains both numeric and categorical data types, which are denoted by N and C, respectively. This study includes four fiber shapes: straight (S), hook-end (H), twisted (T), and no fiber (N). All the features in the dataset are of the numerical data type, except for the steel fiber type. The target variable in the dataset is tensile strength, ranging from 4.4 to 24.9 MPa.

Figure 1 shows Pearson’s correlation coefficient heatmap between the target variable and each feature employed. A positive value in the plot is indicative of a positive correlation, and vice versa, with larger absolute values corresponding to stronger correlations. Alyami et al. [29] posited that the correlation coefficient between the variables should be constrained to an absolute value not exceeding 0.8 to circumvent the issue of multicollinearity. As shown in Figure 1, it is demonstrated that the correlation coefficient between RP/C and S/C reaches 0.83. A thorough examination of the raw data reveals that the substantial increase in the relative amount of sand is attributable to the substitution of cement with GGBS and glass powder. The correlation coefficient would decrease if an absolute amount of each input feature is utilized. Nonetheless, in the present study, an objective is to minimize the number of input features for an efficient application. To this end, cement dosage is not considered an independent feature; rather, the ratio of other materials (with the exception of fiber) to the cement dosage is taken as an input feature. As illustrated in Figure 1, the fiber characteristic index, FRI, exhibits the strongest association with the tensile strength of UHPC, with a correlation coefficient of 0.62.

2.1.2. Data Preprocessing

The initial step in this process is the imputation of missing values. A total of 85 samples from the established database have reported loading rate data, but strain rate data are absent. Additionally, 10 samples have reported no data at all [52]. With regard to the 85 samples, the strain rate is derived as follows:

$$\epsilon ={\displaystyle \frac{v}{l_0}},$$

(1)

where ε is the strain rate (1/s), v represents the loading rate (mm/s), and l₀ denotes the gage length (mm). With regard to the 10 samples that lacked both parameters, it is hypothesized that they undergo pseudo-static loading, with ε set to 9.416 × 10⁻⁶ s⁻¹ corresponding to a loading rate of 0.1 mm/min. Furthermore, for nine samples with unspecified water reducer state (solid/liquid) and anomalously high dosages [25,55,62], the values are adjusted to 30% solid-content equivalent. An additional nine samples, which exhibit an absence of water reducer data [53], are designated as a default agent-to-cement mass ratio of 0.0054. Five samples with undefined steel fiber shapes [55] are imputed as straight fibers (type S).

The following is a discussion of the methods employed for the management of data outliers. The preliminary analysis of residuals from the multilayer perceptron (MLP) is not included, as it is designed to identify physically implausible outliers. The utilization of interquartile range and Z-score methods has been demonstrated to be ineffective in establishing meaningful thresholds. Manual inspection verifies two counter-intuitive yet valid cases in which steel-fiber-reinforced specimens exhibit lower strength than plain samples, thereby confirming the findings of Donnini et al. [58]. The final dataset encompasses all 178 samples to maximize data utility in the present study, with exclusions limited to cases deemed physically unjustifiable.

Data standardization is achieved through the implementation of a formula for Z-score standardization as follows:

$$Z={\displaystyle \frac{(X-\mu )}{\sigma }},$$

(2)

where Z is the standardized value (Z-score), X denotes the original data value, μ is the mean of the dataset, and σ signifies the standard deviation of the dataset.

Data standardization is selectively applied in accordance with the requirements of the underlying algorithm. In the case of distance- or gradient-based methods, such as SVR, ANN, and Bayesian Ridge Regression (BRR), the process of feature scaling plays an essential role. It ensures the standardization of numerical ranges, addresses the issue of magnitude dominance, and enhances model convergence. Conversely, tree-based algorithms such as RF, Gradient Boosting Regression Tree (GBRT), Lightweight Gradient Booster (LightGBM), and Categorical Boosting (CatBoost) employ raw features since their splitting mechanisms are impervious to variations in feature scale. Notably, the CatBoost model’s inherent capacity to manage multiscale features renders standardization particularly unnecessary. This methodology ensures algorithmic integrity while maximizing computational efficiency during the comparative analysis.

The fiber shape type, as defined in the dataset under consideration, is a categorical feature devoid of intrinsic ordering. As such, one-hot encoding is implemented for algorithms such as BRR, SVR, ANN, RF, GBRT, and LightGBM. Given that CatBoost possesses a built-in categorical feature processing function, the program eliminates the necessity for one-hot encoding or other encoders to process the “Fiber type”. This preserves the original format of the feature data and utilizes the advanced categorical processing functionality of CatBoost at its full capacity.

2.2. Algorithm Selection and Hyperparameter Optimization

2.2.1. Algorithm Selection

For the purpose of comparison, seven ML algorithms are selected, BRR, SVR, ANN, RF, GBRT, LightGBM, and CatBoost. The principles of the algorithms are briefly described below.

(1)

Bayesian Ridge Regression (BRR)

BBR is a probabilistic method that incorporates L2 regularization into linear regression within a Bayesian framework [63]. The model assumes Gaussian-distributed observation noise through the following relationship:

$$y=X\beta +ϵ, ϵ~N(0,{\sigma }^{2}I),$$

(3)

where y is the response vector; X represents the design matrix; β denotes the vector of coefficients; and $ϵ$ signifies the error term, which follows a multivariate normal distribution. N denotes the multivariate normal distribution with mean zero and a covariance matrix ${\sigma }^{2}I$, where ${\sigma }^2$ is the common variance in each error term and I represents the identity matrix.

(2)

Support Vector Regression (SVR)

SVR uses an ε-insensitive loss function to construct a “Margin Band” [64,65,66]. The mathematical principle states that for a given training set {(x₁, y₁), …, (x_n, y_n)}, the SVR optimization objective takes the following form:

$$min(1/2{\left|\right|w\left|\right|}^2+C\sum ({\xi }_i+{\xi }_i^{\ast }\left)\right),$$

(4)

$$s.t.|y_i-(w·\phi \left(x_i\right)+b\left)\right|\le \epsilon +{\xi }_i,$$

(5)

$${\xi }_i,{\xi }_i^{\ast }\ge 0,$$

(6)

where min signifies that the objective is to minimize the given expression;$w$ represents the weight defining the separation boundary; C is the penalty coefficient; ${\xi }_i$ and ${\xi }_i^{\ast }$ are the slack variables associated with the i-th training sample, quantifying the deviations above and below the ε-tube, respectively; “s.t.” stands for the abbreviation of “subject to”, introducing the constraints that the solution must satisfy; $y_i$ signifies the i-th value of the observed response value; $x_i$ is the i-th value of feature vector; φ(.) indicates the kernel function mapping; b is the bias; and $\mathsf{\epsilon }$ corresponds to the insensitivity parameter. Through the Lagrangian dyadic transformation, the final solution $f\left(x\right)$ can be expressed as follows:

$$f\left(x\right)=\sum ({\alpha }_i-{\alpha }_i^{\ast })K(x_i,x_j)+b,$$

(7)

where $\alpha$ and ${\alpha }_i^{\ast }$ are the Lagrange multipliers; and $K$ is the kernel function, which is defined by $K(x_i,x_j)=\phi \left(x_i\right)·\phi \left(x_j\right)$.

(3)

Artificial Neural Network (ANN)

An ANN constructs multilayer nonlinear mapping relationships by modeling the structure of biological neural networks [64,67].

Its neuron model is given by:

$$z=\sigma (\sum {\omega }_i{x}_i+b)$$

(8)

where $z$ is the output value of the neuron; σ signifies the activation function; ${\omega }_i$ represents the i-th value of synaptic weight; $x$ denotes the i-th value of input signal; and $b$ is the bias term. This study employs the Rectified Linear Unit (ReLU) as the activation function. ReLU has been shown to be effective in addressing nonlinear regression tasks, such as predicting tensile strength. This is largely due to its high computational efficiency and ability to accelerate gradient descent convergence. As a result, ReLU is well suited for single-hidden-layer ANN models. The loss function is the mean square error (MSE) or Huber loss, etc. Its backpropagation algorithm calculates the gradient via the chain rule through the following expression:

$$\mathsf{\partial }L/\mathsf{\partial }{\omega }_{ij}^l={\delta }_i^{l+1}·a_j^l,$$

(9)

where $L$ represents the loss function; ${\omega }_{ij}^l$ is the weight parameter connecting the j-th neuron in layer l to the i-th neuron in the subsequent layer l + 1; ${\delta }_i^{l+1}$ signifies the error term for the i-th neuron in layer l + 1; $a_j^l$ denotes the output (activation) of the j-th neuron in layer l after applying the activation function. It is combined with regularization techniques such as Dropout and Batch Normalization to prevent overfitting.

An ANN guarantees the ability to fit arbitrary functions by the universal approximation theorem and is capable of automatic feature learning. Its performance is highly dependent on the hyperparameter configuration (number of layers, number of nodes, learning rate, etc.), and it has a powerful nonlinear modeling capability.

(4)

Random Forest (RF)

The core innovation of RF lies in data sampling randomization (Bootstrap) and feature selection randomization [68]. The construction process is to generate n Bootstrap samples from the original dataset with putback sampling, construct a decision tree for each sample, with m features randomly selected when the node splits, and integrate the results by voting (classification) or averaging (regression). The RF regression prediction value takes the following form:

$$\mathrm{ŷ}=(1/k){\sum }_{t=1}^k{T}_t(x),$$

(10)

where $\mathrm{ŷ}$ denotes the final predicted value; $k$ represents the total number of trees; T_t is the predicted value of the tree; and $x$ signifies the feature vector of an input sample. RF is capable of handling high-dimensional data and is insensitive to missing values.

(5)

Gradient Boosting Regression Tree (GBRT)

GBRT adopts the Additive Model and Forward Stepwise Algorithm to reduce the residuals step by step by iteratively constructing a decision tree. The core idea is to use the prediction residuals of the weak learner as a new learning objective [69].

The GBRT optimization process is as follows. First, the negative gradient of the current model is calculated in the m-th iteration:

$$r_m=-\left[\mathsf{\partial }L\left(y_i,{F(x}_i\right)\right)/\mathsf{\partial }{F(x}_i){]}_{F=F_{m-1}}$$

(11)

where $r_m$ is referred to as the pseudo-residual; L denotes the loss function; $F$ represents the prediction of the current ensemble model; $y_i$ denotes the i-th value of observed response; and $x_i$ is the i-th coordinate value of feature vector. Then, a new decision tree is fitted to approximate these residuals. Finally, the model is updated through the following expression:

$$F_m\left(x\right)=F_{m-1}\left(x\right)v{h}_m\left(x\right),$$

(12)

where v is the learning rate (shrinkage coefficient); and $h_m\left(x\right)$ denotes the m-th decision tree. GBRT has a high prediction accuracy and feature combination capability, but its sequential training is difficult to parallelize and sensitive to outliers.

(6)

Lightweight Gradient Booster (LightGBM)

LightGBM uses a histogram-based algorithm (HBA) to discretize continuous features into buckets and a grow-by-leaf (LWG) strategy that selects only the leaf nodes with the highest loss for splitting [70]. The optimal splitting point is determined by the gain criterion:

$$Gain={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{G_L^2}{H_L+\lambda }}+{\displaystyle \frac{G_R^2}{H_R+\lambda }}-{\displaystyle \frac{{\left(G_L+G_R\right)}^2}{{H_L+H}_R+\lambda }}\right)-\gamma ,$$

(13)

where G_L and G_R are the gain sums of the left and right subtrees, respectively; H_L and H_R are the sums of the second-level gradients of the left and right subtrees, respectively; λ denotes the regularization parameter; and γ represents the penalty term for the number of leaf nodes.

(7)

Categorical Boosting (CatBoost)

CatBoost is an advanced GBRT framework specializing in categorical feature processing and bias reduction [71,72]. Its innovations include the following:

Ordered Target Statistics encode categorical features through permutation-isolated target statistics to prevent data leakage. The value for category k is calculated as follows:

$$v_k={\displaystyle \frac{{\sum }_{j=1}^{p-1}\left[x_j^i=x_k^i\right]·y_j+a·P}{{\sum }_{j=1}^{p-1}[x_j^i=x_k^i]+a}},$$

(14)

where p is the sample position, $x_k^i$ denotes the value of the i-th categorical feature for the kth sample, $y_j$ represents the true label value of the j-th sample, a signifies the smoothing parameter, and P corresponds to the target prior (e.g., global mean).

Ordered Boosting trains on multiple permutations while computing gradients exclusively from preceding samples to eliminate bias:

$$g_p={\left.{\displaystyle \frac{\mathsf{\partial }L(y_p,F\left(x_p\right))}{\mathsf{\partial }LF\left(x_p\right)}}\right|}_{F=M_i^{(p-1)}}$$

(15)

where $L$ denotes the loss function, $F$ represents the output of the current ensemble model, $y_p$ signifies the true label value of the p-th sample, $x_p$ is the feature vector of the p-th sample, and $M_i^{(p-1)}$ represents the state of i-th model that is trained using only the samples “preceding” the p-th sample.

Symmetric Trees employ balanced structures with layer-wise identical splits, reducing prediction complexity to O(depth). The advantages of CatBoost include superior categorical handling, overfitting resistance, and fast inference, though with higher memory usage and hyperparameter sensitivity.

Seven algorithms (BRR, SVR, RF, ANN, GBRT, LightGBM, CatBoost) are selected for comparison based on three criteria: (a) model diversity across linear (BRR), kernel-based (SVR), neural network (ANN), and ensemble methods (RF, GBRT, CatBoost), (b) adaptability to UHPC data characteristics such as small sample sizes and mixed variable types, and (c) demonstrated success in material science applications, particularly for strength prediction using ensemble methods [38,45,47]. CatBoost is specifically included for its categorical feature handling and small-data robustness.

2.2.2. Hyperparameter Optimization

Bayesian optimization is utilized in this study for the purpose of hyperparameter tuning. Bayesian optimization employs a Gaussian Process (GP) as the agent model, with the collection function being Expected Improvement (EI).

Table 2. Bayesian optimization of hyperparameters.

Algorithm	Key Hyperparameters	Physical Significance	Optimization Search Range	Type
BRR	alpha_1	Shape parameter of gamma prior	[−8, 2]	Continuous
	alpha_2	Inverse scale parameter of gamma prior	[−8, 2]	Continuous
	lambda_1	Shape parameter of gamma prior	[−8, 2]	Continuous
	lambda_2	Inverse scale parameter of gamma prior	[−8, 2]	Continuous
SVR	C	Penalty coefficient (regularization strength)	[0.1, 100]	Continuous
	gamma	RBF kernel function scale parameter	[0.001, 1]	Continuous
	epsilon	Loss function tolerance	[0.01, 1]	Continuous
	tol	Minimum improvement threshold	[0.00001, 0.01]	Continuous
	max_iter	Maximum iterations	[1000, 10000]	Integer
ANN	hidden_layer_sizes	Hidden layer neuron structures	(50, 200)	Category/integer tuple
	alpha	L2 regularization coefficient (explicit regularization)	[0.0001, 0.1]	Continuous
	learning_rate_init	Initial learning rate	[0.0001, 0.1]	Continuous
	tol	Minimum improvement threshold	[0.00001, 0.01]	Continuous
	max_iter	Maximum number of epochs	[200, 2000]	Integer
RF	n_estimators	Number of trees	[50, 500]	Integer
	max_depth	Maximum depth of single tree (structural regularization)	[3, 20]	Integer
	min_samples_split	Minimum number of samples for node splitting	[2, 10]	Integer
	min_samples_leaf	Minimum number of samples required for leaf nodes	[1, 10]	Integer
	max_features	Maximum number of feature subsets	[0.1, 1.0]	Integer
GBRT	learning_rate	Learning rate (shrinkage step)	[0.01, 0.3]	Continuous
	n_estimators	Number of trees	[50, 500]	Integer
	max_depth	Maximum depth of a single tree	[3, 20]	Integer
	min_samples_split	Minimum number of samples required for a node to continue splitting	[2, 10]	Integer
	min_samples_leaf	Minimum number of samples required for leaf nodes	[1, 10]	Integer
LihgtGBM	learning_rate	Learning rate (shrinkage step)	[0.01, 0.3]	Continuous
	n_estimators	Number of trees	[100, 2000]	Integer
	max_depth	Maximum depth of single tree	[3, 10]	Integer
	num_leaves	Maximum number of leaves in a single tree	[20, 100]	Integer
	min_child_samples	Minimum number of samples required for a leaf node	[5, 50]	Integer
CatBoost	learning_rate	Learning rate	[0.01, 0.3]	Continuous
	depth	Depth of tree	[4, 10]	Integer
	l2_leaf_ reg	L2 regularization coefficient	[1, 10]	Continuous
	border_count	Number of numerical feature bins	[50, 255]	Integer
	iterations	Number of iterations	[100, 2000]	Integer

presents an overview of the number and range of hyperparameter optimization for a variety of algorithms. The initial Bayesian optimization pickup points for the various algorithms are set to 5, with a total of 30 evaluations being conducted for all algorithms under consideration.

2.3. SHAP Interpretability Analysis

2.3.1. Theoretical Basis of SHAP Values

SHAP was introduced into the field of machine learning by Lundberg and Lee in 2017 [39]. The fundamental concept is to consider model prediction as the game gain derived from the cooperation of the feature participants, and to quantify the contribution of each feature to the prediction result through an equitable distribution mechanism.

For the predicted value f(x) of a given sample x, the SHAP value satisfies the additivity axiom:

$$f\left(x\right)={\phi }_0+\sum _{i=1}^M{\phi }_i,$$

(16)

where ${\phi }_0$ is the baseline value (expected output when all features are missing), ${\phi }_i$ denotes the Shapley value of the i-th feature; and M represents the total number of input features. According to cooperative game theory, the feature ${\phi }_i$ can be calculated as follows:

$${\phi }_i=\sum _{S\subseteq N\setminus \left\{i\right\}}{\displaystyle \frac{\left|S\right|!\left(n-\left|S\right|-1\right)!}{n!}}[f(S\cup \left\{i\right\})-f\left(S\right)]$$

(17)

where N is the set of all features, $S\subseteq N\setminus \left\{i\right\}$ denotes the subset S of features that does not contain feature i, n signifies the total number of features, f(S) represents the output value of the model on the subset S of features, and $f(S\cup \{i\left\}\right)$ is the output value of the model on the subset $S\cup \left\{i\right\}$ of features that contains certain features.

2.3.2. Feature Importance Quantification Method

A SHAP value defines the global importance of feature i as the mean of absolute SHAP values:

$$G_i={\displaystyle \frac{1}{m}}\sum _{j=1}^m\left|{\phi }_{i,j}\right|,$$

(18)

where G_i is the average magnitude of i-th attribution across the entire dataset, $m$ signifies the number of individual predictions (rows) in the dataset, and ${\phi }_{i,j}$ denotes the SHAP value of feature i for observation j.

This index can distinguish positive and negative influence features, reflect the marginal contribution of features at any given prediction point, and automatically differentiate the influence of cross features.

2.3.3. Explanatory Analysis Strategies

At the level of the dataset, SHAP has the capacity to reveal the feature action patterns through the use of feature importance plots and beeswarm diagrams. The objective of the present study is to demonstrate that the contribution of each feature and the volume and direction of its influence on the target variable can be visually represented.

Furthermore, SHAP can be utilized to detect nonlinear responses by combining it with PDP to illustrate the relationship curve between the target feature and the SHAP value. The current study investigates the relationships between the primary features (namely, fiber reinforcement index, water–cement ratio, strain rate, and specimen cross-section area) and the tensile strength of UHPC, with a focus on distinguishing the specific impact of each feature.

2.4. Experimental Setup and Evaluation Metrics

2.4.1. Sample Division and Validation Strategy

In order to prevent the adverse effects of the skewed distribution of the sample target variables, this study employs a method of equal-frequency stratified sampling to divide the data into the training set and the test set. According to the findings of previous research conducted by the authors’ team on the sensitivity of the database division ratios of training-to-testing sets of ML models [34], the training set utilizes 80% of the data, while the testing set employs the remaining 20% of the data. The sample data in the testing set are not involved in training and are exclusively used for the evaluation of model performance.

In the training set, the data are randomly partitioned into five folds. Each fold of the validation set contains 28 to 29 samples, with 113 to 114 samples in the remaining training set. Furthermore, the proportion of samples in each box (stratum) in each fold approximates the overall distribution of the training set (20%), with a maximum difference of one sample between boxes. The mean of each fold is employed as the model performance evaluation index of the training set. The efficacy of cross-validation and independent testing is demonstrated in Figure 2. In the figure, green represents the training samples, yellow denotes the validation (test) samples, while the R², RMSE, and MAE values within the chocolate, light gray, and sand brown boxes represent the per-fold validation value, the 5-fold average validation value, and the test value, respectively.

2.4.2. Evaluation Indexes

The present study utilizes three model performance evaluation indices: the coefficient of determination (R²), the root mean square error (RMSE), and the mean absolute error (MAE).

R² value characterizes the variance explanation ability of an ML model, which is calculated using the following formula:

$$R^2=1-{\displaystyle \frac{{\sum }_{i=1}^n{(y_i-{\widehat{y}}_i)}^2}{{\sum }_{i=1}^n{(y_i-{\overline{y}}_i)}^2}},$$

(19)

RMSE is an indicator of absolute error sensitive to outliers, with its calculation formula as follows

$$RMSE=\sqrt{{\displaystyle \frac{1}{n}}\sum _{i=1}^n{(y_i-{\widehat{y}}_i)}^2},$$

(20)

MAE gives a robustness metric reflecting prediction bias, which is determined as follows:

$$MAE={\displaystyle \frac{1}{n}}\sum _{i=1}^n\left|y_i-{\widehat{y}}_i\right|,$$

(21)

In the aforementioned expressions ranging from Equations (19) to (21), $y_i$, ${\widehat{y}}_i$ and ${\overline{y}}_i$ denote the observed value, the predicted value and the mean value, respectively, with n signifying the total number of samples. R² evaluates the goodness of fit of an ML model, and RMSE and MAE measure the prediction errors from different perspectives, with RMSE being more sensitive to large errors. The combination of these three metrics enables a comprehensive evaluation of the accuracy and stability of an ML model.

2.5. Flow Chart

Figure 3 illustrates the flowchart frame of the present study. In the figure, the brown boxes represent the names of the four stages in the process, while the green, brown, cyan, and blue boxes correspond to the specific tasks or content of each respective stage.

This research examines small-sample ML algorithms and analyzes UHPC tensile-strength-influencing factors across four dimensions, including data processing, model establishment, performance evaluation, and feature importance analysis. The main technical procedures undertaken in the course of this study are presented as follows:

• First, sample data are collected through a literature review.
• Second, feature selection, feature fusion, missing value imputation, outlier handling, data standardization, data encoding, and data partitioning are performed on the sample data.
• Third, seven ML algorithms are selected, and models are trained using five-fold cross-validation under both default hyperparameter values and hyperparameter tuning conditions, and model performance is evaluated using an independent test set.
• Fourth, the seven algorithms’ performance is compared both with default and tuned hyperparameters and between their pre- and post-tuning states.
• Finally, based on SHAP values, a global importance-ranking analysis of the factors influencing the UHPC tensile strength is performed, and an in-depth analysis of the nonlinear relationship between tensile strength and key influencing factors is conducted with the combination of PDP.

3. Results and Discussion

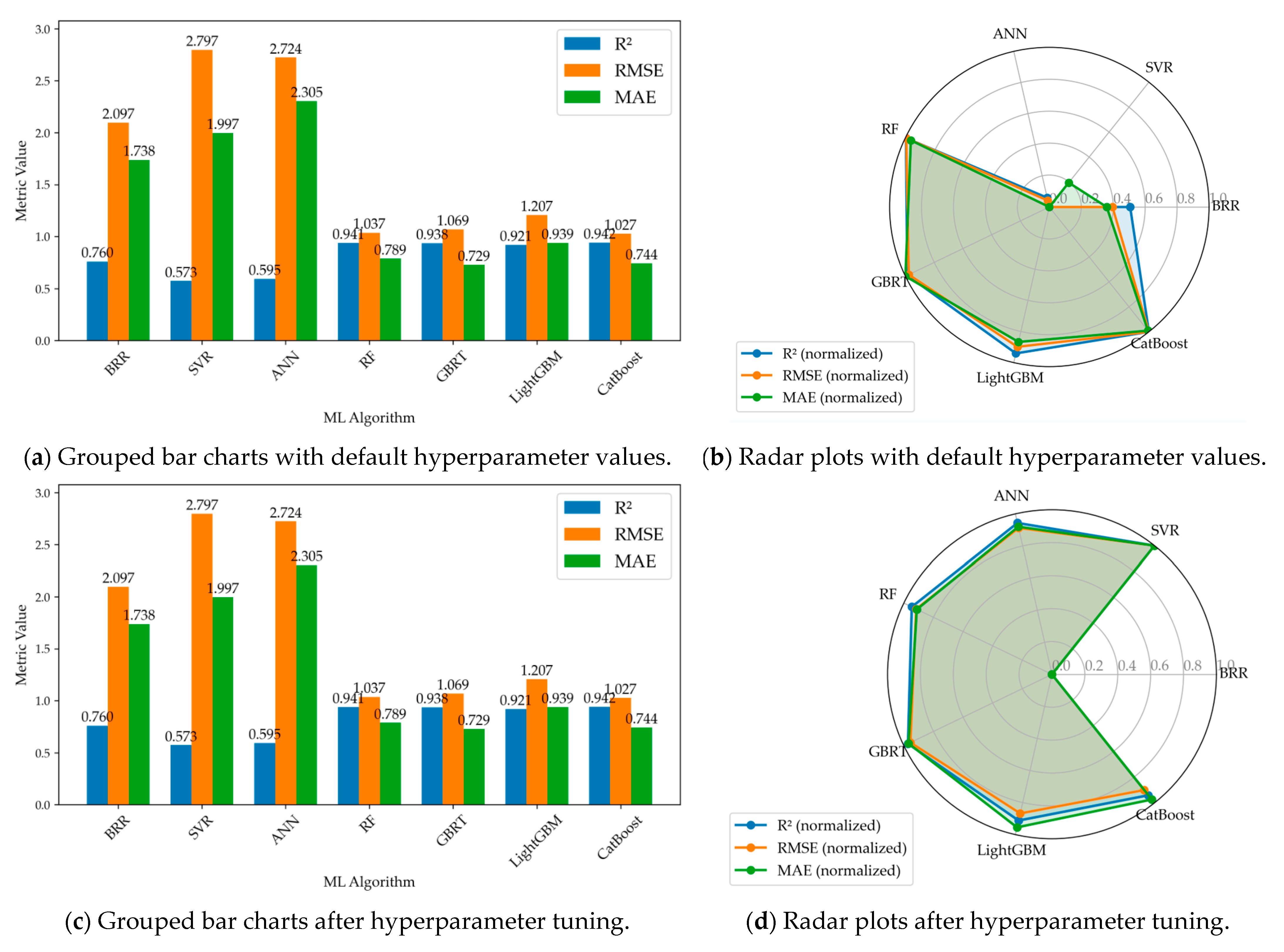
3.1. Multi-Algorithm Comparative Evaluation

In this section, an evaluation of seven ML algorithms (BRR, ANN, SVR, RF, GBRT, LightGBM and CatBoost) is conducted under both default and optimized hyperparameter conditions. This is followed by a comprehensive comparison of model performance.

A comparison of the model performance of various algorithms with default and tuned hyperparameters is presented in Figure 4. Figure 4a,b presents the grouped bar chart and radar plot, respectively, for each algorithm’s performance using default hyperparameters. Figure 4c,d displays the corresponding performance after hyperparameter tuning, with the time required for tuning indicated above the corresponding bars in Figure 4c. To enhance clarity in the representation of performance metrics, all performance values in the radar plots have undergone a process of normalization. As demonstrated in Figure 4, the following observations can be made. First, under default hyperparameters, the ensemble models (RF, GBRT, LightGBM, and CatBoost) clearly outperform conventional models (BRR, SVR, and ANN), with R² values larger than 0.92. If utilizing CatBoost model as a benchmark, the R² values of RF, GBRT, LightGBM, SVR, ANN, and BRR are equivalent to 99.89%, 99.58%, 97.77%, 60.83%, 63.16%, and 80.68%, respectively. Secondly, after hyperparameter tuning, the ensemble models demonstrate only marginal advancements, as evidenced by an increase percentage in the R² values of 0.43% for RF, 1.28% for GBRT, 2.06% for LightGBM, and 0.21% for CatBoost. Conversely, SVR and ANN exhibit substantial grows, with the R² values increasing by 66.67% and 58.82%, respectively. This results in a final performance comparable to that of the ensemble models, with SVR attaining the highest R² value of 0.955. Upon hyperparameter tuning, the SVR, ANN and ensemble models all achieve an R² value above 0.94. Thirdly, although BRR demonstrates some improvement after tuning, its performance remains significantly inferior to that of the other models. Finally, the hyperparameter-tuning time for CatBoost model is 1208.4 s, which is substantially longer than that of the second most computationally expensive algorithm, RF, at 55.6 s.

Ensemble models, which are predicated on tree structures, demonstrate insensitivity to feature scaling and possess the capacity to automatically capture nonlinear relationships and interactions. Furthermore, the regularization mechanisms inherent in bagging (e.g., RF) and boosting (e.g., GBRT, LightGBM, and CatBoost) ensure that these models avoid severe overfitting, even under default settings. Moreover, the default hyperparameters of contemporary ensemble learning libraries have been extensively tuned by communities and developers, rendering them well suited for a substantial range of datasets. It has been well documented within academic research communities that ensemble models frequently exhibit a superior performance in comparison to conventional models [16,34,36,43,44,45]. This phenomenon is primarily attributable to the fact that, in the majority of cases, the default hyperparameters of ensemble models already approach optimal levels, thereby leaving minimal opportunity for additional enhancement through tuning. This assertion is further substantiated by the findings of the study conducted by Ke et al. [33].

In contrast, conventional ML models frequently employ conservative default hyperparameter settings, which may result in underfitting or overfitting when applied to small-sample datasets and often fail to capture complex nonlinear relationships within the data. Therefore, to enhance the efficacy of models such as SVR, it is imperative to adjust the parameters of the penalty, the scale parameter of the radial basis function kernel, the loss function tolerance, and other associated factors. In the case of the ANN model, adjustments are required in the hidden layer neuron structures, the L2 regularization coefficient, and the initial learning rate, among other considerations. In this study, upon the process of hyperparameter tuning, the performance of conventional models exhibited a substantial enhancement, at times even surpassing that of ensemble models. This finding is consistent with previous research conducted by Kim et al. [73], which also demonstrated that, in the case of specific datasets, ANN can outperform ensemble models such as RF and XGBoost through appropriate hyperparameter optimization.

The BRR model has been demonstrated to be generally suitable for small-sample datasets and scenarios with multicollinearity. Given the modest sample size of the database constructed in the present study and the strong correlations between the amounts of cement, reactive powder, inert powder, and water in UHPC, BRR is included in the algorithm selection. However, the findings suggest that BRR does not attain a satisfactory performance, irrespective of hyperparameter tuning. This discrepancy can be attributed, primarily, to the fact that BRR is designed to capture linear relationships, whereas UHPC tensile strength exhibits complex nonlinear interactions with various factors. Moreover, an additional analysis reveals that the sample data in this study follow a non-normal distribution, while BRR assumes normality and is sensitive to noise and outliers, further contributing to its suboptimal performance. Consequently, integrating BRR with other algorithms is a common practice in research to enhance model performance [74].

Figure 4 further suggests that hyperparameter tuning enhances the performance of all algorithms to a variable extent; however, it does require additional computational resources. As demonstrated in Figure 4c, the majority of the algorithms, with the exception of CatBoost, complete hyperparameter tuning rapidly. In contrast, CatBoost requires significantly more time than other ML models despite achieving comparable performance (with the exception of BRR). This phenomenon can be attributed to the CatBoost model’s implementation of ordered boosting, a mechanism that facilitates the automatic handling of categorical features. These characteristics enhance the robustness and accuracy of ML model, and often lead to a strong performance even with default hyperparameters. However, these approaches also incur a substantially higher computational overhead. Consequently, while CatBoost has been demonstrated to outperform numerous other algorithms [34], its considerable tuning time prompts a salient inquiry regarding the trade-off between model efficiency and accuracy in specific practical scenarios.

A comparative analysis of model performance reveals several observations and insights that may offer valuable guidance for similar studies. A careful balancing of data characteristics, model complexity, computational resources, and performance requirements is paramount in the selection of an ML algorithm. If the available data are limited but exhibit clear nonlinearities and interaction effects, and sufficient computational resources are accessible, several ensemble learning algorithms (e.g., RF, LightGBM, CatBoost, and GBRT) can deliver robust and excellent performance even under default hyperparameters. When higher levels of accuracy are desired and hyperparameter tuning is feasible, conventional ML models such as SVR and ANN, after extensive tuning, can achieve a performance comparable or even superior to that of ensemble models, particularly in scenarios where model interpretability is not a major concern. Moreover, in instances where substantial linear relationships or multicollinearity are present in the data, BRR can be utilized as either a baseline model or incorporated within an ensemble framework. The findings emphasize that a single ML algorithm does not consistently perform optimally across all scenarios. A rational selection strategy is predicated on three factors: specific task requirements, data characteristics, and resource constraints. When these factors are taken into consideration, an optimal balance can be achieved between efficiency and accuracy.

3.2. Model Interpretation

Given that the CatBoost model achieves the highest R² values under default hyperparameters, it is selected to analyze the contribution of the input features (i.e., the influencing factors) to the prediction of UHPC tensile strength.

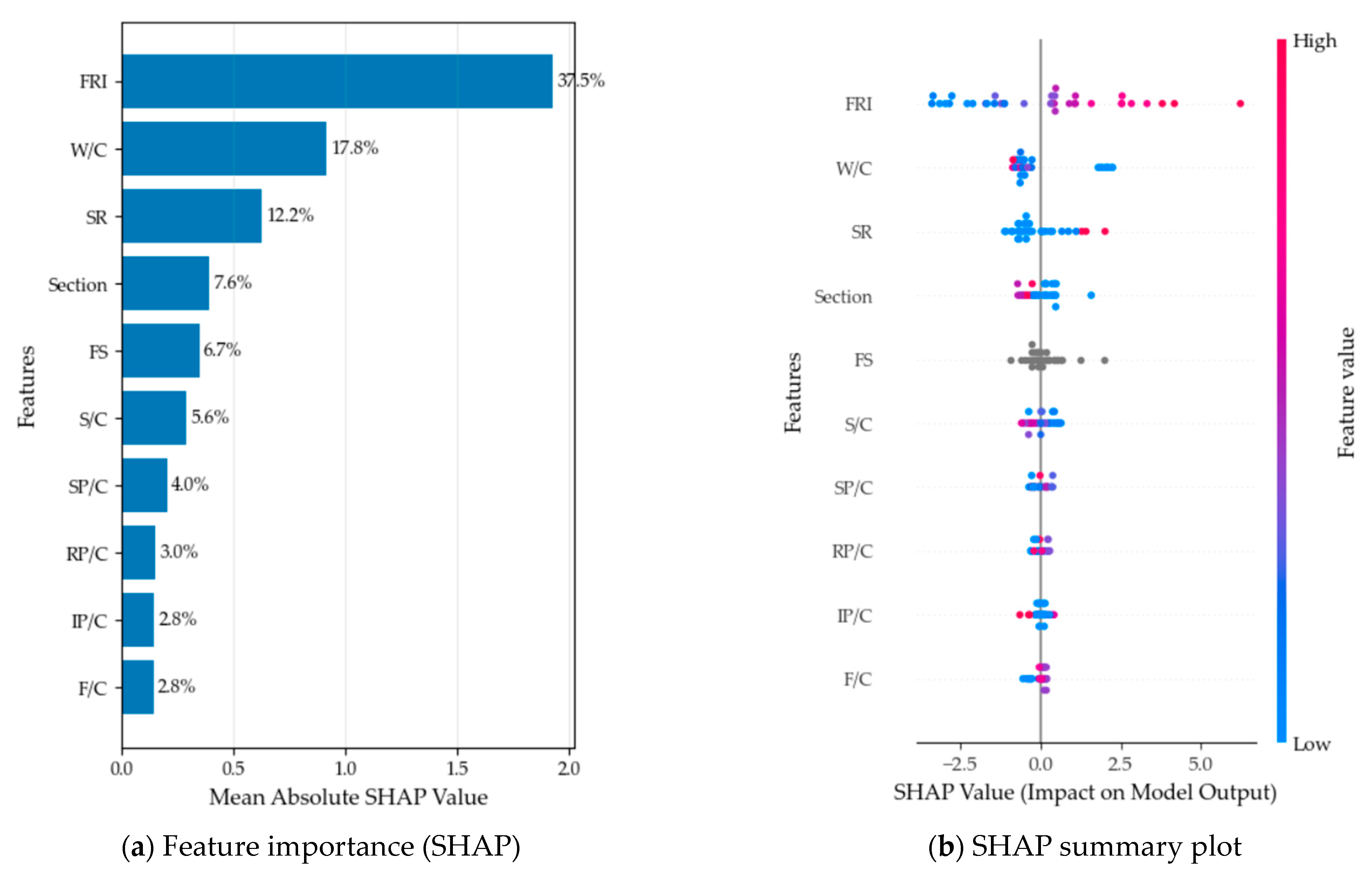
3.2.1. Feature Importance Analysis

A ranking graph and a beeswarm diagram are employed to illustrate the global feature importance. The feature importance ranking is determined by averaging the absolute SHAP values for each feature, providing a quantitative measure of each feature’s global impact on model predictions. In the feature-importance-ranking diagram, the contribution of each variable to the prediction of the target variable is indicated on the right end of the corresponding horizontal bar. The SHAP beeswarm diagram is capable of demonstrating not only the importance and spread of each feature, but also the direction of the influence on the target variable. In the beeswarm plot, the horizontal coordinate corresponds to the magnitude of the SHAP value. In the vertical coordinate, the features are arranged from top to bottom according to the magnitude of their influence, while colors are used to indicate the magnitude of each scatter feature value.

As illustrated in Figure 5a, the most significant influencing factor, the fiber characteristic index (FRI), attains 37.5%, contributing more than one-third of the model’s predictive capacity and emerging as the predominant factor. FRI is a measure of the specific surface area, or the “effective enhancement index”, of the fibers. This finding indicates that, in the context of UHPC, the fiber content, length and diameter—which jointly determine the fiber–matrix contact area and anchorage capacity—are the most critical factors that govern tensile strength. Ouyang et al. [60] observed that fibers are responsible for the majority of the tensile load-bearing capacity due to their ability of bridging, thereby impeding crack growth and propagation. As demonstrated in Figure 5b, an increase in FRI corresponds to a growth in the SHAP value and thus in the magnitude of its effect on the tensile load carrying capacity. Consequently, an appropriate increase in the fiber volume ratio, the incorporation of longer fibers or thinner fibers (or a combination of all three) can remarkably enhance the tensile strength in UHPC design.

The water-to-cement ratio is the second factor that influences the prediction of UHPC tensile strength. Upon the hydration of cementitious components, the excess water will eventually evaporate, resulting in the formation of capillary channels in the concrete matrix. This process increases matrix porosity and thus decreases matrix compactness. The matrix strength (including tensile strength) of UHPC is achieved, to a large extent, by very low porosity. As demonstrated in Figure 5b, the red points of W/C fall within the negative zone of SHAP, indicating that an elevated water–cement ratio results in reduced tensile strength. Therefore, strict control of water consumption is imperative for achieving high tensile strength.

The third most significant factor is the strain rate, indicating that UHPC tensile strength exhibits strain rate sensitivity. In general, the test loading rate has a direct correlation with the resulting strength values. When the specimen is exposed to loading more rapidly, it typically exhibits higher measured strength values. This phenomenon can be attributed to the reduced time available for the material to undergo internal damage during the loading process. Pyo et al. [49] observed that the post-crack peak strength and pre-peak load fracture energy of UHPC both increase with an increasing strain rate. To summarize, when exposed to seismic events and impacts, UHPC demonstrates increased tensile properties, provided the conditions remain otherwise constant.

The cross-sectional area of the specimen emerges as a factor that can be more or less unexpected and is the fourth most affecting factor of UHPC tensile strength. In the case of steel-fiber-reinforced UHPC, the reduction in cross-sectional size leads to a propensity of the fibers to be oriented longitudinally during casting, thereby enhancing the tensile strength of the specimen. This finding is consistent with the experimental results reported by Wille et al. [12]. As illustrated in Figure 5b, the SHAP value increases in proportion to the decrease in the feature Section. Consequently, the size effect of the specimen requires comprehensive consideration in the UHPC tensile strength test.

The contribution of fiber shape is ranked fifth, accounting for 6.7% of the total variance. This outcome indicates that the variation in fiber shape exerts an influence on the tensile strength of UHPC. As observed by Qiu et al. [75], hook-end fibers exhibit a more pronounced strain-hardening plateau compared to straight fibers, a phenomenon attributable to their enhanced mechanical interlocking with the matrix. However, Wille et al. [12] have reported that the discrepancy in tensile strength between smooth, crooked, and twisted fibers is insignificant.

The contribution of the sand-to-cement ratio is ranked sixth. Sand, the primary aggregate of UHPC, serves as the fundamental structural element within the cement matrix. A notable observation in this study is the exclusion of cement amount as an independent feature. Given that the amounts of all components except fibers are entered as ratios to the cement content, the impact of the primary factor of cement amount is reduced in the other materials. Specifically, the sand-to-cement ratio is a critical factor in the analysis, as a higher ratio indicates a lower cement dosage and a lower tensile strength.

The incorporation of highly efficient water-reducing agents is paramount in the formulation of UHPC. However, as illustrated in Figure 5a, its contribution is minimal (4.0%). This may be attributed to its water-saving functionality, and its contribution is obscured or captured by the W/C feature. As depicted in Figure 5a, it can be interpreted that the marginal effect of the water-reducing agent may be reduced at higher dosages.

Reactive powder exhibits a low contribution of 3.0%. Nevertheless, this observation does not diminish its significance. Reactive powder has been demonstrated to be a highly advantageous auxiliary cementitious material, particularly in enhancing the strength of concrete in the later stages of development. Two factors contribute to the observed low contribution. Firstly, there is a strong correlation between the water-to-cement ratio and the sand-to-cement ratio, which serves as a point of reference. The second factor is that the contribution of this feature is diluted due to the limited number of samples with reactive powder.

The primary function of inert powder is to fill the voids between aggregate particles, thereby increasing increase the packing density of UHPC. This, in turn, enhances both the matrix strength and the bond strength of the fiber–matrix interfacial transition zone (ITZ) [53]. However, as shown in Figure 5b, an excessive IP/C ratio may result in a minimal reduction in tensile strength. This is attributed to the fact that an excessive amount of inert material can “dilute” the cementitious system and result in a weakened ITZ.

The contribution of silica fume is 2.8% of the total. The primary functions of silica fume in UHPC are to fill pores, enhance the ITZ, and promote secondary hydration. These processes contribute to a substantial increase in the strength and densification of the matrix. The minimal contribution of silica fume may be attributable to its correlation with water, which functions as a regulator of porosity, and with fiber, which endures the primary tensile force.

The preceding analysis has demonstrated that the combination of characteristic parameters of fibers, denoted by FRI, emerges as the preeminent indicator of tensile strength. This observation underscores the primary role of fibers in bridging cracks and providing tensile load-bearing capacity. The subsequent element is the water-to-cement ratio, the significance of which derives primarily from its substantial impact on matrix porosity. This emphasizes the imperative of meticulously regulating the water-to-cement ratio to attain low porosity and thus high tensile strength characteristic of UHPC. Conversely, the strain rate and cross-sectional area prompt consideration of the discrepancy between the testing conditions and the engineering application. It is imperative that further investigation be conducted into the influence of fiber shape on the tensile strength of UHPC. The sand-to-cement ratio is indicative of the effect of cement amount on tensile strength to a certain extent. The contributions of water reducer, reactive powder, inert powder, and silica fume are not fully understood, primarily due to the complex interactions among the matrix components and a limited sample size of database in this study. This feature-importance-ranking analysis provides a clear direction for optimizing the tensile properties of UHPC: the most effective method for achieving its tensile strength is to optimize the fiber parameters (i.e., volumetric percent and aspect ratio) and to control its water consumption.

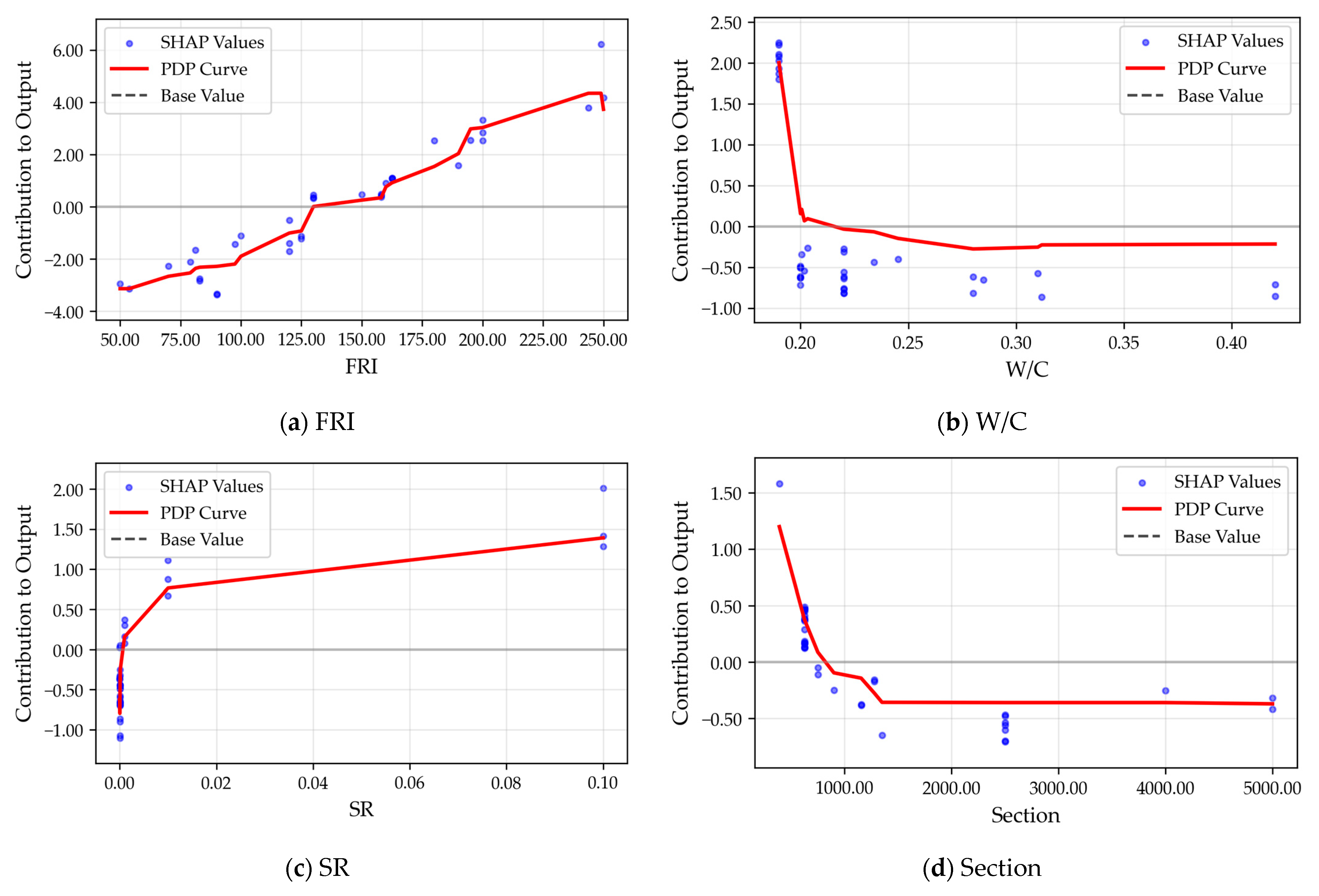
3.2.2. Marginal Effect Analysis of Key Features

The top four features (i.e., fiber reinforcing index, water–cement ratio, strain rate and specimen sectional area) are now considered key elements. PDP is plotted and superimposed with the SHAP scatterplot, as shown in Figure 6. When plotting the PDP, the key feature is taken as a certain fixed value, and all samples are traversed to seek the predicted value. Finally, the predicted values of the various samples are averaged and the offset value of this value from the global mean is calculated. The PDP curve is represented in red, while the SHAP scatter plot is delineated in blue. The PDP plus SHAP scatter plot is a graphical representation that allows for the observation of various information, including the average marginal effect of a particular feature and the contribution of that feature to the model.

Figure 6a presents the PDP superimposed with a SHAP scatterplot for the feature FRI. The horizontal coordinate corresponds to the value of FRI, ranging from 50 to 250, while the vertical coordinate represents the contribution of FRI, ranging from −4 to +6. A comprehensive analysis of the PDP curve reveals its division into two segments, both of which exhibit a linear rise in response to an increase in FRI. The slope of the function is slightly less pronounced between 50 and 90 of FRI, and becomes marginally more sloped between 90 and 200, thereby confirming the increasing average marginal gain from the increase in this eigenvalue. Therefore, the PDP curve evidently demonstrates that the global average effect of FRI is considerably positive, thereby substantiating the feature as a significant positive driver. The decline in the PDP curve at 250 of FRI can be attributed to the anomalous nature of the sample and is not indicative of a general trend. Furthermore, there are evident localized deviations in this PDP curve, suggesting that the positive relationship is not smooth and implying the presence of potential feature interactions or sub-modalities in the data.

The SHAP scatter in Figure 6a provides an individual sample-level perspective, unveiling inherent complexity underlying the global average. A detailed analysis of the data reveals that the trend of the scatter plot distribution is consistent with the PDP curve. This finding serves to validate the model’s capacity to effectively capture the influence of the feature, thereby enhancing the reliability of the interpretation of the PDP curve. In the region of FRI < 125, the SHAP value is negative, indicating that a lower fiber reinforcement index may result in reduced UHPC tensile strength. Conversely, in the case of FRI > 125, the SHAP value increases gradually and is positive, suggesting that optimizing the fiber characteristics significantly enhances the tensile strength. At two specific points, designated as 90 and 250, the SHAP value of FRI exhibits a discernible dispersion with a relatively sparse distribution of scatter points. This observation signifies that there exist substantial variations among individual samples within the specified region, thereby rendering the data susceptible to the influence of external factors. The SHAP plot confirms the considerable positive influence of this feature at the individual level, thereby indicating that increasing the volume fraction Vf and the aspect ratio lf/df of the fibers can foster an enhancement in the UHPC tensile strength. A thorough examination of the data reveals that the distribution of the scattering points is predominantly centered around the PDP curve. Furthermore, the width of the vertical distribution exhibits a notable degree of concentration, suggesting that this particular feature is relatively impervious to the influence of other features. This observation underscores the preeminent role of this feature in determining the tensile strength.

Figure 6b shows the influence of feature W/C on the predicted tensile strength combining PDP curve and SHAP scatter points. The horizontal axis of the graph represents the feature W/C values, ranging from 0.1 to 0.43. The vertical axis is indicative of the contribution of the feature, ranging from −1 to +2.5. Within the PDP curve, two critical thresholds for W/C are identified. When the water-to-cement ratio, W/C, is of less than 0.20, the tensile strength of UHPC decreases sharply with an increase in the W/C ratio. For a W/C between 0.20 and 0.30, the tensile strength of UHPC decreases slowly with an increase in the W/C ratio. However, when the W/C is greater than 0.30, the relationship between the W/C ratio and the tensile strength of UHPC is not significant.

The distribution of scatter points in Figure 6b is predominantly below the PDP curve; however, the direction is largely consistent with the PDP curve. When the W/C is lower than 0.2, the SHAP value is positive, and vice versa. This indicates that a lower water-to-cement ratio is conducive to enhancing UHPC tensile strength, while an excessively high water-to-cement ratio has a detrimental effect on UHPC tensile strength. The distribution of the W/C, ranging from 0.2 to 0.31, exhibits a deviation from the PDP curve, indicating a downward trend and a degree of dispersion. This suggests that the W/C in this section may be influenced by additional factors.

As illustrated in Figure 6c, the horizontal axis of the graph represents the SR value, ranging from 0.00 to 0.10. The vertical axis denotes the contribution ranging from −1 to 2. The predicted tensile strength, as determined by the PDP curve, exhibits a positive correlation with the strain rate. The curve shows a triple fold. When the strain rate is lower than 0.001, the predicted value of tensile strength increases steeply with the growth of strain rate. For a strain rate between 0.001 and 0.01, the slope of the curve exhibits a pronounced decrease. In the case of the strain rate being larger than 0.01, the predicted value of tensile strength increases slowly with the increase in the strain rate.

The distribution direction of the SR scatter points is consistent with that of the PDP curve. Specifically, SHAP assumes a negative value when the strain rate is below 0.001, and a positive value when it is above 0.001. As the strain rate increases from 0.10, the scatterplot deviates from the PDP curve, which may indicate suboptimal model performance at elevated strain rates. As illustrated in Figure 6c, the nonlinear relationship indicates that the optimal loading rate should be determined during the test. Consequently, the tensile strength of UHPC obtained at varying loading rates may not be directly comparable.

Figure 6d shows the influence of feature Section on the combination of PDP curve and SHAP scattering points. The horizontal axis represents the feature values ranging from 625 to 5000, and the vertical axis signifies the contribution, ranging from −1 to +2. A close examination of the PDP curves reveals a discernible nonlinear relationship between the tensile strength of UHPC and the cross-sectional area of the specimens. The curve is roughly subdivided into two segments. As the cross-sectional area of UHPC specimen increases from approximately 625 to 1000, there is a decline in tensile strength. However, when the cross-sectional area is greater than 1000, UHPC tensile strength approaches a constant level, indicating an absence of correlation with the cross-sectional area.

The SHAP scatter plot of Figure 6d demonstrates a comparable trend. As the cross-sectional area of specimen is below 1000 mm², the tensile strength of UHPC is observed to decrease with increasing specimen sectional area. Conversely, when the cross-sectional area exceeds 1000 mm², the tensile strength becomes largely independent of further increases in size. The SHAP scatter is distributed along the alignment of the PDP curve, and the vertical width is narrow, indicating that the feature of the specimen cross-sectional area is minimally affected by the interaction of other features. Yang et al. [50] have demonstrated that the fibers in the specimen of smaller sectional sizes exhibit a higher degree of alignment in the longitudinal direction of the specimen during casting, thereby enhancing the tensile strength. However, as demonstrated in the present study, the orientation of the fibers remains largely unaffected by casting when the cross-sectional size attains a certain threshold of 1000 mm².

4. Conclusions

A review of the existing literature is initially conducted to compile a database of the tensile strength of UHPC, comprising the experimental results of 178 UHPC-based sample with varying design parameters. Then, several feature engineering strategies of both physical and data-driven methods, including feature selection, feature fusion, outlier handling and missing value filling, are proposed to optimize the robustness and generalization ability of the model under the small-sample condition of the established database. Furthermore, seven ML algorithms, namely, BRR, ANN, SVR, RF, GBRT, LightGBM, and CatBoost, are employed to develop an optimized ML model for predicting the tensile strength of UHPC. The performance and efficiency of multiple algorithms are evaluated and compared with default hyperparameter settings and with hyperparameter tuning. The utilization of SHAP values in combination with PDP enables the analysis of the relationships between UHPC tensile strength and various influencing factors. The following conclusions can be drawn:

(1)

To maximize the utility of the limited dataset, several feature engineering strategies are implemented on the basis of material science analysis. These strategies include missing value imputation, outlier handling, feature selection, and feature fusion. This ensures that the feature variables are consistent with the physical and mechanical principles of UHPC while satisfying the data distribution and interpretability requirements of ML algorithms. Consequently, it prevents the occurrence of model bias resulting from the absence of physical laws or improper algorithm adaptation.

(2)

The quantitative evaluation of seven ML algorithms reveals that, under default hyperparameter settings, ensemble algorithms such as RF, GBRT, LightGBM, and CatBoost exhibit superior prediction performance, as indicated by an R² value > 0.92. Conversely, traditional ML algorithms, including BRT, SVR, and ANN, demonstrate a comparatively inferior model performance. After hyperparameter tuning, the model performance of ensemble algorithms exhibits only a marginal improvement. In contrast, the conventional ML algorithms, including SVR and ANN, have shown substantial progress, attaining a model performance that is comparable to that of ensemble models. With regard to the R² value, the performance enhancements for RF, GBRT, LightGBM, CatBoost, ANN, and SVR after hyperparameter tuning are 0.43%, 1.28%, 2.06%, 0.21%, 58.82%, and 66.67%, respectively. Both conventional and ensemble models with hyperparameter tuning consistently achieve R² values greater than 0.94. However, the BRR algorithm demonstrates a suboptimal performance, irrespective of the application of hyperparameter tuning.

(3)

A comparison of the performance of various ML algorithms reveals that CatBoost demonstrates superior performance when evaluated under hyperparameter tuning. Through the implementation of hyperparameter tuning, a modest enhancement in performance is observed, as indicated by an increase in the R² value of 0.21%. However, it should be noted that this process requires a substantial duration of 1208.4 s, which is notably more time-consuming in comparison to all other ML algorithms. This finding suggests that the selection of the algorithm and the tuning of hyperparameters may require a trade-off between model performance and computational cost.

(4)

Feature importance ranking indicates that the fiber reinforcing index, FRI, exerts a predominant influence on UHPC tensile strength prediction, with a contribution of 37.5%, followed by the water-to-cement ratio. Additionally, different tensile test strain rates and specimen cross-sectional dimensions can lead to different experimental results. It is imperative that such disparities be taken into consideration during the formulation of the experimental design, thereby ensuring that conclusions drawn do not deviate from the actual conditions under investigation.

(5)

The utilization of the PDP in conjunction with the SHAP scatter plot is indicative of the nonlinear relationship between UHPC tensile strength and four key factors. The critical thresholds for each factor are identified by FRI, W/C, SR, and Section.

The strategies employed in the present study for feature engineering with limited sample sizes, along with the conclusions on the accuracy and efficiency of ML algorithms, provide valuable references for related research endeavors concerning feature engineering, algorithm selection, and hyperparameter tuning. The findings of this study on the factors influencing tensile strength provide engineering guidance for identifying key elements in the design of UHPC mixes and offer practical theoretical foundations for engineering applications.

In light of the findings from this study, future research efforts will concentrate on expanding the established database through the incorporation of additional experimental samples. It is evident that, given adequate computational resources, further exploration of a comprehensive set of ML algorithms, the extension of the scope of hyperparameter tuning, and the execution of more in-depth feature analysis would contribute to a significant expansion of the conclusions of this study. Additionally, while ML has exhibited a satisfactory degree of accuracy in predicting the tensile strength of UHPC, its black-box nature poses a significant impediment to the broader implementation of ML in engineering applications. To facilitate practical implementation, subsequent research is planned to develop a lightweight graphical user interface (GUI) for predicting UHPC tensile strength. This would allow users to quickly obtain results by inputting feature values without the need for complex coding expertise. Another promising direction involves a physics-informed predictive formula by employing a Gene Expression Programming (GEP) algorithm or other interpretable modeling techniques to derive an explicit mathematical expression between tensile strength and input features, as identified by the proposed ML models.