AI-Enhanced Surrounding Rock Parameter Determination of Deeply Buried Underground Laboratory in Jinping, China
Abstract
1. Introduction
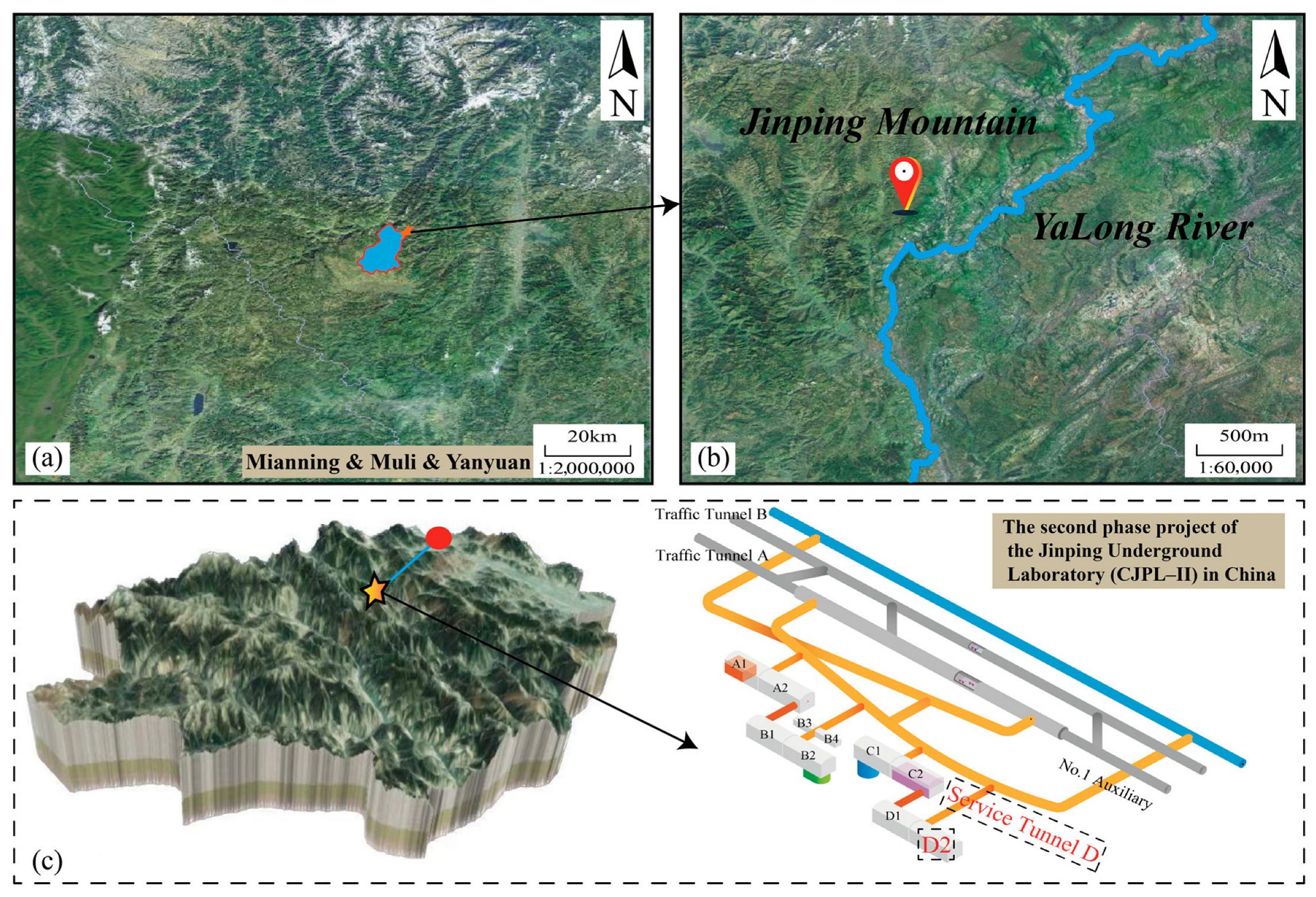
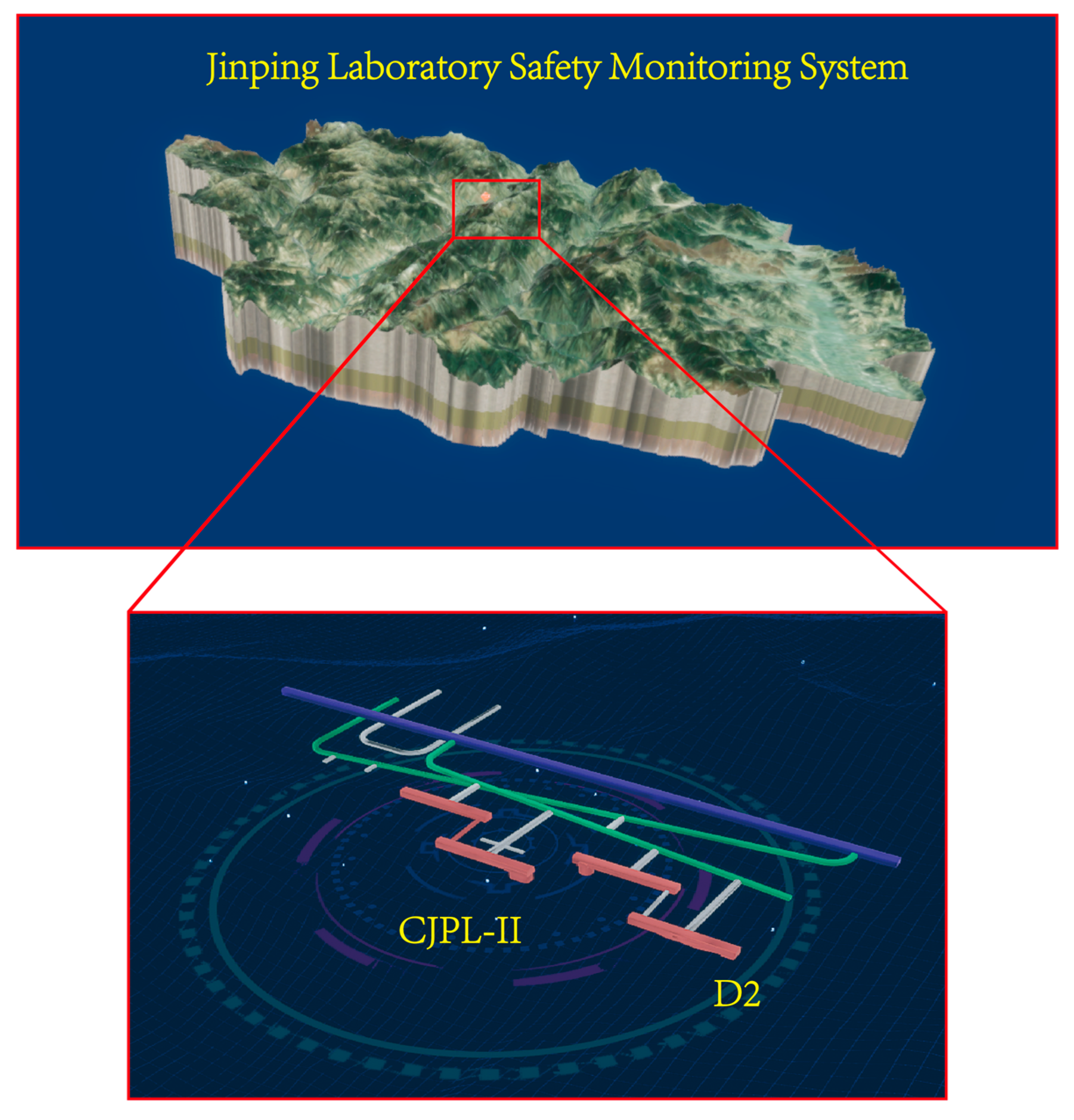
2. Jinping Underground Laboratory
3. AI-Enhanced Rock Mechanical Parameter Determination
3.1. Inverse Analysis
3.2. CatBoost
3.3. Simplicial Homology Global Optimization (SHGO)
- Relative error (RE)
- 2.
- Root mean square error of displacement (RMSE):
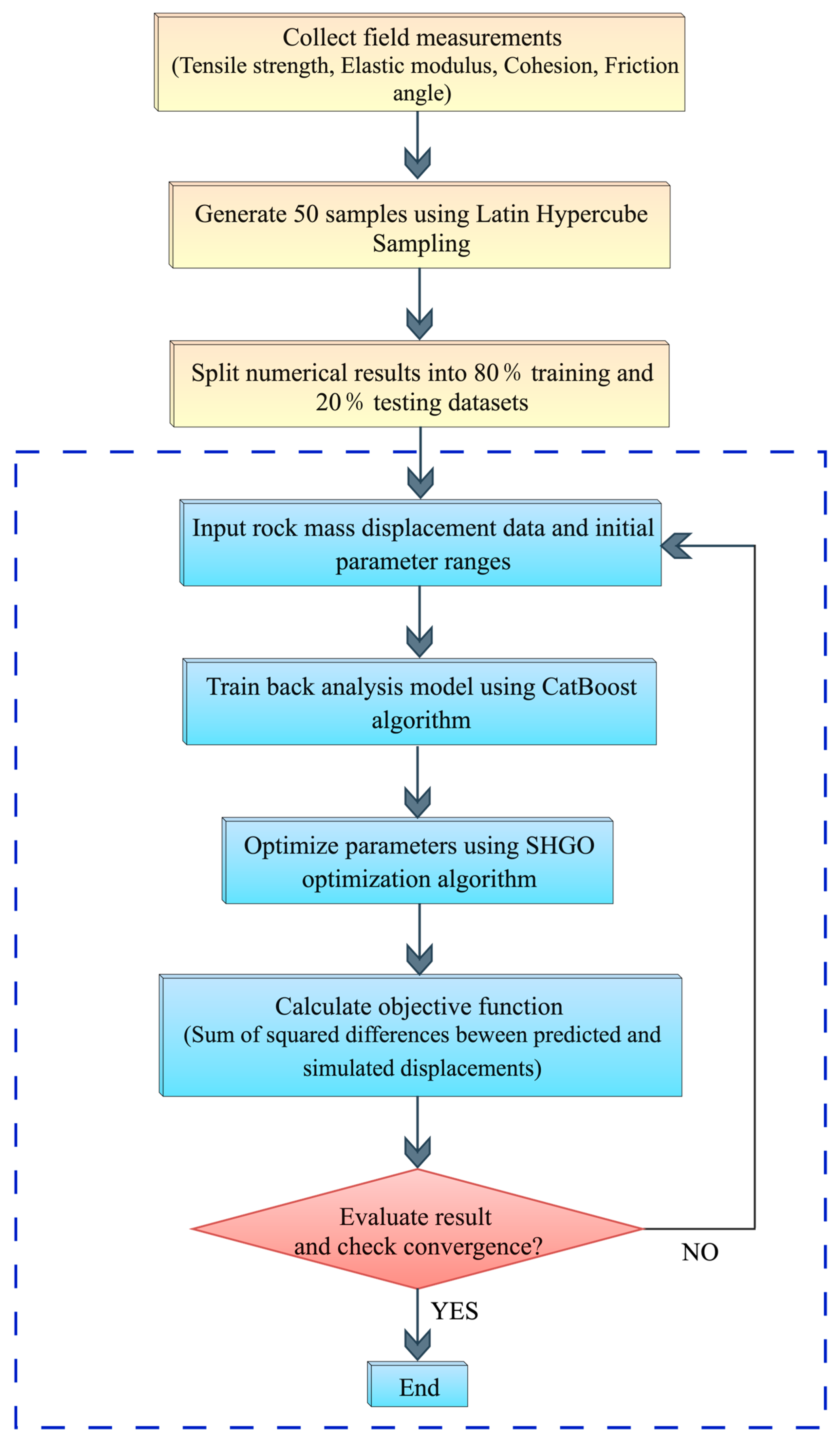
3.4. Procedure of the Comprehensive Algorithm for Inverse Analysis
4. Application
4.1. Numerical Model of Tunnel in Jinping Underground Laboratory
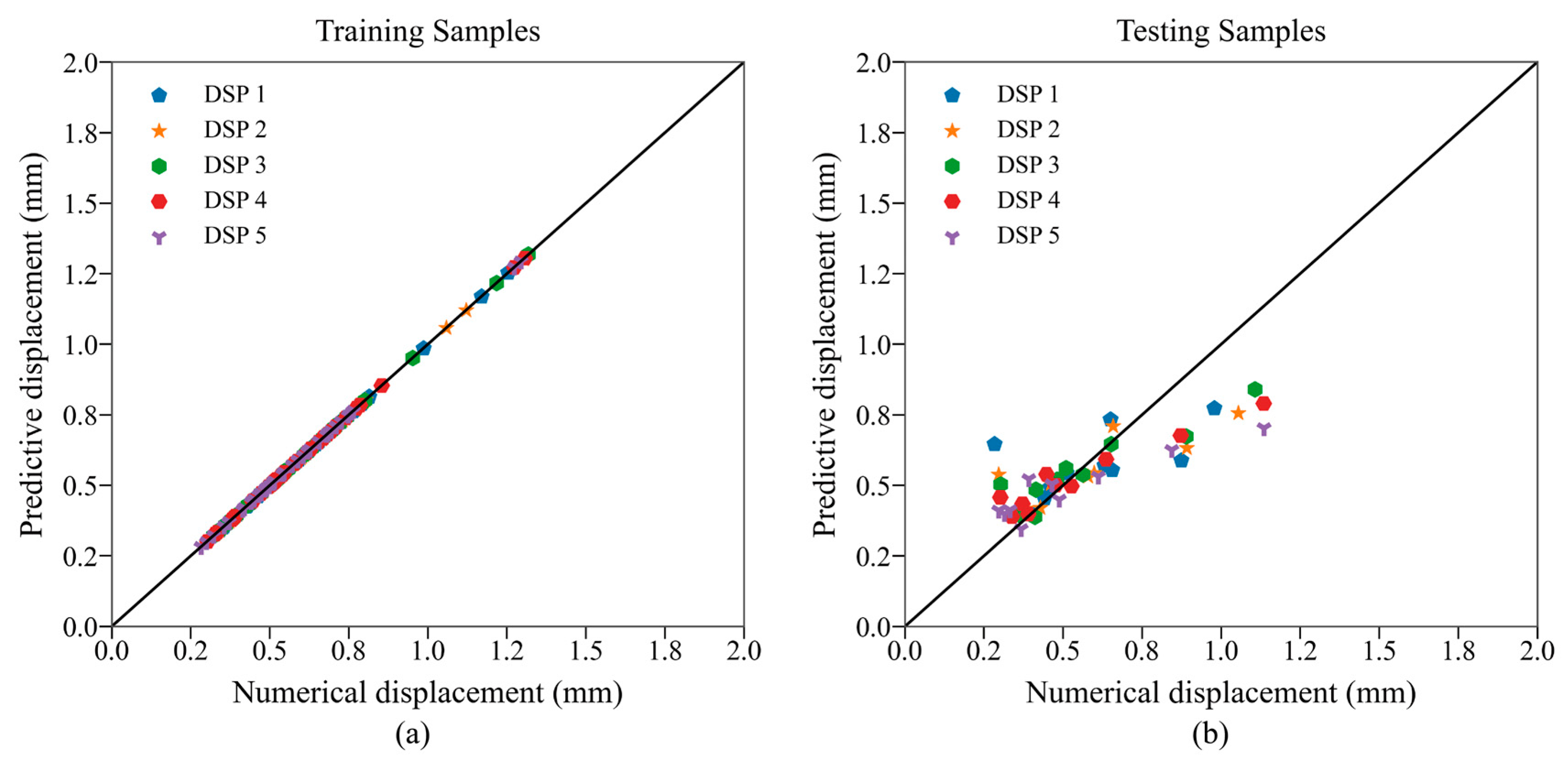
4.2. Results
4.3. Discussions
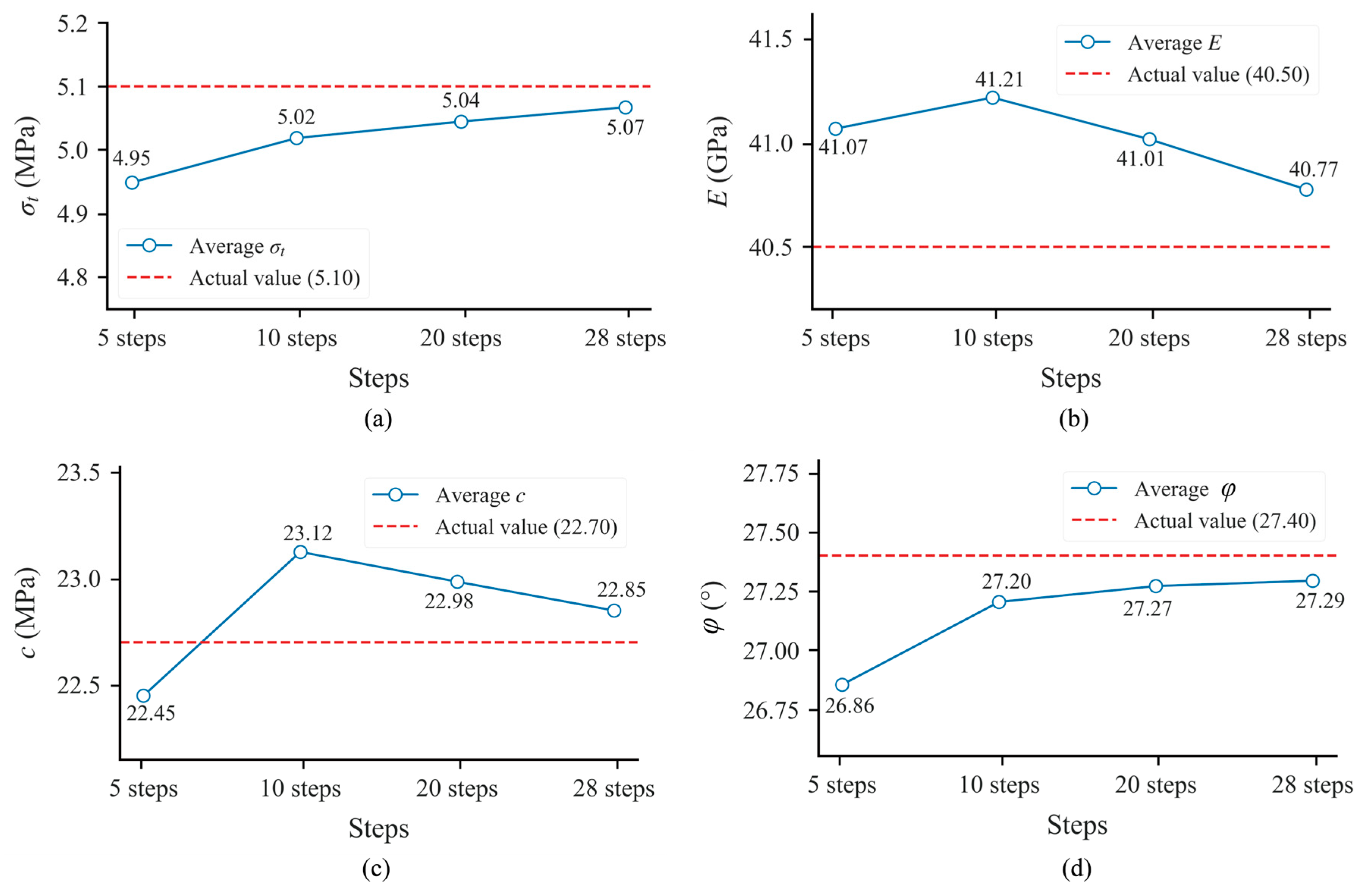
4.3.1. Temporal Evolution of Inversion Accuracy
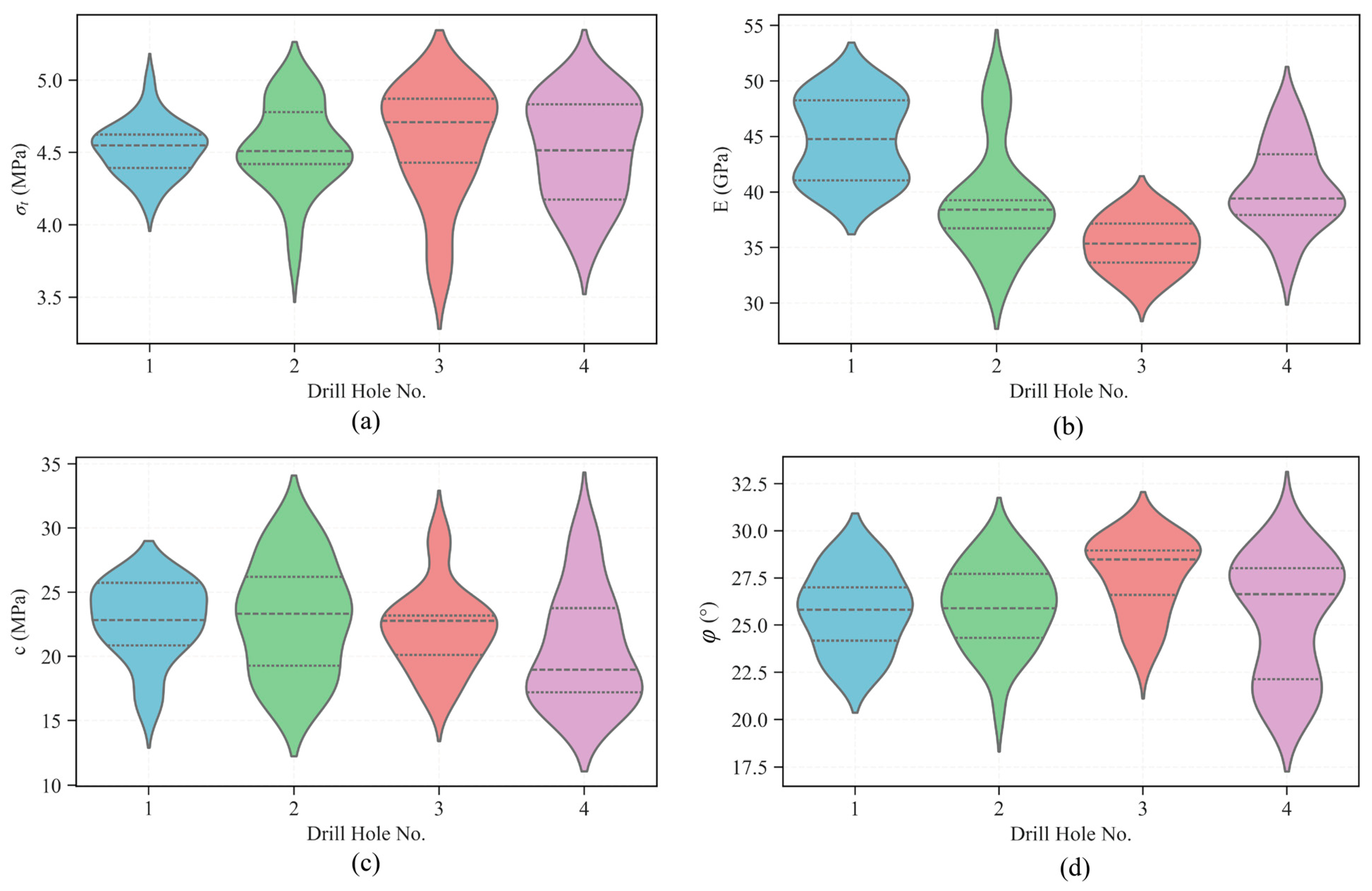
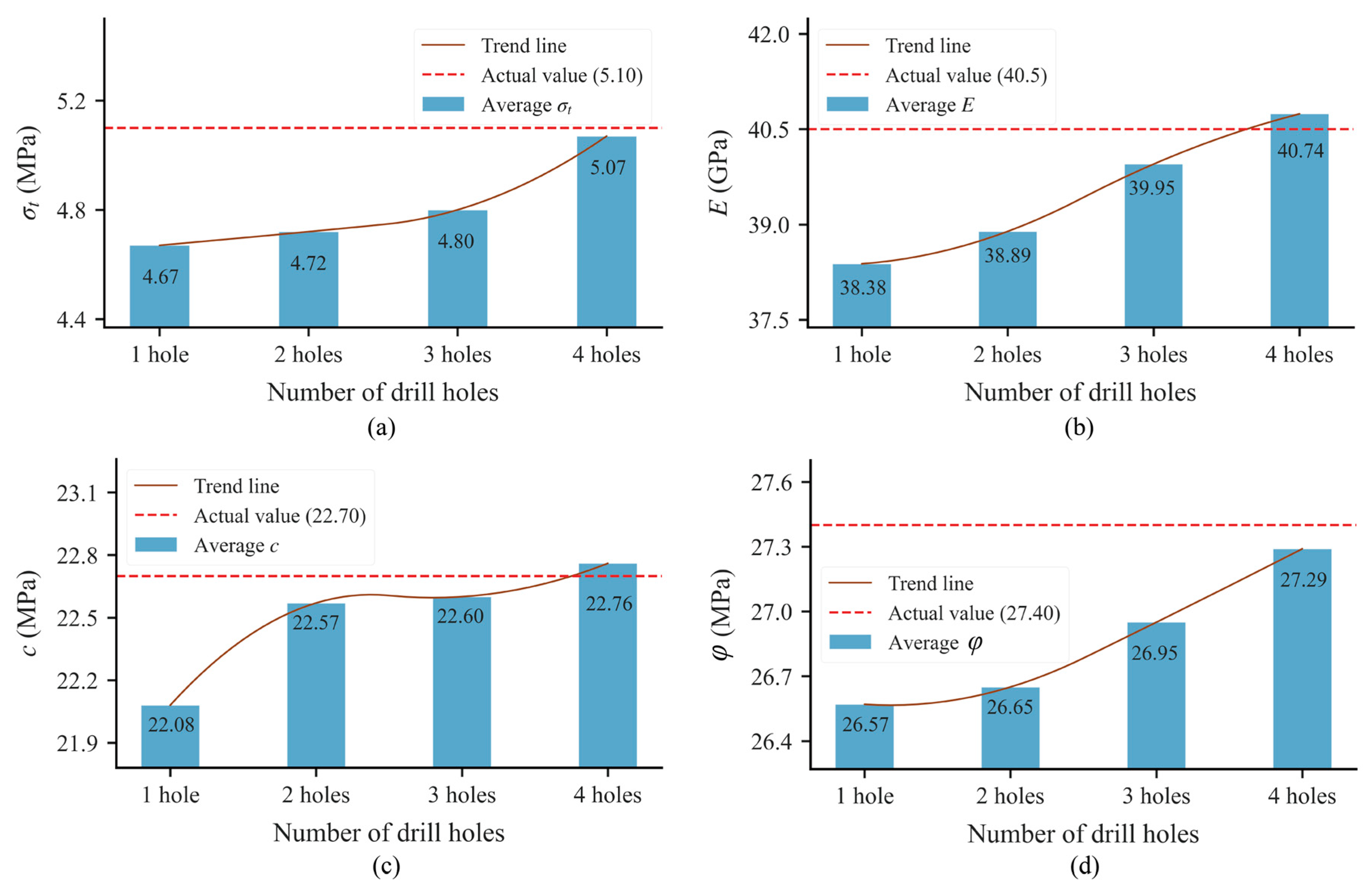
4.3.2. Spatial Robustness with Multiple Boreholes
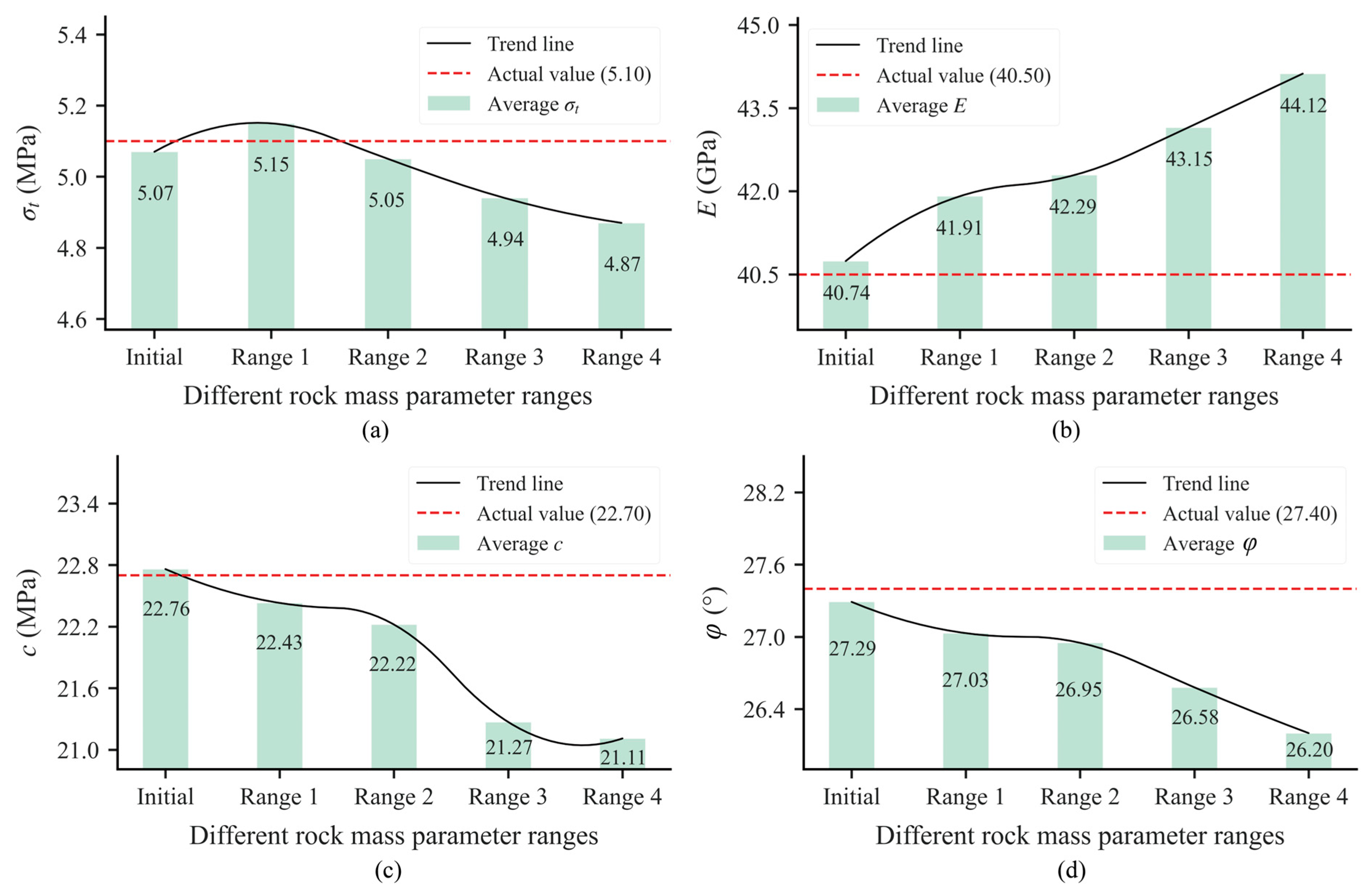
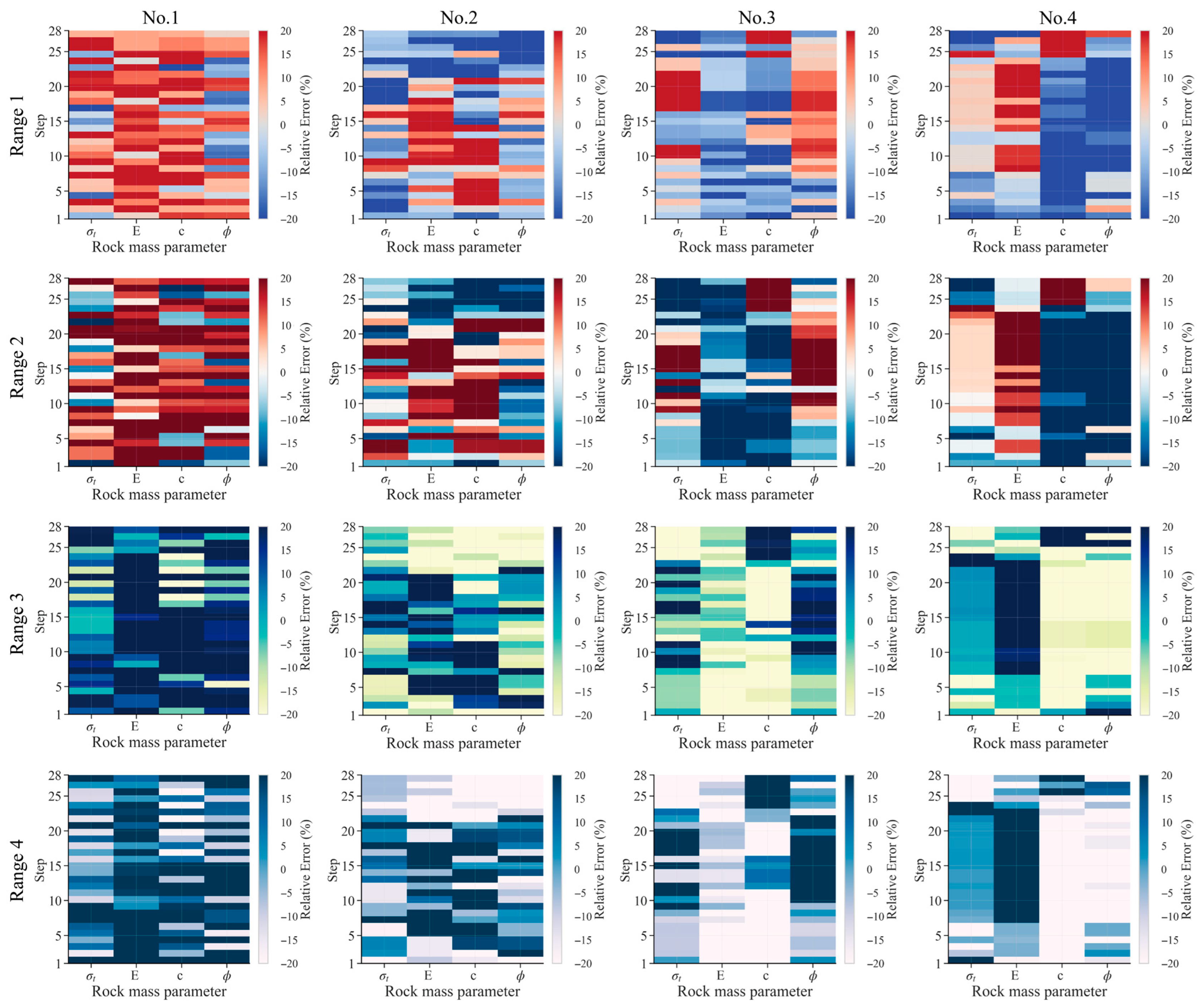
4.3.3. Robustness Against Parameter Range Uncertainty
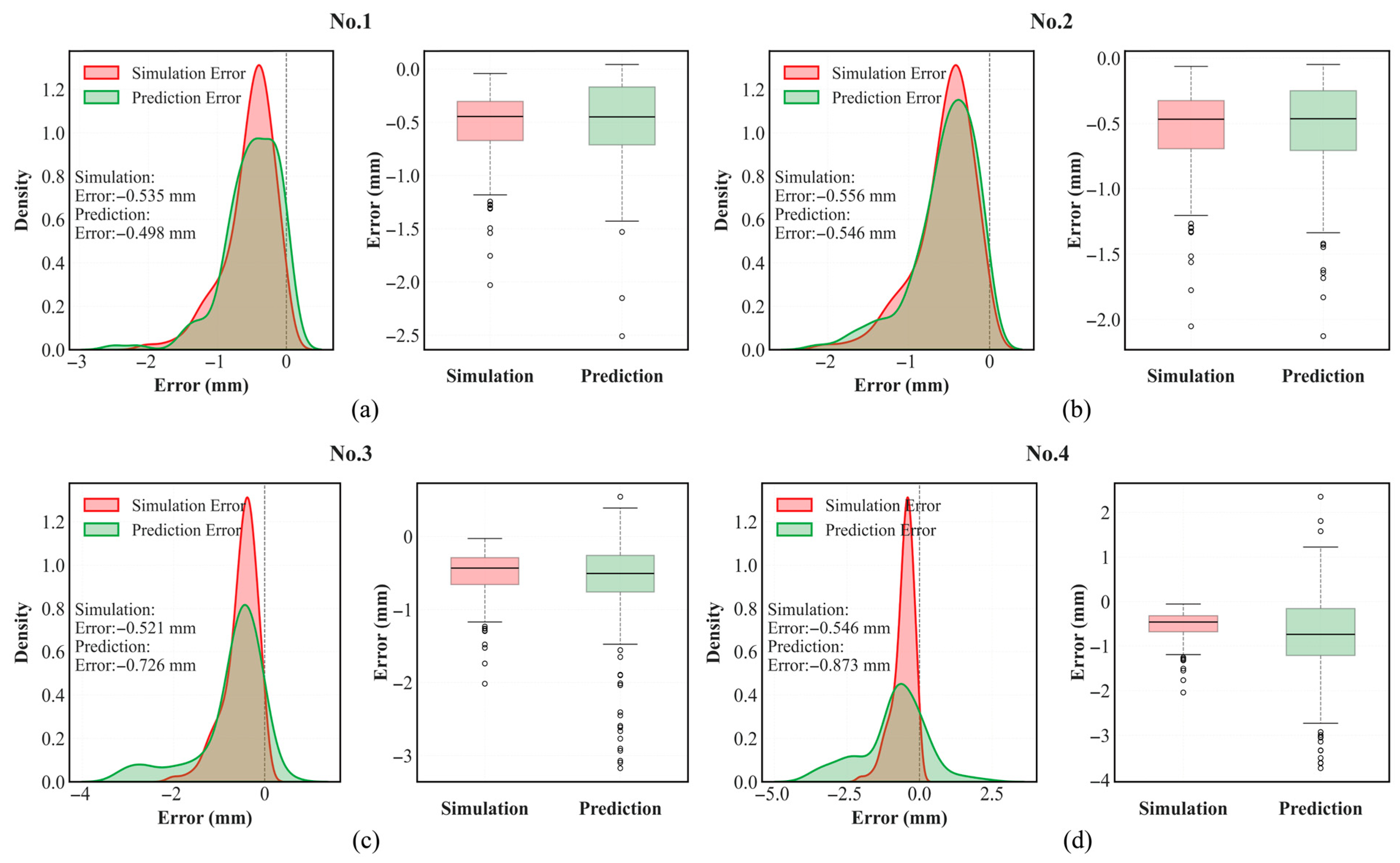
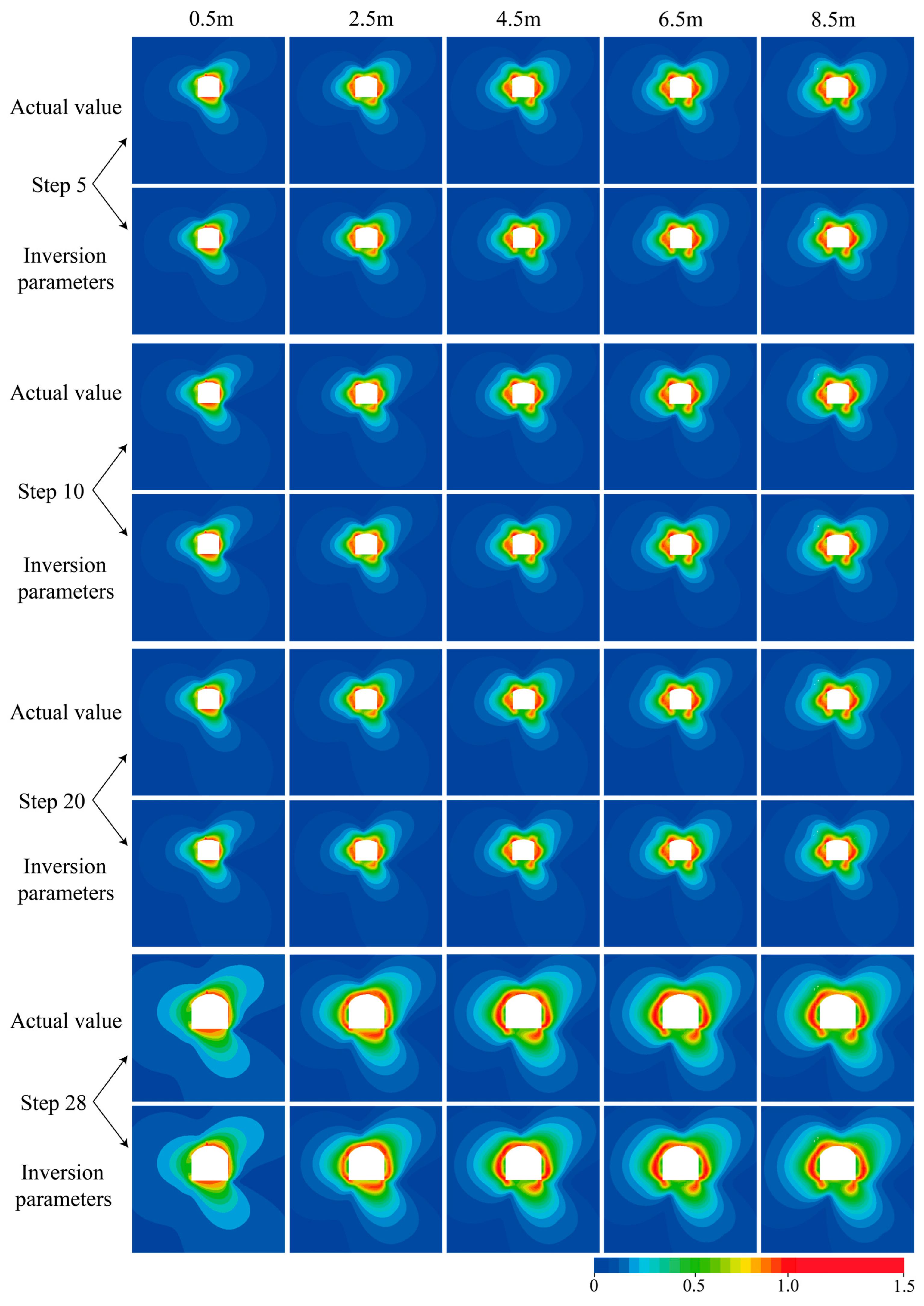
4.3.4. Validation via Mechanical Response Prediction
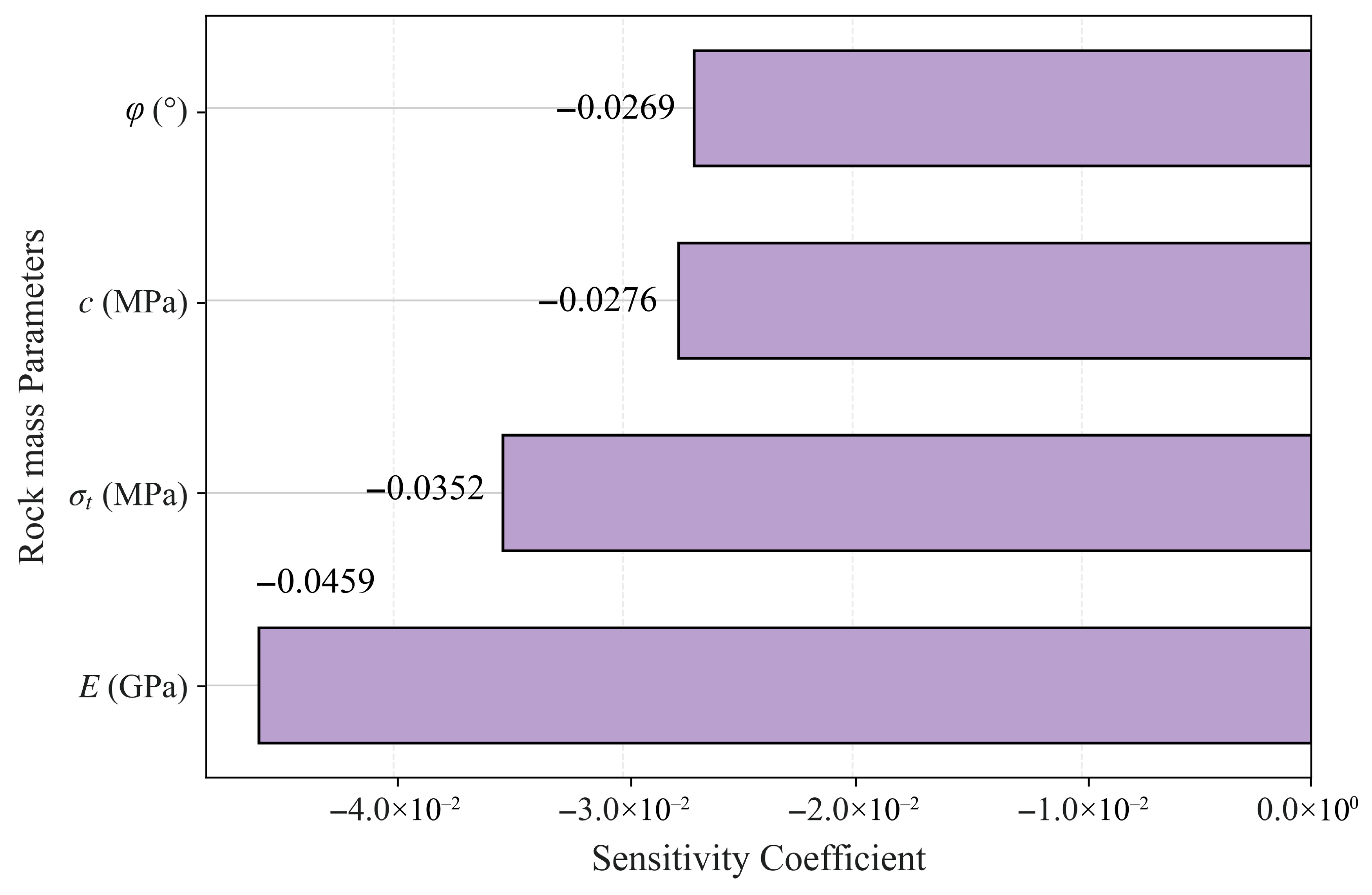
4.3.5. Parameter Interdependence and Sensitivity-Driven Optimization
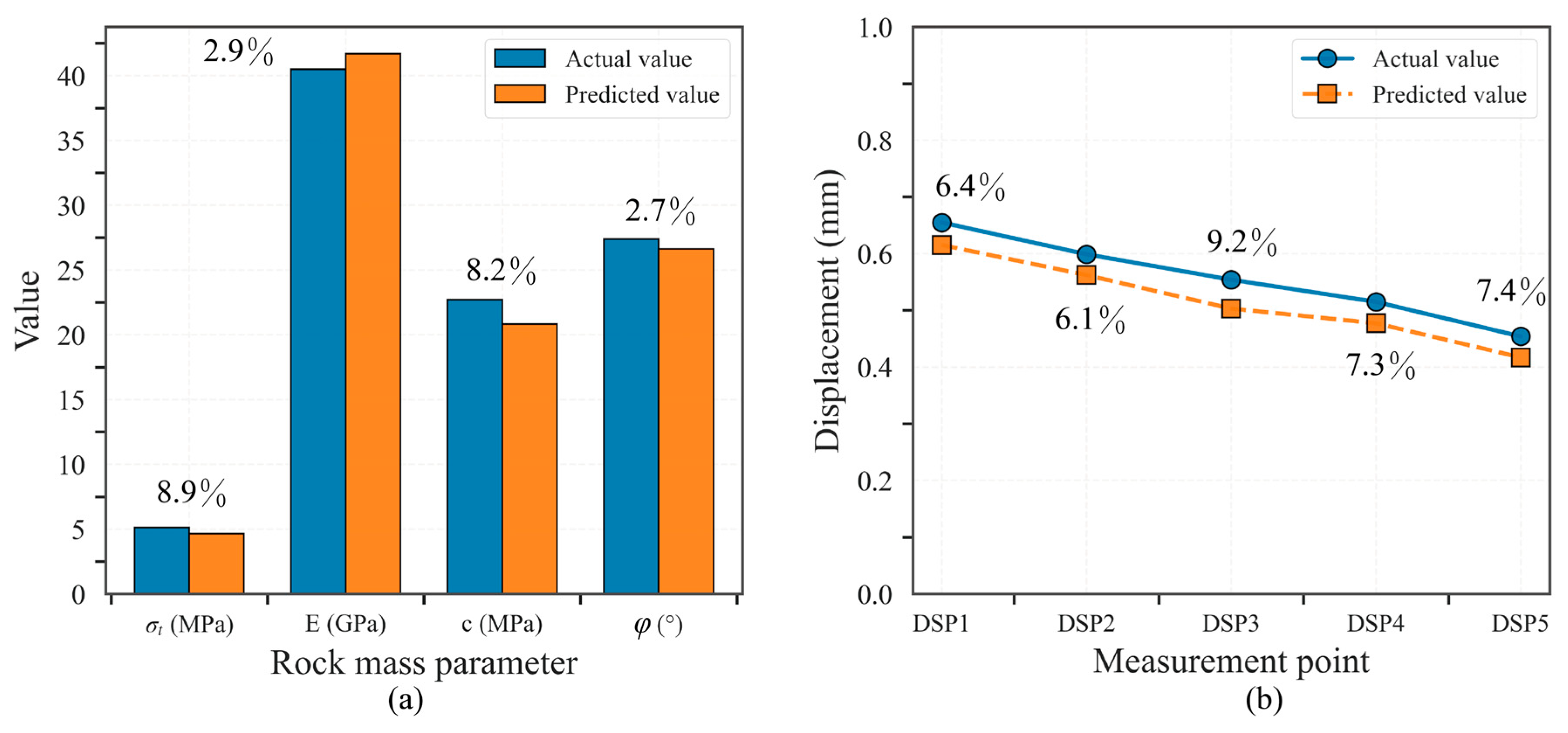
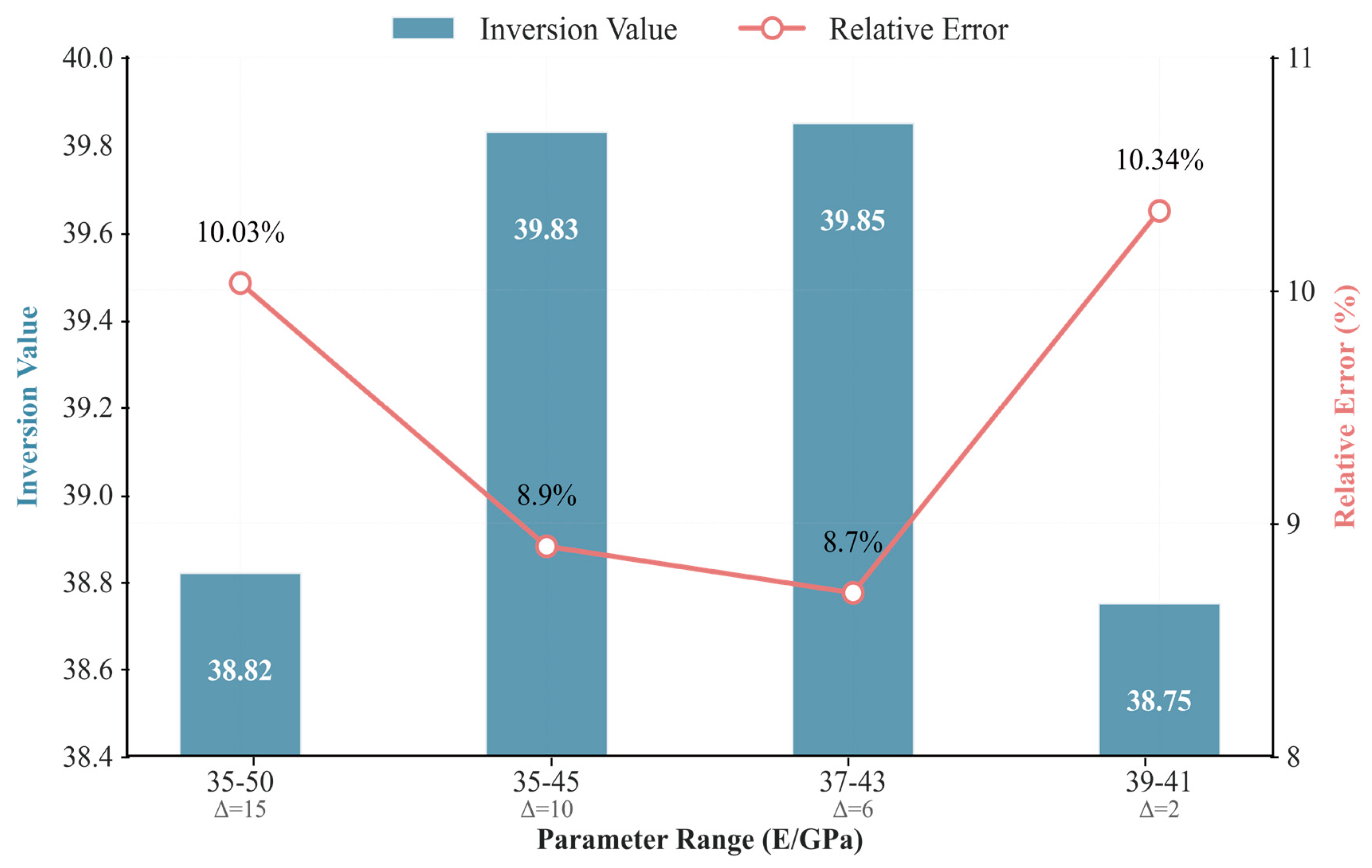
4.4. Validation of D2 Laboratory Operation Data
5. Conclusions
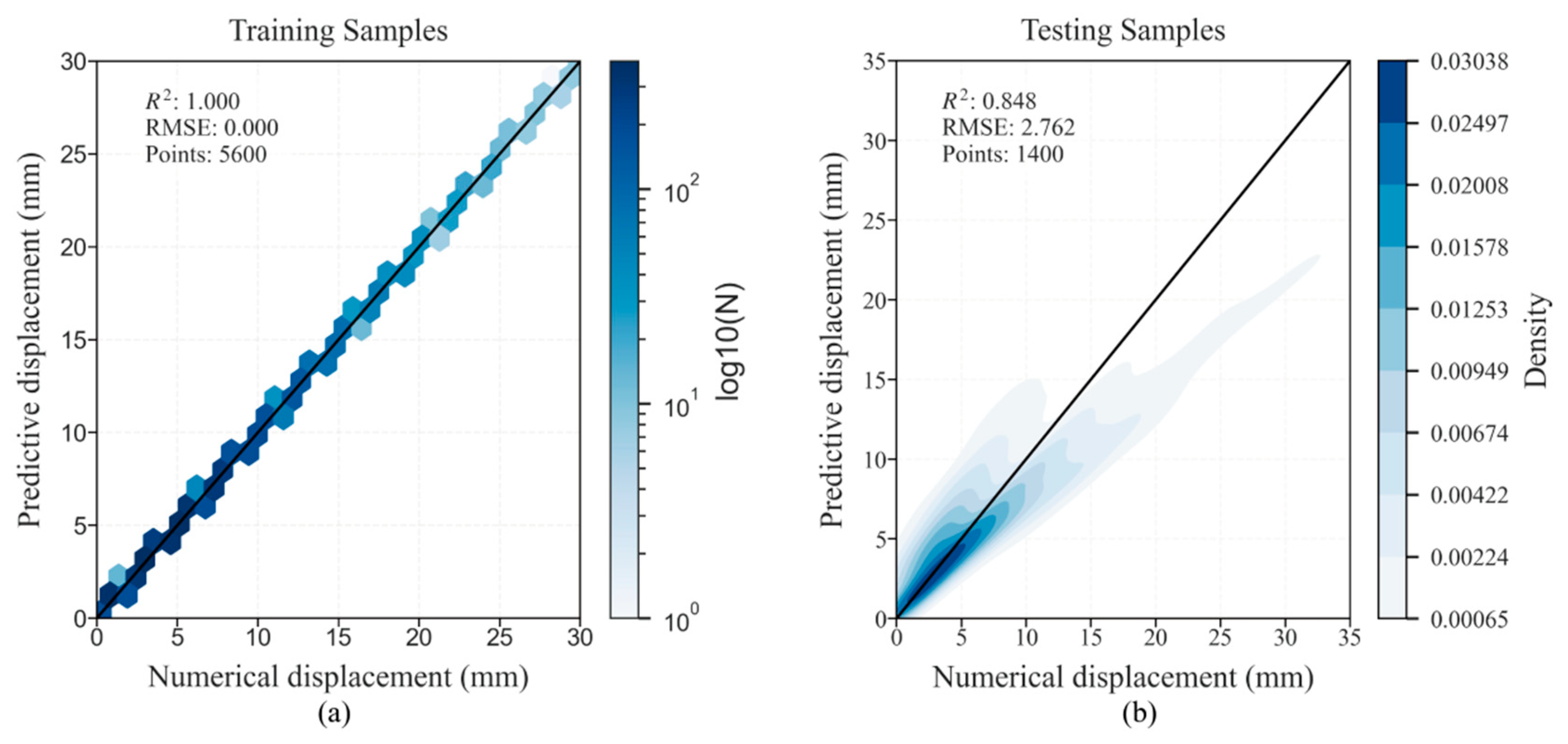
- Validation of the established surrogate model, combined with the SHGO process, yielded optimized surrounding rock parameters with minimal relative errors, confirming satisfactory inverse analysis results. Furthermore, substituting these inverted parameters into the numerical model produced mechanical responses of the surrounding rock that closely matched the true values, demonstrating the model’s reliability.
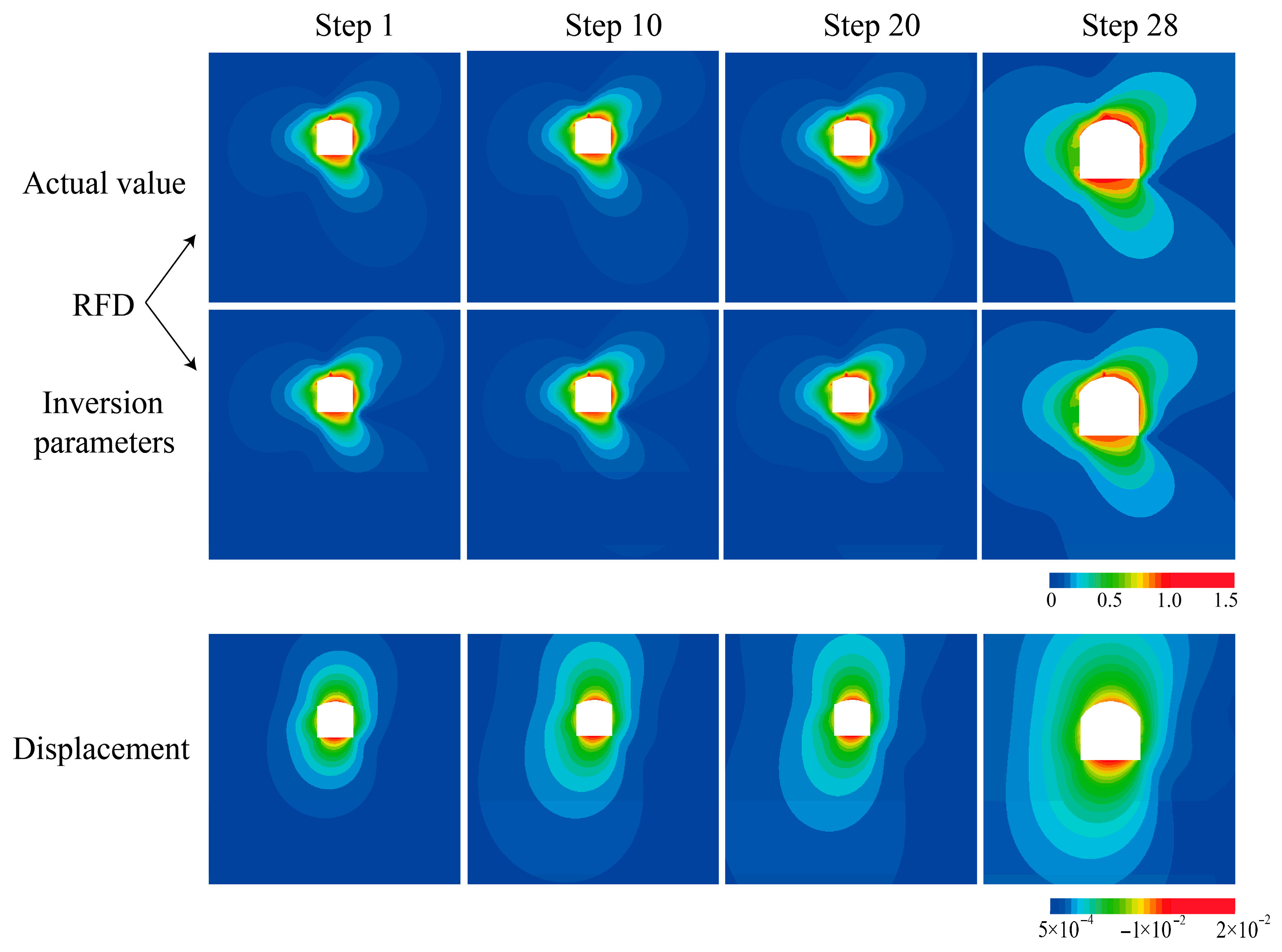
- In practical inverse analysis, using displacement data from the first 28 steps yields rock parameters closer to the true values. Furthermore, increasing the number of measurement holes further enhances the accuracy of the inverted parameter averages.
- As the range of surrounding rock parameters widens, the deviation of the inverted parameter averages from their true values increases. Nevertheless, the maximum error consistently remains below 20%, demonstrating the model’s robust inversion performance and high accuracy.
- In the inverse analysis results, the relative error between RFD cloud diagrams generated using the inverted parameters and those based on the actual parameters is below 5%. Sensitivity analysis revealed the elastic modulus as the most influential parameter.
- The optimization algorithm determined the optimal value to be 39.85, achieving the minimum relative error. These results provide a robust basis for subsequent engineering analysis and design.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Li, C.; Wang, L.; Li, J.; Chen, Y. Application of multi-algorithm ensemble methods in high-dimensional and small-sample data of geotechnical engineering: A case study of swelling pressure of expansive soils. J. Rock Mech. Geotech. Eng. 2024, 16, 1896–1917. [Google Scholar] [CrossRef]
- Ullah, J.; Huan, L.; Zuo, Y.H.; Ehsan, M.; Soupios, P. Enhancing Reservoir Characterization: Genetic Algorithm-Assisted Correction of Pore Aspect Ratio Using CNN-LSTM in Petrophysical Modeling. IEEE Trans. Geosci. Remote Sens. 2025, 63, 5908311. [Google Scholar] [CrossRef]
- Pinheiro, M.; Vallejos, J.; Miranda, T.; Emery, X. Geostatistical simulation to map the spatial heterogeneity of geomechanical parameters: A case study with rock mass rating. Eng. Geol. 2016, 205, 93–103. [Google Scholar] [CrossRef]
- Hu, X.; Shentu, J.; Xie, N.; Huang, Y.; Lei, G.; Hu, H.; Guo, P.; Gong, X. Predicting triaxial compressive strength of high-temperature treated rock using machine learning techniques. J. Rock Mech. Geotech. Eng. 2023, 15, 2072–2082. [Google Scholar] [CrossRef]
- Zhao, H.; Li, S.; Zang, X.; Liu, X.; Zhang, L.; Ren, J. Uncertainty quantification of inverse analysis for geomaterials using probabilistic programming. J. Rock Mech. Geotech. Eng. 2024, 16, 895–908. [Google Scholar] [CrossRef]
- Sakurai, S.; Takeuchi, K. Back analysis of measured displacements of tunnels. Rock Mech. Rock Eng. 1983, 16, 173–180. [Google Scholar] [CrossRef]
- Zhang, F.S.; Dong, L.L.; Wang, H.B.; Zhong, K.; Zhang, P.Y.; Jiang, J.Y. Inverse Analysis of Strata in Seepage Field Based on Regularization Method and Geostatistics Theory. Buildings 2024, 14, 946. [Google Scholar] [CrossRef]
- Chang, X.; Wang, H.; Zhang, Y. Back analysis of rock mass parameters in tunnel engineering using machine learning techniques. Comput. Geotech. 2023, 163, 105738. [Google Scholar] [CrossRef]
- He, J.; Chen, S.-H.; Shahrour, I. Back Analysis of Equivalent Permeability Tensor for Fractured Rock Masses from Packer Tests. Rock Mech. Rock Eng. 2011, 44, 491–496. [Google Scholar] [CrossRef]
- Zhao, H.; Chen, B.; Li, S. Determination of geomaterial mechanical parameters based on back analysis and reduced-order model. Comput. Geotech. 2021, 132, 104013. [Google Scholar] [CrossRef]
- Chen, K.; Olarte, A.A.P. Probabilistic Back Analysis Based on Nadam, Bayesian, and Matrix-Variate Deep Gaussian Process for Rock Tunnels. Rock Mech. Rock Eng. 2024, 57, 9739–9758. [Google Scholar] [CrossRef]
- Shakeri, J.; Pepe, G.; Faradonbeh, R.S.; Ghaderi, Z.; Pappalardo, G.; Cevasco, A.; Mineo, S. Intelligent Approaches for Predicting the Intact Rock Mechanical Parameters and Crack Stress Thresholds. Rock Mech. Rock Eng. 2024, 57, 8499–8528. [Google Scholar] [CrossRef]
- Walton, G.; Sinha, S. Challenges associated with numerical back analysis in rock mechanics. J. Rock Mech. Geotech. Eng. 2022, 14, 2058–2071. [Google Scholar] [CrossRef]
- Leon, F.; Rojas, L.; Peña, A.; Moraga, P.; Robles, P.; Gana, B.; García, J. Mathematical Modelling and Optimization Methods in Geomechanically Informed Blast Design: A Systematic Literature Review. Mathematics 2025, 13, 2456. [Google Scholar] [CrossRef]
- Furtney, J.K.; Thielsen, C.; Fu, W.; Le Goc, R. Surrogate Models in Rock and Soil Mechanics: Integrating Numerical Modeling and Machine Learning. Rock Mech. Rock Eng. 2022, 55, 2845–2859. [Google Scholar] [CrossRef]
- Li, H.; Chen, W.; Tan, X.; Tan, X. Back analysis of geomechanical parameters for rock mass under complex geological conditions using a novel algorithm. Tunn. Undergr. Space Technol. 2023, 136, 105099. [Google Scholar] [CrossRef]
- Wu, K.; Meng, Q.; Li, R.; Luo, L.; Ke, Q.; Wang, C.; Ma, C. A machine learning-based strategy for predicting the mechanical strength of coral reef limestone using X-ray computed tomography. J. Rock Mech. Geotech. Eng. 2024, 16, 2790–2800. [Google Scholar] [CrossRef]
- Yan, H.-C.; Liu, H.-Z.; Li, Y.; Zhuo, L.; Xiao, M.-L.; Chen, K.-P.; Wu, J.-M.; Pei, J.-L. Inversion Analysis of the In Situ Stress Field around Underground Caverns Based on Particle Swarm Optimization Optimized Back Propagation Neural Network. Appl. Sci. 2023, 13, 4697. [Google Scholar] [CrossRef]
- Yin, X.; Huang, X.; Pan, Y.; Liu, Q. Point and interval estimation of rock mass boreability for tunnel boring machine using an improved attribute-weighted deep belief network. Acta Geotech. 2023, 18, 1769–1791. [Google Scholar] [CrossRef]
- Liang, J.; Du, X.; Fang, H.; Li, B.; Wang, N.; Di, D.; Xue, B.; Zhai, K.; Wang, S. Intelligent prediction model of a polymer fracture grouting effect based on a genetic algorithm-optimized back propagation neural network. Tunn. Undergr. Space Technol. 2024, 148, 105781. [Google Scholar] [CrossRef]
- Ding, X.; Hasanipanah, M.; Rouhani, M.M.; Nguyen, T. Hybrid catboost models optimized with metaheuristics for predicting shear strength in rock joints. Bull. Eng. Geol. Environ. 2025, 84, 150. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, R.; Wang, J.; Li, N.; Cao, H. A Rock Mass Strength Prediction Method Integrating Wave Velocity and Operational Parameters Based on the Bayesian Optimization Catboost Algorithm. KSCE J. Civ. Eng. 2023, 27, 3148–3162. [Google Scholar] [CrossRef]
- Liu, Y.; Ren, W.; Liu, C.; Cai, S.; Xu, W. Displacement-Based Back-Analysis Frameworks for Soil Parameters of a Slope: Using Frequentist Inference and Bayesian Inference. Int. J. Geomech. 2022, 22, 04022026. [Google Scholar] [CrossRef]
- Zhao, H.; Zhang, L.; Ren, J.; Wang, M.; Meng, Z. AdaBoost-Based Back Analysis for Determining Rock Mass Mechanical Parameters of Claystones in Goupitan Tunnel, China. Buildings 2022, 12, 1037. [Google Scholar] [CrossRef]
- Acaroglu, O.; Erdogan, C. Stability analysis of roadheaders with mini-disc. Tunn. Undergr. Space Technol. 2017, 68, 187–195. [Google Scholar] [CrossRef]
- Ge, Y.; Tang, H.; Li, C. Mechanical energy evolution in the propagation of rock avalanches using field survey and numerical simulation. Landslides 2021, 18, 3559–3576. [Google Scholar] [CrossRef]
- Sun, Y.; Jiang, Q.H.; Yin, T.; Zhou, C.B. A back-analysis method using an intelligent multi-objective optimization for predicting slope deformation induced by excavation. Eng. Geol. 2018, 239, 214–228. [Google Scholar] [CrossRef]
- Endres, S. A Simplicial Homology Algorithm for Lipschitz Optimisation. Master’s Dissertation, University of Pretoria, Pretoria, South Africa, 2017. [Google Scholar]
- Endres, S.C.; Sandrock, C.; Focke, W.W. A simplicial homology algorithm for Lipschitz optimisation. J. Glob. Optim. 2018, 72, 181–217. [Google Scholar] [CrossRef]
- Zheng, M.; Li, S.; Feng, Z.; Xu, H.; Xiao, Y. Three-dimensional stress variation characteristics in deep hard rock of CJPL-II project based on in-situ monitoring. Int. J. Min. Sci. Technol. 2024, 34, 179–195. [Google Scholar] [CrossRef]
- Li, S.; Feng, X.; Li, Z.; Chen, B.; Jiang, Q.; Wu, S.; Hu, B.; Xu, J. In situ experiments on width and evolution characteristics of excavation damaged zone in deeply buried tunnels. Sci. China-Technol. Sci. 2011, 54, 167–174. [Google Scholar] [CrossRef]
- Li, S.J.; Feng, X.T.; Li, Z.H.; Chen, B.R.; Zhang, C.Q.; Zhou, H. In situ monitoring of rockburst nucleation and evolution in the deeply buried tunnels of Jinping II hydropower station. Eng. Geol. 2012, 137, 85–96. [Google Scholar] [CrossRef]
- Hu, L.; Feng, X.-T.; Xiao, Y.-X.; Feng, G.-L.; Li, S.-J.; Pan, P.-Z.; Yao, Z.-B. Characteristics of the microseismicity resulting from the construction of a deeply-buried shaft. Tunn. Undergr. Space Technol. 2019, 85, 114–127. [Google Scholar] [CrossRef]
- Jiang, Q.; Yang, B.; Yan, F.; Xu, D.; Feng, G.; Li, S. Morphological features and fractography analysis for in situ spalling in the China Jinping underground laboratory with a 2400 m burial depth. Tunn. Undergr. Space Technol. 2021, 118, 104194. [Google Scholar] [CrossRef]
- Chen, H. Underground laboratory in China. Eur. Phys. J. Plus 2012, 127, 105. [Google Scholar] [CrossRef]
- Zhao, H.B.; Chen, B.R. Inverse analysis for rock mechanics based on a high dimensional model representation. Inverse Probl. Sci. Eng. 2021, 29, 1565–1585. [Google Scholar] [CrossRef]
- Cui, K.; Pan, X.K. Back analysis for mass parameters of tunnel surrounding rock. In Proceedings of the 2nd International Conference on Civil Engineering, Architecture and Building Materials (CEABM 2012), Yantai, China, 25–27 May 2012; Volume 170–173, pp. 20–24. [Google Scholar] [CrossRef]
- Yang, C.X.; Wu, Y.H.; Hon, T. A no-tension elastic-plastic model and optimized back-analysis technique for modeling nonlinear mechanical behavior of rock mass in tunneling. Tunn. Undergr. Space Technol. 2010, 25, 279–289. [Google Scholar] [CrossRef]
- Zhang, Z.X.; Wu, S.C.; Wang, Y.K.; Zhang, H.J.; Han, L.Q. Probabilistic back analysis of rock strength parameters in heavily jointed rock slopes based on Bayesian inference. Environ. Earth Sci. 2024, 83, 314. [Google Scholar] [CrossRef]
- An, X.; Zheng, F.; Jiao, Y.; Li, Z.; Zhang, Y.; He, L. Optimized machine learning models for predicting crown convergence of plateau mountain tunnels. Transp. Geotech. 2024, 46, 101254. [Google Scholar] [CrossRef]
- Buehlmann, P.; Yu, B. Sparse boosting. J. Mach. Learn. Res. 2006, 7, 1001–1024. [Google Scholar]
- Liu, Q.; Jiang, Q.; Yu, Y.; Rong, Y.; Sun, Y.; Zhao, H. Extrusion 3D printing circular and horseshoe tunnel physical models: A comparative study of deformation and brittle failure. Theor. Appl. Fract. Mech. 2024, 129, 104229. [Google Scholar] [CrossRef]
- Zhang, C.Q.; Zhou, H.; Feng, X.T.; Huang, S.L. A new interpretation for the polyaxial strength effect of rock. Int. J. Rock Mech. Min. Sci. 2010, 47, 496–501. [Google Scholar] [CrossRef]
- Li, S.; Feng, Z.; Zeng, Z.; Xue, T.; Li, M.; Shen, M.; Yang, J.; Xiao, Y.; Pan, P. Reliability analysis on cavern stability and development of monitoring system for extremely deep underground laboratory. Sci. Sin. Phys. Mech. Astron. 2025, 55, 111019. [Google Scholar] [CrossRef]




| Excavation Step | 5 Monitoring Points on Multi-Point Displacement Meter | ||||
|---|---|---|---|---|---|
| d1(mm) | d2 (mm) | d3 (mm) | d4 (mm) | d5 (mm) | |
| 1 | 1.441 | 0.963 | 0.364 | 0.34 | 0.125 |
| 2 | 1.621 | 1.117 | 0.42 | 0.38 | 0.114 |
| 3 | 1.731 | 1.483 | 0.425 | 0.391 | 0.135 |
| 4 | 1.846 | 1.509 | 0.438 | 0.395 | 0.137 |
| 5 | 2.042 | 1.767 | 0.456 | 0.438 | 0.142 |
| 6 | 2.15 | 1.835 | 0.692 | 0.56 | 0.186 |
| 7 | 2.191 | 2.05 | 0.708 | 0.632 | 0.21 |
| 8 | 2.285 | 1.958 | 0.726 | 0.663 | 0.231 |
| 9 | 2.562 | 2.046 | 0.787 | 0.681 | 0.231 |
| 10 | 2.619 | 2.151 | 0.87 | 0.754 | 0.234 |
| 11 | 2.86 | 2.269 | 0.982 | 0.948 | 0.282 |
| 12 | 3.662 | 2.48 | 1.044 | 0.949 | 0.323 |
| 13 | 4.087 | 2.525 | 1.184 | 1.007 | 0.327 |
| 14 | 4.182 | 2.561 | 1.214 | 1.098 | 0.427 |
| 15 | 5.399 | 2.712 | 1.218 | 1.179 | 0.47 |
| 16 | 5.454 | 2.977 | 1.359 | 1.333 | 0.485 |
| 17 | 6.597 | 3.968 | 1.467 | 1.344 | 0.506 |
| 18 | 6.709 | 4.301 | 1.626 | 1.409 | 0.681 |
| 19 | 6.934 | 4.303 | 1.737 | 1.499 | 0.769 |
| 20 | 8.214 | 4.52 | 1.771 | 1.589 | 0.794 |
| 21 | 8.371 | 5.017 | 1.837 | 1.814 | 1.129 |
| 22 | 8.452 | 5.196 | 2.012 | 2.092 | 1.281 |
| 23 | 10.101 | 5.201 | 2.482 | 2.133 | 1.296 |
| 24 | 11.075 | 6.45 | 2.587 | 2.5 | 1.826 |
| 25 | 11.557 | 6.76 | 2.68 | 2.827 | 2.381 |
| 26 | 11.835 | 7.156 | 3.248 | 3.807 | 2.534 |
| 27 | 11.99 | 7.403 | 3.583 | 3.878 | 2.679 |
| 28 | 12.088 | 7.563 | 4.034 | 3.901 | 2.515 |
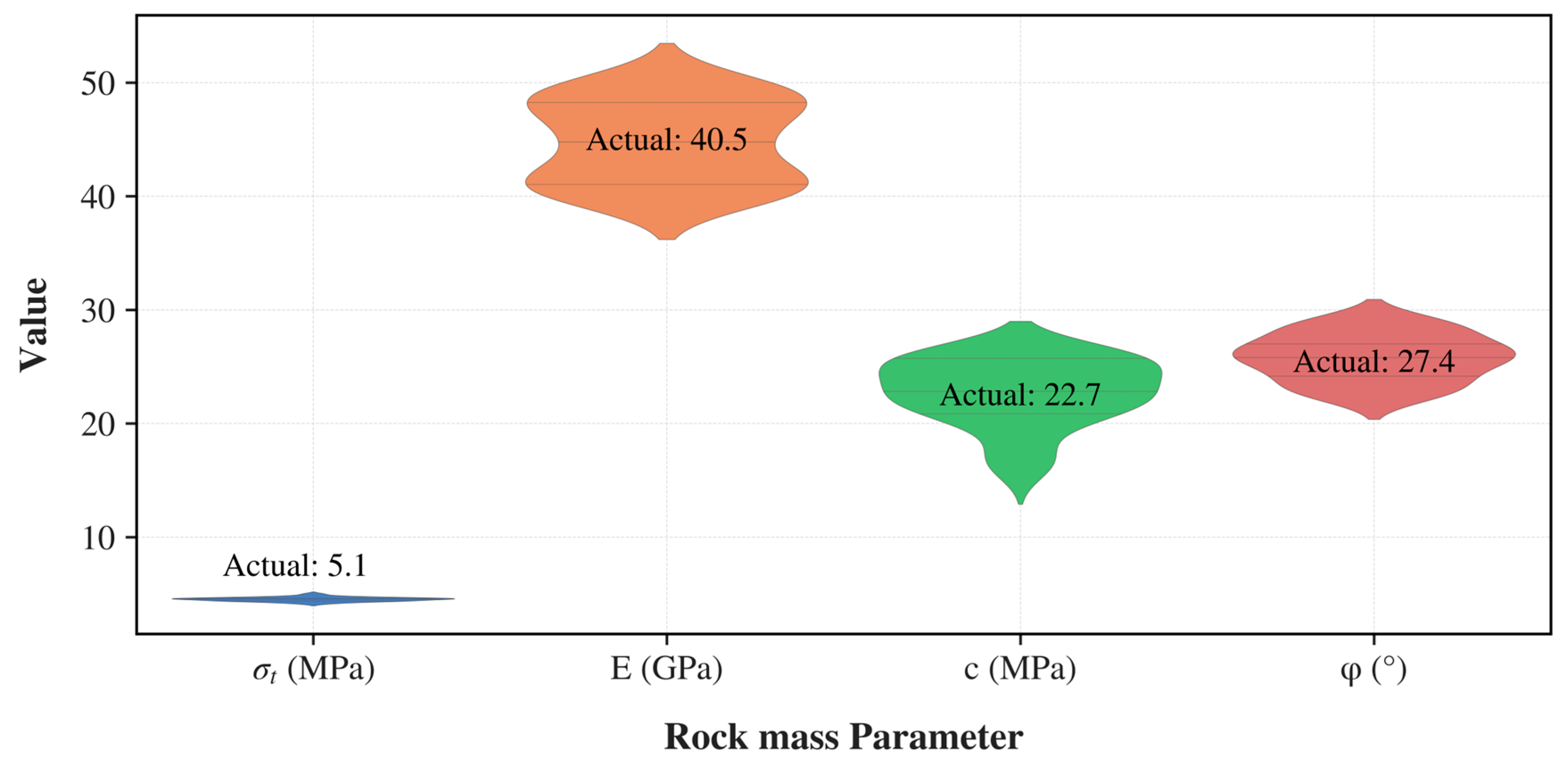
| Properties | Tensile Strength | Yong’s Modulus | Cohesion | Internal Friction |
|---|---|---|---|---|
| Value | 5.1 MPa | 40.5 | 22.7 | 27.4 |
| Properties | Tensile Strength | Yong’s Modulus | Cohesion | Internal Friction |
|---|---|---|---|---|
| Value | 4.75 MPa | 41.74 | 20.87 | 24.97 |
| Tensile Strength | Yong’s Modulus | Cohesion | Internal Friction | |
|---|---|---|---|---|
| Initial range | [3.5, 6.0] | [35, 50] | [15, 30] | [20, 30] |
| Range 1 | [3.125, 6.375] | [25, 55] | [11.25, 33.75] | [17.5, 32.5] |
| Range 2 | [2.75, 6.75] | [20, 60] | [7.5, 37.5] | [15, 35] |
| Range 3 | [2.375, 7.125] | [15, 65] | [3.75, 41.25] | [12.5, 37.5] |
| Range 4 | [2, 7.5] | [10, 70] | [0, 45] | [10, 40] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Z.; Li, S.; Zhao, H.; Shen, M.; Zheng, M.; Yang, J.; Xiao, Y.; Pan, P. AI-Enhanced Surrounding Rock Parameter Determination of Deeply Buried Underground Laboratory in Jinping, China. Buildings 2025, 15, 3187. https://doi.org/10.3390/buildings15173187
Feng Z, Li S, Zhao H, Shen M, Zheng M, Yang J, Xiao Y, Pan P. AI-Enhanced Surrounding Rock Parameter Determination of Deeply Buried Underground Laboratory in Jinping, China. Buildings. 2025; 15(17):3187. https://doi.org/10.3390/buildings15173187
Chicago/Turabian StyleFeng, Zejie, Shaojun Li, Hongbo Zhao, Manbin Shen, Minzong Zheng, Jinzhong Yang, Yaxun Xiao, and Pengzhi Pan. 2025. "AI-Enhanced Surrounding Rock Parameter Determination of Deeply Buried Underground Laboratory in Jinping, China" Buildings 15, no. 17: 3187. https://doi.org/10.3390/buildings15173187
APA StyleFeng, Z., Li, S., Zhao, H., Shen, M., Zheng, M., Yang, J., Xiao, Y., & Pan, P. (2025). AI-Enhanced Surrounding Rock Parameter Determination of Deeply Buried Underground Laboratory in Jinping, China. Buildings, 15(17), 3187. https://doi.org/10.3390/buildings15173187








