Experimental Study on Seismic Performance of Steel-Reinforced Concrete Columns Under Different Loading Protocols
Abstract
1. Introduction
2. Overview of the Experiment
2.1. Specimen Design
2.2. Loading Device and Loading Protocol
- (1)
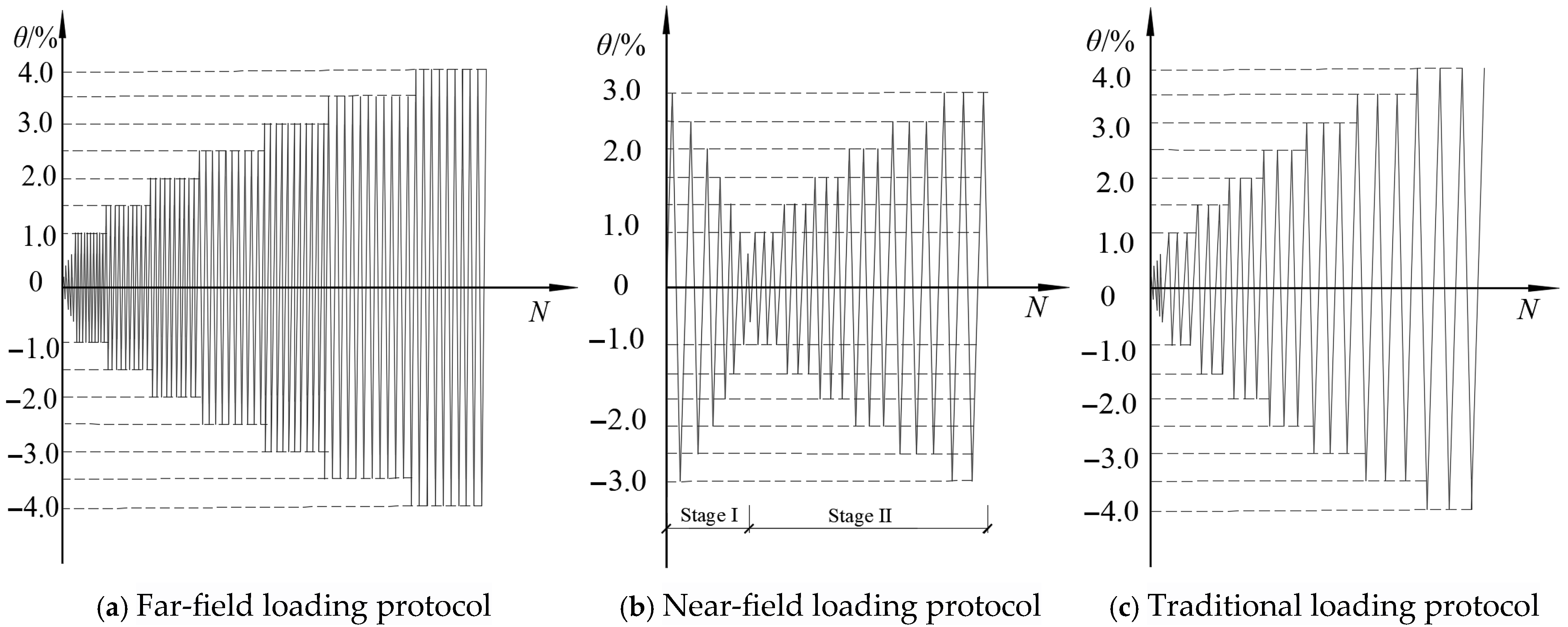
- Far-field loading protocol: Horizontal displacement was cycled 10 times per level after yielding, as shown in Figure 3a. The horizontal displacement shall be incrementally applied based on the column-top horizontal displacement angles θ of 0.09%, 0.18%, 0.23%, 0.3%, 0.36%, 0.45%, 0.6%, 0.73%, and 0.9%, with each displacement level being cycled once. Subsequently, the horizontal displacement was incrementally applied based on θ values of 1.0%, 1.5%, 2.0%, 2.5%, 3.0%, 3.5%, and 4.0%, with ten cycles conducted at each displacement level. The test was terminated when the applied load diminished to less than 85% of the peak load.
- (2)
- Near-field loading protocol: The loading process was divided into two stages, as shown in Figure 3b. In the first stage, the loading displacement was initially applied to the ultimate horizontal displacement ∆u (obtained through traditional loading tests on corresponding specimens), and then the loading displacement was gradually reduced by 5 mm per level until the horizontal displacement decreased to 5 mm, with each level of displacement cycled once, to reveal the impact of near-field ground motions (a strong displacement impulse followed by rapid displacement decay) on the seismic performance of SRC columns. In the second stage, the loading displacement was gradually increased. For specimens SRC5 and SRC6, the horizontal displacements were applied step by step according to the column-top horizontal displacement angles θ = 1.0%, 1.5%, 2.0%, 2.5%, …, with each level of displacement cycled 3 times, to reveal the capacity of already damaged SRC columns to resist subsequent seismic actions. The test was stopped when the applied load started to decrease compared to the load corresponding to the previous level of displacement.
- (3)
- Traditional loading protocol: The horizontal displacements per loading level were the same as those in the “far-field loading protocol”, but after yielding, the horizontal displacements per level were cycled 3 times, as shown in Figure 3c.
3. Failure Process
3.1. Failure Process Description of Specimens
- (1)
- Far-field Loading Specimens (SRC1~SRC2)
- (2)
- Near-field Loading Specimens (SRC3~SRC6)
- (3)
- Traditional Loading Specimens (SRC7~SRC8)
3.2. Influence of Loading Protocol on the Failure Process of Specimens
- (1)
- After the specimen is loaded to the peak load, when cyclically loaded with the same displacement angle, the crack width of the far-field loading specimen increases, and the degree of damage worsens. For example, when the displacement angle is 2.5%, the maximum width of the horizontal cracks in SRC7 is 1.0 mm, while that of SRC1 reaches 2.0 mm.
- (2)
- The displacement angle corresponding to the same failure characteristics decreases for the far-field loading specimen. For example, when the displacement angle of SRC7 is 3%, a large area of spalling appears on the surface of the concrete protective layer, while the displacement angle of the SRC1 specimen is 2.5%; at ultimate failure, the limit displacement angle of SRC7 is 3.5%, while that of SRC1 is 3.0%.
4. Results and Discussion
4.1. Hysteresis Curves
- (1)
- Before reaching the peak load, when loaded with the same displacement, both the far-field loading specimens and the traditional loading specimens exhibit a relatively small reduction in bearing capacity and minimal changes in stiffness. After the peak load, compared to the traditional loading specimens, as the number of cycles at the same displacement level increases, the hysteresis curves of the far-field loading specimens undergo significant changes, the bearing capacity decreases more pronouncedly, stiffness degradation increases markedly, and deformation capacity diminishes, indicating that the cumulative damage to the far-field loading specimens is more severe under the influence of large displacements with multiple cyclic loading.
- (2)
- The near-field loading specimens enter the elastic–plastic descending phase after reaching the peak load during initial loading, with a gradual reduction in bearing capacity and significant residual deformation after unloading, and the hysteresis curves are full. As the loading displacement gradually reduces, the area of the hysteresis loops of the specimens continuously decreases, and the bearing capacity gradually declines. It is also observed that during the second stage, when the loading displacement gradually increases, the hysteresis curves of the specimens before the peak load closely coincide with those of the first stage at the same loading displacement. Subsequently, as the loading displacement increases, the bearing capacity of the specimens decreases, the residual deformation increases significantly, and the damage to the specimens progresses rapidly.
- (3)
- Compared to the far-field loading specimens and the traditional loading specimens, the hysteresis curves of the near-field loading specimens are fuller, indicating stronger energy dissipation capacity. However, due to the damage caused by the initial ultimate displacement, when the loading displacement reduces step by step, the bearing capacity and stiffness of the near-field loading specimens are almost always lower than those of the other specimens with the same loading displacement.
4.2. Bearing Capacity
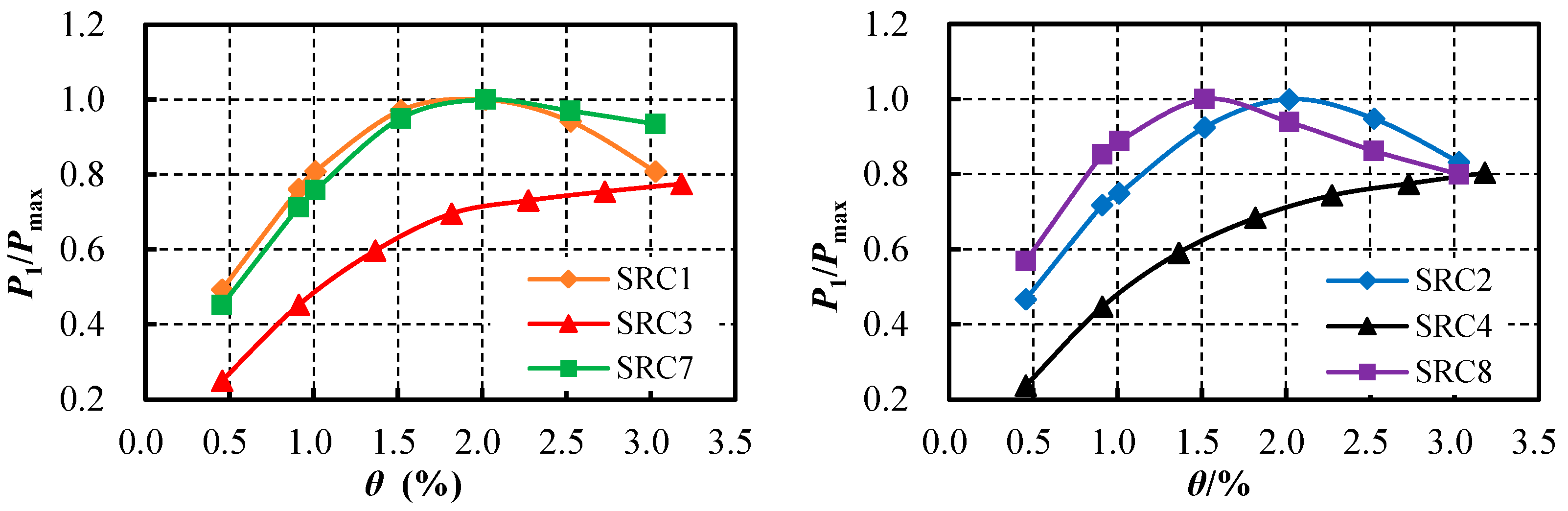
4.2.1. Comparative Analysis of Peak Load
4.2.2. Effect of Far-Field Loading on Bearing Capacity
- (1)
- At the same displacement angle, the P10/P1 of the far-field loading specimens are all smaller than the P3/P1 of the traditional loading specimens under the same conditions, indicating that multiple cycles of the same displacement cause more severe damage to the far-field loaded specimens and a greater reduction in bearing capacity. The bearing capacity indicators measured through three cycles of traditional loading tests are significantly overestimated.
- (2)
- The influence of the number of cycles at the same displacement on the bearing capacity of far-field loading specimens increases with higher displacement amplitudes. Prior to reaching the peak load, the cumulative damage from small displacement cyclic loading is minimal, resulting in only a slight decrease in bearing capacity. For instance, in specimen SRC1, when the displacement angle is below 2.0%, the ratio P10/P1 ranges from 0.924 to 0.95, which is slightly lower than P3/P1, indicating a minor reduction in bearing capacity. Post-peak load, as the number of displacement cycles increases, the reduction in bearing capacity becomes more pronounced. For example, in specimen SRC1, when the displacement angle reaches 2.5%, the ratio P3/P1 is 0.962, showing a reduction of no more than 4.0%. However, after the 10th cycle, the bearing capacity drops by 11.5%, demonstrating that multiple large displacement cycles after the peak load lead to rapid damage progression and significantly diminish the bearing capacity of the specimens.
4.2.3. Effect of Near-Field Loading on Bearing Capacity
- (1)
- Effect of the First Stage of Near-Field Loading on the Bearing Capacity
- (2)
- Effect of the Second Stage of Near-Field Loading on the Bearing Capacity
4.3. Deformation Capacity
4.3.1. Comparative Analysis of Deformation Capacity
4.3.2. Effect of the Second Stage of Near-Field Loading on the Deformation Capacity
4.4. Stiffness Degradation
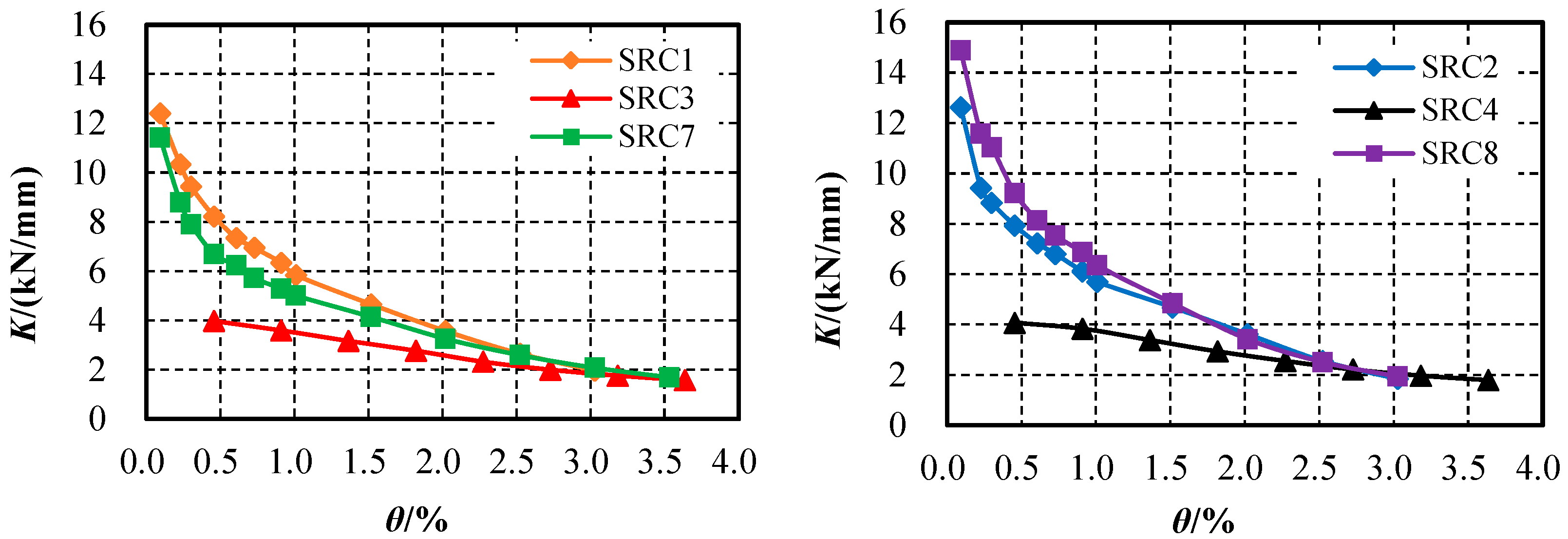
4.4.1. Comparative Analysis of Secant Stiffness
- (1)
- The stiffness of far-field loading specimens and traditional loading specimens initially decreases rapidly and then slows down as the displacement angle increases. When the displacement angle is less than 1.0%, the stiffness degradation rates of far-field loading specimens and traditional loading specimens are basically the same; when the displacement angle is greater than 1.5%, the stiffness degradation of far-field loading specimens is faster than that of traditional loading specimens. This is because, as the loading displacement increases, especially after the peak load, the material property degradation and plastic damage to far-field loading specimens become more severe due to the multiple cyclic loading at the same displacement level.
- (2)
- Near-field loading specimens suffer significant damage after the initial ultimate loading displacement, resulting in low stiffness. Thereafter, as the loading displacement decreases, the stiffness of the specimens increases slowly. When the displacement angle is greater than 2.5%, all specimens, regardless of the loading protocol, have suffered severe damage, with low stiffness and little difference among them. When the displacement angle is less than 2.5%, the stiffness of near-field loading specimens is lower than that of far-field loading specimens and traditional loading specimens at the same loading displacement, and the smaller the loading displacement, the greater the difference in stiffness. For example, at a displacement angle of 2.0%, the stiffness of near-field loading specimens is approximately 0.74 to 0.81 times that of the other specimens, and at a displacement angle of 0.9%, the stiffness of near-field loading specimens is approximately 0.56 to 0.68 times that of the other specimens.
4.4.2. Effect of Far-Field Loading on Stiffness
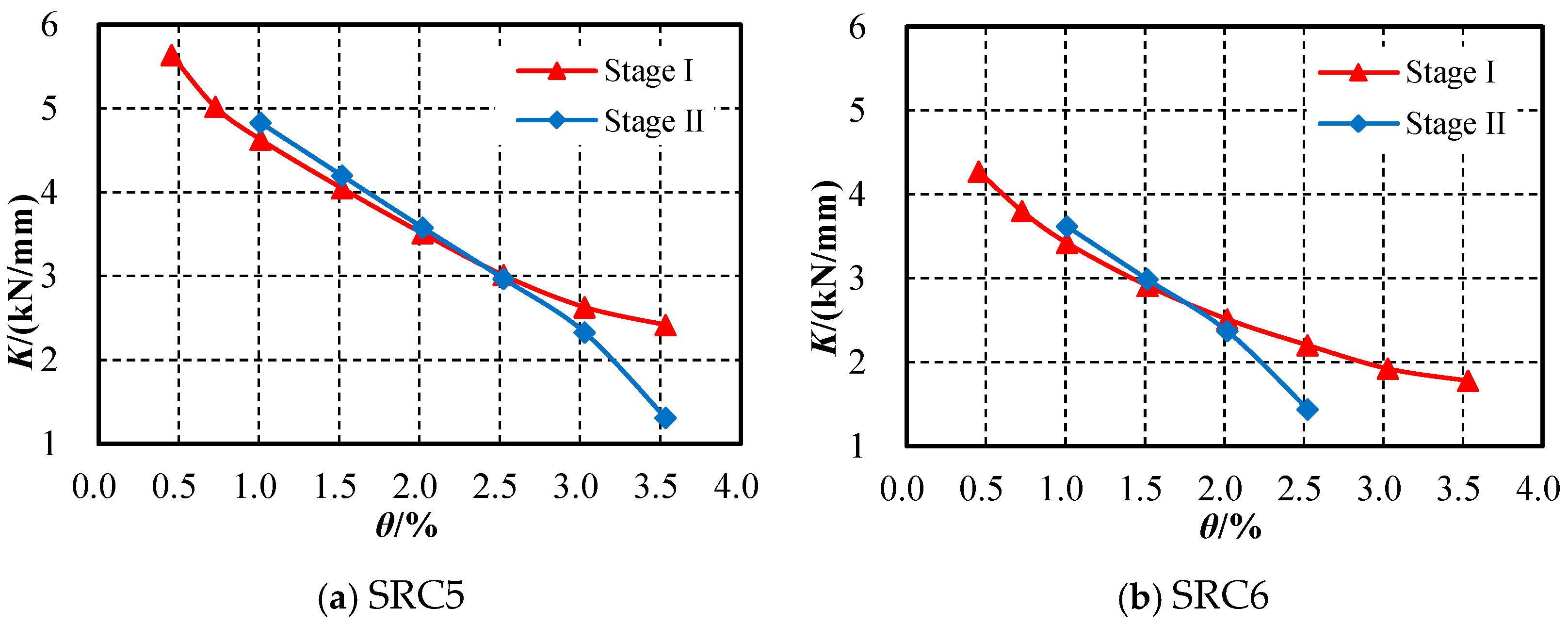
4.4.3. Effect of Second-Stage Near-Field Loading on Stiffness
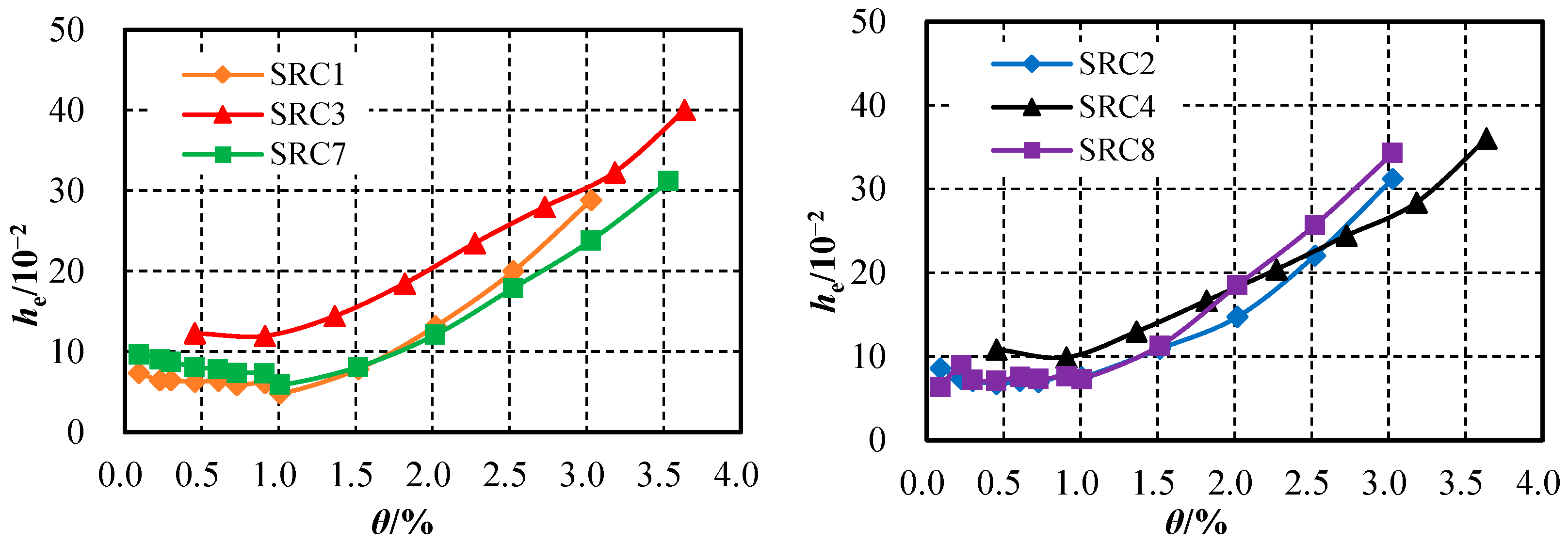
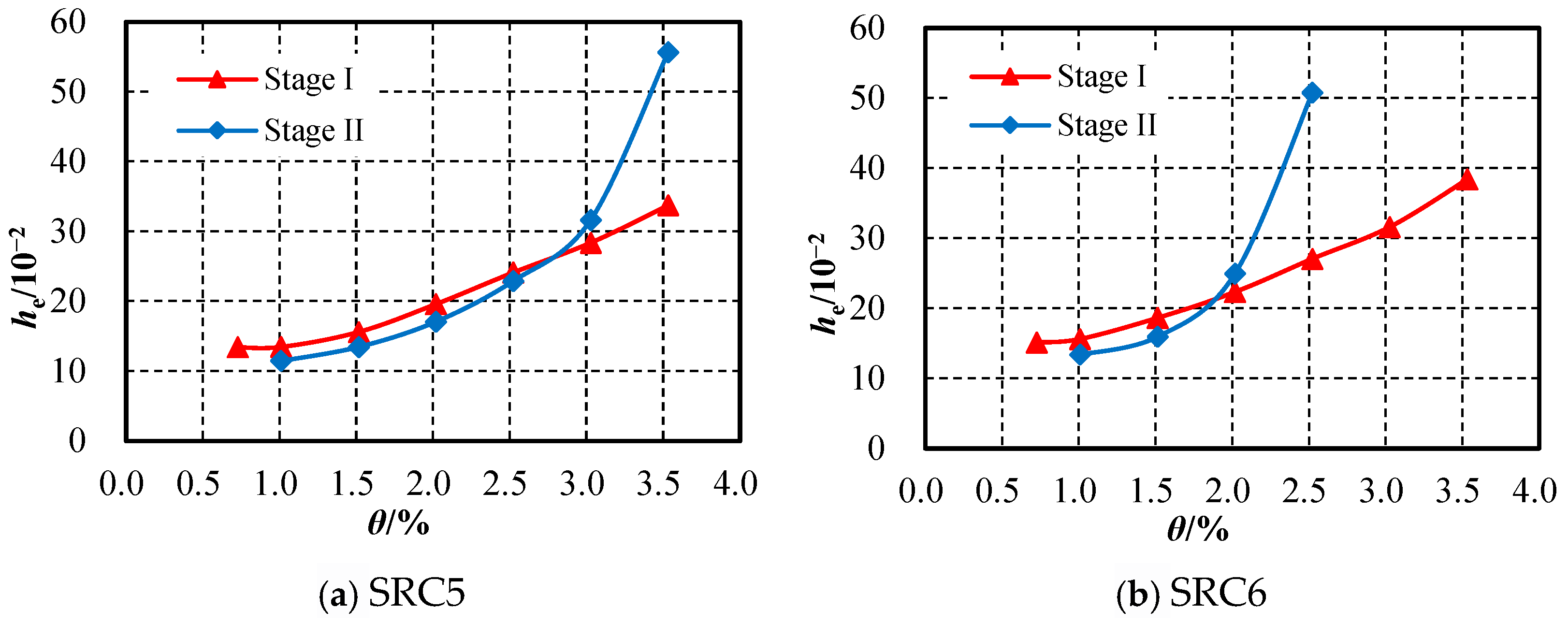
4.5. Energy Dissipation Capacity
4.5.1. Comparative Analysis of Energy Dissipation Capacity
- (1)
- When the displacement angle is less than 1.0%, the specimens have not yielded yet, and he fluctuates slightly with the increase in the displacement angle but generally remains stable. When the displacement angle is greater than 1.0%, as the displacement angle increases, the he of the specimens gradually increases, indicating that the energy dissipation capacity of the specimens continues to increase with the deepening of damage.
- (2)
- Before the peak load, the he of the far-field loading specimens is relatively close to that of the traditional loading specimens, showing basically similar energy dissipation capacities. In the failure stage, the heu of the far-field loading specimens SRC1 and SRC2 are reduced by 14.3% and 9.3%, respectively, compared to the traditional loading specimens SRC7 and SRC8, indicating that the cumulative damage caused by multiple large displacement cyclic loading reduces the ultimate energy dissipation capacity of the far-field loading specimens. The near-field loading specimens directly experience ultimate displacement in a single cycle, and their ultimate energy dissipation capacity is significantly greater than that of the far-field loading specimens and traditional loading specimens. The calculations show that the heu of the near-field loading specimens is approximately 1.54 to 1.68 times that of the far-field loading specimens and approximately 1.33 to 1.44 times that of the traditional loading specimens.
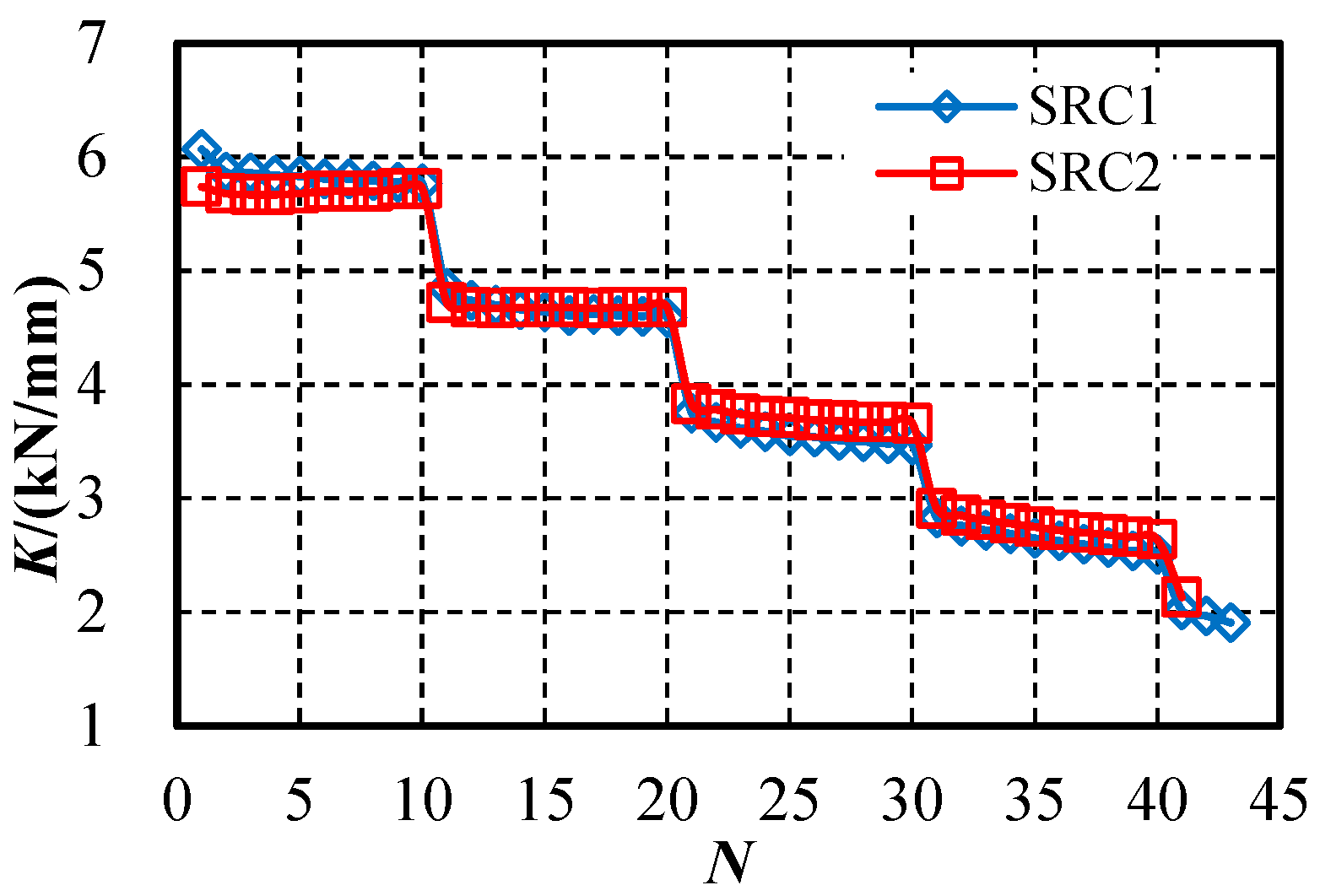
4.5.2. Influence of Far-Field Loading on Energy Dissipation Capacity
- (1)
- Before reaching the peak load (with loading cycles N ranging from 0 to 30), the equivalent viscous damping coefficient (he) of the specimen remains essentially unchanged as the number of cycles N increases under the same loading level. It indicates that multiple cycles of small displacement do not cause sustained damage to the specimen and have no significant impact on its energy dissipation performance.
- (2)
- After the peak load (when N exceeds 30), the equivalent viscous damping coefficient he of the specimen exhibits a notable increasing trend with the rise in displacement amplitude and the number of cycles for the same-level loading. For example, for the specimen SRC1, during multiple cyclic loading with a displacement angle of 2.5%, the value of he for the specimen increased by 4.3% in the 3rd cycle, and by 12.7% in the 10th cycle. For the SRC2 specimens, the increases were 6.5% and 18.1%, respectively. When the displacement angle exceeds 3.0%, it can be observed that the N-he relationship curve of the specimen rapidly shifts upwards, the coefficient he expands rapidly, and the energy dissipation capacity of the specimen is significantly enhanced. It indicates that large-displacement cyclic loading will continuously exacerbate the damage to the specimen. At this point, the internal steel section of the specimen can effectively restrain the core concrete, facilitating the full utilization of the specimen’s energy dissipation capacity.
4.5.3. Influence of Second-Stage Near-Field Loading on Energy Dissipation Capacity
5. Conclusions
- (1)
- Compared to the traditional loading protocol, when loaded at the same displacement, components subjected to far-field loading exhibit larger cracks and increased damage, with a smaller corresponding displacement angle required to reach the same level of failure. The rate of bearing capacity decline accelerates. Therefore, in the case of far-field earthquake action, it is necessary to focus on monitoring the displacement of the structure.
- (2)
- Under the far-field loading protocol, before reaching the peak load, repeated small-displacement cyclic loading does not cause significant damage to the component and has minimal impact on its bearing capacity, stiffness, and energy dissipation capacity. At this stage, the steel-reinforced concrete column still exhibits a certain degree of elasticity. However, after the peak load, the component shows evident damage, with the hysteresis curve becoming less full and stiffness deteriorating significantly.
- (3)
- For near-field loading specimens, due to the large damage caused by the initial ultimate loading displacement, the bearing capacity and stiffness of the specimens during step-wise decreasing loading displacement are lower than those of far-field loading specimens and traditional loading specimens under the same loading displacement. During the second loading stage, before the peak load, the bearing capacity, stiffness, and energy dissipation capacity of the specimens are similar to those during the first loading stage at the same displacement. However, the peak load of the specimens decreases, and after the peak load, the stiffness and deformation capacity of the specimens are significantly lower than those during the first loading stage at the same displacement, greatly reducing their ability to resist subsequent seismic actions.
- (4)
- The loading protocol has a minimal impact on the load-bearing capacity (peak load) of components.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, L.; Hu, J.; Xie, L. On characteristics of ground motion parameters for special long period ground motions. J. Earthq. Eng. Eng. Vib. 2008, 28, 20–27. [Google Scholar]
- Takewaki, I.; Murakami, S.; Fujita, K.; Yoshitomi, S.; Tsuji, M. The 2011 off the Pacific coast of Tohoku earthquake and response of high-rise buildings under long-period ground motions. Soil Dyn. Earthq. Eng. 2011, 31, 1511–1528. [Google Scholar] [CrossRef]
- Chung, Y.; Nagae, A.T.; Hitaka, T.; Nakashima, M. Seismic resistance capacity of high-rise buildings subjected to long-period ground motions: E-Defense shaking table test. J. Struct. Eng. ASCE 2010, 136, 637–644. [Google Scholar] [CrossRef]
- Ji, X.; Fenves, G.L.; Kajiwara, K.; Nakashima, M. Seismic damage detection of a full-scale shaking table test structure. J. Struct. Eng. ASCE 2011, 137, 14–21. [Google Scholar] [CrossRef]
- Liu, Y. Experimental Study on the Seismic Performance of Frame Columns Under Near-Field Earthquakes. Master’s Thesis, Hunan University, Changsha, China, 2010. [Google Scholar]
- Yan, X.; Qi, A.; Mao, H.; Zhang, C. Shaking table test of mega-sub isolated structure under near-field earthquake action. Eng. Mech. 2017, 34, 109–115+144. [Google Scholar]
- Chayut, N.; Sakdirat, K.; Charalampos, B. Far-Field Earthquake Responses of Overhead Line Equipment (OHLE) Structure Considering Soil-Structure Interaction. Front. Built Environ. 2018, 4, 35. [Google Scholar]
- Ren, Q.; Kou, Y.; Xu, Y.; Wei, K. Dynamic stability and collapse analysis of wind tur-bine under near-field ground motion. Structures 2025, 74, 108534. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, W.; Shi, Y.; Li, M.; Wang, S.; Bao, L.; Tian, Y. Experimental and numerical study on seismic behavior of partially steel-reinforced concrete beam-to-steel tube column joint. J. Build. Eng. 2023, 76, 107210. [Google Scholar] [CrossRef]
- Tao, Z.; Wang, Z.; Yu, Q. Finite element modelling of concrete-filled steel stub columns under axial compression. J. Constr. Steel Res. 2013, 89, 121–131. [Google Scholar] [CrossRef]
- Hemanth, B.; Kumar, C.D.J.; Arunakanthi, E. Analysis of dry and wet connections in precast beam-column joint using ABAQUS software. Mater. Today Proc. 2020, 33, 287–295. [Google Scholar]
- Aninthaneni, K.P.; Dhakal, P.R. Analytical and numerical investigation of “dry” jointed precast concrete frame sub-assemblies with steel angle and tube connections. Bull. Earthq. Eng. 2019, 17, 4961–4985. [Google Scholar] [CrossRef]
- Parastesh, H.; Hajirasouliha, I.; Ramezani, R. A new ductile moment-resisting connection for precast concrete frames in seismic regions: An experimental investigation. Eng. Struct. 2014, 70, 144–157. [Google Scholar] [CrossRef]
- Zhu, W.Q.; Meng, G.; Jia, J.Q. Experimental studies on axial load performance of high-strength concrete short columns. Proc. ICE Struct. Build. 2014, 167, 509–519. [Google Scholar] [CrossRef]
- Shi, J.; Bai, G. Restoring force characteristics of hollow steel reinforced concrete frame columns. J. Xi’an Highw. Univ. 2000, 20, 94–97. [Google Scholar]
- Acun, B.; Sucuoğu, H. The effect of displacement history on the performance of concrete columns in flexure. In Advance in Performance-Based Earthquake Engineering, Geotechnical, Eeological, and Earthquake Engineering; Springer: Berlin/Heidelberg, Germany, 2010; Volume 13, pp. 373–382. [Google Scholar]
- Pujol, S.; Sozen, M.A.; Ramirez, J.A. Displacement history effects on drift capacity of reinforced concrete columns. ACI Struct. J. 2006, 103, 253–262. [Google Scholar] [CrossRef] [PubMed]
- Ji, X.; Zhang, M.; Liu, P.; Kang, H.Z.; Qian, J.R.; Zhou, Z.Z.; Hu, H.S. Experimental study on cumulative damage performance of steel-concrete composite columns. J. Build. Struct. 2013, 34, 35–44. [Google Scholar]
- Qian, J.; Li, N.; Ji, X.; Zhao, Z. Experimental study on cumulative damage performance of composite steel tube high-strength concrete columns. J. Civ. Eng. 2014, 47, 30–40. [Google Scholar]
- Zhu, J.; Gong, J.; Xiong, L.; Qiu, J.; Li, X. Experimental study on seismic performance of RC bridge piers under different cycles. J. Southeast Univ. Nat. Sci. Ed. 2019, 49, 652–663. [Google Scholar]
- Qian, J.; Feng, B. Experimental Study on Seismic Performance of Reinforced Concrete Columns with Different Seismic Grades. J. Build. Struct. 2014, 35, 105–114. [Google Scholar]
- Liu, L.; Yi, W.; Xie, C. Displacement performance and simulation of flexural-shear critical square columns under near-fault earthquakes. J. Earthq. Eng. Eng. Vib. 2015, 35, 85–93. [Google Scholar]
- Yi, W.J.; Zhou, Y.; Liu, Y.; Liu, L. Experimental investigation of circular reinforced concrete columns under different loading histories. J. Earthq. Eng. 2016, 20, 654–675. [Google Scholar] [CrossRef]
- Luo, Y. Seismic Performance of Reinforced Concrete Shear Wall Under Near-Field Earthquake. Master’s Thesis, Hunan University, Changsha, China, 2011. [Google Scholar]
- JGJ138-2016; China Academy of Building Research, Code for Design of Composite Structures. China Architecture & Building Press: Beijing, China, 2016.
- Jiang, L.J.; Bai, G.L. Experimental Study on Cumulative Damage Behavior of Steel-Reinforced Concrete Columns. Adv. Civ. Eng. 2020, 2020, 5281725. [Google Scholar] [CrossRef]
- JGJ/T101-2015; China Academy of Building Research, Specification for Seismic Test of Buildings. China Architecture & Building Press: Beijing, China, 2015.
- Chen, Z.; Liu, X. Experimental Study on Seismic Performance of Transversely Ribbed Corrugated Steel Plate–Steel Pipe Concrete Shear Wall. Buildings 2024, 14, 2708. [Google Scholar] [CrossRef]
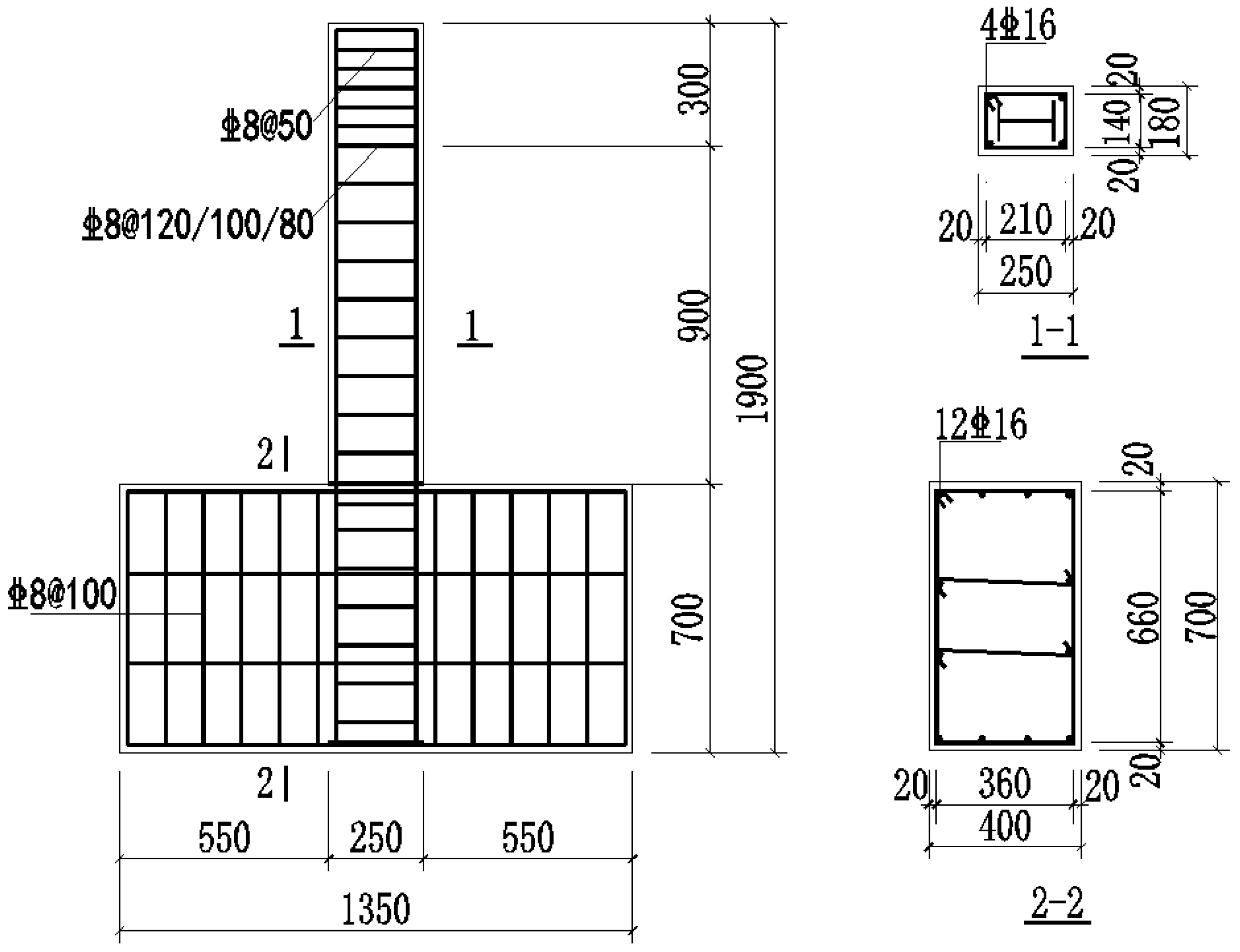
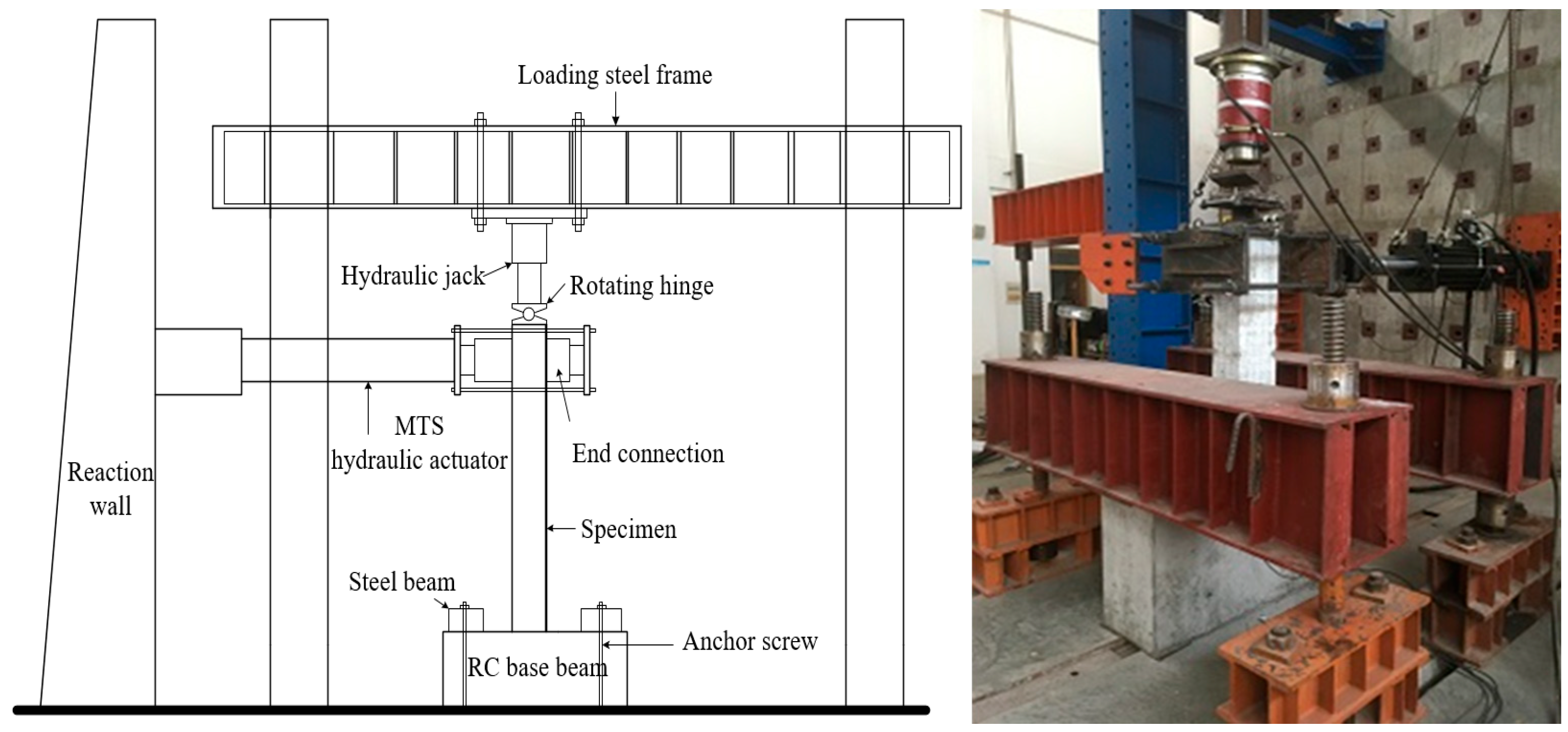





| Specimen | Steel Section | Steel Ratio | Stirrup | Stirrup Ratio | Designed Axial Compression Ratio | Loading Protocol |
|---|---|---|---|---|---|---|
| SRC1 | I14 | 4.8% | C8@100 | 1.2% | 0.3 | far-field loading protocol |
| SRC2 | I14 | 4.8% | C8@80 | 1.5% | ||
| SRC3 | I14 | 4.8% | C8@100 | 1.2% | 0.3 | near-field loading protocol |
| SRC4 | I14 | 4.8% | C8@80 | 1.5% | ||
| SRC5 | I16 | 5.8% | C8@100 | 1.2% | ||
| SRC6 | I14 | 4.8% | C8@120 | 1.0% | ||
| SRC7 | I14 | 4.8% | C8@100 | 1.2% | 0.3 | traditional loading protocol |
| SRC8 | I14 | 4.8% | C8@80 | 1.5% |
| Specimen | θmax | Pmax (kN) | Specimen | θmax | Pmax (kN) |
|---|---|---|---|---|---|
| SRC1 | 2.0% | 82.3 | SRC2 | 2.0% | 85.0 |
| SRC3 | 1.8% | 80.4 | SRC4 | 1.8% | 85.8 |
| SRC5 | 2.6% | 101.7 | SRC6 | 1.9% | 81.0 |
| SRC7 | 2.0% | 75.2 | SRC8 | 1.5% | 82.5 |
| Specimen | Displacement Angle | P3/P1 | P10/P1 | Specimen | Displacement Angle | P3/P1 | P10/P1 |
|---|---|---|---|---|---|---|---|
| SRC1 [26] | 1.0% | 0.964 | 0.950 | SRC2 [26] | 1.0% | 0.989 | 0.997 |
| 1.5% | 0.967 | 0.945 | 1.5% | 0.990 | 0.991 | ||
| 2.0% | 0.965 | 0.924 | 2.0% | 0.977 | 0.956 | ||
| 2.5% | 0.962 | 0.885 | 2.5% | 0.968 | 0.907 | ||
| 3.0% | 0.944 | — | 3.0% | — | — | ||
| SRC7 [26] | 1.0% | 0.981 | — | SRC8 | 1.0% | 0.973 | — |
| 1.5% | 0.964 | — | 1.5% | 0.955 | — | ||
| 2.0% | 0.954 | — | 2.0% | 0.950 | — | ||
| 2.5% | 0.951 | — | 2.5% | 0.967 | — | ||
| 3.0% | 0.962 | — | 3.0% | — | — | ||
| 3.5% | 0.948 | — |
| Specimen | Loading Direction | ∆y/mm | θy | ∆u/mm | θu | μ | μa |
|---|---|---|---|---|---|---|---|
| SRC1 | Positive | 12.92 | 1.15% | 30.45 | 2.90% | 2.36 | 2.52 |
| Negative | −12.39 | −33.30 | 2.69 | ||||
| SRC3 | Positive | 11.97 | 1.07% | 34.53 | 3.27% | 2.88 | 3.06 |
| Negative | −11.57 | −37.39 | 3.23 | ||||
| SRC7 | Positive | 13.76 | 1.26% | 38.90 | 3.54% | 2.83 | 2.81 |
| Negative | −13.97 | −38.90 | 2.78 | ||||
| SRC2 | Positive | 11.43 | 1.09% | 30.42 | 2.90% | 2.66 | 2.67 |
| Negative | −12.44 | −33.30 | 2.68 | ||||
| SRC4 | Positive | 12.47 | 1.16% | 38.24 | 3.56% | 3.07 | 3.08 |
| Negative | −13.00 | −40.00 | 3.08 | ||||
| SRC8 | Positive | 10.76 | 0.94% | 26.36 | 2.71% | 2.45 | 2.90 |
| Negative | −9.93 | −33.30 | 3.35 |
| Specimen | Loading Stage | θy | θu | μ |
|---|---|---|---|---|
| SRC5 | 1 | 1.14% | 3.53% | 3.12 |
| 2 | 1.75% | 3.21% | 1.86 | |
| SRC6 | 1 | 1.13% | 3.43% | 3.03 |
| 2 | 1.48% | 2.32% | 1.57 |
| Specimen | SRC1 | SRC2 | SRC3 | SRC4 | SRC5 | SRC6 | SRC7 | SRC8 |
|---|---|---|---|---|---|---|---|---|
| heu | 0.239 | 0.261 | 0.401 | 0.375 | 0.350 | 0.384 | 0.279 | 0.281 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, Y.; Jiang, L.; Yuan, G.; Guo, L.; Zhou, Q.; Zhu, F. Experimental Study on Seismic Performance of Steel-Reinforced Concrete Columns Under Different Loading Protocols. Buildings 2025, 15, 3180. https://doi.org/10.3390/buildings15173180
Shi Y, Jiang L, Yuan G, Guo L, Zhou Q, Zhu F. Experimental Study on Seismic Performance of Steel-Reinforced Concrete Columns Under Different Loading Protocols. Buildings. 2025; 15(17):3180. https://doi.org/10.3390/buildings15173180
Chicago/Turabian StyleShi, Yun, Lianjie Jiang, Guanglin Yuan, Lu Guo, Qingsong Zhou, and Fangzhi Zhu. 2025. "Experimental Study on Seismic Performance of Steel-Reinforced Concrete Columns Under Different Loading Protocols" Buildings 15, no. 17: 3180. https://doi.org/10.3390/buildings15173180
APA StyleShi, Y., Jiang, L., Yuan, G., Guo, L., Zhou, Q., & Zhu, F. (2025). Experimental Study on Seismic Performance of Steel-Reinforced Concrete Columns Under Different Loading Protocols. Buildings, 15(17), 3180. https://doi.org/10.3390/buildings15173180






