Prediction of Skeleton Curves for Seismically Damaged RC Columns Based on a Data-Driven Machine-Learning Approach
Abstract
1. Introduction
2. Seismic Damaged RC Column Database
2.1. Characteristic Parameters of Columns
2.2. Ground Motion Parameters
3. ML-Based Approach for Skeleton Curves of Seismically Damaged RC Columns
3.1. Input Parameters
3.2. Output Parameters
3.3. Data Preprocessing
3.4. Data Partition
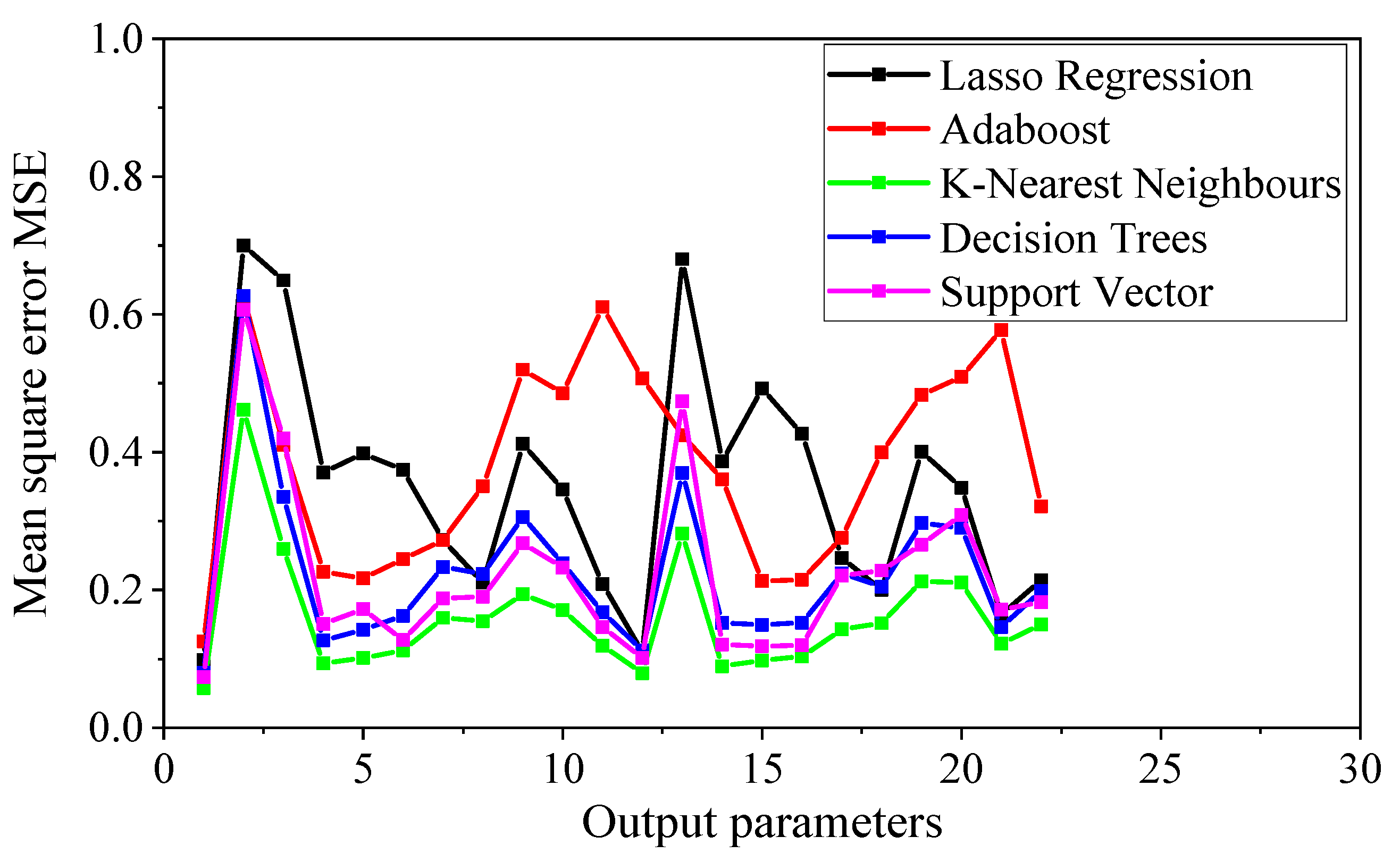
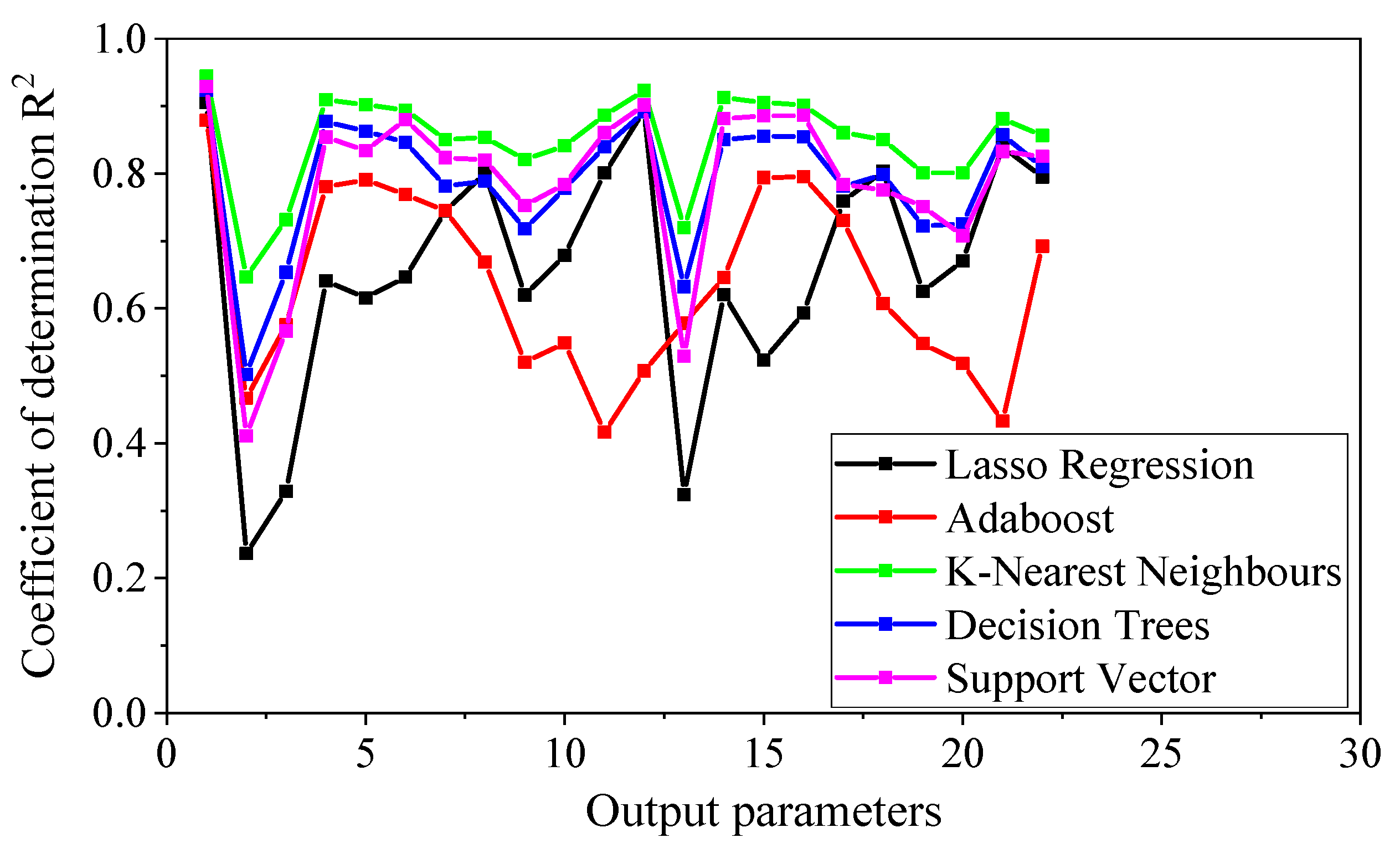
3.5. Model Error Evaluation
- (1)
- Mean squared error (MSE):
- (2)
- Coefficient of determination R-Squared (R2), i.e., the square of the correlation coefficient:
3.6. Machine Learning Algorithms
4. Prediction Results and Analysis
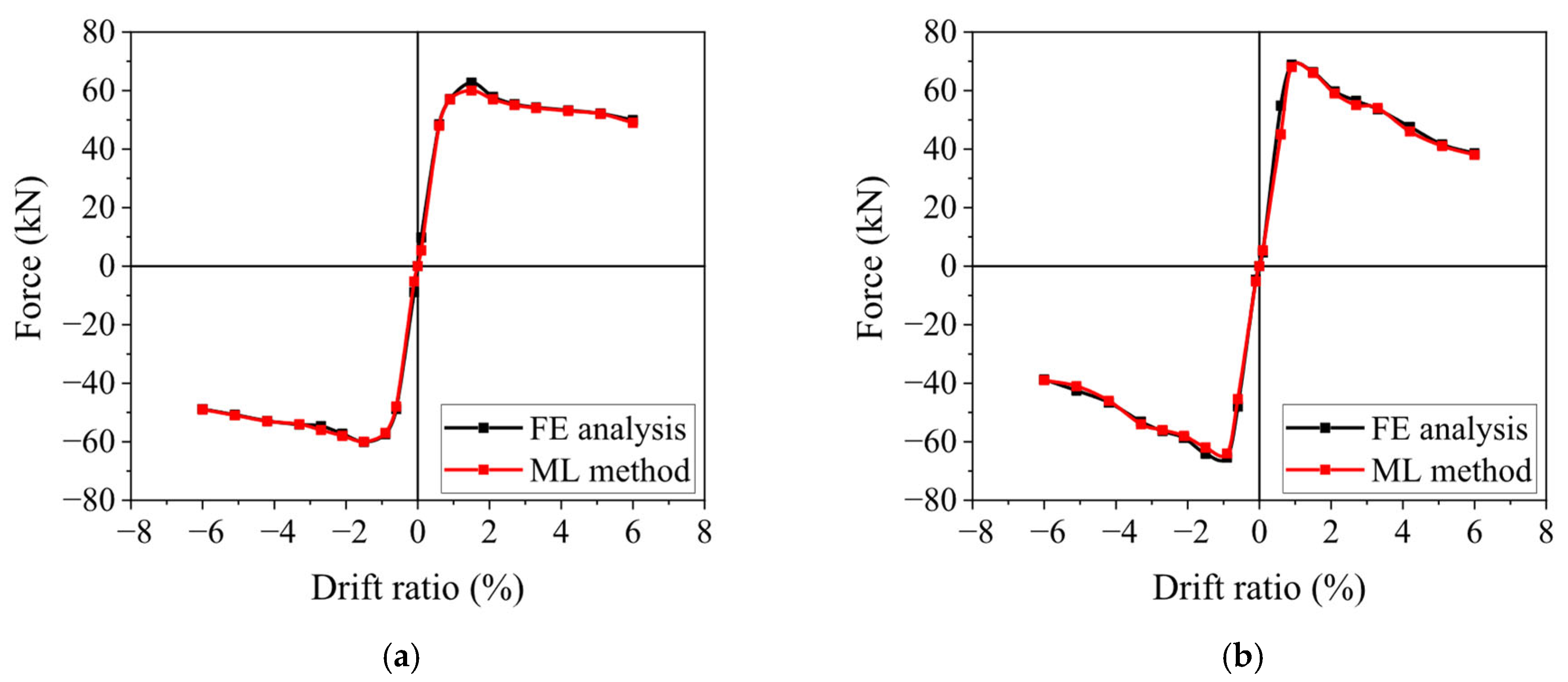
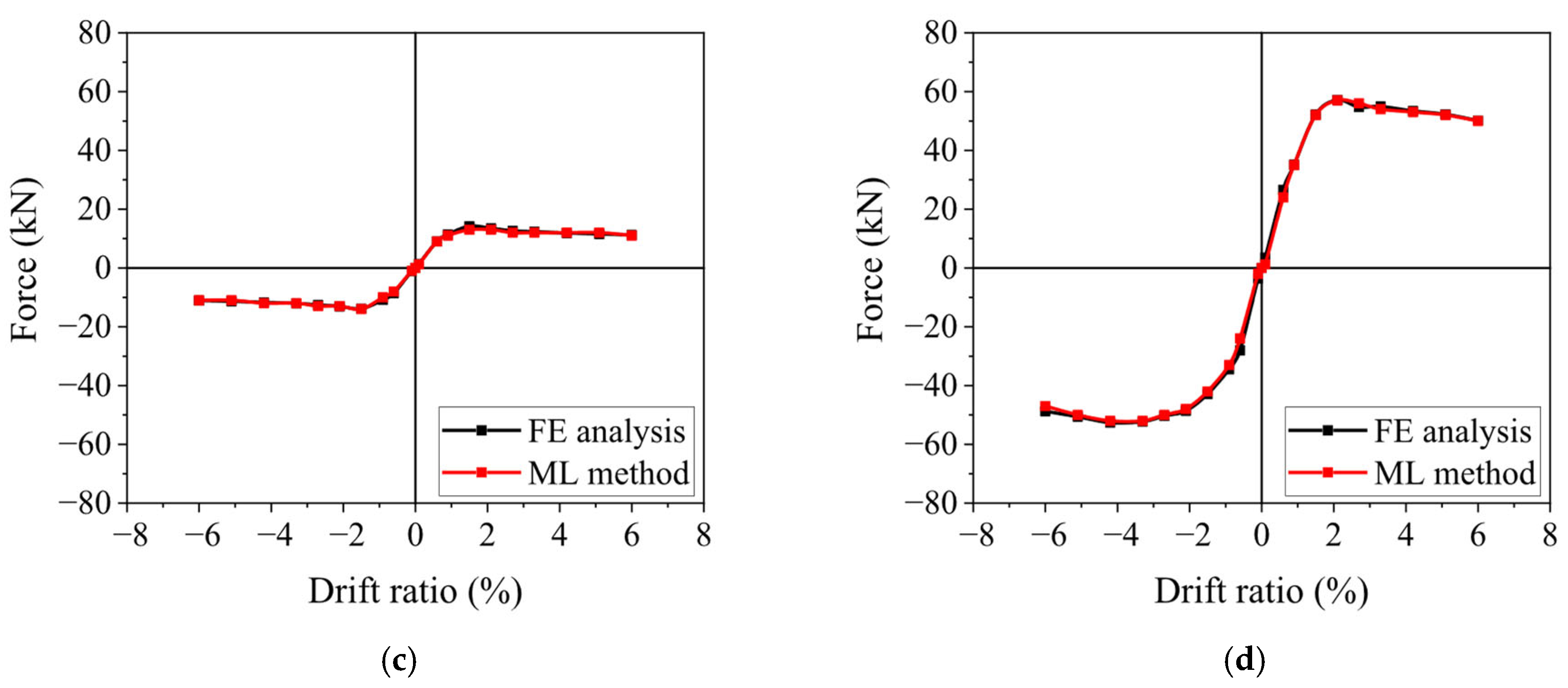
4.1. Prediction Results
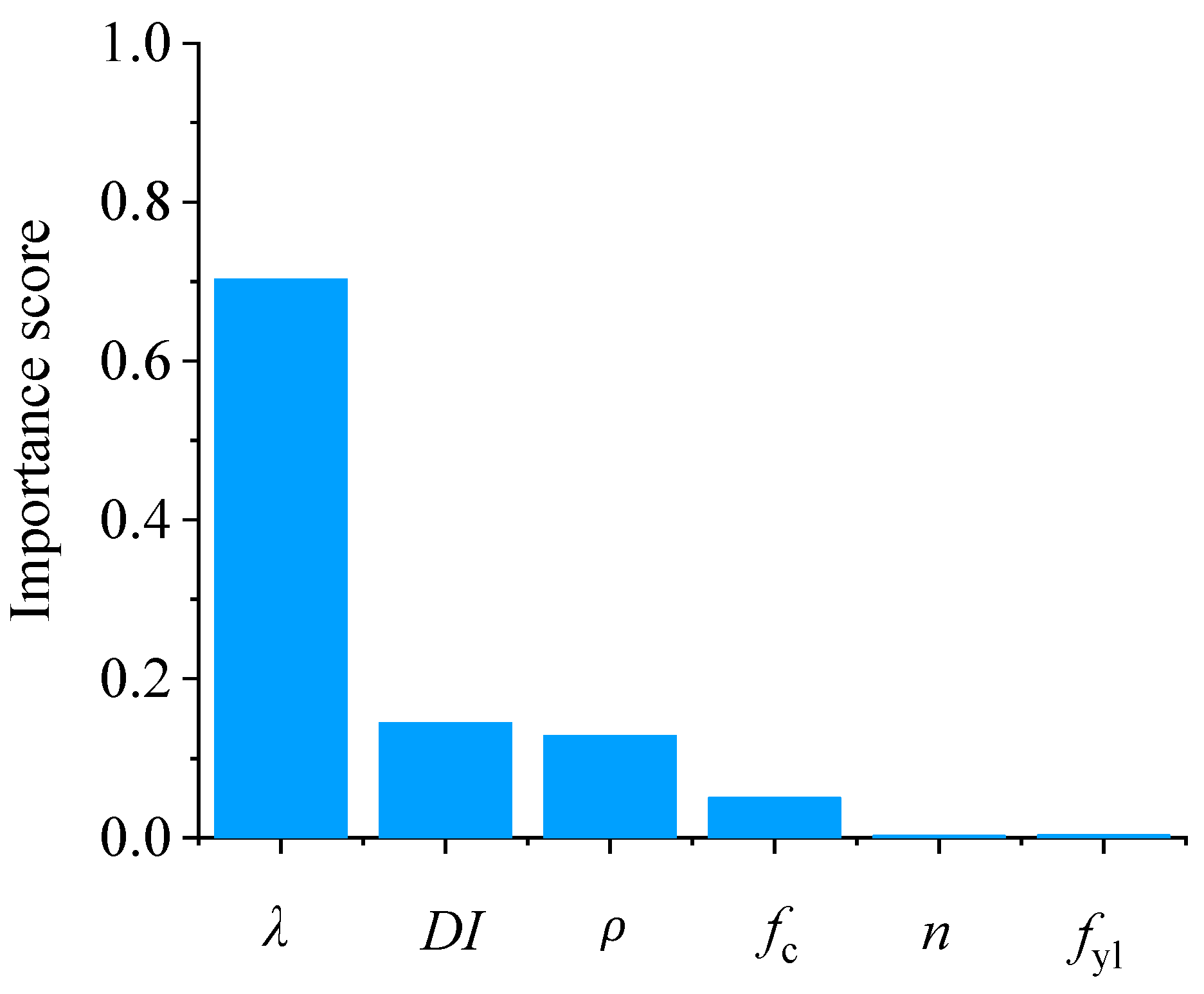
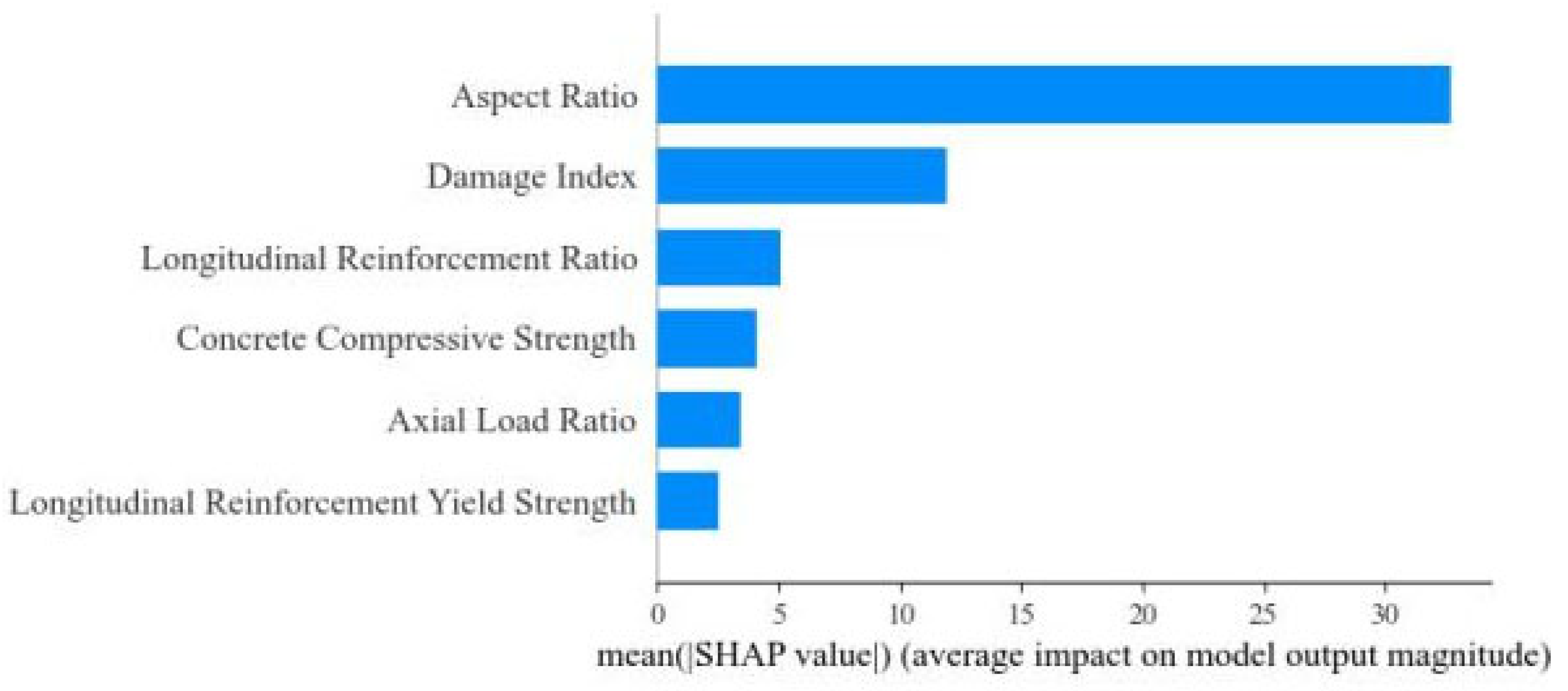
4.2. Influence of Input Variables
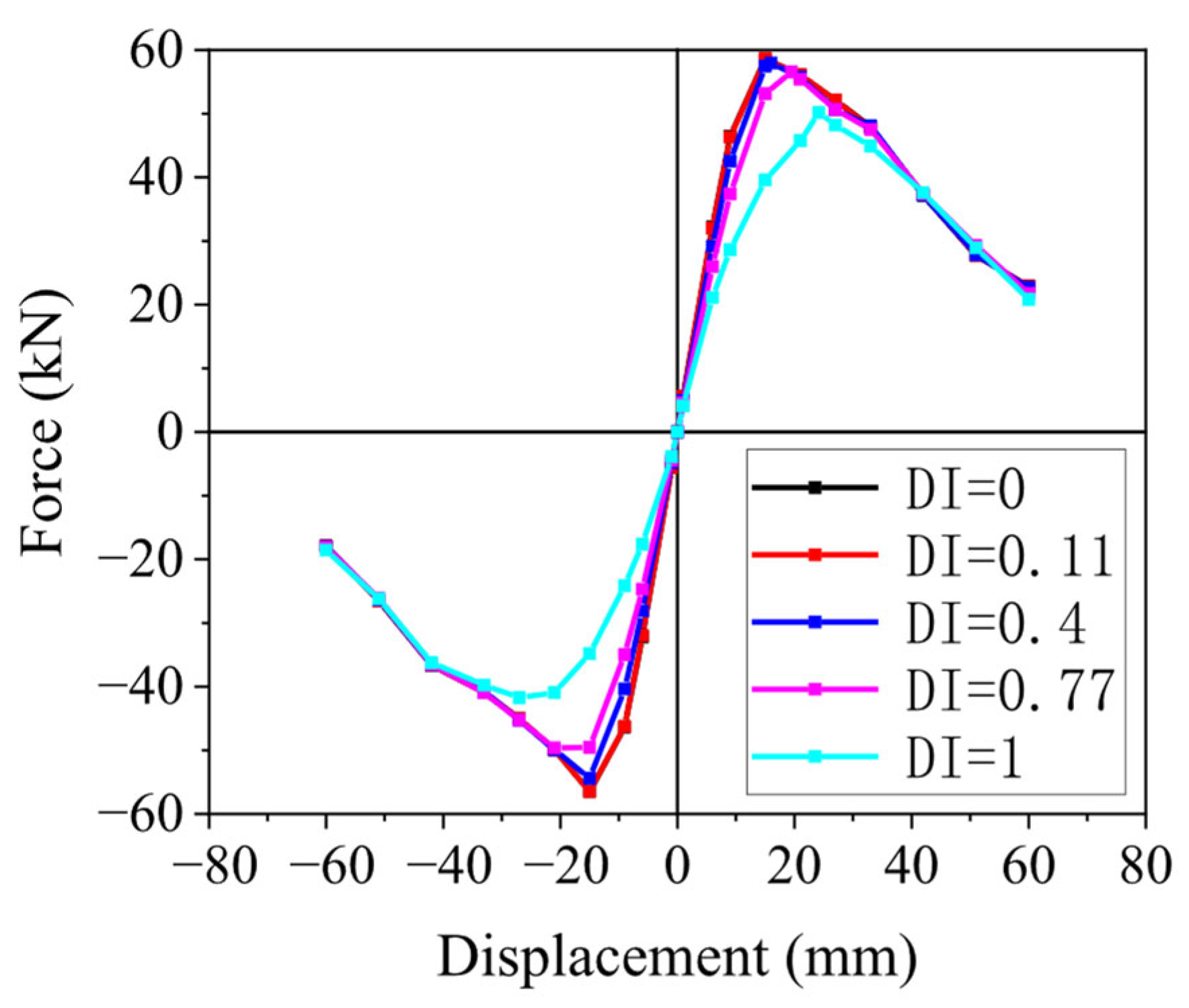
4.3. Quantitative Analysis of Degradation Degree
5. Conclusions
- The research developed an extensive database comprising numerical simulations from common-size column models across all damage levels.
- A machine learning model was developed that predicted the skeleton curve of RC columns as a direct function of their pre-existing damage level, quantified by the damage index, enabling damage-informed prediction of residual structural performance. Machine learning demonstrated excellent ability to predict skeleton curves, particularly in the yielding and descending branches, though prediction performance for coordinate values near zero displacement was less accurate.
- Among the five machine learning algorithms evaluated, K-nearest neighbors achieved the best performance with exceptional accuracy (R2 = 0.978, MSE = 0.022 for peak strength prediction). The approach could reconstruct entire damaged skeleton curves through 22 characteristic points, providing a comprehensive assessment of residual strength, stiffness, and ductility.
- PCA and SHAP identified the aspect ratio as the most influential parameter, followed by the damage index. This study established comprehensive degradation relationships showing negligible capacity reduction for minor damage (DI = 0.11: 99.9% strength retention, 99.6% stiffness retention) versus severe degradation at the collapse level (DI = 1.0: 85.6% strength retention, 54.8% stiffness retention), providing practical insights for post-earthquake evaluation and retrofitting decisions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Naderpour, H.; Mirrashid, M. Proposed soft computing models for moment capacity prediction of reinforced concrete columns. Soft Comput. 2020, 24, 11715–11729. [Google Scholar] [CrossRef]
- Ning, C.-L.; Wang, L.; Du, W. A practical approach to predict the hysteresis loop of reinforced concrete columns failing in different modes. Constr. Build. Mater. 2019, 218, 644–656. [Google Scholar] [CrossRef]
- Luo, H.; Paal, S.G. A locally weighted machine learning model for generalized prediction of drift capacity in seismic vulnerability assessments. Comput. Civ. Infrastruct. Eng. 2019, 34, 935–950. [Google Scholar] [CrossRef]
- Xie, Y.; Ebad Sichani, M.; Padgett, J.E.; Desroches, R. The promise of implementing machine learning in earthquake engineering: A state-of-the-art review. Earthq. Spectra 2020, 36, 1769–1801. [Google Scholar] [CrossRef]
- Asim, K.M.; Martínez-Álvarez, F.; Basit, A.; Iqbal, T. Earthquake magnitude prediction in Hindukush region using machine learning techniques. Nat. Hazards 2016, 85, 471–486. [Google Scholar] [CrossRef]
- Xiong, C.; Li, Q.; Lu, X. Automated regional seismic damage assessment of buildings using an unmanned aerial vehicle and a convolutional neural network. Autom. Constr. 2020, 109, 102994. [Google Scholar] [CrossRef]
- Balz, T.; Liao, M. Building-damage detection using post-seismic high-resolution SAR satellite data. Int. J. Remote. Sens. 2010, 31, 3369–3391. [Google Scholar] [CrossRef]
- Jiang, Y.; Yang, G.; Song, H. Dynamic optimization design of extradosed cable-stayed bridge under earthquake excitation. Eng. Mech. 2020, 37, 313–319. [Google Scholar] [CrossRef]
- Pang, Y.; Dang, X.; Yuan, W. An Artificial Neural Network Based Method for Seismic Fragility Analysis of Highway Bridges. Adv. Struct. Eng. 2014, 17, 413–428. [Google Scholar] [CrossRef]
- Giovanis, D.G.; Fragiadakis, M.; Papadopoulos, V. Epistemic uncertainty assessment using Incremental Dynamic Analysis and Neural Networks. Bull. Earthq. Eng. 2015, 14, 529–547. [Google Scholar] [CrossRef]
- Su, L.; He, H.-J. Decision tree–based seismic damage prediction for reinforcement concrete frame buildings considering structural micro-characteristics. Adv. Struct. Eng. 2019, 22, 2097–2109. [Google Scholar] [CrossRef]
- Kia, A.; Sensoy, S.; Xie, X. Classification of Earthquake-Induced Damage for R/C Slab Column Frames Using Multiclass SVM and Its Combination with MLP Neural Network. Math. Probl. Eng. 2014, 1, 734072. [Google Scholar] [CrossRef]
- Morfidis, K.; Kostinakis, K. Seismic parameters’ combinations for the optimum prediction of the damage state of R/C buildings using neural networks. Adv. Eng. Softw. 2017, 106, 1–16. [Google Scholar] [CrossRef]
- Morfidis, K.; Kostinakis, K. Approaches to the rapid seismic damage prediction of r/c buildings using artificial neural networks. Eng. Struct. 2018, 165, 120–141. [Google Scholar] [CrossRef]
- Morfidis, K.; Kostinakis, K. Comparative evaluation of MFP and RBF neural networks’ ability for instant estimation of r/c buildings’ seismic damage level. Eng. Struct. 2019, 197, 109436. [Google Scholar] [CrossRef]
- Harirchian, E.; Jadhav, K.; Kumari, V.; Lahmer, T. ML-EHSAPP: A prototype for machine learning-based earthquake hazard safety assessment of structures by using a smartphone app. Eur. J. Environ. Civ. Eng. 2021, 26, 5279–5299. [Google Scholar] [CrossRef]
- Zhang, Y.; Burton, H.V.; Sun, H.; Shokrabadi, M. A machine learning framework for assessing post-earthquake structural safety. Struct. Saf. 2018, 72, 1–16. [Google Scholar] [CrossRef]
- Mangalathu, S.; Sun, H.; Nweke, C.C.; Yi, Z.; Burton, H.V. Classifying earthquake damage to buildings using machine learning. Earthq. Spectra 2020, 36, 183–208. [Google Scholar] [CrossRef]
- Palanci, M. Fuzzy rule based seismic risk assessment of one-story precast industrial buildings. Earthq. Eng. Eng. Vib. 2019, 18, 631–648. [Google Scholar] [CrossRef]
- Han, X.; Wu, Z.; Yang, M.; Ji, J. Research on seismic damage assessment of regional RC frame structures based on deep learning. J. Build. Struct. 2020, 41, 27–35. [Google Scholar] [CrossRef]
- Han, X.; Feng, R.; Ji, J.; Wu, Z. Research on parameters of the RC beam lumped plastic hinge model based on deep learning. Eng. Mech. 2021, 38, 160–169. [Google Scholar] [CrossRef]
- Di Ludovico, M.; Polese, M.; D’aRagona, M.G.; Prota, A.; Manfredi, G. A proposal for plastic hinges modification factors for damaged RC columns. Eng. Struct. 2013, 51, 99–112. [Google Scholar] [CrossRef]
- Li, L.; Luo, G.; Wang, Z.; Zhang, Y.; Zhuge, Y. Prediction of residual behaviour for post-earthquake damaged reinforced concrete column based on damage distribution model. Eng. Struct. 2021, 234, 141–296. [Google Scholar] [CrossRef]
- Todorov, B.; Billah, A.M. Post-earthquake seismic capacity estimation of reinforced concrete bridge piers using Machine learning techniques. Structures 2022, 41, 1190–1206. [Google Scholar] [CrossRef]
- Valente, M. Seismic Upgrading Strategies for Non-Ductile Plan-Wise Irregular R/C Structures. Procedia Eng. 2013, 54, 539–553. [Google Scholar] [CrossRef]
- Valente, M.; Milani, G. Alternative retrofitting strategies to prevent the failure of an under-designed reinforced concrete frame. Eng. Fail. Anal. 2018, 89, 271–285. [Google Scholar] [CrossRef]
- GB50010-2010; Code for Seismic Design of Buildings. Ministry of Housing and Urban-Rural Development of P.R. China: Beijing, China, 2010.
- Kunnath, S.K.; Reinhorn, A.M.; Lobo, R.F. A Program for the Inelastic Damage Analysis of Reinforced Concrete Structures, Version 3.0. Technical Report NCEER-92-0022. National Center for Earthquake Engineering Research, SUNY: Buffalo, NY, USA, 1992.
- Kempton, J.J.; Stewart, J.P. Prediction Equations for Significant Duration of Earthquake Ground Motions considering Site and Near-Source Effects. Earthq. Spectra 2006, 22, 985–1013. [Google Scholar] [CrossRef]
- Rathje, E.M.; Abrahamson, N.A.; Bray, J.D. Simplified Frequency Content Estimates of Earthquake Ground Motions. J. Geotech. Geoenviron. Eng. 1998, 124, 150–159. [Google Scholar] [CrossRef]
- Du, W. An empirical model for the mean period (Tm) of ground motions using the NGA-West2 database. Bull. Earthq. Eng. 2017, 15, 2673–2693. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression Shrinkage and Selection Via the Lasso. J. R. Stat. Soc. Ser. B Stat. Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Drucker, H. Improving regressors using boosting techniques. In Proceedings of the Fourteenth International Conference on Machine Learning 1997, Nashville, TN, USA, 8–12 July 1997; pp. 107–115. [Google Scholar]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.; Stone, C.J.; Olshen, R.A. Classification and Regression Trees; Chapman and Hall/CRC: Boca Raton, FL, USA, 2017. [Google Scholar]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Belete, D.M.; Huchaiah, M.D. Grid search in hyperparameter optimization of machine learning models for prediction of HIV/AIDS test results. Int. J. Comput. Appl. 2021, 44, 875–886. [Google Scholar] [CrossRef]


| EQ | Station | Component | Number | EQ | Station | Component | Number |
|---|---|---|---|---|---|---|---|
| ChiChi | TCU071 | N/E | 10 | Northridge | E-RRS | 228/318 | 8 |
| TCU122 | E | FAR | 000/090 | ||||
| TCU129 | N | MU2 | 035/125 | ||||
| CHY101 | E | TUJ | 262/352 | ||||
| HWA032 | N | Petrolia | CE89156 | 000/090 | 2 | ||
| HWA2 | N/E | Umbria Marche | A-AAL | 018/108 | 2 | ||
| CHY046 | N/E | Chalfant Valley | A-LAD | 180 | 1 | ||
| Racha | Ambrolauri | X/Y | 2 | Whittier Narrows | A-ALT | 000/090 | 9 |
| Mt. Hengill Area | Hveragerdi | Y | 1 | A-CAM | 009/279 | ||
| Kefallinia island | Argostoli | X/Y | 4 | A-DEL | 000/090 | ||
| Kefallinia | X/Y | A-MTW | 000 | ||||
| South Iceland | Kaldarholt | Y | 1 | A-GRN | 180 | ||
| Duzce | LDEO | X/Y | 2 | A-SMA | 270 | ||
| Imperial Valley | A-E06 | 140/230 | 4 | WenChuan | 051LXS | NS | 6 |
| A-E08 | 140/230 | 051LXT | EW/NS | ||||
| Darfield | NZHVSC | S64E/S26W | 3 | 051MZQ | NS | ||
| NZLPCC | S10E | 051WCW | EW/NS |
| Categorization | Input Parameters | Value Ranges | Unit | No. | Selection Methods |
|---|---|---|---|---|---|
| Column | Aspect ratio λ | 2.5/3/3.5/4/4.5 | / | 5 | Sequentially selected |
| Longitudinal reinforcement ratio ρl | 0.75/1.15/1.55 | % | 3 | Sequentially selected | |
| Concrete compressive strength fc | 20.1/23.4/26.8/29.6/32.4 | MPa | 5 | Sequentially selected | |
| Reinforcement yield strength fyl | 400/500 | MPa | 2 | Sequentially selected | |
| Axial compression ratio n | 0.1/0.2/0.3/0.4/0.5 /0.6/0.7/0.8/0.9 | / | 9 | Sequentially selected | |
| Earthquake | Damage index DI | 0–1.0 | / | / | Calculated by FE analysis |
| Model | Main Hyperparameter | Selected Value |
|---|---|---|
| Lasso Regression | α | 0.001 |
| K-nearest neighbor | n_neighbors | 16 |
| Support Vector Machine | C | 1000 |
| kernel | RBF (the Radial Basis Function) | |
| Decision Tree | min_samples_split | 9 |
| AdaBoost | n_estimates | 50 |
| learning_rate | 1 |
| DI | Damage Levels | Yield Point (kN, mm) | Peak Point (kN, mm) | Ultimate Point (kN, mm) |
|---|---|---|---|---|
| 0 | Intact | (43.93, 8.47) | (58.57, 15.00) | (46.86, 33.95) |
| 0.11 | Minor damage | (43.92, 8.50) | (58.56, 15.10) | (46.85, 33.80) |
| 0.4 | Moderate damage | (43.44, 9.37) | (57.92, 16.03) | (46.33, 34.53) |
| 0.77 | Severe damage | (42.41, 10.92) | (56.55, 19.47) | (45.24, 35.22) |
| 1 | Collapsed damage | (37.62, 13.24) | (50.16, 24.15) | (40.13, 38.36) |
| DI | Damage Levels | Degradation Ratio of Strength γ1 | Degradation Ratio of Stiffness γ2 |
|---|---|---|---|
| 0 | Intact | 100% | 100% |
| 0.11 | Minor damage | 99.9% | 99.6% |
| 0.4 | Moderate damage | 98.8% | 89.4% |
| 0.77 | Severe damage | 96.5% | 74.9% |
| 1 | Collapsed damage | 85.6% | 54.8% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, P.; Wen, W.; Zhai, C.; Li, Y. Prediction of Skeleton Curves for Seismically Damaged RC Columns Based on a Data-Driven Machine-Learning Approach. Buildings 2025, 15, 3135. https://doi.org/10.3390/buildings15173135
Sun P, Wen W, Zhai C, Li Y. Prediction of Skeleton Curves for Seismically Damaged RC Columns Based on a Data-Driven Machine-Learning Approach. Buildings. 2025; 15(17):3135. https://doi.org/10.3390/buildings15173135
Chicago/Turabian StyleSun, Pengyu, Weiping Wen, Changhai Zhai, and Yiran Li. 2025. "Prediction of Skeleton Curves for Seismically Damaged RC Columns Based on a Data-Driven Machine-Learning Approach" Buildings 15, no. 17: 3135. https://doi.org/10.3390/buildings15173135
APA StyleSun, P., Wen, W., Zhai, C., & Li, Y. (2025). Prediction of Skeleton Curves for Seismically Damaged RC Columns Based on a Data-Driven Machine-Learning Approach. Buildings, 15(17), 3135. https://doi.org/10.3390/buildings15173135







