Research on the Value-Added Pathways of Government-Invested EPC Projects Based on DEMATEL–TAISM–MICMAC

Abstract

Government-invested Engineering, Procurement, and Construction (EPC) projects often encounter challenges, such as ambiguous value-added pathways and undefined key driving mechanisms, which impede efficiency improvements during implementation. To systematically elucidate the value-added pathways and core driving mechanisms in these projects, this study identified and distilled 20 critical influencing factors across four dimensions—contract cost, organization, technology, and environment—through a combination of a literature review, case analysis, and a questionnaire survey yielding 68 valid responses. Employing a DEMATEL–TAISM–MICMAC hybrid model, the research conducted an in-depth analysis: the DEMATEL method quantified the interdependencies among factors and identified key causal elements; a TAISM-directed topological hierarchy diagram was constructed to clearly delineate the hierarchical transmission pathways; and the MICMAC model was utilized for driver–dependency analysis, classifying factor roles and providing cross-validation from three analytical perspectives. The results indicate that S₁₂ (collaborative participation in early planning and design phases) exhibits the highest causal influence and serves as the core driving factor, while S₁ (detailed and explicit contractual clauses) and S₁₂ are positioned at the root level of the hierarchical model, functioning as foundational independent factors that regulate the entire system. The value-added pathways are characterized by a hierarchical transmission logic of “root level → transitional level → direct level”. Based on these findings, the study proposes a system optimization strategy of “strengthening the root level, optimizing the transitional level, and safeguarding the direct level”, thereby offering both theoretical insights and practical guidance for enhancing the value-added efficiency of government-invested EPC projects.

1. Introduction

Amid the rapid development of global infrastructure, the Engineering, Procurement, and Construction (EPC) general contracting model has emerged as the predominant approach in the construction sector due to its highly integrated management structure and efficient collaborative operational mechanisms. By consolidating design, procurement, and construction, the EPC model exhibits significant advantages in enhancing project quality and reducing construction durations. However, as project scale and complexity escalate, the EPC model has encountered a series of practical challenges, including cost overruns, schedule delays, and quality fluctuations. These issues arise not only from the inherent difficulties associated with multi-stakeholder collaboration and deficiencies in the contractual framework but also reflect theoretical gaps in academic research regarding value-added mechanisms within EPC projects. In the context of enhanced public fund performance management, it is crucial to uncover the underlying mechanisms governing the interaction between multidimensional factors and their hierarchical transmission in order to address the bottlenecks that hinder value-added efficiency in government-invested EPC projects.

Value addition is a central pillar of value management in EPC projects, with its theoretical origins rooted in Porter’s value chain theory, which deconstructs corporate value addition into the symbiotic relationship between primary and support activities [1]. This framework provides a foundational model for analyzing the logic of value formation. Expanding on this, Peter Hines’s work [2] shifted the focus to customer-centric value, repositioning customer needs at the core of the value chain and propelling the theory towards a service-oriented paradigm. The practical application of this concept is highly diversified; at the process level, studies by Li and Zhang suggest that full-process tracking audits can dynamically monitor and optimize the value chain flow [3], while other research cautions that excessive monitoring may stifle innovation. Regarding stakeholder dynamics, Du and Wang have shown that the intricate interplay of competition and cooperation between owners and contractors fosters resource and risk sharing, thereby driving value addition [4]. Conversely, Berg et al. identified that organizational friction stemming from business model contradictions within the value chains of architecture, engineering, and construction (AEC) firms can undermine synergistic value addition [5]. In the domain of technological innovation, Liu et al. underscore the critical role of digitalization and service-oriented transformation in redefining value addition pathways [6], though previous studies have raised concerns about the scenario-specific adaptability of technologies like Building Information Modeling (BIM). Within risk management and organizational synergy, Wang et al. quantitatively identified 11 core risk factors influencing decision-making in large-scale projects [7], and Wang and Bai used an evolutionary game model to validate the role of secondary risk management in sustaining value addition under the EPC + PPP model [8]. However, the specific correlation between various risk factors and value addition remains a subject of debate in different studies. From a supply chain perspective, Huang and Li established a significant positive correlation between the degree of supply chain integration and procurement performance in international EPC projects [9]. Similarly, Gao et al. demonstrated that prefabrication rates and logistics coordination are key determinants of construction duration in prefabricated building projects [10]. Despite these findings, a comprehensive understanding of value transmission efficiency across different supply chain links is still fragmented. Methodologically, Bennett and Mayouf introduced a lifecycle value management framework [11], while Wang et al. leveraged an evolutionary game model to reveal the dynamic mechanisms of value co-creation during digital transformation [12]. However, a notable gap persists in the literature: a systematic analysis of the interactive effects of multidimensional factors, particularly in the dynamic characterization of value transmission pathways within complex project environments.

The EPC model for government-invested projects has emerged as a pivotal instrument for enhancing the efficiency of public project delivery, yet its adoption and evolution display considerable regional disparities and ongoing practical debates. In Europe and the Americas, the EPC approach was introduced earlier within municipal engineering, emphasizing the improvement in management efficiency through the implementation of standardized contracts. In contrast, the promotion of EPC in emerging Asian markets is predominantly policy-driven, exemplified by China’s reliance on a suite of regulatory documents to encourage the prioritization of EPC in government-funded initiatives. Current research in this domain primarily follows two trajectories: one examines the adaptability of management models, seeking to optimize performance across the entire project lifecycle [13], while the other investigates the enabling role of digital technologies, with studies such as Li et al. demonstrating that digitalization can enhance sustainable performance through improved stakeholder collaboration [14]. In practice, core controversies persist in four key areas. First, regarding the allocation of responsibilities among multiple stakeholders, Chen et al. underscore the necessity of clearly delineating the roles of government, general contractors, and project management entities [15], although some scholars advocate for maintaining flexibility to accommodate dynamic project adjustments. Second, in the realm of public fund oversight, Sheppard and Beck discuss the delicate balance between transparency and efficiency [16], highlighting divergent approaches between “rigid auditing” and “flexible regulation”. This challenge is further contextualized in emerging economies where innovative financing mechanisms, such as blue bonds, are being introduced under nascent regulatory frameworks, as discussed by Endarto et al. in the case of Indonesia [17]. Third, the tension between policy compliance and engineering flexibility is exemplified by Wacinkiewicz and Słotwiński, who analyze the constraining influence of legal frameworks in the Polish context [18]. This aligns with broader discussions on how legal instruments, including easements, can either facilitate or hinder sustainable infrastructure development, as highlighted by Peráček and Kaššaj in the context of smart cities [19]. Meanwhile, other studies argue for the necessity of adaptive mechanisms in exceptional scenarios. Fourth, in contract design, Aboseif and Hanna advocate for the incorporation of performance quantification metrics [20], yet practical implementation often reveals a disconnect between these metrics and actual project needs. With respect to value-added mechanisms, Lao et al. highlight the importance of design-driven integration capabilities [21], Zhou et al. elucidate the interactive effects among technology, organization, and policy [22], and Huang et al. emphasize the critical role of supply chain management [23]. Nevertheless, existing research has yet to fully elucidate the synergistic mechanisms that reconcile the public interest orientation with the value-added objectives unique to government investment projects, indicating a clear need for further investigation in this area.

A review of existing research reveals that the current research paradigm is highly fragmented, with most studies concentrating on a single aspect or specific perspective, thereby lacking a comprehensive understanding of the underlying logic of value-added systems. In the field of construction engineering in particular, prior research has predominantly examined the role and impact of the value chain in general engineering projects, while insufficient attention has been devoted to the value-added processes of government-invested EPC projects. The mechanism and pathways of value addition constitute the core dimensions of the value formation process in EPC projects. The profound implications and intrinsic interrelationships of these dimensions urgently warrant systematic academic investigation.

This study addresses the critical challenge of enhancing value-added efficiency in government-invested EPC projects by systematically examining their underlying mechanisms. Our core objectives are three-fold:

• To identify the key factors influencing value addition and their synergistic mechanisms across four critical dimensions: contract cost, organization, technology, and environment;
• To reveal the hierarchical transmission pathways of value addition, characterized by a cascading structure from a “root level” to a “transitional level” and a “direct level;”
• To validate the applicability and effectiveness of a DEMATEL–TAISM–MICMAC hybrid model in analyzing complex value-added systems.

Through rigorous scientific inquiry, this study aims to establish a robust theoretical framework and practical management strategies for enhancing the value of government-invested EPC projects. To this end, the following key hypothesis is proposed: “An integrated DEMATEL–TAISM–MICMAC model provides a comprehensive analytical framework capable of effectively revealing the value-added mechanism in government-invested EPC projects. By encompassing a closed-loop process of “quantitative identification, structural decomposition, and functional validation”, the model can accurately pinpoint core drivers, clarify multi-level transmission pathways, and facilitate the classification of factor roles, thereby supporting the formulation of targeted management strategies”.

This main hypothesis is decomposed into three testable sub-hypotheses:

H1 (Identification Efficacy).

The DEMATEL module quantitatively identifies causal relationships among factors, enabling the precise identification of root-level drivers that exert dominant influence within the value-added system.

H2 (Pathway Elucidation).

The TAISM module structurally defines the hierarchical and directional interactions between factors, clearly revealing the transmission logic in “root level → transitional level → direct level”, thereby mapping the value transmission pathways.

H3 (Functional Validation and Strategic Utility).

The MICMAC module classifies factors into functionally distinct clusters (e.g., independent, dependent, linkage, and autonomous), validating the structural findings and providing a scientific basis for developing stratified management strategies.

In summary, this study addresses the fundamental challenges associated with enhancing the value-added efficiency of government-invested EPC projects. By developing a multidimensional integrated framework and employing an innovative hybrid model, the research seeks to uncover the intrinsic driving mechanisms and hierarchical transmission logic underlying value-added pathways. The study systematically identifies key driving factors, clarifies hierarchical structures, and delineates functional roles, thereby proposing a stratified optimization strategy. This approach provides a robust theoretical foundation and practical implementation pathways for optimizing the management systems of government-invested projects.

2. Materials and Methods

2.1. Preliminary Selection of Influencing Factors

To identify the factors influencing the value addition of government-invested EPC projects, this study began with a comprehensive literature review using the Web of Science database. The search, employing the keywords ‘EPC’ and ‘value-added,’ yielded 15 highly relevant articles, which were selected as key references for identifying the factors that contribute to value addition [24,25,26,27,28,29,30,31,32,33,34,35,36,37,38]. In addition, a detailed case analysis of nine government-invested EPC projects implemented across various sectors and regions in China (including Xinjiang and Guangdong provinces) was conducted between 2019 and 2025. These projects span multiple industries, such as housing construction and transportation infrastructure, encompassing a total of nine projects. The analysis aimed to identify key challenges and potential areas for improvement during the project implementation phase. Based on the findings from the literature review and case-based statistical analysis, this study identified 24 critical factors influencing value enhancement in government-invested EPC projects. These factors were categorized into four dimensions—contract cost, organization, technology, and environment—considering both internal and external perspectives.

2.2. Refinement of Core Influencing Factors

2.2.1. Questionnaire Design and Survey

This study involved field visits to construction enterprises and government departments. In-depth interviews were conducted with industry experts possessing extensive experience in EPC contracting projects. A questionnaire survey was employed to accurately identify the key factors influencing value addition. A total of 73 questionnaires were distributed, yielding 68 valid responses. The content of the questionnaire primarily covered the respondents’ personal background information and their assessment of the impact of value-added factors. The participating units included construction companies, general contracting units, and project management departments responsible for handling government-invested projects.

2.2.2. Reliability and Validity Analysis

IBM SPSS Statistics (v26.0) was employed to perform reliability and validity tests on the sample data. The results indicated that the overall Cronbach’s α coefficient of the scale reached 0.864, while the KMO (Kaiser–Meyer–Olkin) value was 0.713. These findings suggest that the questionnaire scale possesses high reliability and validity and that the sample data satisfy the prerequisites for factor analysis. Furthermore, a weight analysis was conducted, as illustrated in Figure 1. In the subsequent model-building phase, to ensure that a limited number of factors could adequately explain all information, four factors with relatively weak influence were excluded from the original 24 factors. This resulted in 20 core value-added influencing factors, which collectively form the value-added influencing factor indicator system, as detailed in

Table 1. Indicator system for value addition influencing factors in EPC projects.

Terms	Code	Influencing Factors
Contract and Cost Aspects	S1	Detailed and explicit contractual clauses
	S2	Simplification of bidding and procurement processes
	S3	Rational allocation of rights, responsibilities, and interests
	S4	Reduction of contract disputes and claims
	S5	Enhancement of oversight during budget preparation
	S6	Control of material and equipment procurement costs
Organizational Aspects	S7	Integrated management and coordination
	S8	Optimized supply chain management
	S9	Enhanced efficiency and quality of information dissemination
	S10	Establishment of an effective change management mechanism
	S11	Continuous monitoring and performance evaluation
	S12	Collaborative participation in early planning and design phases
Technical Aspects	S13	Strengthened technology selection
	S14	Adjustment and optimization of resource allocation
	S15	In-depth design clarification and briefing
	S16	Research and development of advanced construction techniques
	S17	Formulation of specialized technical plans
Environmental Aspects	S18	Policy support and facilitation
	S19	Expeditious land acquisition, relocation, and resettlement
	S20	Effective incentive and penalty mechanisms

.

2.3. Fundamental Scientific Research Methods

In this study, we employed four core scientific research methodologies to ensure the rigor and comprehensive nature of our analysis [19].

1.

Analytical Method

We began by critically reviewing the existing literature, survey data, and expert evaluations to deconstruct the complex value-added mechanism into four key dimensions: contract cost, organization, technology, and environment. This process involved dissecting the collaborative mechanisms among various stakeholders, the contractual framework, and technical processes. Through this, we identified 24 preliminary factors, which were then refined into 20 core indicators using a statistical weighting method.

2.

Deductive Method

Based on Porter’s value chain theory and the principles of EPC project governance, we deduced a series of testable hypotheses regarding the hierarchical value transmission pathways. This deductive logic guided the construction of our hybrid DEMATEL–TAISM–MICMAC model, establishing a causal chain for empirical validation.

3.

Comparative Method

We employed a comparative approach to identify key differences in value drivers and transmission efficiency. This was achieved by contrasting regional implementation paradigms (e.g., China’s policy-driven EPC model versus Europe’s standardized contractual approach) and by cross-validating the causal attributes from DEMATEL, the cluster roles from MICMAC, and the hierarchical positioning from TAISM.

4.

Case Study Method

We conducted an empirical case study on a series of government-invested EPC projects, selecting typical cases from regions such as Xinjiang, China. Core data, including cost overruns, schedule delays, and design change rates, were obtained from official survey reports issued by the 12th Division Government Investment Project Construction Center [39]. To enhance data reliability, we further validated the key findings and causal chains of value erosion events through semi-structured interviews. These interviews, conducted with senior project managers and owner representatives, provided critical insights into the root causes and transmission mechanisms of the issues. Through systematic cross-validation, we robustly confirmed the hierarchical transmission paths and clarified the specific roles of various fundamental factors in value loss.

By integrating these four methods—analytical, deductive, comparative, and case study methods—our research ensures a comprehensive methodology. Each method emphasizes different aspects while working synergistically to support the complete research framework, from foundational analysis to empirical validation. Through the collaboration of quantitative modeling and qualitative analysis, we ensure the rigor and multidimensionality of our conclusions.

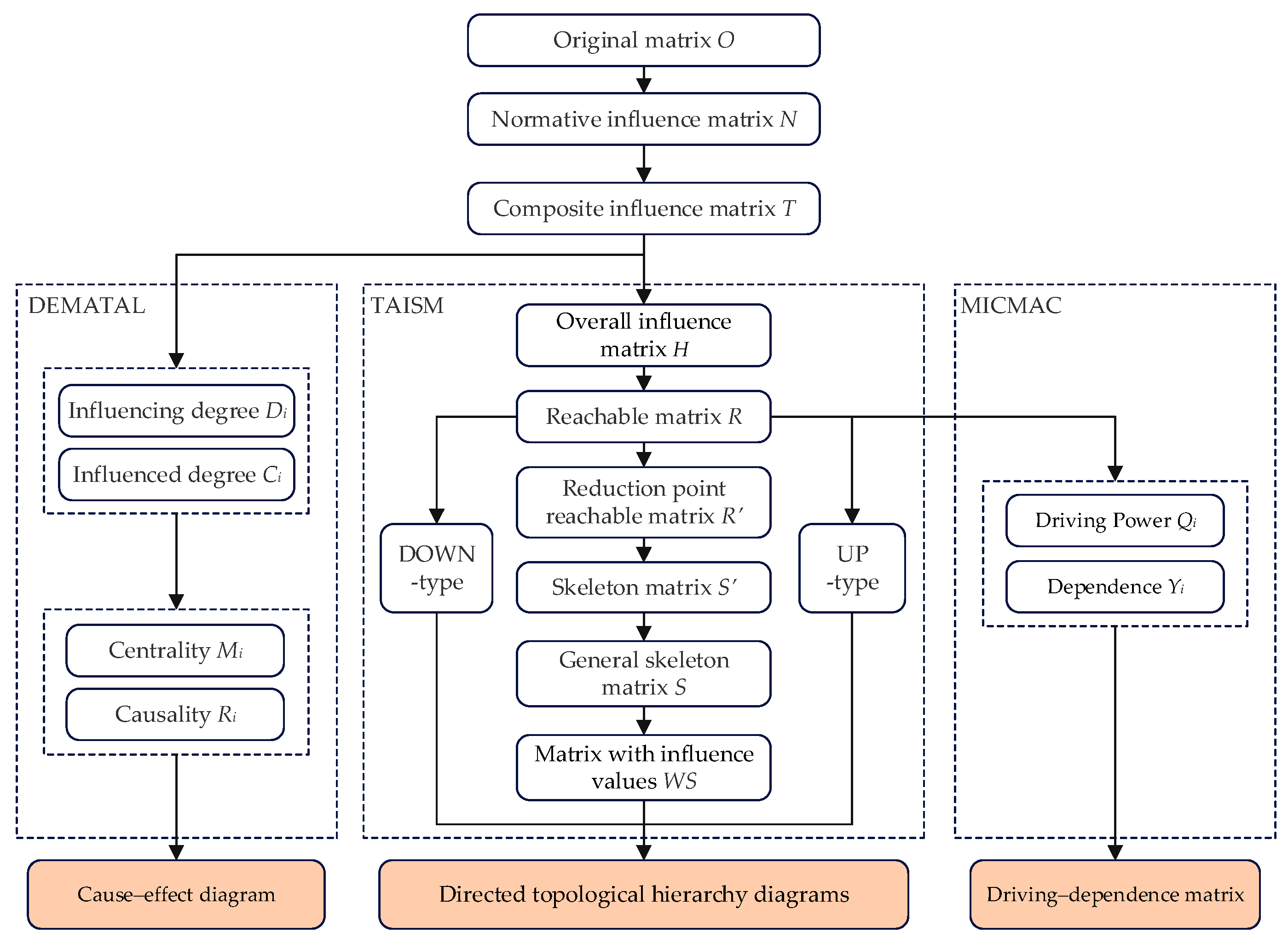
2.4. DEMATEL–TAISM–MICMAC Hybrid Model Analysis Method

To thoroughly investigate the intricate network structure and underlying mechanisms of value creation in government-funded EPC projects, this study proposes and implements a hybrid analytical framework that integrates DEMATEL, TAISM, and MICMAC methodologies (as illustrated in Figure 2). By synthesizing these three complementary approaches, the model addresses the limitations of traditional value-added analyses, which often struggle with ambiguity and a lack of comprehensiveness in capturing complex causal relationships and hierarchical structures among influencing factors. This integrated framework thus enables a systematic and in-depth exploration of the sources, pathways, and principal drivers of value addition in such projects [40].

(1)

The Decision-Making Trial and Evaluation Laboratory (DEMATEL) serves a central quantitative role in this research. Given the inherent complexity of multi-factor interactions in the value-added process, DEMATEL is employed to quantify the interdependencies and strength of influences among various factors. This provides essential data for identifying core variables that significantly impact value output and for clarifying the causal mechanisms governing value-added pathways [41]. The comprehensive influence values derived from DEMATEL not only highlight explicit relationships between factors but also map the transmission efficiency of value within the project system, establishing a solid quantitative foundation for revealing the hierarchical transmission logic underlying value addition [24].

(2)

The Comprehensive Adversarial Interpretation Structure Model (TAISM) is introduced to address the challenges posed by the diverse value aspirations and strategic interactions among the multiple stakeholders involved in EPC projects, including the government, general contractors, and various agencies. In contrast to traditional models, TAISM is particularly adept at capturing the feedback loops in project value-added systems. The UP-type and DOWN-type directed topological hierarchy diagrams constructed by TAISM serve to identify potential leakage points in the value realization process and trace the fundamental drivers of value addition, respectively. This dual “traceability–convergence” perspective provides a powerful analytical tool for harmonizing multi-stakeholder conflicts and optimizing the value distribution framework, effectively addressing the core challenges of value management in government-invested EPC projects [42].

(3)

The Matrix Cross-Multiplication Classification Method (MICMAC) plays a crucial role in systematically categorizing the factors influencing value addition. By evaluating the driving forces and dependencies among the various factors, MICMAC classifies them into distinct roles, such as core drivers, key hubs, or terminal performance factors. This classification not only reveals the unique contributions of each factor within the value-added system but also clarifies the interaction mechanisms between them. The multidimensional cross-validation feature of MICMAC ensures the stability of the relationships, offering a clear depiction of the intrinsic structure and core-periphery dynamics of the value-added system. Consequently, the analysis results provide a robust theoretical foundation for the formulation of hierarchical management strategies [43].

2.5. Construction of the DEMATEL–TAISM Hybrid Model

(1)

Construction of the Direct Original Matrix O

Based on questionnaire survey data, we construct a direct original matrix O among the 20 value-added influencing factors. Factor O_ij represents the degree of direct influence of factor S_i on factor S_j, as shown in Formula (1):

$$O={(O_{ij})}_{m\times m}$$

(1)

(2)

Calculation of the Composite Influence Matrix T

The direct original matrix O is normalized using Formula (2) to obtain the normative influence matrix N. Subsequently, both the direct and indirect influence relationships between factors are considered, and the composite influence matrix T is calculated according to Formula (3):

$$N=({\displaystyle \frac{O_{ij}}{Max\sqrt{{a_i}^2+{b_i}^2}}}{)}_{m\times m}$$

(2)

$$T={\displaystyle \sum _{k=1}^{\infty }{N}^k=N{(I-N)}^{-1}}$$

(3)

(3)

Identification of Factors Influencing Relevant Indicators

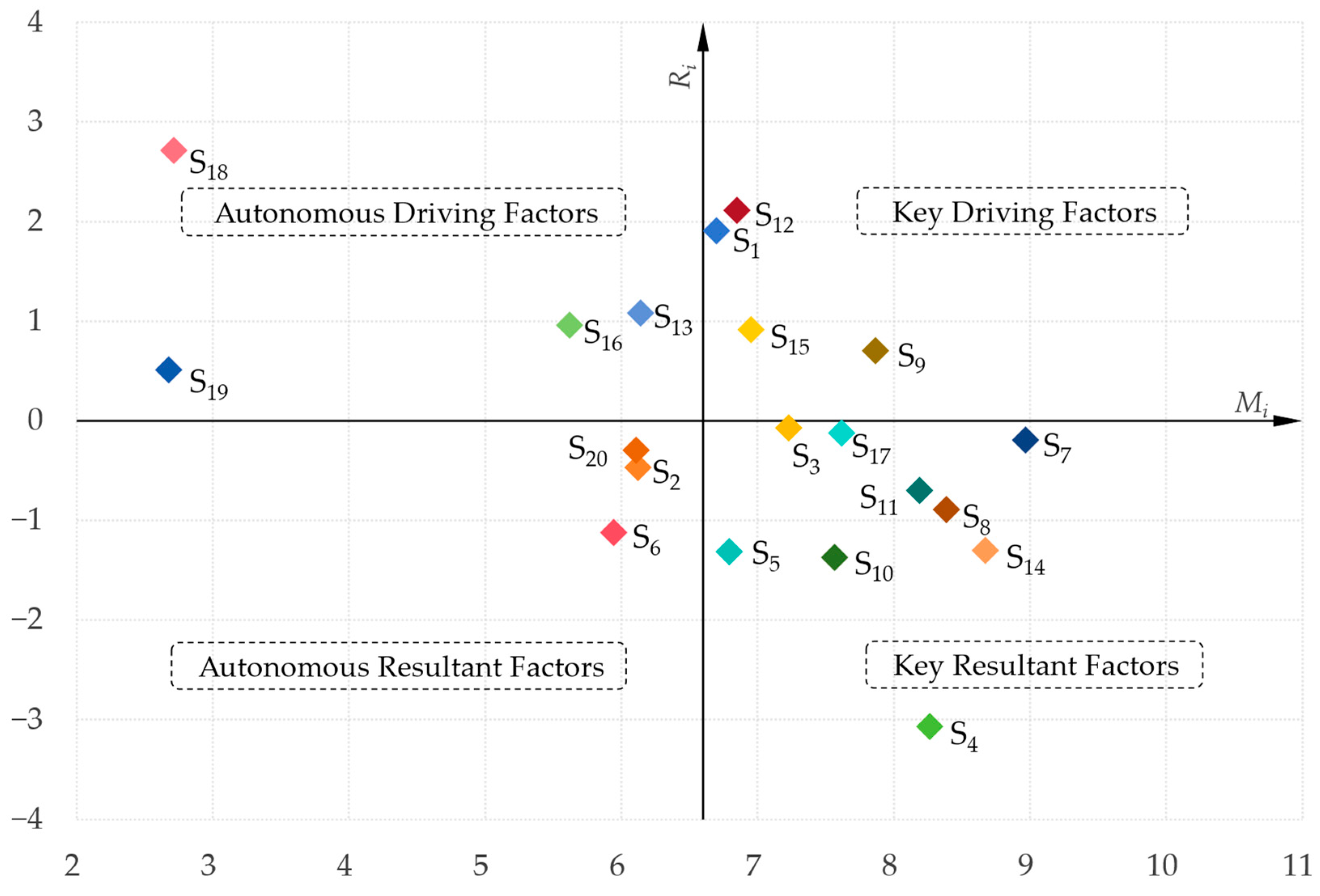
Utilizing the composite influence matrix T, the influencing degree (D_i), influenced degree (C_i), centrality (M_i), and causality (R_i) of each value-added influencing factor are calculated as follows:

$$D_i={\displaystyle \sum _{i=1}^n{t}_{ij}} (i=1,2,3\cdot \cdot \cdot ,n)$$

(4)

$$C_i={\displaystyle \sum _{j=1}^n{t}_{ji}} (i=1,2,3\cdot \cdot \cdot ,n)$$

(5)

$$M_i=D_i+C_i$$

(6)

$$R_i=D_i-C_i$$

(7)

(4)

Computation of the Overall Influence Matrix H

The overall influence matrix H is derived from the composite influence matrix T, representing the complete set of influence relationships across all factors in the system, integrating both direct and indirect influences:

$$H=T+I={(h_{ij})}_{n\times n}$$

(8)

(5)

Formulation of the Reachable Matrix R

To identify the hierarchical structure and critical paths within the system, a threshold value λ is set. The overall influence matrix H is transformed into a binary logical reachable matrix R:

$$R={({\mathrm{r}}_{ij})}_{n\times n} r_{ij}=\left\{\begin{array}{c}1 r_{ij}\ge \lambda \\ 0 r_{ij}<\lambda \end{array}\right.$$

(9)

(6)

Establishing the General Skeleton Matrix S

The reachable matrix R undergoes hierarchical optimization to eliminate redundant connections, resulting in a reduced reachable matrix R′. The nodes are then recovered to form the general skeleton matrix S, which clearly delineates the core hierarchical structure of the system:

$$S^{\prime }=R^{\prime }-{(R^{\prime }-I)}^2-I$$

(10)

(7)

Calculation of the Matrix with Influence Values WS

The values in the composite influence matrix T corresponding to the “1” values in the general skeleton matrix S are retained to form the influence-valued skeletal matrix TS, which contains the influence strength information. This matrix is subsequently used to identify and integrate cyclic relationships among factors, yielding the final matrix WS, which provides quantitative edge weights for constructing hierarchical topological graphs [44].

(8)

Antagonistic Hierarchy Extraction

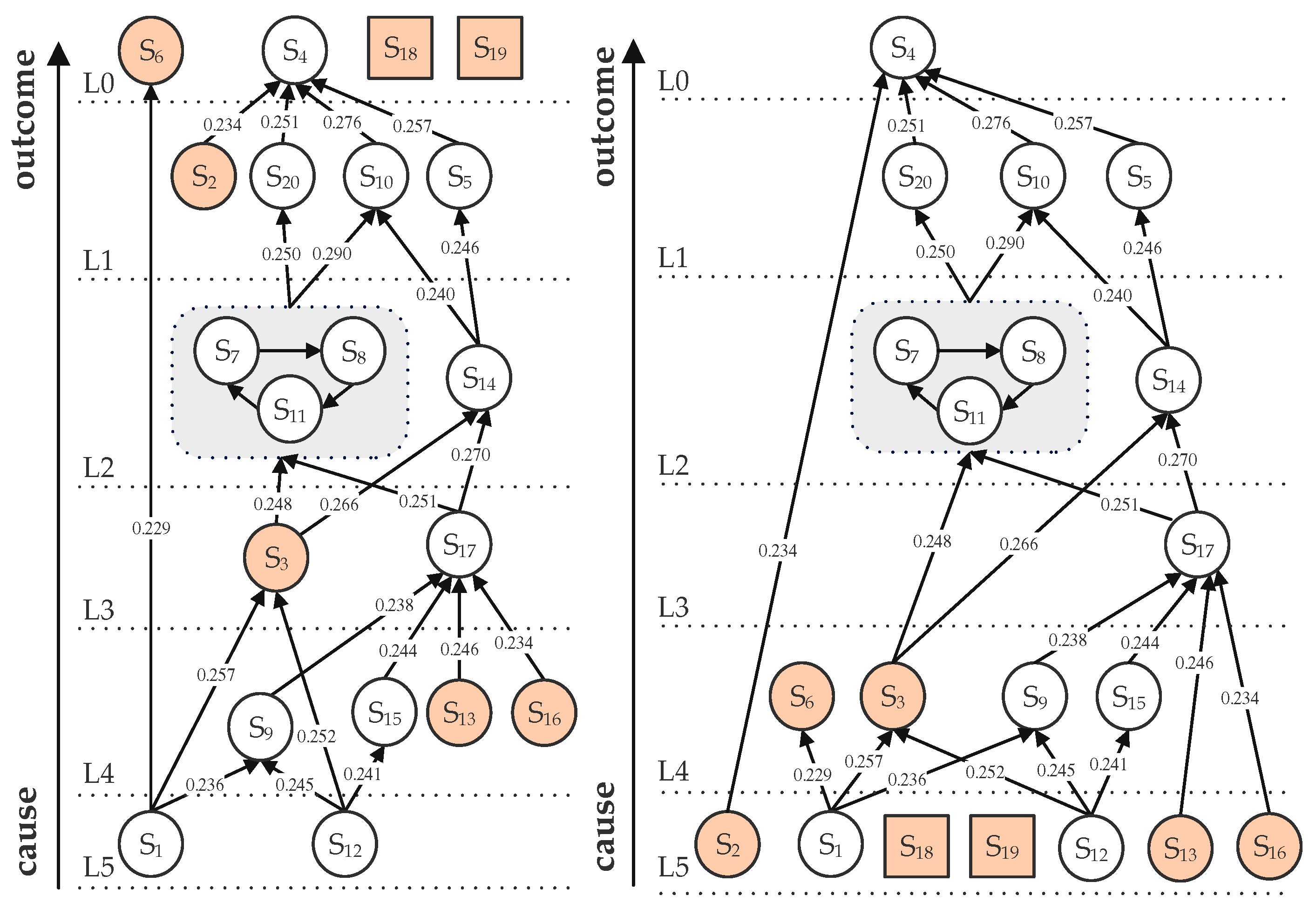
Two types of directed topological hierarchy diagrams are constructed based on the reachable matrix R:

UP type (Result-oriented): Factors that satisfy the condition T(ei) = R(ei) are placed at the lowest level (Level 0), and the hierarchy is subsequently decomposed downward layer by layer, following the reachability relationships.

DOWN type (Cause-priority): Factors meeting the condition T(ei) = Q(ei) are positioned at the lowest level (Level 5), and the hierarchy is constructed upward layer by layer, based on precedence relationships [45].

(9)

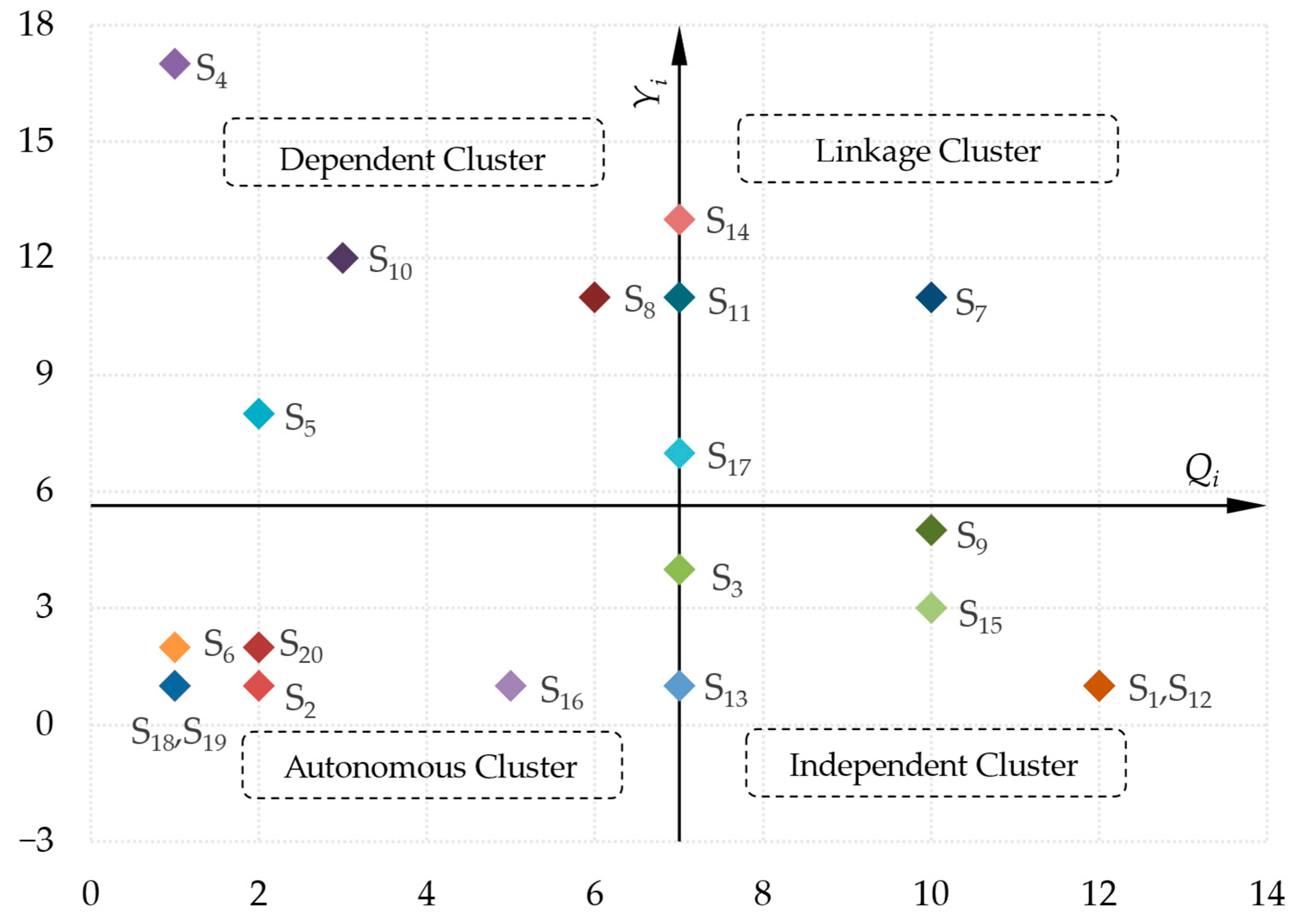
Calculation of Driving Force (Q_i) and Dependence (Y_i), and Construction of the Driving Force–Dependence Matrix

The driving force (Q_i) and dependence (Y_i) of each factor are derived from the row and column sums of the reachable matrix R, respectively:

$$Q_i={\displaystyle \sum _{i=1}^n{r}_{ij}} (i=1,2,3\cdot \cdot \cdot ,n)$$

(11)

$$Y_i={\displaystyle \sum _{j=1}^n{r}_{ij}} (j=1,2,3\cdot \cdot \cdot ,n)$$

(12)

Using the calculated (Q_i) and (Y_i) values, a driving force–dependence matrix is constructed, categorizing the factors into four types: autonomous cluster, dependent cluster, linkage cluster, and independent cluster. This categorization helps clarify the functional roles of each factor within the value-added system.

3. Results and Analysis

3.1. Data Sources

In this study, ten experts were invited to participate in the scoring process. Among them, three were senior scholars from universities and research institutes specializing in EPC general contracting management, all of whom have led relevant research projects and contributed to standards development. Six experts were frontline managers from the 12th Division project in Urumqi, including heads of management, construction, and design departments, each deeply involved in the full-cycle management of EPC projects. Additionally, one expert was a department director from a government agency responsible for project management, possessing 20 years of experience in agency-based project management. The experts evaluated the interrelationships among the value-added factors of EPC projects by completing a questionnaire that utilized a five-point Likert scale ranging from 0 to 4. To ensure the reliability of the survey results, the experts’ opinions were subjected to reliability analysis using IBM SPSS Statistics 26.0, yielding a Cronbach’s α coefficient of 0.962. Since this value exceeds 0.80, the reliability of the survey results is deemed high.

3.2. Calculation Results

3.2.1. DEMATEL Results

The original matrix O is derived by summing the cumulative values, as presented in

Table 2. Original matrix O.

	S1	S2	S3	S4	S5	S6	S7	S8	S9	S10	S11	S12	S13	S14	S15	S16	S17	S18	S19	S20
S1	0	28	35	35	29	23	23	26	26	23	26	15	27	27	20	8	21	0	12	19
S2	7	0	10	22	14	22	28	31	27	12	7	18	8	26	2	6	18	0	0	7
S3	25	12	0	35	23	8	26	25	15	26	32	16	4	27	15	5	18	0	2	28
S4	13	9	16	0	5	8	25	23	19	28	15	17	2	21	3	4	7	0	6	22
S5	19	15	6	33	0	36	16	23	5	17	32	2	3	30	8	1	10	0	4	11
S6	6	24	5	26	30	0	15	30	4	14	12	2	5	36	5	6	12	0	1	4
S7	14	25	30	33	19	20	0	32	40	28	29	31	13	30	21	12	13	0	2	30
S8	10	30	19	30	15	32	33	0	28	24	34	9	4	36	13	8	17	0	0	22
S9	20	23	14	33	26	18	33	28	0	32	28	18	11	29	38	9	22	0	16	20
S10	13	6	18	33	25	11	22	26	22	0	24	9	5	22	11	6	22	0	11	13
S11	4	10	25	36	26	25	25	22	19	24	0	13	21	26	22	10	24	0	1	34
S12	21	19	28	35	25	11	27	25	26	18	26	0	34	24	38	17	35	0	14	8
S13	9	18	14	22	24	24	24	26	9	15	21	9	0	27	24	35	38	0	1	9
S14	8	25	18	27	31	28	26	37	11	25	20	6	18	0	16	25	25	0	8	12
S15	6	14	21	28	23	21	28	23	29	34	24	14	27	25	0	16	31	0	3	12
S16	2	15	21	23	23	8	23	10	10	28	22	12	27	23	19	0	39	0	4	7
S17	20	18	28	28	20	10	23	17	17	31	26	9	26	24	20	27	0	0	4	13
S18	16	8	11	19	8	12	15	8	14	11	13	10	16	12	13	29	16	0	28	11
S19	4	5	10	35	5	6	13	9	4	15	1	10	3	18	5	1	4	0	0	9
S20	13	8	25	30	20	8	17	13	13	20	30	5	9	19	8	17	20	0	7	0

. This calculation reflects the degree of influence among various value-added factors as evaluated by experts. Following this, the original matrix O is normalized through the application of Formulae (1) and (2) to produce the normative influence matrix N. The composite influence matrix T is then generated using Formula (3), as demonstrated in

Table 3. Composite influence matrix T.

	S1	S2	S3	S4	S5	S6	S7	S8	S9	S10	S11	S12	S13	S14	S15	S16	S17	S18	S19	S20
S1	0.120	0.226	0.257	0.358	0.266	0.229	0.280	0.292	0.236	0.274	0.280	0.152	0.181	0.309	0.193	0.131	0.237	0.000	0.077	0.204
S2	0.096	0.112	0.142	0.234	0.165	0.167	0.213	0.224	0.179	0.175	0.164	0.119	0.099	0.223	0.105	0.089	0.165	0.000	0.034	0.123
S3	0.155	0.164	0.154	0.312	0.219	0.167	0.248	0.250	0.185	0.244	0.258	0.135	0.113	0.266	0.158	0.105	0.198	0.000	0.048	0.199
S4	0.102	0.121	0.148	0.172	0.135	0.125	0.194	0.193	0.153	0.197	0.170	0.110	0.079	0.197	0.099	0.077	0.131	0.000	0.046	0.148
S5	0.116	0.140	0.129	0.251	0.130	0.194	0.181	0.202	0.126	0.179	0.210	0.079	0.084	0.226	0.109	0.073	0.141	0.000	0.041	0.129
S6	0.080	0.148	0.112	0.214	0.179	0.104	0.162	0.199	0.110	0.156	0.152	0.070	0.078	0.220	0.092	0.076	0.132	0.000	0.030	0.100
S7	0.154	0.224	0.252	0.360	0.250	0.225	0.236	0.309	0.271	0.290	0.292	0.189	0.156	0.320	0.201	0.142	0.226	0.000	0.058	0.231
S8	0.126	0.210	0.200	0.311	0.211	0.225	0.272	0.206	0.219	0.248	0.267	0.124	0.116	0.296	0.158	0.116	0.203	0.000	0.045	0.191
S9	0.162	0.215	0.213	0.353	0.258	0.217	0.300	0.294	0.181	0.293	0.283	0.158	0.149	0.311	0.231	0.133	0.238	0.000	0.086	0.205
S10	0.116	0.133	0.172	0.276	0.200	0.153	0.214	0.225	0.178	0.163	0.215	0.106	0.100	0.228	0.132	0.094	0.184	0.000	0.062	0.148
S11	0.115	0.166	0.213	0.323	0.234	0.209	0.254	0.252	0.197	0.248	0.196	0.131	0.153	0.274	0.178	0.123	0.219	0.000	0.047	0.215
S12	0.171	0.214	0.252	0.369	0.266	0.210	0.299	0.298	0.245	0.275	0.290	0.124	0.206	0.312	0.241	0.159	0.278	0.000	0.084	0.187
S13	0.119	0.180	0.184	0.283	0.224	0.203	0.245	0.252	0.171	0.223	0.234	0.119	0.107	0.269	0.178	0.175	0.246	0.000	0.043	0.154
S14	0.119	0.197	0.194	0.300	0.240	0.215	0.253	0.280	0.178	0.246	0.235	0.114	0.144	0.215	0.161	0.151	0.218	0.000	0.060	0.164
S15	0.124	0.182	0.213	0.319	0.237	0.209	0.271	0.265	0.228	0.280	0.258	0.139	0.173	0.283	0.138	0.141	0.244	0.000	0.054	0.175
S16	0.097	0.158	0.186	0.266	0.206	0.154	0.226	0.201	0.160	0.234	0.220	0.117	0.156	0.241	0.158	0.090	0.234	0.000	0.047	0.139
S17	0.148	0.183	0.221	0.307	0.222	0.177	0.251	0.241	0.194	0.264	0.252	0.124	0.166	0.269	0.175	0.159	0.169	0.000	0.053	0.171
S18	0.109	0.120	0.140	0.219	0.144	0.135	0.176	0.161	0.142	0.165	0.166	0.097	0.116	0.182	0.124	0.137	0.157	0.000	0.096	0.124
S19	0.054	0.072	0.090	0.181	0.085	0.078	0.114	0.108	0.077	0.117	0.085	0.067	0.051	0.131	0.065	0.044	0.078	0.000	0.020	0.081
S20	0.110	0.128	0.179	0.257	0.181	0.137	0.192	0.186	0.150	0.197	0.217	0.092	0.104	0.210	0.119	0.114	0.173	0.000	0.050	0.112

.

The influencing degree (D_i), influenced degree (C_i), centrality (M_i), and causality (R_i) of each influencing factor were calculated using Formulae (4)–(7), as shown in

Table 4. Calculation results of value addition influencing factors.

Factors	Di	Ci	Mi	Ri	Attributes
S1	4.301	2.396	6.697	1.905	CF
S2	2.827	3.294	6.121	−0.467	OF
S3	3.578	3.651	7.229	−0.073	OF
S4	2.599	5.665	8.264	−3.066	OF
S5	2.739	4.051	6.790	−1.312	OF
S6	2.411	3.533	5.944	−1.122	OF
S7	4.386	4.580	8.966	−0.194	OF
S8	3.747	4.638	8.385	−0.891	OF
S9	4.282	3.581	7.863	0.701	CF
S10	3.098	4.467	7.565	−1.369	OF
S11	3.746	4.443	8.189	−0.697	OF
S12	4.480	2.368	6.848	2.112	CF
S13	3.609	2.529	6.138	1.080	CF
S14	3.686	4.983	8.669	−1.297	OF
S15	3.933	3.016	6.949	0.917	CF
S16	3.290	2.330	5.620	0.960	CF
S17	3.747	3.871	7.618	−0.124	OF
S18	2.713	0.000	2.713	2.713	CF
S19	1.595	1.080	2.675	0.515	CF
S20	2.909	3.200	6.109	−0.291	OF

. Here, OF represents the outcome factor, while CF denotes the cause factor.

To facilitate a clearer and more intuitive analysis of the attributes and characteristics of each factor, a cause–effect diagram was constructed, with centrality (M_i) represented on the x-axis and causality (R_i) on the y-axis [46], as illustrated in Figure 3.

3.2.2. TAISM Results

The inherent relationship between DEMATEL and TAISM allows the overall influence matrix H to be transformed into a reachable matrix R. To determine the threshold λ that ensures the hierarchical structure objectively reflects the system’s interaction nature, the mean (μ_H) and standard deviation (σ_H) of all elements in the overall influence matrix H are first calculated. Using the formula (λ = μ_H + σ_H), a baseline value of (λ = 0.227) is obtained. A sensitivity analysis is then conducted by comparing the hierarchical structure variations within the interval (λ ± 0.03) (i.e., 0.197 to 0.257). The results confirm that (λ = 0.227) optimally preserves the key pathways (e.g., S₁₂ → S₉ → S₁₄ → S₄) while eliminating redundant associations. This outcome is consistent with the practical evaluations of experts in the relevant field [47,48,49]. Ultimately, the reachable matrix R is constructed based on this threshold using Formulae (8) and (9).

Following this, the general skeleton matrix S was calculated according to step (6) and Formula (10). In the resulting matrix, the entries with a value of 1 in S were replaced by their corresponding comprehensive influence values, while the remaining elements (representing loops) were left unchanged. This process yielded a matrix with influence values WS, as presented in

Table 5. Matrix with influence values WS.

	S1	S2	S3	S4	S5	S6	S7	S8	S9	S10	S11	S12	S13	S14	S15	S16	S17	S18	S19	S20
S1	0	0	0.257	0	0	0.229	0	0	0.236	0	0	0	0	0	0	0	0	0	0	0
S2	0	0	0	0.234	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
S3	0	0	0	0	0	0	0.248	0	0	0	0	0	0	0.266	0	0	0	0	0	0
S4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
S5	0	0	0	0.251	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
S6	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
S7	0	0	0	0	0.250	0	0	1	0	0.290	1	0	0	0	0	0	0	0	0	0.231
S8	0	0	0	0	0	0	1	0	0	0	1	0	0	0	0	0	0	0	0	0
S9	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0.238	0	0	0
S10	0	0	0	0.276	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
S11	0	0	0	0	0	0	1	1	0	0	0	0	0	0	0	0	0	0	0	0
S12	0	0	0.252	0	0	0	0	0	0.245	0	0	0	0	0	0.241	0	0	0	0	0
S13	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0.246	0	0	0
S14	0	0	0	0	0.240	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
S15	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0.244	0	0	0
S16	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0.234	0	0	0
S17	0	0	0	0	0	0	0.251	0	0	0	0	0	0	0.270	0	0	0	0	0	0
S18	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
S19	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
S20	0	0	0	0.257	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0

.

Based on the hierarchical extraction method outlined in Section 2.5. (8), the results of the antagonistic hierarchy extraction are presented in

Table 6. Antagonistic hierarchy extraction results.

Level	Result-Prioritized UP Type	Cause-Prioritized DOWN Type
Level 0	S4, S6, S18, S19	S4
Level 1	S2, S5, S10, S20	S5, S10, S20
Level 2	S7, S8, S11, S14	S7, S8, S11, S14
Level 3	S3, S17	S17
Level 4	S9, S13, S15, S16	S3, S6, S9, S15
Level 5	S1, S12	S1, S2, S12, S13, S16, S18, S19

.

To further analyze the interdependent relationships among various factors, a directed topological hierarchy diagram was constructed based on the results shown in Table 6. This diagram uses arrow lines to represent reachable directed relationships, thereby intuitively illustrating the influence paths between factors. As depicted in Figure 4, the hierarchical architecture of the UP-type and DOWN-type directed topological structures is detailed, with factors clustered and layered according to their reachable interaction relationships.

3.2.3. MICMAC Results

The driving force and dependency for each factor were computed based on the reachable matrix R and Formulae (11) and (12). The results are summarized in

Table 7. Driving force (Q_i) and dependence (Y_i) of value-added influencing factors.

Factors	Qi	Yi	Factors	Qi	Yi
S1	12	1	S11	7	11
S2	2	1	S12	12	1
S3	7	4	S13	7	1
S4	1	17	S14	7	13
S5	2	8	S15	10	3
S6	1	2	S16	5	1
S7	10	11	S17	7	7
S8	6	11	S18	1	1
S9	10	5	S19	1	1
S10	3	12	S20	2	2

.

Based on the results presented in Table 7, a driving force–dependence matrix was constructed. The matrix is divided into four quadrants, representing the autonomous cluster, dependent cluster, connected cluster, and independent cluster, as illustrated in Figure 5.

3.3. Results Analysis

3.3.1. DEMATEL Analysis

Centrality (M_i) is defined as the sum of the influencing degree (D_i) and the influenced degree (C_i). A higher centrality degree indicates a more significant impact on value addition [50]. As illustrated in Figure 3, the top-ranked factors by centrality—S₇, S₁₄, S₈, S₄, and S₁₁—exert significant bidirectional influences, meaning they both influence and are influenced by other factors. These factors are thus critical in the value-added process of government-invested EPC projects. These findings suggest that project stakeholders should prioritize the control and optimization of these factors to enhance value.

Causality (R_i) quantifies the net influence of a factor, calculated as D_i − C_i. A positive R_i indicates a driving factor, where a higher R_i value signifies a stronger influence, while a negative R_i indicates a passive factor, where a lower R_i value signifies a greater susceptibility [51]. Figure 3 reveals that S₁₈, S₁₂, S₁, S₁₃, and S₁₆ are dominant driving factors. Prioritizing and controlling these factors facilitates effective decision-making, thereby enhancing project value addition.

3.3.2. TAISM Analysis

(1)

Isolated Factor Analysis

From the directed topological hierarchy diagram (Figure 4), factors S₁₈ and S₁₉ are identified as isolated, exhibiting no significant influence relationships with other factors. In the composite influence matrix T, the row and column sums for S₁₈ and S₁₉ fall below the threshold value λ. Consequently, these isolated factors are excluded from subsequent analyses to facilitate a more focused systemic investigation.

(2)

Hierarchical and Causal Chain Analysis

Analysis of Figure 4 indicates that both UP-type and DOWN-type structural models are divided into six hierarchical levels. After excluding isolated factors, the resulting causal chains are presented in

Table 8. Causal chains.

UP Type	{S4, S6, S18, S19} ≻ {S2, S5, S10, S20} ≻ {[S7, S8, S11], S14} ≻ {S3, S17} ≻ {S9, S13, S15, S16} ≻ {S1, S12}
DOWN Type	{S4} ≻ {S5, S10, S20} ≻ {[S7, S8, S11], S14} ≻ {S17} ≻ {S3, S6, S9, S15} ≻ {S1, S2, S12, S13, S16, S18, S19}

. Notably, factors [S₇, S₈, S₁₁] form a feedback loop, establishing a tightly interconnected cycle.

(3)

Analysis of Root-Level Factors, Transitional-Level Factors, and Direct-Level Factors

As illustrated in Figure 4, the factors influencing the value-added outcome of government-invested EPC projects form a six-level topological structure. The directed segments represent causal relationships, with two distinct transmission chains that do not overlap, consistent with the characteristics of complex activity systems. The structure can be divided into three functional levels: the root level (L5), the transitional level (L1–L4), and the direct level (L0).

The root level (L5) consists of factors S₁, S₂, S₁₂, S₁₃, and S₁₆, which establish the logical foundation for the value-added process. Factors within this layer exhibit outward-directed associations (divergent arrows), indicating that they influence other factors, either directly or indirectly. As the primary components of the system, these factors have a fundamental, foundational impact on value addition.

The transitional level (L1–L4) includes factors S₃, S₅, S₇, S₈, S₉, S₁₀, S₁₁, S₁₄, S₁₅, S₁₇, and S20. These factors act as hubs for the transmission of influence across levels. They possess dual roles: transmitting the influence of higher-level factors and, simultaneously, serving as independent sources of influence for other factors. Situated at the intermediate level of the system, these factors form the core transmission network for value addition and should receive prioritized attention during project implementation.

The direct level (L0) includes the terminal factors S₄ and S₆, which represent the endpoint for value addition and are highly sensitive to upstream influences. This level provides the most direct pathway for realizing value-added outcomes. However, due to its vulnerability to disturbances from preceding factors, a systems-level approach must be applied in management. When intervening in factors in the direct layer, it is essential to concurrently manage the influencing factors from the upstream layers to ensure coordinated and effective outcomes.

3.3.3. MICMAC Analysis

(1)

Analysis of Factor Roles in the Four MICMAC Quadrants

Based on the driving force–dependence diagram (Figure 5), the 20 value-added influencing factors are distributed across the four quadrants according to their driving force and dependence.

1.

Autonomous Cluster (S₂, S₆, S₁₆, S₁₈, etc.): Low Driving Force, Low Dependence

As boundary stabilizers of the system, these factors exhibit minimal internal–external interaction. Such factors are predominantly external environmental variables, independent of the internal feedback loops of the system. For example, S₂ (simplification bidding and procurement processes) primarily impacts procurement-related activities and has a relatively limited influence on the overall project. Similarly, S₁₈ (policy support) is a typical exogenous policy variable, and its dual-low characteristic indicates its independence from the project’s governance system (e.g., S₁–S₁₇). The bidirectional positioning in the directed topological hierarchy diagram (Figure 5) further corroborates this feature.

2.

Dependent Cluster (S₄, S₅, S₈, S₁₀): Low Driving Force, High Dependence

These factors represent the terminal output indicators of the system, exhibiting weak self-influence while being highly governed by upstream factors. They reflect the outcomes of system operations and necessitate optimization of the driving chain for improvement. S₄ (reduction of contract disputes and claims) is a quintessential dependent factor. It is a consequence of conflict management rather than a causal factor. Its high dependence arises from multiple antecedent influences, such as S₁ (detailed and explicit contractual clauses) and S₁₀ (establishment of an effective change management mechanism). Conversely, its low driving force indicates that the reduction of disputes is fundamentally a byproduct of system collaboration and cannot be directly influenced.

3.

Linkage Cluster (S₇, S₉, S₁₁, S₁₇, etc.): Moderate-to-High Driving Force, Moderate-to-High Dependence

These factors serve as dynamic transmission hubs within the system, combining significant influence with high sensitivity. They exhibit bidirectional feedback characteristics and can trigger cascading effects throughout the system. For instance, S₇ (integrated management and coordination) influences multiple areas, such as S₁₀ (establishment of an effective change management mechanism), while its effectiveness is also affected by factors like S₃ (rational allocation of rights, responsibilities, and benefits). S₇ plays a critical linkage role within the project management system, where any changes in one aspect can impact the entire project’s operation.

4.

Independent Cluster (S₁, S₃, S₁₂, S₁₅, etc.): High Driving Force, Low Dependence

These factors represent the fundamental driving sources of the system, exerting strong proactive influence and remaining largely unaffected by other factors. Typically, these factors correspond to the system’s infrastructure or strategic-level variables, governing the long-term evolution of the system. For example, S₁₂ (collaborative participation in early planning and design phases) anchors the technological roadmap and resource framework through multi-stakeholder collaborative decision-making during the project initiation phase. Its high driving force arises from the constraints it imposes on subsequent processes, while its low dependence is attributed to the autonomy granted by policy enforcement.

(2)

Cross-Validation Analysis

A comparison of the results from DEMATEL and MICMAC analyses reveals a high degree of consistency in the classification of core factors (Cohen’s Kappa coefficient = 0.922). Specifically, the causal factors (causal degree > 0) identified in DEMATEL, such as S₁₂, correspond to high driving force and low dependence within the independent cluster of MICMAC. Similarly, result factors (causal degree < 0), exemplified by S₄, are characterized as low driving force and high dependence factors within the dependent cluster of MICMAC. Transition factors (causal degree close to 0), such as S₁₇, demonstrate a balanced driving force and dependence, categorizing them as linkage clusters in MICMAC. Key matching points further validate this consistency, with strong driving factors (S₁, S₉, S₁₂, S₁₅) and strong dependent factors (S₄, S₅, S₁₀, S₁₄) being fully aligned across both methods, alongside autonomous factors (S₁₈, S₁₉) that logically correspond. It is noteworthy that the analysis of S₇ further reinforces this consistent understanding. As a resultant factor in DEMATEL, its high dependency directly reflects significant upstream influence, which is fully consistent with the high dependency identified by MICMAC. Furthermore, MICMAC reveals the strong driving force of S₇ that may be masked by net influence calculations, thereby highlighting the dual influence characteristics of this node through its two-dimensional coordinates. Consequently, the interpretations of S₇ by both methods are essentially unified, with MICMAC providing additional insights into the downstream transmission mechanisms that are not fully characterized by DEMATEL.

Due to the distinct analytical frameworks of the MICMAC classification and TAISM hierarchy, their relationship cannot be validated through conventional consistency testing methods. Instead, consistency characteristics can only be explored through comparative analysis. The comparison results indicate notable correspondence between the two methods in terms of overall characteristics. Specifically, the cause-prioritized (DOWN type) higher levels in TAISM align with the independent cluster (high driving force) in MICMAC, exemplified by S₁ and S₁₂, both situated at the fifth level (the highest level). Conversely, the result-prioritized (UP type) lower levels correspond to the dependent cluster (high dependence) in MICMAC, with S₄ positioned at the 0th level (the lowest level). The linkage cluster in the intermediate levels reveals a balanced driving force and dependence in both methodologies, as seen with S₁₇, which is located at the third level of the UP type and the third level of the DOWN type. Key consistency verification further corroborates the alignment between fundamental causes and terminal results as well as the specific positioning of autonomous factors (S₁₈, S₁₉) within both the UP type and DOWN type. Despite minor discrepancies—such as S₃ exhibiting a higher driving force than dependence and being closer to the cause side in the DOWN type, and S₉ necessitating slight adjustments due to a marginally lower driving force—these differences can be attributed to the nuanced handling of transmission pathways between factors in TAISM.

In summary, the cross-validation results of DEMATEL, MICMAC, and TAISM confirm the overall accuracy of the research model. The triangular validation establishes a closed loop, with the causal attributes identified by DEMATEL, the driving force–dependence relationships established by MICMAC, and the hierarchical pathways delineated by TAISM mutually corroborating one another. Core factors such as S₁, S₄, S₁₂, S₁₈, and S₁₉ demonstrate consistent attributes across all three methods. The minor differences observed for transitional factors, such as S₃ and S₇, can be reasonably attributed to the varying analytical dimensions and the depth of transmission logic characterization inherent in different methods. Specifically, the discrepancy in S₃ arises from TAISM’s refined identification of the relative relationship between driving force and dependency in its hierarchical path analysis. In contrast, the difference in S₇ stems from the dimensional distinctions between DEMATEL’s emphasis on net influence calculation and MICMAC’s two-dimensional coordinate analysis. While DEMATEL does not fully reveal S₇’s potential driving force, MICMAC provides a more comprehensive depiction of its dual influence characteristics. The final assessment substantiates the scientific validity of the calculations, the completeness of the data logical chain, and the consistency of all findings within an acceptable methodological framework, thereby validating the reliability and coherence of the research conclusions.

3.4. Case Data Validation of Model Conclusions

To validate the scientific rigor and applicability of the integrated DEMATEL–TAISM–MICMAC model developed in this study, we conducted an empirical data validation using real-world case studies of government-invested EPC projects [39]. This validation was performed across two dimensions: the direct influence of individual factors and the multi-level transmission pathways. The selected cases not only demonstrate a high degree of consistency between our theoretical findings and real-world scenarios but also provide further insights into the specific manifestations and influence pathways of the value-added mechanism in practice.

1.

Empirical Evidence of the Direct Impact Mechanism of Fundamental Driving Factor S₁₂

In the construction of the Second Middle School for the Twelfth Division of the Production and Construction Corps [52], the owner (the Education Bureau) failed to fully assess the functional requirements in the early stages of the project, resulting in unclear specifications for air-raid shelters. Consequently, facilities such as basketball courts had to be added during the middle stages of the project. This dynamic change in requirements necessitated iterative revisions to the contract terms, ultimately leading to a design change rate of 35%, which significantly increased project costs and extended the construction period. These modifications resulted in additional costs totaling CNY 21.54 million. Similarly, in the construction of the 12th Division Five Halls and One Center [53], the use of unapproved drawings led to conflicts in steel plate shear walls, requiring the demolition and reconstruction of reinforced walls. This delay spanned 62 critical days, equivalent to 34.4% of the contract period, and resulted in an extra cost of CNY 8.4 million. These instances highlight that the absence of S₁₂ directly triggers failures in cost and schedule targets due to design defects and engineering changes. The magnitude of these impacts aligns closely with the high causal degree (R_i = 2.112) attributed to S₁₂ by the DEMATEL model.

2.

Empirical Evidence of the Hierarchical Role of S₁/S₁₂ Under Multi-Level Transmission Pathways

In the construction of the fruit and vegetable cold storage facility for the Twelfth Division of the Production and Construction Corps [54], the absence of S₁₂ (failure to confirm municipal requirements) and S₁₈ (policy mismatch with the pipeline network) resulted initially in information breakdown in S₉ and technical disconnect in S₁₅ (omission of power supply/drainage items). This cascade effect ultimately led to resource misallocation in S₁₄ (inability to operate) and incurred sunk costs in S₄ (CNY 98 million investment scrapped). Similarly, in the construction of the Sanping Farm Hospital [55], the absence of S₁ (contractual constraints on change responsibilities) triggered an imbalance in S₃ responsibilities (abuse of power by the owner) and compromised S₁₀ mechanisms (informal verbal instructions replacing formal procedures). This directly escalated costs in S₄ (30% increase in building area, exceeding the budget by CNY 34.93 million). These cross-case findings mirror the DOWN-type topological path identified by TAISM (root level → transitional level → direct level), validating that root-level factors significantly influence value degradation in government EPC projects through organizational and technological transmission chains.

4. Discussion

To ensure the economic benefits and overall efficiency of government-invested EPC projects and achieve value addition, it is necessary to systematically build a control system from three levels: direct, transitional, and root. These three layers support and influence each other, collectively determining the project’s economic benefits and overall efficiency. The following analysis will systematically examine the key control factors and corresponding management strategies for each level to construct a comprehensive and in-depth project governance framework.

1.

Precise Control of Direct-level Factors to Ensure the Economic Benefits of EPC Project Construction

In government-invested EPC projects, the direct-level factors are pivotal for safeguarding the project’s economic outcomes. Inadequate management of these factors can result in substantial economic losses, which are both immediate and directly observable.

Factor S₄ (reduction of contract disputes and claims) plays a critical role in protecting the economic interests of the project. It is essential for swiftly addressing disputes and minimizing the escalation of improper costs. However, the effectiveness of S4 is heavily contingent upon the stability of upstream processes. Specifically, ambiguities in contract terms at the root level and inefficiencies in change management during the transitional phase can exacerbate risks, increasing the likelihood of claims and disputes, which ultimately diminish project profits. To optimize the effectiveness of S4, it is crucial to continuously monitor contract performance, implement proactive dispute resolution mechanisms, and establish systematic claim prevention strategies. These measures will mitigate value losses caused by upstream risk transmission.

Similarly, S₆ (control of material and equipment procurement costs) is instrumental in determining the competitiveness of the project’s cost baseline; effective cost optimization requires accurate market insights and strong negotiation strategies. However, the performance of S₆ is highly sensitive to fluctuations in upstream and midstream factors. Design oversights or disruptions within the supply chain may lead to procurement cost premiums and project delays, resulting in compounded economic losses. Thus, dynamic cost monitoring and flexible procurement strategies should be incorporated, along with rapid supplier coordination and contingency planning. This proactive approach will enable the real-time detection of cost deviations and prompt adjustments to procurement strategies, thus preventing cost escalations and mitigating schedule risks stemming from design flaws or supply disruptions.

The overall aim of controlling direct-level factors is to establish a robust defense that intercepts upstream risks before they impact the project’s economic value. This strategy reinforces the protective barrier surrounding the project’s economic benefits.

2.

Strengthening Transitional-level Management to Enhance Overall EPC Project Efficiency

The transitional level plays a critical role in EPC projects by serving as the value transmission hub between root-level and direct-level factors. Optimizing the management of transitional-level factors is crucial for enhancing overall project efficiency and preventing the cross-level transmission of risks. Failure to manage this level effectively can result in stagnation of value-added pathways and exacerbate risks, severely undermining project performance.

S₇ (integrated management and coordination) functions as a strategic lever for dismantling professional silos and promoting multi-stage collaboration. Its core objective is to systematically eliminate information barriers through integrated cross-functional platforms (e.g., Project Management Information Systems—PMIS) and establish regular coordination mechanisms. The effectiveness of S₇ is crucial for ensuring the seamless transmission of value across upstream and downstream stages. If S₇ is poorly implemented, root-level design improvements may fail to transition effectively into procurement and construction phases. Additionally, procurement control and dispute mitigation at the direct level may become ineffective due to communication breakdowns, leading to resource misallocation, schedule delays, and interface conflicts. Ensuring the efficient functioning of the S₇ mechanism is, therefore, essential for fostering deep collaboration and the dynamic adaptation of resources across design, procurement, and construction stages.

S₈ (optimized supply chain management) serves as a vital safeguard, ensuring timely and cost-effective resource availability while mitigating the risks associated with supply disruptions. Key strategies include tiered supplier management, strategic agreements, and optimized logistics planning. The stability of S₈ is paramount for maintaining project continuity. During execution, disruptions in the supply chain or improper resource allocation can compromise procurement cost control, leading to cost overruns and delays. Moreover, these disruptions may necessitate adjustments to root-level designs, initiating a cascade of changes that deplete project value. Therefore, it is essential to establish an agile supply chain governance framework, supported by risk-buffering mechanisms, to ensure the uninterrupted delivery of critical resources. This will help shield the design and cost management layers from the adverse effects of supply fluctuations.

S₁₁ (continuous monitoring and performance evaluation) serves as the central mechanism for dynamically calibrating project objectives and fostering continuous improvement. By implementing a multidimensional KPI system that encompasses quality, cost, schedule, safety, and compliance, coupled with periodic diagnostics and early-warning feedback, S₁₁ provides real-time monitoring of project progress and deviations. Its key function is to deliver data-driven insights that inform decision-making at all levels of the project. In the absence of S₁₁, deviations at the root level would remain unaddressed, compromising the effectiveness of transitional-level coordination and supply chain management, which would ultimately undermine direct-level protections. The data generated by S₁₁, therefore, acts as the driving force for refining root-level strategies, optimizing transitional-level processes, and adjusting direct-level controls, ensuring that the project remains on course.

The S₇–S₈–S₁₁ coordination framework creates a closed-loop system that integrates resource management, process coordination, and dynamic regulation. This system bridges the value transmission gap between the root and direct levels, significantly reducing the risk of cross-level risk amplification. Through continuous performance feedback, this framework facilitates comprehensive efficiency improvements, establishing a Pareto improvement paradigm that enhances the overall efficiency of government-invested EPC projects throughout their lifecycle.

3.

Implementing Root-level Strategies to Establish a Solid Foundation for EPC Project Construction

Root-level factors form the bedrock upon which both the economic benefits and overall efficiency of EPC projects are built. Inadequate management of these factors can initiate risk transmission downstream, leading to the erosion of project value and benefits.

S₁ (detailed and explicit contractual clauses) is the foundational safeguard for risk management, ensuring clear definitions of rights, responsibilities, and risk allocation. A well-structured contract provides legal certainty and fosters collaborative stability throughout the project’s execution phase. The clarity of S₁ is crucial in preventing downstream disputes. Previous case studies have demonstrated that ambiguous or poorly defined contract terms are often the root cause of subsequent disputes and claims, amplifying risks during execution. Therefore, investing adequate resources in contract negotiation and refinement during the initiation phase is critical to establishing a solid risk management foundation. This ensures that root-level issues do not evolve into direct conflicts that impact value addition.

S₁₂ (collaborative participation in early planning and design phases) represents a strategic initiative for optimizing design and mitigating source risks. By adopting the Integrated Project Delivery (IPD) model or conducting cross-disciplinary workshops, early collaboration between owners, designers, contractors, key suppliers, and government approval agencies can be facilitated during the conceptualization and schematic design phases. The primary benefit of S₁₂ lies in ensuring that the design solutions are constructible, procurable, and optimized for the project’s lifecycle. However, the effectiveness of S₁₂ is contingent upon the depth of collaboration; insufficient early-stage coordination often results in design defects that initiate a chain of events including cost overruns, frequent revisions, and schedule delays. Strengthening early-stage collaboration, therefore, helps reduce rework costs, enhances overall coordination, and lays a solid foundation for project value addition.

Implementing root-level strategies is akin to establishing a strong foundation for the entire project. By focusing on robust contractual frameworks and optimizing design solutions from the outset, risks can be effectively contained in the early stages, preventing their escalation and ensuring the long-term economic success and efficiency of the project throughout its lifecycle.

Based on the preceding analysis, the implementation of a systematic three-tiered governance model—encompassing the root, transitional, and direct layers—is crucial for ensuring the economic viability and enhancing the value addition of government-invested EPC projects. These three layers are interconnected and mutually reinforcing, forming an organically integrated management framework that mitigates risks and promotes seamless project delivery.

In accordance with the scientific findings presented in previous chapters, this study confirms its core hypothesis: the integrated DEMATEL–TAISM–MICMAC model provides a comprehensive analytical framework capable of effectively revealing the value-added mechanism in government-invested EPC projects. The empirical results are highly consistent with our hypothesis, proving the model’s robustness in dissecting complex value-added pathways and supporting strategic formulation.

5. Conclusions

This study explores value-added pathways of government-invested EPC projects by developing a novel DEMATEL–TAISM–MICMAC hybrid model. Key findings reveal that S₁ (detailed and explicit contractual clauses) and S₁₂ (collaborative participation in early planning and design phases) serve as fundamental drivers of value addition. The value-added process follows a hierarchical transmission path, progressing strategically from the root level (strategic decision-making) through the transitional level (process management) to the direct level (performance output). Furthermore, influencing factors are categorized into four distinct functional clusters: autonomous cluster, dependent cluster, connected cluster, and independent cluster. Theoretically, this work validates the efficacy of hybrid modeling in deciphering complex value-added systems and advances the understanding of underlying value-added mechanisms in EPC project delivery. Practically, the identified hierarchical structure offers a scientifically grounded strategy for optimizing project management systems.

However, the study acknowledges limitations regarding sample diversity across regions, the depth of capturing nonlinear dynamic relationships, and the practical implementation of cross-departmental collaboration strategies. Future research should expand sample sizes across diverse geographical contexts to elucidate differentiated characteristics of value-added pathways. Developing dynamic models integrating fuzzy set theory (e.g., fuzzy DEMATEL, system dynamics) is recommended to provide more accurate characterization of nonlinear factor interactions and system evolution. Additionally, integrating complex network analysis, system resilience concepts, and fuzzy theory could facilitate the construction of a multidimensional evaluation framework encompassing sustainability, interaction mechanisms, and uncertainty. Such focused investigations hold significant potential for enhancing the model’s explanatory power and practical adaptability.