Dynamic Impact and Vibration Response Analysis of Steel–UHPC Composite Containment Under Aircraft Impact
Abstract
1. Introduction
2. FE Models of the Aircraft, S-UHPC Containment, and Validations
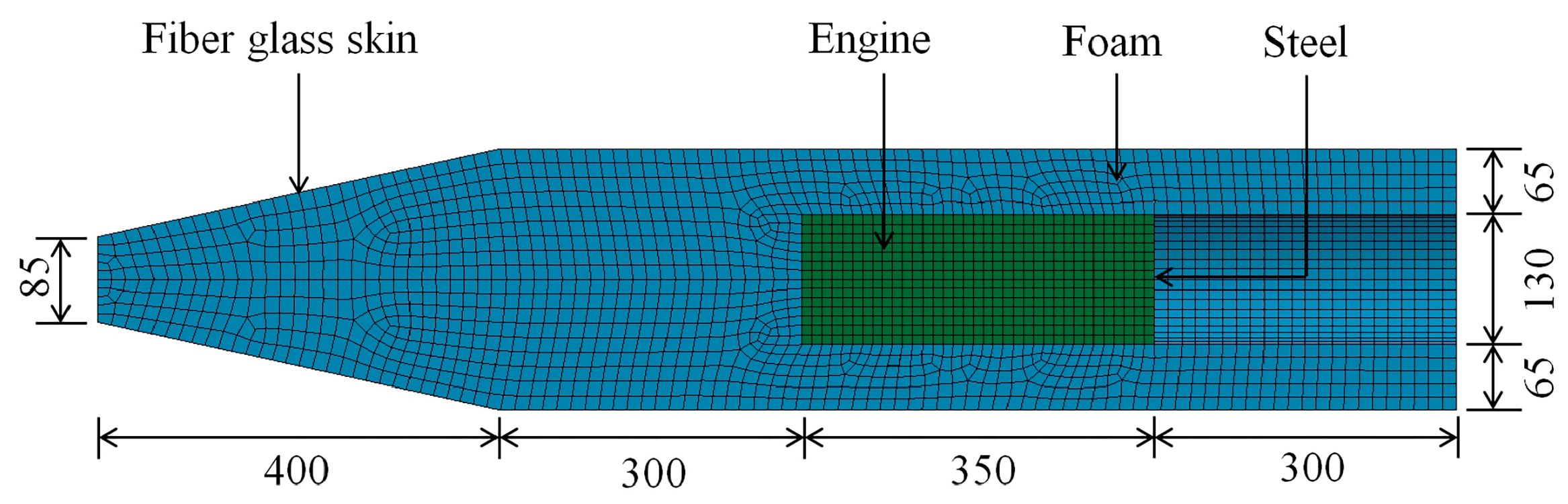
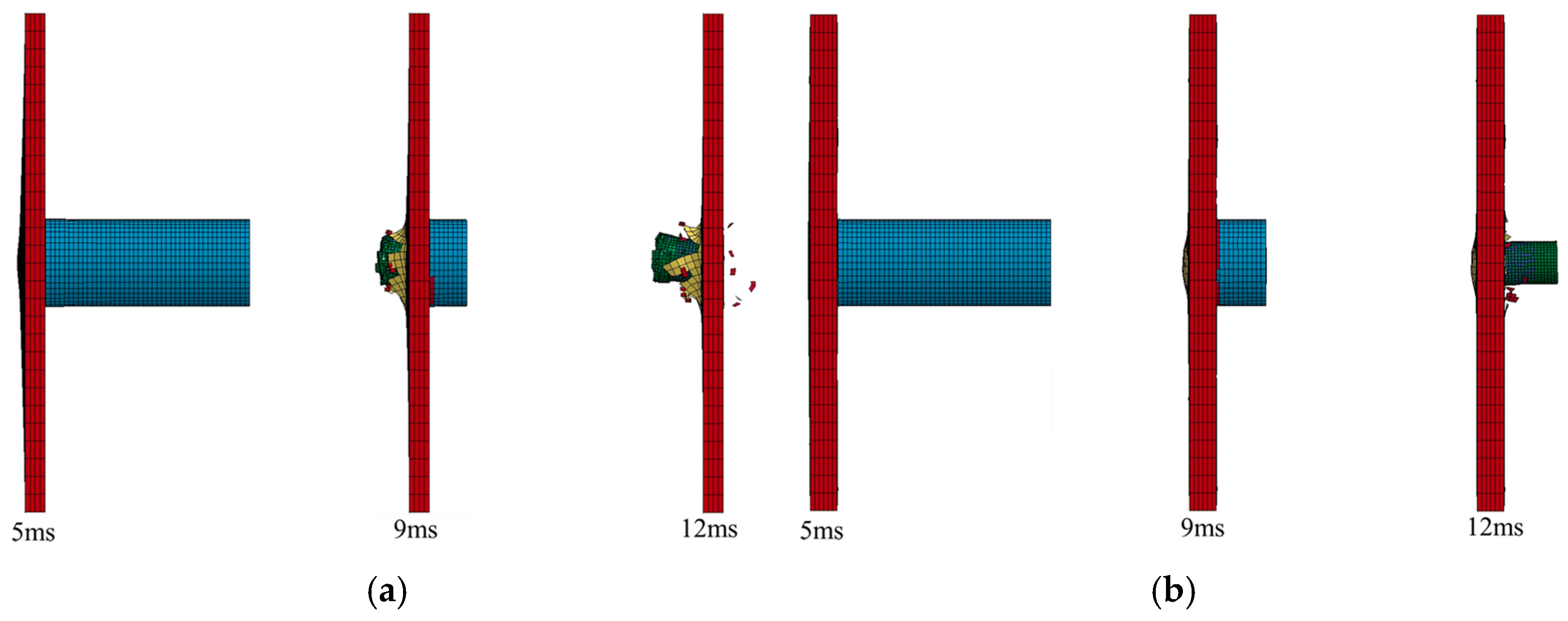
2.1. Aircraft
| Material | Aluminum | Steel |
|---|---|---|
| Density (kg/m3) | 2800 | 7830 |
| Young’s modulus (MPa) | 71,900 | 210,000 |
| Shear modulus (MPa) | 27,800 | 77,000 |
| Poisson’s ratio | 0.33 | 0.3 |
| A (MPa) | 369 | 350 |
| B (MPa) | 684 | 275 |
| N | 0.73 | 0.36 |
| C | 0.0083 | 0.022 |
| M | 1.7 | 1 |
| D1 | 0.13 | 0.05 |
| D2 | 0.13 | 3.44 |
| D3 | −1.5 | −2.12 |
| D4 | 0.011 | 0.002 |
| D5 | 0 | 0.61 |
| Material | Aluminum | Steel |
|---|---|---|
| Density (kg/m3) | 2800 | 7830 |
| Young’s modulus (MPa) | 71,900 | 210,000 |
| Poisson’s ratio | 0.33 | 0.3 |
| Yield stress (MPa) | 503 | 400 |
| Tangent modulus (MPa) | 690 | 1050 |
| C | 40 | 40 |
| p | 5 | 5 |
| FS | 0.05 | 0.1 |
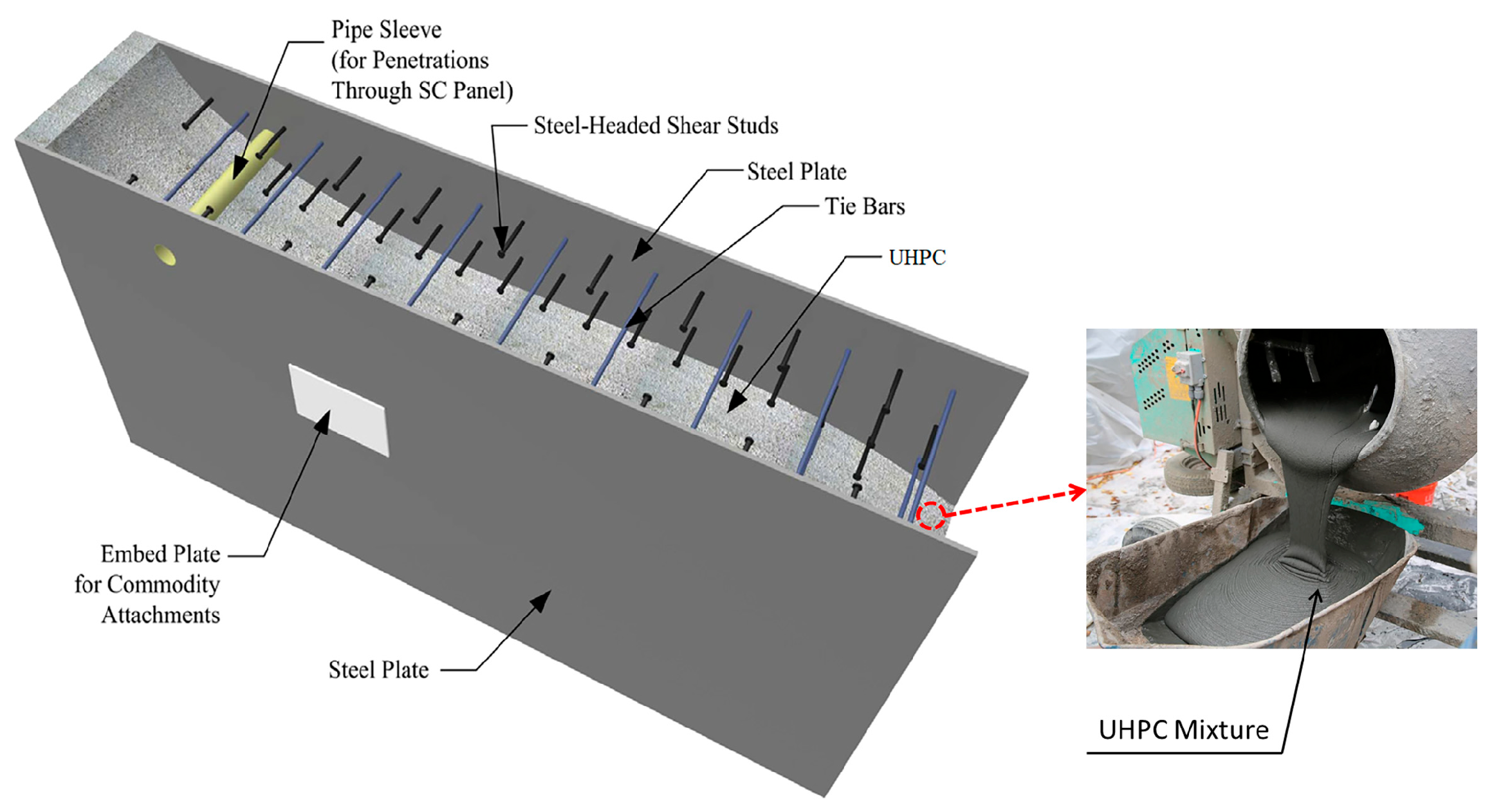
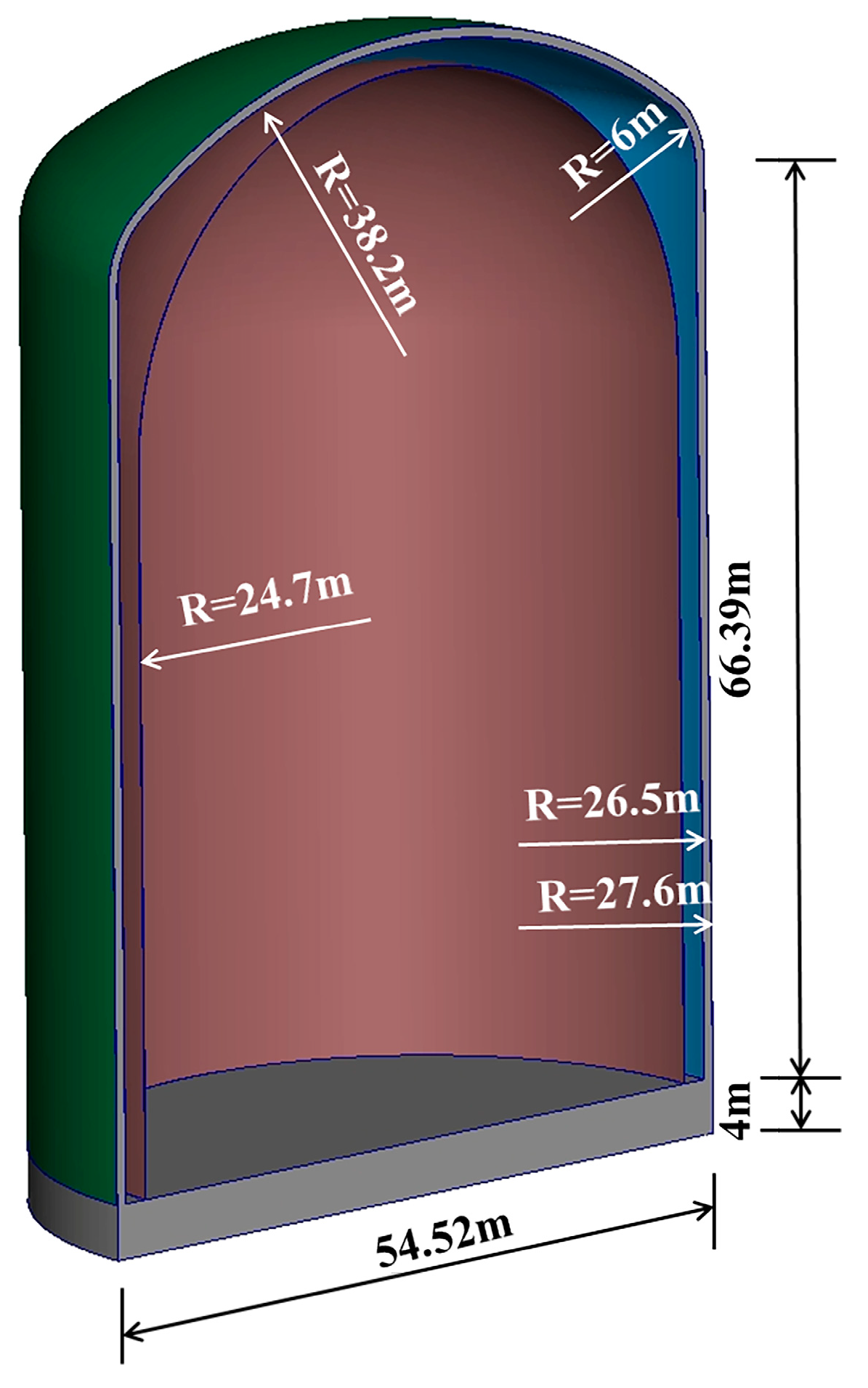
2.2. S-UHPC Containment
2.3. Model Validation
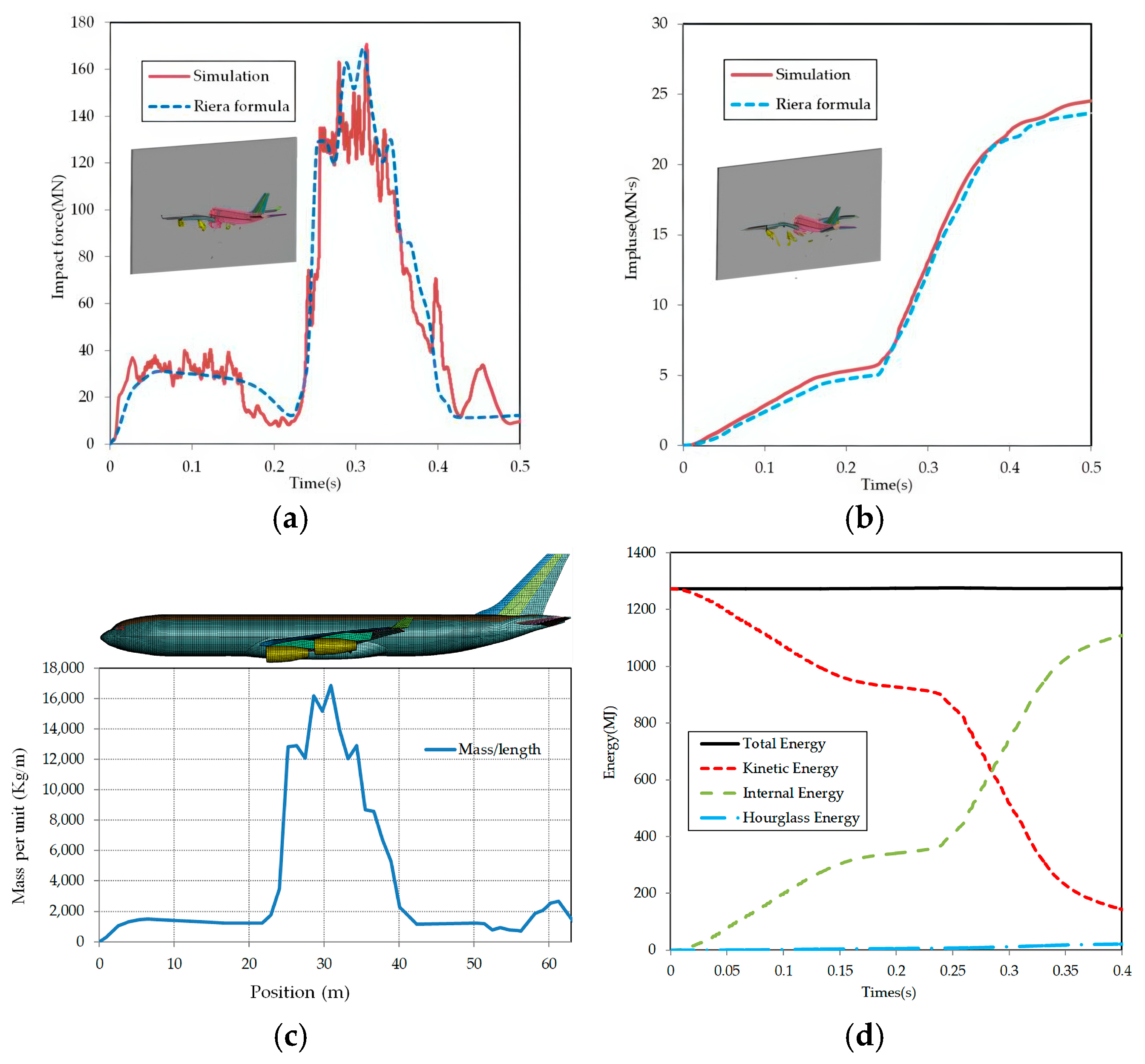
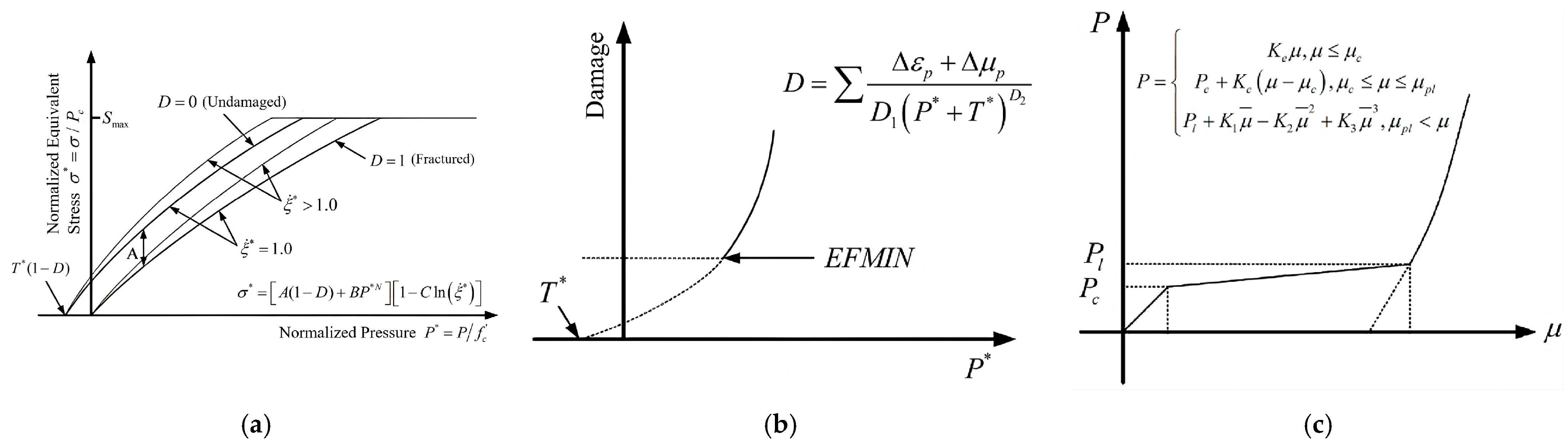
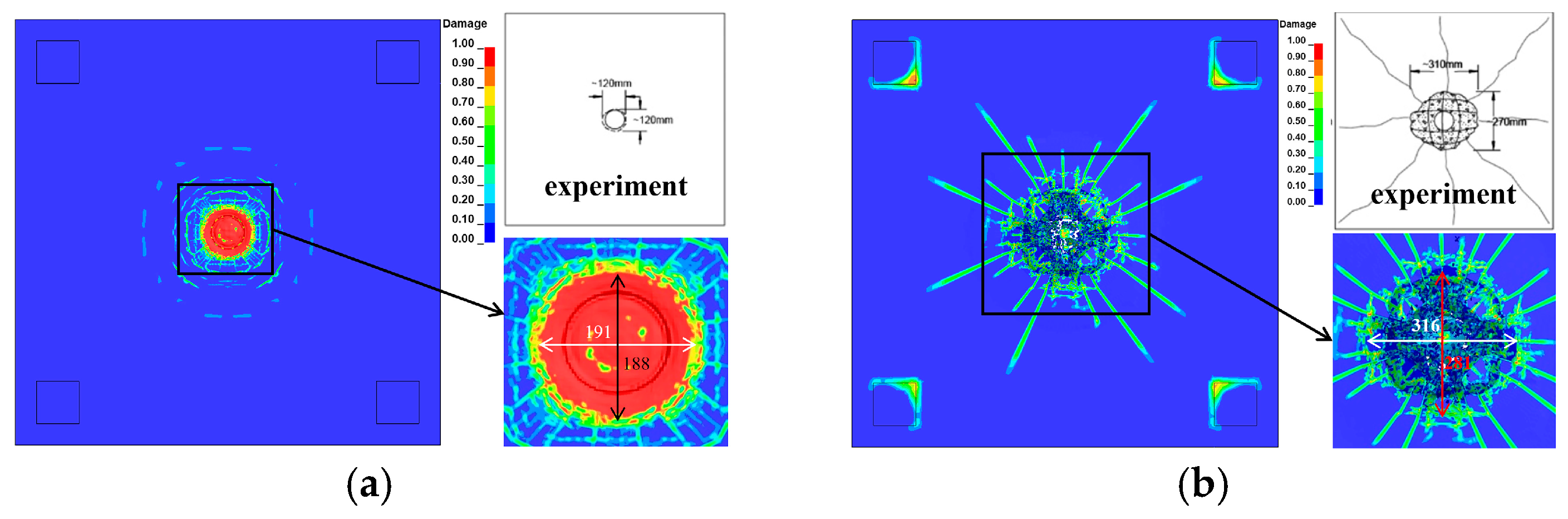
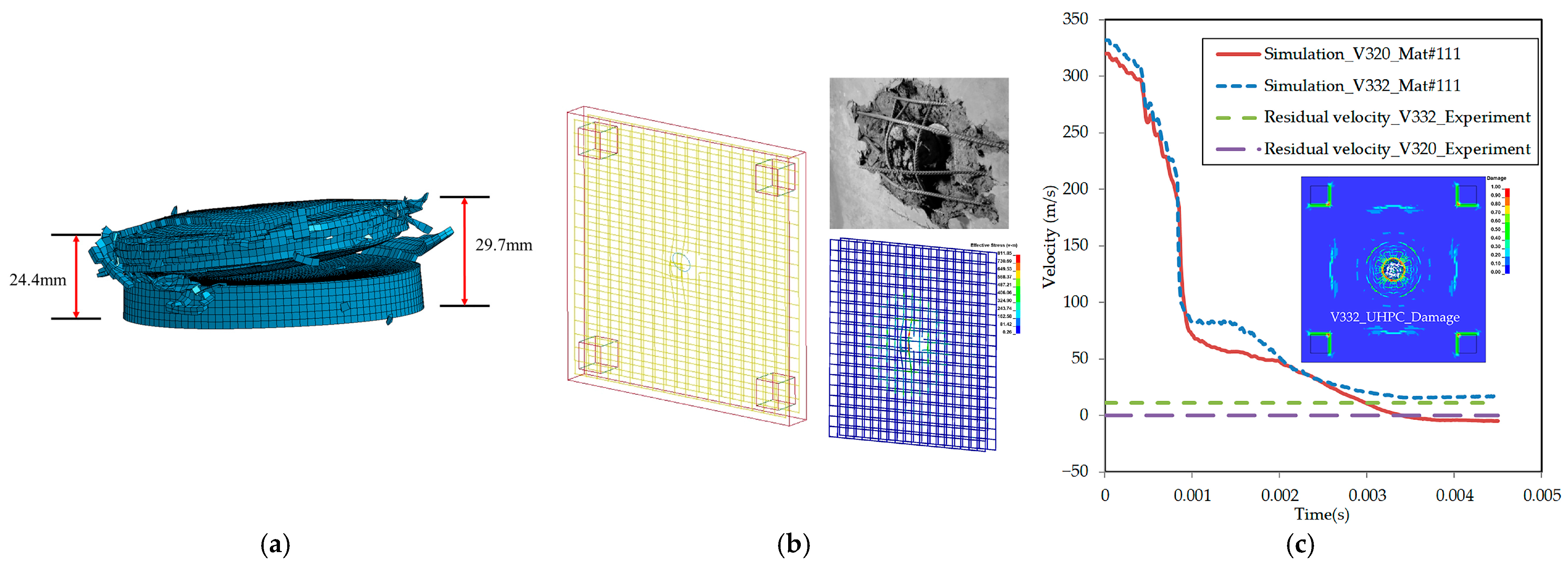
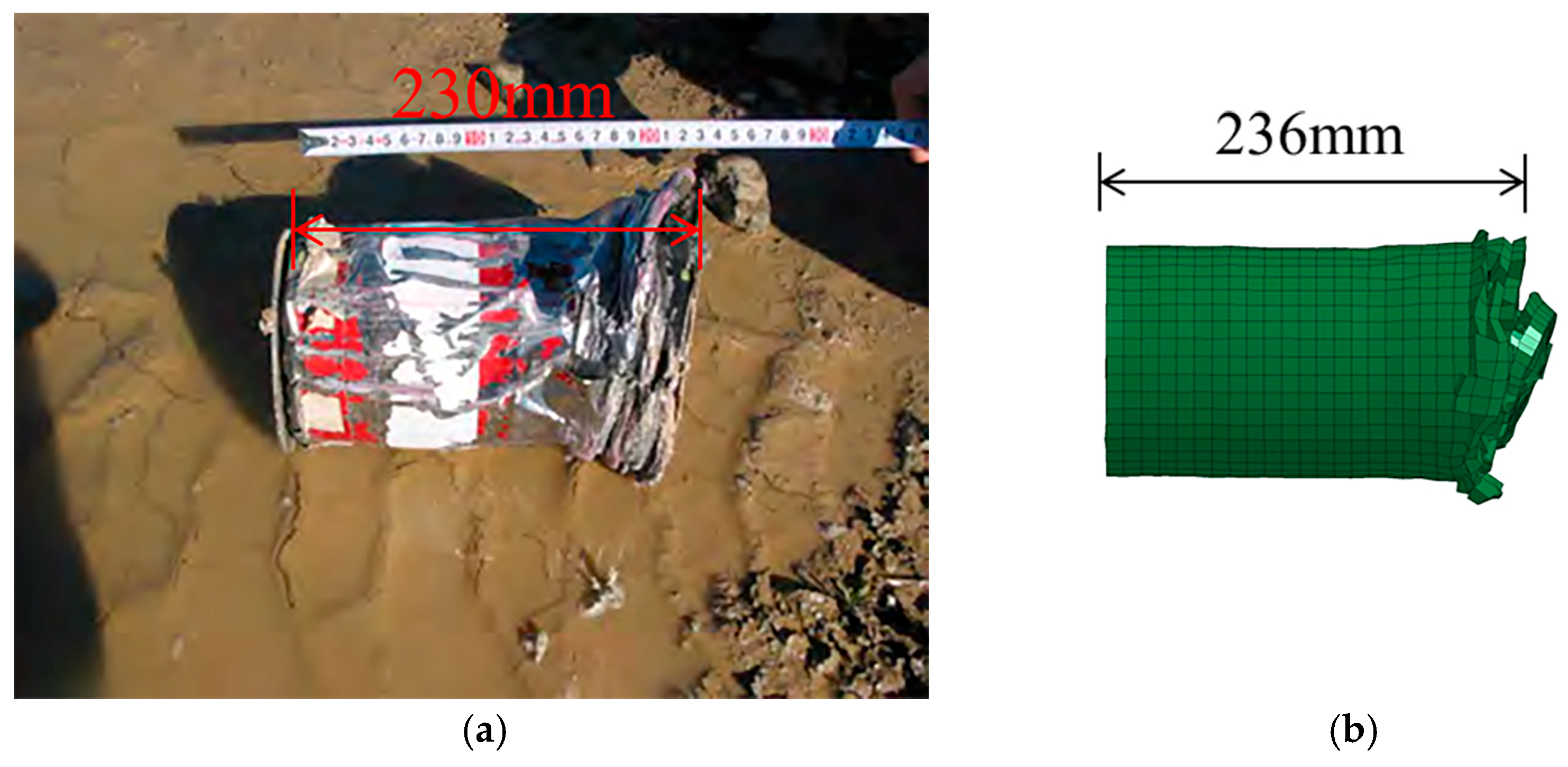
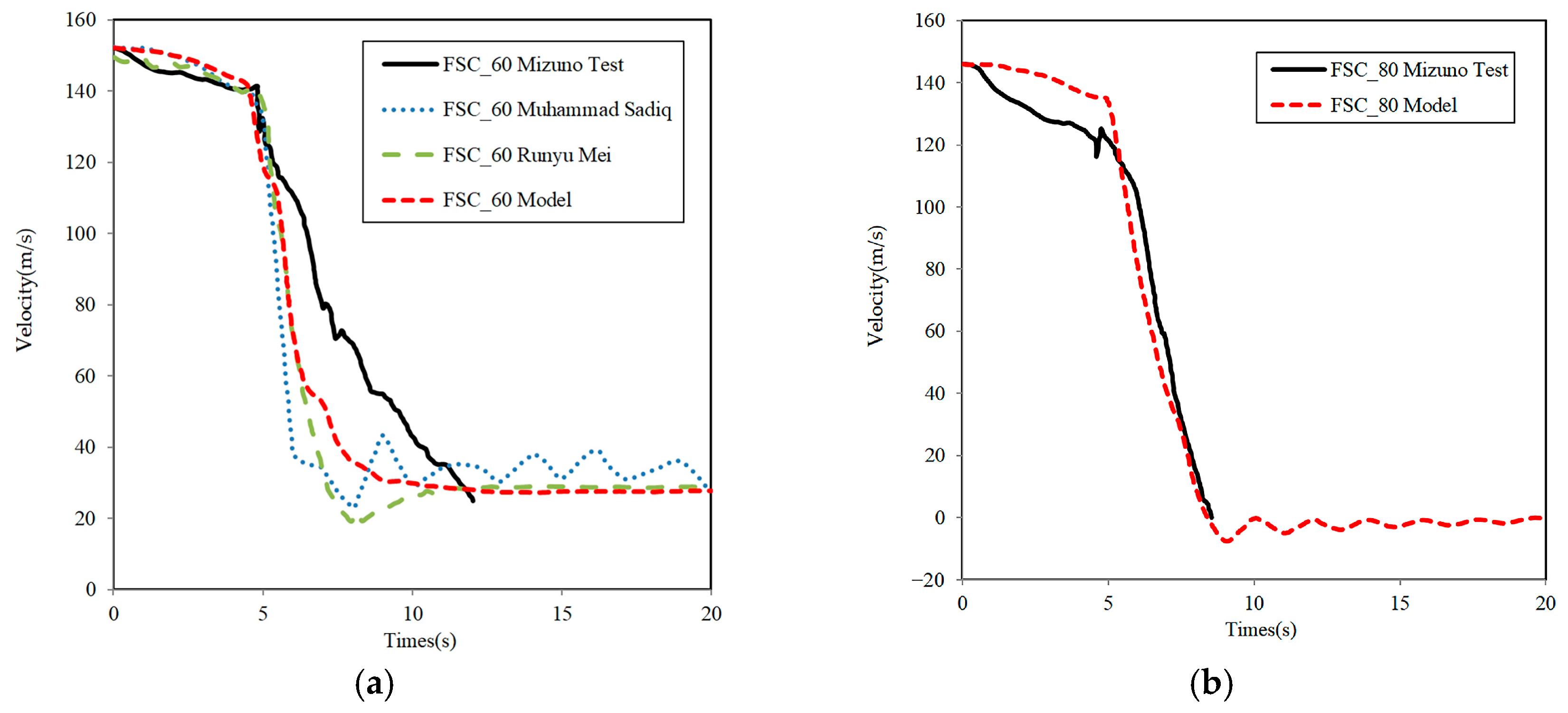
2.3.1. Validation of UHPC
2.3.2. Validation of S-NRC
2.4. Sensitivity Analysis of FE Modeling
2.4.1. Mesh Sensitivity Analysis
2.4.2. Impact Location Sensitivity Analysis
3. Impact Response and Sensitivity Analysis
3.1. Sensitivity Analysis of Different Aircraft Types
3.2. Sensitivity Analysis of Impact Velocity
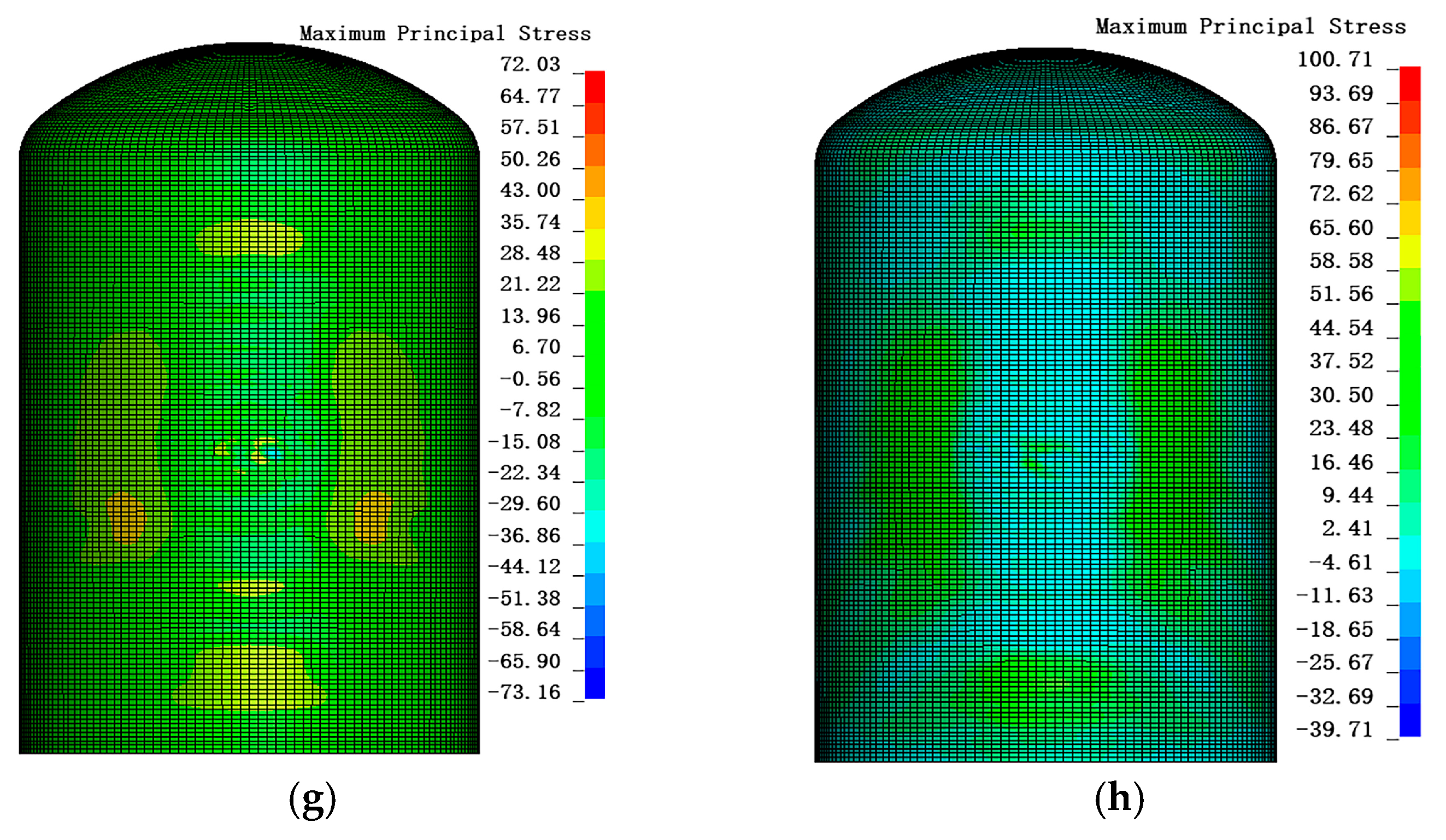
3.3. Sensitivity Analysis of Containment Thickness and Material Type
3.4. Sensitivity Analysis of UHPC Strength Grade
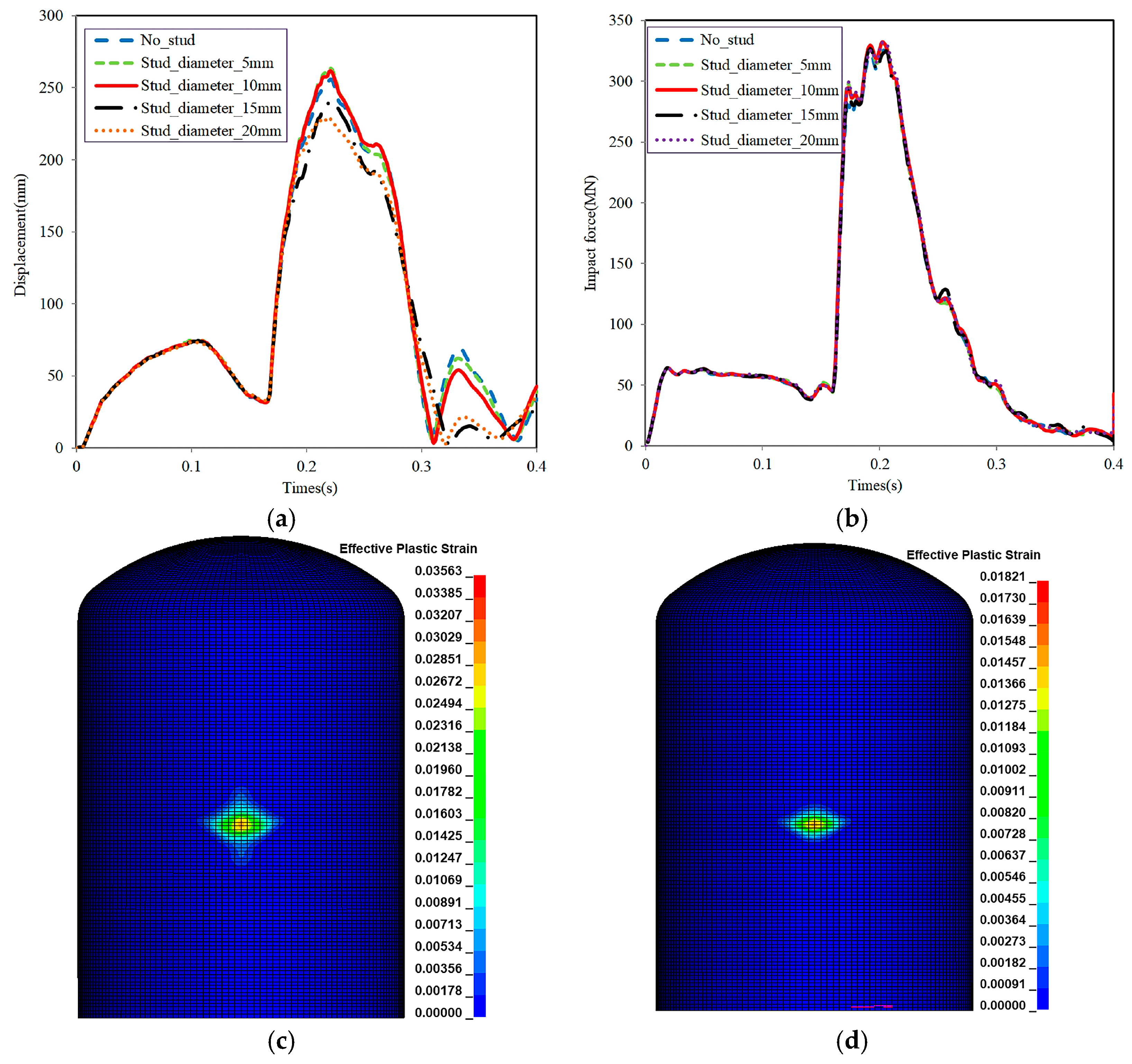
3.5. Sensitivity Analysis of Stud Spacing
3.6. Sensitivity Analysis of Steel Plate Thickness
4. Vibration Response Analysis
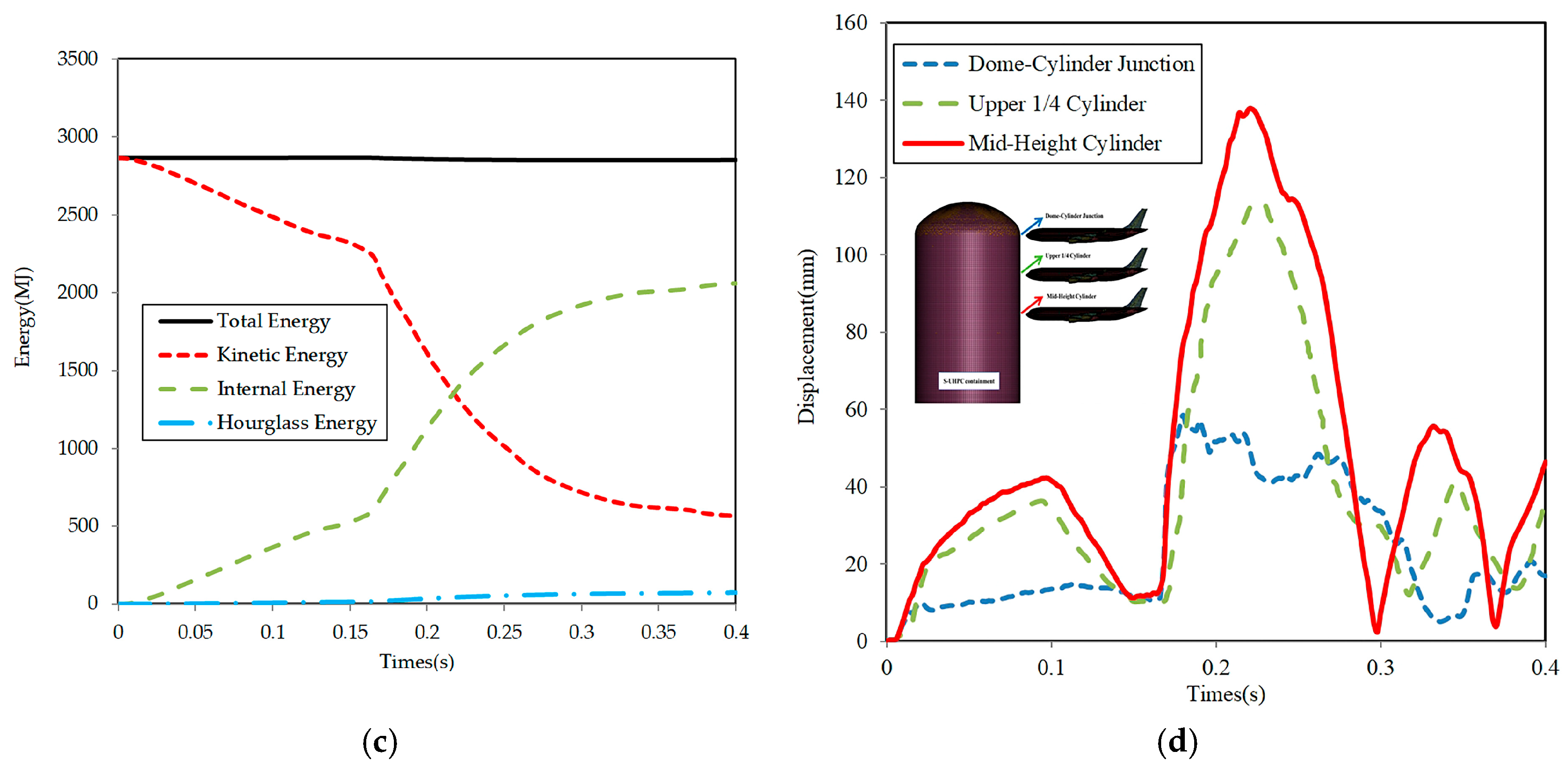
4.1. Modeling Strategy and Monitoring Scheme
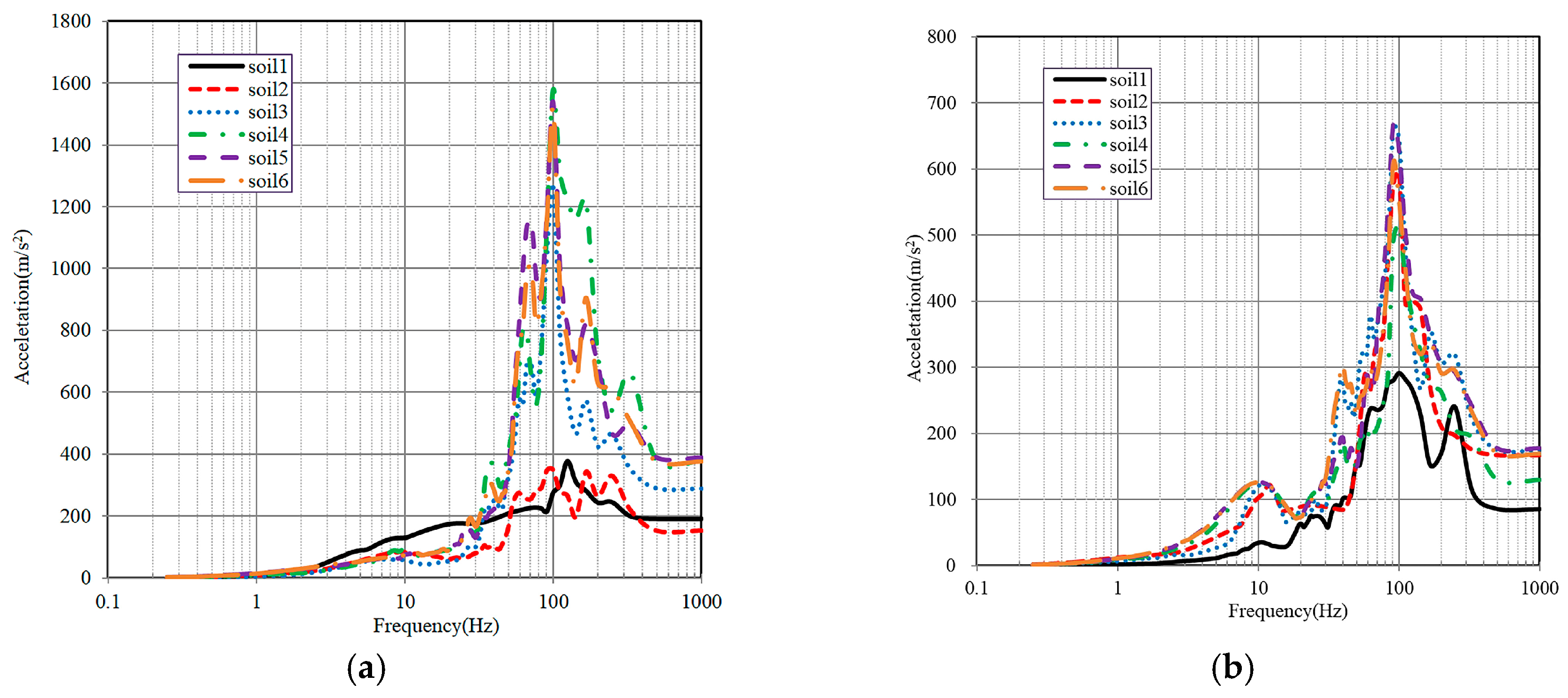
4.2. Floor Response Spectrum Analysis Under Various Soil Conditions
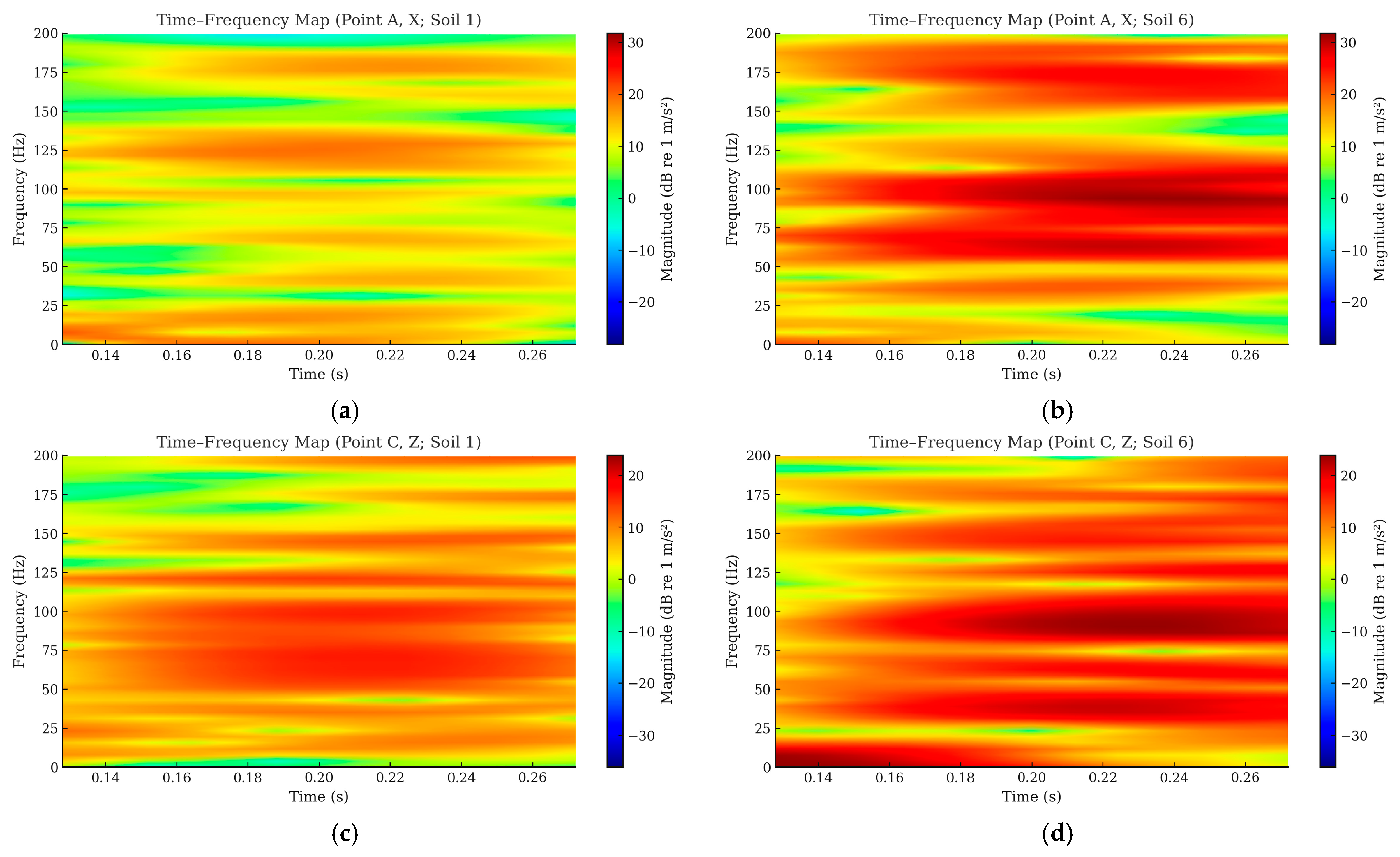
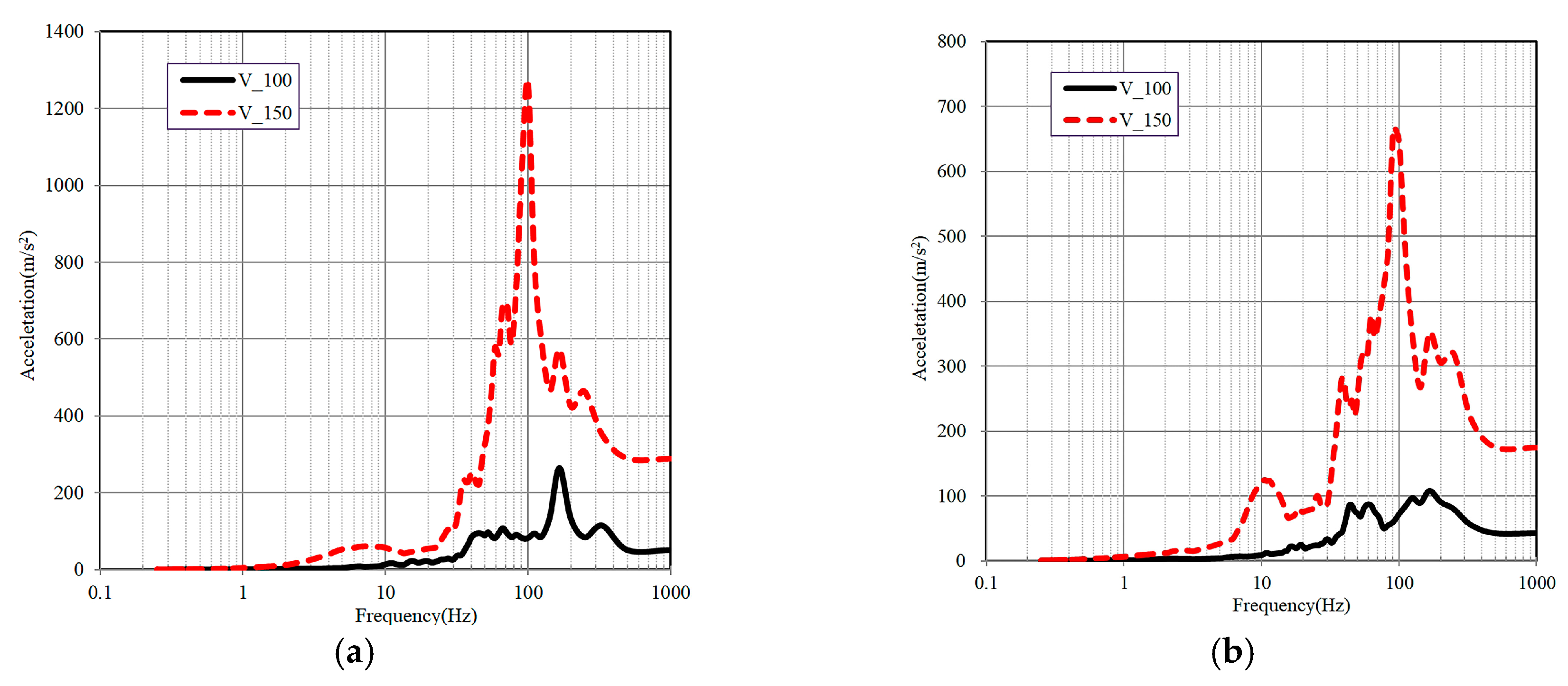
4.3. Influence of Impact Velocity on Floor Response Spectra
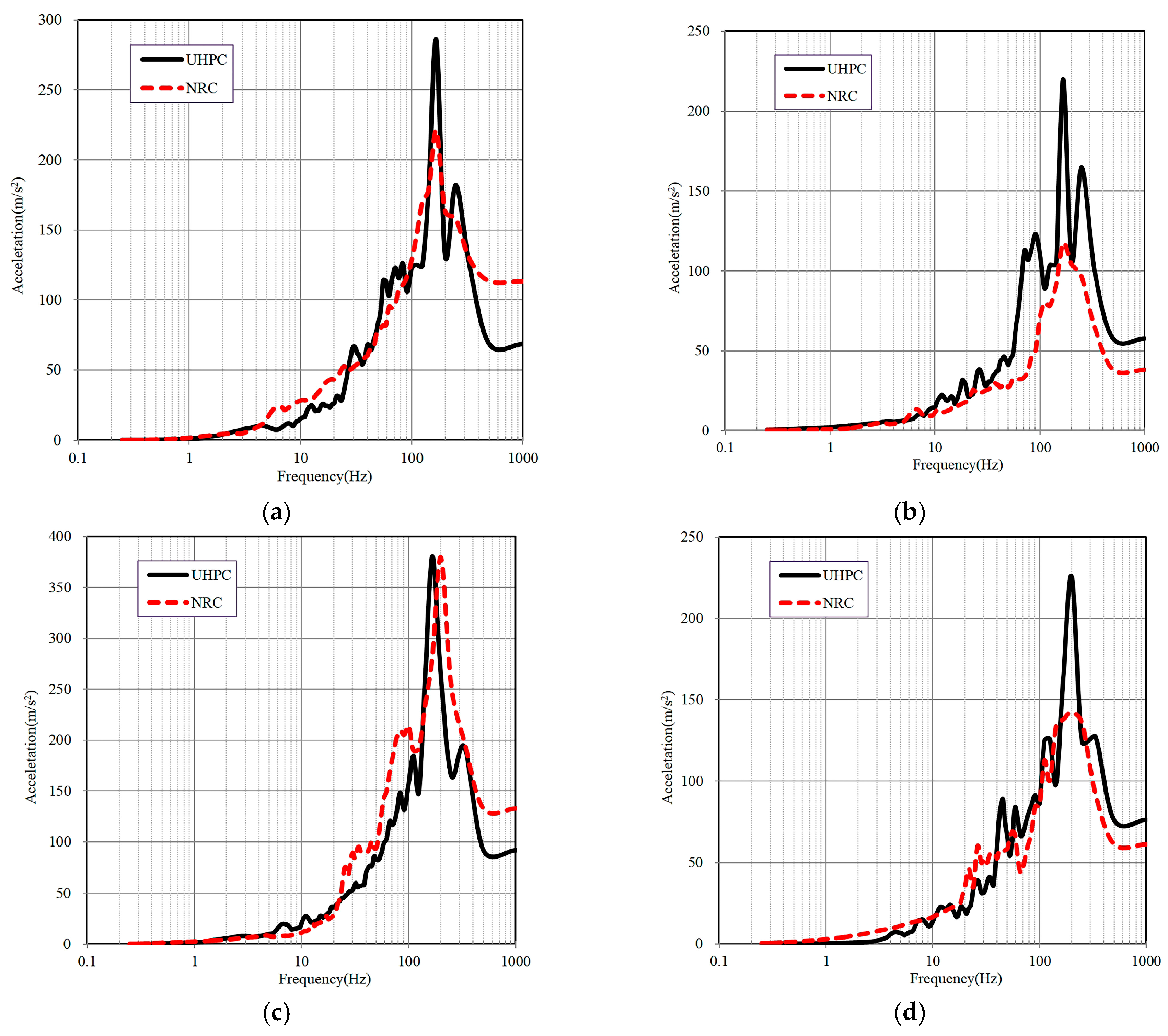
4.4. Influence of Structural Type on Impact-Induced Vibration Response
5. Conclusions
- (1)
- Steel–UHPC nuclear containment structures exhibit up to ~24% lower peak displacement than conventional reinforced concrete at the same wall thickness, demonstrating superior global impact resistance and deformation control under large aircraft impact.
- (2)
- UHPC cores in S-UHPC containment localize damage effectively without through-thickness failure, even at a reduced wall thickness, enabling material savings while maintaining safety margins.
- (3)
- Aircraft impact excites dominant high-frequency vibrations (90–125 Hz), and soft soil conditions amplify acceleration responses by more than four times, highlighting the critical role of site-specific dynamic analysis in containment and equipment design.
- (4)
- Increasing wall and steel plate thickness significantly reduces global deformation and local yielding without substantially altering the peak impact force, providing an effective design strategy for enhancing impact resilience.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| S-UHPC | steel–ultra-high-performance concrete |
| NPPs | nuclear power plants |
| BDBE | beyond-design-basis event |
| SC | steel plate–concrete |
| UHPC | ultra-high-performance concrete |
| HVPI | high-velocity projectile impact |
| SSI | soil–structure interaction |
| FE | finite element |
| PWR | pressurized water reactor |
| HJC | Holmquist–Johnson–Cook |
| S-NRC | Steel–Normal Reinforced Concrete |
| PML | Perfectly Matched Layer |
References
- National Nuclear Safety Administration. Design Safety Regulations for Nuclear Power Plants; HAF102; National Nuclear Safety Administration: Beijing, China, 2016.
- NEI 07-13; Methodology for Performing Aircraft Impact Assessments for New Plant Designs. Nuclear Energy Institute: Washington, DC, USA, 2009.
- Sadiq, M.; Yun, Z.X.; Rong, P. Simulation analysis of impact tests of steel plate reinforced concrete and reinforced concrete slabs against aircraft impact and its validation with experimental results. Nucl. Eng. Des. 2014, 273, 653–667. [Google Scholar] [CrossRef]
- Bruhl, J.C.; Varma, A.H.; Johnson, W.H. Design of composite SC walls to prevent perforation from missile impact. Int. J. Impact. Eng. 2015, 75, 75–87. [Google Scholar] [CrossRef]
- Ren, G.; Pan, R.; Sun, F.; Li, L. Sensitivity Analysis on the Blast Resistance of Steel Concrete Structure Wall Based on CONWEP. In Proceedings of the 2021 28th International Conference on Nuclear Engineering, Virtual, 4–6 August 2021; American Society of Mechanical Engineers: New York, NY, USA, 2021; p. V003T12A022. [Google Scholar]
- Varma, A.H.; Shafaei, S.; Klemencic, R. Steel modules of composite plate shear walls: Behavior, stability, and design. Thin Wall Struct. 2019, 145, 106384. [Google Scholar] [CrossRef]
- Sadiq, M.; Khaliq, W.; Ilyas, M.; Khushnood, R.A.; Khan, S.A.; Rong, P. Analysis of full-scale aircraft impact to reinforced concrete and steel plate reinforced concrete multiple barriers protecting nuclear power plants. Structures 2020, 27, 732–746. [Google Scholar] [CrossRef]
- Kim, K.; Lee, K.; Shin, J.; Lee, J.; Varma, A. A study on the resistance of SC walls subjected to missile impact using large-scale impact tests. Int. J. Impact Eng. 2020, 139, 103507. [Google Scholar] [CrossRef]
- Liu, J.; Han, P. Numerical Analyses of a Shield Building Subjected to a Large Commercial Aircraft Impact. Shock Vib. 2018, 2018, 7854969. [Google Scholar] [CrossRef]
- Russell, H.G.; Graybeal, B.A.; Russell, H.G. Ultra-High Performance Concrete: A State-of-the-Art Report for the Bridge Community; Rep. No. FHWA-HRT-13-060.; Office of Infrastructure Research and Development, Federal Highway Administration: McLean, VA, USA, 2013. [Google Scholar]
- Graybeal, B.A. Characterization of the Behavior of Ultra-High Performance Concrete. Ph.D. Thesis, University of Maryland, College Park, MD, USA, 2005. [Google Scholar]
- Sawab, J.; Lim, I.; Mo, Y.-L.; Li, M.; Wang, H.; Guimaraes, M. Ultra-High-Performance Concrete and Advanced Manufacturing Methods for Modular Construction; Rep. No.13-5282; University of Houston: Houston, TX, USA, 2016. [Google Scholar]
- Magureanu, C.; Sosa, I.; Negrutiu, C.; Heghes, B. Mechanical Properties and Durability of Ultra-High-Performance Concrete. ACI Mater. J. 2012, 109, 177–184. [Google Scholar]
- Graybeal, B.; Tanesi, J. Durability of an Ultrahigh-Performance Concrete. J. Mater. Civil. Eng. 2007, 19, 848–854. [Google Scholar] [CrossRef]
- Hanifehzadeh, M.; Ebad Sichani, M.; Gencturk, B.; Padgett, J.E. Destructive and non-destructive evaluation of reinforced concrete dry casks affected by alkali-silica reactivity damage. Struct. Infrastruct. E. 2019, 15, 1404–1418. [Google Scholar] [CrossRef]
- Graybeal, B. Ultra-High Performance Concrete; Rep. No. FHWAHRT-11-038; Federal Highway Administration: Washington, DC, USA, 2011. [Google Scholar]
- Ning, H.; Ren, H.; Wang, W.; Nie, X. Impact Resistance of Ultra-High-Performance Concrete Composite Structures. Materials 2023, 16, 7456. [Google Scholar] [CrossRef]
- Riedel, W.; Nöldgen, M.; Straßburger, E.; Thoma, K.; Fehling, E. Local damage to Ultra High Performance Concrete structures caused by an impact of aircraft engine missiles. Nucl. Eng. Des. 2010, 240, 2633–2642. [Google Scholar] [CrossRef]
- Wang, Z.; Yan, J.; Lin, Y.; Fan, F.; Yang, Y. Mechanical properties of steel-UHPC-steel slabs under concentrated loads considering composite action. Eng. Struct. 2020, 222, 111095. [Google Scholar] [CrossRef]
- Liu, J.; Li, J.; Fang, J.; Su, Y.; Wu, C. Ultra-high performance concrete targets against high velocity projectile impact—A-state-of-the-art review. Int. J. Impact Eng. 2022, 160, 104080. [Google Scholar] [CrossRef]
- Lin, Y.; Yan, J.; Cao, Z.; Zeng, X.; Fan, F.; Zou, C. Ultimate strength behaviour of S-UHPC-S and SCS sandwich beams under shear loads. J. Constr. Steel Res. 2018, 149, 195–206. [Google Scholar] [CrossRef]
- Wang, Z.; Yan, J.; Lin, Y.; Fan, F.; Sun, M. Experimental and analytical study on the double steel plates-UHPC sandwich slabs under low-velocity impact. Thin Wall Struct. 2023, 184, 110548. [Google Scholar] [CrossRef]
- Sugano, T.; Tsubota, H.; Kasai, Y. Full-scale aircraft impact test for evaluation of impact force. Nucl. Eng. Des. 1993, 140, 373–385. [Google Scholar] [CrossRef]
- Tuñón-Sanjur, L.; Orr, R.S.; Tinic, S.; Ruiz, D.P. Finite element modeling of the AP1000 nuclear island for seismic analyses at generic soil and rock sites. Nucl. Eng. Des. 2007, 237, 1474–1485. [Google Scholar] [CrossRef]
- Islam, M.R.; Turja, S.D.; Van Nguyen, D.; Forcellini, D.; Kim, D. Seismic Soil-Structure Interaction in Nuclear Power Plants: An extensive review. Results Eng. 2024, 23, 102694. [Google Scholar] [CrossRef]
- Hallquist, J.O. LS-DYNA Keyword User’s Manual R8; Livermore Software Technology Corporation: Livermore, CA, USA, 2014. [Google Scholar]
- Johnson, G.R.; Cook, W.H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Karim, M.R.; Fatt, M.S.H. Impact of the Boeing 767 Aircraft into the World Trade Center. J. Eng. Mech. 2005, 131, 1066–1072. [Google Scholar] [CrossRef]
- Cowper, G.R.; Symonds, P.S. Strain-Hardening and Strain-Rate Effects in the Impact Loading of Cantilever Beams; Technical Report No. 28; Division of Applied Mathematics, Brown University: Providence, RI, USA, 1957. [Google Scholar]
- Brown, W.F., Jr.; Mindlin, H.; Ho, C.Y. (Eds.) Aerospace Structural Metals Handbook: CINDAS/USAF CRDA Handbooks Operation; Purdue University: West Lafayette, IN, USA, 1997. [Google Scholar]
- Riera, J.D. On the stress analysis of structures subjected to aircraft impact forces. Nucl. Eng. Des. 1968, 8, 415–426. [Google Scholar] [CrossRef]
- Lee, K.; Jung, J.-W.; Hong, J.-W. Advanced aircraft analysis of an F-4 Phantom on a reinforced concrete building. Nucl. Eng. Des. 2014, 273, 505–528. [Google Scholar] [CrossRef]
- IAEA. Safety Aspects of Nuclear Power Plants in Human Induced External Events: Assessment of Structures; Safety Reports Series No.87; IAEA: Vienna, Austria, 2018. [Google Scholar]
- Li, F.; Chen, G. Nonlinear Seismic Response Characteristics of CAP1400 Nuclear Island Structure on Soft Rock Sites. Sci. Technol. Nucl. Install. 2020, 2020, 8867026. [Google Scholar] [CrossRef]
- Hohnquist, T.; Johnson, G.; Cook, W. A Computational Constitutive Model for Concrete Subjected to Large Strains, High Strain Rates and High Pressures. In Proceedings of the 14th International Symposium on Ballistics, Quebec City, QC, Canada, 26–29 September 1993; American Defense Preparedness Association: Arlington, VA, USA, 1993; pp. 591–600. [Google Scholar]
- Wan, W.; Yang, J.; Xu, G.; Liu, Y. Determination and evaluation of Holmquist-Johnson-Cook constitutive model parameters for ultra-high-performance concrete with steel fibers. Int. J. Impact Eng. 2021, 156, 103966. [Google Scholar] [CrossRef]
- Liu, Y.; Wei, Y. Drop-weight impact resistance of ultrahigh-performance concrete and the corresponding statistical analysis. J. Mater. Civ. Eng. 2022, 34, 04021409. [Google Scholar] [CrossRef]
- Das, N.; Nanthagopalan, P. Ballistic impact resistance of ultra-high-performance concrete (UHPC): A comprehensive experimental investigation and parametric analysis. Int. J. Impact Eng. 2024, 187, 104912. [Google Scholar] [CrossRef]
- Wei, C.; Zhang, Q.; Zhou, Y.; Cheng, Z.; Li, M.; Cui, C. Static and fatigue behaviors of short stud connectors embedded in ultra-high performance concrete. Eng. Struct. 2022, 273, 114888. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, X.; Li, C.; Xu, F.; Wang, G. Friction affected fatigue behavior of steel-UHPC composite structures and the fatigue crack growth in studs. Int. J. Fatigue 2023, 177, 107949. [Google Scholar] [CrossRef]
- Mizuno, J.; Koshika, N.; Sawamoto, Y.; Niwa, N.; Yamashita, T.; Suzuki, A. Investigation on impact resistance of steel plate reinforced concrete barriers against aircraft impact Part 1: Test program and results. In Proceedings of the 18th International Conference on Structural Mechanics in Reactor Technology, Beijing, China, 7–12 August 2005; pp. 2566–2579. [Google Scholar]
- Mei, R.; Li, J.; Lin, G.; Pan, R.; Zhu, X. Evaluation of the vibration response of third generation nuclear power plants with isolation technology under large commercial aircraft impact. Prog. Nucl. Energy 2020, 120, 103230. [Google Scholar] [CrossRef]
- GB 50218-2014; Code for Classification of Rock Mass. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2014.
- Asgari, A.; Ahmadtabar Sorkhi, S.F. Wind turbine performance under multi-hazard loads: Wave, wind, and earthquake effects on liquefiable soil. Results Eng. 2025, 26, 104647. [Google Scholar] [CrossRef]
- American Society of Civil Engineers. Seismic Analysis of Safety-Related Nuclear Structures; American Society of Civil Engineers: Reston, VA, USA, 2017. [Google Scholar]
- Ansys, I. LS-DYNA Help: Perfectly Matched Layer (PML) Absorbing Boundary for SSI Applications. Available online: https://lsdyna.ansys.com/pml/#results (accessed on 27 August 2025).
- Choi, Y.; Ju, H.; Jung, H.-J. Floor Response Spectrum of Nuclear Power Plant Structure Considering Soil-Structure Interaction. In Vibration Engineering for a Sustainable Future: Experiments, Materials and Signal Processing; Springer: Berlin/Heidelberg, Germany, 2021; Volume 2, pp. 161–166. [Google Scholar]

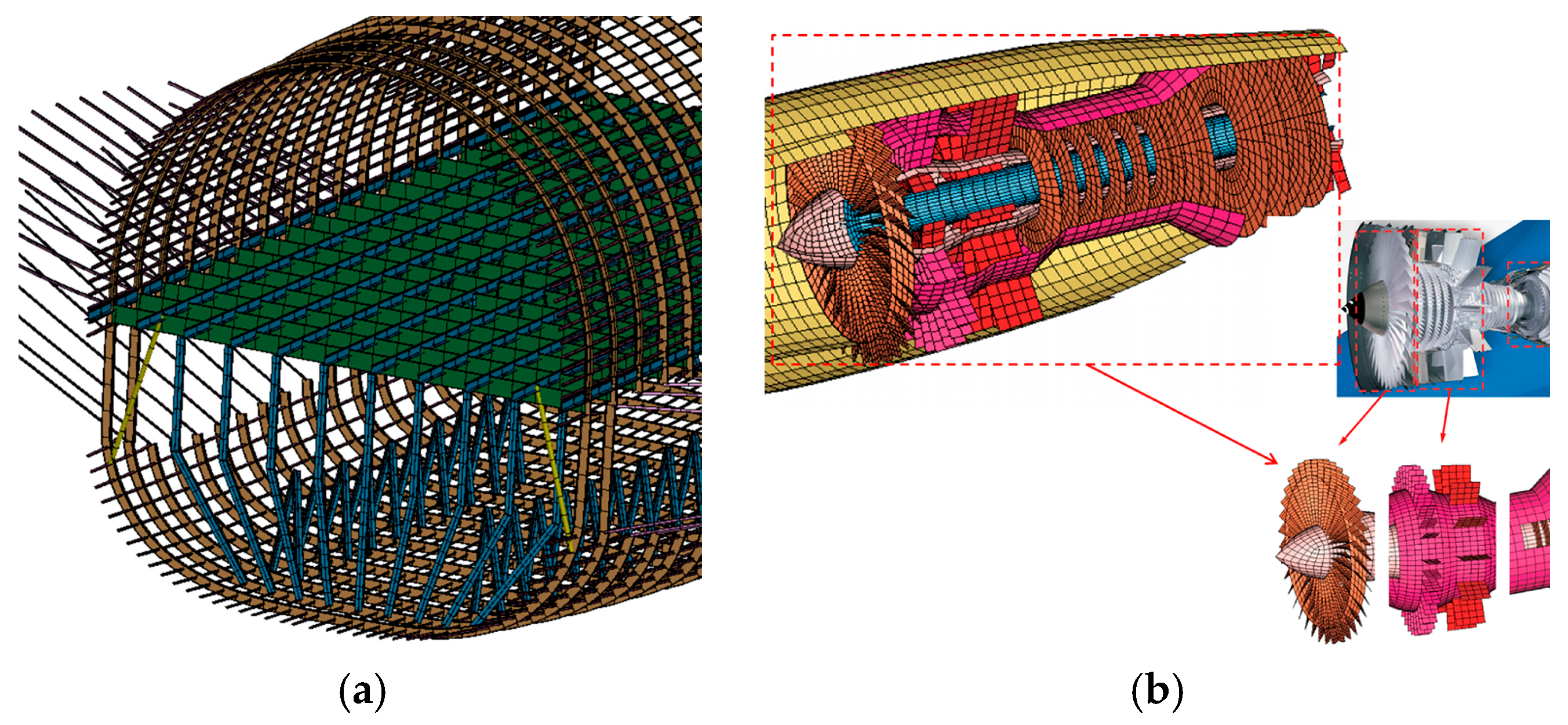



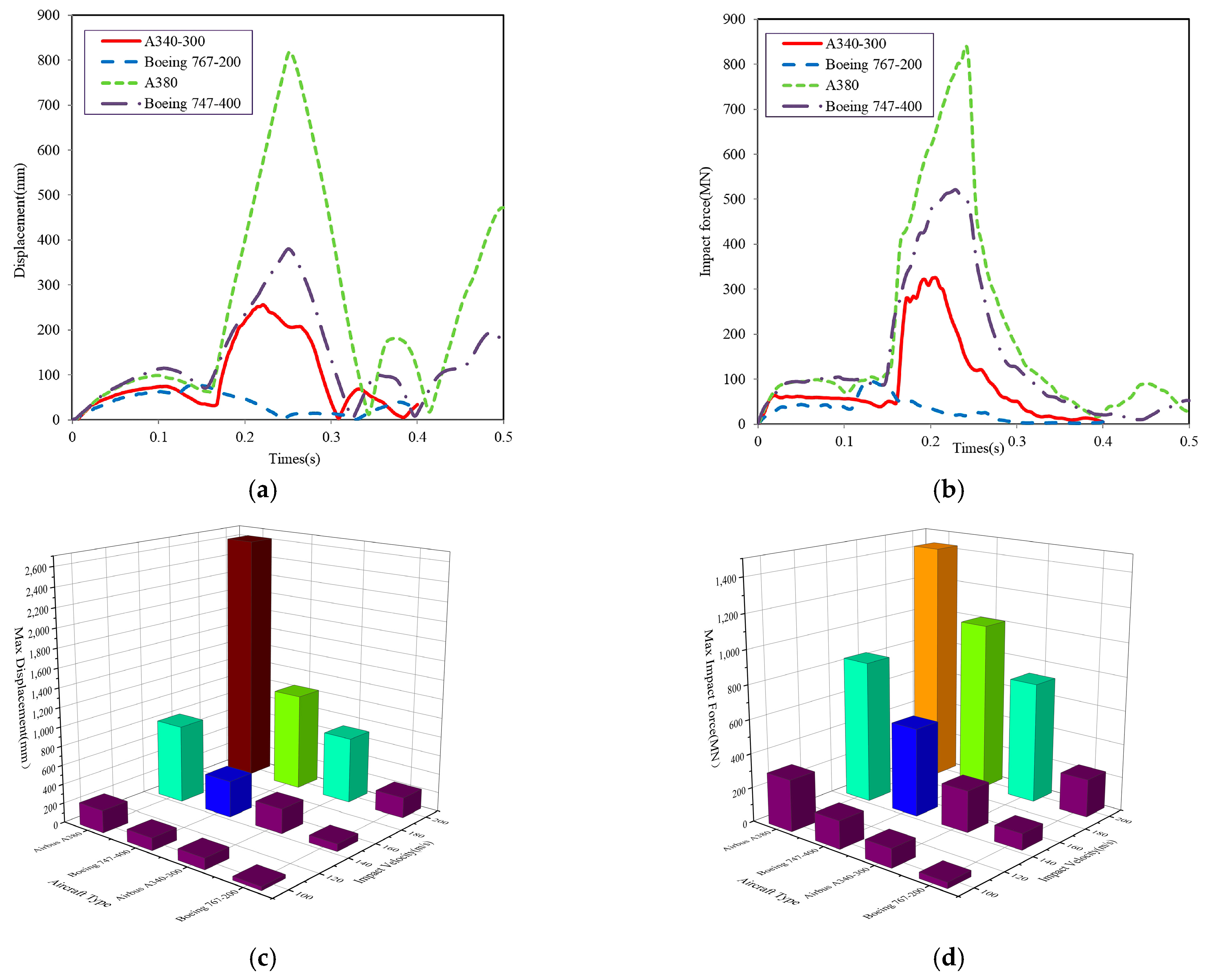

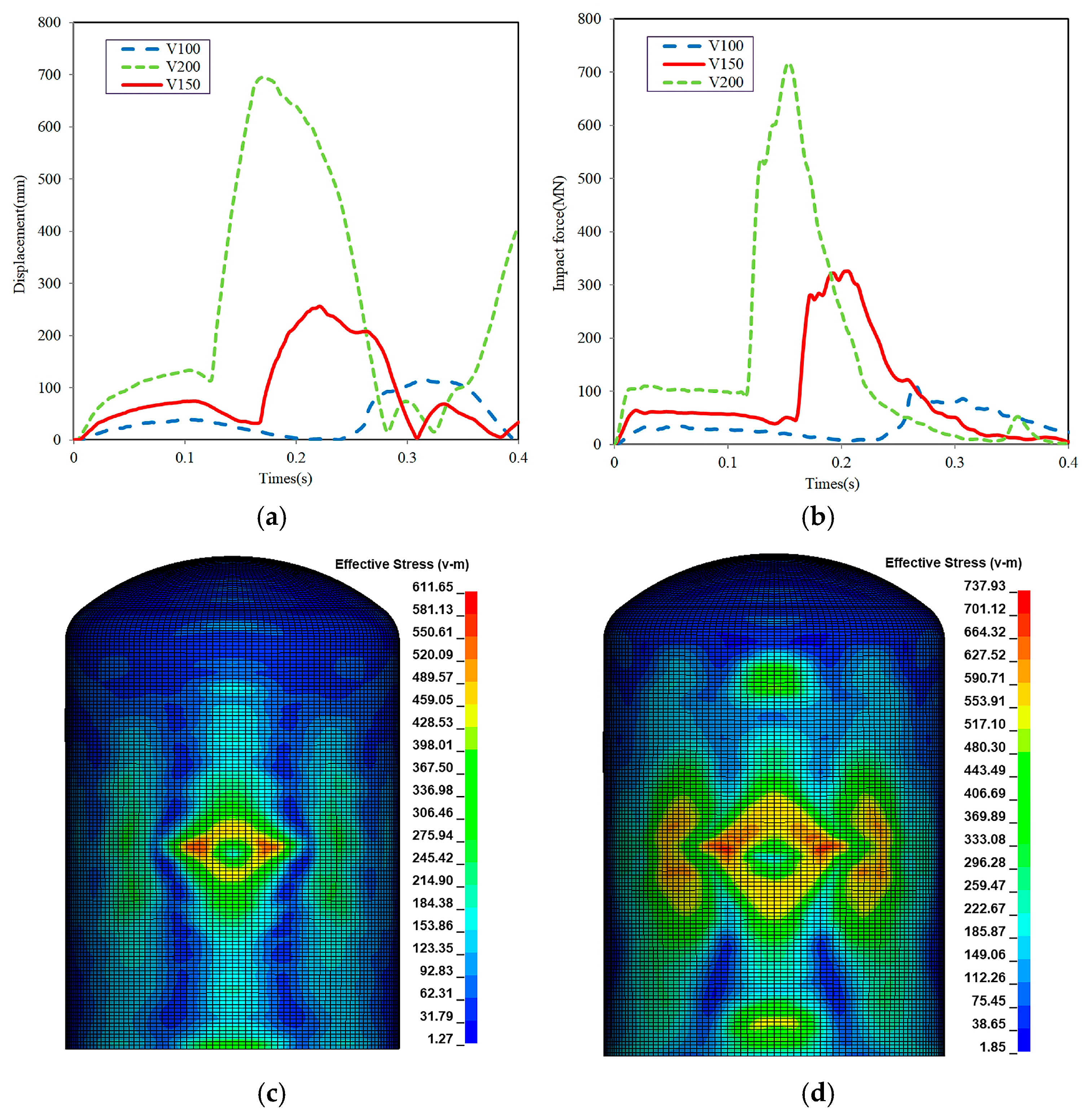
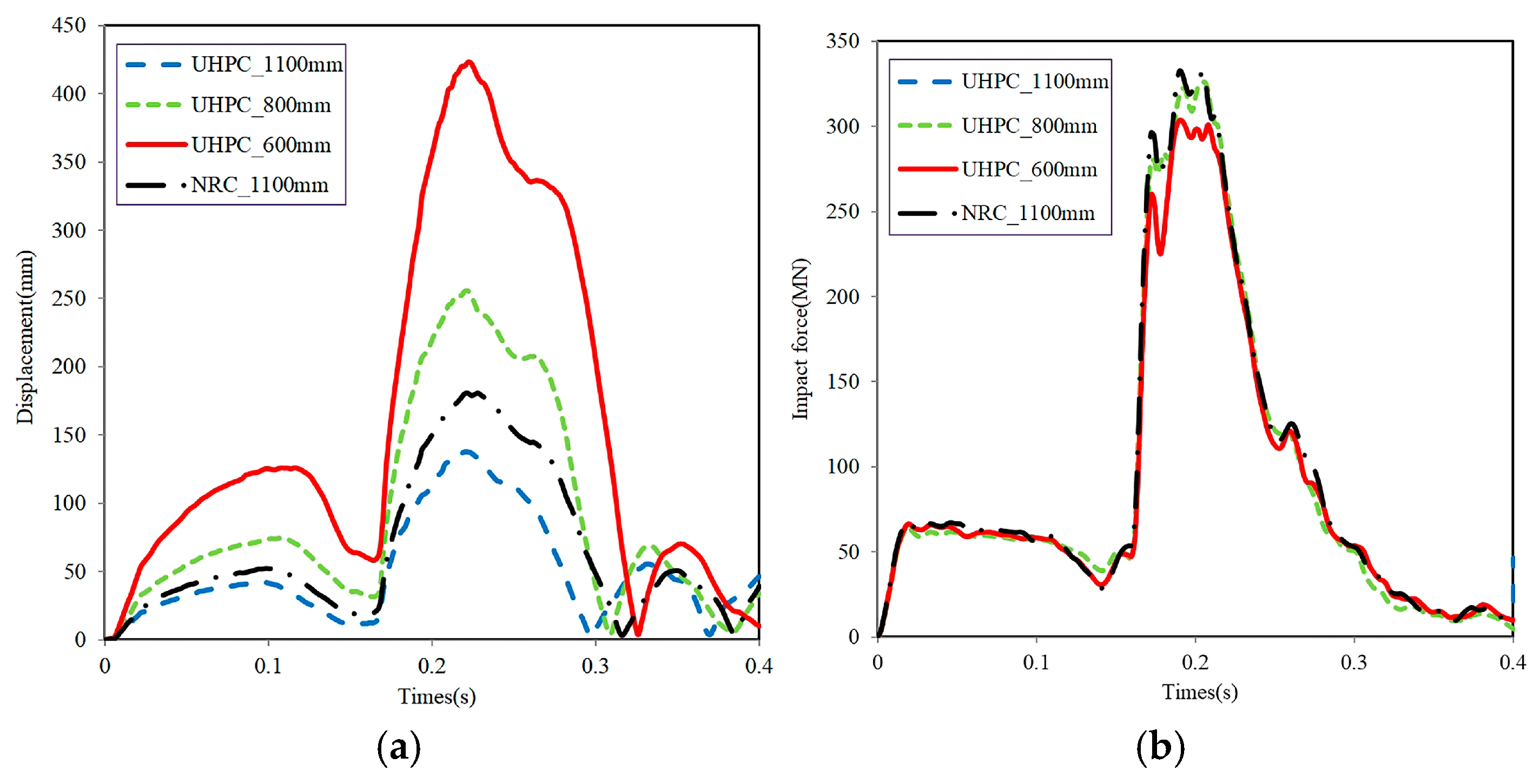






| Aircraft | Maximum Takeoff Weight (t) | Wing Span (m) | Total Length (m) | Number of Passengers |
|---|---|---|---|---|
| A340-300 | 243 | 60.3 | 63.6 | 295 |
| A380 | 560 | 79.8 | 72.8 | 555 |
| B767-200 | 400 | 64.4 | 70.6 | 181 |
| B747-400 | 113 | 47.6 | 48.5 | 416 |
| Material | C120 | C150 | C180 |
|---|---|---|---|
| (kg/m3) | 2600 | 2600 | 2600 |
| (MPa) | 120 | 150 | 180 |
| G (GPa) | 19.55 | 20.83 | 22.92 |
| T (MPa) | 11.2 | 13.3 | 15.0 |
| A | 0.3 | 0.3 | 0.3 |
| B | 1.81 | 1.81 | 1.81 |
| C | 0.019 | 0.019 | 0.019 |
| N | 0.81 | 0.81 | 0.81 |
| SMAX (MPa) | 3.5 | 3.5 | 3.5 |
| D1 | 0.045 | 0.050 | 0.061 |
| D2 | 1.0 | 1.0 | 1.0 |
| EFMIN | 0.011 | 0.012 | 0.016 |
| Pc (MPa) | 40 | 50 | 60 |
| μc | 0.00144 | 0.0018 | 0.0021 |
| Pl (GPa) | 3.63 | 3.63 | 3.63 |
| μpl | 0.117 | 0.117 | 0.117 |
| K1 (GPa) | 101.2 | 101.2 | 101.2 |
| K2 (GPa) | −199.5 | −199.5 | −199.5 |
| K3 (GPa) | 329.2 | 329.2 | 329.2 |
| Material | Steel Plate | Stud/Tie-Bar | Internal Containment |
|---|---|---|---|
| Density (kg/m3) | 7800 | 7800 | 7800 |
| Young’s modulus (MPa) | 21,000 | 20,000 | 21,000 |
| Poisson’s ratio | 0.3 | 0.3 | 0.3 |
| Yield stress (MPa) | 412 | 335 | 500 |
| Tangent modulus (MPa) | 8500 | 8500 | 8500 |
| C | 40 | / | / |
| p | 5 | / | / |
| FS | 0.4 | 0.1 | 0.5 |
| Case | Type | Shear Wave Velocity (m/s) | Shear Modulus (GPa) | Density (kg/m3) | Poisson’s Ratio | Internal Friction Angle (°) | Cohesion (kPa) |
|---|---|---|---|---|---|---|---|
| Soil1 | Hard Rock | 2438 | 15.751 | 2650 | 0.2 | 60 | 2100 |
| Soil2 | Firm Rock | 1067 | 2.846 | 2500 | 0.3 | 40 | 850 |
| Soil3 | Soft Rock | 732 | 1.259 | 2350 | 0.32 | 30 | 430 |
| Soil4 | Soft-to-Medium Soil | 431 | 0.321 | 2000 | 0.35 | 25 | 30 |
| Soil5 | Upper-Bound Soft-to-Medium Soil | 305 | 0.161 | 2000 | 0.36 | 16.7 | 24 |
| Soil6 | Soft Soil | 305 | 0.161 | 2000 | 0.36 | 16.7 | 24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, G.; Pan, R.; Sun, F.; Zhou, G. Dynamic Impact and Vibration Response Analysis of Steel–UHPC Composite Containment Under Aircraft Impact. Buildings 2025, 15, 3130. https://doi.org/10.3390/buildings15173130
Ren G, Pan R, Sun F, Zhou G. Dynamic Impact and Vibration Response Analysis of Steel–UHPC Composite Containment Under Aircraft Impact. Buildings. 2025; 15(17):3130. https://doi.org/10.3390/buildings15173130
Chicago/Turabian StyleRen, Guopeng, Rong Pan, Feng Sun, and Guoliang Zhou. 2025. "Dynamic Impact and Vibration Response Analysis of Steel–UHPC Composite Containment Under Aircraft Impact" Buildings 15, no. 17: 3130. https://doi.org/10.3390/buildings15173130
APA StyleRen, G., Pan, R., Sun, F., & Zhou, G. (2025). Dynamic Impact and Vibration Response Analysis of Steel–UHPC Composite Containment Under Aircraft Impact. Buildings, 15(17), 3130. https://doi.org/10.3390/buildings15173130








