Neural Network-Based Prediction of Compression Behaviour in Steel–Concrete Composite Adapter for CFDST Lattice Turbine Tower
Abstract
1. Introduction
2. Model and Compression Behaviour of SCCA
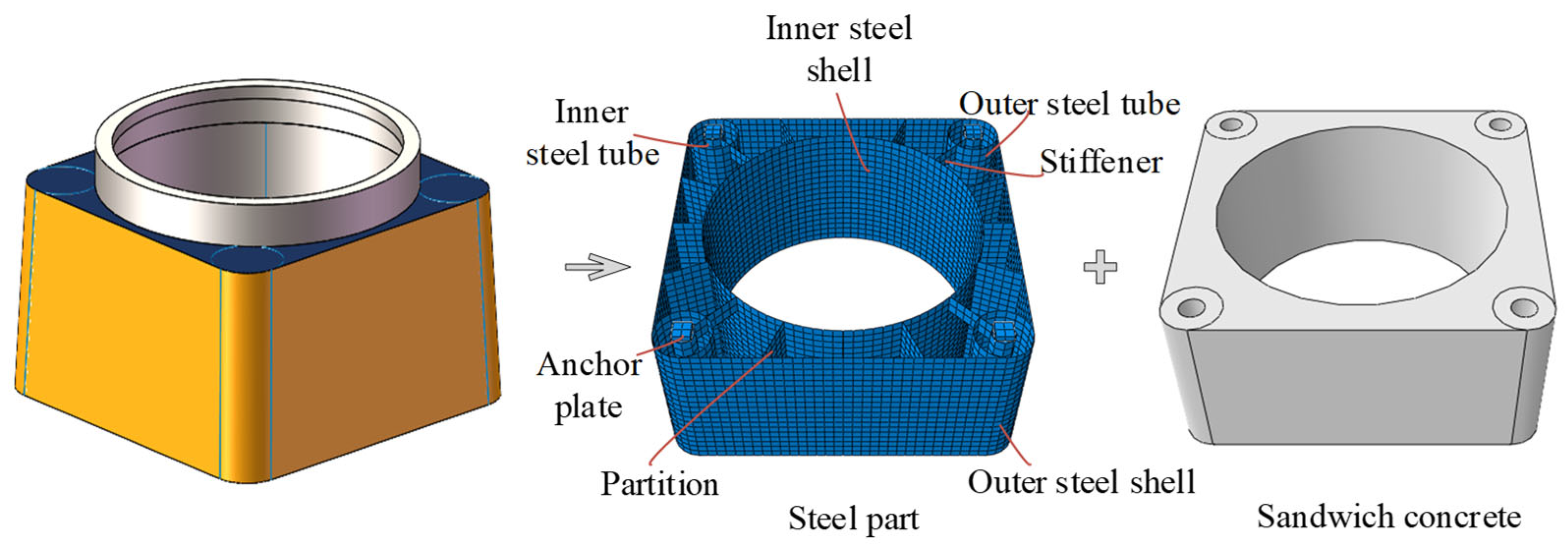
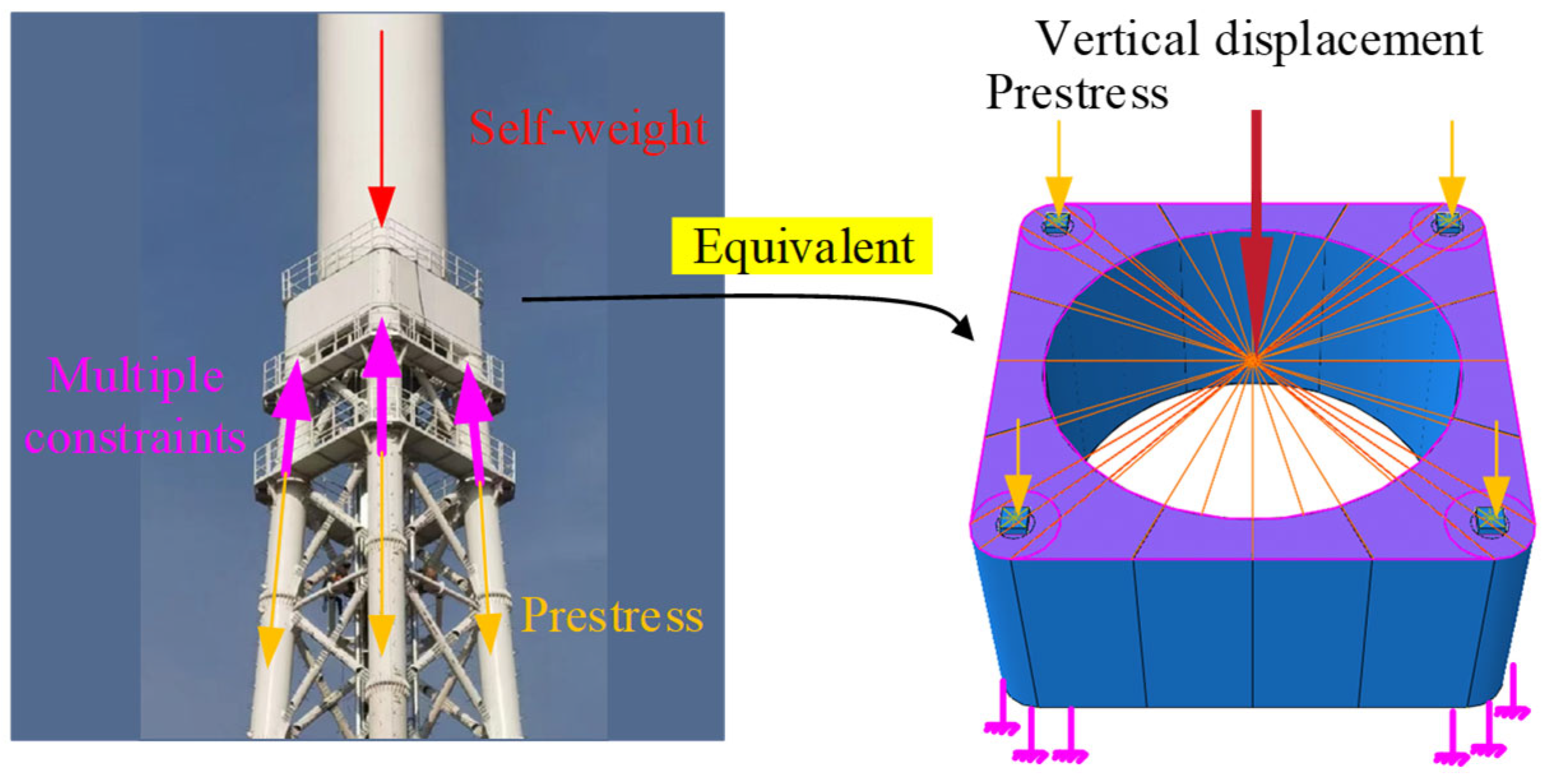
2.1. Modelling
2.2. Structural Response and Failure Mechanism
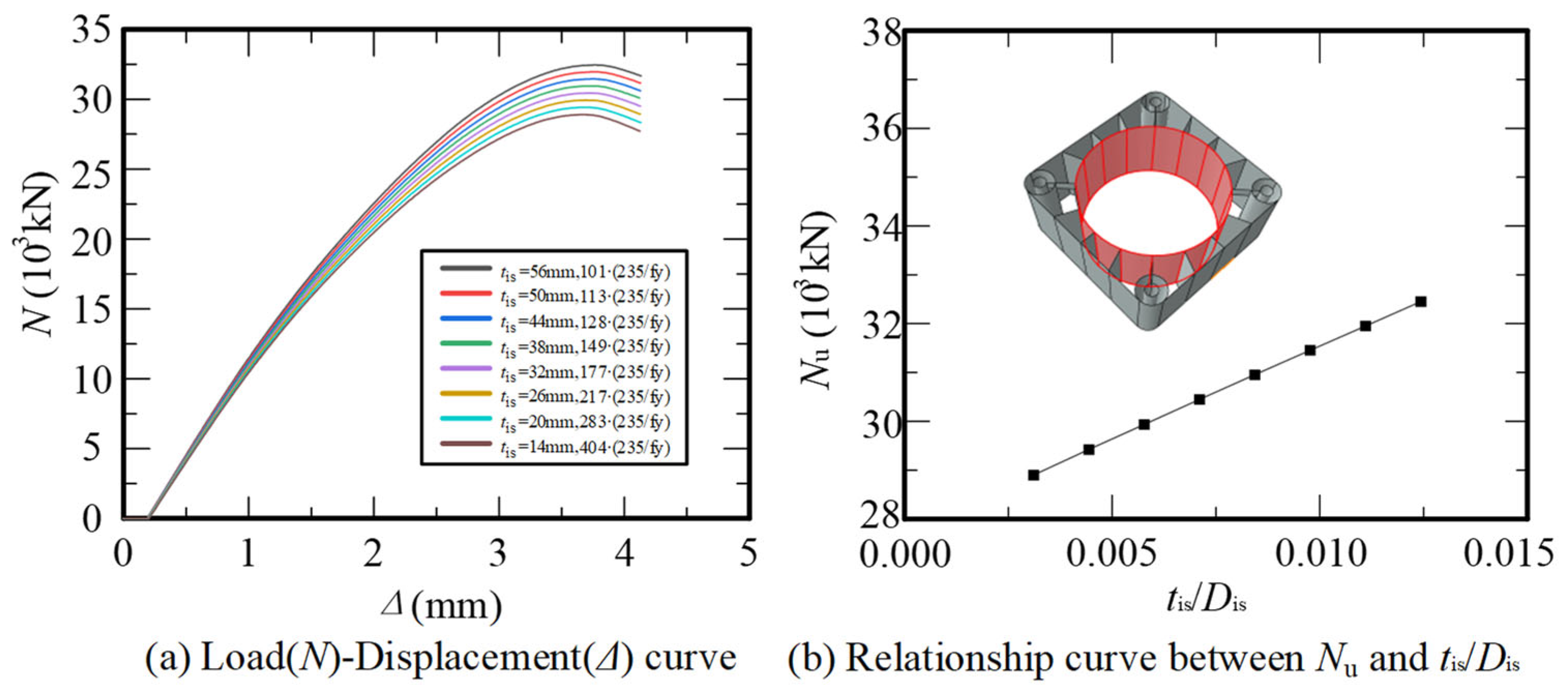
2.2.1. Load–Displacement Behaviour
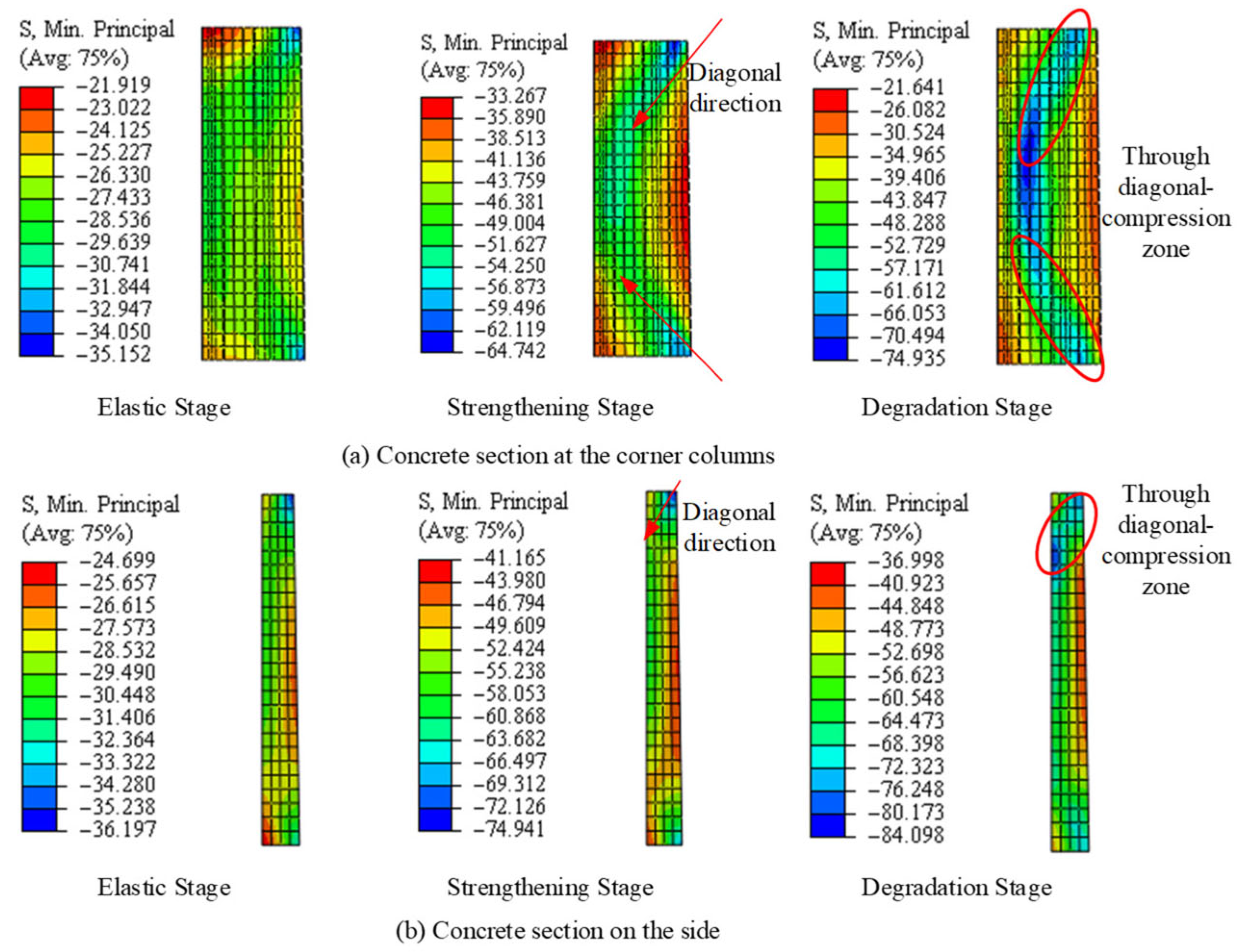
2.2.2. Stress–Strain Distribution and Failure Mechanism
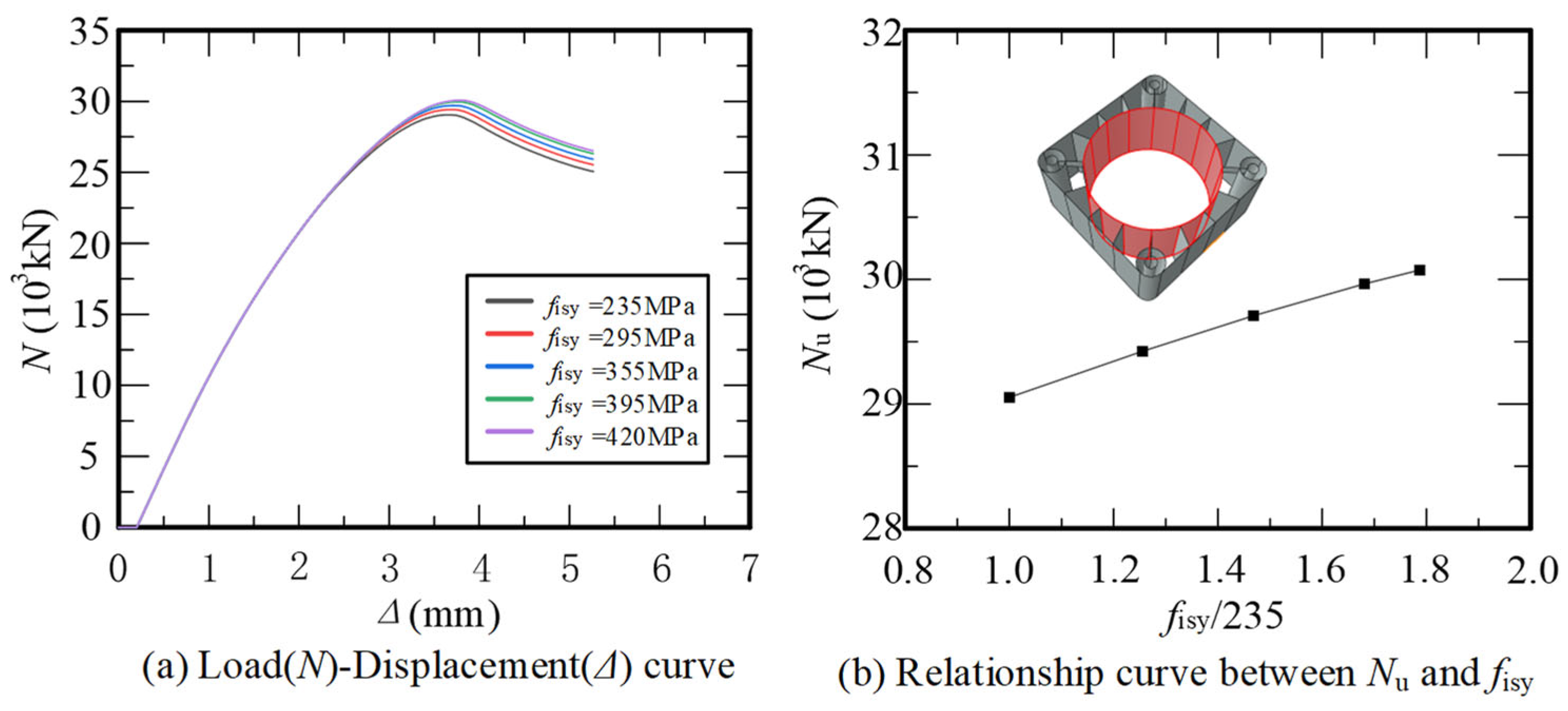
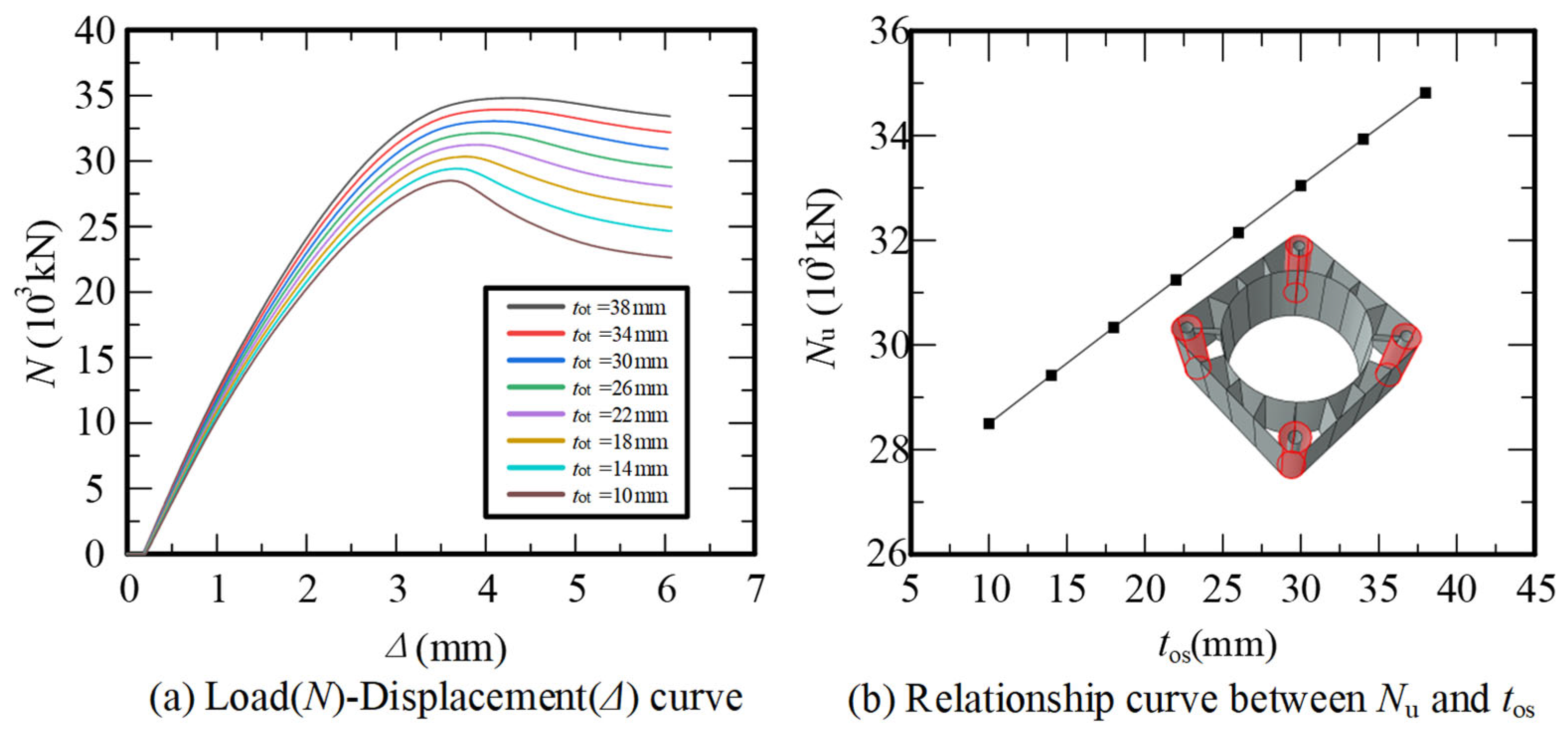
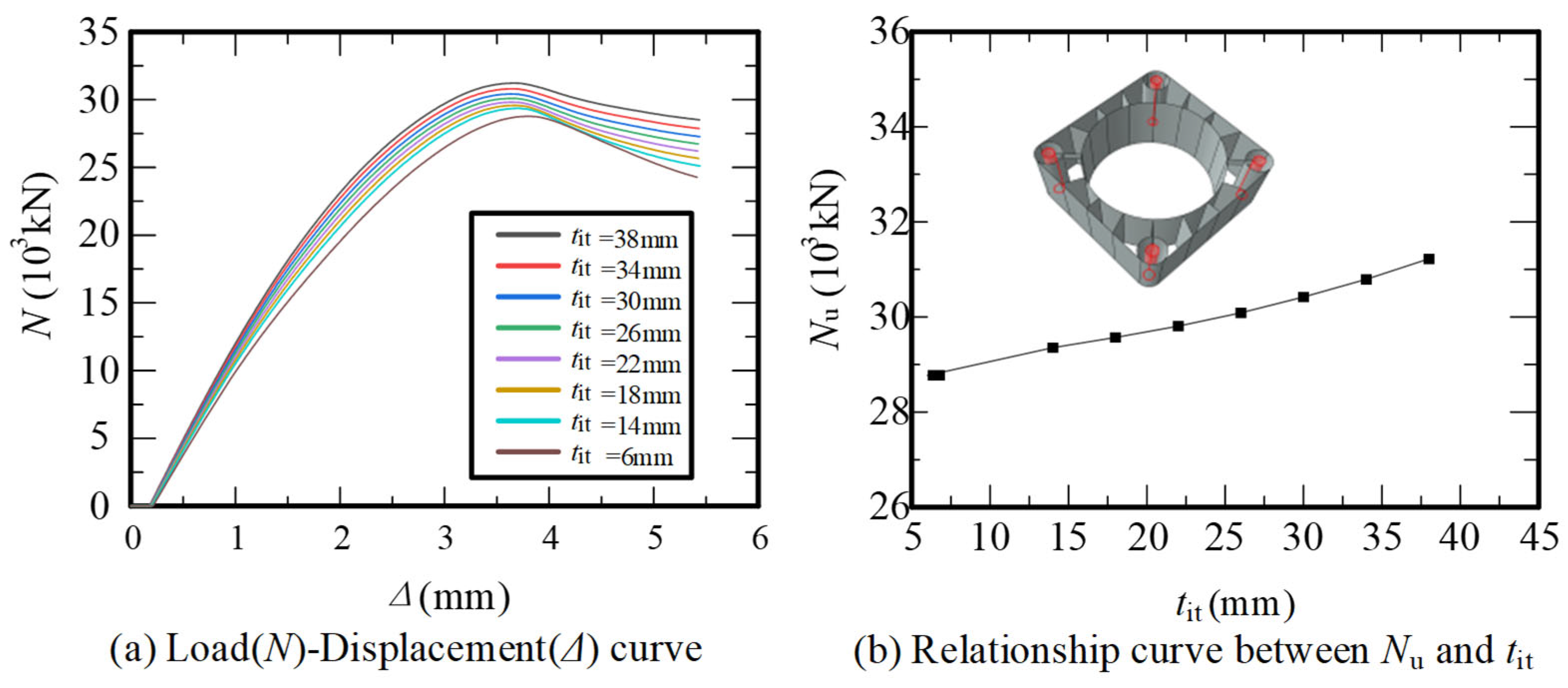
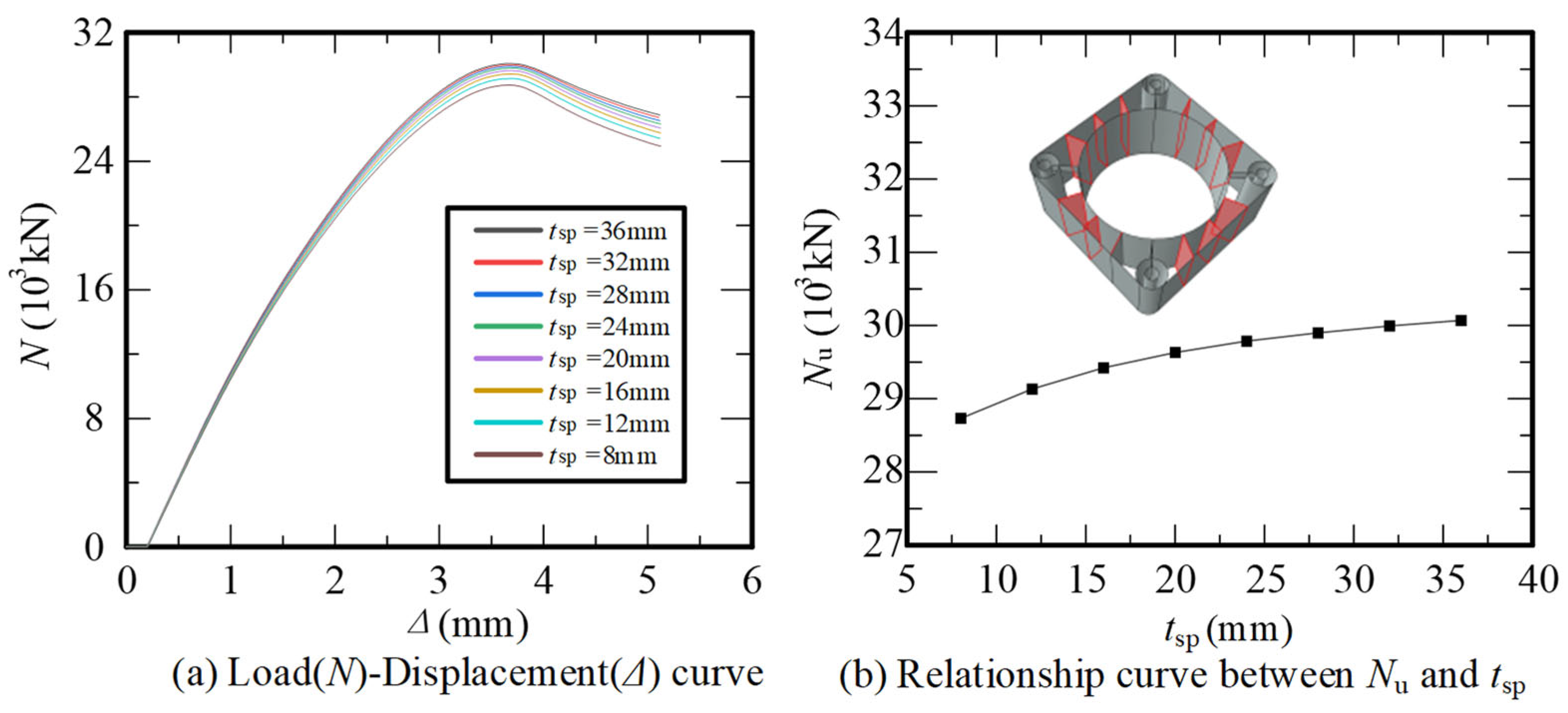
2.3. Parametric Analysis of Influential Factors
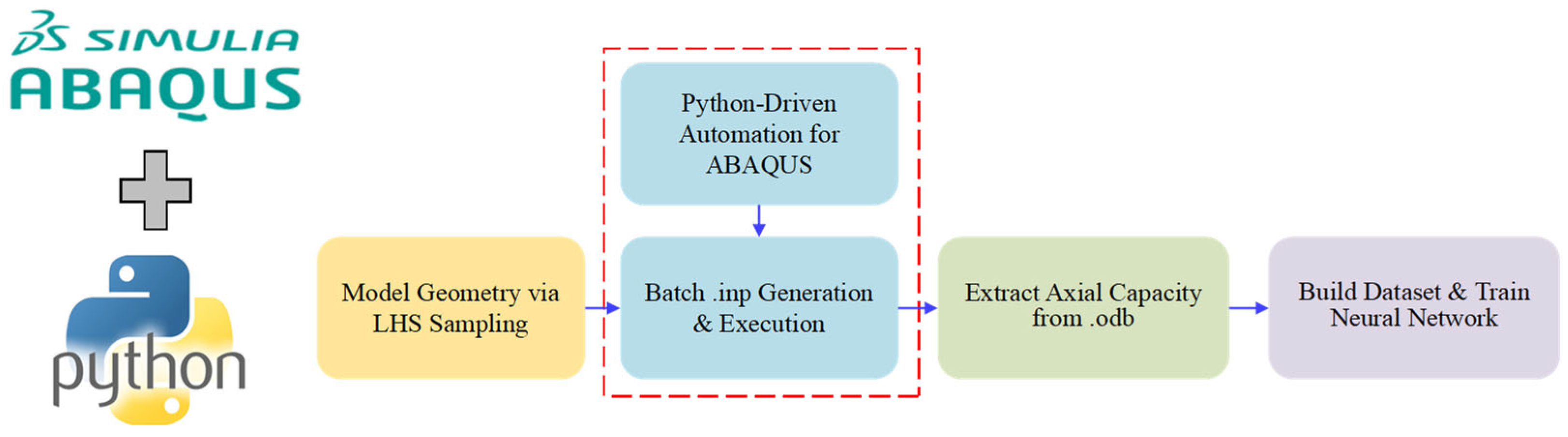
3. Database Establishment for the Axial Capacity of SCCA
3.1. Variable Selection
3.2. Sampling Strategy
3.3. Dataset Statistics
4. Prediction and Application Based on Neural Networks
4.1. Models Used
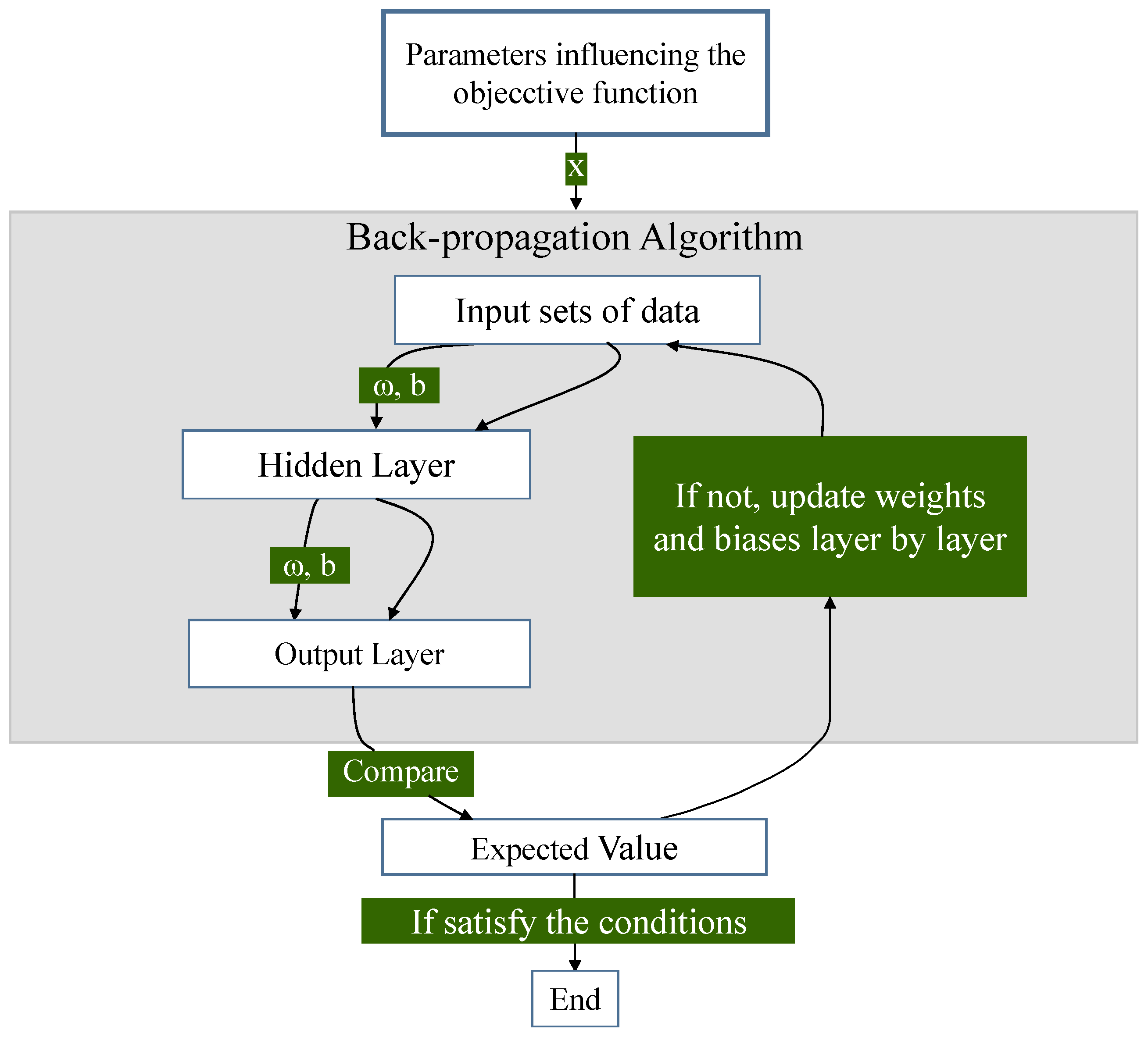
4.2. Neural Network Modelling
4.3. Evaluation Metrics
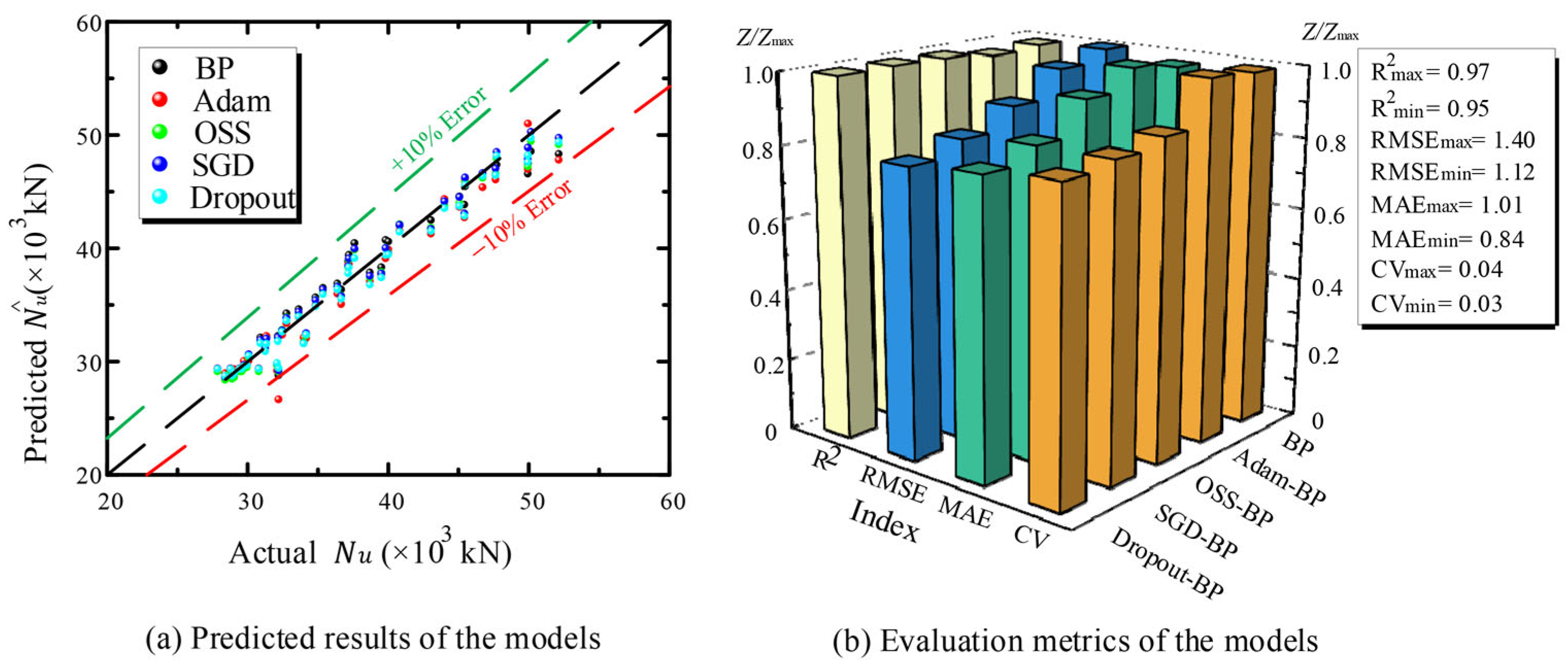
4.4. Performance of the Established Models
4.5. Application in Design Scheme
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
References
- Jin, K.-Y.; Zhou, X.-H.; Hu, C.; Wang, Y.-H.; Lan, Y.-S.; Zhou, Y. Axial Hysterestic Behavior of Prestressed CFDST Columns for Lattice-Type Wind Turbine Towers. Thin Walled Struct. 2024, 205, 112565. [Google Scholar] [CrossRef]
- LaNier, M.W. LWST Phase I Project Conceptual Design Study: Evaluation of Design and Construction Approaches for Economical Hybrid Steel/Concrete Wind Turbine Towers, National Renewable Energy Laboratory, June 28, 2002–July 31, 2004; Report No. NREL/SR-500-36777; National Renewable Energy Lab.: Golden, CO, USA, 2005; p. 15011444. [Google Scholar]
- Stavridou, N.; Koltsakis, E.; Baniotopoulos, C.C. Lattice and Tubular Steel Wind Turbine Towers. Comparative Structural Investigation. Energies 2020, 13, 6325. [Google Scholar] [CrossRef]
- Zhou, Z.; Chen, C.; Shen, X.; Zhou, X.; Hua, X. Conceptual Design of a Prestressed Precast UHPC-Steel Hybrid Tower to Support a 15 MW Offshore Wind Turbine. Eng. Struct. 2024, 321, 118939. [Google Scholar] [CrossRef]
- Gu, Y.-W.; Nie, X.; Liu, Y.-F.; Duan, S.-K.; Fan, J.-S. Experimental and Numerical Study of Steel-to-Concrete Joint Section in Hybrid Cable-Stayed Bridges. J. Constr. Steel Res. 2021, 187, 106982. [Google Scholar] [CrossRef]
- Yao, Y.; Yan, M.; Shi, Z.; Wang, Y.; Bao, Y. Mechanical Behavior of an Innovative Steel–Concrete Joint for Long-Span Railway Hybrid Box Girder Cable-Stayed Bridges. Eng. Struct. 2021, 239, 112358. [Google Scholar] [CrossRef]
- Yang, S.; Pu, Q.; Shi, Z.; Hong, Y. Mechanical Behavior of Steel–Concrete Composite Joints in Railway Hybrid Cable-Stayed Bridges. J. Constr. Steel Res. 2020, 173, 106242. [Google Scholar] [CrossRef]
- Liew, J.Y.R.; Chua, Y.S.; Dai, Z. Steel Concrete Composite Systems for Modular Construction of High-Rise Buildings. Structures 2019, 21, 135–149. [Google Scholar] [CrossRef]
- Ren, W.; Deng, R.; Zhou, X.-H.; Wang, Y.-H.; Cao, F.; Jin, K.-Y. Compressive Behavior of the Steel–Concrete Composite Adapter for Wind Turbine Hybrid Towers. Eng. Struct. 2023, 280, 115703. [Google Scholar] [CrossRef]
- Ren, W.; Deng, R.; Zhou, X.-H.; Cao, F.; Wang, Y.-H.; Jin, K.-Y.; Lan, Y.-S.; Luo, W. Steel-Concrete Composite Adapter for Wind Turbine Hybrid Towers: Mechanism and Ultimate Capacity Prediction under Compression. Structures 2023, 56, 104922. [Google Scholar] [CrossRef]
- Vernardos, S.; Gantes, C. Experimental Behavior of Concrete-Filled Double-Skin Steel Tubular (CFDST) Stub Members under Axial Compression: A Comparative Review. Structures 2019, 22, 383–404. [Google Scholar] [CrossRef]
- Hu, Y.; Zhao, J.; Zhang, D.; Chen, C. Experimental Seismic Performance of CFDST- Steel Beam Frames with Different Construction Details. J. Constr. Steel Res. 2019, 162, 105736. [Google Scholar] [CrossRef]
- Yan, X.-F.; Zhao, Y.-G.; Lin, S.; Zhang, H. Confining Stress Path-Based Compressive Strength Model of Axially Compressed Circular Concrete-Filled Double-Skin Steel Tubular Short Columns. Thin Walled Struct. 2021, 165, 107949. [Google Scholar] [CrossRef]
- Jin, K.-Y.; Zhou, X.-H.; Ren, W.; Wang, Y.-H.; Luo, W. Research on Hexagonal Concrete-Filled Steel Tubular Transition Pieces for Wind Turbine Hybrid Towers under Axial Compression. Thin Walled Struct. 2024, 200, 111956. [Google Scholar] [CrossRef]
- Xu, F.; Chen, J.; Jin, W. Experimental Investigation of Thin-Walled Concrete-Filled Steel Tube Columns with Reinforced Lattice Angle. Thin Walled Struct. 2014, 84, 59–67. [Google Scholar] [CrossRef]
- Liang, W.; Dong, J.; Wang, Q. Mechanical behaviour of concrete-filled double-skin steel tube (CFDST) with stiffeners under axial and eccentric loading. Thin Walled Struct. 2019, 138, 215–230. [Google Scholar] [CrossRef]
- Ekmekyapar, T. Hussein Ghanim Hasan The influence of the inner steel tube on the compression behaviour of the concrete filled double skin steel tube (CFDST) columns. Mar. Struct. 2019, 66, 197–212. [Google Scholar] [CrossRef]
- Li, W.; Chen, B.; Han, L.-H. Dennis Lam Experimental study on the performance of steel-concrete interfaces in circular concrete-filled double skin steel tube. Thin Walled Struct. 2020, 149, 106660. [Google Scholar] [CrossRef]
- Cheng, Z.; Wang, F.; Zhang, D. Analytical model for axially compressed circular concrete-filled double skin steel tubes (CFDSTs): Insights from concrete non-uniformly confined states. Thin Walled Struct. 2023, 192, 111106. [Google Scholar] [CrossRef]
- Huang, H.; Han, L.-H.; Tao, Z.; Zhao, X.-L. Analytical Behaviour of Concrete-Filled Double Skin Steel Tubular (CFDST) Stub Columns. J. Constr. Steel Res. 2010, 66, 542–555. [Google Scholar] [CrossRef]
- Pagoulatou, M.; Sheehan, T.; Dai, X.; Lam, D. Finite element analysis on the capacity of circular concrete-filled double-skin steel tubular (CFDST) stub columns. Eng. Struct. 2014, 72, 102–112. [Google Scholar] [CrossRef]
- Li, W.; Cai, Y.-X. Performance of CFDST stub columns using high-strength steel subjected to axial compression. Thin Walled Struct. 2019, 141, 411–422. [Google Scholar] [CrossRef]
- Yang, B.; Shen, L.; Chen, K.; Feng, C.; Lin, X.; Elchalakani, M.; Xu, S. Mechanical Performance of Circular Ultrahigh-Performance Concrete–Filled Double Skin High-Strength Steel Tubular Stub Columns under Axial Compression. J. Struct. Eng. 2022, 148, 04021298. [Google Scholar] [CrossRef]
- Shi, Y.-L.; Ji, S.-H.; Wang, W.-D.; Xian, W.; Fan, J.-H. Axial compressive behaviour of tapered CFDST stub columns with large void ratio. J. Constr. Steel Res. 2022, 191, 107206. [Google Scholar] [CrossRef]
- Ma, Y.; Yang, Z.; Liu, Y.; Liu, J.; Zhao, W.; Qiu, R.; Chen, X.; Qiao, Y.; Deng, Y. Flexural Behavior of Rectangular Concrete Filled Steel Tubular (RCFST) Composite Truss Bridge. Structures 2025, 72, 108260. [Google Scholar] [CrossRef]
- Wang, J.; Ke, K.; Yam, M.C.H.; Teng, M.; Wang, W. Improving Structural Robustness of Steel Frame Buildings by Enhancing Floor Deck Connections. J. Constr. Steel Res. 2023, 204, 107842. [Google Scholar] [CrossRef]
- Bai, W.; Li, Y.; Ji, J.; Liu, Y.; Zhang, L.; Wang, R.; Jiang, L.; He, L. Axial Compression Behavior of Symmetrical Full-Scale Concrete Filled Double Skin Steel Tube Stub Columns. Symmetry 2022, 14, 223. [Google Scholar] [CrossRef]
- Dong, Z.; Peng, H.; Wang, K.; Liu, T. Performance of Prefabricated Hollow Concrete-Filled Steel Tube Bracings on Transverse Bending: Experimental and Numerical Analyses. J. Mar. Sci. Eng. 2023, 11, 2009. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, A.; Xiong, Q.; Wu, W. Research on the Seismic Performance of Novel Side-Plate Reinforced Beam-Column Composite Joints. J. Constr. Steel Res. 2024, 222, 108935. [Google Scholar] [CrossRef]
- Architectural Institute of Japan. Recommendations for Design and Construction of Concrete Filled Steel Tubular Structures; Architectural Institute of Japan: Tokyo, Japan, 1997. [Google Scholar]
- ANSI/AISC 360-10; Specification for Structural Steel Buildings. American Institute of Steel Construction (AISC-ANSI): Chicago, IL, USA, 2010.
- Han, L.-H.; Lam, D.; Nethercot, D. Design Guide for Concrete-Filled Double Skin Steel Tubular Structures; CRC Press: Boca Raton, FL, USA, 2018; ISBN 0-429-44041-3. [Google Scholar]
- Johnson, R.P.; Anderson, D. Designers' Guide to EN 1994-1-1: Eurocode 4: Design of Composite Steel and Concrete Structures: General Rules and Rules for Buildings; Thomas Telford: London, UK, 2004. [Google Scholar]
- Wang, C.; Chan, T.-M. Machine Learning (ML) Based Models for Predicting the Ultimate Strength of Rectangular Concrete-Filled Steel Tube (CFST) Columns under Eccentric Loading. Eng. Struct. 2023, 276, 115392. [Google Scholar] [CrossRef]
- Nguyen, Q.H.; Ly, H.-B.; Tran, V.Q.; Nguyen, T.-A.; Phan, V.-H.; Le, T.-T.; Pham, B.T. A Novel Hybrid Model Based on a Feedforward Neural Network and One Step Secant Algorithm for Prediction of Load-Bearing Capacity of Rectangular Concrete-Filled Steel Tube Columns. Molecules 2020, 25, 3486. [Google Scholar] [CrossRef]
- Nguyen, H.Q.; Ly, H.-B.; Tran, V.Q.; Nguyen, T.-A.; Le, T.-T.; Pham, B.T. Optimization of Artificial Intelligence System by Evolutionary Algorithm for Prediction of Axial Capacity of Rectangular Concrete Filled Steel Tubes under Compression. Materials 2020, 13, 1205. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Z.Q.; Zhang, M. Prediction of Mechanical Behavior of Concrete Filled Steel Tube Structure Using Artificial Neural Network. Appl. Mech. Mater. 2013, 368–370, 1095–1098. [Google Scholar] [CrossRef]
- Liu, X.; Dangi, S.K.; Yang, Z.; Song, Y.; Sun, Q.; Wang, J. Study on Compression Bearing Capacity of Tapered Concrete-Filled Double-Skin Steel Tubular Members Based on Heuristic-Algorithm-Optimized Backpropagation Neural Network Model. Buildings 2024, 14, 3375. [Google Scholar] [CrossRef]
- Hibbitt, K. ABAQUS/Standard User’s Manual, Version 6.4.1.; Hibbitt, Karlsson, & Sorensen Inc.: Pawtucket, RI, USA, 2003. [Google Scholar]
- Smith, M. ABAQUS/Standard User’s Manual, Version 6.9.; Hibbitt, Karlsson, & Sorensen Inc.: Pawtucket, RI, USA, 2009. [Google Scholar]
- American Concrete Institute. Building Code Requirements for Structural Concrete (ACI 318-05) and Commentary (ACI 318R-05); American Concrete Institute: Farmington Hills, MI, USA, 2005. [Google Scholar]
- Han, L.-H.; Yao, G.-H.; Tao, Z. Performance of Concrete-Filled Thin-Walled Steel Tubes under Pure Torsion. Thin Walled Struct. 2007, 45, 24–36. [Google Scholar] [CrossRef]
- Liu, W. Research on Mechanism of Concrete-Filled Steel Tubes Subjected to Local Compression. Ph.D. Thesis, Fuzhou University, Fuzhou, China, 2005; pp. 64–65. [Google Scholar]
- Shen, J.M.; Wang, C.Z.; Jiang, J.J. Finite Element Analysis on Reinforced Concrete and the Ultimate Analysis on Slab and Shell; Tsinghua University Press: Beijing, China, 1993. [Google Scholar]
- Han, L.H.; Tao, Z.; Huang, H.; Zhao, X.L. Concrete-filled double skin (SHS outer and CHS inner) steel tubular beam-columns. Thin Walled Struct. 2004, 42, 1329–1355. [Google Scholar] [CrossRef]
- Helton, J.C.; Davis, F.J.; Johnson, J.D. A Comparison of Uncertainty and Sensitivity Analysis Results Obtained with Random and Latin Hypercube Sampling. Reliab. Eng. Syst. Saf. 2005, 89, 305–330. [Google Scholar] [CrossRef]
- Du, H.; Pan, J.; Shen, H.; Dong, J. Numerical Analysis of Flexural Behavior of Prestressed Steel-Concrete Continuous Composite Beams Based on BP Neural Network. Comput. Intell. Neurosci. 2022, 2022, 5501610. [Google Scholar] [CrossRef]
- Ahmadi, M.; Naderpour, H.; Kheyroddin, A. Utilization of Artificial Neural Networks to Prediction of the Capacity of CCFT Short Columns Subject to Short Term Axial Load. Arch. Civ. Mech. Eng. 2014, 14, 510–517. [Google Scholar] [CrossRef]
- Hou, C.; Zhou, X.-G. Strength Prediction of Circular CFST Columns through Advanced Machine Learning Methods. J. Build. Eng. 2022, 51, 104289. [Google Scholar] [CrossRef]
- Duong, T.H.; Le, T.T.; Le, M.V. Practical Machine Learning Application for Predicting Axial Capacity of Composite Concrete-Filled Steel Tube Columns Considering Effect of Cross-Sectional Shapes. Int. J. Steel Struct. 2023, 23, 263–278. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Representations by Back-Propagating Errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Robbins, H.; Monro, S. A Stochastic Approximation Method. Ann. Math. Stat. 1951, 22, 400–407. [Google Scholar] [CrossRef]
- Kingma, D.P. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:14126980. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Shen, R.; Gao, L.; Ma, Y.-A. On Optimal Early Stopping: Over-Informative versus under-Informative Parametrization. arXiv 2022, arXiv:2202.09885. [Google Scholar]
- Raskutti, G.; Wainwright, M.J.; Yu, B. Early Stopping and Non-Parametric Regression: An Optimal Data-Dependent Stopping Rule. J. Mach. Learn. Res. 2014, 15, 335–366. [Google Scholar]








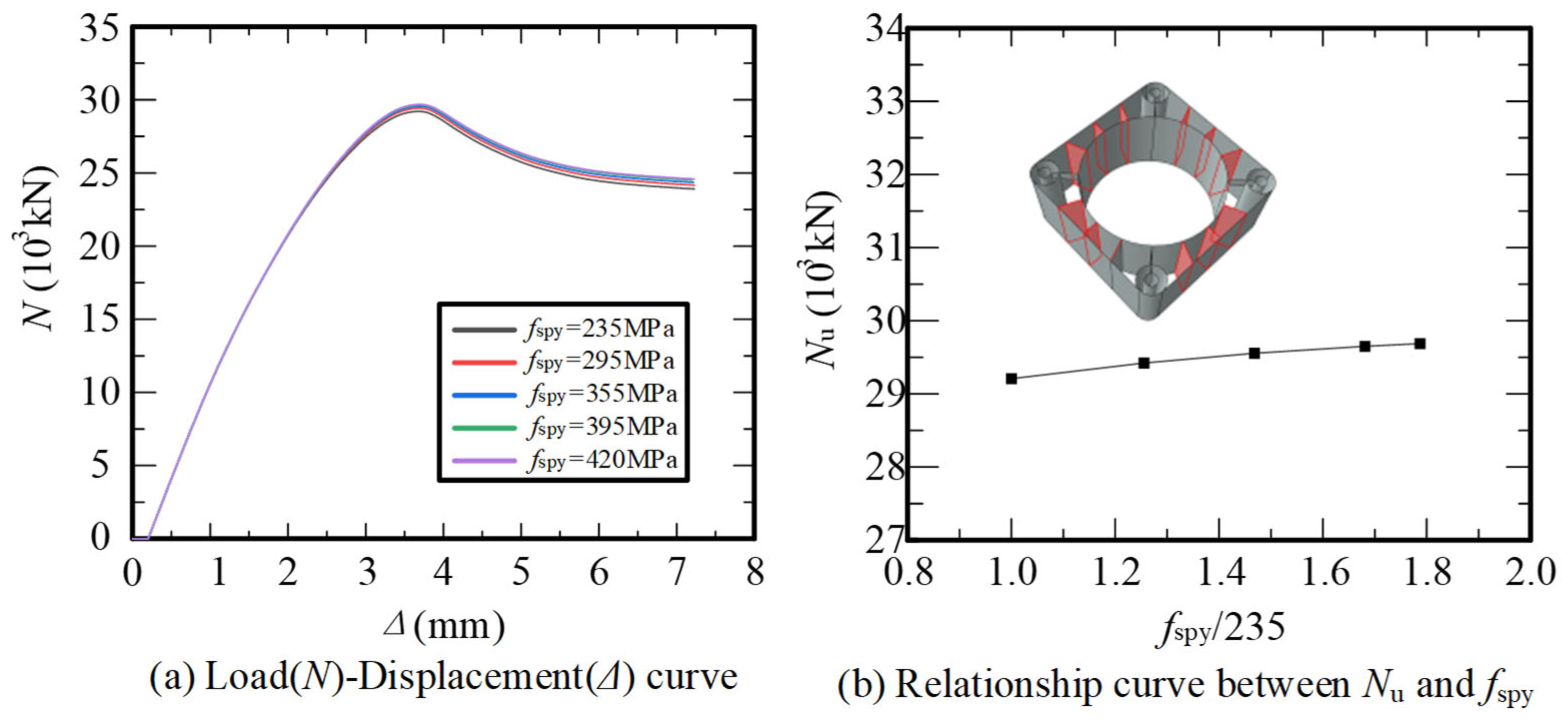
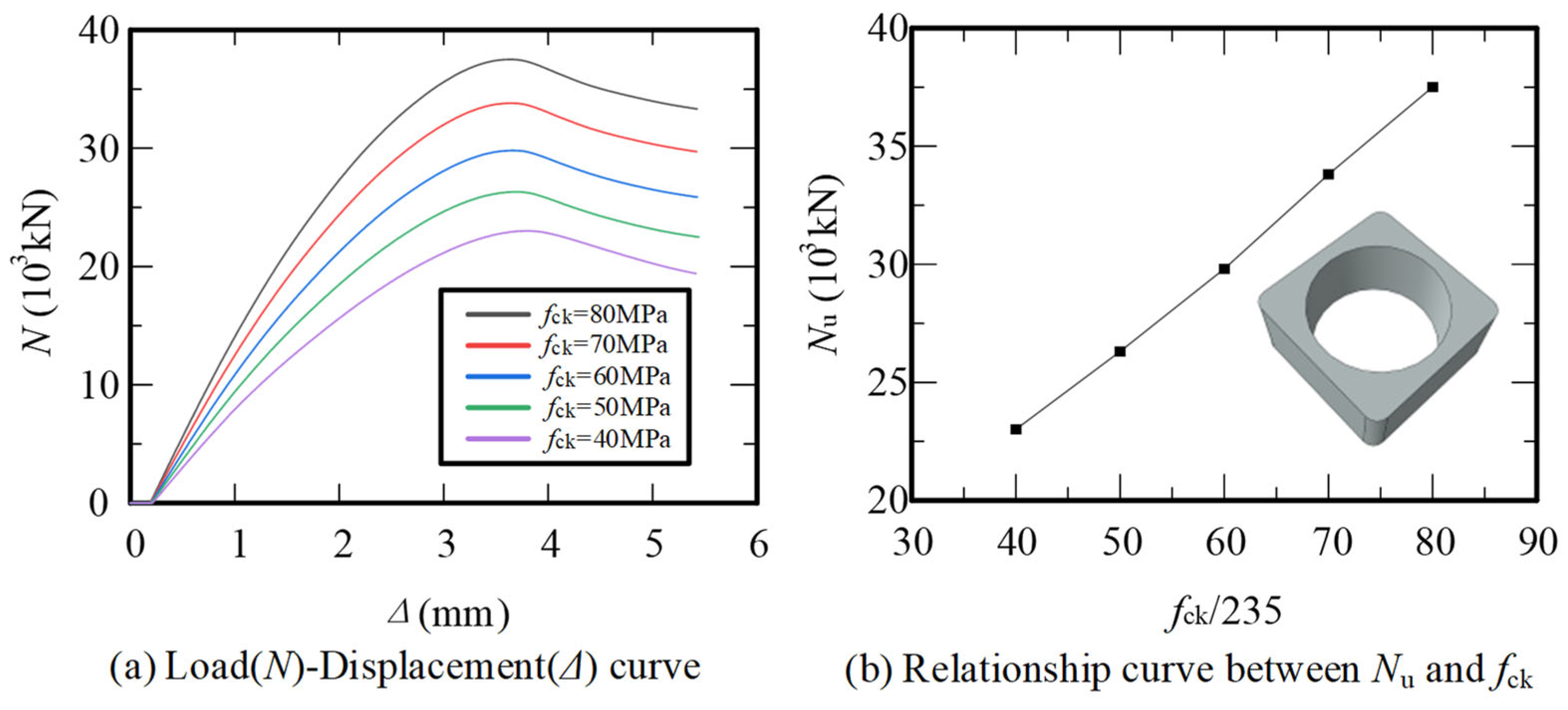
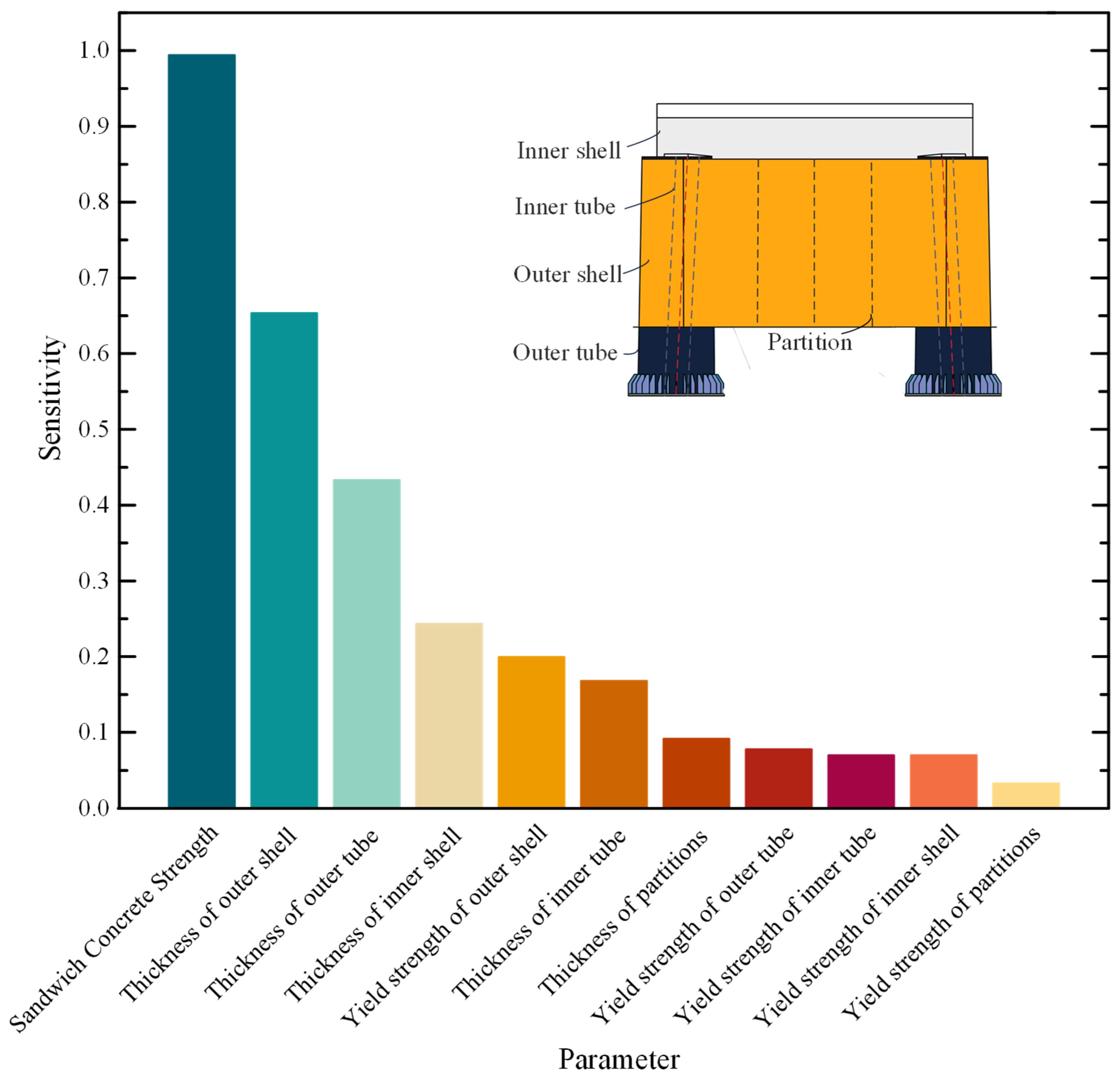



| Parameter | Sensitivity Level | Range (mm/MPa) | Sampling Groups | Sampling Basis |
|---|---|---|---|---|
| Thickness of Outer Shell | High | [10, 42] | 8 | LHS |
| Thickness of Outer Tube | Moderate | [10, 40] | 6 | LHS |
| Thickness of Inner Shell | High | [14, 54] | 8 | LHS |
| Thickness of Inner Tube | Moderate | [10, 34] | 6 | LHS |
| Thickness of Partitions | Low | [8, 32] | 4 | LHS |
| Steel Yield Strength | Low | [40, 80] | 5 | Engineering Grades |
| Concrete Strength | High | [235, 420] | 5 | Engineering Grades |
| Parameters | Notation | Value and Description |
|---|---|---|
| Neurons in input layer | ninput | 11 |
| Number of hidden layers | nlayer | 2 |
| Neurons in hidden layers | nneuron | 64, 32 |
| Neurons in output layer | noutput | 1 |
| Cost function | MSE | Mean square error |
| Activation function | fhidden | Sigmoid |
| Batch size | B | 2 |
| Learning Rate (Initial) | η | 0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, S.-C.; Wen, H.; Zhao, J.-Z.; Liu, Y.-S.; Duan, Y.-J.; Wang, C.-P. Neural Network-Based Prediction of Compression Behaviour in Steel–Concrete Composite Adapter for CFDST Lattice Turbine Tower. Buildings 2025, 15, 3103. https://doi.org/10.3390/buildings15173103
Wei S-C, Wen H, Zhao J-Z, Liu Y-S, Duan Y-J, Wang C-P. Neural Network-Based Prediction of Compression Behaviour in Steel–Concrete Composite Adapter for CFDST Lattice Turbine Tower. Buildings. 2025; 15(17):3103. https://doi.org/10.3390/buildings15173103
Chicago/Turabian StyleWei, Shi-Chao, Hao Wen, Ji-Zhi Zhao, Yu-Sen Liu, Yong-Jun Duan, and Cheng-Po Wang. 2025. "Neural Network-Based Prediction of Compression Behaviour in Steel–Concrete Composite Adapter for CFDST Lattice Turbine Tower" Buildings 15, no. 17: 3103. https://doi.org/10.3390/buildings15173103
APA StyleWei, S.-C., Wen, H., Zhao, J.-Z., Liu, Y.-S., Duan, Y.-J., & Wang, C.-P. (2025). Neural Network-Based Prediction of Compression Behaviour in Steel–Concrete Composite Adapter for CFDST Lattice Turbine Tower. Buildings, 15(17), 3103. https://doi.org/10.3390/buildings15173103






