Abstract
In this study, a new approach was developed for the estimation of optimum parameters (ODP), in terms of materials and design in livestock barns, and for optimal design. For this purpose, two thousand simulations were run using Monte Carlo (MC) techniques and Latin hypercube methods using the Energy Plus program on a 50-head closed dairy farm. In this study, the heat balance in the barn was adapted to Energy Plus using an innovative approach, using heat balance equations according to the ASHRAE Standard. First, data normality was determined using the Shapiro–Wilk (SW) and Kolmogorov–Smirnov (KS) tests. Data on thermal stress duration and energy consumption for dairy cattle welfare were estimated directly from the simulations, and sensitivity (SA) and uncertainty (UA) analyses were conducted. Furthermore, the statistical relationship between thermal comfort and energy consumption was determined using Pearson correlation. The predicted values obtained from the simulations were validated with barn values, and time-series overlay plots and histograms were generated. Furthermore, interpretations of the validation processes were made based on MBE, RSME, and R2 statistical values. The study estimated an indoor thermal comfort temperature of 12 °C, and this value was taken into account in the innovatively developed simulations. The estimated optimum design parameters in the study resulted in energy reductions of 25% and 41% for walls and roofs, 48% and 19% for cooling and heating setpoint temperatures, 43% and 37% for window areas, and 75% and 40% for natural and mechanical ventilation, respectively. When the design parameters were evaluated holistically and analyzed in terms of average values, the new simulation model achieved approximately 50% energy savings. We believe that the newly developed approach will guide future planning for countries, the public, and private sectors to ensure animal welfare and reduce energy consumption.
1. Introduction
Animal-based foods are essential for healthy nutrition. To ensure the production of these foods in the desired quality and quantity for human consumption, high animal productivity is essential. Therefore, to provide animal-based foods, animals should be raised in environments suitable for animal welfare, and the structural, architectural, and climatic characteristics of barns should be planned to create optimal conditions [1]. Planning for optimal conditions should consider many factors. Chief among these are the availability of energy efficiency and thermal comfort, the challenges and opportunities of animal barn design, and pre-design simulation studies to ensure optimal conditions. Therefore, to provide a more comprehensive overview of the literature, the introduction section of the article is divided into subsections. These subsections address challenges and opportunities in animal husbandry building design, the current status and limitations of thermal simulation technologies, key issues in energy efficiency optimization, and the objectives and innovative approaches to the study. These are presented below.
1.1. Challenges and Opportunities in Livestock Building Design
In addition to population growth, the demand for animal products for nutrition has increased due to rising incomes. This has also increased animal production, and projections indicate that this increase will approximately double by 2050 [2]. This increase in animal production has created the necessity of improving the design features of livestock buildings. As with all building types, the energy consumption of buildings designed to house animals must be reduced, and their overall performance must be increased. However, because animal production involves various biological and physiological balances, livestock buildings must be designed with efficiency and animal welfare in mind. This makes the design of livestock buildings more challenging. Furthermore, livestock buildings must be designed specifically to fit the regional landscape [3].
As in all building types, throughout human history, the choice of material for livestock structures has been determined by their abundance, workability, and availability. Accordingly, livestock structures have been designed using materials such as stone, wood, adobe, and clay brick. Over time, solutions have been developed that take into account animal welfare in the designs. Especially in the mid-20th century, animal production began to be carried out in enclosed structures specifically designed for animals [4]. The diversified livestock designs have gained a different dimension with the discovery of materials developed in the construction field, such as iron, steel, and concrete. Furthermore, the developing material technology in the construction sector has been tried to be adapted according to the changing and different parameters of livestock structures. Conditions such as productivity and welfare for livestock have made the design and material selection of livestock structures more difficult and necessary to evaluate in detail [5].
In response to the risks posed by global warming, efforts to reduce energy consumption have accelerated along with increased efficiency in the construction sector. Concepts such as sustainable buildings and green buildings, created through innovative design practices and the selection of appropriate materials, have come to the forefront [6]. This is even more crucial in livestock buildings, where efficiency, welfare, and sustainability must be ensured. Optimal designs for livestock buildings not only ensure sustainable structures but also reduce energy consumption, potentially preventing a factor that could negatively impact global warming. Therefore, technology, innovative design approaches, and the selection of appropriate materials for these designs should be considered as a whole in the design of livestock buildings [7,8].
Livestock buildings are among the primary elements that contribute to local development in terms of rural landscape and environmental sustainability, in addition to food production. Because they involve biological processes, along with efficiency and welfare for animal production, the design of livestock buildings has distinct technical characteristics from other building types. The fact that these designs directly impact the rural landscape necessitates ensuring optimal conditions in the design of these structures [9]. This, coupled with the need for food production, increases the importance that should be given to livestock buildings. This increased importance has increased interest in livestock buildings, which has presented a positive opportunity for them. As a result of comprehensive studies conducted during the design phase of livestock buildings, policies for the development and improvement of rural areas have been developed. Thus, regional development can be achieved alongside animal production [10].
Bringing healthy, high-reproductive animals to the farm to improve the quality and quantity of livestock products, developing an appropriate ration program, and feeding them properly are not sufficient for sustainable animal production. Improving environmental conditions and structural elements is crucial for animal production. Structural, social, and climatic factors within livestock building conditions play a significant role in animal behavior. Deficiencies in structural elements contribute to adverse environmental conditions in livestock buildings. These structural elements include windows, floors, roofs, walls, and bedding. Insufficient window space can lead to ventilation and lighting problems, which can lead to lung diseases in animals. The structural elements used in the architectural planning and design of livestock buildings indirectly affect animal productivity and behavior. From a cost perspective, the design and construction costs of livestock buildings account for 55% of the fixed investment costs [11].
1.2. Current Status and Limitations of Thermal Environment Simulation Technologies
From an animal production perspective, structural, social, and climatic factors play a significant role in animal behavior within livestock buildings. Deficiencies in structural elements within barns lead to adverse environmental conditions. Thermal comfort is the primary impact of these adverse conditions on animals. Numerous studies on livestock buildings indicate that inadequate thermal comfort within barns negatively impacts animal production efficiency. Numerous variables within the barn, such as air quality, natural or artificial ventilation systems, and roof and window positions, are important. In this context, maintaining thermal conditions depends on many factors, the most important of which is the proper planning of building elements. Ensuring thermal comfort also helps control energy consumption [12].
Thermal comfort must be ensured in all buildings, including livestock buildings. Therefore, thermal environment simulation studies are conducted to ensure optimal conditions during the design phase of buildings. Programs such as DesignBuilder, DOE-2, eQuest, Ecotect, Energy-10, EnergyPlus, Green Building Studio, HEED, and IESVE have been developed for building simulations and are being used successfully to simulate the thermal environment in buildings [13].
An examination of the programs used in thermal environment simulations reveals that most of them consist of a simulation engine and a graphical user interface (GUI) connected to this engine. The engines in simulation programs are necessarily developed in computer languages such as FORTRAN, C, and C++. GUIs, which can quickly perform input and output operations, facilitate the preparation of parameters and outputs generated in simulations, ensuring proper operation. In most programs used in thermal environment simulations, the GUIs and the simulation engines are designed separately [14].
Programs such as Ecotect, Radiance, DAYSIM, and EnergyPlus can systematically simulate thermal environments using multiple engines. Thermal conditions are determined in the simulations using data such as sun, daylight, and airflow. These programs also import data using IFC or gbXML via the engine unit and GUIs. These operations are performed using Design Builder and Hevacomp, GUIs developed for EnergyPlus. However, many simulation programs create thermal simulations using advanced IFC and gbXML schemes, but manual simulation checks and modifications are required to determine the optimum conditions for buildings. Limitations of these models include the time-consuming nature of simulation models, the possibility of error, and the need for manual control [15].
1.3. Basic Issues in Energy Efficiency Optimization
Optimization processes in building design are defined as all procedures designed to ensure a building design achieves optimal energy efficiency. Energy efficiency optimization requires preparation. This preparation is followed by optimization processes and, finally, the final stages of optimization. These processes include creating a model for energy efficiency optimization, defining functions for the objectives, and transferring simulations to the software along with independent variable parameters. Following these processes, the phase begins, which involves identifying any existing errors along with the target function and optimization timeframe. The final stage involves interpreting the results [16].
Energy efficiency optimization can be defined to include a single objective. However, if necessary, a function can be created to encompass two or three objectives. Optimizations defined for energy efficiency are designed to reduce annual energy consumption in buildings. However, efficiency performance must be taken into account in the various optimizations created for the algorithms [17].
Along with defining the targets for energy efficiency optimization, independent variable parameters in buildings must also be established. In this context, building design should determine the properties of building materials such as glazing type, window area, and natural and mechanical ventilation in terms of shape [17]. At this point, building shape, in particular, can be evaluated differently in terms of energy efficiency optimization. A general determination can be made for other building materials besides building shape. The most frequently considered variables in terms of building materials and design parameters in energy efficiency optimization are known as glazing type, amount of natural and mechanical ventilation, window-to-wall ratio, and wall material [18].
Studies on energy efficiency optimization in buildings with the aim of reducing negative environmental impacts and energy consumption are rapidly increasing globally [19]. This is even more important for livestock buildings. Reducing energy consumption in livestock buildings, along with environmental impact studies, is essential for sustainable animal production [20]. In addition to reducing energy consumption, it is also possible to increase thermal comfort with optimum architectural design [21]. Many studies on livestock buildings have concluded that many variables, such as natural or artificial ventilation facilities and roof and window positions, are important for energy efficiency. In this context, ensuring energy efficiency in livestock buildings depends on many factors, the most important of which is the correct planning of structural elements. It will be possible to obtain optimum design parameters through correct energy efficiency optimization studies in livestock buildings [22].
1.4. Objectives and Innovative Method of the Study
Air temperature and relative humidity are among the most important physical factors affecting the highest possible productivity in livestock buildings. Dairy cattle, in particular, can tolerate biologically ideal environmental conditions to a certain extent and minimize adverse effects. Therefore, dairy cattle are defined as warm-blooded (homothermic) animals. While individual cattle vary in this regard, breed, type, and productivity factors are the determining factors [23]. The resulting temperature increase allows dairy cattle to eliminate 15% of their internal body heat directly through respiration. Furthermore, when the ambient temperature in livestock buildings exceeds 25 °C, feed consumption begins to decline, and when it exceeds 30 °C, a significant decrease in feed consumption is observed. At 40 °C and above, feed consumption ceases completely. One of the most important reasons for the decrease in feed consumption under high temperatures is that the high respiration rate in animals prevents feed consumption [24].
Heat stress directly affects dairy farming productivity, but it also alters the chemical structure of the milk produced. At low temperatures, the fat content in milk decreases, while at high temperatures, the fat content is higher. Furthermore, high ambient temperature and relative humidity also affect reproduction in dairy cattle [25]. Hormonal activity changes, and the severity of estrus behaviors decreases, or estrus disappears altogether. Furthermore, embryonic mortality and fertility declines occur. This demonstrates that if heat stress is not eliminated in livestock facilities, not only will animal welfare and productivity decline, but the sustainable maintenance of livestock production will be impossible [26].
In livestock buildings, ensuring that energy savings are combined with thermal comfort is of paramount importance. Proper adjustment of livestock barn design parameters positively impacts animal health and productivity. Generally, the building environment can be improved through many design parameters, such as ventilation and construction materials [27]. Geothermal, passive, aerothermal, and biogas solutions are used to reduce fossil fuel consumption in livestock barns [28]. Building (barn) energy simulation (BES) experiments are conducted to determine the effectiveness of these solutions or new barn design parameters and their potential use in barns. The created BES models reveal the building’s climatic environmental conditions and energy performance with specific input and output parameters [29,30]. The creation of BES models, especially in animal barns, has gained importance for animal welfare and productivity. It is envisaged that the increasing BES studies in livestock building research in recent years will form the basis of energy performance certification programs in the future [31].
BES models can play a significant role in assessing many different impacts on livestock buildings, such as climatic environmental conditions, energy consumption, and thermal discomfort duration. While livestock buildings share some characteristics with buildings occupied by people, they require different expertise in certain areas. For example, the need for higher ventilation rates, different airflow rates, and differences in cooling and heating systems are all points that should be considered in the simulation models to be developed. Furthermore, using BES models and housing parameters during the design and management stages of livestock buildings positively impacts energy efficiency [32].
Numerous studies have modeled BES to provide thermal comfort conditions and energy consumption in livestock buildings. Some of these studies simulated periods of thermal stress in animals, while others simulated energy consumption by considering ventilation and various design parameters. This innovative approach examines all aspects of thermal stress, energy consumption, and optimal design parameters and develops a prediction based on indoor thermal comfort temperature. Furthermore, this innovative approach resulted in the creation of a heat balance model according to the ASHRAE Standard to adapt the barn heat balance to Energy Plus.
A review of the studies reveals that Cooper et al. [33] and Liberati and Zappavigna [34] created a general energy simulation model for animal barns with mechanical or natural ventilation systems. In another study, Shin et al. [35] developed a simulation to calibrate the electrical energy consumption of ventilation fans in animal barns. Similarly, Kwak et al. [36], Jackson et al. [37], Axaopoulos et al. [38], and Wang and Xue [39] developed simulation models for energy consumption in animal barns. However, when the BES models in animal barns are examined in terms of thermal stress, it is seen that simulation models have been developed for the climatic conditions inside the barn and for some design parameters. Among these studies, Mikovits et al. [40] developed a simulation to determine the thermal stress in pig barns. In a similar study, Schauberger et al. [41] created a simulation to reveal the thermal stress inside the barn. In a different study evaluating the design parameters, Gonçalves et al. [42] developed a simulation model to reveal potential heat stress by considering different roof tile types. In other studies, simulations were developed by Shin et al. [43], according to climatic environmental conditions, and by Lambert et al. [44], according to humidity values.
In this study, a novel barn energy simulation (BES) was developed to estimate the effects of structural elements in dairy barns on the energy consumed by the barn’s structural elements and the thermal comfort of the animals inside the barn. The simulation is a novel virtual simulation of a dairy barn based on a computer-based mathematical model created according to the basic energy balance equations commonly used in buildings [45]. In addition, a barn simulation was created using simulation tools such as DesignBuilder, EnergyPlus, and TRNSYS, which provide numerical data evaluation across different data sets and are widely used in many thermal analysis studies in buildings and animal barns [35,43,46].
This study examined the most important design parameters required to estimate thermal comfort and energy consumption for animals in dairy barns. The identified parameters were exterior wall construction, roof construction, glazing type, natural and mechanical ventilation ratio, window-to-wall ratio, window area cooling setpoint temperature, heating setpoint temperature, and infiltration rate. The effects of these parameters on thermal comfort and energy consumption were investigated using BES tools. Design parameters were statistically evaluated for thermal comfort and energy consumption using Pearson correlation. In this context, the study estimated the most important design parameters that can reduce energy consumption and increase thermal comfort in dairy barns. A review of simulation studies on animal barns revealed that models are generally developed from the perspective of thermal stress or energy consumption. These models, by simulating various design parameters, only addressed specific issues, such as the relationship between total energy consumption and periods of thermal stress. This study, unlike existing research, considered thermal stress and total energy consumption together and created new simulations considering all barn design parameters. Furthermore, the optimum indoor thermal comfort temperature for the barn was estimated. In this context, a more comprehensive study was conducted for animal barns. Simulated values were also validated against barn values. The study aimed to control total energy consumption by reducing thermal stress levels for animals. To this end, a new approach was developed to estimate the optimum values for various barn design parameters. In this context, the research will contribute to the use of optimal design parameters during the project design phase, increase thermal comfort, positively impact animal welfare and productivity in dairy farming, and reduce energy consumption.
2. Materials and Methods
2.1. Research Area and Shelter Design
The material of the research consists of a 50-head dairy farm operating in the climate conditions of Ankara province of Turkiye, and it was determined as the reference base model in terms of the simulation process. The geographical location of Ankara province, where the research was conducted, is given in Figure 1. However, the dairy farm given in Figure 2 (40 m length × 17.85 m width × 4.25 m height) has an area of 714 m2. In terms of architectural features, the structure has a continental climate in terms of design parameters, such as walls, floors, ventilation windows, and roof systems.
Figure 1.
Research area.
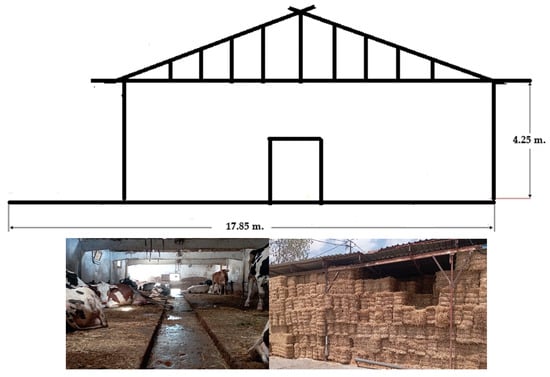
Figure 2.
General view of dairy cattle barn.
The Energy Plus Design Builder (version 6.0.1.019) [47] program was used to prepare different simulations regarding the design parameters of the structural elements in the barn to estimate the thermal stress and total energy consumption of dairy cattle. The EnergyPlus Weather file, which includes the Ankara climate conditions, was obtained to calculate the environmental conditions inside the barn. Weather data were taken from the Ankara 171280 (IWEC) section of the European (WMO Region 6) Turkey file [48]. In addition, a reference model was prepared to represent realistic design practices for the mechanical ventilation (MV) mode for the barn. In this context, a sound and comprehensive evaluation of the different structural elements inside the barn in terms of thermal properties and energy consumption estimation was provided.
2.2. Preparation of Simulations of Design Parameters Research Area and Shelter Design
In this study, Monte Carlo (MC) techniques were used after Shapiro–Wilk (SW) [49] and Kolmogorov–Smirnov (KS) [50] tests were performed to determine the presence of skewness in the data to prepare simulations of various structural elements. The Monte Carlo method is a statistical analysis method widely used in studies conducted in various fields. The MC method uses probability distributions to estimate the averages of mathematical problems that are difficult to solve numerically [51]. Furthermore, sensitivity analysis (SA) and uncertainty analysis (UA) were applied to accurately estimate the impact of different structural elements in the barn on the design process from an architectural perspective. Sensitivity and uncertainty analysis are generally used together in many structural studies [52,53]. Furthermore, the Energy Plus DesignBuilder program, used in many studies to reveal statistical combinations of structural elements in dairy barns, aimed to estimate the effects of the results obtained with the MC method on energy consumption and thermal properties. DesignBuilder is an EnergyPlus (version 6.0.1.019) [47] based software tool used to determine energy and comfort performance in structural design. Parametric analysis is one of the most frequently used methods to describe performance values such as energy and thermal properties in structures [54].
2.2.1. Monte Carlo Technique and Uncertainty Analysis
Monte Carlo Simulation is a type of simulation obtained by repeated random selection of samples and statistical analysis to calculate the results. However, Monte Carlo Simulation is a mathematical technique that allows for quantitative analysis and takes into account the risks that may arise when making decisions according to the results. The technique can be used as a guide in studies to be carried out in many different fields, such as engineering, production, finance, energy, project management, research, and development. Simulations created with the Monte Carlo technique are a technique that can reveal the range of possible results related to a situation and the probabilities that will arise at the point of choice [55].
When we look at the first use of Monte Carlo Simulation, it is seen that it was used by scientists working on atomic bomb studies [56]. The technique takes its name from Monaco’s holiday resort Monte Carlo. In this context, it has been used to model physical and conceptual systems in many studies from the Second World War to the present [57]. Monte Carlo Simulation is one of the most widely used simulation methods in research when evaluated from today’s perspective [58]. The technique substitutes a series of values for any factor with uncertainty. In this context, it creates models of possible results and creates risk analysis. It uses a random set of values and calculates the obtained results repeatedly for a large number of times [59].
Before the uncertainty analysis, a database is created that can be applied to the model in terms of the definition of uncertainties to be created. In order to provide flexibility for the user, the uncertainty magnitude and probability distributions, the model parameters to be analyzed, and the relationships of these model parameters in terms of uncertainty qualities should be included in the created model uncertainty file [60].
The MC technique used in terms of uncertainty analysis is based on the central limit theorem, which was created to provide a general assessment of the uncertainty in the estimates. In this context, uncertainty analysis creates an estimate of the general uncertainty in the estimates in terms of the uncertainties in the input parameters created, independently of the design parameters and their interactions. In this way, it is aimed to eliminate the uncertain situation. In this method, a probability distribution is assigned to each input value created within the scope of the research while performing the process. Thus, the values within the probability distributions for all the parameters created are selected randomly. After the selection process, simulations are performed. The simulations are performed repeatedly with new values selected randomly in the same way. In this way, a large number of successive simulations are performed. The simulations created in large numbers will create a Gaussian distribution in terms of the uncertainty in the output parameters, independent of the probability distributions for the created input parameters. Uncertainty analysis results will be created according to the estimation range, Gaussian distribution, and non-dimensional measurements in the result sets to be obtained [60,61].
2.2.2. Normality Test
Finding an appropriate assumption regarding the distribution of data is crucial for accurate analysis. Appropriate statistical methods can be applied based on the assumed data distribution. Specifically, the model parameters to be generated allow for more specific and efficient calculations. Obtaining accurate results in statistical methods requires a normal distribution of the data. Therefore, performing a normality test before statistical analysis is essential to ensure the accuracy of the analysis results. In this context, the Shapiro–Wilk (SW) [49] and Kolmogorov–Smirnov (KS) [50] methods, the most commonly preferred normality tests, were used to test the data for normality. Based on the results of both methods, a logarithmic transformation was applied to the design parameters with inappropriate distributions to eliminate skewness in the data. The methods used in the normality tests in the study are presented below.
- The Shapiro–Wilk (SW)
The test was developed by Shapiro and Wilk in 1965 to eliminate skewness in data [49]. The general formula for the test statistic is presented below.
Of the variables specified in the formula, (x(i)) is the first-order statistic, and (x) is the sample mean and the resulting constant. The variable specified as ai in the formula is calculated with a separate formula and is presented below.
According to the formula for calculating the ai value, m = (m1, … , mn) T are the expected values of the order statistics of independent and identically distributed random variables sampled from the standard normal distribution set. Furthermore, the value (V) in the formula is the covariance matrix of these order statistics.
- The Kolmogorov–Smirnov (KS)
In order to eliminate skewness occurring outside the normal distribution in a data set, Kolmogorov and Smirnov proposed a normality test known as KS in 1933 [50]. The solution formulation of the test is presented below.
while (zi) represents the cumulative probability of the standard normal distribution, and (D) shows the difference between the observed and expected values.
2.2.3. Energy Plus Program and Sensitivity Analysis
Many programs, such as Ecotect, eQuest, Green Building Studio, Energy-10, Radiance, DAYSIM, and EnergyPlus, are available for creating energy simulations in buildings and determining optimal design parameters [13]. However, among these programs, EnergyPlus is one of the most widely used simulation programs in building sustainability, allowing for analysis and optimization of building performance in terms of energy efficiency [62]. Funded by the US Department of Energy (DOE), EnergyPlus stands out among other programs because it is open source, freely accessible, and functionally interoperable across platforms. In this context, simulations were created using EnergyPlus in this research. The program, which provides numerous integration and extension capabilities, includes a console consisting of text files. .idf files are used for building models. Various graphical interfaces are also available. DesignBuilder, included in these interfaces, facilitates the creation of simulations and is periodically updated [63].
Thanks to the interface and module development in EnergyPlus, it is possible to create building geometric models more easily and accurately than other simulation programs. Furthermore, with jEPlus and the GUI developed as a graphical user interface to support precision and optimization, results can be achieved more easily. Furthermore, with the ability to assign labels in JEPlus, manual editing of .idf files for areas that need to be modified can be performed [64].
The EnergyPlus DesignBuilder program, which is primarily used in energy simulation studies in buildings, is also the most frequently used physics-based simulation modeling tool for livestock buildings [65]. Furthermore, the EnergyPlus DesignBuilder program has been identified as the best option for developing energy models for livestock buildings [35]. The EnergPlus program provides 3D corner coordinates for each surface area in buildings, and the definitions are made using the Building Surface: Detailed class. In this study, the geometric characteristics of the dairy cattle barn were defined in the program using this class. Furthermore, the livestock building’s climatic environmental conditions and design parameters were defined, and the BES model was created.
The energy model creation phase for the barn involves estimating the total energy consumed and the duration of thermal discomfort using a simulation program to produce outputs related to the energy performance of the animal barns. In this context, the program Energy Plus (version 6.0.1.019) [47] was used, and performance measurements were made using Design Builder. The simulation tool used in the research was evaluated for dairy cattle with an innovative approach. In this context, EnergyPlus simulation models were created with heat balance equations suitable for livestock buildings (ANSI/ASHRAE Standard 62.1-2016/ASHRAE Technical Committee on Facilities and Environment 2.2) [66]. In addition, the heat balance equations according to the ASHRAE Standard were used to adapt the heat balance situation in the barn to Energy Plus, which is another innovative aspect of the research. The heat balance equations used were adapted for cattle, taking into account ANSI/ASHRAE Standard 62.1-2016/ASHRAE Technical Committee on Facilities and Environment 2.2. EnergyPlus has input elements for HVAC system components in various building structures [67]. Energy simulations created with EnergyPlus have been successfully applied to livestock buildings.
In the study, after defining the shelter design parameters with their value ranges before the sensitivity analysis, files were created by adding values to the relevant parameters using the LHS method on the model. The creation of these files was achieved using the jEPlus program, an integrated system with the EnergyPlus program [68]. Multiple simulations were created in the EnergyPlus program using the LH method using the IDF files created with the jEPlus program [67].
Sensitivity analysis is performed to estimate the effect of the shelter design parameters determined as inputs in the study in terms of total energy consumption and thermal discomfort, and also to estimate which parameter has the largest effect [69]. In this context, the sensitivity analysis performed within the study provides significant support in explaining the connection between the design parameters for the animal shelter and the simulation results [70]. Sensitivity analysis is generally performed in two different classifications: local and global [71]. In the local sensitivity analysis, only one design parameter is evaluated, while in the global sensitivity analysis, all parameters are evaluated simultaneously [72]. In this context, the global sensitivity analysis method was considered to estimate all design parameters simultaneously in the animal shelter within the study. Before starting the sensitivity analysis in the study, the shelter design parameters and their value ranges to be used in the analysis were determined. The assignment of the determined values can be performed by many different methods. In the study, Latin hypercube sampling (LHS) was used to ensure that the stratification characteristics produce positive results [73].
2.2.4. Pearson Correlation
Pearson correlation reveals the statistical relationship between different data sets represented by variable values. In this context, correlation is a very commonly used similarity measure in determining the direction and intensity of the statistically linear relationship between the attribute values of two different objects. Data sets are determined by a function [74].
Statistical similarity criteria are functions created to determine the degree of statistical similarity between objects. These functions determine the degree of statistical similarity in the range of (0,1) or (−1,1). The correlation coefficient in the study was determined by Formula (1). The change in the value of the obtained correlation coefficient between “+1” and “−1” indicates the transition from a perfect positive correlation to a perfect negative correlation in statistical terms. In this context, the correlation coefficient is based on the comparison of the interaction of two different variables according to the highest possible effect of the two variables. The correlation coefficient created as a result of this statistical function is called the Pearson correlation coefficient [75,76].
The formula is used to test the degree of correlation between two or more variables, where (r) is the product moment correlation coefficient known as Pearson correlation coefficient, (Y) is the independent variable, (X) is the dependent variable, (n) is the sample size symbolized, and xi and yi are the individual midpoints indexed with i.
2.3. Determination of Shelter Design Parameters, Input and Output Variables, and Density Functions
In dairy farms, there is a constant heat loss or gain from structural elements such as floors, walls, windows, and roofs [77]. Keeping the heat loss and gain in balance in terms of environmental conditions for the shelter reveals the energy requirement. In this context, the foundation, shelter floor, walls, doors, windows, carrier system, and roof were taken into account as input variables in providing thermal balance in the shelters. The output variables were determined as energy demand and heat stress conditions in which dairy cattle are thermally uncomfortable.
Two thousand simulated samples were generated using the Latin hypercube sampling (LHS) technique, a widely used sampling method in studies on structures constructed in accordance with uncertainty (UA) and sensitivity (SA) analyses in terms of density functions. LHS is a method that covers the entire sample area, is commonly used in structures, and produces samples without any repetitions [78]. In this respect, the LHS method was used in dairy cattle barns with an innovative perspective. The LHS divides the sample area into equal parts for n sample points. The LHS ensures that each layer is sampled exactly once, thus creating a comprehensive representation of the entire sample area. The structural elements used in the simulated dairy cattle structures were derived from the elements most frequently highlighted in the literature.
2.4. Estimating Indoor Thermal Comfort Temperature in the Preparation of a Barn Energy Simulation (BES)
The heat balance equations used in the study are those suitable for animal barns (ANSI/ASHRAE Standard 62.1-2016/ASHRAE Plant and Environment Technical Committee 2.2) [66]. In this context, two functions were created to estimate energy consumption and thermal comfort. Furthermore, heat balance equations according to the ASHRAE Standard were used to adapt the heat balance situation in the barn to Energy Plus, another innovative aspect of the research. The heat balance equations used were adapted to cattle, taking into account ANSI/ASHRAE Standard 62.1-2016/ASHRAE Plant and Environment Technical Committee 2.2. Furthermore, the optimum indoor temperature estimated for dairy cattle was also taken into account in the simulations, as animals generally have different thermal comfort criteria than humans.
In this context, the optimum temperature, thermal comfort, total energy consumption, and optimal design parameters for dairy barns were estimated based on simulation results. First, unlike existing research, the estimated indoor thermal comfort temperature was considered the optimum value in simulations prepared with Energy Plus and was also considered in simulations for all design parameters. Furthermore, the optimum indoor thermal comfort temperature in the barn was determined as the barn’s input parameter. In this context, statistical analysis was conducted for the distribution characteristics. Furthermore, regression analysis was conducted to determine the effects of indoor thermal comfort temperature on total energy consumption and thermal comfort for the barn, and the significance level was determined.
2.5. Validation of Barn Energy Simulation (BES)
In order to determine the accuracy of the results obtained from the simulation models developed according to the design parameters in buildings, a comparison is generally made with field measurement data. This comparison can be achieved by a statistical analysis method that reveals the similarity of the simulation model in buildings in terms of energy consumption and thermal properties [79].
In the BES model created in the research, the statistical agreement determined between the simulated and measured data was evaluated numerically by comparing them with the limit values determined as a result of international standards and protocols. A field study was conducted to provide the data to be compared with the results of the developed simulation. The data obtained as a result of this process and the simulation results were compared with the limit values determined by international guidelines and protocols. In this context, two different international protocol values were evaluated; these protocols are the 14th Guideline of the American Society of Heating, Refrigerating and Air-Conditioning Engineers (ASHRAE) [66] and the Federal Energy Management Program (FEMP) Measurements and Verification guidelines [79]. A difference of ±10% between the simulated and measured values according to both protocols is the acceptable threshold value [66,79]. In this respect, the reliability of the simulated values according to this ratio determined in the protocols was demonstrated.
An examination of the verification periods in energy simulation studies in livestock farms reveals that verification was generally conducted for periods of 2, 7, 10, 21, 50, and 365 days [32,33,35,37,42,80]. In this context, the verification was conducted using field data during the production cycle between 1 January and 30 August 2024, in a relatively long and comprehensive manner. The long-term study was conducted to ensure that the fieldwork reflected extreme weather conditions, such as extreme cold and heat waves. The verification process was conducted over full-day cycles.
For verification purposes, a total of five equally spaced temperature and humidity meters are located in the livestock building. Five Retmon CHTS-02 temperature and humidity sensors [81] are located equidistantly within the barn, 8 m apart. These sensors are typically used to monitor climatic conditions in closed structures, livestock buildings, and agricultural structures such as greenhouses. In terms of temperature measurement accuracy, the accuracy is less than 0.1 °C, and the humidity accuracy is 3%. Calibration complies with TS EN IEC 61000-6-2 [82] and ISO 9001-2015 [83] standards. The distribution of the sensors within the barn and the remote monitoring system connections are presented in Figure 3.
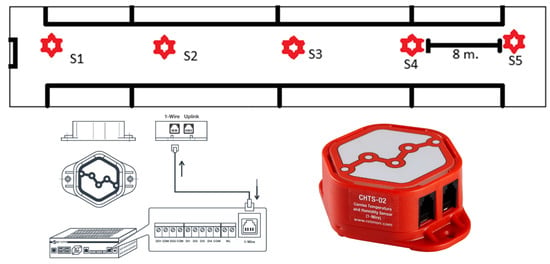
Figure 3.
Sensor remote connection system [81] and distribution inside the barn.
However, some differences may occur between indoor values and simulation models. These differences arise from factors such as heat losses and gains in construction, design errors, and a lack of knowledge and expertise. In this context, it is desirable for the design parameters in buildings to achieve results as close as possible to the values in the simulations. In the research, simulation models were used to estimate the optimum conditions for the barn design parameters based on total energy consumption and thermal stress, and the obtained values were verified. During the validation processes, studies were conducted using the ASHRAE (American Society of Heating, Refrigerating, and Air-Conditioning Engineers), FEMP (Federal Energy Management Program), MBE Mean Bias Error), Cv (RMSE), and R2 methods, where equations are given in the range of 2–5. According to the simulation validation results, a positive value for the MBE value indicates that the data are underestimated, while a negative value indicates that the data are overestimated. In this context, since the sum of the positive and negative numbers can reduce the MBE, the Cv (RSME), which expresses the relative error variability as a percentage, was also used for validation. However, the calculated R2 value shows the closeness of the values measured by the simulations. For the appropriateness of the validation, it is recommended that this value not be less than 0.75 [84,85,86,87].
The variables in the equation (j) are the values whose simulations were created and measurements completed within the time period xj and xj, respectively. Furthermore, n(set) represents the cardinality of the data set considered in the study.
After obtaining the MBE value, the Cv(RMSE) value was calculated. To calculate this value, the RMSE was first determined, and then the Cv(RMSE) value was obtained. The formulas used in the calculations are presented below.
The variables in the RMSE and Cv(RMSE) formulas have the same units as those used in the MBE calculations. In this context, (j) are the values whose simulations were created and measurements completed within xj and xj periods, respectively, and n(set) represents the cardinality of the data set considered in the study.
The verification process performed according to the R2 method is defined by Equation (5), where (mi) is the parameter measurement result, (ḿ) is the mean obtained from the parameter measurement, (si) is the parameter simulation result, and (ś) is the mean obtained from the parameter simulation.
2.6. Methodology
The methodology applied in the research consists of consecutive stages. Detailed aspects of barn design parameters, such as materials, type, service, and climate data, are presented. Two thousand simulations were created using the Latin hypercube sampling (LHS) method from the structural elements determined using the Energy Plus program. Energy consumption data obtained from the heating and cooling load of the animal barn and parameters such as the duration of exposure of dairy cattle to heat stress were evaluated as outputs for the simulation. The simulation outputs obtained were compared with the sampled input parameters in order to determine the effect of each input. In this context, the methodology used in the research is given in Figure 4 with all its stages.
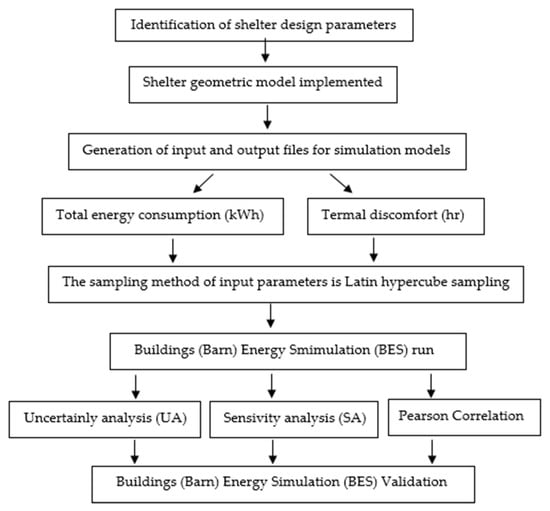
Figure 4.
Barn energy simulation (BES) flowchart.
In the study, UA, SA, energy consumption, and thermal conditions inside the barn are shown as output variables. In addition, the structural elements used in the barn were evaluated as input variables. EnergyPlus DesignBuilder was used for UA and SA in the output analyses. Then, SA, UA, parametric analysis, and Pearson correlation analysis were applied. The Pearson correlation method, which was applied to determine the mutual relationships between heat stress and energy consumption of animals, is a type of analysis that reveals whether there is a linear statistical relationship between two different measurements [88]. As a result of the analyses, it will help designers choose the optimum parameters for dairy cattle barns.
3. Results
In the research, in order to estimate energy consumption, thermal comfort, and the most appropriate design parameters in dairy cattle barns, normality test, the barn inlet and outlet values, uncertainty analysis, sensitivity analysis, the effects of design parameters on the indoor environment, and the relationship between heat stress and energy consumption of animals were determined, and the results were given under subheadings.
3.1. Normality Test of Data
Normality tests were applied before statistical analysis of the design parameters in the study. Both the SW and KS normality tests were evaluated for skewness at a 95% confidence level. According to the normality tests, non-normal data distributions were identified in both tests. Therefore, the design parameters—window floor area ratio, mechanical ventilation rate, and chimney height—were not normally distributed according to either test. Therefore, a logarithmic transformation was applied for these three parameters. The p-values for all design parameters of the livestock structure in the SW and KS tests are presented in Table 1.

Table 1.
Normality analysis of input and output variables.
3.2. Input and Output Variables Inside the Shelter
Climate change is one of the greatest threats to the sustainability of animal production. Extreme climatic events, in particular, directly affect animal welfare and productivity [89]. Therefore, all aspects of animal husbandry will be significantly impacted by extreme climatic changes [90]. Currently, efforts to increase animal production to counter the effects of climate change have accelerated. These increases are made significantly more difficult because they are being implemented in response to extreme climatic conditions. This challenge is experienced regardless of region, as climate change is occurring in nearly every region of the world. Climate change causes increased thermal stress in animals, which has severely negative consequences for their health, welfare, and productivity [91].
The primary objectives in addressing global climate change, which is causing thermal stress to become much more severe in animal production, are to mitigate the effects of climate change and to increase animal welfare and productivity. Technological development efforts aligned with these objectives have gained prominence. In this context, the design of livestock buildings to minimize the effects of climate change has become crucial in reducing thermal stress. The appropriate design of livestock buildings involves a multifaceted approach, considering a wide range of considerations, including shelter needs, meteorological data for appropriate design, and the physiological characteristics and needs of the animals. This multifaceted approach can yield results by determining the optimal design parameters of livestock buildings for climate change. Furthermore, the challenges posed by climate change in the world’s tropical regions, coupled with the increasing nutritional needs of population growth, have necessitated studies on increasing productivity through optimal design parameters for livestock buildings. In this context, innovative efforts have increased to maximize animal production in the limited space available without subjecting animals to thermal stress [92].
Dairy cattle farming is one of the most important units of animal production. In animal production, errors in the design parameters and defective materials of livestock buildings can lead to productivity losses under all climatic conditions and, in the worst cases, to the loss of animal life. Therefore, considering the effects of climate change, the optimum design parameters for livestock buildings must be determined from a scientific and technological perspective [93].
The main factor in the change of internal thermal balance in buildings is heat gain and loss. This situation directly affects energy consumption. In this context, structural elements were determined as design parameters in order to determine heat gain and loss inside the shelter [94]. ASHRAE heat balance equations (ANSI/ASHRAE Standard 62.1-2016/Plant and Environment ASHRAE Technical Committee 2.2) were used for heat balance equations and thermal discomfort duration used in the research, which are suitable for animal shelters [66]. In this context, two functions were created: energy consumption and thermal comfort. Energy consumption and heat stress durations of animals were determined as outputs inside the shelter in the research. Energy Plus is generally designed and programmed for humans. In the research, heat balance equations were used according to the ASHRAE Standard in terms of adapting the heat balance situation in the shelter to Energy Plus. The heat balance equations used were applied in a way that would be suitable for cattle, taking into account ANSI/ASHRAE Standard 62.1-2016/Plant and Environment ASHRAE Technical Committee 2.2. In this respect, as a new approach in the research, simulations were provided in terms of an animal shelter in Energy Plus.
Design parameters for livestock buildings were determined in accordance with regulatory regulations established according to numerous national and international regulations and standards. All regulations were investigated in detail. Design parameters were determined in accordance with regulations related to the raising conditions of bovine animals, the parameters required for animal health and welfare, and the design appropriate for the establishment, operation, and inspection processes of livestock enterprises. Within the scope of the research, design parameter ranges were taken into account in the Regulation on the Identification, Registration, and Monitoring of Bovine Animals [95], the Regulation on Animal Health and Security Law [96], and the Regulation on the Establishment, Operation, and Inspection Procedures and Principles of Livestock Enterprises [97]. In terms of international standards, a conclusion was reached in line with the European Union animal welfare directives [98]. No different parameters were set for the regulatory values under the application conditions. Therefore, the optimum design parameters were determined without deviating from regulatory standards for individual and local applications.
Within the scope of the research, an accuracy analysis was performed in accordance with the uncertainty and sensitivity analysis for the estimated design parameters input variables for the shelter in two thousand simulations. This application was created in accordance with the Latin hypercube method, which is widely used in all structures [99].
The statistical analysis used in the study used the quartile system. The analysis divides the data into four quartiles. In this context, the first quartile is the number midway between the minimum and median values and is defined as Q1. 25% of the data in the first quartile falls below this point. The third quartile is defined as Q3, and 75% of the data falls below this point. The analysis performed is a statistical analysis, including the standard deviation and the square root of the variance [100,101,102]. In this context, a probability function was defined for each structural element to estimate the optimal values of the design parameters for dairy cattle barns. In addition, the frequency distributions of the structural materials used in the structural elements in terms of thermal properties were determined. Thus, the aim was to estimate the optimal design features in dairy cattle barns, taking into account thermal properties and energy savings. In this context, general statistical analyses of the simulations created for the structural elements were performed and presented in Table 2. In addition, the properties and frequency values of the structural materials used in the structural elements are presented in Table 3 [103,104].

Table 2.
Statistical analysis of the distribution characteristics of shelter input parameters.

Table 3.
Frequency values of shelter input parameters and material properties.
3.3. Uncertainty Analysis
In the study, uncertainty analysis of energy consumption and thermal discomfort data was performed for all outputs determined from structural elements in dairy cattle barns, and the determined values are probable energy load and thermal stress intervals and frequency values of these intervals. In this context, according to 2000 simulation studies prepared for structural elements, the highest interval in energy consumption values given in Figure 5 was determined as 305 units, and the total consumption was found to be 54,780–58,788 kWh. However, according to thermal stress periods, the highest value was 390 units and 1626–1736 h. According to the analysis results, the wide variety of interval values reveals the importance of the effect of structural elements in terms of architectural design.
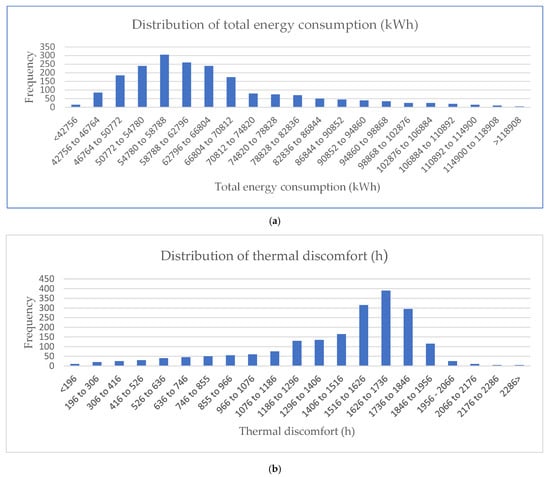
Figure 5.
Uncertainty analysis results. (a) Total energy consumption inside the shelter. (b) Thermal discomfort duration.
3.4. Sensitivity Analysis
Within the scope of the research, regression analysis was used to determine the response that the variables determined as outputs could give to possible changes in the values of the input variables determined in dairy cattle barns. Standardized regression coefficients were created to reveal the sensitivity of all variables; positive values indicate the same direction, and negative values indicate the opposite direction. According to the regression analysis created, the statistical relationship between the variables is presented in Table 4 and Table 5. If the p-value giving the statistical relationship between the input and output variables is less than 0.05, there is a highly reliable and significant relationship between these variables. As the significance level moves away from this value, the statistical relationship level decreases [105].

Table 4.
Regression analysis and significance level of shelter design parameters according to total energy consumption.

Table 5.
Regression analysis and significance level of shelter design parameters according to thermal stress level.
According to the sensitivity analysis results, thermal discomfort in dairy barns is statistically significantly affected by roof construction, indoor thermal comfort temperature, and cooling point set temperature (Table 4). However, there is also a strong statistical relationship between door and window construction, wall construction, window area, natural ventilation opening, mechanical ventilation rate, infiltration rate, and heating point set temperature. A decreasing trend in the statistically strong relationships among window-to-wall ratio, doors and windows, window area, roof construction, natural ventilation opening, mechanical ventilation rate, and heating point set temperature statistically increases thermal stress. Conversely, an increase in indoor thermal comfort temperature and cooling set temperature statistically increases thermal stress.
Energy consumption in the barn is affected by the mechanical ventilation rate, cooling point set temperature, infiltration rate, window area, indoor thermal comfort temperature, doors and windows, and heating point set temperature. (Table 5.) Variables such as window floor-to-wall area ratios, door width, roof type, chimney height, wall construction, and air volume do not significantly affect energy consumption. While a negative statistical relationship was found with energy consumption for the cooling point set temperature and mechanical ventilation rate, a positive statistical relationship was found with doors, walls, and windows, indoor thermal comfort temperature, and heating point set temperature. Within the scope of the research, evaluations were made regarding highly important design parameters, and an attempt was made to establish optimum design conditions in terms of thermal stress and energy consumption.
3.5. Effect of Design Parameters on Shelter Environment
According to regression analysis, sensitivity analysis values were determined for each variable in order to reveal how output variables change due to differences in input variables. In this context, a standardized regression coefficient (SRC) showing sensitivity was created for each variable. A positive SRC value means that there will be an increase in response to an increase among variables, while a negative value means that the changes between variables will be in the opposite direction. However, the p-value shows the level of statistical significance between variables. It is obtained that there will be a very strong effect, especially among variables with a p-value of 0.05. Within the scope of the research, an evaluation was made with both SRC and p-values.
Variables created from the structural elements that must be present in dairy cattle barns in terms of architectural design were compared with total energy consumption and thermal discomfort values. In this context, wall structure, roof covering material, window-to-wall ratio and window area, cooling setpoint temperature, heating setpoint temperature, glass type, mechanical ventilation rate, natural ventilation opening and infiltration rate, and each of the determined outputs were evaluated. The evaluation of each output is given under subheadings.
3.5.1. Indoor Thermal Comfort Temperature
Within the scope of the study, the indoor thermal comfort temperature for animal welfare and productivity was estimated as 12 °C, and simulations were conducted based on this temperature in accordance with the research’s innovative approach. The analysis results showed that the indoor thermal comfort temperature for the shelter was statistically related to total energy consumption and thermal discomfort values. A positive relationship was found between temperature values, thermal discomfort, and total energy consumption. According to the SRC values, positive coefficients of 0.0369 for the shelter’s total energy consumption and 0.4251 for the duration of thermal stress were obtained (Table 3 and Table 4). In addition, the p-values obtained were 0.0001 for energy consumption and 0.0000 for the duration of thermal stress. In this context, a very strong statistical relationship was observed.
According to simulated indoor thermal comfort temperature values for the barn, the lowest energy consumption is observed between 7 and 18 °C. The study’s simulation results of indoor thermal comfort temperature indicate that the optimum value in terms of total energy consumption and thermal comfort is 12 °C. A decrease in indoor thermal comfort temperature below 6 °C results in an increase in energy consumption. Similarly, temperatures above 17 °C lead to an increase in energy consumption. Changes in energy consumption within the barn are similar to changes in thermal stress. Thermal stress levels increase as indoor thermal temperature rises above 17 °C and falls below 5 °C. However, high indoor temperatures have more negative effects than low temperatures. Similarly, another study has shown that the optimum indoor thermal comfort temperature in dairy cattle barns is generally between 10 and 15 °C. Maintaining this temperature within the barn can improve animal welfare and health, maximize yield, and ensure sustainable production. However, in barn applications, varying the indoor thermal comfort temperature between 7 °C and 25 °C has very negative effects on animal welfare and productivity [106]. However, if the indoor thermal comfort temperature rises to the range of 25–35 °C, severe heat stress conditions occur. According to the BES simulation results in the study, the optimum indoor thermal comfort temperature value was determined as 12 °C, and all simulations were prepared by taking this value into account (Figure 6).
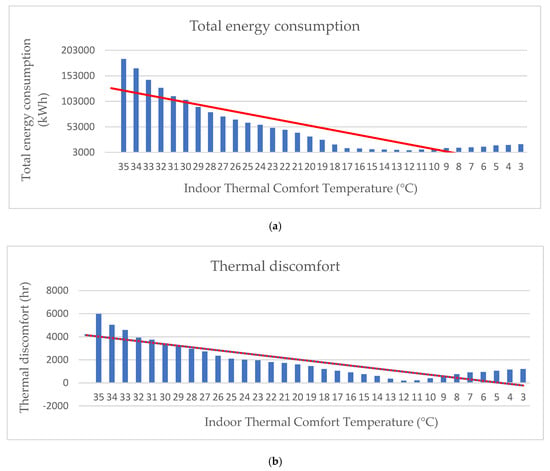
Figure 6.
Effects of indoor thermal comfort temperature on (a) total energy consumption and (b) thermal stress duration.
3.5.2. Wall Structure
The analysis results showed that the wall structure used in the construction of the shelter has a statistical relationship with the total energy consumption and thermal discomfort values. The U-value of the material used in the construction of the wall has a positive effect in terms of thermal discomfort and total energy consumption. According to the obtained SRC values, positive coefficients were obtained with the total energy consumption in the shelter as 0.0698, and with the thermal stress duration as 0.0658 (Table 4 and Table 5). At the same time, there is a very strong statistical relationship in terms of p-values of 0.0004 for energy consumption and 0.0007 for thermal stress duration.
According to the values given in Table 6, the lowest energy consumption in the shelter occurs when the U-value is the lowest, based on the materials used in the shelter wall construction. However, the higher the U-value, the higher the energy consumption. Similar results have been obtained in studies conducted on animal shelters, and appropriate designs have been suggested in terms of wall structure [107]. Similarly, according to the simulation output, thermal stress durations tend to increase positively as the U-value increases. According to the simulations created within the scope of the research, there has been an approximately 25% decrease in energy consumption depending on the type of construction material used in the shelter wall. In addition, there has been a similar decrease in thermal stress durations, and this decrease is around 51% in proportion. The research results show that the wall material has a positive effect on thermal stress and energy consumption.

Table 6.
Effects of wall structure on total energy consumption and thermal stress duration.
3.5.3. Roof Covering Material
As in all structures, roof construction is one of the main factors affecting the conditions inside the structure in animal shelters. Especially solar radiation due to solar energy directly contacts the structure through the roof. Since this situation affects the internal thermal conditions of the structure, it can change factors such as energy consumption and thermal stress duration [43]. In this context, according to the simulations created for dairy cattle shelters, roof construction has a very significant statistical relationship with energy consumption and thermal stress duration. According to the SRC values given in Table 4 and Table 5, total energy consumption was determined as 0.0236, and thermal stress duration as 0.4328. However, when examined in terms of p-value, a very strong statistical relationship was determined, with total energy having coefficients of 0.0020 and thermal stress duration having coefficients of 0.0000.
In the simulations given in Table 7 and created within the scope of the research, the U-values of the materials used as roof covering material in the dairy cattle barn varied between 0.235 W/m2K and 6.227 W/m2K. In the simulations, minimum energy consumption is observed at the U-value of 0.2 W/m2K. Increasing the U-value in the roof covering material also increases energy consumption. In this context, according to the simulation data, a decrease of approximately 41% was achieved in total energy consumption with the roof covering material. This situation is also in the same direction in terms of thermal stress duration. Increasing the U-value in the covering material increased the thermal stress durations. In the simulations, a decrease of approximately 62% was obtained in the thermal stress duration according to the U-value of the roof covering material.

Table 7.
Effects of wall roofing material on total energy consumption and thermal stress duration.
3.5.4. Window Floor Area Ratio and Window Area
In animal shelters, the ratio of the window area to the floor of the shelter is one of the main variables affecting the welfare of the animals. Along with natural ventilation inside the shelter, lighting opportunities also vary according to this ratio. In this context, the ratio of the window area to the floor area was examined in the simulations created together with the window area. The window floor area also affects the climatic environmental conditions inside the buildings, and this directly affects the thermal stress period and energy consumption inside the shelter [108]. In this respect, statistical significance levels were investigated according to the window floor area ratio in the simulations created for the dairy cattle shelter.
According to the values given in Table 4 and Table 5, there is a high statistical relationship between the total energy consumption and thermal stress values and the window floor area ratio. When the SRC values are examined, the values of −0.0501 are seen in the thermal discomfort period and −0.0320 in the total energy consumption. This situation shows that as the window floor area ratio increases, the values of energy consumption and thermal stress duration tend to decrease. The increase in the window area relative to the floor area has increased the natural ventilation opportunities, which has positively contributed to the animal welfare in the shelter. In addition, since the increase in natural ventilation opportunities instead of mechanical ventilation has provided an increase in air volume, energy consumption has also decreased.
When the p-value data obtained in the simulations were evaluated in terms of statistical significance levels, the thermal discomfort duration was determined as 0.0006, and the energy consumption as 0.0000. This situation shows that the window base area ratio, thermal discomfort, and energy consumption have a very high correlation. According to the simulations created, a common decrease is seen in the thermal discomfort and energy consumption values. A constant trend is seen at values higher than this value. In this context, according to the changes in the environmental conditions inside the shelter and the window base area given in Table 8, the total energy consumption decreased by approximately 41%, and the thermal discomfort duration decreased by approximately 53%. In line with previous studies, it is seen that the increase in the window base area has a positive effect on the conditions inside the shelter [109,110]. However, according to the simulations, the optimum value was determined to be 9.2%.

Table 8.
Effects of window floor area ratio on total energy consumption and thermal stress duration.
In the simulations created within the scope of the research, the window area was taken into account in m2 per 500 kg live animal as appropriate for dairy farming. Since the window area inside the shelter affects natural ventilation, it is of great importance in terms of providing environmental conditions inside the shelter [40]. As in the window area values and window floor area ratio values, there is a strong relationship between the thermal conditions inside the shelter and energy consumption. When examined in terms of SRC values, according to the values given in Table 3 and Table 4, −0.3381 was obtained for thermal discomfort duration, and −0.2174 was obtained for energy consumption. In this respect, it is seen that there is a negative statistical relationship between the window area and the thermal discomfort duration and energy consumption.
According to the values given in Table 9, when the p-values of the simulations are examined, they have taken the values of 0.0001 in thermal discomfort duration and 0.0003 in energy consumption. The window area, as in the window-to-wall ratio, has a statistically significant relationship with thermal discomfort and energy consumption. However, the window floor area ratio has a positive effect in terms of decreasing thermal discomfort and energy consumption up to a certain level, and after this level, it remains at a constant level. The window area has also decreased in the same way, and this decrease has continued until the last value. In the simulations, the window area has had a positive effect of approximately 46% in total energy consumption and 28% in thermal discomfort duration. The 0.36 value of the window area in the simulations stands out in terms of providing the most suitable conditions.

Table 9.
Effects of window area on total energy consumption and thermal stress duration.
3.5.5. Cooling and Heating Setpoint Temperature
The internal temperature in dairy cattle barns is generally desired to be between 10 and 15 °C. This temperature range is the range within which optimal productivity and health can be achieved in terms of animal welfare. If necessary, these values can be maintained between 7 °C and 18 °C for short periods. Temperatures above or below these values negatively impact animal welfare. Values close to 25 °C, in particular, have a significant negative impact on animal welfare and productivity [106]. However, the temperature values provided within the range do not provide a clear value. The inability to determine a clear temperature value directly impacts animal welfare and energy consumption. In this context, the aim of the research was to estimate the precise temperature, energy consumption, and optimal design parameters based on the simulations created.
According to the simulation results, when the SRC values of the cooling setpoint temperature given in Table 4 and Table 5 are examined, it is seen that there is a positive statistical relationship with the thermal discomfort duration and a negative statistical relationship with the total energy consumption. The SRC values were determined as 0.6399 for the thermal discomfort duration and −0.7155 for the total energy consumption. The increase in the cooling setpoint temperature increased the thermal discomfort. However, this increase decreases the energy consumption. When the p-values are examined statistically, a very high correlation was obtained, and the correlation coefficients for the thermal discomfort duration were 0.0000, and for the total energy consumption, they were 0.0001. The changes between the cooling setpoint temperature and the values inside the shelter are given in Table 10.

Table 10.
Effects of cooling setpoint temperature on total energy consumption and thermal stress duration.
According to the simulation results of the heating setpoint temperature, there is a negative statistical relationship with total energy consumption (SRC = −0.0229) and a positive relationship with thermal discomfort duration (SRC = 0.0366). An increase in the heating setpoint temperature reduces energy consumption. However, an increase is observed for thermal discomfort durations. A statistically significant relationship is observed, and when the p-values are examined, total energy consumption is 0.0006, and thermal discomfort duration is 0.0079. The change in the heating setpoint according to the variables is given in Table 11.

Table 11.
Effects of heating setpoint temperature (a) on total energy consumption and (b) thermal stress duration.
Within the scope of the research, the indoor thermal comfort temperature for the BES was estimated as a net value of 12 °C. This temperature was considered the optimum condition in the simulations, and changes in the cooling and heating setpoint temperatures significantly reduce energy consumption within the barn [40,111]. However, it has a negative effect on the duration of thermal discomfort. In this context, the optimum barn design values were determined for conditions where the cooling setpoint temperature is 18–19 °C. In dairy cattle, feed consumption begins to decrease when the ambient temperature exceeds 25 °C, and a significant decrease in feed consumption is observed when it exceeds 30 °C. At values of 40 °C and above, feed consumption ceases completely. These responses pose major problems in terms of productivity, reproduction, and animal welfare. In this context, according to the simulation of the cooling setpoint temperature in the research, it was determined that activating ventilation at 19 °C was appropriate. Going above this value significantly increases thermal stress [24]. Specifically, increasing this value to 26 °C increases thermal stress by approximately tenfold and reduces total energy consumption by approximately 48%. In this context, increasing the cooling setpoint temperature to high levels appears to reduce total energy consumption but has significant negative effects on animal welfare and productivity. Furthermore, this can negatively impact animal health and the health of barn workers. Therefore, simulations suggest that the optimum cooling setpoint temperature should not exceed 19 °C. From an animal welfare perspective, the optimal conditions for the heating setpoint temperature are considered to be 7–8 °C. Increasing these values to 17 °C reduces total energy consumption by approximately 19% but increases thermal stress by approximately fourfold. This negatively impacts animal welfare, similar to the cooling setpoint temperature, and can lead to deterioration in both animal health and productivity. Therefore, optimal environmental conditions must be ensured in the barn.
3.5.6. Glass Structure
In determining the type of glass to be used in the shelter as an architectural design, the solar heat gain coefficient (SHGC) was taken into account. SHGC is a variable that has been used in many studies in the selection criteria of glass materials in buildings, and accurate results have been obtained [112]. In this context, the SHGC values of the glass types that can be used in the shelter were compared with the total energy consumption and thermal discomfort duration values in the simulations created.
According to the results obtained in the simulations, a positive correlation was determined between the SHGC values of the glass material and the total energy consumption and thermal discomfort duration. According to the SRC data, energy consumption was 0.3720, and thermal discomfort was 0.4125 (Table 4 and Table 5). This situation shows that the increase in SHCG values increased the negative situation in thermal conditions inside the shelter, together with energy consumption. When the p-values in the correlations were examined, total energy consumption was 0.0002, and thermal discomfort was 0.0005, and a very high statistical relationship was determined. The statistical relationships of the variables according to the SHGC values of the glass to be used in the shelter are given in Table 12.

Table 12.
Effects of glass structure on total energy consumption and thermal stress duration.
An increase in the SHGC value of the glass type increased energy consumption. A change in SHGC value of up to 15% was observed in total energy consumption. This also increased the thermal stress within the barn during the simulation. A change of approximately 47% in thermal stress was obtained (Table 12). In this context, the need for mechanical ventilation increases energy consumption. Generally, the high SHGC value of glass used in buildings increases energy consumption [112]. The same situation was observed in the dairy cattle barn simulations created within the scope of the research. In terms of architectural design within the barn, it was considered important to maintain the SHGC value of the glass material at the optimum value of 0.45 to prevent an increase in thermal stress along with energy consumption.
3.5.7. Natural Ventilation Opening and Mechanical Ventilation Rate
In animal shelters, natural and mechanical ventilation are required to ensure optimum temperatures inside the shelter and animal welfare [113]. In this context, an analysis was performed to determine the optimum values in terms of architectural design in the simulations created for the most suitable natural ventilation opening and mechanical ventilation. According to the values given in Table 4 and Table 5, a negative statistical relationship is seen between the natural ventilation opening and total energy consumption, thermal discomfort, and SCI values. When the SCI values are examined, it is seen that there is a −0.3720 in total energy consumption and −0.4125 in thermal discomfort duration. When examined in terms of p-values, a correlation coefficient of 0.0002 was obtained between the natural ventilation opening and total energy, and 0.0005 with thermal discomfort duration, and there is a very high statistical relationship. The distributions between the variables and the natural ventilation opening obtained in the simulations are given in Table 13.

Table 13.
Effects of natural ventilation opening on total energy consumption and thermal stress duration.
According to the simulation results, an increase in natural ventilation openness resulted in a decrease in total energy consumption. The increase in air volume within the barn positively affected the duration of thermal discomfort through natural ventilation openness. The study found that the optimum value for natural ventilation openness, from an architectural design perspective, was between 0.50 and 0.75. The optimal net value was estimated to be 0.60. According to the simulations, the optimum values obtained based on total energy consumption with natural ventilation opportunities within the barn resulted in an approximately 75% reduction in total energy consumption and an 86% reduction in thermal stress. Similar results have been obtained in similar studies [114]. In this context, natural ventilation is of great importance for animal welfare and productivity.
In animal shelters, in addition to natural ventilation, mechanical ventilation is provided in conditions required by the climatic environmental conditions for animal welfare [110]. In the simulations, the mechanical ventilation rate was taken into account as m3/h/500 kg, taking into account the live weight of dairy cattle. According to the research results, there was a positive relationship between the mechanical ventilation rate and total energy consumption (SRC = 0.0506, p = 0.0000), and a positive relationship was obtained between the duration of thermal discomfort (SRC = −0.0369, p = 0.0001). A very high statistical relationship was obtained between all variables and the mechanical ventilation rate. The changes between the variables in the simulations and the mechanical ventilation rate are given in Table 14.

Table 14.
Effects of mechanical ventilation rate on (a) total energy consumption and (b) thermal stress duration.
According to barn simulations, increases in mechanical ventilation rates increased total energy consumption similarly, as found in various studies [37,55,110,114]. Despite this energy consumption, a reduction in thermal discomfort duration resulted in improved animal welfare. Simulation results indicated that for 500 kg dairy cattle, mechanical ventilation in the range of 133–160 m3/h reduced thermal stress by approximately 88%. Increasing this value to 170 m3/h resulted in an approximately 40% increase in total energy consumption. In this context, mechanical ventilation in the range of 133–160 m3/h was determined to be the optimum value that balances energy consumption while ensuring animal welfare, with a net value estimate of 144 m3/h.
The simulation model outlines the parameters required for optimal ventilation in the barn. For natural ventilation, the window floor area ratio should be 9.2% (Table 8), the window area per animal should be 0.36 m2 (Table 9), and the window opening should be 0.6 m (Table 13). When the research is evaluated based on the 714 m2 area of the barn (40 m length × 17.85 m width × 4.25 m height), it is seen that a design with equal spacing is appropriate based on the window floor area, window area, and window opening values. The space between the windows will be designed as one window area, and an equal spacing is planned. For mechanical ventilation, a fan system generating 144 m3/h per animal should be installed. Depending on the total number of animals in the barn, mechanical ventilation will be required to provide 7200 m3 of air circulation. It would be appropriate to provide this value with multiple fan systems selected according to their capacity.
3.5.8. Infiltration Rate
Infiltration affects the air conditioning load in buildings, the air temperature, and humidity levels inside the building [115,116]. The infiltration rate is affected by many factors, such as climatic environmental conditions, building materials, and building design and age. If there are cracks in the buildings that cause air leakage, closing these areas can reduce the infiltration rate [117]. In this respect, the infiltration rate is a variable that affects energy consumption and thermal conditions in animal shelters.
According to the findings obtained in the study, there is a positive statistical relationship in all values of infiltration rate, total energy consumption, and thermal discomfort duration. When the statistical relationship is examined together with SRC and p-values, total energy consumption (SRC = 0.0427 and p = 0.0003) and thermal discomfort duration (SRC = 0.0658, p = 0.0001) values also increase as a result of the increase in infiltration rate. Since the increase in infiltration rate negatively affects the environmental conditions inside the shelter, an increase in total energy consumption has also occurred, together with the increase in thermal stress. In this respect, insulation conditions should be provided inside the shelter, and structural elements such as walls and windows should be sealed to prevent leakage. According to the simulation results, when the infiltration rate value reaches 1.4, total energy consumption increases by approximately 17%, and thermal discomfort increases by 62%. (Table 15.) In this context, it is of great importance to increase the insulation properties and ensure the sealing inside the shelter in the same way as in different studies [37,118].

Table 15.
Effects of infiltration rate on total energy consumption and thermal stress duration.
3.6. Relationship Between Total Energy Consumption and Thermal Discomfort Duration
After finding the statistical relationship between the energy consumption and thermal performance of the structural elements in the shelter simulations, Pearson correlation was used to statistically examine the relationship between the variables. In this context, firstly, the distributions between the total energy consumption and thermal discomfort duration were created and are given in Figure 7. According to the values given in Figure 7, it is seen that there are normal distributions in terms of thermal comfort and total energy consumption inside the shelter.
Figure 7.
Shelter simulations. (a) Total energy. (b) Heat stress distribution.
According to the Pearson correlation output applied within the scope of the research and the values given in Table 16, a negative statistical relationship was found between total energy consumption and heat stress values. According to the coefficients obtained, there is a high degree of relationship between total energy and heat stress (−0.876). This situation was interpreted as a decrease in heat stress values as a result of the activities of the structural elements that create energy consumption, such as ventilation in the shelter.

Table 16.
Summary of Pearson analysis between total energy consumption and thermal stress in the shelter.
3.7. Validation Results of Barn Energy Simulation (BES) Estimates
In the study, the accuracy of the data estimated using the BES model in a simulated dairy barn was verified by comparing the air temperature, relative humidity, and total energy consumption data within the barn. Data obtained from the field study were used to assess the reliability of the simulation model. Trends observed in air temperature, relative humidity, and energy consumption are presented, along with the trends predicted by the simulation model.
Long-term validation was conducted to demonstrate the effects of cold and hot weather. Temperatures exceeding 30 °C were observed in the region starting in June. However, values of 0 °C or lower were observed in January and February. Furthermore, energy consumption was observed to increase starting in May, when temperatures rise, and to an increasing trend throughout the summer. The observed values indicate that the simulation model produces results quite similar to the field values. It was determined that the main, albeit small, difference in trends stems from the different values at the peaks of the data. Time-series overlay plots of the observed trends are shown in Figure 8.
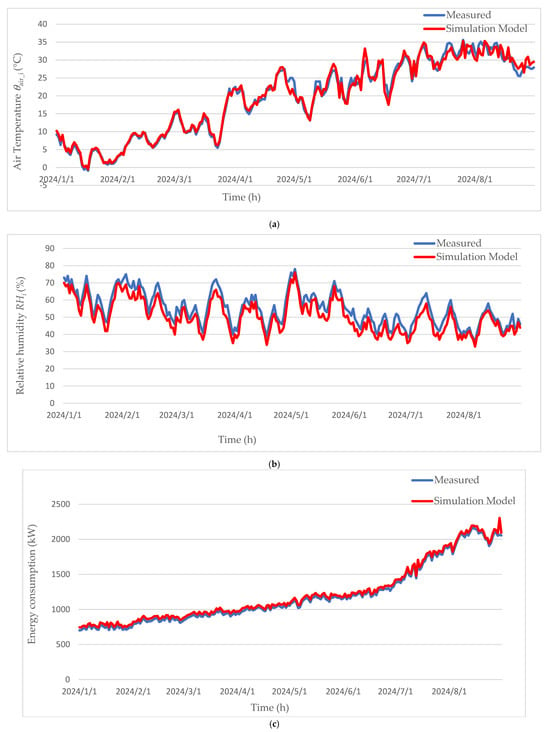
Figure 8.
Time-series overlay plot of simulated and measured data ((a) Air temperature, (b) Relative humidity, and (c) Energy consumption).
Within the scope of the research, histograms were created to determine the distribution groups of simulated and measured data. Histograms are frequently used in computer-based vision, and especially machine learning methods, to identify and capture statistical information about maps, data distributions, or images representing a feature [119]. Similar trends were observed between the simulated and measured data in terms of groups, with some minor differences observed in the most frequently grouped values. Temperature measurements ranged from 28 to 30 °C, and according to the simulation results, the highest group was 30 °C. Similarly, relative humidity measurements ranged from 49% to 52%, and according to the simulation results, the highest group was 50% to 52%. Energy consumption ranged from 1000 to 1300 kW for the highest values, while simulation results determined the range of 950 to 1270 kW. Histogram maps created for temperature, relative humidity, and energy consumption are presented in Figure 9.
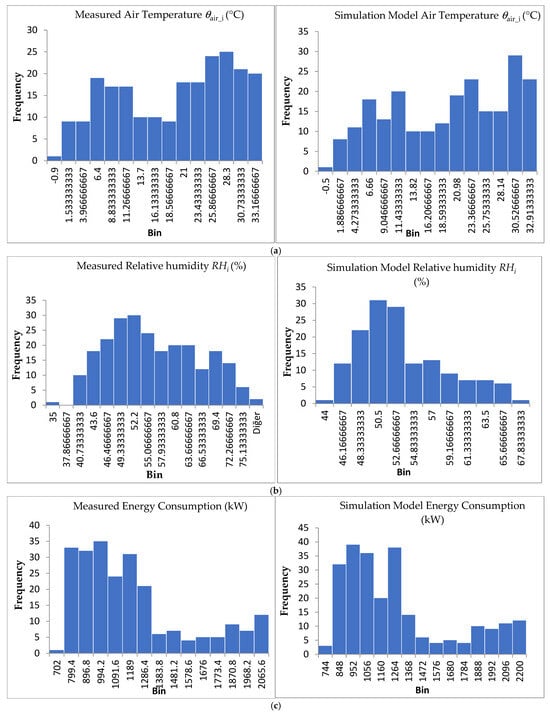
Figure 9.
Histogram graph of simulated and measured data ((a) Air temperature, (b) Relative humidity, and (c) Energy consumption).
According to the verification processes of the shelter simulation values given in Table 17, it has been determined that the model errors of the shelter interior temperature and relative humidity and total energy consumption values in terms of thermal discomfort are less than 10%. This means that the average values of the simulation results are within 10%. According to the values specified in the American Society of Heating, Refrigerating and Air-Conditioning Engineers (ASHRAE) M&V Manual, it is accepted that the simulation verification values are within 10% in terms of error rate of the analysis models [66,79]. In this context, it can be said that the shelter simulation results have high reliability and are verified according to the verification process.

Table 17.
Statistical analysis for barn energy simulation (BES) validation.
4. Conclusions
In this study, a comprehensive analysis was conducted to estimate the design effects of the most important parameters in terms of thermal comfort and energy consumption in livestock buildings and to obtain the most suitable designs to ensure optimal conditions within the shelter. In this context, shelter simulations were created using Monte Carlo techniques and the Energy Plus system, and each design parameter was evaluated. Unlike existing studies, the optimum interior thermal comfort temperature for animal welfare was estimated as 12 °C, and the simulations used this value to estimate total energy consumption and duration of thermal discomfort. Based on uncertainty and sensitivity analyses, the shelter design was analyzed from an animal welfare perspective, including wall structure, roof material, window floor area ratio and window area, cooling and heating setpoint temperature, glazing, natural ventilation openings, mechanical ventilation rate, and infiltration rate. The assessment revealed significant potential for optimization of shelter design parameters based on simulation data.
Based on estimated values from shelter simulations based on the wall structure, a reduction in thermal stress within the shelter of approximately 61% is observed, depending on the U-value of the material used. This reduction is achieved when the wall material has a U-value of 0.354 W/m2K, resulting in an approximately 20% reduction in total energy consumption. Similarly, conditions within the shelter vary depending on the material used for the roof covering. In the simulations, a thermal stress improvement of approximately 73% is achieved when the roof covering material has a U-value of 0.235 W/m2K. Furthermore, a reduction in total energy consumption of approximately 34% is observed.
When the shelter was evaluated in terms of window-to-floor area ratio, the optimal design was estimated at 19.5%, which improved thermal comfort by approximately 45%. It also reduced total energy consumption by approximately 25%. Simulations indicate that shelters with an optimal window area of 0.43 achieved a 53% increase in thermal comfort and a 27% reduction in total energy consumption.
Based on simulations, the optimum value for the cooling point set temperature inside the shelter was estimated to be 18 °C, and the optimum values for the heating point set temperature were estimated to be 7 °C. Under these temperature conditions, maintaining the cooling point set temperature resulted in a reduction of approximately 39% in total energy consumption. When this was evaluated for the heating set temperature, a reduction of approximately 11% was found.
For ventilation conditions within the shelter, it was estimated that optimum simulation results were obtained when the natural ventilation opening was 0.60 and the mechanical ventilation was 144 m3/h. Achieving these values for the shelter resulted in a reduction of approximately 40% in natural ventilation and 38% in mechanical ventilation. Optimum values were obtained when the structural SHGC value of the glass material to be used in the shelter was between 0.45 and 0.50. However, with insulation and no leakage, total energy consumption increased by approximately 10%. According to the Pearson correlation output, examining the simulation results of total energy consumption and thermal stress values within the shelter, increases in total energy consumption generally reduced thermal stress.
The shelter simulation values generated in the study were validated with the shelter interior values, and it was determined that the model errors for total energy consumption values, including indoor temperature and relative humidity and duration of thermal discomfort, were all below 10%. In this context, it can be said that the estimated values of thermal stress, total energy consumption, and optimum design parameters based on the simulations have high reliability.
When the design parameters were evaluated holistically and analyzed in terms of average values, the new simulation model resulted in approximately 50% energy savings. In addition to halving energy consumption, thermal stress in dairy farming was prevented, enabling sustainable animal production. Furthermore, by preventing thermal stress and improving animal welfare, potential animal deaths were also prevented. Furthermore, milk production can be achieved without loss of yield, and the positive nutritional benefits will also have beneficial effects on human health.
In conclusion, the new approach study developed to estimate thermal stress, total energy consumption, and optimal barn design parameters can be used to ensure animal welfare for dairy cattle with minimal energy consumption. Furthermore, it can be said that it will have positive effects on animal welfare and productivity, as well as the health of barn workers. The design parameters estimated from the simulations can provide guidance for barn designers, streamlining construction processes. Furthermore, estimating data that can reduce energy consumption for dairy cattle could lead to a reduction in the amount of energy consumed globally. Furthermore, increased animal welfare and productivity could have positive benefits for food access. The benefits of the research are likely to guide future public and private planning, national energy consumption policies, and efforts to improve animal welfare.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Uzal, S.; Uğurlu, N. Time budget and shelter area use of cattle in free and free stall dairy cattle shelters. Selcuk J. Agric. Food Sci. 2009, 23, 27–37. [Google Scholar]
- Rojas-Downing, M.M.; Nejadhashemi, A.P.; Harrigan, T.; Woznicki, S.A. Climate change and livestock: Impacts, adaptation, and mitigation. Clim. Risk Manag. 2017, 16, 145–163. [Google Scholar] [CrossRef]
- Maialetti, M.; Ciaschini, C.; Quaranta, G.; Salvia, R.; Scarpitta, D.; Bigiotti, S.; Chelli, F.M.; Salvati, L. Investigating ‘Land-Use Trajectories’ in Mediterranean Rural Areas with Official Statistics and a Multiway Factor Analysis. Sustainability 2024, 16, 7644. [Google Scholar] [CrossRef]
- Gunderson, R. The metabolic rifts of livestock agribusiness. Organ. Environ. 2011, 24, 404–422. [Google Scholar] [CrossRef]
- Vázquez-Torres, M.D.R.; Castillo-Reyes, A.R.; Morales Ortega, J.A.; Montero-Urrusquieta, R.Á. Vernacular architecture as heritage. J. Arch. Design 2020, 4, 1–10. [Google Scholar] [CrossRef]
- Rheude, F.; Kondrasch, J.; Röder, H.; Fröhling, M. Review of the terminology in the sustainable building sector. J. Clean. Prod. 2021, 286, 125445. [Google Scholar] [CrossRef]
- Bigiotti, S.; Costantino, C.; Patriarca, A.; Mancini, G.; Provolo, G.; Recanatesi, F.; Ripa, M.N.; Marucci, A. Energy Efficiency and Environmental Sustainability in Rural Buildings: A Life Cycle Assessment of Photovoltaic Integration in Poultry Tunnels—A Case Study in Central Italy. Appl. Sci. 2025, 15, 5094. [Google Scholar] [CrossRef]
- Finocchiaro, A.; Vitaliano, S.; Cinardi, G.; D’Urso, P.R.; Cascone, S.; Arcidiacono, C. Green Wall System to Reduce Particulate Matter in Livestock Housing: Case Study of a Dairy Barn. Buildings 2025, 15, 2280. [Google Scholar] [CrossRef]
- Picuno, P. Use of traditional material in farm buildings for a sustainable rural environment. Int. J. Sustain. Built Environ. 2016, 5, 451–460. [Google Scholar] [CrossRef]
- Bigiotti, S.; Santarsiero, M.L.; Del Monaco, A.I.; Marucci, A. A Typological Analysis Method for Rural Dwellings: Architectural Features, Historical Transformations, and Landscape Integration: The Case of “Capo Due Rami”, Italy. Land 2025, 14, 374. [Google Scholar] [CrossRef]
- Alpan, O.; Aksoy, A.R. Cattle Breeding and Fattening, 7th ed.; Sahin Publisher: Istanbul, Türkiye, 2015; p. 199. [Google Scholar]
- Si, B.; Wang, C.; Cheng, S.; Ma, X.; Xu, W.; Wang, Z.; Li, B.; Wang, Y.; Shi, Z.; Jiang, W. Carbon and Water Footprint Analysis of Pig Farm Buildings in Northeast China Using Building-Information-Modeling Enabled Assessment. Sci. Total Environ. 2023, 888, 164088. [Google Scholar] [CrossRef] [PubMed]
- Attia, S.; Beltrán, L.; Herde, A.D.; Hensen, J. “Architect friendly”: A comparison of ten different building performance simulation tools. In Proceedings of the 11th IBPSA Building Simulation Conference, Glasgow, UK, 27–30 July 2009; pp. 204–211. [Google Scholar]
- Clarke, J.A. Energy Simulation in Building Design; Taylor & Francis: Abingdon, UK, 2001; p. 384. [Google Scholar]
- Kumar, S. Interoperability Between Building Information Models (BIM) and Energy Analysis Programs. Master’s Thesis, University of Southern California, Los Angeles, CA, USA, 2008. [Google Scholar]
- Nguyen, N.H.; Klotsa, D.; Engel, M.; Glotzer, S.C. Emergent collective phenomena in a mixture of hard shapes through active rotation. Phys. Rev. Lett. 2014, 112, 075701. [Google Scholar] [CrossRef]
- Shi, X.; Tian, Z.; Chen, W.; Si, B.; Jin, X. A review on building energy efficient design optimization rom the perspective of architects. Renew. Sustain. Energy Rev. 2016, 65, 872–884. [Google Scholar] [CrossRef]
- Bingham, R.D.; Agelin-Chaab, M.; Rosen, M.A. Whole building optimization of a residential home with PV and battery storage in The Bahamas. Renew. Energy 2019, 132, 1088–1103. [Google Scholar] [CrossRef]
- Cellura, M.; Guarino, F.; Longo, S.; Mistretta, M. Energy life-cycle approach in Net zero energy buildings balance: Operation and embodied energy of an Italian case study. Energy Build. 2014, 72, 371–381. [Google Scholar] [CrossRef]
- Ozocak, M. Management of fertilizer waste systems in animal production structures and vermiculture. Bayburt Univ. J. Sci. 2019, 2, 316–324. [Google Scholar]
- Tabor, J.; Chatterjee, K.; Ghosh, T.K. Smart Textile-Based Personal Thermal Comfort Systems: Current Status and Potential Solutions. Adv. Mater. Technol. 2020, 5, 1901155. [Google Scholar] [CrossRef]
- Qi, F.; Li, H.; Zhao, X.; Huang, J.; Shi, Z. Investigation on Minimum Ventilation, Heating, and Energy Consumption of Pig Buildings in China during Winter. Agriculture 2023, 13, 319. [Google Scholar] [CrossRef]
- Öngel, E.; Özkütük, K. The effect of providing shower opportunities to Holstein cows during hot summer months on milk yield and determination of behavior related to showering habits. Çukurova J. Agric. Food Sci. 2000, 15, 119–126. [Google Scholar]
- Özhan, M.; Tüzemen, N.; Yanar, M. Cattle Breeding; Atatürk University, Faculty of Agriculture Publications: Erzurum, Türkiye, 2001; p. 604. [Google Scholar]
- Özkütük, K. Animal Ecology; Çukurova University, Faculty of Agriculture Publications: Dana, Türkiye, 1990; p. 136. [Google Scholar]
- Willard, S.; Gandy, S.; Bowers, S.; Graves, K.; Elias, A.; Whisnant, C. The effects of GnRH administration postinsemination on serum concentrations of progesterone and pregnancy rates in dairy cattle exposed to mild summer heat stres. Theriogenology 2003, 59, 1799–1810. [Google Scholar] [CrossRef]
- Costantino, A.; Fabrizio, E.; Biglia, A.; Cornale, P.; Battaglini, L. Energy Use for Climate Control of Animal Houses: The State of the Art in Europe. Energy Procedia 2016, 101, 184–191. [Google Scholar] [CrossRef]
- Tyris, D.; Gkountas, A.; Bakalis, P.; Panagakis, P.; Manolakos, D. A Dynamic Heat Pump Model for Indoor Climate Control of a Broiler House. Energies 2023, 16, 2770. [Google Scholar] [CrossRef]
- Chong, A.; Gu, Y.; Jia, H. Calibrating building energy simulation models: A review of the basics to guide future work. Energy Build. 2021, 253, 111533. [Google Scholar] [CrossRef]
- Tomasello, N.; Valenti, F.; Cascone, G.; Porto, S.M.C. Development of a CFD Model to Simulate Natural Ventilation in a Semi-Open Free-Stall Barn for Dairy Cows. Buildings 2019, 9, 183. [Google Scholar] [CrossRef]
- Costantino, A.; Fabrizio, E. Envisioning an Energy Performance Certificate for Livestock Houses: A General Methodological Development and a Specific Application to Growing-Finishing Pig Houses. J. Clean. Prod. 2023, 429, 139279. [Google Scholar] [CrossRef]
- Costantino, A.; Comba, L.; Cornale, P.; Fabrizio, E. Energy impact of climate control in pig farming: Dynamic simulation and experimental validation. Appl. Energy 2022, 309, 118457. [Google Scholar] [CrossRef]
- Cooper, K.; Parsons, D.J.; Demmers, T. A thermal balance model for livestock buildings for use in climate change studies. J. Agric. Eng. Res. 1998, 69, 43–52. [Google Scholar] [CrossRef]
- Liberati, P.; Zappavigna, P. A dynamic computer model for optimization of the internal climate in swine housing design. Trans. ASABE 2007, 50, 2179–2188. [Google Scholar] [CrossRef]
- Shin, H.; Kwak, Y.; Jo, S.-K.; Kim, S.-H.; Huh, J.-H. Calibration of Building Energy Simulation Model for a Mechanically Ventilated Livestock Facility. Biosyst. Eng. 2022, 217, 115–130. [Google Scholar] [CrossRef]
- Kwak, Y.; Shin, H.; Kang, M.; Mun, S.-H.; Jo, S.-K.; Kim, S.-H.; Huh, J.-H. Energy Modeling of Pig Houses: A South Korean Feasibility Study. Energy Strategy Rev. 2021, 36, 100672. [Google Scholar] [CrossRef]
- Jackson, P.; Guy, J.H.; Sturm, B.; Bull, S.; Edwards, S.A. An Innovative Concept Building Design Incorporating Passive Technology to Improve Resource Efficiency and Welfare of Finishing Pigs. Biosyst. Eng. 2018, 174, 190–203. [Google Scholar] [CrossRef]
- Axaopoulos, P.; Panagakis, P.; Axaopoulos, I. Optimization of Exterior Wall and Roof Insulation Thickness of a Growing-Finishing Piggery Building. Trans. ASABE 2017, 60, 489–495. [Google Scholar] [CrossRef]
- Wang, K.; Xue, H. Effects of Roof and Wall Insulation on Thermal Performance of Piglet Building Using Dynamic Simulation and Life Cycle Cost Analysis. Trans. ASABE 2016, 59, 915–922. [Google Scholar] [CrossRef]
- Mikovits, C.; Zollitsch, W.; Hörtenhuber, S.J.; Baumgartner, J.; Niebuhr, K.; Piringer, M.; Anders, I.; Andre, K.; Hennig-Pauka, I.; Schönhar, M.; et al. Impacts of global warming on confined livestock systems for growing-fattening pigs: Simulation of heat stress for 1981 to 2017 in Central Europe. Int. J. Biometeorol. 2019, 63, 221–230. [Google Scholar] [CrossRef] [PubMed]
- Schauberger, G.; Schönhart, M.; Zollitsch, W.; Hörtenhuber, S.J.; Kirner, L.; Mikovits, C.; Baumgartner, J.; Piringer, M.; Knauder, W.; Anders, I.; et al. Reduction of the Economic Risk by Adaptation Measures to Alleviate Heat Stress in Confined Buildings for Growing-Fattening Pigs Modelled by a Projection for Central Europe in 2030. Agronomy 2022, 12, 248. [Google Scholar] [CrossRef]
- Gonçalves, I.C.M.; Turco, S.H.N.; Lopes Neto, J.P.; do Nascimento, J.W.B.; de Lima, V.L.A.; Borges, V.P. Thermal Performance of Aviary Located in the Semiarid Region of Pernambuco Based on Computer Simulation. Rev. Bras. Eng. Agríc. Ambient. 2022, 26, 533–540. [Google Scholar] [CrossRef]
- Shin, H.; Kwak, Y.; Jo, S.-K.; Kim, S.-H.; Huh, J.-H. Development of an Optimal Mechanical Ventilation System Control Strategy Based on Weather Forecasting Data for Outdoor Air Cooling in Livestock Housing. Energy 2023, 268, 126649. [Google Scholar] [CrossRef]
- Lambert, M.; Lemay, S.P.; Barber, E.M.; Crowe, T.G.; Chénard, L. Humidity Control for Swine Buildings in Cold Climate—Part I: Modelling of Three Control Strategies. Can. Biosyst. Eng./Genie Biosyst. Can. 2001, 43, 529–536. [Google Scholar]
- Velten, K. Mathematical modeling and simulation introduction for scientists and engineers. In Mathematical Modeling and Simulation for Scientists and Engineers; Wiley-VCH: Weinheim, Germany, 2009. [Google Scholar]
- Panagakis, P.; Manolakos, D.; Axaopoulos, P. Optimal Financial Insulation Thickness of a Broiler House. Agric. Eng. Int. CIGR J. 2021, 23, 99–110. [Google Scholar]
- EnergyPlus Building Energy Simulation Program of U.S. Department of Energy’s (DOE) Building Technologies Office (BTO) and Managed by the National Renewable Energy Laboratory (NREL). Available online: https://energyplus.net/ (accessed on 10 December 2024).
- World Meteorological Organization WMO. Europe Region 6 Türkiye/Ankara 171280 (IWEC) World Meteorological Organization: Geneva, Switzerland, 2009. Available online: https://wmo.int/about-us/regions/europe (accessed on 15 December 2024).
- Shapiro, S.S.; Wilk, M.B. An analysis of variance test for normality (complete samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Kolmogorov, A. Sulla determinazione empirica di una legge di distribuzione. Inst. Ital. Attuari Giorn. 1933, 4, 83–91. [Google Scholar]
- Andreo, P. Monte Carlo techniques in medical radiation physics. Phys. Med. Biol. 1991, 36, 861–920. [Google Scholar] [CrossRef]
- Leal, S.; Hauer, S.; Zucker, G.; Soucek, S.; Loy, D.; Heinrich, N.; Frank, T.; Drzymalla, T.; Schubert, F. Case Study of a Simplified Building Energy Modeling for Performance Simulation. In Proceedings of the 13th Conference of International Building Performance Simulation Association, Chambéry, France, 26–28 August 2013; pp. 333–339. [Google Scholar]
- Wang, S.; Xu, X. Simplified building model for transient thermal performance estimation using GA-based parameter identification. Int. J. Therm. Sci. 2006, 45, 419–432. [Google Scholar] [CrossRef]
- Jackson, P.; Guy, J.; Edwards, S.A.; Sturm, B.; Bull, S. Application of Dynamic Thermal Engineering Principles to Improve the Efficiency of Resource Use in UK Pork Production Chains. Energy Build. 2017, 139, 53–62. [Google Scholar] [CrossRef]
- Raychaudhuri, S. Introduction to Monte Carlo simulation. In Proceedings of the 2008 Winter Simulation Conference, Miami, FL, USA, 7–10 December 2008; pp. 91–100. [Google Scholar]
- Kochanski, G. Monte Carlo Simulation. Available online: https://kochanski.org/gpk/teaching/0401Oxford/MonteCarlo.pdf (accessed on 24 April 2025).
- Balogh, P.; Golea, P.; Inceu, V. Profit Forecast Model Using Monte Carlo Simulation in Excel. Rom. Stat. Rev. 2013, 61, 33–40. [Google Scholar]
- Saglamci, Y. Simulation; Sekin Publishing House: Ankara, Türkiye, 2021. [Google Scholar]
- Türküm, A. Determination of Distribution, Sources and Health Risks of Volatile Organic Compounds and Inorganic Gases in Kocaeli Atmosphere. Ph.D. Thesis, Kocaeli University, Institute of Science, İzmit, Türkiye, 2018. [Google Scholar]
- Lomas, K.J.; Eppel, H. Sensitivity analysis techniques for building thermal simulation programs. Energy Build. 1992, 19, 21–44. [Google Scholar] [CrossRef]
- Macdonald, I.; Strachan, P. Practical application of uncertainty analysis. Energy Build. 2001, 33, 219–227. [Google Scholar] [CrossRef]
- DOE; NREL. EnergyPlusTM; DOE: Washington, DC, USA; BTO: Tokyo, Japan; NREL: Golden, CO, USA, 2020.
- University of Illinois. LBNL EnergyPlus Documentation-External Interface(s) Application Guide; Guide for Using EnergyPlus with External Interface(s); University of Illinois: Urbana, IL, USA, 2015. [Google Scholar]
- jE+ JEPlus—An Parametric Tool for EnergyPlus and TRNSYS 2019. Available online: http://www.jeplus.org/wiki/doku.php?id=start (accessed on 28 September 2024).
- Costantino, A. Development, validation, and application of building energy simulation models for livestock houses: A systematic review. Agriculture 2023, 13, 2280. [Google Scholar] [CrossRef]
- American Society of Heating, Refrigerating and Air-Conditioning Engineers. ANSI/ASHRAE Standard 62.1-2016 Plant, Animal and Environment; ASHRAE Inc.: Atlanta, GA, USA, 2016; Available online: https://www.ashrae.org/File%20Library/Technical%20Resources/Standards%20and%20Guidelines/Standards%20Addenda/62.1-2016/62_1_2016_n_20190726.pdf (accessed on 10 January 2024).
- Zhang, Y.; Jankovic, L. JEA, An Interactive Optimisation Engine for Building Energy Performance Simulation. In Proceedings of the IBPSA Building Simulation 2017, San Francisco, CA, USA, 7–9 August 2017. [Google Scholar]
- Zhang, Y.; Korolija, I. Performing complex parametric simulations with jEPlus. In Proceedings of the SET2010—9th International Conference on Sustainable Energy Technologies, Shangai, China, 24–27 August 2010. [Google Scholar]
- Harputlugil, G.U. Design Support Evaluation Model that can be used in the First Stage of Energy Performance Priority Architectural Design Process. Ph.D. Thesis, Gazi University Institute of Science, Ankara, Türkiye, 2009. [Google Scholar]
- Solmaz, A.Ş. A Simulation and Multi-Objective Optimization Based Decision Support Model for Determining the Optimum Solution for Improving Building Energy Performance. Ph.D. Thesis, Dokuz Eylül University, Institute of Science, İzmir, Türkiye, 2015. [Google Scholar]
- Saltelli, A.; Ratto, M.; Tarantola, S.; Campolongo, F. Sensitivity Analysis Practices: Strategies for Model-Based Inference. Reliab. Eng. Syst. Saf. 2006, 91, 1109–1125. [Google Scholar] [CrossRef]
- Nguyen, A.T.; Reiter, S. A performance comparison of sensitivity analysis methods for building energy models. Build. Simul. 2015, 8, 651–664. [Google Scholar] [CrossRef]
- Tian, W. A review of sensitivity analysis methods in building energy analysis. Renew. Sustain. Energy Rev. 2013, 20, 411–419. [Google Scholar] [CrossRef]
- Ahlgren, P.; Jarneving, B.; Rousseau, R. Requirements for a cocitation similarity measure, with special reference to pearson’s correlation coefficient. J. Am. Soc. Inf. Sci. Technol. 2003, 54, 550–560. [Google Scholar] [CrossRef]
- Galić, R. Vjerojatnost i Statistika; Elektrotehnički Fakultet Sveučilišta, J.J. Strossmayera u Osijeku: Osijek, Croatia, 1999. [Google Scholar]
- Luchka, A.Y. The Method of Averaging Functional Correction; Academic Press: New York, NY, USA; London, UK, 1963. [Google Scholar]
- Ventura, B.A.; von Keyserlingk, M.A.; Weary, D.M. Animal welfare concerns and values of stakeholders within the dairy industry. J. Agric. Environ. Ethics 2015, 28, 109–126. [Google Scholar] [CrossRef]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 1979, 21, 239–245. [Google Scholar]
- U.S. Department of Energy Federal Energy Management Program. M&V Guidelines: Measurement and Verification for Performance-Based Contracts Version 4.0. DOE/EE-1287-0286; November 2015. Available online: https://www.energy.gov/femp/federal-energy-management-program?nrg_redirect=471333 (accessed on 23 April 2025).
- Nawalany, G.; Sokołowski, P. Interaction between a Cyclically Heated Building and the Ground, for Selected Locations in Europe. Energies 2022, 15, 7493. [Google Scholar] [CrossRef]
- RETMON, URL Temperature and Humidity Sensor|Retmon|Environmental Monitoring Systems. Available online: https://www.retmon.com/en/sensors-and-equipments/temperature-and-humidty-sensor (accessed on 15 November 2023).
- TS EN IEC 61000-6-2; Electromagnetic Compatibility (EMC), Immunity Standard for Industrial Environments. Turkish Standards Institute: Ankara, Türkiye, 2019.
- TS EN ISO 9001: 2015-10; Quality Management Systems. Turkish Standards Institute: Ankara, Türkiye, 2015.
- Bucchianico, A.D. Coefficient of Determination (R2). In Encyclopedia of Statistics in Quality and Reliability; John Wiley & Sons, Ltd.: New Jersey, NY, USA, 2008. [Google Scholar]
- Barrett, G.B. The coefficient of determination: Understanding r squared and R squared. Math. Teach. 2000, 93, 230–234. [Google Scholar] [CrossRef]
- Nevitt, J.; Hancock, G.R. Improving the root mean square error of approximation for nonnormal conditions in structural equation modeling. J. Exp. Educ. 2000, 68, 251–268. [Google Scholar] [CrossRef]
- Hancock, G.R.; Freeman, M.J. Power and sample size for the root mean square error of approximation test of not close fit in structural equation modeling. Educ. Psychol. Meas. 2001, 61, 741–758. [Google Scholar] [CrossRef]
- Benesty, J.; Chen, J.; Huang, Y. On the importance of the Pearson correlation coefficient in noise reduction. IEEE Trans. Audio Speech Lang. Process. 2008, 16, 757–765. [Google Scholar] [CrossRef]
- Frankham, R. Stress and adaptation in conservation genetics. J. Evol. Biol. 2005, 18, 750–755. [Google Scholar] [CrossRef] [PubMed]
- Nardone, A.; Ronchi, B.; Lacetera, N.; Bernabucci, U. Climatic effects on productive traits in livestock. Vet. Res. Commun. 2006, 30, 75–81. [Google Scholar] [CrossRef]
- Bernabucci, U.; Lacetera, N. Metabolic and hormonal adaptations to heat stress in ruminants. J. Anim. 2010, 4, 1167–1183. [Google Scholar] [CrossRef]
- Renaudeau, D.; Gourdine, J.L.; Silva, B.A.N.; Noblet, J. Nutritional routes to attenuate heat stress in pigs. In Livestock and Global Change; Rowlinson, P., Steele, M., Nefzoaoui, A., Eds.; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Suraj, P.T. Effect of environmental stress on dairy cattle under different housing pattern in north and western regions in Tamil Nadu. Ph.D. Thesis, Tamil Nadu Veterinary and Animal Sciences University, Chennai, Tamil Nadu, 2011. [Google Scholar]
- Aye, L.; Charters, W.W.S.; Fandino, A.M.; Robinson, J.R.W. Thermal performance of sustainable energy features. Solar 2005, 2005, 1–10. [Google Scholar]
- Government Gazette, Başbakanlık Mevzuatı Geliştirme ve Yayın Genel Müdürlüğü. Available online: https://www.resmigazete.gov.tr/eskiler/2011/12/20111202-9.htm (accessed on 17 January 2024).
- Government Gazette. Microsoft Word. Available online: https://www.tarimorman.gov.tr/Belgeler/Mevzuat/Yonetmelikler/hayvansagligivezabitasi_yonetmeligi.pdf (accessed on 18 January 2024).
- Government Gazette. Available online: https://www.resmigazete.gov.tr/eskiler/2006/08/20060809-4.htm (accessed on 18 January 2024).
- European Union. Council Directive 98/58/EC of 20 July 1998 Concerning the Protection of Animals Kept for Farming Purposes. Available online: https://eur-lex.europa.eu/legal-content/EN/ALL/?uri=CELEX:31998L0058 (accessed on 16 January 2024).
- Yusuf, Y.; Arsan, Z.D. Identification of the building parameters that influence heating and cooling. Energy 2011, 36, 4287–4429. [Google Scholar] [CrossRef]
- Mishra, P.; Pandey, C.M.; Singh, U.; Gupta, A.; Sahu, C.; Keshri, A. Descriptive statistics and normality tests for statistical data. Ann. Card. Anaesth. 2019, 22, 67–72. [Google Scholar] [CrossRef] [PubMed]
- Vetter, T.R. Descriptive statistics: Reporting the answers to the 5 basic questions of who, what, why, when, where, and a sixth, so what? Anesth. Analg. 2017, 125, 1797–1802. [Google Scholar] [CrossRef]
- Kaliyadan, F.; Kulkarni, V. Types of Variables, Descriptive Statistics, and Sample Size. Indian Dermatol. Online J. 2019, 10, 82–86. [Google Scholar] [CrossRef]
- Mirrahimi, S.; Mohamed, M.F.; Haw, L.C.; Ibrahim, N.L.N.; Yusoff, W.F.M.; Aflaki, A. The effect of building envelope on the thermal comfort and energy saving for high-rise buildings in hot–humid climate. Renew. Sustain. Energy Rev. 2016, 53, 1508–1519. [Google Scholar] [CrossRef]
- Wang, X.; Kendrick, C.; Ogden, R.; Walliman, N.; Baiche, B. A case study on energy consumption and overheating for a UK industrial building with rooflights. Appl. Energy 2013, 104, 337–344. [Google Scholar] [CrossRef]
- Gupta, S.K. The relevance of confidence interval and P-value in inferential statistics. Indian J. Pharmacol. 2012, 44, 143–144. [Google Scholar] [CrossRef]
- Çiftci, M.S. Structural Analysis of Dairy Cattle Shelters in Konya-Güneysınır District. Master’s Thesis, Selcuk University Institute of Science, Konya, Türkiye, 2019. [Google Scholar]
- Costantino, A.; Calvet, S.; Fabrizio, E. Identification of energy-efficient solutions for broiler house envelopes through a primary energy approach. J. Clean. Prod. 2021, 312, 127639. [Google Scholar] [CrossRef]
- Gemeç, E. The contribution of cattle farms to the local economy and the opinions of producers about the sector; the example of Zonguldak Province. Master’s Thesis, Bursa Uludag University Institute of Science, Bursa, Türkiye, 2023. [Google Scholar]
- Wang, Y.; Li, B.; Liang, C.; Zheng, W. Dynamic Simulation of Thermal Load and Energy Efficiency in Poultry Buildings in the Cold Zone of China. Comput. Electron. Agric. 2020, 168, 105127. [Google Scholar] [CrossRef]
- Nguyen-Ky, S.; Penttilä, K. Indoor climate and energy model calibration with monitored data of a naturally ventilated dairy barn in a cold climate. Appl. Eng. Agric. 2021, 37, 851–859. [Google Scholar] [CrossRef]
- Izar-Tenorio, J.; Jaramillo, P.; Griffin, W.M.; Small, M. Impacts of Projected Climate Change Scenarios on Heating and Cooling Demand for Industrial Broiler Chicken Farming in the Eastern U.S. J. Clean. Prod. 2020, 255, 120306. [Google Scholar] [CrossRef]
- Yurttakal, Ö. Evaluation of Thermal Performance of Window Systems at Element and Building Level. Master’s Thesis, Istanbul Technical University Institute of Science, Istanbul, Türkiye, 2007. [Google Scholar]
- Göncü, S.; Önder, D.; Koluman, N.; Mevliyaoğulları, E. Animal shelter features suitable for hot and humid conditions. Tüsedad 2015, 5, 42–47. [Google Scholar]
- Costantino, A.; Fabrizio, E.; Villagrá, A.; Estellés, F.; Calvet, S. The Reduction of Gas Concentrations in Broiler Houses through Ventilation: Assessment of the Thermal and Electrical Energy Consumption. Biosyst. Eng. 2020, 199, 135–148. [Google Scholar] [CrossRef]
- Cho, J.-H.; Lee, I.-B.; Lee, S.-Y.; Park, S.-J.; Jeong, D.-Y.; Decano-Valentin, C.; Kim, J.-G.; Choi, Y.-B.; Jeong, H.-H.; Yeo, U.-H.; et al. Development of Heat Stress Forecasting System in Mechanically Ventilated Broiler House Using Dynamic Energy Simulation. Agriculture 2022, 12, 1666. [Google Scholar] [CrossRef]
- Sadineni, S.B.; Madala, S.; Boehm, R.F. Passive building energy savings: A review of building envelope components. Renew. Sustain. Energy Rev. 2011, 15, 3617–3631. [Google Scholar] [CrossRef]
- Kent, R. Chapter 7—Buildings and Offices. In Energy Management in Plastics Processing, 3rd ed.; Kent, R., Ed.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 345–370. [Google Scholar]
- Lu, Q.; Wen, J.; Zhang, H. Effect of chronic heat exposure on fat deposition and meat quality in two genetic types of chicken. Poult. Sci. 2007, 86, 1059–1064. [Google Scholar] [CrossRef]
- Chai, Z.; He, R.; Sun, Z.; Tan, T.; Méndez-Vázquez, H. Histograms of Gabor ordinal measures for face representation and recognition. In Proceedings of the 2012 5th IAPR International Conference on Biometrics (ICB), New Delhi, India, 29 March–1 April 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 52–58. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).