Parametric Landscape Facilities Aesthetic Design Method Based on SOR Model and Hybrid Kansei Engineering: A Case of Landscape Corridors

Abstract

Parametric design stands out in contemporary landscape facilities design with its distinctive beauty sense. However, understanding this beauty sense and establishing an aesthetic design method is one of the problems needed to be solved. In this context, this study integrates the Stimulus-Organism-Response (SOR) model and hybrid Kansei Engineering establish the aesthetic design method for parametric landscape facilities from the perspectives of cognition and positivist design. Firstly, the SOR model is used to reveal the aesthetic cognitive mechanism of parametric landscape facilities. Secondly, the forward Kansei Engineering is used to extract design features. Thirdly, the extracted design features are combined with shape grammar for parametric modeling in the Grasshopper platform. Fourthly, backward Kansei Engineering is used to evaluate design schemes and analyze their data of beauty sense. Finally, this study takes the landscape corridor as a case to illustrate the proposed method. The results show that (1) in aesthetic cognition, dynamic visual forms, transparency of spatial feeling, and abstract style have a significant positive impact on the beauty perception of parametric landscape facilities, and the beauty perception of parametric design has a unique appeal to the general public. (2) The design case verified the effectiveness of this method, and this study can provide a valuable reference for parametric landscape facilities.

1. Introduction

In the context of the United Nations Sustainable Development Goals (SDGs), landscape facilities designs that promote citizens’ health and well-being are an important trend [1]. Landscape facilities are the integration of aesthetics, functionality, and humanity [2]; aesthetics play a crucial role in improving their design effects.

Aesthetics is a philosophical reflection on various phenomena of beauty and art; its original meaning refers to sensation in Greek [3]. The study of aesthetics was first proposed by the philosopher Baumgarden in German, and the research content is the beauty phenomena and their inherent laws and nature [4]. With the development of aesthetic research, applied aesthetics emerged. Architectural aesthetics is a discipline that intersects architecture and aesthetics, which is based on the practice and creation of architectural art, analyzing its beauty features and theory [5]. In architectural aesthetics, geometric relationships such as scale and proportion are an important aspect. Figure 1a shows the aesthetic of the facade of a Western classical architecture based on the golden section and proportion. This visual proportion analysis of architecture uses mathematical methods to illustrate the harmonious beauty of architecture.

In the context of the development of computer technology, parametric modeling and design is a new design method based on mathematical reasoning. This technology enables rich and systematic variations in design forms [6], as shown in Figure 1b. The creation of parametric design schemes is based on rule-making and modifying in computer programming [7]; this design method based on mathematical relationships offers a new perspective for contemporary aesthetic design.

Parametric design is a design method with mathematical operation. Relevant research indicates that the most prominent feature of this design is variation in continuous differentiation [8]. This new method is the creation of design schemes using computer programming platforms (such as Grasshopper platform), which has been widely concerned in the field of landscape and architecture design research. Tan (2017) conducted a series of practical cases of parametric landscape facilities design based on the Grasshopper platform [9]. Xue (2023) explored the parametric landscape architecture design method with the Grasshopper platform [10]. Lv (2023) constructed a design method for urban public facilities through the extraction of urban regional cultural features and parametric design methods [11]. Zargar S.H. and Alaghmandan M. (2019) developed a parametric design platform for the integration of multiple factors based on the Grasshopper platform [12]. However, there is a lack of research on its beauty features and inherent aesthetic laws.

Aesthetics is originally a philosophical issue. With the development of aesthetic research, various positivist aesthetics studies such as neuroaesthetics [13] and experimental aesthetics have expanded the scope of traditional aesthetics research [14]. Experimental psychology has unraveled the psychological cognitive mechanism of human beings towards beauty sense. The intervention of experimental cognitive science has led the development of aesthetic research towards the direction of positivism.

Aesthetic cognition is an advanced and comprehensive emotional cognitive process [15], representing the user’s overall reaction to both explicit and implicit perceptions of the aesthetic object [16]. This research aims to analyze the cognitive mechanism of people towards beauty objects and reveal the law of beauty appreciation. Neuroscience research shows that beauty stimuli can trigger brain reward mechanisms, thereby enhancing the evaluation and preference for beauty objects [17]. In aesthetic cognitive processes, cognition, association, and feeling interact to create users’ beauty sense [18,19]. The aesthetic cognition process is shown in Figure 2.

The study of aesthetic cognition is usually combined with various psychological models. Users make behavioral responses through psychological reactions to aesthetic stimulation. Among various cognition models, the SOR (Stimulus-Organism-Response) model is frequently used [20]; this theory is similar to aesthetic cognitive activities [21], which was proposed by Mehrabin and Russell in 1974, and it is used to study the influence of stimulation and user behavior [22,23].

The SOR model believes that the stimulus of the external factors causes the organism (user) to produce psychological cognition and then produces corresponding behavioral responses [24]. In this model, the stimulus includes various external factors as well as internal emotional and cognitive factors. The organism is the internal reaction between the external stimulus and the individual’s final behavior, including psychology, emotion, and cognition. Responses are the final behaviors exhibited by the organism under the influence of stimulus, including behavioral intentions, reactive behaviors, and others. In aesthetic cognition research, the SOR model (Stimulus-Organism-Response) is used to reveal the aesthetic cognitive mechanism. Yang et al. (2022) combined the SOR model to construct the analysis framework of heritage tourism aesthetics and explored the aesthetic cognitive mechanism of tourists to cultural heritage [25]. Xin (2023) used the SOR model to study the aesthetic cognition of urban brands [26]. Tan et al. (2024) combined the SOR model to establish a theoretical framework to reveal the mechanism of public art landscape impact on public perception [27]. The SOR model is an effective analytical model in aesthetic cognitive research, however, this model has not yet been studied in the parametric aesthetic cognition.

Kansei Engineering is a method of measuring beauty sense that combines experimental psychology [28], which acquires beauty features and analyzes beauty date through psychological measurement experiment [29]. Compared with qualitative research methods, Kansei Engineering can achieve quantitative research for analysis of beauty sense through scoring, which makes aesthetic research more objective, this technology is widely used in architecture, landscape, product design, and other fields. Nagaoka A. (2013) used the semantic differential (SD) method to analyze the visual effects of landscapes [30]. Matijosaitiene et al. (2014) used the Kansei Engineering method to analyze drivers’ aesthetic needs for road landscape and proposed design guidance for driving road landscape [31]. Karaca E. (2015) used the Kansei Engineering method to transform users’ emotional expectations into design elements and constructed a user-centered landscape design method [32]. Hybrid Kansei Engineering is an extension based on traditional Kansei Engineering: it conducts a two-way study of the beauty data of both the design features and the user, which include forward Kansei Engineering and backward Kansei Engineering [33]. Forward Kansei Engineering mainly converts emotional elements into design features [34], while backward Kansei Engineering mainly analyzes people’s emotional responses to design features [35]. Multicriteria Decision Making (MCDM) methods such as AHP and FCE are frequently used in the research of hybrid Kansei Engineering, and these mathematical methods can quantitatively analyze beauty sense [36,37,38,39].

To sum up, parametric design is a unique design method. However, in current research, there are relatively few studies on the aesthetic research on parametric design; the research on the aesthetic cognitive mechanism and design methods of parametric landscape facilities is especially rare. To solve this problem, this study combines the SOR model and hybrid Kansei Engineering for the first time and proposes a positivist aesthetic design method for parametric landscape facilities, providing a new idea for the design of urban landscape facilities.

This research mainly addresses two key issues:

(1)

What is the aesthetic cognitive mechanism of parametric landscape facilities design?

(2)

Based on the aesthetic cognitive mechanism, how to construct an objective aesthetic design method for parametric landscape facilities?

The research route is illustrated in Figure 3. Firstly, the SOR model was used to reveal the aesthetic cognitive mechanism for parametric landscape facilities. Secondly, based on aesthetic cognition, hybrid Kansei Engineering and parametric modeling is used to establish the aesthetic design method of landscape facilities. Thirdly, the operation process of this method was explained by a case of landscape corridor, providing design suggestions for parametric landscape facilities design.

2. Theory and Method

This section is for constructing the parametric landscape facilities aesthetic design method based on the SOR model and hybrid Kansei Engineering and specifically explains the principle and process framework of this method, shown in Figure 4. This method consists of two parts, aesthetic cognition and aesthetic design.

Firstly, the aesthetic cognition model for parametric landscape facilities is proposed based on the SOR model, which was used to analyze aesthetic cognitive mechanism with the Structural Equation Model (SEM). Secondly, in forward Kansei Engineering, the Design Format Analysis (DFA) and Factor Analysis (FA) were used to obtain the visual features and semantics features, respectively. Thirdly, based on the analysis results of the SOR model and design feature extraction, the shape grammar and parametric modeling method are combined to create the design schemes. Fourthly, in backward Kansei Engineering, the Analytic Hierarchy Process (AHP) and Fuzzy Comprehensive Evaluation (FCE) were used to evaluate design schemes.

2.1. Aesthetic Cognitive Mechanism Based on SOR Model

The analysis method of aesthetic cognitive mechanism based on the SOR model is shown in Figure 5a. Firstly, through the features analysis of parametric landscape facilities, the aesthetic stimulus variables are obtained and the Stimulus-Organism-Response (SOR) model is constructed. Secondly, based on the constructed SOR model, propose hypotheses and design questionnaire questions. Thirdly, the Structural Equation Model is used to analyze the fitting results and path coefficients of the model, thereby verifying the proposed hypotheses and analyzing the influence relationships and degrees among various variables.

Based on the previous analysis of the SOR model, different aesthetic stimulation dimensions are taken as the measurement indication of stimulus (S), and these dimensions can be analyzed from the aspects of visual, space, and style. Visual stimulus refers to the form of a landscape facilities, spatial stimulus refers to its spatial structure, and style stimulus refers to its artistic style. The beauty perception of parametric design is taken as the measurement indication of organism (O). The public’s use intention is taken as the measurement indicator of response (R).

The effect of parametric landscape facilities design is very unique compared with the ordinary landscape facilities. From typical parametric landscape facilities design, it can be known that its visual form is continuous and dynamic change, its space is transparent and changing, and the overall artistic style is novel, as shown in Figure 5b.

The visual effect of parametric landscape facilities exhibits dynamic visual forms, accompanied by the transparency of spatial feeling and an abstract artistic style. Combined with the relevant literature [40], we take dynamic visual forms, transparency of spatial feeling, and abstract style features as sources of aesthetic stimulation. The influence path of different aesthetic stimulus on beauty perception of parametric design is discussed by using the SOR model. The aesthetic cognitive model for landscape facilities design is shown in Figure 5c.

In order to analyze the aesthetic cognition mechanism for the parametric landscape facilities design, explore how dynamic visual forms, changes in spatial feeling and distinctive humanistic features affect the public’s perception, and use intention for this facilities. The following hypotheses are proposed:

H1: 

Dynamic visual forms can significantly influence beauty perception of parametric design.

H2: 

Transparency of spatial feeling can significantly influence beauty perception of parametric design.

H3: 

Abstract style features can significantly influences beauty perception of parametric design.

H4: 

Perception of parametric beauty can significantly influence public use intention.

2.2. Design Feature Extraction Method Based on Forward Kansei Engineering

Based on the SOR analysis, this section is using forward Kansei Engineering to extract explicit visual features and implicit semantic features, respectively, providing a reference for parametric modeling and design.

The forward Kansei Engineering method route is shown in Figure 6. The first step is to collect relevant visual samples based on the design theme, the collection of visual samples can be combined with the analysis results of the SOR model. The second step is to use DFA and FA to extract typical design features and semantic features respectively.

2.2.1. Visual Features Extraction Method Based on DFA

Design Format Analysis (DFA) [41,42,43] is a quantitative analysis of visual features. This method obtains typical features by scoring the correspondence between a series of visual samples and a series of feature descriptions. The process of DFA is shown in Figure 7.

Firstly, through the analysis of the form features of the collected visual samples, the form features collection is obtained, which is evenly distributed. Secondly, the DFA questionnaire was established through the analysis of the correlation degree between visual samples and form features. Thirdly, the scores of different visual samples and form features are calculated through the questionnaire scoring, the calculation formula is shown in Equation (1) [44]. Fourthly, by ranking the visual samples and visual feature scores, typical visual samples and form features are obtained.

$${\overline{X}}_{ijk}={\displaystyle \frac{{\displaystyle \sum _{k=1}^n{X}_{ijk}}}{n}}$$

(1)

where i represents the number of visual samples, j represents the number of feature description, and n represents the number of participants in the questionnaire.

2.2.2. Semantic Features Extraction Method Based on FA

Factor Analysis (FA) [45] is a statistical method that reveals relationships among multiple variables. It reduces dimensionality by explaining the structure of original variables with a few uncorrelated factors, thereby analyzing their underlying nature and patterns. The FA principle is shown in Equation (2) [46].

$$\underset{m\times 1}{Z}=\underset{m\times p}{K}\bullet \underset{p\times 1}{F}+\underset{m\times 1}{B}$$

(2)

where Z = (Z₁, Z₂,…,Z_m) represent the variables with a correlation, F = (F₁, F₂,…,F_p,m ≥ p) are the common factor for Z_m, K_mp represents the factor loading that the i-th variable (Z_i) load on the j-th common factor, and F_j,B = (B₁, B₂,…,B_m) are special factors.

The semantic feature extraction process based on Factor Analysis is shown in Figure 8.

Firstly, collect relevant Kansei words through the analysis of the visual sample, and construct groups of positive and negative based on the collected Kansei words. Secondly, based on the Kansei word pairs, the semantic difference method (generally −3 to 3 or −2 to 2) is used to establish the questionnaire. Thirdly, the data of questionnaire were analyzed through Factor Analysis (generally using SPSS software), the number of factors with high contribution rates is obtained. Based on the rotated component matrix, the factor names are derived, thereby obtaining the typical semantic features.

2.3. Parametric Modeling and Design Method

This section is based on the SOR model and the feature extraction of forward Kansei Engineering, combined with parametric modeling for the creation of design schemes; the process is shown in Figure 9.

Firstly, based on the analysis results of the SOR model and the feature extraction of forward Kansei Engineering, the unit form is further obtained through the integration of visual features and semantic features, and the initial design draft is formed by sketches. Secondly, by combining the unit form and the shape grammar, the design scheme is created in the parametric modeling platform, such as the Grasshopper platform in Rhino. In the parametric modeling, design creation is transformed into rules and parameters, and model shape changes are controlled through programming and numerical adjustments [47]. According to the design effect, a single shape grammar rule can be used, or multiple shape grammar rules can be combined. Finally, the rendering and generation of the design scheme are based on parametric modeling.

The beauty of parametric is based on mathematical reasoning. In graphic computing, shape grammar is a shape reasoning method based on linguistic theories [48], proposed by George Stiny in 1972 [49]. It consists of an initial shape and a set of shape rules that derive new forms through deductive transformations, every shape deduction rule is also a manifestation of beauty. The variation rules of shape grammar include feature creation and feature modification [50,51,52].

In this study, six shape change rules are mainly applied, these shape change rules include translation, scaling, rotation, mirroring, ring array, direction array, as shown in

Table 1. An illustration of the rules of shape grammar.

Rule	Meaning	Mathematical Expression	Rule Expression	Example of the Grasshopper Command
Translation	Moving in a certain direction within a plane	$T=\left[\begin{array}{ccc}1& 0& t_x\\ 0& 1& t_y\\ 0& 0& 1\end{array}\right]$
Scaling	Enlarge or reduce in a certain proportion within a plane	$S=\left[\begin{array}{ccc}{s}_x& 0& 0\\ 0& s_{\mathrm{y}}& 0\\ 0& 0& 1\end{array}\right]$
Rotation	Rotate a fixed angle around a specific point	$R=\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]$
Mirror	Reflection of an object based on a certain plane	$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$
Polar array	Copy the object with a circle as the path around a specified central point	$R_z(\alpha )=\left[\begin{array}{cccc}\cos \alpha & -\sin \alpha & 0& 0\\ \sin \alpha & \cos \alpha & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$
Directional array	Move along a specific direction according to the rules	$T=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ i\cdot \Delta d\cdot x_v& i\cdot \Delta d\cdot y_c& 1\end{array}\right]$

.

The Grasshopper platform in Rhino software is often used for parametric modeling of landscape and architecture. The Grasshopper platform represents the computer language through different containers and operators, and its programming language has excellent visualization advantages [53].

The modeling method in the Grasshopper platform is shown in Figure 10. Firstly, the modification command consists of the command itself and the variable slider in the Grasshopper platform. The command itself controls the modification rules, while the variable slider is used to input variables and change references (such as coordinate axes, planes, etc.). Take the movement command as an example. The variable slider of this command includes the movement direction and the movement distance. The command itself works with the slider variable to change shape. Secondly, the links between each command need to correspond to the interface. For example, the G (geometry) interface should be connected to the same G port. This way, multiple command combinations can be accomplished and multiple form changes can be achieved. Thirdly, by connecting multiple commands according to interface attributes and linking them with the variable slider, a complete parametric programming command in the Grasshopper platform can be formed.

2.4. Design Schemes Evaluation Method Based on Backward Kansei Engineering

Based on design scheme creation, backward Kansei Engineering composed of AHP-FCE can achieve the quantitative evaluation for the beauty sense of design schemes.

The backward Kansei Engineering method route is shown in Figure 11. In backward Kansei Engineering, Analytic Hierarchy Process (AHP) is used to analyze the influence degree of aesthetic evaluation indicators, and Fuzzy Comprehensive Evaluation (FCE) and AHP are combined to evaluate design schemes.

2.4.1. The Calculation Method of Evaluation Indicator Weights Based on AHP

The Analytic Hierarchy Process (AHP) is a structured criteria analysis methodology proposed by T. L. Saaty in the 1970s [54]. This method decomposes the factors of a decision problem into indicators at different levels and analyzes each indicator’s weight based on questionnaire scores [55].

The purpose of constructing the aesthetic evaluation indicators of landscape facilities design based on the AHP is to evaluate its design scheme from different levels, the selection of aesthetic indicators should conform to the public’s evaluation of landscape facilities. Based on the aesthetic cognitive model and the relevant literature on landscape aesthetic evaluation [56,57], the aesthetic indicators for landscape facilities design are constructed form the visual, spatial, and humanistic levels,,the meaning of each aesthetic indicator is shown in

Table 2. Evaluation indicators and definitions.

First Level Indicators	Second Level Indicators	Meaning
Visual level (A)	Decorative element (A1)	The visual effect of the decorative form
	Form combination (A2)	Combination relationship between form elements
	Overall form (A3)	The visual effect of the overall form and structure
Spatial level (B)	Landscape scales (B1)	Spatial perception for landscape scale
	Spatial rhythm (B2)	Rhythm changes in spatial sense
	Spatial harmony (B3)	Coordination and unity in spatial changes
Humanistic level (C)	Cultural feature (C1)	Landscape facilities reflect regional culture
	Symbolic meaning (C2)	The landscape facilities have symbolic significance
	Modern trend (C3)	Landscape facilities reflect the times characteristics

.

Firstly, the judgment matrix A is obtained through comparison and scoring between the two indicators by experts, the scoring method is shown in

Table 3. 1–9 scale value and meaning.

Scale	Significance	Meaning
1	Equally important	Both indicators are equally important
3	Slightly important	The indicator i is slightly more important than the indicators j
5	Moderately important	The indicator i is moderately more important than indicators j
7	Strongly importance	The indicator i is strongly more important than indicator j
9	Absolutely important	The indicator i is absolutely more important than indicator j
2, 4, 6, 8	Midpoint	Indicates the median of the above two elements

.

$$A={\left(a_{ij}\right)}_{nm}=\left[\begin{array}{llll}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ \cdots & \cdots & \cdots & \cdots \\ a_{n1}& a_{n2}& \cdots & a_{nn}\end{array}\right]$$

(3)

Secondly, the weights of each indicator are calculated, the process is as follows (Equations (4)–(9)).

Calculate the product Ai for each row value in the judgment matrix:

$$A_i={\displaystyle \prod _{j=1}^n{\alpha }_{ij}\left(i=1,2,\cdots ,n\right)}$$

(4)

Calculate the geometric mean:

$$\overline{W_{s,i}}=\sqrt[n]{A_i}(i=1,2,\cdots ,n)$$

(5)

The relative weight Wi are obtained after normalization:

$$W_i={\displaystyle \frac{\overline{W_i}}{{\displaystyle \sum _{i=1}^n{\overline{W}}_i}}}\left(i=1,2,\cdots ,n\right)$$

(6)

Calculate the largest eigenvalue:

$$\mathrm{\lambda }\max ={\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}\frac{{\left(A\cdot W\right)}_i}{n{W}_i}}$$

(7)

Calculate consistency index (CI):

$$CI={\displaystyle \frac{\mathrm{\lambda }\max -n}{n-1}}$$

(8)

The consistency ratio (CR) is calculated; the random index (RI) values are shown in

Table 4. Random consistency index.

n	1	2	3	4	5	6	7	8	9	10	11
RI	0	0	0.52	0.89	1.12	1.26	1.36	1.41	1.46	1.49	1.52

.

$$CR={\displaystyle \frac{CI}{RI}}$$

(9)

When CR < 0.1, it indicates that the consistency of the matrix is acceptable. Otherwise, the matrix needs to be readjusted [58].

2.4.2. Aesthetic Evaluation of Design Schemes Based on AHP-FCE

Based on the weight values of the evaluation indicators calculated by the AHP, Fuzzy Comprehensive Evaluation (FCE) is used to evaluate each design scheme to obtain the evaluation data.

FCE is an evaluation method based on fuzzy mathematics [59,60]. This method uses membership functions to evaluate schemes, applies fuzzy mathematics to handle evaluation uncertainties, and provides scientific support for complex decision making.

Firstly, fuzzy evaluation matrix R is obtained by using different evaluation levels questionnaires (e.g., excellent, good, general, poor, very poor).

$$R=\left[\begin{array}{llll}{r}_{11}& r_{12}& \cdots & r_{1m}\\ r_{21}& r_{22}& \cdots & r_{2m}\\ \cdots & \cdots & \cdots & \cdots \\ r_{p1}& r_{p2}& \cdots & r_{pm}\end{array}\right]$$

(10)

Secondly, according to the matrix R and determined weight W, the membership of each evaluation level X is calculated.

$$X=W\bullet R$$

(11)

In this study, the weighted average algorithm M (·, +) is adopted to calculate the membership degree [61], and then the summation normalization method is used to obtain the normalized membership degree. The calculation formula is as follows:

$$Xi={\displaystyle \sum _{i=1}^m(wi\bullet rij)}\hspace{1em}(j=1,2,3\dots ,n)$$

(12)

$$Xm={\displaystyle \frac{X}{{\displaystyle \sum _{i=1}^{n}Xi}}}$$

(13)

Thirdly, based on the membership of each evaluation level X, the comprehensive score Y is calculated. The evaluation set V, V = {10, 8, 6, 4, 2}, and the five grades of excellent, good, general, poor, and very poor resulted in scores of 10, 8, 6, 4, and 2.

$$Y=X\bullet V$$

(14)

3. Case Study

This study taking landscape corridor facilities in a square as the design case to illustrate the proposed design method. The square is spacious and open, and there are no other facilities in the nearby area that may affect it. Landscape corridors are one of the important components of urban landscape facilities, and it is composed of a series of unit forms, making it a case suitable for the application of parametric design methods, which can provide a reference for the other types of parametric landscape facilities. The surrounding environment of the case is shown in Figure 12a, examples of the various landscape corridors are shown in Figure 12b.

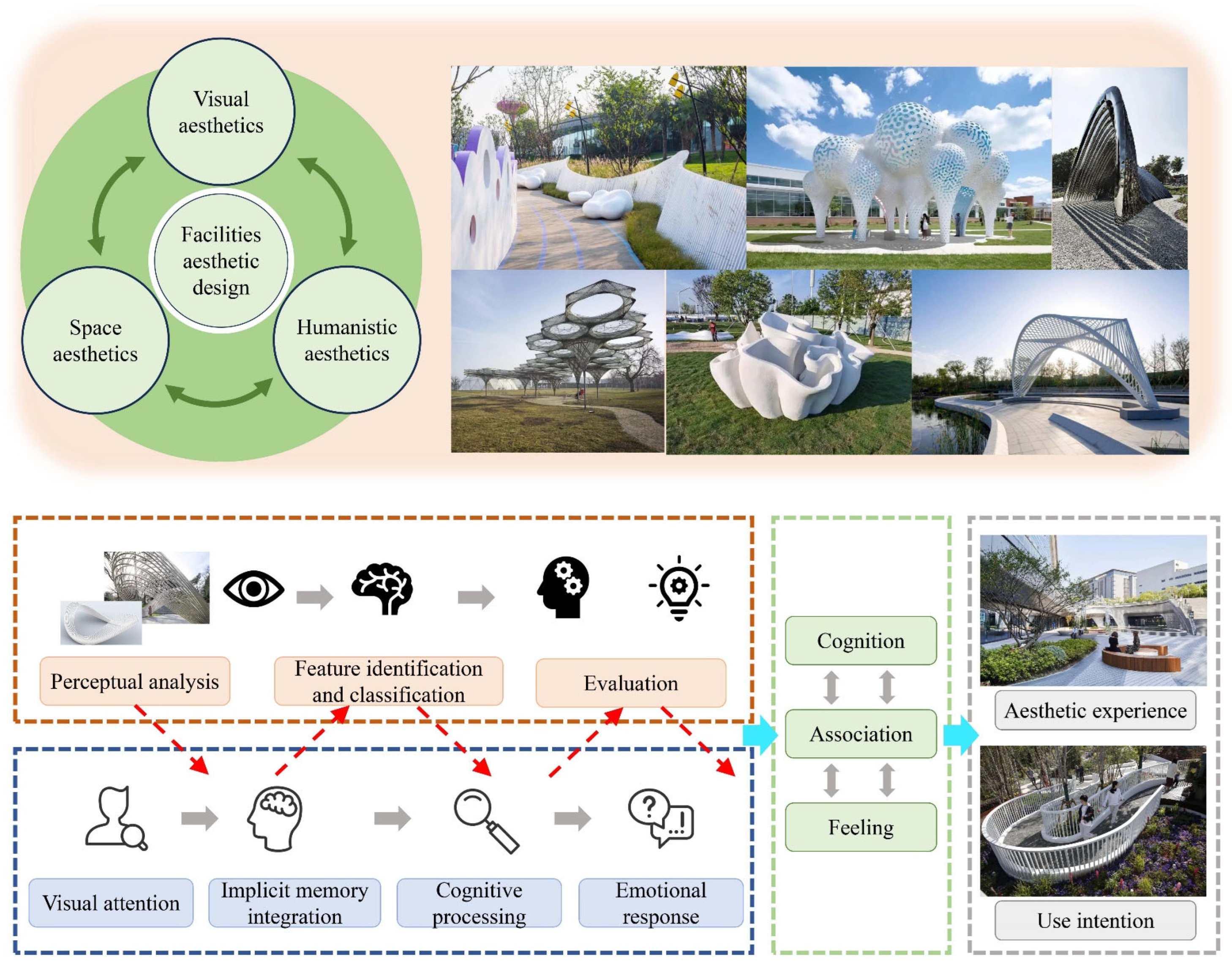
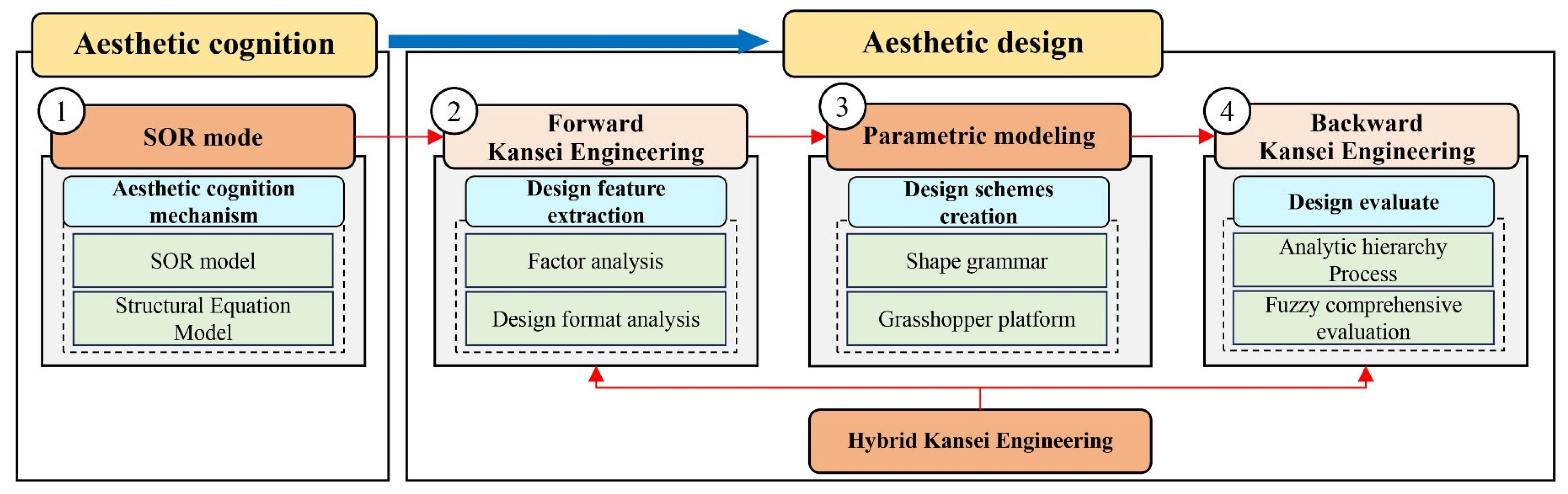
3.1. Analysis of Aesthetic Cognitive Mechanism Based on SOR Model

Based on the analysis of the aesthetic cognitive mechanism of the SOR model in the previous text, the hypothesis proposed in the previous text is verified by combining the Structural Equation Model method, exploring how various aesthetic stimulus variables affect beauty perception of parametric design. The experiment was conducted through questionnaires. Firstly, combining the meanings of each variable and the relevant literature [59,60,61], the detailed measurement items are presented in

Table 5. Measurement questions for each variable.

Latent variables	Number	Question
Dynamic visual forms	A1	I can perceive beauty of parametric from constantly undulating and changing shapes of the landscape facilities.
	A2	I can perceive beauty of parametric from the flowing shape combination of the landscape facilities.
	A3	I can perceive beauty of parametric from with orderly shape combinations of the landscape facilities.
Transparency of spatial feeling	B1	I can perceive the beauty of parametric from the gradual spatial variation of landscape facilities.
	B2	I can perceive beauty of parametric from hollowed-out spatial variations of the landscape facilities.
	B3	I can perceive beauty of parametric from the regular-changing spatial variations of the landscape facilities.
Abstract style features	C1	Landscape facilities with a relatively abstract style allow me to perceive beauty of parametric.
	C2	Landscape facilities with a sense of continuous and repetitive artistry allow me to perceive beauty of parametric.
	C3	Landscape facilities with a minimalist style allow me to perceive beauty of parametric.
Beauty perception of parametric design	D1	Compared with ordinary landscape facilities, I believe the beauty of parametric landscape facilities is more attractive.
	D2	I believe beauty of parametric landscape facilities is distinctive.
	D3	I believe beauty of parametric landscape facilities with is novel.
Use intention	F1	I will actively look for parametric Landscape facilities to use in daily life.
	F2	Compared with ordinary landscape facilities, I would be more willing to use those with parametric beauty again.
	F3	I would recommend landscape facilities that convey parametric beauty to others.

.

Secondly, 300 ordinary adults were selected as the subjects through questionnaire scoring. To ensure the validity of the questionnaire filling, it is necessary to show the subjects pictures of the parametric landscape facilities to let them understand the parametric landscape facilities. The survey questionnaire comprised two parts: (1) respondents’ basic information (gender, age, education level), and (2) scores for the measurement variables. All measurement items were evaluated using a 7-point Likert scale, where 1 indicates “strongly disagree” and 7 indicates “strongly agree”.

The survey participants were all adults with a balanced demographic distribution. A total of 300 questionnaires were distributed, with 294 collected, resulting in an effective response rate of 98.0%, questionnaire collection is acceptable in the study of Structural Equation Models. The details are shown in

Table 6. Characteristics of the sample.

Variable	Category	Frequency	Percentage (%)
Gender	Male	145	48.7%
	Female	153	51.3%
Age	18–25	98	32.9%
	26–35	113	37.9%
	36–45	62	20.8%
	46–55	14	4.7%
	>55	11	3.7%
Educational level	Some high school, no diploma	12	4.0%
	High school graduate	23	7.7%
	Bachelor’s degree	176	59.1%
	Master’s degree	82	27.5%
	Doctorate degree	5	1.7%
Total		298	100%

.

Finally, the experimental data were analyzed through the Structural Equation Model to obtain the final research results. The questionnaire data were analyzed for reliability by using SPSS 22.0 software, and the Cronbach’s α value for each latent variable > 0.7, indicating good reliability of the data.

The model was tested using AMOS 24.0 for confirmatory factor analysis (CFA), as shown in

Table 7. Results of confirmatory factor analysis.

Latent Variables	Number	STD	p	α	CR	AVE
Dynamic visual forms	A1	0.797	***	0.820	0.820	0.603
	A2	0.769	***
	A3	0.763	***
Transparency of spatial feeling	B1	0.817	***	0.828	0.829	0.617
	B2	0.787	***
	B3	0.752	***
Abstract style features	C1	0.833	***	0.841	0.842	0.641
	C2	0.79	***
	C3	0.777	***
Beauty perception of parametric design	D1	0.881	***	0.891	0.891	0.732
	D2	0.87	***
	D3	0.815	***
Use intention	F1	0.829	***	0.850	0.850	0.653
	F2	0.82	***
	F3	0.776	***

Note: *** indicates p < 0.001.

. The fit indices of the model are as follows: X2/df = 1.160, RMSEA = 0.023, GFI = 0.961, CFI = 0.994, NFI = 0.958, TLI = 0.992. The standardized regression weight (STD), composite reliability (CR), and average variance extracted (AVE) of each latent variables are shown in Table 7. All standardized regression weights (STD) were above 0.6, and composite reliability (CR) and average variance extracted (AVE) values were above 0.5. The fit indices of the model demonstrated that this model were considered acceptable [62].

In the test of discriminant validity, the square roots of the AVE values were above each correlation coefficient of the variables, indicating good discriminant validity [63], as shown in

Table 8. Discriminant validity.

	Dynamic Visual Forms	Transparency of Spatial Feeling	Abstract Style Features	Parametric Aesthetic Perception	Use Intention
Dynamic visual forms	0.777
Transparency of spatial feeling	0.348	0.785
Abstract style features	0.415	0.386	0.801
Beauty perception of parametric design	0.41	0.375	0.377	0.856
Use intention	0.431	0.227	0.337	0.268	0.808

.

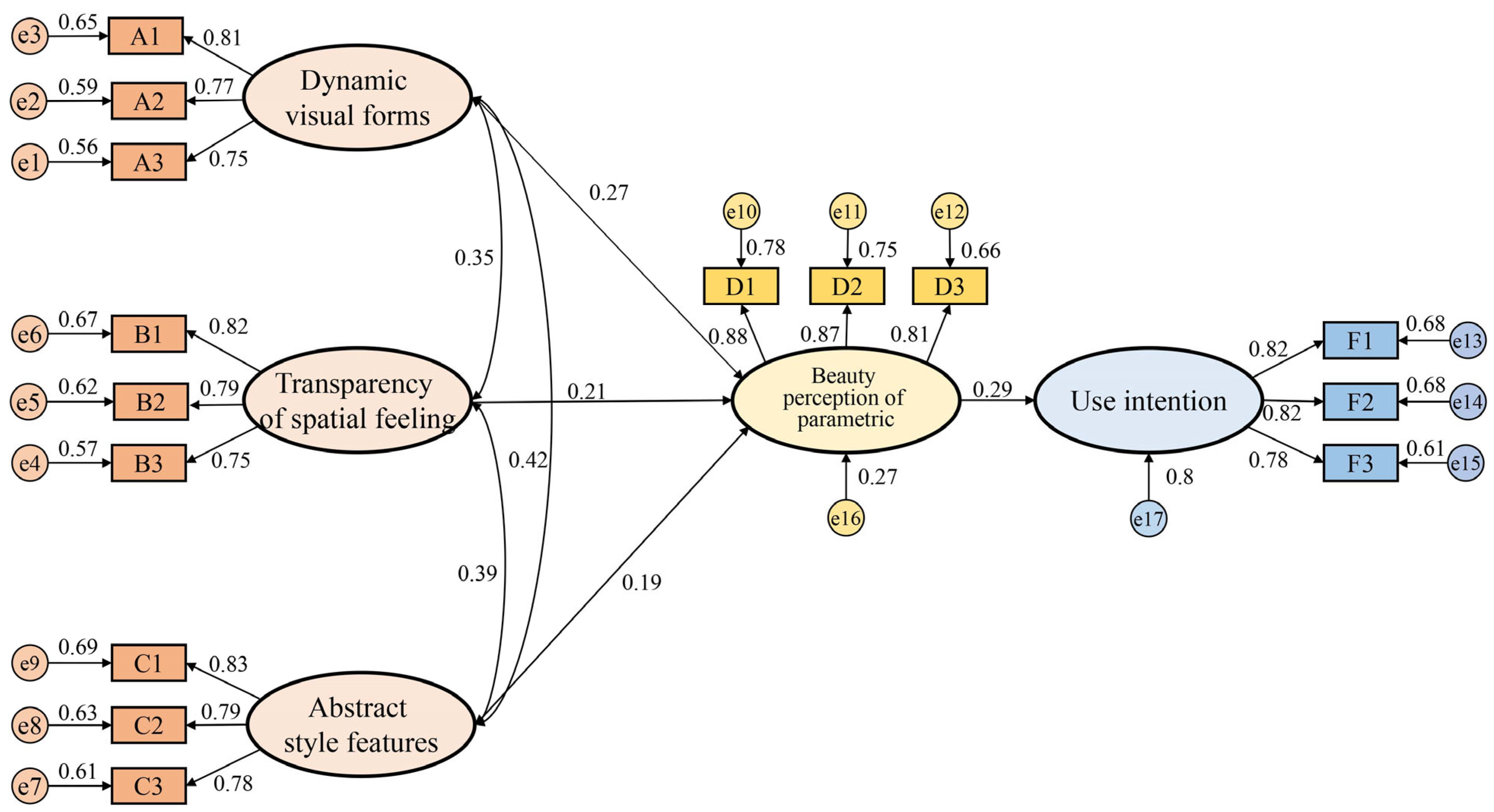
The theoretical model was analyzed by AMOS 24.0 software to calculate the model fit indices. The fit indices of the model are as follows: X2/df = 1.531, RMSEA = 0.042, GFI = 0.947, NFI = 0.942, and CFI = 0.979. All indices are within acceptable limits [64], the fit indices of the model demonstrated that this model were considered acceptable. The results of the model path analysis are shown in

Table 9. Path analysis results.

Hypothesis		STD	S.E.	C.R. (T)	p	Result
H1	Dynamic visual forms → Beauty perception of parametric design	0.27	0.096	3.738	***	Supported
H2	Transparency of spatial feeling → Beauty perception of parametric design	0.211	0.096	3.022	0.003	Supported
H3	Abstract style features → Beauty perception of parametric design	0.192	0.091	2.673	0.008	Supported
H4	Beauty perception of parametric design → Use intention	0.29	0.051	4.38	***	Supported

Note: *** indicates p < 0.001.

and Figure 13.

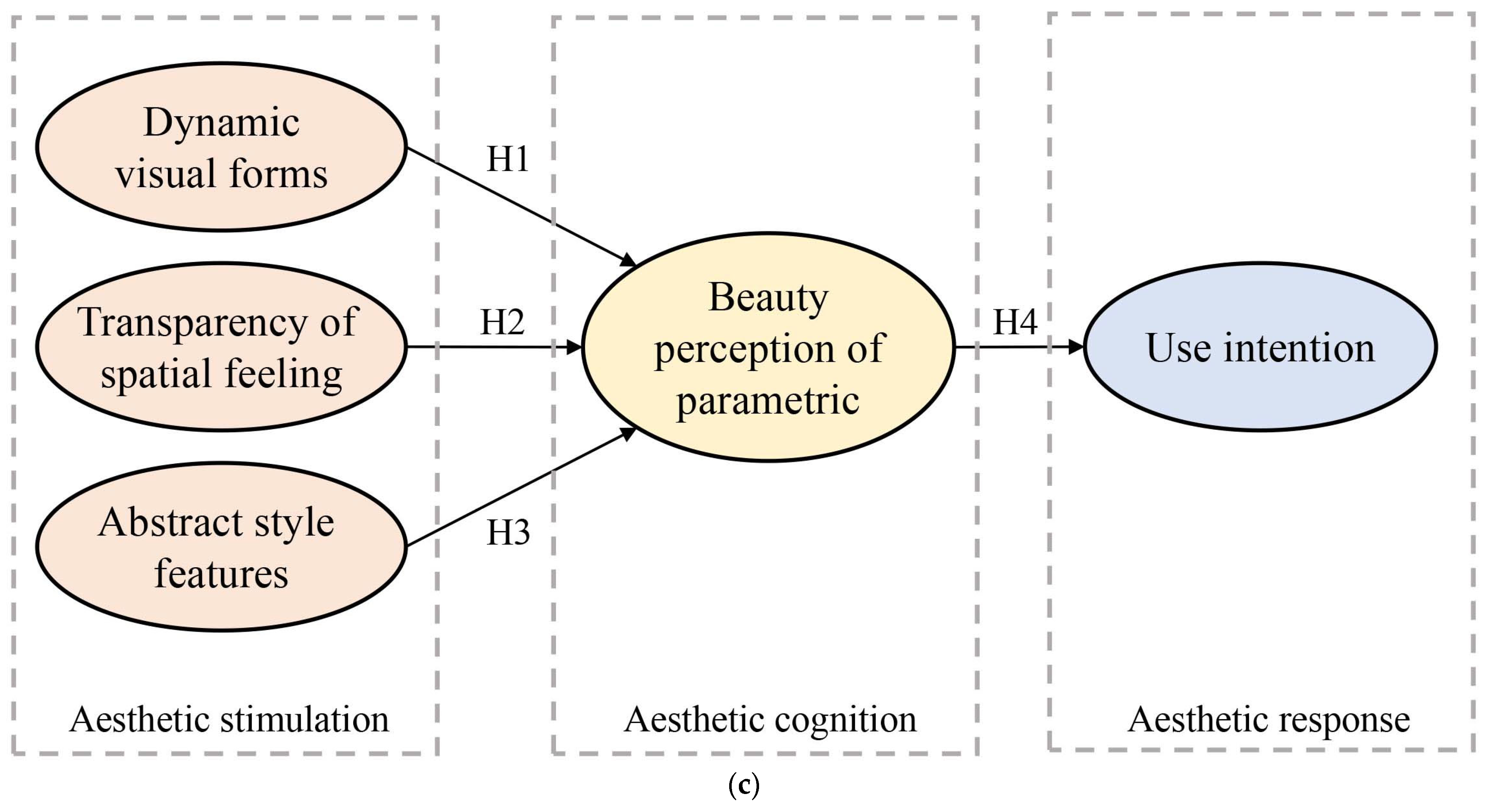
Based on the Structural Equation Model analysis results (Table 9 and Figure 13), all research hypotheses were supported. Dynamic visual forms (β = 0.27, p < 0.001), transparency of spatial feeling (β = 0.211, p < 0.05), and abstract style features (β = 0.192, p < 0.05), all had a significant positive impact on beauty perception of the parametric design. Beauty perception of parametric design (β = 0.29, p < 0.001) can influence the public’s use intention. The results of path analysis indicate that dynamic visual forms, transparency of spatial feeling, and the abstract style features of landscape facilities design are significant influencing factors for beauty perception of parametric design. In the degree of influence, dynamic visual forms are greater than transparency of spatial feeling than the abstract style features. Additionally, beauty perception of parametric design significantly influences the public’s use intention for landscape facilities (β = 0.29, p < 0.001), this indicates that parametric landscape facilities design has a distinctive and novel beauty effect. Compared with other ordinary landscape facilities, it has a unique appeal to the public.

We mediated the effect analysis of the model using the Bootstrap method in AMOS 24.0 software. In this study, the bias-corrected percentile bootstrap method (Bootstrap = 5000) was used to analyze the mediating effect of beauty perception of parametric design between the aesthetic stimulation and the use intention of public. The bootstrap 95% confidence interval does not include 0, indicating that beauty perception of parametric design has a significant mediating effect. The analysis results are shown in

Table 10. Mediating effect test results.

Path	Effect	Effect Size	S.E.	p-Value	Bootstrap 95%CI
					LB	UB
Dynamic visual forms → Beauty perception of parametric design → Use intention	Total Effect	0.078	0.037	0.002	0.022	0.172
	Direct Effect	0.000	0.000	***	0.000	0.000
	Indirect Effect	0.078	0.037	0.002	0.012	0.172
Transparency of spatial feeling → Beauty perception of parametric design → Use intention	Total Effect	0.061	0.029	0.010	0.015	0.133
	Direct Effect	0.000	0.000	***	0.000	0.000
	Indirect Effect	0.061	0.029	0.010	0.015	0.133
Abstract style features → Beauty perception of parametric design → Use intention	Total Effect	0.056	0.032	0.017	0.008	0.136
	Direct Effect	0.000	0.000	***	0.000	0.000
	Indirect Effect	0.056	0.032	0.017	0.008	0.136

Note: *** indicates p < 0.001.

.

To sum up, the four hypotheses proposed in this study are all supported, indicating that the theoretical model constructed can explain the aesthetic cognition mechanism for parametric landscape facilities design.

Firstly, the significance of H1, H2, and H3 (p < 0.05) is supported, which indicates that the aesthetic cognition of landscape facilities is the comprehensive response of users to various beauty stimulus, and these stimulus come from the visual, spatial, and style levels of the facilities. The dynamic visual forms (β = 0.27), transparency of spatial feeling (β = 0.211), and the abstract style features (0.192) will significantly positively influence the public’s beauty perception of parametric design. The aesthetic of landscape facilities design is a complex of visual, spatial, and style, and the dynamic visual effects, transparency of spatial feeling, and abstract style are the key factors for beauty perception of parametric design. In the degree of influence, the perceived influence of dynamic visual forms, transparency of spatial feeling, and the abstract style features on parametric beauty has gradually decreased. This indicates that the dynamic combination of constantly changing shapes, the changing hollowed-out space and the simple geometric style are important factor for aesthetic cognition of parametric landscape facilities design.

Secondly, it is assumed that the significance of H4 (p < 0.001) is supported, which indicates that the beauty perception of parametric design of landscape facilities has a positive impact on the public’s use intention (β = 0.29), and landscape facilities with beauty perception of parametric design can promote the public’s active use of landscape facilities. This indicates that the public considers parametric landscape facilities design to be more attractive compared to other ordinary landscape facilities.

Thirdly, beauty perception of parametric design plays an important mediating role in the public’s willingness to use landscape facilities. Beauty perception of parametric design plays a complete mediating role between various aesthetic stimuli and the public’s usage intentions. This indicates that dynamic visual effects, transparency of spatial feeling, and abstract art styles need to be combined with each other and make the public perceive beauty of parametric landscape facilities, at the same time, this kind of distinctive beauty sense is attractive to the general public.

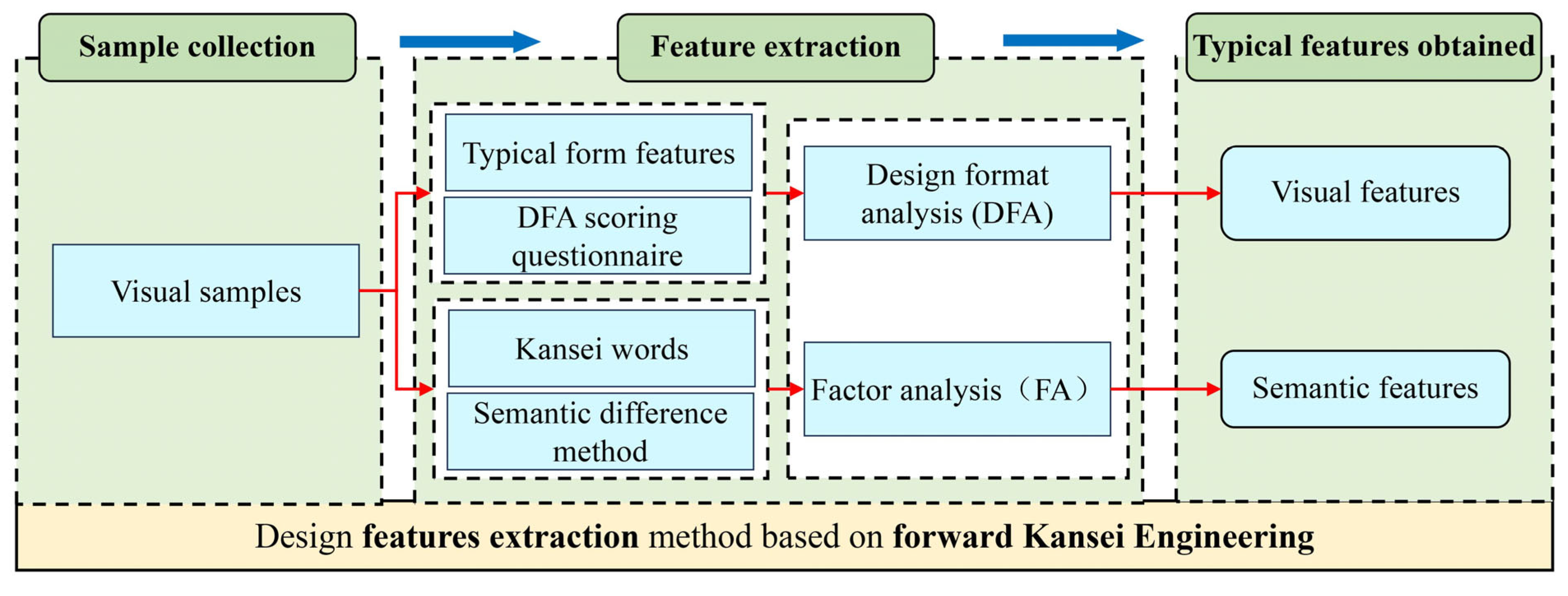
3.2. Design Feature Extraction Based on Forward Kansei Engineering

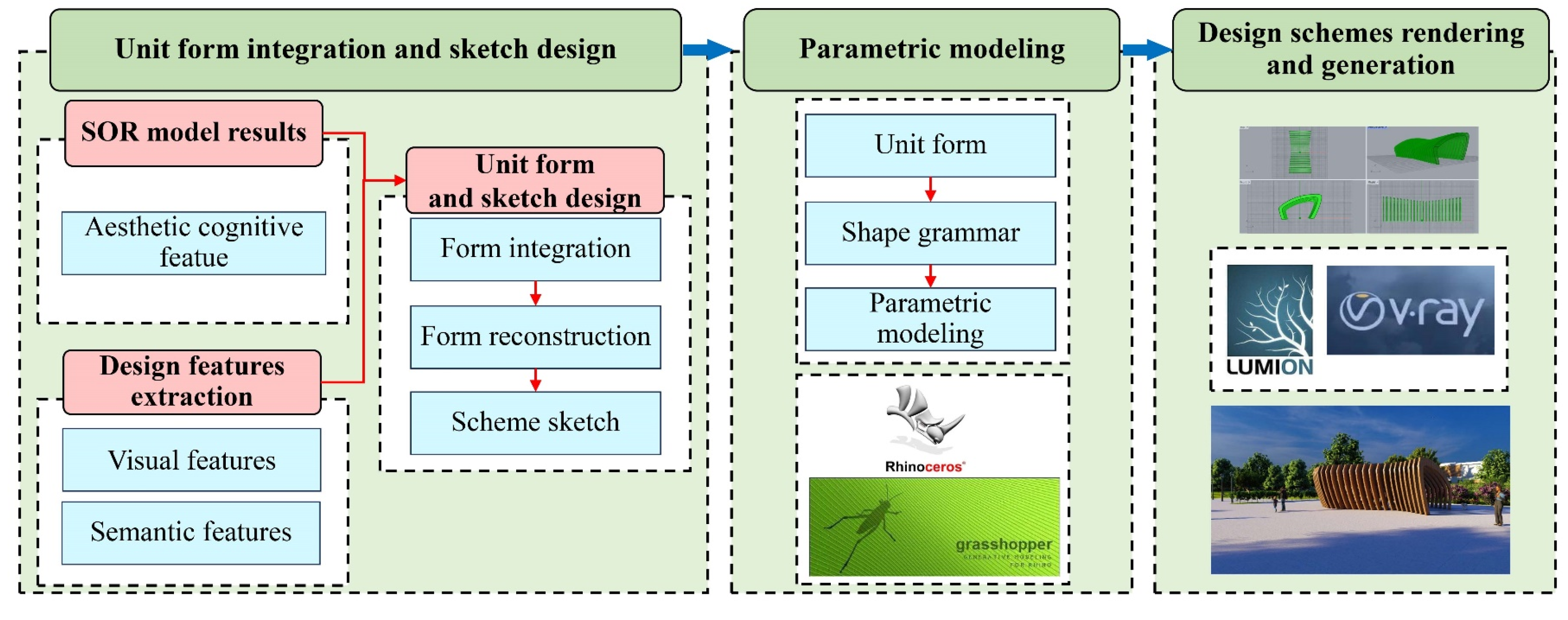
This section is based on analysis results of aesthetic cognition, forward Kansei Engineering is used to extract design features, providing a reference for parametric modeling and design.

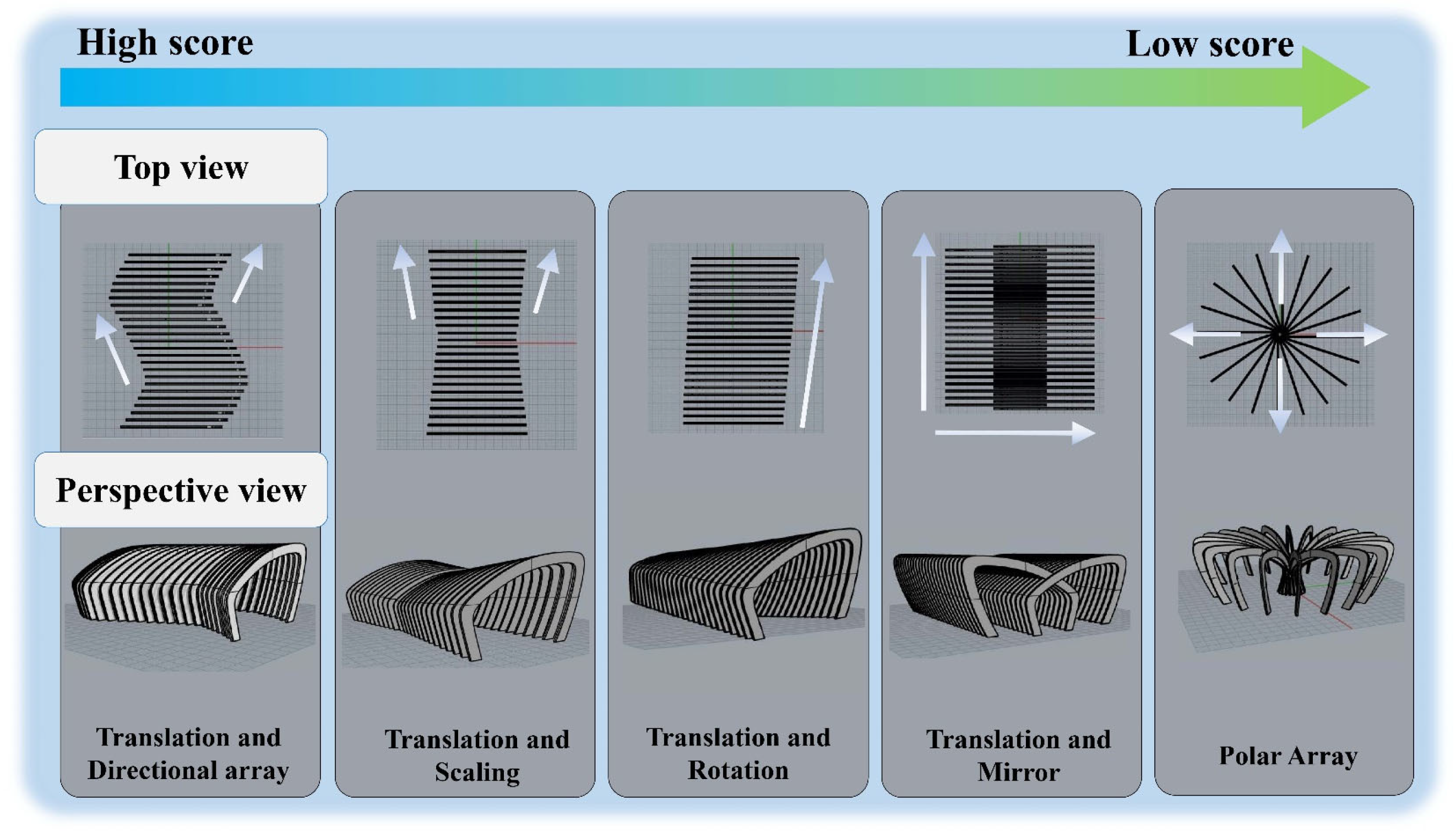
Firstly, based on the analysis results of the SOR model in the previous text, select relatively abstract visual image samples with a dynamic feel. In this study, we select flowers and plants as the sources of visual samples. After screening and comparison, the visual samples that were unclear and had low recognition were removed, nine visual samples (L1–L9) were selected, as shown in Figure 14.

Secondly, and through the analysis of the form features of the visual samples, the form features collection (M1–M6) were extracted, respectively, from the arc shape and the turning shape, as shown in Figure 15.

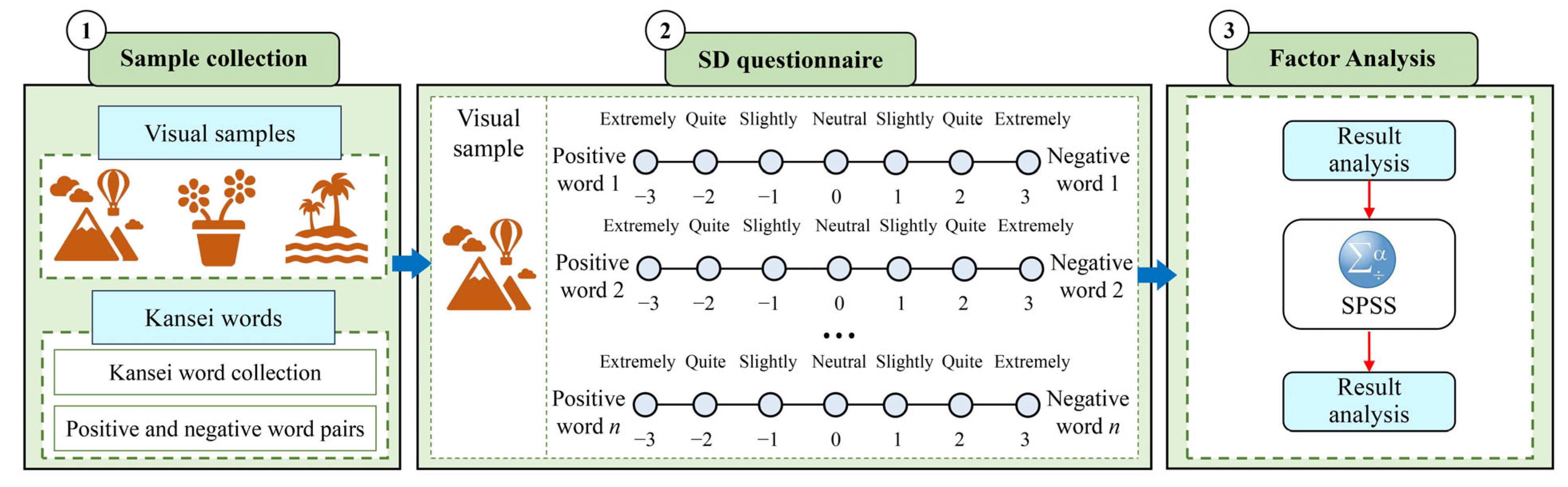
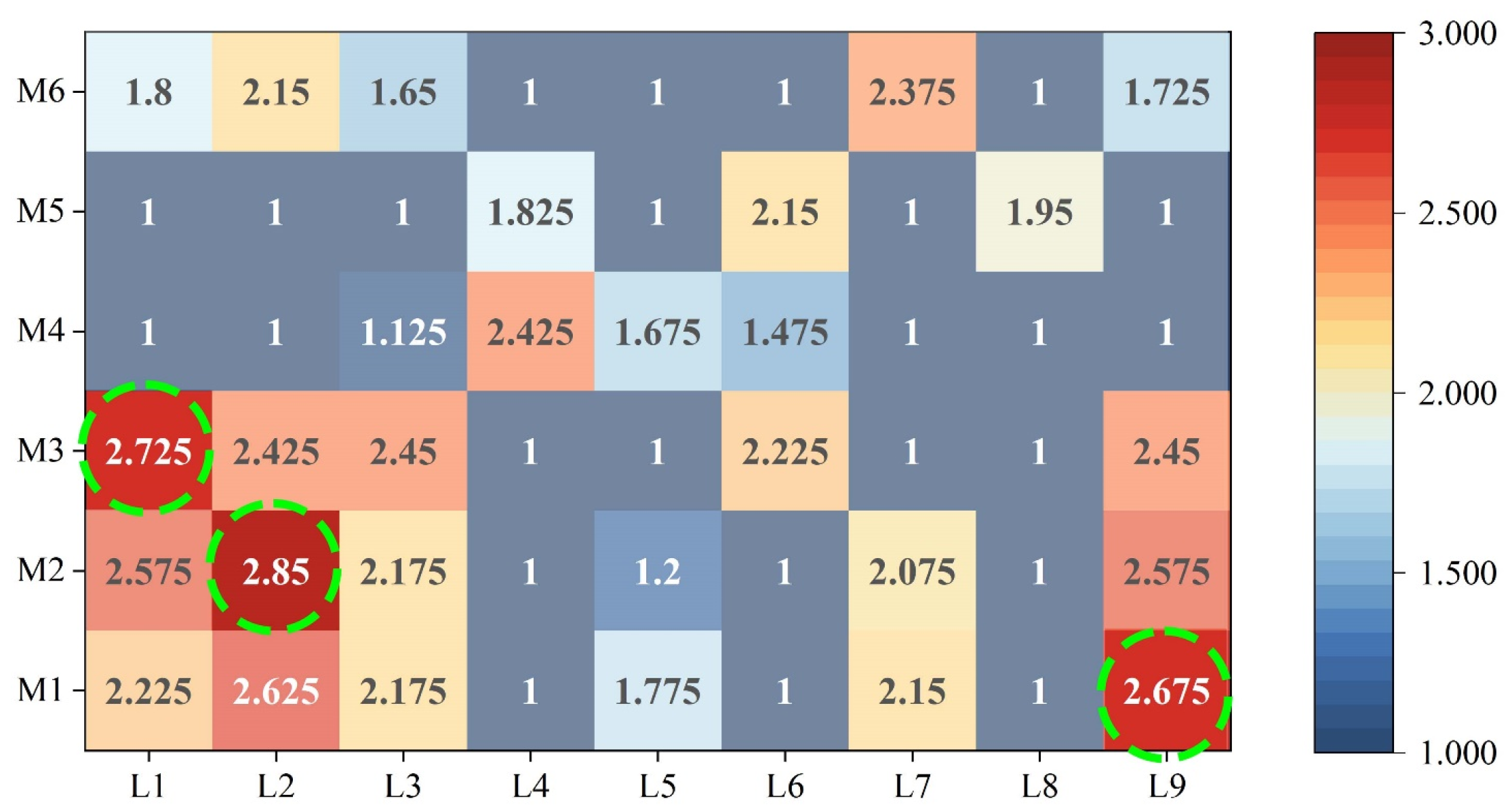
The DFA method is used to extract the typical form features of visual samples. Typical visual features were obtained by scoring the degree of association between nine samples (Figure 14L1–L9) and six form features (Figure 15M1–M6), and the scoring was conducted using a questionnaire. The scale is 1–3 point, higher scores indicate strong correlation of corresponding features.

All subjects are 80 adults who have normal vision and no color deficiencies, and can understand the content and purpose of the questionnaire. Among them, there are 42 males and 38 females, 57 from art and design majors, and 23 from non-art and design majors. A total of 80 valid questionnaires were retrieved, and the effective recovery rate of the questionnaires was 100%. Equation (1) was used to calculate the questionnaire scores, the results are presented in

Table 11. The average score of DFA.

	L1	L2	L3	L4	L5	L6	L7	L8	L9	T 1
M1	2.225	2.625	2.175	1.000	1.775	1.000	2.150	1.000	2.675	16.625
M2	2.575	2.850	2.175	1.000	1.200	1.000	2.075	1.000	2.575	16.450
M3	2.725	2.425	2.450	1.000	1.000	2.225	1.000	1.000	2.450	16.275
M4	1.000	1.000	1.125	2.425	1.675	1.475	1.000	1.000	1.000	11.700
M5	1.000	1.000	1.000	1.825	1.000	2.150	1.000	1.950	1.000	11.925
M6	1.800	2.150	1.650	1.000	1.000	1.000	2.375	1.000	1.725	13.700
T 2	11.325	12.050	10.575	8.250	7.650	8.850	9.600	6.950	11.425

. T1 is the total score of six typical form features (M1–M6), T2 is the total score of nine visual samples (L1–L9).

According to Table 11, at the visual-sample level, the ranking is L2 > L9 > L1> L3 > L7 > L6 > L4> L5 > L8. In the form feature level, M1 >M2 > M3> M6> M5> M4. In this study, we select the top three feature elements as typical features. L1, L2, and L9 were selected as representative visual samples, and M1, M2, and M3 as representative form features, as shown in Figure 16.

Thirdly, the implicit semantic features of flowers and plants were extracted using Factor Analysis (FA). Representative adjectives were selected based on the literature on landscape aesthetic design [65,66,67]. These adjectives were used to constitute positive-inverse phrases, which can be used as Kansei word group, as shown in

Table 12. Kansei word group.

Number	Kansei Word Group	Number	Kansei Word Group
S1	Flow-Static	S5	Exquisite-Rough
S2	Lively-Dull	S6	Soft-Stiff
S3	Elegant-Vulgar	S7	Simple-Complex
S4	Kind-Cold	S8	Fresh-Stale

.

The matching degree between eight Kansei word groups and nine visual samples was measured by a 7-point Likert scale (scale: −3 to 3) via a questionnaire administered to 80 subjects (the composition of the subjects was the same as that of the DFA experiment), the example of Kansei word groups questionnaire is shown in

Table 13. The example of Kansei word groups questionnaire.

Kansei Words	−3	−2	−1	0	1	2	3	Kansei Words
	Extremely	Quite	Slightly	Neutral	Slightly	Quite	Extremely
S1 Flow								Static
S2 Lively								Dull
S3 Elegant								Vulgar
S4 Kind								Cold
S5 Exquisite								Rough
S6 Soft								Stiff
S7 Simple								Complex
S8 Fresh								Stale

.

The effective recovery rate of the questionnaires was 100%, and the mean values of the questionnaire score results are shown in

Table 14. The average score of questionnaire score.

	S1	S2	S3	S4	S5	S6	S7	S8
L1	−2.225	−2.550	−2.850	−2.700	−2.650	−2.900	1.250	−2.650
L2	−2.675	−2.875	−2.925	−2.800	−2.900	−2.825	−2.225	−2.675
L3	−2.350	−2.600	−2.625	2.650	−2.850	−2.800	−2.150	−2.550
L4	−0.950	−1.050	−0.050	−0.450	−0.575	2.150	2.250	1.350
L5	−2.825	−2.250	−2.200	−1.300	−1.650	−2.150	−2.325	−2.625
L6	−2.125	0.375	0.325	0.550	1.650	2.550	1.450	−1.575
L7	−2.650	−2.625	−2.650	−2.750	−2.250	−2.550	−2.625	−2.725
L8	−2.225	1.250	1.225	1.350	1.850	2.650	0.225	−1.150
L9	−2.250	−2.625	−2.600	−2.750	−2.725	−2.450	−2.150	−2.525

.

The questionnaire data were imported into SPSS 22 for Factor Analysis. The Cronbach’s α was 0.922, which indicates that the questionnaire has good reliability. The KMO value was 0.547, and Bartlett’s test yielded 0.000, (<1%), indicating that the data were suitable for Factor Analysis. The total variance explained are presented in

Table 15. Total variance explained.

Components	Initial Eigenvalue			Extract the Sum of Squares of Loads			The sum of the Squares of Rotating Loads
	Total	Percentage of Variance	Accumulate%	Total	Percentage of Variance	Accumulate%	Total	Percentage of Variance	Accumulate%
1	5.671	70.891	70.891	5.671	70.891	70.891	3.913	48.912	48.912
2	1.347	16.834	87.725	1.347	16.834	87.725	3.105	38.813	87.725
3	0.650	8.125	95.850
4	0.281	3.514	99.364
5	0.032	0.395	99.758
6	0.017	0.210	99.969
7	0.002	0.030	99.999
8	0.000	0.001	100.000

.

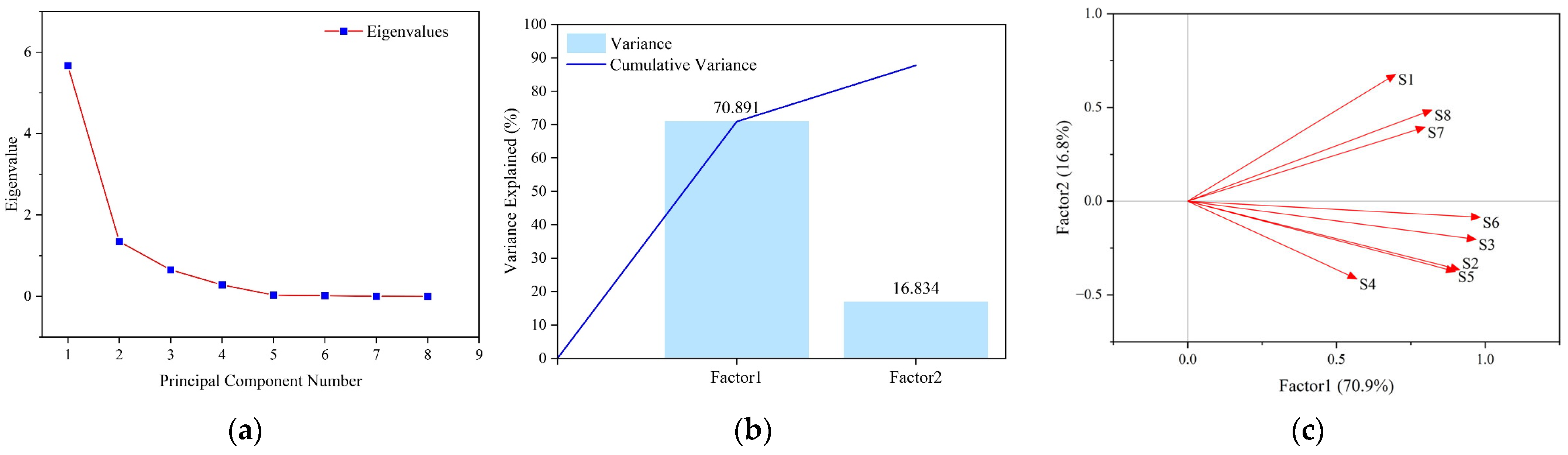
The results of FA are shown in Figure 17. In Figure 17a, the second factor begins to stabilize. In Figure 17b, the first two factors can explain most of the data of the variable. In Figure 17c, the composition of the two factors can be obtained.

The first two factors explain 87.725% of the total variable, so the number of extracted factors was set to two, which can explain most of the information about the variable. The factors were rotated with the maximum variance method, and factor classification of Kansei word groups is according to the absolute value of rotated component matrix; the rotated component matrix is shown in

Table 16. Rotated component matrix.

	Main Ingredient
	Factor 1	Factor 2	Factor Meaning
S2	0.937	0.301	Elegance and affinity
S3	0.877	0.461
S4	0.702	0.043
S5	0.932	0.285
S6	0.811	0.561
S1	0.106	0.968	Flowing simple style
S7	0.363	0.813
S8	0.322	0.898

.

Factor 1 consisted of S2 (lively-dull), S3 (elegant-vulgar), S4 (kind-cold), S5 (exquisite-rough), and S6 (soft-stiff), named the emotional factor, which mainly reflect elegance and affinity of visual samples.

Factor 2 consisted of S1 (flow-static), S7 (simple-complex), and S8 (fresh-stale), named the style factor, which mainly reflects flowing simple style of visual samples.

In conclusion, the semantic features are mainly reflected in the emotional features of elegance and affinity, and it embodies a simple and fluid artistic style.

3.3. Parametric Modeling and Design

This section is based on the design features extracted from forward Kansei Engineering and analysis results of the SOR model, combined with shape grammar rules for parametric modeling and design.

Firstly, the unit forms of aesthetic design were obtained by integrating and reconstructing the typical form features (L1, L2, L9 and M1, M2, M3) and the two factors extracted. Secondly, through the analysis of the unit form, combined with shape grammar to draw the scheme sketch. Thirdly, parametric modeling was carried out in Grasshopper package to create the design scheme. The process is shown in Figure 18.

In this study, we propose five schemes of shape change rules, and each scheme is a combination of two shape change rules, including (1) translation and scaling, (2) translation and rotation, (3) translation and mirror, (4) polar array, and (5) translation and directional array. On the basis of parametric modeling, Lumion 12.0 was applied to render the model and the effect diagram was generated (scheme T1–T5). The five of shape change combinations, Grasshopper commands, and design renderings are shown in

Table 17. Parameterized grammatical representation of shape grammars.

Scheme	Shape Change Combinations	Grasshopper Command Example	Command Explanation	Design Renderings
T1	Translation and Scaling		Firstly, the unit form is translated by 4 unit vectors along the Y-axis. Secondly, among the unit forms, 13 are reduced by a coefficient of 0.98, and 11 are enlarged by a coefficient of 1.02.
T2	Translation and Rotation		Firstly, the unit form is translated by 4 unit vectors along the Y-axis. Secondly, rotate the unit form in the X-Z plane by −0.05° for 24 rotations.
T3	Translation and Mirror		Firstly, the unit form is translated by 2 unit vectors along the Y-axis. Secondly, a total of 24 sets of mirror command were carried out in the Y-Z plane.
T4	Polar Array		Arrange the unit form in a polar array of 30 in the X-Y plane.
T5	Translation and Directional array		The unit forms are arranged in a directional array in the X-Y plane according to the S form, with an offset of 3 unit vectors on the X-axis and 4 unit vectors on the Y-axis.

.

3.4. Evaluation of Design Schemes Based on Backward Kansei Engineering

In this section, based on the scheme creation of parametric design, five design schemes were evaluated using backward Kansei Engineering. The beauty sense data of different design schemes were further analyzed to verify the aesthetic quality of the design schemes.

Firstly, the weights of aesthetic indicators are calculated by using the AHP. Based on Equations (3)–(9), combined with the evaluation indicators of landscape facilities design, this study invited 10 experts to score each indicator, the expert group comes from both theoretical research and design practice fields, including doctor and associate professor in landscape and product design, as well as designers with over 5 years of experience in landscape design. This composition makes the results of the questionnaire data balanced and objective.

Take Expert 1 as an example. The judgment matrix A1 of j based on expert scores is as follows:

$$A_1=\left[\begin{array}{ccc}1& 1/5& 1/7\\ 5& 1& 1/3\\ 7& 3& 1\end{array}\right]$$

The results of the AHP are shown in

Table 18. The judgment matrix and weight value of the A level.

A	A1	A2	A3	ω (A)	λmax	CI	CR
A1	1	0.22	0.138	0.0751	3.032	0.016	0.031
A2	4.544	1	0.366	0.2837
A3	7.260	2.734	1	0.6412

,

Table 19. The judgment matrix and weight value of the B level.

B	B1	B2	B3	ω (B)	λmax	CI	CR
B1	1	0.289	0.179	0.0952	3.042	0.021	0.040
B2	3.464	1	0.338	0.2676
B3	5.578	2.961	1	0.6371

,

Table 20. The judgment matrix and weight value of the C level.

C	C1	C2	C3	ω (C)	λmax	CI	CR
C1	1	0.461	0.244	0.1338	3.01	0.005	0.009
C2	2.169	1	0.392	0.2624
C3	4.102	2.551	1	0.6038

and

Table 21. The judgment matrix and weight value of the first level.

	A	B	C	ω (T)	λmax	CI	CR
A	1	0.847	1.302	0.1338	3.034	0.017	0.033
B	1.180	1	0.882	0.2624
C	0.768	1.134	1	0.6038

.

The calculation results satisfy the criterion CR < 0.1 in Table 18, Table 19, Table 20 and Table 21. This indicates that the consistency of the judgment matrix passes the test. The overall weight can be obtained by multiplying the first-level index weight and the second-level index weight. The weight analysis of evaluation indicators of color design is shown in

Table 22. AHP weight result.

First-Level Indicators	Weight (W1)	Sorting	Second-Level Indicators	Weights (W2)	Sorting	Overall Weights (W3)	Sorting
A	0.3441	1	A1	0.0751	3	0.0258	9
			A2	0.2837	2	0.0976	4
			A3	0.6412	1	0.2206	1
B	0.3375	2	B1	0.0952	3	0.0321	8
			B2	0.2676	2	0.0903	5
			B3	0.6371	1	0.2150	2
C	0.3183	3	C1	0.1338	3	0.0426	7
			C2	0.2624	2	0.0835	6
			C3	0.6038	1	0.1922	3

.

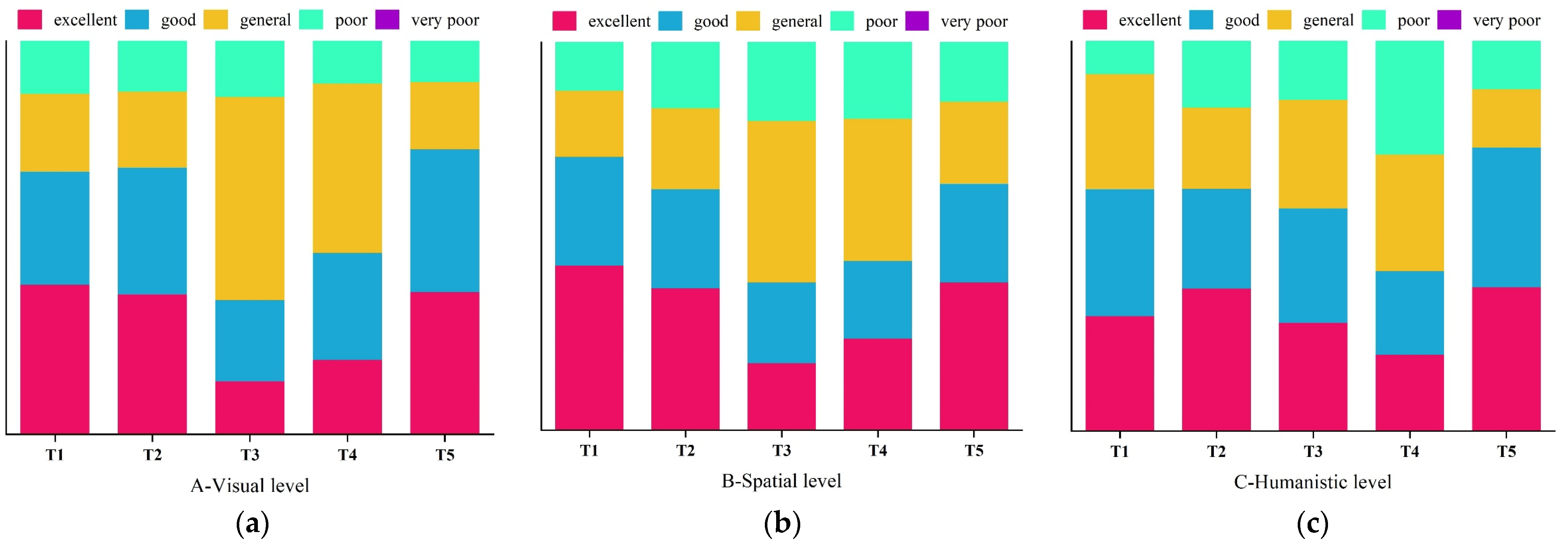
AHP-FCE is used to evaluate the design scheme. The evaluation is divided into five levels: excellent, good, general, poor, and very poor. The purpose of AHP-FCE is to evaluate the beauty sense of five design schemes for the general public. Therefore, the subjects are all randomly selected 50 from the general public and urban residents (in order to ensure that the questionnaire was valid, all participants were adults). Each participant selected the grades of each indicator of the five design schemes (T1–T5), respectively.

The weighted average algorithm M(·, +) is used to calculate the membership degree of the first level. The calculation method is Equations (12) and (13). The excellent, good, general, poor, and very poor membership of first-level indicator levels A (X_1a), B (X_1b), and C (X_1c) of design scheme T1 can be calculated.

$$X_{1\mathrm{a}}=W\times R_{1\mathrm{a}}=(0.0258, 0.0976, 0.2206)\bullet \left[\begin{array}{lllll}0.22& 0.24& 0.42& 0.12& 0\\ 0.38& 0.32& 0.18& 0.12& 0\\ 0.42& 0.26& 0.18& 0.14& 0\end{array}\right]=(0.3808, 0.2883, 0.1980, 0.1328, 0)$$

$$X_{1\mathrm{b}}=W\times R_{1\mathrm{b}}=(0.0321, 0.0903, 0.2150)\bullet \left[\begin{array}{lllll}0.36& 0.26& 0.22& 0.16& 0\\ 0.46& 0.24& 0.18& 0.12& 0\\ 0.44& 0.28& 0.16& 0.12& 0\end{array}\right]=(0.4250, 0.2801, 0.1711, 0.1238, 0)$$

$$X_{1\mathrm{c}}=W\times R_{1\mathrm{c}}=(0.0321, 0.0903, 0.2150)\bullet \left[\begin{array}{lllll}0.24& 0.26& 0.28& 0.22& 0\\ 0.36& 0.28& 0.2& 0.16& 0\\ 0.28& 0.36& 0.34& 0.02& 0\end{array}\right]=(0.2956, 0.3256, 0.2952, 0.0835, 0)$$

By the same method, the excellent, good, general, poor, and very poor membership of the first-level indicator of scheme T2–T5 can be calculated.

The excellent, good, general, poor, and very poor membership of first-level indicator for scheme T2 are as follows.

$$X_{2\mathrm{a}}=W\times R_{2\mathrm{a}}=(0.3567, 0.3227, 0.1932, 0.1275, 0)$$

$$X_{2\mathrm{b}}=W\times R_{2\mathrm{b}}=(0.3664, 0.2555, 0.2086, 0.1694, 0)$$

$$X_{2\mathrm{c}}=W\times R_{2\mathrm{c}}=(0.3460, 0.2951, 0.2496, 0.1092, 0)$$

The excellent, good, general, poor, and very poor membership of the first-level indicator for scheme T3 are as follows.

$$X_{3\mathrm{a}}=W\times R_{3\mathrm{a}}=(0.1356, 0.2067, 0.5166, 0.1410, 0)$$

$$X_{3\mathrm{b}}=W\times R_{3\mathrm{b}}=(0.1734, 0.2085, 0.4163, 0.2018, 0)$$

$$X_{3\mathrm{c}}=W\times R_{3\mathrm{c}}=(0.2787, 0.2936, 0.2784, 0.1494, 0)$$

The excellent, good, general, poor, and very poor membership of the first-level indicator for scheme T4 are as follows.

$$X_{4\mathrm{a}}=W\times R_{4\mathrm{a}}=(0.1902, 0.2717, 0.4310, 0.1072, 0)$$

$$X_{4\mathrm{b}}=W\times R_{4\mathrm{b}}=(0.2368, 0.2002, 0.3667, 0.1963, 0)$$

$$X_{4\mathrm{c}}=W\times R_{4\mathrm{c}}=(0.1966, 0.2142, 0.2994, 0.2898, 0)$$

The excellent, good, general, poor, and very poor membership of the first-level indicator for scheme T5 are as follows.

$$X_{5\mathrm{a}}=W\times R_{5\mathrm{a}}=(0.3627, 0.3627, 0.1717, 0.1030, 0)$$

$$X_{5\mathrm{b}}=W\times R_{5\mathrm{b}}=(0.3814, 0.2549, 0.2112, 0.1525, 0)$$

$$X_{5\mathrm{c}}=W\times R_{5\mathrm{c}}=(0.3697, 0.3587, 0.1491, 0.1225, 0)$$

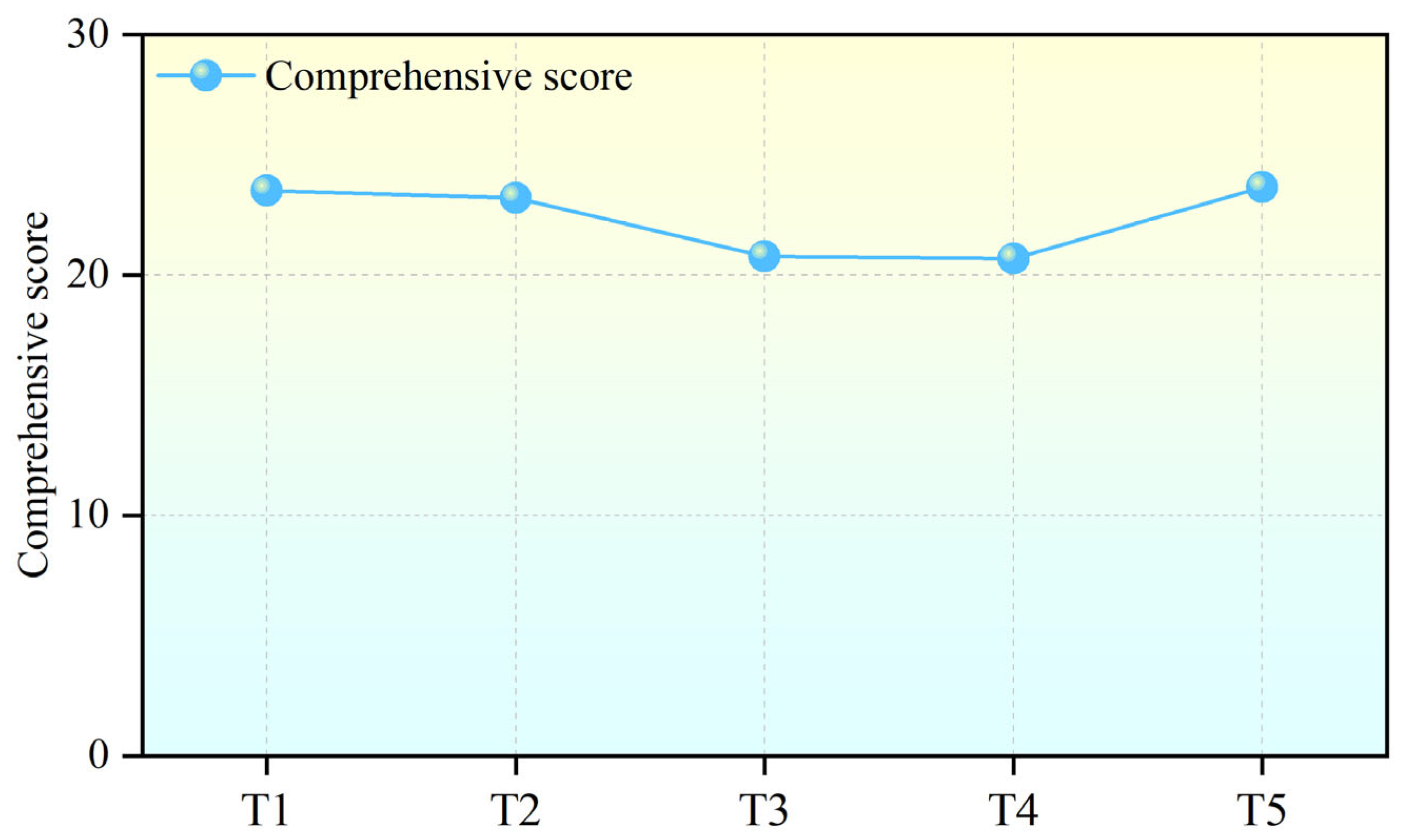
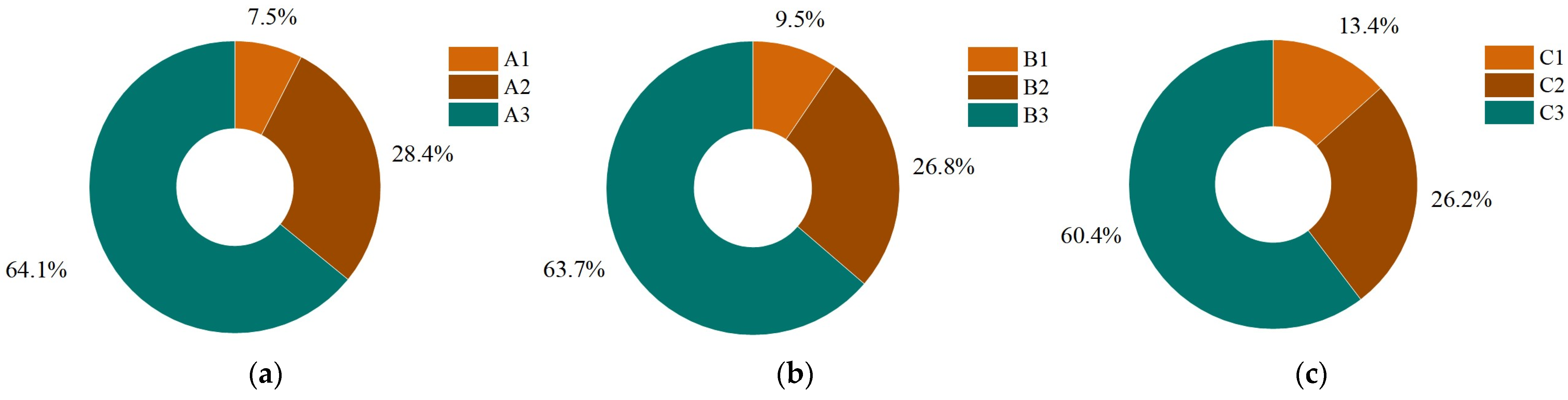
Based on the calculation results of the membership degree, the comprehensive scores of each design scheme can be calculated as according to Equation (14). The calculation process of scheme T1 is as follows.

$$Y_{1\mathrm{a}}=X_{1\mathrm{a}}\times V=0.3808\times 10+0.2883\times 8+0.1980\times 6+0.1328\times 4=7.8336$$

$$Y_{1\mathrm{b}}=X_{1\mathrm{b}}\times V=0.4250\times 10+0.2801\times 8+0.1711\times 6+0.1238\times 4=8.0126$$

$$Y_{1\mathrm{c}}=X_{1\mathrm{c}}\times V=0.2956\times 10+0.3256\times 8+0.2952\times 6+0.0835\times 4=7.666$$

$$Y_1=Y_{1\mathrm{a}}+Y_{1\mathrm{b}}+Y_{1\mathrm{c}}=7.8336+8.0126+7.666=23.5122$$

By using the same method, the comprehensive score of the five design schemes are shown in

Table 23. The comprehensive score of the five schemes.

Scheme No.	T1	T2	T3	T4	T5
Score	23.5122	23.2102	20.784	20.6806	23.6524

.

4. Results and Discussion

The effectiveness of this method was verified through design cases, and the comprehensive score of the five schemes based on Table 23 is shown in Figure 19. The ranking of comprehensive score is T5 > T1 > T2 > T3 > T4.

The schemes T1, T2, and T5 have relatively high total scores, among which scheme T5 has the highest score and can be regarded as the preferred scheme.

To further analyze the aesthetic features of five different design schemes, through the analysis of the membership degree of five schemes in the first-level indicator, the excellent membership of schemes T1, T2, and T5 in visual, spatial, and humanistic levels are relatively high, as shown in Figure 20.

This indicates that the aesthetic of dynamic shape change combinations such as scaling, rotation, and regular direction arrays is better in the visual, spatial, and humanistic levels. In the explicit level, a combination of unit forms with a series of regular shapes and size variations, rotations, and arrangements can be the preferred option for design creation. In the implicit level, this combination of forms has stronger cultural recognition, symbolic meaning, and modern beauty sense.

This research reveals the aesthetic cognitive mechanism for parametric landscape facilities and constructs a design method, this method has excellent operability and can evaluate and optimize the design scheme.

Firstly, in the research on the aesthetic cognitive mechanism of parametric design. Compared with previous study [38,68,69], this study analyzed parametric design from the perspective of aesthetic cognition, and took parametric landscape facilities as the object to explore the aesthetic cognitive features for this specific design object, further enriching the theoretical system of parametric design.

In this study, the SOR model elucidates the aesthetic cognitive mechanism for parametric landscape facilities. Dynamic visual forms, transparency of spatial feeling, and abstract style features are the principal drivers of this perception. Beauty perception of parametric design fully mediates the relationship between aesthetic stimuli and the public’s intention to use the facilities, consequently, parametric landscape facilities are more appealing to general public.

Based on the analysis of the numerical values of standardized regression weights, the path coefficient of dynamic visual forms is greater than transparency of spatial feeling and greater than abstract style features in perceptual stimulation. This indicates that the influence degrees of visual stimulation, spatial stimulation, and artistic style stimulation on beauty perception of parametric design weaken successively. Among these stimulation, dynamic visual forms is the most critical factor influencing the beauty perception of parametric design. In the visual level, orderly and continuous undulating wave shape combinations are the key to parametric landscape facilities design. In the level of spatial perception, regular and gradually changing hollow spatial feeling can significantly influence the beauty perception of parametric design. In the style level, the repetitive expression style of abstraction and simplicity has a significant influence on parametric design. The dynamic form is closely related to the transparency of space and the abstract style. This continuous difference in the changing form is the key to parametric aesthetic design. A schematic of this cognitive mechanism is presented in Figure 21.

In parametric modeling, the variation rules of shape grammars have an intrinsic connection with aesthetics. The top view and perspective view analysis of the shape grammar of the five design schemes are shown in Figure 22. Among various combinations of shaped grammars, the beauty sense of continuous differential changes in shape with more than two directions (direction array, scaling, rotation) is superior to that of symmetrical changes (mirror image and circular array). This indicates that the beauty of the form moving in multiple directions on the plane, the regular scale changes in the form, and the regular rotation of the form is better. The beauty sense of mirror and a circular array is average.

Secondly, this study established an positivist aesthetic design method for parametric landscape facilities based on hybrid Kansei Engineering. Previous research on landscape aesthetic design methods was based on the subjective experience of designers [70], and aesthetic design suggestions were obtained through the discussion and analysis of design cases [71,72]. Forward Kansei Engineering can effectively extract the explicit and implicit features of aesthetic elements, which can be used as a reference for the creation of design schemes. Backward Kansei Engineering can analyze the beauty sense data of different design schemes.

Compared with previous aesthetic research [73,74,75], this study focuses on the quantitative analysis of beauty sense. The chord diagram of the weight value for the aesthetic indicators is shown in Figure 23. The gaps among the first-level indicators are not significant, this indicates that the aesthetic cognition of landscape facilities is an integration of vision, space, and humanity, and the three are interrelated. The gaps among the second-level indicators are significant, which indicates that the weights of aesthetic indicators in the visual, spatial, and humanistic levels are significantly different.

The weight analysis of aesthetic indicators by the AHP is shown in Figure 24. In the weight of visual level, the overall form is the most important, which indicates that compared with the form combination and decorative elements, the overall visual effect has a strong impact on the aesthetic effect of landscape facilities.

In the weight of spatial level, the spatial harmony is the most important. This indicates that the design of landscape facilities needs to reflect the beauty sense of harmony.

In the weight of humanistic level, the modern trend is the most important, which indicates that compared with cultural feature and symbolic meanings, the trend of modern aesthetics is more important to the aesthetic cognition of the general public.

Thirdly, the study also has some limitations. This research only takes the type of landscape corridor facilities as an example, and the design case is only five shape grammar combinations. More combinations of shape grammars can be adopted to analyze the beauty sense of different parametric designs. The data source for this research is based on a single questionnaire survey, and other experimental equipment can also be used to obtain data for aesthetic measurement.

5. Conclusions

This study reveals the aesthetic cognitive mechanism of parametric landscape facilities by using the SOR model, the three main influencing factors were obtained—dynamic visual forms, transparency of spatial feeling, and abstract style features, which provided guidance for design creation. On this basis, a parametric landscape facilities aesthetic design method based on hybrid Kansei Engineering was constructed, taking the landscape corridor as a case to illustrate this method. This research can provide a reference for parametric landscape facilities design.

(1)

In the research of parametric design theory, aesthetic cognition of landscape facilities is primarily driven by three factors—dynamic visual forms, transparency of spatial feeling and abstract style features. Each of these stimuli exerts a significant positive effect on the beauty perception of parametric design. Moreover, the beauty perception of parametric design fully mediates the relationship between aesthetic stimuli and the public’s intention to use the facilities, indicating that users are more inclined to engage with landscape installations; parametric landscape facilities design is attractive to the general public compared to more ordinary landscape facilities

(2)

In the research of parametric design practice, this study established a positivist parametric landscape facilities design method. Based on aesthetic cognition analysis, hybrid Kansei Engineering can obtain more specific design features and evaluate the beauty sense of design schemes. In forward Kansei Engineering, DFA and FA can effectively obtain the explicit and implicit features, respectively. The combination of shape grammar and parametric modeling enables rapid generation of design schemes, reducing reliance on subjective experience. In backward Kansei Engineering, AHP-FCE can effectively evaluate design schemes and measure the beauty sense of different design schemes.

(3)

In future research, beauty data collection can combine questionnaires with emotional measurement equipment, some psychological equipment such as eye-tracking, and other methods. Other types of landscape facilities can be used as cases in the future. Meanwhile, the design scheme can be further improved in this study. Future research can explore more diverse combinations of shape grammars to demonstrate the parametric design effect.