Sustainable Optimization Design of Architectural Space Based on Visual Perception and Multi-Objective Decision Making
Abstract
1. Introduction
- (1)
- An evolutionary deep learning-based approach is proposed for extracting visual features from indoor architectural spaces. This approach integrates a multi-resolution visual information acquisition mechanism and applies linear filtering to enhance the quality of feature representation.
- (2)
- An improved entropy-weighted AHP model is introduced, which fuses data-driven objective weights with expert-informed subjective weights across hierarchical indicators. The final normalized weights yield a robust foundation for sustainable spatial evaluation.
2. Related Work
2.1. Visual Perception Techniques in Spatial Design
2.2. Multi-Objective Decision Frameworks
3. Methodology
3.1. Construction of Visual Information Collection Model
3.2. Implementation of Feature Extraction Based on Evolutionary Deep Learning
3.3. A Multi-Objective Decision-Making Method Based on Improved Entropy Weight Method
3.3.1. Entropy Weighting Method
3.3.2. Analytic Hierarchy Process
- Step 1: Define the overall objective of the system through analysis, and gather relevant decision-making information such as policies and strategic guidelines.
- Step 2: Structure the decision-related elements into hierarchical levels—goal, criteria, and alternatives—where each upper-level element serves as the criterion for evaluating the elements at the subsequent level.
- Step 3: Construct pairwise judgment matrices to compare the relative importance of elements within the same level with respect to an upper-level element.
- Step 4: Calculate the local weights of elements at each level and then synthesize these weights from top to bottom to obtain the overall weights of each indicator relative to the evaluation objective.
3.3.3. Improved AHP
| Algorithm 1: An improved AHP based on the entropy weight method | |
| Step 1: Assuming there are m upper level criteria and n sub criteria. Each upper criterion contains , , and to the nm sub criterion, with . The weight of the upper criterion obtained through the Analytic Hierarchy Process is represented as . The weights of each sub criterion are represented as . Step 2: The entropy weight method is used to obtain the weights of each criterion, which are expressed as: . Step 3: Weight of sub criteria Φ By integrating the weight A obtained from the entropy weight method, the comprehensive weight T of the sub criteria can be expressed as: , where: | |
| (23) | |
| Step 4: According to the correspondence between the sub criteria and the upper criteria, the comprehensive weights of the sub criteria can be re represented as: | |
| (24) | |
| Then, normalize the comprehensive weights of each sub criterion under each upper criterion: | |
| (25) | |
| where Step 5: Multiplying the upper criterion weight B with the obtained comprehensive weight can obtain the weight . | |
| (26) | |
| where Step 6: Represent as . Then normalize , we have: | |
| (27) | |
| where . | |
4. Experimental Results
4.1. Experimental Preparation
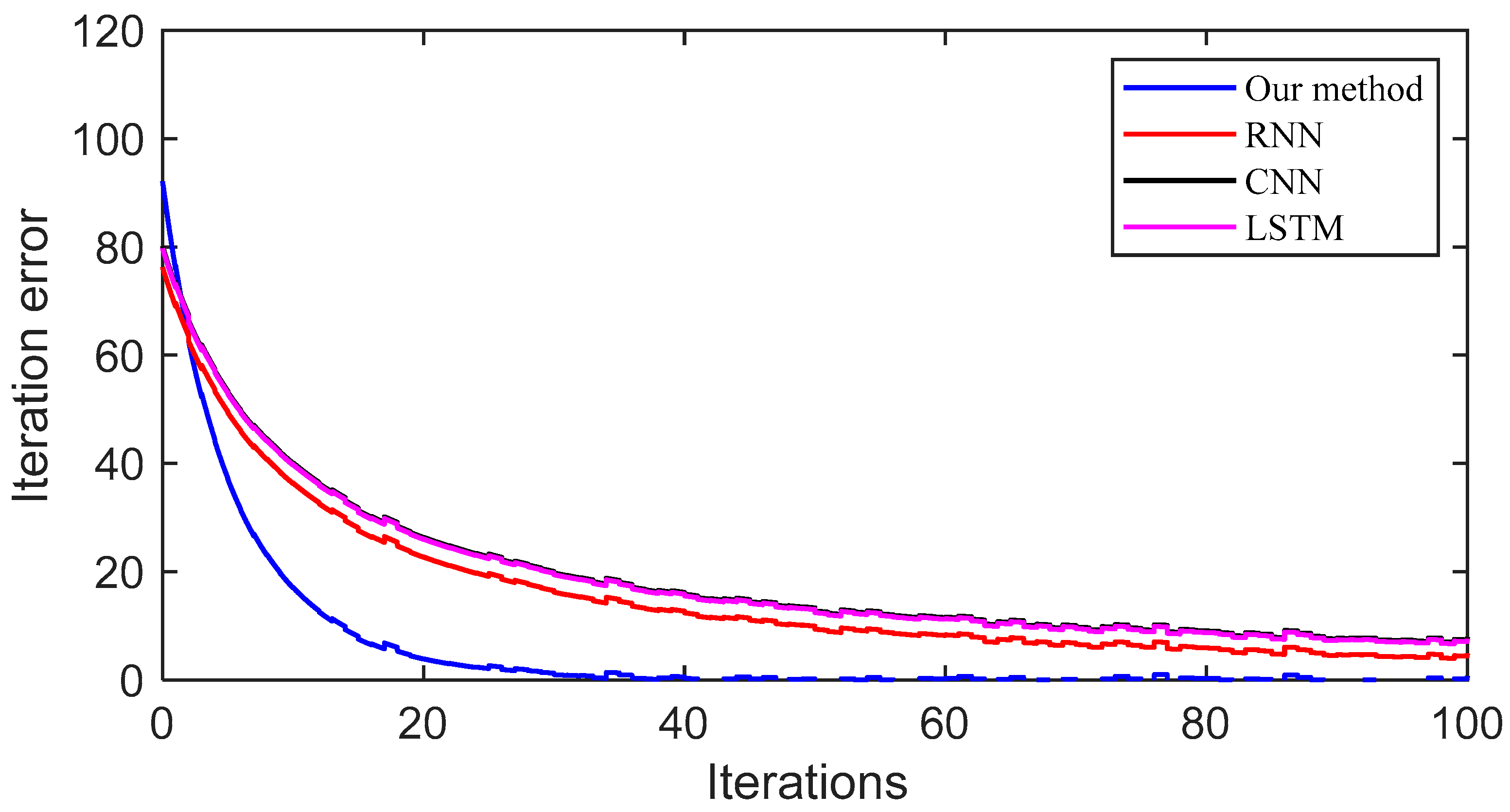
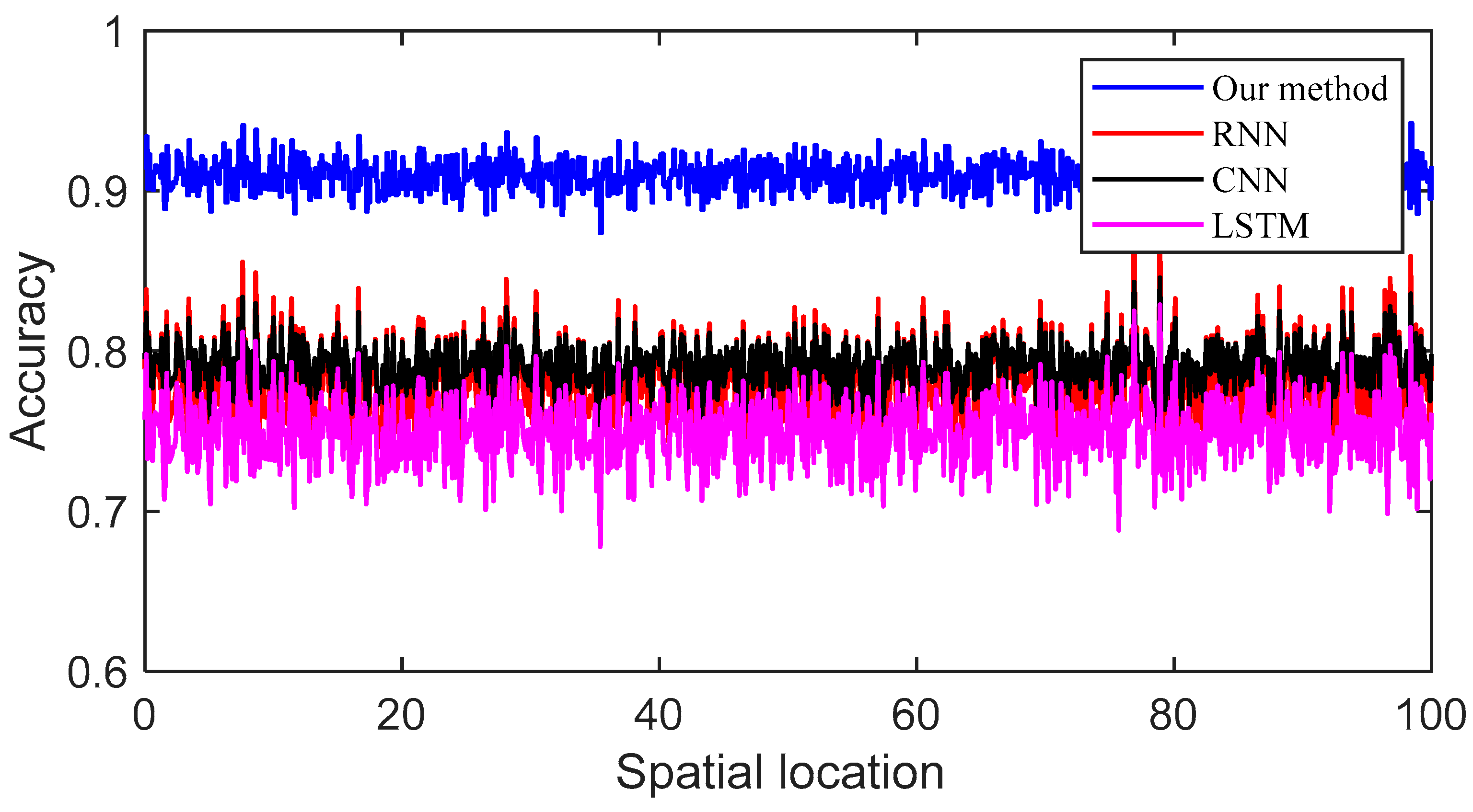
4.2. Experimental Comparison
- (1)
- An evolutionary feature pruning mechanism, which dynamically eliminates low-weight parameters during training to reduce redundant computations;
- (2)
- A hybrid entropy–AHP weighting framework, which accelerates convergence by a factor of 3.2× compared to standard backpropagation, leveraging domain-specific architectural heuristics;
- (3)
- An optimized memory allocation strategy, which minimizes data transfer overhead between computational units.
4.3. Experimental Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AHP | Analytic Hierarchy Process |
References
- Adenaike, F.A.; Olagunju, O.O. A review of recent proposals for addressing climate change impact in the construction industry. J. Adv. Educ. Sci. 2024, 4, 1–8. [Google Scholar]
- Ebekozien, A.; Aigbavboa, C.; Thwala, W.D.; Amadi, G.C.; Aigbedion, M.; Ogbaini, I.F. A systematic review of green building practices implementation in Africa. J. Facil. Manag. 2024, 22, 91–107. [Google Scholar] [CrossRef]
- Chen, H.; Du, Q.; Huo, T.; Liu, P.; Cai, W.; Liu, B. Spatiotemporal patterns and driving mechanism of carbon emissions in China’s urban residential building sector. Energy 2023, 263, 126102. [Google Scholar] [CrossRef]
- Li, W.; Zhang, Z.; Wang, M.; Chen, H. Fabric defect detection algorithm based on image saliency region and similarity location. Electronics 2023, 12, 1392. [Google Scholar] [CrossRef]
- Feng, Y.; Zeng, H.; Li, S.; Liu, Q.; Wang, Y. Refining and reweighting pseudo labels for weakly supervised object detection. Neurocomputing 2024, 577, 127387. [Google Scholar] [CrossRef]
- Liu, X.; Peng, Y.; Lu, Z.; Li, W.; Yu, J.; Ge, D.; Xiang, W. Feature-fusion segmentation network for landslide detection using high-resolution remote sensing images and digital elevation model data. IEEE Trans. Geosci. Remote Sens. 2023, 61, 4500314. [Google Scholar] [CrossRef]
- Wang, H. Multi-sensor fusion module for perceptual target recognition for intelligent machine learning visual feature extraction. IEEE Sens. J. 2021, 21, 24993–25000. [Google Scholar] [CrossRef]
- Chen, M.S.; Liao, Y.C. Applying the Analytical Hierarchy Process to Exploring Demand and Technology Preferences in InsurTech: Focusing on Consumer Concerns. Eng. Proc. 2025, 98, 6. [Google Scholar]
- Yadav, S.; Mohseni, U.; Vasave, M.D.; Thakur, A.S.; Tadvi, U.R.; Pawar, R.S. Assessing Dam Site Suitability Using an Integrated AHP and GIS Approach: A Case Study of the Purna Catchment in the Upper Tapi Basin, India. Environ. Earth Sci. Proc. 2025, 32, 21. [Google Scholar] [CrossRef]
- Sun, J.; Wang, Y.; Jiang, D. 3D Model Topology Algorithm Based on Virtual Reality Visual Features. Meas. Sens. 2024, 33, 101200. [Google Scholar] [CrossRef]
- Geng, L.; Yin, J.; Niu, Y. Lgvc: Language-guided visual context modeling for 3D visual grounding. Neural Comput. Appl. 2024, 36, 12977–12990. [Google Scholar] [CrossRef]
- Flores-Fuentes, W.; Trujillo-Hernández, G.; Alba-Corpus, I.Y.; Rodríguez-Quiñonez, J.C.; Mirada-Vega, J.E.; Hernández-Balbuena, D.; Sergiyenko, O. 3D spatial measurement for model reconstruction: A review. Measurement 2023, 207, 112321. [Google Scholar] [CrossRef]
- Lili, W. Virtual reconstruction of regional 3D images for visual communication effects. Mod. Electron. Technol. 2020, 43, 134–136+140. [Google Scholar]
- Pang, Y.; Miao, L.; Zhou, L.; Lv, G. An Indoor Space Model of Building Considering Multi-Type Segmentation. ISPRS Int. J. Geo-Inf. 2022, 11, 367. [Google Scholar] [CrossRef]
- Chen, G.; Yan, J.; Wang, C.; Chen, S. Expanding the Associations between Landscape Characteristics and Aesthetic Sensory Perception for Traditional Village Public Space. Forests 2024, 15, 97. [Google Scholar] [CrossRef]
- Huang, Z.; Qin, L. Intelligent Extraction of Color Features in Architectural Space Based on Machine Vision. In International Conference on Multimedia Technology and Enhanced Learning; Springer Nature: Cham, Switzerland, 2023; pp. 40–56. [Google Scholar]
- Liu, X.; Wang, C.; Yin, Z.; An, X.; Meng, H. Risk-informed multi-objective decision-making of emergency schemes optimization. Reliab. Eng. Syst. Saf. 2024, 245, 109979. [Google Scholar] [CrossRef]
- Cilali, B.; Rocco, C.M.; Barker, K. Multi-objective decision trees with fuzzy TOPSIS: Application to refugee resettlement planning. J. Multi-Criteria Decis. Anal. 2024, 31, e1822. [Google Scholar] [CrossRef]
- Chen, J.; Wang, S.; Wu, R. Optimization of the integrated green–gray–blue system to deal with urban flood under multi-objective decision-making. Water Sci. Technol. 2024, 89, 434–453. [Google Scholar] [CrossRef]
- Ransikarbum, K.; Pitakaso, R. Multi-objective optimization design of sustainable biofuel network with integrated fuzzy analytic hierarchy process. Expert Syst. Appl. 2024, 240, 122586. [Google Scholar] [CrossRef]
- Chatterjee, S.; Chakraborty, S. A study on the effects of objective weighting methods on TOPSIS-based parametric optimization of non-traditional machining processes. Decis. Anal. J. 2024, 11, 100451. [Google Scholar] [CrossRef]
- Hou, J.; Gao, T.; Yang, Y.; Wang, X.; Yang, Y.; Meng, S. Battery inconsistency evaluation based on hierarchical weight fusion and fuzzy comprehensive evaluation method. J. Energy Storage 2024, 84, 110878. [Google Scholar] [CrossRef]
- Li, C.; Wang, L.; Chen, Y. A comprehensive health diagnosis method for expansive soil slope protection engineering based on supervised and unsupervised learning. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2024, 18, 138–158. [Google Scholar] [CrossRef]
- Guo, J. Research on evaluation of legal risk prevention education quality based on dynamic variable weight analytic hierarchy process. Int. J. Sustain. Dev. 2024, 27, 78–92. [Google Scholar] [CrossRef]
- Nakhaeinejad, M.; Ebrahimi, S.M. Retirement adjustment solutions: A comparative analysis using Shannon’s Entropy and TOPSIS techniques. Int. J. Res. Ind. Eng. 2025, 14, 21–41. [Google Scholar]
- Radhakrishnan, S.; Thankachan, B. Similarity measure, entropy and distance measure of multiple sets. J. Fuzzy Ext. Appl. 2024, 5, 416–433. [Google Scholar]
- Zhou, W.; Wang, R. An entropy weight approach on the fuzzy synthetic assessment of Beijing urban ecosystem health, China. Acta Ecol. Sin. 2025, 25, 3244–3251. [Google Scholar]



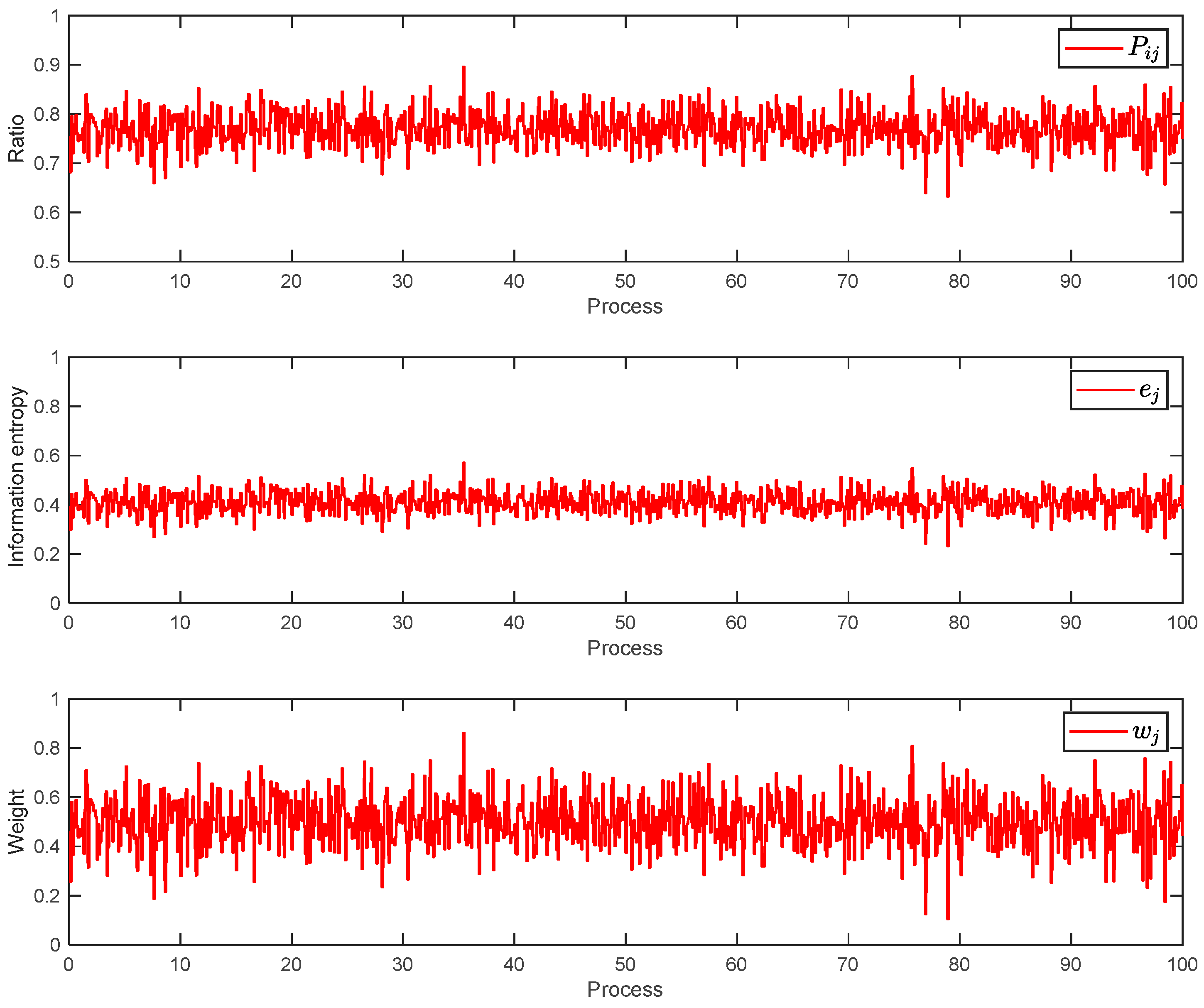
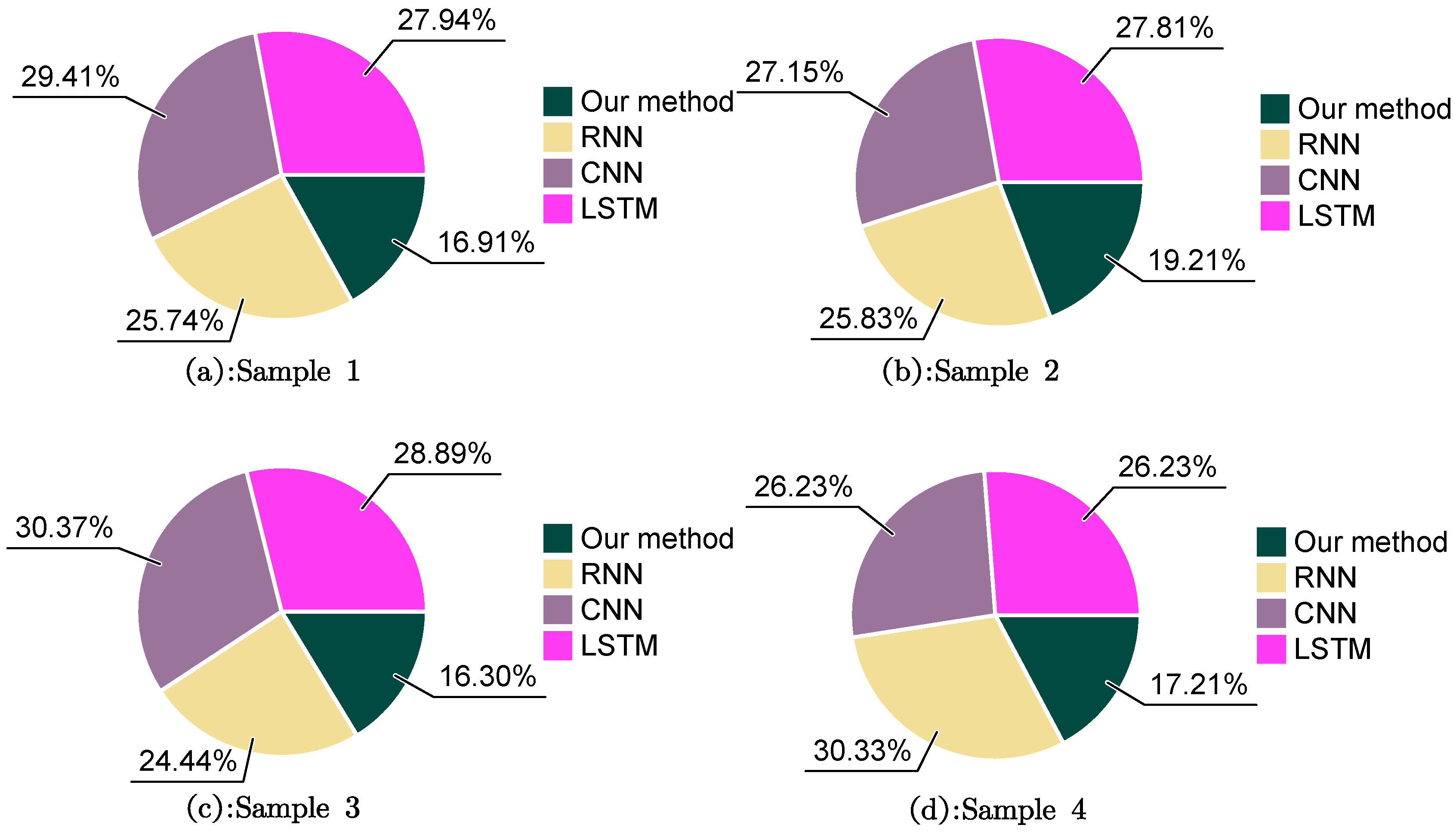

| Number | Pixel Intensity | Poor Visual Fusion | Feature Recognizability (%) |
|---|---|---|---|
| 1 | 16.66758 | 5.910772 | 64.81346565 |
| 2 | 21.54694 | 5.866928 | 63.39476648 |
| 3 | 17.01299 | 5.33094 | 63.39392789 |
| 4 | 21.10643 | 5.015748 | 66.89276182 |
| 5 | 21.94621 | 5.167921 | 70.94626593 |
| 6 | 18.96031 | 5.884936 | 75.49269422 |
| 7 | 19.46771 | 5.147582 | 61.82152966 |
| 8 | 18.19987 | 5.008399 | 68.57931353 |
| 9 | 20.77453 | 5.368025 | 71.79378334 |
| 10 | 19.13333 | 5.484816 | 69.90407186 |
| 11 | 18.84329 | 5.382483 | 64.5673448 |
| 12 | 18.6261 | 5.102322 | 64.93991059 |
| 13 | 21.96934 | 5.697971 | 67.24310694 |
| 14 | 18.9247 | 5.766441 | 60.82588246 |
| 15 | 21.89397 | 5.79092 | 60.46108236 |
| 16 | 16.27069 | 5.205694 | 61.646695 |
| 17 | 16.74956 | 5.453888 | 71.25162764 |
| 18 | 18.17324 | 5.279113 | 62.41718915 |
| 19 | 20.79412 | 5.929543 | 65.1891813 |
| 20 | 18.22117 | 5.871011 | 62.36091272 |
| Sample Quantity | 100 | 200 | 500 | 800 | 1000 |
|---|---|---|---|---|---|
| Our method | 0.12 s | 0.19 s | 0.65 s | 0.88 s | 0.95 s |
| RNN | 1.2 s | 1.6 s | 2.15 s | 2.33 s | 2.89 s |
| CNN | 1.19 s | 1.56 s | 2.01 s | 2.53 s | 3.01 s |
| LSTM | 1.09 s | 1.47 s | 1.98 s | 2.34 s | 2.99 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, Q.; Cai, Y.; Sohaib, O. Sustainable Optimization Design of Architectural Space Based on Visual Perception and Multi-Objective Decision Making. Buildings 2025, 15, 2940. https://doi.org/10.3390/buildings15162940
Ji Q, Cai Y, Sohaib O. Sustainable Optimization Design of Architectural Space Based on Visual Perception and Multi-Objective Decision Making. Buildings. 2025; 15(16):2940. https://doi.org/10.3390/buildings15162940
Chicago/Turabian StyleJi, Qunjing, Yu Cai, and Osama Sohaib. 2025. "Sustainable Optimization Design of Architectural Space Based on Visual Perception and Multi-Objective Decision Making" Buildings 15, no. 16: 2940. https://doi.org/10.3390/buildings15162940
APA StyleJi, Q., Cai, Y., & Sohaib, O. (2025). Sustainable Optimization Design of Architectural Space Based on Visual Perception and Multi-Objective Decision Making. Buildings, 15(16), 2940. https://doi.org/10.3390/buildings15162940








