Dynamic Optimization and Performance Analysis of Solar Thermal Storage Systems for Intermittent Heating in High-Altitude Cold Regions
Abstract
1. Introduction
2. Study on Heat Load Characteristics of Typical Intermittent Heating Buildings and Modification of Design Methods
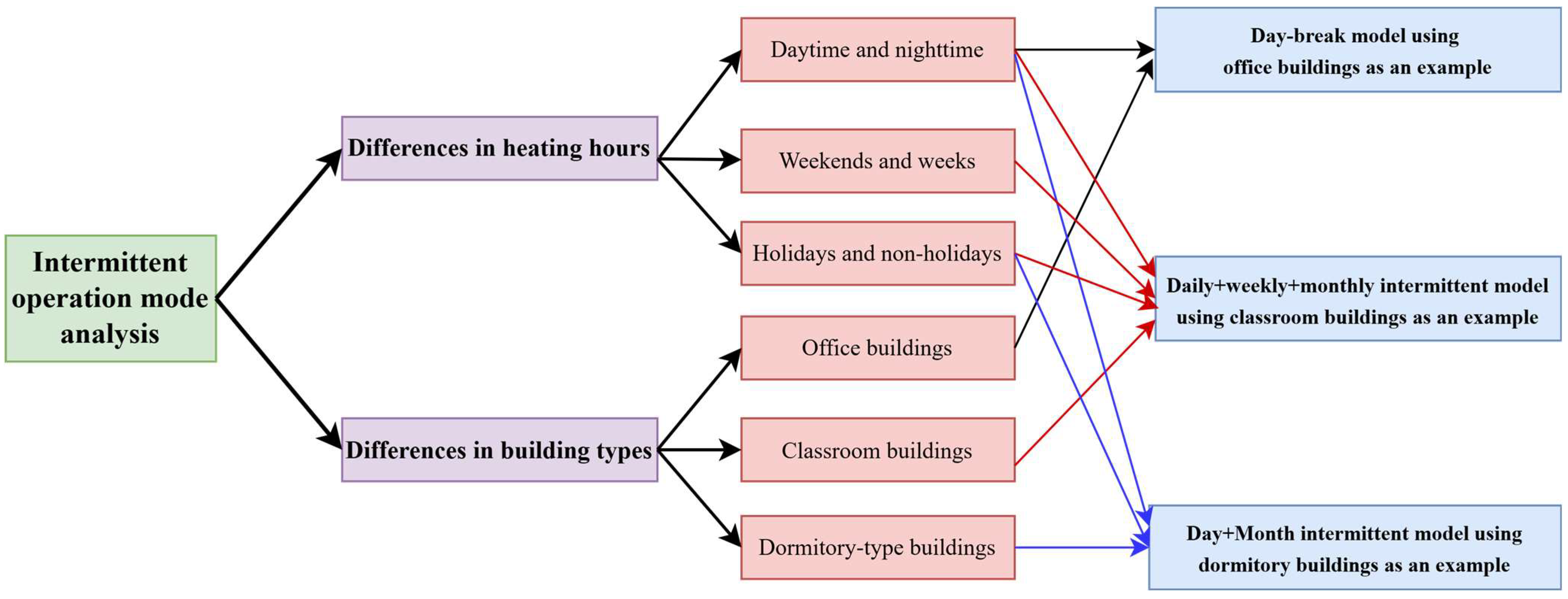
2.1. Classification and Selection of Intermittent Heating Buildings
2.1.1. Classification of Buildings with Intermittent Heating
2.1.2. Selection and Use of Typical Intermittent Buildings
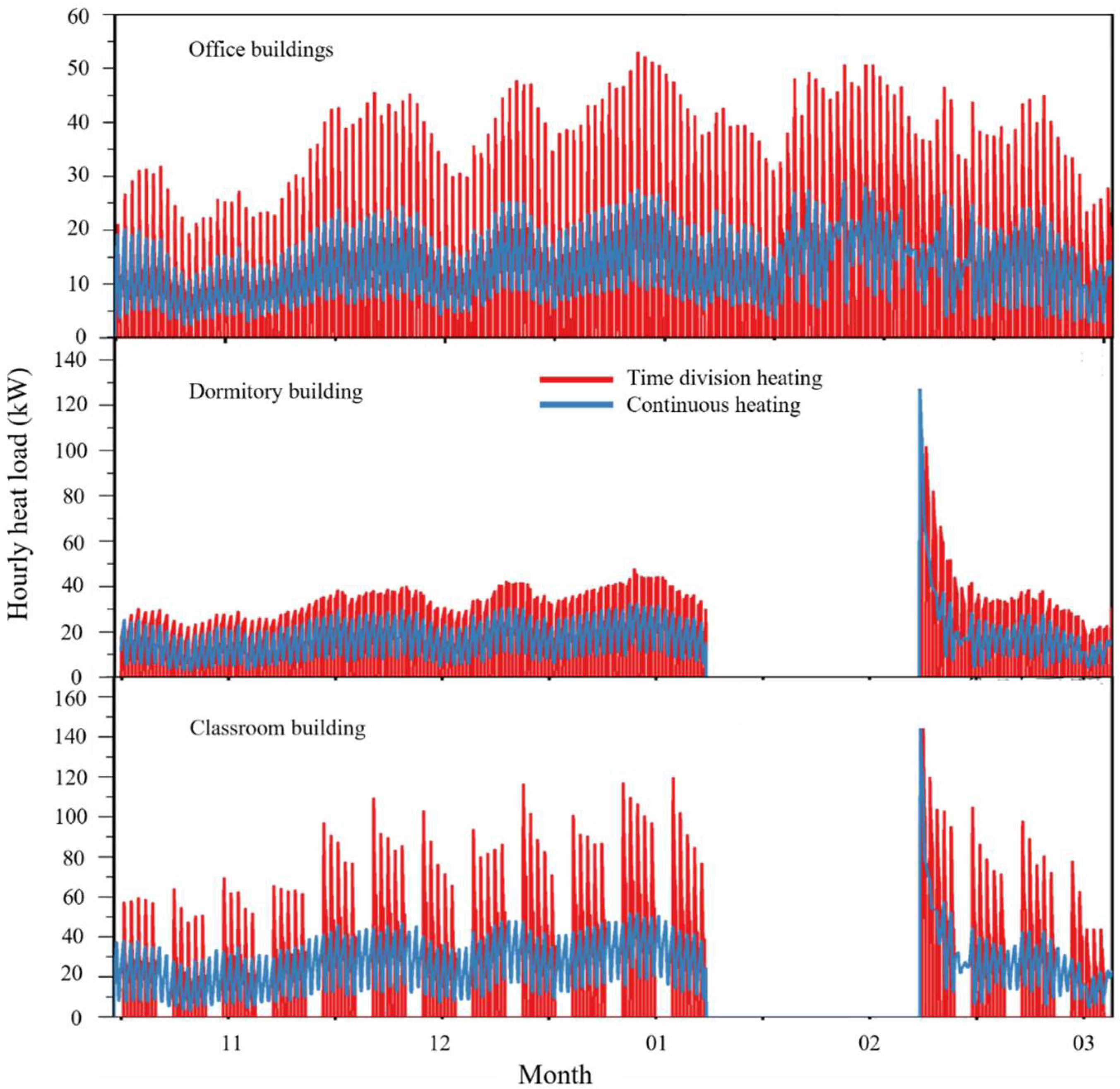
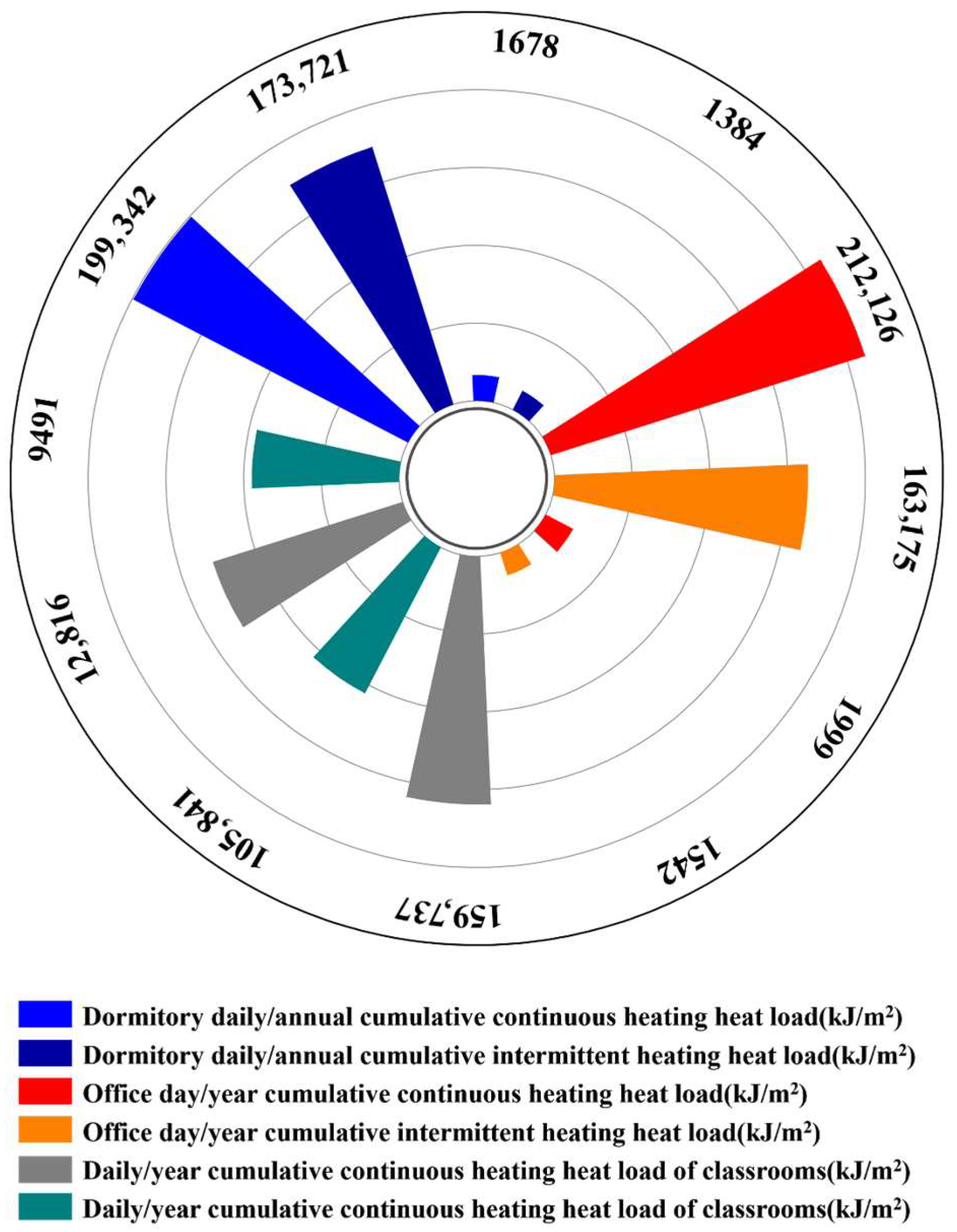
2.2. Analysis of Heat Load Law
2.3. Design Method of Heat Storage for Intermittent Solar Heating System
2.3.1. Design Method of Intermittent Solar Thermal Collector
2.3.2. Design Method of Intermittent Solar Thermal Storage
2.3.3. Design of a Typical Intermittent Solar Thermal Storage System
3. Numerical Simulation
3.1. Building Overview and Heat Load
3.1.1. Selection of Typical Cities and Meteorological Parameters
3.1.2. Typical Intermittent Heating Building Interior Design Parameters
3.1.3. Model Establishment and Parameter Setting
3.2. Mathematical Model
3.2.1. Solar Collector Model
3.2.2. Hot Water Storage Tank Model
3.2.3. Auxiliary Heat Source Model
3.2.4. Radiator Model
3.2.5. Circulating Water Pump Model
3.2.6. Room Thermal Balance Model
3.3. Model Building
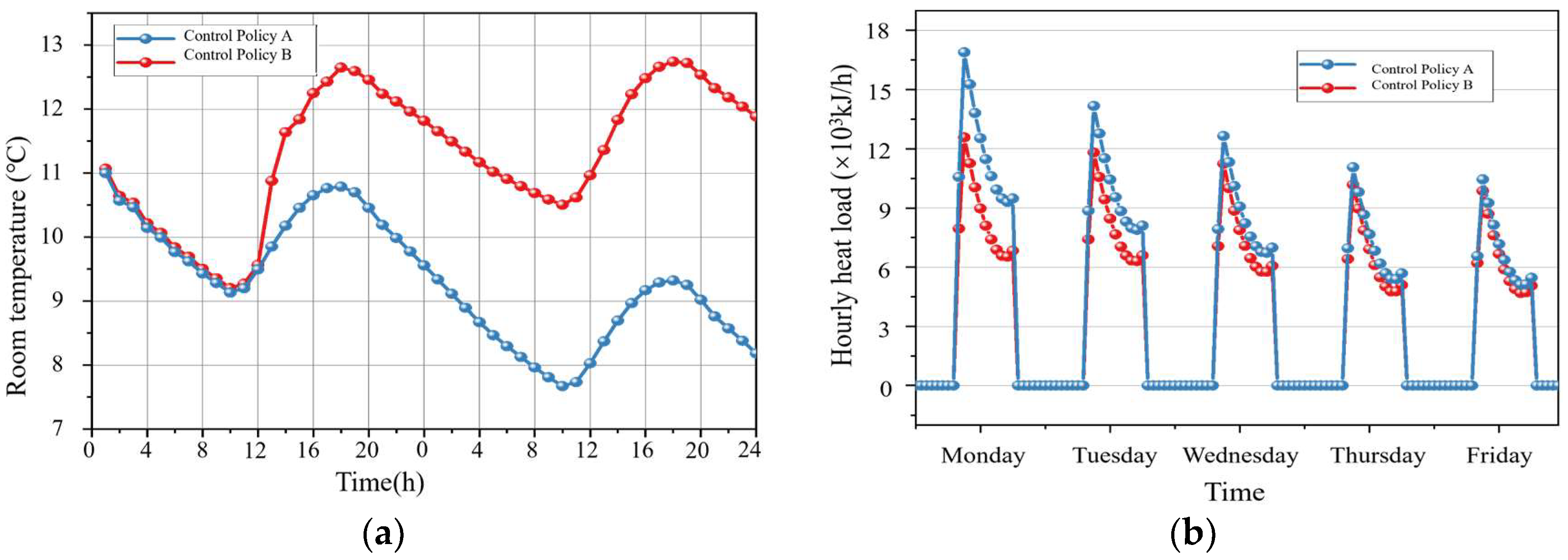
3.4. Intermittent Solar Energy Operation Regulation Strategy
4. Discussion
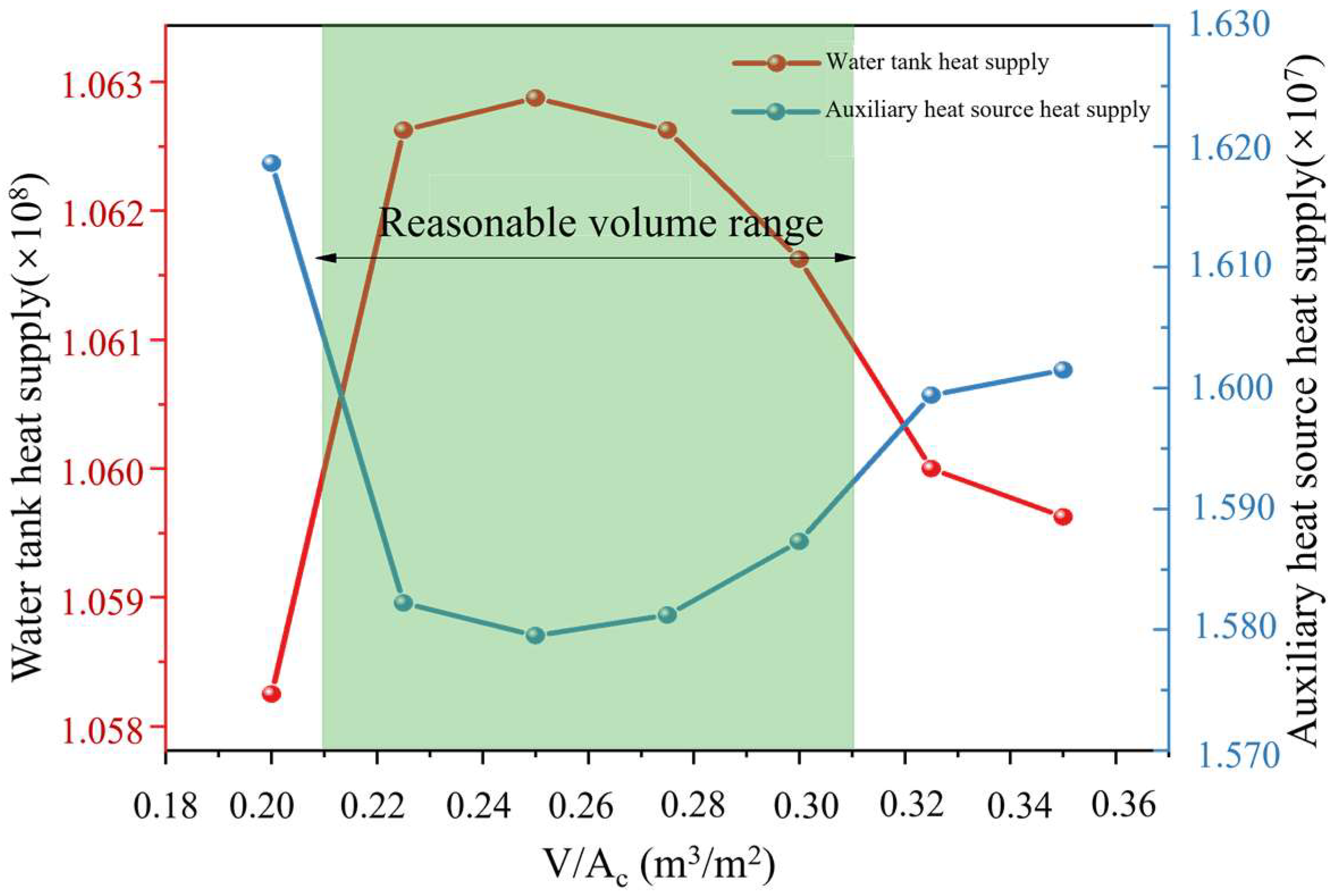
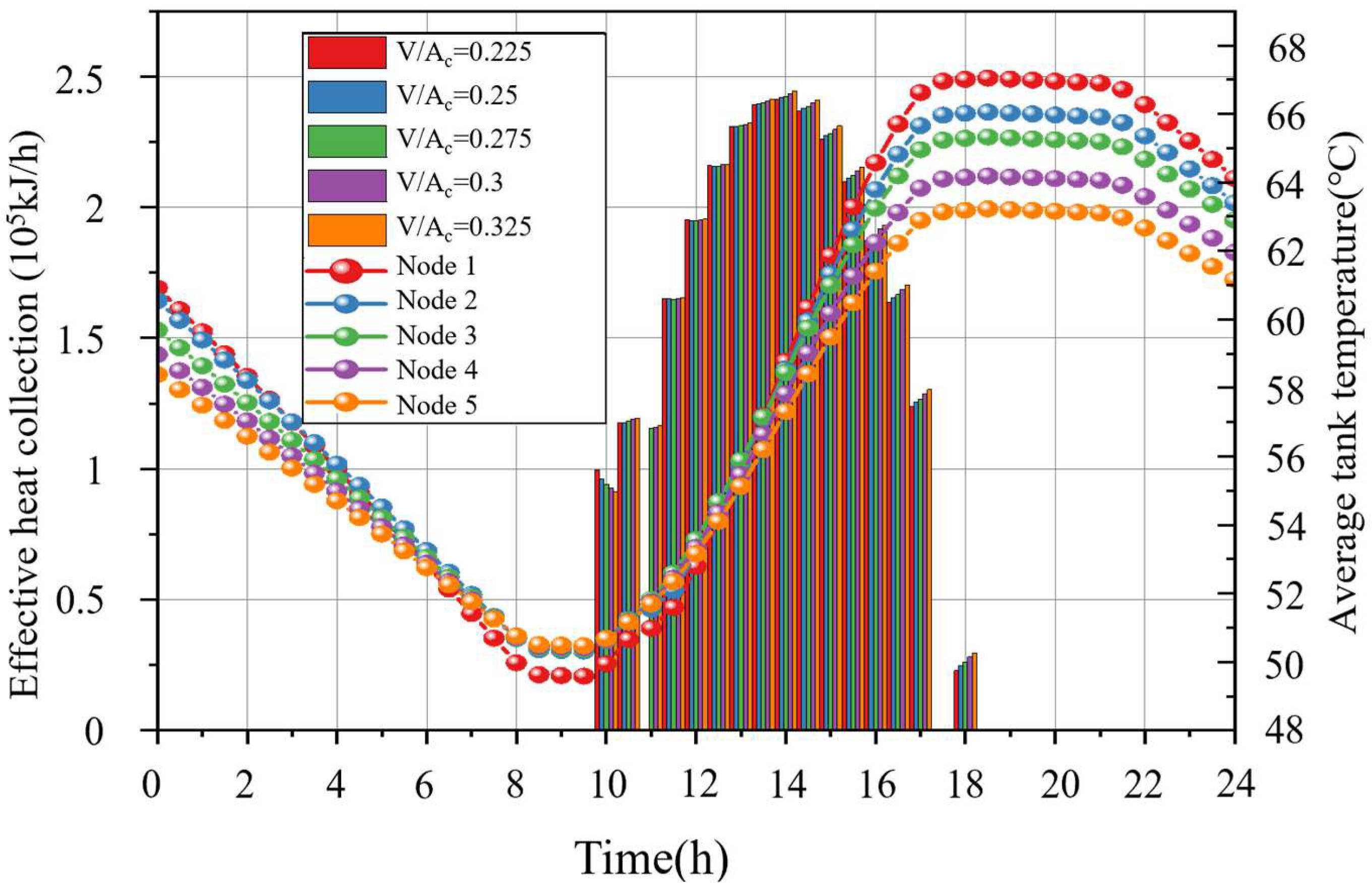
4.1. Effect of Heat Storage Tank Capacity on Intermittent Solar Energy System
4.2. Analysis of Operating Characteristics of Typical Day Simulation Conditions
4.2.1. Operating Characteristics of the Heat Collector Side
4.2.2. Thermal Storage Side Operating Characteristics
4.2.3. Thermal Performance of the Heating Side
4.3. Annual Energy Consumption Analysis of Intermittent Solar Heating System
4.4. Comparative Analysis of Heat Storage Capacity with Traditional Design Methods
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| TRNSYS | Transient System Simulation Tool |
| TMY | Typical Meteorological Year |
| SHS | Solar Heating Systems |
| TCE | standard coal equivalent |
| COMSOL | COMSOL Multiphysics |
| Nomenclature | |
| Ac | Collector area, m2 |
| A′c | Total solar collector area, m2 |
| Aj, Aj−1 | heat loss surface area of the storage tank, m2 |
| a0 | Empirical coefficient (intercept) |
| a1 | First-order temperature coefficient, K−1 |
| a2 | Second-order temperature coefficient, K2 |
| Cp | specific heat capacity of the fluid, kJ/kg·K |
| Cs | heat capacity of the radiator, J/°C |
| Ctank | Heat capacity of the thermal storage tank, kJ/K |
| f par | proportion of pump electrical power converted to heat, kW |
| FR | Solar collector heat transfer factor |
| Fs | heat transfer area, m2 |
| fn | Solar fraction, % |
| G | Total solar irradiance, W/m2 |
| H | Cumulative heat, kJ |
| Iθ(τ) | Solar irradiance on inclined surfaces, W/m2 |
| Lcond,j | Thickness of layer j, m |
| Lcond, j−1 | Thickness of layer j−1, m |
| ṁ | Mass flow rate, kg/s |
| P | pump power consumption, kW |
| Q′L | Cumulative heat consumption during heating period, kJ |
| Q′u | Total radiation during heating operation period, kJ |
| Qu(τ) | Fitting curve of effective solar heat collection |
| Ql(τ) | Hourly heat load fitting curve of the building |
| Qinput | heat supplied to the fluid by the auxiliary heat source |
| Qg(τ) | Water-side thermal load, kW |
| Qin,tank | Heat flow into the tank, kW |
| Qout,tank | Heat flow out of the tank, kW |
| Qcond,j | Conductive heat transfer in direction j, kW |
| Qloss | Total heat loss from the tank, kW |
| Qloss, top | Heat loss from the top of the tank, kW |
| Qloss, bottom | Heat loss from the bottom of the tank, kW |
| Qiu(τ) | Upper-bound heat flow in group I, kJ |
| Qil(τ) | Lower-bound heat flow in group i, kJ |
| Qloss,j | Heat loss from direction j, kW |
| Qloss, edges | Heat loss from the sides/edges, kW |
| ql(τ) | Hourly heat load of building, kW |
| Tenv | ambient temperature surrounding the storage tank, °C |
| To, Ti | outlet and inlet temperatures, respectively, °C |
| Tg, Th | Radiator inlet and outlet water temperature, °C |
| Tj, Tj−1 | Temperatures at layer j and j−1, °C |
| Ttank,j | temperature at node j of the storage tank, m2 |
| tl | Initial temperature of hot water tank, °C |
| tend | Hot water tank termination temperature, °C |
| U | Overall heat transfer coefficient, W/m2·K |
| V′ | The volume of the hot water storage tank, m3 |
| τ1, τ2 | Daily solar radiation time period |
| τa, τb | Intermittent heating start and stop periods |
| ηoverall | Total pump efficiency |
| ηmotor | Motor efficiency |
| ηpumping | Pump operating efficiency |
| ηL | heat loss rate of the storage tank and piping |
| ηcd | average collector efficiency during the heating period |
| ΔQ | heat storage capacity, kJ |
| ΔT | Temperature difference, K |
| εheater | thermal efficiency of the auxiliary heater |
| (τα)e | Effective Projection Absorption Factor |
| Cumulative solar thermal energy supplied to the building | Total useful heat delivered from the solar heating system to meet building demand over a given period, kJ or kWh. |
| Cumulative effective solar thermal energy | Total useful thermal energy collected by the solar collectors over a given period, after accounting for system efficiency and losses, kJ or kWh. |
References
- Abbasi, K.R.; Shahbaz, M.; Zhang, J.; Irfan, M.; Alvarado, R.; Zahid, A.; Khan, Z.A. Analyze the environmental sustainability factors of China: The role of fossil fuel energy and renewable energy. Renew. Energy 2022, 187, 390–402. [Google Scholar] [CrossRef]
- Pan, J.; Chen, X.; Luo, X.; Wang, Y.; Li, Z.; Hu, S.; Liu, Y. Analysis of the impact of China’s energy industry on social development from the perspective of low-carbon policy. Energy Rep. 2022, 8, 14–27. [Google Scholar] [CrossRef]
- China Building Energy Conservation Association. China Building Energy Consumption Annual Report 2020. J. BEE 2021, 49, 1–6. [Google Scholar]
- Xu, S.; Ge, J. Sustainable development of clean heating in rural northern China: Locally tailored energy options. Sustain. Prod. Consum. 2023, 35, 655–667. [Google Scholar] [CrossRef]
- Jiang, Y.; Hu, S.; Liu, X.; Chen, Y.; Zhou, D. Decarbonize Public and Commercial Buildings: China Building Energy and Emission Yearbook 2022; Springer: Singapore, 2022. [Google Scholar] [CrossRef]
- Jiang, Y.; Hu, S. Paths to carbon neutrality in China’s building sector. Heat. Vent. Air Cond. 2021, 51, 1–13. [Google Scholar]
- Wang, X.; Huang, J.; Liu, H. Can China’s carbon trading policy help achieve carbon neutrality?—A study of policy effects from the Five-Sphere Integrated Plan perspective. J. Environ. Manag. 2022, 305, 114357. [Google Scholar] [CrossRef] [PubMed]
- Hepburn, C.; Qi, Y.; Stern, N.; Ward, B.; Xie, C.; Zenghelis, D.; Teng, F.; Jia, J. Towards carbon neutrality and China’s 14th Five-Year Plan: Clean energy transition, sustainable urban development, and investment priorities. Environ. Sci. Ecotechnol. 2021, 8, 100130. [Google Scholar] [CrossRef] [PubMed]
- Ye, A.; Guan, B.; Liu, X.; Chen, L.; Wu, Y.; Wang, Q. Using solar energy to achieve near-zero energy buildings in the Tibetan Plateau. Renew. Energy 2023, 218, 119347. [Google Scholar] [CrossRef]
- Gao, J.; Li, S.; Wu, F.; Wang, Y.; Zhang, H. Study on efficient heating method by solar coupled air source heat pump system with phase change heat storage in severe cold region. Appl. Energy 2024, 367, 123206. [Google Scholar] [CrossRef]
- Georgiev, A.; Popov, R.; Toshkov, E. Investigation of a hybrid system with ground source heat pump and solar collectors: Charging of thermal storage and space heating. Renew. Energy 2020, 147, 2774–2790. [Google Scholar] [CrossRef]
- Wang, Z.; Luo, M.; Geng, Y.; Lin, B.; Hong, J. A model to compare convective and radiant heating systems for intermittent space heating. Appl. Energy 2018, 215, 211–226. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhou, Y.; Zhao, N.; Zhou, J.; Chen, X.; Song, X. Clean heating during winter season in Northern China: A review. Renew. Sustain. Energy Rev. 2021, 149, 111339. [Google Scholar] [CrossRef]
- Dear, R.J.; Akimoto, T.; Arens, E.A.; Brager, G.; Candido, C.; Cheong, K.W.D.; Cheong, B.; Li, N.; Nishihara, S.C.; Sekhar, S.; et al. Progress in thermal comfort research over the last twenty years. Indoor Air 2013, 23, 442–461. [Google Scholar] [CrossRef] [PubMed]
- Pineau, D.; Rivière, P.; Stabat, P.; Marchio, D. Performance analysis of heating systems for low energy houses. Energy Build. 2013, 65, 45–54. [Google Scholar] [CrossRef]
- Liu, G.; Zhou, X.; Yan, J.; Zhang, W.; Liu, M. A temperature and time-sharing dynamic control approach for space heating of buildings in district heating systems. Energy 2021, 221, 119835. [Google Scholar] [CrossRef]
- Yu, H.; Liu, Z.; Li, C.; Xu, X.; Zhang, H.; Wang, Y. Study on pricing mechanism of cooling, heating, and electricity considering demand response in the stage of park integrated energy system planning. Appl. Sci. 2020, 10, 1565. [Google Scholar] [CrossRef]
- Andersen, R.V.; Toftum, J.; Andersen, K.K.; Olesen, B.W. Survey of occupant behavior and control of indoor environment in Danish dwellings. Energy Build. 2009, 41, 11–16. [Google Scholar] [CrossRef]
- Yang, B.; Liu, Y.; Liu, P.; Li, H.; Zhang, X. A novel occupant-centric stratum ventilation system using computer vision: Occupant detection, thermal comfort, air quality, and energy savings. Build. Environ. 2023, 237, 110332. [Google Scholar] [CrossRef]
- Zhou, R.; Gao, P.; Wang, J.; Li, Z.; Zhang, M. Analysis of time-sharing and zoning heat load demand and research on heating control of large heating buildings. Int. J. Heat Technol. 2022, 40, 1105–1113. [Google Scholar] [CrossRef]
- Meng, X.; Huang, Y.; Cao, Y.; Zhang, J.; Li, X. Optimization of the wall thermal insulation characteristics based on the intermittent heating operation. Case Stud. Constr. Mater. 2018, 9, e00188. [Google Scholar] [CrossRef]
- Badran, A.A.; Jaradat, A.W.; Bahbouh, M.N. Comparative study of continuous versus intermittent heating for local residential building: Case studies in Jordan. Energy Convers. Manag. 2013, 65, 709–714. [Google Scholar] [CrossRef]
- Wang, S.; Kang, Y.; Yang, Z.; Zhang, X.; Huang, Y. Numerical study on dynamic thermal characteristics and optimum configuration of internal walls for intermittently heated rooms with different heating durations. Appl. Therm. Eng. 2019, 155, 437–448. [Google Scholar] [CrossRef]
- Wang, D.; Liu, Y.; Wang, Y.; Li, M.; Zhang, Y. Numerical and experimental analysis of floor heat storage and release during an intermittent in-slab floor heating process. Appl. Therm. Eng. 2014, 62, 398–406. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, W.; Zhou, B.; Wang, Y.; Zhang, L. Energy saving effect of different wall structures based on intermittent energy use characteristics in a hot summer and cold winter zone. In Proceedings of the Heat Transfer Summer Conference, Washington, DC, USA, 10–14 July 2016; American Society of Mechanical Engineers: New York, NY, USA, 2016; Volume 50336, p. V002T20A001. [Google Scholar] [CrossRef]
- Sun, S.; Wang, J.; Li, R.; Zhang, T.; Liu, H. Estimation of preheating time for building intermittent heating subject to changes in outdoor temperature and solar radiation. Energy Build. 2024, 317, 114405. [Google Scholar] [CrossRef]
- Tsilingiris, P.T. Wall heat loss from intermittently conditioned spaces—The dynamic influence of structural and operational parameters. Energy Build. 2006, 38, 1022–1031. [Google Scholar] [CrossRef]
- Liu, J.; Xin, Z.; Huang, Y.; Chen, H.; Li, X. Climate suitability assessment on the Qinghai-Tibet Plateau. Sci. Total Environ. 2022, 816, 151653. [Google Scholar] [CrossRef] [PubMed]
- Dordonnat, V.; Koopman, S.J.; Ooms, M.; Dessertaine, A.; Thomas, M. An hourly periodic state space model for modelling French national electricity load. Int. J. Forecast. 2008, 24, 566–587. [Google Scholar] [CrossRef]
- Wang, Z.; Ji, Y.; Su, X. Influence of outdoor and indoor microclimate on human thermal adaptation in winter in the severe cold area, China. Build. Environ. 2018, 133, 91–102. [Google Scholar] [CrossRef]
- An, S.; Chen, X.; Zhang, X.; Zhang, Y.; Zhang, J.; He, C. Precipitation and minimum temperature are primary climatic controls of alpine grassland autumn phenology on the Qinghai-Tibet Plateau. Remote Sens. 2020, 12, 431. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Y.; Yue, T. A new approach for indoor environment design of passive solar buildings in plateau areas. Sustain. Energy Technol. Assess. 2024, 63, 103669. [Google Scholar] [CrossRef]
- Si, P.; Feng, Y.; Lv, Y.; Li, J.; Wang, C. An optimization method applied to active solar energy systems for buildings in cold plateau areas—The case of Lhasa. Appl. Energy 2017, 194, 487–498. [Google Scholar] [CrossRef]
- Lin, B.; Wang, Z.; Liu, Y.; Hong, J.; Zhu, Y. Investigation of winter indoor thermal environment and heating demand of urban residential buildings in China’s hot summer–cold winter climate region. Build. Environ. 2016, 101, 9–18. [Google Scholar] [CrossRef]
- Huang, J.; Wang, S.; Teng, F.; Liang, Q.; Liu, X. Thermal performance optimization of envelope in the energy-saving renovation of existing residential buildings. Energy Build. 2021, 247, 111103. [Google Scholar] [CrossRef]
- Kim, H.; Hong, T.; Kim, J.; Lee, M.; Koo, C. A psychophysiological effect of indoor thermal condition on college students’ learning performance through EEG measurement. Build. Environ. 2020, 184, 107223. [Google Scholar] [CrossRef]
- Wargocki, P.; Wyon, D.P. Providing better thermal and air quality conditions in school classrooms would be cost-effective. Build. Environ. 2013, 59, 581–589. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, C.; Zhang, T.; Li, Y.; Zhang, L. Association of indoor temperature and air quality in classrooms based on field and intervention measurements. Build. Environ. 2023, 229, 109925. [Google Scholar] [CrossRef]
- Bakó-Biró, Z.; Clements-Croome, D.J.; Kochhar, N.; Awbi, H.B.; Williams, M.J. Ventilation rates in schools and pupils’ performance. Build. Environ. 2012, 48, 215–223. [Google Scholar] [CrossRef]
- Xie, M.; Wang, M.; Zhong, H.; Zhang, J.; Liu, P. The impact of urban morphology on the building energy consumption and solar energy generation potential of university dormitory blocks. Sustain. Cities Soc. 2023, 96, 104644. [Google Scholar] [CrossRef]
- Ghiaus, C. Causality issue in the heat balance method for calculating the design heating and cooling load. Energy 2013, 50, 292–301. [Google Scholar] [CrossRef]






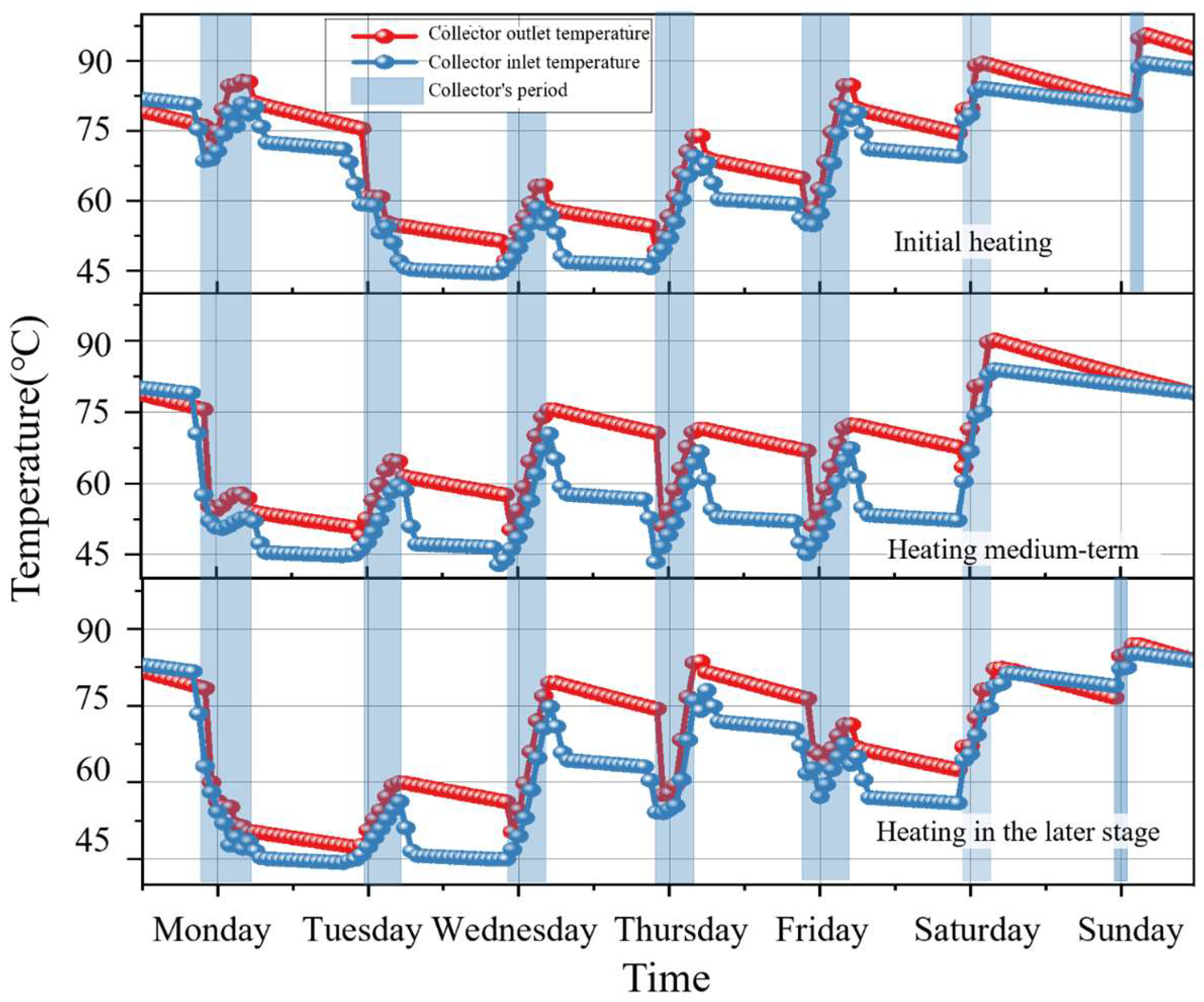
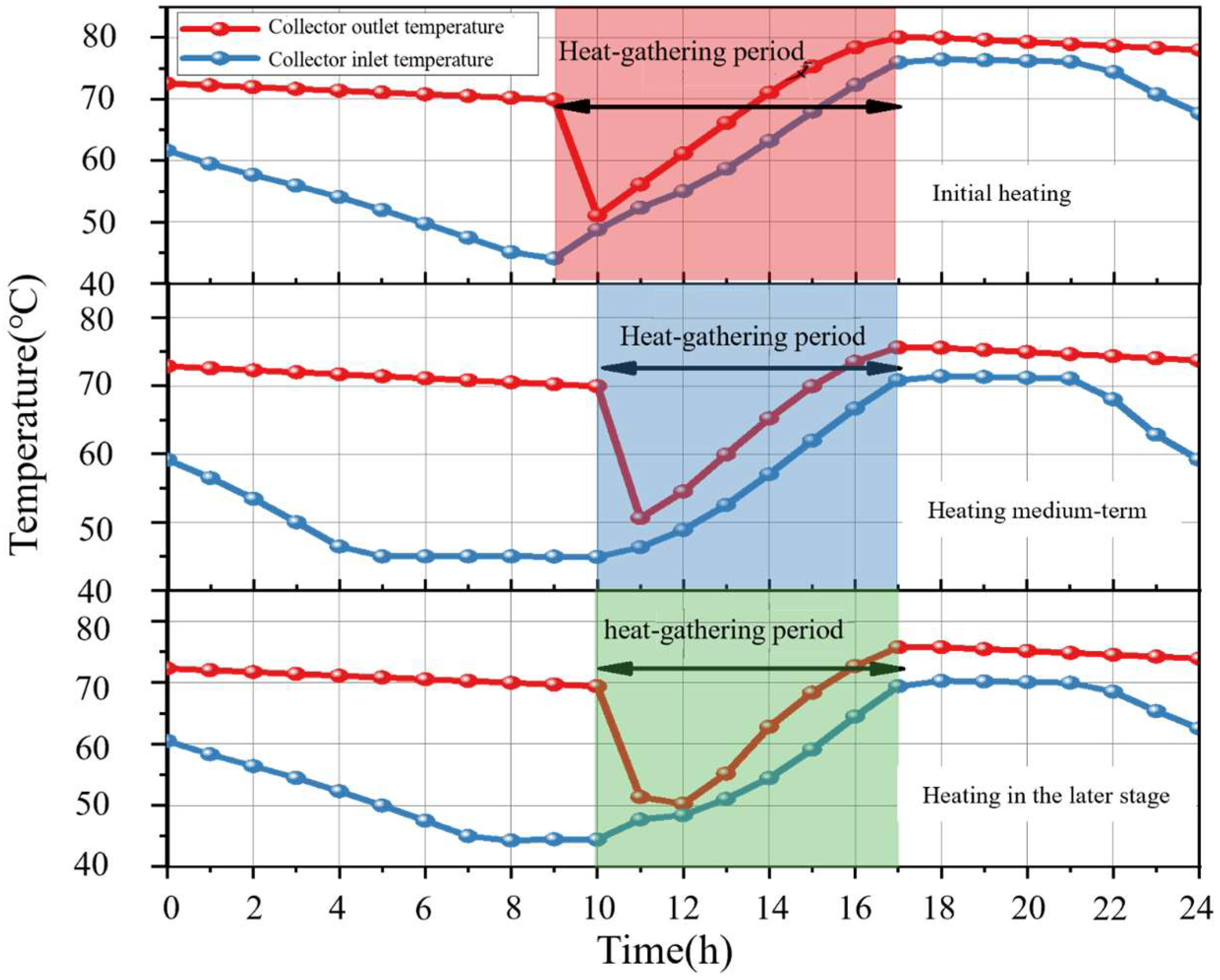


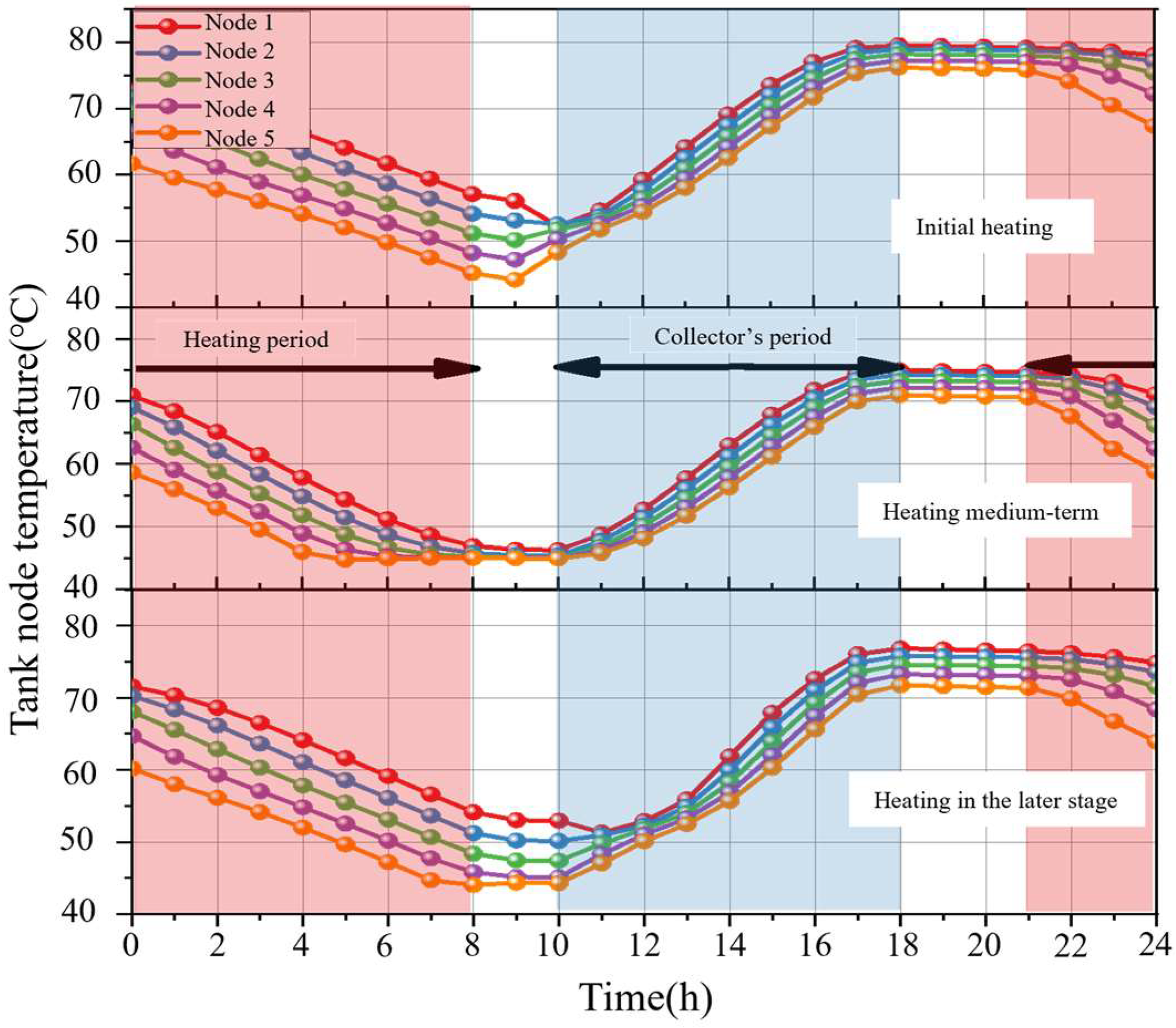
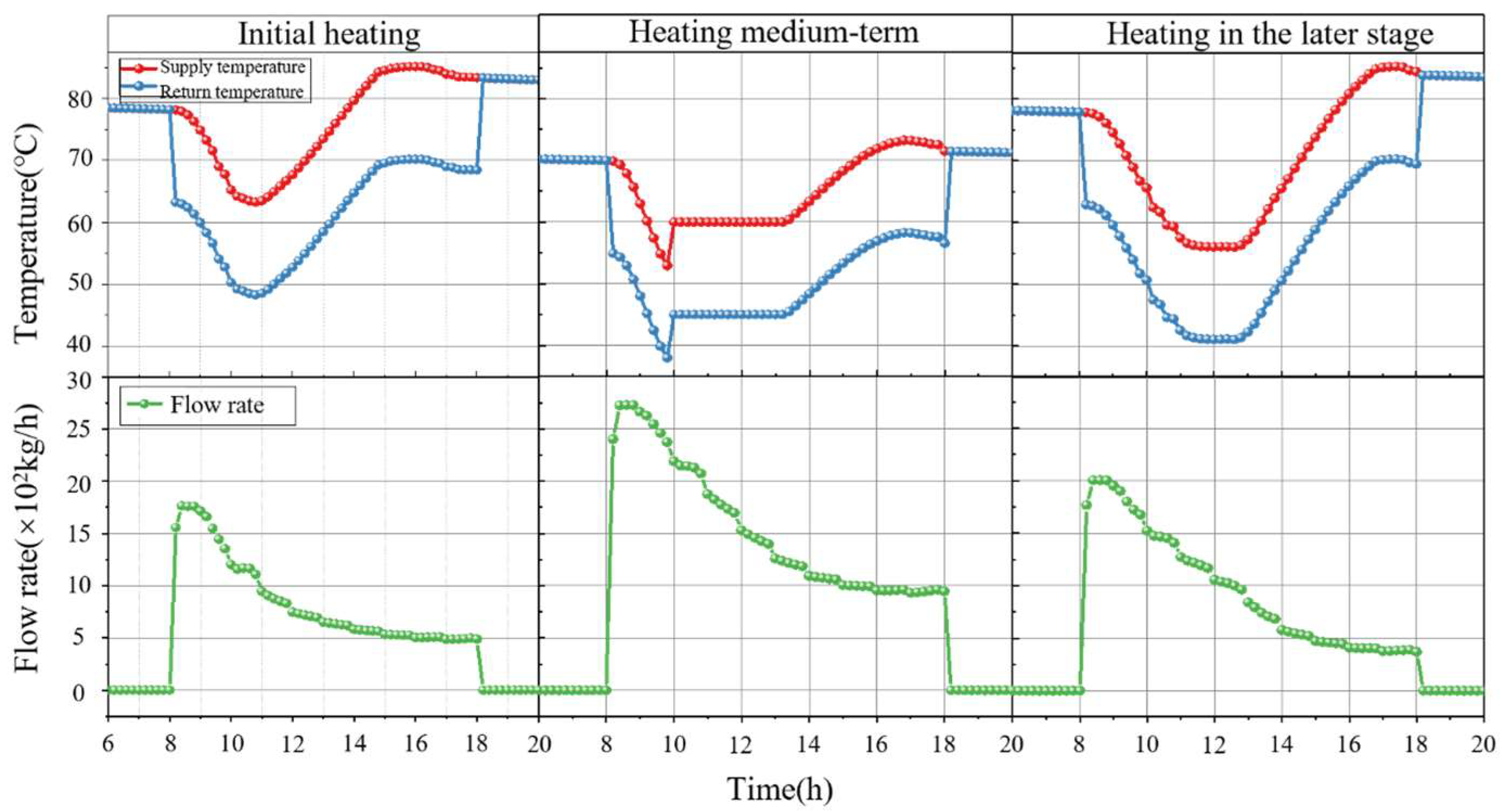


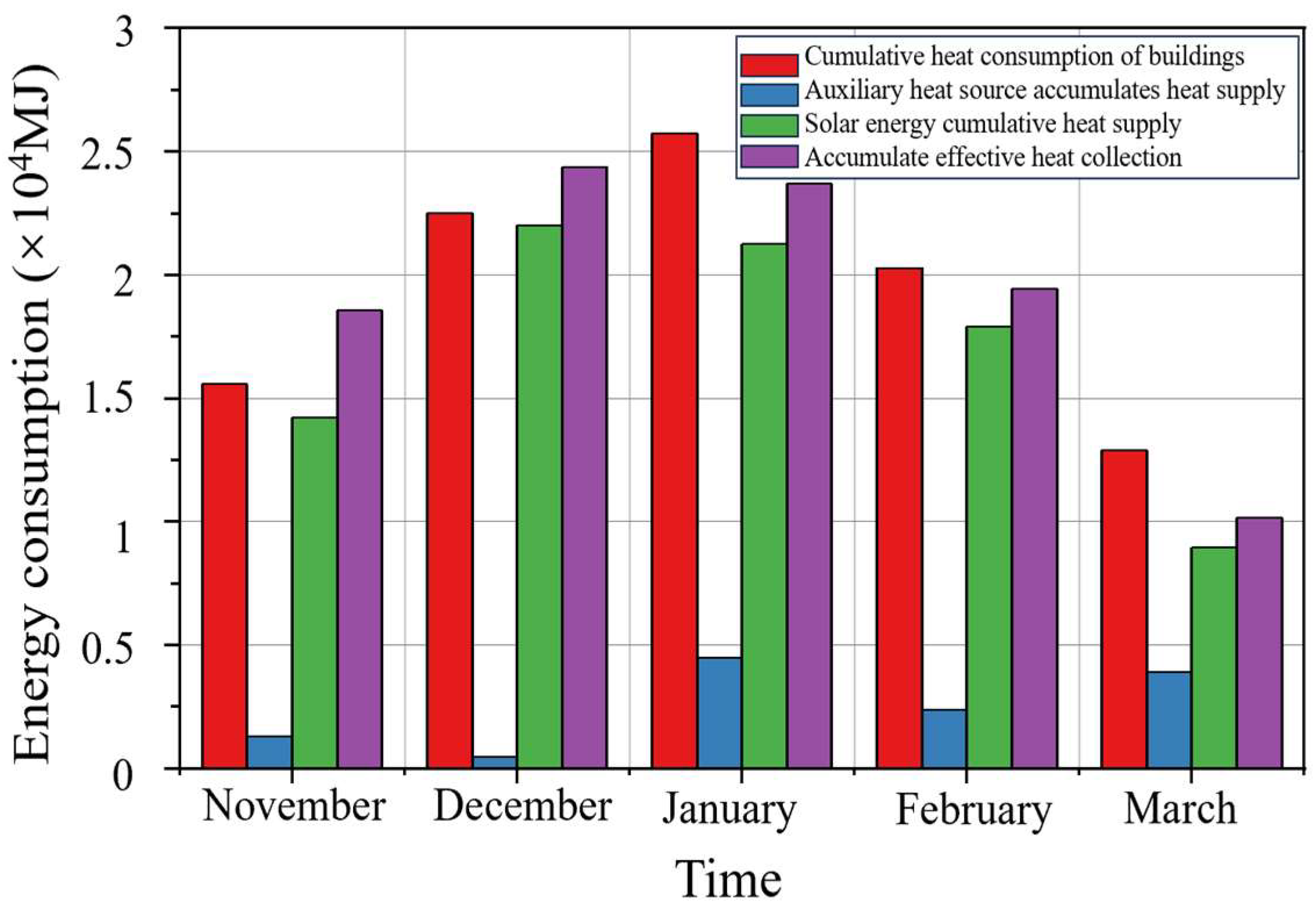
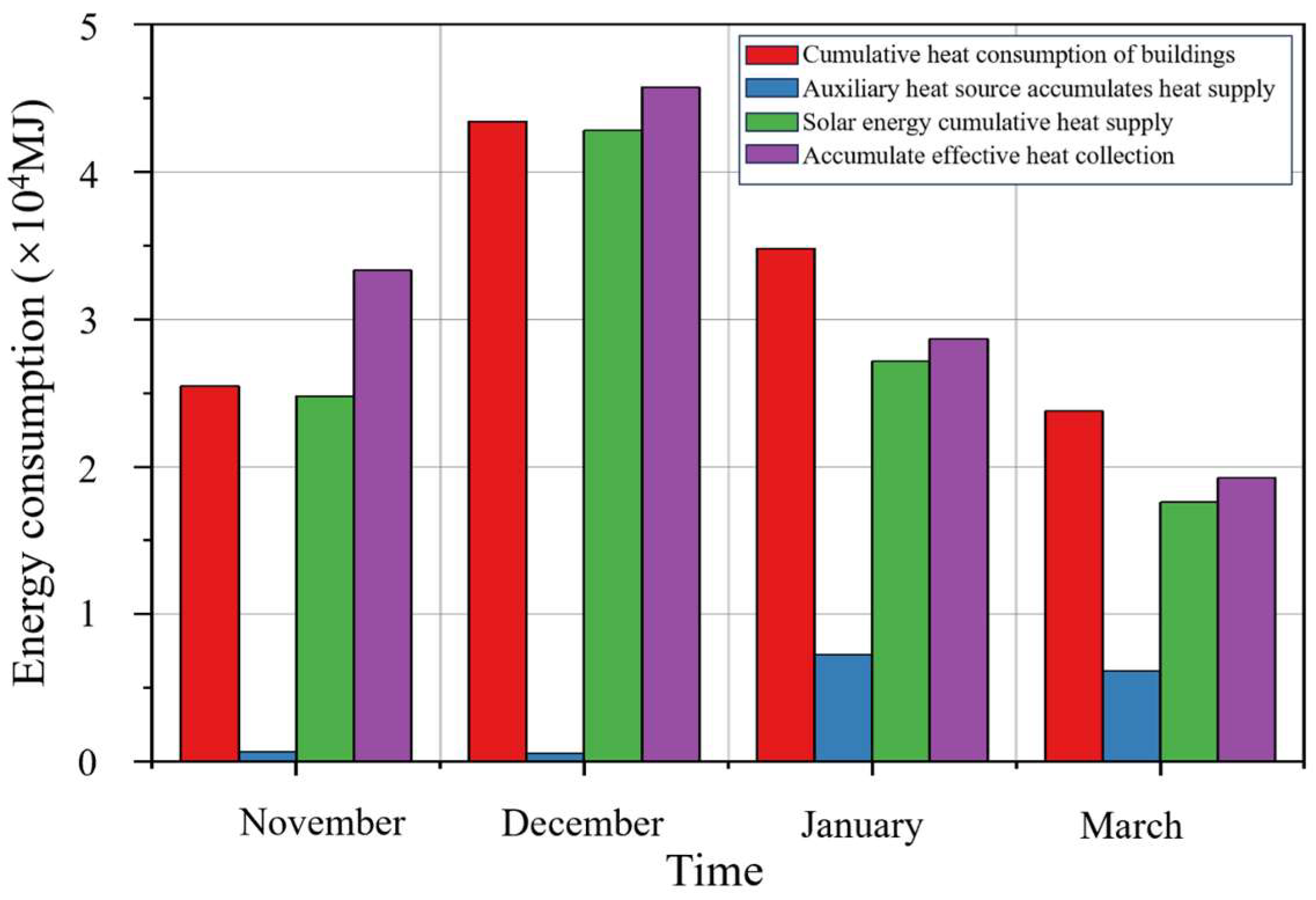
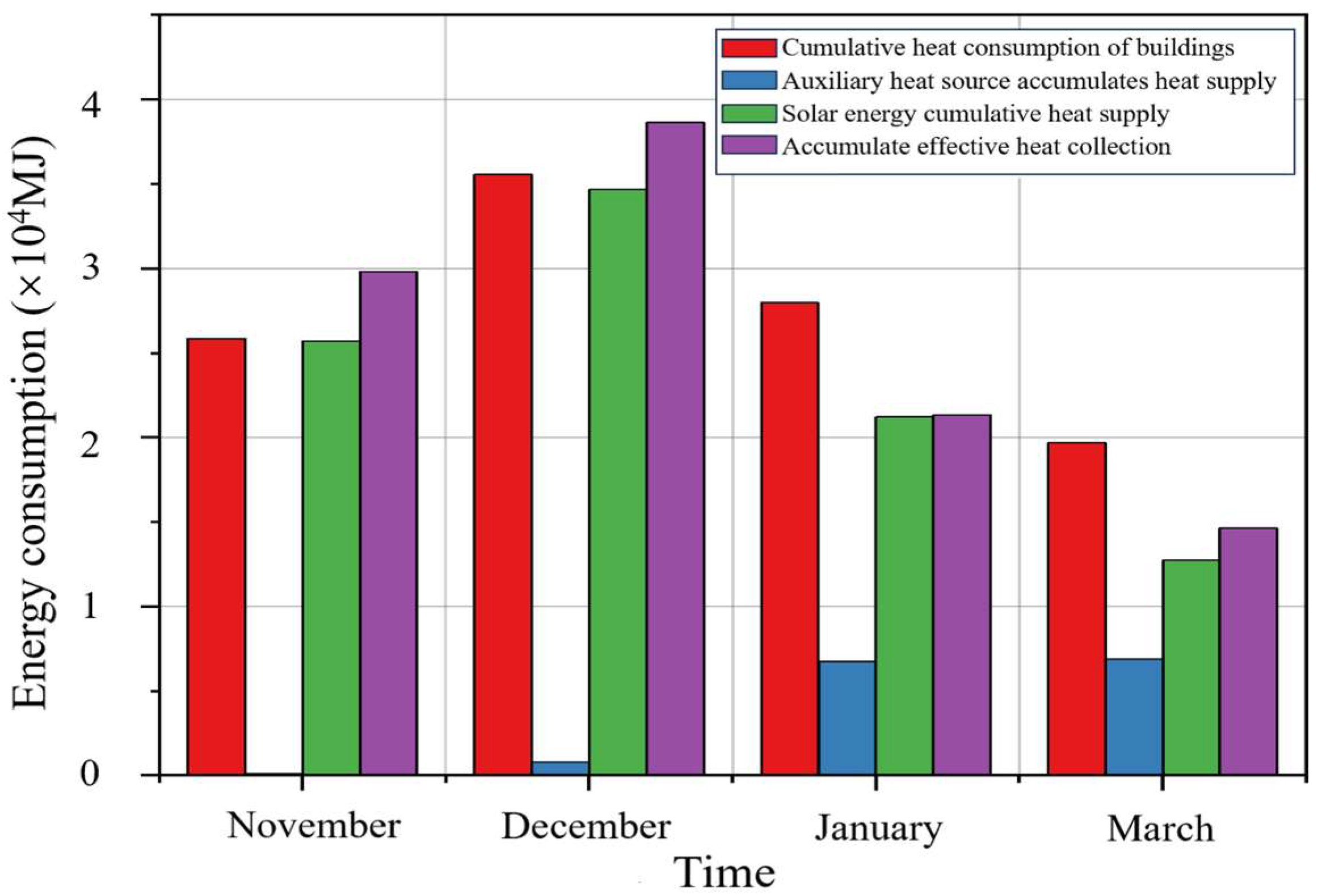
| Intermittent Heating Mode | Day–Night Intermittent Mode | Composite Intermittent Mode | Day–Night + Monthly Intermittent Mode |
|---|---|---|---|
| Cumulative heat load during heating season (MJ) | 100,648 | 137,170 | 121,570 |
| Total radiation during operation period (MJ/m2) | 3489.9 | 2672.5 | 2675.1 |
| Required collector area (m2) | 72 | 128 | 113 |
| The ratio of collector area required per unit heating area is (Ac/m) | 0.119 | 0.099 | 0.158 |
| Building Type | Office Building | Classroom Building | Dormitory Building |
|---|---|---|---|
| Architectural features | The volume is small, so natural ventilation and natural lighting can be used | Central corridor building, large rooms, good lighting, low floors | Square building, simple structure, and layout |
| construction area | 610 m2 | 1296 m2 | 700 m2 |
| Window to wall ratio | 0.4 | 0.5 | 0.3 |
| Building height | 3 floors above ground, 3 m high | 3 floors above ground, 3 m high | 3 floors above ground, 3 m high |
| Structure | Main Material Name | Thickness (mm) | Heat Transfer Coefficient (W/(m2·K)) |
|---|---|---|---|
| External Wall | Cement mortar | 20 | 0.42 |
| EPS insulation board | 76 | ||
| Clay brick | 200 | ||
| Interior Wall | Gypsum mortar | 20 | |
| Clay porous brick | 200 | 2.57 | |
| Cement mortar | 20 | ||
| Floor | Reinforced concrete | 200 | 0.89 |
| Cement mortar | 20 | ||
| Fine stone concrete | 20 | 0.63 | |
| Roofing | Extruded polystyrene board | 40 | |
| Reinforced concrete | 120 | ||
| External windows | Thermal break aluminum window | - | 1.4 |
| Double-layered glass | 24 |
| Serial Number | Module | Procedure |
|---|---|---|
| a | Building Envelope | Utilize the TYPE56 module with SketchUp for architectural modeling |
| b | Meteorological Data | Implement Type15 for TMY weather data processing |
| c | Solar Collection | Configure Type1b flat-plate collector module |
| d | Thermal Storage | Establish a Type158 vertical cylindrical tank with 5-node temperature stratification |
| e | Heat Distribution | Connect TYPE1231 radiator module to the TYPE56 for indoor heat transfer |
| f | Temporal Control | (1) Type14: Intermittent heating cycle regulation; (2) Type95: Weekend/holiday operation control |
| g | Data Output | Configure Type65 for parameter monitoring at specified intervals |
| h | Performance Analysis | Employ Type24 for heating output, energy consumption, and cumulative load calculations |
| Control Mode | Control Principle |
|---|---|
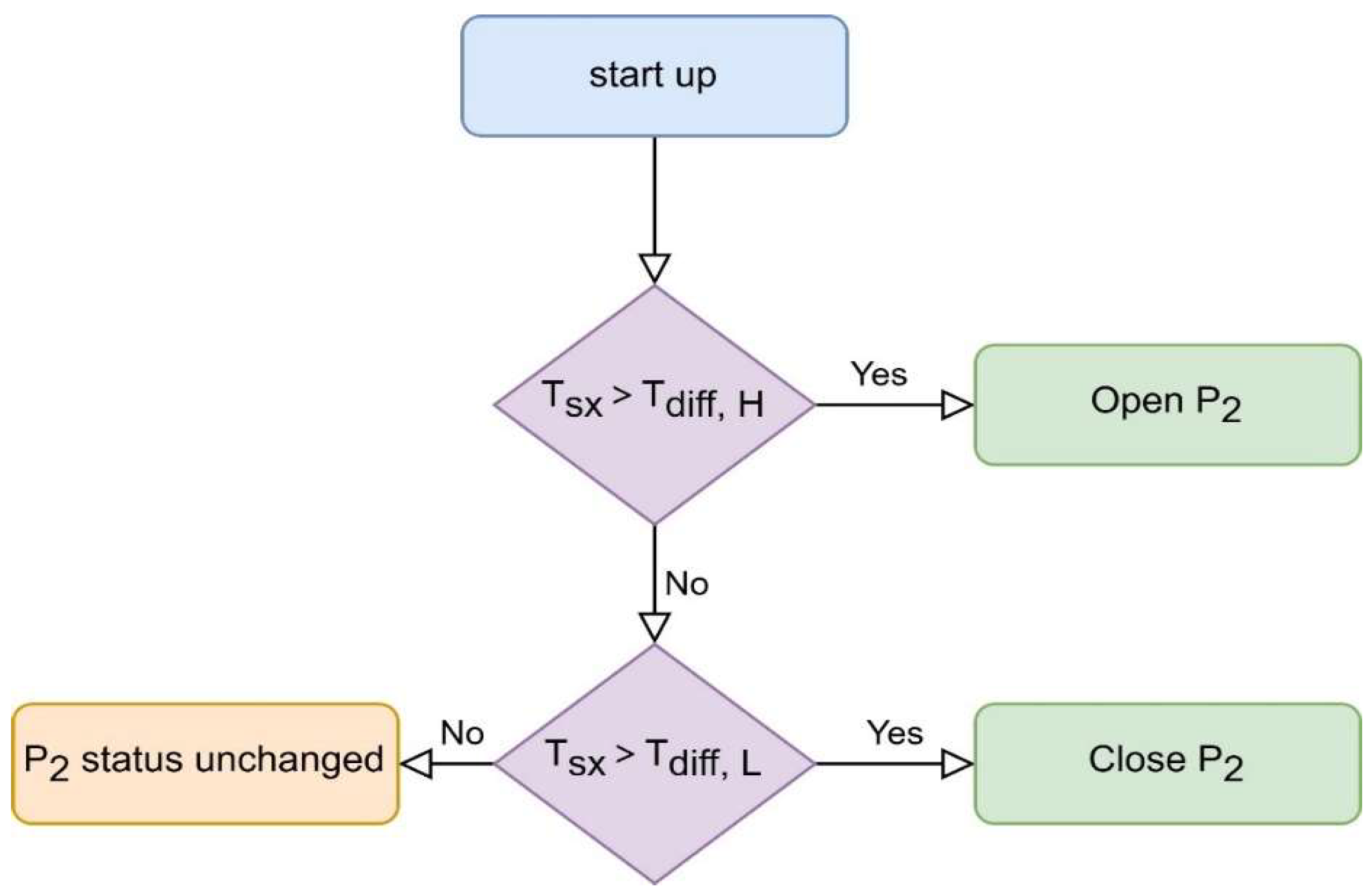
| A (Traditional Control) | When the maximum temperature of the heat storage tank is greater than Tdiff,H °C, turn off the heat collection circulation pump. When it is lower than Tdiff,L, turn on the heat collection circulation pump. |
| B (Traditional Control) | When the maximum temperature of the hot water tank is greater than Tdiff,H °C, the heating circulation water pump is turned on; when it is lower than Tdiff,L, the heating circulation pump is turned off. |
| Cumulative Energy Consumption of the Traditional Operation Strategy Throughout the Year (kWh) | Optimized Operation Strategy for the Cumulative Energy Consumption Throughout the Year (kWh) | |
|---|---|---|
| Heat collector circulation pump | 805 | 813 |
| Heating circulation pump | 573 | 690 |
| Auxiliary heat source | 8754 | 7024 |
| Total system energy consumption | 10,132 | 8527 |
| Period | Solar Radiation (W/m2) | Temperature Range (°C) | Mean Temperature (°C) |
|---|---|---|---|
| Early Season | 600–800 | −2~14 | 6 |
| Mid Season | 500–700 | −14~8 | −2 |
| Late Season | 60–1200 | −5~13 | - |
| System Form | Small Solar Water Heating System | Short-Term Thermal Storage Solar Heating System | Seasonal Heat Storage Solar Heating System |
|---|---|---|---|
| Hot water tank capacity range (L/m2) | 40–100 | 50–150 | 1400–2100 |
| Typical Buildings | Solar Thermal System Heat Supply (kJ) | Solar Energy Guarantee Rate | Average Daily Solar Radiation (kJ/m2·d) | Recommended Water Tank Volume (m3/m2) | Collector Area (m2) | Water Tank Capacity (m3) |
|---|---|---|---|---|---|---|
| Office building | 2,233,440 | 100% | 25,025 | 0.1 | 223 | 22.3 |
| Classroom Building | 3,449,865 | 0.1 | 344 | 34.4 | ||
| Dormitory Building | 2,542,838 | 0.1 | 254 | 25.4 |
| Typical Buildings | Solar Thermal System Heat Supply (kJ) | Solar Energy Guarantee Rate | Average Daily Solar Radiation (kJ/m2·d) | Recommended Water Tank Volume (m3/m2) | Collector Area (m2) | Water Tank Capacity (m3) |
|---|---|---|---|---|---|---|
| Office building | 930,600 | 100% | 25,025 | 0.1 | 93 | 9.3 |
| Classroom Building | 1,581,228 | 0.1 | 158 | 15.8 | ||
| Dormitory Building | 1,165,467 | 0.15 | 116 | 17.4 |
| Comparison of Two Design Methods | Office Building | Classroom Building | Dormitory Building | |
|---|---|---|---|---|
| Collector area required per unit heating area (m2/m2) | Traditional steady-state continuous heating | 0.37 | 0.27 | 0.36 |
| Traditional steady-state intermittent heating | 0.16 | 0.12 | 0.16 | |
| Dynamic intermittent heating method | 0.12 | 0.10 | 0.15 | |
| Water tank volume required per unit collector area (m3/m2) | Traditional steady-state continuous heating | 0.10 | 0.10 | 0.10 |
| Traditional steady-state intermittent heating | 0.10 | 0.10 | 0.15 | |
| Dynamic intermittent heating method | 0.12 | 0.07 | 0.22 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, X.; Bai, P.; Wang, Y.; Du, M. Dynamic Optimization and Performance Analysis of Solar Thermal Storage Systems for Intermittent Heating in High-Altitude Cold Regions. Buildings 2025, 15, 2908. https://doi.org/10.3390/buildings15162908
Hu X, Bai P, Wang Y, Du M. Dynamic Optimization and Performance Analysis of Solar Thermal Storage Systems for Intermittent Heating in High-Altitude Cold Regions. Buildings. 2025; 15(16):2908. https://doi.org/10.3390/buildings15162908
Chicago/Turabian StyleHu, Xiaojia, Pu Bai, Ying Wang, and Menghua Du. 2025. "Dynamic Optimization and Performance Analysis of Solar Thermal Storage Systems for Intermittent Heating in High-Altitude Cold Regions" Buildings 15, no. 16: 2908. https://doi.org/10.3390/buildings15162908
APA StyleHu, X., Bai, P., Wang, Y., & Du, M. (2025). Dynamic Optimization and Performance Analysis of Solar Thermal Storage Systems for Intermittent Heating in High-Altitude Cold Regions. Buildings, 15(16), 2908. https://doi.org/10.3390/buildings15162908






