Abstract
Public–Private Partnership (PPP) procurement is a relatively new approach in Nigeria’s housing sector. This study introduces a Fuzzy Risk Allocation Decision Model (FRADM) designed to address the complex and subjective nature of risk allocation in PPP-procured Mass Housing Projects (MHPs). A structured quantitative approach involving 40 purposively selected PPP housing experts was employed. Using a fuzzy synthetic evaluation (FSE) technique, critical risk factors were assessed based on partners’ risk management capabilities and allocation criteria. Constants (Ci) normalized the risk-carrying capacity indices (RCCIs) of both public and private sectors. Results show that risk attitude ranks highest among nine allocation criteria (MIS = 6.21), with the private sector demonstrating higher overall risk management capability. For instance, the availability of finance risk is optimally shared 53.48% to the private and 46.52% to the public sector. The FRADM was validated as reliable, practical, and replicable. Implications point to enhanced transparency, equitable risk-sharing, and support for SDG 11. The model is a strategic tool for decision-makers in PPP housing delivery in Nigeria and can inform similar efforts in other emerging economies. Further research should examine applications across other infrastructure sectors.
1. Introduction
Sustainable Development Goal (SDG) 11 and its Target 1 stressed the necessity for inclusive, safe, resilient, and sustainable urban environments, promoting universal access to adequate, safe, and affordable housing by 2030. However, in many developing economies such as Nigeria, the housing deficit remains a critical challenge, estimated at over 20 million units due to rapid urbanization, population growth, and inadequate financial and institutional frameworks [1,2,3]. Conventional procurement approaches have proved insufficient in addressing this vast housing gap. Consequently, Public–Private Partnerships (PPPs) have emerged as a strategic procurement method to address the housing deficit [3,4].
PPPs in mass housing enable governments to leverage private sector resources, expertise, and innovation, facilitating the delivery of affordable housing with shared responsibilities and risks [3,4]. In recent years, there has been a noticeable shift in national housing policy frameworks toward PPP-driven mass housing schemes, reflecting global best practices in collaborative infrastructure delivery. Studies such as Nwangwu [3] and Owolabi et al. [5] opined that PPPs offer significant potential for addressing Nigeria’s urban housing crises through structured financing, long-term asset management, and risk-sharing arrangements. However, the success of PPPs in mass housing largely hinges on effective risk allocation strategies. Risk, being inherently subjective and multifaceted, is often poorly allocated in PPP contracts, leading to disputes, cost overruns, and project delays [2,6]. As noted by Nubor [7], misallocation of project risk severely undermines project delivery outcomes, especially when risks are transferred to partners ill-equipped to manage such risk. This challenge is especially prevalent in Nigeria, where PPP housing schemes frequently suffer from irrational and undocumented risk-sharing practices [2,8].
Although extensive research has been conducted on PPP risk allocation models in infrastructural sectors such as water, transportation, and energy [6,9], there is a significant vacuum in the literature regarding PPP Mass Housing Projects (MHPs). These projects differ from conventional infrastructure due to social dimensions, land use acts, and stakeholders’ involvement, exposing the scheme to risk such as affordability gaps, political intervention, and legal uncertainties [1,10]. Moreover, literature underscores the need for context-specific, adaptable risk allocation models that account for housing sector peculiarities [1,2,6,8,10]. Given Nigeria’s renewed commitment to PPP mass housing, evidenced by the Federal Government’s approval of several PPP housing initiatives since 2020, there is an urgent need to adopt a structured and transparent decision-support tool to optimize risk allocation in PPP mass housing [2,6,8,9]. Accordingly, this study is guided by the following research questions viz (a) how can critical risks in PPP mass housing projects be equitably allocated between partners and (b) how effective is a fuzzy synthetic evaluation model in supporting risk allocation decision-making in the Nigerian context? And the objectives of this study are to (a) develop a Fuzzy Risk Allocation Decision Model (FRADM) tailored to Nigeria’s PPP-MHPs, (b) evaluate the relative risk management capabilities of public and private partners, and (c) validate the practicability and reliability of the FRADM for guiding risk allocation decisions. The developed model integrates multi-criteria decision-making techniques with expert judgments to improve objectivity, minimize bias, and ensure that each risk is allocated to the party most capable of managing it, thereby enhancing the efficiency and long-term sustainability of the scheme.
2. Literature Review
2.1. Challenges of Risk Allocation in PPP Mass Housing Procurement
Over the past decade, PPPs have gained traction across developing countries as governments look for new ways to address acute housing shortages. These partnerships aim to draw from private sector funding and technical know-how, especially in the delivery of affordable housing. But while the model holds promise, implementation has often been difficult due to thorny issues around governance and risk [11,12].
The risks inherent in PPP projects are often specific to the different types of each PPP initiative [11]. As such, the effectiveness of PPPs is largely determined by how well resources, risks, and benefits are shared among the parties involved [13]. These risks generally manifest across several phases of construction, such as operations, finance, commerce, and the political landscape. Financial risk, for instance, often stems from inaccurate projections regarding inflation, fluctuations in interest rates, and shifts in foreign exchange markets. In the construction phase, projects are vulnerable to unforeseen delays and escalating costs, while operationally, issues such as accidents or acts of vandalism introduce additional risk and uncertainty. Commercial risks are frequently linked to flawed assumptions about expenditure or traffic flow forecasts.
Other risk factors may include political instability, weak regulatory quality, corruption, and absence of government support; all contribute to investor hesitation and reduced private sector engagement in PPPs, irrespective of PPP procurement types [14].
The complexity of PPP mass housing projects arises from the intersection of long-term contractual obligations, community needs, as well as the above-mentioned risk and uncertainty; therefore, risk allocation remains one of the most contentious elements in these projects, especially in many African countries, including Nigeria, thus limiting sustainable investment in housing schemes [2,11,14]. Several studies emphasize that affordable PPP housing should be approached as a multi-attribute decision process; unfortunately, considerations such as long-term sustainability, transparency in risk sharing, and the preservation of community values are often underplayed, defeating the developmental objectives of housing as a public good. Moreover, risk attitudes and capacities vary significantly across partners in PPPs. While governments may be better positioned to mitigate macroeconomic and political risks such as land acquisition bottlenecks, policy shifts, or inflation—the private sector typically demonstrates stronger capacity in areas like construction performance, cost control, and innovation [15,16,17]. Without a transparent and analytical framework that captures these asymmetries, decision-makers’ risk would undermine the collaborative intent of PPPs in housing procurement.
2.2. Risk Allocation Criteria in PPP Contracts
Effective risk allocation is critical to the success of any PPP initiative. Central to this is the transfer of risks to the parties best equipped to manage them. Olojede et al. [10] noted that a well-structured allocation framework will not only safeguard public and private sector interests but also enhance overall project performance; thus, risk allocation criteria provide valuable insights into how risks should be assessed and shared, emphasizing the importance of collaborative and informed decision-making [18,19].
Key criteria include the ability to anticipate and evaluate risks, allowing the responsible party to implement preventive measures [18]. Lam et al. [20] emphasized the importance of minimizing, monitoring, and controlling risks proactively, rather than reacting only after they occur. Similarly, Li et al. [21] argued that the capacity to manage the consequences of realized risks is vital, such as when a private partner mitigates financial disruptions through flexible payment models. Ameyaw and Chan [16] suggested that when risks cannot be eliminated, they should be absorbed, diversified, or managed to reduce their impact. Cost-efficiency is another essential criterion; Lam et al. [20] maintained that risks should be assumed at the lowest reasonable cost and distributed fairly among project stakeholders. In some cases, taking on risk can be advantageous, enhancing an investor’s reputation, operational efficiency, or financial returns [1,2]. For instance, a private partner demonstrating strong risk management in a mass housing PPP may gain credibility and future opportunities.
Assigning risks to those best positioned to absorb potential losses is equally crucial. Xu et al. [18] advocated for risk distribution based on the ability to mitigate severity, reduce costs, and avoid service delays. However, risk-taking should come at a fair price. Ameyaw and Chan [16] stressed the importance of reasonable and acceptable risk premiums. Governments, for example, must assess whether it is more cost-effective to bear certain risks themselves, such as foreign exchange volatility, rather than compensate private operators charging excessive premiums. Risk attitude also plays a vital role. Risks should be allocated based on each party’s risk tolerance. For instance, governments may assume expropriation risks. Adopting such principles in PPP housing projects promotes fair and efficient risk-sharing, thereby enhancing project sustainability and long-term success [15,22] (see Table 1).

Table 1.
Determinant of equitable risk allocation in PPP procurement.
2.3. Theoretical Risk Allocation Frameworks Used by Researchers
A theoretical framework is a set of interrelated hypotheses aimed at explaining or advancing knowledge within defined boundaries [23]. Takona [24] also described a theoretical framework as a structured representation of key concepts and their assumed interconnections. Leo-Olagbaye et al. [25] emphasized the need for reviewing and adapting existing models to align with a doctoral thesis’s research focus.
Relevant frameworks for this study include the PPP risk allocation model by [21], which categorizes risks among public, private, and third-party stakeholders. Khazaeni et al. [6] proposed a fuzzy TOPSIS decision model incorporating uncertainty and expert judgment. Awodele [26] developed a conceptual framework for risk management in Nigeria’s private finance market using empirical data. Most central to this study is the framework by Ameyaw [15] and Kukah et al. [9], which applies a fuzzy-based, Delphi-guided approach to allocate risks in PPP infrastructure projects based on each party’s capacity to manage them.
2.4. Conceptual Framework for PPP Mass Housing Risk Allocation Optimization
A conceptual framework describes what is occurring with the things being studied and why, in addition to what one is interested in investigating [24]. A graphical model developed by Ameyaw [15] and Kukah et al. [9] to allocate risk in the PPP water and power schemes in Ghana was adopted and improved upon for this study using a Fuzzy synthetic evaluation approach with the introduction of SEM analysis to allocate the critical risk factors and effects on project delivery. According to Ameyaw [15], the model depicted in Figure 1 is a systematic approach where the output of the preceding step is fed into the subsequent steps. It facilitates addressing the subjective and imprecise nature of the risk allocation procedure. The following steps are into consideration in the decision-making process: (i) establishing basic criteria; (ii) defining a set of grade alternatives for the criteria that are expressed in linguistic terms; (iii) establishing a set of weighting by calculating the weight function of the evaluation risk; (iv) develop a fuzzy evaluation matrix for the factors; and (v) applying the weightings in (iii) and matrix to determine the final fuzzy evaluation.
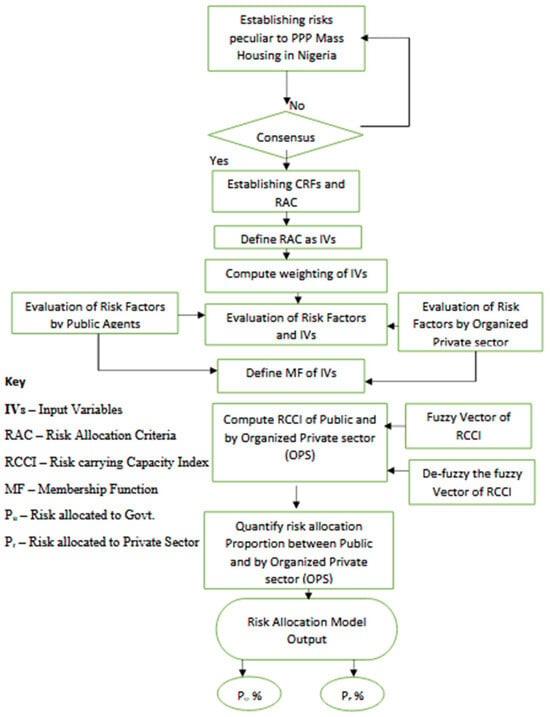
Figure 1.
Fuzzy-SEM-based Risk Allocation Decision Model; Source: Author’s Compilation.
3. Methods
An earlier study assessed the overall risk exposure in Nigeria’s PPP mass housing projects (MHPs), identifying 31 critical risk factors (CRFs) out of 63 for allocation among key stakeholders [1]. Based on this premise, the present study applied risk allocation criteria (RAC) to develop a fuzzy-based decision model, drawing on insights from purposively selected industry experts (see Table 2). The composition of the two expert panels is outlined in the table, while Table 3 presents the grading matrix used to assess both risk transfer proportions and management capabilities.

Table 2.
Profile of respondents.

Table 3.
Evaluation framework/linguistic terms for input variables.
Each panel from the Public and Private sectors comprised 20 professionals actively engaged in PPP-MHPs in Lagos and Abuja, and due to the relatively recent adoption of PPP in Nigeria’s housing sector, a snowball sampling approach was used to identify participants with relevant experience and organizational roles. Their input was considered both credible and essential to the study’s objectives.
The study employed an exponential non-discriminative snowball sampling method, wherein the initial participant referred multiple others. In simpler terms, the researcher engaged a primary respondent, who then connected several additional participants. As Adeoye [27] noted, all referrals should be included to reach a broader and more representative sample. To normalize the Membership Functions (MFs) and the Risk Carrying Capability Index (RCCI) for both parties, a constant (Ci) was derived using the Risk Management Capability (RMC) scale ranging from 0 to 1, as detailed in Table 3.
The model employs the Fuzzy Synthetic Evaluation (FSE) method to simultaneously assess multiple risk allocation criteria (RACs), accommodating the subjective and imprecise nature of PPP housing [15]. Following the identification of nine RACs, the 31 critical risk factors (CRFs) were evaluated and distributed between the public and private sectors using a five-point scale, where 1 indicates extremely low capability and 5 represents very high capability.
Respondents previously engaged in the study were re-contacted via email to validate the findings and assess the proposed risk allocation model for PPP mass housing projects (MHPs) in Lagos and Abuja. Over a three-week period, 20 responses were collected. The validation questionnaire included information on respondent profiles, the identified critical risk factors (CRFs), and the model’s output based on the Risk-Carrying Capability Indices (RCCIs) of both parties. A five-point Likert scale (1 = poor, 5 = excellent) was used to score each item. Respondents evaluated seven dimensions to assess the model’s relevance and practicality as follows: (a) appropriateness of input variables in reflecting the public/private partner’s risk management capacity, (b) reasonableness of variable rankings, (c) realism of risk allocation ratios for actual PPP-MHPs, (d) applicability of the fuzzy model in guiding decision-making, (e) ease of understanding and use by practitioners, (f) clarity and replicability of implementation procedures for both researchers and professionals, and (g) the model’s overall suitability for risk allocation in PPP-driven housing projects.
4. Results
Table 4 presents the mean rankings of the risk allocation criteria used in PPP-MHPs in Nigeria, based on a 7-point Likert scale. Among the evaluated criteria, partners’ risk attitude received the highest mean score (6.21), indicating its perceived importance in risk allocation. This was followed by the capacity to manage the likelihood of risk occurrence (6.18) and the ability to mitigate risks once they arise (6.12). In contrast, the capacity to bear the consequences of risk and to benefit from risk ranked lower, with mean scores of 5.34 and 5.19, respectively. Despite these variations, all criteria were considered relevant, with mean values ranging between 5.19 and 6.21, underscoring their collective significance in allocating perceived risks within PPP-MHPs.

Table 4.
Risk allocation criteria for PPP-MHPs.
4.1. Application of the Fuzzy Risk Allocation Decision Model (FRADM)
A single salient risk factor (Availability of Finance, also referred to as RF1) was selected from among the 31 established critical risk factors to illustrate the operation of the fuzzy allocation decision model. Table 5, Table 6 and Table 7 display the findings of the remaining 30 CRFs.

Table 5.
Input variables and their weighting functions.

Table 6.
RCCI of the government for the availability of finance (RF1).

Table 7.
RCCI of private for the availability of finance (RF1).
4.1.1. Determining the Input Variables’ (IVs’) Weighting Function
In step 1, the Nine (9) Risk Allocation Principles have been established and defined as input variables; therefore, given that the overall mean of IVs is 52.26, the weighting function of the variables is calculated. For instance, the weighting function of “Risk attitude (U1)” is normalized and obtained as follows:
Using this approach, Table 5 reports the weighting function of the other input variables.
4.1.2. Determining the Input Variables’ Membership Function
The membership function for an assessed risk factor’s input variable was determined by the combined expertise of each team. The survey indicates that Team A (Public) evaluated u1 (Risk Attitude) for RF1 in the following manner: 0% indicates very low capability, 40% indicates moderate capability, 60% indicates high capability, and 0% indicates very high capability. As a result, Team A’s membership function (MF) of u1 for RF1 is computed as follows:
It is possible to rewrite the MF of MFu1 (A) as (0.00, 0.00, 0.40, 0.60, and 0.00). The MF of the remaining input variables (u2–u9) is calculated and reported using the same approach, and the fuzzy matrix for RF1 is presented as follows:
| MFu1 | (0.00,0.00,0.40,0.60,0.00) | |
| MFu2 | (0.00,0.20,0.60,0.20,0.00) | |
| MFu3 | (0.00,0.20,0.40,0.40,0.00) | |
| MFu4 | (0.00,0.00,1.00,0.00,0.00) | |
| R(A) = | MFu5 | (0.00,0.00,1.00,0.00,0.00) |
| MFu6 | (0.00,0.20,0.00,0.60,0.20) | |
| MFu7 | (0.00,0.00,0.20,0.80,0.00) | |
| MFu8 | (0.00,0.00,0.40,0.80,0.00) | |
| MFu9 | (0.00,0.00,0.80,0.20,0.00) |
Similarly, Team B’s (Private) evaluation of the memberships function of the input variables for RF1 is expressed as follows: 0% denoting very low capability, 20% denoting moderate capability, 80% denoting high capability, and 0% denoting very high capability, Team B’s membership function (MF) of u1 for RF1 is calculated as follows:
The MF of MFu1(B) is thus rewritten as follows: (0.00, 0.00, 0.20, 0.80, and 0.00); the fuzzy matrix for the remaining input variables (u2–u9) for RF1 by Team B is expressed as follows:
| MFu1 | (0.00,0.00,0.20,0.80,0.00) | |
| MFu2 | (0.00,0.00,0.20,0.80,0.00) | |
| MFu3 | (0.00,0.00,0.60,0.40,0.00) | |
| MFu4 | (0.00,0.00,0.20,0.80,0.00) | |
| R(B) = | MFu5 | (0.00,0.00,0.40,0.60,0.00) |
| MFu6 | (0.00,0.00,0.20,0.80,0.00) | |
| MFu7 | (0.00,0.00,0.20,0.80,0.00) | |
| MFu8 | (0.00,0.00,0.80,0.20,0.00) | |
| MFu9 | (0.00,0.00,0.40,0.60,0.00) |
4.1.3. Determining the Public/Private Partners’ RCCI Membership Functions
Determining the membership function RCCI for both sectors follows after calculating the membership function of the input variable. The MF of the Public Partner’s RCCI for RF1 is thus computed using the fuzzy matrix (RA) and the weighting function (wi) that was calculated through the fuzzy composite operation.
| MFu1 | |||||||||
| MFu2 | |||||||||
| MFu3 | |||||||||
| MFu4 | |||||||||
| MFu5 | |||||||||
| DRRCCIgov = Wi * R(A) = (Wu1, Wu2, Wu3, Wu4, Wu5, Wu6, Wu7, Wu8, Wu9) X | MFu6 | ||||||||
| MFu7 | |||||||||
| MFu8 | |||||||||
| MFu9 | |||||||||
| (0.00,0.00,0.40,0.60,0.00) | |||||||||
| (0.00,0.20,0.60,0.20,0.00) | |||||||||
| (0.00,0.20,0.40,0.40,0.00) | |||||||||
| (0.00,0.00,1.00,0.00,0.00) | |||||||||
| DRRCCIgov = (0.119,0.118,0.117,0.115,0.116,0.109,0.104,0.103,0.099) X | (0.00,0.00,1.00,0.00,0.00) | ||||||||
| (0.00,0.20,0.00,0.60,0.20) | |||||||||
| (0.00,0.00,0.20,0.80,0.00) | |||||||||
| (0.00,0.00,0.20,0.80,0.00) | |||||||||
| (0.00,0.00,0.80,0.20,0.00) | |||||||||
= (0.00,0.08,0.55,0.34,0.03)
The result is shown in Table 8.

Table 8.
RCCI and RMC of government and private partners for the CRFs.
In the same way, the Private Partner determines the MF of RCCI for RF1 as follows:
| (0.00,0.00,0.20,0.80,0.00) | |
| (0.00,0.00,0.20,0.80,0.00) | |
| (0.00,0.00,0.60,0.40,0.00) | |
| (0.00,0.00,0.20,0.80,0.00) | |
| DRRCCIPrivate = (0.119,0.118,0.117,0.115,0.116,0.109,0.104,0.103,0.099) X | (0.00,0.00,0.40,0.60,0.00) |
| (0.00,0.00,0.20,0.80,0.00) | |
| (0.00,0.00,0.20,0.80,0.00) | |
| (0.00,0.00,0.80,0.20,0.00) | |
| (0.00,0.00,0.40,0.60,0.00) |
= (0.00,0.00,0.35,0.65,0.00)
The MF of RCCI of the other important risk factors, established by both parties using the same approach, is shown in Table 8.
4.1.4. Determine the Public and Private Sectors’ RCCI and RCM
By taking into account the scale intervals constant, the MF Public DRRCCIgov and Private DRRCCIPrivate are normalized. The Public Partner RCCI has been normalized for RF1 (finance risk) as follows:
The defuzzified risk management capability level for RF1 is given as follows:
Similarly, the RCCI for RF1 is normalized for the Private Partners as follows:
The defuzzified risk management capability level for RF1 by Private Partners is given as follows:
The scale interval of RMC is interpreted as follows: RMC < 1.5 denotes extremely low-risk management capability; 1.5 ≤ RMC < 2.5 indicates low-risk management capability; 2.5 ≤ RMC < 3.5 signifies moderate risk management capability; 3.5 ≤ RMC < 4.5 represents high-risk management capability; and RMC ≥ 4.2 reflects very high-risk management capability. The outcomes of the remaining CRFs’ RCCI and RMC are computed for both the public and private sectors utilizing the same technique as previously outlined.
4.1.5. Quantify Risk Allocation Proportion
Ameyaw [15] asserted that public and private partners possess distinct capabilities for managing risk associated with a certain risk factor. This study relies on prior research indicating that risk should be allocated to the party capable of managing its consequences. The risk allocation proportions are expressed as a percentage of the RCCI for both parties. The proportion of RF1 (Availability of Finance) that the government assumes is quantified as follows:
Similarly, the percentage of RF1 that the private bears is given as follows:
4.2. Validation of Fuzzy Risk Allocation Decision Model
To validate the proposed model in Figure 1 and the result in Table 9, respondents assessed seven key aspects, including its appropriateness, practicality, applicability, reliability, and overall suitability. As shown in Table 10, there was strong consensus on the relevance of the risk allocation criteria (RAC), with a mean score of 4.20, affirming accurate reflection of public and private partners’ risk management capacities. The prioritization of these criteria was also well supported by a high mean of 4.15, suggesting broader applicability across various PPP projects.

Table 9.
Summary of model results.

Table 10.
Validation results for the risk allocation model.
A mean score of 3.65 for risk allocation proportions indicates agreement that risk sharing should be tailored to individual projects and is feasible in Nigeria’s PPP-MHP context. Respondents also affirmed the model’s utility in decision-making, as reflected in the 3.80 mean score for its practical application. The FSE-based model was rated favorably overall, achieving a validation score of 4.20, indicating substantial expert support. The procedural logic of the model was considered replicable, earning a mean of 4.15, suggesting that both academics and practitioners could apply it across other PPP infrastructure projects. Finally, the model’s overall suitability for risk allocation in PPP-MHPs received a mean score of 4.05, confirming expert confidence in its effectiveness and relevance to the sector.
5. Discussion
Table 9 presents the model output derived using the Fuzzy Synthetic Evaluation (FSE) method, which determines the risk allocation ratios between public and private partners in PPP mass housing projects. The Fuzzy Risk Allocation Decision Model (FRADM) results indicate that risk distribution differs notably between the two sectors. Evaluations were based on a five-point scale, where 1 represents extremely poor capability and 5 represents very good capability. Each risk factor is fully allocated (100%), with proportions ranging from 0% (no responsibility) to 50% (shared responsibility) and up to 100% (full responsibility by one party). A party assuming at least 50% of a risk factor is considered primarily responsible for its management.
The Risk-Carrying Capability Index (RCCI), also ranging from 0 to 1, quantifies each party’s ability to manage specific risks. Higher RCCI values indicate stronger risk-bearing capacity. The findings reveal that the public sector can moderately manage 15 risk factors, each with a minimum 50% allocation. The private sector demonstrates moderate capability for 11 risk factors and high capability for 5, all exceeding the 50% threshold. Given the inherent complexity and risk of PPP-MHPs, it is evident that no single party can assume all risks. Effective collaboration and shared responsibility are essential for achieving the objectives of PPP housing initiatives and advancing SDG Goal 11.
5.1. Risks Allocated to the Public Sector in the PPP Mass Housing Scheme
These risks are inherently tied to the public sector due to its regulatory and leadership roles in PPPs. As shown in Table 4, the sector’s capacity reflects its risk attitude and ability to mitigate and manage potential risk occurrences, and the top 10 risk variables allocated to the sector are discussed as follows:
Currency fluctuation presents a major risk (RCCI = 0.57; allocation = 58.58%) to this sector, thereby increasing project costs and deterring private investment. The government’s recent monetary policies, such as currency redesign to curb excessive cash outside the banking system, are aimed at stabilizing the naira and improving investment conditions in the housing sector [28,29,30]. Economic cycles, including booms and recessions (RCCI = 0.61; allocation = 57.76%), can also be best managed by the public sector. Nigeria’s past experiences with both cycles have influenced household welfare and sectoral stability [31,32,33]. Policy responses like the Economic Recovery and Growth Plan (ERGP) reflect efforts to buffer adverse impacts and build economic resilience [34].
Financial market instability (RCCI = 0.54; allocation = 69.58%) significantly affects PPPs. Nigeria’s underdeveloped financial systems increase market risk, influence investor confidence, and limit credit access [35,36,37]. Enhancing financial infrastructure, especially through better credit mechanisms, remains key to improving housing finance. Interest rate volatility (RCCI = 0.57; allocation = 62.98%) impacts borrowing costs for private developers, while inflation (RCCI = 0.59; allocation = 57.04%) affects cost predictability in construction. Monetary policy adjustments are essential for stabilizing investment conditions in the sector [38,39,40].
Corruption and weak legal compliance (RCCI = 0.49; allocation = 52.60%) undermine PPP execution. This includes inconsistent law enforcement and unethical behavior, often deterring private investment. Effective public sector leadership and adherence to legal frameworks are critical to reducing these risks [2,41,42]. Ineffective execution of housing policies (RCCI = 0.58; allocation = 53.20%) remains a persistent challenge. Despite policy frameworks, poor implementation has hindered sectoral outcomes. Targeted awareness campaigns and stakeholder engagement could improve uptake and performance [2,43]. Flawed decision-making (RCCI = 0.58; allocation = 56.14%) impacts PPP outcomes. Weak institutional performance in areas such as permitting and enforcement constrains infrastructure growth [44,45]. Institutional reform is necessary to reduce bureaucratic delays and promote investor confidence. Changes in government (RCCI = 0.60; allocation = 55.58%) may disrupt long-term housing initiatives due to policy shifts. Strengthening autonomous bodies like the ICRC could enhance policy continuity and protect PPP projects from political fluctuations [2,46].
5.2. Risks Allocated to the Private Sector in the PPP Mass Housing Scheme
These risks are uniquely suited to the private sector, given its operational flexibility, financial expertise, and capacity to manage uncertainties. As shown in Table 4, allocations are guided by the sector’s risk attitude, mitigation ability, and likelihood control.
The availability of finance risk (RCCI = 0.66; allocation = 53.48%) is assigned to the private sector, reflecting its stronger capacity to mobilize capital. Given limited public funds, it is expected that private entities source project financing [14,42]. Similarly, high financing costs (RCCI = 0.66; allocation = 56.77%) fall under private responsibility due to their experience in financial planning and cost control. Lack of creditworthiness (RCCI = 0.56; allocation = 66.67%) is also a private sector risk, as securing loans hinges on financial stability and repayment reliability [2,47]. High bidding costs (RCCI = 0.57; allocation = 62.60%) are attributed to private partners who bear tendering expenses and manage procurement processes efficiently [13,42]. Although some studies argue that the public sector is better positioned to support project viability through incentives [13,42], this study allocates the risk of financial attractiveness (RCCI = 0.67; allocation = 64.42%) to the private sector. For PPP housing, relatively short contract durations offer quicker returns, aligning with private investment goals.
Misinterpretation of housing needs by low-income earners (RCCI = 0.57; allocation = 52.91%) is linked to the private sector’s role in stakeholder engagement. Their responsibility lies in informing end-users of project benefits and clarifying misconceptions related to location and design [2]. Illegal land titles (RCCI = 0.44; allocation = 52.87%) and encroachment (RCCI = 0.57; allocation = 63.13%) are attributed to private entities, particularly when access to land is gained through unofficial channels. This practice often leads to speculation and conflicts among developers, threatening project continuity [2,42]. Liu and Fong [48] argued that the private sector’s motivation, efficiency, and risk-handling expertise make it better suited to manage these risks in a cost-effective manner.
6. Conclusions
The study presents a robust methodology for assessing and assigning risks in PPP mass housing schemes, ensuring that they are allocated to the parties most capable of managing them. Findings reveal that the private sector assumes a larger share of risk due to its expertise, technological capacity, and managerial efficiency, which collectively enhance project delivery. Conversely, public sector risks stem largely from policy, regulatory, and macroeconomic conditions.
As Yuan and Zhang [49] noted, equitable risk distribution is essential for PPP success. This research introduces a Fuzzy Risk Allocation Decision Model (FRADM), which transforms subjective expert opinions and qualitative risk allocation criteria into quantitative outputs using fuzzy set theory. The FRADM offers a transparent and systematic framework for risk allocation, strengthening decision-making in PPP-MHPs. It recommends that stakeholders rigorously assess each party’s risk-handling capabilities prior to allocation to improve accountability and project outcomes. Adopting the nine risk allocation criteria enhances the model’s accuracy and efficiency, offering a credible alternative to subjective, preference-driven approaches. It also functions as a practical negotiation tool, enabling balanced and adaptive risk-sharing between public and private partners. Implementation of this model can reduce project delays and uncertainties while improving the long-term viability of PPP housing schemes globally.
6.1. Practical Implications and Lessons from Global PPP Practice
This study provides valuable insights for PPP stakeholders in Nigeria, especially in optimizing risk allocation for mass housing delivery. Drawing lessons from global experiences such as PPP housing initiatives in India, South Africa, and Malaysia, this emphasizes the need for structured decision-making models like the FRADM to support project viability. In India’s Rajiv Awas Yojana, for instance, clear frameworks for land risk and affordability gaps contributed to improved outcomes. Likewise, South Africa’s Social Housing Program incorporated private innovation with state guarantees, mirroring some of the shared-risk principles applied in this study.
For Nigeria, the FRADM demonstrates how evidence-based tools can improve collaboration, transparency, and long-term sustainability in PPP housing schemes. PPP stakeholders are encouraged to adopt the nine risk allocation criteria and fuzzy logic mechanisms for equitable risk-sharing. This approach not only supports improved project delivery but also aligns closely with national housing goals and SDG 11 on sustainable cities.
6.2. Study Limitations
This study is not without limitations. Firstly, it focuses exclusively on PPP mass housing projects in Nigeria, limiting the generalizability of findings to other infrastructure sectors. Secondly, the fuzzy model relies on expert judgments, which, while validated, are inherently subjective. Finally, the model has not yet been tested in live project environments, which may affect its operational robustness. Future research should explore longitudinal case studies across diverse PPP sectors and regions to further validate and refine the FRADM.
Author Contributions
Conceptualization, B.T.A.; methodology, B.T.A., S.H.P.C. and M.S.R.; validation, B.T.A., S.H.P.C. and M.S.R.; formal analysis, B.T.A., S.H.P.C. and M.S.R.; investigation, B.T.A.; resources, B.T.A.; data curation, B.T.A. and M.S.R.; writing—original draft preparation, B.T.A.; writing—review and editing, B.T.A. and S.H.P.C.; supervision, M.S.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
This study formed part of a PhD research project at Federal University of Technology Akure, Nigeria. Clearance was obtained through the approval of the Postgraduate Advisory Committee, which reviewed the research proposal before data collection.
Informed Consent Statement
Participation in the study was voluntary, and all participants provided informed consent after being adequately briefed on the purpose, confidentiality, and data usage.
Data Availability Statement
All original contributions presented in this study are included in the article. For further information or inquiries, please contact the corresponding author.
Acknowledgments
We appreciate the support of the DUT-FEBE Scientific Research Retreat facilitators (7–11 July 2025), industry experts who contributed to this study, and the editors and anonymous reviewers for their insightful feedback.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Arijeloye, B.T.; Oke, A.E.; Aje, I.O. Evaluation of the Critical risk factors in PPP-procured Mass Housing Projects in Abuja Nigeria-A fuzzy synthetic evaluation (FSE) approach. World J. Civ. Eng. Archit. 2023, 2, 58–85. [Google Scholar]
- Arijeloye, B.T.; Aje, I.O.; Oke, A.E. Evaluating the key risk factors in PPP-procured mass housing projects in Nigeria: A Delphi study of industry experts. J. Eng. Des. Technol. 2024, 22, 60–76. [Google Scholar] [CrossRef]
- Nwangwu, G. Public-Private Partnerships in Nigeria: The Journey so far. J. Commer. Prop. Law. 2021, 8, 97–115. [Google Scholar]
- Kwofie, T.E.; Michael, N.A.; Daniel, Y.A.D.; Aigbavboa, C.O.; Owusu, E.B.; George, F.O. Decision support factors evaluative model for affordable PPP public housing delivery in Ghana. J. Eng. Des. Technol. 2024. [Google Scholar] [CrossRef]
- Owolabi, O.B.; Alamu, O.; Haruna, L.Z. Housing policy and public private partnership in service delivery in Lagos, Nigeria. Int. Conf. Pioneer Innov. Stud. 2023, 1, 312–321. [Google Scholar] [CrossRef]
- Khazaeni, G.; Khazaeni, A. Multi-objective optimal allocation of construction project risks, ant colony optimization algorithm. Int. J. Build. Pathol. Adapt. 2024. [Google Scholar] [CrossRef]
- Nubor, P.K. Public Private Partnership as a Tool for the Provision of Social Housing in Port-Harcourt, Rivers State, Nigeria. J. Environ. Sci. Toxicol. Food Technol. 2020, 14, 56–67. [Google Scholar]
- Zakeri Afshar, A.; Abbasianjahromi, H.; Mirhosseini, S.M.; Ehsanifar, M. Determining the range of negotiable prices for public–private partnership infrastructure projects: A simulation approach. Int. J. Build. Pathol. Adapt. 2024, 43, 50–74. [Google Scholar] [CrossRef]
- Kukah, A.S.K.; Owusu-Manu, D.G.; Badu, E.; Edwards, D.J.; Asamoah, E. Fuzzy quantitative risk allocation model (FQRAM) to guide decision-making on risk allocation in Ghanaian public-private partnership (PPP) power projects. J. Financ. Manag. Prop. Constr. 2024, 29, 83–114. [Google Scholar] [CrossRef]
- Olojede, B.O.; Opawole, A.; Jagboro, G.O.; Alao, O.O. Examination of roles performed by public sector organizations in the procurement of public-private partnership projects. Int. J. Build. Pathol. Adapt. 2023, 41, 495–511. [Google Scholar] [CrossRef]
- Kouton, J.; Sanogo, W.; Djomgoue, N. Risk allocation in energy infrastructure PPPs projects in selected African countries: Does institutional quality, PPPs experience and income level make a difference? Econ. Change Restruct. 2023, 56, 537–580. [Google Scholar] [CrossRef]
- World Bank. Worldwide Governance Indicators (WGI) Database. 2020. Available online: http://info.worldbank.org/governance/wgi/ (accessed on 30 November 2024).
- Tah, J.H.M.; Carr, V. A proposal for construction project risk assessment using fuzzy logic. Constr. Manag. Econ. 2020, 18, 491–500. [Google Scholar] [CrossRef]
- Fleta-Asín, J.; Muñoz, F. How does risk transference to private partner impact on public-private partnerships’ success? Empirical evidence from developing economies. Socio-Econ. Plan. Sci. 2020, 72, 100869. [Google Scholar] [CrossRef]
- Ameyaw, E.E. Risk Allocation Model for Public-Private Partnership Water Supply Projects in Ghana. Ph.D. Thesis, The Hong Kong Polytechnic University, Hong Kong, China, 2015. [Google Scholar]
- Ameyaw, E.E.; Chan, A.P.C. Evaluation and ranking of risk factors in public-private partnership water supply projects in developing countries using fuzzy synthetic evaluation approach. Expert Syst. Appl. 2015, 42, 5102–5116. [Google Scholar] [CrossRef]
- Osei-Kyei, R.; Jin, X.; Nnaji, C.; Akomea-Frimpong, I.; Wuni, I.Y. Review of risk management studies in public-private partnerships: A scientometric analysis. Int. J. Constr. Manag. 2023, 23, 2419–2430. [Google Scholar] [CrossRef]
- Xu, Y.; Yeung, J.F.; Chan, A.P.; Chan, D.W.; Wang, S.Q.; Ke, Y. Developing a risk assessment model for PPP projects in China—A fuzzy synthetic evaluation approach. Autom. Constr. 2010, 19, 929–943. [Google Scholar] [CrossRef]
- Guerrero, A.; Lara-Galera, A.; Alcaraz Carrillo de Albornoz, V.; Arévalo Sarrate, C. Determinant Features to Reduce the Infrastructure Gap in Saudi Arabia Under a Public–Private Partnership Scheme. Buildings 2024, 14, 699. [Google Scholar] [CrossRef]
- Lam, T.; Wang, D.; Lee, P.T.; Tsang, Y.T. Modeling risk allocation decisions in construction contracts. Int. J. Proj. Manag. 2007, 25, 485–493. [Google Scholar] [CrossRef]
- Li Akintoye, A.; Hardcastle, C. Risk analysis and allocation in public-private partnerships projects. In Proceedings of the 17th Arcom Annual Conference, Salford, UK, 5–7 September 2001. [Google Scholar]
- Mazher, K.M.; Chan, A.P.; Zahoor, H.; Ameyaw, E.E.; Edwards, D.J.; Osei-Kyei, R. Modelling capability-based risk allocation in PPPs using fuzzy integral approach. Can. J. Civ. Eng. 2019, 46, 777–788. [Google Scholar] [CrossRef]
- Hirose, M.; Creswell, J.W. Applying core quality criteria of mixed methods research to an empirical study. J. Mix. Methods Res. 2023, 17, 12–28. [Google Scholar] [CrossRef]
- Takona, J.P. Research design: Qualitative, quantitative, and mixed methods approach. Qual. Quant. 2024, 58, 1011–1013. [Google Scholar] [CrossRef]
- Leo-Olagbaye, F.; Odeyinka, H.; Rathnasiri, P. Stakeholders’ Roles in the Delivery of Sustainable Housing Projects in Lagos State, Nigeria. Sustainability 2023, 15, 11709. [Google Scholar] [CrossRef]
- Awodele, O.A. Framework for Managing Risk in Privately Financed Market Projects in Nigeria. Ph.D. Thesis, School of the Built Environment Heriot-Watt University, Edinburgh, UK, 2012. [Google Scholar]
- Adeoye, M.A. Review of Sampling Techniques for Education. ASEAN J. Sci. Educ. 2023, 2, 87–94. [Google Scholar]
- Central Bank of Nigeria. Redesigning of the Currency. 2022. Available online: www.cbn.gov.ng (accessed on 23 January 2025).
- Dada, A.D. Currency Redesign Policy Implementation: Implications for Industrial Performance in Nigeria. Am. J. Ind. Bus. Manag. 2023, 13, 889–910. [Google Scholar] [CrossRef]
- Pillah, T.P. Currency redesign and monetary policy of Nigeria: An evaluation. Int. J. Public Adm. Manag. Res. 2023, 8, 46–53. [Google Scholar]
- De Grauwe, P. Booms and busts in economic activity: A behavioral explanation. J. Econ. Behav. Organ. 2012, 83, 484–501. [Google Scholar] [CrossRef]
- Njoku, O.E.; Lee, Y. Financial Strategies Driving Market Performance During Recession in Nigerian Manufacturing Firms. J. Risk Financ. Manag. 2025, 18, 81. [Google Scholar] [CrossRef]
- Zakari, M. Economic Recovery Growth Plan and Economic Development in Nigeria’s Post-Recession Era. Public Adm. Reg. Stud. 2023, 16, 99–118. [Google Scholar]
- Anam, B.E.; Ijim, U.A.; Ironbar, V.E.; Otu, A.P.; Duke, O.O.; Achuk Eba, M.B. Economic recovery and growth plan, economic sustainability plan and national development plan (2021–2025): The Nigerian experience under President Muhammadu Buhari. Cogent Soc. Sci. 2024, 10, 2289600. [Google Scholar] [CrossRef]
- Lawal, C.; Friday, S.; Ayodeji, D.; Sobowale, A. Advances in public-private partnerships for strengthening national financial governance and crisis response systems. Int. J. Adv. Multidiscip. Res. Stud. 2024, 6, 1700–1719. [Google Scholar] [CrossRef]
- Mukasa, J. Market Risk Analysis in Investment Portfolios in Uganda. J. Mod. Risk Manag. 2023, 1, 1–12. [Google Scholar] [CrossRef]
- Abiloro, T.O.; Ilugbami, J.O. Regulatory Institutions and National Economic Development in Nigeria. Int. J. Res. Innov. Soc. Sci. 2023, 7, 1552–1575. [Google Scholar] [CrossRef]
- Efuntade, O.O.; Efuntade, A.O.; Fcib, A.; Olugbamiye, D.O. Assessing the effect of international lending interest rate volatility on government infrastructural expenditure. Int. J. Econ. Financ. Manag. 2023, 8, 1–17. [Google Scholar] [CrossRef]
- Babayo, M.M.; Milala, S. The Role of Interest Rate Volatility in Shaping Commercial Real Estate Financing Decisions: A Central Bank Perspective: A case study of Nigeria. Int. J. Curr. Res. Sci. Soc. Sci. Lang. 2024, 4, 12–24. [Google Scholar]
- Guobadia, J.O.; Etim, N.M.; Mfon, I.I. The Impact of Monetary Policy Instruments on Nigeria’s Construction Sector: A Focus on Money Supply, Inflation Rate, Exchange Rate, and Interest Rate. Int. J. Dev. Sustain. Environ. Manag. 2024, 4, 1–15. [Google Scholar]
- Zhang, S.; Li, J.; Li, Y.; Zhang, X. Revenue Risk Allocation Mechanism in Public-Private Partnership Projects: Swing Option Approach. J. Constr. Eng. Manag. 2021, 147, 04020153. [Google Scholar] [CrossRef]
- Jiang, W.; Jiang, J.; Martek, I.; Jiang, W. Critical risk management strategies for the operation of public–private partnerships: A vulnerability perspective of infrastructure projects. Eng. Constr. Archit. Manag. 2024, 32, 4771–4795. [Google Scholar] [CrossRef]
- Ichendu, C.; Amadi, D.E. Personalization, flexibility components of housing, the new paradigm in housing development: A panacea to housing deficit in Rivers State, Nigeria. J. Archit. Civ. Eng. 2021, 6, 1–6. [Google Scholar]
- Essien, I.O. Modelling Project Complexity for Leadership Decision Making and Success in the Building Construction Industry in Lagos, Nigeria. Ph.D. Thesis, Oxford Brookes University, Oxford, UK, 2021. [Google Scholar]
- Jiang, W.; Yang, Q.; Jiang, J.; Martek, I.; Gao, F. Operational risk management of public–private partnership infrastructure projects: A bibliometric literature review. Buildings 2022, 12, 1905. [Google Scholar] [CrossRef]
- Justus, N.I.; Nwagbara, A.O.; Nnadi, E.O. Framework for Mitigating the Impact of Risk in the Management of TETfund Building Projects Between 2012–2022 In South East, Nigeria. Contemp. J. Manag. 2024, 6, 80–91. [Google Scholar]
- Li, Z.; Wang, H. Exploring risk factors affecting sustainable outcomes of global public–private partnership (PPP) projects: A stakeholder perspective. Buildings 2023, 13, 2140. [Google Scholar] [CrossRef]
- Liu, T.; Fong, P.S. Towards an Enhanced Business Case Development for Public–Private Partnership (PPP) Projects: A Comparative Study of China and New Zealand. Public–Private Partnerships (PPPs) for Construction Project Deliveries. Buildings 2025, 15, 1154. [Google Scholar] [CrossRef]
- Yuan, R.; Zhang, B. An Evolutionary Game Study on the Collaborative Mechanism for Construction Digitalization Among Governments, Contractors, and Service Providers. Buildings 2025, 15, 1933. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).