Next Article in Journal
Spatio-Temporal Coupling and Forecasting of Construction Industry High-Quality Development and Human Settlements Environmental Suitability in Southern China: Evidence from 15 Provincial Panel Data
Previous Article in Journal
Experimental and Mechanism Study on Axial Compressive Performance of Double Steel Tube Columns Filled with Recycled Concrete Containing Abandoned Brick Aggregate
Previous Article in Special Issue
AI-Based Variable Importance Analysis of Mechanical and ASR Properties in Activated Waste Glass Mortar
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Buildings
Volume 15
Issue 14
10.3390/buildings15142426
buildings-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Research on the Deformation Laws of Adjacent Structures Induced by the Shield Construction Parameters

by
Jinhua Wang
1,2,3,4,5,*,
Nengzhong Lei
2,5,
Xiaolin Tang
1,3 and
Yulin Wang
2,4,*
1
State Key Laboratory of Safety and Resilience of Civil Engineering in Mountain Area, East China Jiaotong University, Nanchang 330013, China
2
College of Civil and Architectural Engineering, Wuyi University, Wuyishan 354300, China
3
School of Civil Engineering and Architecture, East China Jiaotong University, Nanchang 330013, China
4
Engineering Research Center of Prevention and Control of Geological Disasters in Northern Fujian, Fujian Province University, Wuyishan 354300, China
5
Key Laboratory of Smart Town Construction of Hilly Mountains (Wuyi University), Fujian Province University, Wuyishan 354300, China
*
Authors to whom correspondence should be addressed.
Buildings 2025, 15(14), 2426; https://doi.org/10.3390/buildings15142426
Submission received: 19 June 2025 / Revised: 3 July 2025 / Accepted: 8 July 2025 / Published: 10 July 2025
(This article belongs to the Special Issue Urban Renewal: Protection and Restoration of Existing Buildings)
Browse Figures
Versions Notes

Abstract

Taking the shield construction of Xiamen Metro Line 2 tunnel side-crossing the Tianzhushan overpass and under-crossing the Shen-Hai Expressway as the engineering background, FLAC3D 6.0 software was used to examine the deformation of adjacent structures based on shield construction parameters in upper-soft and lower-hard strata. The reliability of the numerical simulation results was verified by comparing measured and predicted deformations. The study results indicate that deformation of the pile will occur during the construction of the tunnel shield next to the pile foundation. The shape of the pile deformation curve in the horizontal direction is significantly influenced by the distance from the pile foundation to the adjacent tunnel’s centerline, as well as by soil bin pressure, grouting layer thickness, and stress release coefficient. During the tunnel shield construction beneath the expressway, increasing the soil bin pressure, the grouting layer thickness, and reducing the stress release coefficient can effectively minimize surface deformation and differential settlement on both sides of the deformation joints between the bridge and the roadbed. The practice shows that, by optimizing shield construction parameters in upper-soft and lower-hard strata, the deformation of nearby bridges and pavements can be kept within allowable limits. This is significant for reducing construction time and costs. The findings offer useful references for similar projects.

1. Introduction

With urbanization accelerating, urban populations are becoming increasingly dense, and ground traffic congestion is becoming increasingly serious. However, the metro is fast, punctual, does not occupy ground space, reduces urban air pollution, and addresses urban congestion effectively, and thus a large number of large cities are vigorously promoting the construction of the metro. However, the metro construction process inevitably has an impact on the existing structures in the strata. Tunnel construction will alter the stress state of the surrounding soil, leading to soil deformation that affects the surface and structures in the strata. When these deformations exceed the allowable deformation, it may jeopardize the structural integrity and normal functionality of the existing structures.
The main methods for assessing the effects of tunnel shield construction on nearby structures include numerical simulation, model testing, analytical solutions, on-site monitoring, etc. On-site monitoring is often used as the verification means for other research methods. Therefore, in the existing research, two or more methods are usually combined for the study, and the reliability of research results are mutually verified through a variety of methods.
From the aspect of numerical simulation research: Liu et al. [1] used numerical simulation to assess the effects of shield tunnel construction on a railway bridge pile foundation, and diverse protective measures were adopted to ensure bridge safety. Kanagaraju et al. [2] conducted an analysis on the effects of tunneling on pile deformation in a sandy soil foundation using PLAXIS3D software. Phutthananon et al. [3] studied how the distance between the palisade surfaces of two tunnels affects the deformation of adjacent monopiles during the construction of parallel two-lane tunnels using numerical simulation. Du et al. [4] combined numerical simulation and on-site monitoring to investigate the horizontal and vertical displacements, as well as stress characteristics of pile foundations during shield construction. Wu et al. [5] performed numerical simulations to examine the deformation of pile foundations for high-speed railway bridges under three working conditions during shield construction. Zhang et al. [6] studied the effects of pile-tunnel spacing, vertical load, and depth of tunnel overburden on piles’ horizontal displacement and bending moment using field tests and numerical methods. Li et al. [7] utilized the finite element method to investigate the effectiveness of different protection schemes in the construction of tunnel side penetration pile groups. Zhang et al. [8] used numerical simulation to assess how shield construction affects the deformation of nearby buildings and their piles. Zhang et al. [9] studied the effects of shield tunneling on surface settlement, the internal forces and deformations in pile foundations based on numerical simulation. Hu et al. [10] carried out a numerical simulation to examine the effects of shield construction on the bearing capacity and deformation of piles situated in water-saturated sand and pebble layers. Wei et al. [11] conducted a numerical simulation to examine the effects of subway tunnel construction on ground surface deformation and the stability of adjacent pile foundations in loess regions. Xin et al. [12] conducted a numerical simulation to investigate the deformation of bridge pile foundations resulting from the construction of adjacent two-lane tunnels. Peng et al. [13] performed a numerical simulation to study surface settlement and pile deformation under two different reinforcement schemes for pile foundations. Gao et al. [14] conducted a simulation to investigate how shield construction affects existing pile foundations’ deformation and proposed control measures for these deformations.
From the aspect of analytical solutions: Huang et al. [15] examined pile–soil–tunnel interactions using a Pasternak-based two-stage analysis and validated the analytical solution by comparing it with on-site data and finite element method (FEM) results from real engineering cases. Wei et al. [16] introduced a simplified analytical method to evaluate the effects of adjacent tunnel excavation on existing pile foundations, confirming its accuracy through multiple approaches. Lei et al. [17] introduced a micro-disturbance control technology system that integrates a “two-stage analysis method for theoretical prediction with active control and passive protection.” Gu et al. [18] investigated the effects of adjacent tunnel excavation on nearby pile foundations using a random finite difference method that accounts for spatial variations in soil properties. Huang et al. [19] derived the equations for calculating vertical settlement and horizontal deformation of adjacent pile foundations during shield construction using the Winkler model, with theoretical calculations aligning well with field measurements. Liu et al. [20] proposed an analytical method to assess the horizontal response of shield tunnels to piles, considering factors like included angle, soil–pile interaction in tunnel environments, and shielding effects of pile groups.
From the aspect of model test research: Ng et al. [21] performed a 3D centrifuge test to study how double-tunnel construction affects an existing single pile. Zhang et al. [22] examined the deformation impacts of large-scale double-hole tunnel excavation on existing pile groups through a 3D centrifuge model test. Song et al. [23] analyzed the redistribution mechanism of pile internal forces near the tunnel excavation area by five centrifuge tests. Ng et al. [24] studied the variation laws of pile settlement, bearing capacity loss, and surface settlement under two different construction sequences through centrifuge model tests and numerical back analysis. He et al. [25] investigated the response of 2×2 pile groups in clay at various minimum distances using a micro shield machine for physical model tests and numerical simulation. Su et al. [26] conducted a comprehensive analysis of how tunnel shield excavation affects the ground and pile foundations under different groundwater conditions, using model tests and numerical simulations.
Upper-soft and lower-hard strata is one of the common composite strata. Generally, the upper strata are softer and the lower strata are harder. These types of strata have different deformation resistances due to the significant disparity in strength between the upper and lower strata. Many scholars have studied how tunneling through soft upper and hard lower strata impacts ground deformation and nearby structures. Wu et al. [27] studied how different soft and hard strata ratios, grouting pressure, and soil bin pressure affect the deformation of upper-soft and lower-hard strata using numerical simulation. Wang et al. [28] proposed a method for predicting surface settlement using numerical simulation, artificial neural networks, and Bayesian networks. This study examined factors affecting surface settlement during shield tunnel construction in upper-soft and lower-hard fractured rock masses. Ding et al. [29] investigated the effect of the ratio between the hard layer depth and the excavation diameter on the shape of the surface settlement. They proposed a predictive method for assessing surface settlement during shield construction in soil–rock mixed strata. Li et al. [30] investigated the surface settlement of shield construction in soil–rock composite strata using on-site monitoring and numerical simulations. They found that composite strata significantly influence maximum settlement more than the width of the settlement trough, with a stronger effect in soil layers compared with rock layers. Liu et al. [31] studied the modified Peck formula’s applicability in upper-soft and lower-hard strata through numerical simulations and on-site monitoring. They analyzed how soil bin pressure and grouting pressure affect surface settlement. Liu et al. [32] studied the collapse mechanisms of shallow tunnels in upper-soft and lower-hard strata through model testing. They proposed a minimum rock-span ratio for different tunnel depths. Jiao et al. [33] investigated the deformation of shield tunnels located beneath existing railways within soil–rock composite strata. Their study clarified how tunnel depth, hard rock ratio, and subgrade reinforcement affect track deformation. Jiao et al. [34] investigated the effects of pipe depth, tunnel curvature radius, hard layer ratio, and other factors on pipeline deformation in soil–rock composite strata. Their research indicates that the hard layer ratio significantly influences pipeline deformation.
In summary, different scholars have examined how tunnel shield construction affects the deformation of adjacent structures under different engineering background conditions, and have achieved certain results, but these research results are carried out for a particular engineering background. At present, there is a scarcity of research addressing the deformation impact of metro tunnel shield construction on nearby structures situated in upper-soft and lower-hard strata. This paper examines the construction of the Xiamen Metro Line 2 Tianzhushan–Dongfu Interval Tunnel, which involves tunneling side-crossing Tianzhushan overpass and under-crossing Shen-Hai Expressway as the engineering background. FLAC3D was utilized to investigate how shield construction parameters affect the differential deformation of the pile foundation at abutment No. 0 of the overpass bridge, as well as the differential deformation at both sides of the deformation joint between the bridge and roadbed, and expressway pavement deformation. The parameters studied include soil bin pressure, grouting layer thickness, and stress release coefficient. The results of the numerical simulations are compared with on-site monitoring data, providing valuable references for similar projects.

2. Project Overview

The Tianzhushan–Dongfu segment of Xiamen Metro Line 2 commences at Tianzhushan Station, turns left with a radius of 800 m, runs southward along Tianzhushan Road, then under-crossing Shen-Hai Expressway with a right deviation curve with a radius of 650 m, then runs southward, and finally enters Dongfu Station with a left deviation of 1000 m. The right track is 1526.975 m long and the left track is 1529.036 m long. The interval section is constructed by the composite EPB shield, and the segments are assembled in the 3 + 2 + 1 mode with staggered joints. The segments are 1200 mm wide and 350 mm thick, the outer diameter is 6200 mm, and the inner diameter is 5500 mm. The interval tunnel side-crossing Tianzhushan overpass and under-crossing Shen-Hai Expressway. The superstructure of Tianzhushan overpass adopts a 3 × 20 m prestressed concrete hollow slab. The No.0 abutment is a pile-connected cap beam abutment, and the No.1 pier is a pile–column pier. The pile foundations are all 1200 mm bored piles, and the pier diameter is 1000 mm. When the tunnel side-crossing Tianzhushan overpass, the distances from the right tunnel’s centerline to the pile foundations of No.0 abutment 1–8 of the overpass are 14.62 m, 13.99 m, 13.31 m, 12.58 m, 11.83 m, 11.01 m, 10.16 m, and 9.25 m. The plane relationship between the shield tunnel and Shen-Hai Expressway and Tianzhushan overpass is shown in Figure 1. The sectional diagram is shown in Figure 2. Table 1 lists the physical and mechanical parameters of soil layers. Table 2 lists the allowable pavement and bridge deformations.

3. The Deformation Laws of Adjacent Structures by the Shield Construction Parameters

3.1. Numerical Modeling

According to Figure 1 and Figure 2, the numerical model dimensions are as follows: the width is 85.00 m, the length is 90.00 m, and the height is 39.80 m. The tunnel is diagonally intersected with the bridge, and the numerical model contains a variety of structures, such as pile foundations, pier columns, tie beams, segments, grouting layers, pavements, etc. It is difficult to use the FLAC3D built-in grid for modeling, which cannot easily meet the modeling of irregular shapes. Therefore, the numerical simulation 3D model was built using Rhino 6 and grid division using Griddle 1.0 software with 8-node hexahedral cells. In the grid division, based on the varying effects of tunnel excavation on nearby strata and structures, the meshing density is different. The grids of the segment, grouting layer, pile foundation, and tunnel perimeter soils are encrypted. Tunnel perimeter soils, segments, and grouting layers within the excavation range of the tunnel are divided into 75 sections along its axis. Each section is 1.2 m long to simulate tunnel excavation. To simplify the model, assuming that each soil layer is uniformly distributed horizontally, and the pavement structure layer is equivalent to one layer, which is named as the pavement structure. The three-dimensional model of the subway tunnel side-crossing Tianzhushan overpass and under-crossing Shen-Hai Expressway can be established as shown in Figure 3. The three-dimensional model of the tunnel and Tianzhushan overpass is shown in Figure 4.
The model boundary conditions are as follows: the bottom and surrounding area are characterized by fixed boundaries, while the top is designated as a free boundary. The overload of the bridge deck and pavement is 20 kN/m2.
Tunnel construction process simulation: the length of each construction section is 1.20 m. The simulation of construction process is as follows: ① the null model is used to deal with the soil unit on the excavation face; ② apply the soil bin pressure to the working face; ③ stress release of soil around the tunnel; ④ segment assembly; ⑤ change the soil layer material outside the segment to simulate increased strength after grouting; ⑥ enter the next cycle. The construction sequence of the two tunnels is as follows: the left tunnel is constructed first, then the right tunnel.
The Mohr–Coulomb strength criterion is extensively utilized in geotechnical engineering due to the ease of obtaining its parameters and its clear physical significance. This criterion can effectively reflect the failure behavior of geotechnical bodies under different stress states. Wu et al. [27], Li et al. [30], Feng et al. [35] and Li et al. [36] used the Mohr–Coulomb strength criterion as the constitutive model for strata, examining how shield construction affects surface deformation in upper-soft and lower-hard layers. Research findings indicate that the Mohr–Coulomb strength criterion demonstrates a certain degree of applicability in upper-soft and lower-hard strata. Therefore, the Mohr–Coulomb strength criterion is applied to the constitutive model of each soil layer in this study. The parameter values for each soil layer are derived from the geotechnical investigation report pertaining to the interval section. The values for each soil layer parameter are listed in Table 1. Linear elastic models are adopted for pile foundation, cover (tie) beam, pier column, bridge deck system, pavement structure, tunnel segment, grouting layer, etc. The parameter values are listed in Table 3.
In the process of numerical calculation, deformation observation points were arranged on the 0#1–0#8 pile foundations. Horizontal displacement observation points were arranged every 3 m from the pile top to bottom, along the side of each pile foundation adjacent to the roadbed. A vertical displacement observation point was arranged at the pile top. A row of surface deformation observation points (hereinafter referred to as “Section 1”) were arranged at the surface. A row of deformation observation points (hereinafter referred to as “section 2”) were arranged on the pavement of Shen-Hai Expressway. A row of observation points were arranged on both sides of the deformation joint at the junction of the bridge and roadbed, and the observation points on both sides of the deformation joint are connected t the center point of pile foundation in the same straight line. Eight observation points were arranged on the abutment side and eight points on the roadbed side to observe uneven deformation at the deformation joint sides caused by tunnel shield construction. A layout diagram of the deformation observation points is shown in Figure 5.

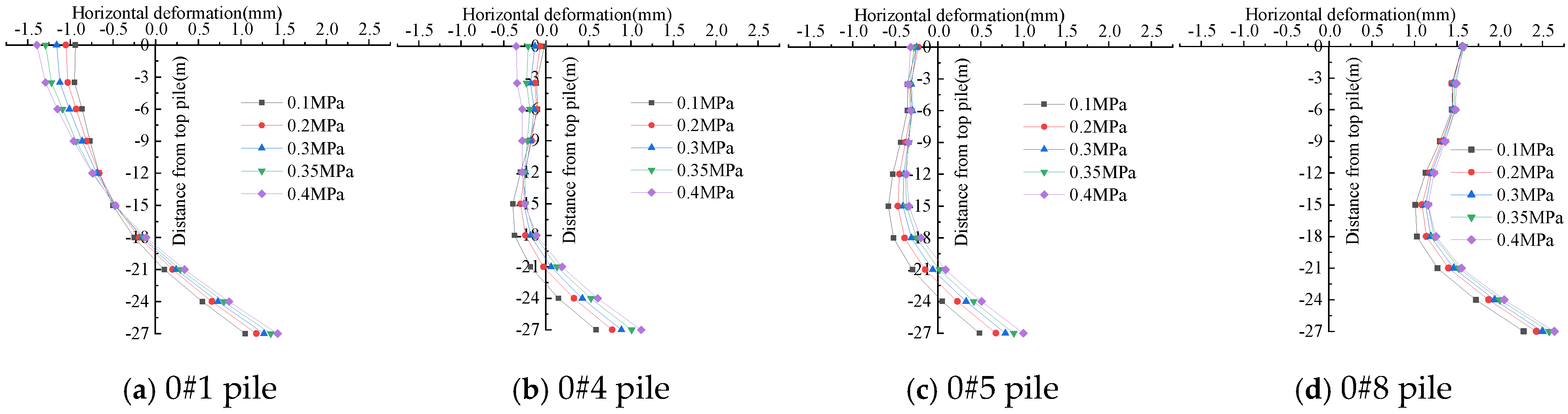
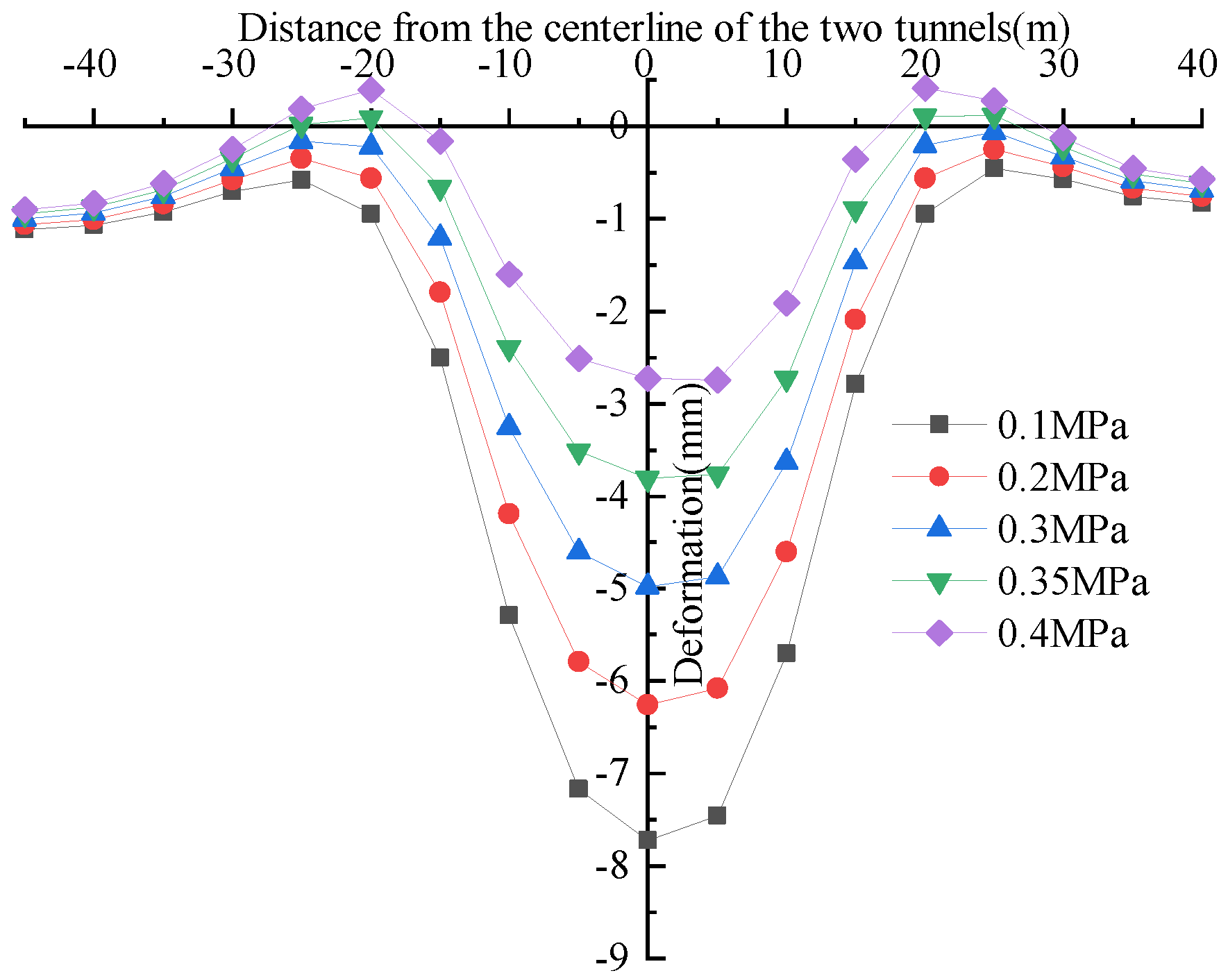
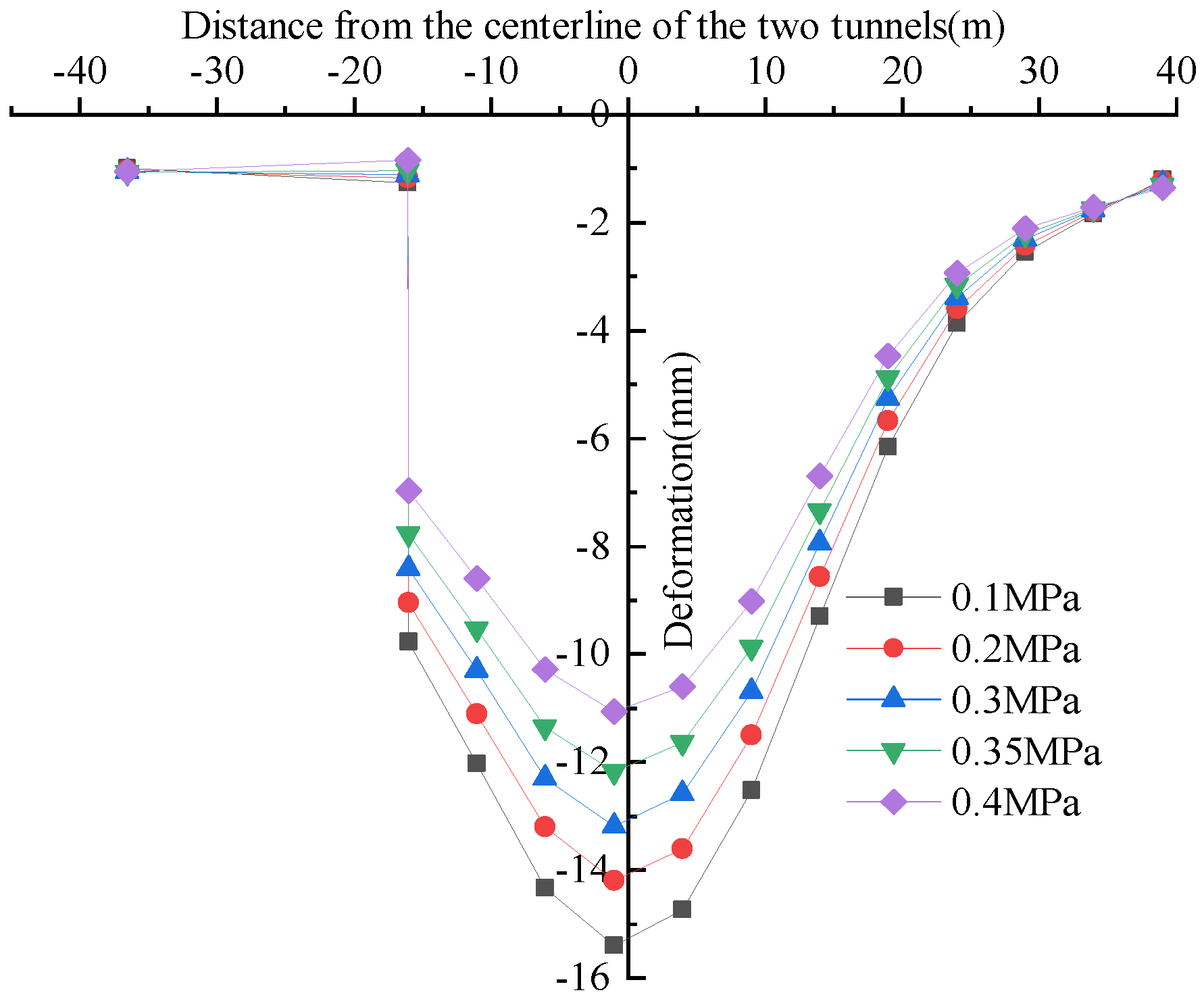
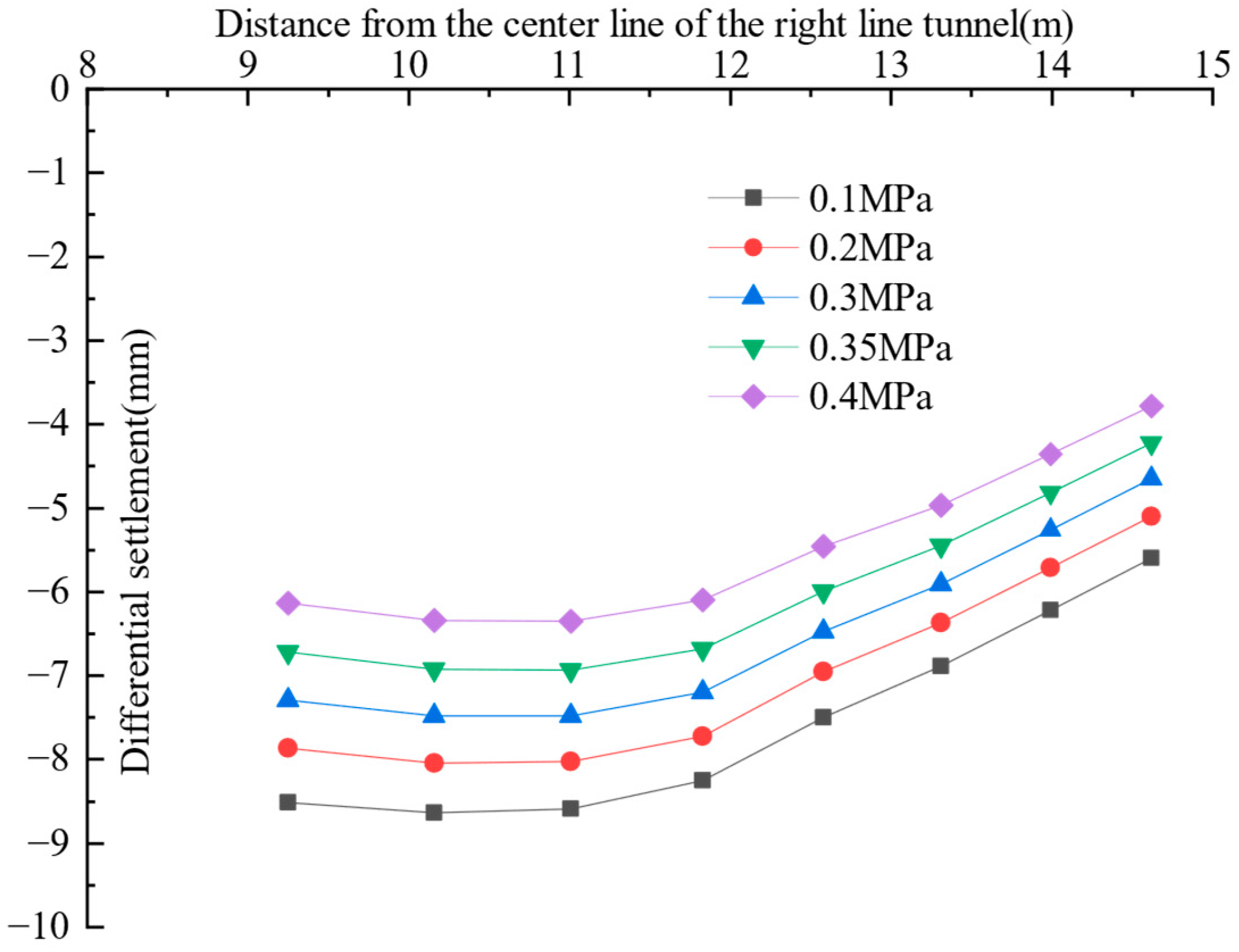
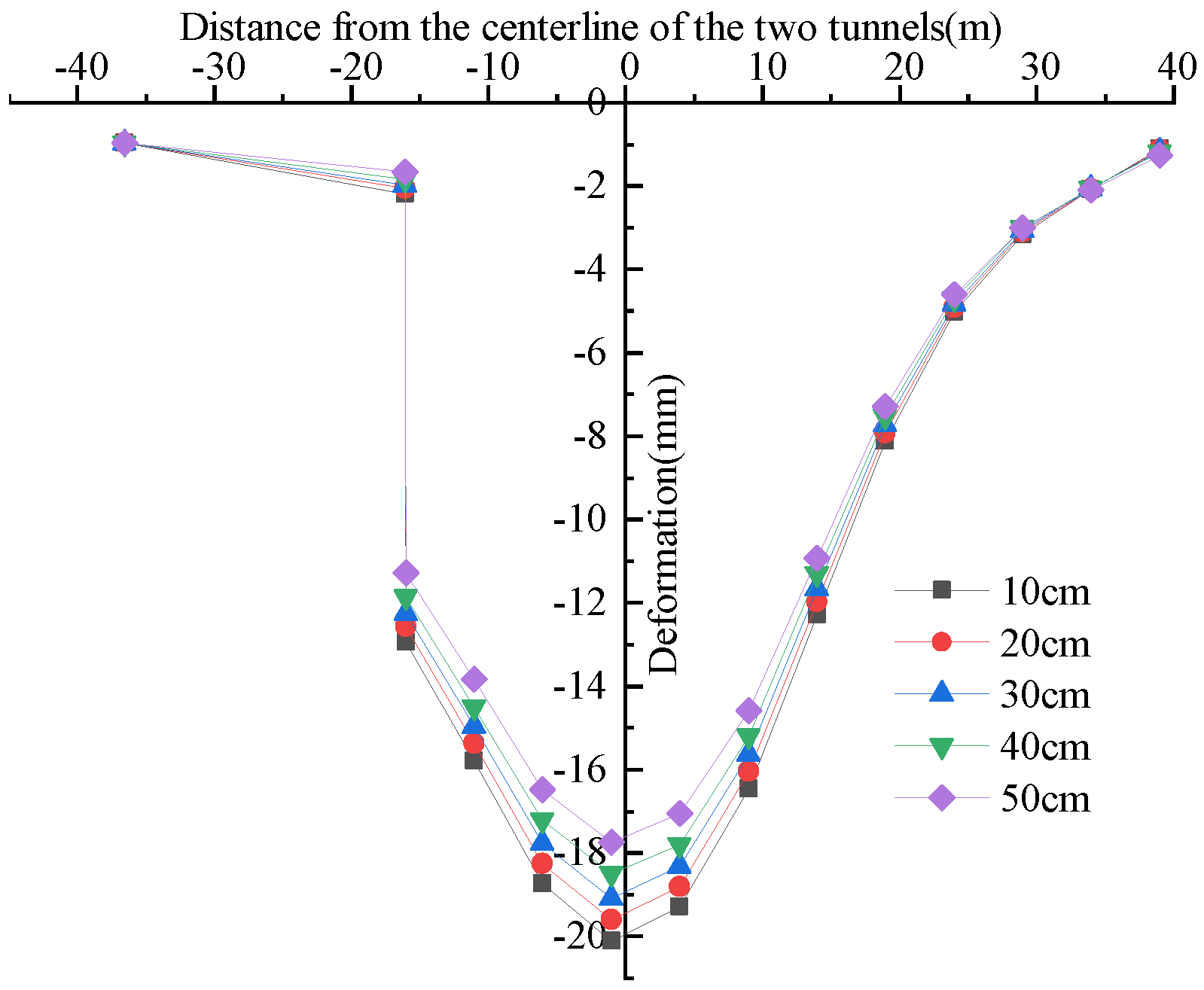
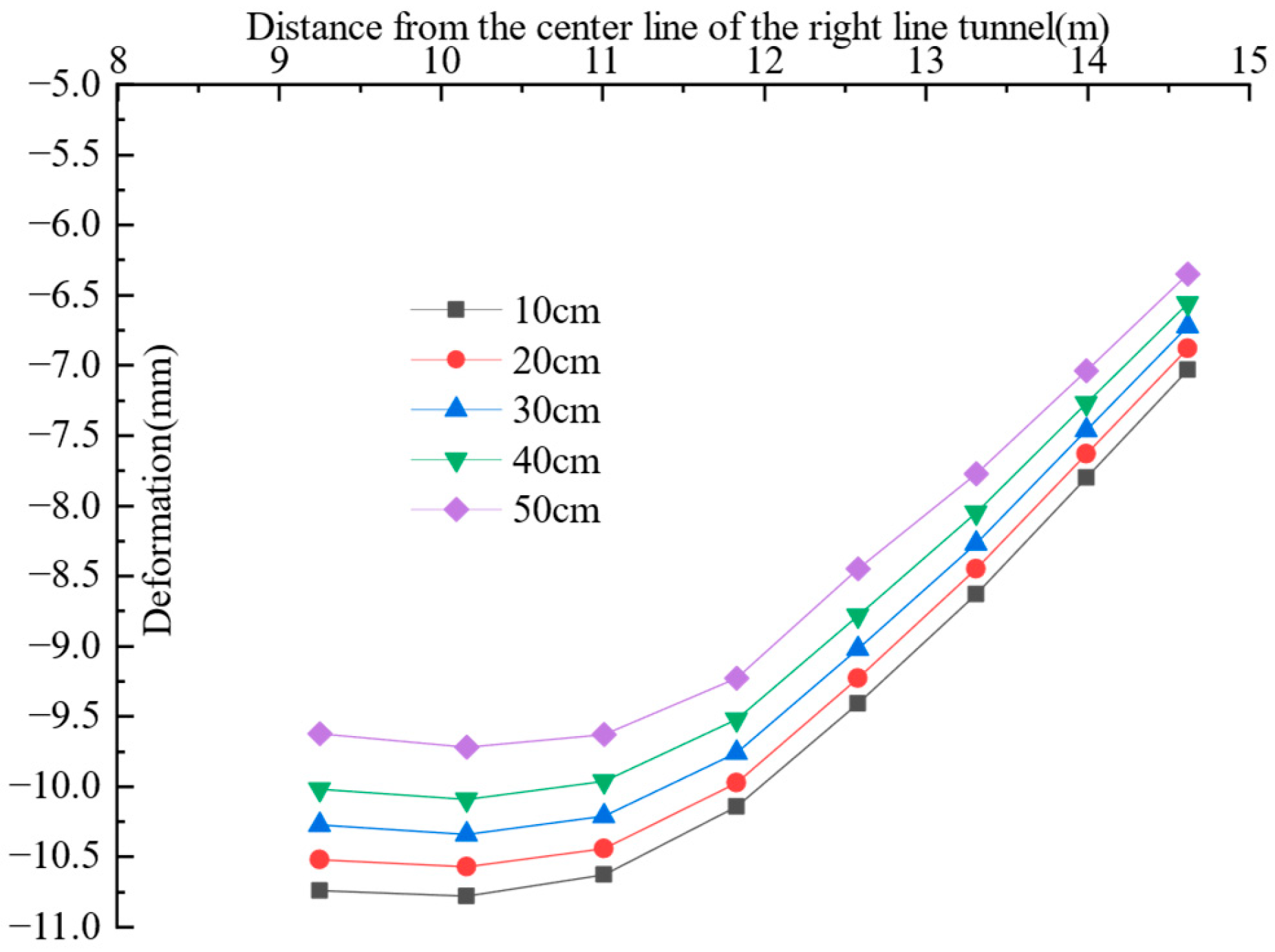
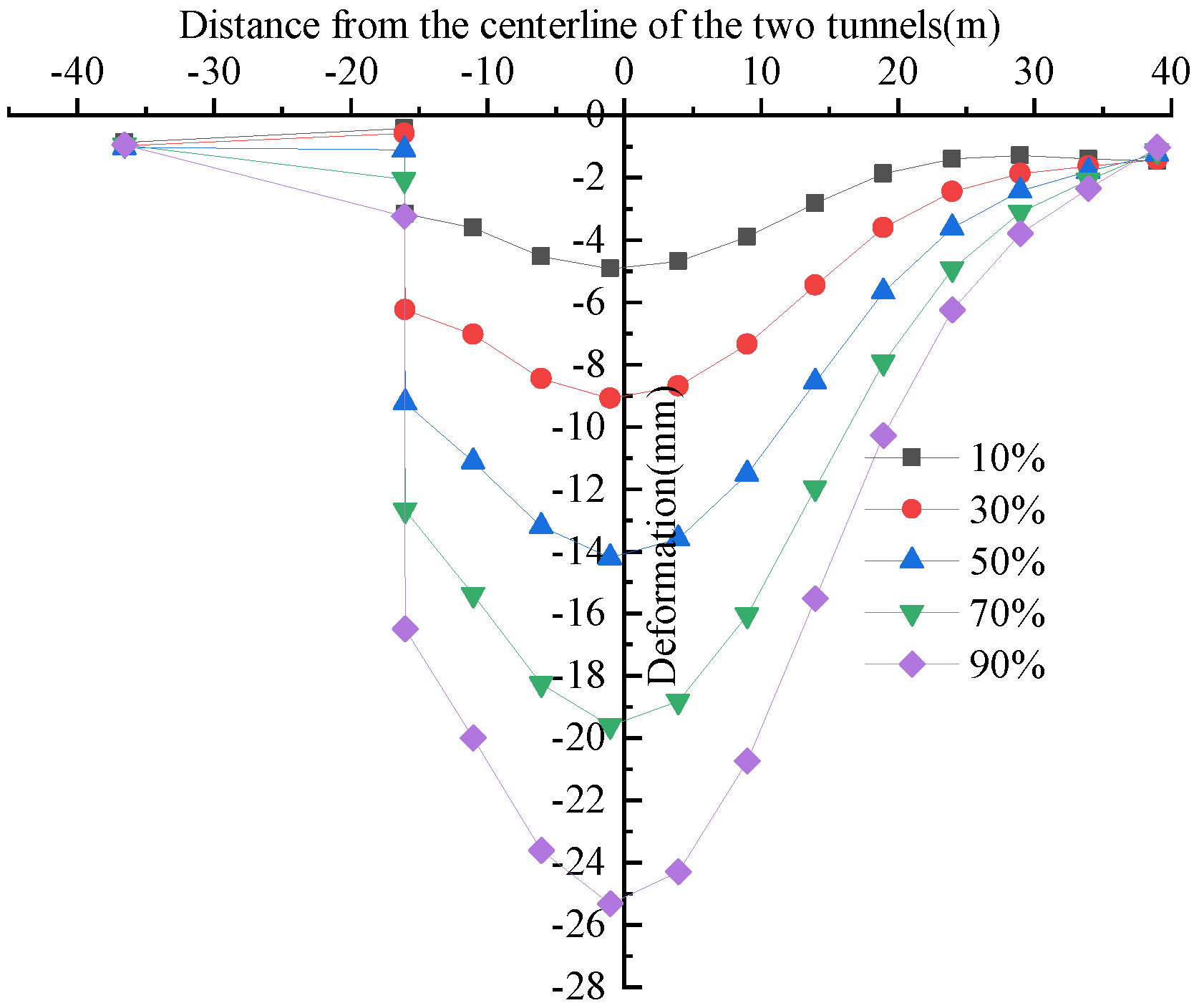
3.2. The Deformation Laws of Pile Foundations and Pavements Under Varying Soil Bin Pressure

The soil bin pressure is the force needed to balance water and soil pressure on the palm surface during EPB shield construction. Setting this pressure correctly is crucial to prevent collapsing or bulging of the soil on the palm surface. To study the impact of soil bin pressure on the deformation of adjacent pile foundation and surface during the tunnel side-crossing Tianzhushan overpass and under-crossing Shen-Hai Expressway shield construction, numerical simulation was used to carry out this study. During this study, only the soil bin pressure is changed, and other parameters remain unchanged. Grouting layer thickness: 20 cm, stress release coefficient: 50%. The soil bin pressures are as follows: 0.1 MPa, 0.2 MPa, 0.3 MPa, 0.35 MPa, and 0.4 MPa. Through numerical calculation, the relationship curve between the pile deformation of 0#1, 0#4, 0#5, and 0#8 along the X-axis and the soil bin pressure are shown in Figure 6.
According to Figure 6, shield tunnel construction adjacent to a pile foundation can cause pile deformation. The curve of pile deformation along the horizontal direction is closely related to the distance from the pile foundation to the nearby tunnel. When the distance from the pile foundation to the adjacent tunnel axis is different, the soil bin pressure affects pile deformation differently. When the distance from the pile foundation to the right tunnel’s centerline is less than 11.01 m (0#6, 0#7, and 0#8), the pile deformation along the X-axis is generally along the positive direction. When the distance from the pile foundation to the right tunnel’s centerline is greater than 11.01 m (0#1–0#5), the upper section of the pile body deforms toward the negative X-axis direction, while the lower section deforms toward the positive X-axis direction. Each pile foundation has a point that is less impacted by soil bin pressure, and the point’s position shifts downward with greater distance from the right tunnel’s centerline, such as 0#8 pile at the top, 0#5 pile at about 3.5 m from the top, 0#4 pile at about 12 m from the top, and 0#1 pile at about 15 m from the top.
According to Figure 6, the deformation of piles 0#1 and 0#8 along the X-axis increases with soil bin pressure. However, their trends differ. For the 0#1 pile, the upper section of the pile body deforms toward the negative X-axis direction, while the lower section deforms toward the positive X-axis direction. The deformation of the pile at various locations is observed to increase with rising soil bin pressure, and the differential deformation across different locations also increases as the soil bin pressure increases. When the soil bin pressure is 0.1 MPa, the difference deformation between the top and bottom of the pile is 1.99 mm, whereas when the soil bin pressure is 0.4 MPa, the difference deformation between the top and bottom of the pile is 2.82 mm. For the 0#8 pile, the pile body is deformed along positive direction of X-axis. With increasing distance from the pile top, deformation decreases to a minimum at 15 m and then gradually increases again. When the distance from the top is under 15 m, the deformation difference of the pile body at various locations decreases as the soil bin pressure increases. Conversely, when the distance exceeds 15 m, this deformation difference increases with higher soil bin pressure. The distance between 0#4 and 0#5 pile foundations and the centerline of the right tunnel is only 1.57 m, the deformation curves of the two pile foundations along the X-axis are essentially similar. The upper section of the pile body deforms toward the negative X-axis direction, while the lower section deforms toward the positive X-axis direction. The differential deformation at various positions of the upper section of the pile decreases as soil bin pressure increases. When the soil bin pressure increases, pile deformation within 15 m from the top becomes more uniform. The variation in the lower section of the pile decreases along the negative X-axis, while it increases in the positive X-axis direction under similar conditions.
The relationship curves between the deformation of each observation points and the soil bin pressure in sections 1 and 2, and at both sides of the deformation joint between bridge abutment and roadbed are shown in Figure 7, Figure 8 and Figure 9.
According to Figure 7 and Figure 8, the deformation of each observation points of sections 1 and 2 decreases as soil bin pressure increases. The deformation curves of the two sections show a similar trend, but the deformation of section 2 is obviously larger than that of section 1. This is because the tunnel depth of section 2 is 5.8 m larger than that of section 1, and the stress exerted by the self-weight of the overlying soil layer is greater. At the same time, there is a vehicle load of 20 kN/m2 at section 2, so the deformation is greater under the same soil bin pressure. Under different soil bin pressures, the deformation of each observation points in section 2 presents as settlement, while the observation points in section 1, which are about 15–25 m away from the centerline of the two tunnels, show upward bulging when the soil bin pressure is greater than 0.35 MPa. When the soil bin pressure is high and the overlying soil layer is thin, it exerts a significant squeezing impact on the surrounding soil near the tunnel. The stress release coefficient is only 50%, preventing timely recovery of soil deformation. Consequently, within 20–40 m from the centerline of both tunnels in section 1, deformation exceeds that beyond 40 m. For a constant increase in soil bin pressure, surface deformation decreases as the thickness of the overlying soil layer increases. For example, when the soil bin pressure increases from 0.1 MPa to 0.2 MPa, the deformation at the center of section 1 decreases from 7.72 mm to 6.26 mm, a decrease of 1.46 mm, while the deformation at the center of section 2 decreases from 15.40 mm to 14.20 mm, a decrease of only 1.20 mm.
According to Figure 8 and Figure 9, when the tunnel side-crossing Tianzhushan overpass, it will cause differential deformation on both sides of the deformation joint between the bridge and the roadbed. The differential deformation is linked to the pile foundation’s distance from the right tunnel’s centerline and soil bin pressure. The differential deformation of the observation points on both sides of the deformation joints decreases as the soil bin pressure increases. When the distance from the pile foundation to the right tunnel’s centerline is less than 11.83 m, changes in distance have little effect on differential deformation. However, when the distance exceeds 11.83 m, differential deformation decreases significantly as distance increases.
The soil bin pressure has a greater impact on the side of the roadbed; increasing the soil bin pressure can reduce the differential deformation on both sides of the deformation joints and mitigate the impacts of shield construction on the driving comfort of the Expressway.

3.3. The Deformation Laws of Pile Foundations and Pavements Under Varying Grouting Layer Thickness

Due to overbreak and underbreak during tunnel shield construction, there will be a specific gap between the tunnel segment and the surrounding soil once the segment has been assembled. The existence of this gap will cause deformation of the strata. Therefore, the gap must be grouted. After grouting, the slurry will penetrate the surrounding strata, and the slurry and the soil form a composite material. The strength of the composite material is higher than that of the soil. When the grouting pressure and volume vary, the thickness of the composite material layer behind the wall changes, leading to different effects on surface deformation. The grouting material’s performance significantly affects the deformation control of surface and adjacent structures. In this project, mortar and double-liquid slurry were used for joint grouting, and the grouting pressure and slurry dosage are adjusted in time according to the site conditions. When studying the effect of grouting layer thickness on deformation, only the thickness was varied while keeping other material parameters constant. The geological radar detection of the grouting layer thickness after subway tunnel shield construction in strongly weathered tuff lava strata shows that it ranges from 10 cm to 50 cm. To study the impact of varying grouting layer thicknesses on pile and surface deformation, a single-variable method was adopted, taking the soil bin pressure as 0.2 MPa, stress release coefficient as 70%, and grouting layer thickness as follows: 10 cm, 20 cm, 30 cm, 40 cm, and 50 cm. After calculation, the relationship curve between the pile deformation of 0#1, 0#4, 0#5, and 0#8 along X-axis and grouting layer thickness are shown in Figure 10.
According to Figure 10, when the distance from the pile foundation to the right tunnel’s centerline exceeds 12.58 m, the pile deformation along the X-axis direction shows that the upper section of the pile body deforms negatively along the X-axis, while the lower part deforms positively. The deformation boundary point of the pile foundation along the X-axis shifts upward with increasing distance from the centerline of the right tunnel and also increases with increasing grouting layer thickness. The pile deformation toward the negative X-axis direction decreases as the grouting layer thickness increases, while deformation toward the positive X-axis direction increases with increasing grouting layer thickness. With the decreasing distance between the pile foundation and the right tunnel’s centerline, pile deformation along the negative X-axis within 18 m from the top gradually decreases. The maximum pile deformation is transmitted from the top to the middle of the pile, with deformation increasing and then decreasing along the depth. When the distance from the pile foundation to the right tunnel’s centerline is 11.83 m, and the grouting layer thickness is below 20 cm, only piles within 3 m from the top deform positively along the X-axis, while other piles deform negatively. Deformation in depth gradually decreases within 0–3 m. When the distance from the top is more than 3 m, the deformation in the depth direction initially increases with depth, peaking at 18 m from the top. As depth increases, deformation gradually decreases. When the distance from the pile foundation to the right tunnel’s centerline is less than 11.01 m, all piles deform positively along the X-axis. The deformation increases with greater grouting layer thickness, while differential deformation at various pile positions decreases as grouting layer thickness increases.
The relationship curves between the deformation of each observation points and grouting layer thickness at monitoring sections 1 and 2, and at both sides of the deformation joint between bridge abutment and roadbed are shown in Figure 11, Figure 12 and Figure 13.
According to Figure 11 and Figure 12, the trend of the deformation curves of sections 1 and 2 is basically the same, and the deformation at each observation points decreases as the grouting layer thickness increases, but section 2 experiences greater deformation than section 1. This is because the tunnel depth of section 2 is 5.8 m larger than that of section 1, the stress exerted by the self-weight of the overlying soil layer is greater, and there is a vehicle load of 20 kN/m2 at section 2. The impact of grouting layer thickness on surface deformation is significant within 15 m from the centerline of the two tunnels, while its effect beyond this range is minimal. When the grouting layer thickness increased from 10 cm to 20 cm, surface deformation decreased by 0.34 mm; with an increase from 20 cm to 30 cm, it decreased by 0.29 mm. As the grouting layer thickness increased, its effectiveness in reducing surface deformation gradually decreased.
According to Figure 12 and Figure 13, the differential deformation at the deformation joint between the bridge and roadbed, caused by shield construction of the tunnel side-crossing Tianzhushan overpass, was influenced by both the thickness of the grouting layer and the distance from the pile foundation to the right tunnel’s centerline. When the distance from the pile foundation to the right tunnel’s centerline is less than 11.01 m, it has little effect on the differential deformation at both sides of the deformation joint. Increasing the grouting layer thickness reduces differential deformation at the deformation joint. Several curves in Figure 13 are basically parallel, indicating that varying grouting layer thicknesses have a similar effect on the differential deformation at both sides of the deformation joint.

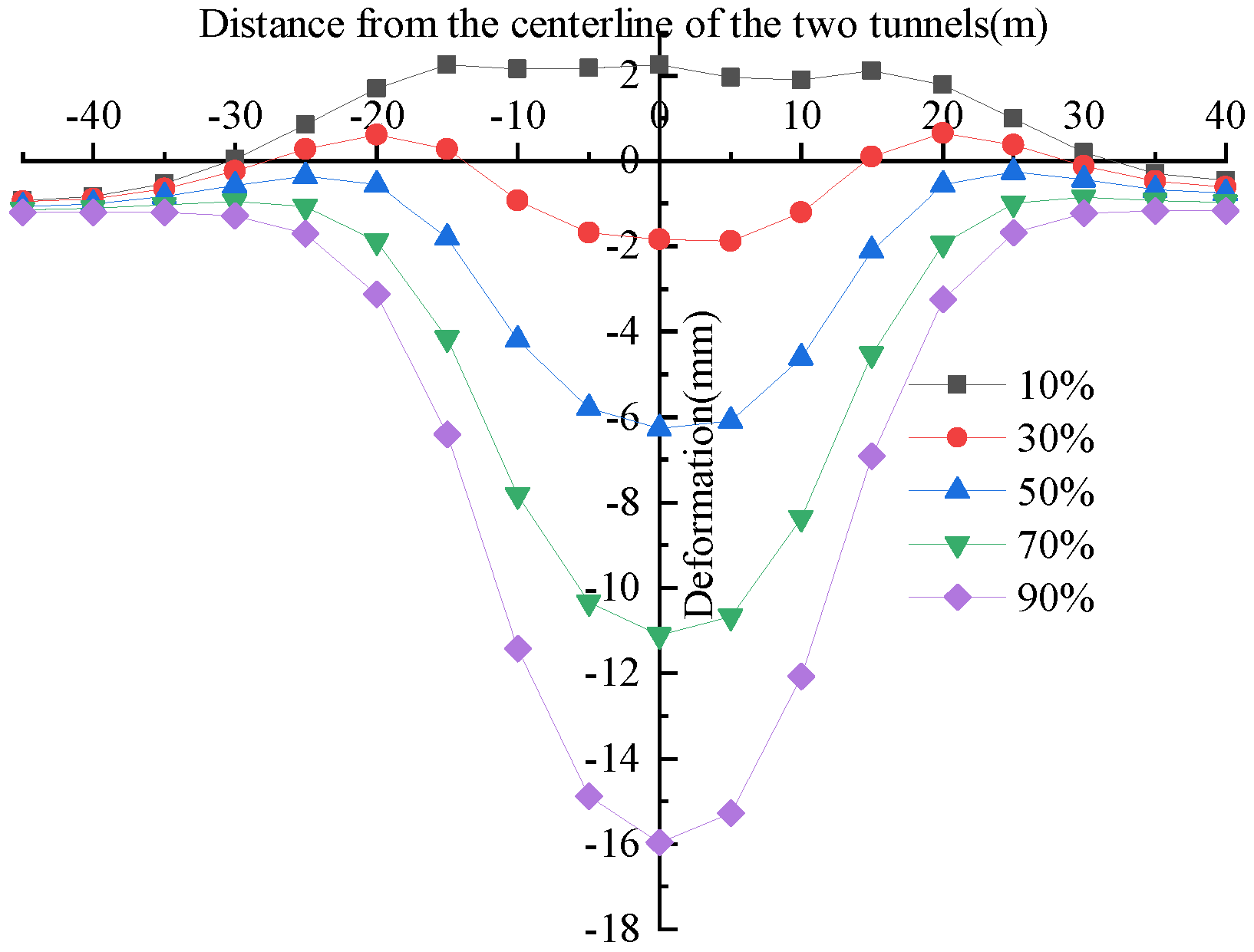
3.4. The Deformation Laws of Pile Foundation and Pavement Under Varying Stress Release Coefficient

The existing research indicates that the deformation of adjacent structures is closely related to the stress release coefficient during tunnel shield construction. In this research, the impact of stress release coefficient on pile and pavement deformation during tunnel shield construction is examined by using various stress release coefficients. After calculation, the relationship curves between the pile deformation of 0#1, 0#4, 0#5, and 0#8 piles along the X-axis and the stress release coefficient is shown in Figure 14.
According to Figure 14, when the stress release coefficient is 10%, the distance from the pile foundation to the right tunnel’s centerline exceeds 11.83 m, the upper section of the pile body deforms toward the negative X-axis direction, while the lower section deforms toward the positive X-axis direction. There is a point of zero deformation in the pile body, and as the distance from the pile foundation to the right tunnel’s centerline decreases, this point moves closer to the pile top. The pile body’s upper section deformation decreases with depth, while that of the lower section increases. As the distance from the pile foundation to the right tunnel’s centerline decreases, the deformation of the upper section of the pile body shifts from negative to positive along the X-axis. When the pile foundation is less than 11.01 m from the right tunnel’s centerline, the deformation of the pile body toward the X-axis is entirely in the positive direction, with minimal deformation at the top. Meanwhile, deformation in the depth direction increases gradually.
When the distance from the pile foundation to the right tunnel’s centerline exceeds 13.31 m, the pile body’s upper section always deforms toward the negative X-axis direction, regardless of stress release coefficient. As the stress release coefficient increases, the point of zero deformation in the pile body shifts downward. The differential deformation decreases, and the lower section of the pile’s deformation decreases along the positive X-axis direction. When the distance from the pile foundation to the right tunnel’s centerline is 12.58–11.83 m, the pile top deformation toward the negative X-axis direction decreases as stress release coefficient increases. When the stress release coefficient increases, the pile top deforms toward the positive X-axis direction, and the maximum deformation shifts from the top or bottom of the pile to its middle.
According to Figure 14, when the stress release coefficient is 70%, the differential deformation of 0#1 pile body is the smallest. When it is 50%, the differential deformation of 0#4 pile body is the smallest. When it is 30%, the differential deformation of 0#5 and 0#8 piles is the smallest. The sensitivity of the pile foundation to the stress release coefficient varies with distance from the right tunnel’s centerline. During tunnel shield construction, adjust the stress release coefficient based on the distance from the pile foundation to the right tunnel’s centerline to minimize differential deformation of the pile foundation in various positions.
The relationship curves between the deformation of each observation point and the stress release coefficient at monitoring sections 1 and 2, and at both sides of the deformation joint between bridge abutment and roadbed are shown in Figure 15, Figure 16 and Figure 17.
According to Figure 15 and Figure 16, the deformation of sections 1 and 2 increases with the stress release coefficient. However, the deformation of section 1 is much lower than that of section 2. This is because the soil thickness at section 1 is 5.8 m lower than that at section 2. With the same stress release coefficient, a thinner overlying soil leads to lower surface deformation. When the tunnel’s overlying soil layer is thin, under the same soil pressure, the surface deformation is uplift or settlement has an important relationship with the stress release coefficient. When the stress release coefficient is below 30%, the soil bin pressure prevents timely dissipation of stress, leading to uplift deformation in the surrounding soil of the tunnel. As the stress release coefficient increases, surface uplift gradually disappears and settlement occurs instead. For equal increments in the stress release coefficient, deformation is greater in thicker layers of overlying soil. For example, when the stress release coefficient increases from 30% to 50%, section 1’s maximum deformation increases by 4.42 mm, while section 2’s maximum deformation increases by 5.11 mm.
According to Figure 16 and Figure 17, it can be seen that the differential deformation on both sides of the deformation joint increases with a higher stress release coefficient and decreases as the distance between the pile foundation and the right tunnel’s centerline decreases. With the increase in stress release coefficient, the differential deformation at different positions on the deformation joint increases. For example, when the stress release coefficient is 10%, the differential deformation at both sides of the deformation joint of 0#1–0#4 piles is 1.18 mm, and that of 0#5–0#8 piles is 0.13 mm. However, when the stress release coefficient is 90%, the differential deformation on both sides of the deformation joint of 0#1–0#4 piles is 2.81 mm, while that of 0#5–0#8 piles is 0.94 mm. Reducing the stress release coefficient effectively minimizes differential deformation at the deformation joint, thereby enhancing driving comfort during tunnel shield construction.

4. Risk Prevention and Control Measures for Shield Structure Side-Crossing Tianzhushan Overpass

(1) The test section is set before the shield side-crossing the overpass to determine the reasonable thrust, torque, and propulsion speed, adjust the shield posture, and reduce unnecessary correction work to ensure that the shield can be continuously advanced.
(2) By monitoring the amount of muck, the over-excavation and under-excavation of the tunnel are calculated, and the grouting pressure and slurry dosage behind the wall are adjusted in a timely manner. If necessary, carry out secondary grouting, minimize the gap at the shield’s tail, and reduce deformation.
(3) Implement construction information management and adjust shield construction parameters in time according to the strata conditions. Through displacement monitoring, stress monitoring, and other means, the strata deformation is timely understood, which offers a scientific foundation for optimizing construction parameters. Reinforcement measures should be implemented for significant deformation, and construction parameters adjusted promptly.

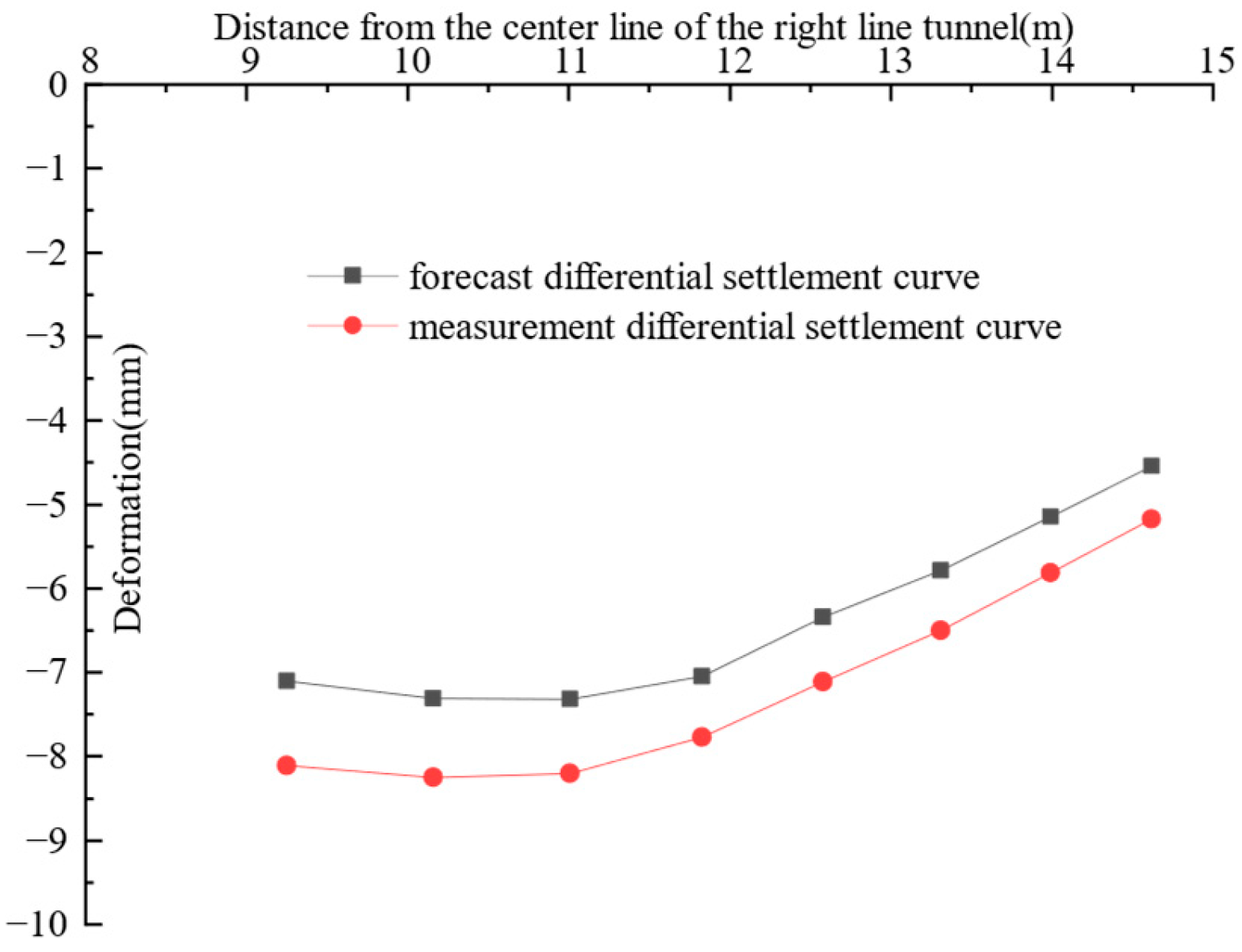
5. Validation of Numerical Simulation Accuracy

To minimize the deformation of the bridge pile foundation and pavement due to the tunnel side-crossing Tianzhushan overpass and under-crossing Shen-Hai Expressway shield construction, numerical simulations were conducted to predict these deformations prior to tunneling. The numerical simulation parameters are as follows: the soil bin pressure is 0.30 MPa, grouting layer thickness is 30 cm, and stress release coefficient is 50%. Numerical calculations show that using these parameters allows for the deformation of the pile foundation and pavement to remain within acceptable limits during construction. To verify the reliability of numerical calculations, the same construction parameters are applied in the field. During construction, the deformation of bridges, pile foundations, and pavements is monitored and compared with predicted deformations from numerical calculations.
The comparison between the on-site monitoring deformation and the predicted deformation along the X-axis direction at the top of 0#1–0#8 piles are shown in Table 4. The comparison of on-site monitoring deformation and predicted deformation at the top of piles for No.0 abutment and No.1 pier are shown in Table 5.
According to Table 4, the on-site monitoring deformation direction of the pile top along the X-axis is consistent with the predicted deformation direction, and the on-site monitoring deformation is less than the allowable deformation. However, the discrepancy between the on-site monitoring deformation and the predicted deformation of the pile foundation varies across different positions. The on-site monitoring of 0#1 to 0#5 piles shows that the deformation in the negative X-axis direction is less than predicted, with a maximum differential deformation of 0.17 mm occurring at No.1 pile. As the distance from the pile foundation to the right tunnel’s centerline decreases, the deformation of the pile foundation along the negative X-axis gradually decreases. The on-site monitoring deformation of piles 0#6 to 0#8 in the positive X-axis direction exceeds the predicted deformation. Additionally, the pile top deformation along this direction increases as the distance between the pile foundation and the right tunnel decreases. However, the differential deformation between the monitored and predicted values decreases with decreased distance.
According to Table 5, the on-site monitoring deformation of the pile top of all pile foundations of No.0 abutment and No.1 pier is basically consistent with the predicted settlement, and the deformation is much less than the allowable deformation, which is 25 mm, and the measured maximum settlement of pile top is 1.40 mm, which is located at 0#4 pile. The measured differential settlement and predicted differential settlement between all longitudinal adjacent piers are far less than the allowable deformation of 2 mm. The maximum measured and predicted differential settlement of pile foundations between longitudinal adjacent piers and abutments is between 0#5 and 1#5, the predicted differential settlement is 0.08 mm, and the measured differential settlement is 0.26 mm. In terms of differential settlement of adjacent pile foundations, the measured deformation closely matches the predicted values. The maximum differential settlement for both is 0.21 mm.
From the analysis, it is evident that, during the shield construction of the tunnel side-crossing Tianzhushan overpass, both the vertical settlement of the bridge pile foundation and the differential settlements of adjacent longitudinal and transverse pile foundations are all within allowable limits. The on-site monitoring deformation closely matches the predicted values, indicating that the method used in this paper is effective for predicting deformation trends caused by the shield construction.
The comparison between on-site monitoring deformation and predicted deformation of sections 1 and 2 are shown in Figure 18, and the comparison between on-site monitoring differential settlement and predicted differential settlement on both sides of deformation joint are shown in Figure 19.
According to Figure 18, the on-site monitoring deformation curves of sections 1 and 2 are basically consistent with the predicted deformation curves, and the on-site monitoring deformation and predicted deformation are within the allowable deformation, but the on-site monitoring shows greater deformation than predicted. The maximum of the on-site monitoring deformation of section 1 is 6.30 mm, and that of section 2 is 14.70 mm. The maximum deformation is located near the centerline of the two tunnels. As the distance from the centerline of the two tunnels increases, surface deformation gradually decreases. For section 1, the thin overlying soil layer causes the surrounding soil to be compressed by significant soil bin pressure, and the stress release coefficient is only 50%; the soil cannot be fully restored after extrusion, which makes the deformation of soil at the distance of 15–35 m from the centerline of the two tunnels less than that at the distance of more than 35 m from the centerline of the two tunnels.
According to Figure 18 and Figure 19, the shield construction of the tunnel side-crossing Tianzhushan overpass will cause differential deformation on both sides of the deformation joint between the bridge and the roadbed. The variation trend of the on-site monitoring differential deformation curve is basically the same as that of the predicted differential deformation curve, but the on-site monitoring differential deformation is about 1 mm larger than the predicted differential deformation. When the distance between the deformation joint and the centerline of the right tunnel is larger, the differential deformation on both sides of the deformation joint caused by tunnel shield construction is smaller. When the distance from the pile foundation to the right tunnel’s centerline is less than 11.01 m, the distance reduction has little effect on the differential deformation on both sides of the deformation joint. According to Figure 19, tunnel shield construction affects the right amplitude of Shen-Hai Expressway more than the left amplitude. Although the deformation of the right amplitude is smaller, the differential deformation along the deformation joint direction is larger. However, although the left amplitude shows greater deformation, the differential deformation is smaller and approaches uniformity.

6. Conclusions

Taking the shield construction of Xiamen Metro Line 2 tunnel side-crossing Tianzhushan overpass and under-crossing Shen-Hai Expressway as the engineering background, the following conclusions can be obtained through this research:
(1)
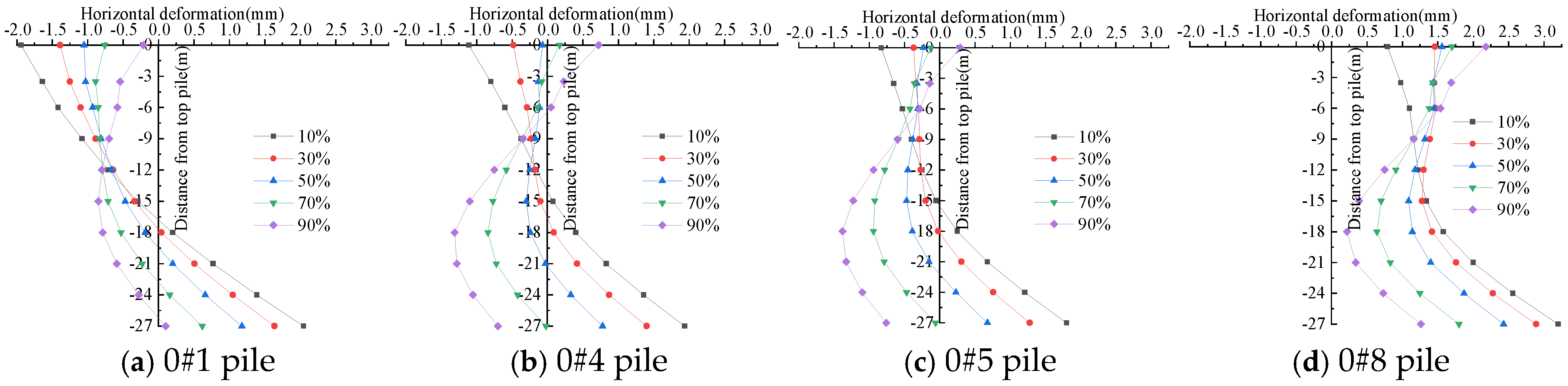
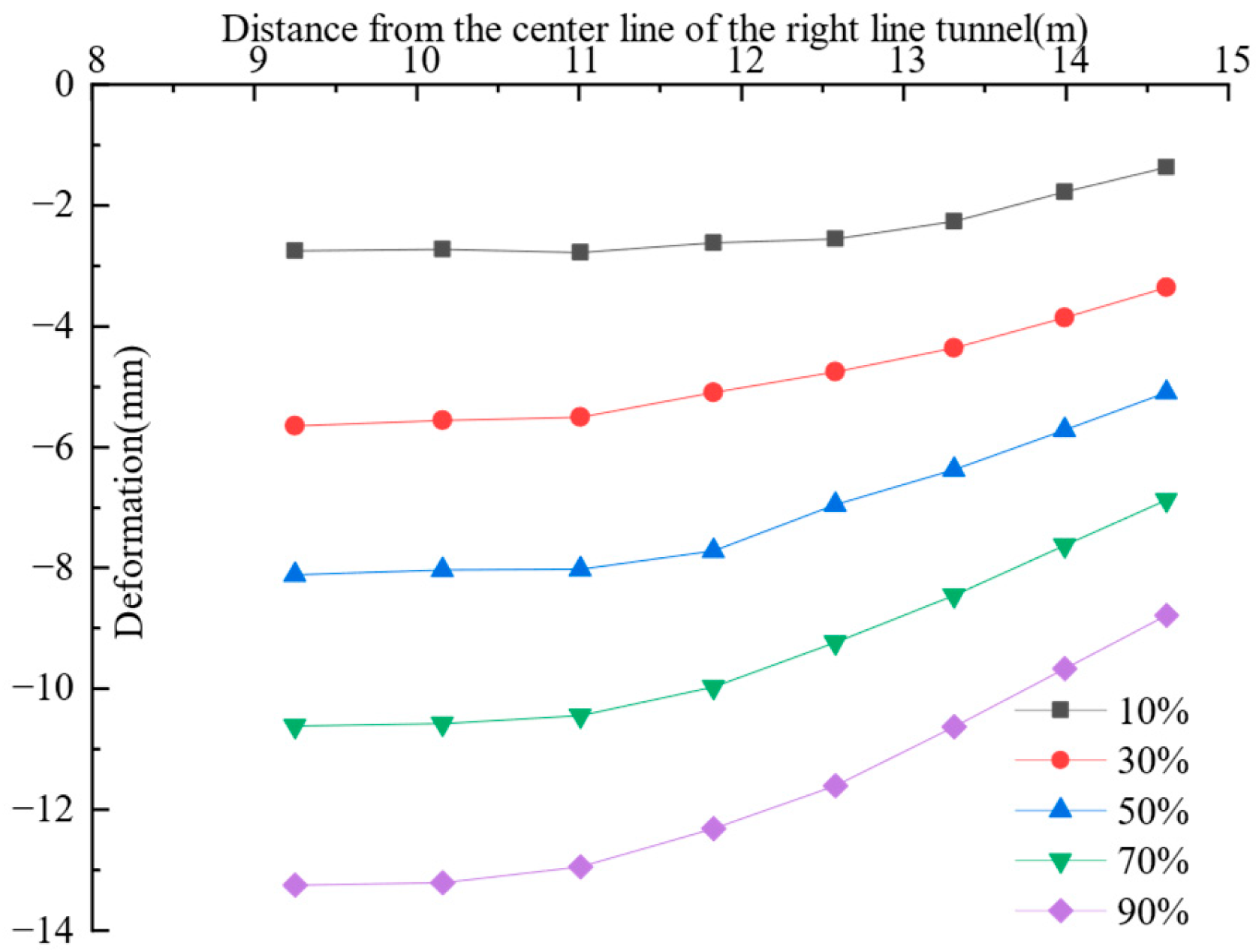
During tunnel shield construction, adjacent pile foundations will deform. The pile deformation curve’s shape is closely linked to the distance between the pile foundation and the adjacent tunnel’s centerline. When the pile foundation is within 11.01 m of the adjacent tunnel’s centerline, the pile body deforms positively along the X-axis. The top and bottom of the pile exhibit greater deformation than the middle, while deformation in depth first decreases and then increases. When the pile foundation is outside 11.83 m of the adjacent tunnel’s centerline, the top of the pile deforms toward the negative X-axis direction, while the bottom deforms toward the positive X-axis direction. Both top and bottom deformations increase with distance.
(2)
When the distance from the pile foundation to the adjacent tunnel’s centerline varies, the impact of soil bin pressure on pile deformation differs. When the pile foundation is within 11.01 m of the adjacent tunnel’s centerline, the pile foundation deformation toward the positive X-axis increases with soil bin pressure, while the differential deformation of the pile body at varying depths decreases as soil bin pressure increases. When the pile foundation is outside 11.83 m of the adjacent tunnel’s centerline, the deformation of the upper section of the pile toward the negative X-axis direction decreases as the soil bin pressure increases, and its differential deformation also decreases with increasing soil bin pressure. In contrast, the deformation of the lower section of the pile toward the positive X-axis direction increases with increasing soil bin pressure. When the pile foundation is outside 12.58 m of the adjacent tunnel’s centerline, the deformation of the upper and lower sections of the pile body increases with soil bin pressure. Increasing soil bin pressure effectively decreases surface deformation and differential deformation at the deformation joint between the bridge and roadbed.
(3)
When the pile foundation is within 11.01 m of the adjacent tunnel’s centerline, the pile body deformation increases with grouting layer thickness, while the differential deformation decreases. When the pile foundation is outside 11.83 m of the adjacent tunnel’s centerline, the deformation of the upper section of the pile body decreases as the grouting layer thickness increases, while the deformation of the lower section increases with increasing grouting layer thickness. Increasing the grouting layer thickness can significantly mitigate surface deformation and diminish the differential deformation on either side of the deformation joint between the bridge and the roadbed. However, as the grouting layer thickness increases, its effectiveness in reducing surface deformation gradually decreases.
(4)
The deformation curve’s shape along the pile’s depth is closely related to the stress release coefficient. When the pile foundation is within 11.01 m of the adjacent tunnel’s centerline, the deformation of the upper section of the pile body toward the negative X-axis decreases as the stress release coefficient increases. When the pile foundation is nearer to the adjacent tunnel’s centerline and the stress release coefficient is higher, the pile top deforms positively toward the X-axis. As the stress release coefficient increases, the lower section of the pile body gradually deforms in the negative X-axis direction. When the distance from the pile foundation to the adjacent tunnel’s centerline is less than 11.0 m, the pile top deformation initially increases and then decreases as the stress release coefficient increases. Reducing the stress release coefficient effectively minimizes surface deformation from tunnel shield construction and differential deformation at the bridge–roadbed joint.
(5)
For upper-soft and lower-hard strata, controlling surface deformation and adjacent structures within allowable limits can be achieved by optimizing shield construction parameters. This is significant for reducing construction time and project costs.

Author Contributions

Conceptualization, Supervision, Funding acquisition, Writing—original draft, Writing—review and editing, J.W.; Formal analysis: N.L.; Investigation and data curation, X.T.; Writing—review and editing, Y.W. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Key R&D Program of China (No: 2023YFC3009400), the National Science Fund of Jiangxi Province (No: 20223BBG71018), and Fujian Natural Science Foundation (No: 2021J011134), Engineering Research Center of Prevention and Control of Geological Disasters in Northern Fujian, Fujian Province University (No: WYERC2024-4), and Construction Service Project of Enterprise Engineering Technology Center (2023-WHFW-012).

Data Availability Statement

The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding authors.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Liu, W.; Zhao, L.; Yao, X.-C.; Zheng, H.-A.; Liu, W.-L. Impact of Shield Tunnel Construction on Adjacent Railway Bridge: Protective Measures and Deformation Control. Buildings 2024, 14, 3024. [Google Scholar] [CrossRef]
  2. Kanagaraju, R.; Krishnamurthy, P.; Ramanagouda, D.G.; Velusamy, S. Numerical Analysis of Displacements in Concrete Pile Foundationsinduced by Adjacent Tunnel Excavation in Sandy Soils. Matéria (Rio J.) 2024, 29, e20240391. [Google Scholar] [CrossRef]
  3. Phutthananon, C.; Lertkultanon, S.; Jongpradist, P.; Duangsano, O.; Likitlersuang, S.; Jamsawang, P. Numerical Investigation on the Responses of Existing Single Piles Due to Adjacent Twin Tunneling Considering the Lagging Distance. Undergr. Space 2023, 11, 171–188. [Google Scholar] [CrossRef]
  4. Du, Y.; Zhang, P.; Zhang, J. Mechanical Response and Control Measures of Pile Foundations under Close-Range Shield Tunneling in Water-Rich Sandy Pebble Strata. Adv. Civ. Eng. 2024, 2024, 4364716. [Google Scholar] [CrossRef]
  5. Wu, N. Environmental Engineering Deformation Control of High-Speed Railway Shield Tunnel Under-crossing Bridge Piles. J. Phys. Conf. Ser. 2021, 2029, 012133. [Google Scholar] [CrossRef]
  6. Zhang, S.; Zhang, X.; Ning, X.; Lu, H.; Jiang, M.; Wei, S.; Xiao, X. Effect of Shield-Tunnel Construction on the Horizontal Response of Adjacent Piles in a Silty Layer. Buildings 2023, 13, 2455. [Google Scholar] [CrossRef]
  7. Li, P.; Lu, Y.; Lai, J.; Liu, H.; Wang, K. A Comparative Study of Protective Schemes for Shield Tunneling Adjacent to Pile Groups. Adv. Civ. Eng. 2020, 2020, 6964314. [Google Scholar] [CrossRef]
  8. Zhang, J.X.; Wu, T.L. Numberical Analysis in the Deformation of Adjacent Buildings and Underground Pile Caused by Tunnel Shield Construction. Appl. Mech. Mater. 2012, 170–173, 1444–1449. [Google Scholar] [CrossRef]
  9. Zhao, Z.-F. Numerical Study on Effect of Shield Tunneling to Adjacent Pile Foundation of Overpass. J. Wuhan Univ. Technol. 2010, 32, 47–50. [Google Scholar] [CrossRef]
  10. Hu, X.Y.; He, C.; Jiang, Y.C.; Wang, J.; Zheng, H.L. Research on the Impact of Shield Tunneling on Adjacent Pile Foundation Using FEM. In ICPTT 2013; American Society of Civil Engineers: Reston, VA, USA, 2013; pp. 651–658. [Google Scholar] [CrossRef]
  11. Wei, Y.-H.; Wang, Y.; Mao, Y.; Chen, L.; Wang, M. Effect of Shield-Tunnel Excavation on Adjacent-Pile Foundation Based on Modified Cam-Clay Model. J. Expressway Transp. Res. Dev. (Engl. Ed.) 2020, 14, 84–92. [Google Scholar] [CrossRef]
  12. Xin, L.; Ye, S.; Wang, D. Numerical Analysis of the Impact of Excavation for Undercrossing Yellow River Tunnel on Adjacent Bridge Foundations. Appl. Rheol. 2023, 33, 20230104. [Google Scholar] [CrossRef]
  13. Kun, P.; Lianjin, T.; Yuchun, G.; Feng, W.; Jun, H. Numerical Analysis of Bridge Pile Deformation Caused by Shield Tunnel Construction underneath. Chin. J. Undergr. Space Eng. 2012, 8, 485–489. [Google Scholar] [CrossRef]
  14. Gao, E.; Chen, Z.; Li, L.; Jiao, T. Effects of Soil Displacement Induced by Subway Shield Tunneling Excavation on Bridge Pile Foundations. Sci. Technol. Rev. 2007, 19, 53–56. [Google Scholar]
  15. Huang, K.; Sun, Y.; Yang, J.; Li, Y.; Jiang, M.; Huang, X. Three-Dimensional Displacement Characteristics of Adjacent Pile Induced by Shield Tunneling under Influence of Multiple Factors. J. Cent. S. Univ. 2022, 29, 1597–1615. [Google Scholar] [CrossRef]
  16. Wei, Z. Analytical Solution for Evaluating the Responses of Existing Pile Caused by Adjacent Tunnel Excavation. Environ. Earth Sci. 2024, 83, 495. [Google Scholar] [CrossRef]
  17. Lei, M.; Shi, Y.; Tang, Q.; Sun, N.; Tang, Z.; Gong, C. Construction Control Technology of a Four-Hole Shield Tunnel Passing through Pile Foundations of an Existing Bridge: A Case Study. J. Cent. S. Univ. 2023, 30, 2360–2373. [Google Scholar] [CrossRef]
  18. Gu, X.; Chen, F.; Zhang, W.; Wang, Q.; Liu, H. Numerical Investigation of Pile Responses Induced by Adjacent Tunnel Excavation in Spatially Variable Clays. Undergr. Space 2022, 7, 911–927. [Google Scholar] [CrossRef]
  19. Huang, K.; Sun, Y.; Zhou, D.; Li, Y.; Jiang, M.; Huang, X. Influence of Water-Rich Tunnel by Shield Tunneling on Existing Bridge Pile Foundation in Layered Soils. J. Cent. S. Univ. 2021, 28, 2574–2588. [Google Scholar] [CrossRef]
  20. Liu, W.; Wang, M.; Luo, G.; Lu, W.; Xiao, H. Horizontal Response of Existing Pile Induced by Adjacent Shield Tunnelling with Large Longitudinal Slope. Tunn. Undergr. Space Technol. 2024, 153, 106036. [Google Scholar] [CrossRef]
  21. Ng, C.W.W.; Lu, H.; Peng, S.Y. Three-Dimensional Centrifuge Modelling of the Effects of Twin Tunnelling on an Existing Pile. Tunn. Undergr. Space Technol. 2013, 35, 189–199. [Google Scholar] [CrossRef]
  22. Zhang, Y.; Ding, C.; Lu, H.; Ji, W. Effects of Large-Scale Twin Tunnel Excavation on an Existing Pile Group: Three-Dimensional Centrifuge Modeling. Soil Mech. Found. Eng. 2022, 58, 500–506. [Google Scholar] [CrossRef]
  23. Song, G.; Marshall, A.M. Centrifuge Study on the Influence of Tunnel Excavation on Piles in Sand. J. Geotech. Geoenviron. Eng. 2020, 146, 04020129. [Google Scholar] [CrossRef]
  24. Ng, C.W.W.; Lu, H. Effects of the Construction Sequence of Twin Tunnels at Different Depths on an Existing Pile. Can. Geotech. J. 2014, 51, 173–183. [Google Scholar] [CrossRef]
  25. He, S.; Lai, J.; Li, Y.; Wang, K.; Wang, L.; Zhang, W. Pile Group Response Induced by Adjacent Shield Tunnelling in Clay: Scale Model Test and Numerical Simulation. Tunn. Undergr. Space Technol. 2022, 120, 104039. [Google Scholar] [CrossRef]
  26. Su, J.; Pan, Y.; Niu, X.; Zhang, C. Effect of Shield Tunneling on Adjacent Pile Foundations in Water-Rich Strata. Transp. Geotech. 2025, 52, 101557. [Google Scholar] [CrossRef]
  27. Wu, X.; Xu, J.; Wang, S.; Sha, P.; Han, Z.; Chen, X.; Shu, S.; Qiao, W.; Zeng, X. Ground Deformation of Shield Tunneling through Composite Strata in Coastal Areas. Buildings 2024, 14, 1236. [Google Scholar] [CrossRef]
  28. Wang, Y.; Zhang, Y.; Zhu, Z.; Du, M.; Qi, Y.; Tao, Z. A Novel Method for Analyzing the Factors Influencing Ground Settlement during Shield Tunnel Construction in Upper-Soft and Lower-Hard Fissured Rock Strata considering the Coupled Hydromechanical Properties. Geofluids 2020, 2020, 6691157. [Google Scholar] [CrossRef]
  29. Ding, J.; Zhang, S.; Zhang, Z.L.H. Ground Settlement Caused by Shield Tunneling in Soil-Rock Composite Strata. J. Perform. Constr. Facil. 2021, 35, 7. [Google Scholar] [CrossRef]
  30. Li, J.; Liu, A.; Xing, H. Study on Ground Settlement Patterns and Prediction Methods in Super-Large-Diameter Shield Tunnels Constructed in Composite Strata. Appl. Sci. 2023, 13, 10820. [Google Scholar] [CrossRef]
  31. Liu, C.; Wang, Z.; Jiang, Y. Settlement Prediction of Double Line Shield Tunnel in Upper-soft and lower-hard Stratas. Soil Mech. Found. Eng. 2022, 59, 385–393. [Google Scholar] [CrossRef]
  32. Liu, C.; Zhang, S.; Zhang, D.; Zhang, K.; Wang, Z. Model tests on progressive collapse mechanism of a shallow subway tunnel in soft upper and hard lower composite strata. Tunn. Undergr. Space Technol. 2023, 131, 104824. [Google Scholar] [CrossRef]
  33. Jiao, N.; Sun, S.; Liu, J.W.X. Analysis of existing railway deformation caused by double shield tunnel construction in soil-rock composite strata. Energy Rep. 2023, 9 (Suppl. 2), 159–165. [Google Scholar] [CrossRef]
  34. Jiao, N.; Wan, X.; Ding, J.; Zhang, S.; Liu, J. Pipeline deformation caused by double curved shield tunnel in soil-rock composite strata. Geomech. Eng. 2024, 36, 131–143. [Google Scholar] [CrossRef]
  35. Feng, J.; Yang, H.J.; Zhang, Y. A Study on Excavation Characteristics of Tunnel with Upper-Soft Lower-Hard Strata. Geofluids 2022, 2022, 1094281. [Google Scholar] [CrossRef]
  36. Li, L.; Du, X.; Zhou, J. Numerical Simulation of Site Deformation Induced by Shield Tunneling in Typical Upper-Soft-Lower-Hard Soil-Rock Composite Strata Site of Changchun. KSCE J. Civ. Eng. 2020, 24, 3156–3168. [Google Scholar] [CrossRef]
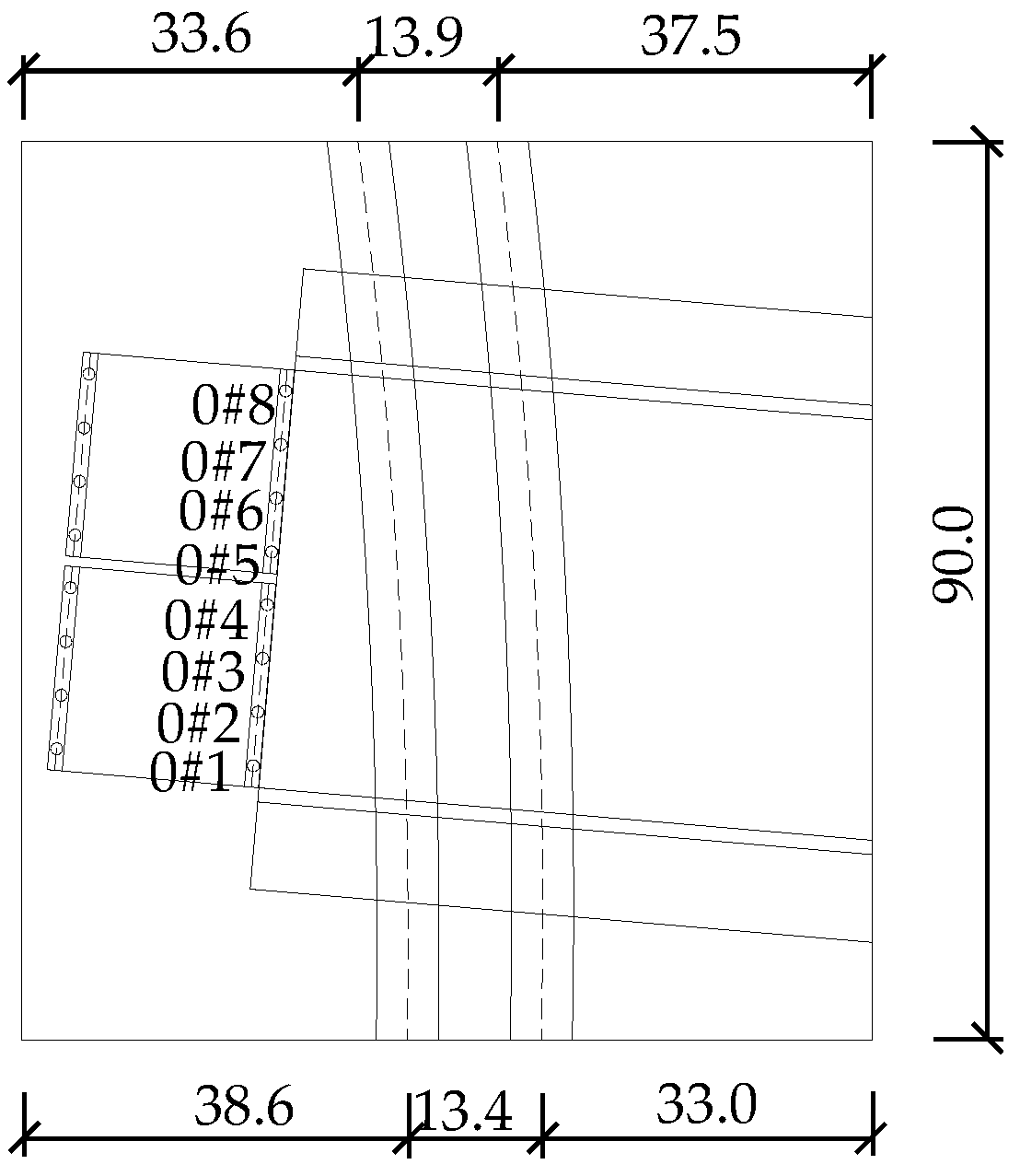
Buildings 15 02426 g001
Figure 1. Plane relationship between shield tunnel and roadbed of Shen-Hai Expressway and Tianzhushan overpass (unit: m).
Figure 1. Plane relationship between shield tunnel and roadbed of Shen-Hai Expressway and Tianzhushan overpass (unit: m).
Buildings 15 02426 g001
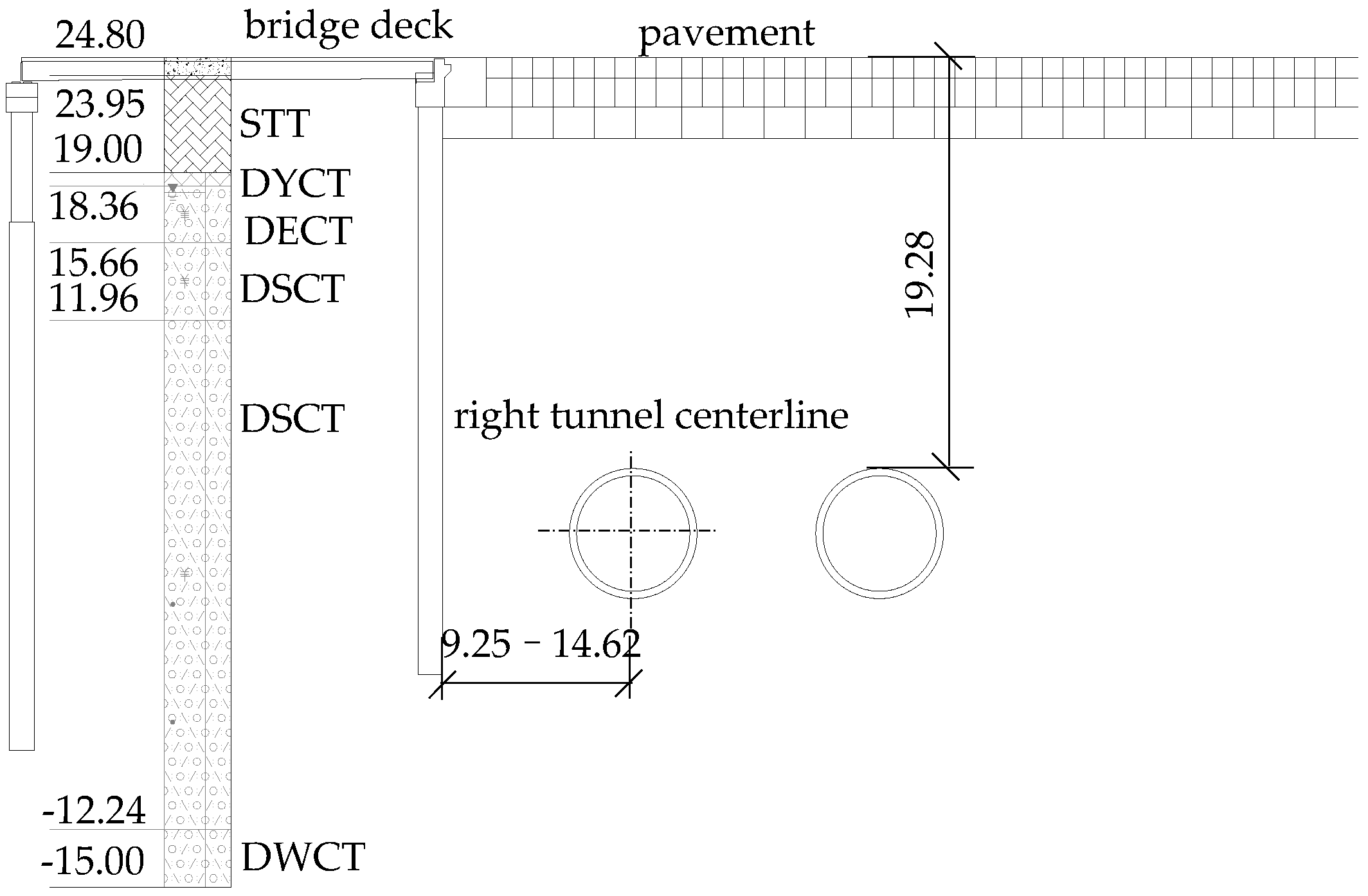
Buildings 15 02426 g002
Figure 2. Sections of shield tunnel side-crossing Tianzhushan overpass and under-crossing Shen-Hai Expressway (unit: m).
Figure 2. Sections of shield tunnel side-crossing Tianzhushan overpass and under-crossing Shen-Hai Expressway (unit: m).
Buildings 15 02426 g002
Buildings 15 02426 g003
Figure 3. Numerical simulation model of shield side-crossing Tianzhu Mountain overpass and under-crossing Shen-Hai Expressway.
Figure 3. Numerical simulation model of shield side-crossing Tianzhu Mountain overpass and under-crossing Shen-Hai Expressway.
Buildings 15 02426 g003
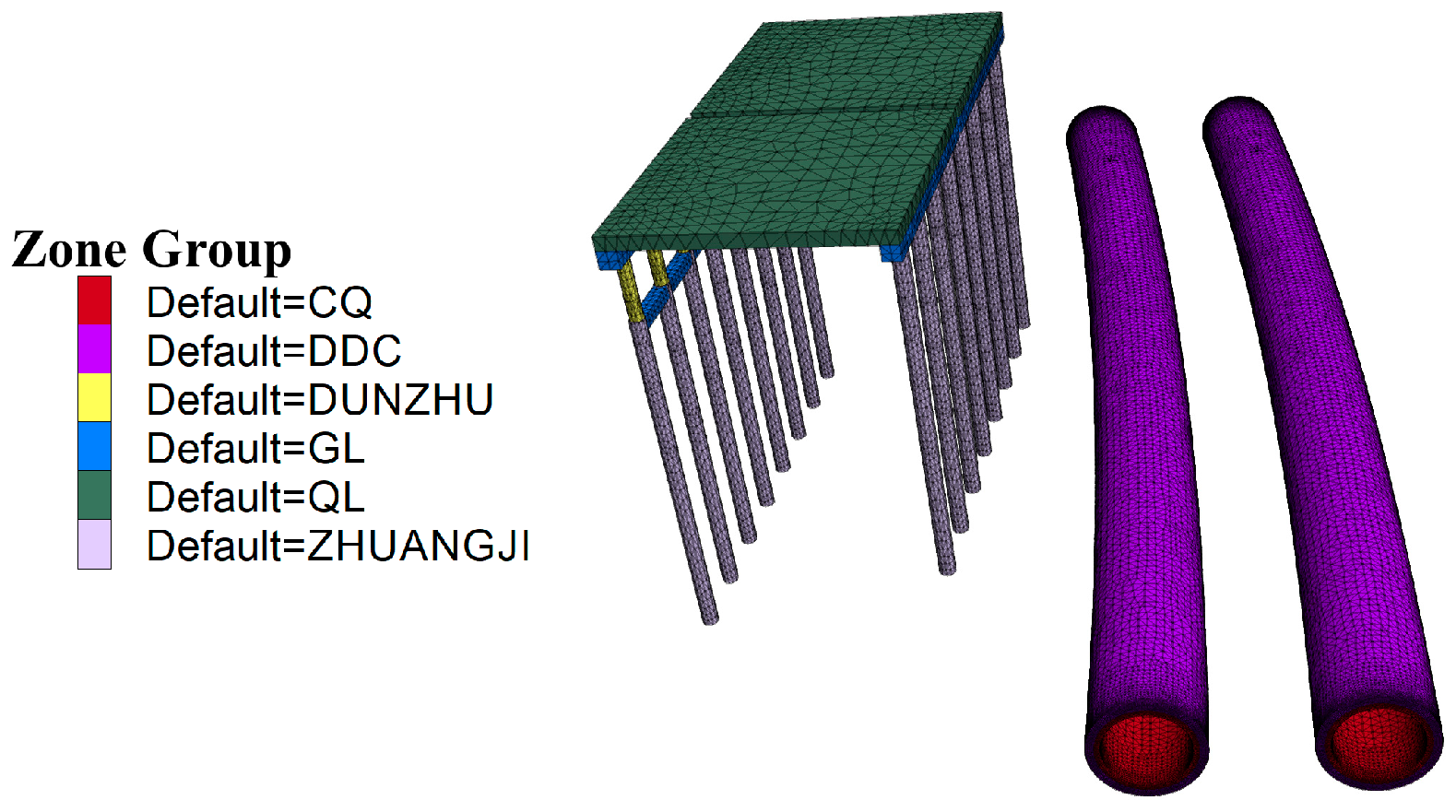
Buildings 15 02426 g004
Figure 4. Three-dimensional model of the tunnel and Tianzhushan overpass.
Figure 4. Three-dimensional model of the tunnel and Tianzhushan overpass.
Buildings 15 02426 g004
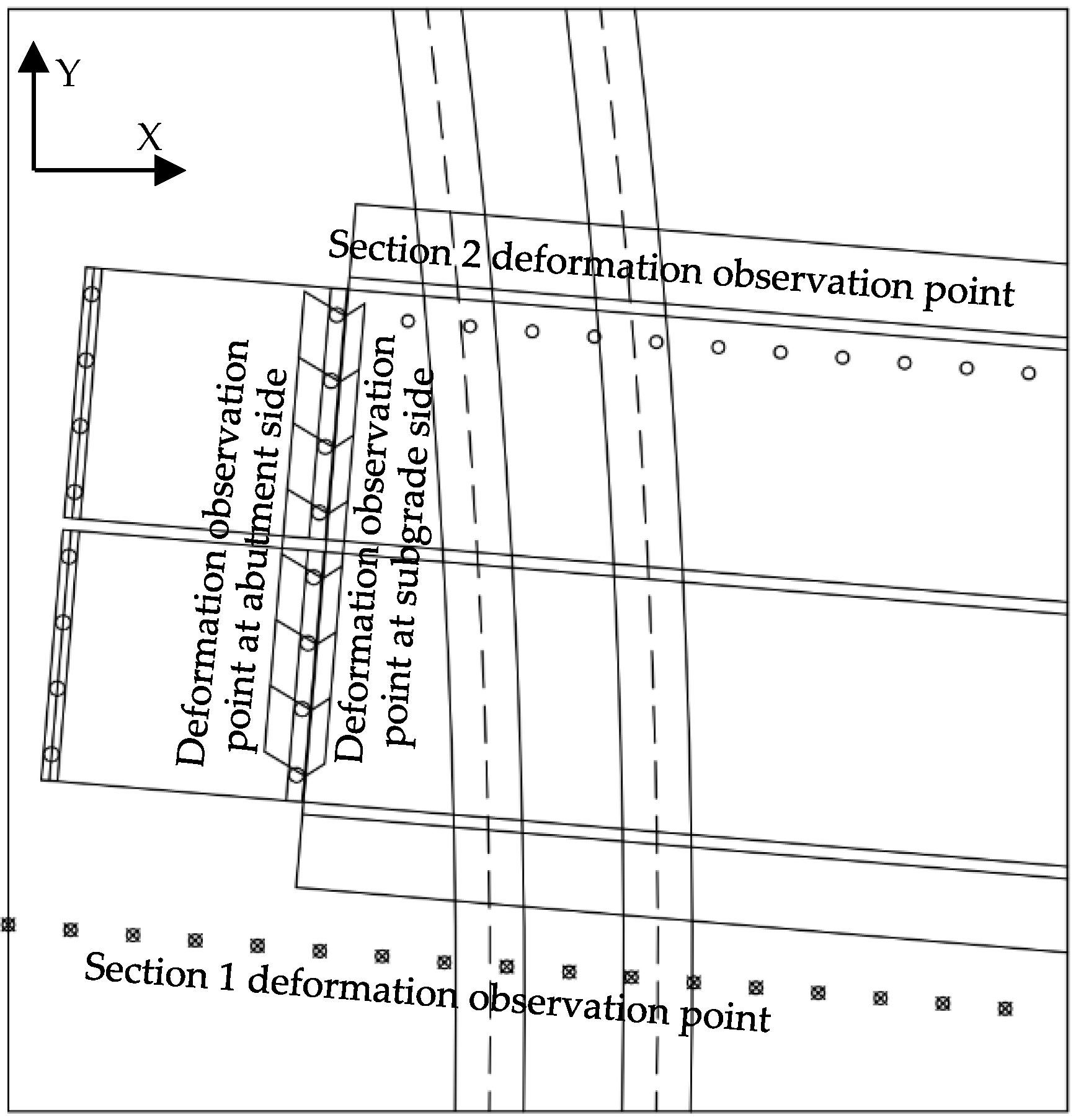
Buildings 15 02426 g005
Figure 5. Layout diagram of deformation observation points.
Figure 5. Layout diagram of deformation observation points.
Buildings 15 02426 g005
Buildings 15 02426 g006
Figure 6. Relationship curve between the pile deformation along X-axis direction and the soil bin pressure.
Figure 6. Relationship curve between the pile deformation along X-axis direction and the soil bin pressure.
Buildings 15 02426 g006
Buildings 15 02426 g007
Figure 7. Relationship curve between deformation of each observation points and soil bin pressure in section 1.
Figure 7. Relationship curve between deformation of each observation points and soil bin pressure in section 1.
Buildings 15 02426 g007
Buildings 15 02426 g008
Figure 8. Relationship curve between deformation of each observation points and soil bin pressure in section 2.
Figure 8. Relationship curve between deformation of each observation points and soil bin pressure in section 2.
Buildings 15 02426 g008
Buildings 15 02426 g009
Figure 9. Relationship curve between differential deformation on both sides of the deformation joint and soil bin pressure.
Figure 9. Relationship curve between differential deformation on both sides of the deformation joint and soil bin pressure.
Buildings 15 02426 g009
Buildings 15 02426 g010
Figure 10. Relationship curve between the pile deformation along the X-axis direction and grouting layer thickness.
Figure 10. Relationship curve between the pile deformation along the X-axis direction and grouting layer thickness.
Buildings 15 02426 g010
Buildings 15 02426 g011
Figure 11. Relationship curve between deformation of each observation points and grouting layer thickness in section 1.
Figure 11. Relationship curve between deformation of each observation points and grouting layer thickness in section 1.
Buildings 15 02426 g011
Buildings 15 02426 g012
Figure 12. Relationship curve between deformation of each observation points and grouting layer thickness in section 2.
Figure 12. Relationship curve between deformation of each observation points and grouting layer thickness in section 2.
Buildings 15 02426 g012
Buildings 15 02426 g013
Figure 13. Relationship curve between differential deformation on both sides of the deformation joint and grouting layer thickness.
Figure 13. Relationship curve between differential deformation on both sides of the deformation joint and grouting layer thickness.
Buildings 15 02426 g013
Buildings 15 02426 g014
Figure 14. Relationship curve between the pile deformation along the X-axis direction and the stress release coefficient.
Figure 14. Relationship curve between the pile deformation along the X-axis direction and the stress release coefficient.
Buildings 15 02426 g014
Buildings 15 02426 g015
Figure 15. Relationship curve between deformation of each observation points and the stress release coefficient in section 1.
Figure 15. Relationship curve between deformation of each observation points and the stress release coefficient in section 1.
Buildings 15 02426 g015
Buildings 15 02426 g016
Figure 16. Relationship curve between deformation of each observation points and the stress release coefficient in section 2.
Figure 16. Relationship curve between deformation of each observation points and the stress release coefficient in section 2.
Buildings 15 02426 g016
Buildings 15 02426 g017
Figure 17. Relationship curve between differential deformation on both sides of the deformation joint and the stress release coefficient.
Figure 17. Relationship curve between differential deformation on both sides of the deformation joint and the stress release coefficient.
Buildings 15 02426 g017
Buildings 15 02426 g018
Figure 18. Comparison between on-site monitoring deformation and predicted deformation of sections 1 and 2.
Figure 18. Comparison between on-site monitoring deformation and predicted deformation of sections 1 and 2.
Buildings 15 02426 g018
Buildings 15 02426 g019
Figure 19. Comparison between on-site monitoring differential settlement and predicted differential settlement on both sides of deformation joint.
Figure 19. Comparison between on-site monitoring differential settlement and predicted differential settlement on both sides of deformation joint.
Buildings 15 02426 g019
Table 1. Soil layer physical and mechanical parameters.
Table 1. Soil layer physical and mechanical parameters.
Name of Soil LayerCodeDensity (kg/m3)Elastic Modulus (E/MPa)Force of Cohesion (c/kPa)Angle of
Internal
Friction (°)		Poisson RatioLamination Thickness (m)
Plain fillSTT18701215.010.00.352.87
Miscellaneous fillDYCT18501012.58.00.360.64
Fully weathered tuff lavaDECT19208025.019.00.322.70
Granular strongly weathered tuff lavaDSCT200050028.025.00.313.70
Fragmented strongly weathered tuff lavaDSICT205080035.0028.00.2924.20
Medium-weathered tuff lavaDWCT2200100050.0032.00.282.76
Table 2. Allowable pavement and bridge deformations.
Table 2. Allowable pavement and bridge deformations.
Monitoring ProjectsAllowable
Settlement of Bridge Piers (mm)		Differential
Settlement Between Longitudinal Adjacent Bridge Piers (mm)		Settlement Between Transverse Adjacent Pier Abutments (mm)Horizontal
Displacement of Bearing
Abutment (mm)		Surface Vertical Displacement (mm)
Allowable deformation25233Sedimentation: 30
Swell: 10
Table 3. The parameter values of each part of the bridge structure and tunnel segments.
Table 3. The parameter values of each part of the bridge structure and tunnel segments.
NameCodeDensity (kg/m3)Elastic Modulus (E/MPa)Poisson RatioNameCodeDensity (kg/m3)Elastic Modulus (E/MPa)Poisson Ratio
LiningCQ2500210,0000.2Pile foundationZHUANGJI2350270,0000.2
Grouting layerDDC240025000.23Pier columnDUNZHU2450270,0000.2
Pavement structureLMJG245050000.22Bridge deck systemQL2500270,0000.2
Cover (tie) beamGL2500270,0000.2
Table 4. Comparison between the on-site monitoring deformation and predicted deformations at the top of 0#1–0#8 piles along the X-axis.
Table 4. Comparison between the on-site monitoring deformation and predicted deformations at the top of 0#1–0#8 piles along the X-axis.
Pile Number
0#10#20#30#40#50#60#70#8
Deformation (mm)
Predicted deformation (mm)−1.19−0.87−0.55−0.24−0.150.421.001.58
Measured deformation (mm)−1.02−0.75−0.48−0.21−0.060.491.051.61
Differential deformation (mm)−0.17−0.12−0.07−0.03−0.090.070.050.03
Table 5. Comparison between the on-site monitoring deformation and predicted deformation of each pile top of No.0 abutment and No.1 pier.
Table 5. Comparison between the on-site monitoring deformation and predicted deformation of each pile top of No.0 abutment and No.1 pier.
Pile Number1#-10#-11#-20#-21#-30#-31#-40#-4
Predicted deformation (mm)−0.62−0.60−0.80−0.80−0.98−1.01−1.15−1.22
Measured deformation (mm)−0.61−0.79−0.80−1.00−0.98−1.21−1.16−1.40
Differential deformation (mm)0.00−0.190.00−0.200.00−0.20−0.01−0.18
Pile number1#-50#-51#-60#-61#-70#-71#-80#-8
Predicted deformation (mm)−0.98−1.06−1.00−1.07−1.02−1.08−1.05−1.09
Measured deformation (mm)−1.01−1.27−1.02−1.26−1.02−1.25−1.03−1.25
Differential deformation (mm)−0.03−0.21−0.02−0.190.00−0.170.02−0.16
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Wang, J.; Lei, N.; Tang, X.; Wang, Y. Research on the Deformation Laws of Adjacent Structures Induced by the Shield Construction Parameters. Buildings 2025, 15, 2426. https://doi.org/10.3390/buildings15142426

AMA Style

Wang J, Lei N, Tang X, Wang Y. Research on the Deformation Laws of Adjacent Structures Induced by the Shield Construction Parameters. Buildings. 2025; 15(14):2426. https://doi.org/10.3390/buildings15142426

Chicago/Turabian Style

Wang, Jinhua, Nengzhong Lei, Xiaolin Tang, and Yulin Wang. 2025. "Research on the Deformation Laws of Adjacent Structures Induced by the Shield Construction Parameters" Buildings 15, no. 14: 2426. https://doi.org/10.3390/buildings15142426

APA Style

Wang, J., Lei, N., Tang, X., & Wang, Y. (2025). Research on the Deformation Laws of Adjacent Structures Induced by the Shield Construction Parameters. Buildings, 15(14), 2426. https://doi.org/10.3390/buildings15142426

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop