Numerical and Experimental Analysis of Thermal Stratification in Locally Heated Residential Spaces
Abstract
1. Introduction
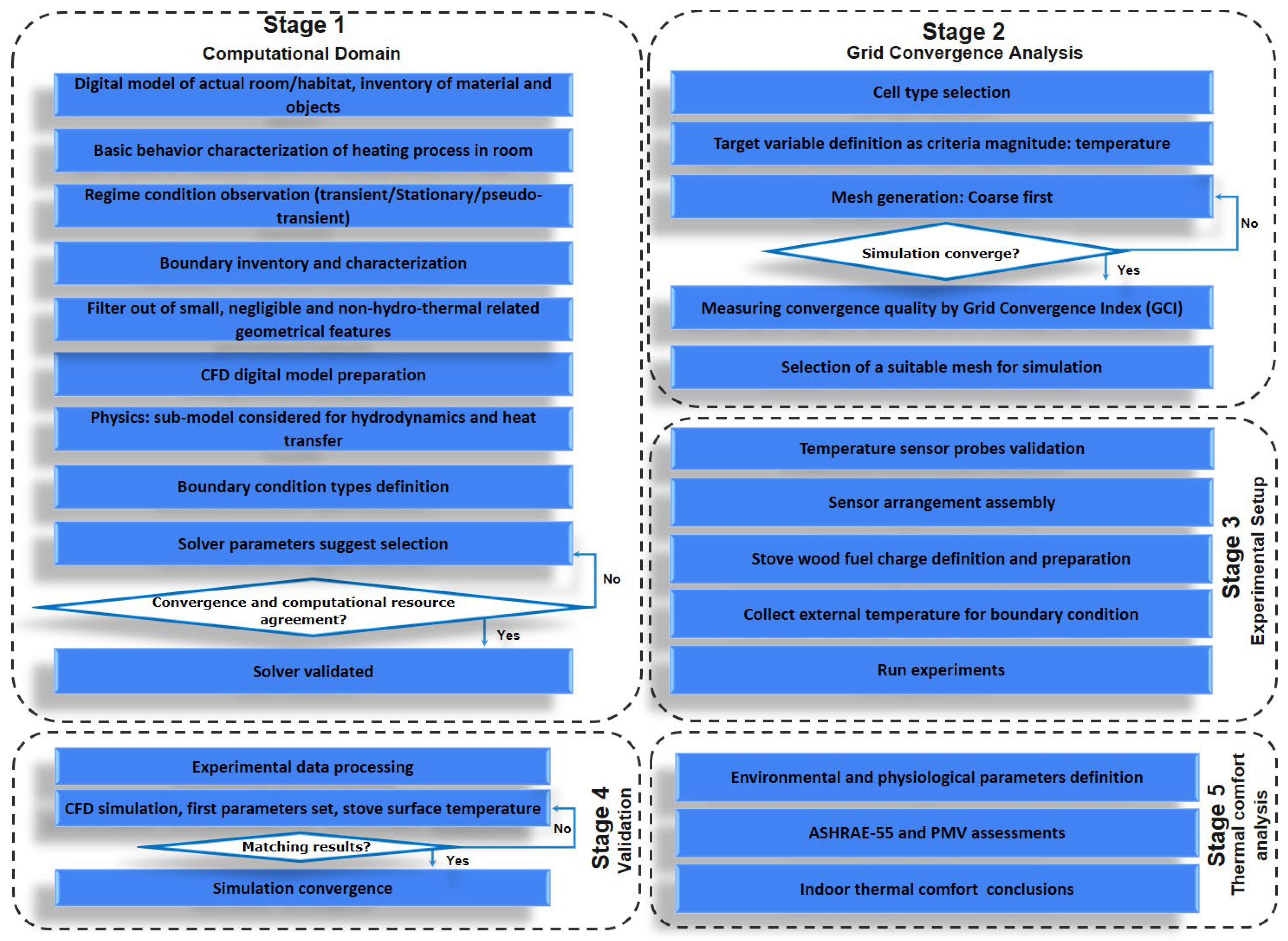
2. Materials and Methods for Capturing Thermal Stratification
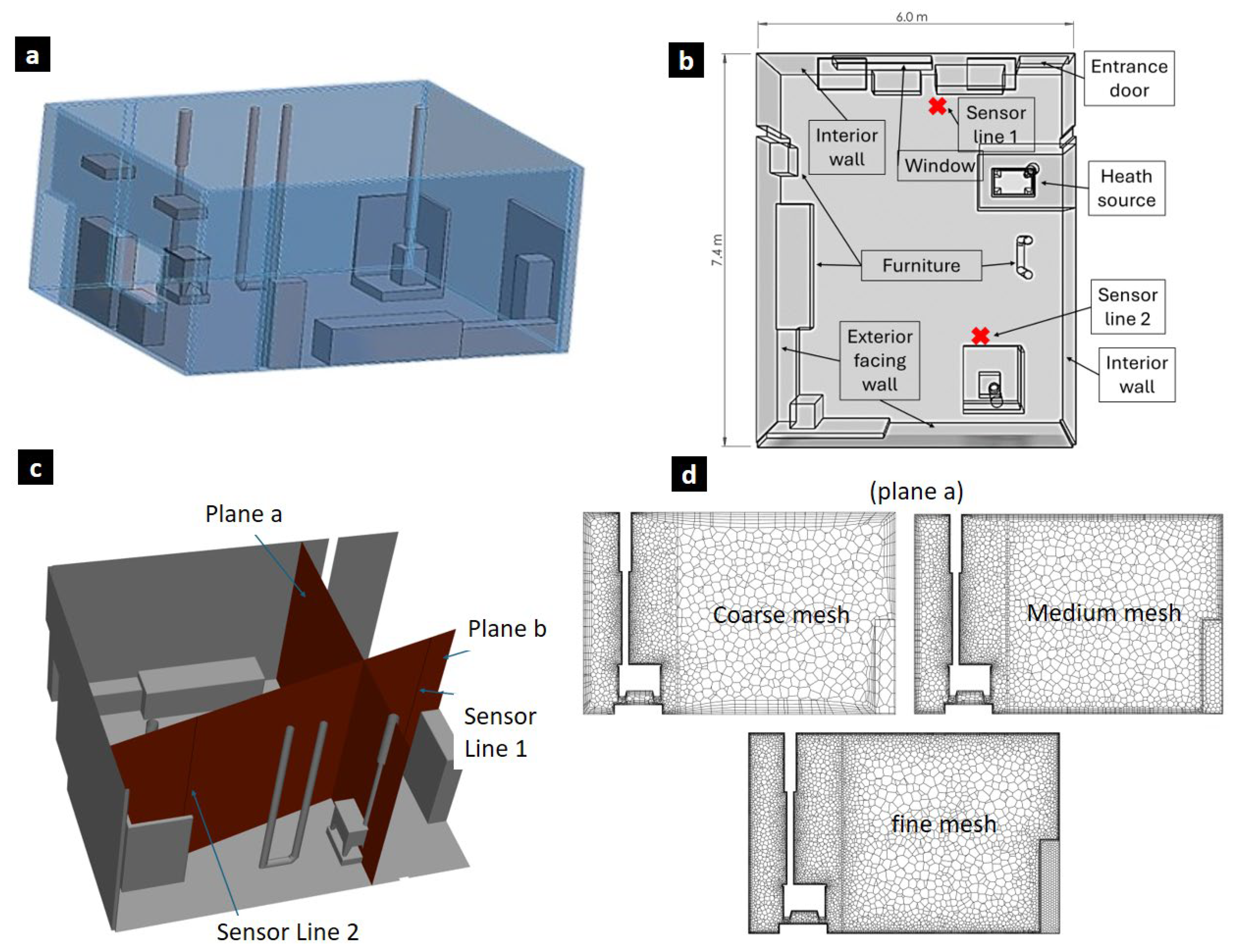
2.1. Computational Model of the Simulated Space Domain
2.2. Selection Criteria for Thermal Comfort Analysis
2.3. Experimental Data Acquisition and Postprocessing of Temporal-Specific Temperature Data
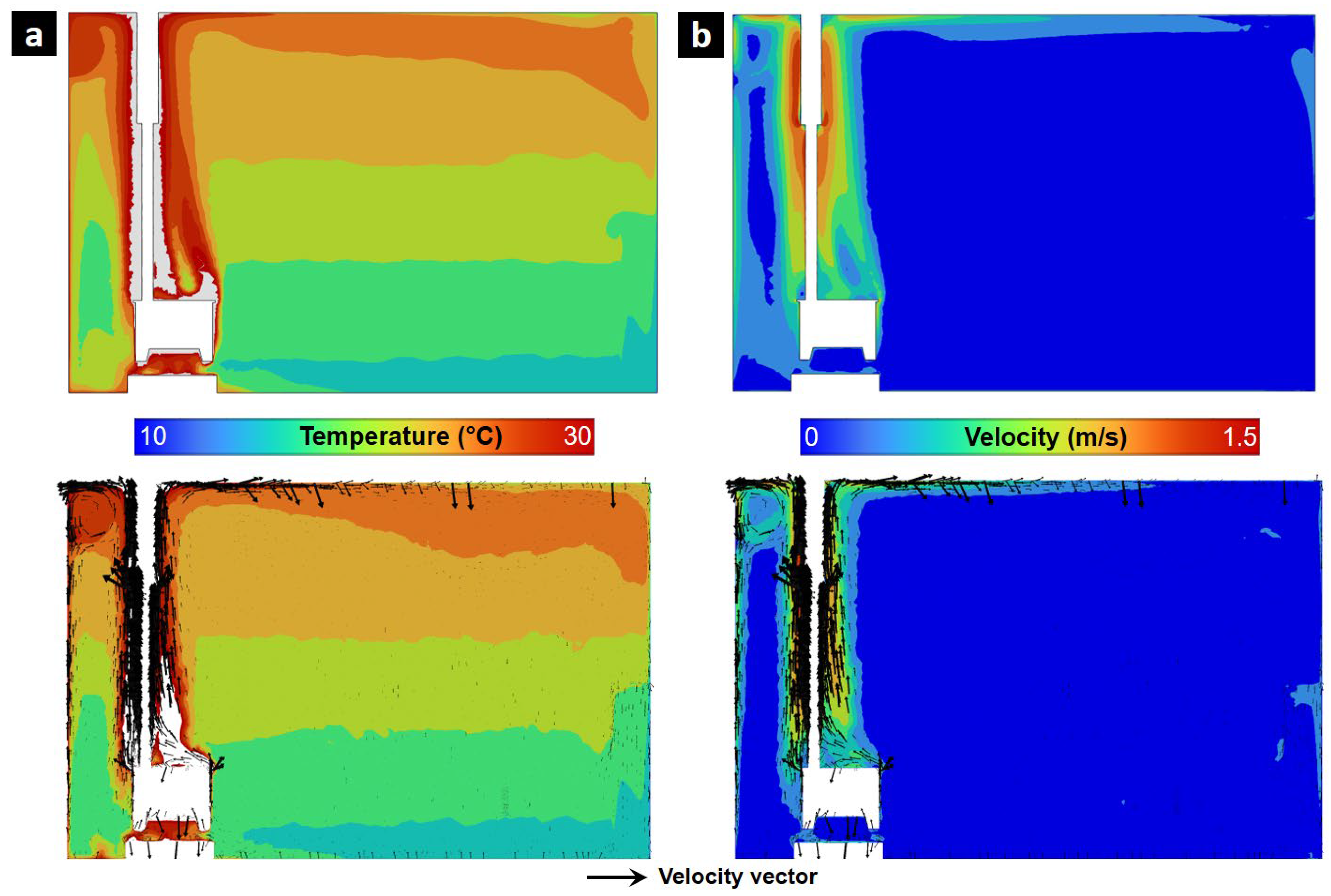
3. Results of Thermal Stratification Analysis Using CFD and Experimental Validation
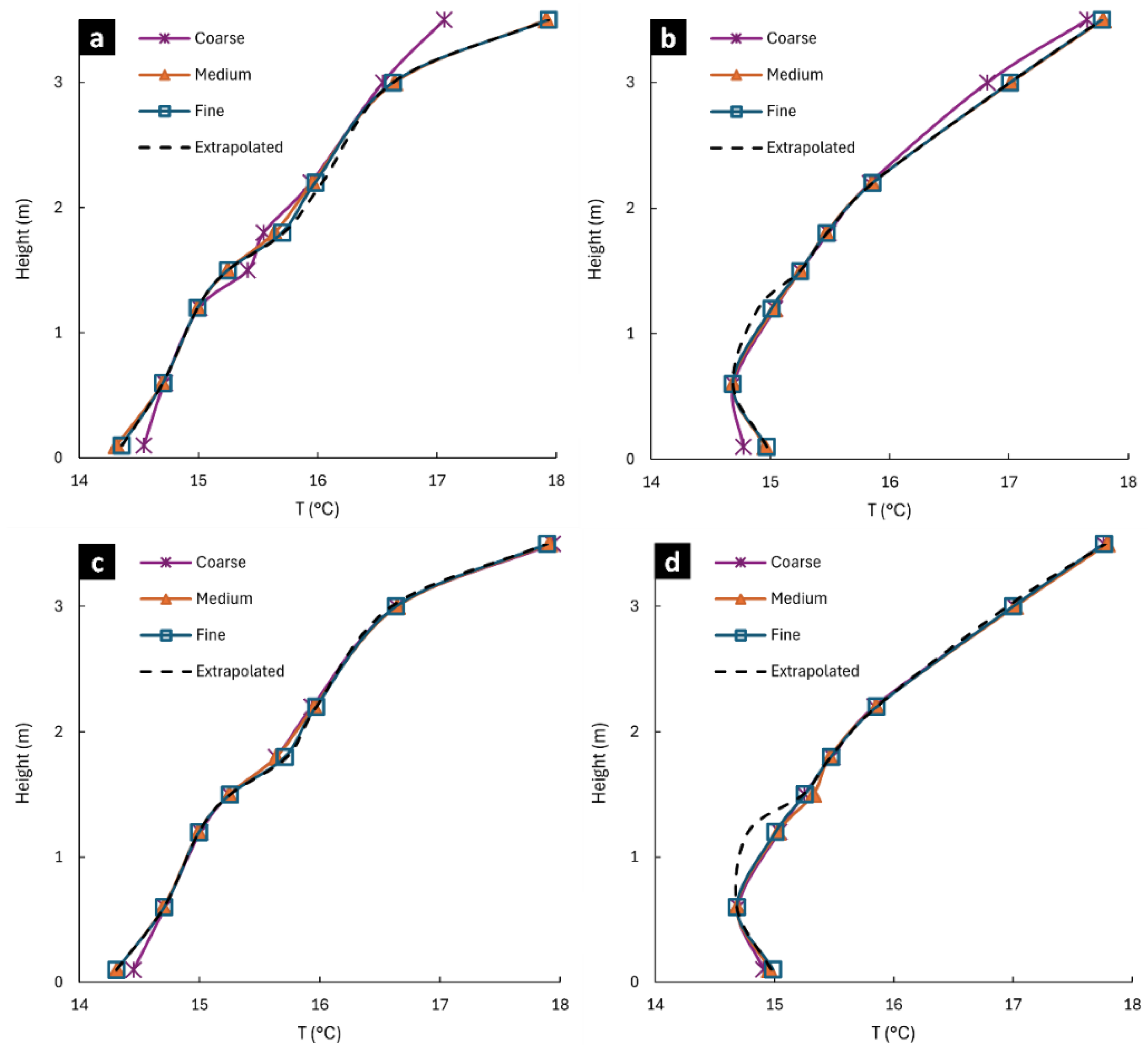
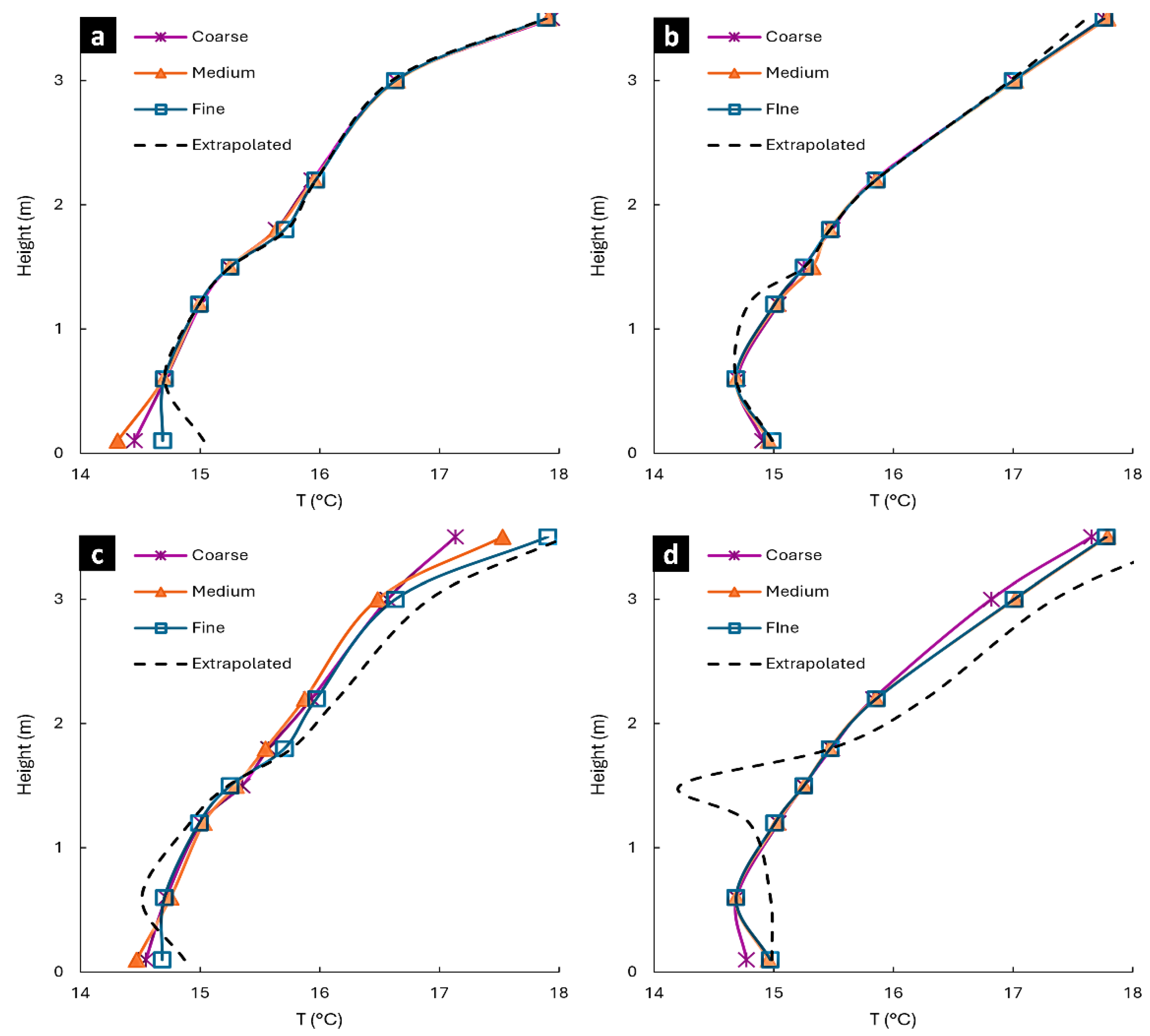
3.1. Temperature Gradient Predictions and Mesh Convergence Analysis in CFD Simulations
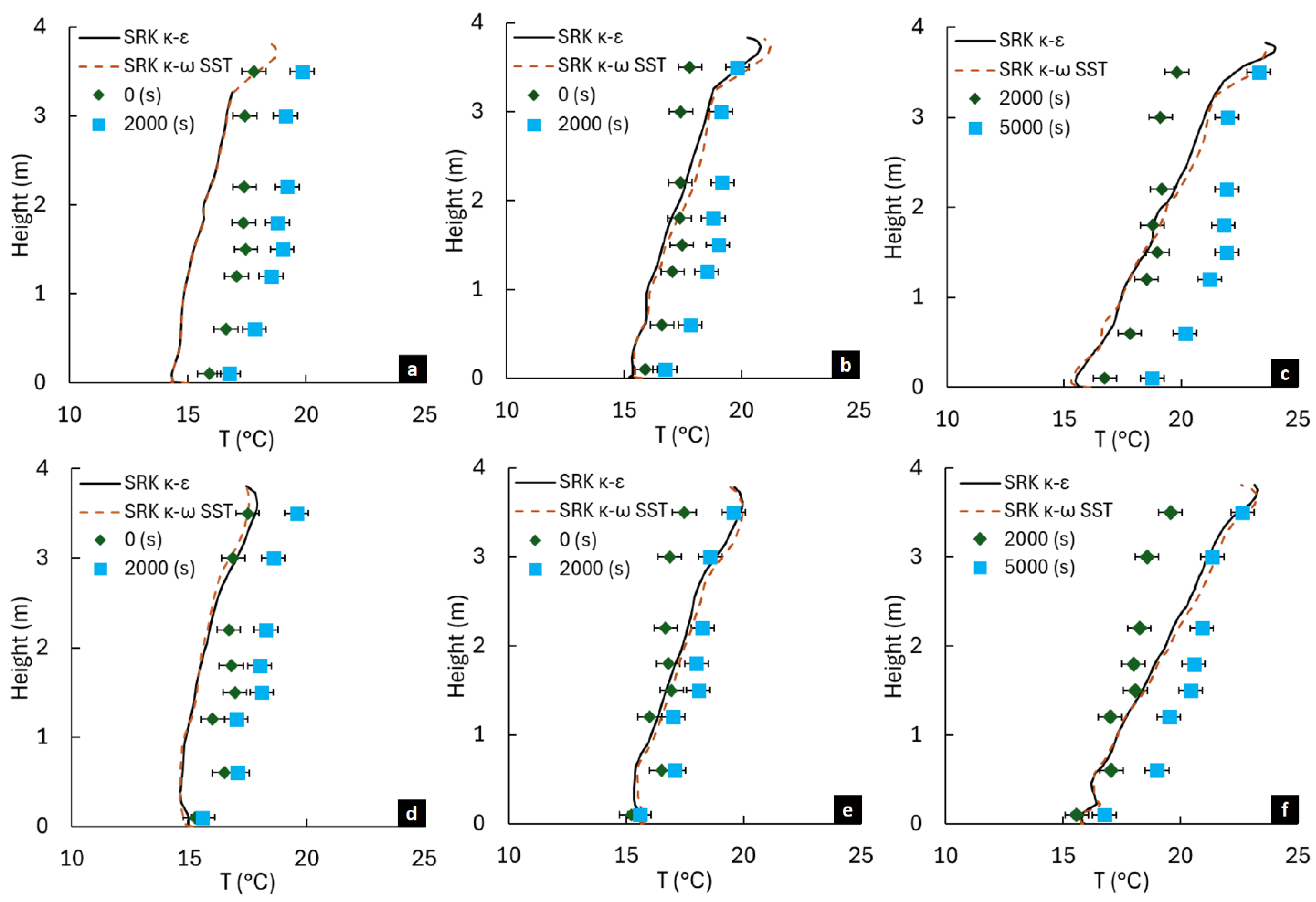
3.2. Thermal Stratification Profile: Experiments Versus Computational Modeling
4. Assessing Indoor Thermal Comfort in Locally Heated Spaces
4.1. PMV-Based Thermal Comfort Assessment and ASHRAE-55 Compliance
4.2. Overcoming Localized Heating Challenges: Strategies for Improving Thermal Comfort and Energy Efficiency
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Valenzuela, M.; Ciudad, G.; Cárdenas, J.P.; Medina, C.; Salas, A.; Oñate, A.; Pincheira, G.; Attia, S.; Tuninetti, V. Towards the development of performance-efficient compressed earth blocks from industrial and agro-industrial by-products. Renew. Sustain. Energy Rev. 2024, 194, 114323. [Google Scholar] [CrossRef]
- Jansen, L. The challenge of sustainable development. J. Clean. Prod. 2003, 11, 231–245. [Google Scholar] [CrossRef]
- Zhong, X.; Yu, H.; Tang, Y.; Mao, H.; Zhang, K. Local Thermal comfort and physiological responses in uniform environments. Buildings 2024, 14, 59. [Google Scholar] [CrossRef]
- Mba, E.J.; Oforji, P.I.; Okeke, F.O.; Ozigbo, I.W.; Onyia, C.D.F.; Ozigbo, C.A.; Ezema, E.C.; Awe, F.C.; Nnaemeka-Okeke, R.C.; Onyia, S.C. Assessment of floor-level impact on natural ventilation and indoor thermal environment in hot–humid climates: A case study of a mid-rise educational building. Buildings 2025, 15, 686. [Google Scholar] [CrossRef]
- Lee, T.C.; Sato, R.; Asawa, T.; Yoon, S. Indoor air temperature distribution and heat transfer coefficient for evaluating cold storage of phase-change materials during night ventilation. Buildings 2024, 14, 1872. [Google Scholar] [CrossRef]
- Longhitano, A.; Costanzo, V.; Evola, G.; Nocera, F. Microclimate Investigation in a conference room with thermal stratification: An investigation of different air conditioning systems. Energies 2024, 17, 1188. [Google Scholar] [CrossRef]
- Wu, X.; Gao, H.; Zhao, M.; Gao, J.; Tian, Z.; Li, X. Experimental study of indoor air distribution and thermal environment in a ceiling cooling room with mixing ventilation, underfloor air distribution and stratum ventilation. Buildings 2023, 13, 2354. [Google Scholar] [CrossRef]
- Van Tran, V.; Park, D.; Lee, Y.-C. Indoor air pollution, related human diseases, and recent trends in the control and improvement of indoor air quality. Int. J. Environ. Res. Public. Health 2020, 17, 2927. [Google Scholar] [CrossRef]
- Fanger, P.O. Assessment of man’s thermal comfort in practice. Br. J. Ind. Med. 1973, 30, 313–324. [Google Scholar] [CrossRef]
- Castilla, M.; Álvarez, J.D.; Berenguel, M.; Pérez, M.; Rodríguez, F.; Guzmán, J.L. Técnicas de control del confort en edificios. RIAI—Rev. Iberoam. Autom. Inform. Ind. 2010, 7, 5–24. [Google Scholar] [CrossRef]
- The American Society of Heating, Refrigerating and Air-Conditioning Engineers. ASHRAE Handbook—Fundamentals; Inch-pound; ASHRAE: Atlanta, GA, USA, 2017; Volume 1, ISBN 9781939200570/1939200571. [Google Scholar]
- Liu, S.; Wang, Z.; Schiavon, S.; He, Y.; Luo, M.; Zhang, H.; Arens, E. Predicted percentage dissatisfied with vertical temperature gradient. Energy Build. 2020, 220, 110085. [Google Scholar] [CrossRef]
- Hedrick, R.L.; Mcfarland, J.K.; Apte, M.G.; Bixby, D.C.; Brunner, G.; Buttner, M.P.; Conover, D.R.; Damiano, L.A.; Danks, R.A.; Fisher, F.J.; et al. ASHRAE standard ventilation for acceptable indoor air quality. Ashrae Stand. 2013, 2010, 1–4. [Google Scholar]
- Wvon, D.P.; Sandberg, M. Discomfort due to vertical thermal gradients. Indoor Air 1996, 6, 48–54. [Google Scholar] [CrossRef]
- Tanaka, M.; Yamazaki, S.; Ohnaka, T.; Tochihara, Y.; Yoshida, K. Physiological Reactions to different vertical (head-foot) air temperature differences. Ergonomics 1986, 29, 131–143. [Google Scholar] [CrossRef]
- Yu, W.J.; Cheong, K.W.D.; Tham, K.W.; Sekhar, S.C.; Kosonen, R. Thermal effect of temperature gradient in a field environment chamber served by displacement ventilation system in the tropics. Build. Environ. 2007, 42, 516–524. [Google Scholar] [CrossRef]
- Liu, S.; Schiavon, S.; Kabanshi, A.; Nazaroff, W.W. Predicted percentage dissatisfied with ankle draft. Indoor Air 2017, 27, 852–862. [Google Scholar] [CrossRef]
- Olesen, B.W.; Schøler, M.; Fanger, P.O. Discomfort Caused by Vertical Air Temperature Differences. In Indoor Climate: Effects on Human Comfort, Performance and Health in Residential, Commercial and Light -Industry Buildings; Fanger, P.O., Valbjorn, O., Eds.; Danish Building Research Institute: Copenhagen, Denmark, 1979; pp. 561–579. [Google Scholar]
- ASHRAE-55; Thermal Environmental Conditions for Human Occupancy. ANSI/ASHRAE: Georgia, GA, USA, 2017.
- Yau, Y.H.; Chew, B.T. A review on predicted mean vote and adaptive thermal comfort models. Build. Serv. Eng. Res. Technol. 2014, 35, 23–35. [Google Scholar] [CrossRef]
- Duan, X.; Yu, S.; Chu, J.; Chen, D.; Chen, Y. Evaluation of Indoor thermal environments using a novel predicted mean vote model based on artificial neural networks. Buildings 2022, 12, 1880. [Google Scholar] [CrossRef]
- Fanger, P.O. Thermal Comfort: Analysis and Applications in Environmental Engineering; McGraw-Hill: New York, NY, USA, 1972; p. 244. ISBN 0070199159. [Google Scholar]
- Ratajczak, K.; Amanowicz, Ł.; Pałaszyńska, K.; Pawlak, F.; Sinacka, J. Recent achievements in research on thermal comfort and ventilation in the aspect of providing people with appropriate conditions in different types of buildings—Semi-systematic review. Energies 2023, 16, 6254. [Google Scholar] [CrossRef]
- Trebilcock, M.; Soto-Muñoz, J.; Yañez, M.; Figueroa-San Martin, R. The right to comfort: A field study on adaptive thermal comfort in free-running primary schools in chile. Build. Environ. 2017, 114, 455–469. [Google Scholar] [CrossRef]
- ISO 7730; Ergonomics of the Thermal Environment-Analytical Determination and Interpretation of Thermal Comfort Using Calculation of the PMV and PPD Indices and Local Thermal Comfort Criteria. International Organization for Standardization: Geneva, Switzerland, 2005.
- Canan, F.; Golasi, I.; Falasca, S.; Salata, F. Outdoor thermal perception and comfort conditions in the köppen-geiger climate category bsk. one-year field survey and measurement campaign in Konya, Turkey. Sci. Total Environ. 2020, 738, 140295. [Google Scholar] [CrossRef]
- Yang, Y.; Shi, N.; Zhang, R.; Zhou, H.; Ding, L.; Tao, J.; Zhang, N.; Cao, B. Study on the effect of local heating devices on human thermal comfort in low-temperature built environment. Buildings 2024, 14, 3996. [Google Scholar] [CrossRef]
- Lee, H.; Lee, K.; Kang, E.; Kim, D.; Oh, M.; Yoon, J. Evaluation of heated window system to enhance indoor thermal comfort and reduce heating demands based on simulation analysis in South Korea. Energies 2023, 16, 1481. [Google Scholar] [CrossRef]
- Hu, Y.; Zhao, L.; Xu, X.; Wu, G.; Yang, Z. Experimental study on thermal environment and thermal comfort of passenger compartment in winter with personal comfort system. Energies 2024, 17, 2190. [Google Scholar] [CrossRef]
- Sauerwein, D.; Fitzgerald, N.; Kuhn, C. Experimental and numerical analysis of temperature reduction potentials in the heating supply of an unrenovated university building. Energies 2023, 16, 1263. [Google Scholar] [CrossRef]
- Venegas, I.; Oñate, A.; Pierart, F.G.; Valenzuela, M.; Narayan, S.; Tuninetti, V. Efficient mako shark-inspired aerodynamic design for concept car bodies in underground road tunnel conditions. Biomimetics 2024, 9, 448. [Google Scholar] [CrossRef]
- Ji, C.; Shi, W.; Ke, E.; Cheng, J.; Zhu, T.; Zong, C.; Li, X. Numerical investigations on the effects of dome cooling air flow on combustion characteristics and emission behavior in a can-type gas turbine combustor. Aerospace 2024, 11, 338. [Google Scholar] [CrossRef]
- Ameen, A.; Bahrami, A.; Elosua Ansa, I. Assessment of thermal comfort and indoor air quality in library group study rooms. Buildings 2023, 13, 1145. [Google Scholar] [CrossRef]
- Das, H.P.; Lin, Y.-W.; Agwan, U.; Spangher, L.; Devonport, A.; Yang, Y.; Drgoňa, J.; Chong, A.; Schiavon, S.; Spanos, C.J. Machine learning for smart and energy-efficient buildings. Environ. Data Sci. 2024, 3, 1–32. [Google Scholar] [CrossRef]
- Moujalled, B.; Cantin, R.; Guarracino, G. Comparison of thermal comfort algorithms in naturally ventilated office buildings. Energy Build. 2008, 40, 2215–2223. [Google Scholar] [CrossRef]
- Dai, B.; Tong, Y.; Hu, Q.; Chen, Z. Characteristics of thermal stratification and its effects on HVAC energy consumption for an atrium building in South China. Energy 2022, 249, 123425. [Google Scholar] [CrossRef]
- Karimipanah, T.; Awbi, H.B. Theoretical and experimental investigation of impinging jet ventilation and comparison with wall displacement ventilation. Build. Environ. 2002, 37, 1329–1342. [Google Scholar] [CrossRef]
- Rohdin, P.; Molin, A.; Moshfegh, B. Experiences from nine passive houses in Sweden—Indoor thermal environment and energy use. Build. Environ. 2014, 71, 176–185. [Google Scholar] [CrossRef]
- Jaime, M.M.; Chávez, C.; Gómez, W. Fuel choices and fuelwood use for residential heating and cooking in urban areas of central-southern Chile: The role of prices, income, and the availability of energy sources and technology. Resour. Energy Econ. 2020, 60, 101125. [Google Scholar] [CrossRef]
- Celis, J.E.; Morales, J.R.; Zaror, C.A.; Inzunza, J.C. A Study of the particulate matter PM10 composition in the atmosphere of Chillán, Chile. Chemosphere 2004, 54, 541–550. [Google Scholar] [CrossRef]
- Ministerio Secretaría General de la Presidencia. Decreto Supremo 78/2009 Establece Plan de Descontaminación Atmosférica de Temuco y Padre Las Casas; Biblioteca del Congreso Nacional de Chile: Santiago, Chile, 2010. Available online: https://bcn.cl/2fdss (accessed on 2 October 2024).
- Ministerio del Medio Ambiente. Decreto 35 Declara Zona Saturada Por Material Particulado Respirable MP10, Como Concentración de 24 Horas, a Las Comunas de Temuco y Padre Las Casas; Biblioteca del Congreso Nacional de Chile: Santiago, Chile, 2005. Available online: https://bcn.cl/2mg2v (accessed on 2 October 2024).
- Ministerio del Medio Ambiente. Seremi Del Medio Ambiente Región De La Araucanía Cuenta Pública Plan De Descontaminación Ambiental; Ministerio del Medio Ambiente: Santiago, Chile, 2020. Available online: https://cuentaspublicas.mma.gob.cl/wp-content/uploads/2021/05/CPP-2020-La-Araucania.pdf (accessed on 2 October 2024).
- Hajdukiewicz, M.; Geron, M.; Keane, M.M. Calibrated CFD simulation to evaluate thermal comfort in a highly-glazed naturally ventilated room. Build. Environ. 2013, 70, 73–89. [Google Scholar] [CrossRef]
- Chen, Q.; Xu, W. A Zero-equation turbulence model for indoor airflow simulation. Energy Build. 1998, 28, 137–144. [Google Scholar] [CrossRef]
- Celik, I.; Karatekin, O. Numerical experiments on application of richardson extrapolation with nonuniform grids. J. Fluids Eng. Trans. ASME 1997, 119, 584–590. [Google Scholar] [CrossRef]
- Risberg, D.; Westerlund, L.; Hellstrom, J.G.I. Computational fluid dynamics simulation of indoor climate in low energy buildings computational set up. Therm. Sci. 2017, 21, 1985–1998. [Google Scholar] [CrossRef]
- Roache, P.J. Perspective: A method for uniform reporting of grid refinement studies. J. Fluids Eng. 1994, 116, 405–413. [Google Scholar] [CrossRef]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J.; Coleman, H.; Raad, P.E. Procedure for estimation and reporting of uncertainty due to discretization in CFD applications. J. Fluids Eng. Trans. ASME 2008, 130, 780011–780014. [Google Scholar] [CrossRef]
- Ghanbari, M.; Ahmadi, M.; Lashanizadegan, A. A Comparison between Peng-Robinson and Soave-Redlich-Kwong cubic equations of state from modification perspective. Cryogenics 2017, 84, 13–19. [Google Scholar] [CrossRef]
- Barrera, E.F.; Aguirre, F.A.; Vargas, S.; Martínez, E.D. Influence of y plus on the value of the wall shear stress and the total drag coefficient through computational fluid dynamics simulations. Inf. Tecnol. 2018, 29, 291–303. [Google Scholar] [CrossRef]
- Cortés, M.; Fazio, P.; Rao, J.; Bustamante, W.; Vera, S. Modelación CFD de Casos Básicos de convección en ambientes cerrados: Necesidades de principiantes en cfd para adquirir habilidades y confianza en la modelación CFD. Rev. Ing. Construcción 2014, 29, 22–45. [Google Scholar] [CrossRef]
- Stamou, A.; Katsiris, I. Verification of a CFD model for indoor airflow and heat transfer. Build. Environ. 2006, 41, 1171–1181. [Google Scholar] [CrossRef]
- Tartarini, F.; Schiavon, S.; Cheung, T.; Hoyt, T. CBE thermal comfort tool: Online tool for thermal comfort calculations and visualizations. SoftwareX 2020, 12, 100563. [Google Scholar] [CrossRef]
- Center For the Built Environment. CBE Thermal Comfort Tool. Available online: https://comfort.cbe.berkeley.edu/ (accessed on 14 October 2024).
- Wang, X.; Xu, W.; Yang, L. Digitalized Approach in Air Pressure and Temperature Data Acquisition System. In Proceedings of the 2011 International Conference of Information Technology, Computer Engineering and Management Sciences, ICM, Nanjing, China, 24–25 September 2011; Volume 1, pp. 126–129. [Google Scholar] [CrossRef]
- Fathoni, A.N.; Hudallah, N.; Putri, R.D.M.; Khotimah, K.; Rijanto, T.; Ma’Arif, M. Design automatic dispenser for blind people based on arduino mega using DS18B20 temperature sensor. In Proceedings of the International Conference on Vocational Education and Electrical Engineering (Icvee): Strengthening the Framework of Society 5.0 Through Innovations in Education, Electrical Engineering and Informatics Engineering, Surabaya, Indonesia, 3–4 October 2020. [Google Scholar] [CrossRef]
- Xu, H.; Wang, W.; Deng, W.; Lun, Z. Design of portable refrigerator based on DS18B20 temperature sensor. In Proceedings of the 2nd International Symposium on Sensor Technology and Control (ISSTC), Hangzhou, China, 11–13 August 2023; pp. 32–36. [Google Scholar] [CrossRef]
- Schafer, R.W. What is a Savitzky-Golay filter? IEEE Signal Process. Mag. 2011, 28, 111–117. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J.E. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- The MathWorks Inc. Signal Processing Toolbox, version 23.2 (R2023b); MathWorks Doc: Natick, MA, USA, 2023. [Google Scholar]
- The MathWorks Inc. MathWorks Documentation for Savitzky-Golay Filtering, version 23.2 (R2023b); MathWorks Doc: Natick, MA, USA, 2023. [Google Scholar]
- Gilani, S.; Montazeri, H.; Blocken, B. CFD simulation of stratified indoor environment in displacement ventilation: Validation and sensitivity analysis. Build. Environ. 2016, 95, 299–313. [Google Scholar] [CrossRef]
- Ghali, K.; Ghaddar, N.; Salloum, M. Effect of stove asymmetric radiation field on thermal comfort using a multisegmented bioheat model. Build. Environ. 2008, 43, 1241–1249. [Google Scholar] [CrossRef]
- Sattari, S.; Farhanieh, B. A parametric study on radiant floor heating system performance. Renew. Energy 2006, 31, 1617–1626. [Google Scholar] [CrossRef]
- Sarbu, I.; Sebarchievici, C. (Eds.) Heat distribution systems in buildings. In Solar Heating and Cooling Systems: Fundamentals, Experiments and Applications; Elsevier: Amsterdam, The Netherlands, 2017; pp. 207–239. [Google Scholar] [CrossRef]

| Boundary | Material | Wall Thickness [m] | Temperature (°C) |
|---|---|---|---|
| Exterior facing wall | Concrete | 0.1 | 10 |
| Interior wall | 15 | ||
| Floor | 15 | ||
| Furniture | Plywood | 0.02 | (0 W/m2 assiged heat flux) |
| Ceiling | Plastic | 0.02 | 15 |
| Window | Glass | 0.0015 | 10 |
| Entrance door | Plywood | 0.1 | 10 |
| Heat source | Carbon steel 1020 | 0.002 | 102 |
| Equation of State | Turbulence Model | Average GCI Fine Mesh (%) | Average GCI Medium Mesh (%) |
|---|---|---|---|
| SRK | k-ω SST | 0.0985 | 0.2215 |
| k-ε | 0.459 | 1.117 | |
| PR | k-ω SST | 0.402 | 0.429 |
| k-ε | 1.555 | 1.980 |
| Air Velocity (m/s) | Metabolic Rate (MET) | Clothing Insulation Level | Comfortable Temperature Range (°C) |
|---|---|---|---|
| 0.01 | Typing: 1.1 | Sweatpants + long-sleeve sweatshirt: 0.74 | 21–27 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tuninetti, V.; Ales, B.; Mora Chandía, T. Numerical and Experimental Analysis of Thermal Stratification in Locally Heated Residential Spaces. Buildings 2025, 15, 2417. https://doi.org/10.3390/buildings15142417
Tuninetti V, Ales B, Mora Chandía T. Numerical and Experimental Analysis of Thermal Stratification in Locally Heated Residential Spaces. Buildings. 2025; 15(14):2417. https://doi.org/10.3390/buildings15142417
Chicago/Turabian StyleTuninetti, Víctor, Bastián Ales, and Tomás Mora Chandía. 2025. "Numerical and Experimental Analysis of Thermal Stratification in Locally Heated Residential Spaces" Buildings 15, no. 14: 2417. https://doi.org/10.3390/buildings15142417
APA StyleTuninetti, V., Ales, B., & Mora Chandía, T. (2025). Numerical and Experimental Analysis of Thermal Stratification in Locally Heated Residential Spaces. Buildings, 15(14), 2417. https://doi.org/10.3390/buildings15142417






