Optimizing Urban Thermal Environments Through 2D/3D Landscape Pattern Analysis: A Machine Learning-Driven Approach for the Yangtze River Delta Urban Agglomeration
Abstract
1. Introduction
2. Materials and Methods
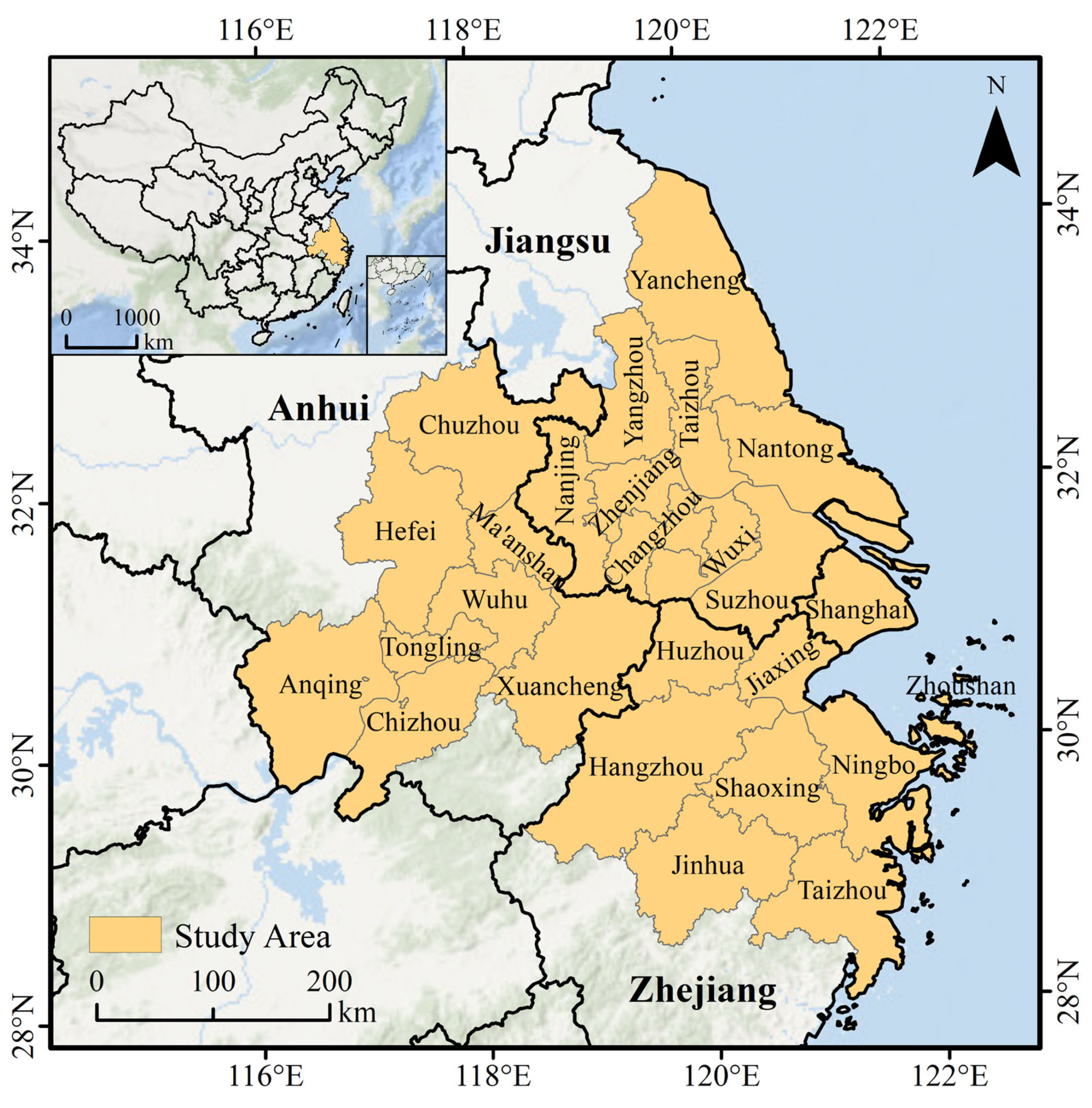
2.1. Study Area
2.2. Data Collection and Preprocessing
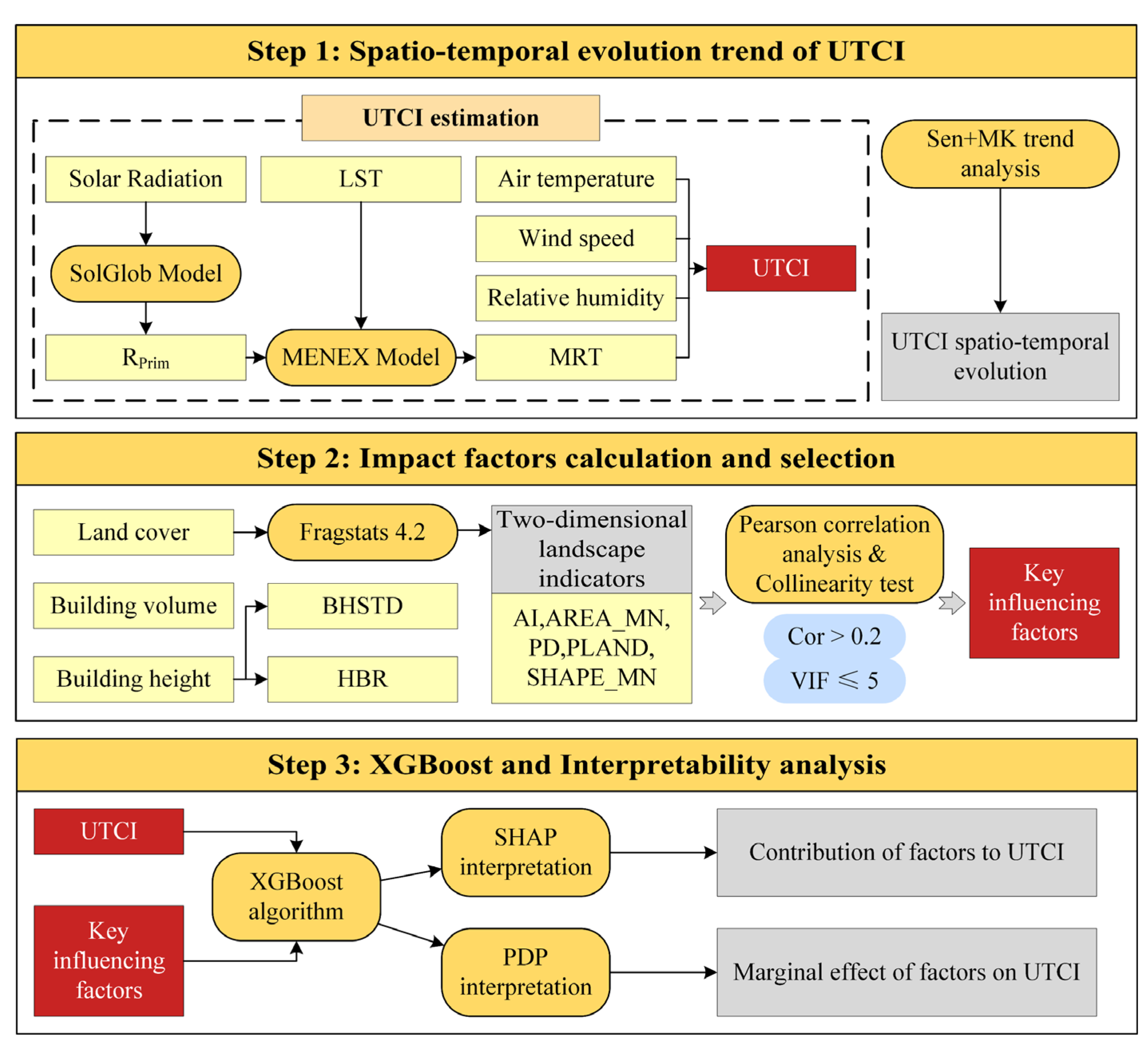
2.3. Overall Workflow
2.4. Estimation of UTCI
2.5. Spatiotemporal Changes in UTCI
2.6. Landscape Indictors
2.7. XGBoost Model
2.8. Explanatory Models
3. Results
3.1. Spatiotemporal Variation in UTCI
3.2. Correlation Analysis Between UTCI and Landscape Indicators
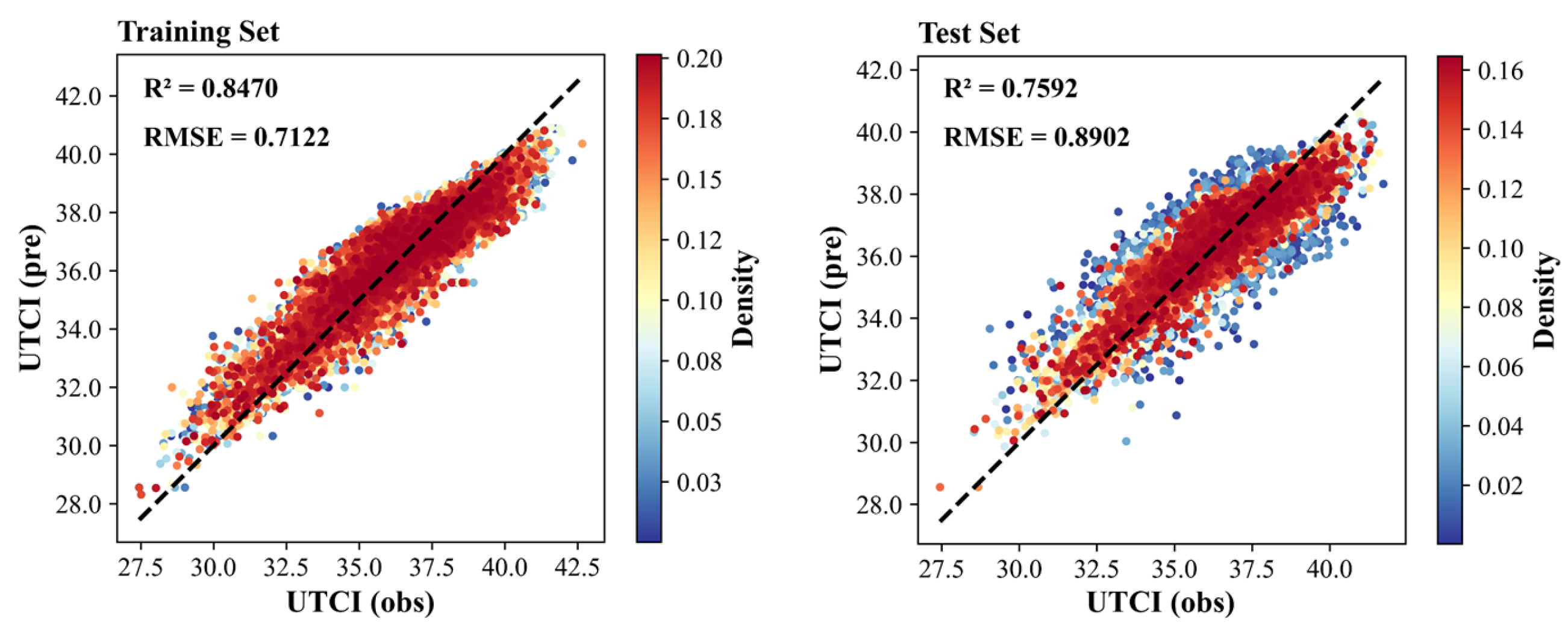
3.2.1. The Accuracy of XGBoost Model
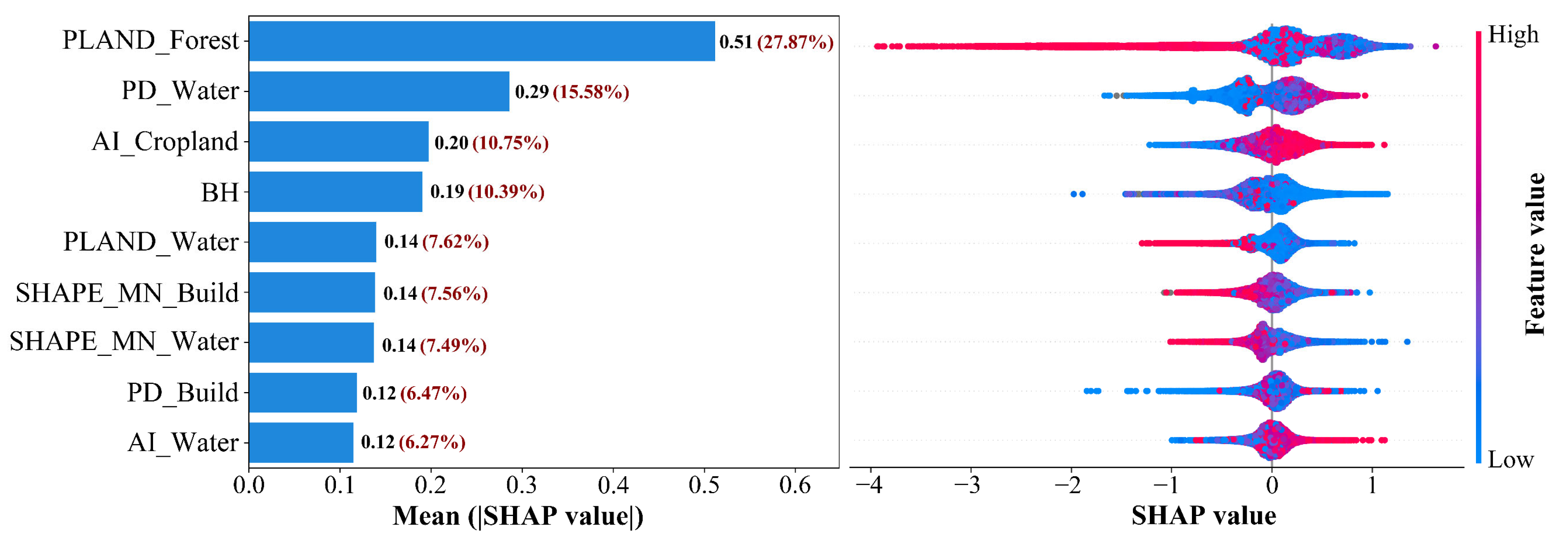
3.2.2. Model Interpretation from SHAP Analysis
3.2.3. Partial Dependency
4. Discussion
4.1. Spatiotemporal Variation Characteristics of UTCI
4.2. Effect of Landscape Factors on UTCI Changes
4.3. Suggestions for Improving Thermal Comfort
4.4. Limitations and Prospects
5. Conclusions
- (1)
- Over 90% of the YRDUA experienced strong or very strong summer heat stress during the study period, with 76.8% of the region showing a statistically significant upward trend in the UTCI at an average rate of 0.09 °C per year.
- (2)
- Areas with forest coverage exceeding 50% exhibited a reduction in the UTCI of up to 2.5 °C, while a higher proportion of water bodies decreased the UTCI by approximately 1.5 °C. Conversely, highly aggregated cropland increased the UTCI by about 1.5 °C, emphasizing the importance of preserving and enhancing blue–green infrastructure and considering land use configuration in mitigating thermal stress.
- (3)
- A moderate increase in building height and shape complexity improved shading and ventilation, leading to an enhancement in thermal comfort by approximately 0.5 °C.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviations | Definition |
| YRDUA | Yangtze River Delta Urban Agglomerations |
| UTCI | Universal Thermal Climate Index |
| TSV | Thermal Sensation Vote |
| WBGT | Wet-Bulb Globe Temperature |
| WCI | Wind Chill Index |
| PET | Physiologically Equivalent Temperature |
| OUT_SET* | Outdoor Standard Effective Temperature |
| Ta | Air Temperature |
| Tmrt | Mean Radiant Temperature |
| WS | Wind Speed |
| RH | Relative Humidity |
| TS | Land Surface Temperature |
| Rprim | Shortwave Radiation Absorbed by the Human Body |
| SR | Solar Radiation |
| La | Longwave Radiation Component from the Atmosphere |
| Lg | Longwave Radiation Component from the Ground |
| AI | Aggregation Index |
| AREA_MN | Mean Patch Area |
| PD | Patch Density |
| PLAND | Percentage of Landscape |
| SHAPE_MN | Mean Shape Index |
| BH | Building Height |
| BHSTD | Building Height Standard Deviation |
| BV | Building Volume |
| HBR | High-Rise Building Ratio |
References
- Ebi, K.L.; Capon, A.; Berry, P.; Broderick, C.; De Dear, R.; Havenith, G.; Honda, Y.; Kovats, R.S.; Ma, W.; Malik, A.; et al. Hot Weather and Heat Extremes: Health Risks. Lancet 2021, 398, 698–708. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Zhao, L.; Dong, W.; Cheng, L.; Cai, W.; Yang, J.; Bao, J.; Liang, X.-Z.; Hajat, S.; Gong, P.; et al. Spatiotemporal Variation of Mortality Burden Attributable to Heatwaves in China, 1979–2020. Sci. Bull. 2022, 67, 1340–1344. [Google Scholar] [CrossRef] [PubMed]
- Lai, D.; Liu, W.; Gan, T.; Liu, K.; Chen, Q. A Review of Mitigating Strategies to Improve the Thermal Environment and Thermal Comfort in Urban Outdoor Spaces. Sci. Total Environ. 2019, 661, 337–353. [Google Scholar] [CrossRef] [PubMed]
- Mazzetto, S. Dynamic Integration of Shading and Ventilation: Novel Quantitative Insights into Building Performance Optimization. Buildings 2025, 15, 1123. [Google Scholar] [CrossRef]
- Ma, J.; Shen, H.; Wu, P.; Wu, J.; Gao, M.; Meng, C. Generating Gapless Land Surface Temperature with a High Spatio-Temporal Resolution by Fusing Multi-Source Satellite-Observed and Model-Simulated Data. Remote Sens. Environ. 2022, 278, 113083. [Google Scholar] [CrossRef]
- Zhao, C.; Zhu, H.; Zhang, S.; Jin, Z.; Zhang, Y.; Wang, Y.; Shi, Y.; Jiang, J.; Chen, X.; Liu, M. Long-term Trends in Surface Thermal Environment and Its Potential Drivers along the Urban Development Gradients in Rapidly Urbanizing Regions of China. Sustain. Cities Soc. 2024, 105, 105324. [Google Scholar] [CrossRef]
- Wen, Z.; Tian, D.; Zhu, Y. Research on Spatial and Temporal Patterns of Heat Island Variability and Influencing Factors in Urban Center Areas: A Case Study of Beijing’s Central Area. Buildings 2023, 13, 1887. [Google Scholar] [CrossRef]
- Hu, Y.; Jia, G.; Gao, H.; Li, Y.; Hou, M.; Li, J.; Miao, C. Spatial Characterization of Global Heat Waves Using Satellite-Based Land Surface Temperature. Int. J. Appl. Earth Obs. Geoinf. 2023, 125, 103604. [Google Scholar] [CrossRef]
- Ren, Z.; Fu, Y.; Dong, Y.; Zhang, P.; He, X. Rapid Urbanization and Climate Change Significantly Contribute to Worsening Urban Human Thermal Comfort: A National 183-City, 26-Year Study in China. Urban Clim. 2022, 43, 101154. [Google Scholar] [CrossRef]
- Jia, S.; Wang, Y.; Wong, N.H.; Weng, Q. A Hybrid Framework for Assessing Outdoor Thermal Comfort in Large-Scale Urban Environments. Landsc. Urban Plan. 2025, 256, 105281. [Google Scholar] [CrossRef]
- Patle, S.; Ghuge, V.V. Evolution and Performance Analysis of Thermal Comfort Indices for Tropical and Subtropical Region: A Comprehensive Literature Review. Int. J. Environ. Sci. Technol. 2024, 21, 10217–10258. [Google Scholar] [CrossRef]
- Azli, M.; Khasri, M.A.; Hariri, A.; Yao, C.Z.; Damanhuri, A.A.M.; Mustafa, M.S.S. Pilot Study on Investigation of Thermal Sensation Votes (TSV) and Students’ Performance in Naturally Ventilated Classroom. Environ. Ecol. Res. 2022, 10, 508–517. [Google Scholar] [CrossRef]
- Lala, B.; Biju, A.; Vanshita; Rastogi, A.; Dahiya, K.; Kala, S.M.; Hagishima, A. The Challenge of Multiple Thermal Comfort Prediction Models: Is TSV Enough? Buildings 2023, 13, 890. [Google Scholar] [CrossRef]
- Liu, Z.; Li, J.; Xi, T. A Review of Thermal Comfort Evaluation and Improvement in Urban Outdoor Spaces. Buildings 2023, 13, 3050. [Google Scholar] [CrossRef]
- Detommaso, M.; Gagliano, A.; Nocera, F. An Overview of Microclimate Simulation Tools and Models for Predicting Outdoor Thermal Comfort. In Urban Heat Stress and Mitigation Solutions; Taylor Francis Group: Abingdon, UK, 2021; pp. 21–39. [Google Scholar]
- Blazejczyk, K.; Epstein, Y.; Jendritzky, G.; Staiger, H.; Tinz, B. Comparison of UTCI to Selected Thermal Indices. Int. J. Biometeorol. 2012, 56, 515–535. [Google Scholar] [CrossRef]
- Jendritzky, G.; De Dear, R.; Havenith, G. UTCI—Why Another Thermal Index? Int. J. Biometeorol. 2012, 56, 421–428. [Google Scholar] [CrossRef]
- Li, W.; Chao, L.; Si, P.; Zhang, H.; Li, Q. Comparisons of the Urbanization Effect on Heat Stress Changes in Guangdong during Different Periods. Remote Sens. 2023, 15, 2750. [Google Scholar] [CrossRef]
- Yu, B.; Hu, Y.; Zhou, X. Can administrative division adjustment improve urban land use efficiency? Evidence from “Revoke County to Urban District” in China. Environ. Plan. B Urban Anal. City Sci. 2025, 0, 23998083251325638. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, G.; Jiang, Y.; Wang, J. Effective Range and Driving Factors of the Urban Ventilation Corridor Effect on Urban Thermal Comfort at Unified Scale with Multisource Data. Remote Sens. 2021, 13, 1783. [Google Scholar] [CrossRef]
- Zou, M.; Zhang, H. Cooling Strategies for Thermal Comfort in Cities: A Review of Key Methods in Landscape Design. Environ. Sci. Pollut. Res. 2021, 28, 62640–62650. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, Y.; Zou, Y.; Xia, D.; Lou, S.; Guo, T.; Zhong, Z. Improving the Thermal Comfort of an Open Space via Landscape Design: A Case Study in Hot and Humid Areas. Atmosphere 2022, 13, 1604. [Google Scholar] [CrossRef]
- Yu, H.; Fukuda, H.; Zhou, M.; Ma, X. Improvement Strategies for Microclimate and Thermal Comfort for Urban Squares: A Case of a Cold Climate Area in China. Buildings 2022, 12, 944. [Google Scholar] [CrossRef]
- Kim, Y.; Yu, S.; Li, D.; Gatson, S.N.; Brown, R.D. Linking Landscape Spatial Heterogeneity to Urban Heat Island and Outdoor Human Thermal Comfort in Tokyo: Application of the Outdoor Thermal Comfort Index. Sustain. Cities Soc. 2022, 87, 104262. [Google Scholar] [CrossRef]
- Feng, L.; Zhao, M.; Zhou, Y.; Zhu, L.; Tian, H. The Seasonal and Annual Impacts of Landscape Patterns on the Urban Thermal Comfort Using Landsat. Ecol. Indic. 2020, 110, 105798. [Google Scholar] [CrossRef]
- Lin, Z.; Xu, H.; Hu, X.; Liu, Z.; Yao, X.; Zhu, Z. Characterizing the Seasonal Relationships between Urban Heat Island and Surface Energy Balance Fluxes Considering the Impact of Three-Dimensional Urban Morphology. Build. Environ. 2024, 265, 112017. [Google Scholar] [CrossRef]
- Kashki, A.; Karami, M.; Zandi, R.; Roki, Z. Evaluation of the Effect of Geographical Parameters on the Formation of the Land Surface Temperature by Applying OLS and GWR, A Case Study Shiraz City, Iran. Urban Clim. 2021, 37, 100832. [Google Scholar] [CrossRef]
- Niu, L.; Zhang, Z.; Peng, Z.; Liang, Y.; Liu, M.; Jiang, Y.; Wei, J.; Tang, R. Identifying Surface Urban Heat Island Drivers and Their Spatial Heterogeneity in China’s 281 Cities: An Empirical Study Based on Multiscale Geographically Weighted Regression. Remote Sens. 2021, 13, 4428. [Google Scholar] [CrossRef]
- Assaf, G.; Assaad, R.H. Modeling the Impact of Land Use/Land Cover (LULC) Factors on Diurnal and Nocturnal Urban Heat Island (UHI) Intensities Using Spatial Regression Models. Urban Clim. 2024, 55, 101971. [Google Scholar] [CrossRef]
- Gu, X.; Wu, Z.; Liu, X.; Qiao, R.; Jiang, Q. Exploring the Nonlinear Interplay between Urban Morphology and Nighttime Thermal Environment. Sustain. Cities Soc. 2024, 101, 105176. [Google Scholar] [CrossRef]
- Wang, W.; Shi, Y.; Zhang, J.; Zhao, X.; Ruan, J.; Wang, C. Exploration of Non-Linear Influence Mechanisms of Traditional Courtyard Forms on Thermal Comfort in Winter and Summer: A Case Study of Beijing, China. Sustain. Cities Soc. 2025, 119, 106124. [Google Scholar] [CrossRef]
- He, J.; Shi, Y.; Xu, L.; Lu, Z.; Feng, M.; Tang, J.; Guo, X. Exploring the Scale Effect of Urban Thermal Environment through XGBoost Model. Sustain. Cities Soc. 2024, 114, 105763. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, X.; Zhou, Y.; Liu, D.; Wang, H. The Dominant Factors and Influence of Urban Characteristics on Land Surface Temperature Using Random Forest Algorithm. Sustain. Cities Soc. 2022, 79, 103722. [Google Scholar] [CrossRef]
- Tanoori, G.; Soltani, A.; Modiri, A. Machine Learning for Urban Heat Island (UHI) Analysis: Predicting Land Surface Temperature (LST) in Urban Environments. Urban Clim. 2024, 55, 101962. [Google Scholar] [CrossRef]
- Guo, F.; Luo, M.; Zhang, C.; Cai, J.; Zhang, X.; Zhang, H.; Dong, J. The Mechanism of Street Spatial Form on Thermal Comfort from Urban Morphology and Human-Centered Perspectives: A Study Based on Multi-Source Data. Buildings 2024, 14, 3253. [Google Scholar] [CrossRef]
- Huang, C.; Liu, K.; Ma, T.; Xue, H.; Wang, P.; Li, L. Analysis of the Impact Mechanisms and Driving Factors of Urban Spatial Morphology on Urban Heat Islands. Sci. Rep. 2025, 15, 18589. [Google Scholar] [CrossRef]
- Zou, B.; Fan, C.; Li, J. Quantifying the Influence of Different Block Types on the Urban Heat Risk in High-Density Cities. Buildings 2024, 14, 2131. [Google Scholar] [CrossRef]
- Cao, Y.; Wang, Q.; Zhou, D. Does Air Pollution Inhibit Manufacturing Productivity in Yangtze River Delta, China? Moderating Effects of Temperature. J. Environ. Manag. 2022, 306, 114492. [Google Scholar] [CrossRef]
- Meng, F.; Qi, L.; Li, H.; Yang, X.; Liu, J. Spatiotemporal Evolution and Influencing Factors of Heat Island Intensity in the Yangtze River Delta Urban Agglomeration Based on GEE. Atmosphere 2024, 15, 1080. [Google Scholar] [CrossRef]
- FANG, Y.; SU, X.; HUANG, Z.; CHENG, X. Spatial Spillover Effect of Urban Resilience on Tourism Economy: A Case Study of the Yangtze River Delta Urban Agglomeration. Prog. Geogr. 2022, 41, 214–223. [Google Scholar] [CrossRef]
- Li, W.; Chen, Z.; Li, M.; Zhang, H.; Li, M.; Qiu, X.; Zhou, C. Carbon Emission and Economic Development Trade-Offs for Optimizing Land-Use Allocation in the Yangtze River Delta, China. Ecol. Indic. 2023, 147, 109950. [Google Scholar] [CrossRef]
- Fiala, D.; Havenith, G.; Bröde, P.; Kampmann, B.; Jendritzky, G. UTCI-Fiala Multi-Node Model of Human Heat Transfer and Temperature Regulation. Int. J. Biometeorol. 2012, 56, 429–441. [Google Scholar] [CrossRef] [PubMed]
- Błażejczyk, K.; Broede, P.; Fiala, D.; Havenith, G.; Holmér, I.; Jendritzky, G.; Kampmann, B.; Kunert, A. Principles of the New Universal Thermal Climate Index (UTCI) and Its Application to Bioclimatic Research in European Scale. Misc. Geogr. 2010, 14, 91–102. [Google Scholar] [CrossRef]
- Matzarakis, A.; Rutz, F.; Mayer, H. Modelling Radiation Fluxes in Simple and Complex Environments: Basics of the RayMan Model. Int. J. Biometeorol. 2010, 54, 131–139. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Zhan, W.; Liu, Z.; Li, J.; Li, L.; Fu, P.; Huang, F.; Lai, J.; Chen, J.; Hong, F.; et al. Satellite-Based Mapping of the Universal Thermal Climate Index over the Yangtze River Delta Urban Agglomeration. J. Clean. Prod. 2020, 277, 123830. [Google Scholar] [CrossRef]
- Blazejczyk, K. Assessment of Recreational Potential of Bioclimate Based on the Human Heat Balance. In Proceedings of the First International Workshop on Climate, Tourism and Recreation. Report of a Workshop, Halkidiki, Greece, 5–10 October 2001; pp. 133–152. [Google Scholar]
- Bröde, P.; Fiala, D.; Błażejczyk, K.; Holmér, I.; Jendritzky, G.; Kampmann, B.; Tinz, B.; Havenith, G. Deriving the Operational Procedure for the Universal Thermal Climate Index (UTCI). Int. J. Biometeorol. 2012, 56, 481–494. [Google Scholar] [CrossRef]
- Chen, J.; Xu, C.; Lin, S.; Wu, Z.; Qiu, R.; Hu, X. Is There Spatial Dependence or Spatial Heterogeneity in the Distribution of Vegetation Greening and Browning in Southeastern China? Forests 2022, 13, 840. [Google Scholar] [CrossRef]
- Zuo, D.; Han, Y.; Xu, Z.; Li, P.; Ban, C.; Sun, W.; Pang, B.; Peng, D.; Kan, G.; Zhang, R.; et al. Time-Lag Effects of Climatic Change and Drought on Vegetation Dynamics in an Alpine River Basin of the Tibet Plateau, China. J. Hydrol. 2021, 600, 126532. [Google Scholar] [CrossRef]
- Fallah Ghalhar, G.; Farhang Dehghan, S.; Asghari, M. Trend Analysis of Humidex as a Heat Discomfort Index Using Mann-Kendall and Sen’s Slope Estimator Statistical Tests. Environ. Health Eng. Manag. J. 2022, 9, 165–176. [Google Scholar] [CrossRef]
- Ye, H.; Li, Z.; Zhang, N.; Leng, X.; Meng, D.; Zheng, J.; Li, Y. Variations in the Effects of Landscape Patterns on the Urban Thermal Environment during Rapid Urbanization (1990–2020) in Megacities. Remote Sens. 2021, 13, 3415. [Google Scholar] [CrossRef]
- Cong, Y.; Zhu, R.; Yang, L.; Zhang, X.; Liu, Y.; Meng, X.; Gao, W. Correlation Analysis of Thermal Comfort and Landscape Characteristics: A Case Study of the Coastal Greenway in Qingdao, China. Buildings 2022, 12, 541. [Google Scholar] [CrossRef]
- Zhou, R.; Xu, H.; Zhang, H.; Zhang, J.; Liu, M.; He, T.; Gao, J.; Li, C. Quantifying the Relationship between 2D/3D Building Patterns and Land Surface Temperature: Study on the Metropolitan Shanghai. Remote Sens. 2022, 14, 4098. [Google Scholar] [CrossRef]
- Sun, F.; Liu, M.; Wang, Y.; Wang, H.; Che, Y. The Effects of 3D Architectural Patterns on the Urban Surface Temperature at a Neighborhood Scale: Relative Contributions and Marginal Effects. J. Clean. Prod. 2020, 258, 120706. [Google Scholar] [CrossRef]
- He, W.; Cao, S.; Du, M.; Hu, D.; Mo, Y.; Liu, M.; Zhao, J.; Cao, Y. How Do Two- and Three-Dimensional Urban Structures Impact Seasonal Land Surface Temperatures at Various Spatial Scales? A Case Study for the Northern Part of Brooklyn, New York, USA. Remote Sens. 2021, 13, 3283. [Google Scholar] [CrossRef]
- Kong, F.; Chen, J.; Middel, A.; Yin, H.; Li, M.; Sun, T.; Zhang, N.; Huang, J.; Liu, H.; Zhou, K.; et al. Impact of 3-D Urban Landscape Patterns on the Outdoor Thermal Environment: A Modelling Study with SOLWEIG. Comput. Environ. Urban Syst. 2022, 94, 101773. [Google Scholar] [CrossRef]
- Wei, J.; Li, Y.; Jia, L.; Liu, B.; Jiang, Y. The Impact of Spatiotemporal Effect and Relevant Factors on the Urban Thermal Environment Through the XGBoost-SHAP Model. Land 2025, 14, 394. [Google Scholar] [CrossRef]
- Tan, J.; Wei, Q.-J.; Liao, Z.-Y.; Kuang, W.-J.; Deng, H.-T.; Yu, D. Relationship between Urban Form and Surface Temperature Based on XGBoost SHAP Interpretable Machine Learning Model. Ying Yong Sheng Tai Xue Bao 2025, 36, 659–670. [Google Scholar] [CrossRef]
- Zhao, X.; Yang, H.; Yao, Y.; Qi, H.; Guo, M.; Su, Y. Factors Affecting Traffic Risks on Bridge Sections of Freeways Based on Partial Dependence Plots. Phys. A Stat. Mech. Its Appl. 2022, 598, 127343. [Google Scholar] [CrossRef]
- Zheng, Z.; Lin, X.; Chen, L.; Yan, C.; Sun, T. Effects of Urbanization and Topography on Thermal Comfort during a Heat Wave Event: A Case Study of Fuzhou, China. Sustain. Cities Soc. 2024, 102, 105233. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, Y.; Hou, H.; Murayama, Y.; Wang, R.; Hu, T. Quantifying the Cooling Effect and Scale of Large Inner-City Lakes Based on Landscape Patterns: A Case Study of Hangzhou and Nanjing. Remote Sens. 2021, 13, 1526. [Google Scholar] [CrossRef]
- Zou, Z.; Yan, C.; Yu, L.; Jiang, X.; Ding, J.; Qin, L.; Wang, B.; Qiu, G. Impacts of Land Use/ Land Cover Types on Interactions between Urban Heat Island Effects and Heat Waves. Build. Environ. 2021, 204, 108138. [Google Scholar] [CrossRef]
- Shu, Y.; Zou, K.; Li, G.; Yan, Q.; Zhang, S.; Zhang, W.; Liang, Y.; Xu, W. Evaluation of Urban Thermal Comfort and Its Relationship with Land Use/Land Cover Change: A Case Study of Three Urban Agglomerations, China. Land 2022, 11, 2140. [Google Scholar] [CrossRef]
- Palanisamy, P.A.; Zawadzka, J.; Jain, K.; Bonafoni, S.; Tiwari, A. Assessing Diurnal Land Surface Temperature Variations across Landcover and Local Climate Zones: Implications for Urban Planning and Mitigation Strategies on Socio-Economic Factors. Sustain. Cities Soc. 2024, 116, 105880. [Google Scholar] [CrossRef]
- Kianmehr, A.; Lim, T.C. Quantifying Interactive Cooling Effects of Morphological Parameters and Vegetation-Related Landscape Features during an Extreme Heat Event. Climate 2022, 10, 60. [Google Scholar] [CrossRef]
- Massaro, E.; Schifanella, R.; Piccardo, M.; Caporaso, L.; Taubenböck, H.; Cescatti, A.; Duveiller, G. Spatially-Optimized Urban Greening for Reduction of Population Exposure to Land Surface Temperature Extremes. Nat. Commun. 2023, 14, 2903. [Google Scholar] [CrossRef]
- Iungman, T.; Cirach, M.; Marando, F.; Pereira Barboza, E.; Khomenko, S.; Masselot, P.; Quijal-Zamorano, M.; Mueller, N.; Gasparrini, A.; Urquiza, J.; et al. Cooling Cities through Urban Green Infrastructure: A Health Impact Assessment of European Cities. Lancet 2023, 401, 577–589. [Google Scholar] [CrossRef]
- Yang, Y.; Lv, Y.; Zhou, D. The Impact of Urban Parks on the Thermal Environment of Built-up Areas and an Optimization Method. PLoS ONE 2025, 20, e0318633. [Google Scholar] [CrossRef]
- Cao, B.; Chen, Q.; Du, M.; Cheng, Q.; Li, Y.; Liu, R. Simulation Analysis of the Cooling Effect of Urban Water Bodies on the Local Thermal Environment. Water 2022, 14, 3091. [Google Scholar] [CrossRef]
- How Jin Aik, D.; Ismail, M.H.; Muharam, F.M.; Alias, M.A. Evaluating the Impacts of Land Use/Land Cover Changes across Topography against Land Surface Temperature in Cameron Highlands. PLoS ONE 2021, 16, e0252111. [Google Scholar] [CrossRef]
- Chen, X.; Gu, X.; Liu, P.; Wang, D.; Mumtaz, F.; Shi, S.; Liu, Q.; Zhan, Y. Impacts of Inter-Annual Cropland Changes on Land Surface Temperature Based on Multi-Temporal Thermal Infrared Images. Infrared Phys. Technol. 2022, 122, 104081. [Google Scholar] [CrossRef]
- He, B.-J.; Ding, L.; Prasad, D. Wind-Sensitive Urban Planning and Design: Precinct Ventilation Performance and Its Potential for Local Warming Mitigation in an Open Midrise Gridiron Precinct. J. Build. Eng. 2020, 29, 101145. [Google Scholar] [CrossRef]
- Han, D.; An, H.; Wang, F.; Xu, X.; Qiao, Z.; Wang, M.; Sui, X.; Liang, S.; Hou, X.; Cai, H.; et al. Understanding Seasonal Contributions of Urban Morphology to Thermal Environment Based on Boosted Regression Tree Approach. Build. Environ. 2022, 226, 109770. [Google Scholar] [CrossRef]
- Li, H.; Li, Y.; Wang, T.; Wang, Z.; Gao, M.; Shen, H. Quantifying 3D Building Form Effects on Urban Land Surface Temperature and Modeling Seasonal Correlation Patterns. Build. Environ. 2021, 204, 108132. [Google Scholar] [CrossRef]
- Han, D.; An, H.; Cai, H.; Wang, F.; Xu, X.; Qiao, Z.; Jia, K.; Sun, Z.; An, Y. How Do 2D/3D Urban Landscapes Impact Diurnal Land Surface Temperature: Insights from Block Scale and Machine Learning Algorithms. Sustain. Cities Soc. 2023, 99, 104933. [Google Scholar] [CrossRef]
- Jiang, Y.; Huang, J.; Shi, T.; Wang, H. Interaction of Urban Rivers and Green Space Morphology to Mitigate the Urban Heat Island Effect: Case-Based Comparative Analysis. Int. J. Environ. Res. Public Health 2021, 18, 11404. [Google Scholar] [CrossRef]
- Wai, C.Y.; Tariq, M.A.U.R.; Muttil, N. A Systematic Review on the Existing Research, Practices, and Prospects Regarding Urban Green Infrastructure for Thermal Comfort in a High-Density Urban Context. Water 2022, 14, 2496. [Google Scholar] [CrossRef]
- Yasa, E. The Interaction of Wind Velocity and Air Gap Width on the Thermal Comfort in Naturally Ventilated Buildings with Multiple Skin Facade. Athens J. Technol. Eng. 2022, 9, 213–266. [Google Scholar] [CrossRef]
- Zhou, H.; Yang, H.; Peng, J. Solar PV Vacuum Glazing (SVG) Insulated Building Facades: Thermal and Electrical Performances. Appl. Energy 2024, 376, 124323. [Google Scholar] [CrossRef]
- Pan, T.; He, S.; Liu, Z.; Jiang, L.; Zhao, Q.; Hamdi, R. Analyzing Changes in Urban Green Spaces and Their Effect on Land Temperature from the Perspective of Surface Radiation Energy Balance in Rizhao City, the Central Coast of China. Remote Sens. 2023, 15, 4785. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, J.; Li, J. Research on Urban Three-Dimensional Greening Design from the Perspective of Climate Change—A Case Study of Beilin District, Xi’an, Shaanxi Province, China. Environ. Sci. Pollut. Res. 2024, 31, 6067–6081. [Google Scholar] [CrossRef]
- Liu, C.; Lu, S.; Tian, J.; Yin, L.; Wang, L.; Zheng, W. Research Overview on Urban Heat Islands Driven by Computational Intelligence. Land 2024, 13, 2176. [Google Scholar] [CrossRef]
- Li, N.; Wu, H.; Ouyang, X. Localized Downscaling of Urban Land Surface Temperature—A Case Study in Beijing, China. Remote Sens. 2022, 14, 2390. [Google Scholar] [CrossRef]
- Wang, B.; Yi, Y.K. Developing an Adapted UTCI (Universal Thermal Climate Index) for the Elderly Population in China’s Severe Cold Climate Region. Sustain. Cities Soc. 2021, 69, 102813. [Google Scholar] [CrossRef]



| Data | Year | Resolution | Source |
|---|---|---|---|
| Air temperature (Ta) | 2000, 2005, 2010, 2015, 2020 | 1 km | National Earth System Science Data Center (https://www.geodata.cn/, accessed on 2 May 2025) |
| Relative humidity (RH) | 1 km | ||
| Wind speed (WS) | 1 km | ||
| Solar radiation (SR) | 1 km | Global resources data cloud (http://www.gis5g.com/, accessed on 2 May 2025) | |
| Land surface temperature (Ts) | 1 km | MODIS MOD11A1 LST Product (https://earthengine.google.com/, accessed on 5 April 2025) | |
| Land use and land cover | 30 m | The 30 m annual land cover datasets in China (https://zenodo.org/records/12779975, accessed on 5 April 2025) | |
| 3D building data | 100 m | Global Human Settlement Layer (https://human-settlement.emergency.copernicus.eu/, accessed on 5 April 2025) |
| UTCI Ranges | Thermal Stress Classification |
|---|---|
| 9–26 °C | No thermal stress |
| 26–32 °C | Moderate heat stress |
| 32–38 °C | Strong heat stress |
| 38–46 °C | Very strong heat stress |
| >46 °C | Extreme heat stress |
| >46 °C | Extreme heat stress |
| β | |Z| | Trend Features |
|---|---|---|
| β > 0 | |Z| > 2.58 | Very significant warming |
| 1.96 < |Z| ≤ 2.58 | Significant warming | |
| |Z| ≤ 1.96 | Slight significant warming | |
| β < 0 | |Z| ≤ 1.96 | Slight significant cooling |
| 1.96 < |Z| ≤ 2.58 | Significant cooling | |
| |Z| > 2.58 | Very significant cooling |
| Dimensions | Indicators | Abbreviation | Formula | Description |
|---|---|---|---|---|
| 2D * | Mean Patch Area (m2) | AREA_MN | Average area of patches. | |
| Aggregation Index (%) | AI | The connectivity among patches within each landscape type. | ||
| Patch Density (patches/km2) | PD | The density of patches within a given landscape area. | ||
| Percentage of Landscape (%) | PLAND | The ratio of patch area to total landscape area. | ||
| Mean Shape Index | SHAPE_MN | The complexity of patch shapes. | ||
| 3D ** | Building Height (m) | BH | Building height. | |
| Building Volume (m3) | BV | Building volume. | ||
| Building Height Standard Deviation (m) | BHSTD | The degree of change in buildings. | ||
| High-Rise Building Ratio (%) | HBR | The proportion of buildings > 24 m. |
| Moderate Heat Stress | Strong Heat Stress | Very Strong Heat Stress | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2000 | 2005 | 2010 | 2015 | 2020 | 2000 | 2005 | 2010 | 2015 | 2020 | 2000 | 2005 | 2010 | 2015 | 2020 | |
| Anqing | 644 | 424 | 634 | 1000 | 705 | 5501 | 3876 | 4913 | 10,913 | 5619 | 7378 | 9223 | 7976 | 1610 | 7199 |
| Changzhou | 0 | 0 | 0 | 14 | 0 | 4159 | 1830 | 3869 | 4356 | 3467 | 211 | 2540 | 501 | 0 | 903 |
| Chizhou | 95 | 68 | 138 | 325 | 133 | 4575 | 2625 | 4725 | 7617 | 4094 | 3696 | 5673 | 3503 | 424 | 4139 |
| Chuzhou | 0 | 0 | 0 | 0 | 0 | 12,321 | 1275 | 2922 | 13,476 | 9293 | 1155 | 12,201 | 10,554 | 0 | 4183 |
| Hangzhou | 738 | 391 | 607 | 1562 | 627 | 15,163 | 10,442 | 14,365 | 14,809 | 14,548 | 470 | 5538 | 1399 | 0 | 1196 |
| Hefei | 0 | 0 | 0 | 27 | 0 | 7684 | 1260 | 2583 | 11,408 | 6945 | 3751 | 10,175 | 8852 | 0 | 4490 |
| Huzhou | 121 | 65 | 117 | 218 | 127 | 5396 | 2520 | 5076 | 5599 | 5256 | 300 | 3232 | 624 | 0 | 434 |
| Jiaxing | 0 | 0 | 0 | 0 | 0 | 3974 | 3940 | 3974 | 3974 | 3974 | 0 | 34 | 0 | 0 | 0 |
| Jinhua | 808 | 302 | 528 | 1021 | 238 | 9281 | 5701 | 8080 | 9683 | 6171 | 864 | 4950 | 2345 | 249 | 4544 |
| Ma’anshan | 0 | 0 | 0 | 0 | 0 | 2630 | 464 | 1444 | 4062 | 2406 | 1432 | 3598 | 2618 | 0 | 1656 |
| Nanjing | 0 | 0 | 0 | 1 | 0 | 6162 | 1351 | 3600 | 6606 | 5557 | 445 | 5256 | 3007 | 0 | 1050 |
| Nantong | 9 | 0 | 0 | 75 | 1 | 8344 | 8353 | 8353 | 8278 | 8352 | 0 | 0 | 0 | 0 | 0 |
| Ningbo | 327 | 62 | 263 | 938 | 189 | 8056 | 7945 | 8120 | 7445 | 8194 | 0 | 376 | 0 | 0 | 0 |
| Shanghai | 1 | 0 | 1 | 89 | 0 | 6214 | 6200 | 6214 | 6126 | 6215 | 0 | 15 | 0 | 0 | 0 |
| Shaoxing | 124 | 14 | 74 | 314 | 64 | 7692 | 5655 | 7143 | 7566 | 6910 | 64 | 2211 | 663 | 0 | 906 |
| Suzhou | 11 | 0 | 0 | 130 | 3 | 8077 | 7375 | 8076 | 7982 | 8093 | 24 | 737 | 36 | 0 | 16 |
| Taizhou (ZJ) | 1565 | 552 | 1119 | 1411 | 510 | 7621 | 8406 | 8049 | 7764 | 8196 | 0 | 228 | 18 | 11 | 480 |
| Taizhou (JS) | 0 | 0 | 0 | 1 | 0 | 5728 | 4797 | 5729 | 5728 | 5673 | 1 | 932 | 0 | 0 | 56 |
| Tongling | 0 | 0 | 0 | 0 | 0 | 1789 | 552 | 1652 | 2997 | 1972 | 1208 | 2445 | 1345 | 0 | 1025 |
| Wuxi | 0 | 0 | 0 | 5 | 0 | 4490 | 3211 | 4209 | 4585 | 4074 | 100 | 1379 | 381 | 0 | 516 |
| Wuhu | 0 | 0 | 0 | 0 | 0 | 4370 | 535 | 2354 | 5995 | 4729 | 1625 | 5460 | 3641 | 0 | 1266 |
| Xuancheng | 236 | 121 | 209 | 425 | 204 | 11,776 | 5716 | 8421 | 11,906 | 9919 | 319 | 6494 | 3701 | 0 | 2208 |
| Yancheng | 89 | 6 | 6 | 100 | 64 | 14,388 | 14,006 | 14,304 | 14,373 | 14,413 | 0 | 465 | 167 | 4 | 0 |
| Yangzhou | 0 | 0 | 0 | 2 | 0 | 6474 | 2283 | 4739 | 6591 | 6488 | 120 | 4311 | 1855 | 1 | 106 |
| Zhenjiang | 0 | 0 | 1 | 0 | 0 | 3746 | 1326 | 3493 | 3837 | 3094 | 91 | 2511 | 343 | 0 | 743 |
| Zhoushan | 46 | 12 | 37 | 229 | 40 | 935 | 969 | 944 | 752 | 941 | 0 | 0 | 0 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, H.; Wang, R.; Hou, H.; Xie, B.; Hu, T. Optimizing Urban Thermal Environments Through 2D/3D Landscape Pattern Analysis: A Machine Learning-Driven Approach for the Yangtze River Delta Urban Agglomeration. Buildings 2025, 15, 2261. https://doi.org/10.3390/buildings15132261
Zhou H, Wang R, Hou H, Xie B, Hu T. Optimizing Urban Thermal Environments Through 2D/3D Landscape Pattern Analysis: A Machine Learning-Driven Approach for the Yangtze River Delta Urban Agglomeration. Buildings. 2025; 15(13):2261. https://doi.org/10.3390/buildings15132261
Chicago/Turabian StyleZhou, Haoshan, Ruci Wang, Hao Hou, Bin Xie, and Tangao Hu. 2025. "Optimizing Urban Thermal Environments Through 2D/3D Landscape Pattern Analysis: A Machine Learning-Driven Approach for the Yangtze River Delta Urban Agglomeration" Buildings 15, no. 13: 2261. https://doi.org/10.3390/buildings15132261
APA StyleZhou, H., Wang, R., Hou, H., Xie, B., & Hu, T. (2025). Optimizing Urban Thermal Environments Through 2D/3D Landscape Pattern Analysis: A Machine Learning-Driven Approach for the Yangtze River Delta Urban Agglomeration. Buildings, 15(13), 2261. https://doi.org/10.3390/buildings15132261








