Cracking Process of Early-Age Concretes: Basis of Numerical Probabilistic Models

Abstract

This paper addresses the modeling of early-age cracking in concrete structures. It explores the application of two probabilistic cracking models, originally developed and validated for analyzing cracks in fully hydrated concrete: the Probabilistic Explicit Cracking (PEC) model and the Probabilistic Semi-Explicit Cracking (PSEC) model. The PEC model is intended for assessing service-level cracking (with crack openings of 300 microns or less), whereas the PSEC model targets larger crack formations. This study introduces a methodology for accounting for the evolution of the models’ probabilistic parameters during the early-age hydration process. Additionally, it outlines specific algorithmic development approaches tailored to each model. The primary aim of this work is to facilitate the implementation of these models by the scientific community through clear and accessible numerical development strategies. This work is fully original because, in the literature, probabilistic cracking numerical models for early-age concrete do not exist. These types of models associated with Monte Carlo approach permits the relevant safety analysis of early-age concrete constructions.

1. Introduction

The interaction between physical and mechanical phenomena in concrete at an early age, particularly the hydration process, its associated thermal effects and their mechanical consequences, especially cracking, represents one of the most critical and complex challenges in the construction of large-scale concrete structures. Such cracking has a significant impact on the long-term durability of these structures.

In this paper, “early age” is defined according to the RILEM TC-254 State-of-the-Art Report [1], which characterizes early-age concrete as the phase following the percolation threshold, during which the material’s properties undergo rapid changes due to hydration. While extensive research has been dedicated to modeling the cracking behavior of concrete during its service life, comparatively little attention has been given to early-age cracking [1]. This gap in the literature is largely due to the inherent complexity of accurately modeling cracking during this early phase. The challenge is further compounded by the need for numerical models to enable the precise prediction of crack openings, which is essential for assessing the durability of structures.

Currently, most commercial finite element models have not proven effective in addressing this specific issue [2]. However, two nonlinear finite element models, based on probabilistic approaches, have been developed and validated for their ability to provide accurate information on crack openings: the Probabilistic Explicit Cracking (PEC) model [3] and the Probabilistic Semi-Explicit Cracking (PSEC) model [4,5].

These models have been successfully applied at various structural scales [3,4,5]. The PEC model primarily targets the analysis of cracking at the serviceability limit state, focusing on crack openings of up to 300 µm. In contrast, the PSEC model is designed for modeling macrocracks with openings greater than 300 µm.

However, neither model currently accounts for early-age cracking behavior. The objective of this paper is to extend these probabilistic models to incorporate early-age concrete behavior. The core contribution and novelty of this work lie in proposing a methodological framework for adapting these probabilistic models to simulate the early-age cracking process in concrete structures

2. Static Cracking Models

The numerical models used to simulate the cracking process in concrete structures can be divided into two primary approaches, which either address kinematic discontinuity discrete implicitly or explicitly, leading to continuum or discrete models. In continuum models, cracks are represented in an implicit manner, and the failure process is understood through the reduction in material stiffness, which modifies its constitutive equation. Key models in the concrete domain include damaged models [6,7,8], smeared crack models [9], and the PSEC model [4,5]. On the other hand, discrete cracking models explicitly treat cracks as geometric entities, appearing as discontinuities in displacement at the interfaces between finite elements or being incorporated into the finite element formulation. The most recognized and commonly used discrete models include the cohesive crack model (also known as the fictitious crack model) [10,11], the lattice model [12], and the PEC model [3].

3. Probabilistic Cracking Models

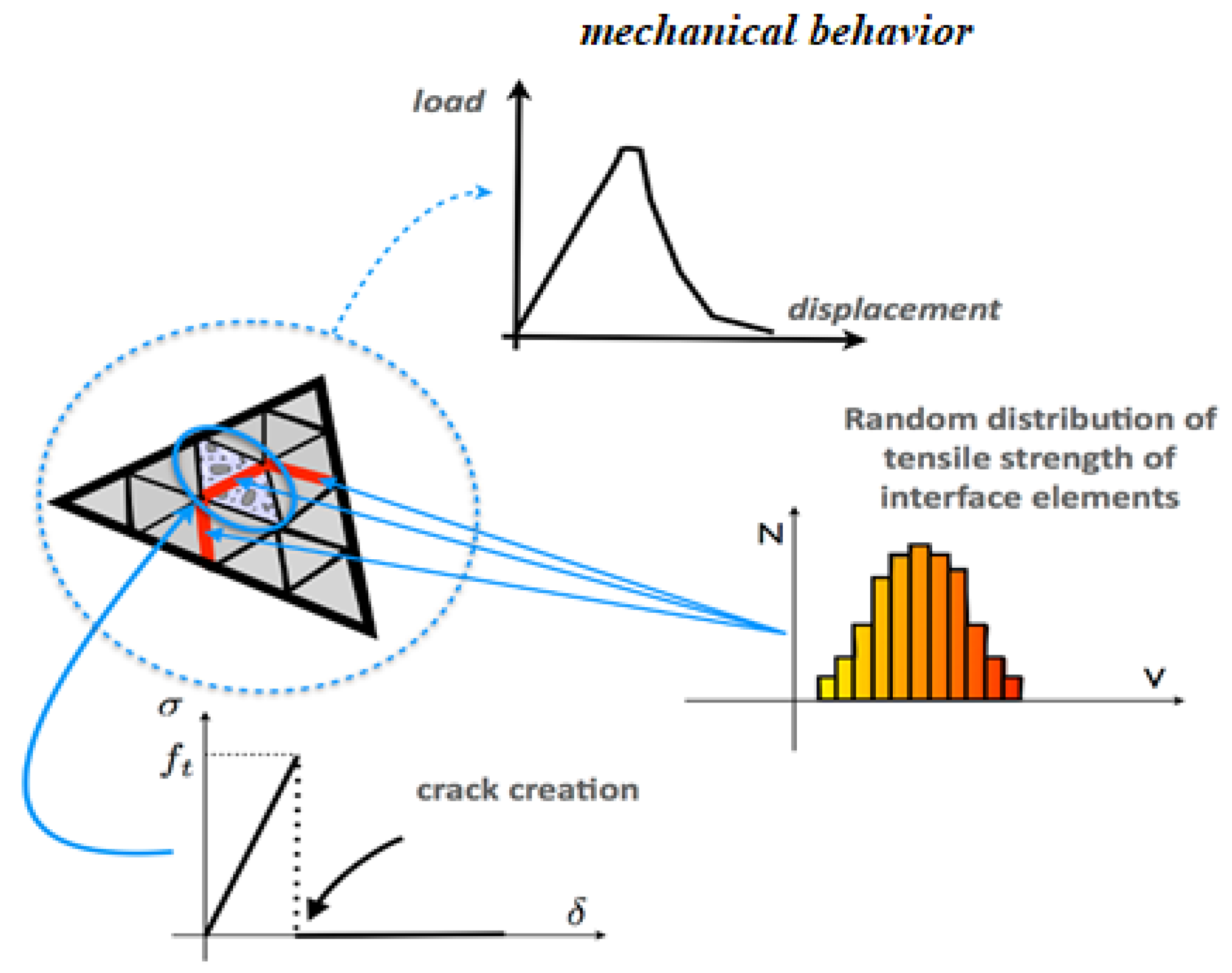
3.1. PEC Model

The PEC model, detailed extensively in reference [3], is built upon several foundational physical assumptions:

• Material heterogeneity: concrete is modeled as a heterogeneous material, with its local mechanical properties randomly distributed.
• Scale dependency: these mechanical properties vary depending on the volume of material considered, reflecting scale effects [13].

From both mechanical and numerical standpoints, the PEC model is characterized by the following features:

• Each volume element in the finite element mesh represents a segment of heterogeneous material.
• The tensile strength is randomly assigned to each element, capturing the probabilistic nature of local failure [3].
• Shear strength is defined deterministically as f_c/2, where f_c denotes the compressive strength of the concrete.
• Cracking is modeled using nonlinear interface elements (quadratic), with failure governed by

  ○

  The Rankine criterion for tension;

  ○

  The Tresca criterion for shear.

• When either criterion is satisfied, the corresponding interface element is considered to have failed. This simulates crack initiation by setting the element’s tensile and shear strength, as well as its normal and tangential stiffness, to zero.

• The randomly assigned tensile strength of a contact interface depends on the volumes of the two adjacent finite elements it connects.

An illustration of the PEC model is provided in Figure 1.

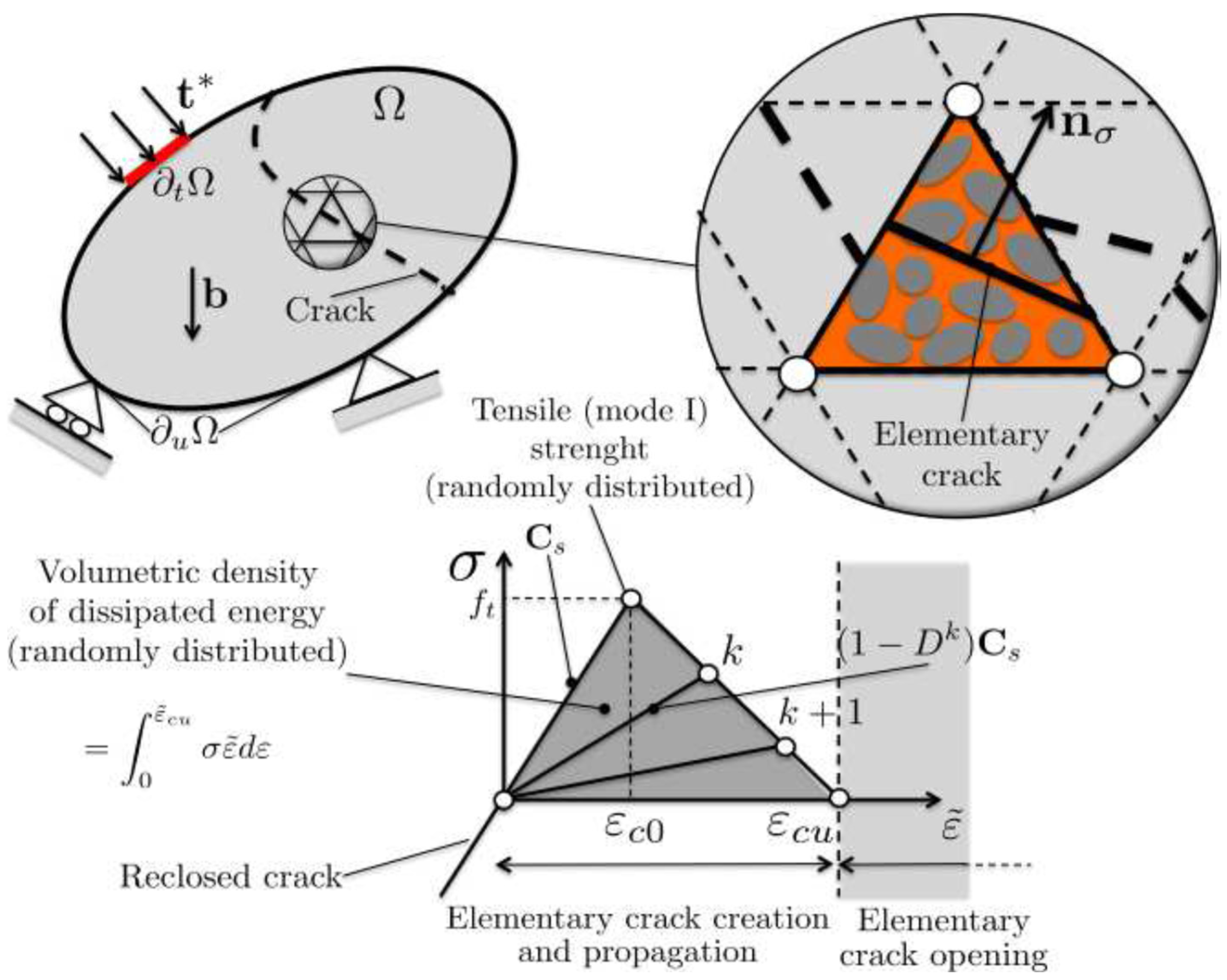
3.2. PSEC Model

The Probabilistic Semi-Explicit Cracking (PSEC) model, a more recent development than the PEC model, governs macrocrack propagation based on two primary criteria:

• Macrocrack initiation: controlled by the uniaxial tensile strength, ft;
• Macrocrack propagation: governed by the mode I critical fracture energy GIC, as defined by the principles of Linear Elastic Fracture Mechanics (LEFMs).

Macrocracks evolve once the entire value of GIC is dissipated, allowing the crack to be explicitly represented as a sequence of fully damaged finite elements. This model differs from classical LEFM formulations in that it utilizes volume elements rather the singular elements typically found in LEFM.

As a result, the PSEC model does not conform to traditional damage mechanics or smeared crack models, where damage zones are treated as physically meaningful regions, and crack openings are inferred from stress–strain behavior in these areas. Instead, the PSEC approach does not model physically damaged zones; the introduction of a damage parameter is purely theoretical, used only as a mechanism to simulate the dissipation of GIC.

Additionally, both mechanical parameters, ft and GIC, are treated as random variables, their values depending on the volume of the finite elements used in the mesh.

A schematic of the PSEC model is shown in Figure 2.

It is important to emphasize that the two probabilistic models presented in this paper must be accompanied by a classical Monte Carlo-type procedure (i.e., multiple simulations in which the probabilistic parameters are distributed differently across the mesh). Indeed, with these numerical models, performing a single simulation is meaningless in terms of the resulting output. For a given structural problem, the set of obtained results allows for a relevant statistical analysis, enabling a safety-oriented assessment of the structure’s behavior.

3.3. Determination of the Values of the Mechanical Parameters of the PEC and PSEC Models

With the exception of the Young’s modulus, Poisson’s ratio, and the shear strength in the PEC model, all mechanical parameters in both the PEC and PSEC models are treated as random variables. Their probabilistic characteristics—namely, the mean value and standard deviation—have been established and validated through previous experimental and numerical studies [3,4,13,14]. These properties are linked to the degree of heterogeneity of each mesh element, denoted as r_e, and defined by the following relation:

r_e = V_e/V_a

(1)

where V_a is the volume of the greatest aggregate size of the concrete, and V_e is the volume of the mesh element.

The probabilistic properties of f_t (PEC and PSEC models) and G_IC (PSEC model) mean that the mean value, μ, and the standard deviation, σ, are given by the following relations:

μ(f_t(r_e)) = a(r_e)^−y

(2)

In Equation (2), a = 6.5 MPa, and y is given by Equation (3), where f_c represents the concrete’s compressive strength in MPa, and α = 1 MPa. The compressive strength is determined by performing a standard test on 160 × 320 mm cylinder specimen.

y = 0.25 − 3.6 × 10⁻³ f_c/α + 1.3 × 10⁻⁵ (f_c/α)²

(3)

σ/μ(f_t(r_e)) = c(r_e)^−d

(4)

In Equation (4), c = 0.35, given by Equation (5), as follows:

d = 4.5 × 10⁻² + 4.5 × 10⁻³ f_c/α − 1.8 × 10⁻⁵ (f_c/α)²

(5)

In the model, the mean value of G_IC, μ(G_IC), is considered as not depending on the size of the mesh elements employed, but the standard deviation of G_IC, σ(G_IC), is considered as depending on the size of the mesh elements [4,5]. The values of μ(G_IC) and σ(G_IC) are given by the following relations [4,5]:

μ(G_IC) = 0.4 f_c + 110

(6)

σ/μ (G_IC(r_e)) = A [1/d ln(c μ(f_t(re)/σ(f_t(re)) + B/A]

(7)

where A = −8.538, and B = 70.88.

Relations (2)–(7) were validated for f_c ≤ 130 MPa and a maximum aggregate size ≥ 10.

The main interest and originality of the two numerical models, beyond their probabilistic nature, lie in the fact that all mechanical parameters related to cracking depend solely on two easily measurable quantities: the compressive strength of the concrete and the maximum aggregate size.

4. Early-Age Cracking

This section focuses on the development of the previously described numerical models to account for the cracking behavior of concrete at an early age.

A recent experimental study [15], investigating the evolution of certain mechanical properties of concrete as a function of its degree of hydration, a key parameter for early-age concrete, led to the following conclusions:

• The mean values of compressive strength, Young’s modulus, and flexural tensile strength increase with the degree of hydration.
• The coefficients of variation of both the compressive strength and flexural tensile strength decrease significantly with increasing hydration, while the reduction is less pronounced for Young’s modulus.

Based on these observations, the following assumptions are proposed:

• The mean value of the uniaxial tensile strength, μ(f_t), increases with both the degree of hydration and the compressive strength of the concrete.
• The coefficient of variation of the uniaxial tensile strength, σ/μ(f_t), decreases with increasing degree of hydration and compressive strength.

Considering Equations (2)–(5), it is reasonable to assume that these relations remain valid during the early ages.

Regarding the fracture energy G_IC, previous studies have demonstrated and validated that this parameter follows the same trends as f_t (i.e., Equations (6) and (7)). Therefore, it is also reasonable to assume that these relations apply to early-age concrete.

Given these assumptions, the next step in this work was to define how they can be incorporated within the framework of the PEC and PSEC numerical models.

This paper specifically addresses the modeling of early-age cracking in concrete. For cracking to occur, internal stresses must develop, more precisely, tensile stresses, in the context of both the PEC and PSEC models.

Modeling the generation of these tensile stresses is beyond the scope of this paper. At COPPE/Universidade Federal do Rio de Janeiro (Brazil), a finite element code, DAMTHE/COPPE, was developed to analyze early-age stress generation. This code utilizes 3D meshing and a parallel computing architecture and is based on a scientific framework that couples thermal, chemical, and mechanical processes [16], with several improvements in recent years [17,18,19,20].

The code simulates the evolution of hydration and temperature using a coupled thermo-chemical approach [16,21], which considers the thermal activation of the hydration process. In this framework, thermal parameters, such as thermal conductivity and specific heat, are explicitly defined for each material and vary with the degree of hydration. The extent of heat release is used to track hydration progress [1]. The mechanical behavior is calculated by enforcing constitutive equations and equilibrium, allowing for the computation of internal stress fields in the hardening concrete.

The numerical simulation is carried out using a time-stepping approach that iteratively solves the thermal, chemical, and mechanical problems.

It is important to emphasize that the adopted coupling strategy is weak coupling, meaning that the cracking process does not influence the thermal and chemical simulations.

This weak coupling constitutes a hypothesis, or rather a strong modeling choice, that is debatable, if not questionable. Regarding the influence of cracking on the evolution of the temperature field, there is no obvious physical reason to believe that this influence is significant. However, the coupling between early-age cracking and physico-chemical mechanisms does in fact exist. This coupling is well known and corresponds to the self-healing of cracks. This self-healing is linked to the continued hydration of unhydrated cement grains that “fill in” the cracks. This self-healing phenomenon is difficult to quantify (the literature is not very precise on this point) and difficult to incorporate into the macroscopic modeling that is the focus of this paper. Moreover, not accounting for this phenomenon is a conservative approach in terms of the cracking risk of concrete structures. This last point serves to justify the proposed choice.

The key new input for the mechanical analysis within the probabilistic models is the evolution of the compressive strength as a function of the degree of hydration. This evolution governs the probabilistic parameters related to early-age cracking behavior.

4.1. PEC Model

The first step in the numerical simulation consists of assigning an initial tensile strength ftif_{ti}fti to each interface element based on the random distribution defined by relations (1) to (5). These initial values correspond to the tensile strength of the fully hydrated material, that is, the strength achieved at the end of the chemical hydration process and the simulation.

The total simulation time, t_T, is set to match the time required for the complete hydration of the concrete. This total time is then divided into a defined number of sub-increments nnn, following standard practice. The simulation progresses through the following steps:

• First Time Sub-Increment (t₁)

• Compute the compressive strength of concrete based on its degree of hydration at time t₁.
• Calculate the mean tensile strength f_tm(t₁) using relations (2) and (3), corresponding to the hydration degree at t₁.
• Determine the difference f_tm1 = f_tm(t_T) − f_tm(t₁)), where f_tm(t_T) is the final mean tensile strength at full hydration.
• Update the tensile strength for each interface element: f_t1 = f_ti − f_tm1.

• This update increases the coefficient of variation of the tensile strength compared to its initial value, consistent with the experimental findings previously discussed.

• Compute the normal tensile stress σ_t1 at the centroid of each interface element using the previously mentioned thermo-chemo-mechanical model [16,21].
• For each interface element, evaluate (σ_t1 − f_t1). If σ_t1 − f_t1 ≥ 0, the element opens, indicating crack formation.

• Second Time Sub-Increment (t₂)

• Calculate the compressive strength of concrete corresponding to its hydration state at t₁ + t₂.
• Determine the mean tensile strength f_tm(t₁ + t₂) for this hydration state.
• Compute the difference f_tm2 = (f_tm(t_T) − f_tm(t₁ + t₂)).
• Update the tensile strength for each interface element: f_t2 = f_ti − f_tm2.
• Evaluate the normal tensile stress σ_t2 at the centroid of each interface element.
• For each interface element, check whether σ_t2 ≥ f_t2; if so, the element opens and cracks propagate.

• Final Time Sub-Increment (t_n)

• At this stage, the simulation time reaches its final value: (t₁ + t₂ +…+t_n) = t_T.
• Each interface element now regains its initial tensile strength f_ti, assigned at the beginning of the simulation.
• Compute the normal tensile stress σ_tn the centroid of each element.
• For each element, evaluate (σ_tn − f_ti). If σ_tn − f_ti ≥ 0, the element opens and cracks are formed.

4.2. PSEC Model

The first step of the numerical simulation involves assigning to each volume element an initial tensile strength, f_ti, using the random distribution described by relations (1) to (5), and an initial fracture energy value, G_ICi, using the distribution described by relations (6) and (7). The subsequent steps of the numerical calculation are as follows:

• First Time Sub-Increment, t₁:

• Compute the compressive strength based on the degree of hydration of the concrete at time t₁.
• Calculate the mean tensile strength, f_tm(t₁), using relations (2) and (3), and the mean fracture energy, G_ICm(t₁), using relation (6), both based on the degree of hydration.
• Determine the differences f_tm1 = (f_tm(t_T) − f_tm(t₁)) and G_ICm1 = (G_ICm(t_T) − G_ICm(t₁)), where (t_T) is the time corresponding to complete hydration.
• Update the tensile strength and fracture energy assigned to each volume element: f_t1= f_ti − f_tm1, G_IC1= G_ICi − G_ICm1.
• Compute the maximum principal tensile stress, σt1, at the centroid of each volume element using the thermo-chemo-mechanical model.
• Evaluate σ_t1 − f_t1 for each volume element:

  ○

  If σ_t1 − f_t1 < 0, the element remains in the linear elastic regime.

  ○

  If σ_t1 − f_t1 ≥ 0, the element enters the non-linear regime, and a damage parameter D = D₁ (specific to each element) is assigned at the end of t_1t.

  ○

  If the energy G_IC1 is fully dissipated during t₁, the element is considered fully damaged (see Section 3.2).

• Second Time Sub-Increment, t₂:

• Recalculate the compressive strength based on the degree of hydration at t₁ + t₂.
• Compute the updated mean tensile strength, f_tm(t₁ + t₂), and mean fracture energy, G_ICm(t₁ + t₂).
• Determine the new differences: f_tm2 = f_tm(t_T) − f_tm(t₁ + t₂), G_ICm2 = G_ICm(t_T) − G_ICm(t₁ + t₂).
• Update the tensile strength and fracture energy values: f_t2 = f_ti − ft_m2, G_IC2 = GICi − G_ICm2.
• Calculate the maximum principal tensile stress, σ_t2, at the centroid of each volume element:

  ○

  For elements still in the linear-elastic regime, use the stiffness matrix based on the degree of hydration (thermo-chemo-mechanical model).

  ○

  For previously damaged elements, use the same stiffness matrix but multiplied by D₁ (this approach ignores self-healing effects in early-age concrete).

• Evaluate σ_t2 − f_t2 for each element:

  ○

  If σ_t2 − f_t2 < 0, the element remains linearly elastic.

  ○

  If σ_t2 − f_t2 ≥ 0, the element either enters the non-linear regime or continues accumulating damage. The damage parameter becomes D₂, specific to each element.

  ○

  If G_IC2 is entirely dissipated during t₂, the element is fully damaged.

• Final Sub-Increment, t_n:

• The simulation concludes at t_T = t₁ + t₂ + ⋯ + t_n.
• Each undamaged volume element retains its initial values f_ti and G_Ici.
• The calculation procedure at this stage follows the same steps described for the second sub-increment t₂.

After this, the calculation process is the same as for the second sub-increment of time, t₂.

5. Conclusions

This paper addresses the modeling of early-age cracking in concrete structures. It focuses on the use of two probabilistic cracking models, originally developed and validated for analyzing cracking in fully hydrated concrete structures: the Probabilistic Explicit Cracking (PEC) model and the Probabilistic Semi-Explicit Cracking (PSEC) model. The PEC model is intended for serviceability cracking (crack openings less than or equal to 300 microns), while the PSEC model is suited for larger cracks. These types of model are associated with the Monte Carlo approach and enable the relevant safety analyses of early-age concrete constructions.

The novelty of this work lies in proposing a strategy to incorporate the evolution of the probabilistic parameters of these models during the early-age hydration process. This strategy is grounded in the experimental data available in the literature. In addition, specific algorithmic implementation strategies are proposed for each numerical model.

The actual numerical developments and validations remain to be completed. A first step of these validations will be based on an experimental study concerning the evolution of the bending tensile strength of concrete as a function of its degree of hydration [15]. Nevertheless, the main contribution and originality of this paper are laying the groundwork for developing probabilistic models tailored to early-age concrete cracking, an area not yet addressed in the existing literature. This work provides a clear and accessible framework for the scientific community to pursue these new numerical developments.