Damage Detection of Seismically Excited Buildings Using Neural Network Arrays with Branch Pruning Optimization
Abstract
1. Introduction
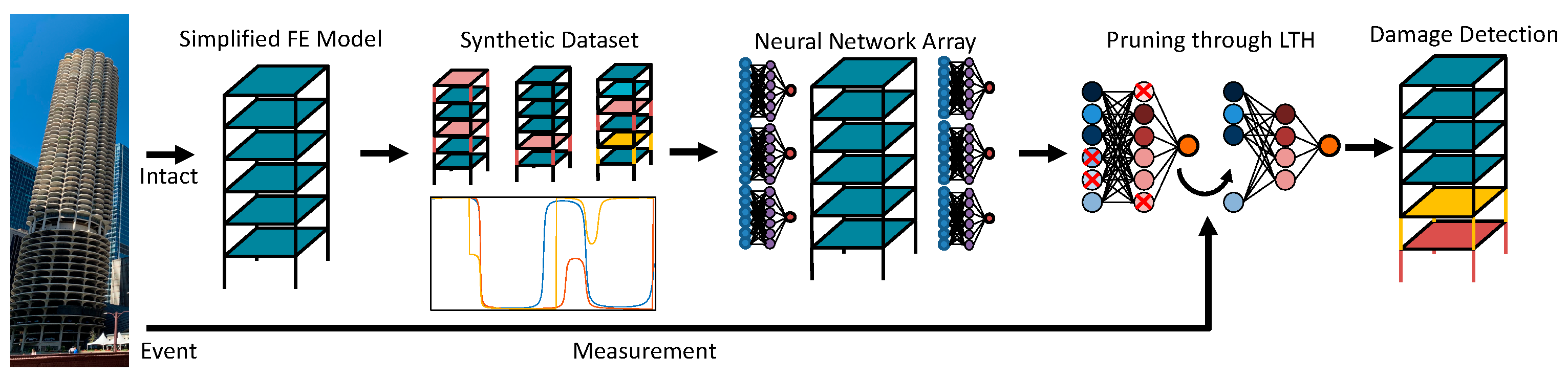
2. Damage Detection Using Neural Network Array with Lottery Ticket Hypothesis
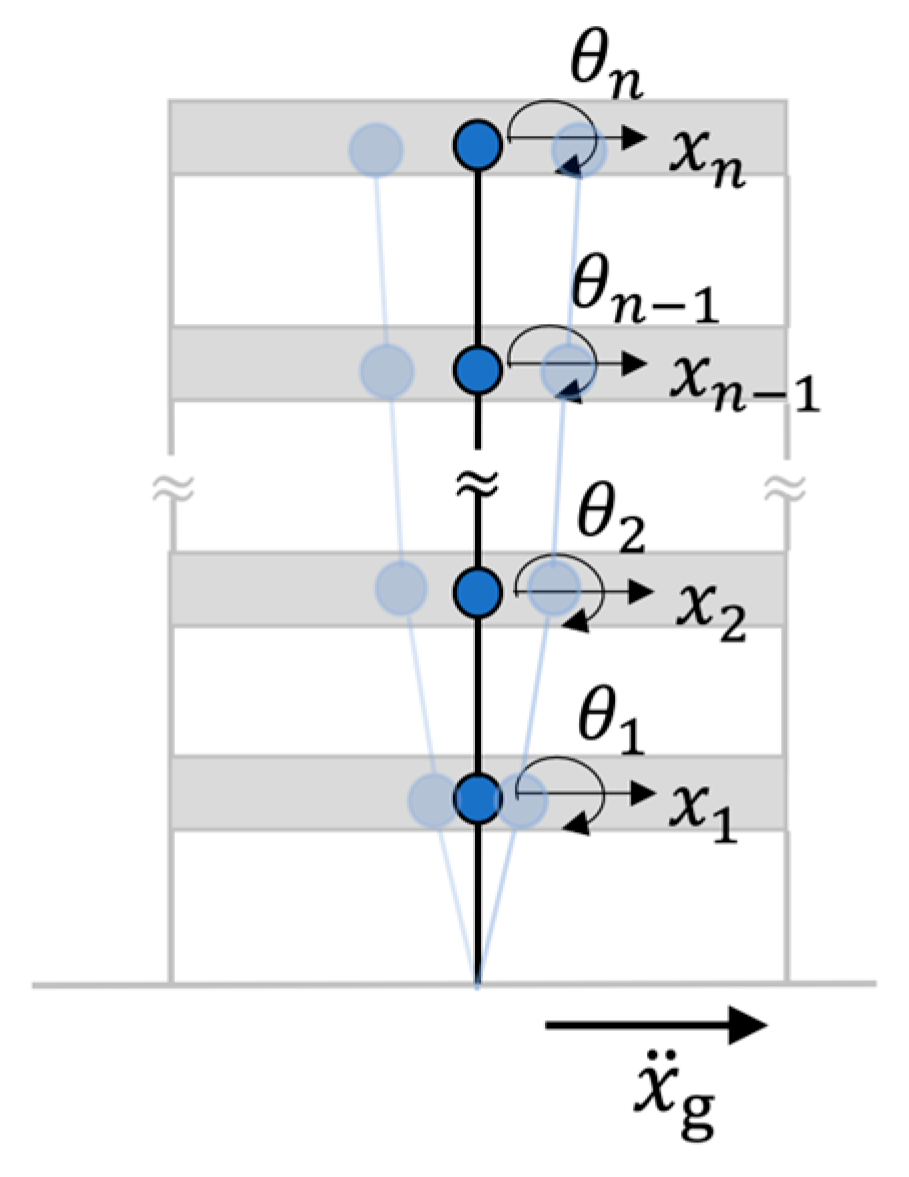
2.1. Numerical Building Model with Floor Flexural Behavior
2.2. Frequency Response Phase Difference
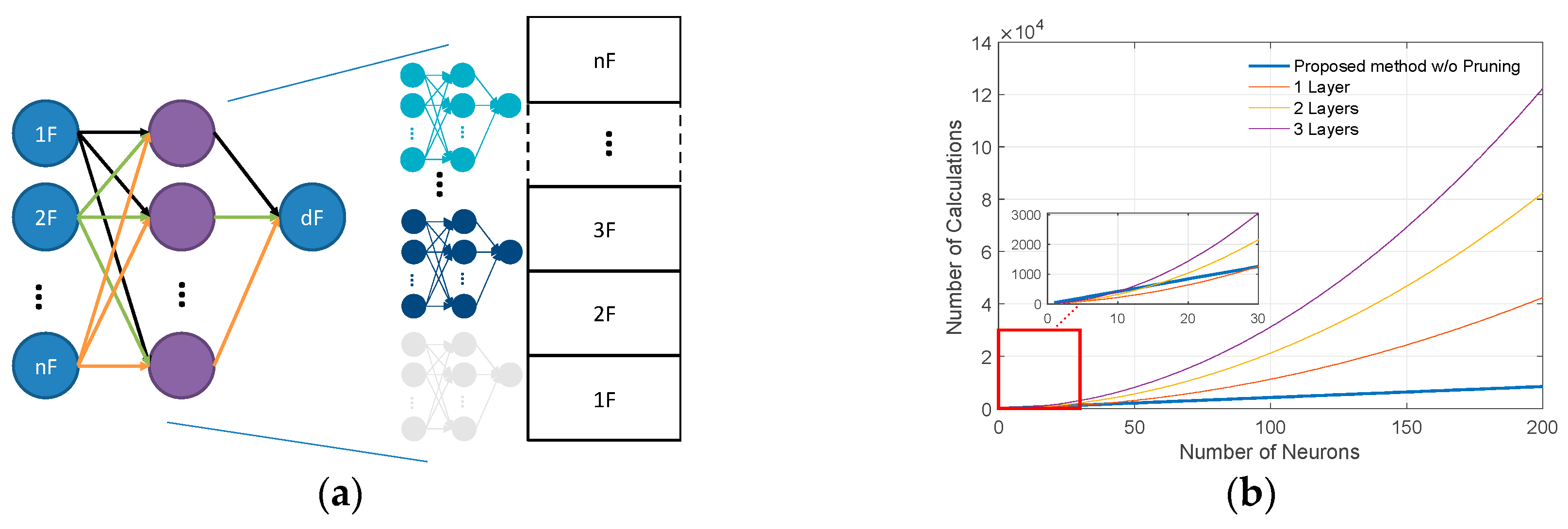
2.3. Artificial Neural Network Model for Damage Detection
2.4. Introduction to Lottery Ticket Hypothesis
3. Numerical Study
3.1. Preparation of Training Samples
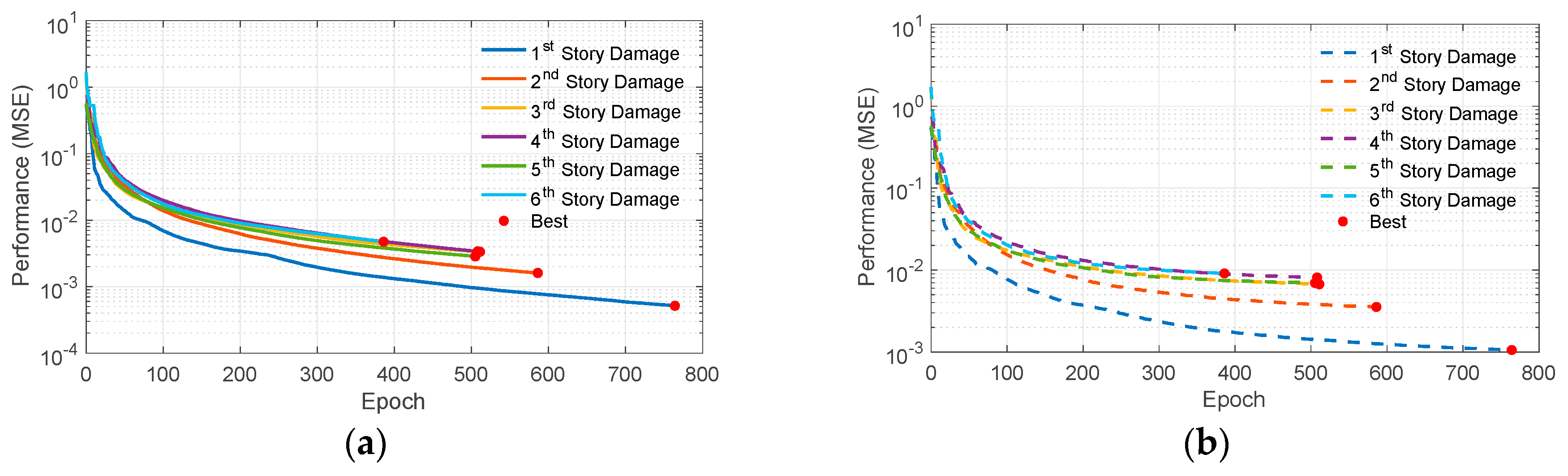
3.2. Training and Validation Process of Initial Neural Network Array
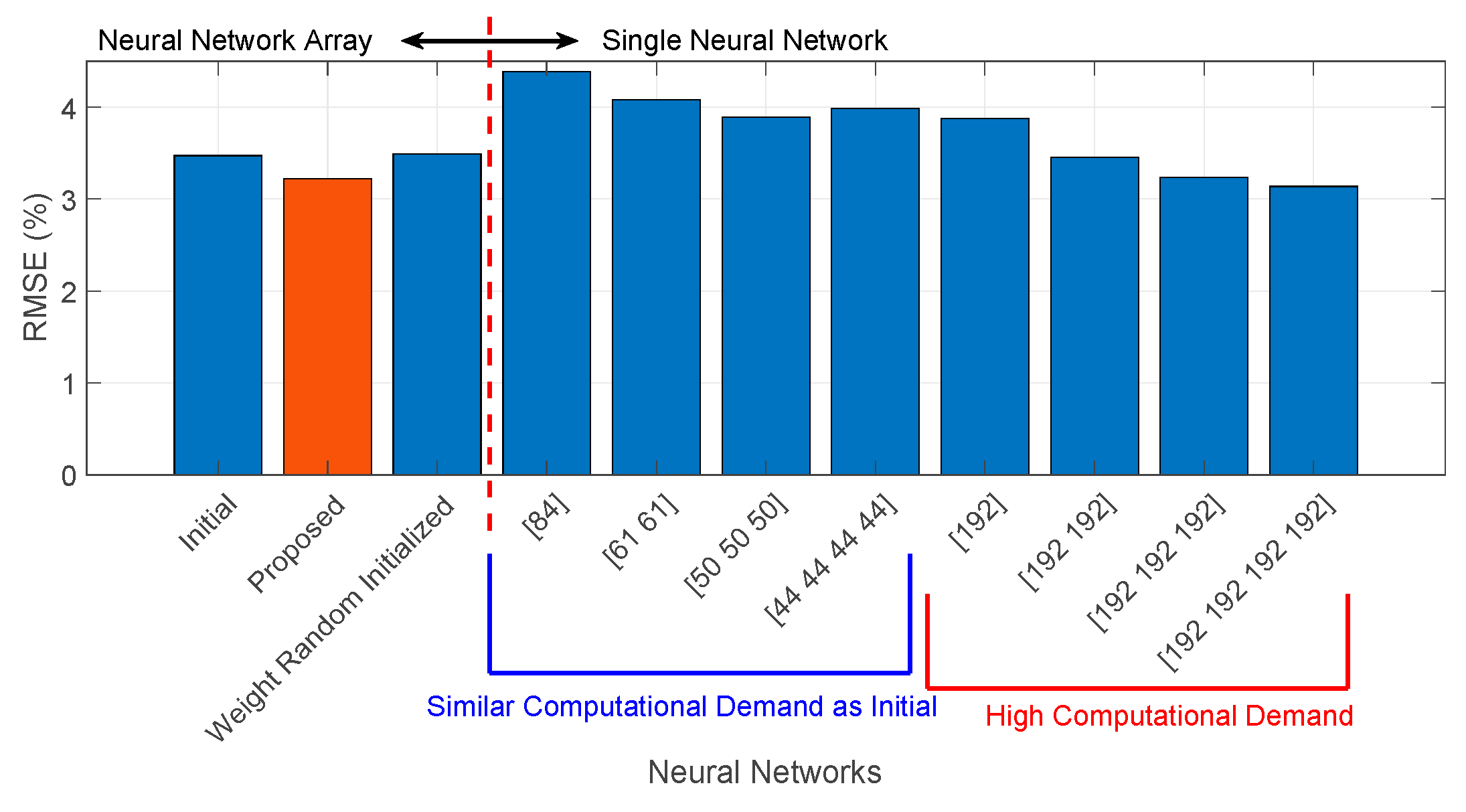
3.3. Neural Network Pruning Using Lottery Ticket Hypothesis
4. Experimental Verification
4.1. Experimental Setup
4.2. Development of Simplified Numerical Model
4.3. Establishment of Proposed Network Array
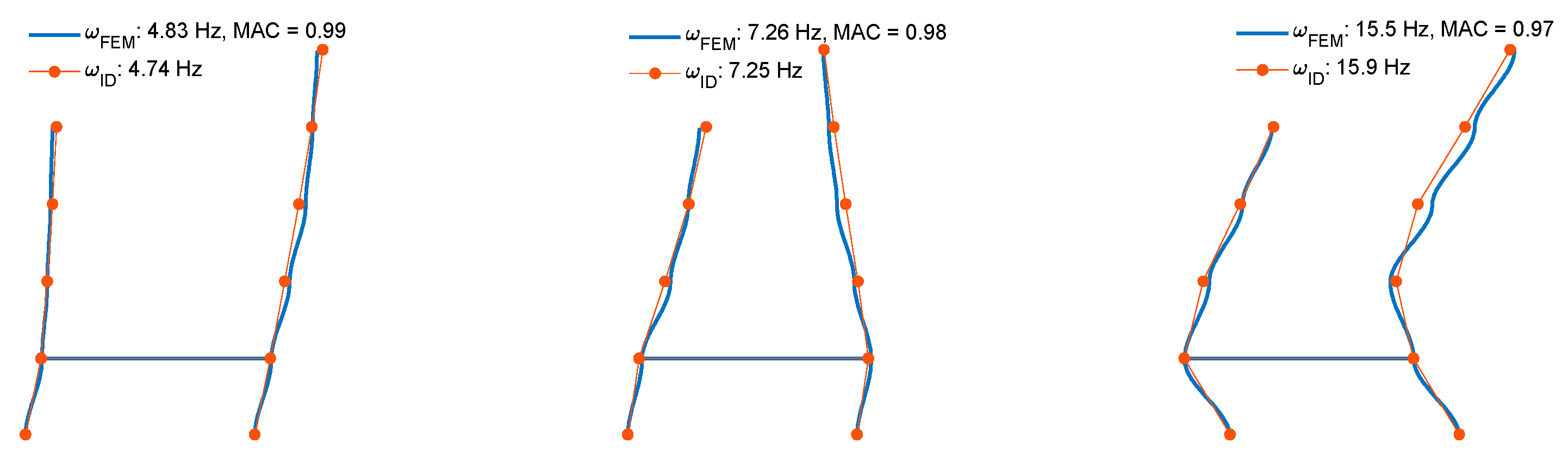
4.4. Damage Detection Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rytter, A. Vibration Based Inspection of Civil Engineering Structures. Ph.D. Dissertation, Aalborg University, Aalborg, Denmark, 1993. [Google Scholar]
- Bandara, R.P.; Chan, T.H.; Thambiratnam, D.P. Frequency response function based damage identification using principal component analysis and pattern recognition technique. Eng. Struct. 2014, 66, 116–128. [Google Scholar] [CrossRef]
- Liu, X.; Lieven, N.; Escamilla-Ambrosio, P.J. Frequency response function shape-based methods for structural damage localisation. Mech. Syst. Sig. Process. 2009, 23, 1243–1259. [Google Scholar] [CrossRef]
- Lee, U.; Shin, J. A frequency response function-based structural damage identification method. Comput. Struct. 2002, 80, 117–132. [Google Scholar] [CrossRef]
- Catbas, F.N.; Gul, M.; Burkett, J.L. Conceptual damage-sensitive features for structural health monitoring: Laboratory and field demonstrations. Mech. Syst. Sig. Process. 2008, 22, 1650–1669. [Google Scholar] [CrossRef]
- Azimi, A.; Eslamlou, A.D.; Pekcan, G. Data-driven structural health monitoring and damage detection through deep learning: State-of-the-art review. Sensors 2020, 20, 2778. [Google Scholar] [CrossRef]
- Ying, Y.; Garrett, H.J., Jr.; Irving, J.; Soibelman, L.; Harley, J.B.; Shi, J.; Jin, Y. Toward data-driven structural health monitoring: Application of machine learning and signal processing to damage detection. J. Comput. Civ. Eng. 2013, 27, 667–680. [Google Scholar] [CrossRef]
- Abdeljaber, O.; Avci, O. Nonparametric structural damage detection algorithm for ambient vibration response: Utilizing artificial neural networks and self-organizing maps. J. Archit. Eng. 2016, 22, 04016004. [Google Scholar] [CrossRef]
- Kostić, B.; Gül, M. Vibration-based damage detection of bridges under varying temperature effects using time-series analysis and artificial neural networks. J. Bridge Eng. 2017, 22, 04017065. [Google Scholar] [CrossRef]
- Abdeljaber, O.; Avci, O.; Kiranyaz, S.; Gabbouj, M.; Inman, D.J. Real-time vibration-based structural damage detection using one-dimensional convolutional neural networks. J. Sound Vib. 2017, 388, 154–170. [Google Scholar] [CrossRef]
- Huang, H.; Burton, H.V. Dynamic seismic damage assessment of distributed infrastructure systems using graph neural networks and semi-supervised machine learning. Adv. Eng. Softw. 2022, 168, 103113. [Google Scholar] [CrossRef]
- Lazaridis, P.C.; Kavvadias, I.E.; Demertzis, K.; Iliadis, L.; Vasiliadis, L.K. Structural damage prediction of a reinforced concrete frame under single and multiple seismic events using machine learning algorithms. Appl. Sci. 2022, 12, 3845. [Google Scholar] [CrossRef]
- Mousavi, Z.; Varahram, S.; Ettefagh, M.M.; Sadeghi, M.H.; Razavi, S.N. Deep neural networks-based damage detection using vibration signals of finite element model and real intact state: An evaluation via a lab-scale offshore jacket structure. Struct. Health Monit. 2021, 20, 379–405. [Google Scholar] [CrossRef]
- Ye, C.; Butler, L.; Calka, B.; Iangurazov, M.; Lu, Q.; Gregory, A.; Girolami, M.; Middleton, C. A digital twin of bridges for structural health monitoring. In Proceedings of the 12th International Workshop on Structural Health Monitoring, Stanford, CA, USA, 10–12 September 2019. [Google Scholar]
- Avci, O.; Abdeljaber, O.; Kiranyaz, S.; Hussein, M.; Gabbouj, M.; Inman, D.J. A review of vibration-based damage detection in civil structures: From traditional methods to machine learning and deep learning applications. Mech. Syst. Signal Process. 2021, 147, 107077. [Google Scholar] [CrossRef]
- Figueiredo, E.; Moldovan, I.; Santos, A.; Campos, P.; Costa, J.C.W.A. Finite element–based machine-learning approach to detect damage in bridges under operational and environmental variations. J. Bridge Eng. 2019, 24, 04019061. [Google Scholar] [CrossRef]
- Mousavi, Z.; Ettefagh, M.M.; Sadeghi, M.H.; Razavi, S.N. Developing deep neural network for damage detection of beam-like structures using dynamic response based on FE model and real healthy state. Appl. Acoust. 2020, 168, 107402. [Google Scholar] [CrossRef]
- Ritto, T.G.; Rochinha, F.A. Digital twin, physics-based model, and machine learning applied to damage detection in structures. Mech. Syst. Signal Process. 2021, 155, 107614. [Google Scholar] [CrossRef]
- Zhao, R.; Yan, R.; Chen, Z.; Mao, K.; Wang, P.; Gao, R.X. Deep learning and its applications to machine health monitoring. Mech. Syst. Signal Process. 2019, 115, 213–237. [Google Scholar] [CrossRef]
- Mangal, L.; Idichandy, V.G.; Ganapathy, C. ART-based multiple neural networks for monitoring offshore platforms. Appl. Ocean Res. 1996, 18, 137–143. [Google Scholar] [CrossRef]
- Mokhatar, S.N.; Shahidan, S.; Jaini, Z.M.; Kamarudin, A.F. An ensemble neural network for damage identification in steel girder bridge structure using vibration data. Civ. Eng. Archit. 2021, 9, 523–532. [Google Scholar]
- Dackerman, U.; Li, J.; Samali, B. Dynamic-based damage identification using neural network ensembles and damage index method. Adv. Struct. Eng. 2010, 13, 1001–1016. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Xu, Z.; Zhang, H.; Wang, Y.; Chang, X.; Liang, Y. L 1/2 regularization. Sci. China Inf. Sci. 2010, 53, 1159–1169. [Google Scholar] [CrossRef]
- Han, S.; Pool, J.; Tran, J.; Dally, W.J. Learning both weights and connections for efficient neural networks. arXiv 2015, arXiv:1506.02626v3. [Google Scholar]
- Zhou, X.; Venigalla, M.; Zhu, S. Bounding box approach to network pruning for efficient path search through large networks. J. Comput. Civ. Eng. 2017, 31, 04017033. [Google Scholar] [CrossRef]
- Wu, R.T.; Singla, A.; Jahanshahi, M.R.; Bertino, E.; Ko, B.J.; Verma, D. Pruning deep convolutional neural networks for efficient edge computing in condition assessment of infrastructures. Comput.-Aided Civ. Infrastruct. Eng. 2019, 34, 774–789. [Google Scholar] [CrossRef]
- Frankle, J.; Carbin, C. The lottery ticket hypothesis: Finding sparse, trainable neural networks. In Proceedings of the ICLR Workshop 2019, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Girish, S.; Maiya, S.R.; Gupta, K.; Chen, H.; Davis, L.; Shrivastava, A. The Lottery Ticket Hypothesis for object recognition. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Virtual Event, 19–25 June 2021. [Google Scholar]
- Ditommaso, R.; Ponzo, F.C. Automatic evaluation of the fundamental frequency variations and related damping factor of reinforced concrete framed structures using the Short Time Impulse Response Function (STIRF). Eng. Struct. 2015, 82, 104–112. [Google Scholar] [CrossRef]
- Ditommaso, R.; Mucciarelli, M.; Ponzo, F.C. Analysis of non-stationary structural systems by using a band-variable filter. Bull Earth Eng. 2012, 10, 895–911. [Google Scholar] [CrossRef]
- Pavelka, A.; Procházka, A. Algorithms for initialization of neural network weights. In Proceedings of the 12th Annual Conference, MATLAB, Prague, Czech Republic, 23–27 August 2004. [Google Scholar]
- LeCun, Y.; Denker, J.S.; Solla, S.A. Optimal brain damage. Adv. Neural Inf. Process. Syst. 1990, 2, 598–605. [Google Scholar]
- The MathWorks Inc. MATLAB Version 9 (R2021a); The MathWorks Inc.: Natick, MA, USA, 2020. [Google Scholar]
- Chou, J.Y.; Chang, C.M. Low-story damage detection of buildings using deep neural network from frequency phase angle differences within a low-frequency band. J. Build. Eng. 2022, 55, 104692. [Google Scholar] [CrossRef]
- Zhang, F.L.; Ventura, C.E.; Xiong, H.B.; Lu, W.S.; Pan, Y.X.; Cao, J.X. Evaluation of the dynamic characteristics of a super tall building using data from ambient vibration and shake table tests by a Bayesian approach. Struct. Contr. Health Monitor. 2018, 25, e2121. [Google Scholar] [CrossRef]
- Chou, J.Y.; Chang, C.M. Decentralized damage detection of seismically-excited buildings using multiple banks of Kalman estimators. Adv. Eng. Inform. 2018, 38, 1–13. [Google Scholar] [CrossRef]
- Chou, J.Y.; Chang, C.M. Modal tracking of seismically-excited buildings using stochastic system identification. Smart Struct. Syst. 2020, 26, 419–433. [Google Scholar]
- Pastor, M.; Binda, M.; Harčarik, T. Modal assurance criterion. Procedia Eng. 2012, 48, 543–548. [Google Scholar] [CrossRef]





| Samples | |||
|---|---|---|---|
| Damage Level | Single-Story Damage | Multiple-Story Damage | Randomized |
| Level 1 (0–18%) | 1000 (Random) | 2 (0%, 18%) | - |
| Level 2 (18–36%) | 1000 (Random) | 1 (36%) | - |
| Level 3 (36–54%) | 1000 (Random) | 1 (54%) | - |
| Level 4 (55–73%) | 1000 (Random) | 1 (72%) | - |
| Level 5 (73–90%) | 1000 (Random) | 1 (90.0%) | - |
| Total Count | 46,656 combinations | 20,000 | |
| Hyperparameter | Value |
|---|---|
| Maximum Epoch | 3000 |
| Mean Square Error (MSE) Threshold | |
| Learning Rate | |
| Batch Size | 128 |
| Momentum | 0.9 |
| Learning Rate Drop Factor | 0.1 |
| Before Pruning | After Pruning | |||||
|---|---|---|---|---|---|---|
| Network Name | Input Layer | Hidden Layer | RMSE (%) | Input Layer—Floor Response | Hidden Layer—Neurons (Pruning Ratio) | RMSE (%) |
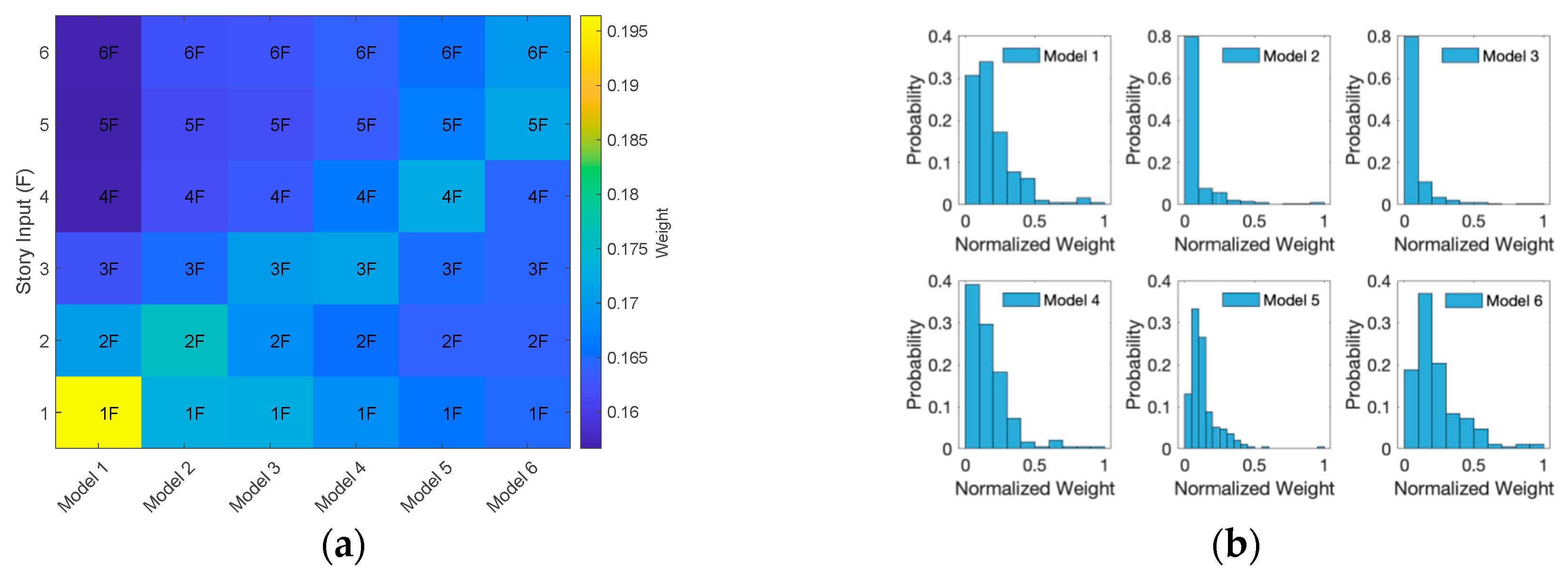
| Model 1 | All story responses | 192 neurons | 1.428% | 1F, 2F, 3F | 17 (91%) | 0.881% |
| Model 2 | 2.650% | 1F, 2F, 3F | 14 (93%) | 1.831% | ||
| Model 3 | 3.690% | 1F, 2F, 3F | 37 (81%) | 3.152% | ||
| Model 4 | 4.218% | 1F, 2F, 3F, 4F, 6F | 173 (11%) | 4.217% | ||
| Model 5 | 3.699% | 1F, 3F, 4F, 5F, 6F | 141 (27%) | 3.653% | ||
| Model 6 | 4.259% | All Stories | 141 (27%) | 4.122% | ||
| (%) | (%) | (%) | (%) | ||
|---|---|---|---|---|---|
| Proposed method | 1F | 0.203% | 0.988% | 0.727% | 0.881% |
| 2F | 0.469% | 1.949% | 1.743% | 1.831% | |
| 3F | 0.721% | 3.538% | 2.642% | 3.152% | |
| 4F | 0.884% | 4.644% | 3.687% | 4.217% | |
| 5F | 0.871% | 4.096% | 3.023% | 3.653% | |
| 6F | 0.836% | 4.474% | 3.756% | 4.217% | |
| 3-layer network | 1F | 0.796% | 2.012% | 1.062% | 1.695% |
| 2F | 0.679% | 2.849% | 1.817% | 2.463% | |
| 3F | 0.746% | 4.076% | 2.544% | 3.512% | |
| 4F | 0.728% | 5.491% | 3.624% | 4.778% | |
| 5F | 0.748% | 5.366% | 3.653% | 4.697% | |
| 6F | 0.749% | 5.619% | 3.975% | 4.957% | |
| Damage Types | Calculation of Synthetic Samples | ||
|---|---|---|---|
| Levels | DoFs | Samples | |
| Single-story damage | 5 | 8 | 40,000 |
| Multiple-story damage | 3 | 8 | 65,536 |
| Randomized-story damage | - | 8 | 20,000 |
| Total count | 125,536 | ||
| Network Name | Initial | After LTH | ||
|---|---|---|---|---|
| RMSE | Input Layer—Floor Response | Hidden Layer—Neurons (Pruning Ratio) | RMSE | |
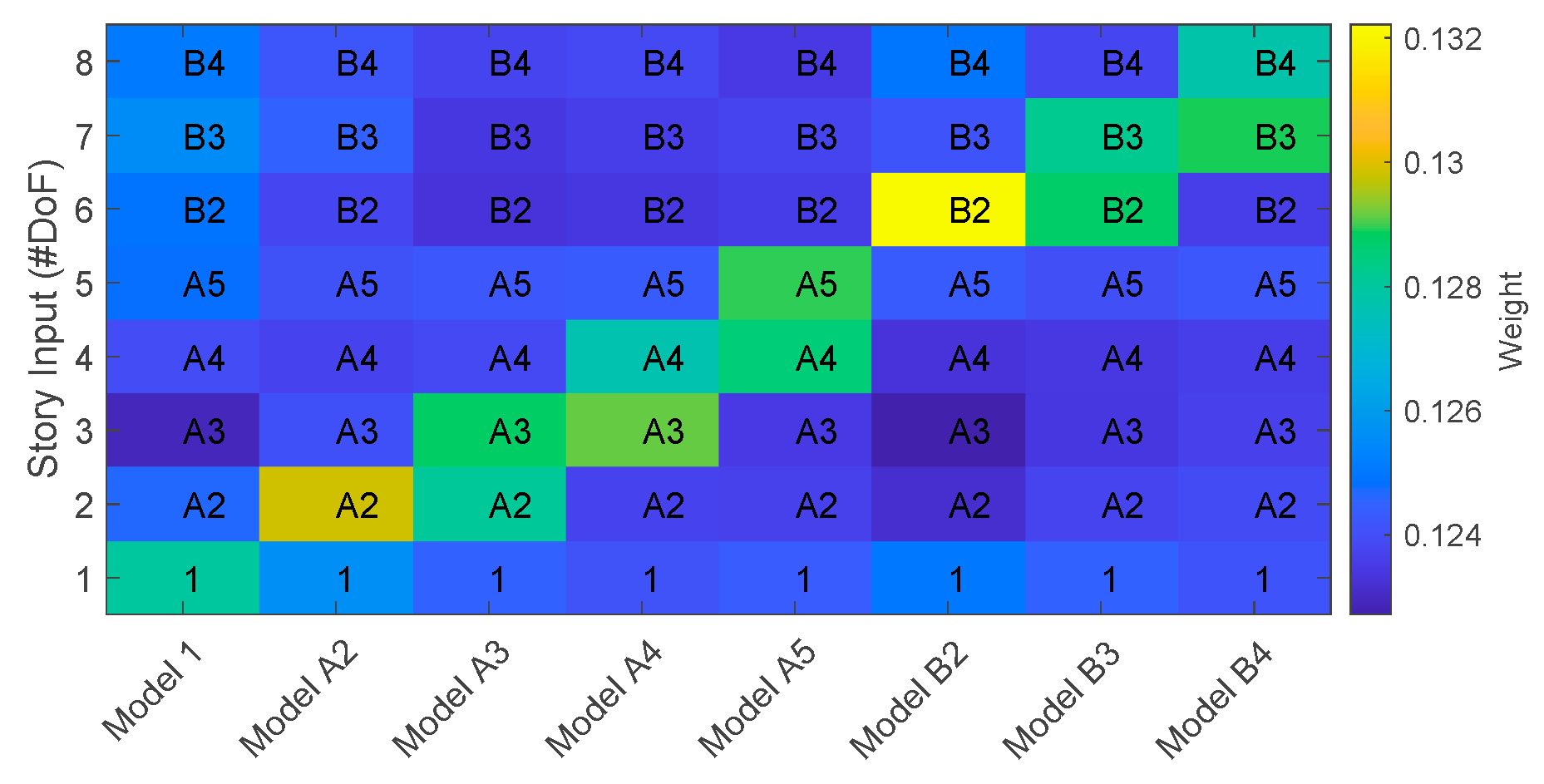
| Model 1 | 2.052% | 1, A2, A4, A5, B3, B4 | 180 (18%) | 1.783% |
| Model A2 | 5.315% | 1, A2, A3, B4 | 147 (33%) | 5.059% |
| Model A3 | 7.168% | 1, A2, A3, A4, A5, B4 | 120 (45%) | 6.735% |
| Model A4 | 9.968% | 1, A3, A4, A5 | 82 (63%) | 8.884% |
| Model A5 | 11.891% | 1, A2, A4, A5, B3 | 120 (45%) | 10.767% |
| Model B2 | 5.181% | 1, A2, A4, A5, B2, B3, B4 | 199 (10%) | 4.986% |
| Model B3 | 9.174% | 1, A2, A4, A5, B2, B3, B4 | 133 (40%) | 8.786% |
| Model B4 | 12.656% | 1, A2, A5, B3, B4 | 46 (79%) | 10.495% |
| 1F | 2F | 3F | 4F | 5F | 6F | 7F | 8F | |
|---|---|---|---|---|---|---|---|---|
| Case 1 | Reference | |||||||
| Case 2 | 11.88% | 0.68% | 0.14% | 0.42% | 1.53% | 0.13% | 0.39% | 0.28% |
| Case 3 | 13.70% | 0.64% | 0.10% | 0.37% | 1.00% | 0.10% | 0.39% | 0.40% |
| Case 4 | 18.65% | 0.73% | 0.07% | 0.64% | 0.20% | 0.10% | 0.56% | 0.54% |
| Case 5 | 88.65% | 2.03% | 0.01% | 12.61% | 5.52% | 5.98% | 14.1% | 0.28% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chou, J.-Y.; Chang, C.-M.; Liu, C.-Y. Damage Detection of Seismically Excited Buildings Using Neural Network Arrays with Branch Pruning Optimization. Buildings 2025, 15, 2052. https://doi.org/10.3390/buildings15122052
Chou J-Y, Chang C-M, Liu C-Y. Damage Detection of Seismically Excited Buildings Using Neural Network Arrays with Branch Pruning Optimization. Buildings. 2025; 15(12):2052. https://doi.org/10.3390/buildings15122052
Chicago/Turabian StyleChou, Jau-Yu, Chia-Ming Chang, and Chieh-Yu Liu. 2025. "Damage Detection of Seismically Excited Buildings Using Neural Network Arrays with Branch Pruning Optimization" Buildings 15, no. 12: 2052. https://doi.org/10.3390/buildings15122052
APA StyleChou, J.-Y., Chang, C.-M., & Liu, C.-Y. (2025). Damage Detection of Seismically Excited Buildings Using Neural Network Arrays with Branch Pruning Optimization. Buildings, 15(12), 2052. https://doi.org/10.3390/buildings15122052







