Abstract
The using of flat slab systems is a common structural solution for residential and commercial buildings as they are a cost-effective structural solution that simplifies and speeds up the construction phase. However, the flat slab systems have complex behavior, particularly in the slab–column connection zones, because of punching shear. Therefore, to prevent brittle flat slab collapse because of punching shear, there are some conditions which must be met in regulations such as Eurocode 2, American Concrete Institute’s Code, and Türkiye Building Earthquake Code—2018. Flat slab collapses because of punching shear can be caused by deficiencies in the design phase as well as deficiencies in the construction phase. The purpose of this study is to investigate the causes of flat slab collapses due to punching shear, focusing on whether these failures arise from design or construction deficiencies. The study highlights the importance of adhering to regulations to prevent brittle flat slab collapses. A case study of an actual building collapse due to punching shear was conducted. Theoretical punching shear strength was calculated based on the Türkiye Building Earthquake Code—2018. A finite element model of the collapsed part of the building was created, and collapse mechanism simulations were performed. It was examined whether the punching collapse mechanism was caused by deficiencies in the design or the construction phase. The findings revealed the critical role of proper design phases and construction practices in ensuring structural integrity.
1. Introduction
Reinforced concrete (RC) slabs are structural elements commonly used in the construction of engineering structures such as residential buildings, bridges, and other infrastructure projects. They are designed to distribute loads over a large area, providing support for floors, roofs, and other structural components. There are several types of reinforced concrete slabs, such as one-way and two-way conventional slabs, ribbed slabs, hollow-tile floor slabs, waffle slabs, and flat slabs.
Flat slab systems are used as common structural solutions for residential and commercial buildings as they are a cost-effective structural solution that simplifies and speeds up the construction phase. In general, flat slabs that are supported directly by columns without beams in between the columns transfer a considerably concentrated load that only impacts a limited area. The term “mushroom slabs” is also used to refer to this building method in the literature. The slab-to-column connection is a crucial component of this system due to the concentration of shear stress created in the connection zone and the possibility of slab punching. The term punching shear refers to a specific kind of brittle slab collapse, particularly in the slab–column connection zone where the concentrated load is applied due to shear stress (Figure 1). This failure mode can have serious consequences for the structural integrity and safety of the building, as it can result in the brittle collapse of the structure. The punching shear strength of an RC slab–column connection is influenced by several factors, including the size and configuration of the column, the thickness and reinforcement of the slab, and the strength and stiffness of the surrounding concrete. The behavior of the connection under punching shear loads is also influenced by the distribution of the load and the stiffness of the surrounding elements, such as beams and walls.
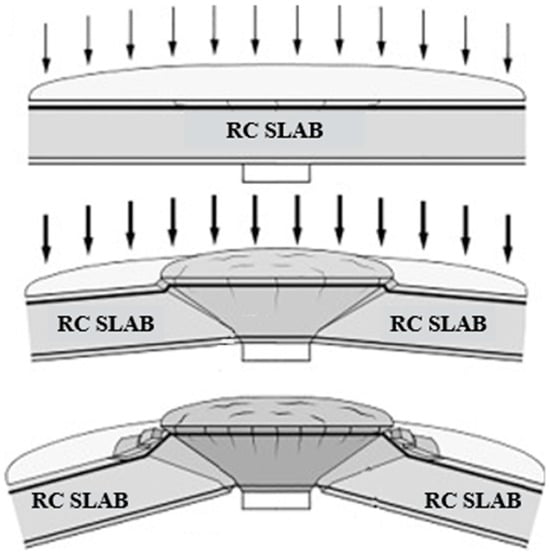
Figure 1.
Schematic view of punching in a flat slab supported by only a column [1].
Many studies in which the punching effect is evaluated are available in the literature. Jia and Chiang [2] examined the influence of capital radius on slab–column punching shear resistance. It was stated that raising the radius of capital clearly improves the node carrying capacity and reduces the moment transfer impact. Bartolac et al. [3] carried out experimental research on the punching shear of slabs with and without shear reinforcement. It was found that the actual carrying capacity of punching shear slabs was underestimated. Genikomsou and Polak [4] studied concrete slab–column connections with shear reinforcement. They compared ultimate loads and crack patterns obtained from experimental and numerical findings. Inácio et al. [5] experimentally evaluated the punching of reinforced high-strength concrete slabs. It was stated that high-strength concrete showed excellent results in terms of punching strength. Schmidt et al. [6] evaluated the concrete and shear reinforcement contributions by systematic punching tests on shear-reinforced flat slabs with closed stirrups. Shu et al. [7,8,9] created finite element (FE) models based on shell and continuum elements that were used to estimate punching behavior and internal force distribution in slabs. Vargas et al. [10] presented a developed database of experiments of flat slabs under eccentric punching shear, and linear FE analyses of all the specimens were considered. Ultimate shear stresses obtained from the experiments were compared to the current codes. Along with these studies, many researchers conducted tests to examine the effect of different types of shear reinforcements (such as bent-up bars, stirrups, and shear heads) on the punching shear failure of the RC slabs [11,12,13,14,15,16]. On the other hand, there are also some experimental studies in the literature on the punching of post-tensioned slabs [17,18,19,20]. Guandalini et al. [21] investigated the punching shear resistance of RC slabs without transverse reinforcement, analyzing the impacts of different flexural reinforcement ratios, specimen dimensions, and aggregate types. Yooprasertchai et al. [22] investigated the effect of the shape (circular and square) on the punching shear capacity of flat slabs, the effect of the distance of an opening from the column’s face, and the applicability of existing punching shear capacity analytical formulations. Alrousan and Alnemrawi [23] studied theoretical and numerical approaches to examine the punching shear capacity of RC flat slabs without shear reinforcement under the loading eccentricity and the presence of an opening adjacent to the column face. Sigrist et al. [24] highlighted the advantages of physical models over empirical formulae. Despite these attempts, classic analytical and empirical models struggle to reliably predict the punching shear strength for complex structural systems. The assumptions of these models often change with different cases and lead to inconsistencies. Recent advancements have attracted interest in the incorporation of machine learning models in the structural fields and the prediction of the punching shear resistance of flat slabs. Artificial neural network-based models have been mostly utilized to estimate the punching shear strength of flat slabs without transverse reinforcement [25].
Including drop panels at the head of the column is an effective way to increase the strength and stiffness of concrete flat slab systems and prevent brittle slab collapse due to punching shear. There are three types of drop panels commonly used in construction: flat drop panels, capital drop panels, and combined flat and capital drop panels (Figure 2). Flat drop panels are the simplest and most common type. They have a uniform depth. Capital drop panels are a type of drop panel that has an additional thicker perimeter surrounding the indentation. A combination of flat and capital drop panels has the features of both of them. The use of drop panels, whether flat, capital, or a combination, can significantly improve the load-carrying capacity of flat slab systems.
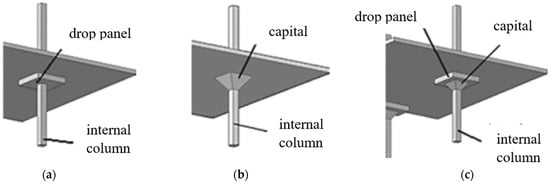
Figure 2.
Types of drop panels: (a) flat, (b) capital, and (c) combined drop panel [2].
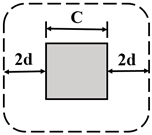
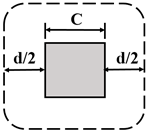
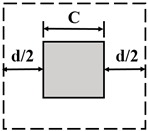
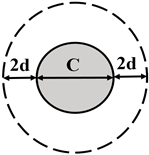
To prevent brittle flat slab collapse because of punching shear, some conditions must be met in the regulations such as Eurocode 2 and American Concrete Institute’s Code (ACI 318-19) [26,27]. Theoretical punching shear strengths are determined with formulations. There are some significant differences in assessing the shear strength of RC slab–column connections in these major regulations. The punching shear strength is assessed along the critical (control) perimeter of columns. Generally, the control perimeter is situated from the column face at a specific distance for the shear strength and just includes the most crucial parameters. Depending on the codes, this distance can range from half to twice the effective depth of the slab. The control perimeters specified in Eurocode 2 Part 1-1 and ACI 318-19 are presented in Table 1 for square, rectangular, and circular columns.

Table 1.
The control perimeters specified in Eurocode 2 Part 1-1 and ACI 318-19 for determination of punching shear strength [26,27].
The ACI 318-19 approach is based on the maximum shear stress υu on the control perimeter of the slab. According to ACI 318-19, the shear stresses do not exceed the least of the following three expressions in slabs without shear reinforcement [26]:
where the values are 40, 30, and 20 for interior, edge, and corner columns, respectively; is the size effect modification factor; is the lightweight factor; and b is the ratio of the long size to the short size of the column.
On the other hand, in Eurocode 2 Part 1-1, the punching shear strength of slabs without shear reinforcement () is calculated as follows [27]:
where is the ratio of reinforcement for bending; is accepted as ; is the concrete material factor; and is the size effect factor. is calculated based on (mm) with the following expression [27]:
In addition to Eurocode 2 Part 1-1 and ACI 318-19, in the Türkiye Building Earthquake Code—2018 (TBEC-2018), stress control is recommended for punching control (TBEC, 2018) [28]. In the flat slabs, punching control can be achieved based on the vertical shear stress formed under the effects of earthquakes, which is obtained from the FE model solution and is augmented by the strength excess coefficient (D) together with the vertical loads. According to TBEC-2018, the following condition must be met for the shear stress value obtained from the finite element solution [28]:
where is the effective depth of the slab; is the design axial tensile strength of concrete; and is the calculated shear force at unit width. The value based on the design should be calculated by determining the control perimeter at the distance from the square and rectangular column surfaces. However, a clear expression is not specified for the determination of the control perimeter in circular columns. Also, it is stated that in case the condition (Equation (6)) is not met, and the slab thickness is not less than 250 mm, the punching shear strength of the slab can be increased by using shear reinforcement [28].
In this study, a building that actually collapsed due to punching shear was selected as a case study. It was determined whether the slab collapse mechanism was caused by deficiencies in the design or the construction phase. The theoretical punching shear strength was determined according to TBEC-2018 for the critical slab–column connection zone of the building. The FE simulation of the collapsed part of the building was performed and the results were compared with the actual collapse mechanism.
2. The Case Study
2.1. Description of the Building
The building chosen as the case study is located in Bolu, Türkiye. It was designed to be used for commercial purposes (marketplace). Some 3D views of the building are given in Figure 3. In addition to the 3D views, plan and section views are also presented in Figure 4.
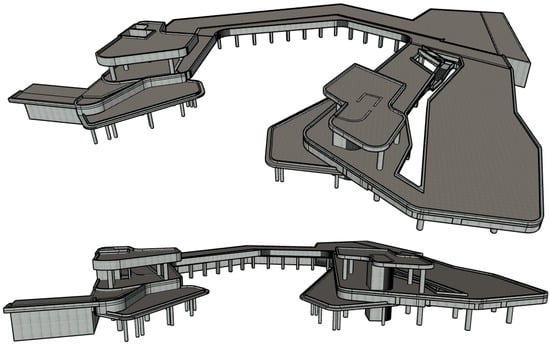
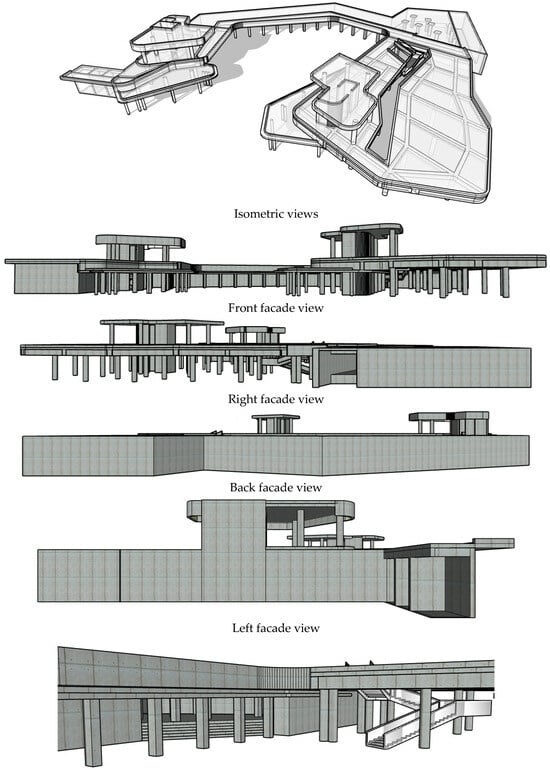
Figure 3.
Some 3D views of the building.
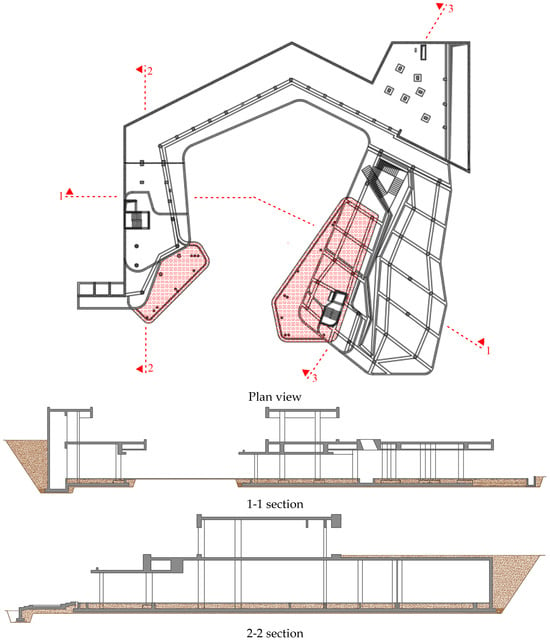

Figure 4.
Plan and section views of the building.
The building was designed according to the upstand beam slab system. As detailed in the section view in Figure 5, beams are placed on the columns in such a way that they remain between two slabs. During the construction phase, the first slab was built on the columns as the first step and the slab system worked as a flat slab. After the first step was completed, the construction of the beams and the second slab was started as the second step. However, in this transitional phase, the flat slab behavior in the first step could not be predicted during design, and a punching effect occurred in the column–slab connection zones, so the brittle slab collapse mechanism was observed. Figure 5 indicates the column–slab connection zone where collapse occurred due to punching stress, and images of the collapsed state of the building are given in Figure 6.
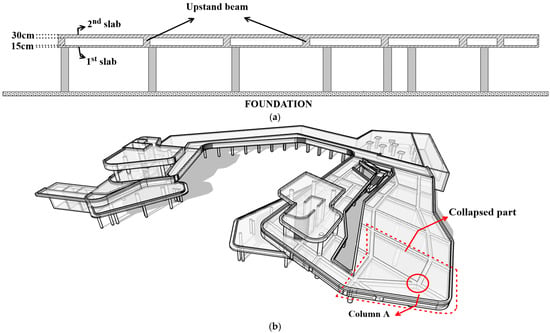
Figure 5.
(a) Upstand beam slab system, and (b) column–slab connection zones where collapse occurred due to punching effect.

Figure 6.
Images of the collapsed part of the building due to the punching effect.
2.2. Punching Shear Strength Calculation
If the construction was completed in accordance with the project, the beams would sit on the column. So, there would be no need to control the punching shear strength in the second step. However, in the first step, a flat slab system was formed, and punching shear strength controls were not carried out since this situation could not be predicted during the design phase. For this reason, the punching shear stress control was achieved theoretically in column A (specified in Figure 5), where punching takes place, according to TBEC-2018.
- Control perimeter
Column A is a circular column with a diameter of 70 cm, but a clear expression is not specified for the determination of the control perimeter in circular columns. So, the expression of “control perimeter shall be permitted to be defined assuming a square column of equivalent area.” specified in ACI 318-19 was considered (Table 2) [26].

Table 2.
Determination of the square column with equivalent area for the circular column [26].
Control perimeter and area were determined by the following formulations:
- Calculation of coefficients reflecting the bending effect ( and ):
- Calculation of the center of gravity of the control area in the direction of the strong and weak axis in the moment direction considered ( and ):
- Calculation of the center of gravity of the control area in the direction of the strong and weak axis in the opposite direction of the moment considered ( and ):
- Calculation of the sum of polar moments of inertia and second moments in the strong and weak axis directions of the surfaces forming the control area ( and ).
Since the axes are equal to each other in the square column, it is sufficient to make a single calculation.
- Calculation of punching shear strength (τpd,1 and τpd,2):where is the design shear force value based on the punching calculation; and are the basic design moments for the slab punching calculation, which is calculated under the combined effect of vertical loads and earthquake loads in the strong and weak axes of the column. When calculating the punching shear strengths ( and ), the bending moment values that occur under the joint effect of vertical loads and earthquake loads calculated by considering the strength excess coefficient () are used [28].
In the FE program, and values were obtained as −8.90 tfm and −1.42 tfm, respectively. In addition, was calculated as 33.01 tf in the FE program. Punching shear strength ( and ) values were obtained by using Equations (17) and (18) as follows:
According to TBEC-2018, the larger of the and values must be equal to or less than the design axial tensile strength of concrete () (Equation (6)). The value is 130.32 tf/m2 for the C30 concrete class, which was used in the construction of the building and has a characteristic compressive strength of 30 MPa. The punching shear strength value () is higher than this value (Equation (20)). For this reason, the punching shear strength condition could not be ensured. In addition, the use of shear reinforcement is not appropriate, since the slab thickness is small than 25 cm according to TBEC-2018 [28].
3. Finite Element Simulations
The FE models of only the collapsed part of the building were generated using Abaqus, v2022 software [29]. The FE models were constituted for both flat slab and upstand beam slab conditions to examine the collapse mechanism of the building (Figure 7). A linear tetrahedron C3D4 finite element with four nodes was used in the models. The optimum mesh size was selected to be 20 cm considering the geometry of the model, the level of accuracy desired to be obtained as a result of the analysis, the availability of calculation resources, and analysis time.
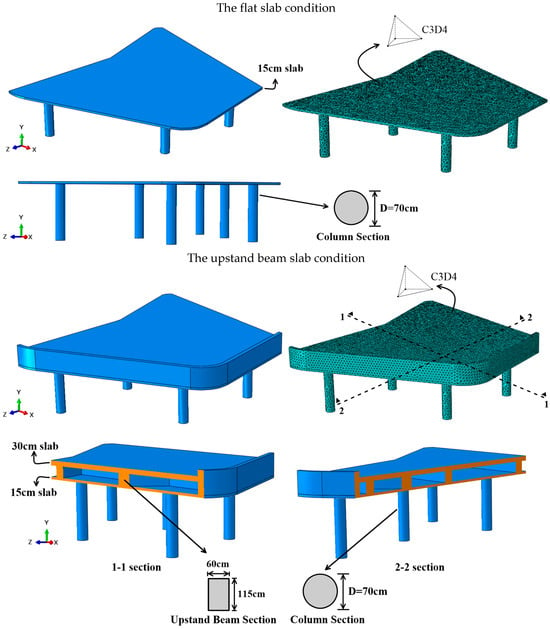
Figure 7.
FE model of the flat slab and upstand beam slab conditions.
The linear material properties, which were used in the analyses, were selected for C30 concrete (Table 3). The Concrete Damage Model (CDP), which is a continuum and plasticity-based damage model, was used to define nonlinear material properties. CDP accepts the main two failure mechanisms as tensile cracking and compressive crushing of the material and has a general capability to model the concrete and other quasi-brittle materials [29]. Equations (21) and (22) define stress–strain relations under uniaxial tension and compression loading.
where and are the total strains in compressive and tension conditions, and are the equivalent plastic strains in compressive and tension conditions, is the initial modulus of elasticity, and and are the compressive and tension damage variables, respectively. These damage variables range from 0, which indicates that the material is undamaged, to 1, which indicates that all strength has been lost. The plastic parameters and stress–inelastic strain values for C30 concrete are given in Table 4 and Table 5. Also, Figure 8 shows the evolution of the compression and tension damage factors ( and ).

Table 3.
The linear elastic material parameters included in the FE model for C30 concrete.

Table 4.
Plastic parameters of C30 concrete for the CDP model [30].

Table 5.
Stress–inelastic strain values for C30 concrete [30].
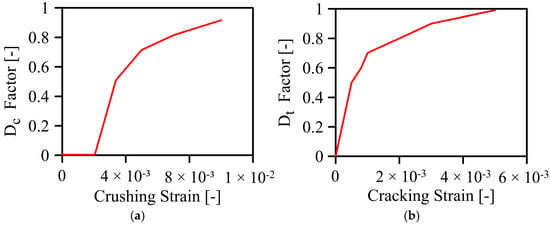
Figure 8.
The compression and tension damage evolutions for C30 concrete [30].
The geometrically nonlinear analyses were carried out by using the explicit procedure. An explicit procedure uses the central-difference operator and a consistent, large-deformation theory or model can undergo large rotations and large deformation, allowing for either automatic or fixed time incrementation to be used. The computational cost involved in running a simulation with a given mesh is proportional to the geometry of the model, mesh size, time period, etc. Nonlinearity of the geometry and material was incorporated in the simulation to accurately model the collapse behavior. During the analyses, the self-weight of the building was only considered. As a result of the analyses, the damage mechanism of the building due to the punching effect was evaluated with the tensile damage. The tensile strain distribution is a good indicator of the damage pattern on the structure. Figure 9 shows that the plastic tensile strain distribution (PEEQT) occurred in the slab systems. While the PEEQT value occurred in the local area of the upstand beam slab model, distribution of the PEEQT value increased in the flat slab model. The concentration of the tensile stress damage distribution (DamageT), which is the tension damage factor (), is similar to that of PEEQT. The evolutions of the damage mechanism for the flat slab and upstand beam slab models are given in Figure 10. Also, Figure 11 shows the ultimate tensile damage condition. As can be seen in Figure 10 and Figure 11, the results similar to the actual collapse mechanism of the building were obtained in the flat slab model. However, collapse did not occur in the upstand beam slab model. Only 45% of local damage was observed (Figure 11).
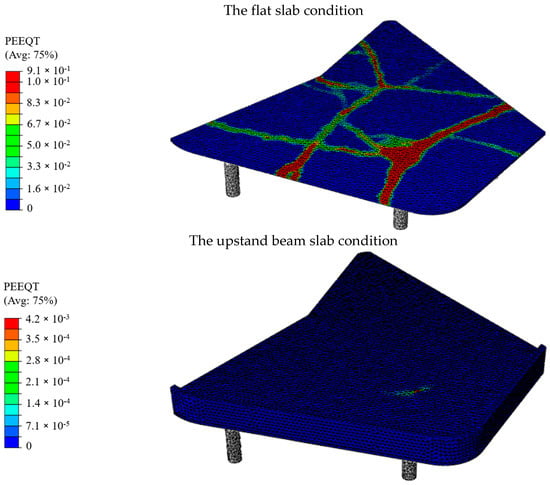
Figure 9.
Plastic tensile strain distributions for the flat slab and upstand beam conditions.
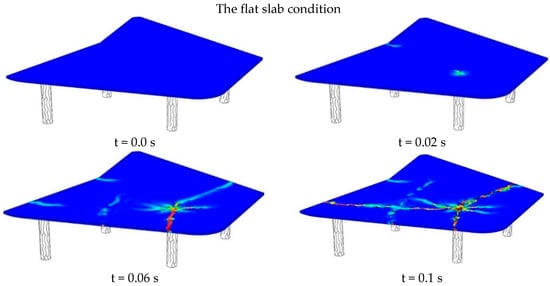
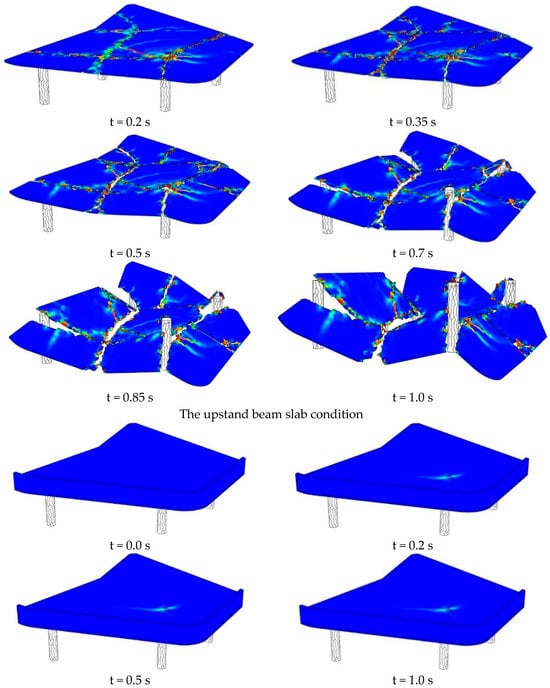
Figure 10.
The evolution of the damage mechanism for the flat slab and upstand beam conditions.
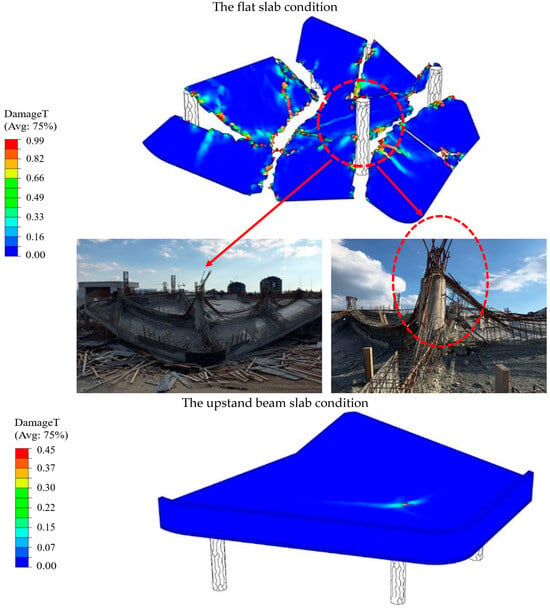
Figure 11.
Ultimate tensile damages for the flat slab and upstand beam slab models conditions.
The findings obtained from the empirical calculations and FE simulations showed a critical role in proper design phases and construction practices in ensuring structural integrity. Potential design deficiencies, such as not planning the design phase considering the construction phase, not providing sufficient punching shear reinforcement at critical connection points, not determining the appropriate slab height, and incorrect load estimates, can cause such failures. In fact, it is clear that the design phase was not planned considering the construction phase in the examined case study. The first construction step should have been foreseen and the punching shear strength should have been calculated. On the other hand, defects during the construction phase, such as failure to carry out the construction phase in accordance with the design phase, inadequate concrete quality, and incorrect reinforcement placement, may also cause slab collapse mechanisms because of the punching shear effect. As a matter of fact, in the case study, construction steps in accordance with the design were not also carried out. Alternative construction steps could have prevented the damage mechanism. Investigation of a detailed analysis of design and construction phases and their accordance with each other would be crucial for enhancing the reliability and safety of similar structures.
In light of the deficiencies identified in the construction and design phases, several recommendations can be proposed to mitigate the risk of similar failures in the future, such as (i) planning the design phase considering the construction phase; (ii) ensuring adequate punching shear reinforcement at critical connection points, particularly in flat slab systems, and selection of an appropriate slab height and concrete class; and (iii) conducting routine on-site inspections to check that the construction phase is carried out in accordance with the design phase and identifying potential construction flaws. Thus, failures of similar flat slab structures can be mitigated, and the safety and integrity of this type of structure can be enhanced.
4. Conclusions
In this study, a building that actually collapsed due to punching shear was evaluated. It was examined whether the reason for collapse is due to the construction phase or the design phase. The building was designed according to the upstand beam slab system. Punching shear control is not necessary to the upstand beam slab system because each beam sits on the columns. However, the building was constructed in two steps. After the first slab was built on the columns as the 1st step, the system behaved like a flat slab. The punching shear strength calculation was carried out for this flat slab system according to the Türkiye Building Earthquake Code. The punching shear strength value (τpd,1) was obtained as 155.23 tf/m2 (1.523 MPa). This value is higher than the condition recommended in the regulation. Hence, the punching shear strength condition cannot be ensured.
In the numerical part of the study, the FE models were constituted for both flat slab and upstand beam slab conditions to examine the collapse mechanism of the building. The geometrically nonlinear analyses were carried out by using the explicit procedure under only self-weight of the building. The plastic tensile strain distribution was examined in the slab systems. Collapse did not occur in the upstand beam slab model and only 45% of local damage was observed. On the other hand, in the flat slab system, brittle slab collapse was observed similar to the actual collapse mechanism of the building. It is concluded that defects during both design and construction phases may cause slab collapse mechanisms because of the punching shear effect. The study addresses flat slab system collapse due to punching shear, and although the results provide specific findings for this structural system, the analysis methods used and the behavioral patterns identified can also be adapted to other structural systems such as various flat slab or slab–column systems with similar critical shear weaknesses. While the findings serve as a focused case study, they also provide insight that could guide further investigation into analogous structural vulnerabilities. Comprehensive multi-case analyses, comparative analyses of international design regulations, examination of how these regulations are incorporated into the construction phase, and sensitivity analyses to assess the impact of the modeling assumptions on the results could provide directions for future research.
Author Contributions
Conceptualization, A.C.A.; Formal analysis, E.E.A. and B.A.; Investigation, E.E.A., M.G. and B.A.; Methodology, E.E.A., A.C.A., M.G. and B.A.; Project administration, A.C.A.; Resources, A.C.A.; Validation, E.E.A., A.C.A., M.G. and B.A.; Visualization, E.E.A.; Writing—original draft, E.E.A., A.C.A., M.G., and B.A.; Writing—review & editing, E.E.A., A.C.A. and B.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data that support the findings of this study are available on request from the corresponding author.
Conflicts of Interest
Author Ahmet Can Altunişik is employed by the Construction Ind. Trade Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
List of Notation
| Control area (TBEC-2018) | |
| b | Ratio of the long size to the short size of the column (ACI 318-19) |
| d | Effective depth of the slab |
| C | Diameter of circular column or size of square/rectangular column |
| Center of gravity of the control area in the direction of the strong axis in the direction of the moment (TBEC-2018) | |
| Center of gravity of the control area in the direction of the weak axis in the direction of the moment (TBEC-2018) | |
| Center of gravity of the control area in the direction of the strong axis in the opposite direction of the moment (TBEC-2018) | |
| Center of gravity of the control area in the direction of the weak axis in the opposite direction of the moment (TBEC-2018) | |
| Strength excess coefficient (TBEC-2018) | |
| Compressive damage variable | |
| Tension damage variable | |
| Initial modulus of elasticity | |
| Design axial tensile strength of concrete (TBEC-2018) | |
| Sum of polar moments of inertia and second moments in the strong axis directions of the surfaces forming the control area (TBEC-2018) | |
| Sum of polar moments of inertia and second moments in the weak axis directions of the surfaces forming the control area (TBEC-2018) | |
| Polar moment of inertia of the control area perpendicular to the axis (TBEC-2018) | |
| Polar moment of inertia of the control area parallel to the axis (TBEC-2018) | |
| Size effect factor (Eurocode 2 Part 1-1) | |
| Design moment calculated about the strong axis of the column under the joint effect of vertical loads and earthquake loads (TBEC-2018) | |
| Design moment calculated about the weak axis of the column under the joint effect of vertical loads and earthquake loads (TBEC-2018) | |
| Control perimeter (TBEC-2018) | |
| 40, 30 and 20 for interior, edge and corner columns (ACI 318-19) | |
| Concrete material factor (Eurocode 2 Part 1-1) | |
| Size effect modification factor (ACI 318-19) | |
| Coefficient reflecting the bending effect (TBEC-2018) | |
| Coefficient reflecting the shear effect (TBEC-2018) | |
| Total strain in compressive condition | |
| Total strain in tension condition | |
| Plastic strain in compressive condition | |
| Equivalent plastic strain in tension condition | |
| Lightweight factor (ACI 318-19) | |
| Ratio of reinforcement for bending (Eurocode 2 Part 1-1) |
References
- Liberati, E.A.P.; Marques, M.G.; Leonel, E.D.; Almeida, L.C.; Trautwein, L.M. Failure analysis of punching in reinforced concrete flat slabs with openings adjacent to the column. Eng. Struct. 2019, 182, 331–343. [Google Scholar] [CrossRef]
- Jia, Y.; Chiang, J.C.L. Finite element analysis of punching shear of reinforced concrete mushroom slab-column connections using ABAQUS. In Advances in Frontier Research on Engineering Structures; Yang, Y., Ed.; Lecture Notes in Civil Engineering; Springer Nature: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Bartolac, M.; Damjanović, D.; Duvnjak, I. Punching strength of flat slabs with and without shear reinforcement. Gradevinar 2015, 67, 771–786. [Google Scholar] [CrossRef]
- Genikomsou, A.S.; Polak, M.A. Finite-element analysis of reinforced concrete slabs with punching shear reinforcement. J. Struct. Eng. 2016, 142, 12. [Google Scholar] [CrossRef]
- Inácio, M.M.G.; Lapi, M.; Ramos, A.P. Punching of reinforced concrete flat slabs—Rational use of high strength concrete. Eng. Struct. 2020, 206, 110194. [Google Scholar] [CrossRef]
- Schmidt, P.; Kueres, D.; Hegger, J. Contribution of concrete and shear reinforcement to the punching shear resistance of flat slabs. Eng. Struct. 2020, 203, 109872. [Google Scholar] [CrossRef]
- Shu, J.; Fall, D.; Plos, M.; Zandi, K.; Lundgren, K. Development of modelling strategies for two-way RC slabs. Eng. Struct. 2015, 101, 439–449. [Google Scholar] [CrossRef]
- Shu, J.; Plos, M.; Zandi, K.; Johansson, M.; Nilenius, F. Prediction of punching behavior of RC slabs using continuum non-linear FE analysis. Eng. Struct. 2016, 125, 15–25. [Google Scholar] [CrossRef]
- Shu, J.; Belletti, B.; Muttoni, A.; Scolari, M.; Plos, M. Internal force distribution in RC slabs subjected to punching shear. Eng. Struct. 2017, 153, 766–781. [Google Scholar] [CrossRef][Green Version]
- Vargas, D.; Lantsoght, E.O.L.; Genikomsou, A.S. Flat slabs in eccentric punching shear: Experimental database and code analysis. Buildings 2022, 12, 2092. [Google Scholar] [CrossRef]
- Broms, C.E. Elimination of flat plate punching failure mode. Struct. J. 2000, 97, 94–101. [Google Scholar] [CrossRef]
- Robertson, I.N.; Kawai, T.; Lee, J.; Enomoto, B. Cyclic testing of slab-column connections with shear reinforcement. Struct. J. 2002, 99, 605–613. [Google Scholar] [CrossRef]
- Kang, T.H.-K.; Wallace, J.W. Dynamic responses of flat plate systems with shear reinforcement. Struct. J. 2005, 102, 763–773. [Google Scholar] [CrossRef]
- Tan, Y.; Teng, S. Interior slab-rectangular column connections under biaxial lateral loadings. In SP-232 Punching Shear in Reinforced Concrete Slabs; American Concrete Institute: Farmington Hills, MI, USA, 2005; pp. 147–174. [Google Scholar]
- El-Salakawy, E.F.; Polak, M.A.; Soudki, K.A. New shears strengthening technique for concrete slab-column connections. Struct. J. 2003, 100, 297–304. [Google Scholar] [CrossRef]
- Adetifa, B.; Polak, M.A. Retrofit of slab column interior connections using shear bolts. Struct. J. 2005, 102, 268–274. [Google Scholar] [CrossRef]
- Silva, R.J.C.; Regan, P.E.; Melo, G.S. Punching resistance of unbonded post tensioned slabs by decompression methods. Struct. Concr. 2005, 6, 9–21. [Google Scholar] [CrossRef]
- Ahn, B.; Kang, T.H.-K.; Kang, S.; Yoon, J.K. Punching shear stress in post-tensioned transfer plate of multi-story building. Appl. Sci. 2020, 10, 6015. [Google Scholar] [CrossRef]
- Binh, T.L.; Cuong, N.-H.; Long, N.-M. Punching shear capacity of unbonded post-tensioned slab—Concrete filled steel tube column joints with innovative connections: Experiment and A new prediction model. J. Build. Eng. 2022, 59, 104974. [Google Scholar] [CrossRef]
- Choi, S.-H.; Hwang, J.-H.; Han, S.-J.; Joo, H.E.; Kim, J.H.; Kim, K.S. Experimental study of punching shear in post-tensioned slabs with unbonded tendons. Struct. Eng. Mech. 2021, 79, 507–516. [Google Scholar] [CrossRef]
- Guandalini, S.; Burdet, O.L.; Muttoni, A. Punching tests of slabs with low reinforcement ratios. Struct. J. 2009, 106, 87–95. [Google Scholar] [CrossRef][Green Version]
- Yooprasertchai, E.; Tiawilai, Y.; Wittayawanitchai, T.; Angsumalee, J.; Joyklad, P.; Hussain, Q. Effect of shape, number, and location of openings on punching shear capacity of flat slabs. Buildings 2021, 11, 484. [Google Scholar] [CrossRef]
- Alrousan, R.Z.; Alnemrawi, B.R. The influence of concrete compressive strength on the punching shear capacity of reinforced concrete flat slabs under different opening configurations and loading conditions. Structures 2022, 44, 101–119. [Google Scholar] [CrossRef]
- Sigrist, V.; Bentz, E.; Ruiz, M.F.; Foster, S.; Muttoni, A. Background to the fib model code 2010 shear provisions—Part I: Beams and slabs. Struct. Concr. 2013, 14, 195–203. [Google Scholar] [CrossRef]
- Khuong, L.-N.; Hoa, T.; Thong, P. Prediction of punching shear strength in flat slabs: Ensemble learning models and practical implementation. Neural Comput. Appl. 2024, 36, 4207–4228. [Google Scholar] [CrossRef]
- ACI 318-19; Building Code Requirements for Structural Concrete and Commentary. American Concrete Institute: Farmington Hills, MI, USA, 2019.
- BS EN 1992-1-1; Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings. British Standards Institution (BSI): London, UK, 2004.
- TBEC-2018; Türkiye Building Earthquake Code. Disaster and Emergency Management Presidency: Ankara, Türkiye, 2018.
- ABAQUS 2022; Dassault Systémes Simulia Corp.: Providence, RI, USA, 2021.
- Husem, M.; Cosgun, S.I. Behavior of reinforced concrete plates under impact loading: Different support conditions and sizes. Comput. Concr. 2016, 18, 389–404. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).