Fire Resistance Performance of Constrained H-Shaped Steel Columns with Uneven Vertical Temperature Distributions
Abstract
1. Introduction
2. Development Law of Temperature Fields under Different Fire Conditions
2.1. Uniform Fire Conditions
2.1.1. Uniform Fire Model Parameters
2.1.2. Early Temperature Rise Pattern under Uniform Fire Conditions
- Changes in the ventilation conditions significantly affected the temperatures at the measuring points. The temperatures at the measuring points rapidly peaked in the early stages of combustion, sharply decreased, and eventually stabilized (Figure 4b). This was because the oxygen near the fire source was rapidly consumed and was not replenished, leading to incomplete combustion. The average temperature at the measuring points after stabilization was 250–300 °C lower compared with the temperatures at points closer to the ventilation opening (Figure 4a).
- During the fire, the upward movement of hot smoke gases resulted in an uneven vertical temperature distribution, with the temperature increasing as the heights of the measuring points increased. Simultaneously, the uneven longitudinal temperature distribution was more pronounced at the measuring points far from the ventilation opening, where poor ventilation conditions led to incomplete combustion. Hence, the measuring points were less influenced by heat radiation from the fire source and more influenced by hot smoke gases.
- 3.
- Regardless of the magnitude of the fire’s HRR, the height of the ventilation opening, and the degree of combustion, an uneven vertical temperature field was consistently present along the steel column’s surface. This was because of the uneven vertical temperature distribution caused by the upward movement of hot smoke during the fire process. The steel column closer to the vent had a more obvious vertical temperature gradient, as part of the hot flue gas closer to the vent was discharged by the vent over time to prevent excessive hot flue gas accumulation. Hence, the vertical temperature stratification was more obvious.
- 4.
- Different ventilation conditions significantly affected the temperatures at the measuring points. The temperature curves of the steel column far from the vent (Figure 5b,d,f) show that the temperatures of the measuring points rapidly reached their highest values in the early stage of combustion, then rapidly decreased and eventually became stable. This was because the rapid consumption of oxygen near the fire source could not be supplemented, which resulted in decreases in the temperatures at the measuring points with inadequate combustion.
2.2. Local Fire Conditions
2.2.1. Model Parameters
2.2.2. Early Temperature Rise Pattern under Local Fire Conditions
2.3. Quasi-Realistic Fire Heating Curves
3. Analysis of the Fire Resistance of Steel Columns Based on Quasi-Realistic Fire Heating Curves
3.1. Heat Transfer Analysis
3.2. Mechanical Analysis
3.2.1. Material Properties
3.2.2. Boundary Conditions
3.3. Comparison of Fire Resistance Performances of Steel Columns under Different Temperature Rise Curves
3.3.1. Comparison of Failure Positions of Steel Columns
3.3.2. Comparison of Fire Resistance Temperatures of Steel Columns
4. Revision of the Formula for the Ultimate Fire Resistance Temperature of Steel Columns
4.1. Parameter Analysis
4.2. Formula Modification
4.3. Applications and Challenges
- Evaluate the applicability of existing codes and standards: Conduct a comprehensive review of existing fire safety codes and standards. Identify which parts may overlook the uneven temperature distribution factors during a fire and assess whether new calculation formulas can be accommodated.
- Develop a revision draft: Based on the revised calculation formulas, define the scope of applicability, calculation methods, parameter definitions, and specific implementation requirements of the new formulas. Ensure that the formulas are clear, accurate, and free of ambiguities and that they align with internationally accepted fire safety standards and practices.
- Expert review and public consultation: Organize reviews of the revised formulas by industry experts and scholars to gather professional opinions and recommendations. Conduct public consultation activities to widely solicit feedback from fire departments and other relevant stakeholders to ensure the reasonableness and feasibility of the revised formulas.
5. Conclusions
- Both local and uniform fires exhibit uneven vertical temperature distributions in the early stages of a fire, with the maximum vertical temperature difference reaching over 500 °C. Therefore, the uneven vertical temperature distribution in the early stages of a fire has to be considered and a simulated temperature rise curve has to be constructed.
- The uneven vertical temperature distribution in the early stages of a fire significantly affects the failure temperatures and locations of steel columns. Additionally, the failure temperature is closely related to parameters such as the load ratio, the vertical temperature difference in the early stages of a fire, and the maximum temperature in the early stages of a fire, among which the load ratio has the most significant effect.
- The revised formula for calculating the fire resistance temperature of steel columns is more accurate and safer compared with that presented in the “Technical Code for Fire Protection of Steel Structures” (GB51249-2017), particularly when the load ratio ranges from 0.2 to 0.5, where the difference can be nearly 200 °C.
- This paper focused on a fire resistance simulation conducted specifically on H-shaped steel columns, which inherently have certain limitations. However, it is believed that similar fire resistance phenomena also occur in other types of steel columns and structural components. An uneven longitudinal temperature distribution shortens the effective fire exposure length of a steel column, thus improving its fire resistance temperature. It is believed that this rule is applicable to various types of steel columns, albeit with different temperature differences.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- EN 1991-1-2; Actions on Structures–Part 1–2: General Actions–Actions on Structures Exposed to Fire. European Committee for Standardization: Brussels, Belgium, 2002.
- Aasen, B. An Experimental Study on Steel Column Behaviour at Elevated Temperatures; Institutt for Stålkonstruksjoner, Universitetet i Trondheim, Norges Tekniske: Trondheim, Norway, 1985. [Google Scholar]
- Ali, F.A.; Shepherd, P.; Randall, M.; Simms, I.; O’Connor, D.J.; Burgess, I. The effect of axial restraint on the fire resistance of steel columns. J. Constr. Steel Res. 1998, 46, 305–306. [Google Scholar] [CrossRef]
- Cai, J.; Feng, J.; Zhao, Y.; Xu, Y. Stability of axially restrained steel columns under temperature action. Sci. China Technol. Sci. 2010, 53, 3349–3355. [Google Scholar] [CrossRef]
- Chiew, S.P.; Zhao, M.S.; Lee, C.K. Mechanical properties of heat-treated high strength steel under fire/post-fire conditions. J. Constr. Steel Res. 2014, 98, 12–19. [Google Scholar] [CrossRef]
- Craveiro, H.D.; Rodrigues, J.P.C.; Laím, L. Cold-formed steel columns made with open cross-sections subjected to fire. Thin-Walled Struct. 2014, 85, 1–14. [Google Scholar] [CrossRef]
- Dellepiani, M.G.; Munoz, G.R.; Yanez, S.J.; Guzmán, C.F.; Flores, E.I.S.; Pina, J.C. Numerical study of the thermo-mechanical behavior of steel–timber structures exposed to fire. J. Build. Eng. 2023, 65, 105758. [Google Scholar] [CrossRef]
- I.S. EN 1993-1-2:2005; Eurocode 3 C. Design of Steel Structures–Part 1–2: General Rules–Structural Fire Design. European Committee for Standardization: Brussels, Belgium, 2005.
- Fan, S.; Zhang, L.; Sun, W.; Ding, X.; Liu, M. Numerical investigation on fire resistance of stainless steel columns with square hollow section under axial compression. Thin-Walled Struct. 2016, 98, 185–195. [Google Scholar] [CrossRef]
- GB 51249-2017; Code for Fire Safety of Steel Structures in Buildings. China Planning Press: Beijing, China, 2017.
- Jiang, B.; Yin, Z.; Zhang, J.; Fan, C.; Li, Y. Effect of rotational restraint conditions on performance of steel columns in fire. Eng. Struct. 2021, 238, 112237. [Google Scholar] [CrossRef]
- Li, G.-Q.; Song, L.-X. Mechanical properties of TMCP Q690 high strength structural steel at elevated temperatures. Fire Saf. J. 2020, 116, 103190. [Google Scholar] [CrossRef]
- Liu, G.; Meng, H.; Qu, G.; Wang, L.; Ren, L.; Lu, H. Real-time monitoring and prediction method of commercial building fire temperature field based on distributed optical fiber sensor temperature measurement system. J. Build. Eng. 2023, 70, 106403. [Google Scholar] [CrossRef]
- Lucherini, A.; Torero, J.L. Defining the fire decay and the cooling phase of post-flashover compartment fires. Fire Saf. J. 2023, 141, 103965. [Google Scholar] [CrossRef]
- Pires, T.A.; do Rêgo Silva, J.J.; dos Santos, M.M.; Costa, L.M. Fire resistance of built-up cold-formed steel columns. J. Constr. Steel Res. 2021, 177, 106456. [Google Scholar] [CrossRef]
- Qiang, X.; Bijlaard, F.; Kolstein, H. Dependence of mechanical properties of high strength steel S690 on elevated temperatures. Constr. Build. Mater. 2012, 30, 73–79. [Google Scholar] [CrossRef]
- Rakshith, B.; Kumar, S. Behaviour of steel columns with realistic boundary restraints under standard fire. Structures 2020, 28, 626–637. [Google Scholar]
- ISO 834-1:1999; Fire-resistance Tests: Elements of Building Construction. General Requirements. International Organization for Standardization: Geneva, Switzerland, 1999.
- Sun, X.; Wang, Q.; Lv, J.; Fang, X.; Han, Y.; Tang, F.; Hu, L. Temperature evolution, flame traveling transition structure inside a compartment of various fire source locations. Fuel 2024, 371, 131911. [Google Scholar] [CrossRef]
- Wang, W.; Li, G. Research progress of fire resistance design theory of high strength steel structures. Ind. Constr. 2016, 46, 61–67. [Google Scholar]
- Wang, W.; Ohmiya, Y.; Ma, G. Fire resistance study of axially loaded high strength steel columns. Procedia Eng. 2013, 62, 690–701. [Google Scholar] [CrossRef]
- Wang, Y.C. The effects of structural continuity on the fire resistance of concrete filled columns in non-sway frames. J. Constr. Steel Res. 1999, 50, 177–197. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, L.; Li, G. Experimental study on fire resistance of high strength Q690 steel columns. J. Build. Struct. 2019, 40, 155–162. [Google Scholar]
- Wu, Y.; Fan, S.; He, B.; Li, C.; Zhou, H. Experimental study and numerical simulation analysis of the fire resistance of high-strength steel columns with rectangular sections under axial compression. Fire Saf. J. 2021, 121, 103266. [Google Scholar] [CrossRef]
- Wu, Y.; Fan, S.; He, B.; Liu, M.; Zhou, H. Research on the fire resistance design of high-strength steel hollow columns under axial compression. Eng. Struct. 2021, 234, 111943. [Google Scholar] [CrossRef]
- Yan, X.; Gernay, T. Numerical modeling of localized fire exposures on structures using FDS-FEM and simple models. Eng. Struct. 2021, 246, 112997. [Google Scholar] [CrossRef]
- Yang, D.; Hu, L.H.; Jiang, Y.Q.; Huo, R.; Zhu, S.; Zhao, X.Y. Comparison of FDS predictions by different combustion models with measured data for enclosure fires. Fire Saf. J. 2010, 45, 298–313. [Google Scholar] [CrossRef]
- Yang, J.; Shi, Y.; Wang, W.; Xu, L.; Al-azzani, H. Experimental and numerical studies on axially restrained cold-formed steel built-up box columns at elevated temperatures. J. Constr. Steel Res. 2020, 171, 106143. [Google Scholar] [CrossRef]
- Yang, J.; Xia, Y.; Wang, W.; Al-azzani, H. Fire resistance of axially restrained Q690 H-shaped welded steel columns: Test, simulation and design. J. Constr. Steel Res. 2021, 177, 106413. [Google Scholar] [CrossRef]
- Yang, K.-C.; Hsu, R. Structural behavior of centrally loaded steel columns at elevated temperature. J. Constr. Steel Res. 2009, 65, 2062–2068. [Google Scholar] [CrossRef]
- Zhao, G.; Beji, T.; Merci, B. Study of FDS simulations of buoyant fire-induced smoke movement in a high-rise building stairwell. Fire Saf. J. 2017, 91, 276–283. [Google Scholar] [CrossRef]

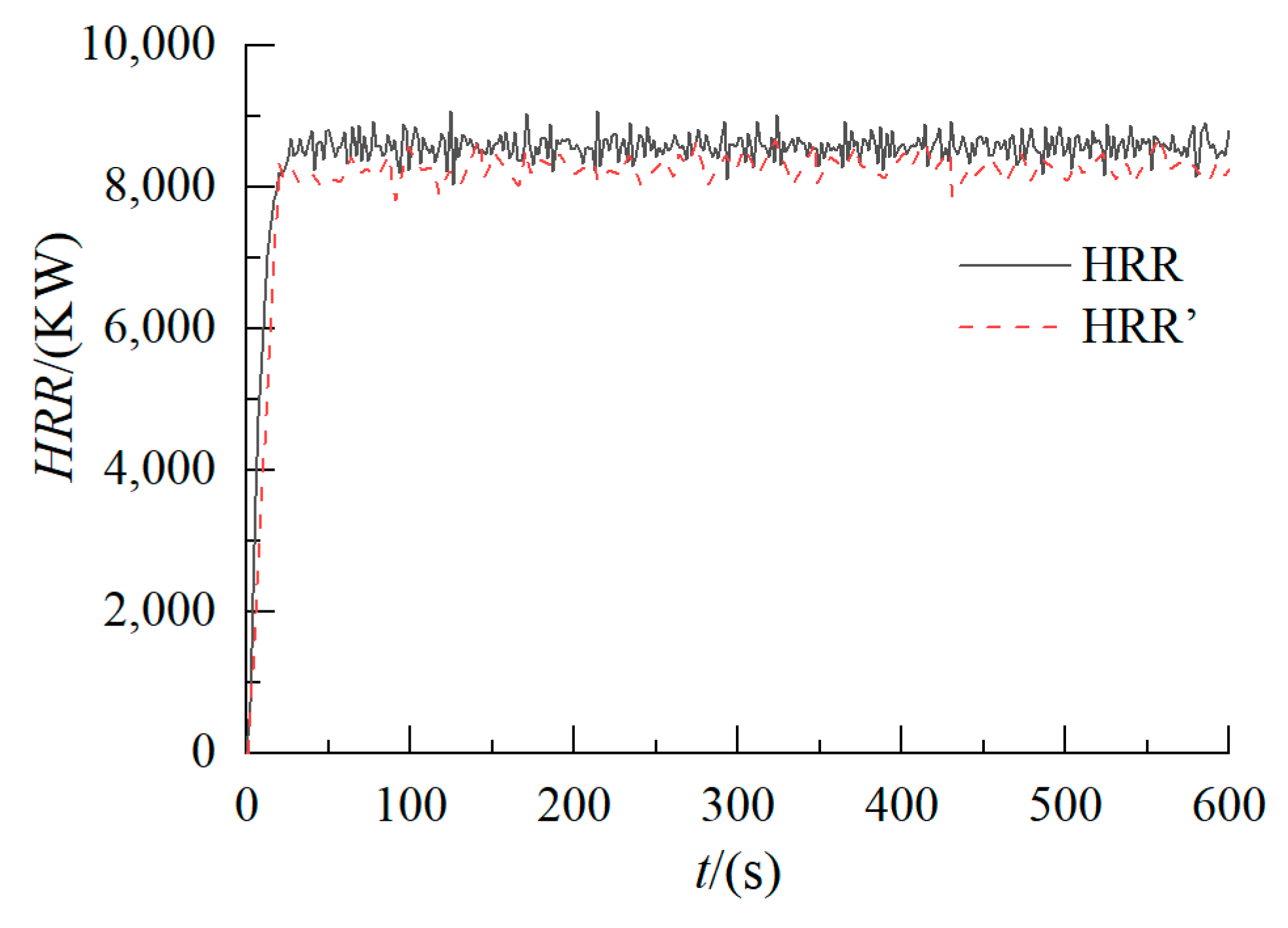





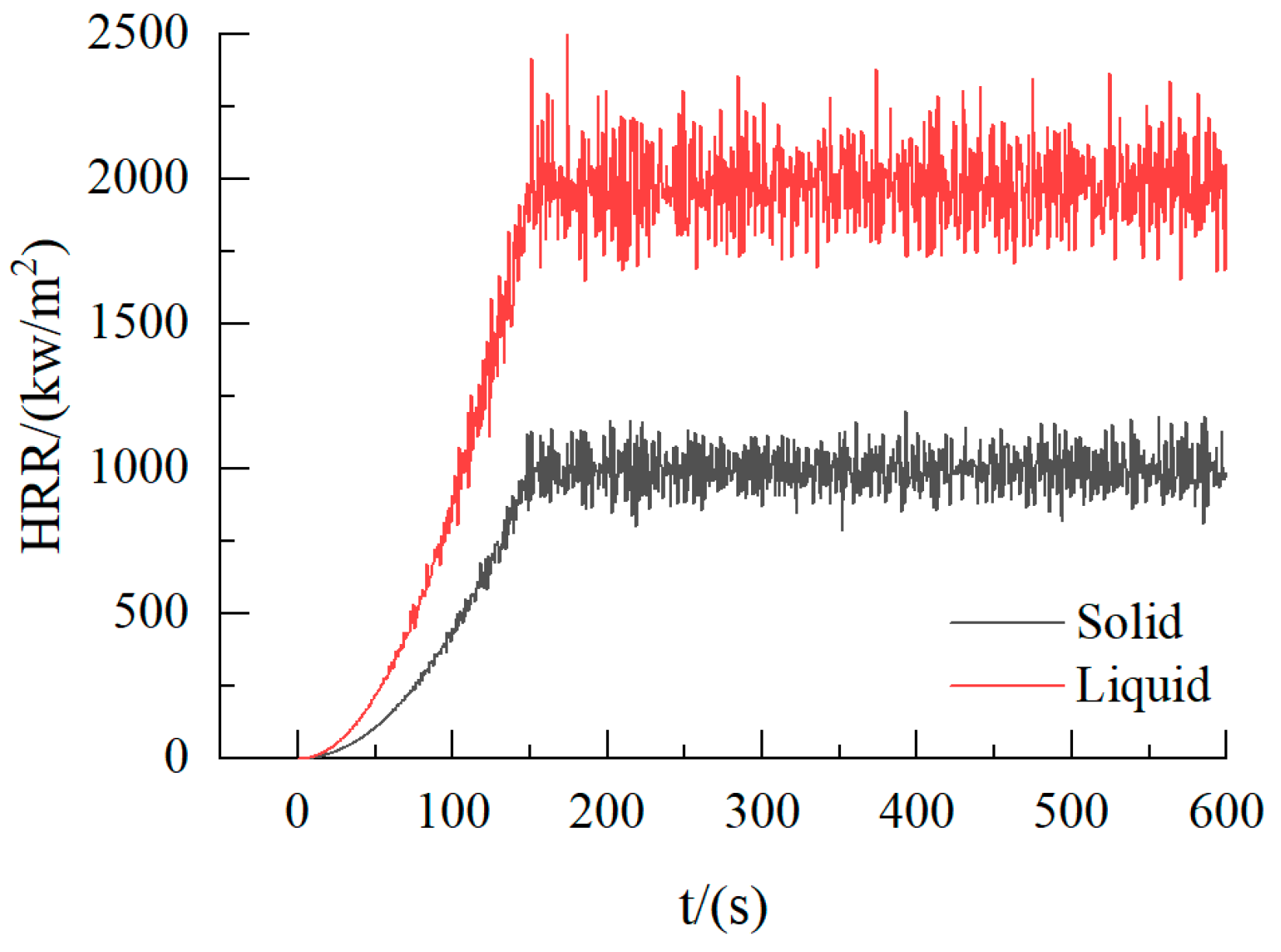
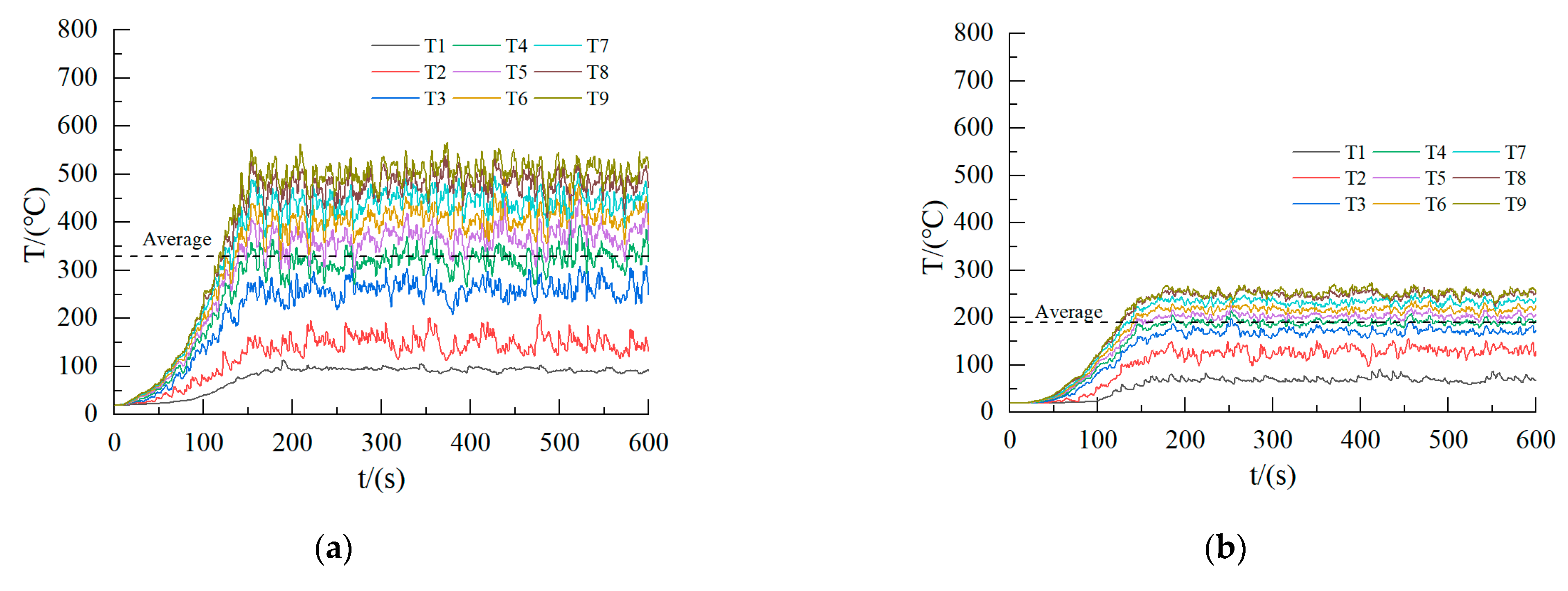












| Model Number | HRRPUA (kW/m2) | H (mm) | D (mm) |
|---|---|---|---|
| E-250-1-500 | 250 | 1500 | 500 |
| E-250-1-3000 | 250 | 1500 | 3000 |
| E-250-2-500 | 250 | 500 | 500 |
| E-250-2-3000 | 250 | 500 | 3000 |
| E-350-1-500 | 350 | 1500 | 500 |
| E-350-1-3000 | 350 | 1500 | 3000 |
| E-350-2-500 | 350 | 500 | 500 |
| E-350-2-3000 | 350 | 500 | 3000 |
| Model Number | HRRPUA (kW/m2) | H (mm) | D (mm) |
|---|---|---|---|
| L-1MW-1 | 1000 | 1000 | 500 |
| L-1MW-2 | 1000 | 1000 | 5000 |
| L-1MW-3 | 1000 | 1500 | 500 |
| L-1MW-4 | 1000 | 500 | 500 |
| L-2MW-1 | 2000 | 1000 | 500 |
| L-2MW-2 | 2000 | 1000 | 5000 |
| L-2MW-3 | 2000 | 1500 | 500 |
| L-2MW-4 | 2000 | 500 | 500 |
| Cross-Section Dimensions | Slenderness Ratio (λ) | Load Ratio (pN) | Axial Restraint Ratio (α) | |
|---|---|---|---|---|
| H200 × 150 × 14 × 14 | 96 | 1.89 | 0.2–0.8 | 0–0.09 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Chen, W.; Li, J.; Yang, T. Fire Resistance Performance of Constrained H-Shaped Steel Columns with Uneven Vertical Temperature Distributions. Buildings 2024, 14, 2826. https://doi.org/10.3390/buildings14092826
Wang X, Chen W, Li J, Yang T. Fire Resistance Performance of Constrained H-Shaped Steel Columns with Uneven Vertical Temperature Distributions. Buildings. 2024; 14(9):2826. https://doi.org/10.3390/buildings14092826
Chicago/Turabian StyleWang, Xiaoming, Wenwen Chen, Jie Li, and Taochun Yang. 2024. "Fire Resistance Performance of Constrained H-Shaped Steel Columns with Uneven Vertical Temperature Distributions" Buildings 14, no. 9: 2826. https://doi.org/10.3390/buildings14092826
APA StyleWang, X., Chen, W., Li, J., & Yang, T. (2024). Fire Resistance Performance of Constrained H-Shaped Steel Columns with Uneven Vertical Temperature Distributions. Buildings, 14(9), 2826. https://doi.org/10.3390/buildings14092826




