Estimation of the Hazardous Chemical Leakage Scale Inside Buildings Using CFD

Abstract

Increased industrialization and aging infrastructure have resulted in leaks of hazardous chemicals, such as CO. Leak modeling is crucial to developing emergency response strategies. Therefore, we simulated the time to criticality (TTC), which is the time to reach the threshold limit for occupational exposure, of a CO leak. The basis of the study is a fire dynamics simulator, a computational fluid dynamics model that was used to investigate the movement of CO in various scenarios, including using different building layouts and areas, temperatures, and leak diameters. Multiple regression analysis was performed to obtain regression equations for the TTC as a function of the independent variables. Ultimately, we found that the type of dispersion varies with respect to the temperature-dependent density of CO, and, among the independent variables, the leak diameter had the strongest effect on the TTC. The regression equations with logarithmic conversion were validated and found to have higher accuracy than those without logarithmic conversion. The findings provide useful information for developing emergency response plans regarding leak size in the case of hazardous chemical leakage. However, empirical studies of different gas types and leakage scenarios are required.

1. Introduction

Hazardous chemical leaks stemming from industrial and chemical processes pose significant safety concerns, and the prompt detection of such leaks and accurate prediction of their magnitude are critical for the prevention of accidents and the development of effective response strategies. Rapid industrialization in South Korea, coupled with the deterioration of infrastructure in dense industrial complexes, has resulted in an increase in gas-related incidents involving tubes, valves, and flanges. These incidents range from leaks to fires, explosions, and the emission of noxious odors. Between 2014 and 2022, there were approximately 740 reported chemical incidents, with a discernible upward trend [1]. Leakages constituted most of these cases, numbering 590. Notably, chemical accidents occurring within confined spaces have a particularly high fatality rate, reaching 50%—a figure 44 times greater than the fatality rate for other types of accidents or disasters, which stands at 1.1% [2].

Substantial research has been conducted on hazardous chemical leaks in both indoor and outdoor environments to discern patterns and forecast variables, including seasonal, climatic, and pollutant factors [3]. For outdoor leak scenarios, the “Areal Locations of Hazardous Atmospheres” (ALOHA) program has been instrumental in assessing diurnal and nocturnal effects, as well as the seasonal impact, on gas leaks [4,5]. Consequently, a variety of simulation tools, such as Phast and ALOHA, have been utilized for these analyses, and computational fluid dynamics (CFD) plays a key role in predicting temporal shifts in concentration or dispersion states [6,7].

For indoor chemical leaks, CFD remains the principal simulation technique. This method enables the investigation of changes with respect to the number and type of sensors deployed to monitor hazardous substances during leak events [8,9]. Within the realm of CFD research, studies focusing on the factors affecting gas dispersion during gas leak modeling in structures such as buildings, hospitals, and ships with ventilation systems have made use of the “Fire Dynamics Simulator” (FDS) [10,11,12]. The efficacy of the FDS in studying hazardous chemical leaks has been validated through comparative analysis with other CFD tools and empirical experiments [13].

Recent advancements in CFD applications for gas leak detection highlight several significant studies. Zhou et al. modeled the diffusion of hazardous gases under various atmospheric stability conditions using a WRF-CFD coupled model, emphasizing the importance of atmospheric stability in gas dispersion [14]. Wang et al. analyzed the leakage and hazardous boundaries of buried gas pipelines, considering underground confined spaces and employing numerical simulations to predict the gas concentrations and distributions [15]. Kim et al. used CFD simulations to model gas explosions in semiconductor facilities, demonstrating the effectiveness of CFD in predicting explosion risks and guiding safety measures [16].

By being able to anticipate the scale of hazardous chemical leaks in advance, it becomes possible to select response methods according to the scale of the leak, enabling flexible responses. Therefore, in this study, we simulated a hazardous chemical leak (of CO) within a building using different room and corridor geometries and hypothesized the time to criticality (TTC), which is the time at which the leaked gas concentration reaches a hazardous level, based on the leak size, storage temperature, and spatial factors that could affect dispersion.

2. Methods

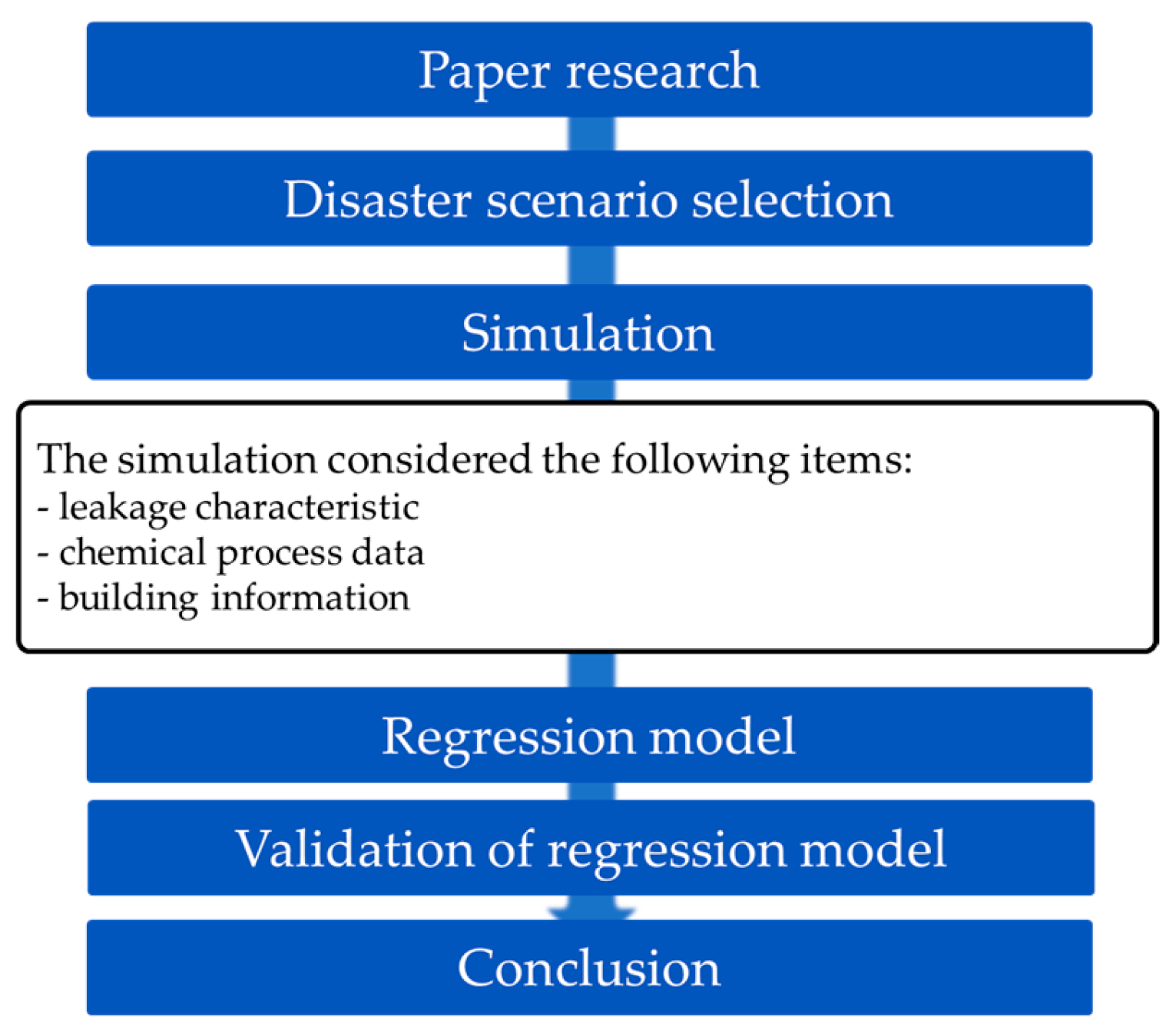
The methods of this study are as shown in Figure 1. A scenario was derived using process information, leakage accident characteristics, and building information. The chemical leak simulation was run accordingly. The simulation software used was FDS Ver 6.7.9, developed by NIST. Regression analysis was performed on the simulation results for each scenario using the time-weighted average (TWA) exceedance time as the dependent variable.

Within Fire Dynamics Simulator (FDS), a robust framework is anchored upon sophisticated fluid dynamics models, which play a crucial role in elucidating the intricate dispersion patterns of gases within confined spaces. By resolving the Navier–Stokes equations and accounting for thermal buoyancy effects, FDS meticulously characterizes airflow phenomena, including turbulent eddies and vortices induced by fire-induced thermal gradients. Moreover, FDS integrates a comprehensive gas diffusion model, enabling the precise simulation of smoke and toxic gas transport. This model intricately considers factors such as ventilation configurations and natural airflow pathways, elucidating the spatial distribution and concentration gradients of airborne contaminants [12,13].

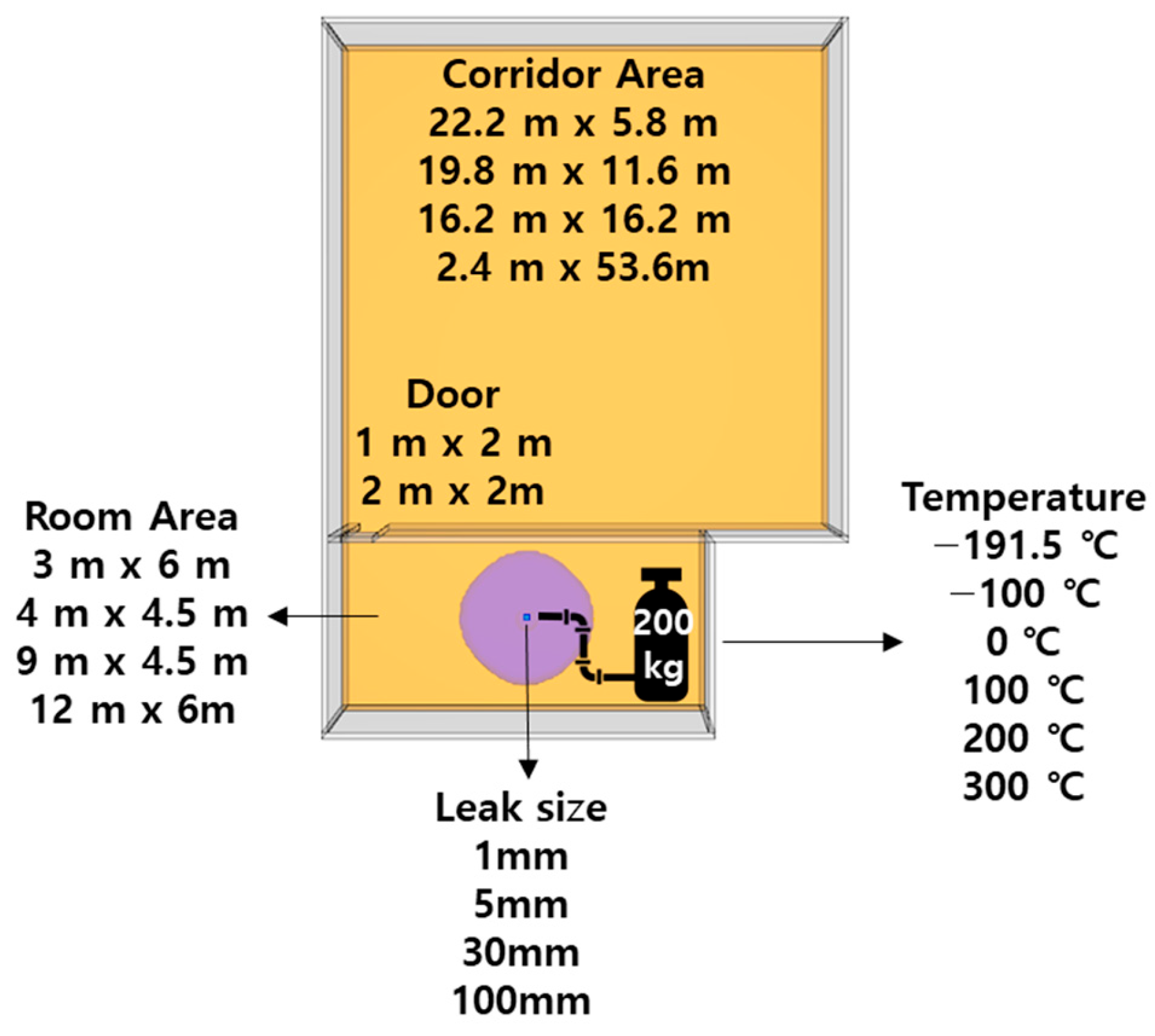
The variables affecting the dispersion of hazardous chemicals during a leakage event include material data, such as the molecular mass of the substance; process data, including the temperature and pressure utilized during operation; and spatial data, which accounts for the building area and geometry. Consequently, variables expected to exert a significant effect on the material, process, and spatial data were selected to prepare different simulation scenarios. As shown in Figure 2, six temperatures, four distinct leak diameters, four room sizes, four corridor dimensions, and two door sizes were used for simulation, yielding 768 simulation scenarios.

2.1. Hazardous Chemical Types and Leak Characteristics

In this study, we focused solely on the leakage of a gas-phase hazardous chemical. Gases characteristically undergo changes in their dispersion with respect to temperature. CO has similar properties to air, having a molecular mass of 28, and as the temperature rises, its density falls, resulting in buoyancy, and vice versa. CO was selected in this study because it was predicted that differences in dispersion type could be examined based on temperature-dependent changes in density.

In the simulations, six temperatures were set, from an initial −191.5 °C, which is the storage temperature of CO in a 200 kg storage tank, to a final 300 °C in increments of approximately 100 °C, and these were used to identify the trends based on the CO temperature. In the preliminary simulations, the leak diameters were set at 0.3, 0.5, 1, 5, 10, 30, 50, and 100 mm; however, the leak diameters of 0.3 and 0.5 mm were excluded because the time-weighted average (TWA) concentration did not reach criticality (see Section 2.2) even after ≥2 h of leakage. Diameters of 10 and 50 mm were used for validation. Therefore, the training data included leak diameters of 1, 5, 30, and 100 mm.

2.2. Spatial Data

The spatial variables were selected based on the criteria of high-risk workplaces stated in the National Fire Protection Association (NFPA) 101 as follows, room area, corridor area, and door area [17], as shown in Figure 3. Based on the NFPA 101 criteria, the room area should be less than 200 ft² (approximately 18.58 m²), and there should be a walking distance of less than 7.6 m. Hence, two areas, 3 m × 6 m and 4 m × 4.5 m, were applied to the simulation, and two more areas, 9 m × 4.5 m and 12 m × 6 m, were used to compare differences with regard to room area. The room height was constant at 3 m.

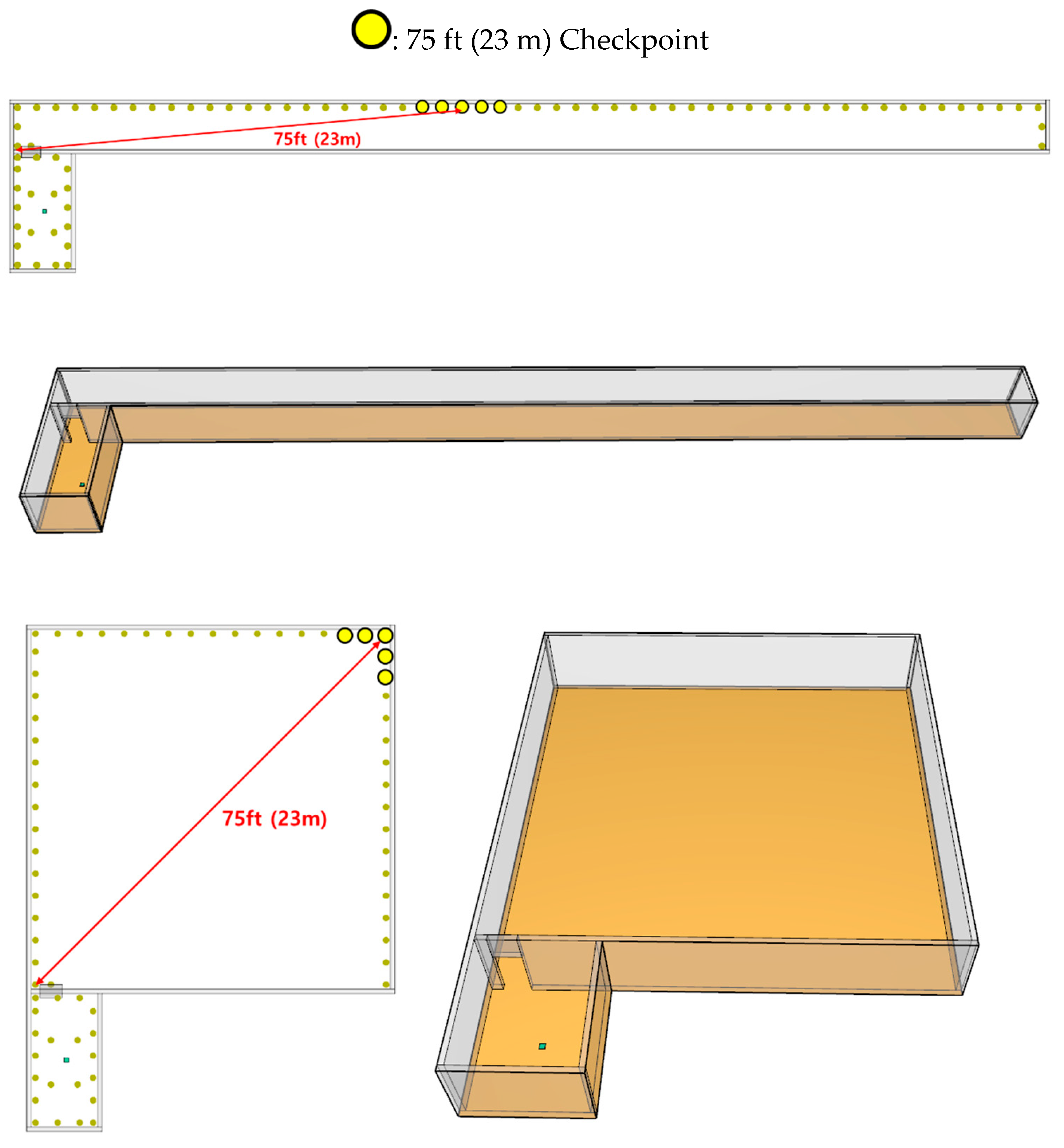
Four distinct corridor configurations were simulated: a 22.2 m × 5.8 m area; a 19.8 m × 11.6 m area; a 16.2 m × 16.2 m area, with the longest diagonal measuring less than 23 m; and another 22.2 m × 5.8 m area to evaluate the impact of the corridor shape when the total area remained constant (Figure 4). Additionally, two standard door sizes were incorporated into the models, measuring 1 and 2 m, to assess their influence on the dispersion of hazardous chemicals.

The concentration of CO was measured with the breathing limit set at 1.8 m. The criteria for the TTC was 30 ppm, which is subsequently denoted as the TWA concentration. The measured concentrations showed irregularity because of turbulence. Therefore, five concentration checkpoints were set at 1 m intervals over a 75 ft (23 m) distance from the door of the room where the leak occurred. The average time at which a CO concentration of 30 ppm was exceeded for the first time at the five measurement points was defined as the TWA exceedance time.

In this study, all doors except the one connecting the room to the corridor were presumed to be closed at the time of the CO leak, and as the mesh, a 0.1 m grid in the room and a 0.2 m grid in the corridor were set to allow for rapid simulation [10] (

Table 1. Simulation parameters.

Category	Set Values
Measurement interval in the room	0.1 m
Measurement height in the corridor	1.8 m
Grid size	Room: 0.1 m Corridor: 0.2 m

). The hazardous chemical was set to be released from a vent of a 0.2 m × 0.2 m size in the center of the room.

2.3. Calculation of Leakage

The degree of leakage with respect to the leak diameter and storage temperature was estimated using the DISC/TVDI discharge model [18], and the leak was presumed to originate from a vent of a 0.2 m × 0.2 m size at the center of the room.

Table 2. Degree of leakage with respect to leak diameter and storage temperature.

	Degree of CO Leakage/(kg/s)
Leak Diameter/(mm)	1	5	30	100
Temperature/(°C)
−191.5	2.35 × 10−2	5.87 × 10−1	2.11 × 10−1	2.35 × 10−2
−100.0	5.91 × 10−4	1.48 × 10−2	5.32 × 10−1	5.91
0.0	2.58 × 10−4	6.44 × 10−3	2.32 × 10−1	2.58
100.0	2.02 × 10−5	5.04 × 10−4	1.82 × 10−2	2.02 × 10−1
200.0	1.79 × 10−5	4.49 × 10−4	1.61 × 10−2	1.79 × 10−1
300.0	1.63 × 10−5	4.07 × 10−4	1.46 × 10−2	1.63 × 10−1

presents the degree of leakage with respect to the leak diameter and storage temperature.

3. Results and Discussion

3.1. Leak Dispersion Type with Respect to Temperature

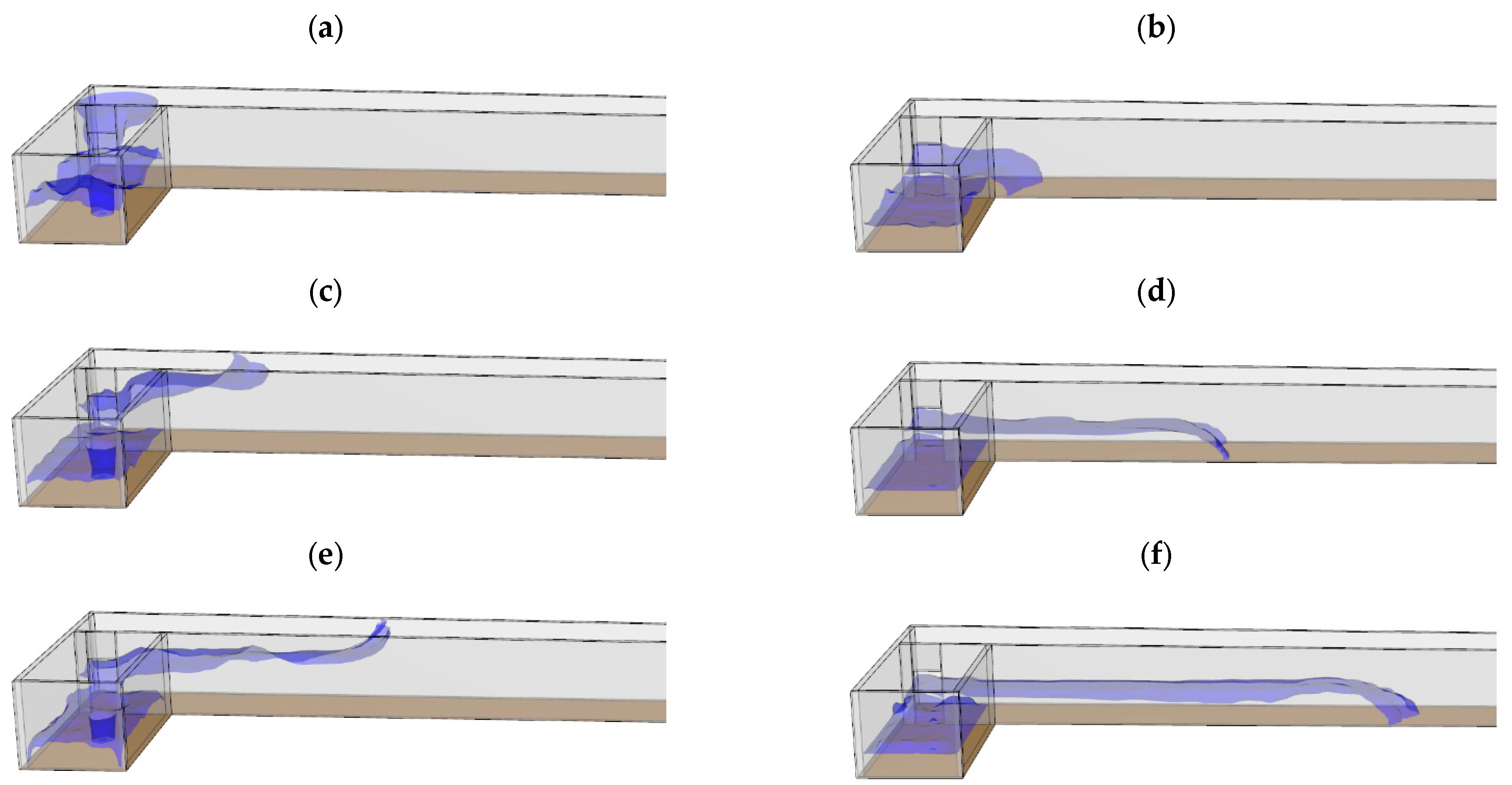
To assess the differences in the dispersion type caused by the differences in the temperature-dependent density, CO gas leakage simulations at 300 and −191.5 °C were compared. Figure 5a and Figure 5b show CO leakages at 300 and −191.5 °C, respectively, with which the gas fills the ceiling and floor areas first in the former and latter cases, respectively, and the results obtained at different times are shown in Figure 6. Thus, the dispersion varied according to the temperature-dependent density. Consequently, analysis of densities above and below that of air is required.

3.2. Correlation Analysis of TWA and Independent Variables

Using the CO leakage simulation results and based on the NFPA 101 criteria, the TWA exceedance time was calculated for the device located 75 ft (23 m) along the diagonal line of the corridor set to satisfy ≤75 ft (≤23 m) between the door and the exit.

3.3. Trend Analysis Using Scatter Plots

The TWA exceedance time was analyzed for a walking distance of 75 ft (23 m) based on the spatial data and leakage data. In Figure 7, the scatter plots display the average TWA exceedance time for the checkpoints for different room and corridor areas. As shown in Figure 6b and Figure 7a, the average TWA increases linearly with an increase in area.

Similarly, as shown in Figure 7c, at temperatures ≤0 °C, the higher density of CO causes the gas to accumulate from the floor area upwards, resulting in an increasing trend in the TWA exceedance time with an increase in temperature. In contrast, Figure 6d shows that at temperatures >0 °C, the lower density of CO compared to air leads to the gas filling the ceiling area first, which may result in quicker detection, and thus a decrease in the TWA exceedance time with an increase in temperature. Figure 6f and Figure 7e show the effect of the leak diameter and inverse leak diameter. As shown in the latter figure, there is a linear increasing trend in the TWA.

3.4. Leakage Regression Equation for Gas with a Density Lower Than That of Air (above 20 °C)

Multiple regression analysis was performed using the TWA exceedance time as the dependent variable and the leak diameter, room area, leak temperature, and corridor area as the independent variables. The fit to the regression equation was increased after the log conversion of the independent variables, and thus non-log and log-converted models were produced [19].

The coefficient of determination (R²) was assessed to evaluate the accuracy of the regression equations. For a multiple regression analysis, an overfitted model can be obtained if a greater number of independent variables are used because this increases R². Thus, to prevent overfitting, the accuracy of the regression equation was evaluated based on the adjusted R² (R²_adj) [20].

Additionally, the model significance outcome was tested by assessing the regression coefficient using the p-value at the 95% confidence interval. That is, statistical significance was set as p < 0.05.

As shown in

Table 3. Statistical parameters for regression equations for a gas with a density lower than that of air.

Model		p-Value	B	β	R2	R2adj
Log applied	(Constant)	3.41 × 10−54	3.596	-	0.952	0.951
	Leak diameter	1.84 × 10−241	0.537	0.915
	Room area	1.58 × 10−85	0.511	0.291
	Leak temperature	2.77 × 10−38	−0.960	−0.164
	Corridor area	6.90 × 10−6	0.162	0.051
Log not applied	(Constant)	2.57 × 10−6	595.145	-	0.728	0.725
	Leak diameter	4.80 × 10−93	1233.316	0.741
	Room area	3.64 × 10−34	10.991	0.361
	Leak temperature	1.38 × 10−13	−1.695	−0.206
	Corridor area	3.21 × 10−3	0.894	0.079

, all the regression coefficients had p < 0.05, demonstrating significance at the 5% level. Although R²_adj did not vary markedly from R² for either regression equation, a higher accuracy was achieved using the log model (R²_adj = 0.951 and 0.725). Furthermore, because the leak diameter exhibited the largest standardized regression coefficient (the so-called beta coefficient, β) for the two equations, it is believed to have a stronger effect on the TWA exceedance time than the other independent variables.

The regression equations to express the TWA exceedance time based on multiple regression analysis for the leakage of gas with a density lower than that of air are shown in Equations (1) and (2).

$$\begin{gathered} \log t_{twa}=3.596+0.537·\log D_{lea{k}_{rev}}+0.511 ·\log A_{room}-0.96 ·\log T_{lea{k}_K}+0.162 ·\log A_{corridor} \\ {t}_{twa}=\frac{{10}^{3.596}\times {D_{leak\_rev}}^{0.537}\times {A_{room}}^{0.511}\times {A_{corridor}}^{0.162}}{{T_{leak\_K}}^{0.96}} \end{gathered}$$

(1)

$$t_{twa}=595.145+1233.316·D_{lea{k}_{rev}}+10.991·A_{room}-1.695·T_{lea{k}_K}+0.894·A_{corridor}$$

(2)

Here, t_twa is the TWA exceedance time at 75 ft (23 m) in seconds, D_{leak_rev} is the inverse of the leak diameter in millimeters, T_{leak_K} is the leak temperature in kelvins, A_room is the area of the room with hazardous chemical leakage in square meters, and A_corridor is the area of the corridor connected to the room in square meters.

3.5. Leakage Regression Equation for Gas with a Density Higher Than That of Air (Below 20 °C)

As shown in

Table 4. Statistical parameters for regression equations for a gas with a density higher than that of air.

Model		p-Value	B	β	R2	R2adj
Log applied	(Constant)	7.63 × 10−137	−5.023	-	0.982	0.982
	Leak diameter	6.96 × 10−298	0.975	0.792
	Room area	3.95 × 10−251	2.551	0.076
	Leak temperature	4.40 × 10−25	0.280	0.590
	Corridor area	0.01	0.115	0.017
Log not applied	(Constant)	3.28 × 10−18	−2311.683	-	0.609	0.604
	Leak diameter	4.20 × 10−58	2734.326	0.619
	Room area	1.75 × 10−4	9.841	0.122
	Leak temperature	3.65 × 10−37	10.46	0.458
	Corridor area	0.27	1.061	0.035

, regression analysis conducted on gas leaks with a density higher that of air revealed a statistically significant result (p < 0.05) when logarithmic transformation was applied to all the variables. However, for the corridor area, the model was not statistically significant (p ≥ 0.05) without logarithmic transformation. The R²_adj remained consistent with the R² for both models, although the log-transformed equation demonstrated enhanced precision, having R²_adj values of 0.982 and 0.604, respectively. As before, the leak diameter, which presented the highest β in both models, should have a greater effect on the TWA exceedance time than the other independent variables.

The regression equations for characterizing the TWA exceedance time for gas leaks denser than air are shown in Equations (3) and (4). The variables incorporated into this equation are analogous to those in Equations (1) and (2).

$$\begin{gathered} \log t_{twa}=-5.023+0.975·\log D_{lea{k}_{rev}}+2.551·\log A_{room}+0.28·\log T_{lea{k}_K}+0.115·\log A_{corridor} \\ {t}_{twa}=\frac{{D_{lea{k}_{rev}}}^{0.975}\times {A_{room}}^{2.551}\times {T_{lea{k}_K}}^{0.28}\times {A_{corridor}}^{0.115}}{{10}^{5.023}} \end{gathered}$$

(3)

$$t_{twa}=-2311.683+2734.326·D_{lea{k}_{rev}}+9.841·A_{room}+10.46·T_{lea{k}_K}+1.061·A_{corridor}$$

(4)

3.6. Validation of the Regression Equations

To validate Equations (1)–(4), 245 random scenarios for the variables shown in

Table 5. Scenarios for regression equation validation.

Leak Gas	Storage Temperature	Corridor Area	Leak Diameter	Room Area
Carbon monoxide	−191.5	22.2 × 5.8	3	6 × 3
	−150
	−100	19.8 × 11.6
	−50		10	9 × 4.5
	0	16.2 × 16.2
	100		50	12 × 6
	300	2.4 × 53.6
	500

were used to obtain calculated values for the simulation and the estimated values of the regression equations. To compare the differences between the calculated and estimated values, the absolute percentage error (APE), as given by Equation (5), was used.

$$APE=\left|\frac{\left(Calculated-Estimated\right)}{Calculated}\right|\times 100\left[\%\right]$$

(5)

The APEs for the regression equations for CO at a temperature-dependent density lower than air (Equations (1) and (2), respectively) were 17.2% and 28%, and for CO at a temperature-dependent density higher than air (Equations (3) and (4), respectively), they were 19.3% and 173.6%. Therefore, a higher fit was shown by the regression equation with log conversion (Equations (1) and (3)) based on the lower APE.

4. Conclusions

In this study, CO leakage from a storage tank was simulated, and a regression model to predict the time-weighted average (TWA) exceedance time at a distance of 75 ft (23 m) from the room experiencing a leak was developed. The study’s findings offer significant insights for developing emergency response plans tailored to specific leak sizes at sites involving hazardous material handling. The results are particularly useful in determining the size of the leak based on real-time data from hazardous chemical leak monitoring sensors deployed at industrial sites.

The study emphasizes that the type of gas leak greatly impacts the regression model due to the gas’s buoyancy, which is influenced by its density. Moreover, this study primarily focused on simulating the leakage of gas-phase hazardous chemicals. Future research should extend to investigating the leakage of liquid-phase chemicals to provide a comprehensive understanding of leak dynamics. Liquid-phase leaks may behave differently from gas-phase leaks due to factors such as viscosity, evaporation rates, and interaction with surfaces, necessitating distinct modeling and response strategies.

Future research directions include further refinement of the regression model to account for different types of hazardous gases, as each gas has unique properties affecting its dispersion and detection. Additionally, studies should explore the integration of advanced sensor technologies and machine learning algorithms to enhance the prediction accuracy and response efficiency. Investigating initial response procedures associated with varying leak sizes will also be crucial for improving on-site safety protocols.

Furthermore, future studies could benefit from exploring the influence of environmental factors such as temperature, humidity, and air currents on gas dispersion patterns. Understanding these factors can lead to more accurate predictions and better preparedness to handle hazardous chemical leaks. Collaborative research involving multidisciplinary teams, including chemical engineers, safety experts, and data scientists, will be essential in advancing this field and ensuring the development of robust, comprehensive safety measures.

Overall, this research sets the foundation for ongoing advancements in the field of hazardous chemical leak detection and response. By leveraging CFD simulations and empirical validations, the findings can significantly contribute to enhancing industrial safety and mitigating the risks associated with hazardous material handling.