Investigation of the Long-Term Performance of Waste Backfill Materials of High Thermal Conductivity in Vertical Ground Heat Exchangers
Abstract
1. Introduction
| Authors | Backfill Material | Additive | Method | Achieving Results |
|---|---|---|---|---|
| Liang B, et al. [16] | Natural sand | Kaolin | Model test | Convective heat-transfer coefficient was improved to 678 W/m2 K. |
| Kim D, et al. [17] | Cement grouting | Steel-making slag | Laboratory test/numerical simulation. | Thermal conductivity exceeds 10%. |
| Erol S, et al. [18] | Silica sand | Graphite | Sand box testing. | Thermal resistance of GHE was reduced and the heat-transfer rate was improved. |
| Blázquez, et al. [19] | Cement grouting | Aluminum shavings | Laboratory test. | Aluminum shavings contribute to increase the thermal conductivity. |
| Treviño, et al. [20] | Cement grouting | Limestone/silica sand, electric arc furnace slag | Laboratory test. | Contact thermal resistance was greatly reduced. |
| Alrtimi, et al. [21] | Mortar of fuel ash | Glass/fluorspar | Laboratory test. | The highest thermal conductivity value could reach 2.88 W/m K. |
| Delaleux, et al. [22] | Bentonite | Graphite | Laboratory test. | High thermal conductivity intensifications were obtained. |
| Muñoz, et al. [23] | Cement mortar | Flake/expanded graphite. | Laboratory test. | Thermal conductivity was improved a lot by the addition of graphite. |
| Lee C, et al. [24] | Cement/bentonite | Silica sand/graphite | Field test. | Thermal performance was improved and thermal interference was reduced. |
2. Methodology
3. Description of Vertical GHEs System
4. Laboratory and Field Test
4.1. Laboratory Test
4.1.1. Methodology
4.1.2. Results and Discussion
4.2. Field Test
4.2.1. Methodology
4.2.2. Results of Field Test
5. Numerical Model Implementation
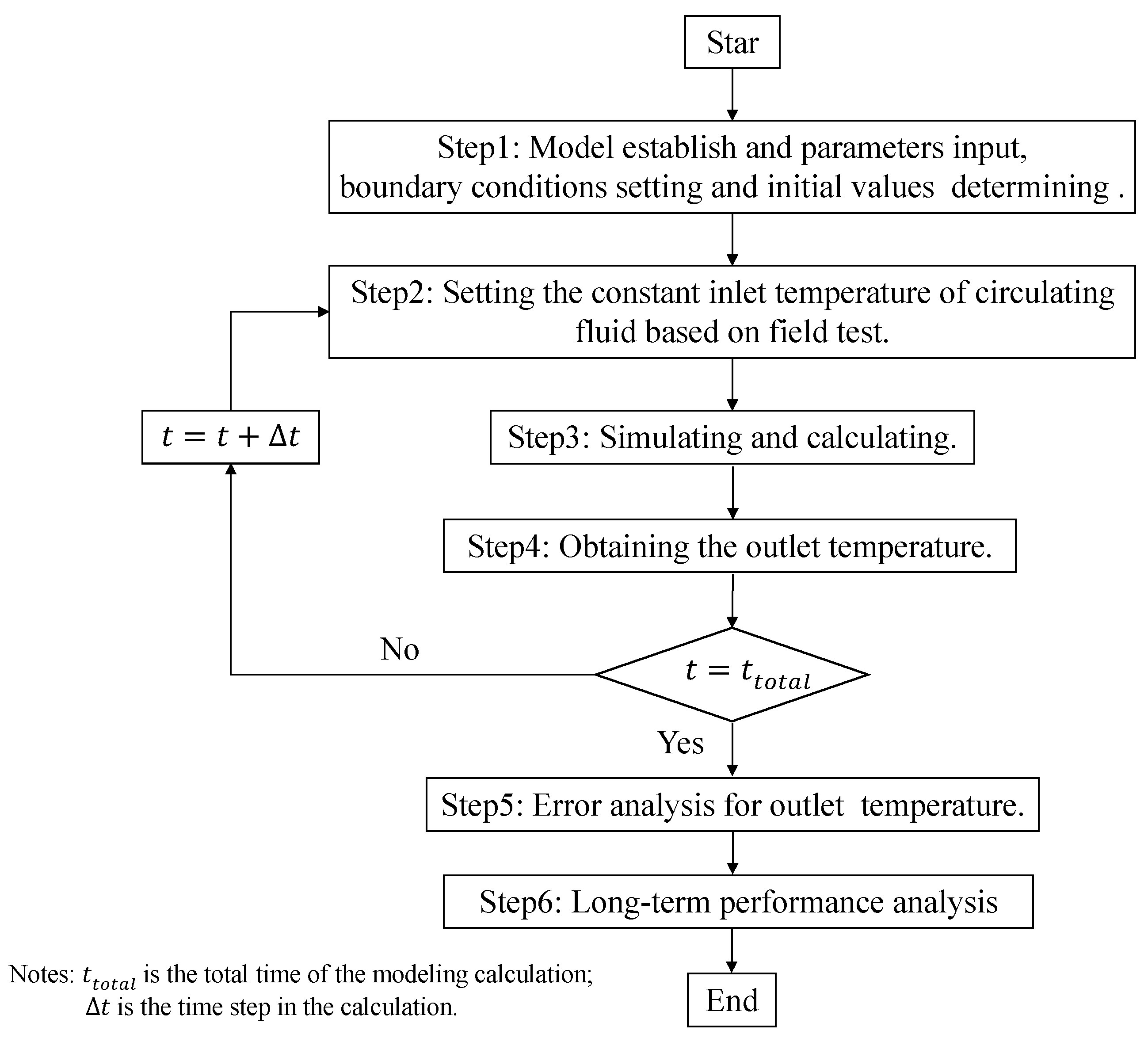
5.1. Methodology
5.1.1. Governing Equations
5.1.2. Geometric Size, Boundary, and Initial Conditions
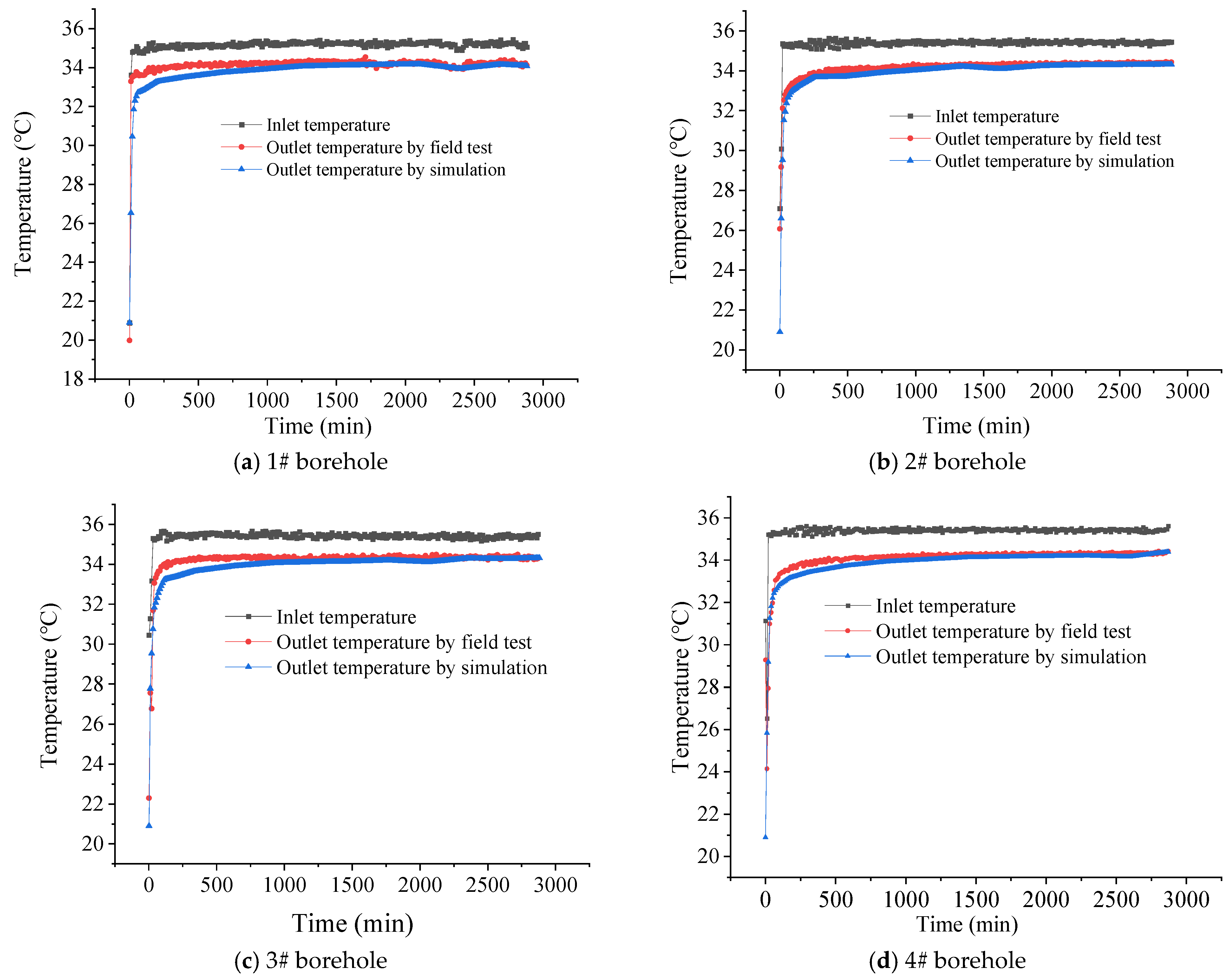
5.2. Results of Numerical Validation
6. Discussion of Numerical Results
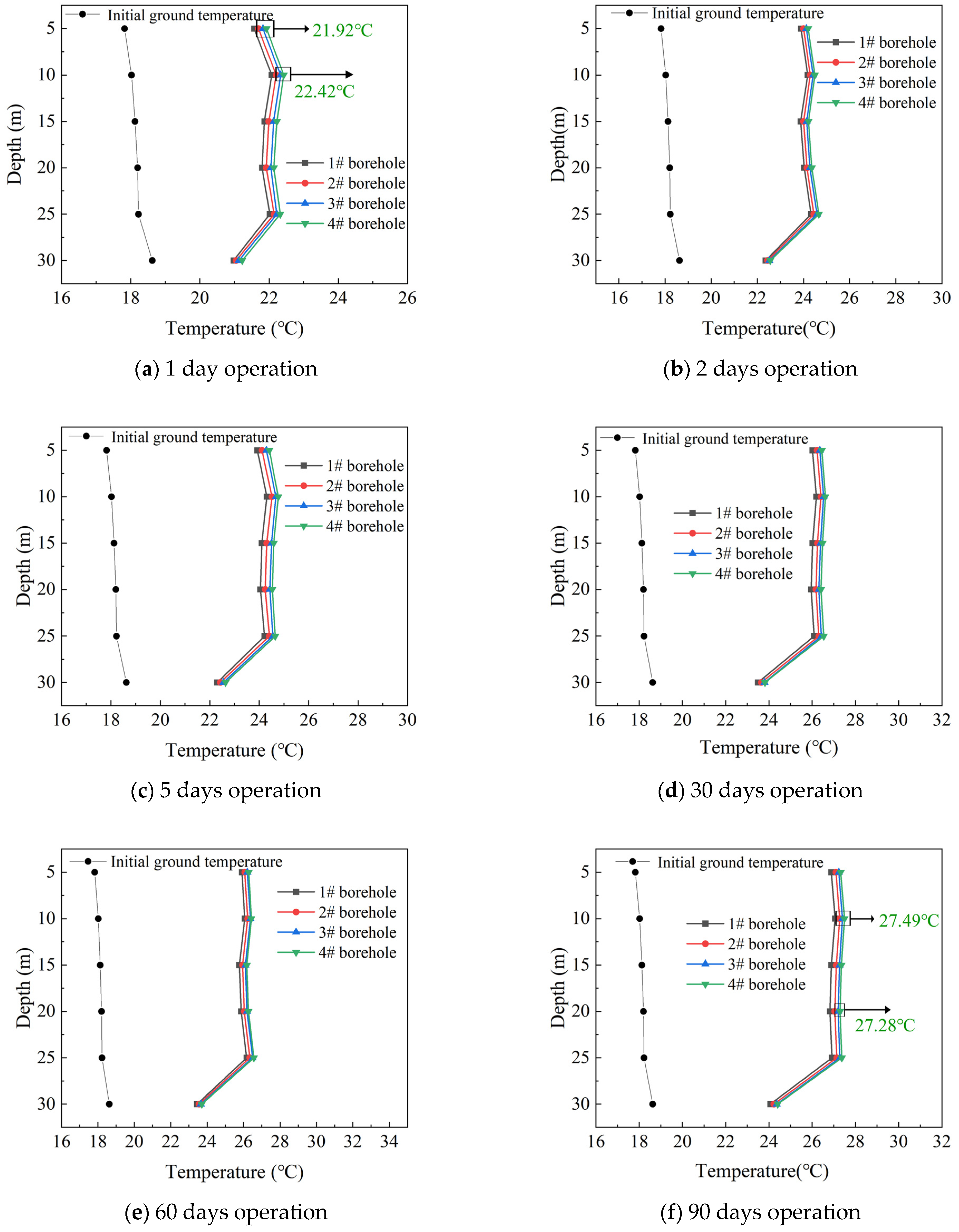
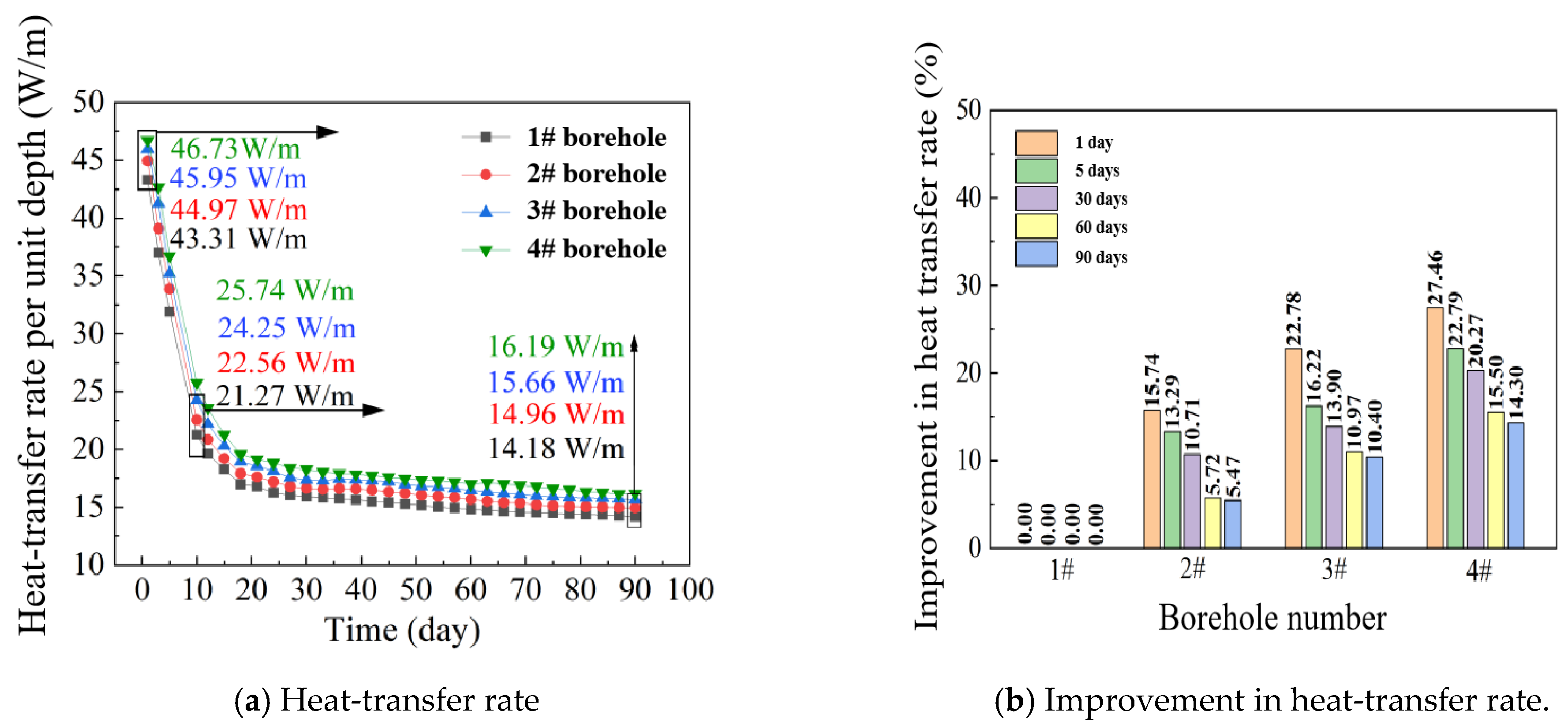
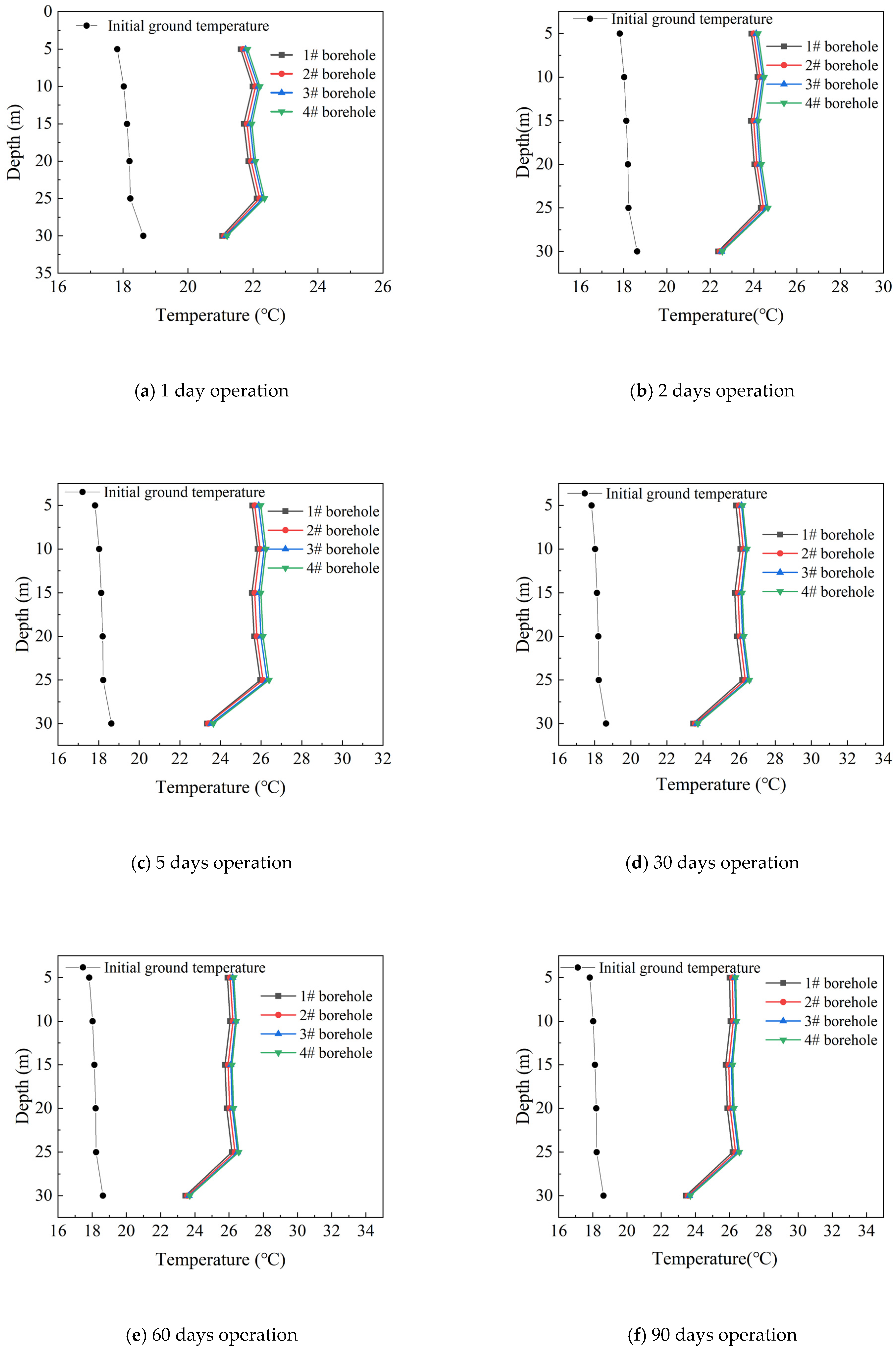
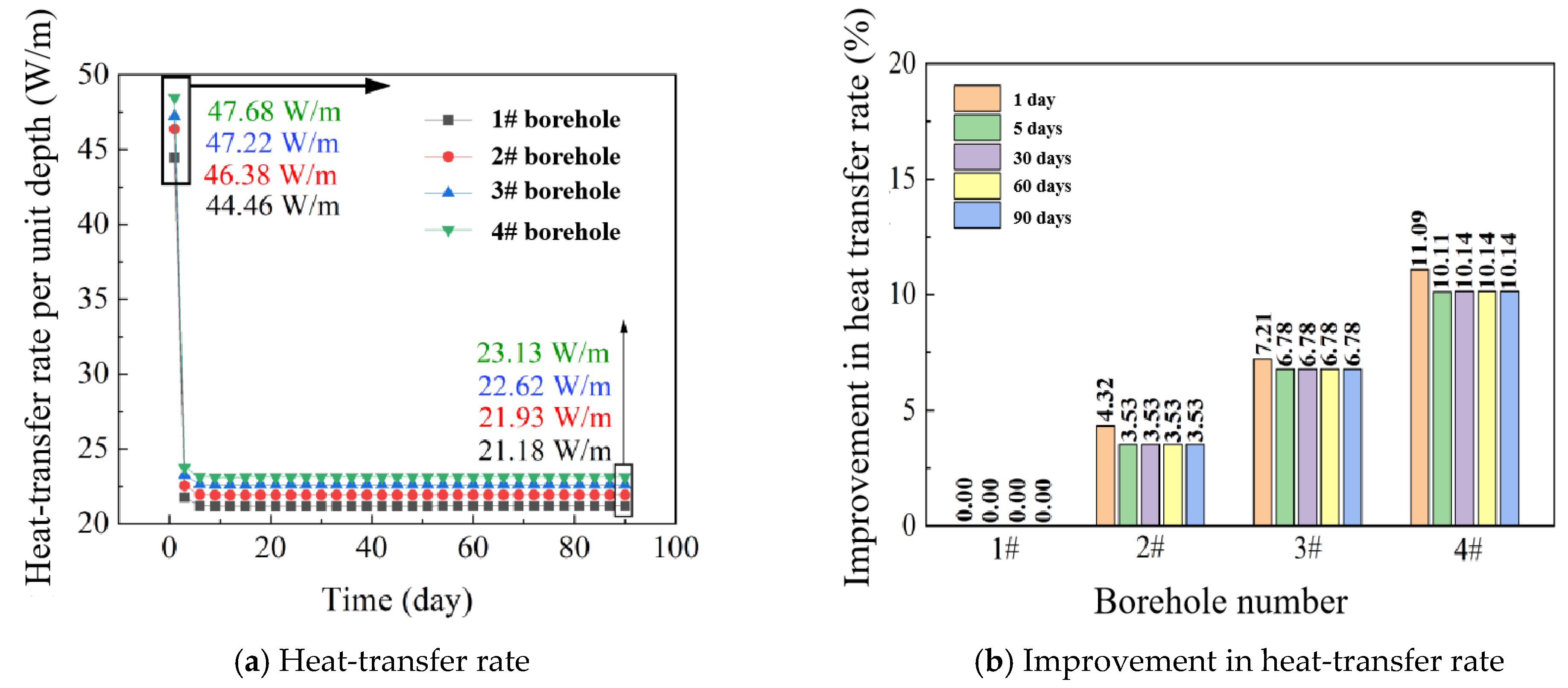
6.1. Long-Term Performance Analysis
6.1.1. Methodology
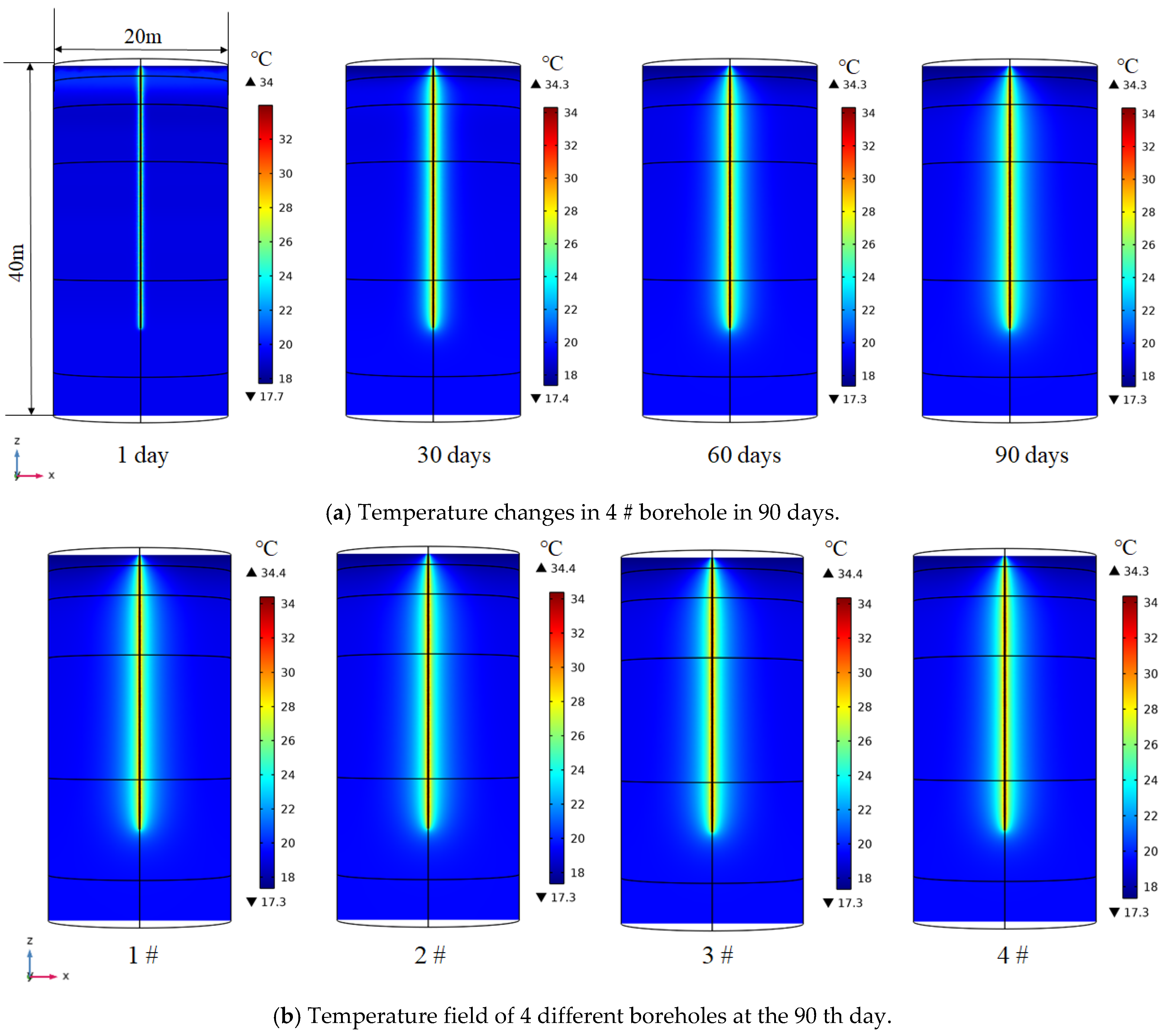
6.1.2. Results and discussion
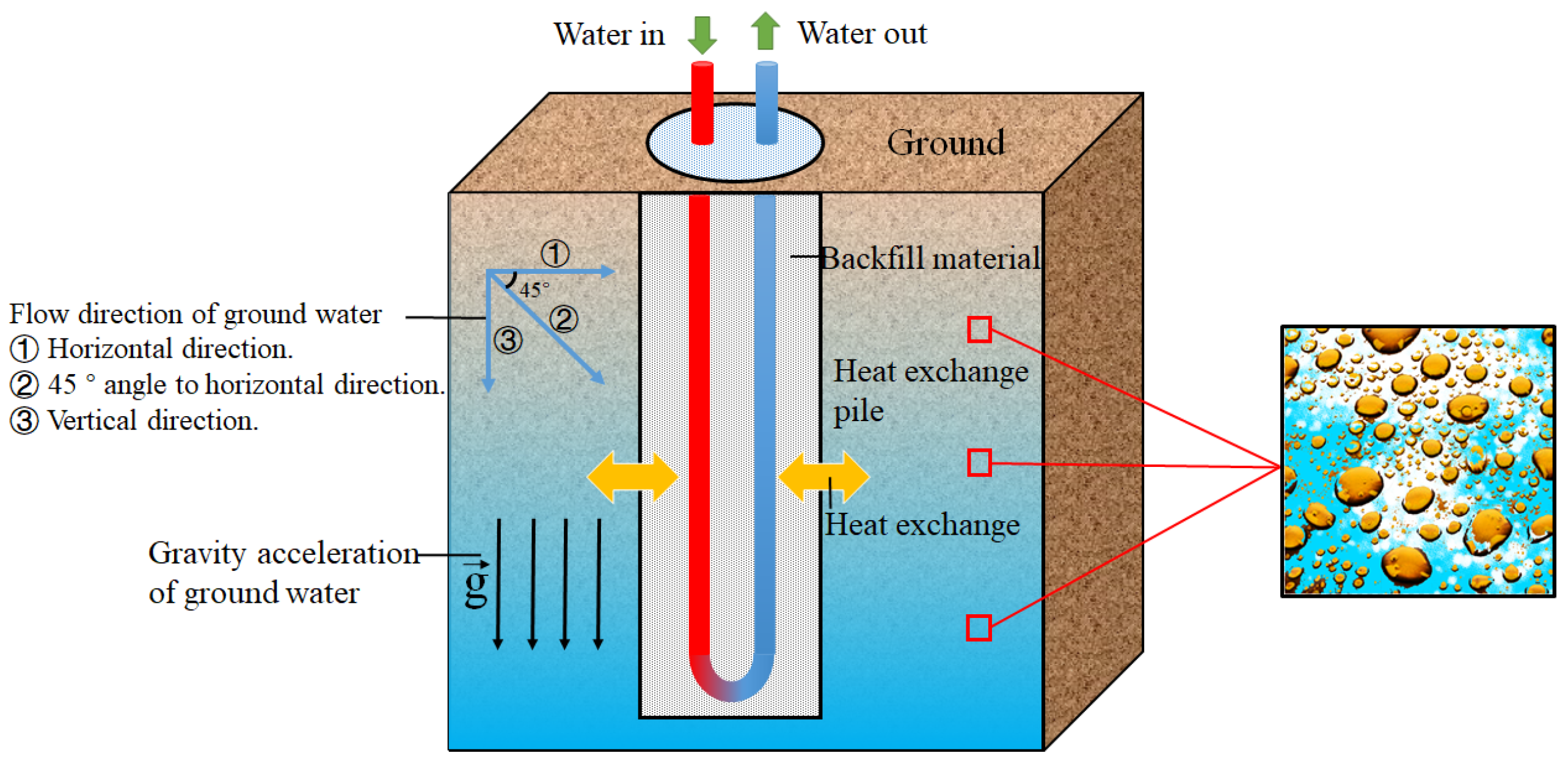
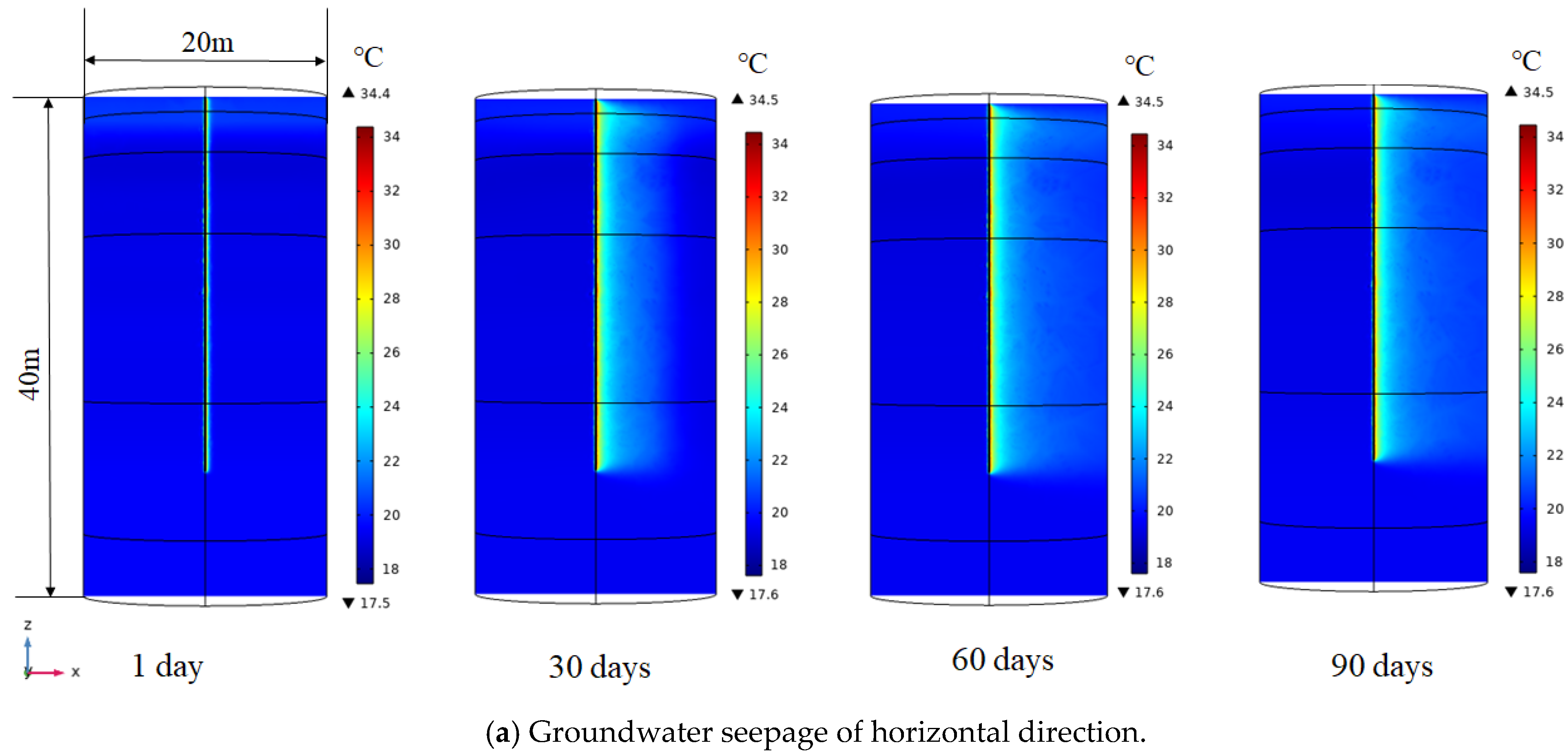
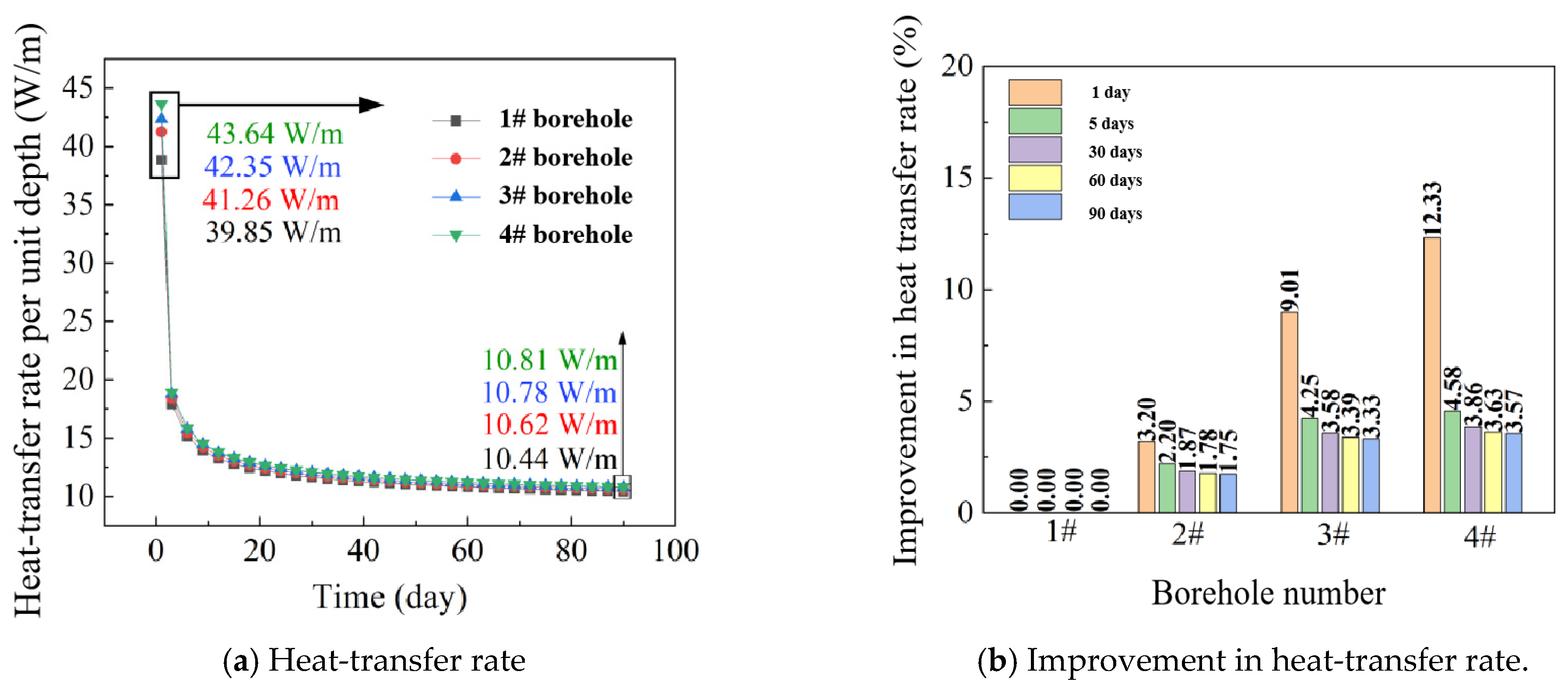
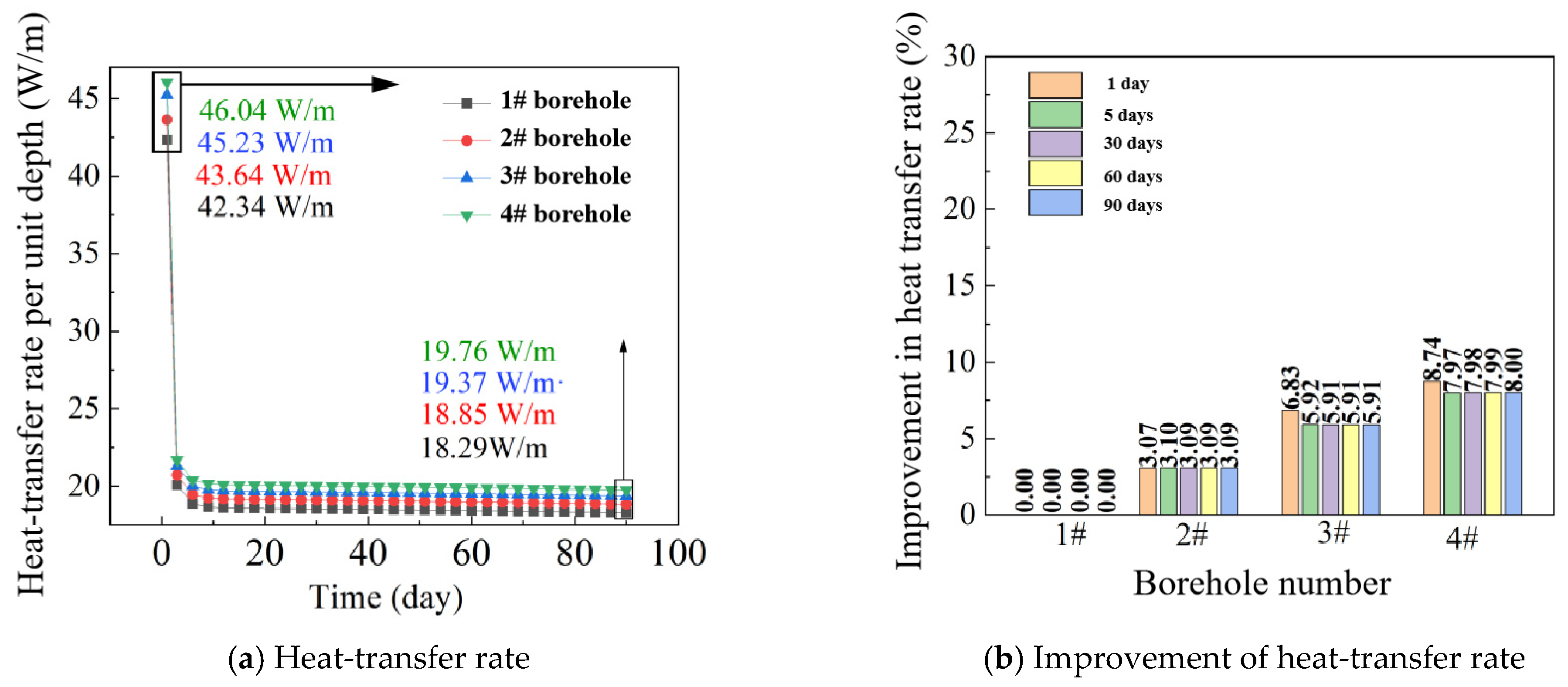
6.2. Influence of Groundwater
6.2.1. Methodology
6.2.2. Results and Discussion
7. Conclusions
- The results of the laboratory tests have shown that graphite could improve the thermal property of cement/fly ash mortar to a relatively high level, in which the thermal conductivity reached 2.317 and 2.391 W/(m K) when the mass ratios of graphite were 5% and 10%, respectively. Then, the numerical model’s accuracy was verified through field tests, with an average outlet temperature of 0.21~0.45 °C and root mean square error of 0.31~0.47 °C, which could be used for long-term performance analysis.
- The long-term heat-transfer rates of four boreholes were evaluated, in which the values of the four boreholes initially decreased from 43.31 for 1#, 44.97 for 2#, 45.95 for 3#, and 46.73 W/m for 4# and then again to 14.18 W/m, 14.96 W/m, 15.66 W/m, and 16.19 W/m, respectively after 90 days operation. A relatively large decline was observed during the first 10 days, then the declines in heat transfer tended to stabilize, and the differences in heat transfer between boreholes gradually reduced.
- Different seepage directions have significant influences on the long-term heat-transfer performance. Horizontal groundwater seepage could take away the heat accumulation generated in the heat-transfer process over time, maintaining a high heat-transfer efficiency during the long-term operation period. The heat-transfer rate in 4# borehole was 23.13 W/m after 90 days of operation, which was still higher than that of 21.18 W/m in the 1# borehole. Vertical groundwater seepage could reduce the overall heat-transfer rates.
- 4.
- The energy-saving potential of ground source heat pumps should be analyzed by reusing high-thermal-conductivity waste materials as backfill materials.
- 5.
- Further assessment of the environmental impact is needed.
- 6.
- Evaluation of the economic benefits is necessary.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Cross-sectional area of pipe, m2. | |
| Specific heat capacity of fluid within the pipe, J/(kg K). | |
| Specific heat capacity of groundwater, J/(kg K). | |
| Specific heat capacity of solid material, J/(kg K). | |
| Specific heat capacity of soil, J/(kg K). | |
| Mean hydraulic diameter, m. | |
| Outer diameter of pipe, m. | |
| Inner diameter of pipe, m. | |
| Darcy friction factor of fluid. | |
| Acceleration of gravity, m/s2. | |
| Heat-transfer coefficient, W/(m2 K). | |
| Convective heat-transfer coefficient, W/(m2 K). | |
| Internal film heat-transfer coefficient of pipe, W/(m2 K). | |
| Depth of borehole, m. | |
| Average error of sample. | |
| Fluid pressure of groundwater, Pa. | |
| Pressure of fluid, Pa. | |
| Prandtl number. | |
| Heat-transfer rate of GHE, W. | |
| Heat-transfer rate of GHE per meter, W/m. | |
| Source term due to heat transfer with the surroundings through the pipe wall, W/m. | |
| Heat-transfer flux at the upper boundary, W/m2. | |
| Mass flow rate of fluid within the pipe, kg/s. | |
| n | Sample size. |
| Nusselt number. | |
| General heat source term of mass (mass source), W/m3. | |
| General heat source term of solid material, W/m3. | |
| General heat source term of soil, W/m3. | |
| Reynolds number. | |
| Root mean square error. | |
| Temperature of fluid within the pipe, °C. | |
| Inlet temperature of fluid, °C. | |
| Outlet temperature of fluid, °C. | |
| Temperature of solid material, °C. | |
| Air temperature around the ground surface, °C. | |
| Exterior temperature outside the pipe, °C. | |
| Initial ground temperature, °C. | |
| Soil temperature, °C. | |
| Time, s. | |
| Velocity of fluid within the pipe, m/s. | |
| Groundwater velocity, m/s. | |
| Pipe wall perimeter, m. | |
| Greek Letters | |
| Soil porosity. | |
| Volume fraction of different phase. | |
| Thermal conductivity of fluid within the pipe, W/(m K). | |
| Thermal conductivity of pipe, W/(m K). | |
| Thermal conductivity of solid material, W/(m K). | |
| Thermal conductivity of soil, W/(m K). | |
| Density of fluid within the pipe, kg/m3. | |
| Density of solid material, kg/m3. | |
| Density of groundwater, kg/m3. | |
| Density of soil, kg/m3. | |
| Penetration of soil. | |
| Fluid dynamic viscosity, Pa s. | |
| Dynamic viscosity of groundwater, Pa s. | |
References
- Ouerghi, F.H.; Omri, M.; Nisar, K.S.; El-Aziz, R.M.A.; Taloba, A.I. Investigating the potential of geothermal energy as a sustainable replacement for fossil fuels in commercial buildings. Alex. Eng. J. 2024, 97, 215–229. [Google Scholar] [CrossRef]
- Verma, V.; Meena, C.S.; Thangavel, S.; Kumar, A.; Choudhary, T.; Dwivedi, G. Ground and solar assisted heat pump systems for space heating and cooling applications in the northern region of India-A study on energy and CO2 saving potential. Sustain. Energy Technol. Assess. 2023, 59, 103405. [Google Scholar] [CrossRef]
- Ashrafi, N.; Ahmadi, R.; Zahedi, A. Technical, economical, and environmental scenario based modeling of the building equipped with ground source heat pump (GSHP) and solar system. Energy Build. 2023, 289, 113048. [Google Scholar] [CrossRef]
- Rashid, L.F.; Dhaidan, N.S.; Hussein, A.K.; Al-Mousawi, F.N.; Younis, O. Ground heat exchanger in different configuration: Review of recent advances and development. Geoenergy Sci. Eng. 2023, 227, 211872. [Google Scholar] [CrossRef]
- Saeidi, R.; Karimi, A.; Noorollahi, Y. The novel designs for increasing heat transfer in ground heat exchangers to improve geothermal heat pump efficiency. Geothermics 2024, 116, 102844. [Google Scholar] [CrossRef]
- Maghrabie, H.M.; Abdeltwab, M.M.; Tawfik, M.H.M. Ground-source heat pumps (GSHPs): Materials, models, applications, and sustainability. Energy Build. 2023, 299, 113560. [Google Scholar] [CrossRef]
- Dai, Y.; Lu, Y.; Sun, Y.; Shi, N. Analysis of heat transfer performance and study of optimum design on geothermal exchanger of ground-source heat pump. Appl. Energy Technol. 2011, 1, 1–5. [Google Scholar]
- Zhang, H.; Han, Z.; Lim, X.; Ji, M.; Zhang, X.; Li, G.; Yang, L. Study on the influence of borehole spacing considering groundwater flow and freezing factors on the annual performance of the ground source heat pump. Appl. Therm. Eng. 2021, 182, 116042. [Google Scholar] [CrossRef]
- Law, Y.L.E.; Dworkin, S.B. Characterization of the effects of borehole configuration and interference with long term ground temperature modelling of ground source heat pumps. Appl. Energy 2016, 179, 1032–1047. [Google Scholar] [CrossRef]
- Bu, X.; Jiang, K.; Li, H.; Wang, L. Performance analysis of deep borehole heat exchanger through filling leakage formation using high thermal conductivity material. Acta Geol. Sin. 2020, 94, 2139–2146. [Google Scholar]
- Liao, L. Numerical study on heat transfer performance of the backfill material of vertical U-tube. Protect. Eng. 2018, 40, 16–21. (In Chinese) [Google Scholar]
- Li, Q.; Yin, Y.; Kong, L.; Qiao, L. Enhancing heat transfer in the heat exchange medium of energy piles. J. Build. Eng. 2021, 40, 102375. [Google Scholar] [CrossRef]
- Castán-Fernández, C.; Marcos-Robredoa, G.; Castro-García, M.P.; Rey-Ronco, M.A.; Alonso-Sanchez, T. Development of a dry mortar with nanosilica and different types of industrial waste for the application in borehole heat exchangers. Constr. Build. Mater. 2022, 359, 129511. [Google Scholar] [CrossRef]
- Lee, C.; Park, M.; Min, S.; Kang, S.-H.; Sohn, B.; Choia, H. Comparison of effective thermal conductivity in closed-loop vertical ground heat exchangers. Appl. Therm. Eng. 2011, 31, 3669–3676. [Google Scholar] [CrossRef]
- Hou, H.; Zhang, S.; Guo, D.; Su, L.; Xu, H. Synergetic benefits of pollution and carbon reduction from fly ash resource utilization-Based on the life cycle perspective. Sci. Total Environ. 2023, 903, 166197. [Google Scholar] [CrossRef] [PubMed]
- Liang, B.; Chen, M.; Orooji, Y. Effective parameters on the performance of ground heat exchangers: A review of latest advances. Geothermics 2022, 98, 102283. [Google Scholar] [CrossRef]
- Kim, D.; Kim, G.; Kim, D.; Baek, H. Experimental and numerical investigation of thermal properties of cement-based grouts used for vertical ground heat exchanger. Renew. Energy 2017, 112, 260–267. [Google Scholar] [CrossRef]
- Erol, S.; François, B. Efficiency of various grouting materials for borehole heat exchangers. Appl. Therm. Eng. 2014, 70, 788–799. [Google Scholar] [CrossRef]
- Blázquez, C.S.; Martín, A.F.; Nieto, I.M.; García, P.C.; Pérez, L.S.S.; Aguilera, D.G. Analysis and study of different grouting materials in vertical geothermal closed-loop systems. Renew. Energy 2017, 114, 1189–1200. [Google Scholar] [CrossRef]
- Treviño, R.B.; Muñoz, P.P.; Pérez, M.Á.C.; Fresno, D.C. Freeze thaw durability of cement-based geothermal grouting materials. Constr. Build. Mater. 2014, 55, 390–397. [Google Scholar] [CrossRef]
- Alrtimi, A.A.; Rouainia, M.; Manning, D.A.C. Thermal enhancement of PFA-based grout for geothermal heat exchangers. Appl. Therm. Eng. 2013, 54, 559–564. [Google Scholar] [CrossRef]
- Delaleux, F.; Py, X.; Olives, R.; Dominguez, A. Enhancement of geothermal borehole heat exchangers performances by improvement of bentonite grouts conductivity. Appl. Therm. Eng. 2012, 33, 92–99. [Google Scholar] [CrossRef]
- Muoñz, P.P.; Vega, I.I.; Barraza, D.Z.; Fresno, D.C. Experimental analysis of enhanced cement-sand-based geothermal grouting materials. Constr. Build. Mater. 2018, 185, 481–488. [Google Scholar]
- Lee, C.; Park, M.; Nguyen, T.-B.; Sohn, B.; Choi, J.M.; Choi, H. Performance evaluation of closed-loop vertical ground heat exchangers by conducting in-situ thermal response tests. Renew. Energy 2012, 42, 77–83. [Google Scholar] [CrossRef]
- Do, T.M.; Kim, H.-K.; Kim, M.-J.; Kim, Y.-S. Utilization of controlled low strength material (CLSM) as a novel grout for geothermal systems: Laboratory and field experiments. J. Build. Eng. 2020, 29, 101110. [Google Scholar] [CrossRef]
- Cao, Z.; Zhang, G.; Liu, Y. Thermal performance analysis and assessment of PCM backfilled precast high-strength concrete energy pile under heating and cooling modes of building. Appl. Therm. Eng. 2022, 216, 119144. [Google Scholar] [CrossRef]
- Zhou, K.; Mao, J.; Li, Y.; Hua, Z. Comparative study on thermal performance of horizontal ground source heat pump systems with Dirichlet and Robin boundary conditions on ground surface. Energy Convers. Manag. 2020, 225, 113469. [Google Scholar] [CrossRef]
- COMSOL Multiphysics, User’s Guide; COMSOL: Stockholm, Sweden, 2020.
- Churchill, S.W. Friction factor equations span all fluid-flow regimes. Chem. Eng. 1977, 84, 91–92. [Google Scholar]
- Dinh, B.H.; Go, G.-H.; Kim, Y.-S. Performance of a horizontal heat exchanger for ground heat pump system: Effects of groundwater level drop with soil-water thermal characteristics. Appl. Therm. Eng. 2021, 195, 117203. [Google Scholar] [CrossRef]
- Go, G.H.; Lee, S.R.; Yoon, S.; Kang, H.B. Design of spiral coil PHC energy pile considering effective borehole thermal resistance and groundwater advection effects. Appl. Energy 2014, 125, 165–178. [Google Scholar] [CrossRef]
- Zhang, G.; Guo, Y.; Zhou, Y.; Ye, M.; Chen, R.; Zhang, H.; Yang, J.; Chen, J.; Zhang, M.; Lian, Y.; et al. Experimental study on the thermal performance of tunnel lining GHE under groundwater flow. Appl. Therm. Eng. 2016, 106, 784–795. [Google Scholar] [CrossRef]
- Tiwari, A.K.; Basu, P. Interpretation of TRT data in the presence of natural convection and groundwater flow in saturated ground. Comput. Geotech. 2021, 140, 104426. [Google Scholar] [CrossRef]
- Sani, A.K.; Singh, R.M. Response of unsaturated soils to heating of geothermal energy pile. Renew. Energy 2020, 147, 2618–2632. [Google Scholar] [CrossRef]
- Zhang, G.; Cao, Z.; Liu, Y.; Chen, J. Field Test and Numerical Simulation on the Long-Term Thermal Response of PHC Energy Pile in Layered Foundation. Sensors 2021, 21, 3873. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, G.; Liu, S. Investigation on the thermal response of full-scale PHC energy pile and ground temperature in multi-layer strata. Appl. Therm. Eng. 2018, 143, 836–848. [Google Scholar] [CrossRef]
- Ma, Q.J.; Wang, P.J. Underground solar energy storage via energy piles. Appl. Energy 2020, 261, 114361. [Google Scholar] [CrossRef]
- Choi, W.; Ooka, R. Effect of natural convection on thermal response test conducted in saturated porous formation: Comparison of gravel-backfilled and cement-grouted borehole heat exchangers. Renew. Energy 2016, 96, 891–903. [Google Scholar] [CrossRef]
- Pandey, U.; Basu, D. Effect of groundwater flow on thermal performance of SBTES systems. J. Energy Storage 2023, 74, 109375. [Google Scholar] [CrossRef]
- Angelotti, A.; Alberti, L.; Licata, I.; La Antelmi, M. Energy performance and thermal impact of a Borehole Heat Exchanger in a sandy aquifer: Influence of the groundwater velocity. Energy Conv. Manag. 2014, 77, 700–708. [Google Scholar] [CrossRef]
- Guo, L.; Zhang, J.; Li, Y.; McLennan, J.; Zhang, Y.; Jiang, H. Experimental and numerical investigation of the influence of groundwater flow on the borehole heat exchanger performance: A case study from Tangshan, China. Energy Build. 2021, 248, 111199. [Google Scholar] [CrossRef]
- Michalski, A.; Klitzsch, N. Temperature sensor module for groundwater flow detection around borehole heat exchangers, Geotherm. Energy 2018, 6, 15. [Google Scholar]



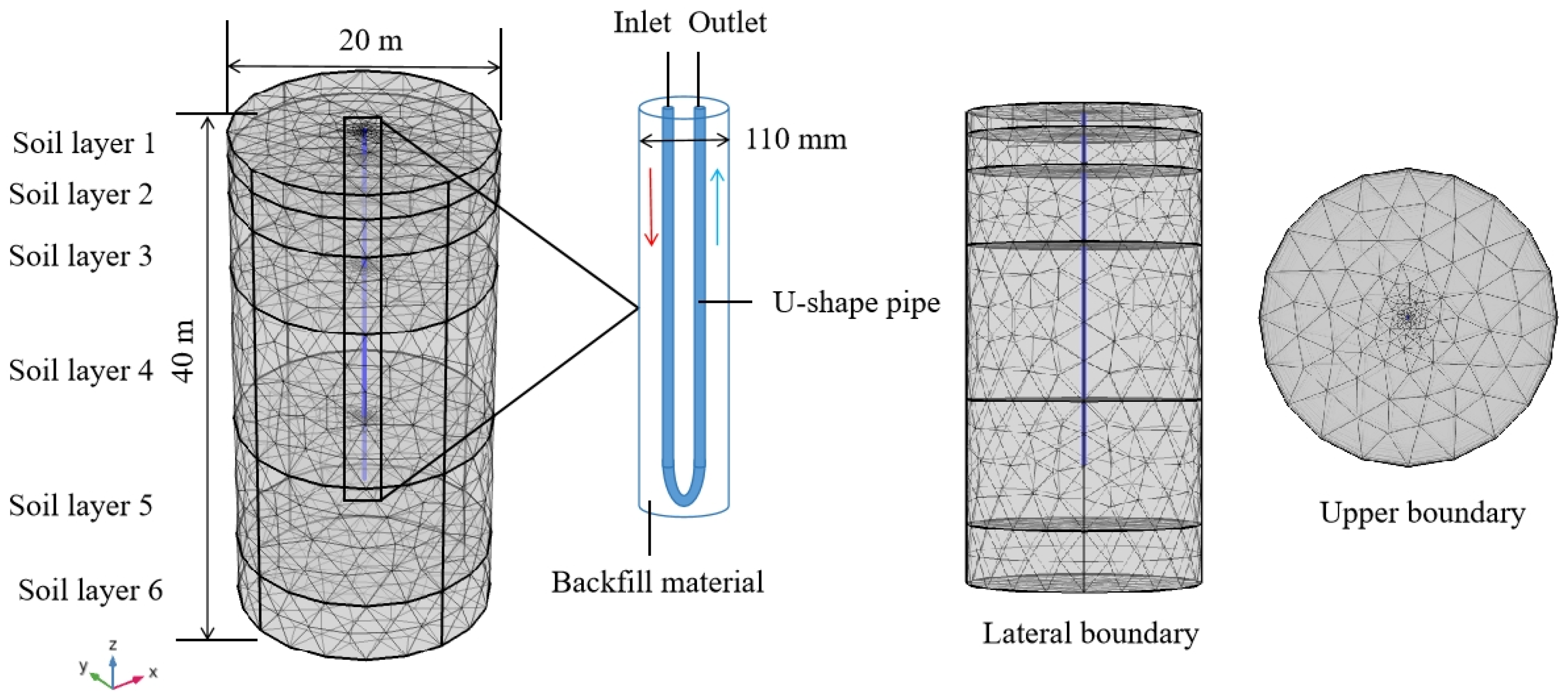

| Borehole Number | Natural Sand | Cement | Fly Ash | Graphite Powder | Water |
|---|---|---|---|---|---|
| 1# | 100 | / | / | / | / |
| 2# | 48 | 5 | 30 | 0 | 17 |
| 3# | 48 | 5 | 25 | 5 | 17 |
| 4# | 48 | 5 | 20 | 10 | 17 |
| Backfill Material in Different Borehole | Thermal Conductivity (W/(m K)) | Specific Heat Capacity (J/(kg K)) | Density (kg/m3) |
|---|---|---|---|
| 1# | 1.620 | 906 | 1420 |
| 2# | 1.933 | 882 | 1955 |
| 3# | 2.317 | 966 | 1870 |
| 4# | 2.391 | 982 | 1855 |
| Soil Layer | Depth Range (m) | Thermal Conductivity (W/(m K)) | Specific Heat Capacity (J/(kg K)) | Density (kg/cm3) |
|---|---|---|---|---|
| Backfill soil | 0–1.9 | 1.66 | 882 | 1780 |
| Silty clay | 1.9–5.0 | 1.73 | 992 | 1830 |
| Silty soil | 5.0–11.3 | 1.61 | 912 | 1750 |
| Silty clay | 11.3–24.4 | 1.75 | 986 | 1870 |
| Silty soil | 24.4–30.0 | 1.71 | 923 | 1850 |
| Borehole Number/ Depth (m) | 1# | 2# | 3# | 4# |
|---|---|---|---|---|
| 2 | 20.1 | 19.5 | 19.8 | 20.2 |
| 4 | 18.8 | 18.1 | 18.6 | 18.0 |
| 6 | 17.5 | 17.9 | 18.1 | 17.8 |
| 8 | 17.7 | 18.1 | 18.3 | 17.9 |
| 10 | 17.9 | 18.1 | 18.3 | 17.8 |
| 12 | 18.1 | 18.2 | 18.1 | 17.8 |
| 14 | 18.3 | 18.2 | 18.1 | 17.9 |
| 16 | 18.2 | 18.2 | 18.3 | 17.8 |
| 18 | 18.2 | 18.3 | 18.3 | 17.9 |
| 20 | 18.2 | 18.3 | 18.3 | 18.0 |
| 25 | 18.1 | 18.3 | 18.4 | 18.1 |
| 30 | 18.3 | 18.5 | 18.5 | 19.2 |
| Average ground temperature | 18.25 | 18.35 | 18.44 | 18.38 |
| Error Calculation Method | 1# | 2# | 3# | 4# |
|---|---|---|---|---|
| Average error (°C), ME | 0.32 | 0.21 | 0.41 | 0.45 |
| Root mean square error (°C), S | 0.47 | 0.31 | 0.42 | 0.43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, R.; Chen, P.; Liu, X.; Xu, H.; Zhang, G.; Chen, A. Investigation of the Long-Term Performance of Waste Backfill Materials of High Thermal Conductivity in Vertical Ground Heat Exchangers. Buildings 2024, 14, 1699. https://doi.org/10.3390/buildings14061699
Wu R, Chen P, Liu X, Xu H, Zhang G, Chen A. Investigation of the Long-Term Performance of Waste Backfill Materials of High Thermal Conductivity in Vertical Ground Heat Exchangers. Buildings. 2024; 14(6):1699. https://doi.org/10.3390/buildings14061699
Chicago/Turabian StyleWu, Ruichun, Panpan Chen, Xinye Liu, Haiqiang Xu, Guozhu Zhang, and Ankang Chen. 2024. "Investigation of the Long-Term Performance of Waste Backfill Materials of High Thermal Conductivity in Vertical Ground Heat Exchangers" Buildings 14, no. 6: 1699. https://doi.org/10.3390/buildings14061699
APA StyleWu, R., Chen, P., Liu, X., Xu, H., Zhang, G., & Chen, A. (2024). Investigation of the Long-Term Performance of Waste Backfill Materials of High Thermal Conductivity in Vertical Ground Heat Exchangers. Buildings, 14(6), 1699. https://doi.org/10.3390/buildings14061699






