Abstract
The study presents a novel meshed horizontal–vertical (H–V) geogrid, offering promising advancements in geotechnical structure performance. The study pioneers a modeling approach for H–V geogrid foundation bearing capacity with discrete element method, expanding understanding and optimizing design strategy. By analyzing the granular displacement, contact force distribution, and vertical stress distribution within the foundation system, the study examines the impact of burial depth, vertical element height, and the number of vertical elements on H–V reinforced foundations. The findings suggest that employing a burial depth equivalent to the width of the footing enhances bearing capacity compared to conventional geogrid applications, with depths set at 0.4 times the width of the footing. This enhancement is attributed to forming a deeper slip surface in H–V systems. Moreover, raising vertical elements to 0.6 times the width of the footing enhances bearing capacity with minimal increase in geogrid usage, indicating a strategic approach to reinforcement. Increasing the number of vertical elements, particularly with three pairs, significantly enhances bearing capacity by reinforcing lateral restraint on the soil and promoting stress homogenization, thereby augmenting the “deep-footing” effect. The technical analysis underscores the efficacy of H–V geogrids in bolstering the bearing capacity of reinforced foundations, which is attributed to the robust grip and interlocking mechanism facilitated by these geogrids’ vertical ribs and mesh structure, which augment lateral confinement and diminish horizontal soil displacement.
1. Introduction
The field of geotechnical engineering has long been concerned with the stability and load-bearing capacity of soil structures reinforced with geogrids [,,,,]. The interface strength between the geogrid and soil is a critical factor in determining the effectiveness of such reinforcement systems [,,]. Insufficient interface strength can lead to premature failure, posing risks to the stability of structures [,,]. Researchers have explored various strategies to enhance reinforcement effectiveness to address challenges associated with inadequate geogrid–soil interface strength [,,,]. Chen et al. [] have indicated that geogrids can significantly enhance peak shear strength by restricting lateral expansion within the reinforced area, effectively reducing the sensitivity of gravel to volumetric expansion. The research findings conducted by Poorahong et al. [] indicate that the number of geogrid layers and their placement significantly affect the ultimate bearing capacity and failure mechanism of reinforced pavements. Furthermore, the results by Du et al. [] show that as the number of geogrid layers and their width increase, there is a corresponding increase in the ultimate bearing capacity of the embankment.
One promising avenue is the development of three-dimensional reinforcement techniques. These techniques involve extending reinforcement both horizontally and vertically within the soil mass, offering the potential for improved interaction with the surrounding soil. Among the recent innovations in this area is introducing a new three-dimensional horizontal–vertical (H–V) geogrid, as depicted in Figure 1. Experimental and theoretical studies have demonstrated the superior interaction strength between H–V geogrids and soil compared to conventional geogrids []. However, despite these advancements, there is still a limited understanding of the reinforcement mechanism of H–V geogrids. This study aimed to fill this knowledge gap by investigating the bearing capacity and reinforcement mechanism of foundations reinforced with H–V geogrids. Leveraging the advanced capabilities of Particle Flow Code in three dimensions (PFC3D), an analysis of the complex behavior of H–V geogrids within the soil matrix was conducted.
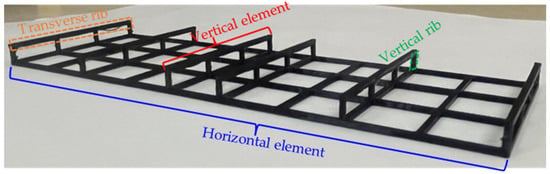
Figure 1.
Photographs of the H–V geogrid.
The study introduces a newly developed meshed H–V geogrid, which is promising to enhance geotechnical structures’ performance and stability. The study also employs a novel approach using Particle Flow Code in three dimensions (PFC3D) to model the bearing capacity of H–V geogrid foundations, thereby expanding understanding of their behavior under load and offering insights into optimizing foundation design and performance. PFC3D outperforms traditional methods like FEM and FDM for handling large deformations. Cheng et al. (2022) [] highlighted CEL as an efficient approach. The discrete element modeling accurately captures particle interactions, which are crucial for granular materials, but it requires precise parameter calibration and entails computational costs. The findings of this study are expected to contribute to the advancement of more robust and reliable reinforcement solutions for civil infrastructure projects.
2. Methodology
2.1. DEM Model
The study utilizes PFC, a widely recognized method in geotechnical engineering research grounded in Newton’s second law and force-displacement principles. This approach iteratively updates contact forces and particle positions through a temporal stepping process, applying these principles alternately [].
The PFC model of the H–V geogrid-reinforced foundation is illustrated in Figure 2. Establishing this PFC model involved four main steps. Initially, the boundaries were established by five walls. Secondly, gravity deposition generated balls, representing the soil in a randomized distribution. Thirdly, the H–V geogrid incorporated stiffness and parallel bonds capable of transmitting tensile force and moment. Lastly, a steep nine-gradient loading, referencing experimental conditions [,], was applied to the plate, representing the strip footing. Microparameters of the PFC models were determined through iterative calculations in numerical tests, employing a trial-and-error approach [,]. Concurrently, particle microparameters were continuously adjusted to align with the macro phenomena observed in model tests, as determined through soil static load tests and geogrid tensile and bending tests [,,]. Meanwhile, Chen et al. (2024) [] and Cundall and Strack (1979) [] emphasized the importance of conducting convergent analyses on parameters like mesh sizes in FEM or particle size in PFC to represent system behavior while optimizing computational resources accurately. The radius of the actual soil particle was increased by tenfold (4 mm) in the PFC model, compared to the model test, which was informed by insights from prior studies and convergence analyses by Zhao et al. (2015) [] and Feng et al. (2022) []. The stiffness of the loading plate was set at ten times the stiffness of the soil granules [,]. The loading velocity was settled at a uniform speed of 2 mm/min during the tests, according to Saha Roy and Deb (2017a, 2017b) [,]. The selection of geogrid was rooted in the model experimental findings, with a specific focus on the steel–plastic composite geogrid []. All other essential mesoscopic parameters for simulation in this study are summarized in Table 1.
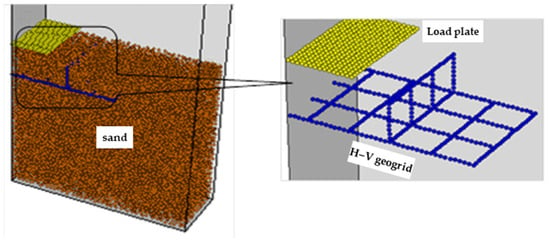
Figure 2.
PFC3D model of H–V reinforced foundation.

Table 1.
Summary of mesoscopic parameters in PFC.
Table 2 summarizes all the test cases conducted in this study. Tests 1 and 2 were designed to investigate the influence of the buried depth of the H–V geogrid on the bearing capacity of foundations. Tests 1 and 4 were devised to scrutinize the effect of the number of vertical elements in the H–V geogrid on the bearing capacity of the foundation. Tests 2 and 3 were structured to assess the impact of the height of the vertical element in the H–V geogrid on the bearing capacity of foundations.

Table 2.
Summary of study’s cases.
2.2. Boundary Condition
To expedite the PFC simulation process while staying within practical computational limits, the numerical model was streamlined by halving the dimensions of the physical specimen. This decision leveraged the inherent symmetry of the H–V geogrid-reinforced foundation model, as advocated by Wang et al. (2020) []. Additionally, insights from model tests indicate that soil particle displacement remained insignificant beyond 2.3 times the footing width (B) and a depth surpassing 2.3B []. Consequently, five walls with equivalent normal and shear stiffness to the soil particles were integrated as boundary conditions to address this issue. Figure 3 illustrates the details of the boundary conditions. The loading plate measured 0.15 m (width) × 0.598 m (length) × 0.025 m (height), while the box dimensions were 0.125 m (width) × 0.35 m (length) × 0.6 m (height). This strategic substitution effectively minimized soil particle displacement and reduced computation time.
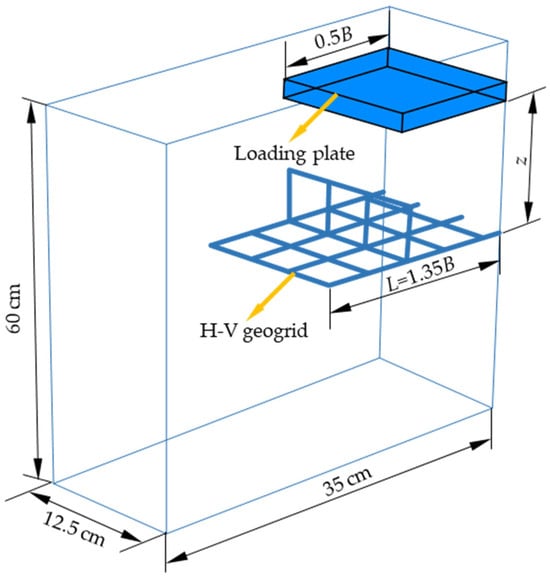
Figure 3.
Schematic diagram of sand bed reinforced with multilayer H–V geogrids.
2.3. Parameters Calibration
The soil particle parameters underwent calibration by establishing an unreinforced foundation model in PFC. Through iterative adjustments of these parameters, the obtained P-s curve from numerical simulations closely matched that of model experiments (Figure 4a). Subsequently, the tensile parameters of the geogrid were calibrated using a PPFC geogrid tensile test model. Tensile specimens, 200 mm long, were subjected to a stretching rate of 2 mm/min. Fine-tuning the geogrid’s microscopic parameters enabled the simulated sample’s tensile curve to closely align with the physical test results (see Figure 4b). The close agreement between the numerical and experimental results suggests that the calibrated PFC model parameters accurately reflect the tensile performance of the geogrids (Figure 4b). Additionally, parameters governing the bending characteristics of the geogrid were calibrated through multiple sets of bending tests (Figure 4c). After calibrating all these parameters, they were input into the PFC model of the H–V geogrid-reinforced foundation.
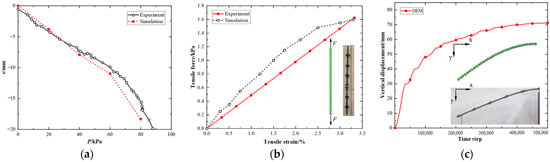
Figure 4.
Parameter calibration results: (a) the P–s curve of unreinforced foundation; (b) experimental and simulated tensile force–strain relationships of geogrid in a tensile test; (c) vertical displacement–time step relationships of DEM geogrid in bending test.
3. Results and Discussion
3.1. P–s Curves
Figure 5 depicts the pressure–settlement (P–s) curve relationship using closed symbols for all four simulated cases. The experimental test results, represented by open symbols and consistent with case 1, are provided for comparison. The observed alignment between experimental and simulation data indicates a firm agreement. The findings unequivocally demonstrate that increasing the H–V geogrid’s buried depth enhanced the bearing capacity of foundations, as evidenced by comparing the red and blue lines. Foundations buried at a depth of 1B demonstrated better bearing capacity than those buried at a depth of 0.4B, which has been identified as the optimal value in conventional geogrid–reinforced foundations [,]. Moreover, increasing the height of the vertical elements also played a significant role in improving bearing capacity. For example, foundations with vertical elements at 0.6B height demonstrated a 1.2 times greater bearing capacity than those with elements at 0.3B height, as indicated by the comparison between the black and red lines, with minimal increase in geogrid consumption. Furthermore, increasing the number of vertical elements led to a significant enhancement in bearing capacity. For instance, foundations equipped with three pairs of vertical elements exhibited a substantial 1.3 times increase compared to those featuring only one pair, as demonstrated by comparing the green and blue lines. It should be noted that this enhancement required only a modest 12% increase in geogrid consumption.
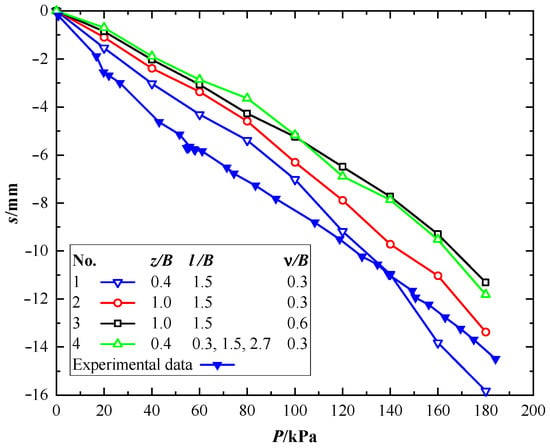
Figure 5.
The P–s curve of reinforced foundations with different H–V geogrid arrangement.
3.2. Displacement in the H–V Geogrid-Reinforced Foundation
Figure 6 illustrates the displacement distribution of the reinforced foundation with the H–V geogrid at embedment depths of 0.4B and 1.0B, respectively. Magnified views of areas A and B were further enlarged to facilitate the analysis of soil granule displacement. Comparing the orange solid arrow in Figure 6a to the dashed arrow in Figure 6b shows that increasing the embedment depth of the H–V geogrid resulted in a deeper slip surface for the footing. This is attributed to the upper soil behaving as a softer layer compared to the lower soil and significant deformation induced by shallow embedment depths potentially warping the soil surface and affecting the effectiveness of the vertical geogrid, especially near the basement. Furthermore, comparing the magnified views of Areas A and B in Figure 6c,d reveals significant differences in soil displacement patterns. When the embedment depth was 0.4B, soil deflection was observed below the H–V geogrid, gradually forming a prominent shear zone as illustrated by the orange solid arrow. However, when the embedment depth was 1B, soil predominantly moved vertically downward, with minor lateral movement towards the sides of the vertical geogrid, as illustrated by the orange dashed arrows. This phenomenon can be attributed to the confinement effect exerted by the vertical elements, suggesting that augmenting the embedment depths of the vertical H–V geogrid can bolster the shear strength of the soil, thereby potentially mitigating shear failure surfaces. This highlights that the H–V geogrid not only influences soil movement in its immediate vicinity but also alters the trajectory of soil over a wider area.
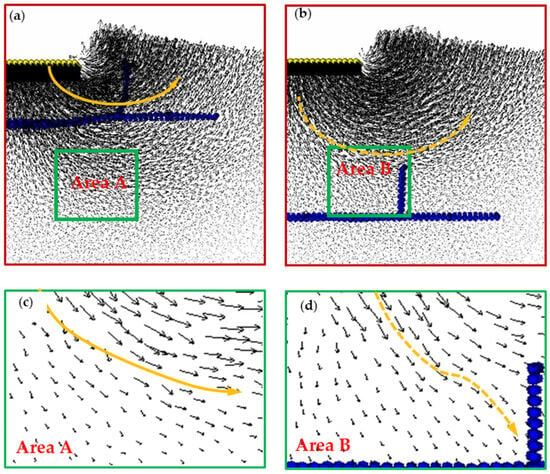
Figure 6.
Displacement distribution of reinforced footings with different H–V geogrid arrangements: (a) z = 0.4B; (b) z = 1.0B; (c) area A; (d) area B.
Figure 7a,b showcase the displacement distribution with vertical element heights of 0.3B and 0.6B in the H–V geogrid. The soil displacement with 0.6B height vertical elements (Figure 7b) displayed minimal variation and improved uniformity compared to that with 0.3B height vertical elements in Figure 7a. Further comparative analysis between the two figures reveals that the soil in Figure 7a exhibits a more pronounced slip surface (see the orange solid arrow) than that in Figure 7b (see the orange dashed arrow). This suggests that increasing the vertical element height mitigated soil displacement, aiding in the adjustment of uneven settlement and delaying the formation of slip surfaces. The magnified views of areas A and B in Figure 7c,d further highlight that soil within 0.3B height vertical elements tended to move upward to the right in Figure 7c, whereas, in Figure 7d, displacement was bifurcated, with some granules moving upward to the right and the majority moving downward to the right. This distinction underscores how the vertical elements of H–V geogrid alter the direction of soil movement, leading to a broader dispersion of soil granules. Consequently, this slows down the formation of slip surfaces and enhances the “deep-footing” effect of the H–V geogrid, as suggested by Huang et al. (1997) [].
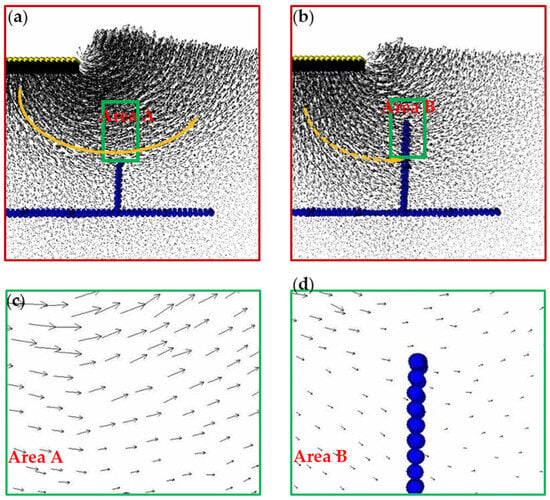
Figure 7.
Displacement distribution of reinforced foundations with different numbers and heights of vertical geogrids: (a) No. 2 ν = 0.3B; (b) No. 3 ν = 0.6B; (c) area A; (d) area B.
Figure 8a,b illustrate the displacement distribution with one pair and three pairs of vertical elements in the H–V geogrid, respectively. A comparison between the two figures shows that with three pairs of vertical elements (Figure 8b), there were notably smaller soil displacement values and surface uplift than the case with only one pair of vertical elements (Figure 8a). This indicates that increasing the number of vertical elements slowed down the formation of slip surfaces, thereby enhancing the bearing capacity of the foundations. Additionally, the deformation and inclination angle of the vertical elements are less pronounced in Figure 8b than in Figure 8a (compare solid and dashed orange arrows). This difference arose because, despite the substantial pressure on the upper part of the vertical element, the minimal difference in soil stress on both sides prevented lateral slipping. Conversely, the vertical element at the edge experienced minimal influence from soil movement due to its distance from the footing. These observations highlight the significant impact of the number and positioning of vertical elements in the H–V geogrid. The magnified views of areas A and B in Figure 8c,d further provide insights into the observation that the included angle between the movement trajectory of soil granules near the vertical elements and the vertical direction is smaller in Figure 8d compared to Figure 8c (compare solid and dashed orange ellipses). This difference is attributed to the increased number of vertical elements in Figure 8d, which exerted a more notable lateral restraint on the soil, directing its movement vertically.
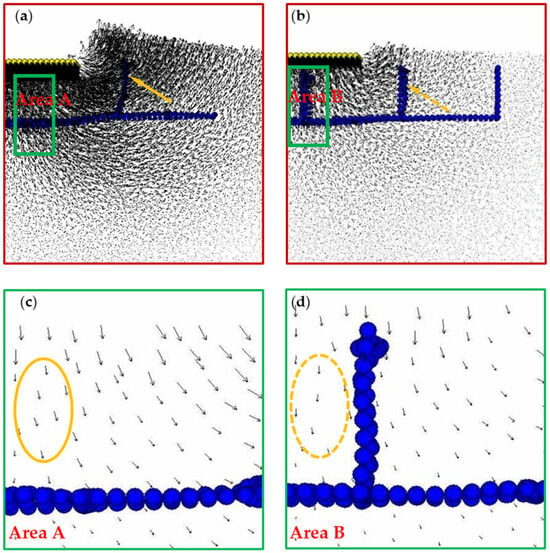
Figure 8.
Displacement distribution of reinforced foundations with different numbers and heights of vertical geogrid: (a) No. 1, 1 pair; (b) No. 4, 3 pairs; (c) area A; (d) area B.
3.3. Stress Distribution in the H–V Geogrid-Reinforced Foundation
Figure 9a,b illustrate the vertical stress distribution diagrams of the reinforced foundation with H–V geogrid within embedment depths of 0.4B and 1.0B, respectively. The black dotted line indicates the location of the loading plate, as seen in Figure 10 and Figure 11. It is indicated that the H–V geogrid-reinforced foundation with an embedment depth of 1B exhibited better stress redistribution across a wider area than the foundation with an embedment depth of 0.4B. This phenomenon may be attributed to the tighter soil compression between the footing and the H–V geogrid at smaller embedded depths. As the embedded depth of the H–V geogrid increased, the vertical stress distribution in the soil became more uniform. This uniformity can be attributed to the redistribution of overburden loading. Conversely, when the embedment depth of the H–V geogrid was shallow, it could only bear the loading within the local range of the bottom of the footing. This limitation highlights the importance of considering the appropriate embedded depth of the H–V geogrid to ensure effective load redistribution and uniform stress distribution within the reinforced foundation.
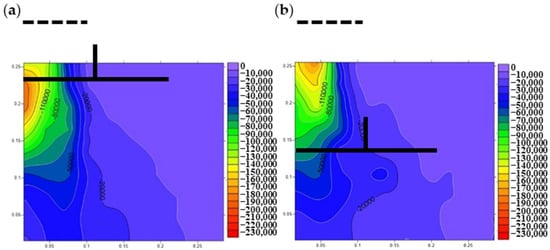
Figure 9.
Vertical stress distribution of reinforced foundations with different H–V geogrid arrangements (the black dotted line is where the loading plate was initially located): (a) No.1 z = 0.4B; (b) No. 2 z = 1.0B.
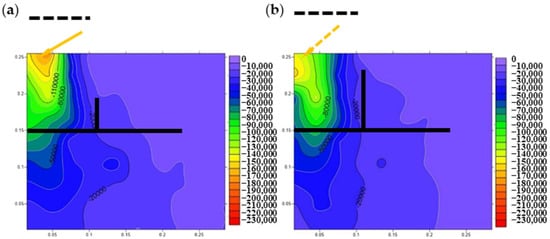
Figure 10.
Vertical stress distribution of reinforced foundations with different H–V geogrid arrangements: (a) No. 2 v = 0.3B; (b) No. 3 v = 0.6B.
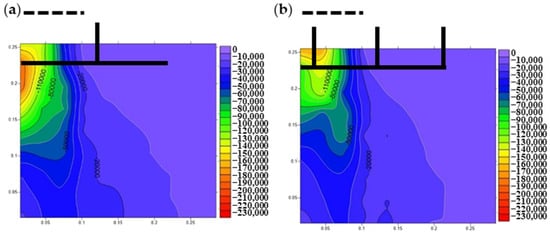
Figure 11.
Vertical stress distribution of reinforced foundations with different H–V geogrid arrangements: (a) No. 1, 1 pair; (b) No. 4, 3 pairs.
Figure 10a,b illustrate the vertical stress distribution with vertical element heights of 0.3B and 0.6B. In Figure 10a, the vertical stress isolines enclosed by the horizontal and vertical elements are almost vertical. However, increasing the height of the vertical element to 0.6B in Figure 10b resulted in a significantly smaller stress concentration area than 0.3B in Figure 10a. This is attributed to the restriction of soil movement to the right after increasing the height of the vertical element, directing more sand downward (compare solid and dashed orange arrows).
Figure 11a,b present the vertical stress distribution with one pair and three vertical elements in the H–V geogrid, respectively. Comparison of the two figures reveals that increased vertical elements promoted stress homogenization within the foundation. The vertical stress on the edge geogrid was the smallest, while the vertical stress on the vertical elements directly below the footing was the largest. The middle vertical elements experienced the densest stress isolines in three pairs of vertical elements, indicating a substantial deformation gradient in the soil within this region.
3.4. Contact Force distribution in the H–V Geogrid-Reinforced Foundation
Figure 12a,b depict the contact force diagrams for reinforced foundations with H–V geogrids embedded at depths of 0.4B and 1.0B, respectively. Comparing area A to area B, it exhibited significant differences in stress homogenization between the depths. The embedded depth of 1.0B demonstrated superior stress distribution, particularly in regions distanced from the footing. This indicates that the deeper embedding enhanced the influence of H–V geogrid on the base, creating a more cohesive and effective reinforced cushion []. Force chains exhibited almost-vertical alignment at 1.0B depth, while deflection and divergence occurred at 0.4B depth (compare solid and dashed orange arrows). This deviation from previous findings suggests that the mesh structure and vertical element components significantly minimized the force chain deflection. Increasing the H–V geogrid embedded depth enhanced the lateral restraint of reinforced area, similar to the “deep-footing” effects observed in conventional geogrids [,].

Figure 12.
The contact force of reinforced footings with different H–V geogrid arrangements: (a) No. 1 z = 0.4B; (b) No. 2 z = 1.0B; (c) area A; (d) area B.
Figure 13a,b depict the contact force diagram for vertical geogrid heights of 0.3B and 0.6B in the H–V geogrid. The magnified views of areas A and B in both figures provide detailed insights into the observations. Comparing Figure 13a,b, it is apparent that the contact force of soil in the area below the H–V geogrid showed little difference with the increase in the height of the vertical elements. However, the contact force of soil above the geogrid appeared more uniform, aligning with the stress analysis. Further examination between Figure 13c,d reveals notable differences in the contact force distribution. The contact force between the geogrid and soil primarily concentrated in the lower-left part of the vertical element at lower vertical element heights. Conversely, as the height of the vertical element increased, the contact force between the soil on the left side of the vertical element became more homogenized. This indicates that increasing the height of the vertical geogrid led to a more uniform distribution of contact force, reflecting a more even transmission of the force chain.

Figure 13.
Contact force of reinforced footing with different heights of vertical geogrid: (a) No. 2 v = 0.3B; (b) No. 3 v = 0.6B; (c) area A; (d) area B.
It should be noted that increasing the height of vertical geogrid elements plays a pivotal role in achieving a more uniform contact force distribution within a reinforced foundation system. As vertical elements are extended, they interact with a larger soil volume, enabling better stress distribution over a broader vertical section. Taller elements offer an increased surface area for load transfer and stress absorption, effectively spreading forces from the overlying structure more evenly and reducing stress concentrations that may lead to localized failures. Moreover, taller elements more effectively restrict lateral soil movements, maintaining soil structure under loading conditions and ensuring a uniform contact force distribution. This restriction is vital when soil settlement under load may occur unevenly.
Figure 14a,b depict the contact force diagram for one pair and three pairs of vertical elements within the H–V geogrid. The magnified views of areas A and B provide detailed insights into the distribution of force chains. A comparison between Figure 14a,b illustrates that the force chain within three pairs of vertical elements in Figure 14b appeared thinner and more uniform than that within one pair of vertical elements in Figure 14a, both beneath the strip footing and in the lower right area distanced from the footing. This observation suggests that increasing the vertical elements of the H–V geogrid contributed to a more homogenized stress distribution within the foundation. Further comparison between Figure 14c,d reveals significant differences in the stress distribution of soil surrounded by three pairs of vertical elements in Figure 14d compared to one pair of vertical elements in Figure 14c. The force chains on the left and right sides of the three pairs of vertical elements in Figure 14d exhibited minimal penetration, with most force chains bypassing the upper part of the vertical elements. Additionally, some force chains deflected when passing through the mesh of the vertical elements, as illustrated in Figure 14d, resembling a membrane reinforcement mechanism. This behavior is attributed to the occlusion and locking between the soil and the geogrid meshes, effectively integrating the vertical elements and adjacent soil into a cohesive whole (compare solid and dashed orange ellipses).

Figure 14.
Contact force of reinforced footing with different number of vertical bars: (a) No. 1, 1 pair; (b) No. 4, 3 pairs; (c) area A; (d) area B.
3.5. Failure Theories
The failure of foundations under load, often attributed to insufficient subsoil bearing capacity, typically presents a general and local shear failure []. When the vertical rib was small, the number was few, and the burial depth was shallow (see Figure 6a), the H–V geogrid tended to experience general shear failure while interacting with the soil. However, it is essential to note that more extended vertical ribs may induce significant uplift forces. When the vertical rib was small, the number was few, but the burial depth was deep (see Figure 6b), the H–V geogrid still leaned towards general shear failure while working with the soil. Nonetheless, there is a higher likelihood of potential local shear failure in the soil above the geogrid. When the vertical rib was more prominent, the number was few, but the burial depth was deep (see Figure 7b), the H–V geogrid primarily experienced general shear failure at deeper distances while interacting with the soil. When the vertical rib was small, the number was more, and the burial depth was shallow (see Figure 8b), the H–V geogrid behaved similarly to a “deep-footing” within the soil. Hence, in practical applications, careful consideration should be given to factors such as buried depth, vertical element height of the H–V geogrid, and the number of vertical elements. Meanwhile, it is essential to note that soil properties, such as cohesion, internal friction angle, and water content, type, and stiffness of the geogrid, were not the main focus of this study. However, these factors still need to be considered when using H–V geogrids in real-world practical engineering applications.
3.6. The Deformation of the H–V Geogrid
Figure 15a provides insights into the deformation characteristics of the H–V geogrid, focusing on both transverse and longitudinal deformation within the orange box area (the dashed red box outlines the location of the strip footing above). It is suggested that the horizontal deformation of the transverse rib was more pronounced than that of the longitudinal rib. Furthermore, comparing the deformation among the transverse ribs, it is indicated that the geogrids closer to the center of the footing experienced more significant deformation. The confinement effect of the vertical element diminished as the horizontal space from the center exceeded 1.5B. Meanwhile, the displacement pattern of the vertical element, as observed in Figure 15b, showed a gradual increase from the bottom to the top, with the displacement predominantly to the right. This movement was influenced by the connection of the bottom of the vertical element to the longitudinal geogrid, causing a clockwise movement around its bottom. Additionally, two inflection points can be observed in Figure 15b, approximately 1B (solid circle and arrow) and 1.5B (dashed circle and arrow) away from the center of the footing. These points are attributed to the rigid connections between the vertical and horizontal elements of the H–V geogrid. The bending of the vertical element caused a specific rotation angle at the rigid connection points, altering the distribution of the inverse bending points of the geogrid. This reduced the buckling degree of the horizontal element, equalizing the deformation difference of the horizontal element in the vertical direction and enhancing the uniformity of the reinforcement effect provided by the H–V geogrid.
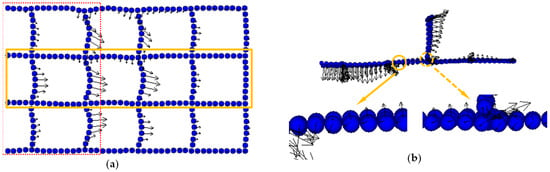
Figure 15.
The deformation of the H–V geogrid: (a) top view; (b) elevation.
4. Conclusions
This paper employed PFC to investigate the bearing capacity and reinforced mechanism of H–V reinforced geogrid foundation. The results are as follows:
- (1)
- An embedment depth equivalent to the footing width improves the bearing capacity of the H–V geogrid-reinforced foundation compared to depths of 0.4 times the footing width, which has been identified as the optimal value in conventional geogrid-reinforced foundations. This increased embedment depth creates a deeper slip surface, impacting soil movement trajectory beyond immediate effects.
- (2)
- Boosting the height of vertical elements and introducing more of them significantly improves the bearing capacity of the H–V reinforced foundation. Foundations equipped with three pairs of vertical elements experience a significant boost, reaching 1.3 times the capacity compared to just one pair, and raising the vertical elements to 0.6 times the width of the footing results in 1.2 times the increase in capacity compared to those set at 0.3 times the footing width, with only a modest 12% uptick in geogrid usage. This underscores the strategic and economically beneficial reinforcement of vertical elements.
- (3)
- The vertical elements increase lateral restraint on the soil, reducing its movement and enhancing the “deep-footing” effect of the H–V geogrid. Heightened vertical elements also decrease soil displacement, aid in settling unevenness, and delay slip surface formation. They ensure uniform horizontal stress distribution during footing loading and minimize force chain deflection. Increasing the embedded depth of the H–V geogrid further strengthens lateral restraint, akin to conventional geogrids.
- (4)
- The H–V geogrid analysis reveals that transverse ribs deform more prominently near the footing’s center than longitudinal ribs. The confinement effect of vertical elements weakens with increasing horizontal distance from the center. Displacement of vertical elements rises from bottom to top, mainly towards the right, influenced by their connection to the longitudinal geogrid. Inflection points at around 1B and 1.5B from the center result from rigid connections between vertical and horizontal elements, reducing buckling and ensuring uniform reinforcement across the geogrid.
- (5)
- The approach provides a comprehensive understanding of how H–V geogrids differ from conventional geogrids and influence the overall performance of the reinforced foundation system. However, it is essential to note that soil properties such as cohesion, internal friction angle, water content, and the type and properties of the geogrid can significantly influence the bearing capacity of the H–V geogrid-reinforced foundation. Further investigation is warranted before its application in real-world practical engineering projects.
Author Contributions
Conceptualization, J.H.; methodology, J.W., F.Z. and J.H.; data curation writing—original draft preparation, J.W., F.Z., L.G. and J.H.; writing—review and editing, J.H.; visualization, J.W. and F.Z.; project administration, J.W. All authors have read and agreed to the published version of the manuscript.
Funding
Qinghai Provincial Department of Transportation Science and Technology Project (2022–02) provided financial support for Wu’s contributions to this study.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
Authors Jinjun Wu, Fabin Zhang and Liang Gao were employed by the company Qinghai Transportation Planning and Design Institute Co., Ltd. The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Latha, G.M.; Venkateswarlu, H.; Krishna, A. Geocell Anchor Cage for enhanced load support in soil structures. Constr. Build. Mater. 2024, 425, 135998. [Google Scholar] [CrossRef]
- Dash, S.K.; Sireesh, S.; Sitharam, T.G. Model studies on circular footing supported on geocell reinforced sand underlain by soft clay. Geotext. Geomembr. 2003, 21, 197–219. [Google Scholar] [CrossRef]
- Zhang, M.X.; Javadi, A.A.; Min, X. Triaxial tests of sand reinforced with 3D inclusions. Geotext. Geomembr. 2006, 24, 201–209. [Google Scholar] [CrossRef]
- Boushehrian, A.H.; Hataf, N.; Ghahramani, A. Modeling of the cyclic behavior of shallow foundations resting on geomesh and grid-anchor reinforced sand. Geotext. Geomembr. 2011, 29, 242–248. [Google Scholar] [CrossRef]
- Makkar, F.M.; Chandrakaran, S.; Sankar, N. Behaviour of Model Square Footing Resting on Sand Reinforced with Three-Dimensional Geogrid. Int. J. Geosynth. Ground Eng. 2017, 3, 3. [Google Scholar] [CrossRef]
- Alimohammadi, H.; Zheng, J.; Schaefer, V.R.; Siekmeier, J.; Velasquez, R. Evaluation of geogrid reinforcement of flexible pavement performance: A review of large-scale laboratory studies. Transp. Geotech. 2021, 27, 100471. [Google Scholar] [CrossRef]
- Esmaeili, M.; Naderi, B.; Neyestanaki, H.K.; Khodaverdian, A. Investigating the effect of geogrid on stabilization of high railway embankments. Soils Found. 2018, 58, 319–332. [Google Scholar] [CrossRef]
- Bai, X.-H.; Huang, X.-Z.; Zhang, W. Bearing capacity of square footing supported by a geobelt-reinforced crushed stone cushion on soft soil. Geotext. Geomembr. 2013, 38, 37–42. [Google Scholar] [CrossRef]
- Xiao, C.; Gao, S.; Liu, H.; Du, Y. Case history on failure of geosynthetics-reinforced soil bridge approach retaining walls. Geotext. Geomembr. 2021, 49, 1585–1599. [Google Scholar] [CrossRef]
- Luo, F.; Huang, R.; Zhang, G. Centrifuge modeling of the geogrid-reinforced slope subjected to differential settlement. Acta Geotech. 2020, 15, 3027–3040. [Google Scholar] [CrossRef]
- Hegde, A.; Kadabinakatti, S.; Sitharam, T.G. Protection of Buried Pipelines Using a Combination of Geocell and Geogrid Reinforcement: Experimental Studies. In Ground Improvement and Geosynthetics; American Society of Civil Engineers (ASCE): Shanghai, China, 2014; pp. 289–298. [Google Scholar]
- Cicek, E.; Guler, E.; Yetimoglu, T. Effect of reinforcement length for different geosynthetic reinforcements on strip footing on sand soil. Soils Found. 2015, 55, 661–677. [Google Scholar] [CrossRef]
- Yetimoglu, T.; Wu Jonathan, T.H.; Saglamer, A. Bearing Capacity of Rectangular Footings on Geogrid-Reinforced Sand. J. Geotech. Eng. 1994, 120, 2083–2099. [Google Scholar] [CrossRef]
- Ghosh, A.; Ghosh, A.; Bera, A.K. Bearing capacity of square footing on pond ash reinforced with jute-geotextile. Geotext. Geomembr. 2005, 23, 144–173. [Google Scholar] [CrossRef]
- Bhandari, A.; Han, J. Investigation of geotextile–soil interaction under a cyclic vertical load using the discrete element method. Geotext. Geomembr. 2010, 28, 33–43. [Google Scholar] [CrossRef]
- Chen, J.; Bao, N.; Ma, C.; Sun, R. Triaxial behavior of unreinforced and geogrid-reinforced calcareous gravelly sand: Experiment and discrete element modelling. Constr. Build. Mater. 2024, 430, 136405. [Google Scholar] [CrossRef]
- Poorahong, H.; Jamsawang, P.; Thanasisathit, N.; Jongpradist, P.; Jing, G. Performance of a triaxial geogrid-reinforced crushed rock base underlain by a soft clay subgrade. Case Stud. Constr. Mater. 2024, 20, e03198. [Google Scholar] [CrossRef]
- Du, W.; Nie, R.; Qi, Y.; Ruan, B.; Mo, F. Investigation on the static performance of geogrid reinforced aeolian sand railway embankment: Field test and discrete element simulation. Geotext. Geomembr. 2024. [Google Scholar] [CrossRef]
- Hou, J.; Zhang, M.; Li, P. Simulation study of foundations reinforced with horizontal-vertical inclusions using particle flow code. J. Shanghai Jiaotong Univ. (Sci.) 2013, 18, 311–316. [Google Scholar] [CrossRef]
- Cheng, P.; Liu, Y.; Li, Y.P.; Yi, J.T. A large deformation finite element analysis of uplift behaviour for helical anchor in spatially variable clay. Comput. Geotech. 2022, 141, 104542. [Google Scholar] [CrossRef]
- Mahmood, A.A.; Elektorowicz, M. A review of discrete element method research on particulate systems. IOP Conf. Ser. Mater. Sci. Eng. 2016, 136, 012034. [Google Scholar] [CrossRef]
- Xu, F.; Moayedi, H.; Foong, L.K.; Moghadam, M.J.; Zangeneh, M. Laboratory and numerical analysis of geogrid encased stone columns. Measurement 2021, 169, 108369. [Google Scholar] [CrossRef]
- Zheng, G.; Yu, X.; Zhou, H.; Yang, X.; Guo, W.; Yang, P. Influence of geosynthetic reinforcement on the stability of an embankment with rigid columns embedded in an inclined underlying stratum. Geotext. Geomembr. 2021, 49, 180–187. [Google Scholar] [CrossRef]
- Han, J.; Bhandari, A.; Wang, F. DEM Analysis of Stresses and Deformations of Geogrid-Reinforced Embankments over Piles. Int. J. Geomech. 2012, 12, 340–350. [Google Scholar] [CrossRef]
- Ngo, N.T.; Indraratna, B.; Rujikiatkamjorn, C. DEM simulation of the behaviour of geogrid stabilised ballast fouled with coal. Comput. Geotech. 2014, 55, 224–231. [Google Scholar] [CrossRef]
- Zhou, W.; Yang, L.; Ma, G.; Chang, X.; Cheng, Y.; Li, D. Macro–micro responses of crushable granular materials in simulated true triaxial tests. Granul. Matter 2015, 17, 497–509. [Google Scholar] [CrossRef]
- Zhou, W.; Yang, L.; Ma, G.; Chang, X.; Lai, Z.; Xu, K. DEM analysis of the size effects on the behavior of crushable granular materials. Granul. Matter 2016, 18, 64. [Google Scholar] [CrossRef]
- Hou, J.; Li, H.; Liu, L.; Wang, S.; Teng, Y.; Bao, S. A DEM analysis of geomembrane-lined landfill subject to vertical loading. Geotext. Geomembr. 2021, 49, 369–375. [Google Scholar] [CrossRef]
- Chen, X.-J.; Fang, P.-P.; Chen, Q.-N.; Hu, J.; Yao, K.; Liu, Y. Influence of cutterhead opening ratio on soil arching effect and face stability during tunnelling through non-uniform soils. Undergr. Space 2024, 17, 45–59. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Zhao, T.; Dai, F.; Xu, N.; Liu, Y.; Xu, Y. A composite particle model for non-spherical particles in DEM simulations. Granul. Matter 2015, 17, 763–774. [Google Scholar] [CrossRef]
- Feng, S.-J.; Wang, Y.-Q.; Chen, H.-X. DEM simulation of geotextile-geomembrane interface direct shear test considering the interlocking and wearing processes. Comput. Geotech. 2022, 148, 104805. [Google Scholar] [CrossRef]
- Calvetti, F.; Di Prisco, C.; Nova, R. Experimental and Numerical Analysis of Soil–Pipe Interaction. J. Geotech. Geoenviron. Eng. 2004, 130, 1292–1299. [Google Scholar] [CrossRef]
- Wang, Z.; Klapperich, H.; Ziegler, M. Discrete Element Modeling of Geogrid Reinforced Soil; Lehrstuhl für Geotechnik im Bauwesen und Institut für Grundbau: Aachen, Germany, 2016. [Google Scholar]
- Saha Roy, S.; Deb, K. Bearing capacity of rectangular footings on multilayer geosynthetic-reinforced granular fill over soft soil. Int. J. Geomech. 2017, 17, 04017069. [Google Scholar] [CrossRef]
- Saha Roy, S.; Deb, K. Effects of aspect ratio of footings on bearing capacity for geogrid-reinforced sand over soft soil. Geosynth. Int. 2017, 24, 362–382. [Google Scholar] [CrossRef]
- Hou, J.; Liu, S.; Nam, B.; Ma, Y. Bearing Capacity and Mechanism of the H–V Geogrid-Reinforced Foundation. Polymers 2023, 15, 2606. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Jacobs, F.; Ziegler, M.; Yang, G. Visualisation and quantification of geogrid reinforcing effects under strip footing loads using discrete element method. Geotext. Geomembr. 2020, 48, 62–70. [Google Scholar] [CrossRef]
- Huang, C.; Hong, L. Ultimate Bearing Capacity and Settlement of Footings on Reinforced Sandy Ground. Soils Found. 2000, 40, 65–73. [Google Scholar] [CrossRef]
- Huang, C.C.; Menq, F.Y. Deep-Footing and Wide-Slab Effects in Reinforced Sandy Ground. J. Geotech. Geoenviron. Eng. 1997, 123, 30–36. [Google Scholar] [CrossRef]
- Zhang, T.-T.; Zhang, M.-X.; Juan, H. Bearing Capacity Behavior and Failure Modes of HV Reinforcement Foundation Based on Strength Reduction Finite Element Method. J. Shanghai Jiaotong Univ. 2011, 45, 757. [Google Scholar]
- Li, J.; Tian, Y.; Cassidy, M.J. Failure mechanism and bearing capacity of footings buried at various depths in spatially random soil. J. Geotech. Geoenviron. Eng. 2015, 141, 04014099. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).