Numerical Evaluation of the Punching Shear Strength of Flat Slabs Subjected to Balanced and Unbalanced Moments
Abstract
1. Introduction
2. Experimental Test
3. Numerical Models
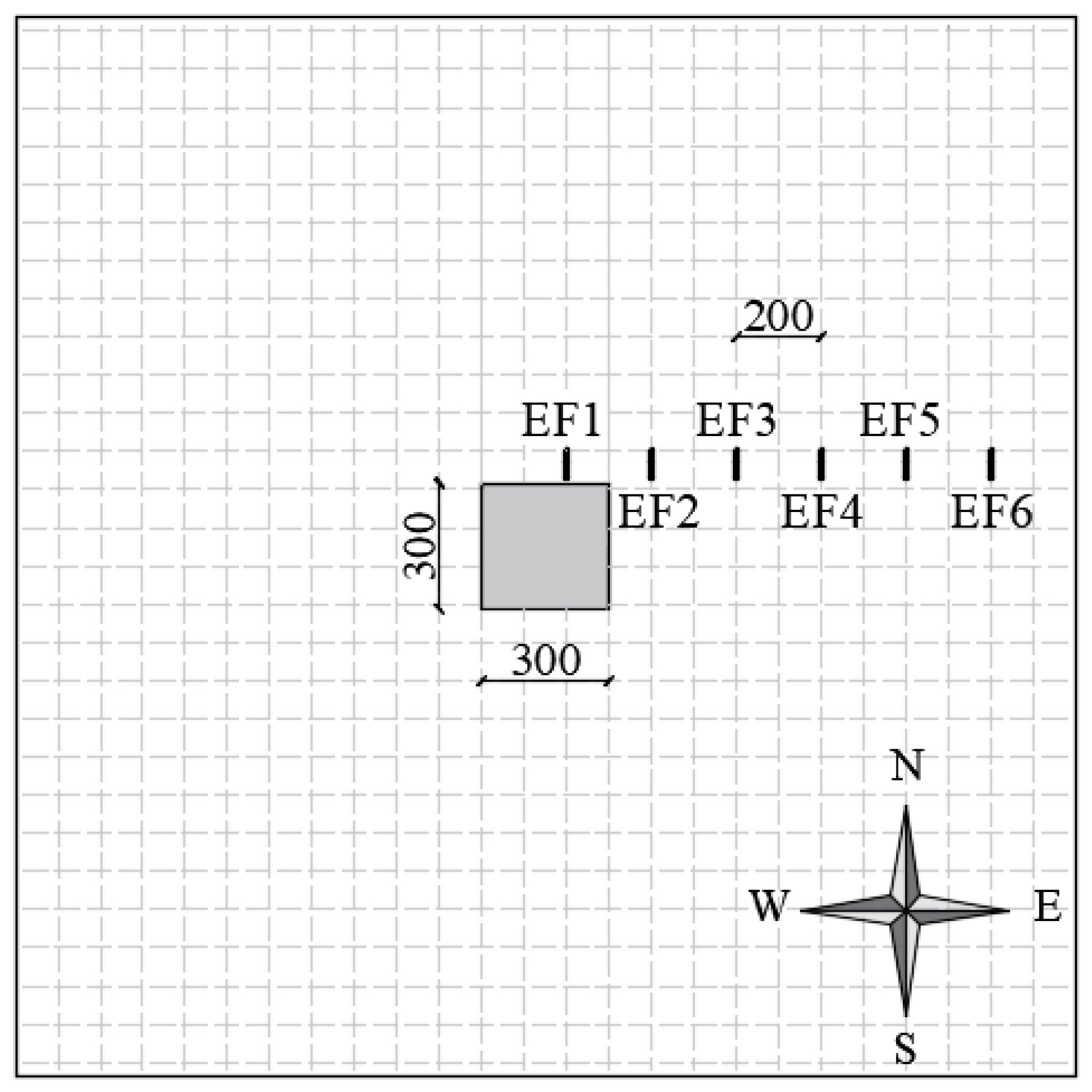
3.1. Geometrics Parameters
3.2. Boundary Conditions and Reference Points
3.3. Load Conditions
3.4. Reinforcement Bars and Concrete
3.5. Finite Element Mesh
4. Validation of the F.E. Models
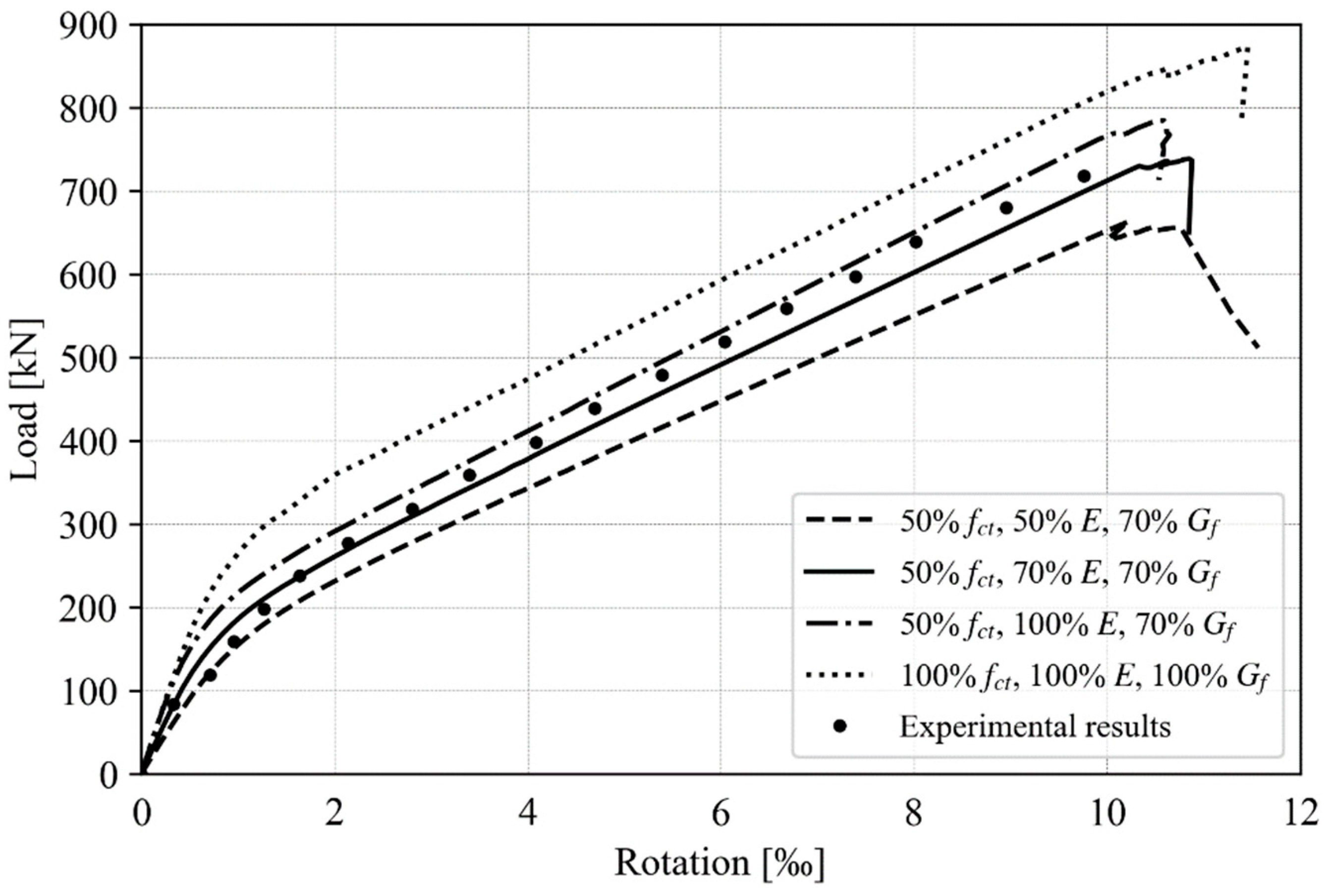
4.1. Concrete Parameters
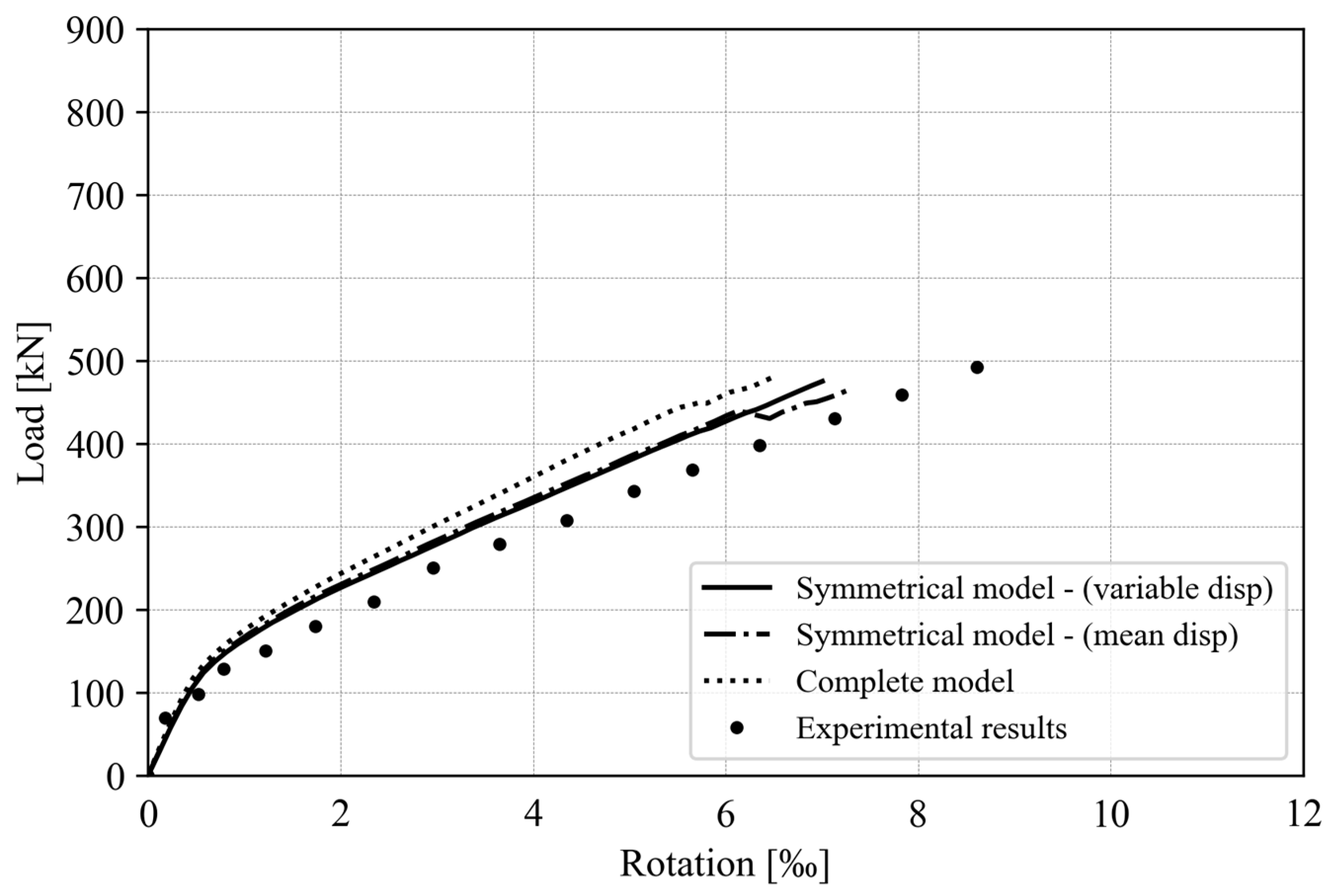
4.2. Symmetry Conditions
4.3. Ultimate Shear Force and Rotation
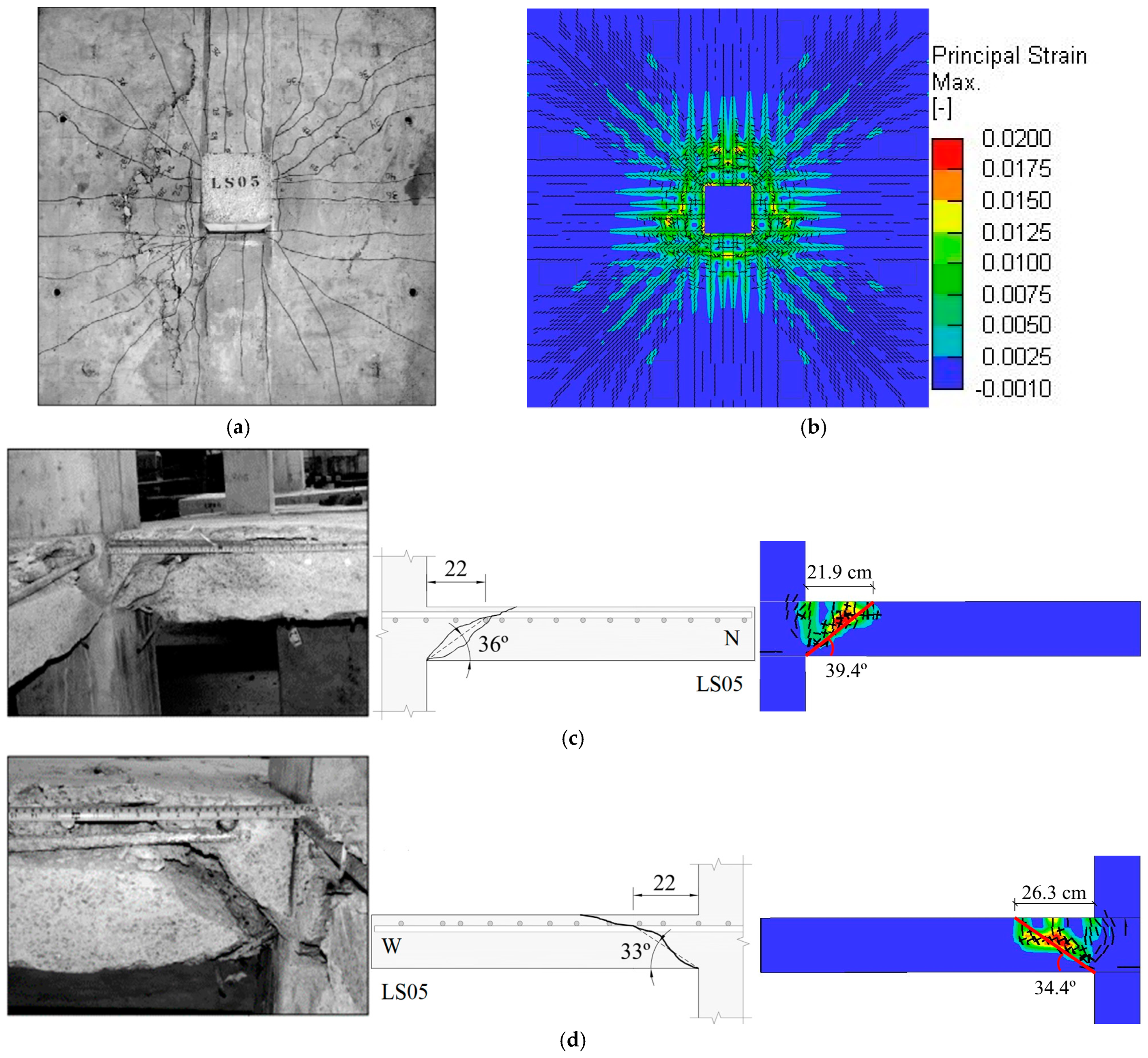
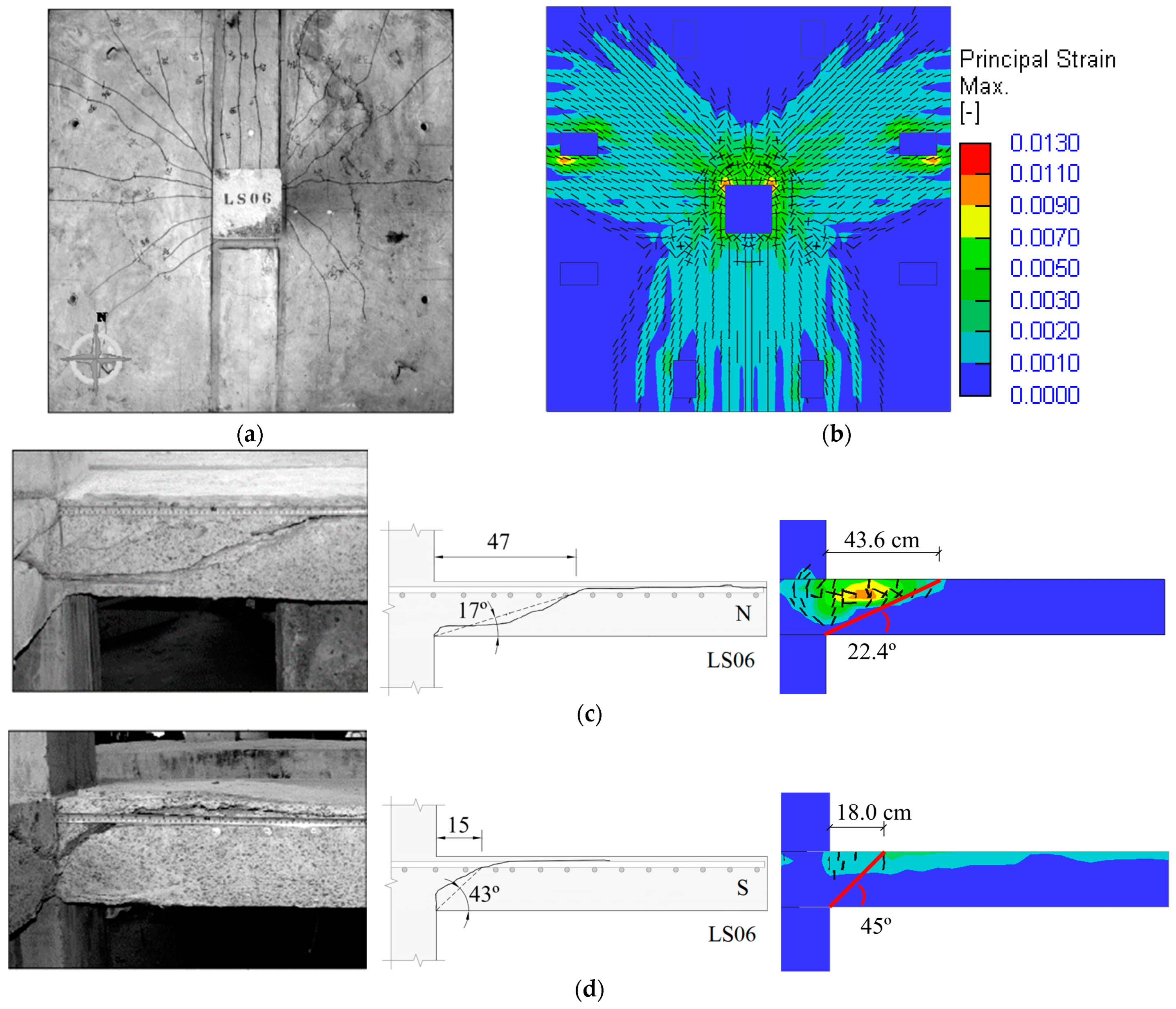
4.4. Crack Distribution
4.4.1. Slab LS05
4.4.2. Slab LS06
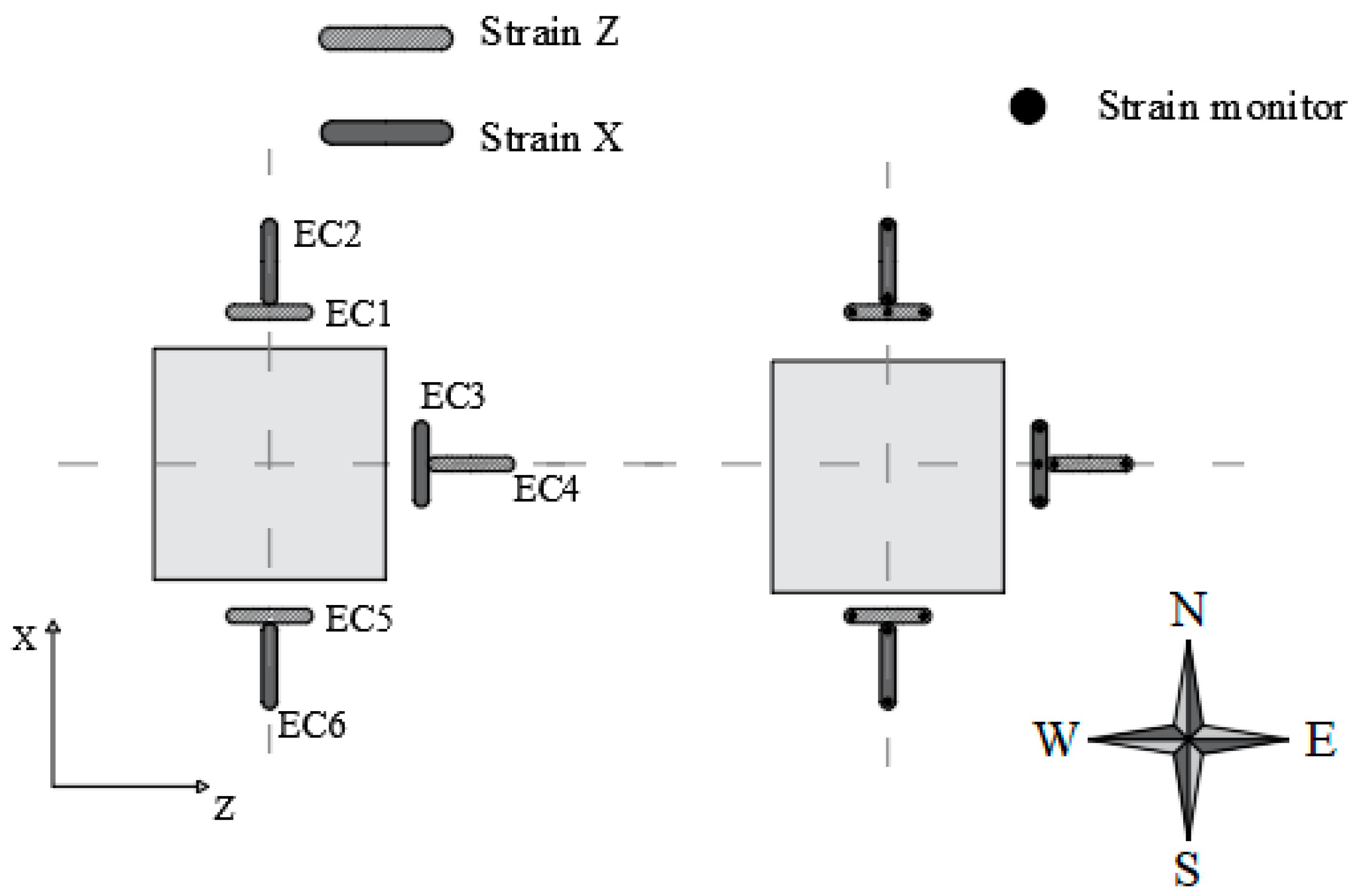
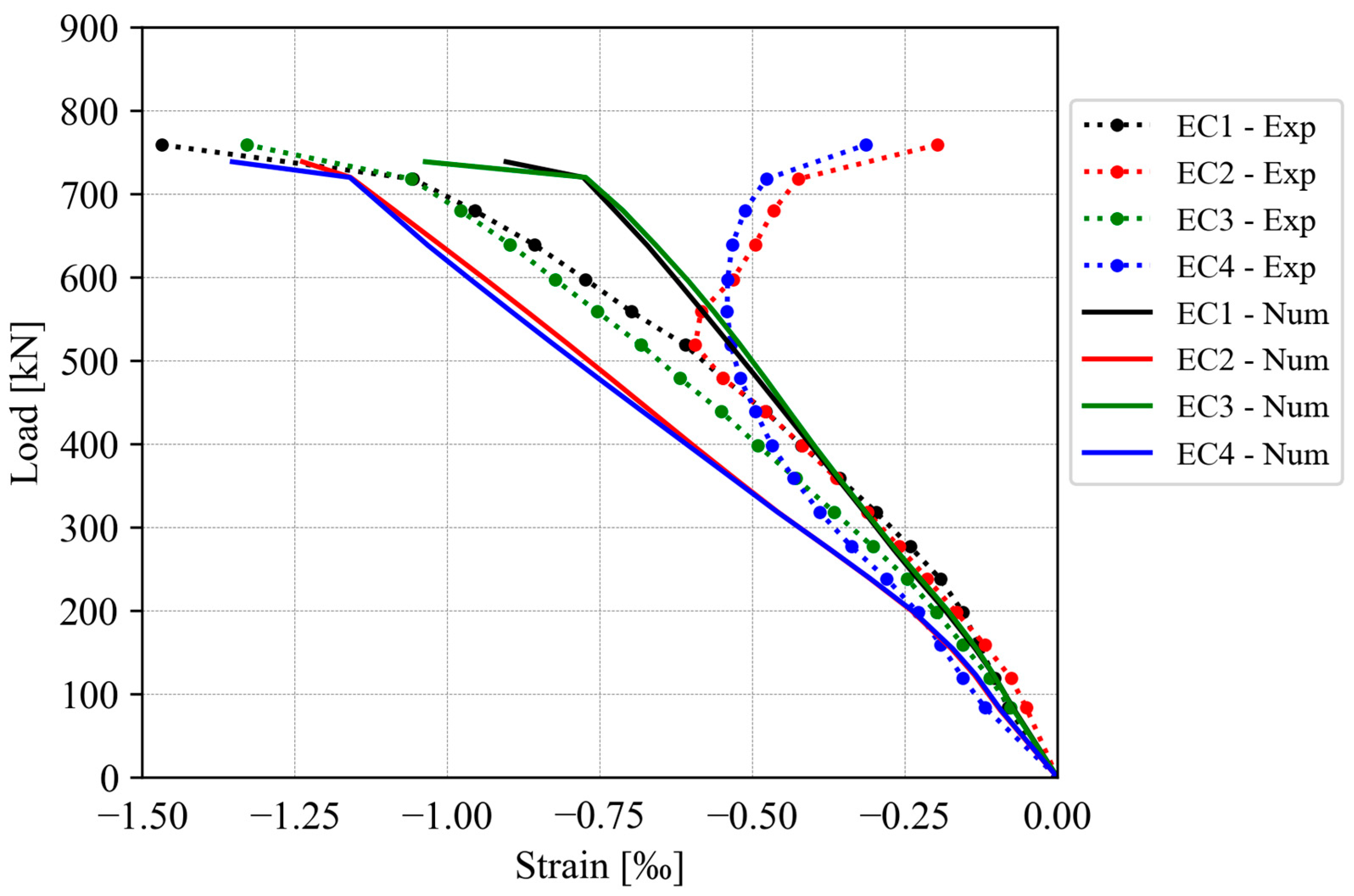
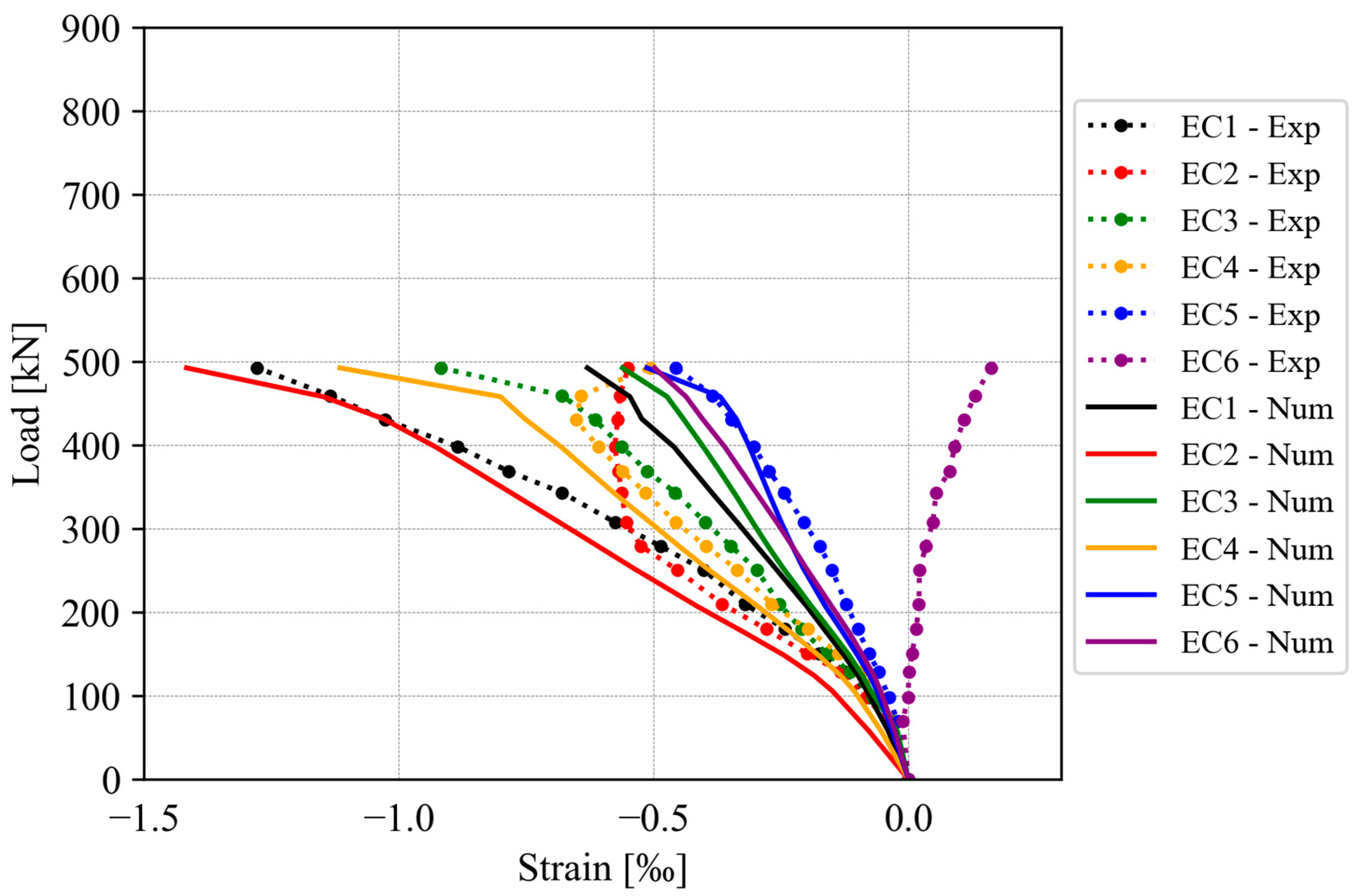
4.5. Steel Strains
4.5.1. Slab LS05
4.5.2. Slab LS06
4.6. Concrete Strains
4.6.1. Slab LS05
4.6.2. Slab LS06
5. Parametric Study and Design Codes Comparison
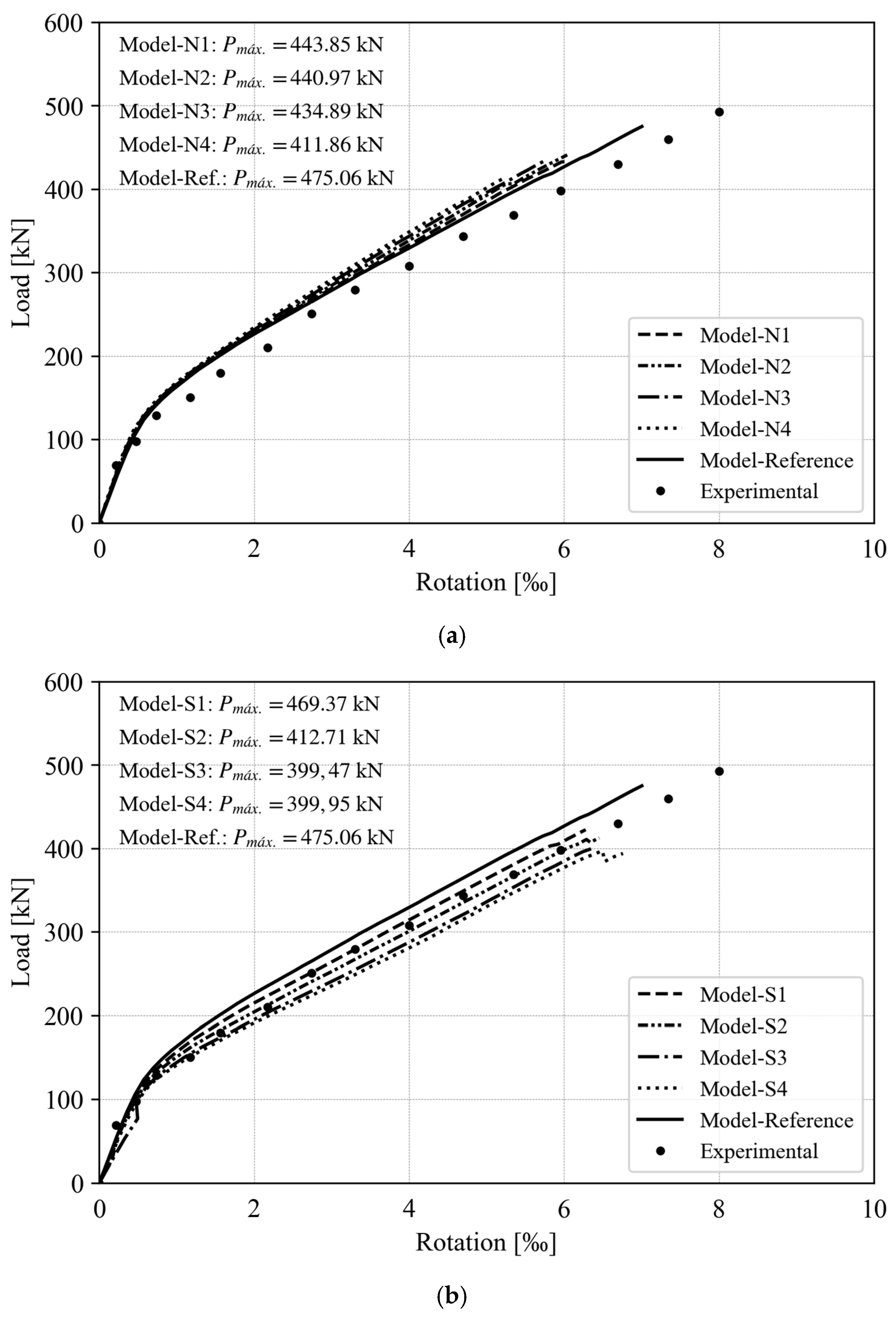
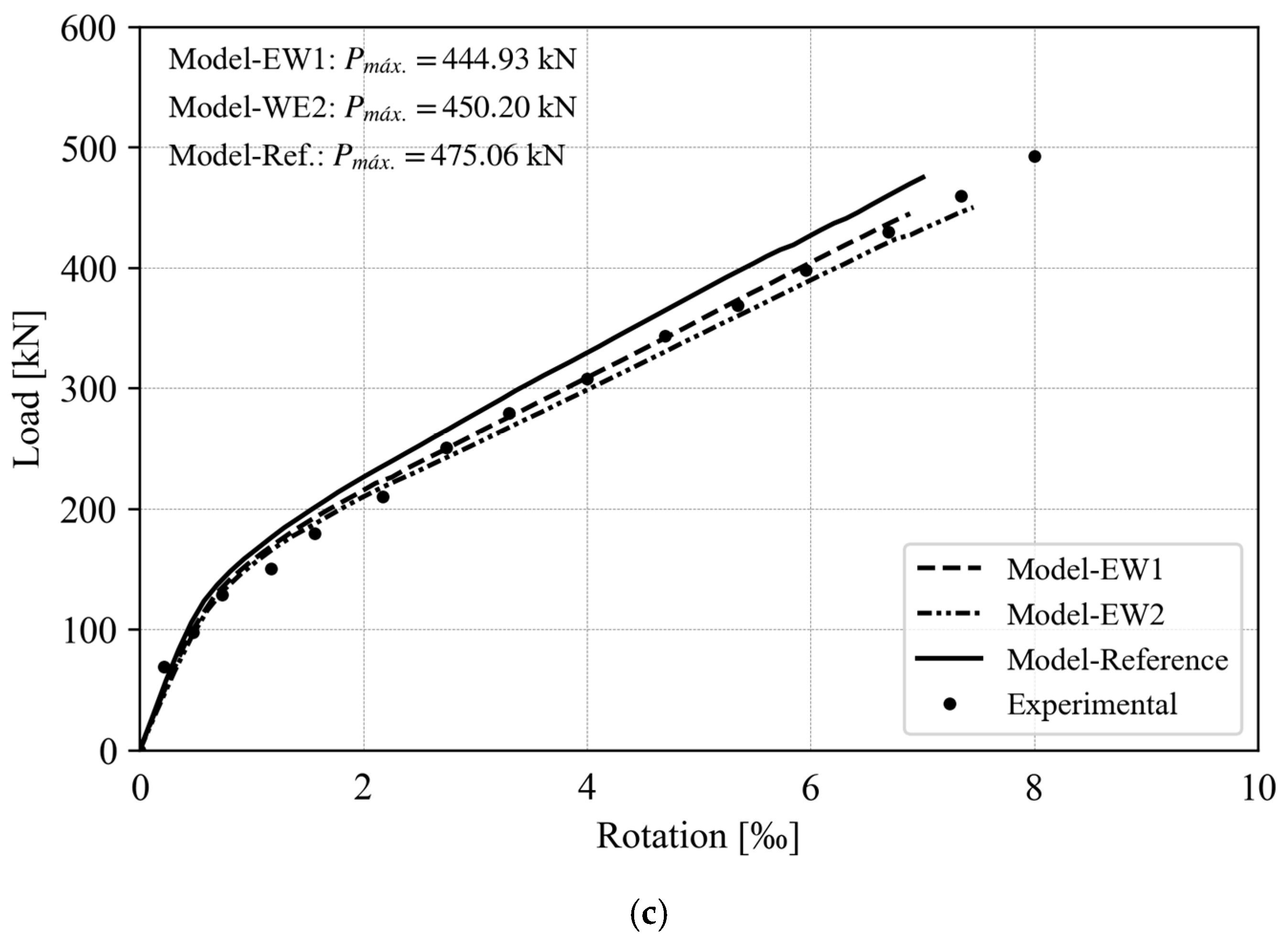
5.1. Ultimate Shear Forces and Rotations
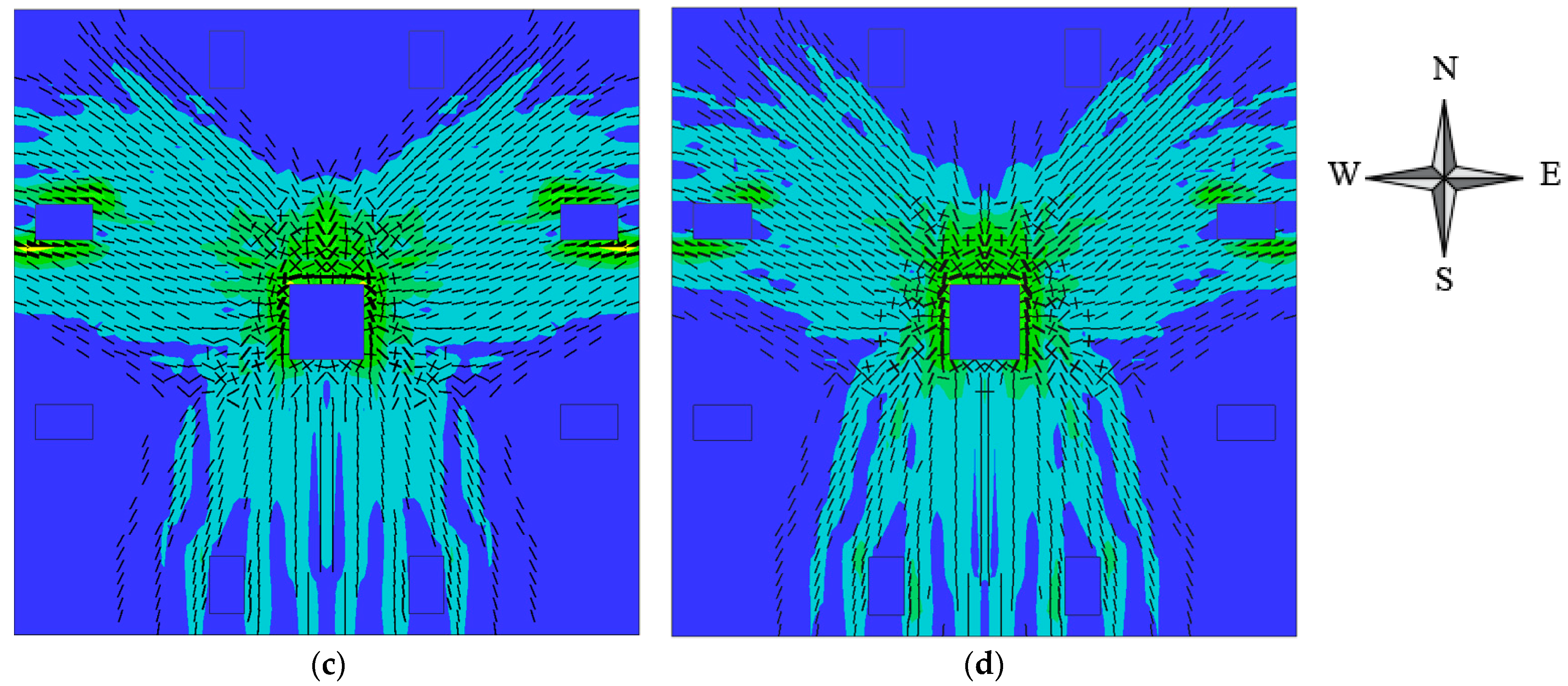
5.2. Cracking Pattern
5.3. Desing Codes Comparison
6. Conclusions and Remarks
- The numerical results of both loading cases (non-eccentric and eccentric) agreed well with the experimental results. The most significant discrepancy between the ultimate experimental and computational shear forces was 11%, referring to the LS06 model (eccentric load) with one plane of symmetry.
- Regarding cracking, all F.E. models exhibited cracking patterns identical to those found experimentally by the reference authors.
- The strains in the concrete slab were the parameters that showed the most significant discrepancies. Such differences can be attributed to several factors, including the proximity between the strain gauge sensors and the column, uncertainties associated with the mechanical properties of the material, numerical errors generated from approximations in the analysis of F.E. models, the size and conditions of adherence of the strain gauges during the application of the load, the boundary conditions, and characteristics of the loading process.
- All aspects allow us to conclude that the F.E. models developed are valid and capable of adequately representing the mechanical behaviour of smooth slabs subjected to balanced and unbalanced moments.
- The parametric study results confirmed that the increase in the unbalanced moment negatively impacts the punching strength of the slab–column connections.
- In summary, the unbalanced moment results in an increase in shear stress in the slab–column connection, a phenomenon observed by all numerical models in Groups 1, 2, and 3, and corroborated by the design codes.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Punching Shear Provisions in Design Codes
| Crushing of compression strut: |
| Diagonal tension: |
| Examples of control perimeters: |
 |
| Crushing of compression strut: |
| Diagonal tension: |
| Example of control perimeter: |
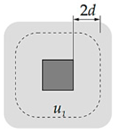 |
| Stress corresponding to the nominal shear strength without shear reinforcement: |
| Examples of control perimeters: |
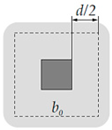 |
| Maximum shear force resistance: |
| without shear reinforcement: |
| Examples of control perimeters: |
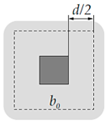 |
References
- Sagaseta, J.; Muttoni, A.; Ruiz, M.F.; Tassinari, L. Non-Axis-Symmetrical Punching Shear around Internal Columns of RC Slabs without Transverse Reinforcement. Mag. Concr. Res. 2011, 63, 441–457. [Google Scholar] [CrossRef]
- Durucan, C.; Anil, Ö. Effect of Opening Size and Location on the Punching Shear Behavior of Interior Slab-Column Connections Strengthened with CFRP Strips. Eng. Struct. 2015, 105, 22–36. [Google Scholar] [CrossRef]
- Ismail, E.S.I.M. Non-Linear Finite Element Analysis of Reinforced Concrete Flat Plates with Opening Adjacent to Column under Eccentric Punching Loads. HBRC J. 2018, 14, 438–449. [Google Scholar] [CrossRef]
- Živković, S.; Bešević, M.; Purčar, M.V.; Kozarić, L. Nonlinear Finite Element Analysis of Punching Shear Strength of Eccentrically Loaded RC Flat Slabs with Opening. KSCE J. Civ. Eng. 2019, 23, 4771–4780. [Google Scholar] [CrossRef]
- Marques, M.G.; Liberati, E.A.P.; Pimentel, M.J.; de Souza, R.A.; Trautwein, L.M. Nonlinear Finite Element Analysis (NLFEA) of Reinforced Concrete Flat Slabs with Holes. Structures 2020, 27, 1–11. [Google Scholar] [CrossRef]
- Bursać, S.; Bešević, M.; Vojnić Purčar, M.; Kozarić, L.; Đurić, N. Experimental Analysis of Punching Shear Strength of Eccentrically Loaded Slab with the Opening along the Face of the Internal Column. Eng. Struct. 2021, 249, 113359. [Google Scholar] [CrossRef]
- Ungermann, J.; Schmidt, P.; Christou, G.; Hegger, J. Eccentric Punching Tests on Column Bases—Influence of Column Geometry. Struct. Concr. 2022, 23, 1316–1332. [Google Scholar] [CrossRef]
- Vargas, D.; Lantsoght, E.O.L.; Genikomsou, A.S. Flat Slabs in Eccentric Punching Shear: Experimental Database and Code Analysis. Buildings 2022, 12, 2092. [Google Scholar] [CrossRef]
- Aguiar, A.; Oliveira, D.; Reis, L.; Nzambi, A. Punching Shear Strength of Waffle Flat Slabs with Opening Adjacent to Elongated Columns. Eng. Struct. 2021, 243, 112641. [Google Scholar] [CrossRef]
- Brigo, H.; Ashihara, L.J.; Marques, M.G.; Liberati, E.A.P. Non-Linear Analysis of Flat Slabs Prestressed with Unbonded Tendons Submitted to Punching Shear. Buildings 2023, 13, 923. [Google Scholar] [CrossRef]
- Krüger, G.; Burdet, O.; Favre, R. Punching Strength of R.C. Flat Slabs with Moment Transfer; International Workshop on Punching Shear: Stockholm, Sweden, 2000; pp. 1–8. [Google Scholar]
- Ferreira, M.d.P.; Oliveira, M.H.; Melo, G.S.S.A. Tests on the Punching Resistance of Flat Slabs with Unbalanced Moments. Eng. Struct. 2019, 196, 109311. [Google Scholar] [CrossRef]
- Secci, L.; Lapi, M.; Teoni, E.; Pinho Ramos, A.; Orlando, M. Eccentric Punching Strength of Continuous Flat Slabs—Analysis of Different Experimental Setups. Struct. Concr. 2021, 22, 1183–1204. [Google Scholar] [CrossRef]
- Al-Bayati, A.F.; Lau, T.L.; Clark, L.A. Punching Shear Design of Waffle Slabs at Internal Column Connections. Pract. Period. Struct. Des. Constr. 2023, 28, 1–8. [Google Scholar] [CrossRef]
- El-Naqeeb, M.H.; Abdelwahed, B.S. Numerical Assessment of Punching Shear Strength of Eccentrically Loaded Footings with Nonconventional Shear Reinforcement. Structures 2023, 49, 716–729. [Google Scholar] [CrossRef]
- European Committee for Standardization. Eurocode 2—Design of Concrete Structures of Concrete Part 1: General and for Buildings Rules; European Committee for Standardization: Brussels, Belgium, 2004. [Google Scholar]
- American Concrete Institute. 318-19 Building Code Requirements for Structural Concrete and Commentary; American Concrete Institute: Indianapolis, IN, USA, 2019; ISBN 9781641950565. [Google Scholar]
- Associação Brasileira de Normas Técnicas. NBR 6118—Projeto de Estruturas de Concreto; Associação Brasileira de Normas Técnicas: Rio de Janeiro, Brazil, 2014; p. 238. [Google Scholar]
- Obaidat, Y.T.; Barham, W.; Obaidat, A.T.; Al-Khazaaleh, N.A.A. Modeling of Confined Circular RC Columns Using Artificial Neural Network and Finite Element Method. Structures 2022, 40, 74–87. [Google Scholar] [CrossRef]
- Yang, J.; Xia, J.; Zhang, Z.; Zou, Y.; Wang, Z.; Zhou, J. Experimental and Numerical Investigations on the Mechanical Behavior of Reinforced Concrete Arches Strengthened with UHPC Subjected to Asymmetric Load. Structures 2022, 39, 1158–1175. [Google Scholar] [CrossRef]
- Aghani, K.; Afshin, H.; Abedi, K. Finite Element-Based Prediction of the Long-Term Deflection of Reinforced Concrete Beams Strengthened with Prestressed Fiber-Reinforced Polymers. Structures 2022, 43, 358–373. [Google Scholar] [CrossRef]
- da Paz, G.L.G.; Marques, M.G.; Ruas, S.R.C. Numerical Analysis of Reinforced Concrete Columns Strengthened with Sleeve Wedge Bolts and a Self Compacting Concrete Layer. Structures 2022, 43, 726–737. [Google Scholar] [CrossRef]
- CIMNE GiD—The Personal Pre and Post Processor 2020. Available online: https://edisciplinas.usp.br/mod/url/view.php?id=3168131 (accessed on 30 March 2024).
- Cervenka Consulting ATENA—Computer Program for Nonlinear Finite Element Analysis of Reinforced Concrete Structures 2023. Available online: https://www.cervenka.cz/products/atena/ (accessed on 30 March 2024).
- Fédération Internationale du Béton. Model Code 2010; FIB Bulletins; FIB. The International Federation for Structural Concrete: Lausanne, Switzerland, 2010; ISBN 978-2-88394-095-6. [Google Scholar]
- de Boer, A.; Hendriks, M.; Uijl, J.; Belletti, B.; Damoni, C. Nonlinear FEA Guideline for Modelling of Concrete Infrastructure Objects. In Computational Modelling of Concrete Structures; CRC Press: Boca Raton, FL, USA, 2014; Volume 2, pp. 977–985. ISBN 9781138026421. [Google Scholar]
- Guandalini, S.; Burdet, O.L.; Muttoni, A. Punching Tests of Slabs with Low Reinforcement Ratios. ACI Struct. J. 2009, 106, 87–95. [Google Scholar] [CrossRef][Green Version]
- European Committee for Standardization. FprEN 1992-1-1—Eurocode 2. Design of Concrete Structures—Part 1-1: General Rules—Rules for Buildings, Bridges and Civil Engineering Structures; European Committee for Standardization: Brussels, Belgium, 2021. [Google Scholar]
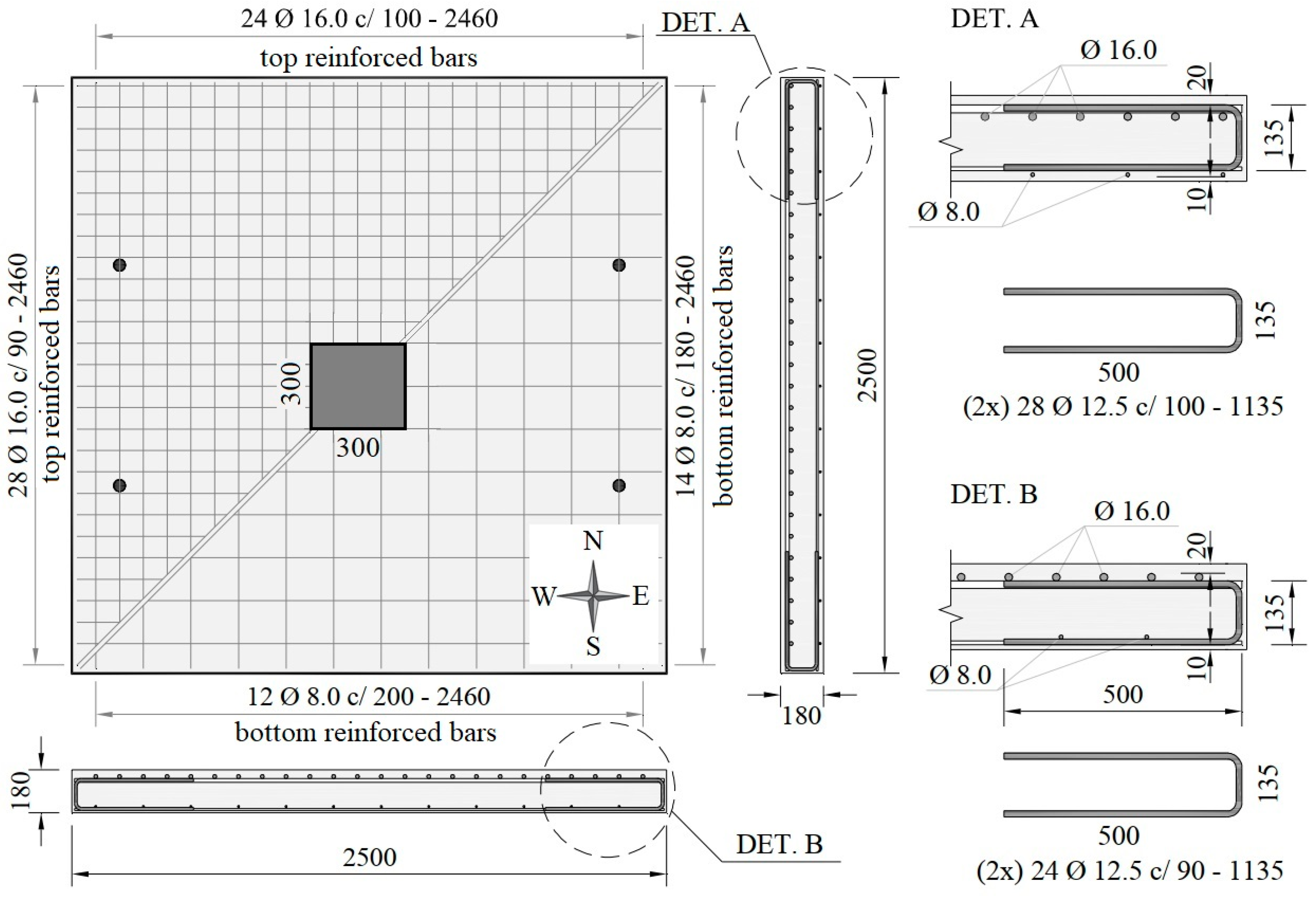
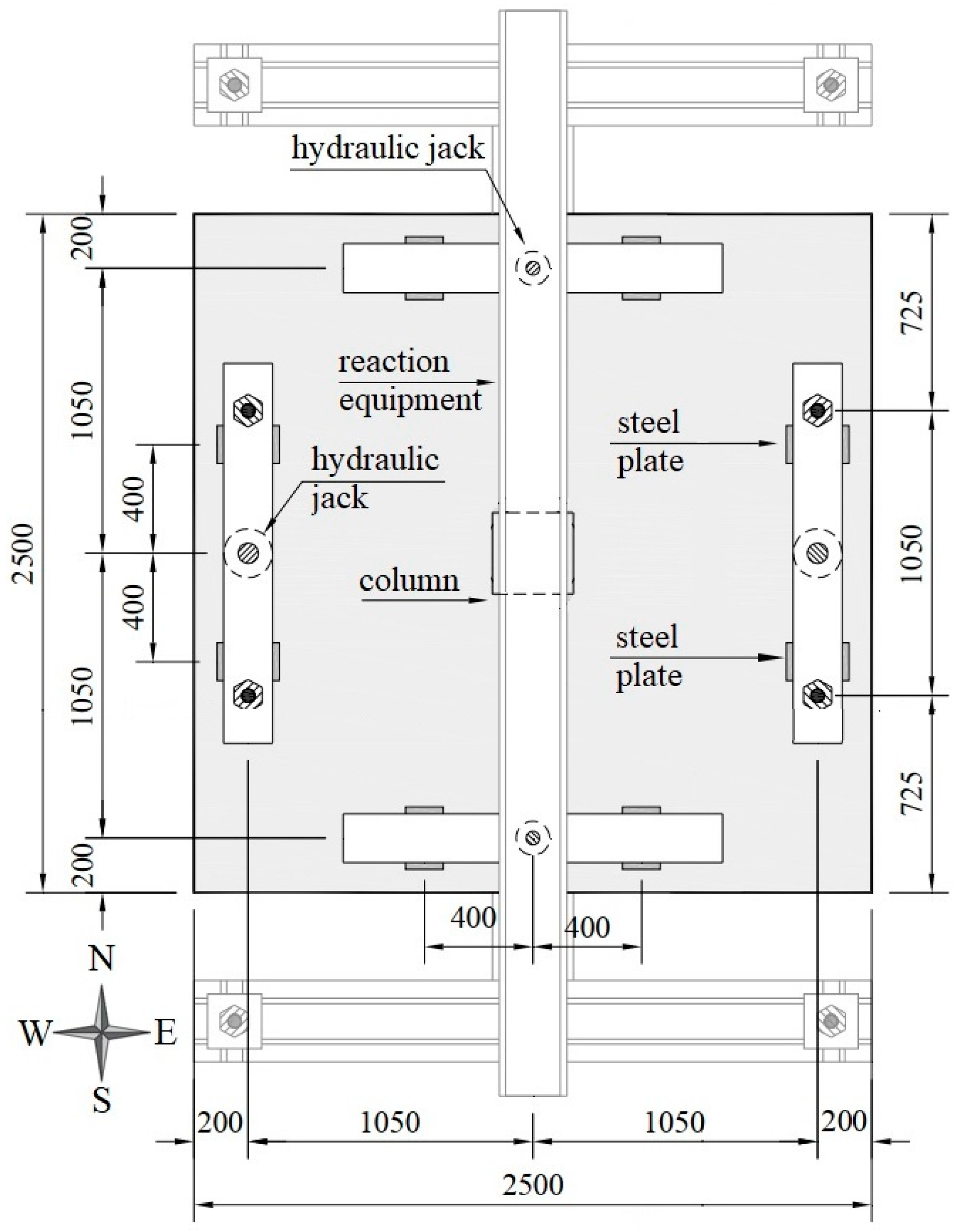
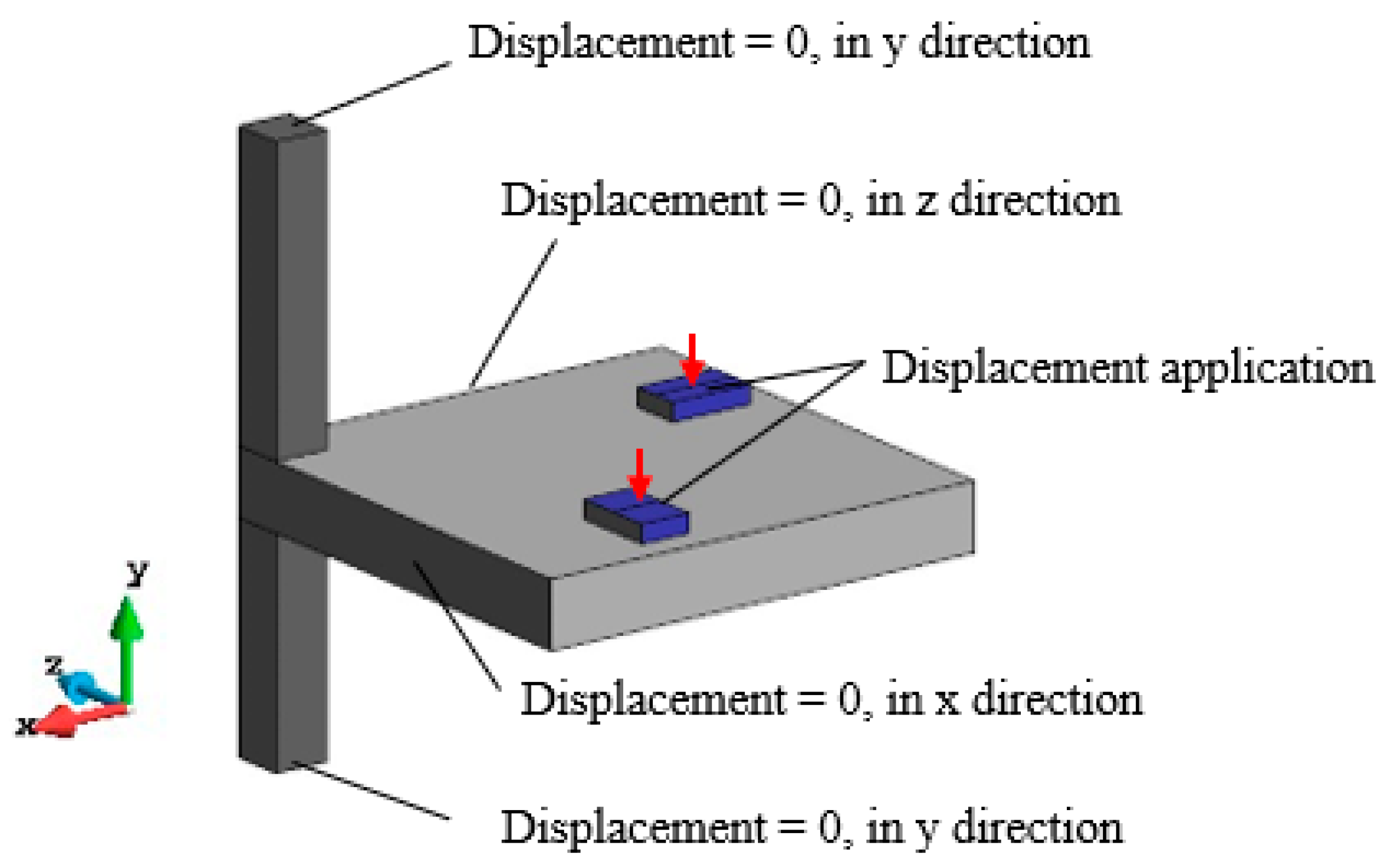
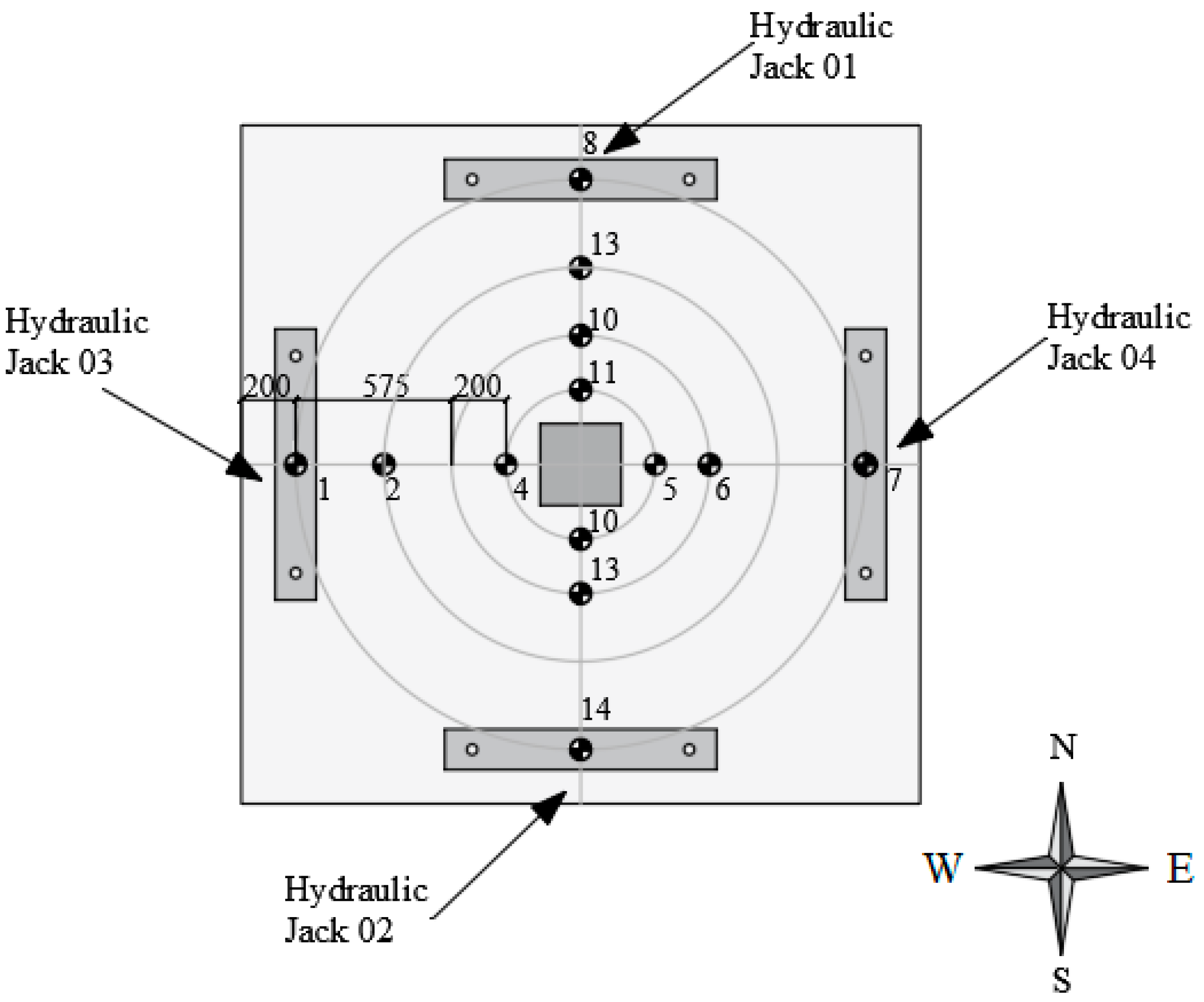

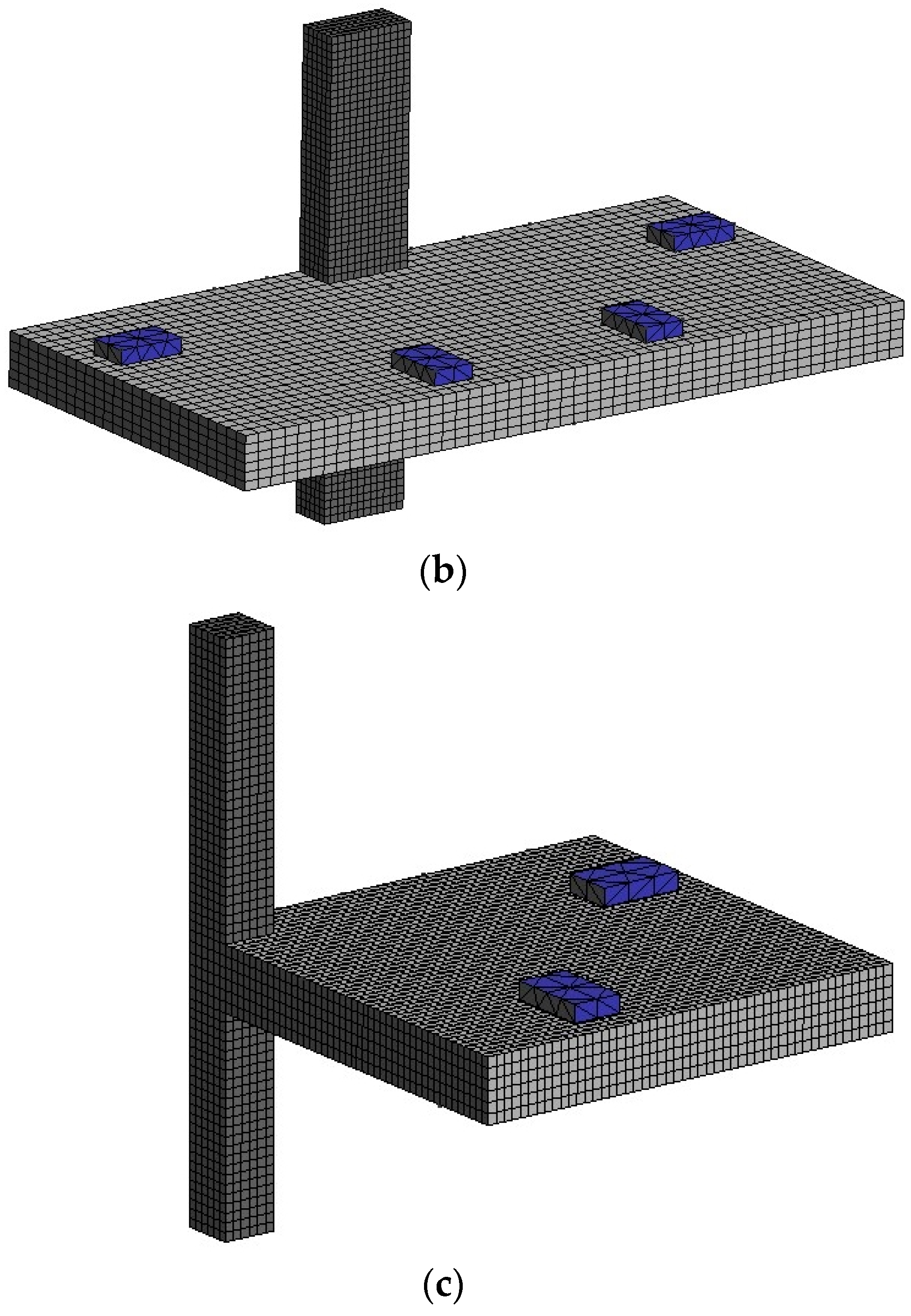



| Load Step | Experimental Response | Displacement Increment (Each Rigid Plate—Figure 4) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Jack 01 L1 (kN) | Jack 02 L2 (kN) | Jack 03 L3 (kN) | Jack 04 L4 (kN) | Total Load TL (kN) | L1/TL | L2/TL | L3/TL | L4/TL | |
| 1 | 12.5 | 3.8 | 8.0 | 7.4 | 69.2 | 0.090 | 0.027 | 0.058 | 0.053 |
| 2 | 24.1 | 6.0 | 15.1 | 15.3 | 98.0 | 0.123 | 0.031 | 0.077 | 0.078 |
| 3 | 36.1 | 9.5 | 22.6 | 22.9 | 128.6 | 0.140 | 0.037 | 0.088 | 0.089 |
| 4 | 48.0 | 12.0 | 29.9 | 29.8 | 157.2 | 0.153 | 0.038 | 0.095 | 0.095 |
| 5 | 59.9 | 15.0 | 37.2 | 37.4 | 187.0 | 0.160 | 0.040 | 0.099 | 0.100 |
| 6 | 72.1 | 18.0 | 44.8 | 44.6 | 217.0 | 0.166 | 0.041 | 0.103 | 0.103 |
| 7 | 83.8 | 21.5 | 54.7 | 53.2 | 250.7 | 0.167 | 0.043 | 0.109 | 0.106 |
| 8 | 96.8 | 25.0 | 60.0 | 59.8 | 279.1 | 0.173 | 0.045 | 0.107 | 0.107 |
| 9 | 107.9 | 27.3 | 67.4 | 67.5 | 307.6 | 0.175 | 0.044 | 0.110 | 0.110 |
| 10 | 121.0 | 32.0 | 76.7 | 76.0 | 343.2 | 0.176 | 0.047 | 0.112 | 0.111 |
| 11 | 132.2 | 33.0 | 83.0 | 83.0 | 368.7 | 0.179 | 0.045 | 0.113 | 0.113 |
| 12 | 144.1 | 36.5 | 90.0 | 90.0 | 398.1 | 0.181 | 0.046 | 0.113 | 0.113 |
| 13 | 156.7 | 39.5 | 98.4 | 98.0 | 430.1 | 0.182 | 0.046 | 0.114 | 0.114 |
| 14 | 168.5 | 42.5 | 105.1 | 105.8 | 459.4 | 0.183 | 0.046 | 0.114 | 0.115 |
| 15 | 181.0 | 47.5 | 112.5 | 114.0 | 492.5 | 0.184 | 0.048 | 0.114 | 0.116 |
| Mean displacement of each hydraulic jack [mm] | 0.163 | 0.042 | 0.103 | 0.103 | |||||
| Model | ||||||
|---|---|---|---|---|---|---|
| LS05 | 779.0 | 735.6 | 1.06 | 9.76 | 10.62 | 0.92 |
| LS06 (symmetrical model) | 528.0 | 475.1 | 1.11 | 8.61 | 7.00 | 1.23 |
| LS06 (complete model) | 528.0 | 480.4 | 1.10 | 8.61 | 6.50 | 1.32 |
| Position | Mean Value (1) | Group 1 | Group 2 | Group 3 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| N1 | N2 | N3 | N4 | S1 | S2 | S3 | S4 | EW1 | EW2 | ||
| North | 0.163 | 0.170 | 0.180 | 0.190 | 0.200 | 0.163 | 0.163 | 0.163 | 0.163 | 0.163 | 0.163 |
| South | 0.042 | 0.042 | 0.042 | 0.042 | 0.042 | 0.030 | 0.020 | 0.010 | 0.005 | 0.042 | 0.042 |
| East/West | 0.103 | 0.103 | 0.103 | 0.103 | 0.103 | 0.103 | 0.103 | 0.103 | 0.103 | 0.120 | 0.130 |
| Model | [kN] | ||||
|---|---|---|---|---|---|
| Group 1 | N1 | 443.85 | 1.07 | 6.27 | 1.12 |
| N2 | 440.97 | 1.08 | 6.04 | 1.16 | |
| N3 | 434.89 | 1.09 | 5.77 | 1.21 | |
| N4 | 411.86 | 1.15 | 5.20 | 1.35 | |
| Group 2 | S1 | 469.37 | 1.01 | 6.28 | 1.12 |
| S2 | 412.71 | 1.15 | 6.45 | 1.09 | |
| S3 | 399.47 | 1.19 | 6.50 | 1.08 | |
| S4 | 393.95 | 1.21 | 6.76 | 1.04 | |
| Group 3 | EW1 | 444.93 | 1.07 | 6.89 | 1.02 |
| EW2 | 450.20 | 1.06 | 7.46 | 0.94 |
| Pmáx | ACI 318 | Pmáx/ PACI | Eurocode 2 | Pmáx/ PEC2 | Model Code | Pmáx/ PMC | FprEN | Pmáx/ PFprEN | ABNT NBR 6118 | Pmáx/ PNBR | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Experimental Test | 528.0 | 354.2 | 1.49 | 416.6 | 1.27 | 258.9 | 2.04 | 404.9 | 1.30 | 300.8 | 1.76 |
| LS06 (symmetrical model) | 475.1 | 354.2 | 1.49 | 416.6 | 1.27 | 288.7 | 1.83 | 333.0 | 1.59 | 300.8 | 1.76 |
| N1 | 443.9 | 277.9 | 1.60 | 426.4 | 1.04 | 352.5 | 1.26 | 338.4 | 1.31 | 307.9 | 1.44 |
| N2 | 441.0 | 278.9 | 1.58 | 415.1 | 1.06 | 336.5 | 1.31 | 336.8 | 1.31 | 299.8 | 1.47 |
| N3 | 434.9 | 281.0 | 1.55 | 404.4 | 1.08 | 323.6 | 1.34 | 335.2 | 1.30 | 292.1 | 1.49 |
| N4 | 411.9 | 289.2 | 1.42 | 394.2 | 1.04 | 322.5 | 1.28 | 333.5 | 1.23 | 284.7 | 1.45 |
| S1 | 469.4 | 269.6 | 1.74 | 420.7 | 1.12 | 327.5 | 1.43 | 353.4 | 1.33 | 303.8 | 1.54 |
| S2 | 412.7 | 288.9 | 1.43 | 409.7 | 1.01 | 346.5 | 1.19 | 351.3 | 1.17 | 295.9 | 1.39 |
| S3 | 399.5 | 293.8 | 1.36 | 399.3 | 1.00 | 338.8 | 1.18 | 349.2 | 1.14 | 288.4 | 1.39 |
| S4 | 394.0 | 295.9 | 1.33 | 394.2 | 1.00 | 334.5 | 1.18 | 350.2 | 1.12 | 284.7 | 1.38 |
| EW1 | 444.9 | 277.6 | 1.60 | 389.5 | 1.14 | 294.7 | 1.51 | 351.2 | 1.27 | 281.3 | 1.58 |
| EW2 | 450.2 | 275.8 | 1.63 | 434.6 | 1.04 | 361.6 | 1.25 | 383.4 | 1.17 | 313.9 | 1.43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mendes, R.P.; Mesquita, L.C.; Ferreira, M.P.; Trautwein, L.M.; Marvila, M.T.; Marques, M.G. Numerical Evaluation of the Punching Shear Strength of Flat Slabs Subjected to Balanced and Unbalanced Moments. Buildings 2024, 14, 985. https://doi.org/10.3390/buildings14040985
Mendes RP, Mesquita LC, Ferreira MP, Trautwein LM, Marvila MT, Marques MG. Numerical Evaluation of the Punching Shear Strength of Flat Slabs Subjected to Balanced and Unbalanced Moments. Buildings. 2024; 14(4):985. https://doi.org/10.3390/buildings14040985
Chicago/Turabian StyleMendes, Roberta Prado, Leonardo Carvalho Mesquita, Maurício Pina Ferreira, Leandro Mouta Trautwein, Markssuel Teixeira Marvila, and Marília Gonçalves Marques. 2024. "Numerical Evaluation of the Punching Shear Strength of Flat Slabs Subjected to Balanced and Unbalanced Moments" Buildings 14, no. 4: 985. https://doi.org/10.3390/buildings14040985
APA StyleMendes, R. P., Mesquita, L. C., Ferreira, M. P., Trautwein, L. M., Marvila, M. T., & Marques, M. G. (2024). Numerical Evaluation of the Punching Shear Strength of Flat Slabs Subjected to Balanced and Unbalanced Moments. Buildings, 14(4), 985. https://doi.org/10.3390/buildings14040985


_Su.png)





