Dynamic Characteristics Analysis and Finite Element Simulation of an Ancient Timber Building under Environmental Excitation

Abstract

This study investigates the vibration response and dynamic characteristics of the Shigudeng Pavilion under environmental excitation, employing a comprehensive approach that includes vibration response measurements, theoretical analysis, and finite element numerical simulation. An in-depth examination of the appearance and stress status of the Shigudeng Pavilion in Yao Ancient Village in southern Hunan was conducted, and the horizontal acceleration of different floors of the pavilion under environmental excitation was ascertained through field measurements. The NExT-ERA method was utilized to identify the modal parameters (frequency, damping ratio, and vibration pattern) of the measured timber construction. Subsequently, a finite element analysis model of the ancient timber building was developed and refined using ANSYS Workbench finite element software. This study proposes a specific repair plan addressing apparent defects and structural damage in the measured ancient timber building, offering theoretical and technical references for the conservation and repair of similar structures.

1. Introduction

A timber structure is typical of historical buildings in south Hunan Province, China, which are characterized by peculiar shapes, exquisite timber carvings, and remarkable regional culture. Historical buildings are widely distributed throughout the traditional villages of Yongzhou, in particular, a relatively large proportion of which are listed on the inventory of National Cultural Heritage Timber Buildings. As timber buildings are continually affected by external loads, the environment, moths, timber aging, and other factors, which make the timber structures prone to crippling, cracking, groove rotting, uneven settlement, and other forms of damage during their life span, there is an urgent need to carry out health monitoring, assessment, and repair of building damage [1].

Scholars have previously carried out modal identification and finite element analyses of local nodes of timber structures, and based on their findings, they have proposed assessment and repair methods for ancient timber buildings as follows:

(1) Sun Xianlun [2], Song Dukuo [3], Gu Xinqiang [4], and Zhang Dong [5], respectively, used random vibration theory to analyze the vibrations of different ancient timber buildings under traffic excitation, and conducted modal analysis identification, enriching the application experience and reference knowledge of the using random vibration theory in ancient architecture. Their research revealed that the self-vibration frequencies of timber buildings were relatively low, and damage to component nodes could lead to a significant decrease in structural stiffness and self-vibration frequencies. Furthermore, Zhang Shaoxiong [6] obtained the dynamic characteristics of the Drum Tower of Xi’an under the influence of traffic vibration, from the perspective of the time domain and frequency domain combined with random vibration theory. Additionally, Antonella Saisi et al. [7] conducted dynamic measurements on a masonry bell tower and iron arch bridge under ambient excitation, and determined the modal parameters of two key vibration modes of historical buildings based on the dynamic measurement data.

(2) Fujita et al. [8] compared the frequency, load-displacement curves, and static calculation results of various types of timber structures, and established a mathematical model for ancient timber buildings. In another study, Chen Zhiyong [9] created a finite element model of a timber bucket arch, and the beam-column node and column base node of a timber tower, carried out finite element analysis on local nodes of the timber tower, and obtained a mechanical model of the timber arch’s initial vertical bearing stiffness. Elsewhere, Yu Maohong and Zhao Junhai [10], through finite element analysis of a simplified model of the Xi’an East Gate City Tower, established a finite element model with the node contact of a mortise and tenon bucket arch and other nodes as a semi-rigid connection, and calculated the modal parameters of the structure with different stiffness values. In their study, Wu Yanhui [11,12], through finite element analysis of Guangyue Tower under the excitation of traffic, proposed and verified a relationship equation for the horizontal vibration velocity of this timber structure. Meanwhile, regarding the repair of ancient timber buildings, Duan Chunhui et al. [13,14] summarized the characteristics of existing ancient timber building damage and proposed a metal reinforcement method. In another contribution, by comparing the structurally intact and current Yingxian timber tower, using two types of finite element model analysis to assess the dynamic properties of the structure, seismic load, seismic response, and other force performance, Chen Zhiyong [9] proposed the addition of diagonal bracing in reinforcement design.

(3) Yves Vanhellemont et al. [15] proposed a component restoration program for the repair of ancient buildings through digital technology, and based on the current state of technology in Flanders, outlined the possibility of implementing a variety of technologies and their prospects for application. Elsewhere, Kloiber M [16] and other scholars used soil mortar mixed with lime, casein, and wheat straw to repair locally decayed timber components, and the results showed that this mixture had very similar physical properties compared to general mortar. Meanwhile, Angiolilli M [17] and other scholars added the mechanical properties of short glass-fiber-reinforced mortar with different contents and aspect ratios to fiber-reinforced polymers (FRPs) and the fiber-reinforced cementitious matrix (FRCM) to repair cracks. Their experiments showed that this material offers a suitable solution when strong crack repair is needed. In their study, Zhu Chuanwei [18] used basalt-fiber-reinforced polymer (BFRP) material to strengthen the nodes and components of traditional timber residential buildings, which can effectively suppress the impact of natural defects in timber on the load-bearing capacity of construction and improve the load-bearing capacity and seismic performance of timber components. Finally, Tetsuro Ono et al. [19] proposed a strengthening program based on their measured data for Japanese timber-frame ancient temples, and successfully applied this to a real-life situation.

2. Introduction and Measurement of Shigudeng Pavilion

2.1. Introduction to Shigudeng Pavilion

Lanxi Yao Village, located in Jiangyong County, Hunan Province, China, is an ancient fortress-style settlement that received significant recognition between 2014 and 2019, including the titles of China’s Famous Historical and Cultural Village, Hunan Province’s Most Beautiful Minority Characteristic Village, and recognition from the National Key Cultural Relics Protection Unit. The Shigudeng Pavilion, a nationally protected cultural relic within the village, was built in the Song Dynasty and reconstructed in the 8th year of Daoguang in the Qing Dynasty. The pavilion covers 70 m², has floor space of 150 m², and reaches 9 m high. The three-layer structure is supported by 16 timber pillars, each approximately 30 cm in diameter, embellished by 16 intricately carved stone drums at their bases. The front view of the Shigudeng Pavilion is presented in Figure 1.

2.2. Research Methods

Dynamic characteristics of timber gatehouses have rarely been obtained through field measurements and finite element simulation research. Nonetheless, in this research, we investigated the appearance and force status of the Shigudeng Pavilion by adopting a field measurement method to ascertain its dynamic characteristics, combined with the use of the ANSYS Workbench to create and correct a three-dimensional model, propose a repair program based on the timber building’s apparent damage, and provide theoretical and technical references for similar buildings in terms of conservation and restoration. The experimental flow is presented in Figure 2.

The first-floor axial network is presented in Figure 3 (the numbers and letters in the figure define subsequent 2/B and 3/E columns), and the first eaves are presented in Figure 4. The gold columns of double eaves are load-bearing components of the overall structure, which extend as gable columns outwards along the beam direction on the front and hill faces; carried externally, the gable columns intersect with gable beams, for a total of 12 eaves columns.

2.3. Surface and Structural Damage Survey

The Shigudeng Pavilion was rebuilt 195 years ago, but under the influence of natural and artificial factors over a long period, some timber components have suffered minor cracks or been lost. Details of apparent and structural damage are presented in Figure 5.

Based on these, the safety of the Shigudeng Pavilion was evaluated in conjunction with the “Technical Standard for Maintenance and Reinforcement of Ancient Timber Buildings GB-T 50165-2020”. The following conclusions were drawn:

(1) Brick wall deterioration assessment: The brick wall is chalked in the mortar joints, with a maximum depth of 10 mm, and the mortar has completely lost its effect in many places. Furthermore, there are vertical and diagonal cracks along the breaks of bricks, so the brick wall was assessed to be moderately crippled.

(2) Evaluation of overall structural soundness: The upper timber structure and brick wall are connected by a simple lap; the lateral support is weak and easily affected by horizontal vibration, which has caused much damage in the nodes of the beam-column mortise and tenon joints; and there are missing beams in the middle part of the third floor along with defective members, as well as missing beams on the second floor. Accordingly, the overall solidity of the structure was evaluated as a C grade.

2.4. Test Systems and Test Solutions

The vibration test system includes four parts: the target test system, vibration sensors, signal transmission channels, and data analysis equipment. The test consists of 991B pickup sensors, a 32-channel YZKJ-DIAK dynamic signal acquisition and analysis system, and UT data analysis software. The flow of test data analysis is presented in Figure 6.

Ancient timber buildings subject to the vibration frequency of environmental excitation mainly receiving the low-frequency vibration band; in this research setting, we sampled a frequency of 128 Hz, set the 991B pickup vibration to 1 (acceleration gear), set the X-axis normal to the north-south direction, and set the Y-axis normal to the east-west direction. The Shigudeng Pavilion was divided into the first-floor mezzanine (2.6 m), the second floor (3.9 m), the third floor (6.6 m), and the roof level (8.4 m), and we arranged our 991B horizontal acceleration sensors in the four layers of the 2/B and 3/E columns, as well as placing two on each floor. The two sensors in the layer-two mezzanine faced the X- and Y-direction, respectively, the layer-three sensors were oriented in the same directions as in the mezzanine layer, and the remaining sensors were placed on the vertical and horizontal beams of the corresponding columns and layers. The sensor arrangement is presented in Figure 7.

3. Measurement Data Analysis

3.1. Acceleration Signal Frequency Characteristics

Samples of X- and Y-direction time-domain curves of the 2/B and 3/E columns under ambient excitation with a step size of 30 s were intercepted and analyzed. Examples of the acceleration time-domain curves of the 2/B column with a step size of 30 s are presented in Figure 8, and those for the acceleration time-domain curves of the 3/E column with a step size of 30 s are presented in Figure 9.

3.2. Identification Methods of Modal Parameters and Results

3.2.1. NExT-ERA

The NExT-ERA method is a combination of the Eigen System Realization Algorithm (ERA [20]) and Natural Excitation Technique (NExT [21]) (Chang et al., 2012 [22]; Chang and Pakzad, 2013 [23]), which uses a combination of NExT and ERA, based on the vibration response of the structure alone. This method is aimed at identifying the modal parameters of the system under ambient excitations using a multipoint correlation function as the input. This method is widely used in the identification of the performance of large geotechnical constructions under ambient excitation. During modal parameter identification using the time-domain algorithm, owing to the influence of system noise interference and local vibration, the development of approaches for effectively determining the system order is a hot topic in modal identification research. In the NExT-ERA algorithm, the method of combining the acceleration power spectra and stability diagrams can allow researchers to intuitively determine the system order, and if the difference in the modal parameters of the two neighboring orders is within a reasonable range, then it can be surmised that the identified eigenvalues are stable. Furthermore, if the acceleration power spectrum (PSD) under these eigenvalues has obvious wave peaks, then the real modes can be better distinguished from the noisy modes in a PSD plot and steady-state plot.

3.2.2. Modal Identification Results

We used the NExT-ERA system identification method for the modal analysis of signals. As shown in the X-direction PSD diagram in Figure 10, the X-direction forward third-order self-oscillation frequencies of the Shigudeng Pavilion are 1.015 Hz, 2.716 Hz, and 5.043 Hz, and the Y-direction PSD diagram in Figure 11, the Y-direction are 1.056 Hz, 2.394 Hz, and 4.839 Hz. X- and Y-direction forward third-order vibration patterns are presented in Figure 12 and Figure 13, and the frequencies and damping ratios of the X- and Y-directions are presented in

Table 1. X-direction frequencies and damping ratios.

Location	First-Order		Second-Order		Third-Order
	Frequency/Hz	Damping Ratio/%	Frequency/Hz	Damping Ratio/%	Frequency/Hz	Damping Ratio/%
2/B column	1.014	3.98	2.406	1.65	5.048	1.35
3/E column	1.016	2.73	3.026	1.58	5.037	1.07
Average value	1.015	3.36	2.716	1.62	5.043	1.21

and

Table 2. Y-direction frequencies and damping ratios.

Location	First-Order		Second-Order		Third-Order
	Frequency/Hz	Damping Ratio/%	Frequency/Hz	Damping Ratio/%	Frequency/Hz	Damping Ratio/%
2/B column	0.937	2.90	2.400	2.37	4.758	0.97
3/E column	1.174	5.56	2.387	3.46	4.920	3.32
Average value	1.056	4.23	2.394	2.92	4.839	2.15

. The maximum damping ratio of the X-direction is 3.98% for the 2/B column in the first-order vibration pattern, that for the Y-direction is 5.56% for the 3/E column, and the two directions damping ratios decrease with self-oscillation frequency.

4. Finite Element Analysis

4.1. Finite Element Model

To ensure the calculation accuracy of the finite element model and improve the analysis efficiency, the geometric model of the Shigudeng Pavilion was simplified as follows: Firstly, the smaller external eave columns of the pavilion have little effect on the mechanical properties of the overall structure, so they were ignored. Secondly, we extracted the main stress components to create the model. The simplified model of the Shigudeng Pavilion is presented in Figure 14.

The Shigudeng Pavilion was built in the Song Dynasty, and through a field investigation, we determined that the timber building material was cedar. By reviewing the literature Special Topics on Wood Physics [24] and the Wood Structure Design Manual [25], we obtained relationship equations for the timber all directional shear modulus as follows based on the finite element simulation analysis results and comparison [26,27], carried out multiple adjustments to the cedar parameters, thereby ensuring that the simulated first-order natural frequency matched the measured first-order natural frequency. Finally, determine the parameters in

Table 3. Cedar parameters.

Material	Density (kg/m3)	Elastic Modulus (GPa)			Poisson’s Ratio			Shear Modulus (GPa)
Cedar	390	EL	ER	ET	μLR	μLT	μRT	GLR	GLT	GRT
		11.6	0.9	0.5	0.47	0.37	0.25	0.87	0.70	0.21

for finite element analysis.

$$G_{RT}\approx 0.018E_L$$

$$G_{LR}\approx 0.075E_L$$

$$G_{LT}\approx 0.06E_L$$

Next, we imported the cedar material into the simplified model, created a surface-to-surface contact method for the joints of timber components, constrained the translational displacement of the base in the X-, Y-, and Z-direction, and used a fixed hinge joint for the column base. Finally, the simplified model was divided into meshes, and automatic partitioning using module mesh allowed us to create about 660,000 units and 1.1 million nodes in total. The mesh details are presented in Figure 15 (where the blue line is the enlarged local reference line).

4.2. Finite Element Analysis Results

We used ANSYS Workbench to analyze the Shigudeng Pavilion simplified model, and we obtained the first eight orders of self-vibration frequencies, as presented in

Table 4. Simplified model of self-oscillating frequency.

Order	Frequency/Hz
1	1.0037
2	1.6432
3	2.1641
4	2.5846
5	2.8601
6	2.8733
7	3.5091
8	4.0789

.

4.3. Comparison of Recognition Results

The results of the finite element method were compared with measured data to check the reliability of the method. The errors of the first three measured self-vibration frequencies were small, and the large error of the first-order mode in the Y-direction may have been caused by actual damage. Our comparison of the ANSYS simulated structural vibration modes with the measured modal parameters indicated that the first-order modes in the X- and Y-direction were dominant. A comparison of the measured and finite element simulated self-vibration frequencies is presented in

Table 5. Comparison of self-vibration frequencies.

Order	Direction	Calculation Results/Hz	Measurement Results/Hz	Error Rate
First-order frequency	X	1.0037	1.015	1.11%
	Y	1.6432	1.056	55.61%
Second-order frequency	X	2.8601	2.716	5.31%
	Y	2.5846	2.394	7.96%
Third-order frequency	X	5.2854	5.043	4.81%
	Y	4.8559	4.839	0.35%

, and a comparison of the X- and Y-direction first-order modes is presented in Figure 16.

5. Repair Program Analysis

5.1. Repair Program

5.1.1. Ancient Building Repair Background

In the 1930s, researchers in the field of Chinese architecture, led by Liang Sicheng and others, began to survey and map the existing ancient buildings, summarizing much valuable information. Today, research related to ancient buildings is still based on their initial findings [28,29]. Since the mid 20th century, projects aimed at protecting cultural relics have increased year by year, and a lot of experience has been accumulated. It is generally recognized that the principle of not changing the original state of an ancient building should be observed in restoration work (the original state refers to a healthy state of cultural relics). Therefore, for cultural relics that have had their original appearance changed, early restoration work should be carried out [30,31]. The current specification “Wooden Structure of Ancient Buildings Maintenance and Reinforcement Technical Standards GB-T 50165-2020” puts forward the method of structural identification and the reinforcement damage point method, which are standardized for the reinforcement of ancient buildings as follows:

(1) To maintain the original appearance of buildings, highlight the historical period characteristics of an ancient architectural structure or group of structures, providing historical evidence and adequate technical justifications.

(2) Maintenance works on ancient buildings should preserve the original building form, structure, materials, technology, and art.

(3) In a maintenance and reinforcement project for ancient buildings, modern technology and materials can be used, but their use must comply with the following: it is appropriate to use modern materials for repairs but not to use modern materials to completely replace the originals; such works should be tried out through experimentation first, and then gradually expand the scope of use; and works must comply with the norms of operating procedures and quality measurement guidelines.

(4) The management and use authorities of ancient buildings must protect ancient buildings and thus mandate that they may not be freely altered or expanded. If repairs are needed, proposals should be reported to the competent authorities in charge of cultural relics for approval.

5.1.2. Repair Model

According to the results of of investigations into the appearance and structural damage to the Shigudeng Pavilion, we can propose a repair and reinforcement program: Works should proceed to use timber column supports instead of the brick wall support, so that it restores the original appearance of the ancient building, and decorative balustrades should be placed between the columns in the same fashion as those in the south brick wall. A model of the restoration is presented in Figure 17.

5.2. Comparison of Repair Model Dynamic Characterization

A finite element model has been established for the repair model (as presented in Figure 17) to validate the feasibility of the proposed scheme. The structural mode parameters after the repair process were forecasted via finite element analysis. The natural frequencies of the repair model are presented in

Table 6. Self-vibration frequencies of the restoration model.

Order	Frequency/Hz
1	1.5095
2	2.5296
3	2.7837
4	3.4663
5	3.7645
6	5.0999
7	5.1358
8	6.2212

. The first eight-order vibration modes are presented in Figure 18. The calculation results of the repair model were compared with those of the original model. The first- and second-order natural frequencies are presented in

Table 7. Comparison of first- and second-order self-vibration frequencies.

Order	Direction	Calculation Results/Hz	The Result after Repair/Hz	Measurement Results/Hz
First-order	X	1.0037	1.5095	1.015
	Y	1.6432	2.7837	1.056
Second-order	X	2.8601	3.7645	2.716
	Y	2.5846	3.4663	2.394

. The results of the finite element analysis show that the first- and second-order frequencies of the repair model are higher than the measured frequencies, indicating that the stiffness after the repair is larger than that before reinforcement, while the dynamic characteristics meet the requirements of structural use. A comparison of the first eight orders of self-oscillating frequencies between the repair model and the original model is presented in Figure 19.

The following restoration recommendations can be made further to the damage survey:

(1) In the case of missing components, matching timber can be obtained locally for the repairs, and the reinforcement can be retro so that the old and new materials are consistent in appearance, preserving the architectural features and avoiding a sense of dissonance.

(2) Replacement may be considered for floor slabs that have trough decay, and some slack floor slabs will need to be refastened or replaced.

(3) Sun Yong [32], through a study of Anhui’s historical and cultural towns’ timber buildings, reported that there are many timber diseases to look out for. According to their characteristics, we advise the use of broken timber and adhesives to fill the cracks, and the use of new materials, such as targeted repairs of nodes by wrapping them with carbon fiber cloth, to ensure the original appearance of the building and, at the same time, to enhance its strength. When the cracks do not exceed the radius of the column, new materials [33,34] can be considered to fill them, which will improve the strength of the column. For example, carbon-, glass-, and basalt-fiber-reinforced materials may be applied.

(4) The Shigudeng Pavilion is surrounded by mountains and thus susceptible to insect damage. To prevent termite erosion, consideration should be given to applying oil-based termite control drugs or mixing relevant drugs to coatings.

6. Conclusions

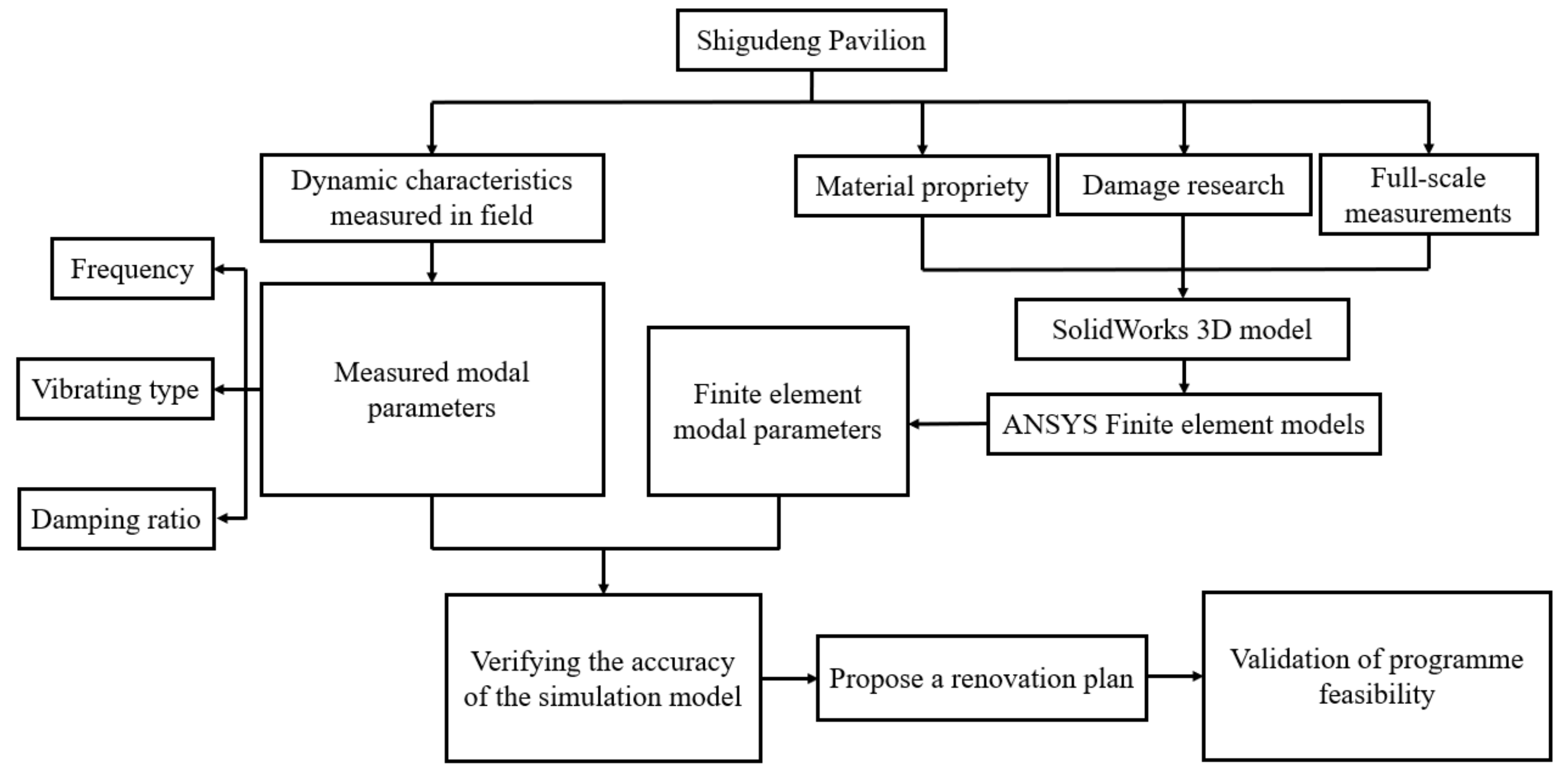
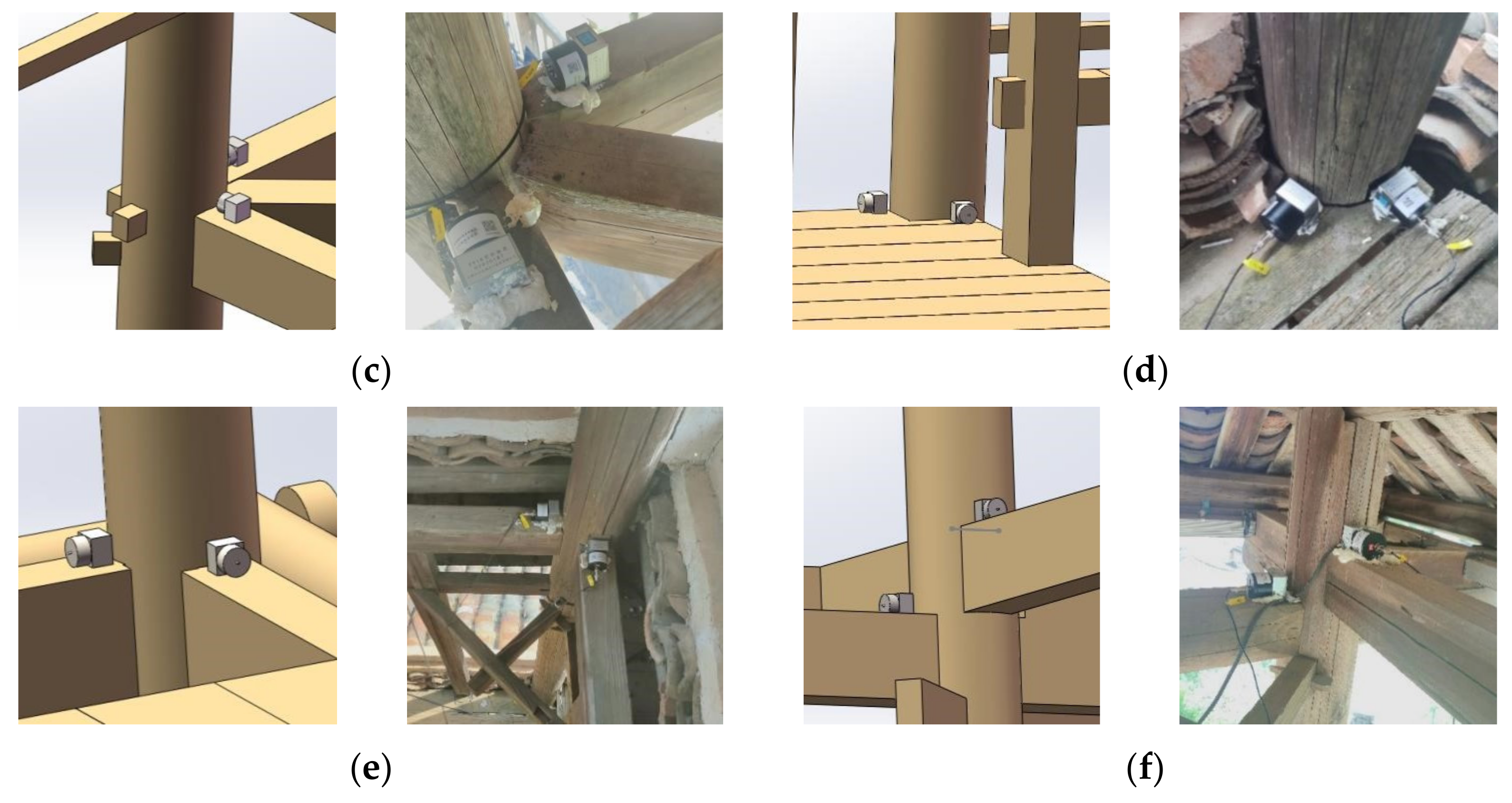
This study was based on field measurement of the vibration response of the Shigudeng Pavilion to environmental excitation, along with the use of stochastic vibration theory to analyze its dynamic responses. Combining the findings from our finite element simulation results and field measurements, and the repair program we proposed based on those results, we offer the following contributions:

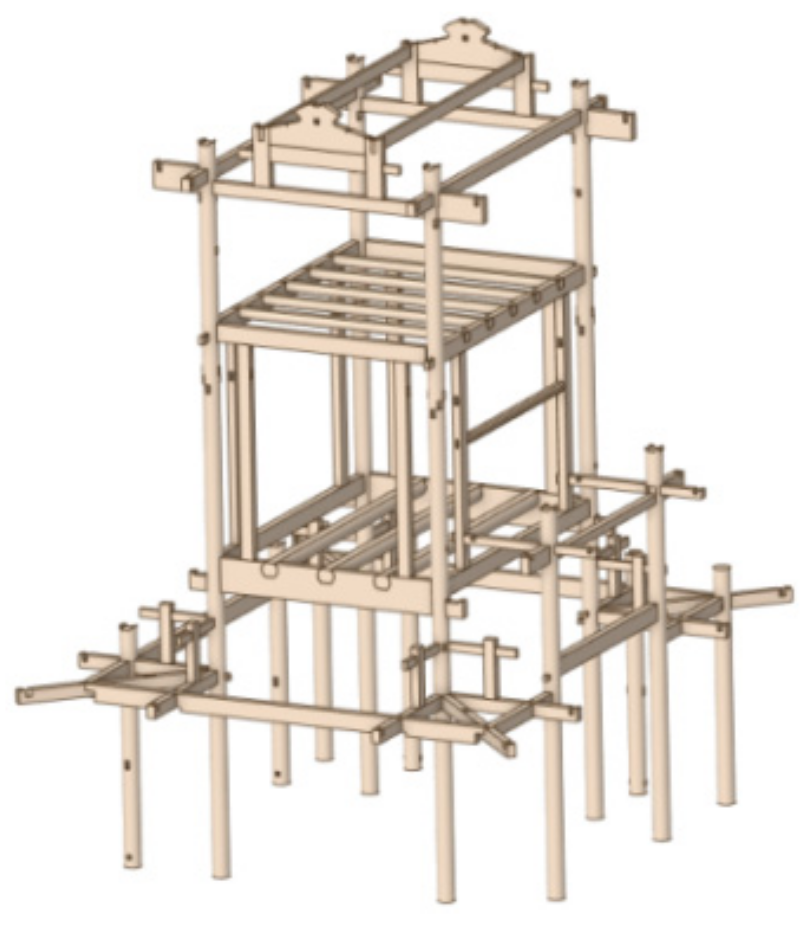
(1) Through our study of the Shigudeng Pavilion, its damage status was identified and a full-sized refined three-dimensional model was established;

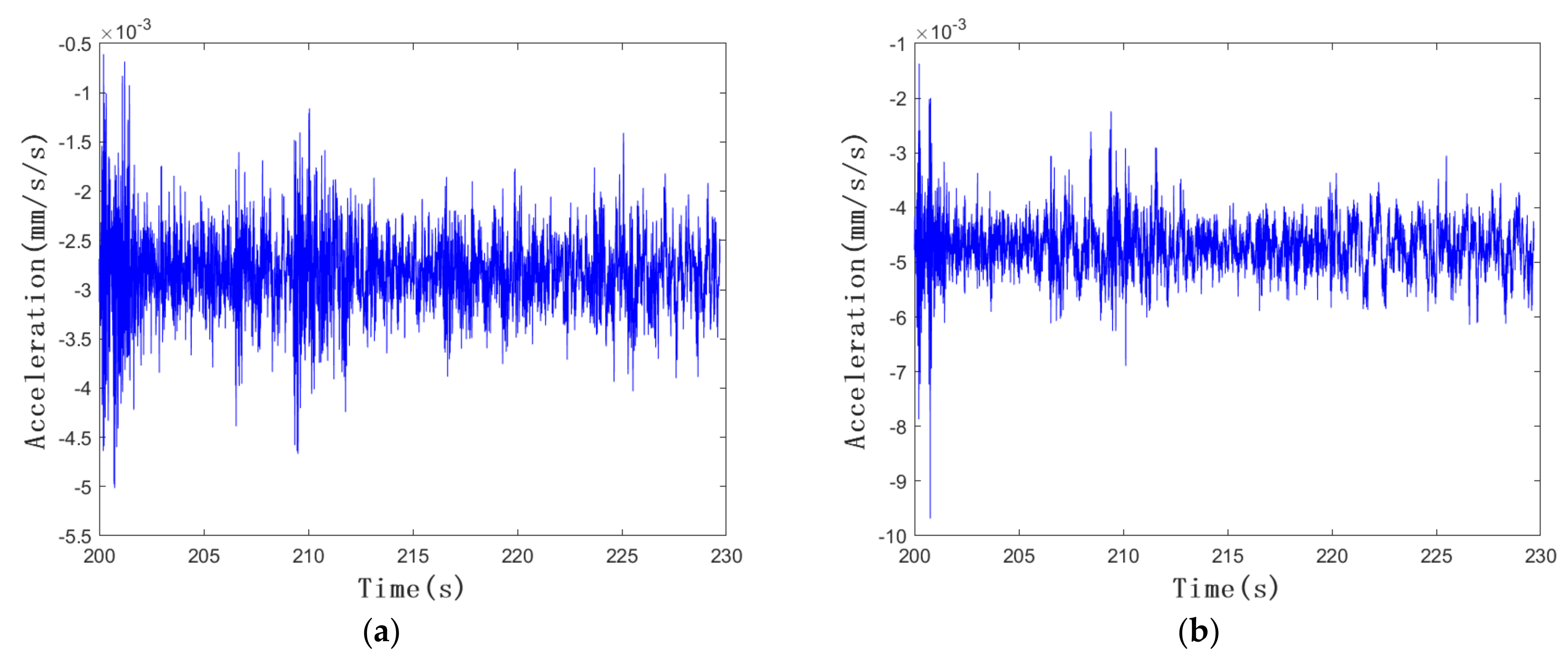
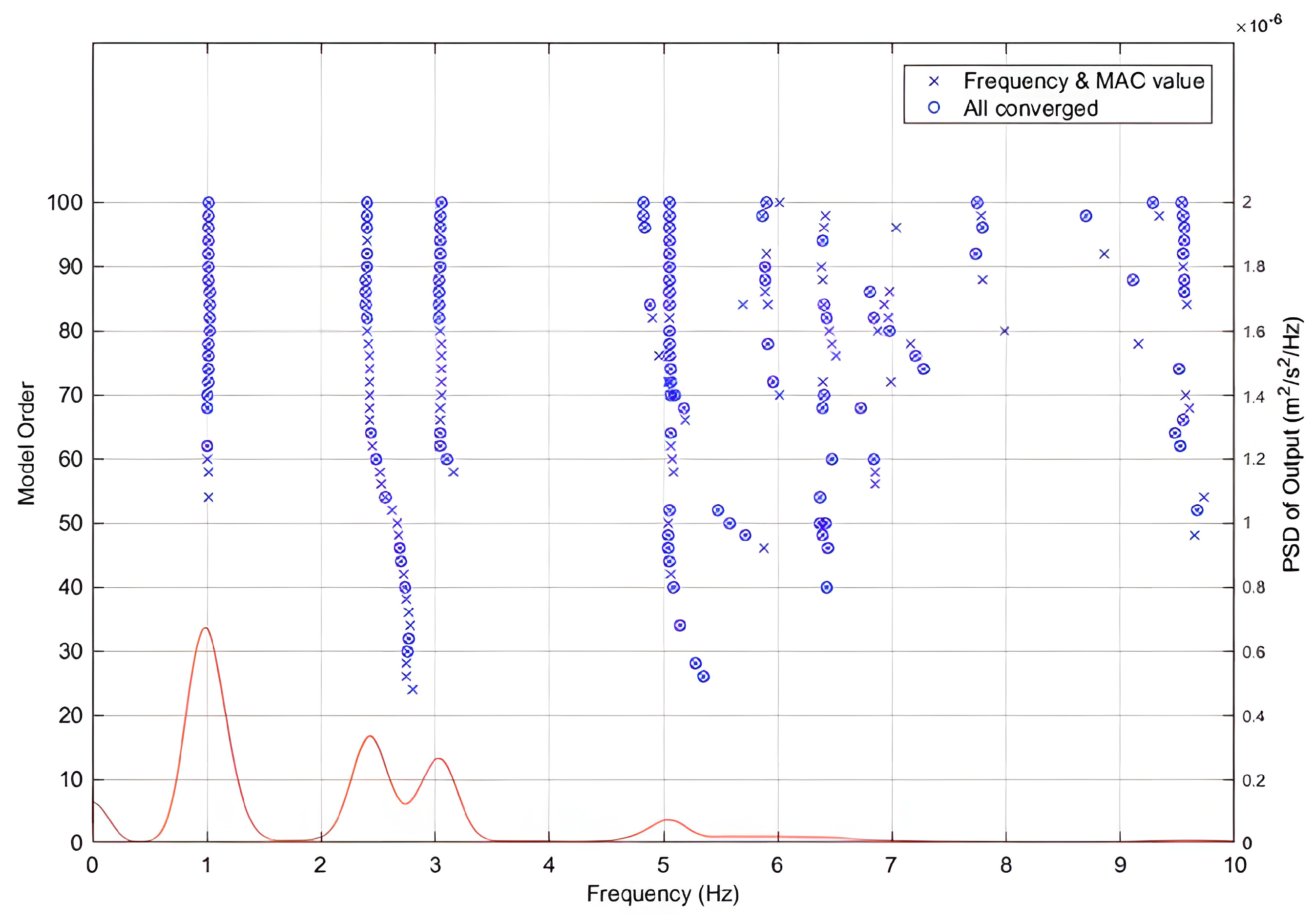
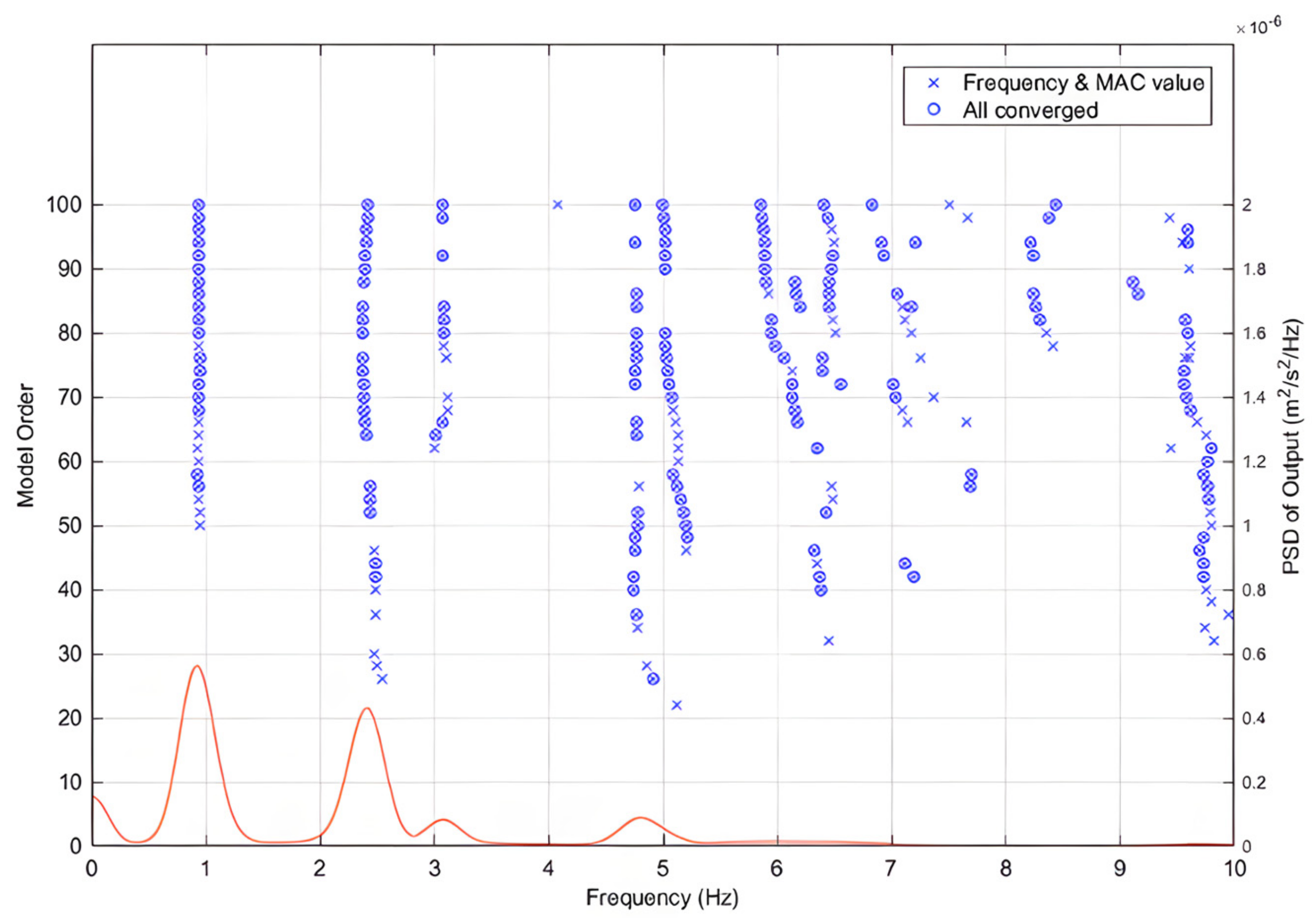
(2) Under environmental excitation, we found that the vibration response of the Shigudeng Pavilion was mainly concentrated between 0.8 and 5.1 Hz, and the first-order self-vibration frequencies in the X- and Y-direction were all at around 1 Hz;

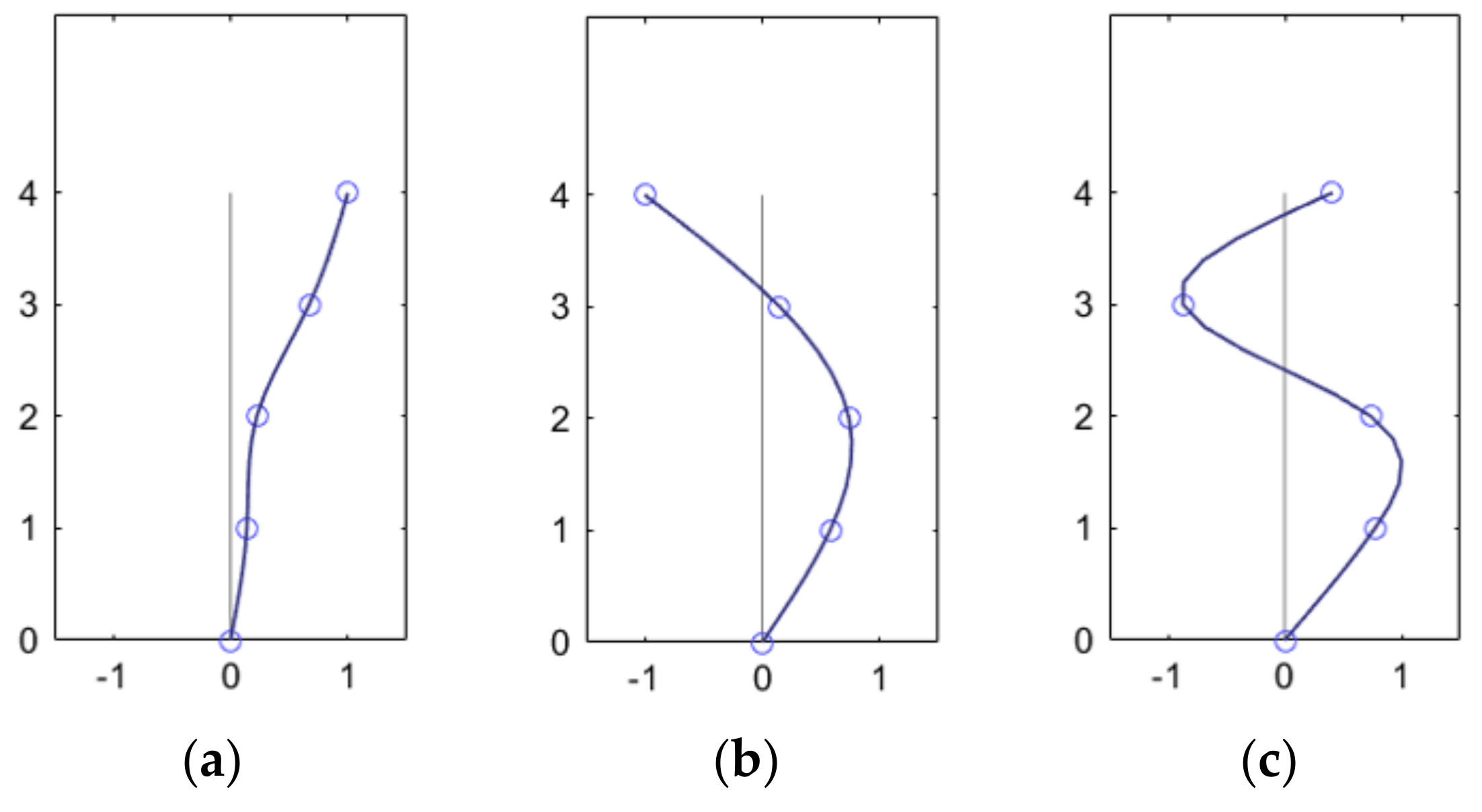
(3) Modal calculation of vibration signals was carried out to obtain the modal parameters of the Shigudeng Pavilion in the X- and Y-direction, and we found that the first three self-vibration frequencies in the X-direction were 1.015 Hz, 2.716 Hz, and 5.043 Hz in order, those in the Y-direction were 1.056 Hz, 2.394 Hz, and 4.839 Hz in order, the first-order vibration patterns were dominant in the X- and Y-direction; and the damping ratios in both directions decreased with the increase in self-vibration frequencies;

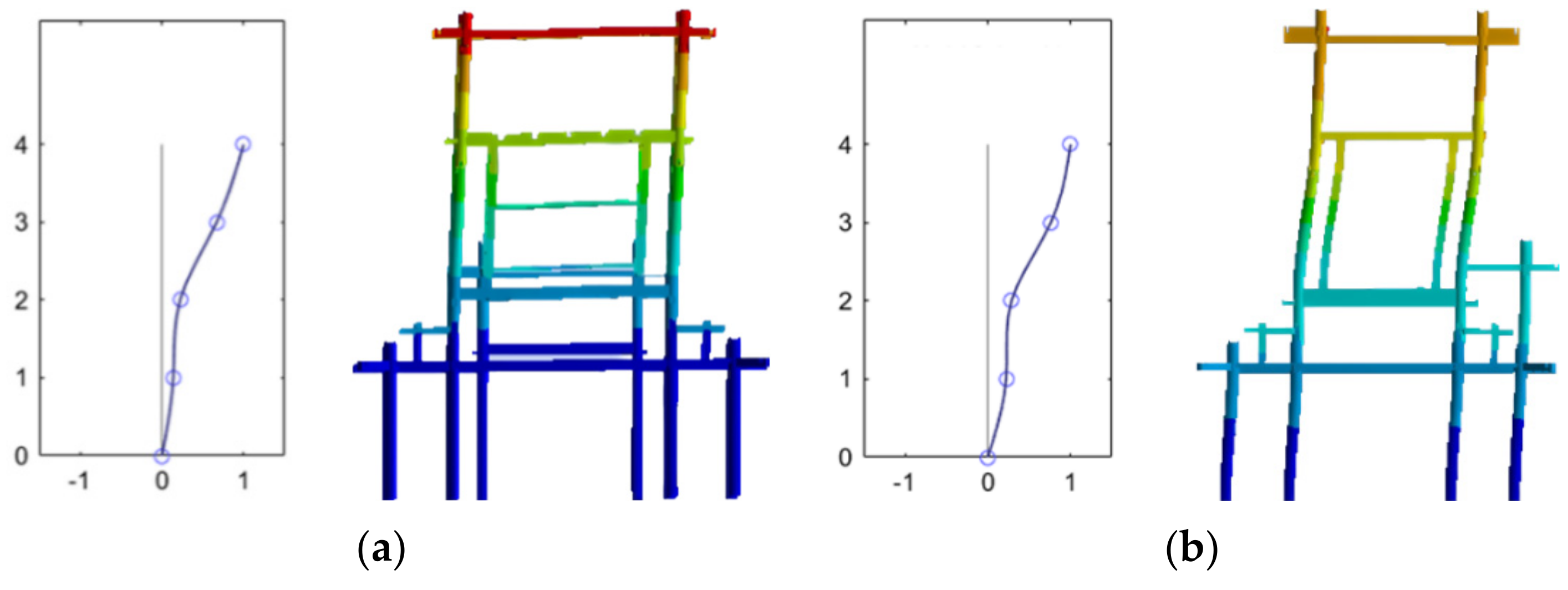
(4) Based on the geometric model established in the preliminary stage, a finite element model of the timber components was set up, and when comparing the simulation results with the measured modal parameters, we found that the results for the dynamic properties were basically in line with the actual situation;

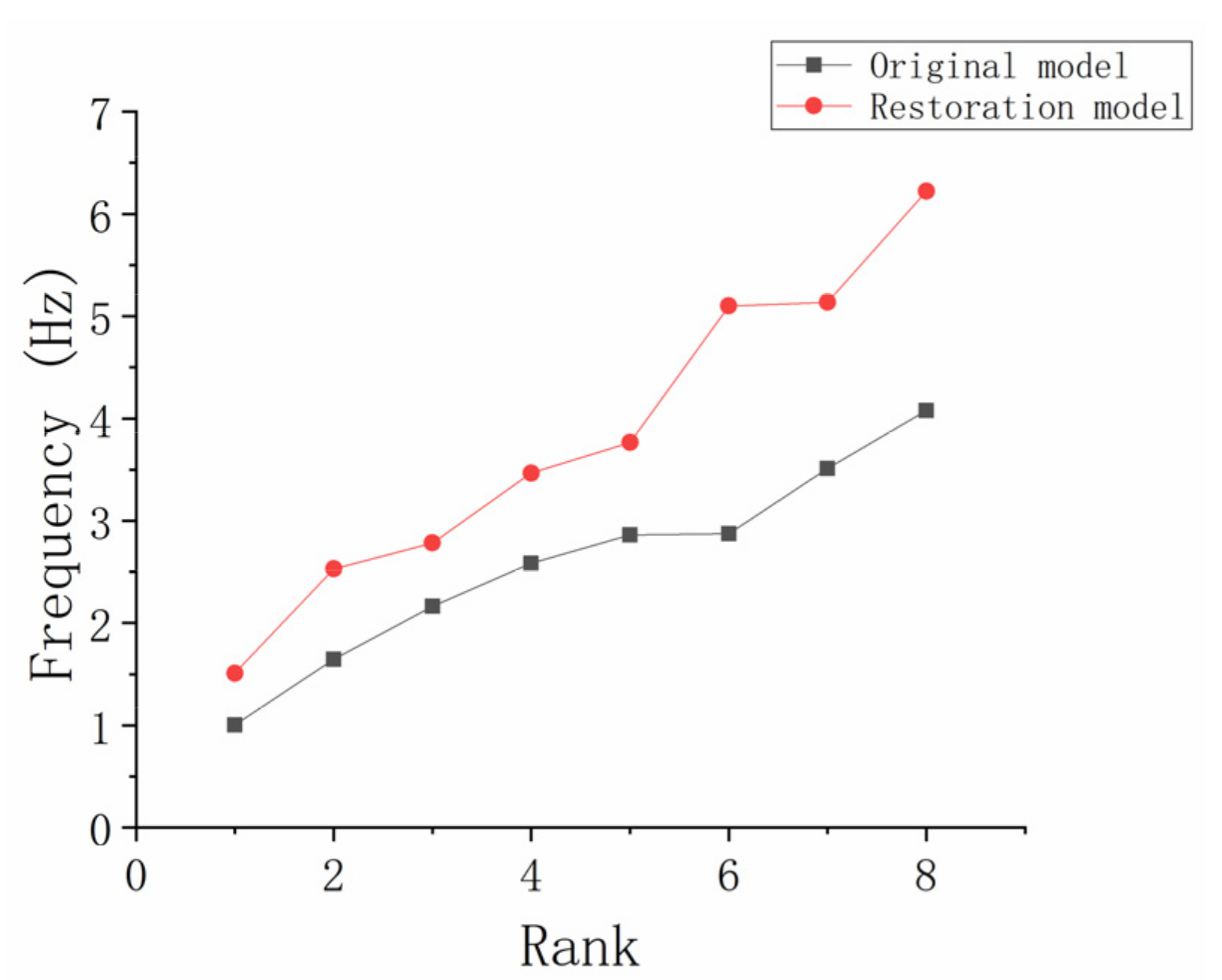
(5) A preliminary proposal for repair of the Shigudeng Pavilion was offered, in which we proposed replacing the north brick wall with timber columns to support the superstructure and restore the original appearance of the building. After verifying the accuracy of the finite element method (FEM), a repair model was established and finite element calculations were carried out, and the results indicated that the first- and second-order self-vibration frequencies were higher than the measured and existing models. As such, the feasibility of the repair program was preliminarily verified;

(6) Based on the damage and disease survey, recommendations were made for addressing the localized corrosion, cracking, defects, and insect infestation of the Shigudeng Pavilion.